COMBAT: A Combined Association Test for Genes Using Summary Statistics

Many gene-based association tests have been proposed for genomewide association studies (GWAS). However, the power of existing gene-based tests is...

Abstract

Genome-wide association studies (GWAS) have been widely used for identifying common variants associated with complex diseases. Traditional analysis of GWAS typically examines one marker at a time, usually single nucleotide polymorphisms (SNPs), to identify individual variants associated with a disease. However, due to the small effect sizes of common variants, the power to detect individual risk variants is generally low. As a complementary approach to SNP-level analysis, a variety of gene-based association tests have been proposed. However, the power of existing gene-based tests is often dependent on the underlying genetic models, and it is not known a priori which test is optimal. Here we propose a combined association test (COMBAT) for genes, which incorporates strengths from existing gene-based tests and shows higher overall performance than any individual test. Our method does not require raw genotype or phenotype data, but needs only SNP-level P-values and correlations between SNPs from ancestry-matched samples. Extensive simulations showed that COMBAT has an appropriate type I error rate, maintains higher power across a wide range of genetic models, and is more robust than any individual gene-based test. We further demonstrated the superior performance of COMBAT over several other gene-based tests through reanalysis of the meta-analytic results of GWAS for bipolar disorder. Our method allows for the more powerful application of gene-based analysis to complex diseases, which will have broad use given that GWAS summary results are increasingly publicly available.

GENOME-WIDE association studies (GWAS), which examine millions of common single nucleotide polymorphisms (SNPs) across the genome, have been widely used for identifying common variants associated with complex diseases. These studies have uncovered numerous risk variants and provided novel insights into disease biology. Despite these successes, genetic variants identified to date explain only a small fraction of the heritability for most complex diseases, which raises the question of “missing heritability” (Manolio et al. 2009). One explanation is that a large number of common variants remain to be discovered, but their effect sizes are generally too small to be detected individually (Eichler et al. 2010). In the search for additional common risk variants, one approach is to amass ever larger samples, in order to have adequate power to detect their small effects when variants are analyzed individually. However, collecting both genotypic and phenotypic data on large samples is time-consuming and expensive. As an alternative strategy, more sophisticated analyses of existing GWAS data can enhance the capture of true genetic signals in an efficient and cost-effective manner.

As a complementary approach to SNP-level analysis, gene-based association analysis has been proposed for GWAS (Neale and Sham 2004). Gene-based analysis aims to derive an overall gene-level P-value by examining associations of all SNPs within a gene with a trait of interest. Compared with SNP-level analysis, gene-based analysis has several advantages. First, a susceptibility gene may contain multiple independent causal variants. In this case, gene-based analysis may increase power by aggregating the disparate signals within a gene. Second, gene-based analysis may further increase power by reducing the multiple testing burden from one based on ∼1,000,000 million SNPs to one based on ∼20,000 genes. Third, gene-based analysis can deal with the problem of allelic heterogeneity and hence lead to more consistent results across studies. Fourth, gene-based analysis can provide greater insights into disease biology since the genes are basic functional units of the genome. In addition, the gene-based P-value approach can be readily extended to pathway or network-based analysis of GWAS.

A variety of methods have been proposed for gene-based association analysis, many of which involve the combination of SNP-level P-values. One group of methods has the advantage of detecting genes with a single causal variant, for example, the smallest P-value method (Wang et al. 2007). This type of approach takes the smallest P-value over all SNPs within a gene as an overall gene-based P-value. Because larger genes tend to have SNPs with smaller P-values by chance, permutation is usually needed to adjust for the total number of SNPs within a gene. However, permutation is not only computationally demanding, but, in addition, there are situations in which permutation is not easy or possible, such as in family-based GWAS designs and gene-based analyses for GWAS meta-analytic results from large consortia. There are also scenarios in which multiple independent SNPs within a gene contribute to disease risk. Accordingly, another group of methods were developed to detect genes with multiple independent causal variants. For example, to capture multiple independent weak signals and increase detection power, the Fisher’s combination test of P-values method has been proposed (Curtis et al. 2008). However, because of the extensive linkage disequilibrium (LD) between SNPs within the gene, there are no theoretical distributions for the test statistics. Permutation is still needed to estimate the empirical P-value.

To overcome the limitations of permutation, Liu et al. proposed a versatile gene-based test (VEGAS) that computes a gene-level P-value using simulations from a multivariate normal distribution (Liu et al. 2010). One major advantage of VEGAS is that the method does not require raw genotype data; rather it only needs SNP-level P-values and genotype data of ancestry-matched reference samples. Furthermore, the test statistic is flexible because it can be constructed for the most significant SNP or for the most significant subsets of SNPs. Therefore, the test statistics of VEGAS have the potential to detect genes with either one or many causal variants. However, it is unknown which test statistic is optimal in real data analysis, because the power of a test statistic is dependent on the underlying true genetic architecture of susceptibility genes that is usually unknown. For example, if a gene contains only one causal variant, a test statistic that uses the most significant SNP may be the most powerful; in contrast, the same test will be less powerful for another gene that contains multiple independent causal variants. To further improve the efficiency and accuracy of P-value computation, Li et al. proposed GATES (gene-based association test using extended Simes procedure), to rapidly compute a gene-level P-value without using either permutation or simulation (Li et al. 2011). While GATES is more computationally efficient and analytically accurate, it suffers from power loss when a gene contains multiple independent causal variants.

Theoretically, there are no uniformly powerful gene-based analytical methods, and the best methods vary depending on the underlying genetic architecture. Although we do not know which method is optimal in real data, we do know that some methods are more powerful than others under certain circumstances. Therefore, it is statistically important and challenging to choose the best method for real data analysis. Here we propose a combined gene-based association test (COMBAT), which incorporates strengths from a variety of gene-based tests. Intuitively, the method that produces the smallest P-value will be the most powerful. COMBAT was developed to capture the best method by choosing the one with the smallest P-value, but will also correct for the number of gene-based tests using the extended Simes procedure. Extensive simulations showed that COMBAT has appropriate type I error rates, maintains higher power across a wide range of genetic models, and is more robust than any single test. When applied to GWAS meta-analysis results for bipolar disorder from the Psychiatric Genomic Consortium (PGC) (Psychiatric GWAS Consortium Bipolar Disorder Working Group 2011), COMBAT outperformed alternative gene-based tests. The proposed test allows for the more powerful application of gene-based analysis to complex diseases, which will have broad use given that GWAS summary results are increasingly publicly available.

Materials and Methods

An overview of COMBAT

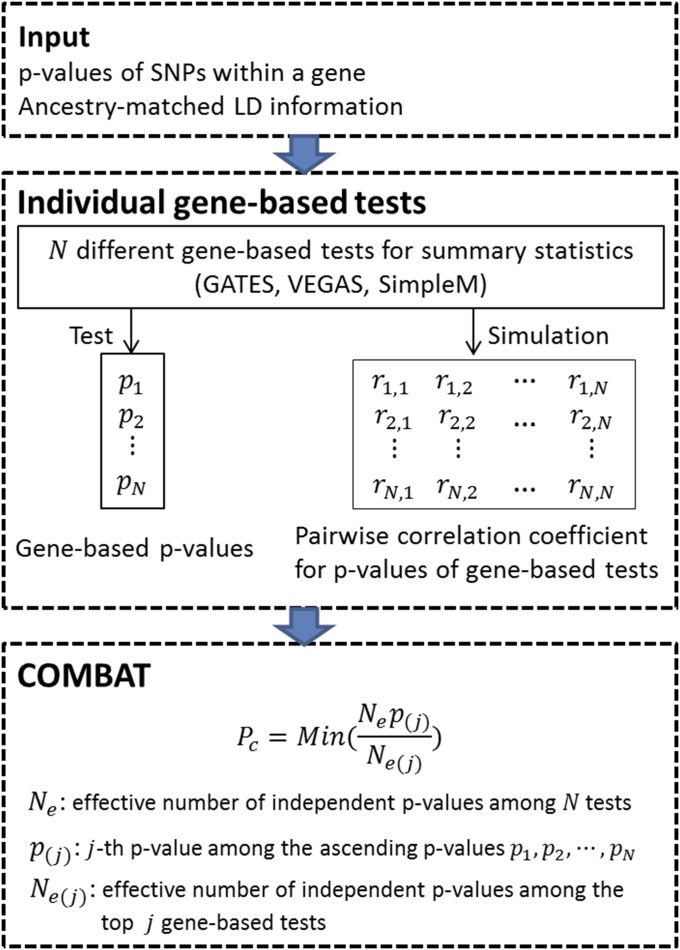
An overview of COMBAT is provided in Figure 1. Briefly, given the SNP-level P-values within a gene, and genotype data of ancestry-matched reference samples, we first compute $N$ gene-based P-values for the gene using $N$ different gene-based association tests, which can take SNP-level P-values as input, including GATES, a number of VEGAS test statistics, and SimpleM (Gao et al. 2008). COMBAT will then scan all individual gene-based tests and identify the most powerful test while controlling for correlations among different tests. It must be noted that COMBAT is flexible in its ability to take statistics from other gene-based association tests as input. Under the null hypothesis of no association, we use a simulation-based approach to estimate the correlation coefficient matrix of P-values from $N$ different gene-based tests. We note that the correlation coefficient matrix of P-values can be estimated based on the LD information of ancestry-matched reference samples as shown in Supplemental Material, Figure S1 and File S2. Once the P-value correlation coefficient matrix is estimated, COMBAT then applies the extended Simes procedure to combine the P-values of $\text{N}$ different gene-based tests to an overall gene-level P-value.

Figure 1.

Overview of the COMBAT method. First, the input includes P-values of SNPs mapped to a given gene and ancestry-matched LD information. Second, it computes a gene-based P-value using each individual gene-based test. It further derives the correlations of P-values of individual gene-based tests under the null hypothesis using a simulation-based approach. Third, COMBAT applies the extended Simes procedure to combine the P-values of individual gene-based tests to an overall gene-level P-value.

Extended Simes procedure

Let ($p_{\left(1\right)},p_{\left(2\right)},\cdots ,p_{\left(N\right)}$) be the ascending P-values from $N$ different gene-based tests. COMBAT applies the extended Simes procedure to combine the $N$ P-values to an overall P-value $P_{combat}$ as follows:

$$P_{combat}=Min\left(\frac{N_e{p}_{\left(j\right)}}{N_{e\left(j\right)}}\right), 1\le j\le N,$$

where $N_e$ is the effective number of independent P-values among the $N$ association tests and $N_{e\left(j\right)}$ is the effective number of independent P-values among the top $j$ association tests. To obtain $N_e$ and $N_{e\left(j\right)},$ we apply a robust technique as proposed in GATES (Li et al. 2011). Specifically, $N_e$ is estimated by

$$N_e=N-{\displaystyle \sum _{i=1}^N\left({\lambda }_i-1\right)I\left({\lambda }_i-1\right)},$$

where ${\lambda }_i$ is the $i$th eigenvalue of the P-value correlation coefficient matrix of $N$ association tests, and $I\left({\lambda }_i-1\right)$ is an indicator function taking the value of $0$ if ${\lambda }_i\le 1$ and $1$ if ${\lambda }_i>1.$ When the $N$ association tests are independent (correlation coefficient of P-values is $0$ between tests), then eigenvalues are all one, thus $N_e=N.$ When the $N$ association tests are the same (correlation coefficient of P-values is $1$ between tests), the first eigenvalue is $N$ and the rest are 0, so that $N_e=1.$ For intermediate situations, the correlations of P-values from different association tests are between $0$ and $1,$ thus $N_e$ will usually be smaller than $N,$ but >$1.$ The computation of $N_{e\left(j\right)}$ is similar to that of $N_e,$ but the eigenvalues are computed for the P-value correlation coefficient matrix of the top $j$ association tests.

Estimation of P-value correlation matrix under the null hypothesis

To apply the extended Simes procedure, it is necessary to obtain the correlation matrix of P-values among different gene-based tests under the null hypothesis. We estimated the correlation of P-values for each pair of gene-based tests based on the LD matrix of SNPs within the gene. The LD information can be obtained from ancestry-matched reference samples, such as those from HapMap, 1000 Genomes, or a custom set of individuals if genotype data are available. Figure S1 and File S2 show the schematic diagram of our simulation process to estimate the correlation of P-values between two gene-based tests. The simulation is based on the premise that under the null hypothesis of no association, the joint $z$ statistics of SNPs should follow a multivariate normal distribution with mean 0 and covariance matrix being the pairwise correlations of SNPs within the gene (Conneely and Boehnke 2007). Briefly, for a list of SNPs within a given gene, we first generate $K$ number of multivariate normal vector $\mathit{Z}$ with mean $0$ and covariance matrix of pairwise LD values ($r$) between SNPs. $\mathit{Z}$ is then transformed into a two-tailed P-value vector $\mathit{P}.$ For each P-value vector, we computed a gene-level P-value for each gene-based test. Therefore, we can get $K$ number of gene-level P-values for each gene-based test. The correlation of P-values between two gene-based tests can then be calculated based on the $K$ P-values obtained for each test.

To investigate the validity of this LD-based simulation approach, we compared COMBAT P-values estimated by the simulation approach to those obtained from a permutation-based approach, which can be considered a gold standard for the correlations of P-values between different tests. Specifically, we constructed null data sets with individual level genotype data for genes with varying numbers of SNPs (10, 30, 50, and 100) using GWAS data from the Atherosclerosis Risk in Communities (ARIC) study (ARIC Investigators 1989). For simplicity without loss of generality, 10 genes were randomly sampled for each size (i.e., number of SNPs). We randomly selected 1000 samples and assigned them quantitative trait values from a standard normal distribution. The phenotype values were permuted 1000 times. For each permuted phenotype, we computed SNP-level association P-values, followed by computing a gene-based P-value for each gene-based association test. We thus obtained 1000 gene-based P-values for each gene-based test, which were subsequently used to compute the correlation between gene-based tests.

A brief review of gene-based tests underlying COMBAT

COMBAT is built upon a number of gene-based tests, which do not require raw genotype or phenotype data, but need only the SNP-level P-values and pairwise SNP correlations from ancestry-matched reference samples. The power of these tests is often affected by the number of causal SNPs within a gene. When there is only one or a few causal SNPs, tests that aim to capture the most significant SNP, such as GATES, VEGAS-max, and SimpleM, are more powerful. In the case of multiple independent causal SNPs, methods that aggregate signals across SNPs, such as VEGAS-sum, tend to be more powerful. Below we briefly review these tests underlying COMBAT.

GATES:

This method uses an extended Simes procedure to derive a gene-based P-value. Basically, it combines P-values of SNPs into an overall gene-based P-value by $p=Min\left(\frac{N_e{p}_{\left(j\right)}}{N_{e\left(j\right)}}\right),$ where $N_e$ and $N_{e\left(j\right)}$ are the effective number of independent P-values among all, and the top $j$ SNPs, respectively. The number of effective independent SNPs is estimated by the correlation matrix of SNP P-values, which can be approximated by a high order polynomial function of the allelic correlation matrix. Neither permutation nor simulation is needed in GATES.

VEGAS:

This is a versatile gene-based association test, which combines SNP-level chi-square statistics into an overall gene-based test statistic. The test statistic can be constructed for either the top SNP or subsets of the most significant SNPs. The empirical distribution of the test statistic is estimated by simulating sufficient numbers of multivariate normal vectors with mean zero and the covariance matrix being the LD between SNPs. While the method is flexible in its test statistics, it is not known in advance which of these is optimal in real data. To capture the test statistic that is most likely to be powerful, COMBAT scans a series of test statistics from the one that considers only the top SNP to those that combine various proportions of top significant SNPs (e.g., the top 10, 20, and 100% of the most significant SNPs).

SimpleM:

This method computes a gene-based P-value by taking the smallest P-value of SNPs within a gene while correcting for the effective number of independent tests through a Bonferroni correction procedure (Gao et al. 2008). Specifically, $p=1-{\left(1-\min \left\{p_{\left(1\right)},p_{\left(2\right)},\cdots ,p_{\left(m\right)}\right\}\right)}^k,$ where $k$ is the effective number of independent tests estimated from the correlation matrix of SNPs using a principal component analysis approach. We set $k$ so that the corresponding eigenvalues explain 99.5% of the variation for the SNP data.

Conventional SNP-level analysis

To compare the performance of gene-based association analysis with conventional SNP-level analysis in simulations, we also calculated the SNP-level P-value, which was defined as the smallest P-value of SNPs within a gene with Bonferroni correction for the total number of SNPs.

Simulation of genotype data

We evaluated the performance of COMBAT using simulated genotype data. The simulation involved the generation of genotype data for a gene with 50 SNPs. We set the minor allele frequencies of all SNPs as a random number from 0.05 to 0.5. All SNPs were biallelic and under Hardy–Weinberg equilibrium. We considered three different scenarios in terms of LD structure: (1) SNPs are in linkage equilibrium (LE, i.e., r = 0); (2) SNPs are located in four moderate LD blocks with r = 0.5 for all pairwise SNP correlations within each block; and (3) SNPs are located in four strong LD blocks with r = 0.9 for all pairwise SNP correlations within each block. The numbers of SNPs in the four LD blocks are 10, 5, 15, and 20, respectively.

Type I error rate estimation

To examine the type I error rates of COMBAT, we generated null data sets by simulating a continuous phenotype of sample size 1000 from a standard normal distribution. We then permuted this phenotype 1000 times to generate 1000 null data sets. For each null data set, we tested the association of each SNP with the phenotype using linear regression. After obtaining the SNP-level P-values, we applied individual gene-based tests (GATES, VEGAS, and SimpleM) and COMBAT to get gene-level P-values. The empirical type I error rate was calculated as the proportion of 1000 P-values from the null data that was equal to or less than a given nominal $\alpha$ level (0.05 and 0.01). To evaluate the effect of sample size on type I error rates, we repeated the simulation for a sample size of 2000.

As the above simulations might not reflect realistic gene or LD structure, we also evaluated the type I error rates of COMBAT and individual gene-based tests using real GWAS genotype data from the ARIC study. In this analysis, 30 genes with different numbers of SNPs (30, 50, or 100) were randomly sampled from the real genotype data in such a way that there were 10 genes for each SNP size. Null phenotype data were generated from a standard normal distribution and the type 1 error rate was estimated for each gene-based test in a similar way as described for simulated genotype data analysis.

Power analysis

To compare the power of COMBAT and individual gene-based tests, we used simulated genotype data with different LD blocks, as described above, and generated phenotype data under alternative hypotheses of various genetic models. Specifically, we generated a quantitative trait of sample size 1000 using a linear regression model:

$$y={\beta }_1{g}_1+{\beta }_2{g}_2+\cdots +{\beta }_K{g}_K+\epsilon ,$$

where $K$ is the number of causal SNPs, ${\beta }_i\left(i=1,2,\cdots ,K\right)$ are the additive effects for causal SNPs, $g_i\left(i=1,2,\cdots ,K\right)$ are the effect allele counts for causal SNPs, and $\mathrm{\epsilon }$ is a random term that follows a standard normal distribution. Within each LD block, one causal SNP was randomly chosen with a genetic effect of $\log \left(1.1\right).$ We considered four genetic models: (1) one causal SNP; (2) two causal SNPs; (3) three causal SNPs; and (4) four causal SNPs. We created 1000 causal data sets under each model. For each causal data set, COMBAT and each individual gene-based test were run to get a gene-level P-value. The power was defined as the proportion of P-values from 1000 causal data sets that were less than or equal to a given $\alpha$ level of 0.01. To evaluate the effect of sample size on power, we repeated the simulation for a sample size of 2000.

Real data analysis

To evaluate the performance of COMBAT on real data and compare it with other individual gene-based tests, we applied COMBAT and other methods to GWAS meta-analysis results for bipolar disorder from the PGC. Summary results for 2,427,220 autosomal SNPs were downloaded from the PGC website (https://www.med.unc.edu/pgc/). The sample included 7481 subjects with bipolar disorder and 9250 controls. We focused our analysis on autosomal SNPs with MAF ≥ 0.01 and imputed quality score >0.8. To reduce systematic bias and minimize the chance of false positive findings, we used genomic control-corrected SNP-level P-values. Considering the potentially important roles of noncoding variants in complex traits and diseases (Ward and Kellis 2012) and previous studies that have performed gene-based analyses with noncoding variants (Gamazon et al. 2015; Kilaru et al. 2016), we also included noncoding variants in gene-based tests for bipolar disorder. We assigned an SNP to a gene if it was located within the gene, based on NCBI 37.3 gene annotation, or within 20 kb upstream or downstream of the gene, to capture regulatory variants. We limited analysis to genes with at least five SNPs. In total, there are 20,701 genes with 1,174,071 SNPs. We estimated pairwise SNP correlations within a gene based on the genotype data of unrelated CEU samples from the 1000 Genomes Project.

Data availability

The method, along with each individual gene-based test, has been implemented in the R package COMBAT, which is available on CRAN (https://cran.r-project.org/web/packages/COMBAT/).

Results

Estimation of simulations needed for computing COMBAT P-values

Using a simulation-based approach, we first estimated the correlation matrix of P-values among different gene-based tests under the null hypothesis, which was then used for computing COMBAT P-values. To investigate how many simulations are needed to get a stable estimate of a COMBAT P-value, we varied the number of simulations and compared the corresponding results with those from standard permutations. Table 1 summarizes the correlation coefficients between simulation-based and permutation-based COMBAT P-values for genes with varying number of SNPs. In all simulation settings, a high correlation (r ≥ 0.97) was observed between simulation-based and permutation-based approaches. It turned out that the smaller the gene size, the fewer the number of simulations were required to achieve a high correlation. Based on our empirical observations, 10 to 50 simulations will generally be sufficient for a stable and accurate estimate of P-value compared to a permutation-based approach (r > 0.98).

Table 1. Correlation coefficients between simulation-based and permutation-based COMBAT P-values.

Number of simulations	Gene size (number of SNPs)
	10	30	50	100
5	0.98	0.98	0.97	0.97
10	0.99	0.99	0.98	0.98
20	0.99	0.99	0.98	0.98
30	0.99	0.99	0.98	0.98
40	0.99	0.99	0.98	0.98
50	0.99	0.99	0.99	0.98
60	0.99	0.99	0.99	0.98
70	0.99	0.99	0.99	0.99
80	0.99	0.99	0.99	0.99
90	0.99	0.99	0.99	0.99
100	0.99	0.99	0.99	0.99

Type I error

We evaluated the type I error of COMBAT, conventional SNP-level analysis, and individual gene-based tests. Table 2 shows the empirical type I error rates at two α levels (α = 0.05 and α = 0.01) for simulated genes with different LD patterns, using a sample size of 1000. Overall, COMBAT and all individual gene-based tests maintained an appropriate type I error rate under different LD structures. Conventional SNP-level analysis tended to be conservative when there was strong LD among SNPs. We found a similar pattern of type I error rates based on simulations with a sample size of 2000 (Table S1 in File S1).

Table 2. Empirical type I error rates for SNP-level analysis and various gene-based tests based on simulated genotype data and real genotype data of 1000 individuals.

	α	SNP	GATES	VEGAS (max)	VEGAS (10%)	VEGAS (20%)	VEGAS (30%)	VEGAS (40%)	VEGAS (sum)	SimpleM	COMBAT
LD (r)
0	0.05	0.042	0.042	0.043	0.044	0.044	0.044	0.041	0.045	0.042	0.05
	0.01	0.009	0.009	0.007	0.01	0.008	0.006	0.007	0.01	0.009	0.01
0.5	0.05	0.04	0.044	0.045	0.051	0.049	0.045	0.046	0.045	0.041	0.049
	0.01	0.007	0.009	0.008	0.011	0.009	0.008	0.011	0.01	0.009	0.012
0.9	0.05	0.027	0.051	0.051	0.049	0.044	0.04	0.047	0.044	0.028	0.051
	0.01	0.005	0.01	0.01	0.01	0.011	0.009	0.009	0.011	0.009	0.013
Number of SNPs
30	0.05	0.024	0.051	0.050	0.050	0.051	0.049	0.050	0.050	0.037	0.056
	0.01	0.005	0.010	0.009	0.009	0.009	0.009	0.009	0.011	0.009	0.011
50	0.05	0.026	0.055	0.054	0.050	0.048	0.048	0.049	0.049	0.045	0.056
	0.01	0.005	0.012	0.010	0.010	0.009	0.010	0.010	0.010	0.010	0.012
100	0.05	0.030	0.055	0.051	0.051	0.048	0.047	0.048	0.048	0.046	0.054
	0.01	0.006	0.012	0.010	0.009	0.009	0.008	0.008	0.008	0.010	0.010

We further evaluated type I error rates using real GWAS genotype data from the ARIC study. As shown in Table 2, all the methods still offered effective control of false positive rates at two α levels (α = 0.05 and α = 0.01), suggesting the appropriate type I error rates of individual gene-based methods and of COMBAT in analysis of real genotype data. Type I error rates were conservative for conventional SNP-level analysis in all real genotype data.

Power

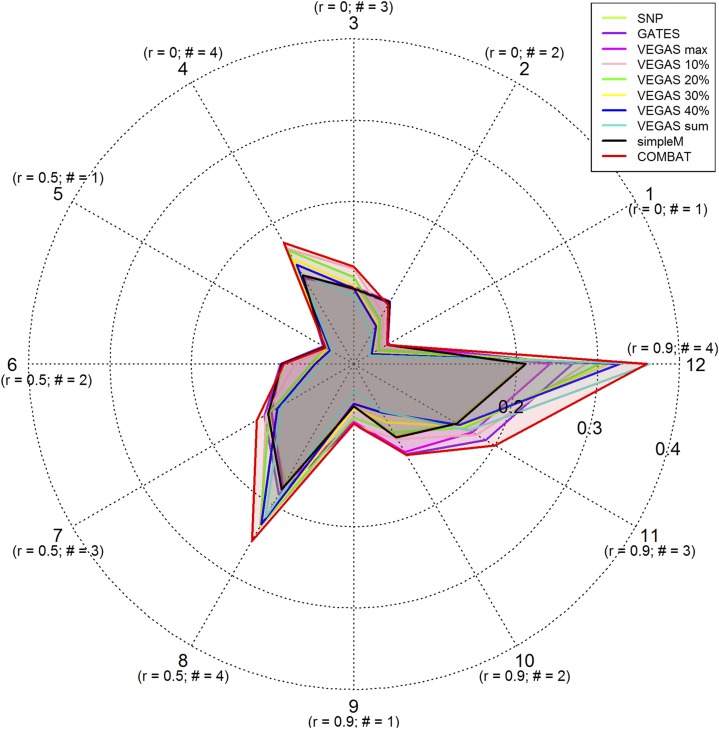
Using a number of simulated genetic models, we investigated the power of COMBAT and compared its performance with individual gene-based tests and conventional SNP-level analysis. We considered 12 genetic models with combinations of various numbers of causal SNPs (1, 2, 3, and 4) and different LD patterns (LE, moderate LD, and strong LD). Figure 2 shows the radial power plot for COMBAT and individual gene-based tests across 12 genetic models with a sample size of 1000 and a P-value significance level of 0.01. As expected, the statistical power is affected by the number of independent causal SNPs and LD patterns for all individual gene-based tests. When there was only one causal SNP and the SNPs were in LE, we observed the highest power for the tests that aim to capture the top significant SNPs within a gene, such as GATES, VEGAS-max, and SimpleM. On the other hand, for disease models with multiple independent causal SNPs, the highest power was observed for the tests that aggregate signals across SNPs within the gene, e.g., the VEGAS tests that combine a certain proportion of SNPs. In comparison with all individual gene-based tests, COMBAT was clearly the winner in all simulated genetic models. COMBAT was similar to or superior in power to the best performing individual gene-based tests in all situations. When there was no LD, the performance of conventional SNP-level analysis was similar to gene-based tests that capture the top significant SNPs, but was less powerful when strong LD existed. We observed a similar pattern for genetic models with moderate and strong LD patterns, but the statistical power was generally increased for all tests due to the increased signal to noise ratio. Power simulations using a larger sample size of 2000 yielded the same conclusions (Figure S2 and File S2). The empirical power values at two α levels (α = 0.05 and α = 0.01) for all gene-based tests across 12 genetic models and conventional SNP-level analysis are shown in Table S2 in File S1 (sample size = 1000) and Table S3 in File S1 (sample size = 2000).

Figure 2.

Radial power plots for SNP-level analysis and various gene-based tests under 12 different genetic models given a sample size of 1000 and a P-value significance threshold of 0.01. Genes with 50 SNPs were simulated and the SNPs formed 4 LD blocks. One or zero SNP was chosen as a causal SNP in each LD block. r, correlation among SNPs within each LD block; #, number of causal SNPs. Dotted tracks denote power levels.

Application to meta-analysis of GWAS for bipolar disorder

We applied COMBAT, as well as all individual gene-based tests, to the GWAS meta-analysis results for bipolar disorder downloaded from the PGC website. At a genome-wide significance level of 0.05, COMBAT detected more significant genes than any other individual gene-based test or SNP-level analysis (minimum P-value within a gene, with genome-wide significant threshold of 5.0 × 10⁻⁸). All significant genes identified by the individual gene-based tests were also significant by COMBAT. Table 3 shows nine genes identified by COMBAT that remained significant after Bonferroni correction (P_corrected < 0.05). It was noteworthy that none of the individual gene-based tests could detect all of these nine genes at a significance level that survives Bonferroni correction (P < 2.4 × 10⁻⁶). For example, GATES did not identify SYNE1, DDN, PRKAG1, and ITIH3; VEGAS-sum did not identify ANK3; both VEGAS-max and SimpleM missed SYNE1, KMT2D, DDN, PRKAG1, and ITIH3. Among these nine genes identified by COMBAT, ANK3 and SYNE1 were reported to be associated with bipolar disorder in the primary meta-analysis from PGC. Of note, none of the individual gene-based tests detected both ANK3 and SYNE1 as genome-wide significant after Bonferroni correction. Interestingly, COMBAT also detected another two genes, ITIH3 and DDN, which were not genome-wide significant in the primary SNP-level PGC meta-analysis, but did meet the genome-wide threshold for association with BP in larger samples (Psychiatric GWAS Consortium Bipolar Disorder Working Group 2011; Hou et al. 2016).

Table 3. Results of bipolar disorder GWAS data application: genes with genome-wide significance (P-value < 2.4 × 10⁻⁶) by COMBAT and corresponding results by SNP-level analysis (minimum P-value) and individual gene-based tests.

Genes	SNP (minP)	GATES	VEGAS (max)	VEGAS (10%)	VEGAS (20%)	VEGAS (sum)	SimpleM	COMBAT	Pcorrected
RHEBL1	9.43E−09	2.59E−07	4.00E−07	4.00E−07	6.00E−07	2.00E−07	3.83E−07	2.98E−07	6.12E−03
DHH	9.39E−09	3.27E−07	6.00E−07	9.00E−07	9.00E−07	5.00E−07	3.83E−07	4.19E−07	8.58E−03
LMBR1L	9.39E−09	3.88E−07	1.00E−06	1.30E−06	1.20E−06	1.90E−06	4.78E−07	5.31E−07	1.09E−02
SYNE1	4.33E−09	7.19E−06	8.50E−06	3.00E−07	6.00E−07	1.70E−06	2.54E−06	7.08E−07	1.45E−02
KMT2D	8.27E−08	2.03E−06	2.60E−06	2.10E−06	1.50E−06	5.00E−07	2.52E−06	7.48E−07	1.53E−02
ANK3	5.54E−10	9.92E−07	1.00E−06	4.73E−05	3.32E−04	3.12E−03	3.87E−07	8.72E−07	1.78E−02
DDN	1.79E−07	4.10E−06	4.70E−06	4.70E−06	1.60E−06	9.00E−07	4.94E−06	1.16E−06	2.36E−02
PRKAG1	8.27 E−08	2.74E−06	3.10E−06	1.90E−06	2.00E−06	1.00E−06	3.16E−06	1.64E−06	3.32E−02
ITIH3	1.99E−07	1.78E−05	2.17E−05	1.39E−05	8.00E−06	1.30E−06	1.49E−05	2.32E−06	4.66E−02

Discussion

Motivation for the proposed COMBAT method is based on the key considerations that the genetic underpinnings may vary across susceptibility genes, and that the statistical power of existing gene-based tests is often dependent on the true genetic architecture underlying susceptibility genes. Therefore, it is important and desirable to develop a robust test statistic that can take into account the unique association patterns of susceptibility genes. Accordingly, COMBAT was designed to choose the most powerful method from a variety of gene-based tests while correcting for the correlations among methods. Our extensive simulations demonstrated the superior performance of COMBAT as compared to several individual gene-based tests over a wide range of genetic models. Moreover, COMBAT requires only SNP-level P-values and ancestry-matched LD information, and therefore it can be applied to almost any GWAS design for which results have been generated.

We previously developed a Flexible and Adaptive test for Gene Sets (FLAGS) using summary statistics (Huang et al. 2016), which adaptively combines gene signals for gene set-based association tests, taking into account the unique association patterns of gene sets. The intuitions underlying both FLAGS and COMBAT are similar: there is no universally powerful approach for either gene-based or gene set-based testing; both methods are designed to identify the best test among a group of different tests. But their ways of correcting for the number of tests are different: FLAGS uses a simulation-based approach, whereas COMBAT uses an extended Simes procedure.

Although the COMBAT method has been developed for GWAS summary data, we reason that the same framework can be applied to gene-based tests for rare variants, such as those generated from whole genome or exome sequencing studies. As with common variations, disease susceptibility genes may also have differing genetic architectures when it comes to rare causal variants, and the statistical power of gene-based tests for these variants may also depend on the underlying genetic models. Therefore, COMBAT can be designed to scan a number of gene-based tests of rare variants and choose the best one while controlling for correlations among tests. However, since raw data are required for most gene-based tests for rare variants, a permutation-based approach would be necessary to estimate the correlations of P-values among different methods under the null. Nonetheless, our experience with common variants leads us to expect that a limited number of permutations should generally be sufficient to obtain a stable and accurate estimation of P-value correlations among methods.

In the analysis of GWAS meta-analytic data for bipolar disorder, COMBAT detected a number of significant genes that may underlie the illness. Of these, ANK3 and SYNE1 were reported in the primary meta-analysis from the PGC; however, none of the individual gene-based tests could detect both of them after multiple testing correction, reinforcing the advantage of COMBAT. It was noteworthy that COMBAT not only detected genes reported in the primary meta-analysis from PGC, but also identified two genes (ITIH3 and DDN) that were not genome-wide significant in the original PGC meta-analysis, but were in studies with larger samples. In particular, DDN reached genome-wide significance in a recent large-scale meta-analysis of GWAS for bipolar disorder (Hou et al. 2016). This gene encodes a synaptic protein, dendrin, which has been linked to synaptic plasticity, memory formation (Kremerskothen et al. 2006), and sleep deprivation (Neuner-Jehle et al. 1996), a core symptom of bipolar disorder, and therefore is a biologically plausible candidate. ITIH3 was genome-wide significant in the cross-disorder analysis of bipolar disorder and schizophrenia from the PGC (Psychiatric GWAS Consortium Bipolar Disorder Working Group 2011), suggesting it may be a common susceptibility gene for both disorders. ITIH3 belongs to the family of inter-α-trypsin inhibitors and plays an important role in regulation of differentiation of neural stem cells (Han et al. 2015). A recent study showed that a variant within ITIH3 influences response to antipsychotic medication (Brandl et al. 2016).

This work should be viewed in light of two limitations. First, our simulations indicated that gene-based association analyses are more powerful than SNP-level analyses for genes with multiple independent causal variants. If a gene contains only one causal variant, however, the inclusion of a large number of noncausal variants may reduce the power for detecting risk genes. Therefore, gene-based methods should not be seen as a replacement for traditional SNP-level analyses, but rather a complement. Second, COMBAT utilizes summary test statistics rather than raw genotype data from association studies, and caution must be taken when the test statistics at different SNPs involve different subsets of individuals from across the multiple samples. In fact, it is not uncommon that association tests of different SNPs were generated from different subsets of samples, especially in large-scale GWAS meta-analyses. However, this is a common issue to most, if not all, existing gene-based tests that use summary statistics. Accordingly, COMBAT, which is built upon existing gene-based tests, is also affected by the same issue. When raw genotype is available, the missing genotype data in a subset of samples can be imputed to a common reference panel to avoid sample inconsistency. In the absence of such raw data, each individual gene-based test should be extended with more advanced modeling techniques to tackle this issue.

In summary, we have developed a robust and powerful gene-based test for common variants using summary statistics. Given the fact that GWAS summary results are increasingly publicly available, and given the difficulties that can arise in accessing raw data, our method will allow for the broader application of gene-based analysis to GWAS of complex diseases.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300257/-/DC1.