Interpreting short tandem repeat variations in humans using mutational constraint

Abstract

Identifying regions of the genome that are depleted of mutations can reveal potentially deleterious variants. Short tandem repeats (STRs), also known as microsatellites, are among the largest contributors of de novo mutations in humans. However, per-locus studies of STR mutations have been limited to highly ascertained panels of several dozen loci. Here, we harnessed bioinformatics tools and a novel analytical framework to estimate mutation parameters for each STR in the human genome by correlating STR genotypes with local sequence heterozygosity. We applied our method to obtain robust estimates of the impact of local sequence features on mutation parameters and used this to create a framework for measuring constraint at STRs by comparing observed vs. expected mutation rates. Constraint scores identified known pathogenic variants with early onset effects. Our metric will provide a valuable tool for prioritizing pathogenic STRs in medical genetics studies.

Introduction

Mutations that have negative fitness consequences tend to be eliminated from the population. Thus, identifying regions of the genome that are depleted of mutations has proven a useful strategy for interpreting the significance of de novo variation in developmental disorders¹, prioritizing rare disease variants², and identifying genes or non-coding regions of the genome that are under selective constraint^3,4. The key idea of these approaches is that mutations occurring at sites evolving under a neutral model are likely to have little effect on reproductive fitness, whereas mutations at intolerant sites are more likely to be involved in severe early-onset disorders.

So far, the genetics community has developed a multitude of methods to assess genetic constraint. These studies have highlighted the importance of a carefully calibrated model of the background mutation process to establish a neutral expectation. For instance, Samocha et al.¹ determine the expected number of de novo variants per gene based on a neutral model obtained by counting mutations for each possible trinucleotide context in intergenic SNPs. In a different approach, fitCons³ aggregates non-coding regions with similar functional annotations and compares observed variation in those regions to an expectation obtained from presumably neutral flanking regions. Notably, these methods have mainly focused on single nucleotide polymorphisms (SNPs) and to a lesser extent on small indels. As of today, computational methods to analyze and assess the functional impact of repetitive elements in the genome are lacking. Thus, repeat variants are commonly excluded from medical genetics analyses.

To expand the range of interpretation tools to repeat elements, we focused on short tandem repeats (STRs), also known as microsatellites, in the human genome. STRs consist of repeated motifs of 1–6bp and represent about 1.6 million loci⁵, rendering them one of the largest repeat classes. STR mutations are responsible for over 30 Mendelian disorders⁶, many of which are thought to arise spontaneously from de novo mutations^7,8. Emerging evidence suggests STRs play an important role in complex traits⁹ such as gene expression¹⁰ and DNA methylation¹¹. In addition, analyses of cancer cell lines have shown that STR instability is a chief clinical sign for tumor prognosis¹², but the functional impact of these instabilities is largely unknown.

Evaluating genetic constraint requires two fundamental components: an accurate mutation model and a deep catalog of existing variation. Both of these have been difficult to obtain for repetitive regions of the genome. Current knowledge of the STR mutation process is based on low-throughput studies focusing on an ascertained panel of loci that are highly polymorphic. These include genealogical STRs on the Y chromosome^13,14, approximately a dozen autosomal STRs from the CODIS (Combined DNA Index System) set used in forensics, and several thousand STRs historically used for linkage analysis¹⁵. These studies suggest an average mutation rate of approximately 10⁻³ to 10⁻⁴ mutations per generation^13–17. However, these loci likely have significantly higher mutation rates than most STRs. Moreover, well characterized STRs consist almost entirely of tetra- or di-nucleotide repeats, which may mutate with different rates and processes compared to other repeat classes. Finally, STR mutation rate studies have been based on small numbers of families and show substantial differences regarding absolute mutation rates and their patterns (Supplementary Table 1).

Here, we developed a framework to measure constraint at individual STRs that benefits from a novel method to obtain observed and expected mutation rates at each locus. We developed a robust quantitative model that harnesses population-scale genomic data to estimate locus-specific mutation dynamics at each STR by correlating local SNP heterozygosity with STR variation. After extensive validation, we applied this model to estimate mutation rates at more than one million STRs using whole genome sequencing of 300 unrelated samples from diverse populations¹⁸. Using these results, we built a model to predict mutation parameters from local sequence features and measured constraint at each STR locus. One caveat is that our method is primarily applicable to STRs that can be completely spanned by short reads and does not accurately describe large expansion mutations observed in conditions such as Huntington’s Disease or Fragile X Syndrome. We show that our constraint metric can be used to predict clinical relevance of individual STRs, including those in genes with known implications in developmental disorders. This framework will likely enable better assessment of the role of STRs in human traits and will inform future work incorporating STRs into human genetics studies.

Results

A method to estimate local mutation parameters

We first sought to develop a method to estimate mutation parameters at each STR in the genome by fitting a model of STR evolution to population-scale data. A primary requirement of our method is a model of the STR mutation process that fits observed variation patterns. Motivated by the poor fit of the widely used generalized stepwise mutation model (GSM) to our data (Supplementary Note), we developed a novel length-biased version of the GSM that closely recapitulates observed population-wide trends (Supplementary Note, Supplementary Figures 1,2), including a saturation of the STR molecular clock over time. Our model includes three parameters: μ denotes the per-generation mutation rate, β describes the strength of the directional bias of mutation, and p paramaterizes the geometric mutation step size distribution. Recently, we developed a method called MUTEA that employs a similar model to precisely estimate individual mutation rates for Y chromosome STRs (Y-STRs) from population-scale sequencing of unrelated individuals. MUTEA models STR evolution on the underlying SNP-based Y phylogeny¹⁹. We found good concordance (r²=0.87) between MUTEA and traditional trio-based methods and high reproducibility (r²=0.92) across independent datasets. However, the main limitation of this approach is that it requires full knowledge of the underlying haplotype genealogy, which is difficult to obtain for autosomal loci.

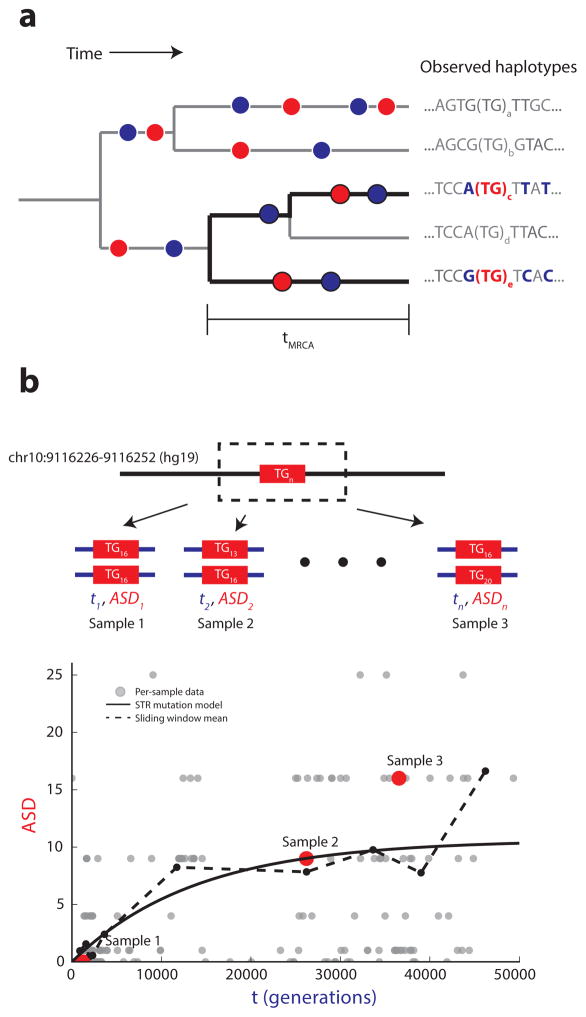
To analyze the mutation rates of autosomal STRs, we extended MUTEA to analyze pairs of haplotypes. The key insight of our mutation rate estimation procedure is that different classes of mutations provide orthogonal molecular clocks (Figure 1). Consider a pair of haplotypes consisting of an STR and its surrounding sequence. The SNP heterozygosity is a function of the time to the most recent common ancestor (TMRCA) of the haplotypes and the SNP mutation rate. On the other hand, the squared difference between the numbers of repeats of the two STR alleles (allele squared distance, or ASD) is a separate function of the TMRCA. The distribution of ASD values observed for a given TMRCA is determined by our STR mutation model. Using known parameters of the SNP mutation process, we can estimate the local TMRCA and calibrate the STR molecular clock¹⁵.

Figure 1. Estimating STR mutation parameters from diploid data.

(a) SNPs and STRs give orthogonal molecular clocks. The tree represents an example evolutionary history of an STR locus. Red dots denote STR mutation events. Blue dots represent SNP mutation events. Black branches denote an observed diploid locus, consisting of two haplotypes from the tree. Bolded nucleotides represent sequence differences between the two haplotypes. (b) Correlating local TMRCA with STR genotypes allows per-locus mutation rate estimation. For each diploid STR call, we use SNP heterozygosity to estimate the TMRCA of the surrounding region and we compute the squared difference between the two STR alleles. Our STR mutation model describes the expected ASD for a given TMRCA (solid black line).

Our method takes as input unphased STR and SNP genotypes and returns maximum likelihood estimates of STR mutation parameters. The TMRCA is approximated by local SNP heterozygosity using a pairwise sequentially Markovian coalescent model²⁰ (Methods). ASD is calculated directly from a diploid STR genotype as the squared difference in the number of repeats of each allele. Our maximum likelihood framework allows us to estimate parameters at a single STR or jointly across many loci. A potential caveat is that haplotype pairs may have shared evolutionary history and thus are not statistically independent, which is not expected to bias our estimates but will artificially shrink standard errors. To account for this non-independence, we adjust standard errors by calibrating to ground truth simulated and capillary electrophoresis datasets (Supplementary Note, Supplementary Figure 3).

Validating parameter estimates

We first evaluated our estimation procedure on STR and SNP genotypes simulated on haplotype trees using a wide range of mutation parameters. To evaluate our method on unphased diploid data, we formed a set of 300 “diploids” by randomly selecting leaf pairs and recording the TMRCA and STR allele lengths. To test the effects of genotyping errors, we simulated “stutter” errors using the model described in Willems et al.¹⁹ and used the expectation-maximization framework we developed previously²¹ to estimate per-locus stutter noise and correct for STR genotyping errors.

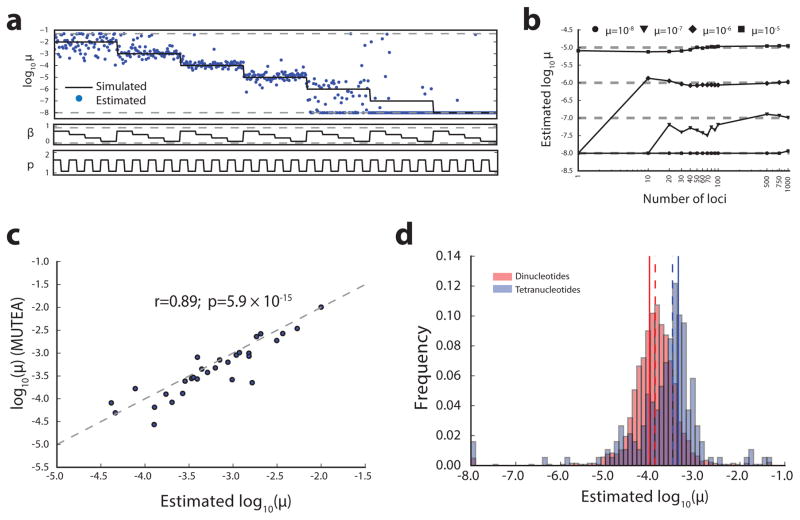
Our method obtained accurate per-locus estimates for μ for most biologically relevant parameter ranges (Figure 2a). Notably, estimates for p and β were less precise (Supplementary Figure 4) and thus downstream analyses focused on mutation rates. The main limitation of our method is an inability to capture low mutation rates. Informative estimates could be obtained for rates >10⁻⁶. This presumably stems from the low number of total mutations observed (median 1 mutation for μ = 10⁻⁶ in 300 samples). Aggregating loci or analyzing larger sample sizes gives higher power to estimate low mutation rates due to the higher number of total mutations observed. By analyzing loci jointly, we could accurately estimate mutation rates down to 10⁻⁶ with 30 or more loci and 10⁻⁷ with 70 or more loci (Figure 2b). As expected, inferring and modeling stutter errors correctly removed biases induced by stutter errors (Supplementary Figure 5).

Figure 2. Accurate estimation of STR mutation parameters from simulated data.

(a) Per-locus estimates of mutation rate. Dashed gray lines give boundaries enforced during numerical optimization. (b) Jointly estimating parameters across loci allows inference of low mutation rates. Black lines give joint estimates for different simulated mutation rates. Dashed gray lines give simulated values. (c) Y-STR mutation rate parameters are concordant across estimation methods. Mutation rate estimates from this study compared to those generated by MUTEA. Gray dashed lines denote the diagonal (N=41). (d) Autosomal mutation rate estimates are concordant with de novo studies. Histograms gives the distribution of per-locus mutation rates estimated by this study. Dashed lines give median estimates across loci. Solid lines give empirical mutation rates from trio data analyzed by Sun et al.¹⁵

We next evaluated the ability of our method to obtain mutation rates from population-scale sequencing of Y-STRs whose mutation rates have been previously characterized. We analyzed 143 males sequenced to 30–50x by the Simons Genome Diversity Project¹⁸ (SGDP) and 1,243 males sequenced to 4–6x by the 1000 Genomes Project²². We used all pairs of haploid Y chromosomes as input to our maximum likelihood framework. We compared our results to two orthogonal mutation rate estimates: our previous MUTEA method¹⁹ and a study that examined 2,000 father-son duos¹³. We found that our mutation rate estimates were consistent across sequencing datasets (r=0.90; two-tailed p=1.5×10⁻¹⁸; n=48) (Supplementary Figure 6). Encouragingly, our rate estimates were similar to those reported by MUTEA on the SGDP dataset (r=0.89; two-tailed p=5.9×10⁻¹⁵; n=41) (Figure 2c). Furthermore, our estimates were significantly correlated with those reported by Ballantyne et al. (r=0.78; two-tailed p=2.0×10⁻⁹; n=41) (Supplementary Figure 6), a substantial improvement over results obtained using a traditional stepwise mutation model (r=0.37; two-tailed p=0.0150; n=41), validating our choice of mutation model.

Finally, we evaluated our method on a subset of well characterized autosomal diploid loci. We first analyzed the forensics CODIS markers, which have well-characterized mutation rates estimated across more than a million meiosis events (see URLs). Mutation rates were concordant with published CODIS rates (r=0.90; two-tailed p=0.00016; n=11) (Supplementary Figure 7). We also compared to di- and tetranucleotide mutation rates previously estimated by Sun et al. by aggregating data from 1,634 loci in 85,289 Icelanders¹⁵. Mutation rates were in strong agreement (Figure 2d, Supplementary Figure 8), which is especially encouraging given that the Sun et al. STR genotypes were obtained using an orthogonal capillary electrophoresis method.

Genome-wide characterization of the STR mutation process

Next, we applied our mutation rate estimation method genome-wide. We analyzed 300 individuals from diverse genetic backgrounds sequenced to 30–50x coverage by the SGDP Project¹⁸. We aligned reads to the hg19 reference genome using BWA-MEM²³ and the resulting alignments were used as input to lobSTR²⁴ (Methods). High quality SNP genotypes were obtained from our previous study¹⁸. We used these as input to PSMC²⁰ to estimate the local TMRCA between haplotypes of each diploid individual. For each locus, we adjusted genotypes for stutter errors (Supplementary Figure 9, Supplementary Table 2, Methods) and used adjusted genotypes as input to our mutation rate estimation technique. After filtering (Methods), 1,251,510 STR loci with an average of 249 calls/locus remained for analysis. Results were concordant with mutation rates predicted by extrapolating MUTEA to autosomal loci (r=0.71; two-tailed p<10⁻¹⁶; n=480,623) (Supplementary Figure 10), suggesting that our mutation rate estimation is robust even in the case of unphased genotype data from modest sample sizes.

Per-locus mutation rates for each repeat motif length varied over several orders of magnitude, ranging from 10⁻⁸ to 10⁻² mutations per locus per generation (Supplementary Figure 11, Supplementary Table 3). Median mutation rates were highest for homopolymer loci (log₁₀μ = −5.0) and decreased with the length of the repeat motif, with most pentanucleotides and hexanucleotides below our detection threshold. Interestingly, homopolymers also showed markedly higher length constraint compared to other loci, suggesting an increased pressure to maintain specific lengths. Step size distributions also differed by repeat motif length. Homopolymers (median p = 1.00) and to a lesser extent repeats with motif lengths 3–6 (median p = 0.95) almost always mutate by a single repeat unit. On the other hand, dinucleotides are more likely to mutate by multiple units at once, consistent with previous studies¹⁵. Overall, our results highlight the diverse set of influences on the STR mutation process and suggest there is limited utility to citing a single set of STR mutation parameters.

A framework for measuring STR constraint

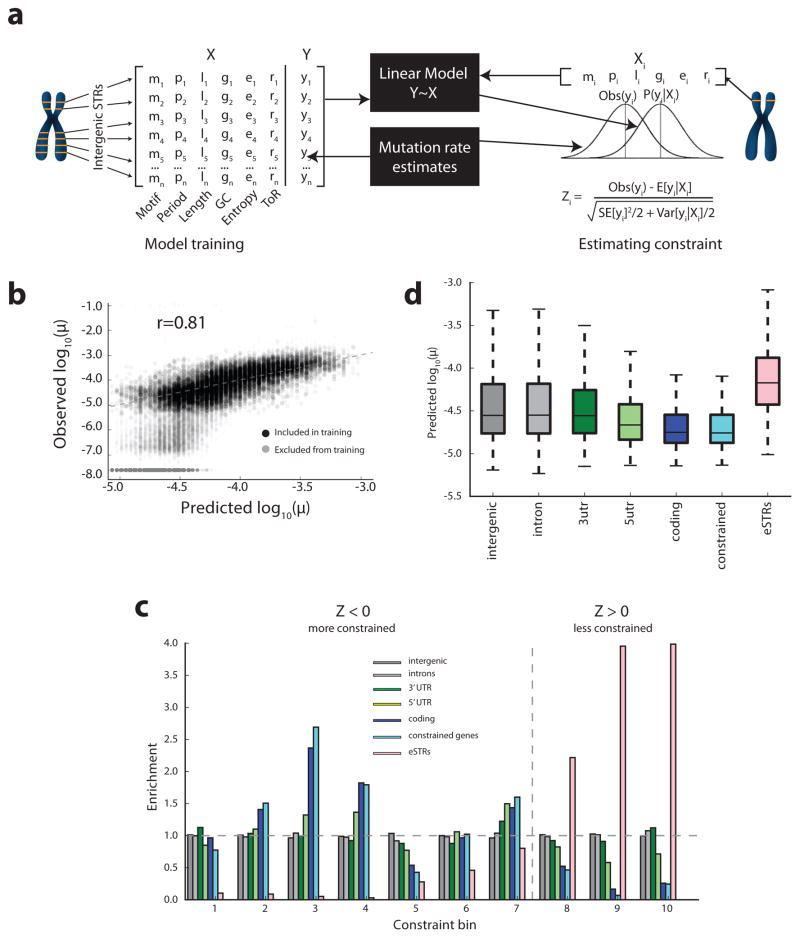
Encouraged by the accuracy of our per-locus autosomal parameter estimates, we sought to create a framework to evaluate genetic constraint at STRs by comparing observed to expected mutation rates. Our framework relies on generating robust predictions of per-locus mutation rates based on local sequence features and comparing the departure of the observed rates from this expectation (Figure 3a). STRs whose observed mutation rates are far lower than expected are assumed to be under selective constraint and thus more likely to have negative fitness consequences.

Figure 3. A framework for measuring STR constraint.

(a) Schematic of constraint framework. In the model training phase, a linear model is trained to predict mutation rates from local sequence features. In the estimation phase, constraint is measured by comparing predicted mutation rates to observed rates. (b) Sequence features are predictive of mutation rate. Comparison of predicted vs. observed mutation rates for a held out test set of intergenic loci. Gray dots denote loci with high or undefined standard errors that were excluded from model training. (c) Enrichment of gene annotations by constraint bin. X-axis gives bins defined by Z-score deciles. Y-axis gives the fold enrichment of each annotation in each bin. The dashed line gives the boundary between constrained (Z<0) and non-constrained (Z>=0) scores. (d) Predicted mutation rates by annotation. Center lines denote medians, boxes span the interquartile range, and whiskers extend beyond the box limits by 1.5 times the interquartile range. For (c) and (d), constrained denotes STRs in genes with missense constraint score >3 as reported by ExAC.

We began by evaluating whether local sequence features can accurately predict STR mutation rates. We examined the relationship between STR mutation rate and a variety of features, including total STR length, motif length, replication timing, and motif sequence (Supplementary Figure 12). While all features were correlated with mutation rate (Supplementary Table 4), total uninterrupted repeat sequence length and motif length were by far the strongest predictors, as has been previously reported by many studies^15,19. These features were combined into a linear regression model to predict per-locus mutation rates. We stringently filtered the training data to consist of presumably neutral (intergenic) loci with the best model performance. Analysis was restricted to STRs with motif lengths of 2–4bp with reference length ≥ 20bp and small standard errors (Methods), since this subset showed mutation rates primarily in the range that our model can detect. Using this filtered set of markers, a linear model explained 65% of variation in mutation rates in an independent validation set (Figure 3b).

We next developed a metric to quantify constraint at each STR by comparing observed to expected mutation rates. Our constraint metric is calculated as a Z-score, taking into account errors in both the predicted and observed values (Methods). Negative Z-scores denote loci that are more constrained than expected, and vice versa. Constraint scores for loci with detectable mutation rates followed the expected standard normal distribution (Supplementary Figure 13). However, loci with mutation rates below our detection threshold of 10⁻⁶ do not have reliable standard error estimates and had downward biased scores. Nevertheless, these loci are informative of a constraint signal in cases where the predicted mutation rate is high but the observed rate is below our detection threshold. Thus, rather than analyzing distributions of raw constraint scores, we binned scores by deciles and examined enrichments for functional annotations in each bin. For comparison, we also calculated mutation rates and constraint scores assuming a generalized stepwise model (Methods) and found that mutation rates and constraint scores were similar (r=0.88 and r=0.56 for mutation rates and constraint scores, respectively). All constraint scores analyzed below were calculated using the length-constrained model.

STR constraint scores give insights into human phenotypes

Observed Z-scores are concordant with biological expectations across genomic features. Introns, intergenic, and 3′-UTR regions closely matched neutral expectation (Figure 3c). On the other hand, STRs in coding exons showed significantly reduced mutation rates compared to the null model. These trends were recapitulated in the expected mutation rates (Figure 3d), suggesting that STRs under constraint are also under evolutionary pressure to maintain sequence features contributing to lower mutability. Additional analysis of STR constraint in coding regions is given in Supplementary Note and Supplementary Figure 14. In contrast to strong levels of constraint in coding exons, the STRs that we had previously identified to act as expression quantitative trait loci (eQTLs)¹⁰ showed a marked lack of constraint, consistent with observations in the Exome Aggregation Consortium (ExAC) dataset²⁵ showing highly constrained genes are depleted for eQTLs.

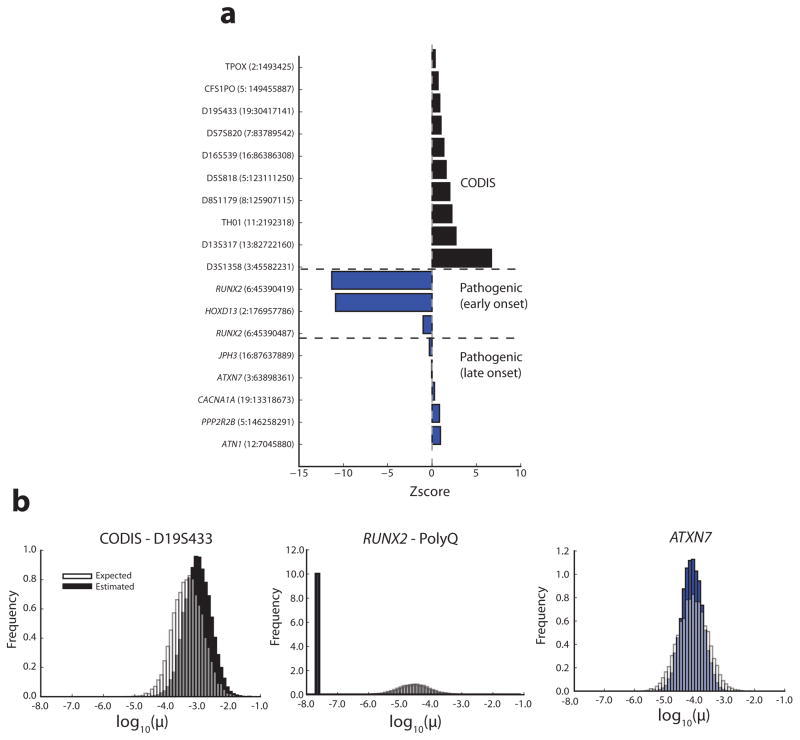
Constraint can provide a useful metric to prioritize potential pathogenic variants and interpret the role of individual loci in human conditions. Notably, this metric is most sensitive to early-onset disorders, as mutations involved in later onset disorders generally do not affect fitness and are thus expected to follow neutral patterns. Additionally, constraint is most sensitive to deleterious mutations following dominant inheritance patterns, since recessive mutations are eliminated at much slower rates. Consistent with this theory, STRs implicated in early onset dominant diseases show significantly higher constraint than expected (Figure 4). We focused on STRs that can be genotyped from high throughput sequencing data and are involved in congenital disorders. Notably, this excludes most large repeat expansions such as those involved in Huntington’s Disease or Fragile X Syndrome. First, we examined polyalanine and polyglutamine tracts in RUNX2. Even mild expansion of four glutamine residues has been shown to result in congenital cleidocranial dysplasia (OMIM: 119600)^26,27. Both repeats showed constrained mutation rates, with the polyglutamine repeat in the most constrained bin (Z=−11.3). Next, we tested a polyalanine expansion in HOXD13, which causes a severe form of synpolydactyly (OMIM: 186000). Again, a mild expansion (7 additional residues) has been shown to be pathogenic²⁸. This repeat was on the boundary of the most severe constraint bin (Z=−10.9). As a negative control, we also tested constraint at the CODIS loci used in forensics, which have been specifically ascertained for their high polymorphism rates and are likely neutral. As expected, the CODIS markers have weak constraint scores, and exhibit slightly higher mutation rates than expected (Z>0) (Figure 4).

Figure 4. Constraint scores can be used for STR prioritization.

(a) Z-scores for example loci. Black indicates CODIS forensics markers. Blue indicates known pathogenic STRs. For each STR, the CODIS marker or gene name is given and the chromosomal location (GRCh37) is indicated in parentheses. (b) Example distributions of estimated vs. expected mutation rates. The left panel shows a CODIS STR (D19S433), a presumably neutral STR. The middle panel shows a highly constrained polyglutamine repeat in RUNX2 for which a mild expansion is implicated in cleidocranial dysplasia, an early onset disorder. The right panel shows a polyglutamine repeat in ATXN7, implicated in spinocerebellar ataxia type 7, a late onset disorder and accordingly not highly constrained.

More broadly, we found protein-coding STRs are highly enriched in genes that are involved in developmental processes (Fisher’s exact test p=1.88×10⁻³⁶; n_fg=1,133; n_bg=20,913). Consistent with this result, three of the ten most highly constrained coding STRs in our dataset are in genes with previously reported developmental disorders following autosomal dominant inheritance patterns that have yet to be associated with pathogenic STRs: GATA6 (congenital heart defects, OMIM: 600001), SOX11 (mental retardation, OMIM: 615866), and BCL11B (Immunodeficiency 49, OMIM: 617237) (Supplementary Table 5). On the other hand, we found that pathogenic STRs of late onset STR expansions disorders such as spinocerebellar ataxias were not highly constrained and showed mutation rates very close to predicted values (Figure 4). These disorders often do not occur until the fourth or fifth decade of life²⁹, and thus are not expected to be under strong purifying selection. Taken together, these results suggest STR constraint scores will provide a useful metric by which to prioritize rare pathogenic variants involved in severe developmental disorders.

To facilitate use by the genomics community, genome-wide results of our mutational constraint analysis are provided in BED format (see Data Availability), which can be analyzed with standard genomics tools such as BEDtools³⁰.

Discussion

Metrics for quantifying genetic constraint by comparing observed to expected variation have provided a valuable lens to interpret the impact of de novo SNP variants. These have been widely used for applications including quantifying the burden of de novo variation in neurodevelopmental disorders^1,31, identifying individual genes constrained for missense or loss of function variation²⁵, and more recently to measure constraint in non-coding elements^4,32. However, the mutation rate at SNPs is sufficiently low that any given nucleotide has a low probability of being covered by a polymorphism even in very large datasets of human variation (e.g. a dataset of more than 60,000 exomes contained about 1 polymorphism per 8 nucleotides²⁵). Thus, the information provided by SNP variation is never sufficient to provide a direct measurement of the likely evolutionary constraint on a particular mutation. In contrast, the much higher mutation rate at STRs makes it possible to precisely measure constraint on a per-locus basis even with as few as 300 whole genomes.

We combined a deep catalog of STR variation¹⁸ with a novel model of the STR mutation process to develop an accurate method for measuring per-locus STR mutation parameters. We used this method to estimate individual mutation rates for more than 1 million STRs in the genome. Observed STR mutation rates vary over several orders of magnitude, suggesting it is not useful to cite a single mutation rate for all STRs. Median genome-wide mutation rates were far lower than previously reported^15–17,33. This is consistent with the fact that most well studied STR panels were specifically ascertained for their high heterozygosity, needed for traditional STR applications such as forensics or genetic linkage analysis. Our estimates confirm many known trends in STR mutation, such as the dependence of mutation rate on total STR length and the tendency of dinucleotide repeats to mutate in larger units than tetranucleotides¹⁵. Moreover, this large dataset allows us to exclude the possibility that certain sequence features such as local GC content play a strong role in determining STR mutation rates.

By comparing observed to expected mutation rates, we showed that we can measure genetic constraint at individual loci and use our constraint metric to prioritize potentially pathogenic variants. Importantly, our approach provides a biologically agnostic approach to assessing the importance of individual loci, as it relies entirely on observed genetic variation. While our analyses focused on STRs, the framework developed here can be easily extended to any class of repetitive variation for which accurate genotype panels are available. In future studies, we envision this work will provide a much needed framework to interpret the dozens of de novo variants at STRs and other repeats arising in each individual, especially in the context of severe early onset disorders. Beyond analyzing de novo variation, accurate models of STR mutation will enable scans for STRs under selection³⁴, help identify rapidly mutating markers for forensics or genetic genealogy^19,35, and improve statistical methods for incorporating STRs into quantitative genetics studies.

Our mutation rate estimation method and constraint metric face several limitations. First, estimating mutation rates in several hundred samples is only accurate for mutation rates down to approximately 10⁻⁶. Loci with slower mutation rates produce biased results, limiting our ability to predict and measure mutation rates at a large number of loci, including the majority of protein coding STRs. While we can detect general signals of constraint for slowly mutating STRs, larger sample sizes will allow for more accurate constraint scores and thus more informative prioritization. Second, our method analyzes pairs of haplotypes rather than the entire evolutionary history of a locus. While this has the advantage of allowing estimation across unphased data, it discards valuable information present in the full haplotype tree and limits the scope of models that can be considered. For example, it precludes modeling allele length-specific mutation rates, which requires estimating ancestral states on the full haplotype tree. Finally, there are additional aspects of the STR mutation process not modeled here. Our method focuses on short stepwise mutations occurring at relatively stable STRs. Unstable expansions, such as those occurring in trinucleotide repeat disorders, likely mutate by different models. Our model also ignores the effect of sequence interruptions and putative interactions between alleles, both of which have been hypothesized to influence STR mutation patterns^19,36.

Future bioinformatic advances will likely overcome many of these issues and improve the precision of our estimates. In particular, while our method works on unphased data, phased STR and SNP haplotypes would allow analysis of the entire haplotype tree at a given locus as is done by MUTEA, improving our accuracy and allowing us to consider a broader range of mutation models. Additionally, our current tools are limited to STRs that can be spanned by short reads, and thus exclude many well known pathogenic loci such as those involved in trinucleotide repeat expansion disorders. We envision that long read and synthetic long read technologies will both enable analysis of a broader class of repeats and provide an additional layer of phase information. Finally, larger sample sizes will allow more accurate analysis of constraint for slow-mutating loci. Taken together, these advances will provide a valuable framework for interpreting mutation and selection at hundreds of thousands of STRs in the genome and will help prioritize STR mutations in clinical studies.

Online Methods

STR mutation model

We model STR mutation using a discrete version of the Ornstein-Uhlenbeck process described in detail in the Supplementary Note. Our model assumes STR mutations occur at a rate of μ mutations per locus per generation according to a step-size distribution with first and second moments:

$$\begin{gathered} E[(a_{i+1}-a_i)\mid a_i]=-\beta a_i \\ E[{(a_{i+1}-a_i)}^2\mid a_i]={\sigma }^2 \end{gathered}$$

where a_i is the length of the STR allele after mutation i and a_i+1 is the length after mutation i +1. This implies that long alleles (>0) tend to decrease back toward 0 and short alleles (<0) tend to increase toward 0. For all analyses, all alleles are assumed to be relative to the major allele, which is set to 0.

Mutation parameter estimation

We extended the MUTEA framework to estimate parameters at diploid loci for which the underlying haplotype tree is unknown. For each sample genotyped at locus j, we obtain t_ij, the TMRCA between the two haplotypes of sample i, and a distribution G_ij, where G_ij(a,b) gives the posterior probability that sample i has genotype (a,b). We initially assume that haplotype pairs are independent and maximize the following likelihood function at locus j:

$$\begin{gathered} L_j(\theta \mid D_j)={\mathit{\Pi }}_{i}P(G_{ij}\mid \mathit{\Theta },t_{ij}) \\ P(G_{ij}\mid \mathit{\Theta },t_{ij})={\mathit{\sum }}_{(a,b)}{G}_{ij}(a,b)A({(a-b)}^2\mid t_{ij}) \end{gathered}$$

Where θ = {μ, β, p}, D_j = {(G_1j, t_1j), (G_2j, t_2j)...(G_nj, t_nj)}, n is the number of samples, and A(x|t) gives the probability of observing a squared distance of x between alleles on haplotypes with a TMRCA of t. We used the Nelder-Mead algorithm to minimize the negative of the log-likelihood and imposed boundaries of μ ∈ [10⁻⁸, 0.05], β ∈ [0,0.9], p ∈ [0.7, 1.0].

To compute the function A, we first build a transition matrix M of size L × L, where L is the number of allowed alleles. M[a,b] gives the probability that allele a mutates to allele b in a single generation. Step sizes were set based on the model described in Supplementary Note:

$$\begin{gathered} M[a_t,a_t+k]=\mu u_{t}p{(1-p)}^{k-1}k>0 \\ M[a_t,a_t+k]=\mu d_{t}p{(1-p)}^{-k-1}k<0 \\ M[a_t,a_t+k]=(1-\mu )k=0 \end{gathered}$$

where $u_t=\frac{1-\beta p{a}_t}{2}$ and $d_t=\frac{1+\beta p{a}_t}{2}$.

M represents a stochastic process, and thus M^T gives transition probabilities along a branch T generations long. A single row M^T[a,:] gives the expected allele frequency spectrum of a locus for which the ancestral allele was a and the MRCA was T generations ago. We can use this to derive the probability of observing a given squared distance between two alleles separated by t generations:

$$A(x\mid t,a)=\sum _{i=\mathrm{1..}L-\sqrt{x}}{M}^t[a,i]M^t[a,i+\sqrt{x}]$$

In our data, we do not know the ancestral allele a for each pair of haplotypes. However, under our model of STR evolution, A does not depend on the ancestral allele and so we assume 0 as the ancestral allele for simplicity. Notably, we have assumed haplotype pairs are statistically independent. While this does not bias our results, standard errors must be adjusted as described in the Supplementary Note.

Estimating mutation parameters using a generalized stepwise model

Under a generalized stepwise model (GSM), the ASD should be linearly related to the TMRCA between a pair of haplotypes³⁷:

$${(a_i-a_j)}^2=2{\mu }_{\mathit{eff}}{t}_{ij}$$

Where a_i and a_j are the repeat lengths of STR alleles on two haplotypes i and j, t_ij is the TMRCA between that pair of haplotypes, and μ_eff is the effective mutation rate. The effective mutation rate is defined as ${\mu }_{\mathit{eff}}=\mu {\sigma }_m^2$, where μ is the per-generation mutation rate of the locus and step sizes are drawn from a distribution with mean 0 and variance ${\sigma }_m^2$.

For each locus, we calculated μ_eff by regressing ASD on TMRCA and dividing the resulting slope by 2.

Joint estimation of mutation parameters across multiple loci

The MUTEA approach can be easily extended to estimate mutation parameters in aggregate by jointly maximizing the likelihood across multiple loci at once:

$$L(\theta \mid D)={\mathit{\Pi }}_j(\theta \mid D_j)$$

To minimize computation and because β and p tended to be less consistent across loci, we first perform per-locus analyses to obtain individual estimates for β and p. We then hold these parameters constant at the mean value across all loci and only maximize the joint likelihood across μ

Simulating SNP-STR haplotypes

We used fastsimcoal³⁸ to simulate coalescent trees for 600 haplotypes using an effective population size of 100,000. We then forward-simulated a single STR starting with a root allele of 0 using specified values of μ, β, and ${\sigma }^2=\frac{2-p}{p^2}$. Mutations were generated according to a Poisson process with rate $\lambda =\frac{1}{\mu }$ and following the model described above. We chose 300 random pairs of haplotypes to form “diploid” individuals to use as input to our estimation method. We simulated reads for each locus assuming 5x sequencing coverage, with each read equally likely to originate from each allele. Stutter errors were simulated using the model described in Willems et al.¹⁹ with u = 0.1, d = 0.05, and ρ_s = 0.9. This indicates that stutter noise causes the true allele to expand or contract with 10% or 5% frequency, respectively, and that error sizes are geometrically distributed with 10% probability of mutating by more than one repeat unit. For estimating per-locus parameters, we performed 10 simulations with each set of parameters.

Datasets

Previously published mutation rate estimates

MUTEA mutation rate and length bias estimates for the 1000 Genomes dataset were obtained from Table S1 in Willems et al.¹⁹ De novo Y-STR mutation rate estimates were obtained from Table S1 of Ballantyne et al.¹³ CODIS mutation rates were obtained from NIST (see URLs).

Annotations

Local GC content and sequence entropy were obtained from the “strinfo” file included in the lobSTR hg19 reference bundle. Missense constraint scores were downloaded from the ExAC website (see URLs).

STR genotyping

Profiling STRs from short reads

Raw sequencing reads for the SGDP dataset were aligned using BWA-MEM²³. Alignments were used as input to the allelotype tool packaged with lobSTR²⁴ version 4.0.2 with non-default flags “—filter-mapq0 –filter-clipped –max-repeats-in-ends 3 –min-read-end-match 10 –dont-include-pl –min-het-freq 0.2 –noweb”. STR genotypes are available on dbVar under accession nstd128. Y-STRs for the 1000 Genomes data were previously profiled²⁴ and were preprocessed as described in¹⁹.

Filtering to obtain high quality STR calls

Y-STR calls for SGDP were filtered using the lobSTR_filter_vcf.py script available in the lobSTR download with arguments “--loc-max-ref-length 80 --loc-call-rate 0.8 --loc-log-score 0.8 --loc-cov 3 --call-cov 3 --call-dist-end 20 --call-log-score 0.8” and ignoring female samples. Autosomal samples were filtered using “--loc-max-ref-length 80 --loc-call-rate 0.8 --loc-log-score 0.8 --loc-cov 5 --call-cov 5 --call-dist-end 20 --call-log-score 0.8”.

Calculating local TMRCA

As described in Mallick et al.¹⁸, we used the pairwise sequential Markovian coalescent (PSMC)²⁰ to infer local TMRCAs across the genome in each sample. For each region overlapping an STR, we calculated the geometric mean of the upper and lower heterozygosity estimates returned by PSMC. We scaled heterozygosity to TMRCA based on the genome-wide average PSMC estimate (0.00057) of a French sample with a previously estimated genome-wide average TMRCA of 21,000 generations¹⁵. To accommodate errors in this scaling process, final mutation rate estimates were scaled to match the mean values of published de novo rates (see below).

Pairwise Y chromosome analysis

For each pair of SGDP Y-chromosomes, we first calculated the pairwise sequence heterozygosity. We then scaled this to TMRCA using the relationship t_i = h_i/2μ_YSNP, where h_i is the heterozygosity of pair i and μ_YSNP is the Y-chromosome SNP mutation rate. μ_YSNP was set to 2.1775×10⁻⁸ as reported by Helgason et al.³⁹ For the 1000 Genomes set, we obtained a Y-phylogeny that was built by the 1000Y analysis group⁴⁰. We scaled the tree using a method described previously¹⁹. For each dataset, we used pairwise TMRCA and allele squared distance estimates as input to our maximum likelihood procedure.

Scaling mutation parameters

Our TMRCA estimates, and thus mutation rate estimates, scale linearly with the choice of SNP mutation rate. To account for this and to compare estimates between datasets, we scaled our mutation rates by a constant factor such that the mean STR mutation rates between datasets were identical. Genome-wide estimates are scaled based on the comparison with CODIS rates.

Measuring STR constraint

Predicting mutation rates from local sequence features

We trained a linear model to predict log₁₀ mutation rates from local sequence features including GC content, replication timing, sequence entropy, motif sequence, motif length, total STR length, and uninterrupted STR length. The model was built using presumably neutral intergenic loci, with 75% of the loci reserved for training and 25% for testing. While all features were correlated with mutation rates, the best test performance was achieved using only motif length and uninterrupted STR length. Models were built using the python statsmodels package (see URLs).

Model training was restricted to STRs whose mutation rates could be reliably estimated. We filtered STRs with total reference length <20bp, since the majority of shorter STRs returned biased mutation rates at the optimization boundary of 10⁻⁸. We further filtered STRs with standard errors equal to 0, >0.1, or undefined (usually indicating the lower optimization boundary of 10⁻⁸ was reached). However, these loci were included in testing and in downstream analysis as the majority of coding STRs fell into this category.

Calculating Z-scores

Constraint scores are calculated for each locus i as:

$$Z_i=\frac{{\mu }_i-E[{\mu }_i]}{\sqrt{SE{[{\mu }_i]}^2/2+\mathit{Var}[{\mu }_i]/2}}$$

Where μ_i is the observed mutation rate, SE[μ_i] is the standard error of the observed mutation rate, E[μ_i] is the predicted mutation rate, and Var[μ_i] is the variance of the prediction. In all cases, μ_i refers to the log₁₀ mutation rate, with the log₁₀ notation omitted for simplicity.

Constraint score analysis

GO analysis was performed using goatools (see URLs). OMIM disease annotations were accessed on December 8, 2016.

Data availability

Per-locus mutation parameters are available at https://s3-us-west-2.amazonaws.com/strconstraint/Gymrek_etal_SupplementalData1_v2.bed.gz. The file format is described in https://s3-us-west-2.amazonaws.com/strconstraint/readme_v2.txt.

Code availability

Code used in this study is available at https://github.com/gymreklab/mutea-autosomal.