Building Predictive Models of Genetic Circuits Using the Principle of Maximum Caliber

Abstract

Learning the underlying details of a gene network is a major challenge in cellular and synthetic biology. We address this challenge by building a chemical kinetic model that utilizes information encoded in the stochastic protein expression trajectories typically measured in experiments. The applicability of the proposed method is demonstrated in an auto-activating genetic circuit, a common motif in natural and synthetic gene networks. Our approach is based on the principle of maximum caliber (MaxCal)—a dynamical analog of the principle of maximum entropy—and builds a minimal model using only three constraints: 1) protein synthesis, 2) protein degradation, and 3) positive feedback. The MaxCal-generated model (described with four parameters) was benchmarked against synthetic data generated using a Gillespie algorithm on a known reaction network (with seven parameters). MaxCal accurately predicts underlying rate parameters of protein synthesis and degradation as well as experimental observables such as protein number and dwell-time distributions. Furthermore, MaxCal yields an effective feedback parameter that can be useful for circuit design. We also extend our methodology and demonstrate how to analyze trajectories that are not in protein numbers but in arbitrary fluorescence units, a more typical condition in experiments. This “top-down” methodology based on minimal information—in contrast to traditional “bottom-up” approaches that require ad hoc knowledge of circuit details—provides a powerful tool to accurately infer underlying details of feedback circuits that are not otherwise visible in experiments and to help guide circuit design.

Introduction

Biological function is largely dictated by gene networks that control protein expression in single cells. Understanding details of these networks and consequently building quantitative models is essential to control gene expression and ultimately regulate cellular dynamics. However, model development has been limited due to the lack of information about the complex web of interactions (including feedback regulation) that defines these networks. Typical experiments only provide partial information by measuring the expression levels of one or two proteins of interest using fluorescent tags, much less than the actual number of entities (mRNAs, promoters, nucleotides, and amino acids) involved in the process of gene expression. This problem of partial information is a key challenge for model building. Although the number of species monitored is limited, experimental read-outs contain crucial information, as they record the entire time trajectory of fluctuating protein expression levels. The stochastic nature of the trajectories is due to small copy numbers of molecules involved in these reactions (1, 2, 3, 4, 5, 6, 7, 8, 9). The details of noise statistics encode the details of network architecture. This provides a potentially useful avenue for inferring details of network architecture by analyzing noisy protein expression levels (10, 11, 12, 13, 14, 15). Despite realizing the power of this approach (10, 12, 14, 15), such efforts are still in their infancy. Existing models are either too simple, with limited single-cell-level predictive power, or too detailed, requiring too many unknown parameters (16). The most common stochastic approaches first define sets of reaction networks to be simulated using a Gillespie algorithm (17) or related methods and then fit different observables to determine the corresponding reaction rate parameters. A major drawback of these methods is that they are “bottom-up” and require detailed knowledge of the underlying reaction network. This is particularly challenging when networks involve feedback, a common feature in many natural networks and synthetic biology. It is currently impossible to test many of these ad hoc assumptions independently. Furthermore, these approaches can involve too many parameters that can fit the same data with multiple models, creating additional challenges for efficient parameter estimation (11). The challenge of having too many parameters is also problematic for circuit design (18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30), as it requires ways to efficiently explore parameter space to test different models, thus demanding models with the least possible number of parameters.

To circumvent these obstacles, we propose a “top-down” approach for modeling these networks. We use the principle of maximum caliber (MaxCal) to model stochastic trajectories with minimal information. We show the application of MaxCal on a simple auto-activating circuit, a common motif in many biological circuits (31). MaxCal maximizes path entropy subject to constraints, similar to maximum entropy on state space, and directly works with path trajectories. This makes MaxCal directly applicable to experimentally measured time trajectories of protein numbers. We establish the methodology on synthetic data generated using Gillespie simulations (17) of a known auto-activating circuit. These trajectory data serve as the input data—a proxy for experimental data—for MaxCal. The minimal model of MaxCal is then applied to the raw trajectory statistics in conjunction with maximum likelihood (ML) to determine representative parameters for the model. These parameters can predict other statistics of the data and quantitatively infer several underlying physical variables that are not visible otherwise. In the next section, we first describe the synthetic circuit and generation of in silico data that mimic experimental data. Next, we introduce MaxCal and its specific application to the circuit. We show how MaxCal, along with ML, can be used to infer model parameters and make predictions. Comparing these predictions against the known model allows us to benchmark the predictive capabilities of MaxCal. Finally, we discuss how the methodology can be applied when the input data are not in protein number but in arbitrary fluorescence, a common challenge in interpreting experimental data.

Materials and Methods

Generating synthetic data for an auto-activating circuit

Considering the complexity of natural networks with many unknown or incompletely understood interactions, synthetic biologists are building mimics of frequently occurring parts of bigger networks, called network motifs (32, 33, 34). One natural network motif with important biological function that has inspired the design of many synthetic gene circuits is feedback regulation. Our previous work (35) has demonstrated the application of MaxCal on double-negative (overall positive) feedback circuits, where two genes mutually repress each other, commonly referred to as a toggle-switch circuit (36, 37). Here, we consider a positive feedback circuit where a single gene auto-activates itself. As a proof of concept, we apply MaxCal to synthetic data generated in silico using a model for which the underlying parameters are known. This will serve as a proxy for experimental data and provide us with a gold standard to which we can compare when demonstrating how well MaxCal performs given stochastic trajectories. Among several models of auto-activation in different biological contexts (38, 39, 40, 41, 42, 43, 44, 45), we adopt the one below (Eq. 1), studied by Kepler and Elston (46), to generate stochastic synthetic data that will serve to mimic experimental time traces:

$$\mathit{\alpha }\stackrel{g}{\to }\mathit{\alpha }+A;A\stackrel{r}{\to }\mathrm{\oslash };A+A\underset{b_{\text{d}}}{\overset{f_{\text{d}}}{\rightleftarrows }}{A}_2$$ (1)

$$\mathit{\alpha }+A_2\underset{b_{\text{p}}}{\overset{f_{\text{p}}}{\rightleftarrows }}{\mathit{\alpha }}^{\ast };{\mathit{\alpha }}^{\ast }\stackrel{g^{\ast }}{\to }{\mathit{\alpha }}^{\ast }+A.$$

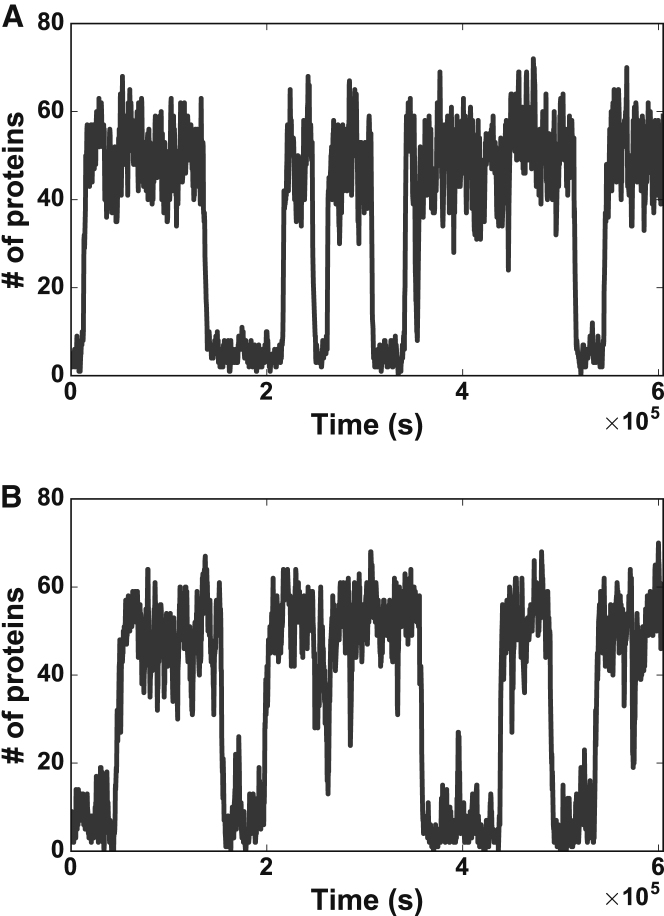
In this scheme, some generic protein, A, is created from its corresponding gene, α, at a rate g, degrades at a rate r, and dimerizes into $A_2$ with forward and backward rates $f_{\text{d}}$ and $b_{\text{d}}$, respectively. $A_2$ can then bind and unbind to the promoter site of α at rates $f_{\text{p}}$ and $b_{\text{p}}$, respectively, sending α into or out of its activated state, ${\alpha }^{\text{∗}}$. In this activated state, ${\alpha }^{\text{∗}}$ creates protein A at a much faster rate, $g^{\text{∗}}$, capturing the essentials of a positive-feedback mechanism. Rates are chosen to produce switching times that are representative of experiments (31) while maintaining protein synthesis and degradation rates in the realm of typical rates (47). A Gillespie algorithm (17) was used to generate stochastic trajectories of protein (A) levels as shown in Fig. 1 A. Three major features are worth noting: 1) two clearly separated high and low states, 2) a large amount of fluctuation within each state, and 3) stochastic switching between the two states. In the next section, we first attempt to reproduce these three basic features in MaxCal using as simple a framework as possible.

Figure 1.

Positive feedback circuit. (A) Typical time trace of the number of proteins in a self-promotion circuit using the reaction scheme in Eq. 1 ($g=5.0\times {10}^{-3}{\text{ s}}^{-1}$, $g^{\text{∗}}=50.0\times {10}^{-3}{\text{s}}^{-1}$, $r=1.0\times {10}^{-3}{\text{s}}^{-1}$, $f_{\text{d}}=5.0\times {10}^{-3}{\text{s}}^{-1}$, $b_{\text{d}}=50{\text{s}}^{-1}$, $f_{\text{p}}=6.0\times {10}^{-3}{\text{s}}^{-1}$, $b_{\text{p}}=3.0\times {10}^{-5}{\text{s}}^{-1}$, assuming the intrinsic time unit is seconds). Data are recorded every $300\text{s}$. (B) Typical time trace of the number of proteins in the minimal model of self-promotion using MaxCal ($h_{\alpha }=-0.512$, $h_A=0.585$, $K_A=0.0298$, $M=15$, $\Delta t=300\text{s}$).

MaxCal model for auto-activating circuit

Maximum caliber is a variational principle that gives a prescription for inferring dynamics by maximizing the path entropy (35, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58), or caliber, subject to known constraints enforced via Lagrange multipliers. For the gene circuit of interest, there are three minimal constraints that must be in place: 1) protein synthesis, 2) protein degradation, and 3) auto-activation/positive feedback. We enforce the first two by restricting the average number of proteins that are created in a discrete time interval $\left(\Delta t\right)$ as well as the average number of proteins that are destroyed (35, 55). To do this, we define ${\ell }_{\alpha }$ as the production-state variable, which describes the number of proteins that are created in the time interval and ranges as integer values between zero and some predefined maximal value (M), i.e., $0\le {\ell }_{\alpha }\le M$. We also define ${\ell }_A$ as the degradation-state variable, which describes the number of previously existing proteins that still exist at the end of the time interval. Clearly, ${\ell }_A$ ranges as integer values between zero and the number of proteins present at the beginning of the time interval $\left(N_A\right)$, i.e., $0\le {\ell }_A\le N_A$. The corresponding Lagrange multipliers for these two constraints are $h_{\alpha }$ and $h_A$, and the probability of observing a particular combination of ${\ell }_{\alpha }$ and ${\ell }_A$ is defined as $P_{{\ell }_{\alpha },{\ell }_A}$. Next, we implement the constraint of positive feedback, the idea that a high number of proteins $\left(N_A\right)$ should positively correlate with the production of A. This is done by introducing a third Lagrange multiplier, $K_A$, that enforces a coupling between protein production and the presence of proteins by constraining the average of ${\ell }_{\alpha }{\ell }_A$. This is the lowest-order term in the coupling of these two variables that must be imposed to capture the essence of feedback. Similar arguments were used to build models to describe negative feedback in toggle-switch circuitry (35). The four basic ingredients of the model, described above, yield the caliber as

$$C=-\sum _{{\ell }_{\alpha }=0}^M\sum _{{\ell }_A=0}^{N_A}{P}_{{\ell }_{\alpha },{\ell }_A}\text{log}{P}_{{\ell }_{\alpha },{\ell }_A}+h_{\alpha }\sum _{{\ell }_{\alpha }=0}^M\sum _{{\ell }_A=0}^{N_A}{\ell }_{\alpha }{P}_{{\ell }_{\alpha },{\ell }_A}+h_A\sum _{{\ell }_{\alpha }=0}^M\sum _{{\ell }_A=0}^{N_A}{\ell }_A{P}_{{\ell }_{\alpha },{\ell }_A}+K_A\sum _{{\ell }_{\alpha }=0}^M\sum _{{\ell }_A=0}^{N_A}{\ell }_{\alpha }{\ell }_A{P}_{{\ell }_{\alpha },{\ell }_A},$$ (2)

and the corresponding caliber-maximized path probabilities are

$$P_{{\ell }_{\alpha },{\ell }_A}=Q^{-1}\left(\begin{array}{c}{N}_A\\ {\ell }_A\end{array}\right)\text{exp}\left(h_{\alpha }{\ell }_{\alpha }+h_A{\ell }_A+K_A{\ell }_{\alpha }{\ell }_A\right);Q=\sum _{{\ell }_{\alpha }=0}^M\sum _{{\ell }_A=0}^{N_A}\left(\begin{array}{c}{N}_A\\ {\ell }_A\end{array}\right)\text{exp}\left(h_{\alpha }{\ell }_{\alpha }+h_A{\ell }_A+K_A{\ell }_{\alpha }{\ell }_A\right).$$ (3)

Using this path probability distribution, stochastic trajectories are generated using a Monte Carlo method to select a path for each time point. The system then creates and destroys the number of proteins corresponding to the ${\ell }_{\alpha }$ and ${\ell }_A$ of the selected path and the time of the system advances by the predetermined $\Delta t$. A quick search of the parameter phase space ($h_{\alpha }$, $h_A$, $K_A$, M) reveals that even with just these four parameters, bimodal behaviors like the ones seen in the self-promotion circuit of the previous section (characterized with seven parameters in Fig. 1 A) can be reproduced (see Fig. 1 B). For efficient computation, protein number probability distributions are generated using the method of finite-state projection (FSP) of Munsky and Khammash (59). This method is needed to provide a systematic way to truncate the infinite phase space of possible states, since protein number does not have an upper bound. FSP provides a rigorous self-consistent approach to ensure that the truncation error is within a pre-determined error bound (see Supporting Material for exact application).

Furthermore, the state variables ${\ell }_{\alpha }$ and ${\ell }_A$ directly relate to effective protein synthesis and degradation rates analogous to g, $g^{\text{∗}}$, and r in the auto-activation circuit (Eq. 1). Specifically,

$$g=\frac{{\langle {\ell }_{\alpha }\rangle }_{N_A=N_L}}{\Delta t},g^{\text{∗}}=\frac{{\langle {\ell }_{\alpha }\rangle }_{N_A=N_H}}{\Delta t},r\left(N\right)=\frac{N-{\langle {\ell }_A\rangle }_{N_A=N}}{N\Delta t},r=\sum _{N}P\left(N\right)r\left(N\right),$$ (4)

where $N_{\text{L}}$ and $N_{\text{H}}$ are the peak values of the number of proteins in the low and high states, respectively, and $P\left(N\right)$ is the probability of having N proteins within the system (calculated via FSP).

An additional metric that could be of interest in genetic circuit design is the effective feedback metric, F. We define F as the average Pearson correlation coefficient between ${\ell }_{\alpha }$ and ${\ell }_A$:

$$F=\sum _{N}P\left(N\right)\frac{\langle {\ell }_{\alpha }{\ell }_A\rangle -\langle {\ell }_{\alpha }\rangle \langle {\ell }_A\rangle }{{\sigma }_{{\ell }_{\alpha }}{\sigma }_{{\ell }_A}},$$ (5)

where ${\sigma }_{{\ell }_{\alpha }}$ and ${\sigma }_{{\ell }_A}$ represent the standard deviations of ${\ell }_{\alpha }$ and ${\ell }_A$, respectively. The averages (in the numerator) and standard deviations (in the denominator) are first evaluated for a given N and then the ratio is further averaged over the protein number distribution, $P\left(N\right)$, to yield effective feedback, F. This parameter is designed to be restricted between $-1$ and 1 as a way to quantify the relative feedback within the system and will help to objectively compare two independent gene circuits. Although in the application presented here we expect $0<F<1$, we anticipate $0>F>-1$ while describing negative-feedback circuits.

Parameter estimation via maximum likelihood

The exercise above ensures that the minimal model of MaxCal with only four parameters is capable of producing the general features of a bimodal system. Next, we proceed to benchmark the performance of the model quantitatively when given a particular stochastic trajectory to characterize. This will allow us to learn about quantitative details of the underlying network by decoding information hidden in the noisy raw trajectory. For example, we may be interested in inferring the effective synthesis/degradation rates or the degree of feedback (F), quantities that are not directly available from the raw experimental trajectory. Below, we provide the framework to quantitatively infer these specific characteristics of a network from the stochastic trajectory.

Consider an experimentally observed trajectory of sufficiently long time, T, expressed in the units of the typical timescale $\left(\Delta t\right)$ used for sampling the data. In this intrinsic time unit $\left(\Delta t\right)$, we have $T+1$ frames at which the protein number has been recorded. Now consider a particular transition between two subsequent frames, say t and $t+1$, in which the protein number changed from i to j. We denote the probability of this one-step (single-frame) transition as $P\left(j,t+1;i,t\right)$, which is abbreviated as $P_{i\to j}$. These one-step transition probabilities can be determined from MaxCal as

$$P_{i\to j}=\sum _{{\ell }_{\alpha }=0}^M\sum _{{\ell }_A=0}^i\delta \left({\ell }_{\alpha }+{\ell }_A-j\right)P_{{\ell }_{\alpha },{\ell }_A},$$ (6)

where δ is the Dirac delta function, and $P_{{\ell }_{\alpha },{\ell }_A}$ are functions of the Lagrange multipliers, described by Eq. 3. The likelihood $\left(\mathcal{L}\right)$ of observing the experimental trajectory given a specific set of MaxCal parameters ($h_{\alpha }$, $h_A$, $K_A$, and M) can then be calculated as

$$\mathcal{L}=\prod _{t=0}^{T-1}P\left(N_{t+1},t+1;N_t,t\right)=\prod _{\left\{i\to j\right\}}{P}_{i\to j}^{{\omega }_{i\to j}},$$ (7)

where $N_t$ is the number of proteins present in frame t, ${\omega }_{i\to j}$ is the total number of $i\to j$ one-step transitions, and the second product is over all possible transitions between different values of i and j. As outlined above (Eq. 6), $P_{i\to j}$ values are determined using MaxCal, hence the likelihood is a function of $h_{\alpha }$, $h_A$, $K_A$, and M. Thus, we can maximize the likelihood of the trajectory to select $h_{\alpha }$, $h_A$, $K_A$, and M.

Experiments (and our Gillespie simulations) have no upper limit on production analogous to M in MaxCal. Rare fluctuations leading to unusually large jumps in protein number (>M) in one time step will severely penalize the likelihood of parameter values that are otherwise most likely. This discontinuous jump in likelihood will erroneously eliminate the most likely set of parameters. We avoid this problem by calculating transition probabilities over multiple intervals (m frames) for a given set of MaxCal parameters. We denote the probability of a multi-step (multiple-frame) transition as $P\left(j,t+m;i,t\right)$, abbreviated as $P_{\left(i\to j\right),m}$. This slightly modifies our likelihood function, $\mathcal{L}$, as

$$\mathcal{L}=\prod _{n=1}^{\mathcal{N}}P(N_{t+m},t+m;N_t,t=m(n-1))=\prod _{\left\{i\to j\right\}}{P}_{\left(i\to j\right),m}^{{\omega }_{\left(i\to j\right),m}},$$ (8)

where $\mathcal{N}$ is $T/m$ rounded down to the nearest integer and ${\omega }_{\left(i\to j\right),m}$ is the total number of $i\to j$ transitions over m frames. An objective choice of m can be provided by using the average residence times (in frames) in the high and low states . However, our result is not sensitive to the choice of m and is robust for a range of values around the typical value.

Dealing with experimental data

Although the procedure above is applicable to synthetic data in terms of protein number, typical experimental read-outs are in arbitrary fluorescence units. Furthermore, the amount of fluorescence measured per protein is noisy and requires one to de-convolute fluorescence fluctuations from protein number fluctuations. To mimic typical experimental readouts with these challenges, we use the same synthetic data from the auto-activating circuit, but “corrupt” it to create a fluorescence trajectory in silico that is likely to be observed in an experiment. We assume the probability distribution of fluorescence intensity (I) measured per protein to be a Gaussian distribution (60, 61, 62) centered at a with a standard deviation of b, i.e., $\langle I\rangle =a$ and $\langle I^2\rangle -{\langle I\rangle }^2=b^2$. With this assumption, the fluorescence measured from N proteins would follow a probability distribution that is a convolution of N protein fluorescence distributions leading to a Gaussian distribution with mean $Na$ and variance $N{b}^2$. To “corrupt” simulated trajectories of protein numbers, we select a fluorescence for each time point from this distribution where the mean and variance depend on the protein number, N. Although the procedure described here assumes that the fluorescence per protein follows a Gaussian distribution, we used a similar approach for Γ distributions (63, 64) as well.

With this “synthetic fluorescence trajectory” closely mimicking realistic experimental situations, we propose two strategies to infer the underlying model. In the first strategy, we assume the average fluorescence intensity per protein $\left(\langle I\rangle =a\right)$ is known, possibly obtained by carrying out low-intensity photobleaching (65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77). We use a as a conversion factor to determine protein number (N) from the fluorescence intensity, f, as

$$N=\text{Int}\left(f/a\right),$$ (9)

where the Int function yields the nearest integer with negative protein numbers being rounded to zero. Parameter estimation then proceeds in the same fashion as before when analyzing trajectories in terms of protein number over time. In this strategy, parameter estimation takes place in two steps serially: first, fluorescence to number conversion (using Eq. 9), and then MaxCal with ML (as described earlier). We call this method serial fluorescence-to-number conversion, or simply SFNC.

We propose a second strategy in which the fluorescence fluctuation is included when calculating the likelihood of a set of MaxCal parameters. In this second approach (termed parallel FNC, or PFNC), we assume that the variance—in addition to the average—in intensity fluctuation per protein is also known, i.e., both a and b are given. This can be obtained using the same photobleaching experiment mentioned above to measure the probability distribution of fluorescence per protein (65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77). With this information, we can incorporate the fluorescence distribution in the likelihood function (Eq. 8), modifying it to

$$\mathcal{L}=\prod _{n=1}^{\mathcal{N}}\left(\sum _{N_t}\sum _{N_{t+m}}\text{Φ}\left(N_t|f_t\right)P\left(N_{t+m},t+m;N_t,t=m\left(n-1\right)\right)\text{Φ}\left(N_{t+m}|f_{t+m}\right)\right)$$ (10)

where $f_t$ is the fluorescence at frame t, and $\text{Φ}\left(N_t|f_t\right)$ is the conditional probability that $N_t$ proteins are present given a fluorescence measurement of $f_t$. These probabilities are known and used as previously with the knowledge of the known variance and mean. The probability $P\left(N_{t+m},t+m;N_t,t\right)$ is determined as above using MaxCal and is a function of the Lagrange multipliers and M. The new likelihood function (Eq. 10) is then maximized to determine $h_{\alpha }$, $h_A$, $K_A$, and M.

Results and Discussion

MaxCal accurately infers underlying rate parameters

Using the procedures described above, we determine $h_{\alpha }$, $h_A,K_A$, and M for a given stochastic trajectory in terms of either protein number or fluorescence readout. These fully specify the minimal MaxCal model and are capable of making multiple predictions, such as of the underlying rate parameters. Effective values for the underlying production and degradation rates can be predicted using the average value of the production- and degradation-state variables, respectively (see Eq. 4). To see how well these inferred rates compare to the true values, we applied our inference method to input trajectories that are ∼2000 frames long with an intrinsic sampling rate of 5 min $\left(\Delta t=300\text{s}\right)$, equivalent to trajectories of 7 days. Furthermore, we used 100 such trajectories, equivalent to tracking protein numbers in 100 cells. These numbers were chosen to closely match typical experimental conditions (31). To quantify the variance of the effective rate estimates, we apply our method to 10 different sets of these simulations and present the average and standard deviation of the 10 sets of predicted rates. Using simulations from the reaction rates listed in Table 1, the predicted values compare well against the “true” values used to generate the synthetic data (see Table 1). The robustness of the prediction was further tested by creating synthetic data using different values of g, $g^{\text{∗}}$, and r, and similar accuracies were produced. In addition, the inference scheme was applied to an alternate model of positive feedback—different from Eq. 1—to generate the synthetic data, and again, the inferred rates matched well with input values (see Supporting Material for details). However, it is important to realize that Eq. 4 is only an approximation to infer the intrinsic production and degradation rates. Thus, it is possible to have deviations between the inferred and true rates—higher than the ones reported in Table 1—whereas MaxCal captures the temporal statistics well (e.g., fluctuations in the high/low states and transitions between states).

Table 1.

Comparison of True Rates and Predicted Rates Using MaxCal

	True Values	Predicted Values
$g\left({\text{s}}^{-1}\right)$	$5.0\times {10}^{-3}$	$5.8\pm 0.3\times {10}^{-3}$
$g^{\text{∗}}\left({\text{s}}^{-1}\right)$	$50.0\times {10}^{-3}$	$43.0\pm 2.2\times {10}^{-3}$
$r\left({\text{s}}^{-1}\right)$	$1.0\times {10}^{-3}$	$0.95\pm 0.05\times {10}^{-3}$
${\tau }_{L\to H}$ (s)	$71.5\times {10}^3$	$99.0\pm 11.5\times {10}^3$
${\tau }_{H\to L}$ (s)	$86.0\times {10}^3$	$117.6\pm 12.9\times {10}^3$
$S_{\text{I}}$ (bits)	8.84	9.24 ± 0.03
$S_{\text{h}}$ (bits)	9.42	9.07 ± 0.02
$S_{\text{l}}$ (bits)	6.20	7.66 ± 0.04
$S_{\text{cg}}$ (bits)	1.03	1.02 ± 0.01

The first column reports the “true” underlying protein synthesis and degradation rates used to create synthetic input data ($f_{\text{d}}=5.0\times {10}^{-3}{\text{s}}^{-1}$, $b_{\text{d}}=50{\text{s}}^{-1}$, $f_{\text{p}}=6.0\times {10}^{-3}{\text{s}}^{-1}$, $b_{\text{p}}=3.0\times {10}^{-5}{\text{s}}^{-1}$), average residence times in the high and low states, and corresponding path informational entropies. Synthetic input data were recorded at $\Delta t=300\text{s}$. The second column reports the average and standard deviation of the same quantities of interest, but extracted using the MaxCal model on 10 sets of synthetic data, each consisting of 100 trajectories of 7 days.

Distributions predicted from MaxCal agree well with data

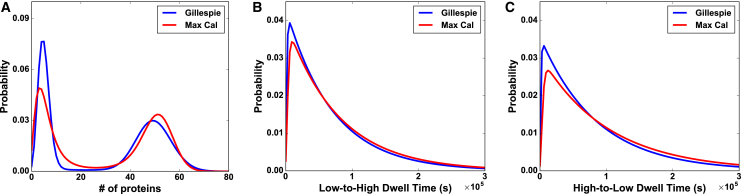
For a more detailed demonstration of how well MaxCal describes data, we further compared MaxCal-predicted distributions to that of the input data (generated from the reaction network in Eq. 1). Fig. 2 A shows that the protein number distribution predicted from MaxCal agrees well with the input data in that the locations and widths of the two peaks are comparable between the two approaches. Next, we compare the distribution of dwell times predicted by MaxCal to that obtained from the synthetic data. The agreement for the shape of the distribution and the average dwell times in the low and high states (see Fig. 2, B and C; Table 1) are reasonable.

Figure 2.

Predicted distributions agree well with the “true” distributions. (A) Protein-number probability distributions from synthetic input trajectories (blue) and predicted MaxCal trajectories (red). (B) Low-state and (C) high-state residence time probability distributions for synthetic input trajectories (blue) and predicted MaxCal trajectories (red). The underlying Gillespie reaction rates are the same as those used in Table 1 and the extracted MaxCal parameters used are a representative example from the 10 sets extracted to make Table 1. To see this figure in color, go online.

The comparisons between “true” and predicted values for multiple observables show that the minimal model of MaxCal with only four parameters can make reasonable predictions for data generated with more complex models (with seven parameters). To further quantify the quality of the parameter extraction and performance of our minimal model against those of the actual model with more parameters, we compare the informational content in the “synthetic” Gillespie trajectories and trajectories generated by MaxCal using these parameters. We compute path informational entropy as (78)

$$S_I=-\sum _{i,j}{P}_i{P}_{i\to j}{\text{log}}_2\left(P_i{P}_{i\to j}\right),$$ (11)

where $P_i$ is the probability of having i proteins in the system and $P_{i\to j}$ is the probability of transitioning from i proteins to j proteins after a single frame. If our MaxCal model is too simple and cannot adequately capture the dynamics of the Gillespie trajectories used, its $S_I$ will be notably different from that of the Gillespie model. We find that the MaxCal model selected by ML has only a 4.5% difference in path informational entropy compared to the “synthetic” input data from Gillespie simulations (see Table 1). This provides quantitative verification that the minimal constraints used in Eq. 2 are sufficient to describe the auto-activating circuit modeled here. The overall path entropy has contributions from three types of fluctuations: 1) within the high state, 2) within the low state, and 3) transitions between the high and low states. To further explore how MaxCal-generated path entropy captures details of these fluctuations, we compute three additional path entropies: $S_{\text{h}}$, $S_{\text{l}}$, and $S_{\text{cg}}$. $S_{\text{h}}$ and $S_{\text{l}}$ are computed in the same fashion as $S_I$, but only consider parts of the trajectory in the high state and low state respectively (see Supporting Material for high/low state assignment). To measure $S_{\text{cg}}$, the trajectory is first coarse-grained into a binary trajectory between the low state $\left(N_{cg}=0\right)$ and the high state $\left(N_{cg}=1\right)$. $S_{\text{cg}}$ is then calculated in the same manner as Eq. 11. We find that MaxCal generated estimates of $S_{\text{h}}$ and $S_{\text{cg}}$ are in excellent agreement with the input data, whereas $S_{\text{l}}$ differs by ∼24% from the input (see Table 1). The analysis above provides a quantitative measure of performance for MaxCal with a given set of constraints. These measures can be further used to determine the need for incorporating higher-order combinations of the state variables to the caliber function (Eq. 2; e.g., $\langle {\ell }_{\alpha }{\ell }_A^2\rangle$, $\langle {\ell }_{\alpha }^2{\ell }_A\rangle$, etc.) to develop models of higher complexity (51).

MaxCal provides an effective feedback parameter for the circuit

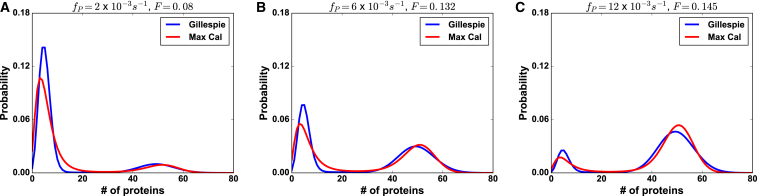
We also extract the effective feedback parameter, F, using Eq. 5. As a demonstration of its usefulness, if we compared the MaxCal parameters extracted from experimental traces with varying concentrations of inducer (31), the effective production and degradation rates might be similar, but F would be expected to vary with different amounts of inducer, representing the degree of coupling between the production of A and the concentration of A. To mimic the effect of varying inducer concentrations, we generated synthetic data with higher or lower promoter binding rates, $f_{\text{p}}$, to effectively increase or decrease the amount of self promotion in the system. Next, we applied our MaxCal framework to these trajectories with different levels of self-promotion. Fig. 3, A–C, shows that MaxCal reproduces comparable protein number distributions regardless of the degree of self-promotion. Table 2 further demonstrates that although MaxCal infers very similar production and degradation rates between the three levels of self-promotion, the effective feedback, F, changes accordingly.

Figure 3.

MaxCal can capture distributions under varying degrees of feedback. Protein-number probability distributions from synthetic input trajectories (blue) and predicted MaxCal trajectories (red) for different levels of self-promotion, specifically (A) $f_{\text{P}}=2\times {10}^{-3}{\text{s}}^{-1}$, (B) $f_{\text{P}}=6\times {10}^{-3}{\text{s}}^{-1}$, and (C) $f_{\text{P}}=12\times {10}^{-3}{\text{s}}^{-1}$. The underlying Gillespie reaction rates are the same as those used in Table 2 and the extracted MaxCal parameters used are a representative example from the 10 sets extracted to make Table 2. To see this figure in color, go online.

Table 2.

Comparison of Feedback Parameter Using Different Promoter Binding Rates

$f_{\text{p}}$	Extracted g	Extracted $g^{\text{∗}}$	Extracted r	F
$2.0\times {10}^{-3}{\text{s}}^{-1}$	$4.3\pm 0.3\times {10}^{-3}{\text{s}}^{-1}$	$34.9\pm 2.5\times {10}^{-3}{\text{s}}^{-1}$	$0.81\pm 0.06\times {10}^{-3}{\text{s}}^{-1}$	$0.080\pm 0.006$
$6.0\times {10}^{-3}{\text{s}}^{-1}$	$5.8\pm 0.3\times {10}^{-3}{\text{s}}^{-1}$	$43.0\pm 2.2\times {10}^{-3}{\text{s}}^{-1}$	$0.95\pm 0.05\times {10}^{-3}{\text{s}}^{-1}$	$0.132\pm 0.005$
$12.0\times {10}^{-3}{\text{s}}^{-1}$	$5.7\pm 0.4\times {10}^{-3}{\text{s}}^{-1}$	$38.8\pm 2.9\times {10}^{-3}{\text{s}}^{-1}$	$0.80\pm 0.06\times {10}^{-3}{\text{s}}^{-1}$	$0.145\pm 0.006$

Each row reports the average and SD of the extracted production and degradation rates as well as the effective feedback, F, for different values of $f_{\text{p}}$. Similar to Fig. 2, for all three cases, $g=5.0\times {10}^{-3}{\text{s}}^{-1}$, $g^{\text{∗}}=50.0\times {10}^{-3}{\text{s}}^{-1}$, $r=1.0\times {10}^{-3}{\text{s}}^{-1}$, $f_{\text{d}}=5.0\times {10}^{-3}{\text{s}}^{-1}$, $b_{\text{d}}=50{\text{s}}^{-1}$, $b_{\text{p}}=3.0\times {10}^{-5}{\text{s}}^{-1}$, and 10 sets of synthetic data, each equivalent to 100 trajectories of 7 days, were used to extract predicted values and standard deviations.

Estimating the effective feedback parameter can be important, as it determines the onset of bimodality from unimodality as well as the relative population in the high and low states. Bimodal protein distributions and stochastic switching between the two states often dictate phenotypic variability, a characteristic of bet-hedging strategies used by microbes to evade stress such as antibiotic (31, 79, 80). Consequently, different strains that have evolved under different selection pressures may differentially tune their level of feedback (81). Similarly, it may be interesting to see whether strains using “resistance” or “tolerance” mechanisms to evade antibiotics (82) evolve their feedback parameters differently. Applying MaxCal on experimental trajectories of different strains evolved under different conditions to infer these feedback parameters can give us further insights into evolvability and selection. Similarly, this metric can be useful when describing circuits with negative feedback as well.

The ability to extract an effective feedback parameter is a special feature of MaxCal that provides a coarse-grained description of feedback. This is in contrast to traditional parameterization schemes that invoke auxiliary species and multiple reactions involving many parameters to describe feedback. As a result, MaxCal can provide a model with fewer parameters compared to traditional bottom-up approaches. This is true even when describing circuits with multiple species beyond the single-gene expression circuit used in this study (35, 55). The success of MaxCal presented here motivates the need for future studies on synthetic data generated using more intermediate steps, such as RNA synthesis before protein synthesis. Further research must also be performed on circuits involving more species that mutually regulate each other, possibly leading to oscillatory behaviors as in the repressilator circuit of Elowitz and Liebler (83). It is also important to note that MaxCal is exactly equivalent to the master equation when describing systems without feedback, e.g., biochemical cycles where states interconvert among themselves (52, 55, 84).

MaxCal can be applied when dealing with noisy fluorescence trajectories

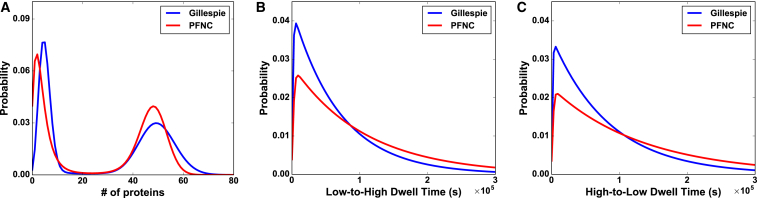
The results above illustrate the applicability of MaxCal when experimental trajectories are expressed in protein-number fluctuations. We now proceed to demonstrate the applicability of MaxCal when data are reported in noisy fluorescence trajectories instead of protein-number trajectories. We use both methodologies, SFNC and PFNC, as described earlier, to infer the underlying model from the noisy data. Fig. 4 and Table 3 show the performance of these strategies tested against “corrupted” synthetic data. SFNC, based on only the knowledge of average intensity per protein, performs well when the fluctuation in fluorescence per protein is sufficiently small compared to the average fluorescence (see Table 3). However, SFNC starts to deviate significantly from the “true” values when noise increases, e.g., noise is >100% of the average fluorescence. In fact, at these levels of noise, it becomes increasingly difficult to determine the unique ML function, and the corresponding values of rate parameters start to deviate largely from the true values. Considering this deficiency, SFNC should not be used for noise levels >100%. PFNC, on the other hand, does not suffer from any such issues. PFNC infers rates with reasonable accuracy even when noise is as high as 200% (see Table 3, bottom rows). The success of PFNC is further demonstrated by comparing “true” and predicted distributions of protein numbers and dwell times (see Fig. 4) at this level of noise. PFNC performs better than SFNC due to the incorporation of fluorescence fluctuation within its ML procedure. Although the above results were extracted from data using a Gaussian fluorescence distribution, we carried out similar exercises using a Γ distribution for the fluorescence per protein (63, 64), with similarly accurate results. This highlights the need for carrying out controlled photobleaching experiments to learn about the average as well as the noise in the fluorescence per protein to faithfully infer underlying dynamics. In summary, the exercise above demonstrates broad applicability of MaxCal, even when experimental data are not in protein number but in fluorescence with high fluctuation.

Figure 4.

Predicted distributions from fluorescence trajectories with 200% noise using PFNC. (A) Protein-number probability distributions from “true” synthetic input trajectories (blue) and MaxCal trajectories using PFNC inference strategy (red). Comparisons between “true” and PFNC are also shown for (B) low-state and (C) high-state residence time probability distributions. The underlying Gillespie reaction rates are the same as those used in Table 3 and the extracted MaxCal parameters are a representative example from the 10 sets extracted to make the last row of Table 3. To see this figure in color, go online.

Table 3.

Effective Rates from Fluorescence Trajectories

Noise	$g\left({\text{s}}^{-1}\right)$	$g^{\text{∗}}\left({\text{s}}^{-1}\right)$	$r\left({\text{s}}^{-1}\right)$	$\text{Method}$
True	$5.0\times {10}^{-3}$	$50.0\times {10}^{-3}$	$1.0\times {10}^{-3}$
0%	$5.8\pm 0.3\times {10}^{-3}$	$43.0\pm 2.2\times {10}^{-3}$	$0.95\pm 0.05\times {10}^{-3}$	MaxCal
50%	$6.1\pm 0.3\times {10}^{-3}$	$46.2\pm 2.6\times {10}^{-3}$	$1.03\pm 0.06\times {10}^{-3}$	SFNC
50%	$5.3\pm 0.3\times {10}^{-3}$	$41.5\pm 2.1\times {10}^{-3}$	$0.93\pm 0.05\times {10}^{-3}$	PFNC
100%	$6.8\pm 0.4\times {10}^{-3}$	$50.5\pm 2.7\times {10}^{-3}$	$1.08\pm 0.05\times {10}^{-3}$	SFNC
100%	$5.7\pm 0.3\times {10}^{-3}$	$48.0\pm 2.5\times {10}^{-3}$	$1.09\pm 0.06\times {10}^{-3}$	PFNC
150%	$6.1\pm 0.3\times {10}^{-3}$	$55.2\pm 3.5\times {10}^{-3}$	$1.26\pm 0.08\times {10}^{-3}$	PFNC
200%	$6.6\pm 0.3\times {10}^{-3}$	$63.3\pm 3.9\times {10}^{-3}$	$1.47\pm 0.08\times {10}^{-3}$	PFNC

The first row reports the “true” underlying protein synthesis and degradation rates used to create synthetic input data (same rates and conditions as in Table 1). The second row reports the average and standard deviation of MaxCal-inferred rates when trajectories are in protein number. Rows 3–8 report extracted rates for synthetically corrupted trajectories generated using different levels of noise in fluorescence per protein compared to the average (indicated in column 1) and different methods of extraction (SFNC and PFNC, as indicated in column 5).

Conclusions

We use the principle of maximum caliber (MaxCal)—akin to the principle of maximum entropy applied to describe path probabilities—to model protein-number fluctuations as observed in genetic circuits. We demonstrate the application of MaxCal in a positive feedback circuit, a common motif in many naturally occurring and synthetic circuits. Specifically, we consider a single-gene auto-activating circuit where a minimal model based on MaxCal was developed with three physical constraints: protein synthesis, protein degradation, and positive feedback. Through this analysis, we make four key conclusions. First, the minimal model is capable of producing the switch-like behavior of the circuit. Second, the model shows its usefulness to quantitatively infer underlying parameters. To mimic raw data from experiment, synthetic data were generated using a Gillespie algorithm with a known reaction network model to produce trajectories of fluctuating protein numbers. MaxCal correctly infers underlying rates when compared to the “known” values. Furthermore, MaxCal-predicted distributions agree well with the ones derived from the input data. Third, MaxCal provides an effective feedback parameter to characterize these circuits that can be useful for circuit design as well as analysis of differently evolved strains. Finally, we show how similar methods can be applied when the raw trajectory is in fluorescence rather than protein number, a typical attribute of experimental data. We demonstrate this by “corrupting” the same synthetic protein number trajectories with Gaussian fluctuation to create noisy fluorescence trajectories. In the regime of low fluorescence noise, the average fluorescence per protein can be used to convert traces back to protein number, followed by MaxCal to infer the model (SFNC). However, higher levels of noise require a more integrated approach (PFNC), where a model’s likelihood is calculated by combining both MaxCal-generated transition probabilities and fluorescence fluctuation. Using fluorescence-corrupted trajectories, we show that PFNC can infer underlying rates and distributions of observables even when the relative noise is fairly high. The method presented here demonstrates the potential application of MaxCal to broader problems in gene networks involving feedback, even when data are presented in fluorescence.

Author Contributions

T.F., G.B., and K.G. designed research. T.F. performed research. T.F. and K.G. analyzed data, and T.F., G.B., and K.G. wrote the article.

Editor: Nathalie Balaban.