Abstract
Background
Recent progress in electrophysiological and optical methods for neuronal recordings provides vast amounts of high-resolution data. In parallel, the development of computer technology has allowed simulation of ever-larger neuronal circuits. A challenge in taking advantage of these developments is the construction of single-cell and network models in a way that faithfully reproduces neuronal biophysics with subcellular level of details while keeping the simulation costs at an acceptable level.
New Method
In this work, we develop and apply an automated, stepwise method for fitting a neuron model to data with fine spatial resolution, such as that achievable with voltage sensitive dyes (VSDs) and Ca2+ imaging.
Result
We apply our method to simulated data from layer 5 pyramidal cells (L5PCs) and construct a model with reduced neuronal morphology. We connect the reduced-morphology neurons into a network and validate against simulated data from a high-resolution L5PC network model.
Comparison with Existing Methods
Our approach combines features from several previously applied model-fitting strategies. The reduced-morphology neuron model obtained using our approach reliably reproduces the membrane-potential dynamics across the dendrites as predicted by the full-morphology model.
Conclusions
The network models produced using our method are cost-efficient and predict that interconnected L5PCs are able to amplify delta-range oscillatory inputs across a large range of network sizes and topologies, largely due to the medium afterhyperpolarization mediated by the Ca2+-activated SK current.
Keywords: multi-compartmental neuron models, biophysically detailed modeling, model fitting using imaging data, automated fitting methods, parameter peeling
1. Introduction
Automated methods for neuron model fitting have replaced the need for manual tuning of model parameters [1]. Due to the ease of their use, they could provide a solution for exploiting computational properties of single neurons and neural circuits [2]. Novel algorithms and strategies for automated neuron model fitting have been proposed [3, 4, 5, 6, 7, 8, 9]. These methods span a wide range of types of neurons and their electrophysiological characteristics. Many of these strategies only use voltage traces recorded from the soma, while others rely on electrophysiological recordings at one or more additional dendritic locations in order to reproduce the correct membrane-potential dynamics distributed across the sub-cellular compartments. However, recording with multiple intracellular electrodes is an experimentally demanding procedure ultimately limited by the number of micromanipulators that can fit in a setup, the experimenter’s skills, and integrity of the cell in the presence of multiple recording electrodes [10]. By contrast, recent developments of optical imaging technologies and engineering of novel voltage-sensitive dyes (VSDs) and Ca2+ indicators have enabled high-resolution sampling of transmembrane voltage and intracellular Ca2+ concentration in single neurons with sub-cellular resolution [11, 12, 12, 13, 14, 15, 16]. In this work, we develop an automated, stepwise procedure for fitting a multicompartmental neuron model to data from somatic patch-clamp recordings in combination with VSD and Ca2+-imaging data.
Interactions between synaptic inputs to the dendrites and firing of the soma are a hallmark of neural computation [17]. This is especially true for L5PCs, which are characterized by a long apical dendrite that spans across cortical layers and receives inputs from various neuron populations in different parts of the dendritic tree [18]. The apical dendrite is rich in voltage-gated Ca2+ channels that contribute to the generation of a dendritic Ca2+ spike [19]. This Ca2+ spike plays an important role in integration of synaptic inputs to the apical tuft, communication of these signals to the soma, and coincidence detection in the form of the back-propagating action potential-activated Ca2+ spike (BAC) firing [18]. L5PCs express many types of voltage-gated ion channels [20, 21, 22], and a number of computational models have been developed accounting for these biophysical properties [3, 7, 23, 24, 25, 26, 27]. The multitude of types of voltage-gated ion channels, however, represents a challenge for modeling of the membrane-potential dynamics: unless specific care is taken, the role of a specific ion-channel species may be assigned to another ion-channel species when both conductances are fitted simultaneously, i.e., constrained by the same objective functions [28]. To tackle this problem, in [25], a parameter peeling experimental procedure was introduced, in which specific types of ion channels in L5PC are blocked sequentially using drugs, and the neuron response to different stimuli are recorded at each stage. The ion-channel conductances are then fitted step-by-step to these data. Another strategy was explored in [7], where experimental data from L5PCs with and without apical dendrite (occluded using a “pinching” method [29]) were used during one of the three stages of fitting. In this case, the data for different stages of fitting were obtained from separate experiments. Both techniques facilitate the optimization procedure by reducing the number of free parameters that are fitted simultaneously.
Reduced-morphology models may be crucial in simulations of large networks due to the lighter computational load they impose. While the level of detail in the morphologies obtained from 3D reconstructions is high, the electrophysiological properties of the distal dendritic segments, as well as the heterogeneity of ion-channel populations between different dendritic branches, remain elusive [30] and are generally not taken into account in the models. However, in many neuron types, dendritic electrophysiological properties vary monotonically with the distance from the soma [31], which favors the use of simplified (yet multi-compartmental) morphologies. These simplified models should reproduce the experimentally observed properties of communication between perisomatic and (proximal to mid-distal) dendritic sections of the considered neuron while reducing the computational load in comparison to full-morphology models.
In this work, we use the experimentally validated model introduced in [26] (“Hay model”) to generate simulated VSD and Ca2+-imaging data as well as simulated electrophysiological recordings in a L5PC. We simulate the parameter peeling procedure by sequentially setting channel conductances of different ion-channel species to zero in the Hay model and measuring the neuron responses to different stimuli under these blockades. We then fit the channel conductances in a four-compartment model to reproduce these data. We propose and apply a four-step scheme, where the three first steps utilize information on voltage and intracellular Ca2+ concentrations along the dendrites with high spatial resolution. The first step fits the parameters of reduced morphology, in a similar fashion as in [7], and parameters controlling passive membrane properties. The second step fits the non-specific ion-channel conductances. These are important for correctly describing the distal dendritic excitability. The third step fits the Ca2+ channel conductances and SK channel conductances and the parameters describing Ca2+ dynamics. The fourth step fits the rest of the active conductances, including the conductances responsible for the spiking behavior. We show that the obtained reduced-morphology L5PC model is cost-efficient and faithfully reproduces the membrane dynamics and spiking behavior, including the BAC firing. Furthermore, we test our method for fitting a neuron model with a full, reconstructed morphology, and find that acceptable fitting results are obtained also when using this complex dendritic morphology.
The obtained reduced-morphology model is especially useful in network simulations due to its lighter requirements of random access memory and computation time. We validated our model by introducing it in a biophysically detailed L5PC microcircuit model [32], which originally included the full-morphology Hay model neurons, and showing that the two models yielded similar network dynamics. Our circuit model of reduced-morphology L5PCs predicts that interconnected L5PCs amplify certain delta-range frequencies due to the large contributions of the Ca2+-activated K+ currents (SK currents) to the cell electrophysiology.
2. Materials and methods
2.1. The L5PC model
The Hay model of an L5PC, as well as the reduced-morphology model developed here, include the following ionic currents: fast inactivating Na+ current (INat), persistent Na+ current (INap), non-specific cation current (Ih), muscarinic K+ current (Im), slow inactivating K+ current (IKp), fast inactivating K+ current (IKt), fast non-inactivating K+ current (IKv3.1), high-voltage-activated Ca2+ current (ICaHV A), low-voltage-activated Ca2+ current (ICaLV A), small-conductance Ca2+-activated K+ current (ISK), and finally, the passive leak current (Ileak). The current balance equation of each segment of the neuronal membrane can thus be written as
where each current species, except for the axial current, is a product of activation and inactivation variables as
Here, ḡ is the maximal conductance of the ion channels, m and h are the activation and inactivation variables, Nm and Nh are constants describing the gating mechanisms of the channel, and E is the reversal potential corresponding to the ionic species. Reversal potentials of Na+ and K+ are constants (ENa = 50mV, EK = −85 mV), while the reversal potential of Ca2+ is determined through the Nernst equation by the intracellular [Ca2+] (typically, values of ECa in the Hay model vary between 96 and 120 mV [33]). The axial current Iaxial is determined by the axial resistance and the voltage difference between the considered membrane segment and its neighbors. For details on the model equations, see [26].
The intracellular [Ca2+] obeys the following dynamics:
where ICaHV A and ICaLV A are the high and low-voltage activated Ca2+ currents entering the considered cell segment, γ represents the fraction of Ca2+ ions entering the cell that contribute to the intracellular [Ca2+], F the Faraday constant, d is the depth of the sub-membrane layer considered for calculation of concentration, cmin the resting intracellular [Ca2+], and τdecay is the decay time constant of the intracellular [Ca2+].
In this work, we run parameter-fitting tasks where we assume the ion-channel dynamics fixed, and only vary the parameters governing the maximal conductances, namely, gNat, gNap, gh, gm, gKp, gKt, gKv3.1, gCaHV A, gCaLV A, gSK, and gl, and parameters γ and τdecay that control the Ca2+ dynamics.
2.1.1. Synapse model
The model for synaptic currents, which are used in simulations including in vivo-like background synaptic firing, is adopted from [32]. Each excitatory synapse conducts AMPA- and NMDA-mediated currents, and each inhibitory synapse conducts GABAA-mediated currents. These are modeled as follows:
Here, wAMPA, wNMDA, and wGABA are synaptic weights, gGlu = 0.0004 μS is the baseline conductance of a single glutamatergic synapse and gGABA = 0.001 μS that of an inhibitory synapse. Variables BAMPA, AAMPA, BNMDA, ANMDA, BGABA, and AGABA are increased by a positive constant (chosen such that the peak conductance of the synaptic current after a long silent period would be gGlu or gGABA) at each time of synaptic activation, and otherwise decay towards zero, A faster than B, as follows:
| (1) |
Time constants for the different synaptic species are τA,AMPA = 0.2 ms, τB,AMPA = 1.7 ms, τA,NMDA = 0.29 ms, τB,NMDA = 43 ms, τA,GABA = 0.2 ms, and τB,GABA = 1.7 ms. Variable cMg2+ represents the Mg2+ block of the NMDA-activated channel, and its value is determined by the membrane potential [34]. Variables EGlu = 0 mV and EGABA = −80 mV are the reversal potentials of the glutamatergic and inhibitory synapse, respectively.
The background synapses are activated at Poisson-distributed activation times, while the intra-network synapses that are exclusively glutamatergic (when present) are activated immediately after a spike in the pre-synaptic neuron. The activations of the synapses follow a probabilistic rule [35] that allows the modeling of both short-term depression and facilitation. For details, see [32].
2.1.2. Model implementation
Throughout the work, the NEURON software [36] is used for simulating the L5PC. For single-cell simulations, the adaptive time-step integration method is used, while for the multi-neuron simulations, the fixed time step 0.025 ms is used. Our NEURON and Python scripts both for running the parameter fittings and simulating the fitted models are publicly available at https://senselab.med.yale.edu/ModelDB/showModel.cshtml?model=187474—in addition, the principal model for a single reduced-morphology L5PC is described using NeuroML-2 [37]. The NEURON scripts are based on the publicly available models published in [26] and [32]. When implementing the model of [32] using our reduced-morphology L5PCs, we updated the background synapse model as follows. We grouped the background synapses that were located in the same segment into one synapse group, where the individual synapses shared the variables A and B (see Equation 1) — only the activation times of each individual synapse were saved into the memory. This radically decreased the computational load imposed by solving the differential equations (Equation 1).
2.2. Stepwise fitting procedure
We present a flexible stepwise neuron model-fitting framework and apply it to fit a four-compartment model to simulated electrophysiology and imaging data from an L5PC. The fitted parameters are listed in Table 1. The parameter value ranges are taken from Table 2 in [26], with certain exceptions (see Supplementary material, Section S1). During each step, we use a Python implementation (published by the authors of [7]) of the non-dominated sorting genetic algorithm II (NSGA-II) [38] for the parameter optimization. The crossover and mutation parameters and the probability of mutation per parameter are kept fixed as ηc = 20, ηm = 20 and pm = 0.5. The three first fitting steps are performed using Nsamp=1000 samples and Ngen=20 generations, the fourth fitting step using Nsamp=2000 samples and Ngen=20 generations — these values were found adequate for obtaining an acceptable fit to the data, although no convergence to a local optimum is guaranteed. The capacity of the genetic algorithm is double the population size.
Table 1. The table of parameters used in each step and their boundaries and reference values.
The first column shows the step in which the parameter is fitted. The second column names the parameters, and the third and fourth column show the values used by the optimization algorithm as the lower and upper limits, respectively. The fifth column shows the corresponding values in the full model — note that in the full model, the apical dendritic tree is divided into two equally long sections, and in case the parameters vary spatially, the values shown are the minimum and maximum of the values across these sections. Conductances are given in S/cm2, lengths in μm, axial resistances in Ωcm, and capacitances in μF/cm2.
| Step | Parameter | Lower | Upper | Full model | |
|---|---|---|---|---|---|
| 1 | Lsoma | 11.58 | 46.34 | 23.17 | |
| 1 | Lbasal | 141.06 | 564.26 | 282.12 | |
| 1 | Lapic | 325.0 | 1300.0 | 650 | |
| 1 | Ltuft | 325.26 | 1301.06 | 650.53 | |
| 1 |
|
20 | 500 | 100 | |
| 1 |
|
10 | 1000 | 100 | |
| 1 |
|
10 | 1000 | 100 | |
| 1 |
|
10 | 1000 | 100 | |
| 1 |
|
0.5 | 2.0 | 1.0 | |
| 1 |
|
0.5 | 4.0 | 2.0 | |
| 1 |
|
0.5 | 4.0 | 2.0 | |
| 1 |
|
0.5 | 4.0 | 2.0 | |
| 1 |
|
2×10−5 | 0.0001 | 3.38×10−5 | |
| 1 |
|
1.5×10−5 | 0.0001 | 4.67×10−5 | |
| 1 |
|
1.5×10−5 | 0.0001 | 5.89×10−5 | |
| 1 |
|
1.5×10−5 | 0.0001 | 5.89×10−5 | |
|
| |||||
| 2 | Eh | −55 | −35 | −45 | |
| 2 |
|
0 | 0.0008 | 1.29×10−6 | |
| 2 |
|
0 | 0.0008 | 1.30×10−6 – 1.71×10−6 | |
| 2 |
|
0 | 0.008 | 1.78×10−6 – 0.000127 | |
| 2 |
|
2×10−5 | 0.0001 | 3.38×10−5 | |
| 2 |
|
1.5×10−5 | 0.0001 | 4.67×10−5 | |
| 2 |
|
1.5×10−5 | 0.0001 | 5.89×10−5 | |
| 2 |
|
1.5×10−5 | 0.0001 | 5.89×10−5 | |
|
| |||||
| 3 |
|
0 | 0.001 | 3.66×10−10 | |
| 3 |
|
0 | 0.0025 | 5.55×10−5 | |
| 3 |
|
0 | 0.025 | 5.55×10−5 – 0.000555 | |
| 3 |
|
0 | 0.01 | 3.86×10−8 | |
| 3 |
|
0 | 0.1 | 0.000187 | |
| 3 |
|
0 | 1.0 | 0.000187 – 0.0187 | |
| 3 | γsoma | 0.0005 | 0.05 | 0.000501 | |
| 3 | γapic | 0.0005 | 0.05 | 0.000509 | |
| 3 | γtuft | 0.0005 | 0.05 | 0.000509 | |
| 3 | τdecaysoma | 20.0 | 1000.0 | 460.0 | |
| 3 | τdecayapic | 20.0 | 200.0 | 122.0 | |
| 3 | τdecaytuft | 20.0 | 200.0 | 122.0 | |
| 3 |
|
0 | 0.1 | 4.18×10−5 | |
| 3 |
|
0 | 0.005 | 0.0012 | |
| 3 |
|
0 | 0.005 | 0.0012 | |
|
| |||||
| 4 |
|
0 | 4.0 | 2.04 | |
| 4 |
|
0 | 0.01 | 0.00172 | |
| 4 |
|
0 | 0.1 | 0.0812 | |
| 4 |
|
0 | 1.0 | 0.00223 | |
| 4 |
|
0 | 2.0 | 0.693 | |
| 4 |
|
0 | 0.0005 | 6.75×10−5 | |
| 4 |
|
0 | 0.02 | 0.0213 | |
| 4 |
|
0 | 0.02 | 0.000261 | |
| 4 |
|
0 | 0.0005 | 6.75×10−5 | |
| 4 |
|
0 | 0.02 | 0.0213 | |
| 4 |
|
0 | 0.02 | 0.000261 | |
The objectives are given in Table 2 — see Section 2.2.5 for details of the used objective functions. During each step, the parameters that were optimized during the previous steps are kept fixed, while the parameters that will be optimized in the following steps are set to zero (simulating a perfect blockade of the corresponding ion channels).
Table 2. Objective functions used in each step.
The first column names the objectives such that the number left of the dot indicates the step and the number right of the dot indicates the objective number. The second column describes the type of objective function, the third column indicates the site of recording in the neuron, and the fourth column describes the type of stimulus used. The fifth column refers to the equation corresponding to the type of objective function (see Section 2.2.5). The sixth column lists the amplitudes of the stimuli: each value represents an individual run where only the shown stimulus with the shown amplitude is applied to the neuron, except for objective 4.3, where a combination of two stimuli with a 5 ms inter-stimulus interval is applied.
| Objective number | Objective function | Where measured | Stimulus type | Eq. | Stimulus amplitude |
|---|---|---|---|---|---|
| 1.1 | Difference in distribution of steady-state membrane potential | Dendrites | 3000-ms DC pulse at soma | (5) | 0.5 nA |
| 1.2 | Difference in distribution of peak membrane potential | Dendrites | EPSP-like current injection at the apical dendrite 620 μm from soma | (5) | 0.5 nA |
| 1.3 | Difference in membrane potential time series | Soma | 100-ms DC pulse at soma | (2) | −1.0 nA 0.0 nA 1.0 nA |
| 2.1 | Difference in distribution of steady-state membrane potential | Dendrites | 3000-ms DC pulse at soma | (5) | 0 nA 0.5 nA 1.0 nA |
| 2.2 | Difference in membrane potential time series | Soma | 100ms DC pulse at soma | (2) | 0.5 nA 1.0 nA |
| 3.1 | Difference in membrane potential time series | Soma | 100ms DC pulse at soma | (2) | 1.0 nA 2.0 nA |
| 3.2 | Difference in distribution of steady-state membrane potentials | Dendrites | 3000-ms DC pulse at soma (5) | 0.5 | nA 1.0 nA |
| 3.3 | Difference in distribution of steady-state intracellular [Ca2+ ] | Apical dendrite | 3000-ms DC pulse at soma (5) | 0.5 | nA 1.0 nA |
| 3.4 | Difference in distribution of peak membrane potential | Dendrites | EPSP-like current injection at the apical dendrite 620 μm from soma | (5) | 0.5 nA 1.0 nA |
| 3.5 | Difference in distribution of peak intracellular [Ca2+ ] | Apical dendrite | EPSP-like current injection at the apical dendrite 620 μm from soma | (5) | 0.5 nA 1.0 nA |
| 4.1 | Difference in membrane potential time series and numbers of spikes | Soma | 100-ms DC pulse at soma | (4) | 0.25 nA 0.5 nA |
| 4.2 | Difference in membrane potential time series and numbers of spikes | Soma | 5-ms DC at soma | (4) | 1.9 nA |
| 4.3 | Difference in membrane potential time series and numbers of spikes | Soma | 5-ms DC at soma and EPSP-like current at apical dendrite | (4) | 1.9 nA (soma) + 0.5 nA (apical) |
| 4.4 | Difference in numbers of spikes | Soma | 3000-ms DC at soma | (3) | 0.78 nA 1.0 nA 1.9 nA |
2.2.1. First step: Morphology
We follow the procedure of the first fitting step as presented in [7], with certain changes. In [7], the leak conductances were set to fixed values both in the target model and in the reduced-morphology model under optimization. Here, we do not change the leak conductance in the target model but keep it fixed. However, similarly as in [7], we fit the leak conductances again in the second step. Thus, the output parameters of our first step can be interpreted as optimal lengths, axial resistances and membrane capacitances for which the considered objectives can be well met with some values the of leak conductances. In the Supplementary material, Section S7, we show that the method used in [7] produces valid fitting results in our framework as well, and in Section S9, we show that the first step can be combined with the second one when fitting a neuron model with reconstructed morphology.
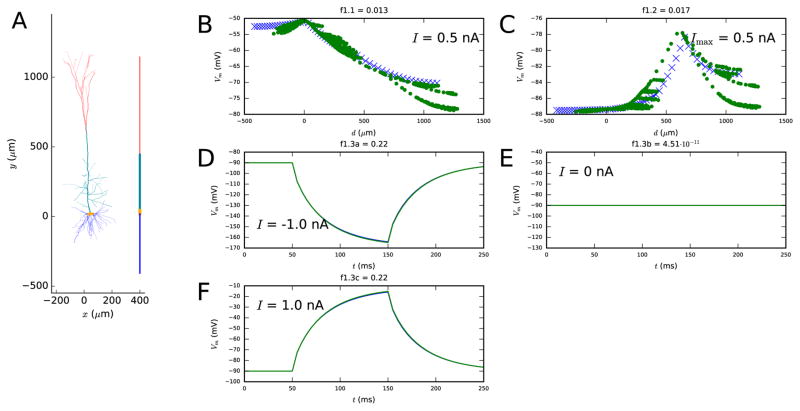
Following [7], we reset the diameters of each compartment during each iteration of the optimization algorithm such that the membrane area of the compartment is equal to the total membrane area of the corresponding segments of the full model. The objective functions are chosen such that the response of a reduced-morphology model neuron with optimal parameters to somatic and apical inputs is as similar as possible to the corresponding response in the full-morphology neuron. The accuracy of the model neuron response to somatic inputs is measured in terms of both somatic membrane-potential time series (objective 1.3) and dendritic steady-state voltage distribution (objective 1.1), while the accuracy of the response to apical inputs is measured only in the latter terms (objective 1.2).
2.2.2. Second step: Passive and “nearly passive” properties
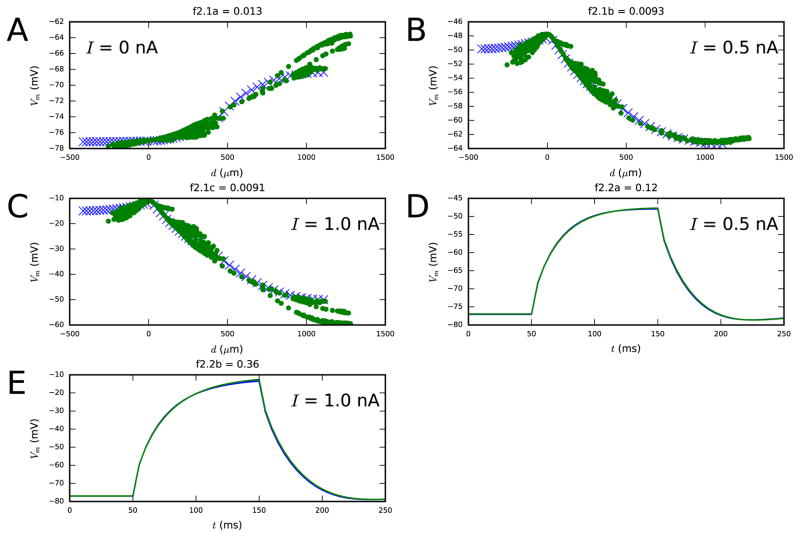
After fixing the morphological parameters (compartment lengths, axial resistances and membrane capacitances), we optimize the rest of the parameters that are major contributors to membrane response properties at rest. These are the leak conductances, non-specific ion-channel conductances (gh), and the reversal potential of the non-specific ion current (Eh). In the same way as in the first step, we set the objectives such that a neuron model with optimal parameter values would respond accurately to somatic input both in terms of membrane-potential time series (objective 2.1) and its steady-state distribution across dendrites (objective 2.2). We assume the leak reversal potential known (−90 mV), but if it is unknown, it should be fitted here as well.
2.2.3. Third step: Ca2+ dynamics and SK currents
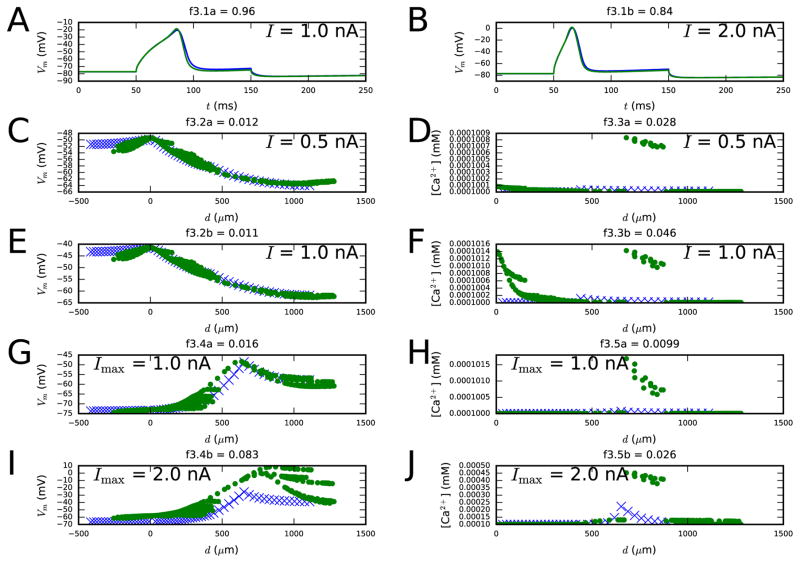
Once the passive properties and non-specific ion channel properties have been optimized, we search for the optimal parameters that govern Ca2+ currents, Ca2+ dynamics, and Ca2+-dependent K+ currents. These parameters are in the Hay model the following: high-voltage activated (HVA) and low-voltage activated (LVA) Ca2+ channel conductances (gCaHVA and gCaLVA), percentage of Ca2+ current inclusion into sub-membrane space (γ), time constant of decay of free Ca2+ (τdecay), and the SK channel conductance (gSK). It may be important that these parameters be fitted simultaneously, as the Ca2+ currents have a strong feedback effect on the membrane potential through the SK channels. For this reason, we use objective functions that promote both a correct membrane-potential response and an accurate [Ca2+] response to different stimuli. A good fit postulates that the steady-state membrane potential (objective 3.2) and Ca2+ concentration (objective 3.3) distributions across the dendrites, as a response to somatic DC, are similar to those in the target neuron, and that the maximal membrane potential (objective 3.4) and Ca2+ concentration (objective 3.5) responses to an EPSP-like current injection are accurate as well. The distribution of membrane potential is measured across the whole neuron, while the Ca2+ concentration only needs to be measured at the apical dendrite: as the signal propagation in the basal dendrites of an L5PC was nearly passive [39], the Hay model does not include Ca2+ channels in the basal dendritic compartments [26]. In addition, the membrane-potential time series at soma during a 100-ms DC pulse should be as close as possible to the one in the target neuron (objective 3.1). The correct temporal activation and deactivation of the Ca2+ and SK currents at the soma is a prerequisite for an accurate spiking behavior, especially regarding the medium afterhyperpolarization (AHP) period.
2.2.4. Fourth step: Correct spiking behavior
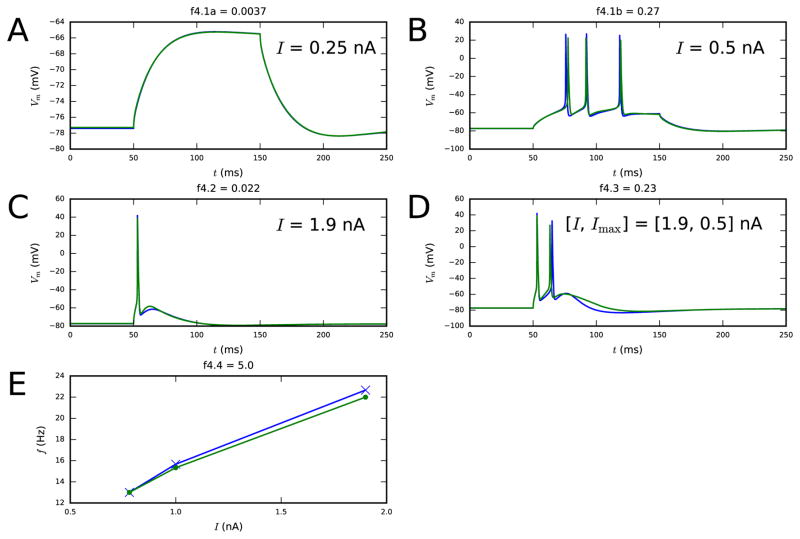
After fixing the parameters governing Ca2+ dynamics and SK currents, we optimize the rest of the parameters to make the model produce acceptable spiking behavior. We require that the f–I curve be close to that in the target neuron (objective 4.4), and that the somatic membrane-potential time series be similar to that in the target neuron, both when given somatic sub-threshold and supra-threshold DC (objective 4.1 and 4.2) and a combination of somatic and apical stimuli that induces BAC firing (objective 4.3). This step is computationally the most challenging one, both because of the cost of evaluating the f–I curves (albeit here done for only three values of current amplitude), and because of the large genetic population that is needed to secure that the objective functions be met closely enough. It might be advisable to divide this step further into two steps, where, e.g., first the slower ion-channel conductances (Im, IKp, INap) are optimized, and finally the conductances of the faster ones (IKt, INat, IKv3.1). This is left for future studies.
2.2.5. Distance metrics of the objective functions
The objective functions of Table 2 are designed to capture correct membrane-potential behavior across the spatial extent of the neuron. Certain objective functions only consider the quantities measured at soma (objectives 1.3, 2.2, 3.1, and 4.1–4.4). These objectives are further categorized to those that aim at capturing the correct time series (objectives 1.3, 2.2, 3.1, 4.1), those that only aim at capturing the correct numbers of spikes (objective 4.4), and those that aim at capturing both (objectives 4.2 and 4.3). The difference in time series is quantified using the L1 norm (mean absolute difference) between the target and candidate membrane potential (a function of parameters p) across a time window ranging from 50 ms before the start of the stimulus to 200 ms after the start of the stimulus:
| (2) |
The L1 norm is relatively less strict against differences in spike timings between the target and candidate data (but elaborates more the breadth of the time window in which differences in membrane potentials occur) than the L2 norm. The difference in f–I curves is quantified by the 2-norm, i.e.,
| (3) |
when no other measures are considered (objective 4.4). However, objectives 4.2 and 4.3 use a combination of spike number and timing data and the time course data — in these objectives all the differences are quantified using 1-norms:
| (4) |
We chose the coefficients as and , which means that an average difference of 12 mV is penalized as much as the summed distance of 20 ms between the spike timings, and furthermore as much as a difference of one spike in spike counts. These values gave the error function a desired empirical balance, such that voltage traces that looked (by eye) more different from the target data than others also received larger error values.
The rest of the objectives, namely, objectives 1.1–1.2, 2.1, and 3.2–3.5, concern quantities measured along the dendrites — both near to and far from soma. For these objectives, the membrane potentials V (either the steady-state membrane potential following a long stimulus as in objectives 1.1, 2.1, and 3.2, or maximal membrane potential during a pulse stimulus as in objectives 1.2 and 3.4) or Ca2+ concentrations c (objectives 3.3 and 3.5) are quantified across the spatial extent. This is done using either 20 (in simulations of reduced-morphology L5PCs when synaptic background inputs are not modeled) or 5 (in simulations of reconstructed-morphology L5PCs and reduced-morphology L5PCs with spontaneous synaptic inputs) recording sites per compartment. With four compartments in the reduced-morphology neuron and 193 in the full-morphology neuron, this implies that the total numbers of recording sites are (for objectives 1.1–3.5) and . For each recording site, a spatial coordinate d is determined by its distance from soma; negative values of d are assigned to recording sites along the basal dendrite and positive values along the apical dendrite. The difference of these 2-dimensional data, and is quantified as follows. First, we disregard the data corresponding to those recording sites at the reduced morphology that are further away from the soma than the farthest sites in the reconstructed morphology. In our work, this is done for recording sites for which d < −282 μm or d > 1301 μm (i.e. d outside the spatial extent of cell #1 in [26]). Second, we normalize the remaining data by the maximal range ( or ), and hence the resulting data are in ℝ2 plane, where the average distance of the reduced-morphology-neuron data from their nearest neighbor in the reconstructed-morphology-neuron data is used as the distance metric. In mathematical terms, we can thus write
| (5) |
where Nacc is the number of accepted data points, i.e., data points for which d(i) ≥ −282 μm and d(i) ≤ 1301 μm. Note that the limitation of the accepted data points allows neurons that are significantly longer to be created. However, as the diameters of the segments are restricted by the rule that conserves the total membrane area, neurons with too long dendrites end up having too thin diameters, which is likely to prevent a good fit to the data.
2.2.6. Combining the steps
As we use a genetic multi-objective optimization algorithm, at the end of each step we have a population of Pareto-efficient (see, e.g., [1]) parameter sets. We apply an exploratory scheme, where the best parameter sets of each objective and parameter sets that perform well in two separate objectives are handed on to the next step. In the interest of reducing the number of the parameter sets that are fixed during the early steps, we reduce the number of objective functions by grouping some of them together.
Firstly, most of the objectives of Table 2 consist of stimuli of different amplitudes (objectives 1.3–4.1 and 4.4). In these cases, the objective functions are defined as sums of the sub-objective functions. As an example, for objective 1.3, we have
where functions f1.3,I(p) are of the form of Equation 2.
Secondly, we further combine the objectives for correct membrane-potential distribution across the dendrites as a response to somatic DC and that as a response to EPSP-like stimulus. Namely, we group together objectives 1.1 and 1.2 as f1.1+1.2(p) = f1.1(p)+5f1.2(p), objectives 3.2 and 3.4 as f3.2+3.4(p) = f3.2(p)+f3.4(p), objectives 3.3 and 3.5 as f3.3+3.5(p) = f3.3(p)+f3.5(p), and objectives 4.2 and 4.3 as f4.2+4.3(p) = f4.2(p)+f4.3(p). The factor 5 is chosen for f1.2(p) due to the small effect of EPSP-like stimulus on dendritic peak membrane potentials when all active conductances are blocked compared to that of the somatic DC; in other objectives the effects are approximately of the same order of magnitude (data not shown).
Due to this grouping, the multi-objective optimization algorithm is given two objective functions for the first and second steps, and three for the third and fourth steps. In practice, this means that the first step optimization is performed once, and three candidate parameter sets are obtained — one that performs best in f1.1+1.2, one that performs best in f1.3, and one that performs well in both. When picking the parameter set that produces a good fit to two objective functions, we first normalize the error function values of both objectives by their medians (across the whole population of parameters at the end of the optimization) and then sum them together: the parameter set pi that produce the smallest value of the sum
| (6) |
is chosen. The second step optimization is then performed three times (once using each of these three parameter sets) and nine candidate parameter sets are obtained. The third step optimization is thus performed nine times, and each optimization gives six candidate parameter sets (one that performs best in f3.1, one that is best in f3.2+3.4, one that is best in f3.3+3.5, and three intermediate ones that perform well in two of the three objective functions), and therefore, the final step is performed for a maximum number of 54 parameter sets. Note that some of the optimizations performed during the first three steps may give parameter sets that do not produce a good fit to the data. In such cases, only the feasible parameter sets are handed over to the final fitting step.
2.3. Power spectra
We illustrate and quantify the possible oscillations in the neuronal network dynamics using the power spectra of the population spike trains. The power spectrum of a spike train , where variables tj represent the spike times, is determined as
where Fs(f) is the Fourier component for the frequency f. This component can be determined as
where i is the imaginary unit.
3. Results
3.1. Morphology parameters and ion-channel conductances for the reduced model can be fitted to the full model data
We applied the stepwise model-fitting procedure using simulated data (obtained from simulations of the Hay model with reconstructed morphology) as the target data for the objective functions. We used the multi-objective optimization algorithm developed in [38] to find the optimal parameter values, in a similar fashion as done in [7]. Figures 1, 2, 3, and 4 show the performance of the fitted model in fulfilling the objectives, and Table 3 lists the obtained parameter values.
Figure 1. First step fit.
A: The reconstructed and reduced (fitted) morphology. B–F: Illustration on how well the reduced model (blue crosses and curves) approximates the behavior of the full model (green dots and curves) with regard to the objective functions. The panel B (objective 1.1) shows the membrane-potential values at each recorded location after a 3-second somatic DC injection, and the panel C (objective 1.2) shows the maximal membrane-potential values during or after an EPSP-like current injection at the apical dendrite. This current is injected at a 620 μm distance from the soma, and it has a double-exponential pulse shape with rise time 0.5 ms and decay time 5 ms. The panels D–F (objective 1.3) show the somatic membrane-potential time series as a response to somatic 100-ms DC pulses with three different amplitudes: the blue and green curves are tightly overlapping. The spatial coordinate d in objectives 1.1 and 1.2 represents the distance (along the dendrites) from soma — negative values are given to locations at the basal dendrite and positive to locations at the apical dendrite. Colors available in the online version of the article.
Figure 2. Second step fit.
Panels A–C show the membrane-potential distribution along the dendrites both at rest and as a steady-state response to long, somatic DCs with amplitudes 0.5 and 1.0 nA (objective 2.1). Panels D–E show the membrane-potential time series response to 100-ms somatic DCs of two different amplitudes (objective 2.2). Blue: reduced-morphology neuron, green: full-morphology neuron. Colors available in the online version.
Figure 3. Third step fit.
Panels A–B show the membrane-potential time series as a response to 100-ms somatic DCs of two different amplitudes (objective 3.1). Panels C–F show the distributions of the steady-state membrane potentials (left) and Ca2+ concentrations (right) along the dendrites using long, somatic DC pulses with amplitudes 0.5 and 1.0 nA (objectives 3.2 and 3.3) as the stimulus. Panels G–J, in turn, show the distributions of the maximum membrane potential (left) and Ca2+ concentration (right) along the dendrites as a response to EPSP-like current injection (objectives 3.4 and 3.5). Blue: reduced-morphology neuron, green: full-morphology neuron. Colors available in the online version.
Figure 4. Fourth step fit.
Panels A–B show the membrane-potential time series as a response to 100-ms somatic DCs (objective 4.1), both sub-threshold (left) and supra-threshold (right). Panel C shows the membrane-potential time series as a response to a somatic DC (objective 4.2). Panel D shows the membrane-potential time series as a response to a combination of 5-ms somatic DC and EPSP-like apical current injection (objective 4.3). This combination of stimuli should induce BAC firing in the model L5PC, as happens with the Hay model [26]. Panel E shows the somatic f–I curves (objective 4.4). Blue: reduced-morphology neuron, green: full-morphology neuron. Colors available in the online version.
Table 3. Parameter values obtained from the multi-objective optimizations of Figures 1–4.
Note that the passive leak conductances are initially fitted at the first step, but refitted at the second step. Conductances are given in S/cm2, lengths in μm, axial resistances in Ωcm, and capacitances in μF/cm2. The first step parameter set was the one that minimized f1.3, while the second step parameter set minimized f2.1. The third step parameters minimized the sum of f3.2+3.4 and f3.3+3.5 and the fourth step parameters the sum of f4.2+4.3 and f4.4, where the function values were normalized by the medians of the corresponding functions across the genetic algorithm population (e.g., see Equation 6).
| STEP 1 | ||
|---|---|---|
| Variable | Value | |
|
| ||
| Lsoma | 24.5 | |
| Lbasal | 426 | |
| Lapic | 400 | |
| Ltuft | 702 | |
|
|
380 | |
|
|
197 | |
|
|
958 | |
|
|
224 | |
|
|
1.22 | |
|
|
1.94 | |
|
|
1.45 | |
|
|
2.6 | |
|
|
7.8.10−5 | |
|
|
2.56.10−5 | |
|
|
5.92.10−5 | |
|
|
6.75.10−5 | |
| STEP 2 | ||
|---|---|---|
| Variable | Value | |
|
| ||
| Eh | −40.7 | |
|
|
0.000279 | |
|
|
0.000294 | |
|
|
0 | |
|
|
0.00493 | |
|
|
4.37.10−5 | |
|
|
3.79.10−5 | |
|
|
5.29.10−5 | |
|
|
6.83.10−5 | |
| STEP 3 | ||
|---|---|---|
| Variable | Value | |
|
| ||
|
|
0.000838 | |
|
|
0 | |
|
|
0.000977 | |
|
|
0.00311 | |
|
|
0 | |
|
|
0.000487 | |
| γsoma | 0.0005 | |
| γapic | 0.0347 | |
| γtuft | 0.0005 | |
| τdecaysoma | 488 | |
| τdecayapic | 142 | |
| τdecaytuft | 95.4 | |
|
|
0.0479 | |
|
|
0.000231 | |
|
|
0.00365 | |
| STEP 4 | ||
|---|---|---|
| Variable | Value | |
|
| ||
|
|
2.41 | |
|
|
0.00206 | |
|
|
0.0239 | |
|
|
0.000176 | |
|
|
0.701 | |
|
|
0.000143 | |
|
|
0.0135 | |
|
|
0.00121 | |
|
|
0.000113 | |
|
|
0.0131 | |
|
|
0 | |
The reduced model shows a good fit to most of the measured quantities. However, the third step reveals that all aspects of the ion channel distributions cannot be accurately preserved in the four-compartment model: the responses of the full model were best reproduced by letting the Ca2+ channel conductances go to zero in the apical trunk, while keeping the corresponding values at the apical tuft relatively large. By contrast in the original model, the Ca2+ channel conductances were non-zero all along the apical dendrite, but had extremely large values at segments 685–885 μm away from the soma (in the “hot zone of Ca2+ channels”). Figure S1 (Supplementary material Section S2) shows that the error functions for the spatial distributions of membrane potential and Ca2+ concentration in the third step fitting could be decreased by including an extra compartment that represented the hot zone in the reduced-morphology neuron. Nevertheless, this would make the model a six-compartment model, as the furthest compartment would have to be divided to three compartments. Furthermore, in a recent study [27], the Ca2+ channels were better fitted by using linear increases Ca2+ channel densities than a Gaussian-shaped distribution with largest conductances around the main bifurcation point along the apical dendrite. Therefore, we applied the parameters obtained from the fitting of the four-compartment model (Figure 3) in the rest of this work.
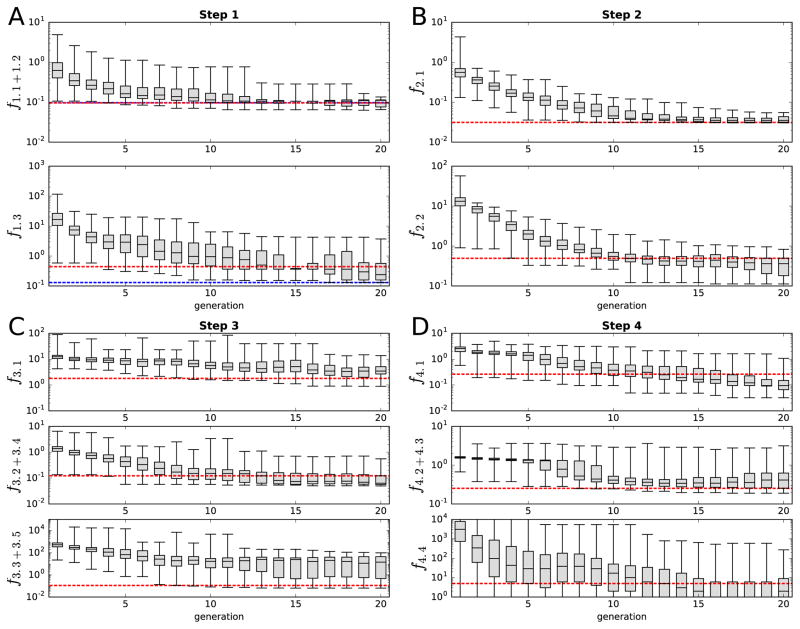
Figure 5 shows the evolution of the objective functions across the generations in all four steps of fitting: in most cases the values of the error function dramatically decreased during the first five to ten generations, after which only modest improvement was achieved. For the results shown in Figures 1–4, only the final parameter set was used, but to make sure the fitting procedure is robust, we repeated the final fitting step 10 times. All of these 10 samples showed the correct numbers of spikes in response to the stimuli of Figure 4B–D (data not shown).
Figure 5. The evolution of the minimum, lower quartile, median, upper quartile, and maximum of the objective function values.
Panels A–D show the steps 1–4, respectively, and the separate subpanels show the values of the objective functions separately. The red dashed lines represent the objective function values of the final parameter set (see Figures 1–4). The blue dashed lines in panel A show the objective function values of the optimal parameter set chosen after the first step: the passive conductances are reassigned for the red dashed line parameters during the second step, otherwise the parameters are the same. The values of the minimal errors that are outside the plotted range in panel D represent zero values (number of spikes exactly same as in the target data for all three DC amplitudes). Colors available in the online version.
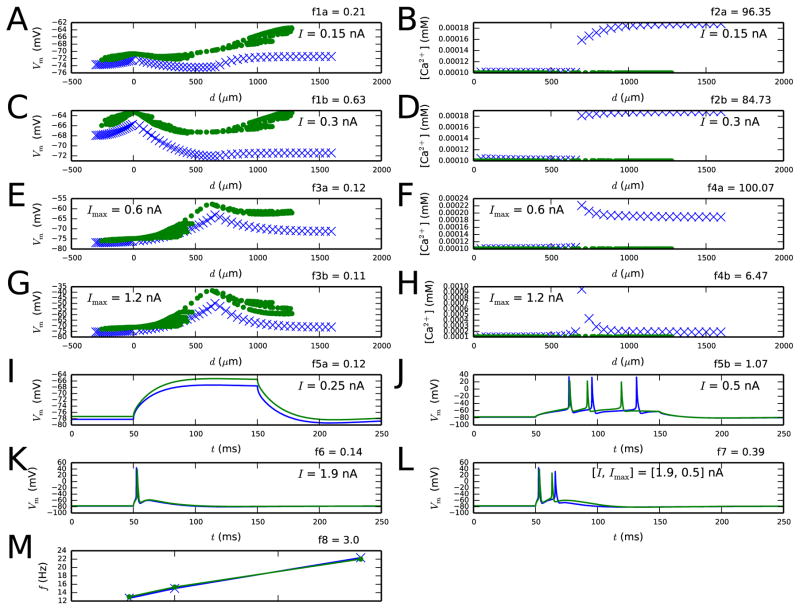
The stepwise approach gains advantage from the fact that the parameter search space is smaller than when all parameters are fitted at once. In Figure 6, we show that fitting all model parameters simultaneously (without simulation of ion channel blockades) did not produce as good fitting results as the stepwise method: out of ten trials, only one of the obtained parameter sets produced the correct number of spikes as response to the stimuli of objectives 4.1–4.3. This parameter set was characterized by relatively strong Ca2+ currents and very fast Ca2+ dynamics in the apical dendrite, but the SK currents, by contrast, were weaker (see Supplementary material, Section S3 for details). Although the numbers of spikes were correctly reproduced in Figure 6I–L, the spike timing in the BAC firing experiment (panel L) was not as accurate as in Figure 4. Furthermore, the response to sub-threshold stimulus (Figure 6I) was less accurately predicted by this model than by the standard reduced model (see Figure 4A). In the Supplementary material, Section S4, we show that qualitatively similar results were obtained using indicator-based evolutionary algorithm (IBEA) [40], which has been shown to outperform other multiobjective optimization methods in certain neuron model fitting tasks [41]. Out of fifteen trials, only one IBEA optimization succeeded in producing the correct number of spikes as response to the stimuli of objectives 4.1–4.3. The best solution is shown in Figure S2, and the underlying parameter values are listed in Table S4. Similarly to the abovementioned NSGA solution, this IBEA solution underestimated the somatic SK conductances and showed a mismatch in membrane potential response to a sub-threshold stimulus.
Figure 6. Results from the experiment where all parameters model parameters were simultaneously fitted.
A population of Nsamp=2000 samples was iterated for Ngen=20–29 generations. The optimization was repeated ten times, and the best fit is shown here. See Table S2 for the objective functions and Table S3 for the parameter values.
To further show the flexibility of our method, we present alternative fitting results in the Supplementary material. In Section S5 and Figures S7–S10, we show that our fitting method worked well also when noisy measurements at dendritic locations are used. In these optimizations, the target VSD data were added a Gaussian white noise component up to 5-mV SD (the mean absolute error for this component is approximately 4 mV) and the Ca2+ concentration data were multiplied by a log-normal noise component with σ up to 0.2 (positive errors of this component are on average +177% while negative errors are on average −52%). We also assessed the effect of lower temporal resolution on the quality of the fit. When we reduced the temporal resolution of the dendritic VSD and Ca2+ concentration measurements to 200 and 20 Hz, respectively, the mean errors of the membrane potentials along the dendrites in the three first fitting steps were 0.03–0.09 mV and the relative errors of the Ca2+ concentration were 0.002–0.8%. If yet smaller resolutions of (100 Hz and 10 Hz) were used, the corresponding errors were on average 0.11–0.34 mV and 0.005–1.6%. These errors were small but systematic in the way that the magnitude of the response was always underestimated. In Section S6, we showed that errors stemming from using smaller temporal resolutions (100-Hz membrane-potential measurements and 10-Hz Ca2+ concentration measurements) do not have a significant effect on the fitting. Figure S11 shows the objective function values after the second step fit when either accurate or temporally downsampled (dendritic) target data were used, and Figures S12 and S13 show the swarms of parameter values and their relation to the objectives f2.1 and f2.2, respectively. The obtained parameter and objective function values obtained by fitting to downsampled data were indistinguishable from those obtained by fitting to accurate target data. Section S7 and Figures S14–S17, in turn, show that the fitting of leak conductance during both the first and second step was not necessary from the optimization point of view, as acceptable results could also be obtained by setting the leak conductances to a predetermined value in the first step (as done in [7]) and fitting them during the second step (obviously, this is not possible in fitting to experimental data as the leak conductances cannot be controlled by the experimenter).
We also confirmed that our method performs well when different rules of particle selection were applied, both within an optimization and between different steps of optimization. Firstly, we confirmed that our four-step method also works when IBEA-selection based optimization is used instead of the NSGA-II, as shown in Figures S3–S6. Secondly, Section S8 introduces an alternative stepwise fitting method where no particular best candidate from an earlier step was chosen. Instead, at the end of a fitting step, the whole population was passed on to the next step, where the earlier-step parameters of each particle were assigned a randomly chosen parameter set from this population (the fitted parameters were, however, drawn randomly from the uniform distribution as in the default method). Figures S18–S21 show that this approach gave a fair fit to the objective functions as well. This approach could be useful if there were more than four steps or much more objective functions than in those in Table 2, which would make the tree-like parameter optimization scheme (see Section 2.2.6) computationally heavy. This approach might, however, benefit from a more sophisticated rule for the crossover procedure in the genetic algorithm. In the scheme of Figures S18–S21, the parameters fitted during the earlier steps were picked in an all-or-none fashion from one of the two candidates in the crossovers, and only the parameters fitted during the performed step were applied to the NSGA crossover mechanism (see [38]). This prevented the parameters fitted during earlier steps to be mixed in a way that would abolish the fit to the objective functions of the earlier steps. This is an important requirement in the stepwise scheme, as the quality of the fit to the objective functions of the later steps need not correlate with that of the earlier steps.
Finally, we demonstrate that our step-wise method shows promise also when applied to reconstructed morphologies. We fitted the passive membrane properties and the ionic conductances along the dendritic tree (cell #2 in [26]) in three steps, see Supplementary material, Section S9 for details. The resulting model showed an acceptable fit to the target data, as shown in Figures S22–S24.
Both the four-compartment model of Figures 1–4 and the morphologically detailed model of Figures S22–S24 are models that reproduce the spiking properties and the spatial distribution of membrane potential dynamics in the (simulated) target data. While the morphologically detailed model provides better means for studying the integration of inputs from different parts of the dendritic tree, the four-compartment model is faster to simulate and hence more useful in large network simulations. Table 4 shows the reductions in simulation times attained by the use of reduced model, compared to the model of Figures S22–S24, on a standard personal computer. The reduced model was on average 7–27 times faster to simulate than the morphologically detailed model with variable numbers of segments (as in [26]), depending on the chosen number of segments in the reduced model (5–20 per compartment) and the choice of solving method. The speed-up factors obtained when both the morphologically detailed and the reduced-morphology model were simulated using the fixed time step method were close to the theoretical speed-up factor (27.13) estimated by comparing the numbers of differential equations solved in the two cases.
Table 4.
Speed-up factors attained by using the reduced-morphology models on a standard PC. The first column indicates the objective functions to which the simulation contributes (see Table 2), and the lower-case letter indicates the amplitude (‘a’ for smallest current, ‘c’ for largest) if more than one stimulus amplitudes were given. The second and third columns show the factors (mean ± SD, Nsamp = 5) by which the simulation times were shortened by the use of models with reduced morphology using 20 or 5 spatial segments per compartment, respectively, when variable time step method was used. The fourth column shows the corresponding factor (for reduced-morphology model with 5 spatial segments per compartment) when fixed time step method was used. In the reconstructed morphology (cell #2 of [26]), the default numbers of segments were used; these varied between 1 and 15 and summed up to 715. The numbers of differential equations solved were 5833 in the full model and 215 or 860 in the reduced-morphology model with 5 or 20 segments per compartment, respectively, giving theoretical speed-up-factor estimates 27.13 and 6.78. The data are grouped according to the steps to which the objective functions belong. All simulations were run with the NEURON software using a single central processing unit (CPU).
| Objective | 20 segments adaptive dt | 5 segments adaptive dt | 5 segments fixed dt |
|---|---|---|---|
| f1.1 | 6.9±0.5 | 23.8±3.7 | 27.7±0.7 |
| f1.2 | 7.8±1.1 | 28.0±3.7 | 27.7±0.6 |
| f1.3a | 6.3±0.8 | 22.9±3.1 | 27.6±0.7 |
| f1.3b | 8.0±1.0 | 27.9±4.1 | 27.7±0.6 |
| f1.3c | 6.7±0.8 | 24.0±3.5 | 27.6±0.7 |
| Objective | 20 segments adaptive dt | 5 segments adaptive dt | 5 segments fixed dt |
|---|---|---|---|
| f2.1a | 19.0±0.8 | 60.6±4.6 | 27.6±0.7 |
| f2.1b | 14.9±1.3 | 48.7±5.2 | 27.6±0.6 |
| f2.1c | 17.9±1.9 | 51.1±3.7 | 27.6±0.6 |
| f2.2a | 13.2±0.9 | 35.9±4.6 | 27.6±0.6 |
| f2.2b | 14.6±1.2 | 36.7±5.0 | 27.7±0.6 |
| Objective | 20 segments adaptive dt | 5 segments adaptive dt | 5 segments fixed dt |
|---|---|---|---|
| f3.1a | 4.6±0.4 | 15.5±2.9 | 27.6±0.6 |
| f3.1b | 4.6±0.4 | 16.5±2.7 | 27.5±0.7 |
| f3.2a | 5.6±0.5 | 20.1±2.5 | 27.5±0.7 |
| f3.2b | 5.3±0.6 | 17.8±1.8 | 27.2±0.7 |
| f3.3a | 5.1±0.4 | 17.5±2.0 | 27.3±0.7 |
| f3.3b | 5.9±0.5 | 21.4±3.0 | 27.3±0.7 |
| Objective | 20 segments adaptive dt | 5 segments adaptive dt | 5 segments fixed dt |
|---|---|---|---|
| f4.1a | 14.9±1.5 | 27.6±5.2 | 27.2±0.5 |
| f4.1b | 7.1±0.8 | 18.8±2.2 | 27.2±0.6 |
| f4.2 | 9.6±1.0 | 18.3±1.4 | 27.2±0.6 |
| f4.3 | 8.7±0.8 | 17.3±1.7 | 27.2±0.6 |
| f4.4a | 8.7±0.5 | 29.7±3.0 | 27.2±0.5 |
| f4.4b | 8.2±0.8 | 29.2±3.1 | 27.2±0.6 |
| f4.4c | 7.0±0.6 | 25.5±2.9 | 27.2±0.5 |
3.2. Validation of the reduced model without synaptic inputs
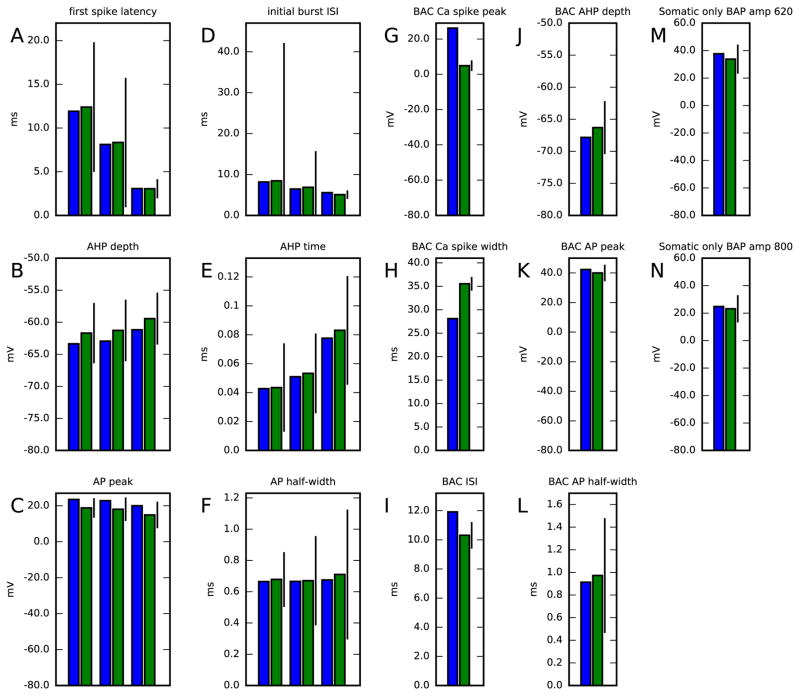
We validated the obtained reduced-morphology model by evaluating the quantities of the objective functions used in the construction of the original Hay model [26]. These objectives are different from ours in that they do not consider distribution of membrane potential across dendrites but mostly in soma (response to one of the somatic stimuli measured also in two locations along the apical dendrite, though), and many of the considered quantities include statistical features obtained from a sequence of spikes. The quantities used for validation are the following: first spike latency (A), initial burst inter-spike interval (D), fast AHP depth (B,J) and time (E), action potential peak (C,K) and half-width (F,L), Ca2+ spike peak (G) and width (H), inter-spike interval mean (I), and membrane-potential maximum at 620 (M) or 800 μm (N). Of these, quantities A–F concern firing induced by somatic DC of amplitudes 0.78, 1.0 and 1.9 nA, quantities G–L concern BAC firing induced by a combination of a somatic square pulse of duration 5 ms and amplitude 1.9 nA and an apical (at 620 μm) EPSP-like stimulus of rise time 0.5 ms, decay time 5 ms, and maximum amplitude of 0.5 nA, and quantities M–N concern the spatial decay of an action potential induced by a somatic square pulse of duration 5 ms and amplitude 1.9 nA. Figure 7 shows these quantities in both the reduced model (blue) and the original Hay model (green).
Figure 7. Reduced model validation against data from full model.
Panels A–F show the reduced (blue) and full (green) model cell responses to a somatic DC. The bar represents the SD in the corresponding experimentally measured quantities — note, however, that here the reduced model response is compared only against the full model response, not against the mean of the experimentally measured data (which were shown in Table 1 in [26]). The values shown correspond to three different simulations, where the DC amplitudes were 0.78, 1.0 and 1.9 nA. Panels G–L show the responses to stimuli that induce BAC firing, i.e., a combination of a square pulse of duration 5 ms and amplitude 1.9 nA and an EPSP-like stimulus at the apical dendrite, separated by a 5-ms delay (somatic stimulus is applied first). Panels M–N show the membrane-potential responses to a tonic, somatic stimulus-induced spike at distant apical dendrite. Colors available in the online version.
Except for two of these quantities, namely, the width and maximum membrane potential of a Ca2+ spike, all the differences between the quantities in the reduced model and original model were less than three times the experimentally observed SD (see Table 1 in [26]). The discrepancy in Ca2+ spike amplitude could already be anticipated in the simulations of the third step model, where Na+ and K+ channels, except for SK channel, were blocked. In these simulations, a strong EPSP-like stimulus caused 5 to 20 mV larger peak membrane potentials in the full model than in the reduced model along the first 700 μm of the apical dendrite, and even larger differences in the distal tuft (see Figure 3). In the simulations of the intact models, the difference in Ca2+ spike amplitude was of the same magnitude (20 mV), however, in the opposite direction: BAC firing caused the peak membrane potential to be higher in the reduced than in the full model, as shown in Figure 7. This switch is made possible by the contribution of Na+ channels to the BAC firing [26, 27]. Correcting this behavior might require a use of objective functions that more accurately restrict the spatial aspects of the neuron response also in the fourth step.
Both the model fitting and validation of Figure 7 were carried out by dividing each of the four compartments into nseg = 20 segments. Figure S25 (Supplementary material, Section S10) shows that the model validation results are acceptable even when each compartment was divided into nseg = 5 segments. Thus, in the following sections, we keep nseg = 5 in the interest of fast numerical integration.
3.3. Validation of the reduced model with network interactions
We implemented the obtained reduced-morphology L5PC model in a circuit model of L5PCs [32]. For model validation purposes, we compared the predictions of our reduced network model with the predictions of the full network model of [32]. Similarly to the procedure applied in [32], we randomly connected 150 L5PCs such that two neurons had a probability of 0.13 of being connected in a unidirectional manner and 0.06 of having a bidirectional connection [42]. Each intra-network connection was represented by a set of five synaptic contacts, randomly distributed along the dendrites. These synapses conducted AMPA and NMDA currents with the same characteristics as the background excitatory inputs (except that they were non-depressing and had a 25% release probability, while the background synapses had a 60% baseline release probability) and synapses between reciprocally connected L5PCs were 1.5 times stronger than others.
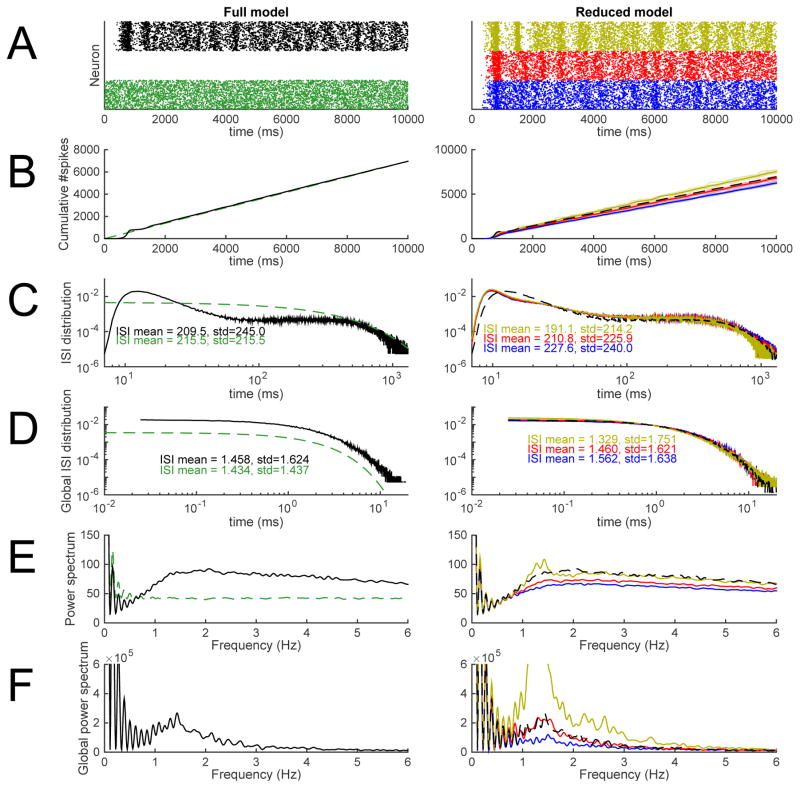
We performed 10-second network simulations for the model network with reduced-morphology neurons. The background synaptic conductances were up-scaled (AMPA, NMDA and GABA conductances all in proportion) such that a single reduced-morphology neuron produce the same spiking rate as a single full-morphology neuron — to achieve this, the conductances were increased by 11%. The intra-network synapses were up-scaled in a similar manner to make a network of reduced-morphology neurons have similar firing rate as the network of full-morphology neurons. Here we did not fix the up-scaling factor, but instead considered a range of values close to the optimal in order to see the effect of the scaling factor on other network properties than the firing rate. Figure 8 shows example population spike trains, cumulative firing-rate curves, inter-spike interval (ISI) distributions, and power spectra for both the full network model and the networks of reduced-morphology neurons where the intra-network synapses are up-scaled using three different factors (1.1, 1.25, and 1.4). The statistics from the reduced network models are very similar to those from the full network model. Differences arise in the shapes of the ISI distributions and the power spectra. The mean of the (single-cell) ISI distributions were almost equal between the full network and the reduced network with the intra-network synapse-scaling factor 1.25, but the standard deviation was larger in the former (see Figure 8C), indicating a slight underrepresentation of ISI values smaller and larger than mean in the reduced network in comparison to the full network (note that although the ISI probability distribution had larger values in the reduced network at very low values of ISIs, the peak at medium-low values of ISI was altogether thicker in the full network distribution). Consequently, the (single-cell) power spectrum of the reduced network had less power at low frequencies than the full network, except the reduced network with the intra-network synapse-scaling factor 1.4, which due to the increased spiking rate had an altogether elevated power spectrum. By contrast, the global ISI distribution and the global power spectra (where the spiking events were pooled across neurons) were very similar between the full and the reduced network with intra-network synapse-scaling factor 1.25.
Figure 8. The network consisting of model L5PCs with reduced morphology reproduced the main features of a network model with reconstructed-morphology neurons and dense background synaptic inputs.
The left-hand panels show predictions of the full network model [32], and the right-hand panels show the predictions of the network model with reduced-morphology neurons. Black: full network model. Green: Poisson process with λ fitted to reproduce the spiking frequency of the full network model. Blue, red, and yellow: reduced-morphology networks where the intra-network synapses are up-scaled to reproduce the spiking frequency of the full network (red, up-scaling factor 1.25), or produce slightly smaller (blue, up-scaling factor 1.1) or higher (yellow, up-scaling factor 1.4) spiking frequency. A: Population spike trains. B: Cumulative spike counts since the beginning of the simulations. C: Single-neuron inter-spike interval distributions. In the right-hand panel, the full network model ISI distribution is smoothened for large ISIs to remove jitter. D: Network inter-spike interval distributions, i.e., distribution of intervals in pooled spike trains. In the right-hand panel, the full network model ISI distribution is smoothened for large ISIs to remove jitter. E: Power spectra of single-neuron spike trains. F: Network power spectra, i.e., power spectra of pooled spike trains. The data of panels C–F are extracted from time moment t=1000 ms onward. Panel A shows only one sample population spike train, but the data of panels B–F are extracted from 30–100 independent samples (except for the ISI distributions of Poisson processes, which are theoretically determined). Colors available in the online version.
Both the network model with reduced-morphology neurons and the full network model are rather memory-consuming, but the reduced network model is computationally much less expensive than the original network model. The original network model was parallelized on 150 CPUs (running on a single CPU with up to 48GB of random access memory was impossible due to the need of even more memory), and a single simulation took 0.74±0.07 (mean ± SD) hours to finish. The network model with reduced-morphology neurons could be run both parallelized and on a single CPU: when parallelized on 150 CPUs, a network simulation took 0.066±0.001 hours (3.9 minutes, speed-up factor 11.3) to finish, while a single-CPU simulation took 2.3±0.41 hours (speed-up factor 47.6 when compared to the total simulation time of the parallelized runs) and required less than 7GB of memory.
3.4. Predictions of the reduced model
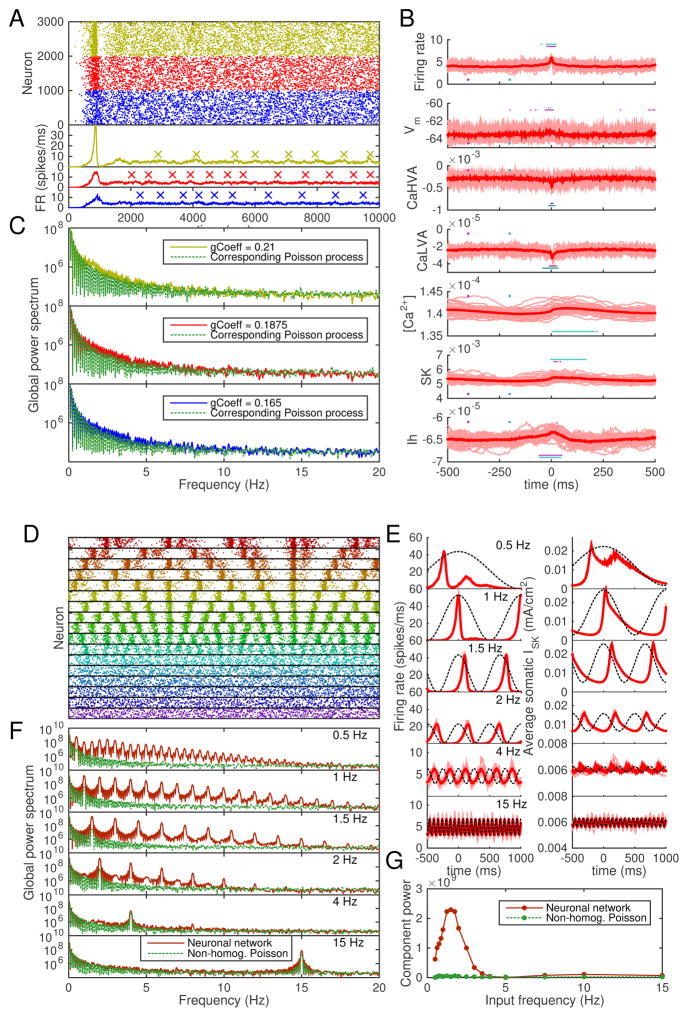
In the final part of our work, we studied the network response of interconnected L5PCs to oscillatory background input, which is an important function in in vivo cortical circuits. We implemented a 1000-neuron network of reduced-morphology L5PCs, using the same model parameters as in Figure 8, except for the intra-network synaptic weights, which were downscaled to counterbalance the increase in network size. Figure 9 shows example population spike trains, average SK current and intracellular Ca2+ concentration time series, and frequency spectra of the population spike trains in these networks and their relation to the frequency spectra of Poisson processes with corresponding event rates. In Figure 9A–C, the background synaptic inputs were stationary (no oscillations in inputs). In Figure 9D–G, the background synaptic input times follow a non-homogeneous Poisson process dynamics, where the average input rate term λ varies by ±25% in a sinusoidal curve with a given frequency.
Figure 9. The model predicts amplified L5PC network responses to delta-range oscillations.
A: Population spike trains of networks of 1000 neurons, each of which receives background synaptic inputs that obey homogeneous Poisson statistics. For clarity, only every fifth spike is plotted. Blue: predictions with synaptic weight 0.165, red: predictions with weight 0.1875, yellow: predictions with weight 0.21. Different random number seeds were used in the three network simulations. The lower subpanel shows the total firing rates of the networks, smoothened with a Gaussian with 3.5-millisecond SD. Local maxima of the firing-rate curves above the 90%-percentile of the data were detected for further use (see panel B). The peaks that were at a distance < 500 ms from other (higher) peaks were rejected — the accepted peaks are shown with crosses (‘×’). B: Intracellular and membrane properties at the somata of the neurons before and after the peaks in network firing rate (as detected in panel A). The x axis shows the time from 500 ms before the peak until 500 ms after the peak, and the y axis shows the values of the measured quantity. Panels from top to bottom: network firing rate (spikes/millisecond), membrane potential at soma (mV, averaged across the 1000 neurons), Ca2+ currents ICaHV A and ICaLV A (mA/cm2, measured at soma and averaged across neurons), intracellular [Ca2+] (mM, measured at soma and averaged across neurons), SK and HCN channel currents ISK and Ih (mA/cm2, measured at soma and averaged across neurons). The dim thin curves show peak-wise curves in single network samples (i.e., up to 20 curves obtained per network), and the red thick curve shows the mean across these peak-wise curves. The horizontal cyan and magenta bars show the time instants during which the medians of the data underlying the thin red curves are statistically different (U-test, p < 0.001, 64 samples) from the medians of the same data at time instants 200 ms and 400 ms before the firing-rate peak (marked with cyan and magenta dots). C: Power spectra of the population spike trains of panel A and corresponding Poisson processes. Only spikes from t = 2000 ms to t = 10000 ms considered, and the mean of five independent network simulations is shown. The Poisson processes were generated to have the same numbers of events during the considered interval as the compared network (sample-wise one-to-one correspondence). D: Population spike trains of networks of 1000 neurons, each of which receives background synaptic inputs that obey non-homogeneous Poisson statistics. In these non-homogeneous Poisson processes, λ varies ±25% from the baseline value of that used in panel A with a frequency (from top to bottom) 0.5, 0.625, 0.75, 0.875, 1.0, 1.25, 1.5, 1.75, 2.0, 2.5, 3.0, 3.5, 4.0, 5.0, 7.5, 10.0, or 15 Hz. For clarity, only every 40th spike is plotted. E: The firing-rate curves (left) and SK currents ISK (right) of the simulations of panel D. See panel B for details. Here, x axis shows the time from 500 ms before the peak of the oscillatory background inputs until 1000 ms after the peak. The phase of the background input oscillation is illustrated with the dashed line. Note that the y-axes are zoomed in for the two highest input frequencies. F: Power spectra of some of the population spike trains of panel D and the corresponding non-homogeneous Poisson processes. Means of five independent network simulations are shown. G: Power amplitude of the frequency component corresponding to the background input frequency, plotted against the background input frequency.
In Figure 9A and C, we can observe from the spike trains and frequency spectra that oscillations emerge in a similar fashion as in Figure 8. Figure 9B shows that the emergence of the oscillations is contributed by the delayed activation of SK currents (delayed with respect to the phase of the average firing rate). Figure S26 (Supplementary material, Section S11) shows that these oscillations disappear if the SK current — or the high-voltage-activated Ca2+ current ICaHV A that is a major contributor to the SK current — is blocked, as the neurons of the network enter a high-frequency firing state. Blockade of other currents have smaller effects, except for the blockade of transient Na+ currents, which fully inhibits the spiking behavior (data not shown).
Figure 9D shows example spike trains for networks receiving oscillatory inputs with different frequencies. Figure 9E shows for some of these frequencies the average firing-rate curves and SK currents before and after the peak background input. We can observe that for input frequencies 1–2 Hz, the delay between the firing-rate and SK-current peaks is small compared to the oscillation wavelength, while for 4 Hz, the SK currents are still active by the next peak background input, and hence the following response is weaker. The global effects can be observed in Figure 9F, where the power spectra of the output population spike trains are plotted against the power spectra of corresponding non-homogeneous Poisson processes. In these processes, the rate term λ was identical to that of the background synaptic input process and the numbers of events were identical to the numbers of spikes in the networks. The powers of the frequency components corresponding to the input frequencies are plotted across the input frequencies in Figure 9G. Figures 9F–G show that frequencies approximately 0.5–4 Hz are amplified by the network (in comparison to non-homogeneous Poisson processes).
To test the robustness of our predictions, we repeated the experiment of Figure 9D–G using different network topologies and smaller network size. Instead of the Erdős-Rényi-type of random network connectivities used above and in [32], we now used the Watts-Strogatz [43] connectivity pattern. In this pattern, the nodes (neurons) are first located on the perimeter of a ring and connected to their closest neighbors, and each of the connections is then randomly rewired with a probability 0 ≤ q ≤ 1 to an arbitrary node of the network. Depending on the rewiring probability q, the networks may express the “small world” behavior, where local connections are abundant but the global path length is small [43]. Figure S27 (Supplementary material, Section S12) shows that the trend of delta-range frequencies being amplified by the L5PC network, as seen in Figure 9G, is reproduced with all tested Watts-Strogatz networks. The amplitudes of the amplification vary in Watts-Strogatz networks with different rewiring probabilities, but these differences are not large compared to the variation that stems from the random placement and activation times of the synapses.
4. Discussion
Conclusions
We introduced a stepwise neuron model-fitting strategy designed for data obtained from VSD and Ca2+ imaging. We tested our method on simulated data from L5PCs where ion channels were sequentially blocked, and the ion-channel conductances of the remaining channels were fitted stepwise to produce a reduced-morphology version of the Hay model presented in [26]. The obtained model, which is more than 20 times faster to simulate, preserves the properties of communication between soma and apical dendrite in a single L5PC. Furthermore, when interconnected to form a network and added background synaptic inputs, our model neurons reproduce the network dynamics predicted by the full model [32].
Towards application of our approach to experimental data
VSD imaging can be readily performed in slices to obtain high-resolution single-neuron data. To get the correct calibration, the VSD measurement may have to be accompanied by a patch-electrode [44] or fluorescence lifetime imaging [45]. While the spatial resolutions obtained using VSD imaging techniques have increased all the way to the level of dendritic spines [46], the temporal resolutions are usually lower than those in electrophysiological measurements. However, the differences are decreasing with the development of novel voltage sensors with improved performance [47]. The temporal resolution used in Ca2+ imaging experiments is yet lower, ranging from several to tens of Hz, which is mostly due to the slower underlying Ca2+ dynamics [48]. In this work, we showed that the membrane-potential dynamics along the dendrites of a reduced-morphology neuron model can be fitted with an adequate accuracy to corresponding data in simulations of a full-morphology neuron model (Figures 1–4). Furthermore, using a complex morphology also for the fitted model, we showed that our stepwise scheme yielded an acceptable fit that preserved the membrane-potential dynamics along the main apical and basal dendritic branches of a reconstructed morphology (Figures S22–S24). Development of this approach could allow for generation of morphologically detailed neuron models where ion-channel conductances for each segment of the dendritic tree are fitted directly to the imaging data obtained from the corresponding segments instead of having the ion-channel conductances follow statistical rules as in [26], [27], and many other models.
Besides the challenges of temporal resolution, the VSD and Ca2+ optical imaging techniques suffer from noise levels that are significantly larger than those in electrophysiological experiments. Therefore, in many cases, averaging is performed to increase signal-to-noise ratio. However, recent advances in probe design and optical imaging instrumentation, accelerated by the BRAIN Initiative [49], open the door for detection of signal in single trials capturing trial-to-trial variability. In addition, Ca2+ imaging techniques are prone to systematic errors imposed by buffering of Ca2+ ions by the indicator molecules, which interferes with the measured Ca2+ dynamics [50, 51]. In this work, we demonstrated high fidelity reconstruction of dendritic membrane-potential dynamics in the presence of measurement noise with a size comparable or larger than in many VSD and Ca2+ imaging applications (Figures S7–S10). An additional source of error is the low temporal resolution itself, but Figures S11–S13 show that its effect on our fitness functions and the parameter optimization results are small. It is, however, crucial that the higher resolution (1 kHz or larger) be used for measuring the membrane potential at the soma of the intact (spiking) neuron, as the number and timing of spikes may not be faithfully captured in the data with lower resolution.
To assure that the right role is given to the right ion channels and to obtain a successful fit using limited resources, we used the stepwise protocol where only a subset of the ion-channel conductances are fitted simultaneously, and the fitted values are passed on to the next stage where another subset of ion-channel conductances are fitted. Experimentally, this procedure requires cumulative use of pharmacological blockers of different ion channels [52]. We designed the model-fitting steps as a trade-off between experimentally validated procedures (such as those in [25] and [27]) and fitting-wise effective strategies. In the fourth model-fitting step, we fitted all voltage-gated Na+ channel conductances and all voltage-gated K+ channel conductances, while in the third step we fitted the Ca2+ channel conductances and Ca2+-activated K+ channel conductances, and in the second step the HCN channel conductances. Experimentally, this could be carried out by first (after recording the responses of the intact neuron for the fourth step fitting) applying a solution with a Na+ channel blocker, such as tetrodotoxin (TTX), and K+ channel blockers that do not block the apamin-sensitive SK channels, such as tetraethylammonium (TEA) [53] and 4-aminopyridine (4-AP) [54], and then record the data needed for third step fitting. To obtain data for the second step fitting, the SK channels have to be blocked by apamin and Ca2+ channels either by some of the pharmacological blockers, such as dihydropyridine variants, or by replacing the Ca2+ ions in the intracellular medium by Cd2+ or Co2+ [25] (note that blocking Ca2+ channels might be sufficient to abolish the SK currents as well, as the major source of Ca2+ entry into the cell is blocked). To record data for the first step fitting, the HCN currents have to be blocked, which could be done for example with ZD7288 [55]. However, it may be an unrealistic demand to require a blockade of all voltage-gated ion channels in an experimental setting, and thus the first two steps might have to be combined to fit the passive membrane properties and the HCN channel conductances simultaneously. It should be noted, however, that pharmacological blockers of ion channels are never ideal, but they on one hand often have side-effects that limit their use and on the other hand do not necessarily completely block the targeted ion channels. In [25], probably for this reason, blockade of K+ channels was replaced by careful choice of stimulating currents and repeated fitting of the passive parameters after the K+ channel conductances had been estimated — methods of this kind could be highly useful in our framework as well.
Comparison to other methods
The single-cell model fitting we carried out resembles that done by the authors of [7] in that we used their Python implementation of the NSGA-II algorithm [38] to a similar task: to construct a reduced-morphology model of an L5PC using a stepwise fitting strategy. There are, however, three main differences in the fitting methods between our work and theirs.
Firstly, their approach does not employ the parameter peeling strategy (such as that presented in [25]), where data from the same neuron under different pharmacological blockades is used. Instead, they constrain all the active conductances responsible for spiking behavior during the second step, and then use data from separate experiments to constrain the Ca2+ dynamics and SK conductances during the third and final step. Their approach yielded a successful fit for six out of ten models, and the effects of the conductances added during the third step on the second step fit were reported to be small [7]. The reason for the small effects is likely to lie in the choice of objective functions and parameters varied. In their second step, the model parameters (both somatic and dendritic) were fitted using membrane-potential traces at soma (both in intact and pinched neurons though). In their third step, only parameters concerning apical dendrite were fitted, as in their model the Ca2+ and SK channels were assumed to be present only in the apical tuft. As for our study, we generated the data by simulating the Hay model [26], which contains a large SK conductance not only in the apical dendrite but also in the soma — the mutual expression of these channels and their distinct roles are also backed by recent experiments [56]. Therefore, applying the third step of the approach of [7] to our data would imply a major change to the second step fits (for reference, see the effect of SK blockade in the network experiment of Figure S26 and our earlier analysis on the contribution of SK currents to the single-cell dynamics [33]).
Secondly, our model included a slightly larger set of ion channels but (in the default fitting task) smaller number of functionally different compartments. We applied the same ion channel selection as was used in the Hay model [26], which includes the LVA Ca2+ channels and Kv3.1 channels in addition to those included in the model of [7]. While in our model the action potentials are generated in the soma, their model describes the action potential initiation zone and the axon as well. Thirdly, our approach concentrates on producing an accurate representation of membrane-potential dynamics in the dendrites across a continuum of distances from soma in all except the last step, while in [7], only the first step employs objective functions that constrain membrane-potential dynamics in the dendrites.
Although our fitting method was inspired by the possibilities that lie in its application to experimental data, we mainly used it for making a reduced-morphology version of an existing, experimentally validated L5PC model. Model-reduction schemes have been applied previously to many neuron models, including models for L5PCs. In [57], simple conservation rules were applied to convert a full-morphology model of L5PC into a reduced-morphology L5PC. In their work, both the full model and the reduced model had passive dendrites, and thus no rules for the scaling of active conductances were applied. In [6], different degrees of reduction and their effects were tested when simplifying a full-morphology model of a globus pallidus neuron into a reduced-morphology model. In a similar manner as done in [57], the authors of [6] considered simple schemes, where the total membrane area of neuron compartments and their electrotonic lengths (as defined in passive signal propagation experiments) were conserved. However, the authors of [6] also studied whether varying the active conductances in the dendrites of the reduced model could improve the fit to the data from the full-morphology neuron (which also had active dendrites), but could not significantly improve the fits obtained by the simple rules they used for model reduction. It should be noted that these experiments were done using hand-tuning of the active conductances — thus, it is likely that applying suitable objective functions and letting the active conductances vary between different spatial segments could introduce improvements to the quality of their fit.
Our parameter optimizations were carried out using relatively few (20) generations. This was less than in [7] (100–1000 generations used) and [26] (500 generations used), but we found it sufficiently large for obtaining a good fit. Larger numbers are expected to further improve the fit, but at the expense of increased computational load for the fitting procedure. Our population size, by contrast, was as large or larger than in [7] (350–1000 samples) and [26] (1000 samples). We did not vary other genetic algorithm parameters as done in [7], but we expect that fine-tuning the crossover and mutation parameters would boost the genetic algorithm performance.
Network simulations
In creating neuron models, it is important to ensure the usability of the model in network simulations. Simulations of realistic activity in cortical circuits would require the description of many neuron types and their dynamics, such as those sketched in [58] and [2]. However, circuit models of many cell types are difficult to control as the number of connectivity-related parameters grows as the square of the number of cell types [58]. In this work, we implemented a network model of L5PCs, following the choices made in [32]. We replaced the thick-tufted L5PCs in the model of [32] by our reduced-morphology neurons to gain speed and allow simulations of larger networks. We fitted the background synaptic conductances based on single-cell activity produced by the model of [32], but we also validated the obtained network model against data obtained from 10-second network simulations of the full model. The network model, although consisting of L5PCs only, gives an insight to the cortical network responses that arise from the L5PC-to-L5PC connections. These connections are relatively abundant in the neocortical microcircuitry (a connectivity of 11.6% observed in [42], and 6% – 18%, depending on the subtype of L5PC, in [2]), and hence the emergent properties of a L5PC network could be of interest also in the absence of the surrounding network (cf. [32]).
In the network simulations of the present study, we concentrated on network properties with longer time scales than those studied in [32]. These include network responses to oscillatory inputs with delta-range frequencies (0.5–5 Hz): our model predicts that the lowest delta-range frequencies (0.5–3 Hz) be significantly amplified by the network (see Figure 9). On the other hand, amplification of low delta-range frequencies is present also when the timings of the background synaptic inputs follow stationary (non-oscillatory) Poisson statistics. These results are of particular interest as L5PCs were proposed in a recent review to be key players in generating or maintaining the cortical up and down states that shift periodically in a delta-range frequency [59]. Another review proposes that delta oscillations are composed of two components: one originating in (1) neocortex and the other in (2) thalamus [60]. Our modeling results support the contributions of L5PCs to both components: (1) since the underlying Hay model is based on neocortical (although murine) in vitro data [26] and our model predicts that oscillations emerge spontaneously in interconnected L5PCs (Figures 8 and 9A–C), and (2) since an important part of excitatory synaptic inputs to the L5PCs comes from thalamus [18] and our model predicts that oscillatory inputs with delta-range frequencies are amplified by the interconnected L5PCs (Figure 9D–G). The large contribution of Ca2+-dependent K+ currents to the prevalence of the oscillations, as predicted by our model, has also been proposed in the literature of slow (<1 Hz) oscillations [61, 62], which are likely to be generated by the same mechanism as the delta oscillations originating in the neocortex [62].
The results showing amplification of delta-range frequencies (Figure 9D–G) are robust to the underlying network architecture, as shown in Figure S27. The differences between the amplifications in networks with different topologies are small, but systematic analysis of the effects of the underlying structure could reveal contributions from different graph-theoretic measures as shown for another system in [63]. To achieve this, a large set of various models of network architecture, both theoretical [64, 65, 66] and data-oriented [67, 2], should be used. This is left for future work.
Our results showing the prevalence of oscillations in spontaneous L5PC network dynamics (Figures 8 and 9A–C) also provides an additional mechanistic view point to the results shown in [32]. In their work, they considered the network response to a synchronous stimulus at time t = 2000 ms following the spontaneous background synaptic firing. Our model predicts a variability in the network firing rate curves (see Figure 9A) and the timing of the local maxima of these curves. Furthermore, we showed that the time passed since the previous local maximum significantly affects the average amplitude of SK currents in the network (Figure 9B), which are a major contributor to single-cell and network activity (Figure S26). Therefore, the large SDs in Figures 2, 4, 5, and 6 of [32] could be decreased if only networks that are in the same phase in relation to the spontaneous oscillations were considered.
Outlook and future directions
Our stepwise method is automated in the sense that no hand-tuning of model parameters is needed at any stage [1]. However, constructing a unique model for a large number of neurons would greatly benefit from a degree of “meta-automaticity”, where automated experimental procedures stimulate and record the cell responses and choose the amplitudes of the stimuli used for neuron fitting (such as those in Table 2) based on the responses. This is important, since neurons of the same type can possess radically different electrophysiological properties [68, 2]. Furthermore, automated methods would be needed in choosing the final parameter set out of the Pareto-optimal population given by the multi-objective optimization algorithm. Stepwise strategies, such as the one we presented, are as well suited for this task as the strategies that fit all parameters simultaneously, yet the stepwise strategies gain advantage from dealing with a smaller parameter space [7] and are less likely to mix the roles of different ion-channel conductances (see, e.g., the discussion on compensatory mechanisms in [28]). The increased automaticity would also allow systematic generation of reduced-morphology versions of the neuron models that are currently available in public databases. Furthermore, the reduced-morphology model obtained using the method is in itself immediately applicable in e.g. studying mental disease [33].
Future experimental techniques are likely to permit the use of VSD and Ca2+ imaging in parallel with automated cell patching. Automatic cell-patching methods [69] have already been implemented in a number of systems, including in vivo neurons [70]. Furthermore, VSD imaging techniques may allow a resolution of dendritic compartment scale also in vivo in the near future. Computational model-fitting methods should be updated to take advantage of these new technologies in order to allow more faithful reproduction of dendritic membrane-potential dynamics than that attained by using patch-clamp data alone. We have shown that reliable reproduction of the communication between soma and dendrites can be obtained by fitting a reduced-morphology model of an L5PC to a combination of simulated VSD, Ca2+ imaging, and electrophysiological data. Future work should validate this method experimentally and extend the framework to permit it to be efficiently used as part of fully automated model-fitting techniques.
Supplementary Material
Highlights.
New VSD and Ca2+-imaging techniques allow high-resolution imaging of neurons.
We present a stepwise model-fitting scheme with possibilities to apply to such data.
We apply our method to simulated data to construct a reduced-morphology L5PC model.
Our model is cost-efficient and reproduces the main features of the original model.
Our model predicts that interconnected L5PCs can amplify low-frequency inputs.
Acknowledgments
NOTUR resources were used for heavy simulations. Funding: NIH grant 5 R01 EB000790-10, EC-FP7 grant 604102 (“Human Brain Project”), Research Council of Norway (216699, 213837, 223273, and 248828), South East Norway Health Authority (2013-123), and KG Jebsen Foundation.
Footnotes
Financial disclosures
The authors declare that there are no conflicts of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.VanGeit Werner, DeSchutter Erik, Achard Pablo. Automated neuron model optimization techniques: a review. Biological Cybernetics. 2008;99(4–5):241–251. doi: 10.1007/s00422-008-0257-6. [DOI] [PubMed] [Google Scholar]
- 2.Markram Henry, Muller Eilif, Ramaswamy Srikanth, Reimann Michael W, Abdellah Marwan, Sanchez Carlos Aguado, Ailamaki Anastasia, Alonso-Nanclares Lidia, Antille Nicolas, Arsever Selim, et al. Reconstruction and simulation of neocortical microcircuitry. Cell. 2015;163(2):456–492. doi: 10.1016/j.cell.2015.09.029. [DOI] [PubMed] [Google Scholar]
- 3.Keren Naomi, Peled Noam, Korngreen Alon. Constraining compartmental models using multiple voltage recordings and genetic algorithms. Journal of Neurophysiology. 2005;94(6):3730–3742. doi: 10.1152/jn.00408.2005. [DOI] [PubMed] [Google Scholar]
- 4.Druckmann Shaul, Banitt Yoav, Gidon Albert A, Schürmann Felix, Markram Henry, Segev Idan. A novel multiple objective optimization framework for constraining conductance-based neuron models by experimental data. Frontiers in Neuroscience. 2007;1:1. doi: 10.3389/neuro.01.1.1.001.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Druckmann Shaul, Berger Thomas K, Schürmann Felix, Hill Sean, Markram Henry, Segev Idan. Effective stimuli for constructing reliable neuron models. PLoS Computational Biology. 2011;7(8):e1002133. doi: 10.1371/journal.pcbi.1002133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hendrickson Eric B, Edgerton Jeremy R, Jaeger Dieter. The capabilities and limitations of conductance-based compartmental neuron models with reduced branched or unbranched morphologies and active dendrites. Journal of Computational Neuroscience. 2011;30(2):301–321. doi: 10.1007/s10827-010-0258-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bahl Armin, Stemmler Martin B, Herz Andreas VM, Roth Arnd. Automated optimization of a reduced layer 5 pyramidal cell model based on experimental data. Journal of Neuroscience Methods. 2012;210(1):22–34. doi: 10.1016/j.jneumeth.2012.04.006. [DOI] [PubMed] [Google Scholar]
- 8.Brookings Ted, Goeritz Marie L, Marder Eve. Automatic parameter estimation of multicompartmental neuron models via minimization of trace error with control adjustment. Journal of Neurophysiology. 2014;112(9):2332–2348. doi: 10.1152/jn.00007.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rumbell Timothy H, Draguljić Danel, Yadav Aniruddha, Hof Patrick R, Luebke Jennifer I, Weaver Christina M. Automated evolutionary optimization of ion channel conductances and kinetics in models of young and aged rhesus monkey pyramidal neurons. Journal of Computational Neuroscience. 2016:1–26. doi: 10.1007/s10827-016-0605-9. [DOI] [PubMed] [Google Scholar]
- 10.Wang Guangfu, Wyskiel Daniel R, Yang Weiguo, Wang Yiqing, Milbern Lana C, Lalanne Txomin, Jiang Xiaolong, Shen Ying, Sun Qian-Quan, Julius Zhu J. An optogenetics-and imaging-assisted simultaneous multiple patch-clamp recording system for decoding complex neural circuits. Nature Protocols. 2015;10(3):397–412. doi: 10.1038/nprot.2015.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Göbel Werner, Helmchen Fritjof. New angles on neuronal dendrites in vivo. Journal of Neurophysiology. 2007;98(6):3770–3779. doi: 10.1152/jn.00850.2007. [DOI] [PubMed] [Google Scholar]
- 12.Peterka Darcy S, Takahashi Hiroto, Yuste Rafael. Imaging voltage in neurons. Neuron. 2011;69(1):9–21. doi: 10.1016/j.neuron.2010.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hochbaum Daniel R, Zhao Yongxin, Farhi Samouil L, Klapoetke Nathan, Werley Christopher A, Kapoor Vikrant, Zou Peng, Kralj Joel M, Maclaurin Dougal, Smedemark-Margulies Niklas, et al. All-optical electrophysiology in mammalian neurons using engineered microbial rhodopsins. Nature Methods. 2014;11(8):825–833. doi: 10.1038/nmeth.3000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Grienberger Christine, Chen Xiaowei, Konnerth Arthur. Dendritic function in vivo. Trends in Neurosciences. 2015;38(1):45–54. doi: 10.1016/j.tins.2014.11.002. [DOI] [PubMed] [Google Scholar]
- 15.Antic Srdjan D, Empson Ruth M, Knöpfel Thomas. Voltage imaging to understand connections and functions of neuronal circuits. Journal of Neurophysiology. 2016;116(1):135–152. doi: 10.1152/jn.00226.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lou Shan, Adam Yoav, Weinstein Eli N, Williams Erika, Williams Katherine, Parot Vicente, Kavokine Nikita, Liberles Stephen, Madisen Linda, Zeng Hongkui, et al. Genetically targeted all-optical electrophysiology with a transgenic cre-dependent optopatch mouse. Journal of Neuroscience. 2016;36(43):11059–11073. doi: 10.1523/JNEUROSCI.1582-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Smith Spencer L, Smith Ikuko T, Branco Tiago, Häusser Michael. Dendritic spikes enhance stimulus selectivity in cortical neurons in vivo. Nature. 2013;503(7474):115–120. doi: 10.1038/nature12600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Larkum Matthew. A cellular mechanism for cortical associations: An organizing principle for the cerebral cortex. Trends in Neurosciences. 2013;36(3):141–151. doi: 10.1016/j.tins.2012.11.006. [DOI] [PubMed] [Google Scholar]
- 19.Schiller Jackie, Schiller Yitzhak, Stuart Greg, Sakmann Bert. Calcium action potentials restricted to distal apical dendrites of rat neocortical pyramidal neurons. Journal of Physiology. 1997;505(Pt 3):605–616. doi: 10.1111/j.1469-7793.1997.605ba.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Korngreen Alon, Sakmann Bert. Voltage-gated k+ channels in layer 5 neocortical pyramidal neurones from young rats: subtypes and gradients. Journal of Physiology. 2000;525(3):621–639. doi: 10.1111/j.1469-7793.2000.00621.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Christophe Elodie, Doerflinger Nathalie, Lavery Daniel J, Molnár Zoltán, Charpak Serge, Audinat Etienne. Two populations of layer v pyramidal cells of the mouse neocortex: development and sensitivity to anesthetics. Journal of Neurophysiology. 2005;94(5):3357–3367. doi: 10.1152/jn.00076.2005. [DOI] [PubMed] [Google Scholar]
- 22.Almog Mara, Korngreen Alon, et al. Characterization of voltage-gated ca (2+) conductances in layer 5 neocortical pyramidal neurons from rats. PLoS ONE. 2009;4(4):e4841–e4841. doi: 10.1371/journal.pone.0004841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mainen Zachary F, Sejnowski Terrence J. Influence of dendritic structure on firing pattern in model neocortical neurons. Nature. 1996;382(6589):363–366. doi: 10.1038/382363a0. [DOI] [PubMed] [Google Scholar]
- 24.Durstewitz Daniel, Seamans Jeremy K, Sejnowski Terrence J. Dopamine-mediated stabilization of delay-period activity in a network model of prefrontal cortex. Journal of Neurophysiology. 2000;83(3):1733–1750. doi: 10.1152/jn.2000.83.3.1733. [DOI] [PubMed] [Google Scholar]
- 25.Keren Naomi, Bar-Yehuda Dan, Korngreen Alon. Experimentally guided modelling of dendritic excitability in rat neocortical pyramidal neurones. Journal of Physiology. 2009;587(7):1413–1437. doi: 10.1113/jphysiol.2008.167130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hay Etay, Hill Sean, Schürmann Felix, Markram Henry, Segev Idan. Models of neocortical layer 5b pyramidal cells capturing a wide range of dendritic and perisomatic active properties. PLoS Computational Biology. 2011;7:e1002107. doi: 10.1371/journal.pcbi.1002107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Almog Mara, Korngreen Alon. A quantitative description of dendritic conductances and its application to dendritic excitation in layer 5 pyramidal neurons. Journal of Neuroscience. 2014;34(1):182–196. doi: 10.1523/JNEUROSCI.2896-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Achard Pablo, De Schutter Erik. Complex parameter landscape for a complex neuron model. PLoS Computational Biology. 2006;2(7):e94. doi: 10.1371/journal.pcbi.0020094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bekkers John M, Häusser Michael. Targeted dendrotomy reveals active and passive contributions of the dendritic tree to synaptic integration and neuronal output. Proceedings of the National Academy of Sciences. 2007;104(27):11447–11452. doi: 10.1073/pnas.0701586104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Häusser Michael, Spruston Nelson, Stuart Greg J. Diversity and dynamics of dendritic signaling. Science. 2000;290(5492):739–744. doi: 10.1126/science.290.5492.739. [DOI] [PubMed] [Google Scholar]
- 31.Migliore Michele, Shepherd Gordon M. Emerging rules for the distributions of active dendritic conductances. Nature Reviews Neuroscience. 2002;3(5):362–370. doi: 10.1038/nrn810. [DOI] [PubMed] [Google Scholar]
- 32.Hay Etay, Segev Idan. Dendritic excitability and gain control in recurrent cortical microcircuits. Cerebral Cortex. 2015;25(10):3561–3571. doi: 10.1093/cercor/bhu200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mäki-Marttunen Tuomo, Halnes Geir, Devor Anna, Witoelar Aree, Bettella Francesco, Djurovic Srdjan, Wang Yunpeng, Einevoll Gaute T, Andreassen Ole A, Dale Anders M. Functional effects of schizophrenia-linked genetic variants on intrinsic single-neuron excitability: A modeling study. Biological Psychiatry: Cognitive Neuroscience and Neuroimaging. 2016;1 doi: 10.1016/j.bpsc.2015.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jahr Craig E, Stevens Charles F. Voltage dependence of nmda-activated macroscopic conductances predicted by single-channel kinetics. Journal of Neuroscience. 1990;10(9):3178–3182. doi: 10.1523/JNEUROSCI.10-09-03178.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ramaswamy Srikanth, Hill Sean L, King James G, Schürmann Felix, Wang Yun, Markram Henry. Intrinsic morphological diversity of thick-tufted layer 5 pyramidal neurons ensures robust and invariant properties of in silico synaptic connections. Journal of Physiology. 2012;590(4):737–752. doi: 10.1113/jphysiol.2011.219576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hines Michael L, Carnevale Nicholas T. The NEURON simulation environment. Neural Computation. 1997;9(6):1179–1209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- 37.Cannon Robert C, Gleeson Padraig, Crook Sharon, Ganapathy Gautham, Marin Boris, Piasini Eugenio, Angus Silver R. Lems: a language for expressing complex biological models in concise and hierarchical form and its use in underpinning neuroml 2. Frontiers in Neuroinformatics. 2014;8:79. doi: 10.3389/fninf.2014.00079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Deb Kalyanmoy, Pratap Amrit, Agarwal Sameer, Meyarivan TAMT. A fast and elitist multiobjective genetic algorithm: Nsga-ii. IEEE Transactions on Evolutionary Computation. 2002;6(2):182–197. [Google Scholar]
- 39.Nevian Thomas, Larkum Matthew E, Polsky Alon, Schiller Jackie. Properties of basal dendrites of layer 5 pyramidal neurons: a direct patch-clamp recording study. Nature Neuroscience. 2007;10(2):206–214. doi: 10.1038/nn1826. [DOI] [PubMed] [Google Scholar]
- 40.Zitzler Eckart, Künzli Simon. International Conference on Parallel Problem Solving from Nature. Springer; 2004. Indicator-based selection in multiobjective search; pp. 832–842. [Google Scholar]
- 41.Van Geit Werner, Gevaert Michael, Chindemi Giuseppe, Rössert Christian, Courcol Jean-Denis, Muller Eilif B, Schürmann Felix, Segev Idan, Markram Henry. Bluepyopt: Leveraging open source software and cloud infrastructure to optimise model parameters in neuroscience. Frontiers in Neuroinformatics. 2016;10 doi: 10.3389/fninf.2016.00017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Song Sen, Sjöström Per Jesper, Reigl Markus, Nelson Sacha, Chklovskii Dmitri B. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 2005;3(3):e68. doi: 10.1371/journal.pbio.0030068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Watts Duncan J, Strogatz Steven H. Collective dynamics of ‘small-world’ networks. Nature. 1998;393(6684):440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 44.Popovic Marko, Gao Xin, Zecevic Dejan. Voltage-sensitive dye recording from axons, dendrites and dendritic spines of individual neurons in brain slices. JoVE (Journal of Visualized Experiments) 2012;(69):e4261–e4261. doi: 10.3791/4261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Brinks Daan, Klein Aaron J, Cohen Adam E. Two-photon lifetime imaging of voltage indicating proteins as a probe of absolute membrane voltage. Biophysical Journal. 2015;109(5):914–921. doi: 10.1016/j.bpj.2015.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Acker Corey D, Hoyos Erika, Loew Leslie M. EPSPs measured in proximal dendritic spines of cortical pyramidal neurons. eNeuro. 2016;3(2):ENEURO.0050–15. doi: 10.1523/ENEURO.0050-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gong Yiyang, Huang Cheng, Li Jin Zhong, Grewe Benjamin F, Zhang Yanping, Eismann Stephan, Schnitzer Mark J. High-speed recording of neural spikes in awake mice and flies with a fluorescent voltage sensor. Science. 2015;350(6266):1361–1366. doi: 10.1126/science.aab0810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Grewe Benjamin F, Langer Dominik, Kasper Hansjörg, Kampa Björn M, Helmchen Fritjof. High-speed in vivo calcium imaging reveals neuronal network activity with near-millisecond precision. Nature Methods. 2010;7(5):399–405. doi: 10.1038/nmeth.1453. [DOI] [PubMed] [Google Scholar]
- 49.Insel Thomas R, Landis Story C, Collins Francis S. The nih brain initiative. Science. 2013;340(6133):687–688. doi: 10.1126/science.1239276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Markram Henry, Roth Arnd, Helmchen Fritjof. Competitive calcium binding: implications for dendritic calcium signaling. Journal of Computational Neuroscience. 1998;5(3):331–348. doi: 10.1023/a:1008891229546. [DOI] [PubMed] [Google Scholar]
- 51.Sabatini Bernardo L, Oertner Thomas G, Svoboda Karel. The life cycle of ca 2+ ions in dendritic spines. Neuron. 2002;33(3):439–452. doi: 10.1016/s0896-6273(02)00573-1. [DOI] [PubMed] [Google Scholar]
- 52.Roth Arnd, Bahl Armin. Divide et impera: optimizing compartmental models of neurons step by step. The Journal of Physiology. 2009;587(7):1369–1370. doi: 10.1113/jphysiol.2009.170944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Rudy Bernardo, Iverson Linda E. Ion channels. Vol. 207. Gulf Professional Publishing; 1997. [Google Scholar]
- 54.Artym Vira V, Petty Howard R. Molecular proximity of kv1. 3 voltage-gated potassium channels and β1-integrins on the plasma membrane of melanoma cells effects of cell adherence and channel blockers. Journal of General Physiology. 2002;120(1):29–37. doi: 10.1085/jgp.20028607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wu Xing, Liao Liping, Liu Xiangming, Luo Fang, Yang Tianming, Li Chenhong. Is zd7288 a selective blocker of hyperpolarization-activated cyclic nucleotide-gated channel currents? Channels. 2012;6(6):438–442. doi: 10.4161/chan.22209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Rudolph Stephanie, Thanawala Monica S. Location matters: somatic and dendritic sk channels answer to distinct calcium signals. Journal of Neurophysiology. 2015;114(1):1–5. doi: 10.1152/jn.00181.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Bush Paul C, Sejnowski Terrence J. Reduced compartmental models of neocortical pyramidal cells. Journal of Neuroscience Methods. 1993;46(2):159–166. doi: 10.1016/0165-0270(93)90151-g. [DOI] [PubMed] [Google Scholar]
- 58.Traub Roger D, Contreras Diego, Cunningham Mark O, Murray Hilary, LeBeau Fiona EN, Roopun Anita, Bibbig Andrea, Bryan Wilent W, Higley Michael J, Whittington Miles A. Single-column thalamocortical network model exhibiting gamma oscillations, sleep spindles, and epileptogenic bursts. Journal of Neurophysiology. 2005;93(4):2194–2232. doi: 10.1152/jn.00983.2004. [DOI] [PubMed] [Google Scholar]
- 59.Harmony Thalía. The functional significance of delta oscillations in cognitive processing. Frontiers in integrative Neuroscience. 2013;7 doi: 10.3389/fnint.2013.00083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Timofeev Igor, Chauvette Sylvain. Thalamocortical oscillations: local control of eeg slow waves. Current Topics in Medicinal Chemistry. 2011;11(19):2457–2471. doi: 10.2174/156802611797470376. [DOI] [PubMed] [Google Scholar]
- 61.Steriade Mircea, Nunez A, Amzica F. A novel slow (¡ 1 hz) oscillation of neocortical neurons in vivo: depolarizing and hyperpolarizing components. Journal of Neuroscience. 1993;13(8):3252–3265. doi: 10.1523/JNEUROSCI.13-08-03252.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Neske Garrett T. The slow oscillation in cortical and thalamic networks: mechanisms and functions. Frontiers in Neural Circuits. 2015;9 doi: 10.3389/fncir.2015.00088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Mäki-Marttunen Tuomo, Aćimović Jugoslava, Ruohonen Keijo, Linne Marja-Leena. Structure-dynamics relationships in bursting neuronal networks revealed using a prediction framework. PLoS ONE. 2013;8(7):e69373. doi: 10.1371/journal.pone.0069373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Zhao Liqiong, Beverlin Bryce, II, Netoff Tay, Nykamp Duane Quinn. Synchronization from second order network connectivity statistics. Frontiers in Computational Neuroscience. 2011;5:28. doi: 10.3389/fncom.2011.00028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Aćimović Jugoslava, Mäki-Marttunen Tuomo, Linne Marja-Leena. The effects of neuron morphology on graph theoretic measures of network connectivity: the analysis of a two-level statistical model. Frontiers in Neuroanatomy. 2015;9 doi: 10.3389/fnana.2015.00076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Mäki-Marttunen Tuomo. An algorithm for motif-based network design. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2016 doi: 10.1109/TCBB.2016.2576442. [DOI] [PubMed] [Google Scholar]
- 67.Perin Rodrigo, Berger Thomas K, Markram Henry. A synaptic organizing principle for cortical neuronal groups. Proceedings of the National Academy of Sciences. 2011;108(13):5419–5424. doi: 10.1073/pnas.1016051108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Druckmann Shaul, Hill Sean, Schürmann Felix, Markram Henry, Segev Idan. A hierarchical structure of cortical interneuron electrical diversity revealed by automated statistical analysis. Cerebral Cortex. 2013;23(12):2994–3006. doi: 10.1093/cercor/bhs290. [DOI] [PubMed] [Google Scholar]
- 69.Jones Kenneth A, Garbati Nicoletta, Zhang Hong, Large Charles H. High Throughput Screening: Methods and Protocols. 2. 2009. Automated patch clamping using the qpatch; pp. 209–223. [DOI] [PubMed] [Google Scholar]
- 70.Kodandaramaiah Suhasa B, Franzesi Giovanni Talei, Chow Brian Y, Boyden Edward S, Forest Craig R. Automated whole-cell patch-clamp electrophysiology of neurons in vivo. Nature Methods. 2012;9(6):585–587. doi: 10.1038/nmeth.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.