Electroencephalographic Resting-State Networks: Source Localization of Microstates

Abstract

Using electroencephalography (EEG) to elucidate the spontaneous activation of brain resting-state networks (RSNs) is nontrivial as the signal of interest is of low amplitude and it is difficult to distinguish the underlying neural sources. Using the principles of electric field topographical analysis, it is possible to estimate the meta-stable states of the brain (i.e., the resting-state topographies, so-called microstates). We estimated seven resting-state topographies explaining the EEG data set with k-means clustering (N = 164, 256 electrodes). Using a method specifically designed to localize the sources of broadband EEG scalp topographies by matching sensor and source space temporal patterns, we demonstrated that we can estimate the EEG RSNs reliably by measuring the reproducibility of our findings. After subtracting their mean from the seven EEG RSNs, we identified seven state-specific networks. The mean map includes regions known to be densely anatomically and functionally connected (superior frontal, superior parietal, insula, and anterior cingulate cortices). While the mean map can be interpreted as a “router,” crosslinking multiple functional networks, the seven state-specific RSNs partly resemble and extend previous functional magnetic resonance imaging-based networks estimated as the hemodynamic correlates of four canonical EEG microstates.

Introduction

Studying the spontaneous activity of the brain

Functional magnetic resonance imaging (fMRI) studies have revealed that the brain at rest exhibits spontaneous blood oxygen-level-dependent (BOLD) fluctuations over time that correlate with functionally connected brain areas (Biswal et al., 1995). This discovery and the use of advanced neuroimaging techniques led to a fundamental paradigm shift in the understanding of how the brain works. The current prevailing hypothesis is that the brain is inherently active in an organized way so as to be better prepared for stimulus processing rather than the brain being considered as in an idle state activated by external stimuli.

Studies of resting-state networks (RSNs) with fMRI summarize several minutes of recording based on the assumption that the functional connections between the different areas of a network remain stationary. This assumption is challenged by recent time-resolved fMRI studies that showed that RSNs vary over time (Hutchison et al., 2013; Zalesky et al., 2014) and they strongly overlap in space and time (Karahanoğlu and Van De Ville, 2015; Smith et al., 2012), suggesting dynamic interactions between RSNs.

Using temporal rather than spatial independent component analysis (ICA) of accelerated fMRI data, Smith et al. (2012) described temporally distinct but spatially overlapping correlated and anticorrelated networks with several brain regions being part of multiple networks, supporting the notion that “functional integration among brain areas means that large-scale neuronal dynamics can share a substantial anatomical infrastructure” (Friston, 1998). Also using accelerated fMRI, Zalesky and colleagues (2014) showed that these temporally alternating patterns of correlation and anticorrelation of spatially distributed regions are not continuous, but partitioned into different epochs. The authors compared these brief intervals of increased activity in spatially distributed brain regions with electrophysiological findings of epochs of synchronous activity (Deco et al., 2008) that may allow the individual segregated networks to have access to a global cognitive workspace necessary for conscious processing. This idea is the basis of the global workspace model of consciousness that suggests that a resting state represents a microstate of cognition and that cognitive processing evolves through a succession of such microstates (Dehaene and Changeux, 2011). During each of these states, several brain areas communicate in a coordinated manner to prepare for incoming stimuli (Bressler and Kelso, 2001; Bressler and Tognoli, 2006). Based on electroencephalography (EEG) measurements, Bressler (1995) estimated that the duration of such conscious brain states is in the range of a few hundred milliseconds.

The concept of “microstate of cognition” is supported by Lehmann and colleagues' (1987) electrophysiological observation that a given configuration of the global scalp electric field (a.k.a. a topography) measured with multichannel EEG remains stable for periods of ∼100 msec and then switches to a new configuration. Lehmann's team hypothesized that these broadband EEG “microstates” represent the building blocks of human cognition, the “atoms of thought” (Lehmann, 1990). In this sense, these microstates could be the electrophysiological correlates of the periods of stable spatial patterns proposed in the global workspace theory (Baars, 2002; Baars, 1988; Changeux and Michel, 2004; Dehaene and Changeux, 2011): these “thoughts” (or states), by coming in and out of focus, could reach various levels of consciousness as described by Dehaene and Changeux (2011) and the information broadcast between states can encode the smooth transition from thought to thought.

Several studies conducted during the last 20 years have shown that the presence and temporal dynamics of EEG microstates are modulated by different levels of consciousness (Brodbeck et al., 2012; Katayama et al., 2007; Singh and Telles, 2015), and diseases [e.g., in schizophrenia (Kindler et al., 2011; Lehmann et al., 2005; Strelets et al., 2003)]. What is largely missing is a reliable identification of the neuronal sources generating these different EEG states, that is, the brain areas that are synchronized with each other during each of these microstates.

Two main approaches have been explored for filling the gap: (1) the analysis of simultaneously recorded EEG-fMRI data to identify the brain areas of hemodynamic changes matching the temporal fluctuations of the resting-state topographies, and (2) EEG source imaging to estimate the neuronal networks generating each resting-state topography.

EEG-fMRI resting-state networks

Two independent studies on combined EEG-fMRI appeared in the same issue of NeuroImage (Britz et al., 2010; Musso et al., 2010) and were accompanied by two editorial comments (Lehmann, 2010; Laufs, 2010). Musso and colleagues focused on resting-state EEG-BOLD analysis at the individual level, that is, resting-state topographies (and corresponding BOLD correlates) were estimated independently for each subject. They showed that, on average, half of the individuals' resting-state topographies elicited BOLD activation with spatial patterns that resembled those usually described in fMRI resting-state studies. On the group level, seven aggregation factors were identified, but only one of the factors was able to elicit significant BOLD activation in brain areas within the visual as well as the default mode network.

Britz and colleagues estimated topographies (and BOLD correlates) at a group level. Using k-means cluster analysis, they determined four dominant resting-state topographies across all subjects. They then determined the time course of these template maps in each subject and convolved them with a hemodynamic response function. Group-level general linear modeling identified distinct BOLD networks for each of the four EEG topographies, corresponding to known fMRI-based RSNs: auditory, visual, salience, and attention networks.

Yuan and colleagues (2012) identified EEG resting-state topographies by a temporal ICA and then compared 13 selected EEG components with those estimated from the fMRI ICA. Out of the 13 components, six were associated with one or two fMRI RSNs, while the remaining seven correlated with more than two fMRI networks. Despite methodologically different approaches, all three studies showed that the dominant EEG topographies are fairly well related to the fMRI-defined RSNs, but with considerable spatial overlap.

EEG resting-state networks

Instead of estimating the resting-state topography BOLD correlates (indirectly correlated to the topography fluctuations), in the present work, we estimate directly the (electrophysiological) neural networks generating the resting-state scalp topographies. To the best of our knowledge, only one team used this direct approach to estimate the sources of EEG resting-state topographies [Pascual-Marqui et al. (2014); and related work from Milz et al. (2016)]. They analyzed a publicly available data set of 109 subjects recorded with 61-channel EEG, in which the data were filtered between 2 and 20 Hz.

They used first-level group k-means clustering to estimate four resting-state maps and then estimated individual versions of each of the four maps by spatial fitting. They then computed the source distributions of the group maps (1) and the individual maps (2) by projecting each topography into source space using eLORETA. The individual solutions were tested for nonzero mean at each solution point across subjects. Both approaches (1) and (2) resulted in greatly overlapping source distributions, primarily involving the posterior cingulate and occipital/parietal cortices (except for the third map that also involved the anterior cingulate). Pascual-Marqui's approach does not distinguish resting states based on their temporal signature but it focuses on the distinctive spatial characteristics of the potential fields.

We recently proposed the method topographic electrophysiological state source-imaging (TESS) (Custo et al., 2014) for spontaneous or evoked EEG source localization inspired by classic fMRI analysis of BOLD evoked responses. TESS is based on general linear model (GLM) regression and it estimates the spatial source distribution of a given scalp topography (e.g., an average epileptic spike map) by selecting the spatial locations (solution points) with time courses matching that of the topography of interest.

In this article, we use TESS to estimate the sources of EEG resting-states topographies, that is, to estimate the EEG-based RSNs (eRSNs). We analyze a set of 164 healthy subjects recorded with 256-channel EEG during 3–7 min of rest with eyes closed; we estimate the optimal set of resting-state topographies representing this data set, compute the time course of each of these maps, and determine the distribution of the underlying time-correlated sources. We quantify the reproducibility of the observed source distributions using bootstrapping and we interpret and classify our results based on their spatial patterns.

Materials and Methods

EEG data set

We recorded 164 healthy subjects (age 6 to 87 years, mean/standard deviation 38.11 ± 24.15, 89 females) for 3–7 min during rest in an electrically shielded room. The subjects were sitting upright with their eyes closed and were instructed to relax and let their minds wander. A high-density sensor cap (256-channel HydroCel Geodesic Sensor Net; Electrical Geodesics, Inc., Eugene, OR) was used to record EEGs at a sampling rate of 1000 Hz and with a vertex reference. Following acquisition, the data were filtered between 1 and 40 Hz, and infomax-based ICA was applied to remove oculomotor and cardiac artifacts (Jung et al., 2000). The data were downsampled to 125 Hz, bad electrodes were interpolated using a three-dimensional spherical spline (Perrin et al., 1989), and the reference was recomputed as the average of all the channels. Only 204 electrodes were processed in this manner, the sensors on the cheeks and neck were omitted. The data were spatially smoothed to account for small groups of sporadically bad electrode signals with an approach similar to an interquartile mean (IQM), in which the cumulative density function is split into six intervals instead of four. All the preprocessing steps were done using Cartool toolbox (https://sites.google.com/site/cartoolcommunity/home) and MATLAB.

Resting-state topography estimation

We use Cartool's adapted k-means clustering method to estimate the optimal set of topographies explaining the input EEG signal (Brunet et al., 2011; Murray et al., 2009; Pascual-Marqui et al., 1995). To determine the optimal number of clusters, we calculate 11 independent optimization criteria and combine them as follows: 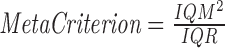, where IQM is the IQM of the criteria and IQR is the interquartile range of the criteria (see Supplementary Data, Supplementary Fig. S1, and Supplementary Table S1 for details; Supplementary Data are available online at www.liebertpub.com/brain). The criteria are Cross-Validation (its second derivative), Cubic Clustering Criterion (its first derivative), Davies and Bouldin, Dunn, Frey and Van Groenewoud, Hartigan (its first derivative), Krzanowski-Lai Index, Marriott, Point-Biserial, Tau, and Trace (W) (its second derivative) (Charrad et al., 2014; Krzanowski and Lai, 1988; Milligan and Cooper, 1985; Murray et al., 2008; Pascual-Marqui et al., 1995). In Supplementary Data, we report more details on these 11 methods and the type of cost function they implement.

We cluster the EEG data at the global field power (GFP) peaks to maximize the signal to noise ratio and focus on moments of high global neuronal synchronization (Britz et al., 2010; Koenig et al., 2002; Pascual-Marqui et al., 1995; Tomescu et al., 2014), for a discussion on the advantages and limits of this approach (Gärtner et al., 2015; Koenig and Brandeis, 2016). Typically, the topography around a GFP peak remains stable and is at its highest SNR at the GFP peak.

The k-means clustering is performed in two iterations: first, we cluster each individual EEG (at the GFP peaks) into its optimal number of clusters (see Supplementary Data for more details on the optimal criterion), assigning an EEG time frame to a cluster only if its correlation with the cluster map is above 0.5; we use temporal smoothing of strength 10 on half window size 1 (Besag factor 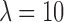and 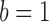in Equation 13 (Pascual-Marqui et al., 1995). For a given k, we randomly select a starting set of k topographies 100 times (where k is the number of clusters) to find the set of cluster maps that maximize the global explained variance. Then, the mean cluster map, or template topography, will represent the optimal individual's cluster centroid (i.e., explaining most of the variances) for a specific k. This procedure is repeated for k ranging from 1 to 15 and the optimal criterion described in Supplementary Data is applied to the individual clustering results to find each subject's optimal k. We then group cluster these individual template topographies (500 trials) again not assigning maps to a cluster if their correlation is below 0.5.

Resting-state topography source analysis (TESS)

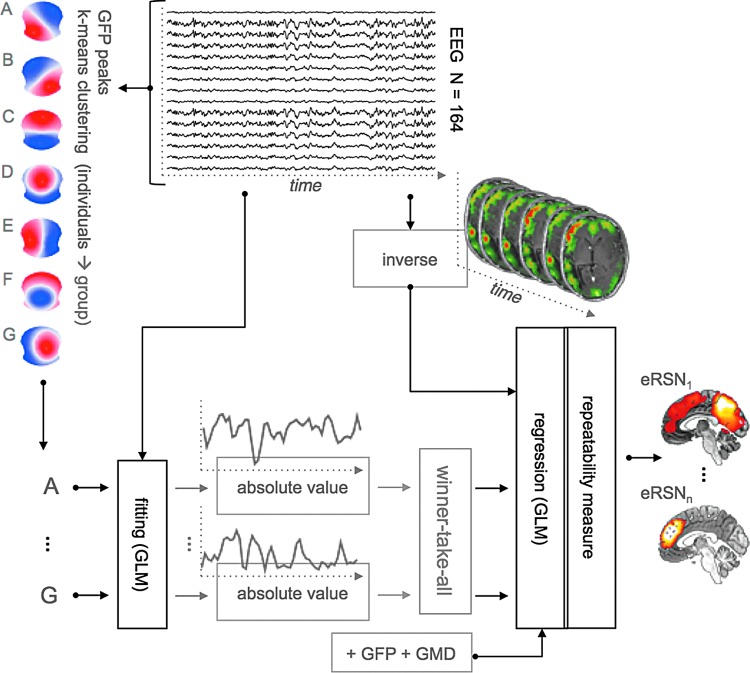
Figure 1 depicts the source analysis steps for the seven estimated broadband EEG resting-state topographies using TESS (Custo et al., 2014). The seven resting-state maps form the design matrix that is fitted to each subject's continuous EEG using a GLM. The GLM estimates the coefficients 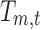for the linear combination of the seven input maps m minimizing their distance from each EEG time point t (i.e., minimizing the squared sum of the difference between the EEG values measured at time t and their linear approximation, that is, the linear combination of the input maps). The fitting result is a time course of coefficients for each resting-state map for each subject. Using a winner-takes-all approach, we compute an index function attributing each time point to the topography with the highest GLM coefficient:

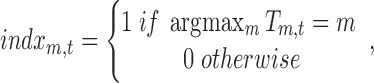FIG. 1.

We use TESS (Custo et al., 2014) to estimate the sources associated with the seven resting-state topographies A–G. The method is based on the idea that we can separate noise and the sources generating a topography based on their time course. Using a GLM, we estimate the time course of each resting-state topography (“fitting” box of the diagram) and through a second GLM, we estimate the set of sources matching the temporal profile of each topography (“regression” box of the diagram). The seven resting-state topographies are estimated separately using a two-level k-means clustering approach. GFP indicates the global field power, GMD stands for global map dissimilarity, and the final output eRSN corresponds to the EEG-based RSN associated with a resting-state topography. EEG, electroencephalography; RSN, resting-state network; TESS, topographic electrophysiological state source-imaging. Color images available online at www.liebertpub.com/brain

where 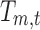is the coefficient assigned by the GLM fitting to a subject's EEG time frame t for the resting-state topography m.

In parallel, a distributed linear inverse solution is applied to each time point of the individual EEG [LAURA from Cartool's toolbox; (Grave de Peralta Menendez et al., 2004)], and the time course of the current density of 5000 solution points equally distributed in the gray matter of a template brain is estimated: 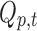for each solution point p and time point t (Michel et al., 2004). A second temporal GLM is then used to fit the two time courses ( 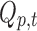and 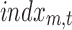), resulting in an estimate of the coefficient for each solution point p (or “voxel”) and each of the seven resting-state topographies m [see Custo et al. (2014) for more details].

The topography time courses used as regressors in the final GLM are fit together with the GFP and the global map dissimilarity (GMD). The GMD for each pair of consecutive maps, u and v, in a subject's EEG time series is defined as follows:

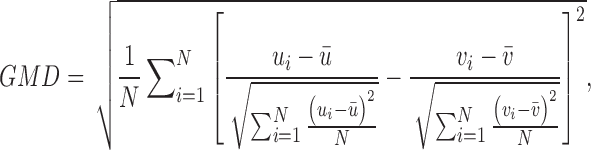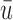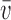where N is the number of electrodes, u_i and v_i are the voltages at electrode i of maps u and v, respectively, and and are the average voltages of all electrodes of these maps.

The GFP regressor helps eliminate the bias induced by the signal power fluctuations; the GMD regressor can diminish the contributions of the moments of transitions between states, when the SNR is very low and the signal association to a particular state is weak (Lehmann and Skrandies, 1980). Similarly to an fMRI GLM-based analysis, the result of this process is a beta variable distribution associating “activity” to voxels matching a certain temporal pattern.

Reproducibility analysis

We perform bootstrapping to assess the accuracy of our measures (Hastie et al., 2009). This analysis is performed in two steps: in the first step we compute the z scores of randomly selected samples of the estimated activity maps (random sampling with replacement of the output of TESS, 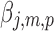, the p^th solution point of the m^th resting-state source map for the j^th subject); in the second step we compute second-level z scores of the samples' z scores from step one. 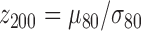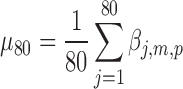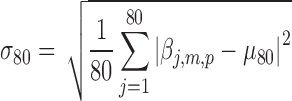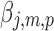In more details: in the first step, for each random sample (200 repetitions, sample size 80), we compute the sample mean divided by its standard deviation, , where , , and are the p^th solution point of the m^th estimated source map for the j^th subject. 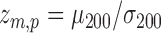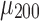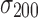In the second step, we compute the bootstrap ratio (Hastie et al., 2009): , where and are the mean and standard deviation of the 200 z scores computed on each sample ().

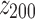The result is a z score representing the generators of each resting-state topography that we call the eRSN: a sizeable value of 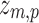indicates robust estimation of brain activity in the population. To control for multiple comparison, we applied Bonferroni correction to the t-values of the contrast 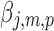, that is, the 164 beta variables estimated with TESS (not shown, p < 0.05) that were similarly spatially distributed and had maximum values of 16–18 for any of the seven maps.

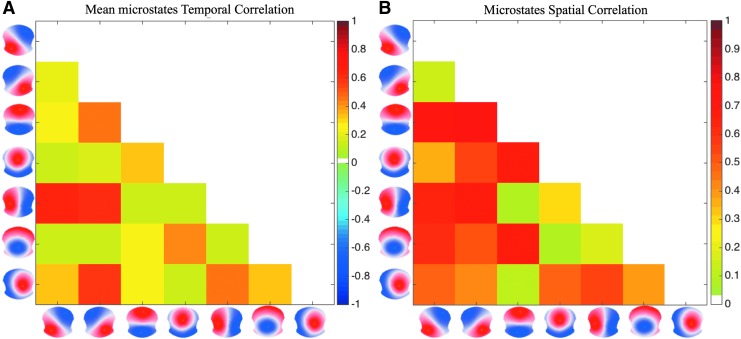
To test whether the resting-state topographies are spatially and/or temporally correlated, which might indicate a redundancy in the set of state topographies, we compute their pairwise spatial and temporal correlations. In the temporal domain, we compute the Pearson correlation coefficients of the absolute value of the time courses estimated by GLM fitting the seven resting-state topographies to a subject's EEG. Then, we compute the mean and standard deviation across subjects of these correlation coefficients. The spatial correlation is calculated by computing the absolute value of the Pearson correlation between the seven estimated normalized resting-state topographies, measuring the covariance between the spatial distributions of the topography scalp potentials. Taking the absolute value of the correlation coefficients makes them invariant to the topography's polarity.

Results

Resting-state topography estimation

The two-step k-means clustering (individual level and group level, see Materials and Methods for details), at the individual level, revealed between 3 and 11 topographies (mean k = 5.8 ± 1.6) as the optimal number of clusters (totaling 952 maps), and, at the group level, seven clusters provided optimal explanation of the data. These seven maps explained 84.8% of the global variance. The first column of Table 1 shows the topographies of these maps, which are the centroid of the respective clusters of maps; the second column shows the number of individual template maps assigned to each cluster; the third column displays the number of subjects contributing with at least one map to the cluster; finally, the fourth column shows the mean global variance of the individual data explained by each cluster map, that is, by each resting-state topography (indicated by GEV, global explained variance).

Table 1.

Resting-State Topography Parameters

Maps	Maps × cluster	No. of subjects	GEV
	160	145	14
	168	148	15
	205	161	19
	115	100	10
	127	120	11
	105	93	9
	71	70	6

GEV, global explained variance. Color images available online at www.liebertpub.com/brain

The result shows that maps A, B, C, and D, the four of the seven maps most conventionally described in the literature (Khanna et al., 2015), together explain ∼60% of the variance when using seven clusters. The other three maps, E–G, explain an additional 25% of the variance. Figure 2 shows the temporal and spatial correlations among the seven maps. The highest temporal correlations are found between map E and the canonical maps A and B (0.63 and 0.62, respectively), and between map G and map B (0.57). The variability of the microstate temporal correlations across subjects is low (standard deviation range is 0.105–0.181). The spatial correlation matrix (Fig. 2B) reveals a lower correlation between the four canonical maps and the three additional ones (<0.68) than the correlation between canonical maps themselves (as high as 0.76).

FIG. 2.

Mean temporal (A) and spatial (B) correlation coefficients of the seven resting-state topographies. Color images available online at www.liebertpub.com/brain

EEG-based RSNs

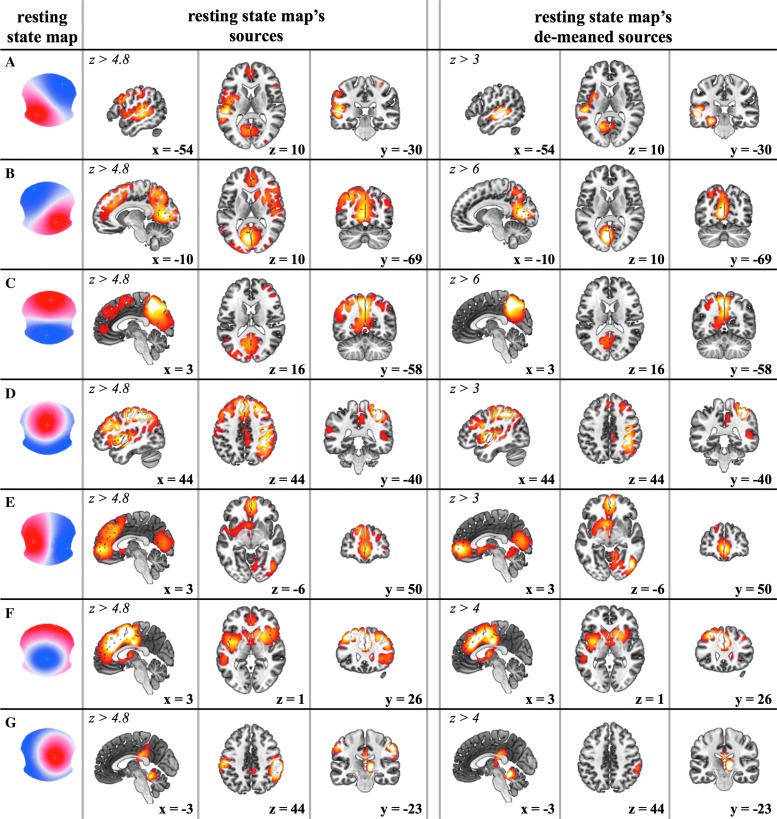
The seven resting-state topography sources were estimated with TESS and tested for reproducibility. The resulting z-scores are shown in Figure 3: in the left-most column we display the seven resting-state topographies (A–G). In the second, third, and fourth columns we show the network generating each resting-state map over the MNI brain (Fonov et al., 2011) in the sagittal, transverse, and coronal slices of local maximal activity (z score >4.8).

FIG. 3.

The estimated seven RSNs (and corresponding scalp topographies, A–G, in the first column) displayed over the MNI brain. The z scores resulting from bootstrapping (p < 0.005) are thresholded at z > 4.8 (second to fourth column). The de-meaned EEG-based RSNs are shown in the last three columns (z at least greater than 3). Color images available online at www.liebertpub.com/brain

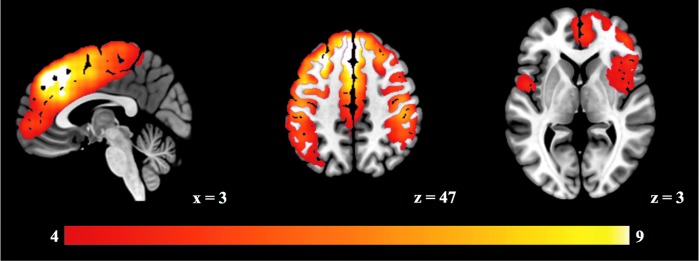
In Figure 3 (columns 2–4), we can notice several brain structures with high z-scores common to most microstates. To determine which brain regions are common to the majority of the EEG topographies, we average the z-scores of the seven eRSNs. This mean map is shown in Figure 4 (z score >4). The most dominant areas of overlap are in the anterior/posterior medial axes, including the superior frontal cortex extending ventrally to the anterior cingulate and caudally to the postcentral gyrus. Also, the insula and the superior parietal cortex belong to this set of common regions. We subtract this mean map from each individual eRSN to highlight the state-specific portion of the RSNs. These de-meaned maps are shown in Figure 3 (last three columns) together with their corresponding microstate topographies. In Table 2, we summarize the active regions for each topography. We define an area “active” when it is statistically significantly present after de-meaning (p < 0.005, z scores at least larger than 3).

FIG. 4.

The mean of the seven eRSNs (z > 4). Color images available online at www.liebertpub.com/brain

Table 2.

Electroencephalographic Resting-State Network Summary

Resting-state map	List of maxima ROIs
A	Left Heschl's gyrus
	Left Wernicke area
	Left insula
	Left lingual gyrus
B	Cuneus
	Right insula
	Right claustrum
	Right frontal eye field
C	Precuneus
	PCC
	Left angular gyrus
D	Right inf. par. lobe
	Right mid fr. gyrus
	Right sup. fr. gyrus
	Right insula
E	Left mid frontal gyrus
	ACC
	PCC
	Cuneus
F	Dorsal ACC
	Sup. fr. gyrus
	Mid fr. gyrus
	Insula
G	Right inf. par. lobe
	Sup. tmp. gyrus
	Cerebellum

ACC, anterior cingulate cortex; PCC, posterior cingulate cortex; ROIs, regions of interest.

The following are the main cortical regions distinctly associated with each microstate topography:

• • Map A: left middle and superior temporal lobe, including Brodmann areas 41 (BA41, primary auditory cortex) and 22 (BA22, Wernicke), and the left insular cortex. There is also a circumscribed but lower activation of the left lingual gyrus (BA19).

• • Map B: very strong activity in the left and right occipital cortices (cuneus), including Brodmann areas 17 and 18 (primary visual cortex). Second smaller areas of activity are located in the right insular cortex extending to the right claustrum and the right frontal eye field (BA8).

• • Map C: major activity is found in the precuneus and the posterior cingulate cortex (PCC). A second weaker activated area is the left angular gyrus.

• • Map D: strong activation is found in the right inferior parietal lobe (BA40) and the right middle and superior frontal gyri. The right insula (BA13) is activated as well.

• • Map E: the left middle frontal gyrus, including the frontal eye field (Brodmann area 8), and the dorsal part of the anterior cingulate are strongly activated together with the cuneus, extending to the PCC. The thalamus is activated as well, even though the ability of EEG to localize these deep structures is debated.

• • Map F: very strong activation is seen in the dorsal anterior cingulate cortex (ACC; BA32) extending to the superior frontal gyrus. The list of main activated areas is completed by the bilateral middle frontal gyrus and bilateral insula.

• • Map G: strongest activations are found in the right inferior parietal lobe extending to the superior temporal gyrus. The cerebellum is also activated.

Discussion

EEG microstates reflect the synchronous activity of large-scale neuronal networks that persist phase-locked for some tens of milliseconds and are suggested to represent the basic building blocks of free-floating mental processes. Determining the dominant active brain areas during each of these states and linking them to brain functions associated with these areas can help understanding the functional significance of these states. The present work estimated the EEG microstate networks from a large sample of subjects recorded with high-density EEG using spatial and temporal linear modeling. We found that:

• (1) Seven distinct EEG spatial patterns (topographies) best describe our large data set of spontaneous electrophysiological activity, among which we can identify the four canonical microstate maps frequently described in literature.

• (2) In line with time-resolved fMRI resting-state studies and combined EEG-fMRI resting-state studies, we identified brain regions shared by most eRSNs (Fig. 4).

• (3) Each resting-state topography is reliably associated with a distributed network of estimated sources (p < 0.005), in which we distinguished common (Fig. 4) and more network-specific regions (Fig. 3, last three columns).

Seven EEG resting-state topographies

The combination of 11 different optimization criteria identified 7 EEG scalp potential maps as the optimal number of clusters best explaining the variance of our large data set of subjects aged between 6 and 87. Many previous studies described only four microstate maps (our maps A–D). When using seven clusters, the four maps A–D explain ∼60% of our data's variance, and the additional three maps contribute to another 25% of the variance (in total 84.8%, see Supplementary Data for more details on our k-means clustering optimal criteria). Very few of the studies finding four maps estimated the optimal number of states independently; most selected the four dominant cluster maps based on the existing microstate literature: see reviews by Khanna et al. (2015) and Rieger et al. (2016).

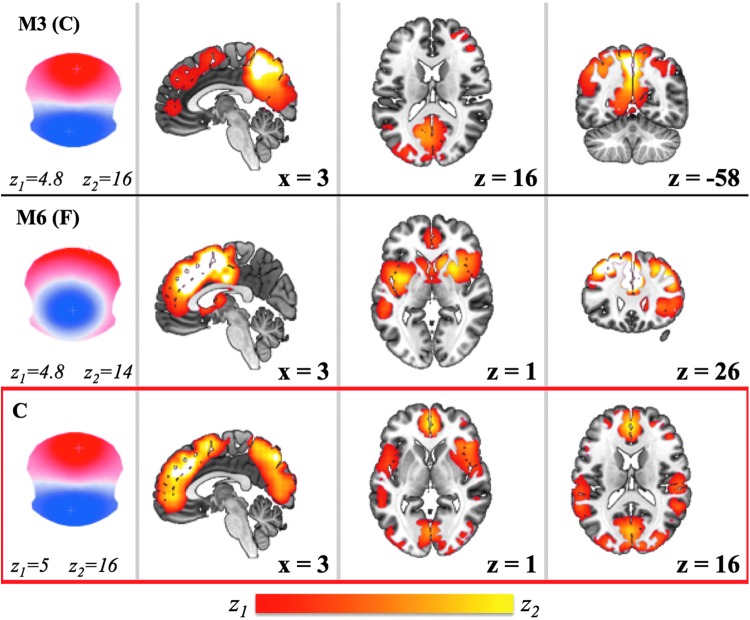
Although the topographies of these four maps are fairly stable across studies, examples are found of atypical maps in which the classification into canonical A–D classes and the subsequent functional interpretations may be too restrictive. Our analysis of 164 subjects led to the estimation of EEG resting-state topographies that include the four canonical maps, A–D, and an additional three maps, E–G, spatially distinct from the four canonical maps. Using a data-driven approach, we estimated two distinct networks generating microstates C and F (Fig. 3). However, in the literature, we find nuances of inconsistent labeling of C-like and F-like resting-state maps as representations of the same state and network. If researchers determine differences in the temporal characteristics of EEG maps (e.g., occurrences and durations) based only on the four most dominant spatial patterns, care should be taken with the interpretation of their associated RSNs [for a discussion see Seitzman et al. (2017)]. We test the hypothesis that, when only four microstates are used, C becomes a combination of map C and map F, by repeating our GLM analysis using only map A–D (the “canonical” four topographies). We observe that indeed (Fig. 5) when our GLM-based method for source localization has fewer maps to fit the data with, it ends up merging into a single network, the sources belonging to map C and those generating map F, including the anterior and posterior cingulate cortices.

FIG. 5.

Resting-state topography M3 (corresponding to map C from the seven maps A–G) and resting-state topography M6 (corresponding to map F from the seven maps A–G) and their corresponding networks (from Fig. 3, z > 4.8) are shown next to resting-state topography “C” and its corresponding network, in the bottom red box (z > 5). Resting-state map “C” is obtained by analyzing the same data set of 164 subjects but using only maps A, B, C, and D (from the set of seven resting-state maps) for the GLM fitting, instead of using the full set A–G. Color images available online at www.liebertpub.com/brain

The seven maps described in the present study and their corresponding RSNs could serve as a starting point for future research aimed at a more exhaustive and accurate classification of resting-state topographies and their corresponding networks.

Spatially overlapping networks

We estimated the neuronal generators of seven resting-state topographies using spatial and temporal general linear modeling and obtained highly reproducible results. This analysis revealed a few brain areas consistently activated in nearly all seven networks. The fact that most of the EEG RSNs share these brain areas might explain the partial spatial overlaps of the scalp potential maps (i.e., the resting-state topographies). We argue that although the low spatial resolution of EEG source imaging contributes to the smoothness and spatial overlap of any EEG-based network analysis, our reproducibility analysis conducted on a large data set of rest EEG leads to the unequivocal definition of brain areas shared by distinct resting states (p < 0.005, z > 4, see Fig. 4). These common regions include areas along the anterior/posterior medial axes as well as the insula and superior parietal cortex.

Network analyses based on fMRI, DTI, and graph theory have consistently identified these regions to be densely anatomically and functionally connected (Collin et al., 2014; Hagmann et al., 2008; van den Heuvel et al., 2012), taking a central role as major hubs in large-scale brain networks [for a review see van den Heuvel and Sporns (2013)]. Their consistent contribution to the time course of all seven EEG microstates might reflect their involvement in a broad range of cognitive processes that crosslink multiple functional domains (Karahanoğlu and Van De Ville, 2015; Mesulam, 1998; Yeo et al., 2014). The existence of and need for common communication channels well fit into the global workspace model (Dehaene and Changeux, 2004); any brain state, evoked or spontaneous, when consciously accessed, generates a high activity in its state-specific network, but it also broadcasts information to shared cortical areas for integration of information in an efficient and flexible way.

Microstate-specific networks

When subtracting from each eRSN their mean, unique areas of activity characterize each microstate. The four networks generating microstate A, B, F, and D have patterns similar to the four described in Britz et al. (2010), where the RSNs were estimated based on temporal correlation between EEG topographies and fMRI BOLD activity. This is an interesting finding because these two methodological approaches are based on very different time scales: slow-fluctuating fMRI-based networks are captured by Britz's BOLD signal analysis, whereas fast-fluctuating electrophysiological states are localized by our source analysis approach. We have previously shown that the scale-free dynamics of EEG microstates explains the link between these two time scales (Van De Ville et al., 2010). Nevertheless, in our study, the EEG networks include additional areas in comparison to the four fMRI-based networks described in Britz et al. (2010). This difference can be explained by the fact that by convolving the time course of the four microstates with the hemodynamic response function, only very slow fluctuating dynamics is kept. Such approaches do not capture fast and nonstationary properties of brain activity (Hutchison et al., 2013).

Electrophysiological studies have repeatedly shown that neural signals at rest fluctuate at much faster time scales to be effectively prepared for any possible external or internal stimulus (Bressler and Kelso, 2001; Malsburg et al., 2010). Such fast and dynamically changing systems of networks cannot be estimated with methods hypothesizing slowly fluctuating functional networks, as done in conventional fMRI analysis. New fMRI studies looking at spontaneous dynamic BOLD functional connectivity [see Preti et al. (2016) for a recent review] promote a redefinition of metabolic RSNs closer to the EEG (Hutchison et al., 2013; Zalesky et al., 2014). Similar to the results reported here, such time-resolved fMRI studies show spontaneous brain activity fluctuations that are quite different from the conventional fMRI RSNs (Smith et al., 2012).

We provide a tentative interpretation of our findings by comparing the electrophysiological networks we estimated for microstate A–D with the hemodynamic networks estimated by Britz and colleagues (2010). In our study, the left temporal lobe and the left insula are identified as major generators of microstate A. In Britz et al. (2010), the microstate A time course is correlated with fMRI BOLD activity primarily in bilateral superior and middle temporal gyri as well as the left middle frontal gyrus, areas partly corresponding to the sources we estimated in our study. Microstate B's generators are mainly localized in the occipital cortex, similarly to Britz' results. Microstate D is highly concordant with the study by Britz et al., which identifies its BOLD correlates in the right superior and middle frontal gyri and the right superior and inferior parietal lobules.

A clear difference concerns microstate C; that is, while in the study by Britz et al., BOLD correlates include the anterior cingulate, inferior frontal gyrus and insula, our results estimate microstate C being generated in parietal brain regions (the PCC and the precuneus). The network C described in the study by Britz et al. rather corresponds to our new microstate F. As described above, microstate C and F are spatially correlated (correlation coefficient of 0.7), causing previous studies to easily collapse these two states into one (especially when limiting the number of clusters to 4), with a resulting topography resembling more often microstate C, or causing mislabeling of microstate F as if it were C. As described above, when only four microstate maps are used in our analysis, C becomes a combination of map C and map F, including the anterior and posterior cingulate cortices.

Microstates E and G are two newly identified states not described in previous studies, with the exception of an E-like microstate appearing in a study by Grieder et al. (2016). Microstate E involves areas typically attributed to the default mode network: ACC, PCC, and precuneus. Microstate G, finally, might be related to the sensorimotor network mainly because of its strong activation of the cerebellum.

The extension to seven microstates instead of the canonical four not only separates previously collapsed microstates but it also identifies new microstate topographies and corresponding networks. In particular, we estimate the generators of one of these new states (microstate E) to belong to the default mode network, namely, the anterior and posterior cingulate cortices. Other microstates also include areas that belong to the default mode network, particularly microstate C, with sources in the PCC and precuneus, and microstate F, with sources in the medial prefrontal cortex. Moreover, we identify the medial prefrontal cortex as one of the sources generating most of the other microstates and, as discussed above, we interpret this region as a major hub in large-scale networks.

The functional role of the different areas of the default mode network and its common attribution to a task-negative network is discussed in depth in recent fMRI literature (Spreng, 2012; Salomon et al., 2014). In this regard, an interesting contribution comes from Andrews-Hanna and collaborators who show that the default mode network is task active in tasks that implicate self-referential cognitive processes, but also that this network can be divided into several subsystems communicating with each other through common hubs. In this proposed system, the medial prefrontal cortex and the PCC play the role of hubs, while the subsystems with distinct functional roles comprise a dorsal medial cortex subsystem (responsible for internally guided cognition) and a medial temporal subsystem (responsible for memory-guided imagery) (Andrews-Hanna et al., 2010; Andrews-Hanna, 2012; Christoff et al., 2016). A recent meta-analysis by the same group shows that besides the default mode network, other distinct networks are implicated in spontaneous thoughts (Fox et al., 2015).

Such a differential view on the default mode network and its role in the emergence of spontaneous thoughts fits well with our findings: a set of common microstate hubs and of subsystems that include, but are not limited to, areas of the default mode network, generating distinct spatiotemporal activity patterns recorded with scalp EEG.

A final point worth discussing is whether our estimated microstate networks identify areas of functional activation or deactivation. Alpha activity dominates the EEG when subjects close their eyes and is commonly associated to functional deactivation or “cortical idling” (Pfurtscheller et al., 1996). One could therefore argue that the occurrence of a microstate (and the activity in the corresponding brain areas) indicates cortical deactivation rather than activation (Milz et al., 2016).

However, while such interpretation probably holds for suppression of activity in areas not involved in stimulus processing, there is ample evidence that alpha power is increased during different cognitive task demands, questioning the idea that alpha synchronization merely reflects reduced mental activity (for a detailed discussion see Fink and Benedek (2014). For example, in a combined EEG-fMRI study, Fink et al. (2009) show that creative cognition tasks are associated with frontal alpha synchronization as well as increase of the BOLD response in frontal brain regions. Other studies also show alpha power increase during mental imagery and imagination tasks (Cooper et al., 2006; Stein and Sarnthein, 2000), suggesting that the increase of alpha activity during resting state actually reflects free-floating associations and mental imagery, a conscious cognitive activity that could be mainly responsible for generating the microstates that we observe in our study.

Conclusions

Our study combines EEG resting-state topographical analysis with a recently published EEG source localization method for estimating neural networks based on temporal pattern matching (Custo et al., 2014). We analyze a large data set of high-density EEG and estimate a set of seven microstates that explain 84.8% of the data's variance and consistently present across subjects, diverging from the conventional assumption that there are only four relevant microstates. Comparing our topographic source analysis using seven or four maps leads to the conclusion that the best policy is to estimate each data set's optimal number of clusters, rather than using a fixed number. This is particularly critical when comparing different conditions or groups, for example, patients versus controls, to avoid matching or merging “similar” maps as if they represented the same state.

The estimated sources generating the seven resting-state topographies can be separated into two components: one comprises several state-specific neural activation patterns that are unique to each state (e.g., resting state map A is generated by brain regions mainly associated with the auditory-language network, and resting state map B is associated with visually related regions), whereas the other component comprises a single map of brain regions shared among microstate networks. These two components might reflect what is proposed in the global workspace model of consciousness (Dehaene and Changeux, 2011) that hypothesizes that the brain fluctuates in two different levels of consciousness, both when elicited by a stimulus and spontaneously during rest: higher levels of consciousness (i.e., conscious access) are achieved by information made globally available to multiple networks via brain regions with dense long-range axons, while another level corresponds to state-specific neural activation patterns processed at a subliminal level.

Thanks to such new insights into rapidly fluctuating brain resting states, further studies focusing on their temporal dynamics in the millisecond time range, their transition rules, and their variability under different experimental and pathological conditions are now within reach.

Acknowledgments

This work was supported by the Swiss National Science Foundation (grant no. 320030_159705) to C.M.M. and D.V.D.V., by the National Center of Competence in Research (NCCR) “SYNAPSY—The Synaptic Bases of Mental Diseases” funded by the Swiss National Science Foundation (grant no. 51AU40_125759 to C.M.M.), and the NIH grant P41EB015902 to W.M.W.

Author Disclosure Statement

No competing financial interests exist.