NF-κB dynamics discriminate between TNF doses in single cells

SUMMARY

Although cytokine dependent dynamics of NF-κB are known to encode information that regulates cell-fate decisions, it is unclear whether single-cell responses are switch-like or encode more information about cytokine dose. Here, we measure the dynamic subcellular localization of NF-κB in response to a range of TNF stimulation conditions to determine the prevailing mechanism of single-cell dose discrimination. Using an information theory formalism that accounts for signaling dynamics and non-responsive cell subpopulations, we find the information transmission capacity of single cells exceeds that predicted from a switch-like response. Instead, we observe that NF-κB dynamics within single cells contain sufficient information to encode multiple, TNF-dependent cellular states and have an activation threshold that varies across the population. By comparing single-cell responses to an internal, experimentally observed reference, we demonstrate that cells can grade responses to TNF across several orders of magnitude in concentration. This suggests that cells contain additional control points to fine-tune their cytokine responses beyond the decision to activate.

eTOC

Using an information theory framework and single cell data, Zhang et al. set out to distinguish between different mechanisms for activation of intracellular signals. They show that heterogeneity between cellular states can lead to underestimates in the capabilities of single cells. In contrast with a switch-like model for pathway activation, they find that single cells can encode multiple levels of response that increase with stimulation strength.

INTRODUCTION

To mediate cell fate decisions, cytokines such as tumor necrosis factor (TNF) initiate dynamic alterations in the abundance and activity of signaling proteins in each cell (Aggarwal, 2003; Kawai and Akira, 2007). IkB kinases (IKKs) are recruited to ubiquitin structures near the plasma membrane and activated through induced proximity with other signaling proteins (Tarantino et al., 2014; Workman and Habelhah, 2013). NF-kB inhibitor proteins (IkB) are phosphorylated by active IKK and rapidly degraded, leading to nuclear accumulation of NF-kB transcription factors and expression of anti-apoptotic and pro-inflammatory regulators (Hayden and Ghosh, 2004; Pahl, 1999; Wajant and Scheurich, 2011). In addition to canonical roles, NF-kB responses are context-sensitive and in certain settings also drive transcription of pro-apoptotic and anti-inflammatory cytokines (Kasibhatla et al., 1998; Lawrence, 2009; Tak and Firestein, 2001). Since deregulation of NF-kB contributes to disease (Lewis and Pollard, 2006; Marx, 2004; Schottenfeld and Beebe-Dimmer, 2006), responses to cytokines must be robust to sources of biochemical noise (Kaern et al., 2005; Raj and van Oudenaarden, 2008) that limit the accuracy of information transmission in each cell (Cheong et al., 2011; Selimkhanov et al., 2014).

Temporal properties of activated NF-kB in the nucleus control diverse transcriptional programs that can be clustered based on the timing of their expression (Hoffmann et al., 2002; Lee et al., 2014; Tian et al., 2005a; Tian et al., 2005b; Werner et al., 2005). Early-response genes encode secreted cytokines and negative regulators of the NF-κB pathway such as A20 and IκBα that peak after 1 hour, whereas expression of mid- and late-response genes does not peak until hours later (Ashall et al., 2009; Tian et al., 2005b). When measured in a cell population, the duration and concentration of cytokine stimulation differentially regulates the expression of gene clusters (Ashall et al., 2009; Kellogg et al., 2015; Tian et al., 2005a; Zambrano et al., 2016) giving the impression of a tunable signaling system where graded responses regulate different physiological functions.

When viewed in single cells, the abundance and timing of nuclear NF-kB localization show substantial cell-to-cell variability (Ashall et al., 2009; Kellogg et al., 2015; Lee et al., 2014; Tay et al., 2010). Models parameterized to single-cells exposed to limiting concentrations of TNF or other NF-κB agonists suggest that pathway activation may be switch-like, in which the strength of an inducing signal changes the probability of a stochastic all-or-nothing response in each cell (Kellogg et al., 2015; Lipniacki et al., 2007; Tay et al., 2010; Turner et al., 2010). Switch-like mechanisms for pathway activation reduce sensitivity to noise by filtering low-level environmental fluctuations and preventing spurious inflammatory responses (Kellogg et al., 2015; Turner et al., 2010). However, at the single-cell level, a switch cannot transmit dosage information and restricts the range of responses in each cell’s to either ‘on’ or ‘off’ when exposed to time-varying stimuli. It’s difficult to reconcile how cytokines control diverse cell fate decisions using a mechanism that transmits little information in each cell.

Here, we use models to show how mechanisms of cytokine responses can be discerned from single-cell data. We measure time courses of nuclear NF-κB in 1000s of single cells exposed to TNF over a range of concentrations and durations, and use an information theory formalism to quantify the channel capacity of the system. Although we find evidence of a threshold for pathway activation that varies between cells, we also find that single-cell dynamics encode sufficient information for multiple states of responses to cytokine conditions. Despite significant heterogeneity when comparing between single cells in the same condition, repeat stimulation experiments reveal dose-dependence when different conditions are compared in the same cell. Our results reveal that single cells can discriminate and grade multiple levels of responses to cytokine doses across orders of magnitude in concentration.

RESULTS

Single-cell Data are Necessary to Discriminate Between Models for Switch-like and Graded Signal Transduction

To determine how switch-like and graded mechanisms for cytokine responses differ when viewed at the levels of single cells and cell populations, we developed a set of heuristic models to simulate a heterogeneous population of cells exposed to a range of cytokine doses. Each model represents one of three distinct mechanisms for pathway activation (Figure 1A). For all models we simulated 100 single cells, each initialized with a distinct ‘cell state’ (integers between 1 and 100) which determines how strongly it will respond to stimulus, and a random threshold for activation (See Figures 1B and S1). All models included terms for basal and inducible noise to better approximate biological systems (Figure S1).

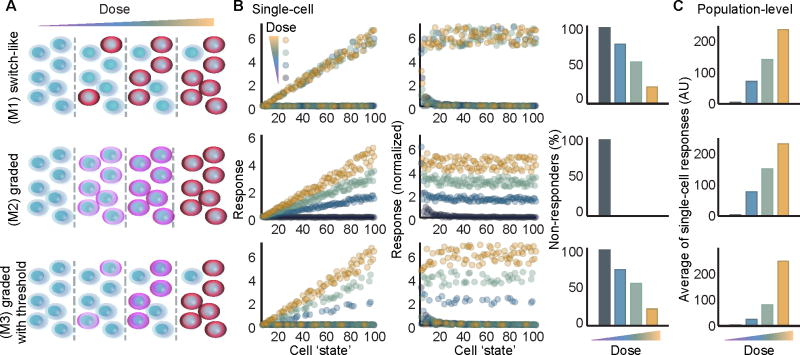
Figure 1. Population-level data cannot distinguish between switch-like and graded response mechanisms.

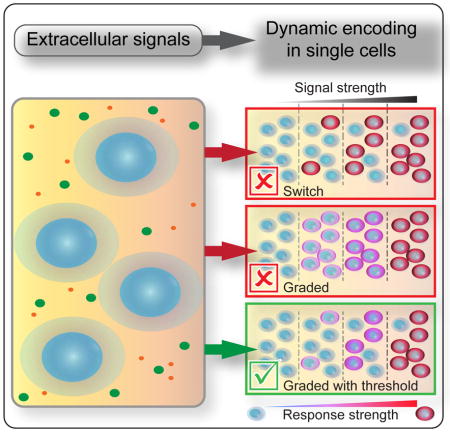
(A) Schematic for (M1) a switch-like mechanism for activation where a cytokine dose increases the probability of an all-or-nothing response in each cell; (M2) a graded mechanism for single-cell activation in which each cell’s response is graded in proportion with increasing cytokine dose; and (M3) a combined threshold with graded mechanism where single cells responses are graded in proportion with cytokine dose only if the dose is greater than the cell’s threshold for activation. (B) Simulated responses of single cells modeled with extrinsic noise (described in Figure S1). Each cell is initialized in a unique ‘cell state’ that approximates its responsiveness to cytokine. Responses to 4 doses are compared in each model plotted as a raw response (left), or a normalized response that divides each cell’s response by its ‘cell state’ (middle). The fraction of non-responder cells is quantified for each dose (right). (C) Three mechanistically distinct models are indiscernible when using the average of single cell responses to approximate a population-level measurement. See also, Figure S1.

Each model describes a plausible yet distinct scenario, with differences apparent at the single-cell level (Figure 1B). For Model 1 (M1), pathway activation is switch-like and a cell exposed to any dose greater than its activation threshold will respond fully as determined by its ‘cell state’. Response distributions overlap between doses in M1 for responsive and non-responsive cells respectively. For M2, there are no non-responder cells at any non-zero dose (Figure 1B, right column), and single-cell responses are graded with ‘dose’ and ‘cell state’. Model 3 (M3) combines M1 and M2, where cell responses increase with ‘dose’ and ‘cell state’, but only for doses greater than the cell’s activation threshold. For M3, non-responsive cells exist with overlapping distributions for all non-saturating doses. When each cell’s response is normalized to its cellular state in M2 and M3, the response strength to a single input dose is nearly invariant across activated cells (Figure 1B, middle column). In contrast for M1, there is no dosage information transmitted beyond sub- or supra-threshold cytokine concentration. Remarkably, when viewed as population-level averages, for example as may be observed for western blots, these models are indistinguishable (Figure 1C).

Cell Lines Show Differing Sensitivity and Responsiveness to Cytokine Stimulation

To investigate mechanisms of dose discrimination, we set out to identify a cell line that responds strongly to TNF. We used fixed-cell immunofluorescence to characterize subcellular NF-κB localization in a panel of human cancer cell lines. Because the duration of exposure to cytokines can distinctly coordinate downstream signal transduction pathways (Hoffmann et al., 2002; Kellogg et al., 2015; Lee et al., 2016; Zambrano et al., 2016), cells were exposed to a range of TNF concentrations as a single pulse or continuously. The average nuclear abundance of the RelA subunit of NF-κB was measured from fixed-cell images (Figure 2A; thick lines) to compare cell lines and rank their relative sensitivities.

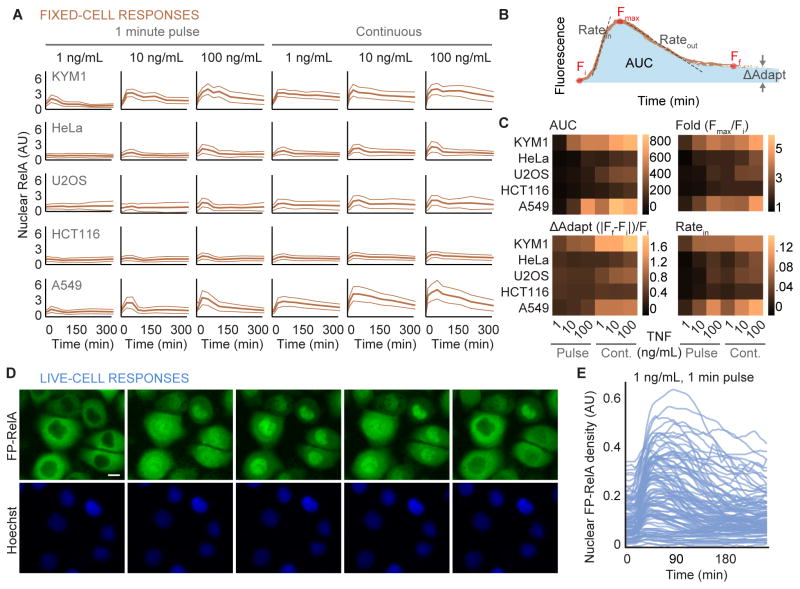
Figure 2. Heterogeneity of responses to TNF between cell lines and single cells.

(A) Time courses for average nuclear RelA from fixed cells are shown for a panel of human cell lines exposed to indicated concentrations of TNF continuously or as a single 1-minute pulse (solid orange curve). On average, 11374 single cells were measured across the time points for each cytokine condition. Light colored lines indicate the standard deviation of approximately 1274 cells measured at each time point. Time points for fixation included 0, 10, 30, 60, 90, 120, 180, 240, and 360 minutes following exposure to TNF. (B) Descriptors used to quantify the response of cells to a cytokine. F_i, F_max, and F_f respectively describe the initial, maximal, and final amount of nuclear RelA fluorescence. AUC defines the area under the curve for the cytokine response and ΔAdapt quantifies the deviation from a perfect adaptive response. Rate_in and Rate_out quantify the maximal rate of nuclear entry and exit respectively for average of fixed-cell data. (C) Heatmaps for each descriptors quantified in a panel of cell lines exposed to indicated cytokine conditions. Formulae used to calculate ΔAdapt and fold change (Fold) are shown. See also, Figure S2. (D) Time-lapse images of FP-RelA stably expressed in KYM1 cells exposed to a single 1-minute pulse of 1ng/mL TNF; scale bar, 10 μm, see also Movie S1. (E) Time courses of nuclear FP-RelA density measured in single cells treated with a 1-minute pulse of 1 ng/mL TNF. See also, Figure S2 and Table S1.

The intensity of nuclear RelA varied among single cells of the same type when exposed to TNF (Figure S2A). To quantify pathway activation for each cell line, time courses of nuclear RelA averages were decomposed into a series of descriptors (Figure 2B; (Behar et al., 2013; Cohen-Saidon et al., 2009; Lee et al., 2014)) and plotted as heat maps (Figure 2C). Using the area under the curve (AUC) and the maximum fold change (F_max/F_i), KYM1 and A549 cells showed the strongest responses to TNF. Although both cell lines had comparable rates of nuclear change (Rate_in and Rate_out) and deviations from adaptation (Figures 2C and S2B), KYM1 cells were selected for further study because they are sensitive to the broadest range of TNF concentrations (0.1 ng/mL; Figure S2C).

Temporal properties of molecules within single cells can be quantified over multiple time points using live-cell experiments (Ashall et al., 2009; Hoffmann et al., 2002; Lee et al., 2014; Purvis et al., 2012; Selimkhanov et al., 2014). To further characterize TNF-induced dynamics of RelA, KYM1 cells that stably express fluorescent protein-RelA (FP-RelA) fusions (Figure S2D–F) were imaged by time-lapse in growth medium with trace amounts of a live-cell dye to assist with nuclear segmentation (Zambrano et al., 2016). Compared between single cells, FP-RelA showed transient and variable translocation into the nucleus (Figures 2D and 2E). Consistent with previous results in HeLa (Lee et al., 2014), coefficient of variation (CV) for descriptors for nuclear RelA that approximate response dynamics (such as fold change F_max/F_i, or adaptation F_f/F_i) showed significantly less variability than others (Figure S2G; non-overlapping 95% CI).

If response dynamics are less variable between cells and also encode condition-specific signals (Purvis and Lahav, 2013), then they may more accurately convey information about the environment. Indeed, calculations for the information transmission using multivariate vectors to describe dynamic responses of single-cells, such as RelA dynamics in cells exposed to lipopolysaccharides, yield significantly greater values than those calculated from single time-points (Selimkhanov et al., 2014). Although TNF-induced pathway activation was previously characterized as a <1-bit system using measurements of nuclear RelA at a single time-point (Cheong et al., 2011), more information may be encoded by dynamics.

Dynamics of TNF-responses Carry More Information but are Confounded by Populations of Non-responsive Cells

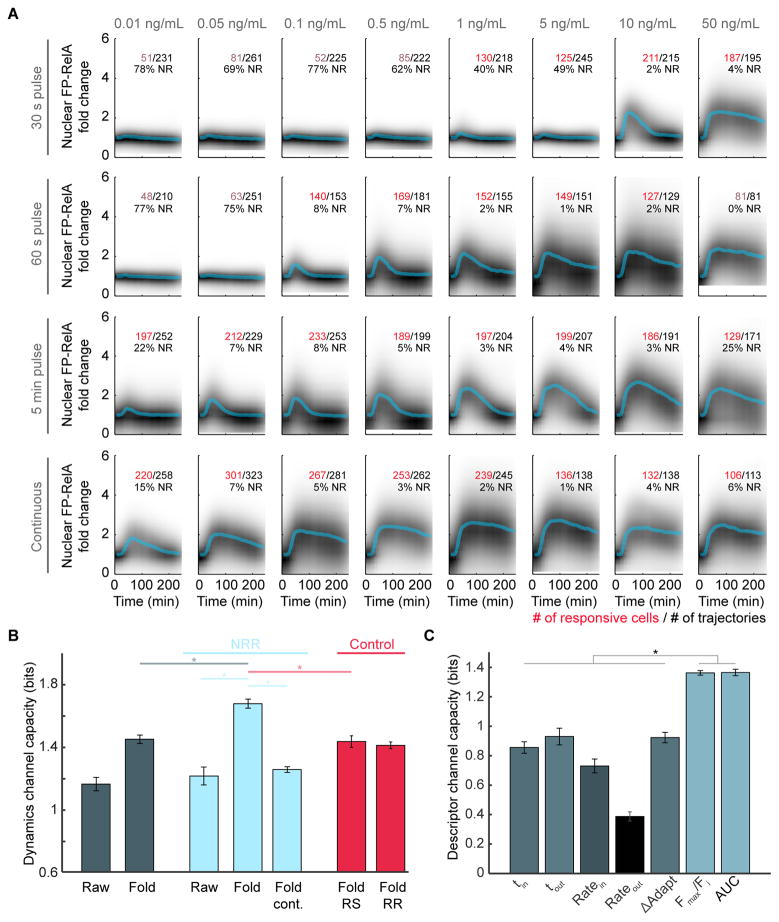
To determine if NF-κB dynamics contain more information about TNF dose, we measured single-cell responses to a broad range of TNF concentrations. Cells were also exposed to a single pulse of TNF with a 30-second, 1-minute, or 5-minute duration using the same range of concentrations (Figure 3A, in addition to an untreated control in Figure S3A) to reflect conditions that cells may encounter in vivo (Kellogg et al., 2015; Lee et al., 2016). Time courses for each cell’s nuclear FP-RelA was described by a vector, and a k-nearest neighbors approach was used to calculate the information transmission capacity (Selimkhanov et al., 2014). Because experimental data is subject to measurement noise, the resulting channel capacity estimates a lower bound for mutual information between single-cell responses and TNF conditions or, alternatively, the number of distinguishable dose-response pairs (Levchenko and Nemenman, 2014). Using a subset of 26 conditions (Figure 3A, where the number of responsive cells is labeled in red in addition to untreated control; see STAR methods), the information transmission capacity converged to 1.2 bits or 1.4 bits when representing single-cell time courses in arbitrary units (‘Raw’) or as fold change (‘Fold’) respectively (Figures 3B, S3A, S3B and S3E).

Figure 3. Information Transmission Capacity of the TNF-NF-κB pathway.

(A) Density plots of single-cell FP-RelA time courses for responses to TNF with indicated concentration and duration. Median of single-cell responses for each condition is shown in blue. Inset numbers indicate the total number of single-cell time courses collected (black), the number of cells with a significant amount of FP-RelA translocation (red or pink), and the fraction of non-responders (NR) for each condition. (B) Channel capacity values calculated for each data set: (dark blue) ‘Raw’ and ‘Fold’ data sets where each single-cell time course is represented in arbitrary units or fold change (Figure S3A); (light blue) ‘NRR’, data sets where time courses for non-responder cells are removed, the ‘Fold cont.’ data set only includes conditions from the Fold-NRR with continuous exposure to TNF (bottom row of panel A); (red) Average of 20 subsample control data sets where the same number of cell trajectories are removed from the ‘Fold’ data set as in the NRR, but cells were either ‘Randomly Selected’ (Fold RS) or ‘Responding cells were targeted for Removal’ (Fold RR) (See STAR methods). For all data sets, conditions with fewer than 100 responder cells (pink numbers in panel A) were removed from channel capacity calculations; p < 10⁻¹², t test. (C) Channel capacity values for scalar descriptors of FP-RelA dynamics (p ≪ 10⁻¹³, t test). Error bars represent standard deviation. See also Figure S3.

NF-κB was previously characterized as a system with digital properties, having fewer cells that respond to low strength stimulus (Kellogg et al., 2015; Lee et al., 2016; Tay et al., 2010; Turner et al., 2010). Since the channel capacity estimates the number of distinct response distributions a system can achieve, we asked whether calculations are affected by distributions of non-responsive cells that are likely to exist and overlap in all conditions. We developed a statistical model of an 8-state system (S₀ through S₇) with a channel capacity of 3 bits (Figures S3C and S3D; see STAR methods). Simulations compared scenarios where each of the excited states (S₁ through S₇) contained a predefined fraction of non-responders sampled from the ground state distribution (S₀). Even though the channel capacity of the excitable subpopulation remained constant, simulations showed that bit depths for the whole system drop in proportion with the non-responder fraction (Figure S3C) suggesting that information transmitted accurately by responders may be concealed by cells that do not respond to stimulation.

We set out to determine whether non-responsive cells in our data set impact the channel capacity of TNF-induced signals. Previously, we demonstrated that cells exposed to TNF with less than 1.2-fold change in nuclear FP-RelA are unlikely to activate transcription (Lee et al., 2016), so we applied the same threshold to categorize cells as TNF-responsive and non-responsive (NR; listed in Figure 3A) in each condition. The fraction of NR varies widely between TNF conditions, with fewer cells responding to low concentration or short duration TNF exposure. By removing these trajectories from our data, we created a data set with Non-Responder cells Removed (‘NRR’). Although channel capacity of the Raw-NRR showed a marginal yet significant increase in bit depths over unfiltered data (p < 0.05; Figure 3B), the Fold-NRR had significantly greater channel capacity (1.7 bits) than the ‘Fold’ data set (p < 10⁻¹²) in addition to a subset from the Fold-NRR with only continuous treatment conditions (1.3 bits; p < 10⁻¹⁶; bottom row of Figure 3A) which shows that cells transmit information about pulse-treatment that is distinct from continuous conditions.

Since descriptors can summarize dynamic properties of a cell’s response, we asked whether certain descriptors transmit more information about TNF. Single-cell responses in the Fold-NRR were fit to two sigmoid functions (Figure S3F; (Chechik and Koller, 2009)), used to compute descriptors described above (Figure 2B) in addition to two temporal descriptors for the time of maximal rates for nuclear entry or exit (t_in and t_out respectively). We calculated the channel capacity for each descriptor (Figure 3C) and found that the AUC, a summary statistic that approximates the whole time course of a cell’s response, carries the most information (1.4 bits), followed closely by the maximum fold change.

Our results show that a subpopulation of cells can accurately resolve at least 1.7 bits of information about TNF-exposure conditions. Although the channel capacity using vectors of single cell dynamics are higher than scalars by definition (Potter et al., 2017), we also find the system transmits approximately 1.4 bits of information using scalar descriptors. These results suggest that single cells are capable of more than ‘on’ or ‘off’ responses to TNF, but do not ensure that single cells can achieve multiple distinct levels of response that grade with cytokine dose.

Single Cells can Grade Multiple Levels of Responses with TNF Dose

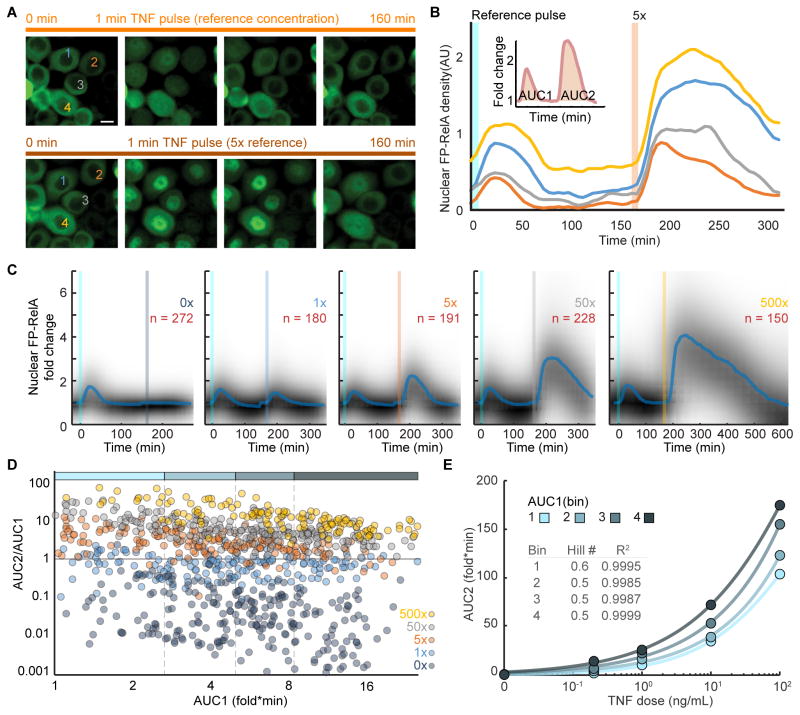
We used repeat TNF stimulation to determine whether graded responses can be observed in the same cell. From our matrix of live-cell responses (Figure 3A), we reasoned that a 1 minute pulse of 0.2 ng/mL TNF should induce a detectable yet weak response in most cells leading to minimal perturbation. Following exposure to a pulse of TNF, we measured expression for A20 and IκBα and observed that the abundance for mediators of negative feedback return to nearly baseline after 3 hours (Figure S4A–B; compare 0.2 and 10 ng/mL). Subsequently we refer to a 1 minute pulse of 0.2 ng/mL as a ‘reference’, used as a common condition to compare same-cell responses to other TNF conditions. AUC1 and AUC2 (inset Figure 4B) were measured from a manually curated data set of single cells exposed to a ‘reference’ followed by a 3 hour recovery period and then a 1 minute ‘test pulse’ of indicated concentration (Figure 4A–C). Only cells that were responsive to ‘reference’ stimulation were included in the data set. Results from control experiments comparing a 6 hour recovery period were similar, but there were clear indicators of tolerance when using a high concentration reference (Figure S4C–E).

Figure 4. Repeat TNF Stimulation Reveals a Graded Mechanism of Dose Discrimination in Single Cells.

(A) Time-lapse images of FP-RelA in live cells stimulated with a 1 minute reference pulse of 0.2 ng/mL TNF, followed by a 1 minute pulse with 5x the reference dose (1 ng/mL TNF). Same cells are marked; scale bar, 10 μm; see also Movie S2. (B) Representative single-cell time courses for the cells labeled in (A). Inset shows schematic of area under the curve calculations for single-cell responses to the first (AUC1) and second (AUC2) TNF pulse (C) Density plots of single-cell FP-RelA time courses for cells exposed to a reference TNF pulse followed by a range of increasing test doses. Median of single-cell responses is shown in blue and inset numbers indicate the number of single cell time courses collected in each condition. (D) Scatter plots showing AUC2/AUC1 stratified along AUC1 across the range of test conditions. Colored bar along top depicts bins of single cells based on AUC1 into an approximately equal number of cells per condition. (E) Average response of single cells (AUC2) to increasing ‘test pulse’ concentrations (0, 0.2, 1, 10, or 100 ng/mL TNF) for each bin in panel D; inset describes hill coefficients and goodness of fit for logistic regression. See also, Figure S4 and Table S2.

Comparing ‘test pulse’ only, histograms for AUC2 showed overlap, with a significantly smaller bit depth than values calculated above for response dynamics (p < 10⁻¹⁰; Figures S4F and S4G). By contrast, when AUC2 was normalized by AUC1 for the same cell (AUC2/AUC1) and plotted against AUC1 we saw clearer separation between conditions in proportion with TNF concentration (Figure 4D; p < 10⁻⁸⁴ one-way ANOVA; pairwise comparisons in Table S2) analogous to normalized response patterns of M2 and M3 in Figure 1B. To compare cells with similar responsiveness to TNF, data were binned by AUC1, and within each bin sigmoid fits were calculated for AUC2 plotted against dose (Figure 4E). Although there was a trend that cells with large AUC1 in response to the reference also have proportionately larger AUC2 for the same ‘test pulse’ condition, all data sets were well-fit by sigmoid functions with comparable hill coefficients much smaller than 1 (Figure 4E, inset). These results demonstrate that the dose-response curve of single cells is not switch-like (Ferrell and Ha, 2014). Similarly, even though responses to ‘reference’ are independent of the ‘test pulse’, channel capacity values calculated for [AUC1, AUC2] are significantly larger (p < 10⁻¹¹) and comparable with the channel capacity calculated from the matrix of live-cell responses (Figure S4G), suggesting that the accuracy of responses increase when conditioned on the cell state. Together, our results demonstrate that single cells are capable of multiple levels of responses that grade in proportion with TNF concentration.

DISCUSSION

A key question is how coarse-grained is a single cell’s ability to detect and respond to inflammatory cytokines in its environment – do activating signals increase the probability of a stochastic all-or-nothing response, or do cells precisely grade their responses to a range of stimulus levels? In this work, channel capacity calculations and repeat stimulation experiments show that some cells can accurately grade multiple levels of responses to cytokine conditions. Although these observations contradict a purely switch-like model for pathway activation proposed by model M1 (Figure 1), we also observed in all conditions a subpopulation of cells with a non-responder phenotype. The fractional abundance of non-responder cells varies widely depending on the intensity of cytokine conditions (Figure 3A) which contradicts the purely graded model of pathway activation described by M2 (Figure 1B, right column). Taken together our results support M3, in which low-level cytokine fluctuations are filtered by a threshold for pathway activation that varies between cells, and responses to supra-threshold conditions are graded with dose.

Several factors that were not considered in previous studies were critical to observe greater than 1.5 bits of information in the ‘Fold-NRR’ (Figure 3B): (1) By analyzing the subpopulation of responder cells in isolation from non-responders the channel capacity was increased by ~0.3 bits (c.f. ‘Fold’ and ‘Fold-NRR’); (2) by representing single-cell time courses as fold change, the channel capacity was increased by ~0.5 bits (c.f. ‘Raw-NRR’ and ‘Fold-NRR’). This is consistent with incoherent feedforward network motifs in many signaling systems that more robustly encode and detect fold-change dynamics (Cohen-Saidon et al., 2009; Goentoro and Kirschner, 2009; Lee et al., 2014); (3) finally, ~0.5 bits of information was gained by exposing cells to TNF as a pulse in addition to continuous treatment conditions across a range of concentrations (c.f. ‘Continuous-Fold-NRR’ and ‘Fold-NRR’). Although each factor contributes to the channel capacity, their combined effects are non-linear and synergistic. Above all, repeat stimulation experiments that compare responses to a reference in the same cell were essential to demonstrate the capabilities of single cells.

Cellular information processing can be divided into categories of ‘cell autonomous’, such as the channel capacity of a single cell studied here, and ‘cell population’ in which cells share ligands through paracrine feedbacks to coordinate decisions over longer timescales (Suderman et al., 2017). Underlying both is the impression that signal transduction networks have an intrinsic capacity to transmit information that is the same in every cell, yet our results suggest that this may not be the case. Although non-responder cells share a similar ‘response-phenotype’, their abundance varies between TNF conditions which suggests they are a heterogeneous subpopulation that cannot be defined by a unique network state. For example, cells that do not express a critical component of the TNF-receptor complex may be completely refractory to any TNF stimulus yet biochemically distinct from other non-responsive cells. Whereas stochastic fluctuation in the abundance of regulatory proteins in a cell may broaden or restrict the range of stimulus conditions to which it can respond. It’s therefore conceivable that cell subpopulations have distinct information transmission capacities that are conditioned by their biochemical state, and that mixtures of these subpopulations lead to underestimates of the network’s capacity to transmit information.

Sources of noise make biological systems appear unpredictable, but that does not mean they are unreliable. Through accounting for heterogeneity in cell states, the information transmission capacity of single cells is better approximated and it is found that cells can grade multiple levels of responses to cytokines over a range of doses. Although it remains to be determined whether grading is biologically important for cell fate decisions, either cell autonomous or through cell-cell communication, grading provides additional control points for cells to fine-tune and diversify responses to stimuli.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Requests for resources should be directed to the Lead Contact, Robin Lee (robinlee@pitt.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Cell culture

Parental KYM1 (female), HeLa (female), U2OS (female), HCT116 (male), and A549 (male) cell lines (ATCC) were cultured in RPMI, DMEM, McCoy’s 5A, McCoy’s 5A, and F12K media respectively at 37°C and 5% CO2. Parental KYM1 and KYM1 cells infected with a retroviral construct to express mVenus-RelA under control of the CMV were kindly provided as a gift from Suzanne Gaudet. From these cells, a clonal cell line was selected based on FP-RelA expression, localization, and responsiveness to TNF. All media was supplemented with 10% Corning Regular FBS, 100 U/mL penicillin, 100 μg/mL streptomycin and 0.2mM L-glutamine (Invitrogen).

METHOD DETAILS

Fixed-cell immunofluorescence

For fixed-cell experiments, cells were seeded into plastic bottom 96-well imaging plates (Fisher) at the following densities: KYM1 12000 cell/well 24 hours prior to treatment, HeLa 7000 cell/well 24 hours prior to treatment, U2OS 6000 cell/well 24 hours prior to treatment, HCT116 20000 cell/well 24 hours prior to treatment, and A549 5000 cell/well 48 hours prior to treatment or 6000 cell/well 24 hours prior to treatment for low cytokine concentration test. On the day of the experiment, media containing cytokine (TNF) was prepared at 15X the desired concentration for each well. Timing of cytokine treatment was planned so that fixation for all time points (0, 10, 30, 60, 90, 120, 180, 240, and 360 minutes) occurred simultaneously at time zero. For continuous treatments, 12.3μL of pre-warmed 15X cytokine mixture was spiked into wells and mixed. For pulse treatments, 12.3μL of 15X cytokine was mixed into wells and after 1 minute all the media was removed, cells were washed in PBS, and 185μL of fresh media was added to each well. Between treatments the cells remained in environmentally controlled conditions (37°C and 5% CO2) and 15X cytokine solutions were kept at 4°C to prevent degradation.

At time zero, media was removed from the wells, 185 μL of PBS was used to wash the wells, and wells were incubated at room temp in 120 μL of 4% paraformaldehyde (PFA) in 1X PBS for 10 minutes. Wells were washed 3X three minutes with 185 μL 1X PBS and then incubated in 120 μL 100% methanol for 10 min at room temp. Next, wells were washed 3X three minutes in PBS-T (1XPBS 0.1% Tween 20) followed by 120 μL of primary antibody solution (3% BSA in PBS-T) with a primary antibody (selected from: 1 μg/mL α-RelA [sc-8008; Santa Cruz]; 5 μg/mL α-A20 [ab13597; Abcam]; or, 1:400 α-IκBα [#4818; CST]). Plates were wrapped in para-film and left to incubate at 4°C overnight. The following morning, wells were washed 3X five minutes in 185 μL PBS-T followed by incubation for 1 hour in 120 μL of the secondary antibody solution (3% BSA PBS-T, 4 μg/mL Goat anti-Mouse IgG Alexa Fluor 647 (Thermo Fisher)). 185 μL PBS-T was used to wash the wells for 5 minutes and they were put into 120ul Hoechst solution (PBS-T, 200ng/mL Hoechst) for 20 min. Finally wells were washed five minutes with PBS-T and then 185 μL PBS was used to fill the wells and keep the cells hydrated during imaging. Cells were imaged using Delta Vision Elite imaging system at 20x magnification with a LUCPLFLN objective (0.45NA; Olympus).

Live-cell imaging

Live cells were imaged in an environmentally controlled chamber (37°C, 5% CO₂) on a DeltaVision Elite microscope equipped with a pco.edge sCMOS camera and an Insight solid-state illumination module (GE). KYM1 cells expressing FP-RelA were seeded at a density of 25000 cells/well 24 hours prior to live-cell imaging experiments on no. 1.5 glass bottom 96 well imaging plates (Matriplate). 2 hours before imaging, live-cells were pre-stained with 300ng/mL Hoechst 33342 for 1 hour. Following this all growth medium contained trace concentrations of Hoechst (60 ng/mL) to maintain the nuclear stain and assist with segmentation in downstream applications. Consistent with previous studies (Zambrano et al., 2016), cells continued to grow and divide normally for at least 10 hours while imaged in these conditions. Wide-field epifluorescence and DIC images of KYM1 cells were collected using a 20x LUCPLFLN objective (0.45NA; Olympus). For all treatments, cytokine mixtures were prepared and pre-warmed so that addition of 120μL added to wells results in a final concentration as indicated. For wash-out experiments, cytokine-containing media was aspirated, wells were washed with pre-warmed media, and fresh media was added to each well. FP-RelA, time-lapse images were collected over at least 4 fields per condition with a temporal resolution of 5 minutes per frame before and after exposure to TNF. Cells were imaged for at least 30 minutes prior to addition of TNF.

Western blots and analysis

Kym1 cells stably expressing FP-RelA were cultured for 24 hours in complete growth medium. After treatments, cells were lysed in SDS-based lysis buffer consisting of 112 mM Tris-Cl, pH 6.8, 4% SDS supplemented with protease and phosphatase inhibitors at 4°C for 30 min. Protein extracts were clarified by centrifugation at 4°C at 12,000 × g for 10 min. Nuclear extracts were isolated using NE-PER^™ Nuclear and Cytoplasmic Extraction Reagents (Pierce). Lysate protein levels were quantified by BCA assay (Pierce). Samples were separated by SDS-PAGE, 25 μg total protein per lane, then transferred to PVDF membranes. Blocking was done in 5% milk in TBS for 1 hour. Primary antibodies directed at RelA, A20, IκBα, β-actin, Lamin A/C(#4764, #5630, #4814, #3700, and #4777 respectively; Cell Signaling Technology), GAPDH (sc25778; Santa Cruz) were diluted in 5% milk in TBS-T and incubated overnight at 4°C. Alexa 680/800-conjugated secondary antibodies (LI-COR) were used in combination with an Odyssey (LI-COR) scanner for detection and quantification of band intensities.

Gaussian model

An 8-input system (S₀ through S₇) was modeled by sampling 200 points from each of eight 2 dimensional Gaussians with unit variance and means separated by a scalar in one dimension and 0 in the other dimension. Here, S₀ can be thought of as a ground state and each additional state is excited by a scalar multiple to model a dose-response system with a theoretical maximum channel capacity of 3 bits. Models with 6 units (no overlap) and 2 units (partial overlap) of separation were compared (Figure S3C). To simulate the effects of a non-responsive fraction f, 200 * f points were sampled from the first Gaussian distribution (ground state S₀), and 200(1− f) points sampled from the Gaussian for each of the excited states (S₁ through S₇). Channel capacity calculations were carried out for 7 values of f, ranging from 0 to 0.6 to match the range of experimentally observed fractions of non-responders.

In a complementary set of experiments, we simulated the effects of sub-sampling on channel capacity calculations (Figure S3D). Here, we started with a mixed population that contains 50% non-responders and 50% cells capable of dose discrimination (i.e. f = 0.5). Selecting for removal the fraction of cells as indicated on the x-axis either randomly (red) or by targeting non-responders (blue), mutual information was calculated. We see that random subsampling does not increase the channel capacity, whereas targeting non-responders does.

QUANTIFICATION AND STATISTICAL ANALYSIS

Fixed-cell image analysis

Cell Profiler (Carpenter et al., 2006) was used to segment the nuclear compartment cells using the Hoechst channel, and quantify median nuclear intensity values from each cell in fixed-cell images. Data were compiled and statistical analysis performed using MATLAB. Cell numbers used to calculate mean and standard deviations for fixed-cell experiments are summarized in Table S1.

Live-cell analysis

Custom scripts in MATLAB were used to flat-field correct, background correct, and register movies of FP-RelA. Nuclear regions were segmented using the Hoechst channel and single-cell trajectories of nuclear FP-RelA were tracked using Cell Profiler (Carpenter et al., 2006). For each cell at each time point, median nuclear intensity of FP-RelA was reported by Cell Profiler and represented as three-frame running averages to reduce the influence of high-frequency noise. The fold-change transform was carried out by dividing each single-cell time course by its average nuclear fluorescence from four imaging frames before the time point at which TNF was added (Figure S3A). Cells that were observed to die, divide or leave the field of view within the experimental timeframe were excluded from analysis. Trajectories for each condition were shown as a density plot in MATLAB (Eilers and Goeman, 2004). Cell numbers collected in each live-cell experiment are listed in their respective figure panels.

Channel capacity calculations

All channel capacity calculations were performed using updated MATLAB scripts (2017-08-15) provided by Roy Wollman and used as described previously (Selimkhanov et al., 2014). Briefly the algorithm uses a k-nearest neighbor density estimation to compute the conditional probability density of each single-cell response. These are used to compute the entropy of the response, and the entropy of the response conditioned on the signal. The difference in these two terms gives the mutual information, which is maximized over all possible probability distributions of the signal, using the MATLAB optimization function fmincon. The method is described in more detail in Selimkhanov et al., 2014.

A k value of 5 was used for all the k-nearest neighbor probability density estimation steps. The values reported are the mean and standard deviation of 10 jackknife iterations. At each iteration, the channel capacity was estimated by subsampling from the data set 20 different sample size (SS) fractions ranging from 0.6 to 0.95. To reduce sample size bias and estimate channel capacity variance, linear regression was used to extrapolate the channel capacity value at a sample size of infinity, i.e. 1/SS = 0 (See red dots in Figure S3B). The flatness of the resulting slopes are consistent with observations from Selimkhanov et al., suggesting that the size of our data set is sufficient to accurately estimate channel capacity values, i.e. values calculated for the finite sample size are similar to the extrapolated values.

Time courses of nuclear RelA were collected for thousands of single cells across conditions and the information transmission capacity was calculated for the dynamics of TNF-driven signaling. We next described single cell responses using vectors of increasing dimension to compare channel capacities (Figure S3E). For these calculations, each single-cell time course was sub-sampled into a multivariate vector of dimension ‘d’ using a uniform grid centered on the middle time point as described previously (Selimkhanov et al., 2014). We used jackknife resampling to correct for sample size bias and determine the variance of calculated bit depths as described by Selimkhanov et al. (Figure S3B). Using a subset of 26 of the tested conditions, discussed below in further detail (Figure 3A; conditions where the number of responsive cells is labeled in red), calculations for channel capacity converged to a maximum value of 1.2 bits in fewer than 5 dimensions (Figure S3E, orange line for the ‘Raw’ data set). Jackknifing to estimate sample size bias confirmed that we had sufficient data to accurately estimate the channel capacity at a vector dimension of 5 (Figure S3B). We therefore use d = 5 to compare channel capacity estimates in subsequent experiments.

To maintain adequate sample sizes for channel capacity calculations and ensure that equal numbers of conditions are compared between data sets, we filtered conditions with fewer than 100 trajectories in the NRR data set for all channel capacity calculations (Figure 3A; conditions with pink numbers). All data sets therefore include a total of 26 conditions: 25 TNF-response conditions with at least 100 trajectories in the NRR, in addition to the untreated control sample that was not filtered for non-responder cells. The channel capacity was calculated for each data set using uniformly sampled vectors with an increasing number of dimensions. As previously shown (Selimkhanov et al., 2014), we see that that increasing the number of dimensions increases the estimate of the channel capacity at first, but after a certain point convergence is achieved upon which adding more vector dimensions does not increase the estimated channel capacity.

For the “NRR” datasets, all single-cell trajectories with a maximum fold change of less than 1.2 were removed from the analysis (Lee et al., 2016). We found that channel capacity calculations were robust to slight variations in this threshold. To show that the increase in the estimated channel capacity on removing non-responder cells is not a trivial effect of subsampling the data set, we generated two control data sets, “Fold RS” and “Fold RR”. To get “Fold RS” we calculate the total number of non-responding cells in our “fold” data set and remove an equivalent number of trajectories randomly distributed throughout the data set. To get “Fold RR”, we remove an equivalent number of ‘responder’ trajectories randomly distributed among responding cells in the data set. The channel capacity estimated from both of these is similar to that obtained using the “fold” dataset. The randomized controls were generated 20 times, and for each we performed 10 jackknife replicates. The values reported are the mean and variance of the channel capacity obtained from each of the 20 randomized data sets.

Sigmoid Fits to Estimate t_in and t_out

To estimate the times of maximum rate of FP-RelA nuclear entry and exit, the following two-sigmoid model was used:

$$\begin{array}{cc}y(t)=\frac{1}{p_1+p_2\ast {\mathrm{e}}^{-{\mathrm{p}}_{3}t+p_4}}+p_5,& t\le t_{\mathit{max}}\\ y(t)=\frac{1}{p_6+p_7\ast {\mathrm{e}}^{-{\mathrm{p}}_{8}t+p_9}}+p_{10},& t>t_{\mathit{max}}\end{array}$$

Where t_max is the time of max fold change of nuclear NF-κB. The sigmoid is fit to the data using the genetic algorithm function (ga) in MATLAB to minimize the objective function:

$${\mathit{\sum }}_t{\left(\frac{(y(t)-y_{\mathit{true}}(t))}{y_{\mathit{true}}(t)}\right)}^2.$$

Sigmoid Fits to Calculate Hill Coefficients

The bin boundaries for AUC1 were specified as follows: [0.25 2.8 5.5 9.4 50]. This was done to maintain roughly equal numbers of cells per bin. For cells that fall within a certain bin, i.e. they have similar values of AUC1, a 4 parameter logistic equation (L4P) was fit to describe the relationship between AUC2 and dose, i.e.

$$\mathit{AUC}2=D+\frac{A-D}{1+{\left(\frac{\mathit{dose}}{C}\right)}^B}$$

The hill coefficient, i.e. B obtained for each of these fits was less than 1.

Extracting Descriptors from NF- kB dynamics

Max fold change, $\frac{{\mathit{F}}_{\mathit{max}}}{{\mathit{F}}_{\mathit{i}}}$: the maximum value calculated from the fold-change transformed FP-RelA time course. The fold-change transform is carried out by dividing the time course by the average of the first four imaging frames leading to the time point at which TNF was added (F_i).

^*Time of max, t_max: the time at which the nuclear FP-RelA fluorescence is maximum. If t_max is more than 170 minutes after stimulation, the descriptor could not be determined and the time course was discarded from analysis for this descriptor.

^*The time of max rate in, t_in: the time at which the rate of FP-RelA entry into the nucleus is maximum as determined from the slope of the first sigmoid fit. If t_in could not be determined within 155 minutes of TNF stimulation, then the time course is discarded from analysis for this descriptor.

^*Maximal rate of nuclear entry, Rate_in: was calculated from the data as the slope of the straight line fit to three points on the single-cell time course centered at t_in.

^*The time of max rate out, t_out: the time at which the rate of nuclear FP-RelA exit from the nucleus is maximum as determined from the slope of the second sigmoid fit.

^*Maximal rate of nuclear exit, Rate_out: was calculated from the experimental data as the slope of the straight line fit to three points on the single-cell time course centered at t_out.

Adaptation, ΔAdapt: is the ratio of the absolute difference in the final and initial nuclear FP-RelA to the initial amount of nuclear FP-RelA.

$$\mathrm{\Delta }\mathit{Adapt}=\frac{|F_{\mathit{final}}-F_{\mathit{initial}}|}{F_{\mathit{initial}}}$$

F_final is calculated by averaging the last 4 frames of the nuclear FP-RelA time course, and F_initial is calculated by averaging 4 frames of the nuclear FP-RelA time course preceding TNF stimulation.

Area under the curve, AUC: is the area bounded by the nuclear FP-RelA time course and the baseline amount of nuclear FP-RelA, i.e. for fold change where initial nuclear FP-RelA value of 1, i.e. ${\mathit{\sum }}_{i=\mathit{time}of\mathit{stimulus}}^{i=\mathit{end}\mathit{point}of\mathit{response}}(max(1,X(i))-1)$. The end point of a response is marked as the frame at which the second sigmoid becomes flat after t_out, i.e. $\frac{\mathit{\Delta }\mathit{fold}}{\mathit{\Delta }t}<0.0002$, or the last frame, whichever occurs first.

DATA AND SOFTWARE AVAILABILITY

Requests for datasets and code should be directed to the Lead Contact, Robin Lee (robinlee@pitt.edu).

Supplementary Material

1. Movie S1, related to main figure 2. TNF-induced nuclear translocation of FP-RelA in live KYM1 cells.

Time course of nuclear translocation in live KYM1 cells exposed continuously to 1 ng/mL TNF.

2. Movie S2, related to main figure 4. Nuclear translocation of FP-RelA during repeat stimulation in live KYM1 cells.

Time course of nuclear translocation in live KYM1 cells exposed first to a 1 minute ‘reference pulse’ of 0.2 ng/mL TNF, followed 3 hours later by a 1 minute ‘test pulse’ of 1 ng/mL TNF (i.e. a 5x increase in concentration).

3

Figure S1, related to main figure 1. Description for 3 models of single cell dose responses. (A) Formulae for (M1) Switch-like, (M2) Graded, and (M3) Graded with threshold (top, middle and bottom respectively) models of single cell responses. M1 and M3 differ from M2 because they incorporate a heavyside function to model a switch-like behavior. For all models 100 cells were simulated, each initialized with a unique integer value between 1 and 100 to approximate heterogeneity in the cellular state. During initialization each cell was also assigned a threshold for activation (thresh) used in models M1 and M3 to determine whether a cell responds to a given dose. In all models, the strength of response to a dose of cytokine scales linearly with the cell’s state, whereby a cell with state 100 and a cell with state 0 will have the strongest and weakest responses respectively. (B) Parameter values used for simulations described in (A) as well as Figure 1 of the main text. Basal noise (η_basal) was used as a cut-off to quantify the non-responsive fraction in the right column of Figure 1B. That is, a non-responders are defined as: ≤ (η_basal)_MAX

Figure S2, related to main figure 2. Subcellular localization of endogenous RelA in human cancer cells. (A) Fixed-cell RelA immunofluorescence images of KYM1, HeLa, U2OS, HCT116, and A549 cells. Cells were treated with a 1 minute pulse of 100 ng/mL of TNF and fixed at the indicated time after cytokine exposure; scale bar 10 μm. (B) Heatmap for Rate_out descriptor does not show a significant trend. (C) KYM1 cells show greater sensitivity to low concentrations of TNF when compared with A549 cells, the second most responsive cell line to TNF. (D) Western blot of RelA in lysates from parental KYM1 cells (P) and KYM1 cells that express mVenus-RelA (FP-RelA). Biological replicates are shown. (E) Quantification of bands from (D) show that FP-RelA is overexpressed 2.9-fold when compared with P KYM1 cells. For FP-RelA, endogenous and FP-RelA bands were summed; ±SEM. (F) Western blot of nuclear lysates (top) from FP-RelA cells collected at indicated times after exposure to a 1 minute pulse of 10 ng/mL TNF. Quantification of endogenous and FP-RelA bands (bottom) show qualitatively similar dynamics to each other. (G) Bar graphs of the coefficients for variation for descriptors (described in Figure 2B) of nuclear FP-RelA density in cells exposed to TNF conditions as indicated. Error bars represent 95% confidence interval of the coefficient of variation.

Figure S3, related to main figure 3. Details of control analysis, models, and features used in channel capacity calculations. (A) Density plots for nuclear FP-RelA in KYM1 cells exposed to a 5 minute TNF pulse of indicated concentration. Raw trajectories (top) and fold-transformed trajectories (bottom) are shown with the untreated control sample in the left-most column. (B) Plots showing jackknife analysis for channel capacity calculations. To correct for sample size bias and determine the variance of channel capacity values, the data set was jackknifed at sequentially increasing fractions, SS (points shown in blue) followed by linear regression to extrapolate the channel capacity at a sample size of infinity (i.e. 1/SS = 0; points shown in red). The lines obtained via linear regression are relatively flat, indicating that the size of our dataset is large enough to accurately estimate the channel capacity. (C) Plots showing the degradation in channel capacity of a system of eight 2-D Gaussians, when subpopulations of non-responders are considered. Fully separated Gaussians show the theoretical maximum channel capacity of 3 bits for this system (middle top). Overlap in the Gaussians (middle bottom), or the presence of bimodal distributions with an overlapping basal population (right) significantly reduces the values of channel capacity calculations (left); k = 10; ± standard deviation. (D) The effects of subsampling were simulated for the Gaussian system described in (C), except starting with 50% of the population sampled from the basal distribution for fully separated Gaussians (top) or overlapping Gaussians (bottom). In contrast with randomly targeted removal (red), channel capacity values after selectively removing a defined fraction of non-responders (blue) increases the channel capacity up to the defined limit revealing the true channel capacity of the responsive subpopulation; ± standard deviation. (E) Channel capacity values calculated for each data set over a range of vector dimensions (d = 5 is reported in the manuscript): Single-cell trajectories for ‘Raw’ data sets are in arbitrary fluorescence units; for ‘Fold’ data sets, each single-cell time course is represented as fold change (A); for ‘NRR’ data sets, single-cell trajectories with < 1.2-fold change in nuclear FP-RelA are removed; the continuous data set only includes conditions with continuous exposure to TNF (bottom row of Figure 3A). Green stars compare Fold-NRR and Raw-NRR (p < 10⁻⁶, t test). (F) Representative sigmoid fits of five single cell time courses. The red lines show representative experimental trajectories for a single cell’s nuclear FP-RelA time course. Black lines show two sigmoid fits used to approximate phases of nuclear entry and exit for FP-RelA and to calculate t_in and t_out. Rate_in and Rate_out were calculated from the slopes of adjacent time points from the experimental trajectory (teal line segments). The region used to calculate the AUC is indicated by the shaded area.

Figure S4 related to main figure 4. Negative feedback and dampened responses in cells exposed to a high concentration reference pulse of TNF. (A) Western blots (top) for regulators of negative feedback A20 and IκBα in KYM1 cells 3 hours after exposure to a 1 minute reference pulse of TNF at indicated concentration. GAPDH-normalized band intensities quantified in bar graphs (bottom) show that negative regulators are perturbed greater in response to a high concentration reference pulse (10 ng/mL) in comparison with a low concentration reference (0.2 ng/mL); ±SEM of biological duplicate. (B) Results from (A) are confirmed by time courses for average cellular A20 (left) and IκBα from fixed-cell immunofluorescence KYM1 exposed to indicated TNF conditions. Light colored lines indicate the standard deviation. (C) Scatter plots showing AUC2/AUC1 stratified along AUC1 across the range of test conditions in cells after a 6 hour recovery period. (D) Density plots of single-cell FP-RelA time courses for cells exposed to a high concentration (10 ng/mL) reference pulse of TNF followed by a TNF pulse with a 10x increase in concentration 3 hours (left) or 6 hours (right) later. (E) Jitter plots comparing AUC2/AUC1 responses in single cells exposed to a low concentration reference pulse (0.2 ng/mL) or a high concentration reference pulse (10 ng/mL) of TNF with either a 3 hour or 6 hour intervening recovery window. Responses to test pulses are significantly dampened when cells are exposed to a high concentration reference pulse regardless of the duration of the recovery window. (F) Frequency distributions of AUC2 across the range of test conditions. (G) Channel capacity values calculated using AUC2 are compared with a vector that includes reference information about each cell ([AUC1, AUC2]). Red line indicates the channel capacity calculated from the full matrix of conditions (Figure 3); ± standard deviation; p < 10⁻¹¹.

4

Table S1, related to main Figure 2. Summary of cell numbers for fixed cell experiments. For each condition cells were exposed continuously or to a pulse of cytokine, and fixed after 0, 10, 30, 60, 90, 120, 180, 240, or 360 minutes. ‘Total’ is the aggregate number of cells measured across all time points, ‘Avg #’ quantifies the average number of cells measured in each time point, and ‘StDev’ quantifies the standard deviation across time points for indicated condition.

Table S2. Related to main Figure 4. Summary of pairwise p-values for AUC2/AUC1 compared between test pulse conditions. For each pair of test pulse conditions in Figure 4D, p-values are lower than listed. Concentrations listed are relative to a test pulse concentration of 0.2 ng/mL TNF.

HIGHLIGHTS.

• Graded dose discrimination provides more control points to fine-tune cell responses

• Mechanisms of dose discrimination cannot be determined from population data

• Information transmission capacity varies between subpopulations of isogenic cells

Single cells are capable of graded responses with respect to cytokine strength