Meta-Analysis Approaches to Combine Multiple Gene Set Enrichment Studies

Abstract

In the field of gene set enrichment analysis (GSEA), meta-analysis has been used to integrate information from multiple studies to present a reliable summarization of the expanding volume of individual biomedical research, as well as improve the power of detecting essential gene sets involved in complex human diseases. However, existing methods, Meta-Analysis for Pathway Enrichment (MAPE, [1]), may be subject to power loss because of (i) using gross summary statistics for combining end results from component studies and (ii) using enrichment scores whose distributions depend on the set sizes. In this paper, we adapt meta-analysis approaches recently developed for genome-wide association studies, which are based on fixed effect (FE) and random effects (RE) models, to integrate multiple GSEA studies. We further develop a mixed strategy via adaptive testing for choosing RE versus FE models to achieve greater statistical efficiency as well as flexibility. In addition, a size-adjusted enrichment score based on a one-sided Kolmogorov-Smirnov statistic is proposed to formally account for varying set sizes when testing multiple gene sets. Our methods tend to have much better performance than the MAPE methods, and can be applied to both discrete and continuous phenotypes. Specifically, the performance of the adaptive testing method seems to be the most stable in general situations.

1. Introduction

In transcriptome studies, great attention has been drawn to identification of pathways, or more broadly, groups of biologically related genes involved in complex human diseases or other biological processes. A major type of such analysis is called Gene Set Enrichment Analysis (GSEA), which determines whether a gene set is over-represented by genes associated with a trait of interest. Gene sets can be pre-defined according to a variety of criteria, including genes/proteins participating in common pathways, sharing similar annotated functions or related sequence motifs, interacting with and co-regulating each other, and serving as oncogenic, immunologic or other disease signature genes. In general, GSEA is designed to detect coordinated expression changes in a group of related genes, and such changes are, in whole or in part, cellular reactions to changes related to disease phenotypes or therapeutic treatments. Thus, gene sets identified from GSEA can provide key insights into biological processes underlying disease pathogenesis or treatment effects.

Various statistical methods have been developed for GSEA using a single mRNA dataset. An early method for GSEA is to associate gene expression with phenotype changes to identify differentially expressed (DE) genes based on a statistic measuring the degree of differential expression, and then determine whether a gene set contains significantly more DE genes than would be expected by chance using Fisher’s exact test [2]. Subramanian et al. [3] proposed an improved GSEA method, which has become one of the most well-known and currently widely used GSEA algorithms. It makes use of the ranks of genes according to the degree of differential expression, to compute the enrichment score of a gene set based on a weighted Kolmogorov-Smirnov (KS) test. Then it estimates the statistical significance of the gene set using an empirical null distribution of the enrichment score obtained from a permutation procedure. Later, many other methods for GSEA were further developed. For example, [4] modified the GSEA algorithm by [3] using a max–mean statistic and a re-standardization procedure; and [5] proposed a random set approach. For a detailed review about the methodological development of GSEA, see [6, 7]. Due to mature statistical analytics, GSEA has been widely applied in biomedical fields, where GSEA plays critical roles in the innovation of disease prevention and intervention strategies, including revealing novel genes and key regulatory modules, detecting ensembles of diagnostic and prognostic markers, and discovering potential therapeutic targets [8–13].

In the past decades, enormous amounts of data have been generated from various biomedical experiments; and the volume continues to expand. Consortia have been recently formed and public databases have been constructed and regularly updated, making it increasingly feasible to access data from multiple research projects. Despite significant successes GSEA has achieved, it is striking that findings are often unstable and thus are inconsistent among independent studies targeting the same disease or biological problem. This is partly because of small sample sizes relative to an overwhelming number of genes, as is typical in individual genome-wide transcriptomic studies, making estimation and inference highly volatile. Thus, there is an increasingly urgent need to perform integrative GSEA, i.e., integrating multiple relevant GSEA studies, to turn individual data into collective knowledge.

Integrative GSEA (iGSEA), when performed properly, can effectively increase the sample size of the analysis, greatly facilitate information sharing, and improve the power of detecting truly interesting gene classes, as well as increasing the reproducibility and interpretability of research results. However, methods for iGSEA are rather scant. [1] systematically developed and evaluated three methods for Meta-Analysis of Pathway Enrichment (MAPE), including MAPE-P, MAPEG and MAPE-I. All these methods use the maximum, minimum or Fisher’s statistic to combine p-values from multiple studies, and so inevitably lose power by using such gross summaries. Further, when testing multiple pathways, the MAPE methods do not account for different set sizes in their permutation-based procedures. In addition, the lack of ability to formally handle between-study heterogeneity, which may exist in GSEA studies due to the varying quality of experiments and the noisy nature of genomic data, can affect the performance of the MAPE methods. More recently, a Bayesian method has been proposed for integrative GSEA by [14] to improve the detection of enriched gene sets, which simultaneously models gene set information and original gene expression data from all component studies. This method can only be applied to binary phenotypes. When the number of genes or gene sets or component studies gets large, it can become computationally formidable. In addition, detecting the convergence of Markov chains and selecting starting points may require great human efforts.

Motivated by the room for improvement of the existing methods, we focus on the development of new methods for iGSEA that are (i) statistically efficient; (2) computationally affordable and (3) applicable to both discrete and continuous phenotypes. Here, we adapt and extend meta-analysis approaches [15–17] newly developed for genome-wide association studies (GWAS), which are based on fixed effect (FE) and random effects (RE) models, to integrate multiple GSEA studies. Specifically, we propose a hybrid strategy for choosing RE versus FE models, with an attempt to achieve great statistical efficiency as well as stability in performance in various practical situations. In addition, unlike the MAPE methods, our proposed iGSEA methods formally account for different set sizes when testing a database of gene sets.

In the next section of this paper, we describe our modeling and testing strategy in an individual study, where a generalized linear model (GLM) is used to fit the relationship between the expression of an individual gene and the phenotype, and then gene-level statistics are constructed to quantify the strength of the association. In Section 3, we propose several meta-analysis methods to compute an overall gene-level statistic that integrates the gene-level statistics from individual studies. In Section 4, we focus on gene set analysis, where we propose size-adjusted set-level statistics via a one-sided KS test, estimate their significance based on permutation, and adjust for multiple testing when more than one gene set is tested. Sections 5 and 6 present results from simulation studies and an example using gene expression data from five lung cancer studies. Section 7 concludes the paper with a brief discussion. The algorithm for the proposed iGSEA methods is outlined in the appendix.

2. Modeling and testing in an individual study

We are interested in combining K independent GSEA studies that share a common phenotype Y. Suppose there are G genes in a genome that appear at least once in the K studies. Let J_k be the sample size in study k, where k = 1, … K; let Y_jk be the phenotype of sample j in study k, where j = 1, …, J_k; and let X_jgk be the expression level of gene g for sample j in study k, where g = 1, …, G. We use β_gk to denote the effect of gene g’s expression on the phenotype Y in study k. We assume that different studies may have different genes from the same genome (i.e., some genes’ information can be missing in one or more studies), which allows us to include more studies in our integrative analysis.

For each gene g included in study k, we use a GLM to model the relationship between X_jgk and Y_jk:

$$l(E(Y_{jk}))={\alpha }_{gk}+{\beta }_{gk}{X}_{\mathit{jgk}},$$ (1)

where l(·) is the link function, and Y_jk is assumed to follow an exponential family distribution.

To test the null hypothesis H₀: β_gk = 0, we can compute the score statistic U_gk and its corresponding variance V_gk based on the distribution of Y, whose probability distribution function can be written as

$$p(Y_{jk})=exp\left\{\frac{Y_{jk}{\theta }_{jk}-b({\theta }_{jk})}{a({\varphi }_k)}+c(Y_{jk},{\varphi }_k)\right\},$$

where ϕ_k is the dispersion parameter, and θ_jk is the natural parameter. Here, a(·), b(·), and c(·) are known functions, determined by the type of distribution of the phenotype Y. For example, if Y is binary, then the distribution is Bernoulli so that a (ϕ) = 1, b (θ) = log (1 + e^θ) and c (Y, ϕ) = 0. We use b′ (·) and b″ (·) to denote the first and second derivatives of b(·). Since E(Y_jk) = b′ (θ_jk), θ_jk is equal to b′ ⁻¹ ∘ l⁻¹(α_gk + β_gkX_jgk). We can therefore construct the likelihood function and then derive the score statistic and the corresponding estimated variance:

$$\begin{gathered} U_{gk}=a{\left({\widehat{\varphi }}_{gk}\right)}^{-1}\sum _{j=1}^{J_k}\left\{\left[\frac{Y_{jk}-l^{-1}\left({\widehat{\alpha }}_{gk}+{\widehat{\beta }}_{gk}{X}_{\mathit{jgk}}\right)}{b^{″}({\widehat{\theta }}_{\mathit{jgk}})}\right]{(l^{-1})}^{\prime }\left({\widehat{\alpha }}_{gk}+{\widehat{\beta }}_{gk}{X}_{\mathit{jgk}}\right)X_{\mathit{jgk}}\right\}, \\ {V}_{gk}=a{\left({\widehat{\varphi }}_{gk}\right)}^{-1}\sum _{j=1}^{J_k}\left\{\frac{1}{b^{″}({\widehat{\theta }}_{\mathit{jgk}})}{\left[{(l^{-1})}^{\prime }\left({\widehat{\alpha }}_{gk}+{\widehat{\beta }}_{gk}{X}_{\mathit{jgk}}\right)X_{\mathit{jgk}}\right]}^2\right\}, \end{gathered}$$

where ϕ̂_gk and α̂_gk are the maximum likelihood estimates, and θ̂_jgk = b′⁻¹ ∘ l⁻¹(α̂_gk + β̂_gkX_jgk). Note that under the null hypothesis of no association between X_gk and Y_k, β̂_gk ≡ 0; and $U_{gk}^2/V_{gk}$ asymptotically follows a chi-square distribution with one degree of freedom ( ${\chi }_1^2$).

3. Computing overall gene-level statistics

To combine multiple GSEA studies, we rely on meta-analysis to compute a statistic per gene, using the gene-level statistics (U_gk, V_gk) from individual studies, for measuring the overall strength of association between gene g’s expression and the phenotype. Below we consider three approaches: (1) testing based on a fixed-effect (FE) model; (2) testing based on a random-effects (RE) model; and (3) adaptive testing (AT). The first two adapt the recent FE and RE testing methods for GWAS meta-analysis [15–17] into iGSEA, respectively. The third aims to combine the strength of the first two and achieve robustness against model mis-specification.

3.1. FE testing

A fixed-effect model that assumes no heterogeneity among GSEA studies is specified as follows:

$${\beta }_{gk}\equiv {\mu }_g,k=1,\dots ,K,$$ (2)

where μ_g stands for the common genetic effect of gene g among the different studies. Let T_gk indicate whether gene g is included in study k (1 if included; 0 otherwise). Motivated by [18] and [17], we use the following statistic to test the null hypothesis H₀: μ_g = 0:

$$C_g^{FE}=\frac{{\left({\sum }_{k=1}^K{T}_{gk}{U}_{gk}\right)}^2}{{\sum }_{k=1}^K{T}_{gk}{V}_{gk}},$$ (3)

where $C_g^{FE}$ follows an asymptotic distribution of ${\chi }_1^2$ under H₀. Here, we do not need to calculate the P-value of $C_g^{FE}$ and decide whether H₀ is rejected. This is because in the latter sections, a gene set will be tested based on the ordering of $C_g^{FE}$s as larger values of $C_g^{FE}$s indicate more evidence to reject H₀ and so imply smaller P-values no matter what the actual reference distribution of $C_g^{FE}$ is.

Although meta-analysis is generally believed to be less statistically efficient than mega-analysis (i.e., joint analysis of individual-level raw data from all component studies), [18] proved that under the FE model, meta-analysis based on score statistics can achieve the same efficiency as mega-analysis. Thus, unlike using the coarse summary statistics in the MAPE methods, this model-based method has almost no information loss when testing the common effect in (2).

3.2. RE testing

To accommodate between-study heterogeneity, one can specify β_gk as a random effect. The results from different studies for gene g are therefore combined based on a random effects model specified by

$${\beta }_{gk}={\mu }_g+{\epsilon }_{gk},k=1,\dots ,K,$$ (4)

where μ_g stands for the mean genetic effect among studies, and ε_gk is the random effect representing the study-specific deviation of the effect from the mean effect μ_g. It is assumed that ε_gks are independent and follow a normal distribution with mean 0 and variance τ_g.

In GWAS, however, researchers prefer to using the FE approach to combine multiple genomic studies, even when between-study heterogeneity exists, due to a controversial phenomenon [19]. That is, the traditional RE approach that tests H₀: μ_g = 0 usually provides less significant P-values than the corresponding FE approach so that RE does not give any new findings compared with FE in most cases. [16] investigated this conservative nature of the traditional RE approach and proposed an improved RE approach that tests the hypothesis H₀: μ_g = 0 and τ_g = 0 in genomic settings. The new approach has been shown to achieve higher power than FE when there is heterogeneity. Here, we adapt this approach and test the null hypothesis H₀: μ_g = 0 and τ_g = 0 rather than H₀: μ_g = 0 under the RE model. The test statistic is specified as follows:

$$C_g^{RE}=\frac{{\left({\sum }_{k=1}^K{T}_{gk}{U}_{gk}\right)}^2}{{\sum }_{k=1}^K{T}_{gk}{V}_{gk}}+\frac{{\left[{\sum }_{k=1}^K{(T_{gk}{U}_{gk})}^2-{\sum }_{k=1}^K{T}_{gk}{V}_{gk}\right]}^2}{2{\sum }_{k=1}^K{(T_{gk}{V}_{gk})}^2}.$$ (5)

The first term is the statistic $C_g^{RE}$ to test μ_g = 0 under the FE model (i.e., τ_g = 0) and the second term is to test τ_g = 0 given μ_g = 0. Again, we do not need to calculate the P-value because we will rely on the ordering of $C_g^{RE}$ for testing a gene set.

3.3. Adaptive testing

The above FE and RE methods apply the same class of models to all genes. In practical situations, however, some genes, especially those “silent” with zero effect, tend to fit in the FE model while the others are likely to fit in the RE model. For instance, in lung cancer research, it is found that the effect size of gene “SLC35A5” seem to be quite stable, but that of gene “CYCS” differs greatly from study to study [20–22]. Thus, we propose a data-adaptive testing procedure that is robust to model mis-specification.

We begin with the more general RE model (4) and for each gene g, we first test the between-study heterogeneity $H_0^{(1)}:{\tau }_g=0$. If $H_0^{(1)}$ is rejected, then no more testing is needed because H₀: μ_g = 0 and τ_g = 0is also rejected, meaning that this gene is associated with the phenotype in at least one of the studies. If $H_0^{(1)}$ is not rejected, we switch to the FE model to test $H_0^{(2)}:{\mu }_g=0$ using $C_g^{FE}$. Note that if ${\sum }_{k=1}^K{T}_{gk}=1$, we directly go to $H_0^{(2)}$.

Let p_1g and p_2g be the P-value in stage 1 and 2, respectively. We can calculate p_2g based on the asymptotic distribution of $C_g^{FE}$ under $H_0^{(2)}$, as mentioned in Section 3.1, or based on a standard permutation procedure. In Section 3.3.1, we explain how to compute p_1g when testing $H_0^{(1)}$. In Section 3.3.2, we compute an overall P-value of the two-stage test, denoted by $p_g^{AT}$, for each gene to combine p_1g and p_2g. When testing a gene set, the ordering of the genes will be produced based on the overall P-value from this adaptive testing method.

3.3.1. Testing the existence of between-study heterogeneity

Under the RE model, a classical approach to test the between-study heterogeneity τ is Cochran’s Q test [23, 24], where the Q statistic is computed by summing the squared deviation of each study’s estimated effect size from the estimated overall effect size, with the contribution of each study weighted by its inverse variance. More recently, three measures including the H, R, and I² statistics have been proposed to assess the between-study heterogeneity in meta-analysis, each of which has its own characteristics as discussed in [25]. In this paper, we use the Q statistic to test the heterogeneity of gene g’s effect because its asymptotic distribution is relatively simple and the other three statistics are all computed based on the Q statistics. Under our context, the Q statistic of gene g can be defined by

$$Q_g=\sum _{k=1}^K{T}_{gk}{w}_{gk}{\left({\widehat{\beta }}_{gk}-{\widehat{\beta }}_g\right)}^2,$$ (6)

where β̂_gk is the estimator of β_gk fit by the GLM with variance ${\sigma }_{gk}^2,w_{gk}\equiv 1/{\widehat{\sigma }}_{gk}^2$ is the estimated precision of β̂_gk within study k, and β̂_g is a weighted average of the study estimates, using the estimated precisions as weights:

$${\widehat{\beta }}_g=\frac{{\sum }_{k=1}^K{T}_{gk}{w}_{gk}{\widehat{\beta }}_{gk}}{{\sum }_{k=1}^K{T}_{gk}{w}_{gk}}.$$

We can set p_1g to be the P-value of Q_g based on its asymptotic null distribution; that is, when $H_0^{(1)}:\tau =0$ holds, Q_g asymptotically follows a chi-square distribution with degrees of freedom $df={\sum }_{k=1}^K{T}_{gk}-1$.

Alternatively, we can use a permutation-based method to test the heterogeneity τ_g in a meta-analysis. [26] summarized seven methods, which include the variance component type estimator (VC), the method of moments estimator (MM), the maximum likelihood estimator (ML), the restricted maximum likelihood estimator (REML), the empirical Bayes estimator (EB), the model error variance type estimator (MV), a variation of the MV estimator (MVvc), for estimating τ_g under the RE model; and among them, MVvc and EB are found to be the most accurate in general, particularly when τ_g is moderate to large. Below we describe a permutation procedure based on the MVvc estimator of τ_g because of its good performance as well as its computational ease based on a non-iterative procedure.

Let ${\widehat{\tau }}_g^{VC}$ be the VC estimator of τ, where

$${\widehat{\tau }}_g^{VC}=\frac{1}{{\sum }_{k=1}^K{T}_{gk}-1}\sum _{k=1}^K{T}_{gk}{({\widehat{\beta }}_{gk}-{\overline{\beta }}_g)}^2-\frac{1}{{\sum }_{k=1}^K{T}_{gk}}\sum _{k=1}^K{T}_{gk}{\widehat{\sigma }}_{gk}^2,$$

and ${\overline{\beta }}_g={\sum }_{k=1}^K{T}_{gk}{\widehat{\beta }}_{gk}/{\sum }_{k=1}^K{T}_{gk}$. Let ${\widehat{r}}_{gk}\equiv {\widehat{\sigma }}_{gk}^2/{\widehat{\tau }}_g^{VC}$ be the plug-in estimator for the ratio of within-study vs. between-study heterogeneity, i.e., ${\sigma }_{gk}^2/{\tau }_g$; and v̂_gk ≡ r̂_gk + 1. Then according to [27], the MVvc estimator of τ_g can be calculated by

$${\widehat{\tau }}_g^{\mathit{MVvc}}=\frac{1}{{\sum }_{k=1}^K{T}_{gk}-1}\sum _{k=1}^K{T}_{gk}{\widehat{v}}_{gk}^{-1}{({\widehat{\beta }}_{gk}-{\stackrel{\sim }{\beta }}_g)}^2,$$ (7)

with

$${\stackrel{\sim }{\beta }}_g=\frac{{\sum }_{k=1}^K{T}_{gk}{\widehat{v}}_{gk}^{-1}{\widehat{\beta }}_{gk}}{{\sum }_{k=1}^K{T}_{gk}{\widehat{v}}_{gk}^{-1}}.$$

In case that ${\widehat{\tau }}_g^{VC}\le 0$, we replace it with a small value (e.g., 0.01) to compute r̂_gk. We permute sample labels over different studies to obtain the empirical null distribution of ${\widehat{\tau }}_g^{\mathit{MVvc}}$ and then calculate the P-value of the observed statistic.

3.3.2. Combining P-values

We first discuss how to combine P-values from individual stages for a two-stage test defined by a set of general decision rules (the subscript g is dropped whenever there is no ambiguity). Let α be the overall size of the two-stage test, and α_i be the size of the ith-stage test, satisfying 0 < α_i < α for i = 1, 2. Further, let α₀ be a predetermined upper limit such that 0 < α < α₀ ≤ 1. Typically, the test uses the following decision rules: (1) if p₁ ≤ α₁, reject $H_0^{(1)}$; if p₁ > α₀, fail to reject $H_0^{(1)}$; and in either case, the test stops. (2) If α₁ < p₁ ≤ α₀, the test proceeds to the second stage: $H_0^{(2)}$ is rejected if and only if F(p₁, p₂), a predetermined function, is less than or equal to f, and f is determined by the following equality

$${\alpha }_1+{\int }_{{\alpha }_1}^{{\alpha }_0}{\int }_0^1\mathrm{I}\{F(x,y)\le f\}\mathit{dydx}=\alpha ,$$

where I(·) is the indicator function. Then according to [28], the overall P-value of the two-stage test can be given by

$$p=\{\begin{array}{ll}{p}_1,\hfill & \text{if}{p}_1\le {\alpha }_1\text{or}{p}_1¿{\alpha }_0,\hfill \\ {\alpha }_1+{\int }_{{\alpha }_1}^{{\alpha }_0}{\int }_0^1\mathrm{I}\{F(x,y)\le F(p_1,p_2)\}\mathit{dydx},\hfill & \text{otherwise.}\hfill \end{array}$$

Many existing methods for computing the overall P-value use the framework above, such as the Fisher’s weighted product test [29] and the weighted inverse normal method [30].

For our adaptive testing procedure, it is obvious that α₀ is set to 1. We further set F(p₁, p₂) = p₂, proposed by [31]. Thus, the overall P-value of our test is given by

$$p^{AT}=\{\begin{array}{ll}{p}_1,\hfill & \text{if}{p}_1\le {\alpha }_1,\hfill \\ {\alpha }_1+p_2(1-{\alpha }_1),\hfill & \text{otherwise.}\hfill \end{array}$$

If the tests in the two stages are independent, then the following relationship holds:

$${\alpha }_1+(1-{\alpha }_1){\alpha }_2=\alpha .$$ (8)

In our context, it might be plausible to argue that the result of the second stage is not related to that of the first stage as they involve testing the mean and variance of the effect sizes, respectively, which are two distinctive characteristics of data. As mentioned in [31], the above method to combine P-values is easy to implement and only depends on one parameter α₁, which lies in (0, α) and can be determined by prior information about the existence of between-study heterogeneity or the common effect size. When prior information is not available, we could simply set α₁ = α₂ and then solve the equality (8), yielding ${\alpha }_1=1-\sqrt{1-\alpha }$; or alternatively, we could set α₁ based on some exploratory data analysis for assessing the heterogeneity.

4. Gene set analysis with size-adjusted enrichment scores

If there is only one gene set (say set s) to test, a straightforward approach to enrichment analysis is to choose some reasonable set-level statistic as the enrichment score v_s and compute its significance through a permutation procedure. In detail, we randomly shuffle the gene labels B times (so that a different set of genes randomly selected from the larger pool of G genes is included in set s each time) and compute the permuted enrichment scores, say $v_s^{(b)}$, 1 ≤ b ≤ B. The P-value of the observed v_s can be approximated by

$$p(v_s)=\frac{{\sum }_{b=1}^{B}I\left(v_s^{(b)}\ge v_s\right)}{B}.$$

When more than one gene set is tested, the Q-value is computed to account for multiplicity ([1, 7, 32]), which is defined as the minimum false discovery rate (FDR) at which a set is claimed to be statistically significant. The Q-value of the observed v_s is evaluated by

$$q(v_s)=\frac{{\widehat{\pi }}_0{\sum }_{s^{\prime }=1}^S{\sum }_{b=1}^{B}I\left(v_{s^{\prime }}^{(b)}\ge v_s\right)}{B{\sum }_{s^{\prime }=1}^{S}I(v_{s^{\prime }}\ge v_s)},$$ (9)

where π̂₀ is a rough estimate of the proportion of non-enriched sets and S is the number of gene sets being tested. We calculate π̂₀ using the method described in [32], which is implemented in an R package called “qvalue” [33]. Note that for the MAPE methods, π̂₀ is always set to 1 ([1]), a conservative choice. Our preliminary simulation has found that using qvalue with MAPEs leads to worse results in FDR control. Gene sets with a Q-value < δ are claimed to be enriched. Throughout this paper, δ is set to the default value 0.05.

As to choosing an enrichment score, we consider a one-sided KS test, which is to determine whether the distribution of the overall gene-level statistic (say u_g) for genes in set s is stochastically larger/smaller than the distribution of the same statistic for genes out of the set. To keep the direction of the one sided KS test the same over the different meta-analysis approaches, we set $u_g=C_g^{FE}$ for the FE method, $u_g=C_g^{FE}$ for the RE method, and $u_g=-p_g^{AT}$ for the AT method. Suppose set s contains G_s genes. We order the total G genes according to one of the three overall gene-level statistics. For example, let A and B denote the statistic $C_g^{FE}$ for genes in and out of set s, respectively. The order statistics are A₍₁₎,A₍₂₎, …,A_(Gs) and B₍₁₎,B₍₂₎, …,B_(G−s), where G_−s ≡ G − G_s. Let F_A and F_B denote the underlying cumulative distribution functions (CDF) for A and B, respectively. Then the null and alternative hypotheses are H₀: F_A = F_B for all x, and H_a: F_A ≤ F_B for all x, F_A < F_B for some x.

The one-sided two sample KS test statistic for set s is given by

$$h_s=\underset{x}{max}[{\widehat{F}}_B(x)-{\widehat{F}}_A(x)],$$

where F̂_A(x) is the empirical CDF of A, defined by

$${\widehat{F}}_A(x)=\{\begin{array}{ll}0\hfill & \text{if}x<A_{(1)}\hfill \\ \frac{m}{G_s}\hfill & \text{if}{A}_{(m)}\le x<A_{(m+1)}\text{for}m=1,2,\dots ,G_s-1,\hfill \\ 1\hfill & \text{if}x\ge A_{(G_s)}\hfill \end{array}$$

and F̂_B(x) is defined similarly.

We mention that the KS-type statistics have been commonly used as enrichment scores in the literature. For example, the popular GSEA algorithm by [3] used a weighted version of the two-sided KS statistic; and the existing MAPE methods for integrative GSEA by [1] used the one-sided KS statistic as well, but for testing the opposite direction. However, an important fact about the KS-type statistics is often ignored: for gene sets of different sizes, their KS statistics follow different distributions. While enrichment analysis is commonly applied to a database of gene sets, whose sizes vary in a wide range, none of the existing methods adjust the KS-type statistics to formally account for varying set sizes when computing the Q-value to control the FDR. [3] obtained normalized enrichment scores from separately rescaling the positive and negative scores by dividing by the mean of the permuted scores. However, there is no theoretical ground provided for their adjustment and so it is ad hoc.

Below we propose a size-adjusted KS statistic as our enrichment score:

$$v_s=\frac{h_s}{\sqrt{\frac{1}{G_s}+\frac{1}{G_{-s}}}}.$$ (10)

According to [34] and [35], v_s has an asymptotic distribution whose CDF is given by

$$F(z)=1-exp(-2z^2),z>0,$$ (11)

which is independent of the size of the gene set. A comparison of the empirical CDF of 1000 replicates and the asymptotic CDF is given in Section 1 of Supplementary Material. We find that they are very close, especially when G_s ≥ 30. Therefore, the size-adjusted KS statistics for gene sets of varying sizes approximately follow the same distribution, making the permutation-based computation of Q-value considerably improved.

5. Simulation

We designed two simulation studies, one for binary phenotypes and the other for continuous phenotypes, to assess the performance of the proposed iGSEA methods and compare them with the existing methods under default settings. Our methods are labeled by iGSEA-FE, iGSEA-RE and iGSEA-AT, respectively, according to the meta-analysis strategies used, as discussed in Section 3. In each study, we first compared the power in identifying enrichment via a one-gene-set simulation model as in [1]; and we further examined the sensitivity and specificity of the methods via a multiple-gene-set simulation model. Throughout this section, we fixed the significance level at 0.05 for every test conducted; and we set B = 500 for the one-gene-set model and B = 200 for the multiple-gene-set model. For iGSEA-AT, we set the first-stage significant level α₁ ∈ {0.02, 0.03, 0.04} in our simulation and find that its performance was not sensitive to the change of α₁. Thus we report the results based on α₁ = 0.02. We also note that due to the mixed strategy of using the FE and RE models, as discussed in Section 3.3, it is unrealistic to expect that iGSEA-AT outperforms iGSEA-FE and iGSEA-RE uniformly; instead, we anticipate that its performance can mimic the better of the two closely in most cases.

5.1. Binary phenotypes

Power comparison

Suppose there are G = 500 genes in a genome and the first 100 genes belong to the gene set of interest. For DE genes, we simulated both down-regulated (DR) and up-regulated (UR) genes. We generated a random variable d_g to indicate whether gene g is an UR, DR, or equally expressed (EE) gene, which is represented by d_g = 1, −1, and 0, respectively. There are ${\sum }_{g=1}^{100}\mid d_g\mid =100·\omega$ DE genes out of the first 100 genes that belong to the gene set and ${\sum }_{g=101}^{500}\mid d_g\mid =400·{\omega }_0$ DE genes out of the rest 400 genes. We fixed ω₀ = 0.2 in the simulation, and so the gene set is enriched if ω > 0.2. We assume there are (ω − 10%) UR and 10% DR genes in the gene set, and 10% UR and 10% DR genes out of the gene set. We set ω ∈ {0.2, 0.3, 0.4, 0.5} to represent zero, weak, medium and strong enrichment signals, respectively.

For the purpose of meta-analysis, we simulated four independent studies in each generated dataset. The chance of each gene to be included in study k is determined by a universal sampling rate λ, where we set λ ∈ {0.5, 0.6, 0.7, 0.8, 0.9, 1}. Each study has J = 40 samples, including 20 normal samples with Y_j = 0 and 20 tumor samples with Y_j = 1. For a DE gene, we generated a random binary variable r_g to indicate whether the effects of this DE gene across different studies are random or fixed. If r_g = 1, this DE gene is called a RE gene, otherwise r_g = 0. The proportion of the RE genes out of the DE genes is represented by γ, where we set γ ∈ {0, 0.2, 0.4, 0.6, 0.8, 1}.

Since Y is binary, we used a logistic regression model: for sample j in study k, logit(E(Y_kj = 1|X_gkj = x)) = α_gk + β_gkx. According to the Bayes theorem, we can generate the expression levels X_gkj from N(β_gk, 1) given the value of Y_kj ([36]), where β_gk = d_gμ if Y_kj = 1 and r_g = 0 (i.e., DE genes from the FE model); β_gk ~ N(d_gμ, τ²) if Y_kj = 1, r_g = 1 (i.e., DE genes from the RE model); and β_gk = 0 otherwise (i.e., EE genes or Y_kj = 0).

We mainly consider those situations where a wise choice about which method to use can make a difference in identifying an enriched gene set, so we set the mean effect size of the DE genes μ ∈ {0.3, 0.45, 0.6} to make the signal-to-noise ratio not too high (otherwise, all the methods perform well). We further set τ ∈ {0.5², 1}. A total number of 500 (1000 for ω = 0.2) independent replicate datasets were simulated for each combination of the design parameters (ω, λ, γ, μ, τ).

We first examined the test size for all the methods compared. For the cases with ω = 0.2 where the null hypothesis of no enrichment holds for the gene set, we computed type I errors (i.e., test sizes) and then compared them with the nominal significance level 0.05. We report the results of simulated test sizes in Section 2.1 of Supplementary Material. We find that under the null, our iGSEA methods and MAPE-G seem to be a bit conservative and so tend to reject the null less than expected; MAPE-P seems to be aggressive and so tend to reject the null more than expected, especially for large γ; and MAPE-I is often somewhere between MAPE-G and MAPE-P. Thus, for a fair comparison in power, we need to match the type 1 errors of all the methods. To do so, for each non-null setting (i.e., ω ≠ 0.2), we used 1000 replicates under ω = 0.2 to simulate the critical value from the empirical reference distribution of the enrichment score; and we computed the power based on the simulated critical value so that the type I error of each method was controlled at 0.05.

We examined the power for all the combinations of (ω, λ, γ, μ, τ); and in Section 2.2 of Supplementary Material, we report the results for all the non-null settings except for those in which all the three proposed iGSEA methods worked well and have nearly 100% power. In our simulation, we observe that among the three existing methods, their power typically follows the order MAPE-P>MAPE-I>MAPE-G. Thus, to reduce the number of lines in the figures, we only plot the maximum power of the three MAPE methods in each setting, labeled by maxMAPE, instead of each individual power. As we expect, the increase of the enrichment signal ω or the mean effect size μ would boost the power of all the involved tests. The increase of the sampling rate λ also has a positive impact on the power. Among all the methods, either iGSEA-AT or iGSEA-RE appears to be the top performer in most of the settings; and maxMAPE has lower power than the above two methods except for only a few settings where ω = 0.3.

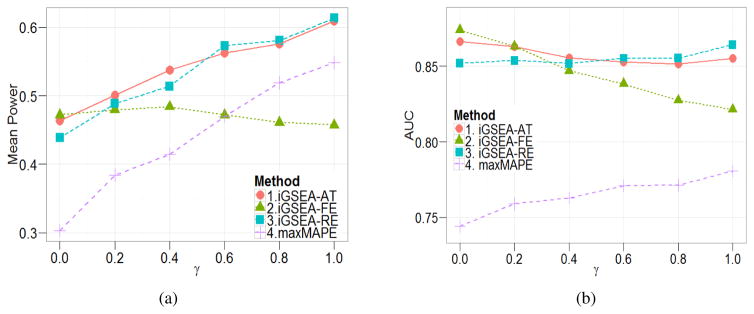
Figure 1(a) displays the mean power over the different settings stratified by the proportion of the RE genes γ. It seems that γ plays an important role in the relative performance of the three proposed iGSEA methods. When γ = 0 (i.e., all genes follow the FE model), it is not surprising to observe that iGSEA-FE has the highest mean power; and iGSEA-AT has mean power quite close to iGSEA-FE. When γ is small, iGSEA-AT outperforms both iGSEA-FE and iGSEA-RE. As γ is moving to 1, iGSEA-RE tends to outperform the other methods; however, the performance of iGSEA-AT is very close to that of iGSEA-RE. Overall, in terms of the mean power, iGSEA-AT is better than iGSEA-RE when there is no or a small proportion of RE genes; and it is much better than iGSEA-FE when there exist RE genes. In addition, iGSEA-AT is better than maxMAPE for all γ. Thus, in realistic situations where γ is unknown, we recommend iGSEA-AT as a safe choice for its stable performance.

Figure 1.

Simulation results for binary phenotypes: (a) the mean power (b) the mean AUC stratified by the proportion of RE genes γ.

Sensitivity vs. specificity

We proceed to compare the sensitivity and specificity of the methods via ROC curves by generating multiple gene sets. We assume that each generated dataset contains four independent studies, each having 20 normal samples and 20 tumor samples as before; and there are 1000 genes in the genome of interest, of which the first 100 are UR genes, the last 100 are DR genes, and the rest are EE genes. We generated 100 gene sets of varying sizes, of which the first 30% are enriched by UR genes, the next 30% are enriched by DR genes and the last 40% are non-enriched. For each of these gene sets, its size was independently generated from N(100, 30²) and then left-truncated at 25; and UR, DR and EE genes were randomly chosen from the corresponding populations. We set ω = 0.3, μ = 0.45, τ = 0.5², and λ = 0.7. The detail about constructing the different types of gene sets and generating expression levels for the different types of genes can be found in Section 2.3 of Supplementary Material.

We present an example of ROC curves in each setting of γ using one randomly generated dataset in Section 2.4 of Supplementary Material. The curves show that all the three iGSEA methods have better performance than the MAPE methods. Among them, iGSEA-FE seems to be the best for small γ but the poorest for large γ while iGSEA-RE shows an opposite pattern; and iGSEA-AT is the best for medium γ, and otherwise, it is somewhere between the other two. We further examine the average AUC (area under the ROC curve) of each method by simulating 200 datasets under each setting considered. As clearly shown in Figure 1(b), the three iGSEA methods have much higher AUC than the MAPE methods. Further, as γ increases, the AUC of iGSEA-FE tends to decrease and the AUC of iGSEA-RE tends to increase while that of iGSEA-AT is steadier. Overall, iGSEA-AT has the best performance in terms of AUC as it is close to iGSEA-FE for small γ, close to iGSEA-RE for large γ and it is the best in the middle. This pattern is similar to what we observed from power results in Figure 1(a), which leads to the same conclusion that iGSEA-AT should be chosen in situations when γ is not known.

We report the mean AUC values for each proposed iGSEA method before and after our size adjustment in Table 1. It is clear that the use of the size-adjusted KS statistic in (10) consistently improves the mean AUC of all the three iGSEA methods. In addition, the performance of all the six methods in FDR control is reported in Section 2.5 of Supplementary Material, where we find that the iGSEA methods outperform the MAPE methods, regardless of the γ value.

Table 1.

Mean AUC values of the proposed iGSEA methods before and after our size adjustment.

Method	Adjustment	γ = 0	γ = 0.2	γ = 0.4	γ = 0.6	γ = 0.8	γ = 1
iGSEA-FE	Before	0.862	0.848	0.832	0.824	0.810	0.805
	After	0.874	0.863	0.847	0.838	0.827	0.821
iGSEA-RE	Before	0.837	0.839	0.840	0.842	0.841	0.851
	After	0.852	0.854	0.852	0.855	0.855	0.864
iGSEA-AT	Before	0.852	0.848	0.842	0.840	0.838	0.839
	After	0.866	0.863	0.856	0.853	0.852	0.855

5.2. Continuous phenotypes

In practice, many continuous response data can be approximated closely by normal distributions, especially after appropriate transformation. As a typical example of continuous phenotypes, we assume that the response Y follows a normal distribution, where the GLM (1) becomes a linear regression model: E(Y_kj|X_jgk = x) = α_gk + β_gkx.

Power comparison

We used the same settings for the total number of genes in the genome (G), the size of the generated gene set (G_s), the number of GSEA studies (K), the numbers of the UR, DR, EE genes, and the proportion of RE genes (γ ∈ {0, 0.2, 0.4, 0.6, 0.8, 1}) as in the binary case. We set λ = 0.7, ω₀ = 0.2, and ω ∈ {0.2, 0.3}. We assume that X_jgk and Y_jk follow a bivariate normal distribution BV N(μ_x, μ_y, σ_x, σ_y, ρ_gk) for j = 1, ⋯, 20, where μ_x = μ_y = 0, and σ_x = σ_y = 1, and ρ_gk = β_gk. So we simulated Y_jk from N(0, 1) and then simulated the expression levels based on the conditional distribution $X_{\mathit{jgk}}\mid Y_{jk}=y~N\left({\beta }_{gk}y,1-{\beta }_{gk}^2\right)$. For a RE gene, we set β_gk ~ N(μ_g, 0.25²), where μ_g ~ N(0.3d_g, 0.1²); otherwise, we set β_gk = μ_g, where μ_g ~ N(0.3d_g, 0.1²) for a DE gene and μ_g = 0for an EE gene. Note that β_gk ∈ (−1, 1), we truncated its value at -0.9 and 0.9 if β_gk > 0.9 and β_gk < −0.9.

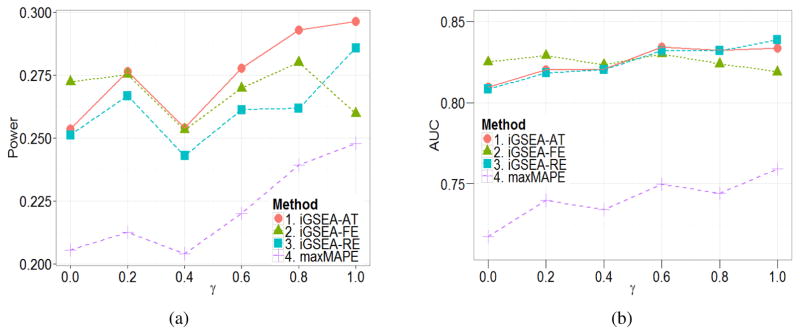
By examining the type I errors of the methods under the settings with the enrichment signal ω = 0.2, we find that the three iGSEA methods are relatively conservative, which is similar to what we find in the case of binary phenotypes. Thus, we used simulated critical values for each method to control the type I error at 0.05 and compared the power in Figure 2(a). Again, all the three proposed methods work better than the three MAPE methods for all γ. Unlike the binary case, iGSEA-FE seems to outperform iGSEA-RE except for γ = 1; and iGSEA-AT seems to outperform iGSEA-FE for medium or large γ. Overall, iGSEA-AT seems to be the best in terms of power.

Figure 2.

Simulation results for continuous phenotypes: (a) the power; (b) the mean AUC stratified by the proportion of RE genes γ.

Sensitivity vs. specificity

The way we generated the different types of genes and gene sets is the same as in the multiple-gene-set model for the binary case; and we generated μ_g, β_gk, Y_jk and X_jgk as in the single-gene-set model for the normal case. The average AUC over 200 datasets for each γ value is shown in Figure 2(b). It is clear that the three iGSEA methods outperform the MAPE methods. For small γ, iGSEA-AT is slightly better than iGSEA-RE; and it is better than iGSEA-FE for large γ.

6. Data example

Here, we illustrate the proposed methods using real expression data and real gene sets. To identify pivotal gene sets involved in lung cancer, we conducted integrative GSEA of five studies using pathways in Kyoto Encyclopedia of Genes and Genomes (KEGG), which is a comprehensive public database containing a large collection of human curated pathways [37]. The data contain four microarray mRNA datasets, including three from [21] and the other from [20], and one RNA-seq dataset [22]. Each of the five expression datasets contains both case and control samples. The detail of the datasets, including the source, the type of experiment and the sample size, is given in Section 3 of Supplementary Material. All expression data were log2-transformed and then standardized.

6.1. Performance Evaluation

To draw ROC curves, we constructed 60 benchmark pathways, including 30 positive controls (PC) and 30 negative controls (NC). A PC pathway includes 25 “essential” genes and 25 “non-essential” genes while a NC pathway includes 50 “nonessential” genes. To randomly generate PCs and NCs, we used the list of “essential” genes given in [14], which contains genes that are believed to be highly related to lung cancer according to the literature, while the list of “non-essential” genes contains those excluded from the list of “essential” genes and any KEGG pathway.

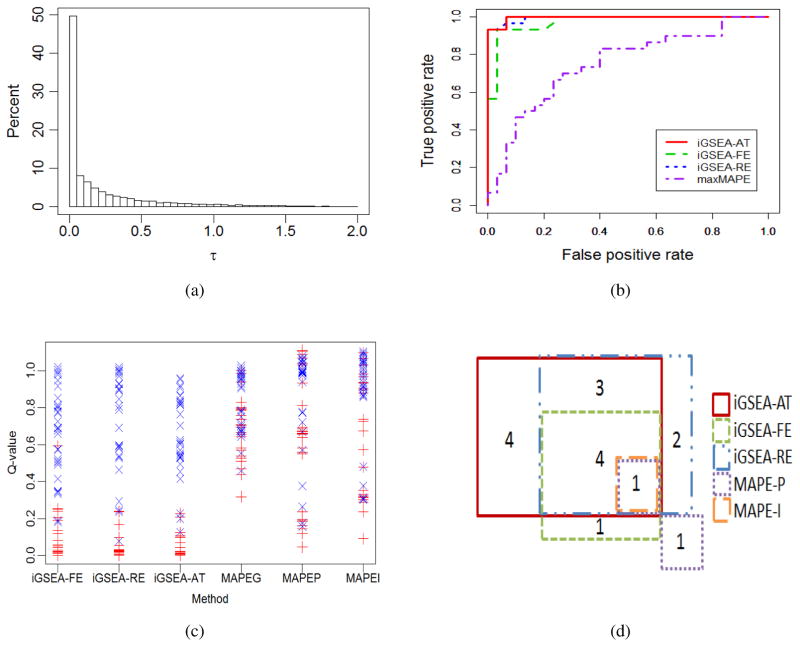
Through an exploratory analysis of the data, we find that although the estimated between-study heterogeneity is close to zero for 50% of the genes, it varied largely among potentially DE genes and 16% of the genes have estimated values greater than 0.5, as seen in Figure 3(a). This obviously indicates neither the FE nor RE model holds for all the genes considered. Due to the conservative nature of iGSEA-AT, we set α₁ = 0.04, making it a bit easier to reject $H_0^{(1)}:{\tau }_g=0$ than the default value 0.0253. Figure 3(b) shows the ROC curves of the three iGSEA methods and MAPEI, since MAPEI is slightly better than MAPEG and MAPEP in this example; and Table 2 presents the AUC value for each of the six methods. The three iGSEA methods clearly have better performance than the three MAPE methods. As seen from the AUC table, the performance of iGSEA-AT and iGSEA-RE is quite comparable, and both have greater AUC than iGSEA-FE. Recall that in our simulation for the binary case, iGSEA-AT and iGSEA-RE often performed better than iGSEA-FE when γ is large. Thus, the above AUC results might hint that the between-study heterogeneity cannot be ignored for a large portion of the DE genes in this example. Figure 3(c) further shows the estimated Q-values of the benchmark pathways computed from the six methods. The three iGSEA methods separate the PC pathways (red “×”s) from the NC pathways (blue “+”s) very well, while the three MAPE methods yield a much poorer distinction.

Figure 3.

Data example: (a) the histogram of estimated between-study heterogeneity ${\widehat{\tau }}_g^{\mathit{MVvc}}$; (b) ROC curves of the three iGSEA methods and MAPEI using 60 constructed benchmark pathways; (c) Estimated Q-values of benchmark pathways from the six methods, where red “×”s and blue “+”s represent positive and negative controls, respectively; (d) Venn diagram of enriched KEGG pathways identified by at least one of the methods.

Table 2.

Data example: area under the ROC curve of each method considered.

	FE	RE	AT	MAPE-G	MAPE-P	MAPE-I
AUC	0.972	0.994	0.996	0.707	0.709	0.748

6.2. Results

We tested KEGG pathways and report the estimated Q-values of those identified by any of the methods in Section 3 of Supplementary Material. In total, iGSEA-FE, iGSEA-RE and iGSEA-AT reported 6, 10 and 12 enriched pathways, respectively. By contrast, MAPE-P, MAPE-G and MAPE-I only reported 2, 0 and 1, respectively, even with π̂₀ = 0.5 in (9). Figure 3(d) shows the Venn diagram for the methods. There are four pathways can be detected by all the three iGSEA methods but none of the MAPE methods. For example, “glyoxylate and dicarboxylate metabolism” is a pathway that has been found to be significantly correlated with loss of tumor differentiation [38]. Also, there are four pathways that were detected only by iGSEA-AT. Among them, “primary immunodeficiency” is a complex series of diseases, and may be associated with adenocarcinoma [39]. This pathway has been reported by [40] to be associated with early-stage lung adenocarcinoma. Also, for the pathway “glycosaminoglycan degradation”, it is known that the structural characteristics of glycosaminoglycans and enzymes involved in their degradation are involved in cancer progression [41]. Thus, these findings are consistent with recent studies in lung cancer while none of the other methods identified them.

7. Discussion

We have shown that the proposed iGSEA methods typically outperformed the MAPE methods through simulation and a data example. In particular, iGSEA-AT has good overall performance; and unlike iGSEA-FE and iGSEA-RE, it seems not to be sensitive to model specification in meta-analysis, due to a data-adaptive strategy of choosing FE vs. RE models. Thus, we recommend iGSEA-AT for combining multiple GSEA studies in practical situations where there is typically no one-size-fits-all model.

We mention that in our numerical studies, for iGSEA-AT, we used Cochran’s Q test to estimate the first-stage P-value p_1g and the asymptotic test of $C_g^{FE}$ to estimate the second-stage P-value p_2g. In our preliminary simulation, we find that using permutation-based methods led to similar results. This is because whether the permutation or asymptotic methods are used may not affect the ordering of $p_g^{AT}$ much. However, the permutation procedures were much slower when the number of genes is large.

Computational efficiency is critical in practice given the increasingly large numbers of genes, gene sets, samples, and available datasets. The three iGSEA methods are fairly fast to conduct and numerically stable. To illustrate the relative efficiency in computing, we report the time to run each method with B = 500 for a randomly generated dataset of four studies with λ = 1 under the one-gene-set model for the binary case in Section 5.1: it takes iGSEA-FE and iGSEA-RE less than 1 second to finish, iGSEA-AT about 4 seconds, and the three MAPE methods 83–86 seconds, using a machine with Windows 8.1 64-bit Operating System, Intel(R) Core(TM) i7-4700MQ CPU @2.40GHz and 8 GB of memory.

In some applications, it would be desirable to adjust for individual-level confounding covariates/factors such as age, race, environmental exposures, etc. Using the GLM setup described in Section 2, the proposed iGSEA methods can easily provide covariate-adjusted estimates as well as covariate-adjusted score statistics and associated variances within each study, and then they can be combined in the same way as we discussed in Section 3. [18] mentioned that using meta-analysis methods based on score statistics, the numbers and types of covariates even need not be the same among the component studies.

Although it covers a wide range of models and distributions, the GLM is not the best way to model censored survival outcomes. Instead, a standard approach is to use Cox proportional hazards models [42]. We note that the extension of our iGSEA methods to survival outcomes is straightforward. Here, we define Y_jk as the observed time (either censoring or event time) for sample j in study k. Using the partial likelihood function under the Cox model, U_gks and V_gks can be constructed accordingly, and all the subsequent steps in our iGSEA methods remain unchanged.

The proposed methods are applicable to situations when expression data are from both microarray and NGS experiments, as shown in our data example. To enhance comparability among studies and ensure estimation of the same parameter, we should carefully review inclusion criteria and adjustments of covariates, and conduct appropriate data preprocessing including annotation and alignment across all different platforms and versions, background correction and normalization of expression data, removal of batch effects whenever possible. For highly complex datasets where the above could fail, blindly applying the proposed methods would be inappropriate; and we suggest to develop robust iGSEA methods based on aggregation of ranked lists from component studies. We further note that although presented in the context of gene expression studies, the proposed iGSEA methods seem to be equally applicable to meta-analysis of other omics data, e.g., epigenomics/methylation studies in large consortia.

Finally, software for the proposed methods is available as an R package named “iGSEA” and is freely distributed on CRAN after testing.

Supplementary Material

Supp info

Figure 1: Comparison of the empirical CDF of v_s with the asymptotic CDF.

Table 1: Type I errors of each method when λ = 0.5, μ = 0.3 and τ = 1.

Table 2: Type I errors of each method when λ = 0.5, μ = 0.45 and τ = 1.

Table 3: Type I errors of each method when λ = 0.5, μ = 0.6 and τ = 1.

Figure 2: Power comparison for the settings with ω = 0.3, μ = 0.3 and τ = 0.5².

Figure 3: Power comparison for the settings with ω = 0.3, μ = 0.3 and τ = 1.

Figure 4: Power comparison for the settings with ω = 0.3, μ = 0.45 and τ = 0.5².

Figure 5: Power comparison for the settings with ω = 0.3, μ = 0.45 and τ = 1.

Figure 6: Power comparison for the settings with ω = 0.3, μ = 0.6 and τ = 0.5².

Figure 7: Power comparison for the settings with ω = 0.3, μ = 0.6 and τ = 1.

Figure 8: Power comparison for the settings with ω = 0.4, μ = 0.3 and τ = 0.5².

Figure 9: Power comparison for the settings with ω = 0.4, μ = 0.3 and τ = 1.

Figure 10: Power comparison for the settings with ω = 0.4, μ = 0.45 and τ = 0.5².

Figure 11: Power comparison for the settings with ω = 0.4, μ = 0.45 and τ = 1.

Figure 12: Power comparison for the settings with ω = 0.5, μ = 0.3 and τ = 0.5².

Figure 13: Power comparison for the settings with ω = 0.5, μ = 0.3 and τ = 1.

Table 4: Design detail in constructing gene sets; 30% of the gene sets are enriched by UR genes, another 30% are enriched by DR genes, and the remaining 40% are non-enriched.

Table 5: Design detail in generating expression levels for different types of genes. Genes 1–100 are UR genes, Genes 101–900 are EE genes, and Genes 901- 1000 are DR genes.

Figure 14: ROC curves for detecting multiple enriched gene sets using iGSEA-FE, iGSEA-RE, iGSEA-AT, and maxMAPE. The purple curve on the plots actually represents the performance of MAPE-P because it is the best of its kind.

Table 6: Empirical FDRs of each method in the multiple-gene-set simulation for binary phenotypes.

Table 7: Lung adenocarcinoma datasets involved in data analysis

Table 8: The estimated Q-values of identified KEGG pathways

Appendix: Algorithm

I. Computing gene-level statistics

1. For each study k, compute the estimated effect β̂_gk, the estimated precision w_gk, the score statistic U_gk, and the corresponding variance estimate V_gk for the genes involved in study k, where g = 1, …, G and k = 1, …, K.

II. Meta-analysis

1. For each gene g, compute the overall gene-level statistic u_g, where $u_g=C_g^{FE}$ for the FE method, $u_g=C_g^{RE}$ for the RE method, and $u_g=-p_g^{AT}$ for the AT method.

III. Gene set analysis

1. For each gene set s, order the genes in and out of the set according to the values of u_g (from small to large), and then compute the enrichment score using the size-adjusted one-sided KS statistic v_s.

2. Randomly assign genes to set s B times and compute the permuted statistics, $v_s^{(b)}$ , 1 ≤ b ≤ B, 1 ≤ s ≤ S.

3. Estimate the P-value of set s by

   $$p(v_s)=\frac{{\sum }_{s^{\prime }=1}^S{\sum }_{b=1}^{B}I\left(v_{s^{\prime }}^{(b)}\ge v_s\right)}{BS}$$

4. Estimate the Q-value of gene set s by (9).

5. Report those gene sets with Q-value< δ as enriched.