Using a FRET Library with Multiple Probe Pairs To Drive Monte Carlo Simulations of α-Synuclein

Abstract

We describe a strategy for experimentally-constraining computational simulations of intrinsically disordered proteins (IDPs), using α-synuclein, an IDP with a central role in Parkinson’s disease pathology, as an example. Previously, data from single-molecule Förster Resonance Energy Transfer (FRET) experiments have been effectively utilized to generate experimentally constrained computational models of IDPs. However, the fluorophores required for single-molecule FRET experiments are not amenable to the study of short-range (<30 Å) interactions. Using ensemble FRET measurements allows one to acquire data from probes with multiple distance ranges, which can be used to constrain Monte Carlo simulations in PyRosetta. To appropriately employ ensemble FRET data as constraints, we optimized the shape and weight of constraining potentials to afford ensembles of structures that are consistent with experimental data. We also used this approach to examine the structure of α-synuclein in the presence of the compacting osmolyte trimethylamine-N-oxide. Despite significant compaction imparted by 2 M trimethylamine-N-oxide, the underlying ensemble of α-synuclein remains largely disordered and capable of aggregation, also in agreement with experimental data. These proof-of-concept experiments demonstrate that our modeling protocol enables one to efficiently generate experimentally constrained models of IDPs that incorporate atomic-scale detail, allowing one to study an IDP under a variety of conditions.

Introduction

Intrinsically disordered proteins (IDPs) and proteins containing disordered regions are exceptionally responsive to changes in solution conditions, making them prone to misfolding and aggregation. One such IDP is α-synuclein (αS), a 140-amino-acid neuronal protein, the aggregation of which is implicated in Parkinson's disease pathogenesis (1, 2). αS is primarily expressed at presynaptic termini and is suspected to play roles in regulating neurotransmitter release and maintaining synaptic function and plasticity (3). Likely the most recognized aspect of αS is its ability to misfold and self-associate, resulting in the production of toxic amyloid fibrils. These fibrils are the primary components of Lewy Bodies, which have been long been recognized as a postmortem hallmark of Parkinson’s disease (1). The protein is comprised of three domains: the N-terminal domain (residues 1–60), comprised of four imperfect 11-amino-acid repeats featuring a KTKEGV motif found in amphipathic helices; the nonamyloid β-component, or NAC domain (residues 61–95), which contains two additional KTKEGV repeats and forms the β-sheet rich core of amyloid aggregates; and the acidic C-terminal domain, which is highly charged and is considered to be largely disordered. The first two domains adopt an α-helical structure in the presence of lipid membranes or detergent micelles whereas, in solution, the αS monomer is largely disordered (2, 4, 5, 6, 7, 8). The structural plasticity of αS and most IDPs is attributed to a lack of hydrophobic residues and an excess of charged residues, producing systems that are self-repulsive and unable to form a collapsed hydrophobic core (6). Despite these characteristics, αS has been shown to be partially collapsed and to deviate from a true random coil structure (9, 10, 11, 12, 13, 14). Moreover, the dynamic structure of αS has high environmental sensitivity that has largely hindered development of a cohesive characterization of the structural ensemble of monomeric αS in solution (6, 10, 11, 12, 13, 14, 15, 16, 17, 18). Solution conditions including temperature, salt concentration, and pH all have substantial effects on the partial folding and collapse of αS. Furthermore, cosolvents and osmolytes have been shown to drive conformational readjustment of αS (6, 19, 20, 21, 22). In particular, seminal work by Uversky, Fink, and coworkers (23) demonstrated the ability of trimethylamine-N-oxide (TMAO) to promote compaction and partial helical folding of αS monomers, and in high concentrations drive the formation of helical oligomers. Intriguingly, these helical conformations are morphologically distinct from the helical structure formed on membranes, and the presence of osmolytes has been show to affect fibril formation (24).

TMAO is a naturally occurring amphiphilic osmolyte that is found in several aquatic organisms, where it counteracts the destabilizing effects of high concentrations of urea required for regulation of osmotic pressure (25, 26, 27). Experimental and theoretical efforts have afforded an effective model by which preferential exclusion of TMAO from the protein backbone and sequestration of water by TMAO promotes the formation of intramolecular hydrogen bonds and a reduction in exposed surface area for the protein (28, 29, 30, 31, 32, 33, 34). Solution studies of TMAO have revealed that the large 4.67 D dipole moment prompts significant water ordering around each molecule (35). Comprised of a total of ∼13 water molecules, direct coordination of water to the oxygen along with formation of a clathrate like structure about the methyl groups produces a first solvation shell with a 6 Å radius, and elicits an excluded volume effect that entropically drives protein compaction (28, 35, 36, 37). In addition to the effects of excluded volume and water arrangement, TMAO has been proposed to act as a nanocrowder and also serves as a poor solvent of the peptide backbone (38, 39). Single-molecule Förster resonance energy transfer (FRET) has been previously used by Deniz and coworkers (24, 40) to investigate the compact structure of αS in TMAO. These studies were performed with a limited set of measurements and demonstrated that successive compaction of αS occurs with increasing concentrations of TMAO while maintaining a single, broadly distributed conformational state. Moreover, the work by Deniz and coworkers showed that despite the emergence of a partially helical secondary structure, the folding pathway and resulting structure were distinct from helices formed on membranes. Although a putative structural ensemble was not proposed in this work, our laboratory and others have demonstrated the ability to apply distances and distributions obtained from single molecule FRET data as constraints for Monte Carlo (MC) simulations (15). In the context of the present problem of TMAO compaction of αS, we wish to further develop a method for employing FRET constraints to generate experimentally constrained models of IDP ensembles.

Although the use of FRET data has not been extensively explored as a basis for generating structural ensembles of IDPs, the application of other long-range measurements has demonstrated success. Work by Forman-Kay, Zweckstetter, Blackledge, and others has shown the efficacy of utilizing data from paramagnetic relaxation enhancement (PRE) NMR experiments as restraints for simulating ensembles of IDPs (12, 13, 14, 41, 42). Dobson, Vendruscolo, and Eliezer have also applied NMR-based methods to study the disordered ensemble of αS (10, 11). Moreover, efforts by Langen have demonstrated the similar usefulness of electron paramagnetic resonance (5, 43). To date, most studies have focused on the application of PRE data, which lacks description of the underlying distribution of states (42). Single-molecule FRET has demonstrated an exceptional ability to visualize subpopulations of disordered ensembles (44). Furthermore, Best and Schuler have addressed some of the major concerns surrounding distance extraction from FRET data (17, 18). Studies of chemically denatured ubiquitin have shown that FRET and small angle x-ray scattering (SAXS) data afford comparable molecular sizes, and that the inclusion of large hydrophobic probe molecules does not significantly impact the structural ensemble (17). Moreover, recent work by Schuler has verified that distributions extracted from single-molecule FRET data display a high degree of agreement with distributions compiled from structural ensembles generated from molecular dynamics simulations restrained with NMR and SAXS data (18).

In this report, we focus on elucidating the structural changes associated with TMAO-induced compaction of αS by combining MC simulations in PyRosetta with experimental constraints from ensemble FRET measurements. Although single-molecule FRET measurements provide additional information regarding the number of distributions as well as the distribution breadth associated with a particular average value, the photophysical requisites for these measurements (i.e., bright, visible wavelength fluorophore pairs, which tend to have 30–70 Å working ranges) generally preclude accurate measurement of distances below ∼30 Å. This limitation is important, as we wish to generate atomically detailed computational models of αS and therefore need short distance constraints for our simulations. Based on the aforementioned results from Deniz and coworkers (24, 40, 44), we assume that the observed ensemble FRET efficiencies are resultant from single distributions, well described by polymer physics models, allowing us to rely on distances obtained from single distribution analysis. Furthermore, we propose that the most effective set of constraints would encompass not only long distances, such as those traditionally afforded from single-molecule FRET, but also short distances closer to those obtained via PRE measurements, which should more effectively limit the conformational variability within the ensemble.

Previously, we have studied αS compaction using the p-cyanophenylalanine (Cnf) and thioamide probe pair, which has a short Förster radius (R₀, the distance of half-maximal energy transfer) of 18 Å (45, 46, 47). We showed that increases in FRET efficiency (E_FRET) indicating compaction are observable as αS is incubated with increasing concentrations of TMAO. However, these Cnf-thioamide-labeled proteins required semisynthesis through native chemical ligation, a method with insufficient throughput for FRET library construction. Herein, we employ Cnf-tryptophan (Trp) as a genetically incorporable, short-range probe pair allowing for more facile production of a library of labeled constructs for measuring distinct intramolecular distances in the presence of TMAO (48, 49). Additionally, we have incorporated a second, longer-range probe pair, fluorescein-5-maleimide (Fam) conjugated to cysteine and tetramethylrhodamine azide (Raz) conjugated to an O-propargyl tyrosine unnatural amino acid (50). The Fam-Raz pair has a working distance around 50 Å and provides accuracy in ranges equivalent to those accessible through single-molecule FRET.

By applying measurements from these two complementary FRET libraries as weighted constraints for atomically detailed MC simulations in PyRosetta, we construct model conformational ensembles that agree well with experimental data such as fluorescence correlation spectroscopy (FCS), reporting on the overall average size of the protein. This strategy of using FRET data to direct all atom models in MC simulations provides a means to generate structure-guided hypotheses for allosteric transitions in αS to understand the effects of changes in environment or interactions with ligands.

Materials and Methods

Protein overexpression and purification

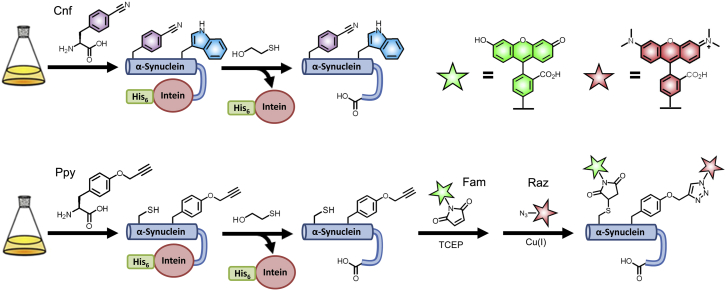
Protein expression was performed in Escherichia coli, where unnatural amino acids were incorporated via amber stop codon suppression and traceless purification was facilitated via attachment of a C-terminal intein containing a C-terminal His-tag (Fig. 1). For the Cnf-Trp library, all native tyrosine residues were mutated to phenylalanine to assure that all energy transfer occurred exclusively between Cnf and Trp. Details of postexpression dye attachment, purification, and construct confirmation are reported in the Supporting Material.

Figure 1.

Scheme for labeled protein production. Top: Direct incorporation of p-cyanophenylalanine (Cnf) and tryptophan (Trp) via unnatural amino acid mutagenesis and conventional mutagenesis, respectively. Bottom: Incorporation of Cysteine (Cys) and O-propargyl tyrosine (Ppy) with subsequent labeling by fluorescein-5-maleimide (Fam) and tetramethylrhodamine azide (Raz), respectively. To see this figure in color, go online.

FRET measurements in TMAO

All labeled αS variants were dialyzed into 20 mM Tris, 100 mM NaCl (pH 7.5). TMAO containing buffers were also prepared with 20 mM Tris, 100 mM NaCl, and the pH was adjusted to 7.5 after the addition of TMAO. Concentrations for the Cnf-Trp library were determined using the Sigma-Aldrich FluoroProfile Quantification Kit, whereas concentrations for the Fam-Raz library were determined via ultraviolet-visible absorbance. Steady-state measurements for the Cnf-Trp library and time-correlated single photon counting (TCSPC) measurements of the Fam-Raz library were performed at a 1 μM concentration, whereas steady-state measurements for the Fam-Raz library were performed at a 100 nM concentration. Measurements were taken in triplicate in 0, 2, and 4 M TMAO. TCSPC measurements were performed for Fam-Raz constructs under solution conditions identical to the steady-state measurements. Intramolecular FRET measurements were performed at concentrations of 1 μM, whereas intermolecular FRET measurements were performed by mixing single-labeled αS containing Fam with single-labeled αS containing Raz, at a concentration of 1 μM for each labeled construct.

Analysis of steady-state and TCSPC data

E_FRET values from steady-state measurements were determined by minimizing the squared difference between the spectrum from the double-labeled construct and a linear weighted sum of two single-labeled constructs using the equation

$$\sum _{\lambda }{\left(I{\left(\lambda \right)}_{\text{DA}}-AI{\left(\lambda \right)}_{\text{D}}-BI{\left(\lambda \right)}_{\text{A}}\right)}^2\to \min .$$ (1)

In Eq. 1, I(λ) represents the intensity as a function of wavelength for the construct indicated by the subscript, where A, D, and DA refer to constructs containing the acceptor fluorophore, the donor fluorophore, and both fluorophores, respectively. The weighting values A and B were used to determine E_FRET values from donor quenching and donor-sensitized emission of the acceptor to produce an error-weighted E_FRET value as described in the Supporting Material. The interresidue distances were calculated from E_FRET using a polymer-scaled version of the Förster equation:

$$E_{FRET}=\sum _r{P}_n\left(r,x\right)/\left(1+{\left(r/R_0\right)}^6\right),$$ (2)

$$P_1\left(r,x\right)=4\pi r{\left(\frac{3}{2\pi x^2}\right)}^{3/2}\text{exp}\left(-\frac{3}{2}\frac{r^2}{x^2}\right),$$ (3)

$$P_2\left(r,x\right)|=\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{exp}\left(-\frac{1}{2}\frac{{\left(r-x\right)}^2}{{\sigma }^2}\right),$$ (4)

where r and x represent the interresidue distance and the average interresidue distance. The reported distances determined from E_FRET values are the average interresidue distances. Two different polymer distributions, P(r,x), based on the Gaussian chain model (Eq. 3) and a semiempirically derived normal distribution (Eq. 4), where the standard deviation, σ, was determined from polymer-liked simulation (detailed in the Supporting Material), were used to determine average distances. Additionally, fluorescence lifetimes from constructs containing only Fam (τ_D) and from constructs containing both Fam and Raz (τ_DA) were used to calculate the ratiometric change in lifetime (τ_DA/τ_D), and thus E_FRET values for comparison with steady-state data. Full details regarding TCSPC analysis are provided in the Supporting Material.

FCS

FCS measurements of 20 nM αS labeled with Alexa Fluor 488 at positions 9, 114, and 130 were taken in the presence of 0, 2, and 4 M TMAO using a laboratory-built instrument based on an Olympus IX71 microscope described in further detail in the Supporting Material. Before addition of labeled protein, chambers were incubated with 400 μM wild-type αS to prevent sticking of the labeled protein to the surface. Free Alexa Fluor 488 dye was measured in each concentration of TMAO to account for changes in viscosity. Additional information regarding FCS measurement and analysis can be found in the Supporting Material.

PyRosetta simulations

MC simulations were performed in PyRosetta on the University of Pennsylvania School of Arts and Sciences General Purpose Cluster. The simulation sampling includes ∼1.5 × 10⁶ backbone φ/ψ torsion angle changes in a simulated annealing score function gradient along with sample of side-chain rotamers. Constraints were applied either in the form of a harmonic potential or a potential derived from the Gaussian chain probability distribution. Output structures represent the lowest energy structures generated over the course of the simulation as determined by the sum of the “beta” Rosetta score function and the constraint energy. Additional details and the base PyRosetta script are provided in the Supporting Material.

Results

We began by generating two libraries of proteins, labeled with either Cnf-Trp or Fam-Raz pairs, and making FRET measurements in varying concentrations of TMAO. For both FRET pairs, we observed changes in photophysical parameters impacting the extraction of distance information from FRET data that necessitated performing control fluorescence measurements using single-labeled proteins. When calculating R₀ (Eq. S8 in the Supporting Materials and Methods) for these experiments, there were four parameters of interest, Φ_D, J, κ² and n, which represent the quantum yield of the FRET donor, the overlap integral between donor emission and acceptor absorbance, the orientation factor between the two fluorophores, and the refractive index of the solution, respectively. Of these parameters, we determined that changes in Φ_D as a function of environment contributed most significantly to changes in R₀ for both Cnf and Fam. Additionally, Zheng et al. (18) previously demonstrated that for disordered proteins, the orientations of the fluorophores are sufficiently isotropic to warrant the approximation of κ² = 2/3, which is the value for an isotropic distribution of orientations. Fluorescence measurements made on donor-only and acceptor-only proteins enabled us to not only account for changes in Φ_D to enhance our accuracy in calculating R₀, but also allowed us to easily overcome the difficulties of interpreting highly overlapped spectra and extract distances from E_FRET measurements for use in modeling.

Cnf-Trp library

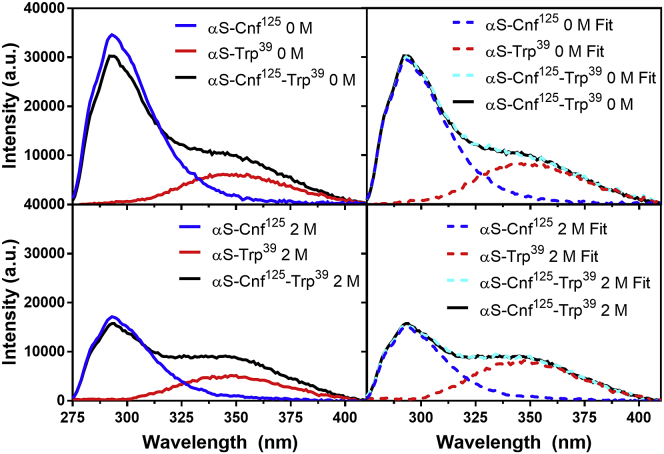
The Cnf-Trp construct library consisted of a total of 27 proteins (17 double-labeled and 10 single-labeled αS mutants) spanning 16 unique intramolecular distances. Acquiring concentration-matched emission spectra for each single-labeled construct in varying TMAO conditions allowed for tracking of changes in the quantum yield and spectral shape of Cnf and Trp emission. The sensitivity of these photophysical properties to increasing concentrations of TMAO was initially assessed for the free amino acids (Fig. S43). Although a decrease in the quantum yield was observed for both Cnf and Trp, no major change in emission maximum was observed in the Trp spectrum. In contrast to the free amino acid measurements, Trp-containing αS mutants successively blue-shifted in increasing concentrations of TMAO, as a result of changes in local environment upon compaction. Thus, measuring single-labeled spectra was not only crucial for tracking spectral changes due to environmental effects, but was also essential for deconvoluting the highly overlapped Cnf and Trp emission spectra in constructs containing both fluorophores. E_FRET values were obtained for each probe pair in buffer containing 0, 2, and 4 M TMAO. Fig. 2 shows the deconvolution of a 0 M measurement as well as a 2 M measurement for the Cnf₁₂₅-Trp₉₄ pair. As expected, E_FRET increases, correlating with the expected decrease in interresidue distance resulting from compaction in TMAO. Without TMAO, in most cases this probe pair is not able to accurately capture the apparent intraresidue distance, as seen in low E_FRET values outside of the most reliable FRET range (E_FRET = 0.3–0.7). This is most clearly observed in Fig. 3, where the distances extracted from these data are largely invariant above sequence separations of 50 residues. However, in cases where the probes are relatively close in primary sequence, the utility of this short-range pair is clearly demonstrated. In the presence of 2 M, and especially 4 M TMAO, a significant number of the probed regions display E_FRET values within the optimal range for accurate distance determination.

Figure 2.

Determination of E_FRET. Left: Background subtracted fluorescence emission spectra of constructs labeled with Cnf, Trp, or both Cnf and Trp in 0 M (top) and 2 M TMAO (bottom). Right: Double-labeled Cnf-Trp spectrum compared to weighted sum of Cnf-only and Trp-only spectra, along with the contributions from each single-labeled spectrum shown for 0 M (top) and 2 M TMAO (bottom) spectra. To see this figure in color, go online.

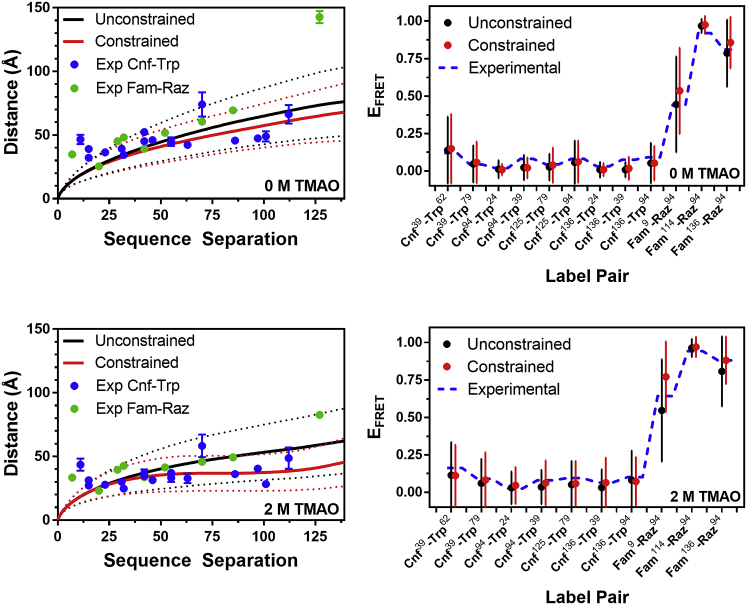
Figure 3.

Comparison of experimental and simulated data. Left: Distances extracted from E_FRET measurements of the Cnf-Trp and Fam-Raz libraries shown with interresidue distances for a given primary sequence separation in unconstrained or constrained MC simulations. The average (solid line) and standard deviation (dashed line) of interresidue distances are shown for the simulated ensembles. Right: Experimental and simulated E_FRET values. Dashes represent average E_FRET values for each pair of labeled residues, with interconnecting lines to guide the eye. The average (point) and standard deviation (line) of E_FRET values obtained based on interresidue separations in the unconstrained or constrained simulated ensembles. To see this figure in color, go online.

Fam-Raz library

To complement our Cnf-Trp data, we also performed FRET measurements with a probe pair with a longer working range. A set of 21 constructs, consisting of 10 dual-labeled and 11 single-labeled analogs containing Fam and/or Raz, was produced to accurately monitor long-range distance changes during the compaction of αS by TMAO. In cases where exceedingly low E_FRET was observed with the short-range probe pair, we observed efficiencies much closer to the optimal efficiency range for the Fam-Raz pair. This was most significant in the absence of TMAO. However, our measurements approached the short end of the working range for the Fam-Raz pair in some instances in 2 M TMAO, and exhausted its utility in 4 M TMAO.

In 4 M TMAO, the long working range of this probe pair was effective for assessing the formation of oligomers, which were reported by Uversky et al. (23). When mixing Fam and Raz single-labeled species in 4 M TMAO, there was a significant reduction in the lifetime of the Fam labeled construct, consistent with intermolecular FRET (Figs. S48–S50). In buffer or 2 M TMAO, there was no observed change in the lifetime of the Fam-labeled protein due to the presence of the protein containing Raz. FCS and atomic force microscopy measurements also demonstrate the formation of oligomers in 4 M TMAO (Figs. S51 and S52). As a result of these observations, we decided to forego modeling the 4 M structure due to the complexity of deconvoluting intra- and intermolecular FRET in oligomers.

Interpretation of FRET data

Because αS is disordered, the interresidue distance separating any given label pair is widely distributed. To accurately obtain an average distance value, this distribution needs to be taken into account. Therefore, the corresponding interresidue distances were calculated using a polymer-scaled Förster equation, Eq. 2, taking into account changes in R₀ resulting from changes in quantum yield for each labeling position. Distances were calculated using both the Gaussian chain (Eq. 3) and semiempirical (Eq. 4) models, which produced significantly different sets of results. Conceptually, two positions labeled with two FRET pairs with different R₀ values should have distinct FRET efficiencies, but comparable extracted distances. Since the Cnf-Trp and Fam-Raz libraries contained a limited number of labeled positions in common, for comparison the distances were plotted in Fig. S44 as a function of probe pair primary sequence separation. We reasoned that the consistency between data from the Cnf-Trp and Fam-Raz libraries on a Flory scaling plot should help us to identify the more accurate probability distribution. In Fig. S44, it is clear that there is substantially better agreement between the Cnf-Trp and Fam-Raz data sets when applying the Gaussian chain distribution to extract distance data from the E_FRET values.

Simulations

After data collection, simulations were performed in PyRosetta to generate structural ensembles that represent the changes observed by FRET. Before introducing FRET-based constraints, we optimized a PyRosetta script to effectively produce ensembles of structures in general agreement with previously published radius of gyration (R_g) and radius of hydration (R_h) values (21, 51). Simulations were performed where the weighting of the FRET constraints relative to other Rosetta energy terms (a, Eqs. S18 and S19 in the Supporting Materials and Methods) was varied, and different shapes for the FRET constraint function were assessed. These constraint function shapes were based on the Gaussian chain (Eq. 3) or semiempirical (Eq. 4) distance distributions used in the FRET analyses. Given the greater consistency between Cnf-Trp and Fam-Raz data when using the Gaussian chain probability distribution (above), we favored using this function for implementing constraints as well. However, we tested all combinations to ensure that no bias was introduced based on the pairing of distribution functions used in FRET data analysis and in constraint implementation. The results of these tests are detailed in the Supporting Material (Figs. S53–S64) and are discussed further below. We found that setting the weight of the constraints relative to the other score function components to unity allowed the FRET constraints to influence the structure without overconstraining, and that reasonable variations of the shape of the constraint function did not dramatically influence the simulation results. Thus, in the main text, we exclusively report simulations performed using the Gaussian chain distribution, with all other simulations reported in the Supporting Material. The 2 M TMAO simulations were performed with the solvation term removed in an effort to account for the significant change in solvation. Unconstrained simulations performed with this altered score function provided a more compact starting point for introducing FRET constraints, whereas constrained ensembles were noticeably more compact (Figs. S56–S58). Moreover, for simulations of the 2 M ensemble, fragment insertion was incorporated within the MC search to increase the amount of resultant secondary structure, which has been observed by circular dichroism studies of the TMAO-induced conformation (23). Although this significantly increased the number of helices, there was no marked improvement in the match of simulated structures with experimental FRET data (Figs. S56–S58).

Initially, we compared the constrained simulations to the FRET data using Flory scaling plots, where the average interresidue distance (between α-carbons) as a function of sequence separation was plotted for the ensemble of 1000 lowest energy structures with experimental FRET data overlaid as discrete points (Fig. 3, left). All experimental data were close to the average simulation distance or within the standard deviation for both 0 and 2 M ensembles, with the notable exception of the Fam₉-Raz₁₃₆ FRET data. It is notable that the distance determined for this FRET pair using the harmonic potential (Fig. S44) does not show such dramatic discord with the other distances, potentially suggesting a limitation of the Gaussian chain model for very long distance ranges. We also predicted FRET values for all of the pairs of label sites for comparison to the experimental FRET data (Fig. 3, right). Distances between the α-carbons of the amino acids at the label sites were extracted from each structure in a simulated structural ensemble and converted to E_FRET values using the classical Förster equation (Eq. 2, where P(r,x) = 1). Since the variations in conformation in the ensemble explicitly capture the distribution of interresidue distances, the average E_FRET was computed as a simple average of the values extracted from each structure with no further correction for polymer scaling of the distance distribution. We found good agreement, with an average absolute E_FRET difference of 0.09 and all experimental values falling within the standard deviation of the simulated values. As discussed below, the close match between these values helps to validate our choice of a polymer-scaled distance distribution function in interpreting E_FRET values to input constraints in the simulations.

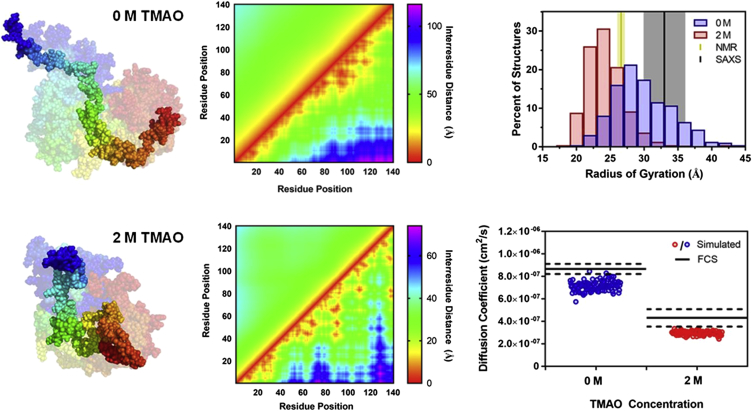
Fig. 4 shows the 10 lowest energy structures from the 0 and 2 M simulations, aligned and with a single structure darkened for clarity. One can see significant compaction of the 2 M ensemble, which can be quantified using histograms of the R_g for each structure in the ensemble. The average radius of gyration in 0 M TMAO is 29.3 ± 4.6 Å, which shrinks to 23.5 ± 3.4 Å in 2 M TMAO. Interestingly, despite this compaction, αS remains disordered in 2 M TMAO. The disorder can be visualized using a plot of the distribution of interresidue distances as a two-dimensional “heat map,” with interresidue distances for the entire ensemble plotted above the diagonal and interresidue distances for the single darkened structure below the diagonal. As seen in the middle plots in Fig. 4, in both 0 and 2 M TMAO, the average interresidue distance scales with primary sequence separation, despite the fact that long-range contacts occur in individual structures within the ensembles (Fig. S67). This combined information indicated that, in the presence of 2 M TMAO, αS populates a compacted disordered ensemble that still maintains a high degree of structural heterogeneity. To confirm that the structure ensembles were consistent with other experimental observables, we calculated the diffusion coefficient for each structure of the 0 and 2 M ensembles using HydroPro (52). As seen in Fig. 4, the calculated diffusion coefficients are slightly (16%) smaller, but in reasonable agreement with those measured in our FCS experiments.

Figure 4.

Analysis of αS structural ensembles. Left: Representative structures from 0 and 2 M simulations. The darkened structure in the foreground is the lowest energy structure and the faded ensemble in the background includes the 10 lowest energy structures. Middle: Heat maps showing the average interresidue distances in the simulated ensembles. Each heat map shows the average distance for the full simulated ensemble of structures above the diagonal and distances from the single lowest energy structure below the diagonal. Top right: Histograms of radii of gyration of structures from simulations, plotted with literature values of R_g determined from SAXS data and the hydrodynamic radius from NMR studies. Bottom right: Diffusion coefficients from FCS and simulated structures. To see this figure in color, go online.

Comparison of structure ensembles to data from literature

We compared our structural models in the absence of TMAO to data from the literature as well as other published models. The average R_g of our 0 M ensemble matched well with reported values of R_g from SAXS experiments and R_h (typically 30% larger than R_g) from NMR experiments (21, 51). Furthermore, our models agreed remarkably well with both the primary NMR PRE data (Fig. S66) and Flory scaling plots of the resulting models (Fig. S65) reported by Allison et al. (10). We do observe rare contacts between regions of the protein that are distant in primary sequence (Fig. S67), consistent with reports of transient C-terminal contacts with the NAC and N-terminus (14). Although there is limited information on the structure of αS in 2 M TMAO, we find that our models agree with the available information. Similar to previous studies, our circular dichroism measurements made in 0 or 2 M TMAO show little change in αS helicity (Fig. S73), consistent with our models which show that the 2 M ensembles are still highly disordered. Previously, Uversky and coworkers monitored fibrillization of αS in TMAO using thioflavin T (ThT) fluorescence, and found that aggregation was accelerated, but that the final level of ThT fluorescence was lower. Our own studies with Congo Red (Fig. S71) corroborated this observation, although, intriguingly, changes in fluorescence polarization (Fig. S72) were slower in 2 M TMAO, possibly indicating that the ThT and Congo Red spectroscopic properties are changed in TMAO. Thus, although compacted, αS remains disordered and able to sample conformations that lead to fibril formation. This can be seen in Figs. S69 and S70 where, despite compaction observed by changes in solvent-accessible surface area, metrics such as numbers of intramolecular hydrogen bonds and backbone dihedral angles do not indicate the presence of persistent structure.

Discussion

Our previous study of αS structures using MC simulations with only a repulsive Lennard-Jones potential and harmonic constraints based on single-molecule FRET data gave structural ensembles with global properties that matched well to experimental measurements such as R_g. This modeling protocol, with constrained simulations utilizing exclusively a repulsive van der Waals potential, was extremely efficient in its simplicity, but the resulting models lacked atomic-scale details that could be used in generating hypotheses or interpreting mechanisms of conformational change. We and others have also performed unconstrained simulations which included the amino acids using single-sphere “centroid” representations of the side chains, as well as all-atom molecular dynamics simulations of αS, which do provide such detailed information, but are much more computationally intensive and generally limited in the conformational space explored. We wished to find an intermediate level of simulation wherein we could include side chains in MC simulations and maintain efficient sampling. However, we reasoned that the previous long-range constraints (>30 Å) derived from single-molecule FRET data would not provide sufficient information on short-range interactions to properly direct these simulations. Thus, we here included data from the short-range Cnf-Trp pair along with data from the Fam-Raz pair, which has a comparable FRET range to the previous single-molecule FRET probes. These short-range probe pairs may be crucial for identifying contacts or collapsed regions that can exist under varied solution conditions or in the presence of allosteric molecules.

Assessing the validity of P(r)

We reasoned at the outset that the Gaussian chain P(r) was more accurate because it led to greater consistency between the distances obtained from the Cnf-Trp and Fam-Raz libraries. However, this method of analysis was complicated by the limited numbers of intramolecular distances in a range that could be accurately captured by both pairs, as these probes were selected specifically for their efficacy across different distance ranges. Furthermore, one can observe that the Cnf-Trp distances are largely invariant after reaching a sequences separation of ∼50 residues due to a working range that extends to only ∼35 Å. Therefore, our assignment of the Gaussian chain P(r) as the more accurate distribution function arises from visual inspection of the Flory scaling plots in Fig. S44 in the 25–45 Å range, which encompass the upper and lower bounds of the Cnf-Trp and Fam-Raz probe pairs, respectively. It is important to note that at very short (<15 residues) and very long (>115 residues) sequence separations, the calculated distances are likely unable to be accommodated by any conformation of the protein. Furthermore, the functional form of the distribution may also be dependent on the number of residues between two probes (e.g., short sequence separations cannot have truly polymer-like behavior and may need to be treated with classical FRET equations) or heterogeneity not accounted for by polymer-scaling behaviors (53).

Differences between constraint methods

Since IDPs have relatively flat energetic landscapes, improper introduction of constraints can easily result in ensembles where the resultant conformations are not sufficiently diverse, especially proximal to constrained sites. This arises primarily from constraining potentials that are too deep or too narrow, but can also occur when conformational space is not effectively sampled. The latter problem could be caused by poor parameterization of the Metropolis criterion (such as selection of a kT value that is too low) or by not having an appropriate score function to produce the multiple local minima present within a single pair-wise constraint potential. By expanding our score function from a single repulsive van der Waals term to the current optimal score function utilized by Rosetta, we assure that output states populate local minima that allow us to extract high-resolution information and provide an effective buffer for constraint introduction. Achieving unconstrained simulations of this quality required significant adjustment of PyRosetta scripts, which normally are used to model folded proteins rather than IDPs. These optimization efforts will be reported in detail elsewhere. In addition to improved modeling scripts, we hypothesized that issues related to the constraint functional form could be circumvented by directly employing appropriate distance distributions for disordered ensembles to analyze the FRET data.

Nonetheless, we performed simulations with all four combinations of the two P(r) functions used to obtain distances and the two corresponding constraining functions. This allowed us to consider how the ensembles were influenced by the method of constraining in addition to the sets of distances used as constraints. Figs. S56–S63 demonstrate that neither the method of constraint nor the P(r) utilized for the distance determination through Eq. 2 had a dramatic impact on the resulting structures. This likely arises from the fact that distances from the unconstrained simulation are already very close to the distances obtained from the experiments. Despite the relative agreement between the ensembles produced across all constraining methods for a given concentration of TMAO, there are several noteworthy observations. Figs. S60–S63 show that in all cases in which a harmonic potential was employed, the structural diversity, most clearly observable in the dispersion of R_g values, is visibly decreased. Moreover, harmonic constraints consistently produced deviations in the scaling behavior, where the heat maps (Figs. S60–S64) reveal distances between the N-terminal region and the NAC domain that are, on average, longer than those between the C-terminal region and the NAC. This observation is independent of the input data, as these nuances are observed for both data sets, with constraints from data obtained utilizing P₂(r,x) further enhancing these trends. These observations demonstrate that there are significant differences between these ensembles which result exclusively from the functional form of the constraining potential.

The relative impacts of changes in the score function or in the constraints are evident in comparisons between 2 M simulations performed using Gaussian chain derived data with or without constraints or solvation term modification (Figs. S56, S60–S63). FRET constraints alone compacted the 2 M ensemble (2 M GC-GC) relative to the 0 M ensemble (0 M GC-GC), but were not sufficient to generate ensembles that were consistent with the 2 M experimental data. However, it is important to note the marked differences between the 0 and 2 M ensembles, as these demonstrate that simulations in PyRosetta can be significantly influenced by constraints, which was not evident from the 0 M simulations alone. The fact that these constraints alone were unable to produce ensembles in full agreement with the 2 M data suggests that αS in the presence of molar quantities of TMAO populates a subset of conformations that are not accessible with the standard score function. With the solvation term removed, comparison of the 2 M constrained (2M GC-GC^†, see Fig. S62) and unconstrained (Unconstrained^†, see Fig. S61) simulations demonstrate that the constraints serve to exclude extended structures. This further suggests that the application of constraints does not produce new conformations not present in the unconstrained population, but can effectively remove unfavorable structures from an ensemble based on experimental data. Overall, we see this as a favorable compromise as the necessity to modulate the unconstrained population through changes to the PyRosetta scoring is likely driven by the dramatic change in buffer conditions, which would not be present in many other applications. Systems where dramatic changes in solvent conditions occur (as in this study) can be effectively represented by adjusting the score function, whereas intramolecular (or intermolecular) contacts can be accounted for by changing the constraint functional form to accurately represent experimental data.

Comparison of experimental and simulated data

Initial comparisons between the experimental and simulated distances in Figs. 3 and S56 demonstrate that most of the obtained distances fall within 1 SD of the average interresidue distance for the given sequence separation. The observed disagreements at high and low sequence separation are likely due to inaccuracies in the determination of the experimental distance arising from either the working range of the probe or the polymer-scaling function, as previously discussed. Moreover, agreement in simulated and experimental FRET efficiencies in Figs. 3, S57, and S58 demonstrate that the underlying conformation dispersion is accurately captured, since appropriate efficiencies are obtained for both probe pairs. The FCS measurements herein also demonstrate that the simulated ensembles are of approximately the correct overall size and that the degree of compaction is qualitatively accurate. The quantitative disagreement between the simulated diffusion coefficients observed in Fig. 4, where the simulated diffusion coefficients are systematically lower than the experimental values, could arise from several different factors. Given that the overall size agrees with previously published NMR and SAXS data, it is possible that we encountered small, systematic inaccuracies in determining diffusion coefficients resulting from a combination of the treatment of the disordered ensemble in HydroPro, the need for an empirical conversion factor, or accounting for the change in viscosity induced by TMAO. Importantly, we have demonstrated in Figs. S65 and S66, respectively, that our 0 M ensembles agree with previously published PRE data and the structural ensembles generated from those data (10, 11).

It is worth noting that in our effort to establish an efficient, intermediate level of simulation, we chose not to pursue some elements that could have further improved the accuracy or tested the boundaries of our simulations. For example, we elected not to incorporate probe/linker spatial exploration. Although we acknowledge that simulations would be made more accurate by including representations of the probes, with FRET based on distances between fluorophore transition dipoles instead of α-carbons, this would have significantly increased the computational time, undermining our intention of creating an efficient approach. Additionally, we envision that coupling our method with the strategy previously employed by Dobson and Vendruscolo, where constraining functions were iteratively updated, could produce a more refined, but computationally intensive, version of our modeling protocol (11). Moreover, this method circumvents the need to assume a probability distribution function when interpreting the FRET data, as the constraints would be applied directly as FRET efficiencies. Finally, since introduction of a new constraint functional form is as simple as writing a new function in Python, we hypothesize that our method of constraint introduction, where assumptions regarding underlying distributions are directly converted into a potential, is not only useful for applying FRET data from disordered systems, but would also allow for efficient incorporation of other types of experimental data such as PRE data (10, 13, 41).

Conclusions

We have developed a Rosetta modeling protocol using explicit protein side chains and sophisticated score functions in combination with appropriately weighted distance constraints to generate models of IDPs. By performing simulations that were constrained with experimental FRET data from two libraries containing different FRET pairs, we were able to model the ensemble of αS in buffer and in the presence of 2 M TMAO. Our models agreed well with independent measurements of αS structure from FCS, NMR, PRE, and SAXS data, and were computationally less taxing than traditional molecular dynamics simulations. In future work, we intend to explore the degree to which ensembles generated in PyRosetta capture residual secondary structure and the accuracy of values computed from these ensembles, such as chemical shifts or J-couplings in comparison with NMR experiments. The modifications made to our Rosetta modeling protocol allowed us to produce reasonable αS starting models in the absence of constraints. The quality of these unconstrained models gives us greater confidence in interpreting the interactions observed in the constrained structural ensembles, and makes the simulations more robust to the inclusion of an inconsistent constraint. After careful consideration of constraint function shape and weight, we have found a form that allows them to influence the structural ensemble without overconstraining. Future investigations could employ different weights for different FRET pairs, or different functional forms for different distance ranges.

Our modeling protocol for IDPs incorporates atomic detail relevant to the study of chemical-, ligand-, or environment-induced conformational changes, and yet is sufficiently rapid both in data collection and simulation time to be applied in a moderate throughput fashion. Once libraries of labeled proteins have been generated, FRET measurements of the type reported here could easily be acquired under a variety of conditions, potentially even in a multiwell format. The collection of FRET constraints could then be used to generate structural ensembles to explore hypotheses for mechanisms of conformational change or to rationalize trends among molecules and modifications that modulate IDP conformation. For example, Kakish et al. (54) have recently shown that bis-heterocycles linked by a flexible tether are able to bind to αS and induce conformational changes in the monomer that inhibit its propensity to aggregate. The procedures used here to study the effects of TMAO on αS structure could be applied to study such molecules with therapeutic potential. Furthermore, recent work has shown that modifications such as serine glycosylation and tyrosine phosphorylation affect aggregation and membrane binding respectively (55, 56). Subsequent modification of the current labeled library, or production of a new library, would allow one to utilize the method reported herein to visualize the effect of these and other posttranslational modifications on the disordered ensemble. Although certain classes of molecules or solution conditions may spectroscopically interfere with our FRET probes, it is important to note that we can easily vary these probes using essentially the same labeling strategies. For example, we have recently reported a methoxycoumarin-acridonylalanine FRET pair that can be introduced by a combination of cysteine modification and unnatural amino acid mutagenesis (57). Finally, it is important to note that our methods are not restricted to pure IDPs like monomeric αS, but can be applied to disordered regions of folded proteins or ordered aggregates such as the N- and C-terminal regions of fibrillar αS (58, 59).

Author Contributions

J.J.F. prepared the Cnf-Trp library and performed all steady-state and lifetime measurements and simulations. C.M.H. prepared the Fam-Raz library. J.Y. assisted in preparation of the Cnf-Trp library. B.P. performed FCS measurements (advised by E.R.). Y.-C.L. performed atomic force microscopy measurements (advised by Z.F.). A.N. and J.J.F. designed and performed computational modeling. J.J.F. and E.J.P. drafted the manuscript. All authors contributed to manuscript editing.

Editor: David Eliezer.