The generational scalability of single-cell replicative aging

Specific mathematical forms can explain survival probability and generation-duration dynamics of replicatively aging cells.

Abstract

Despite the identification of numerous genes able to modulate lifespan, it remains unknown whether these genes interact to form a regulatory network that governs aging. Here we show that genetic interventions that extend or shorten replicative lifespan in Saccharomyces cerevisiae elicit proportional scaling of survival curve dynamics. The scalable nature of replicative lifespan distributions indicates that replicative aging is governed by a global state variable that determines cell survival by integrating effects from different risk factors. We also show that the Weibull survival function, a scale-invariant mathematical form, is capable of accurately predicting experimental survival distributions. We demonstrate that a drift-diffusion model of aging state with random challenge arrival effectively captures mortality risk. Measuring single-cell generation durations during aging, we uncover power-law dynamics with strain-specific speeds of increase in generation durations. Our application of quantitative modeling approaches to high-precision replicative aging data offers novel insights into aging dynamics and lifespan determinants in single cells.

INTRODUCTION

While the molecular determinants of how cells of an initially isogenic population experience heterogeneity in their lifespan are not fully understood, two distinct frameworks (1–3) are thought to describe the organization of lifespan determinants. In the first framework (competing risks model), a death event occurs when the state of a single aging factor falls below its threshold for causing cell death, even if the other factors have not reached their thresholds yet. In the second framework (dependency network model), coordinated interactions among the aging factors lead to the formation of a global state variable (X) which determines cell death.

A recent study (3) has shown that interventions, such as temperature and gene disruptions, altered the chronological lifespan (CLS) distributions of Caenorhabditis elegans in a scalable manner by stretching or shrinking of the time. CLS (4–6) is a lifespan metric that quantifies the length of time an organism is alive in a nonmitotic state. Supporting the dependency network model, results from the C. elegans study suggested that, through such temporal scaling, the physiological determinants of the death risk were altered to the same extent by each intervention throughout the adult life of the organism (3).

For organisms whose cells go through mitotic divisions, replicative lifespan (RLS) (4, 7) is an alternative quantitative metric to measure the lifespan of mitotically dividing cells. RLS is defined as the total number of division events a mother cell completes before death. Here, using the yeast Saccharomyces cerevisiae as a model, we experimentally and computationally investigate whether or not genetic interventions change RLS distributions in a scalable manner. We show the scalability of the distributions and identify Weibull and Strehler-Mildvan models as scale-invariant empirical and mechanistic models, respectively, that can mathematically describe the experimental distributions. Further, we elucidate that the power law provides a quantitative link between generation durations and the number of generations before cell death.

RESULTS

Experimental measurement of single-cell RLS

To explore whether RLS distributions would display scalable behavior with respect to the number of generations, we tracked mitotically dividing mother yeast cells throughout their full RLS by starting from their first generation. Using our microfluidic “yeast replicator” device (8) to automate the measurements of yeast RLS in liquid medium, we collected high-precision cell survival data (Fig. 1, A to C). The probability of a cell’s being alive at a specific age (g) formed a survival distribution S(g) (Fig. 1D). An average lifespan of 23.5 generations was measured from the distribution of lifespan values obtained from the wild-type cells (Fig. 1E).

Fig. 1. Experimental measurement of single-cell lifespan and generation durations.

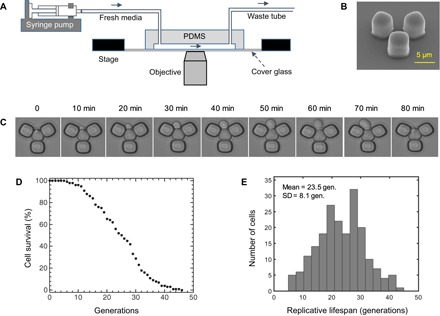
(A) Schematics of the experimental setup with the microfluidic chip and a stage-automated inverted microscope. (B) Scanning electron microscope picture of the functional unit of the microfluidic chip. Scale bar, 5 μm. (C) Time-dynamic bright-field images of a sample mother cell giving birth to a daughter cell. (D) Cell survival as a function of the number of generations (gen.) of the wild-type yeast cells. Cell survival was quantified by taking the fraction of initial cells (n = 200) that were still alive at a specific generation. (E) RLS distribution from 200 wild-type mother cells analyzed. The average RLS is 23.5 generations. PDMS, polydimethylsiloxane.

By deleting specific genes from the yeast genome, the average lifespan of yeast cells can be made shorter or longer compared to the average lifespan displayed by the wild-type cells. We picked seven genes (Table 1) and deleted them from the wild-type genome. The choice to include these specific gene deletions was based on either their canonical nature or the desire to represent a wide range of lifespan values (8, 9). Performing single-cell aging experiments on these seven strains using our microfluidic setup, we found that the absence of SIR2, RIF1, or TVP15 shortened the average lifespan, whereas yeast cells lived longer when SGF73, TOR1, GPA2, or FOB1 gene was deleted (Table 1).

Table 1. Descriptions of the genes deleted from the wild-type background.

RLS values for the gene-deleted strains are given in mean ± SD generations. Wild-type cells lived 23.5 ± 8.1 generations. n = 200 cells.

Gene	Description	Lifespan
SIR2	NAD+-dependent histone deacetylase of the sirtuin family.	14.0 ± 4.8
RIF1	Protein involved in telomere length control, silencing, and DNA replication.	15.4 ± 5.0
TVP15	Integral membrane protein. Localizes to late Golgi vesicles.	19.0 ± 7.5
SGF73	Protein with roles in anchoring deubiquitination module into SAGA and SLIK complexes.	33.2 ± 13.0
TOR1	PIK-related protein kinase and rapamycin target. Subunit of the TORC1 complex.	30.0 ± 10.7
GPA2	Nucleotide binding α subunit of the heterotrimeric G protein.	28.3 ± 8.5
FOB1	Nucleolar protein that is required for replication fork blocking.	31.9 ± 11.8

Scalability of RLS distributions across different genetic interventions

Independent of any particular parametric form of S(g), between any two genetic backgrounds Δ₁ and Δ₂, if S_Δ1(g) = S_Δ2(λ^{− 1}g), then the genetic perturbations introduced to the yeast genome would be expected to affect cell survival statistics through a generational rescaling of the survival probability, with λ being the scaling factor (3). To quantitatively evaluate the presence or absence of scalability, we applied an accelerated failure time (AFT) regression model to the survival data (Fig. 2, A to G, and the Supplementary Materials). For lifespan distributions that can overlap by a simple generational rescaling, one would expect to obtain identically distributed residuals as a result of the AFT regression. To evaluate the degree of differences between AFT residual distributions, we applied a Kolmogorov-Smirnov test (see the Supplementary Materials). We did not observe (Kolmogorov-Smirnov at 0.05 significance level; fig. S1 and tables S1 and S2) any significant deviations from perfect scaling across the different genetic backgrounds, confirming that a diverse set of genetic interventions produce a generational scaling of cell survival probabilities for single yeast cells.

Fig. 2. Scalability of RLS distributions across multiple genetic interventions.

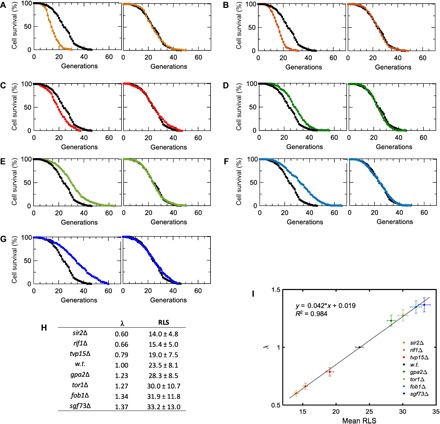
(A to G) Experimental (left) and scaled (right) survival curves are shown for sir2Δ (A), rif1Δ (B), tvp15Δ (C), gpa2Δ (D), tor1Δ (E), fob1Δ (F), and sgf73Δ (G) strains. n = 200 cells for all strains, and wild-type survival data are shown in black in all panels. (H) The scaling factor λ and the RLS (mean ± SD generations) values for all strains characterized. (I) Linear fit applied to λ and mean RLS values. To compute the error bars, we generated 1000 virtual samples for each strain. Each virtual sample consists of 200 RLS data points sampled from a pool of 200 RLS measurements (with replacement) available for each strain. Sampling is done using MATLAB’s bootstrp function. Using wild-type (w.t.) strain as the template, λ and mean RLS for each sample are computed. The error bars (SD) of λ and mean RLS are then computed respectively based on the λ and mean RLS values of the 1000 virtual samples for each strain. The linear fit is performed on the pooled λ and mean RLS values of all the virtual samples.

As expected, the values of λ that were extracted after scaling the survival curve of each gene-deleted strain to the wild-type survival curve displayed a linear relationship with respect to the average RLS of the strains measured (Fig. 2, H and I). The scalability indicates that these seven genes have a concerted influence on the global aging factor X(g) (3). Such an influence could be through direct or indirect interactions among these genes. Some of these interactions have already been characterized mechanistically. For example, the deletion of SIR2 shortens yeast lifespan through increasing both ribosomal DNA (rDNA) recombination and extrachromosomal rDNA circle formation (10), whereas the deletion of TOR1 extends lifespan through reduced signaling in the TOR pathway (9), resulting in down-regulation of ribosome biogenesis. As another example, when combined in the same yeast strain, SIR2 and FOB1 deletions compensate the effects of each other to a large degree (10). FOB1 is a key gene whose deletion decreases the rate of rDNA recombination (11) and extends yeast lifespan (12).

Empirical Weibull model fits and predicts the experimental survival distributions

To ascertain whether an exact mathematical form (describing the experimental survival distributions and satisfying the scalability requirement) can be associated to S(g), we considered the gamma, Gompertz, and Weibull distributions that have been historically (13–16) used to describe morbidity statistics of living systems, with the survival functions

Gamma (r, α): $\frac{\mathit{S}}{{\mathit{S}}_0}=\frac{{\mathit{r}}^{\mathrm{\alpha }}}{\mathrm{\Gamma }(\mathrm{\alpha })}{\displaystyle {\int }_{\mathit{g}}^{\infty }}{\mathit{t}}^{\mathrm{\alpha }-1}{\mathit{e}}^{-\mathit{r}\mathit{t}}\mathit{d}\mathit{t}$

Gompertz (r, α): $\frac{\mathit{S}}{{\mathit{S}}_0}={\mathit{e}}^{\frac{\mathrm{\alpha }}{\mathit{r}}(1-{\mathit{e}}^{\mathit{r}\mathit{g}})}$

Weibull (r, α): $\frac{\mathit{S}}{{\mathit{S}}_0}={\mathit{e}}^{-{(\mathit{r}\mathit{g})}^{\mathrm{\alpha }}}$

In these equations, g describes the replicative age of a cell, S is the number of cells that are alive at g, and S₀ is the initial number of cells to be followed during their aging process (see the Supplementary Materials). Performing a least-squares fit against the experimental survival distribution of the wild-type yeast cells, we saw that the Weibull distribution was superior in its fitting ability compared to the gamma and Gompertz distributions (Fig. 3 and table S3). The robustness of the fits was further confirmed across different initial values of the parameters by systematically sampling them from large ranges (fig. S2). Furthermore, an inspection of the gamma and Gompertz survival functions showed us that they could not be scale-invariant. Finally, the Weibull survival function could be reduced to a one-parameter form without diminishing its fit accuracy (fig. S3 and tables S4 and S5), and it could support scale invariance with respect to changes in its scaling parameter r, lending further support to its selection to represent S(g).

Fig. 3. Performance comparisons among the empirical models.

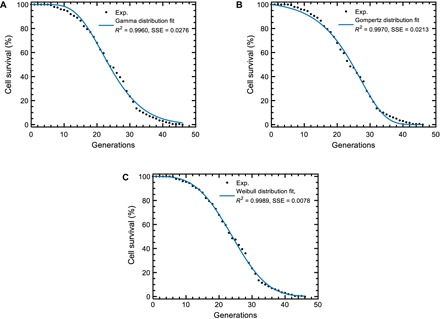
(A to C) Least-squares fit results for the three empirical survival distributions. Experimental wild-type cell survival curve (black dots) was fitted to two-parameter gamma (A), Gompertz (B), or Weibull (C) distributions. The blue line was generated using the best-fitting parameter values extracted from each fit. Higher R² and lower sum of squared errors (SSE) values show the superior performance of the Weibull distribution. n = 200 wild-type cells formed the experimental survival curve.

The observation that the survival probabilities of single yeast cells at specific generation numbers follow the form of the one-parameter Weibull survival function suggests that it may be possible to predict their full survival dynamics by using only a fraction of the data obtained at young ages. To test the predictive power of the Weibull survival function, we performed least-squares fitting procedures by using only a fraction (10 to 90%) of the wild-type cell survival data (table S6). Using the extracted value of the fit parameter (scaling parameter), we then calculated the full survival curve and examined the degree of similarity between each result and the empirical curve (fig. S4). Feeding the initial 30% of the experimental survival data into the fitting process turned out to be sufficient for predicting the full survival curve reasonably well. When we analyzed and included a higher number of cells (1000 cells instead of 200) to compose the survival curve of the wild-type strain (fig. S5 and table S7), the smoothness of the curve slightly improved as expected; however, the fraction of data needed for strong predictions did not change drastically.

We next showed that the predictive capacity of the Weibull survival function was not specific to the survival curve obtained from the wild-type yeast strain, but it could also predict the full survival curves of the strains experiencing different genetic interventions reasonably well (figs. S6 to S12 and table S8). These findings reaffirmed the ability of the Weibull survival function to mathematically represent cell survival as a function of generations. What biological insights into the aging process can be gained from the knowledge that the Weibull survival function with a constant shape parameter α quantitatively describes empirical cell survival dynamics? With the variable g corresponding to “time to failure,” Weibull survival function provides a distribution for which the failure rate is proportional to a power of time (measured in generations), with α > 1 indicating that the failure rate increases over time (as would be expected in an aging process). Therefore, we conclude that the aging process in yeast is accompanied by a specific nonlinear increase in failure rate dictated by the fixed value of α (3.28). Intriguingly, after factoring in the scaling parameter, our data suggest that the nonlinear dynamics of failure rate increase is kept constant across the specific genetic backgrounds we investigated. In this system, the failure represents cell death, that is, when the global state variable X reaches the threshold necessary to trigger the death event. Therefore, the constant nonlinear dynamics of the failure rate indicates that the scaled rate of change of X(g) is invariant across the strains we tested.

Stochastic Strehler-Mildvan model provides mechanistic insights into single-cell aging

To gather mechanistic insights into the dynamics of yeast aging at the microscopic level, we explored how our experimental results related to specific stochastic models that can potentially describe the aging process in single cells and the impact of aging on cell survival. For this, we tested three different microscopic models for their ability to capture the survival dynamics of the wild-type yeast cells (see the Supplementary Materials). Among the stochastic models we tested were semi-infinite random walk, drift-diffusion process with drift heterogeneity, and Strehler-Mildvan model with drift-diffusion-based survival mode. Importantly, the analytical cell survival distributions corresponding to each of these microscopic models satisfy the scalability requirement (3). However, we found that the Strehler-Mildvan model was superior to the other two models in terms of its ability to capture the dynamics of the cell survival distribution using the optimal model parameters (Fig. 4, A to C, figs. S14 to S16, and table S9).

Fig. 4. Performance comparisons among the mechanistic models.

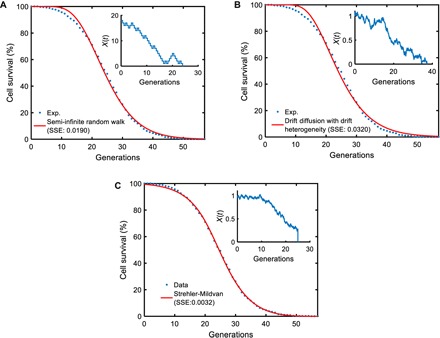
For each microscopic process, n = 200,000 parameter sets were sampled from the parameter ranges (table S9) and fed into the analytical survival functions (see the Supplementary Materials) corresponding to each microscopic model. For each parameter set, the SSE between the simulated survival curve and the experimental survival curve (obtained from the tracking of 1000 wild-type cells) was computed. The parameter sets corresponding to the smallest SSE values for the different models were then used as initial values for the final optimization process using MATLAB’s fminsearch function. The red curve in each panel was generated by using the optimized/fitted parameter values in each analytical survival function. The experimental survival curve is denoted by the blue dots in each panel. The insets show schematic trajectories reflecting the nature of each microscopic process. (A) Semi-infinite random walk (SSE = 0.0190). (B) Drift diffusion with drift heterogeneity (SSE = 0.0320). (C) Strehler-Mildvan model with viability drift diffusion (SSE = 0.0032).

Compared to the other two models we tested, the distinguishing feature of the Strehler-Mildvan model with drift-diffusion-based survival mode is that it splits the age-dependent and age-independent causes of cell death. An age-dependent cause leads to a linear loss in survival governed by the drift-diffusion model, while an age-independent sudden catastrophe leads to cell death if its randomly sampled value is equal to or larger than the survival level at a given time. Therefore, the success of the Strehler-Mildvan model to fit to our cell survival data suggests that the generation-specific probability of death for yeast cells has microscopic contributions from both age-dependent and age-independent random factors. However, further exploration on the relative importance of the parameters describing the Strehler-Mildvan model showed us that the diffusion parameter was not essential for realizing the differential survival distributions observed from the wild-type, short-living (sir2Δ), and long-living (fob1Δ) yeast strains (fig. S17 and table S10), indicating that the drift process is the primary determinant of the aging state in the age-dependent module of the Strehler-Mildvan model (see the Supplementary Materials). To understand the generation-dependent dynamics of the aging state X in these three strains, we ran stochastic simulations of the Strehler-Mildvan model using strain-specific parameter values. We saw that the mean of the aging state X (or vitality) followed nonlinear decrease dynamics toward cell death (fig. S18). The speed of the vitality decrease was the highest for the short-living sir2Δ strain, while it was the lowest for the long-living fob1Δ strain.

The fitting abilities of the empirical Weibull and mechanistic Strehler-Mildvan models together with their generational scaling features suggest the existence of a link between these models. Applying the same strain-specific scaling factor value to the scalable parameters of the Strehler-Mildvan and Weibull survival functions made the two functions’ output overlap (fig. S19). This indicates that the scalable parameters μ,σ²,γ of the mechanistic Strehler-Mildvan survival function collectively play the same role as the scalable parameter r of the empirical Weibull survival function through the scaling parameter λ. Further characterization of the specific analytical connection between the two parameter sets could not be performed because of the complex nature of the survival function associated with the Strehler-Mildvan model (see the Supplementary Materials).

Power law governs the dynamics of mean generation durations during aging

Next, we considered single-cell generation durations as a reporter of death risk that integrates the effects of the age-dependent and age-independent microscopic contributions to the risk of death, and we sought to explore empirical connections between replicative age and generation durations. Results from a previous study (17) showed that old yeast cells contained higher levels of reactive oxygen species (ROS) compared to young cells. Expecting that higher ROS levels lead to more DNA damage and considering the time needed for damage repair, we hypothesized that old cells will have longer cell cycle durations, though we were unable to predict the dynamics of duration increases as a function of generations. Thus, throughout the full lifespan of single cells, we measured generation durations from wild-type, short-living (sir2Δ), and long-living (fob1Δ) yeast strains and quantified mean generation durations at single-generation resolution (Fig. 5).

Fig. 5. Analysis of single-cell generation times during aging.

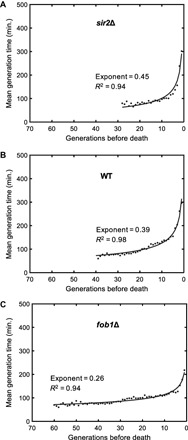
Mean generation times as a function of generations toward the death event for sir2Δ (A), wild-type (WT) (B), and fob1Δ (C) strains. For each generation, single-cell generation durations of all cells experiencing that generation were averaged. The generation times of 121 wild-type, 122 sir2Δ, and 122 fob1Δ cells were analyzed. Solid lines depict the results from fitting the mean generation time data of each strain to a power law function. Fit statistics are provided on the panels.

In all three genetic backgrounds, mean generation durations increased in a nonlinear fashion while cells were approaching their last generation before death (Fig. 5, A to C). The generation-dependent increase in mean generation durations is consistent with a power law f(g) = ag^k. The strain-specific power law exponent k quantifying the speed of increase in generation durations was the highest for the short-living sir2Δ strain, and it was the lowest for the long-living fob1Δ strain. This observation together with the power law being a scale-invariant functional relationship supported the idea of using generation duration as a reporter of death risk.

Although we do not exactly know the specific molecular mechanism that leads to the power law–governed increases in generation durations during aging, one of the plausible mechanisms is that aging-associated accumulation of DNA damage and/or aging-associated deficiency in the fidelity of DNA repair or genome maintenance pathways cause the observed phenotype. In this framework, the deletion of the histone deacetylase SIR2 could be expected to lead to a speedier increase in generation durations compared to the wild type due to reduced levels of genome silencing, making DNA more prone to damage. In addition, the facts that SIR2 and FOB1 deletions compensate the effects of each other on RLS to a large degree (10) and that the fob1Δ genome experiences relatively less DNA replication fork blocking (11) compared to the wild type (therefore, less need for repair and slower increase in generation durations) could be taken as additional support on this plausible mechanism.

DISCUSSION

Here, we show that the RLS distributions measured from single yeast cells are scalable across several different genetic backgrounds tested. On the basis of detailed numerical analyses (2, 3) performed for two phenomenological aging models (competing risks model and dependency network model), the scale-invariant nature of cell survival suggests that replicative aging in yeast can be described in terms of generational changes in a global state variable X(g). This variable determines cell survival by integrating the effects of different risk factors present. This integration can be intuitively understood by considering the effects of each risk factor on X(g) to be simultaneously and equally rescaled throughout lifespan.

Despite the fact that the different genetic interventions we studied here turned out to be part of the same aging network due to the scalability across the genetic backgrounds we tested, we cannot rule out the possible presence of additional, modularly independent, aging networks in the yeast genome. These networks and their components can be identified by performing high-throughput lifespan measurements on gene-deletion libraries followed by the grouping of the scaled survival curves based on pairwise similarities.

Our results also elucidated that the age-dependent dynamics of survival decrease in yeast populations can be mathematically described and predicted by the scale-invariant one-parameter Weibull survival function, meaning that the aging process in yeast is accompanied by a specific nonlinear increase in failure rate. Despite this deterministic description introduced, we note that the stochastic effects experienced by a single cell during its lifespan can still make the cell deviate from the deterministic lifespan trajectory followed by the population. A stochastic model we tested, the Strehler-Mildvan model, shows that the drift-guided diffusion process together with random challenge arrival explains how the measured cell survival dynamics can be realized. Finally, using single-cell generation durations as an integrative probe of cell health and fitness, this study also uncovers an empirical connection between aging and generation durations through a power-law model of decaying cell health during aging.

MATERIALS and METHODS

Yeast strains used in this study

All S. cerevisiae strains (table S8) used in this study have the BY genetic background. The haploid gene-deletion strains fob1Δ, sgf73Δ, tor1Δ, sir2Δ, gpa2Δ, tvp15Δ, and rif1Δ were obtained from Dharmacon Inc. with the following catalog numbers, respectively: YSC6273-201935800, YSC6273-201936107, YSC6273-201937801, YSC6273-201935296, YSC6273-201921174, YSC6273-201935791, and YSC6273-201938023.

Growth medium and experimental protocol followed during the aging experiments

The design and fabrication of the PDMS chip used in this study and the experimental protocols for setting up and running the aging experiments were described in detail in our previous publication (12). In summary, cells were grown in complete synthetic medium (CSM) supplemented with amino acids and 2% glucose as the carbon source. Overnight-grown yeast cells (10 ml of culture volume in a shaker at 30°C) were diluted so that the cell density (optical density at 600 nm) was around 0.1. Diluted cells were loaded into the microfluidic platform using a syringe pump operating at the flow rate of 20 μl/min for a duration between 2 and 3 min. Using Nikon’s Elements software, 200 mother cells were analyzed from each strain (1000 cells were analyzed for the wild-type strain) for their lifespan values by starting from their first generation until the end of their RLS. For tracking the cells, 60× oil and 40× air objectives were used. Bright-field images were acquired with 10-min intervals in the CSM minimal media environment containing 2% glucose, and the single-cell lifespan values were counted and recorded after the completion of the aging experiment. The generation time data plotted in Fig. 5 were collected at the single-cell level by measuring the time each mother cell took between consecutive S phase initiations which were marked by consecutive bud initiations. From each strain, 122 mother cells were analyzed for their generation times across their lifespan. For the wild-type strain, we included 121 cells, because one cell was excluded as an outlier due to its abnormally long generation duration of 2340 min during its fifth generation.

During the aging experiments, the syringe pump was programmed to push fresh minimal medium into the microfluidic chip at two different medium flow rates: the continuous rate at 2 μl/min for 18 min followed by the flushing flow rate of 30 μl/min for 2 min. These flow rates cycled repeatedly until the end of the RLS experiment. The growth temperature during the lifespan experiments was ~30°C.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/1/eaao4666/DC1

fig. S1. Evaluating the Kolmogorov-Smirnov test on differentially scaled survival curves using simulated data.

fig. S2. Parameter sweeps.

fig. S3. Fit performance comparisons between one- and two-parameter Weibull survival functions.

fig. S4. Predictive capacity characterization for the one-parameter Weibull survival function on 200 wild-type cells.

fig. S5. Predictive capacity characterization for the one-parameter Weibull survival function on 1000 wild-type cells.

fig. S6. Predictive capacity characterization for the one-parameter Weibull survival function on sir2Δ.

fig. S7. Predictive capacity characterization for the one-parameter Weibull survival function on rif1Δ.

fig. S8. Predictive capacity characterization for the one-parameter Weibull survival function on tvp15Δ.

fig. S9. Predictive capacity characterization for the one-parameter Weibull survival function on gpa2Δ.

fig. S10. Predictive capacity characterization for the one-parameter Weibull survival function on tor1Δ.

fig. S11. Predictive capacity characterization for the one-parameter Weibull survival function on fob1Δ.

fig. S12. Predictive capacity characterization for the one-parameter Weibull survival function on sgf73Δ.

fig. S13. Quantifying deviations from perfect scaling.

fig. S14. Simulation results for the Strehler-Mildvan model with vitality drift diffusion.

fig. S15. Performance of the exponential challenge arrival process.

fig. S16. Results from the application of AIC and BIC tests on the stochastic models tested.

fig. S17. Sensitivity characterization for the Strehler-Mildvan model parameters.

fig. S18. The generation-dependent dynamics of the aging or viability state X.

fig. S19. Numerical connection between the Strehler-Mildvan and Weibull survival functions.

table S1. Results from the Kolmogorov-Smirnov statistic sup|S_i − S_j|, where sup is the supremum (maximum) function.

table S2. P values computed using ks.test function of R.

table S3. Fit results from the use of the two-parameter Gompertz, gamma, and Weibull survival functions.

table S4. Fit performance of the two-parameter Weibull survival function.

table S5. Fit performance of the one-parameter Weibull survival function (α is fixed at 3.28).

table S6. Fit and prediction results from the use of the one-parameter Weibull survival function.

table S7. Fit and prediction results from the use of the one-parameter Weibull survival function.

table S8. Yeast strains used in this study.

table S9. For each microscopic process, parameter ranges used during the sampling process and the fitted parameter values.

table S10. Predicted parameter values for sir2Δ and fob1Δ strains, obtained after applying scaling.

Materials and Methods

References (18, 19)