SUMMARY
Detecting dependence between two random variables is a fundamental problem. Although the Pearson correlation coefficient is effective for capturing linear dependence, it can be entirely powerless for detecting nonlinear and/or heteroscedastic patterns. We introduce a new measure, G-squared, to test whether two univariate random variables are independent and to measure the strength of their relationship. The G-squared statistic is almost identical to the square of the Pearson correlation coefficient, R-squared, for linear relationships with constant error variance, and has the intuitive meaning of the piecewise R-squared between the variables. It is particularly effective in handling nonlinearity and heteroscedastic errors. We propose two estimators of G-squared and show their consistency. Simulations demonstrate that G-squared estimators are among the most powerful test statistics compared with several state-of-the-art methods.
Keywords: Bayes factor, Coefficient of determination, Hypothesis test, Likelihood ratio
1. INTRODUCTION
The Pearson correlation coefficient is widely used to detect and measure the dependence between two random quantities. The square of its least-squares estimate, popularly known as R-squared, is often used to quantify how linearly related two random variables are. However, the shortcomings of the R-squared statistic as a measure of the strength of dependence are also significant, as discussed recently by Reshef et al. (2011), which has inspired the development of many new methods for detecting dependence.
The Spearman correlation calculates the Pearson correlation coefficient between rank
statistics. Although more robust than the Pearson correlation, this method still cannot
capture nonmonotone relationships. The alternating conditional expectation method was
introduced by Breiman & Friedman (1985) to
approximate the maximal correlation between  and
and
 , i.e., to find optimal transformations of the
data,
, i.e., to find optimal transformations of the
data, 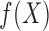 and
and 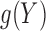 , such
that their correlation is maximized. The implementation of this method has limitations,
because it is infeasible to search through all possible transformations. Estimating mutual
information is another popular approach due to the fact that the mutual information is zero
if and only if
, such
that their correlation is maximized. The implementation of this method has limitations,
because it is infeasible to search through all possible transformations. Estimating mutual
information is another popular approach due to the fact that the mutual information is zero
if and only if  and
and  are
independent. Kraskov et al. (2004) proposed a method
that involves estimating the entropy of
are
independent. Kraskov et al. (2004) proposed a method
that involves estimating the entropy of 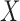 ,
, 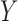 and
and
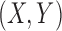 separately. The method was claimed to
be numerically exact for independent cases, and effective for high-dimensional variables. An
energy distance-based method (Szèkely et al., 2007;
Szèkely & Rizzo, 2009) and a kernel-based
method (Gretton et al., 2005, 2012) for solving the two-sample test problem appeared separately in the
statistics and machine learning literatures, and have corresponding usage in independence
tests. The two methods were recently shown to be equivalent (Sejdinovic et al., 2013). Methods based on empirical cumulative distribution
functions (Hoeffding, 1948), empirical copula (Genest & Rémillard, 2004) and empirical characteristic
functions (Kankainen & Ushakov, 1998; Huskova & Meintanis, 2008) have also been proposed for
detecting dependence.
separately. The method was claimed to
be numerically exact for independent cases, and effective for high-dimensional variables. An
energy distance-based method (Szèkely et al., 2007;
Szèkely & Rizzo, 2009) and a kernel-based
method (Gretton et al., 2005, 2012) for solving the two-sample test problem appeared separately in the
statistics and machine learning literatures, and have corresponding usage in independence
tests. The two methods were recently shown to be equivalent (Sejdinovic et al., 2013). Methods based on empirical cumulative distribution
functions (Hoeffding, 1948), empirical copula (Genest & Rémillard, 2004) and empirical characteristic
functions (Kankainen & Ushakov, 1998; Huskova & Meintanis, 2008) have also been proposed for
detecting dependence.
Another set of approaches is based on discretization of the random variables. Known as
grid-based methods, they are primarily designed to test for independence between univariate
random variables. Reshef et al. (2011) introduced the
maximum information coefficient, which focuses on the generality and equitability of a
dependence statistic; two more powerful estimators for this quantity were suggested by
Reshef et al. (arXiv:1505.02213). Equitability requires that the same value of the statistic
imply the same amount of dependence regardless of the type of the underlying relationship,
but it is not a well-defined mathematical concept. We show in the Supplementary Material that the
equitability of G-squared is superior to all other independence testing statistics for a
wide range of functional relationships. Heller et al.
(2016) proposed a grid-based method which utilizes the 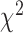 statistic to test independence and is a distribution-free test. Blyth (1994) and Doksum et al.
(1994) discussed using the correlation curve to measure the strength of the
relationship. However, a direct use of nonparametric curve estimation may rely too heavily
on the smoothness of the relationship; furthermore, it cannot deal with heteroscedastic
noise.
statistic to test independence and is a distribution-free test. Blyth (1994) and Doksum et al.
(1994) discussed using the correlation curve to measure the strength of the
relationship. However, a direct use of nonparametric curve estimation may rely too heavily
on the smoothness of the relationship; furthermore, it cannot deal with heteroscedastic
noise.
The 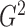 statistic proposed in this paper is
derived from a regularized likelihood ratio test for piecewise-linear relationships and can
be viewed as an integration of continuous and discrete methods. It is a function of both the
conditional mean and the conditional variance of one variable given the other, so it is
capable of detecting general functional relationships with heteroscedastic error variances.
An estimate of
statistic proposed in this paper is
derived from a regularized likelihood ratio test for piecewise-linear relationships and can
be viewed as an integration of continuous and discrete methods. It is a function of both the
conditional mean and the conditional variance of one variable given the other, so it is
capable of detecting general functional relationships with heteroscedastic error variances.
An estimate of 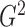 can be derived via the same likelihood
ratio approach as
can be derived via the same likelihood
ratio approach as 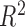 when the true underlying relationship
is linear. Thus, it is reasonable that
when the true underlying relationship
is linear. Thus, it is reasonable that 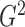 is almost identical to
is almost identical to
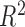 for linear relationships. Efficient
estimates of
for linear relationships. Efficient
estimates of 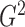 can be computed quickly using a dynamic
programming method, whereas the methods of Reshef et al.
(2011) and Heller et al. (2016) consider
grids on two variables simultaneously and hence require longer computational times. We will
also show that, in terms of power,
can be computed quickly using a dynamic
programming method, whereas the methods of Reshef et al.
(2011) and Heller et al. (2016) consider
grids on two variables simultaneously and hence require longer computational times. We will
also show that, in terms of power, 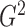 is one of the best
statistics for independence testing when considering a wide range of functional
relationships.
is one of the best
statistics for independence testing when considering a wide range of functional
relationships.
2. MEASURING DEPENDENCE WITH G-SQUARED
2.1. Defining 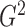 as a generalization of
as a generalization of
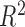
The R-squared statistic measures how well the data fit a linear regression model. Given
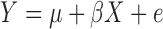 with
with
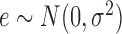 , the standard estimate
of R-squared can be derived from a likelihood ratio test statistic for testing
, the standard estimate
of R-squared can be derived from a likelihood ratio test statistic for testing
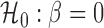 against
against
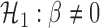 , i.e.,
, i.e.,
where 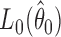 and
and
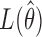 are the maximized
likelihoods under
are the maximized
likelihoods under 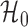 and
and 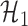 .
.
Throughout the paper, we let 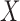 and
and 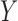 be
univariate continuous random variables. As a working model, we assume that the
relationship between
be
univariate continuous random variables. As a working model, we assume that the
relationship between 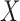 and
and 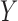 can be
characterized as
can be
characterized as 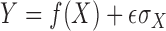 , with
, with
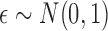 and
and
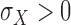 . If
. If 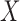 and
and
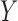 are independent, then
are independent, then
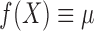 and
and 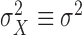 . Now let us look at
the piecewise-linear relationship
. Now let us look at
the piecewise-linear relationship
where 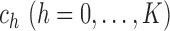 are called the
breakpoints. While this working model allows for heteroscedasticity, it requires constant
variance within each segment between two consecutive breakpoints. Testing whether
are called the
breakpoints. While this working model allows for heteroscedasticity, it requires constant
variance within each segment between two consecutive breakpoints. Testing whether
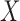 and
and 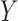 are
independent is equivalent to testing whether
are
independent is equivalent to testing whether 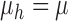 and
and
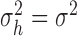 . Given
. Given
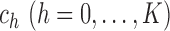 , the likelihood ratio
test statistic can be written as
, the likelihood ratio
test statistic can be written as
where
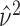 is the overall sample variance
of
is the overall sample variance
of 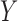 and
and 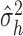 is the residual variance
after regressing
is the residual variance
after regressing 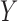 on
on 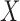 for
for
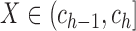 . Because
. Because
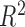 is a transformation of the likelihood
ratio and converges to the square of the Pearson correlation coefficient, we perform the
same transformation on
is a transformation of the likelihood
ratio and converges to the square of the Pearson correlation coefficient, we perform the
same transformation on 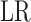 . The resulting test statistic
converges to a quantity related to the conditional mean and the conditional variance of
. The resulting test statistic
converges to a quantity related to the conditional mean and the conditional variance of
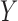 on
on 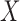 . It is
easy to show that as
. It is
easy to show that as 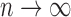 ,
,
| (1) |
When 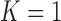 , the relationship degenerates to a
simple linear relation and
, the relationship degenerates to a
simple linear relation and 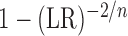 is exactly
is exactly
 .
.
More generally, because a piecewise-linear function can approximate any almost everywhere
continuous function, we can employ the same hypothesis testing framework as above to
derive (1) for any such approximation.
Thus, for any pair of random variables  , the following
concept is a natural generalization of R-squared:
, the following
concept is a natural generalization of R-squared:
in which we require that 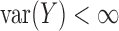 . Evidently,
. Evidently,
 lies between 0 and 1, and
is equal to zero if and only if both
lies between 0 and 1, and
is equal to zero if and only if both 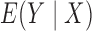 and
and
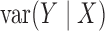 are constant. The
definition of
are constant. The
definition of 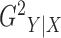 is closely related to the
R-squared defined by segmented regression (Oosterbaan
& Ritzema, 2006), discussed in the Supplementary Material. We symmetrize
is closely related to the
R-squared defined by segmented regression (Oosterbaan
& Ritzema, 2006), discussed in the Supplementary Material. We symmetrize 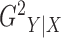 to arrive at the following
quantity as the definition of the G-squared statistic:
to arrive at the following
quantity as the definition of the G-squared statistic:
provided 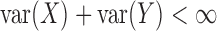 .
Thus,
.
Thus, 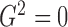 if and only if
if and only if
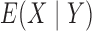 ,
, 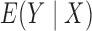 ,
, 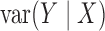 and
and
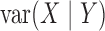 are all constant,
which is not equivalent to independence of
are all constant,
which is not equivalent to independence of 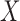 and
and
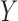 . In practice, however, dependent cases
with
. In practice, however, dependent cases
with 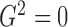 are rare.
are rare.
2.2. Estimation of 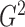
Without loss of generality, we focus on the estimation of 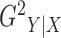 ;
; 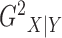 can be estimated in the same
way by interchanging
can be estimated in the same
way by interchanging 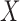 and
and 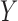 . When
. When
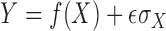 with
with
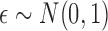 for an almost
everywhere continuous function
for an almost
everywhere continuous function 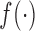 , we can use a
piecewise-linear function to approximate
, we can use a
piecewise-linear function to approximate 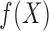 and estimate
and estimate
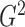 . However, in practice the number and
locations of the breakpoints are unknown. We propose two estimators of
. However, in practice the number and
locations of the breakpoints are unknown. We propose two estimators of
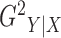 , the first aiming to find
the maximum penalized likelihood ratio among all possible piecewise-linear approximations,
and the second focusing on a Bayesian average of all approximations.
, the first aiming to find
the maximum penalized likelihood ratio among all possible piecewise-linear approximations,
and the second focusing on a Bayesian average of all approximations.
Suppose that we have 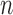 sorted independent observations,
sorted independent observations,
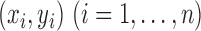 , such that
, such that
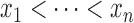 . For the set of
breakpoints, we only need to consider
. For the set of
breakpoints, we only need to consider 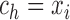 . Each interval
. Each interval
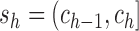 is called a slice of the
observations, so that
is called a slice of the
observations, so that 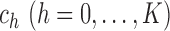 divide the range of
divide the range of
 into
into  non-overlapping slices. Let
non-overlapping slices. Let 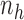 denote the number of observations in
slice
denote the number of observations in
slice 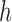 , and let
, and let 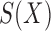 denote a slicing scheme of
denote a slicing scheme of 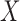 , i.e.,
, i.e., 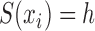 if
if 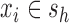 , which is abbreviated as
, which is abbreviated as
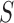 whenever the meaning is clear. Let
whenever the meaning is clear. Let
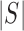 be the number of slices in
be the number of slices in
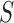 and let
and let 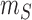 denote the minimum size of all the slices.
denote the minimum size of all the slices.
To avoid overfitting when maximizing loglikelihood ratios both over unknown parameters
and over all possible slicing schemes, we restrict the minimum size of each slice to
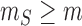 and maximize the loglikelihood
ratio with a penalty on the number of slices. For simplicity, let
and maximize the loglikelihood
ratio with a penalty on the number of slices. For simplicity, let
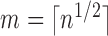 . Thus, we focus on
the penalized loglikelihood ratio
. Thus, we focus on
the penalized loglikelihood ratio
| (2) |
where 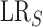 is the likelihood ratio for
is the likelihood ratio for
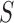 and
and 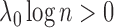 is the penalty incurred
for one additional slice. From a Bayesian perspective, this is equivalent to assigning the
prior distribution for the number of slices to be proportional to
is the penalty incurred
for one additional slice. From a Bayesian perspective, this is equivalent to assigning the
prior distribution for the number of slices to be proportional to
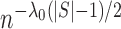 . Suppose that each
observation
. Suppose that each
observation 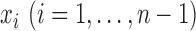 has probability
has probability
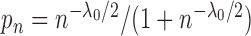 of being the breakpoint independently. Then the probability of a slicing scheme
of being the breakpoint independently. Then the probability of a slicing scheme
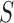 is
is
When 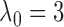 , the statistic
, the statistic
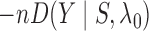 is equivalent to
the Bayesian information criterion (Schwarz, 1978)
up to a constant.
is equivalent to
the Bayesian information criterion (Schwarz, 1978)
up to a constant.
Treating the slicing scheme as a nuisance parameter, we can maximize over all allowable slicing schemes to obtain that
Our first estimator of 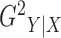 , which we call
, which we call
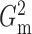 with m standing for the
maximum likelihood ratio, can be defined as
with m standing for the
maximum likelihood ratio, can be defined as
Hence, the overall G-squared can be estimated as
By definition, 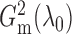 lies between 0
and 1, and
lies between 0
and 1, and 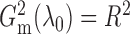 when the
optimal slicing schemes for both directions have only one slice. Later, we will show that
when
when the
optimal slicing schemes for both directions have only one slice. Later, we will show that
when  and
and  follow
a bivariate normal distribution,
follow
a bivariate normal distribution, 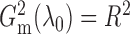 almost surely
for large
almost surely
for large 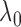 .
.
Another attractive way to estimate 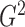 is to integrate out
the nuisance slicing scheme parameter. A full Bayesian approach would require us to
compute the Bayes factor (Kass & Raftery,
1995), which may be undesirable since we do not wish to impose too strong a
modelling assumption. On the other hand, however, the Bayesian formalism may guide us to a
desirable integration strategy for the slicing scheme. We therefore put the problem into a
Bayes framework and compute the Bayes factor for comparing the null and alternative
models. The null model is only one model while the alternative is any piecewise-linear
model, possibly with countably infinite pieces. Let
is to integrate out
the nuisance slicing scheme parameter. A full Bayesian approach would require us to
compute the Bayes factor (Kass & Raftery,
1995), which may be undesirable since we do not wish to impose too strong a
modelling assumption. On the other hand, however, the Bayesian formalism may guide us to a
desirable integration strategy for the slicing scheme. We therefore put the problem into a
Bayes framework and compute the Bayes factor for comparing the null and alternative
models. The null model is only one model while the alternative is any piecewise-linear
model, possibly with countably infinite pieces. Let 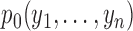 be the marginal
probability of the data under the null. Let
be the marginal
probability of the data under the null. Let 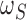 be the prior
probability for slicing scheme
be the prior
probability for slicing scheme 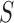 and let
and let
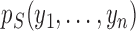 denote the marginal
probability of the data under
denote the marginal
probability of the data under 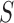 . The Bayes factor can
be written as
. The Bayes factor can
be written as
| (3) |
where
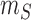 is the minimum size of all the slices
of
is the minimum size of all the slices
of 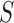 . The marginal probabilities are not easy
to compute even with proper priors. Schwarz (1978)
states that if the data distribution is in the exponential family and the parameter is of
dimension
. The marginal probabilities are not easy
to compute even with proper priors. Schwarz (1978)
states that if the data distribution is in the exponential family and the parameter is of
dimension 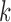 , the marginal probability of the data can
be approximated as
, the marginal probability of the data can
be approximated as
| (4) |
where
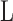 is the maximized likelihood. In
our set-up, the number of parameters
is the maximized likelihood. In
our set-up, the number of parameters 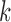 for the null model is
2, and for an alternative model with a slicing scheme
for the null model is
2, and for an alternative model with a slicing scheme 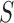 it is
it is
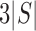 . Inserting expression (4) into both the numerator and the
denominator of (3), we obtain
. Inserting expression (4) into both the numerator and the
denominator of (3), we obtain
| (5) |
If we take 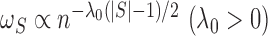 ,
which corresponds to the penalty term in (2) and is involved in defining
,
which corresponds to the penalty term in (2) and is involved in defining 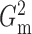 , the
approximated Bayes factor can be restated as
, the
approximated Bayes factor can be restated as
| (6) |
As we will discuss in § 2.5,
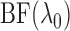 can serve as a
marginal likelihood function for
can serve as a
marginal likelihood function for 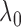 and be used to
find an optimal
and be used to
find an optimal 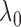 suitable for a particular
dataset. This quantity also looks like an average version of
suitable for a particular
dataset. This quantity also looks like an average version of 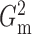 , but with an additional
penalty. Since
, but with an additional
penalty. Since 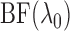 can take values below
1, its transformation
can take values below
1, its transformation 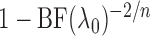 , as in the
case where we derived
, as in the
case where we derived 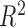 via the likelihood ratio test, can
take negative values, especially when
via the likelihood ratio test, can
take negative values, especially when 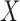 and
and
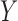 are independent. It is therefore not an
ideal estimator of
are independent. It is therefore not an
ideal estimator of 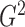 .
.
By removing the model size penalty term in (5), we obtain a modified version, which is simply a weighted average of the likelihood ratios and is guaranteed to be greater than or equal to 1:
We can thus define a quantity similar to our likelihood formulation of R-squared,
which we call the total G-squared, and define
We show later that 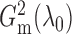 and
and
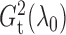 are both
consistent estimators of
are both
consistent estimators of 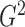 .
.
2.3. Theoretical properties of the 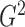 estimators
estimators
In order to show that 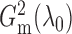 and
and
 converge to
converge to
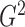 as the sample size goes to infinity,
we introduce the notation
as the sample size goes to infinity,
we introduce the notation 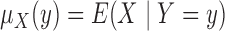 ,
,
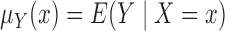 ,
,
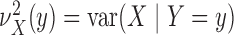 and
and
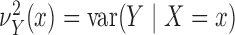 , and
assume the following regularity conditions.
, and
assume the following regularity conditions.
condition 1.
The random variables
and
are bounded continuously with finite variances such that
almost everywhere for some constant
.
condition 2.
The functions
,
,
and
have continuous derivatives almost everywhere.
condition 3.
There exists a constant
such that
almost surely.
With these preparations, we can state our main results.
Theorem 1.
Under Conditions 1–3, for all
,
almost surely as
. Thus,
and
are consistent estimators of
.
A proof of the theorem and numerical studies of the estimators’ consistency are provided
in the Supplementary Material.
It is expected that 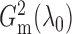 should converge
to
should converge
to 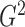 because of the way it is constructed.
It is surprising that
because of the way it is constructed.
It is surprising that 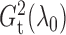 also converges to
also converges to
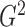 . The result, which links
. The result, which links
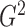 estimation with the likelihood ratio
and Bayesian formalism, suggests that most of the information up to the second moment has
been fully utilized in the two test statistics. The theorem thus supports the use of
estimation with the likelihood ratio
and Bayesian formalism, suggests that most of the information up to the second moment has
been fully utilized in the two test statistics. The theorem thus supports the use of
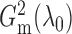 and
and
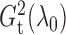 for testing
whether
for testing
whether 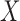 and
and 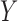 are
independent. The null distributions of the two statistics depend on the marginal
distributions of
are
independent. The null distributions of the two statistics depend on the marginal
distributions of 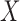 and
and 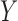 , and
can be generated empirically using permutation. One can also perform a quantile-based
transformation on
, and
can be generated empirically using permutation. One can also perform a quantile-based
transformation on 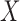 and
and 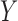 so
that their marginal distributions become standard normal; however, the
so
that their marginal distributions become standard normal; however, the
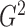 based on the transformed data tends
to lose some power.
based on the transformed data tends
to lose some power.
When 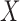 and
and 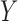 are
bivariate normal, the G-squared statistic is almost the same as the R-squared statistic
when
are
bivariate normal, the G-squared statistic is almost the same as the R-squared statistic
when 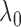 is large enough.
is large enough.
Theorem 2.
If
and
follow a bivariate normal distribution, then for
large enough,
So, for
and
, we have
almost surely.
The lower bound on 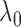 is not tight and can be relaxed
in practice. Empirically, we have observed that
is not tight and can be relaxed
in practice. Empirically, we have observed that 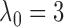 is large
enough for
is large
enough for 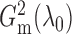 to be very close
to
to be very close
to 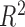 in the bivariate normal setting.
in the bivariate normal setting.
2.4. Dynamic programming algorithm for computing 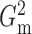 and
and 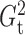
The brute force calculation of either 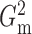 or
or
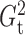 has a computational
complexity of
has a computational
complexity of 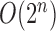 and is prohibitive in practice.
Fortunately, we have found a dynamic programming scheme for computing both quantities with
a time complexity of only
and is prohibitive in practice.
Fortunately, we have found a dynamic programming scheme for computing both quantities with
a time complexity of only 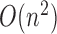 . The algorithms for computing
. The algorithms for computing
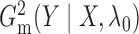 and
and
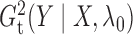 are
roughly the same except for one operation, namely maximization versus summation, and can
be summarized by the following steps.
are
roughly the same except for one operation, namely maximization versus summation, and can
be summarized by the following steps.
Step 1.
(Data preparation). Arrange the observed pairs
according to the
values sorted from low to high. Then normalize
such that
and
.
Step 2.
(Main algorithm). Define
as the smallest slice size,
and
. Initialize three sequences,
with
and
. For
, recursively fill in entries of the tables with
where
,
and
, with
being the residual variance of regressing
on
for observations
.
Step 3.
The final result is
Here, 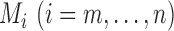 stores the partial
maximized likelihood ratio up to the ordered observation
stores the partial
maximized likelihood ratio up to the ordered observation 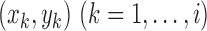 ;
;
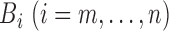 stores the partial
normalizing constant; and
stores the partial
normalizing constant; and 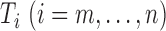 stores the partial
sum of the likelihood ratios. When
stores the partial
sum of the likelihood ratios. When 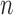 is extremely large, we
can speed up the algorithm by considering fewer slice schemes. For example, we can divide
is extremely large, we
can speed up the algorithm by considering fewer slice schemes. For example, we can divide
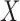 into chunks of size
into chunks of size
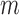 by rank and consider only slicing schemes
between the chunks. For this method, the computational complexity is
by rank and consider only slicing schemes
between the chunks. For this method, the computational complexity is
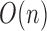 . We can compute
. We can compute
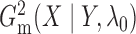 and
and
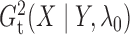 similarly
to get
similarly
to get 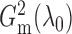 and
and
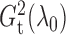 . Empirically, the
algorithm is faster than many other powerful methods, as shown in the Supplementary Material.
. Empirically, the
algorithm is faster than many other powerful methods, as shown in the Supplementary Material.
2.5. An empirical Bayes strategy for selecting 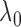
Although the choice of the penalty parameter 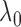 is not critical
for the general use of
is not critical
for the general use of 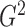 , we typically take
, we typically take
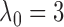 for
for 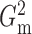 and
and 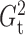 because
because
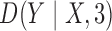 is equivalent to the
Bayesian information criterion. Fine-tuning
is equivalent to the
Bayesian information criterion. Fine-tuning 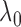 can improve the
estimation of
can improve the
estimation of 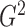 ; we therefore propose a data-driven
strategy for choosing
; we therefore propose a data-driven
strategy for choosing 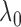 adaptively. The quantity
adaptively. The quantity
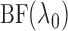 in (6) can be viewed as an approximation to
in (6) can be viewed as an approximation to
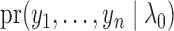 up to a normalizing constant. Hence we can use the maximum likelihood principle to choose
the
up to a normalizing constant. Hence we can use the maximum likelihood principle to choose
the 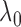 that maximizes
that maximizes
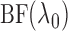 . We then use
the chosen
. We then use
the chosen 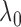 to compute
to compute
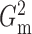 and
and
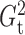 as estimators of
as estimators of
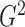 . In practice, we evaluate
. In practice, we evaluate
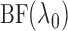 for a finite
set of
for a finite
set of 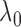 values, such as
values, such as
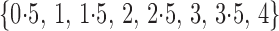 ,
and pick the
,
and pick the 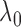 value that maximizes
value that maximizes
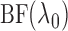 ;
;
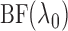 can be
computed efficiently via a dynamic programming algorithm similar to that described in
§2.4. As an illustration, we consider the sampling distributions of
can be
computed efficiently via a dynamic programming algorithm similar to that described in
§2.4. As an illustration, we consider the sampling distributions of
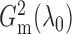 and
and
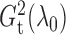 with
with
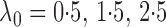 and
and 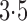 for the following two
scenarios:
for the following two
scenarios:
Example 1.
and
with
.
Example 2.
and
with
.
We simulated 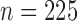 data points. For each model, we set
data points. For each model, we set
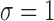 so that
so that 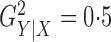 and performed 1000
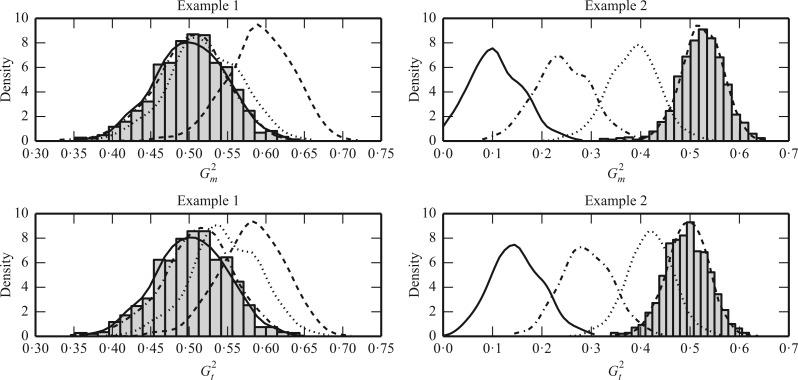
replications. Figure 1 shows histograms of
and performed 1000
replications. Figure 1 shows histograms of
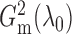 and
and
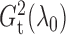 with different
with different
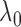 values. The results demonstrate
that for relationships which can be approximated well by a linear function, a larger
values. The results demonstrate
that for relationships which can be approximated well by a linear function, a larger
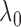 is preferred because it penalizes
the number of slices more heavily, so that the resulting sampling distributions are less
biased. On the other hand, for complicated relationships such as trigonometric functions,
a smaller
is preferred because it penalizes
the number of slices more heavily, so that the resulting sampling distributions are less
biased. On the other hand, for complicated relationships such as trigonometric functions,
a smaller 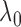 is preferable because it allows
more slices, which can help to capture fluctuations in the functional relationship. The
figure also shows that the empirical Bayes selection of
is preferable because it allows
more slices, which can help to capture fluctuations in the functional relationship. The
figure also shows that the empirical Bayes selection of 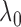 worked very well, leading to a
proper choice of
worked very well, leading to a
proper choice of 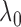 for each simulated dataset from
both examples and resulting in the most accurate estimates of
for each simulated dataset from
both examples and resulting in the most accurate estimates of 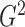 .
Additional simulation studies and discussion of the consistency of the data-driven
strategy can be found in the Supplementary Material.
.
Additional simulation studies and discussion of the consistency of the data-driven
strategy can be found in the Supplementary Material.
Fig. 1.
Sampling distributions of 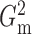 and
and
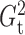 under the two models
described in §2.5 with
under the two models
described in §2.5 with 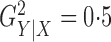 for
for
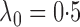 (dashed),
1
(dashed),
1 5 (dotted),
2
5 (dotted),
2 5 (dot-dash) and
3
5 (dot-dash) and
3 5 (solid). The density function
in each case is estimated by the histogram. The sampling distributions of
5 (solid). The density function
in each case is estimated by the histogram. The sampling distributions of
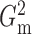 and
and
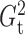 with the empirical
Bayes selection of
with the empirical
Bayes selection of 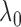 are shaded grey and
overlaid on top of the other density functions.
are shaded grey and
overlaid on top of the other density functions.
3. POWER ANALYSIS
Next, we compare the power of different independence testing methods for various
relationships. Here we again fixed 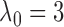 for both
for both
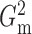 and
and 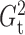 . Other methods we tested include
the alternating conditional expectation (Breiman & Friedman, 1985), Genest’s test (Genest & Rémillard, 2004), Pearson correlation,
distance correlation (Szèkely et al., 2007), the
method of Heller et al. (2016), the characteristic
function method (Kankainen & Ushakov, 1998),
Hoeffding’s test (Hoeffding, 1948), the mutual
information method (Kraskov et al., 2004), and two
methods,
. Other methods we tested include
the alternating conditional expectation (Breiman & Friedman, 1985), Genest’s test (Genest & Rémillard, 2004), Pearson correlation,
distance correlation (Szèkely et al., 2007), the
method of Heller et al. (2016), the characteristic
function method (Kankainen & Ushakov, 1998),
Hoeffding’s test (Hoeffding, 1948), the mutual
information method (Kraskov et al., 2004), and two
methods, 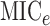 and
and
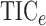 , based on the maximum
information criterion (Reshef et al., 2011). We
follow the procedure for computing the powers of different methods as described in Reshef et
al. (arXiv:1505.02214) and a 2012 online note by N. Simon and R. J. Tibshirani.
, based on the maximum
information criterion (Reshef et al., 2011). We
follow the procedure for computing the powers of different methods as described in Reshef et
al. (arXiv:1505.02214) and a 2012 online note by N. Simon and R. J. Tibshirani.
For different functional relationships 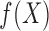 and different noise
levels
and different noise
levels 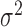 , we let
, we let
where 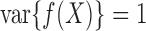 . Thus
. Thus
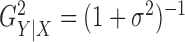 is a monotone
function of the signal-to-noise ratio, and it is of interest to observe how the performances
of different methods deteriorate as the signal strength weakens for various functional
relationships. We used permutation to generate the null distribution and to set the
rejection region in all cases.
is a monotone
function of the signal-to-noise ratio, and it is of interest to observe how the performances
of different methods deteriorate as the signal strength weakens for various functional
relationships. We used permutation to generate the null distribution and to set the
rejection region in all cases.
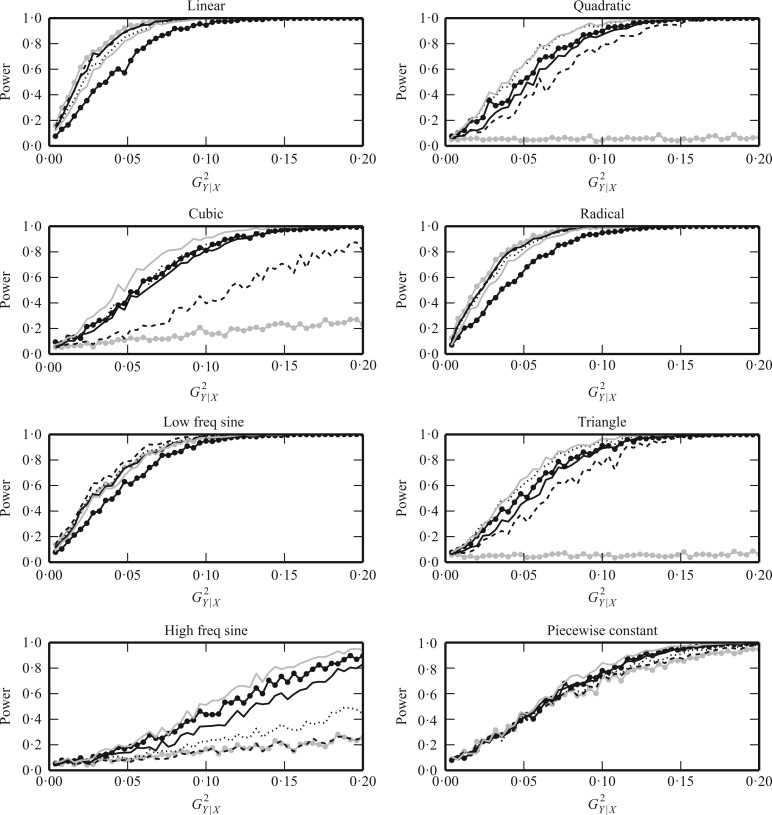
Figure 2 shows power comparisons for eight functional
relationships. We set the sample size to 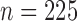 and performed 1000
replications for each relationship and each
and performed 1000
replications for each relationship and each 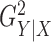 value. For
the sake of clarity, here we plot only Pearson correlation, distance correlation, the method
of Heller et al. (2016),
value. For
the sake of clarity, here we plot only Pearson correlation, distance correlation, the method
of Heller et al. (2016), 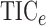 ,
, 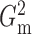 and
and 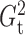 . For any method with tuning
parameters, we chose the parameter values that resulted in the highest average power over
all the examples. Due to computational concerns, we chose
. For any method with tuning
parameters, we chose the parameter values that resulted in the highest average power over
all the examples. Due to computational concerns, we chose 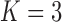 for
the method of Heller et al. (2016). It can be seen
that
for
the method of Heller et al. (2016). It can be seen
that 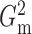 and
and 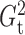 performed robustly, and were
always among the most powerful methods, with
performed robustly, and were
always among the most powerful methods, with 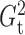 being
slightly more powerful than
being
slightly more powerful than 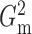 in nearly all the examples.
They outperformed the other methods in cases such as the high-frequency sine, triangle and
piecewise-constant functions, where piecewise-linear approximation is more appropriate than
other approaches. For monotonic examples such as linear and radical relationships,
in nearly all the examples.
They outperformed the other methods in cases such as the high-frequency sine, triangle and
piecewise-constant functions, where piecewise-linear approximation is more appropriate than
other approaches. For monotonic examples such as linear and radical relationships,
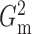 and
and 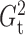 had slightly lower power than
Pearson correlation, distance correlation and the method of Heller et al. (2016), but were still highly competitive.
had slightly lower power than
Pearson correlation, distance correlation and the method of Heller et al. (2016), but were still highly competitive.
Fig. 2.
The powers of 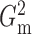 (black solid),
(black solid),
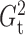 (grey solid), Pearson
correlation (grey circles), distance correlation (black dashed), the method of Heller et al. (2016) (black dotted) and
(grey solid), Pearson
correlation (grey circles), distance correlation (black dashed), the method of Heller et al. (2016) (black dotted) and
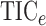 (black circles)
for testing independence between
(black circles)
for testing independence between 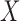 and
and
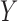 when the underlying true functional
relationships are linear, quadratic, cubic, radical, low-frequency sine, triangle,
high-frequency sine, and piecewise constant. The horizontal axis represents
when the underlying true functional
relationships are linear, quadratic, cubic, radical, low-frequency sine, triangle,
high-frequency sine, and piecewise constant. The horizontal axis represents
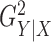 , a monotone function of
the signal-to-noise ratio, and the vertical axis is the power. We chose
, a monotone function of
the signal-to-noise ratio, and the vertical axis is the power. We chose
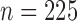 and performed 1000 replications
for each relationship and each
and performed 1000 replications
for each relationship and each 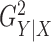 value.
value.
We also studied the performances of these methods for 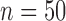 , 100
and 400, and found that
, 100
and 400, and found that  and
and 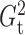 still had high power regardless
of
still had high power regardless
of 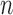 , although their advantages were much less
obvious when
, although their advantages were much less
obvious when 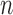 was small. More details can be found in the
Supplementary Material.
was small. More details can be found in the
Supplementary Material.
4. DISCUSSION
The proposed G-squared statistic can be viewed as a direct generalization of the R-squared statistic. While maintaining the same interpretability as the R-squared statistic, the G-squared statistic is also a powerful measure of dependence for general relationships. Instead of resorting to curve-fitting methods to estimate the underlying relationship and the G-squared statistic, we employed piecewise-linear approximations with penalties and dynamic programming algorithms. Although we have considered only piecewise-linear functions, one could potentially approximate a relationship between two variables using piecewise polynomials or other flexible basis functions, with perhaps additional penalty terms to control the complexity. Furthermore, it would be worthwhile to generalize the slicing idea to testing dependence between two multivariate random variables.
Supplementary Material
ACKNOWLEDGEMENT
We are grateful to the two referees for helpful comments and suggestions. This research was supported in part by the U.S. National Science Foundation and National Institutes of Health. We thank Ashley Wang for her proofreading of the paper. The views expressed herein are the authors’ alone and are not necessarily the views of Two Sigma Investments, Limited Partnership, or any of its affiliates.
SUPPLEMENTARY MATERIAL
Supplementary material available at Biometrika online includes proofs of the theorems, software implementation details, discussions on segmented regression, a study of equitability, and more simulation results.
References
- Blyth S. (1994). Local divergence and association. Biometrika 91579–84. [Google Scholar]
- Breiman L. & Friedman J. H. (1985). Estimating optimal transformations for multiple regression and correlation. J. Am. Statist. Assoc. 80580–98. [Google Scholar]
- Doksum K. Blyth S. Bradlow E. Meng X. & Zhao H. (1994). Correlation curves as local measures of variance explained by regression. J. Am. Statist. Assoc. 89571–82. [Google Scholar]
- Genest C. & Rémillard B. (2004). Test of independence and randomness based on the empirical copula process. Test 13335–69. [Google Scholar]
- Gretton A. Gousquet O. Smola A. & Schlkopf B. (2005). Measuring statistical dependence with Hilbert–Schmidt norms. Algor. Learn. Theory 373463–77. [Google Scholar]
- Gretton A. Borgwardt K. M. Rasch M. J. Schlkopf B. & Smola A. (2012). A kernel two-sample test. J. Mach. Learn. Res. 13723–73. [Google Scholar]
- Heller R. Heller Y. Kaufman S. Brill B. & Gorfine M. (2016). Consistent distribution-free $K$-sample and independence tests for univariate random variables. J. Mach. Learn. Res. 171–54. [Google Scholar]
- Hoeffding W. (1948). A non-parametric test of independence. Ann. Statist. 19546–57. [Google Scholar]
- Huškovà M. & Meintanis S. (2008). Testing procedures based on the empirical characteristic functions I: Goodness-of-fit, testing for symmetry and independence. Tatra Mt. Math. Publ. 39225–33. [Google Scholar]
- Kankainen A. & Ushakov N. G. (1998). A consistent modification of a test for independence based on the empirical characteristic function. J. Math. Sci. 891486–94. [Google Scholar]
- Kass R. E. & Raftery A. E. (1995). Bayes factors. J. Am. Statist. Assoc. 90773–95. [Google Scholar]
- Kraskov A. Stogbauer H. & Grassberger P. (2004). Estimating mutual information. Phys. Rev. E 69.6066138. [DOI] [PubMed] [Google Scholar]
- Oosterbaan R. J. & Ritzema H. P. (2006). Drainage Principles and Applications. Wageningen, Netherlands: International Institute for Land Reclamation and Improvement, pp. 217–20. [Google Scholar]
- Reshef D. N. Reshef Y. A. Finucane H. K. Grossman S. R. McVean G. Turnbaugh P. J. Lander E. S. Mitzenmacher M. & Sabeti P. S. (2011). Detecting novel associations in large data sets. Science 3341518–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwarz G. (1978). Estimating the dimension of a model. Ann. Statist. 6461–4. [Google Scholar]
- Sejdinovic D. Sriperumbudur B. Gretton A. & Fukumizu K. (2013). Equivalence of distance-based and RKHS-based statistics in hypothesis testing. Ann. Statist. 412263–91. [Google Scholar]
- Szèekely G. J. & Rizzo M. L. (2009). Brownian distance correlation. Ann. Appl. Statist. 121236–65. [Google Scholar]
- Székely G. J. Rizzo M. L. & Bakirov N. K. (2007). Measuring and testing dependence by correlation of distances. Ann. Statist. 122769–94. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.