Rogue waves and large deviations in deep sea

Significance

Quantifying the departure from Gaussianity of the wave-height distribution in the seas and thereby estimating the likelihood of appearance of rogue waves is a long-standing problem with important practical implications for boats and naval structures. Here, a procedure is introduced to identify ocean states that are precursors to rogue waves, which could permit their early detection. Our findings indicate that rogue waves obey a large deviation principle—i.e., they are dominated by single realizations—which our method calculates by solving an optimization problem. The method generalizes to estimate the probability of extreme events in other deterministic dynamical systems with random initial data and/or parameters, by using prior information about the nature of their statistics.

Abstract

The appearance of rogue waves in deep sea is investigated by using the modified nonlinear Schrödinger (MNLS) equation in one spatial dimension with random initial conditions that are assumed to be normally distributed, with a spectrum approximating realistic conditions of a unidirectional sea state. It is shown that one can use the incomplete information contained in this spectrum as prior and supplement this information with the MNLS dynamics to reliably estimate the probability distribution of the sea surface elevation far in the tail at later times. Our results indicate that rogue waves occur when the system hits unlikely pockets of wave configurations that trigger large disturbances of the surface height. The rogue wave precursors in these pockets are wave patterns of regular height, but with a very specific shape that is identified explicitly, thereby allowing for early detection. The method proposed here combines Monte Carlo sampling with tools from large deviations theory that reduce the calculation of the most likely rogue wave precursors to an optimization problem that can be solved efficiently. This approach is transferable to other problems in which the system’s governing equations contain random initial conditions and/or parameters.

Rogue waves, long considered a figment of sailors’ imaginations, are now recognized to be a real, and serious, threat for boats and naval structures (1, 2). Oceanographers define them as deep-water waves whose crest-to-trough height $H$ exceeds twice the significant wave height $H_s$, which itself is four times the SD of the ocean surface elevation. Rogue waves appear suddenly and unpredictably and can lead to water walls with vertical size on the order of $20$–$30$ m (3, 4), with enormous destructive power. Although rare, they tend to occur more frequently than predicted by linear Gaussian theory (5, 6). While the mechanisms underlying their appearance remain under debate (7–9), one plausible scenario has emerged over the years: It involves the phenomenon of modulational instability (10, 11), a nonlinear amplification mechanism by which many weakly interacting waves of regular size can create a much larger one. Such an instability arises in the context of the focusing nonlinear Schrödinger (NLS) equation (11–17) or its higher-order variants (18–22), which are known to be good models for the evolution of a unidirectional, narrow-banded surface wave field in a deep sea. Support for the description of rogue waves through such envelope equations recently came from experiments in water tanks (23–26), where Dysthe’s modified NLS (MNLS) equation in one spatial dimension (18, 19) was shown to accurately describe the mechanism creating coherent structures which soak up energy from its surroundings. While these experiments and other theoretical works (27, 28) give grounds for the use of MNLS to describe rogue waves, they have not addressed the question of their likelihood of appearance. Some progress in this direction has been recently made in ref. 29, where a reduced model based on MNLS was used to estimate the probability of a given amplitude within a certain time, and thereby compute the tail of the surface height distribution. These calculations were done by using an ansatz for the solutions of MNLS, effectively making the problem 2D. The purpose of this work is to remove this approximation and study the problem in its full generality. Specifically, we consider the MNLS with random initial data drawn from a Gaussian distribution (30). The spectrum of this field is chosen to have a width comparable to that of the Joint North Sea Wave Project (JONSWAP) spectrum (31, 32) obtained from observations in the North Sea. We calculate the probability of occurrence of a large amplitude solution of MNLS out of these random initial data and thereby also estimate the tail of the surface height distribution. These calculations are performed within the framework of large deviations theory (LDT), which predicts the most likely way by which large disturbances arise and therefore also explains the mechanism of rogue wave creation. Our results are validated by comparison with brute-force Monte Carlo simulations, which indicate that rogue waves in MNLS are indeed within the realm of LDT. Our approach therefore gives an efficient way to assess the probability of large waves and their mechanism of creation.

1. Problem Setup

Our starting point will be the MNLS equation for the evolution of the complex envelope $u(t,x)$ of the sea surface in deep water (18), in terms of which the surface elevation reads $\eta (t,x)=\mathrm{\Re }(u(t,x)e^{i(k_{0}x-{\omega }_{0}t)})$ (here $k_0$ denotes the carrier wave number, ${\omega }_0=\sqrt{g{k}_0}$, and $g$ is the gravitational acceleration). Measuring $u$ and $x$ in units of $k_0^{-1}$ and $t$ in ${\omega }_0^{-1}$, we can write MNLS in nondimensional form as

$${\partial }_{t}u+{\displaystyle \frac{1}{2}}{\partial }_{x}u+{\displaystyle \frac{i}{8}}{\partial }_x^{2}u-{\displaystyle \frac{1}{16}}{\partial }_x^{3}u+{\displaystyle \frac{i}{2}}{|u|}^{2}u+{\displaystyle \frac{3}{2}}{|u|}^2{\partial }_{x}u+{\displaystyle \frac{1}{4}}{u}^2{\partial }_x\overline{u}-{\displaystyle \frac{i}{2}}\left|{\partial }_x\right|{|u|}^2=0,\hspace{1em}x\in [0,L],$$ [1]

where the bar denotes complex conjugation. We will consider Eq. 1 with random initial condition $u_0(x)\equiv u(0,x)$, constructed via their Fourier representation,

$$u_0(x)=\sum _{n\in \mathbb{Z}}{e}^{i{k}_{n}x}{(2{\widehat{C}}_n)}^{1/2}{\theta }_n,\hspace{1em}{\widehat{C}}_n=A{e}^{-k_n^2/(2{\mathrm{\Delta }}^2)},$$ [2]

where $k_n=2\pi n/L$, ${\theta }_n$ are complex Gaussian variables with mean zero and covariance $𝔼{\theta }_n{\overline{\theta }}_m={\delta }_{m,n}$, $𝔼{\theta }_n{\theta }_m=𝔼{\overline{\theta }}_n{\overline{\theta }}_m=0$. This guarantees that $u_0(x)$ is a Gaussian field with mean zero and $𝔼(u_0(x){\overline{u}}_0(x\prime ))=2{\sum }_{n\in \mathbb{Z}}{e}^{i{k}_n(x-x\prime )}{\widehat{C}}_n$. To make contact with the observational data, the amplitude $A$ and the width $\mathrm{\Delta }$ in Eq. 2 are picked so that ${\widehat{C}}_n$ has the same height and area as the JONSWAP spectrum (31, 32); see Supporting Information for details.

Because the initial data for Eq. 1 are random, so is the solution at time $t>0$, and our aim is to compute

$$P_T(z)\equiv \mathbb{P}(F(u(T))\ge z),$$ [3]

where $\mathbb{P}$ denotes probability over the initial data and $F$ is a scalar functional depending on $u$ at time $T>0$. Even though our method is applicable to more general observables, here we will focus on

$$F(u(T))=\underset{x\in [0,L]}{\max }|u(T,x)|.$$ [4]

2. LDT Approach

A brute-force approach to calculate Eq. 3 is Monte Carlo sampling: Generate random initial conditions $u_0(x)$ by picking random ${\theta }_n$’s in Eq. 2, evolve each of these $u_0(x)$ deterministically via Eq. 1 up to time $t=T$ to get $u(T,x)$, and count the proportion that fulfill $F(u(T))\ge z$. While this method is simple, and will be used below as benchmark, it loses efficiency when $z$ is large, which is precisely the regime of interest for the tails of the distribution of $F(u(T))$. In that regime, a more efficient approach is to rely on results from LDT which assert that Eq. 3 can be estimated by identifying the most likely initial condition that is consistent with $F(u(T))\ge z$. To see how this result comes about, recall that the probability density of $u_0$ is formally proportional to $\exp (-\frac{1}{2}{\parallel u_0\parallel }_C^2)$, where ${\parallel u_0\parallel }_C^2$ is given by

$${\parallel u_0\parallel }_C^2=\sum _{n\in \mathbb{Z}}\frac{{|{\widehat{a}}_n|}^2}{{\widehat{C}}_n},\hspace{1em}{\widehat{a}}_n=\frac{1}{L}{\int }_0^L{e}^{-i{k}_{n}x}{u}_0(x)dx.$$ [5]

To calculate Eq. 3 we should integrate this density over the set $\mathrm{\Omega }(z)=\{u_0:F(u(T,u_0))\ge z\}$, which is hard to do in practice. Instead, we can estimate the integral by Laplace’s method. As shown in Materials and Methods, this is justified for large $z$, when the probability of the set $\mathrm{\Omega }(z)$ is dominated by a single $u_0(x)$ that contributes most to the integral and can be identified via the constrained minimization problem

$$\frac{1}{2}\underset{u_0\in \mathrm{\Omega }(z)}{\min }{\parallel u_0\parallel }_C^2\equiv I_T(z),$$ [6]

which then yields the following LDT estimate for Eq. 3

$$P_T(z)\asymp \exp \left(-I_T(z)\right).$$ [7]

Here, $\asymp$ means that the ratio of the logarithms of both sides tends to 1 as $z\to \mathrm{\infty }$. As discussed in Materials and Methods, a multiplication prefactor can be added to Eq. 7, but it does not affect significantly the tail of $P_T(z)$ on a logarithmic scale.

In practice, the constraint $F(u(T,u_0))\ge z$ can be imposed by adding a Lagrange multiplier term to Eq. 6, and it is easier to use this multiplier as control parameter and simply see a posteriori what value of $z$ it implies. That is to say, perform for various values of $\lambda$ the minimization

$$\underset{u_0}{\min }\left(\frac{1}{2}{\parallel u_0\parallel }_C^2-\lambda F(u(T,u_0))\right)\equiv S_T(\lambda ),$$ [8]

over all $u_0$ of the form in Eq. 2 (no constraint), then observe that this implies the parametric representation

$$I_T(z(\lambda ))=\frac{1}{2}{\parallel u_0^{\star }(\lambda )\parallel }_C^2,\hspace{1em}z(\lambda )=F(u(T,u_0^{\star }(\lambda ))).$$ [9]

where $u_0^{\star }(\lambda )$ denotes the minimizer obtained in Eq. 8. It is easy to see from Eqs. 6 and 8 that $S_T(\lambda )$ is the Legendre transform of $I_T(z)$ since:

$$S_T(\lambda )=\underset{z\in ℝ}{sup}(\lambda z-I_T(z))=\underset{z\in ℝ}{sup}\left(\lambda z-\frac{1}{2}\underset{u_0\in \mathrm{\Omega }(z)}{inf}{\parallel u_0\parallel }_C^2\right),$$ [10]

3. Results

We considered two sets of parameters. In set 1, we took $A=5.4\cdot {10}^{-5}{k}_0^{-2}$ and $\mathrm{\Delta }=0.19k_0$. Converting back into dimensional units by using $k_0^{-1}=36$ m consistent with the JONSWAP spectrum (31, 32), this implies a significant wave height $H_s=4\sqrt{C(0)}=3.3$ m classified as a “rough sea” (33). It also yields a Benjamin–Feir index (BFI)$=2\sqrt{2C(0)}/\mathrm{\Delta }=0.34$, (32, 34), meaning that the modulational instability of a typical initial condition is of medium intensity. In set 2, we took $A=3.4\cdot {10}^{-4}{k}_0^{-2}$ and $\mathrm{\Delta }=0.19k_0$, for which $H_s=8.2$ m is that of a “high sea” and the BFI is 0.85, meaning that the modulational instability of a typical initial condition is stronger.

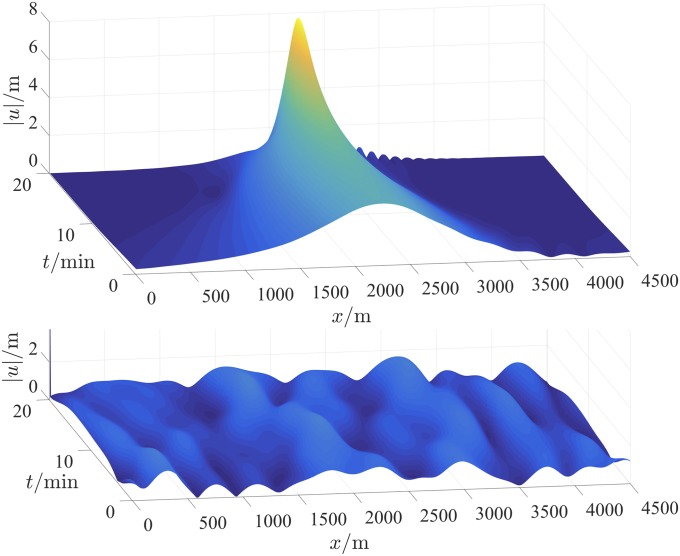
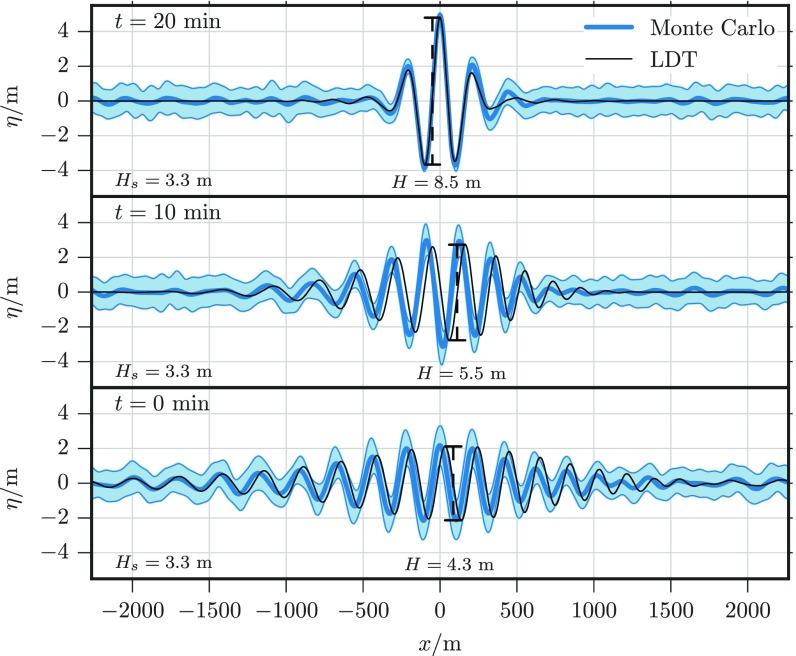
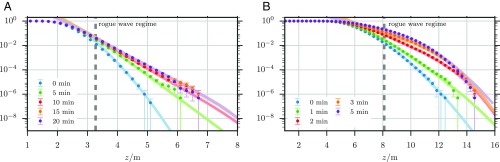
Fig. 1, Upper shows the time evolution of $|u(t,x)|$ starting from an initial condition from set 1 optimized so that ${\max }_x|u(T,x)|=8$ m at $T=20$ min. For comparison, Fig. 1, Lower shows $|u(t,x)|$ for a typical initial condition drawn from its Gaussian distribution. To illustrate what is special about the initial conditions identified by our optimization procedure, in Fig. 2, we show snapshots of the surface elevation $\eta (t,x)$ at three different times, $t=0,10,20$ min (black lines), using the constraint that ${\max }_x|u(T,x)|\ge 4.8$ m at $T=20$ min. Additionally, we average all Monte Carlo samples achieving ${\max }_x|u(t,x)|\ge 4.8$ m, translated to the origin. Snapshots of this mean configuration are shown in Fig. 2 (blue lines). They agree well with those of the optimized solution (black lines). The one SD spread around the mean Monte Carlo realization (light blue) is reasonably small, especially around the rogue wave at final time. This indicates that the event ${\max }_x|u(T,x)|\ge 4.8$ m is indeed realized with probability close to 1 by starting from the most likely initial condition consistent with this event, as predicted by LDT. The usefulness of LDT is confirmed in Fig. 3, depicting the probabilities of ${\max }_x|u(T,x)|$ for both sets 1 and 2 calculated via LDT optimization (lines), compared with Monte Carlo sampling (dots). As can be seen, the agreement is remarkable, especially in the tail corresponding to the rogue wave regime. As expected, the Monte Carlo sampling becomes inaccurate in the tail, since there, the probabilities are dominated by unlikely events. The LDT calculation, in contrast, remains efficient and accurate far in the tail.

Fig. 1.

(Upper) Time evolution of $|u(t,x)|$ from an initial condition optimized for ${\max }_x|u(T,x)|\ge 8$ m at $T=20$ min. (Lower) Same for a typical Gaussian random initial condition.

Fig. 2.

Comparison between the average realization reaching ${\max }_x|u(T,x)|\ge 4.8$ m at $T=20$ min (dark blue) and one SD around this mean (light blue), with the solution reaching the same amplitude starting from the maximum-likelihood initial condition (black) for $t=0,10,20$ min.

Fig. 3.

Probabilities $P_T(z)$ of ${\max }_x|u(T,x)|$ for different times $T$ for sets 1 (A) and 2 (B). The probabilities estimated by Monte Carlo sampling with ${10}^6$ realizations (dots) are compared with those predicted by LDT (lines). These probabilities agree over $\sim$5 orders of magnitude in probability, although LDT allows for the calculation of the tail where Monte Carlo becomes prohibitively costly. The error bars in the Monte Carlo results represent the statistical error of 2 SD ($95\%$ confidence interval) for the Bernoulli distribution with parameter $P_T(z)$.

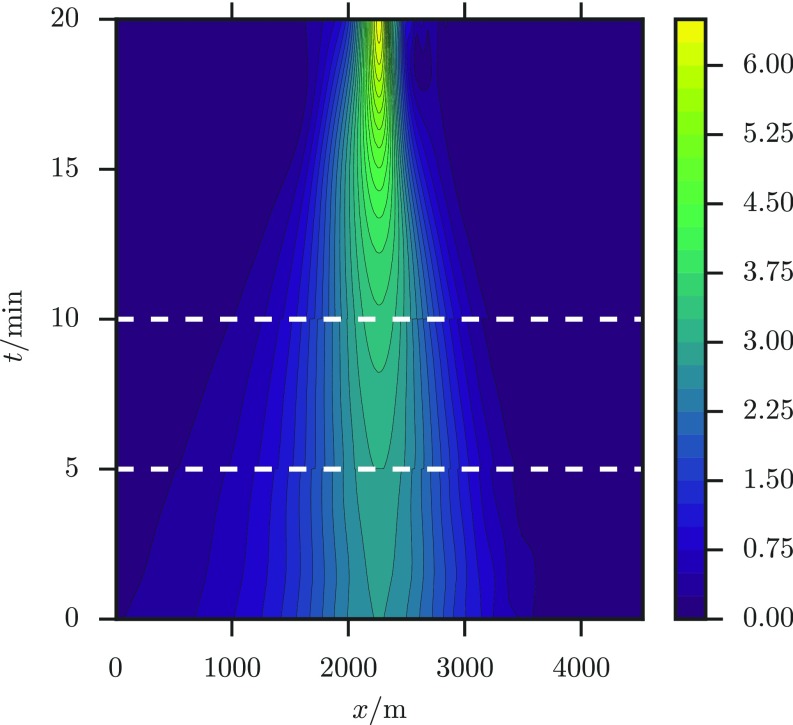
The probabilities plotted in Fig. 3 show several remarkable features. First, they indicate that, as $T$ gets larger, their tails fatten significantly. For example, in set 1 $P_{T=20\text{min}}(6\text{m})\approx {10}^{-5}$, which is $5$ orders of magnitude larger than initially, $P_{t=0\text{min}}(6\text{m})\approx {10}^{-10}$. Secondly, the probabilities converge to a limiting density for large $T$. This occurs after some decorrelation time ${\tau }_c\approx 10$ min in set 1 and ${\tau }_c\approx 3$ min in set 2. Similarly, the LDT results converge. In fact, this convergence can be observed at the level of the trajectories generated from the optimal $u_0^{\star }$. As Fig. 4 shows, reading these trajectories backward from $t=T$, their end portions coincide, regardless of whether $T=20$ min, $T=15$ min, or $T=10$ min. The implications of these observations, in particular on the mechanism of creation of rogue waves and their probability of appearance within a time window, are discussed in Interpretation.

Fig. 4.

Contour plot of the optimal trajectories from LDT for $T=10$, 15, and 20 min in set 1. The trajectories, superposed to match at $t=T$, coincide, which is consistent with the convergence of the probabilities $P_T(z)$ for large $T$.

Before doing so, let us discuss the scalability of our results to larger domain sizes; see Supporting Information for more details. As shown above, the optimization procedure based on LDT predicts that the most likely way a rogue wave will occur in the domain is via the apparition of a single large peak in $|u(t,x)|$. In the setup considered before, this prediction is confirmed by the brute-force simulations using Monte Carlo sampling. It is clear, however, that for increased domain size—e.g., by taking a domain size of $NL$ with $N\gg 1$—it will become increasingly likely to observe multiple peaks, for the simple reason that large waves can occur independently at multiple sufficiently separated locations. In these large domains, the large deviation predictions remain valid if we look at the maximum of $|u(t,x)|$ in observation windows that are not too large (that is, about the size of the domain $L$ considered above). However, they deteriorate if we consider this maximum in the entire domain of size $NL$, in the sense that the value $\mathbb{P}({\max }_{x\in [0,NL]}|u(t,x)|\ge z)$ predicted by LDT matches that from Monte Carlo sampling at values of $z$ that are pushed further away in the tails. This is an entropic effect, which is easy to correct for: Events in different subwindows must be considered independent, and their probabilities superposed. That is, if we denote by

$$P_T^N(z)=\mathbb{P}(\underset{x\in [0,NL]}{\max }|u(T,x)|\ge z),$$ [11]

it can be related to $P_T(z)=\mathbb{P}({\max }_{x\in [0,L]}|u(T,x)|\ge z)$ via

$$P_T^N(z)=1-{\left(1-P_T(z)\right)}^N.$$ [12]

This formula is derived in Supporting Information and shown to accurately explain the numerical results. For efficiency, $L$ is chosen to be the smallest domain size for which boundary effects can be neglected, in the sense that the shape of the optimal trajectories does no longer change if $L$ is increased further. In effect, this provides us with a method to scale up our results to arbitrary large observation windows.

4. Interpretation

The convergence of $P_T(z)$ toward a limiting function $P(z)$ has important consequences for the significance and interpretation of our method and its results. Notice first that this convergence can be explained if we assume that the probability distribution of the solutions to Eq. 1 with Gaussian initial data converges to an invariant measure. In this case, for large $T$, the Monte Carlo simulations will sample the value of ${\max }_x|u|$ on this invariant measure, and the optimization procedure based on LDT will do the same. The timescale ${\tau }_c$ over which convergence occurs depends on how far this invariant measure is from the initial Gaussian measure of $u_0(x)$. Interestingly, the values we observe for ${\tau }_c$ are in rough agreement with the time scales predicted by the semiclassical limit of NLS that describes high-power pulse propagation (35, 36). As recalled in Supporting Information, this approach predicts that the timescale of apparition of a focusing solution starting from a large initial pulse of maximal amplitude $U_i$ and length-scale $L_i$ is ${\tau }_c=\sqrt{T_{\text{nl}}{T}_{\text{lin}}}$, where $T_{\text{nl}}={\left(\frac{1}{2}{\omega }_0{k}_0^2{U}_i^2\right)}^{-1}$ is the nonlinear timescale for modulational instability and $T_{\text{lin}}=8{\omega }_0^{-1}{k}_0^2{L}_i^2$ is the linear timescale associated with group dispersion. Setting $U_i=H_s$ (the size at the onset of rogue waves) and $L_i=\sqrt{2\pi }{\mathrm{\Delta }}^{-1}$ (the correlation length of the initial field) gives ${\tau }_c\simeq 18$ min for set 1 and ${\tau }_c\simeq 8$ min for set 2, consistent with the convergence times of $P_T(z)$. This observation has implications in terms of the mechanism of apparition of rogue waves, in particular, their connection to the so-called Peregrine soliton, that has been invoked as prototype mechanism for rogue wave creation (5, 13, 37–40), in particular for water waves (24, 25, 41), plasmas (42), and fiber optics (36, 43, 44). This connection is discussed in Supporting Information.

Our findings also indicate that, even though the assumption that $u_0(x)$ is Gaussian is incorrect in the tail [that is, $P_{T=0}(z)$ is not equal to the limiting $P(z)$ in the tail], it contains the right seeds to estimate $P(z)$ via $P_T(z)$ if $T\gtrsim {\tau }_c$. (This convergence occurs on the timescale ${\tau }_c$ which is much smaller than the mixing time for the solutions of Eq. 1, i.e., the time it would take from a given initial condition, rather than an ensemble thereof, to sample the invariant measure.) Altogether, this is consistent with the scenario put forward by Sapsis and coworkers in refs. 45 and 46 to explain how extreme events arise in intermittent dynamical systems and calculate their probability: They occur when the system hits small instability pockets which trigger a large transient excursion. In this scenario, as long as the initial probability distribution in these pockets is accurate, the dynamics will permit precise estimation of the distribution tail. In some sense, the distribution of the initial condition plays a role of the prior distribution in Bayesian inference, and the posterior can be effectively sampled by adding the additional information from the dynamics over short periods of time during which instabilities can occur. [Note in particular that the Gaussian field in Eq. 2 is the random field that maximizes entropy given the constraint on its covariance $C(x)$.] In ref. 45, this picture is made predictive by using a 2D ansatz for the initial condition $u_0(x)$ to avoid having to perform sampling in high dimension over the original $u_0(x)$. What our results show is that this approximation can be avoided all together by using LDT to perform the calculations directly with the full Gaussian initial condition in Eq. 2.

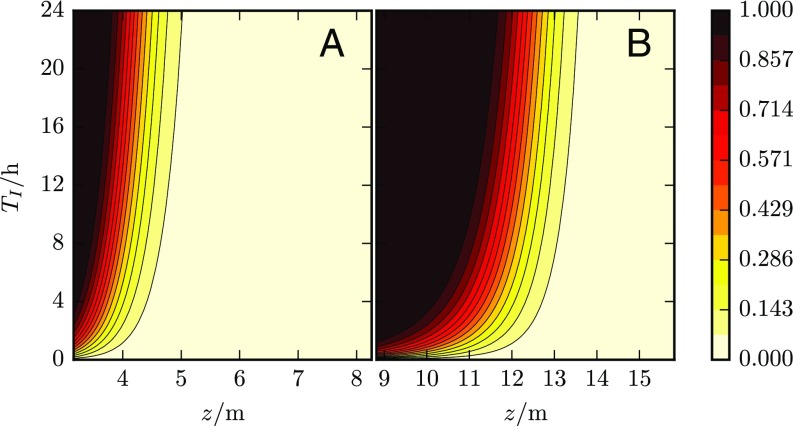
Interestingly, we can use the results above to calculate the probability of occurrence of rogue waves in a given time window. More precisely, the probability $p(z,T_I)$ that a rogue wave of amplitude larger than $z$ be observed in the domain $[0,L]$ during $[0,T_I]$ [i.e., that ${\max }_{t\in [0,T_I]}{\max }_{x\in [0,L]}|u(t,x)|\ge z$] can be estimated in terms of $P(z)$ and ${\tau }_c$ as

$$p\equiv \mathbb{P}(\underset{t\in [0,T_I]}{\max }\underset{x\in [0,L]}{\max }|u(t,x)|\ge z)\sim 1-{(1-P(z))}^{T_I/{\tau }_c},$$ [13]

where we use the fact that rogue waves can be considered independent on timescales larger than ${\tau }_c$ and assume $T_I\gg {\tau }_c$. The function $p$ is plotted in Fig. 5 as a function of $z$ and $T_I$. For example, for set 1, Eq. 13 indicates a 50% chance to observe a rogue wave of height $z=4$ m (that is, $\sim$8 m from crest-to-trough) after 11 h [using ${\tau }_c=10$ min and $P(z=4\text{m})=1.1\cdot {10}^{-2}$]; if we wait 30 h, the chance goes up to 85%. Similarly, for set 2, the chance to observe a wave of 11 m height is $\sim$50% after 3 h and $\sim$85% after 8 h (${\tau }_c=3$ min and $P(z=11\text{m})=1.2\cdot {10}^{-2}$).

Fig. 5.

Contour plots of the probability to observe a wave whose amplitude exceeds $z$ in the time window $[0,T_I]$ for sets 1 (A) and 2 (B).

5. Concluding Remarks

We have shown how an optimization problem building on LDT can be used to predict the pathway and likelihood of appearance of rogue waves in the solutions of MNLS fed by random initial data consistent with observations. This setup guarantees accuracy of the core of the initial distribution, which in turn permits the precise estimation of its tail via the dynamics. Our results give quantitative estimate for the probabilities of observing high-amplitude waves within a given time window. These results also show that rogue waves have very specific precursors, a feature that was already noted in ref. 47 in the context of a reduced model and could potentially be used for their early detection.

6. Materials and Methods

Laplace Method and Large Deviations.

Here, we recall some standard large deviation results that rely on the evaluation of Gaussian integrals by Laplace’s method and are at the core of the method we propose. It is convenient to rephrase the problem abstractly and consider the estimation of

$$P(z)=\mathbb{P}(\varphi (\theta )>z),$$ [14]

where $\theta \in {ℝ}^D$ are Gaussian random variables with mean zero and covariance Id, and $\varphi :{ℝ}^D\to ℝ$ is some real valued function—as long as we truncate the sum in Eq. 2 to a finite number of modes, $|n|\le M$, the problem treated in this work can be cast in this way, with $\theta$ playing the role of $C^{-1/2}{u}_0$ and $\varphi (\cdot )$ that of $F(u(T,C^{-1/2}\cdot ))$. The probability $P(z)$ in Eq. 14 is given by

$$P(z)={(2\pi )}^{-D/2}{\int }_{\mathrm{\Omega }(z)}{e}^{-\frac{1}{2}{|\theta |}^2}d\theta ,$$ [15]

where $\mathrm{\Omega }(z)=\{\theta :\varphi (\theta )>z\}$. The interesting case is when this set does not contain the origin, $0\notin \mathrm{\Omega }(z)$, which we will assume is true when $z>0$. We also make two additional assumptions:

• 1.
  The point on the boundary $\partial \mathrm{\Omega }(z)$ that is closest to the origin is isolated: Denoting this point as

  $${\theta }^{\star }(z)=\underset{\theta \in \partial \mathrm{\Omega }(z)}{\text{argmin}}{|\theta |}^2,$$ [16]
  we assume that

  $$\begin{array}{c}{\displaystyle \frac{1}{2}}{|{\theta }^{\star }(z)|}^2\hspace{0.17em}\text{is strictly increasing with}\hspace{0.17em}z\ge 0\text{;}\hfill \\ \underset{z\to \mathrm{\infty }}{lim}{\displaystyle \frac{1}{2}}{|{\theta }^{\star }(z)|}^2=\mathrm{\infty }.\end{array}$$ [17]
• 2.The connected piece of $\partial \mathrm{\Omega }(z)$ that contains ${\theta }^{\star }(z)$ is smooth with a curvature that is bounded by a constant independent of $z$.

The point ${\theta }^{\star }(z)$ satisfies the Euler–Lagrange equation for Eq. 16, with the constraint incorporated via a Lagrange multiplier term:

$${\theta }^{\star }(z)=\lambda \nabla \varphi ({\theta }^{\star }(z))$$ [18]

for some Lagrange multiplier $\lambda$. This implies that

$$\frac{{\theta }^{\star }(z)}{|{\theta }^{\star }(z)|}=\frac{\nabla \varphi ({\theta }^{\star }(z))}{|\nabla \varphi ({\theta }^{\star }(z))|}=\widehat{n}(z).$$ [19]

where $\widehat{n}(z)$ denotes the inward pointing unit vector normal to $\partial \mathrm{\Omega }(z)$ at ${\theta }^{\star }(z)$. If we move inside the set $\mathrm{\Omega }(z)$ from ${\theta }^{\star }(z)$ in the direction of $\widehat{n}(z)$, the norm ${|\theta |}^2$ increases under the assumptions in Eq. 17. Indeed, setting $\theta ={\theta }^{\star }(z)+\widehat{n}(z)u$ with $u\ge 0$, we have

$$\begin{array}{c}{|\theta |}^2={|{\theta }^{\star }(z)|}^2+2⟨\widehat{n}(z),{\theta }^{\star }(z)⟩u+u^2\\ ={|{\theta }^{\star }(z)|}^2+2|{\theta }^{\star }(z)|z+z^2\text{,}\end{array}$$ [20]

where we use Eq. 19. In fact, if we were to perform the integral in that direction, the natural variable of integration would be to rescale $u\to u/|{\theta }^{\star }(z)|$. In particular, if we were to replace $\mathrm{\Omega }(z)$ by the half space $P(z)=\{\theta |\widehat{n}(z)\cdot (\theta -{\theta }^{\ast }(z))>0\}$, it would be easy to estimate the integral in Eq. 15 by introducing a local coordinate system around ${\theta }^{\ast }(z)$, whose first coordinate is in the direction of $\widehat{n}(z)$. Indeed, this would give:

$$\begin{array}{c}{(2\pi )}^{-D/2}{\int }_{P(z)}{e}^{-\frac{1}{2}{|\theta |}^2}d\theta \\ ={(2\pi )}^{-D/2}{\int }_0^{\mathrm{\infty }}{e}^{-\frac{1}{2}{|{\theta }^{\star }(z)|}^2-|{\theta }^{\star }(z)|u-\frac{1}{2}{u}^2}du{\int }_{{ℝ}^{N-1}}{e}^{-\frac{1}{2}{|\eta |}^2}d\eta \\ ={(2\pi )}^{-1/2}{e}^{-\frac{1}{2}{|{\theta }^{\star }(z)|}^2}{\int }_0^{\mathrm{\infty }}{e}^{-|{\theta }^{\star }(z)|u-\frac{1}{2}{u}^2}du\\ ={(2\pi )}^{-1/2}|{\theta }^{\star }(z){|}^{-1}{e}^{-\frac{1}{2}{|{\theta }^{\star }(z)|}^2}{\int }_0^{\mathrm{\infty }}{e}^{-v-\frac{1}{2}{|{\theta }^{\star }(z)|}^{-2}{v}^2}dv\\ \sim {(2\pi )}^{-1/2}|{\theta }^{\star }(z){|}^{-1}{e}^{-\frac{1}{2}{|{\theta }^{\star }(z)|}^2}\hspace{1em}\text{as}\hspace{0.17em}z\to \mathrm{\infty }.\end{array}$$ [21]

The last approximation goes beyond a large deviations estimate (i.e., it includes the prefactor), and it implies

$$\underset{z\to \mathrm{\infty }}{lim}{|{\theta }^{\star }(z)|}^{-2}\log \left({(2\pi )}^{-D/2}{\int }_{P(z)}{e}^{-\frac{1}{2}{|\theta |}^2}d\theta \right)=-\frac{1}{2}.$$ [22]

This log-asymptotic estimate is often written as

$${\int }_{P(z)}{e}^{-\frac{1}{2}{|\theta |}^2}d\theta \asymp e^{-\frac{1}{2}{|{\theta }^{\star }(z)|}^2}\hspace{1em}\text{as}\hspace{0.17em}z\to \mathrm{\infty }.$$ [23]

Interestingly, while the asymptotic estimate in Eq. 21 does not necessarily apply to the original integral in Eq. 15 [that is, the prefactor may take different forms depending on the shape of $\partial \mathrm{\Omega }(z)$ near ${\theta }^{\star }(z)$], the rougher log-asymptotic estimate in Eq. 23 does as long as the boundary $\partial \mathrm{\Omega }(z)$ is smooth, with a curvature that is bounded by a constant independent of $z$. This is because the contribution (positive or negative) to the integral over the region between $\mathrm{\Omega }(z)$ and $P(z)$ is subdominant in that case, in the sense that the log of its amplitude is dominated by $|{\theta }^{\star }(z)|$. This is the essence of the large deviations result that we apply in this work.

Numerical Aspects.

To perform the calculations, we solve Eq. 1 with $L=40\pi$ and periodic boundary conditions, and check that this domain is large enough to make the effect of these boundary conditions negligible (Supporting Information). The spatial domain is discretized by using $2^{12}$ equidistant grid points, which is enough to resolve the solution of Eq. 1. To evolve the field $u(t,x)$ in time, we use a pseudospectral second-order exponential time-differencing (ETD2RK) method (48, 49).

When performing the Monte Carlo simulations, we use ${10}^6$ realizations of the random initial data constructed by truncating the sum in Eq. 2 over the $M=23$ modes with $-11\le n\le 11$—i.e., $-3\mathrm{\Delta }\le k_n\le 3\mathrm{\Delta }$: These modes carry most of the variance, and we check that adding more modes to the initial condition did not affect the results in any significant way (Supporting Information).

Optimization Procedure.

As explained above, the large deviation rate function $I_T(z)$ in Eq. 6 can be evaluated by solving the dual optimization problem in Eq. 8, which we rewrite as $S_T(\lambda )={\text{inf}}_{u_0}E(u_0,\lambda )$, where we define the cost function

$$E(u_0,\lambda )\equiv \frac{1}{2}{\parallel u_0\parallel }_C^2-\lambda F(u(T,u_0)).$$ [24]

We perform this minimization using steepest descent with adaptive step (line search) and preconditioning of the gradient (50). This involves evaluating the (functional) gradient of $E(u_0,\lambda )$ with respect to $u_0$. Using the chain rule, this gradient can be expressed as (using compact vectorial notation)

$$\frac{\delta E}{\delta u_0}=C^{-1}{u}_0-\lambda J^T(T,u_0)\frac{\delta F}{\delta u}$$ [25]

where $J(t,u_0)=\delta u(t,u_0)/\delta u_0$ is the Jacobian of the transformation $u_0\to u(t,u_0)$. Collecting all terms on the right-hand side of the MNLS Eq. 1 into $b(u)$, this equation can be written as

$${\partial }_{t}u=b(u),\hspace{1em}u(t=0)=u_0,$$ [26]

and it is easy to see that in this notation $J(t,u_0)$ satisfies

$${\partial }_{t}J=\frac{\delta b}{\delta u}J,\hspace{1em}J(t=0)=\text{Id}.$$ [27]

Consistent with what was done in the Monte Carlo sampling, to get the results presented above, we truncate the initial data $u_0$ over $M=23$ modes using the representation

$$u_0(x)=\sum _{n=-11}^{11}{e}^{i{k}_{n}x}{\widehat{a}}_n,\hspace{1em}{k}_n=2\pi n/L.$$ [28]

This means that minimization of Eq. 24 is performed in the $2M-1=45$ dimensional space spanned by the modes ${\widehat{a}}_n$, accounting for invariance by an overall phase shift—to check convergence, we also repeat this calculation using larger values of $M$ and find no noticeable difference in the results (Supporting Information).

In practice, the evaluation of the gradient in Eq. 25 is performed by integrating both $u(t)$ and $J(t)$ up to time $t=T$. Eq. 27 is integrated by using the same pseudospectral method as for Eq. 1 on the same grid. To perform the steepest descent step, we then precondition the gradient through scalar multiplication by the step-independent, diagonal metric with the components of the spectrum ${\widehat{C}}_n$ as diagonal elements.