Protein Structure Prediction: Making AWSEM AWSEM-ER by Adding Evolutionary Restraints

Abstract

Protein sequences have evolved to fold into functional structures, resulting in families of diverse protein sequences that all share the same overall fold. One can harness protein family sequence data to infer likely contacts between pairs of residues. In the current study, we combine this kind of inference from coevolutionary information with a coarse-grained protein force field ordinarily used with single sequence input, the Associative memory, Water mediated, Structure and Energy Model (AWSEM), to achieve improved structure prediction. The resulting Associative memory, Water mediated, Structure and Energy Model with Evolutionary Restraints (AWSEM-ER) yields a significant improvement in the quality of protein structure prediction over the single sequence prediction from AWSEM when a sufficiently large number of homologous sequences are available. Free energy landscape analysis shows that the addition of the evolutionary term shifts the free energy minimum to more native-like structures, which explains the improvement in the quality of structures when performing predictions using simulated annealing. Simulations using AWSEM without coevolutionary information have proved useful in elucidating not only protein folding behavior, but also mechanisms of protein function. The success of AWSEM-ER in de novo structure prediction suggests that the enhanced model opens the door to functional studies of proteins even when no experimentally solved structures are available.

1 Introduction

The process by which proteins fold to their native structure has been of intense interest both because of the practical desire to predict protein structure from easily obtained sequence data and due to deeper scientific curiosity about the nature of biological self-organization. The fact that a protein can overcome entropy to fold into an ensemble of structures that fluctuates about the functional configuration almost seems paradoxical.[1] It is now understood that protein sequences can fold because their sequences have evolved to minimize the degree of frustration in the functional structure. Sequences favored by evolution have funneled landscapes that guide the molecule to fold into the native functional structure while avoiding non-native, partially folded “traps”.[2, 3] While understanding the general principles of protein folding is of scientific interest, this understanding is also helpful for devising algorithms that can be used to predict protein structure. Nevertheless, predicting detailed high-resolution structures of particular proteins remains an important but difficult task in practice.

The structure prediction problem can be stated in the following way. Given the sequence of amino acids for a specific protein, without doing additional experiments on the protein, can we predict the native structure into which that protein will fold? For an ever-growing number of sequences the answer is now “yes”. With the dramatic increases in computational power and the number of experimentally known structures in the protein data bank (PDB)[4], knowledge-based prediction methods are proving able to achieve usefully accurate predictions of structure.

For some time now, the most accurate method of protein structure prediction has been homology modeling, which involves exploiting knowledge of evolutionary descent.[5] Homology modeling involves searching for sequences that are globally similar to the target sequence and then, hopefully, finding a match to a protein whose structure has been solved already. One can generally assume that, if two sequences are sufficiently similar, they must have evolved from a common ancestor and will also share similar structures. Homology modeling works as a consequence of evolutionary restraints: in order for a modern protein along with all its ancient ancestors and cousins to have always functioned in the same way, they all must have folded throughout history into structures which must not have changed much. As the number of solved protein structures has increased, so has the power of homology modeling based on analogy to known structures. It has become increasingly rare to find globally novel folds. Nevertheless, at least in some cases, it remains a challenge to recognize whether or not a specific protein has a homolog with a solved structure prior to the experimental determination of the structure. Such proteins are sometimes said to be in a “twilight zone” of homology inference.[6]

A relatively recent development in protein structure prediction involves using evolutionary sequence data in a different way by looking at residue pair covariation within families of protein sequences. Even if none of the family members have had their structures determined, correlated changes in sequence can be used to predict native contacts. Similar reasoning was used by Levitt for tRNA and Fox and Woese in their early predictions of rRNA structure from coevolution of bases which must have remained paired.[7, 8] Since, over the course of time, naturally occurring proteins have undergone random mutations but nevertheless have had to still maintain the same functional structure, variations of pairs of residues that are in contact in the folded structure are correlated. Building global probability models of multiple sequence alignments allows one to distinguish between direct and indirect correlations.[9] Many of the strong direct correlations will correspond to the native contacts in a minimally frustrated protein. The accurate prediction of native contacts by coevolutionary analysis depends on there being a sufficient number of sequences available in the multiple sequence alignment relative to the size of the protein. One needs roughly five times as many sequences as the number of residues in the target sequence to be assured of a reasonably accurate prediction of a large number of native contacts.[10]

One way to employ the predictions of contacts from coevolutionary analysis of protein families is to use the predicted contacts as the basis of a perfectly funneled structure-based model for a single protein. Sułkowska et al. have shown that this approach can yield reasonably accurate structure predictions.[11] Alternatively, one could use coevolutionarily predicted contacts as evolutionary constraints combined with a more complex structure prediction protocol as Marks et al. have shown.[12, 13] Ovchinnikov et al. have enjoyed signal success in recent iterations of CASP by incorporating coevolutionary information as additional constraints into their ROSETTA algorithm for ab initio structure prediction.[14] Using this approach, Ovchinnikov et al. have successfully predicted structures for hundreds of proteins.[15, 16] Being tied to function, ultimately, coevolutionary data contain information that goes beyond an individual protein’s structure. Aside from having information about intramonomer protein contacts, strong coevolutionary variation sometimes contains information that does not refer to the monomer but that deals with interdomain contacts for proteins when they form oligomers. Several studies have been carried out that show the utility of using such coevolutionary information for predicting oligomeric interfaces.[17, 18, 19] In addition to containing static structural information about native proteins, coevolutionary analysis also reveals functional aspects for proteins that arise from their having multiple conformations. Recognizing this fact, Morcos et al. have used coevolutionary analysis to uncover multiple protein conformations of receptors/binding proteins.[20] Another recent study has shown the potential for using coevolutionary information to study disordered regions in proteins.[21]

While the methods outlined above yield sufficiently accurate predictions for many proteins, they also can come up short in some cases. Proteins that contain regions not covered by sequence homology are tricky for homology methods. Also, if there are no known homologues of a protein that possesses an already solved structure, the direct homology modeling strategy obviously fails. Finding out with certainty which proteins are homologues to a given sequence is at times difficult, especially for distantly related proteins in the “twilight zone”, which are those with a sequence identity of about 25-30 percent.[6] As we noted, an analogous “twilight zone” also exists for coevolutionary methods if there are few related sequences. For coevolutionary inference of contacts to be accurate, a protein with L amino acids typically requires at least 5L homologous sequences that are significantly different from one another.[10] A sequence with fewer related sequences is in the “coevolutionary twilight zone”, where the number and quality of predicted contacts based solely on coevolutionary analysis begins to degrade. In this work, we investigate whether structure prediction efforts on target sequences in the “coevolutionary twlight zone” can benefit from the addition of physically motivated terms to the energy function being used to guide structure formation.

Though structural predictions obtained by purely physically motivated algorithms are not generally as accurate as homology models, purely physical methods based on a single sequence already perform moderately well for many structure prediction tasks. They are especially useful where existing structural knowledge is lacking, for example, for predicting structures of misfolded oligomers or aggregates.[22] Detailed physical models based on fully atomistic force fields have been shown to successfully fold small proteins.[23] Routinely employing such all-atom models, however, quickly becomes computationally prohibitive for larger proteins. Coarse-grained models of proteins can overcome the computational expense of using more detailed atomistic models.[24] Our group has developed a series of coarse-grained protein force fields that have been shown to accurately predict protein structures from single sequences alone, without exploiting structural knowledge about homologues.[25, 26] The optimization of the coarse-grained force field takes advantage of insights from energy landscape theory to learn both the form of the energy function as well as the corresponding parameters in the coarse-grained force field. The resulting model is called the Associative memory, Water mediated, Structure and Energy Model, or AWSEM. The physically motivated nature of the model also allows for a variety of both functional and misfolding phenomena to be studied by combining simulations with thermodynamic and kinetic analyses.[22] Most algorithms aimed purely at structure prediction cannot be used directly for such mechanistic studies. The success of AWSEM-ER inde novo structure prediction means that the ability of AWSEM to investigate mechanistic questions can now be leveraged for studying proteins in families that do not have any experimentally determined structures in them.

Although using a single algorithm may be sufficient to predict the structure of some proteins, experience suggests that a more robust strategy is to exploit the synergy of a variety of approaches. The AWSEM protein force field is comprised of several different terms, some of which are physically motivated, while other terms involve input from bioinformatic searches or atomistic simulations. The contact term in AWSEM accounts for physically relevant tertiary interactions, enabling prediction even when there are no homologues. But we note also that information about structures of homologous sequences, when available, can be added into the model to enrich the fragment memory term, which markedly improves performance. A previous study has shown that the energies obtained from coevolutionary inference are indeed correlated with the physically motivated terms of AWSEM.[27] The correlation is not perfect however, suggesting that each may contain some information lacking in the other. AWSEM does not have any terms based on nonlocal coevolutionary information. Because of the correlation of the physical and evolutionary landscapes, some of the contact inferences from coevolution may be redundant in predicting the structure of a given protein, but some information may not be redundant. In this paper, we show how coevolutionary information can be encoded as an evolutionary restraint term into AWSEM, making it AWSEM-ER, the Associative memory, Water mediated, Structure and Energy Model with Evolutionary Restraints. We will explore how this enhanced algorithm that takes advantage of the synergy of physics and evolution fares in structure prediction tasks where varying amounts of sequence information is available as input to the coevolutionary model.

In this work, we first benchmark AWSEM-ER on a panel of α-helical proteins that we have previously studied using AWSEM[28], which employs a database search for fragment input but employs no homologue information, and also using AAWSEM[25], a version of AWSEM that employs no bioinformatics in any form but only uses the results of all atom simulations of fragments of the protein in solvent to construct the fragment memory term. The latter method might be described as truly ab initio. For the purpose of mimicking de novo structure prediction tasks, we have run these test simulations using a version of AWSEM that deliberately avoids using structural information from sequences that are globally homologous to the prediction target sequence. (For comparison, in the supplementary information, we also show results when homology is used to choose fragments, a strategy useful in practical situations.) We also simulate models that employ no transferable contact term but instead use only contacts predicted from coevolutionary information. Finally, we test the AWSEM-ER algorithm, which combines the physically motivated and coevolution-based force fields into a single hybrid. For the panel of previously studied α-helical proteins, we find that AWSEM-ER yields predictions that are better than any of the other protocols that we tested. The predictions that use only the evolutionary restraint term often yield quite good predictions when many native contacts can be correctly inferred due to the abundance of sequence information for some protein families. We also examined another test panel of proteins for which there are not as many sequences available for the coevolutionary analysis (below the typical 5L threshold). For this panel of proteins, where the coevolutionary inference of contacts is less robust, we find the AWSEM-ER model still shows some improvement over the simpler algorithms for many of the proteins, but in this case the improvements over pure AWSEM based on a single sequence are more modest. To better understand how adding evolutionary restraints improve prediction quality, we also carry out free energy analyses for several proteins. These analyses show that the landscapes generated by AWSEM-ER are typically more strongly funneled than the landscapes constructed from “single sequence” AWSEM alone or the landscape based on the coevolutionary contact model by itself.

2 Methods

2.1 Coevolutionary analysis

Several methods have been developed to infer native contacts in a given protein family using a large number of aligned sequences as input. Of the coevolutionary analysis methods developed so far, plmDCA[29] and GREMLIN[30] seem to predict contacts most accurately.[10] Both methods work by using a pseudo-likelihood maximization framework to infer an evolutionary energy function over sequence space. For a more comprehensive overview of these methods, see the review by Stein et al.[31] The predicted contacts that we use in this study were obtained using the GREMLIN web server with default settings. For proteins with fewer available sequences (panel 2 below), we used jackhmmer[32] instead of HHblits[33] for the sequence alignments. The GREMLIN webserver yields the top 1.5L contacts for each prediction, as ranked by the GREMLIN score. For panel 1, we used all 1.5L predicted contacts in the coevolutionary contact model. For panel 2, where the co-evolutionarily inferred contacts are less reliable, we chose to use only those contacts with a probability greater than 0.5, as estimated by GREMLIN. Contact maps containing the GREMLIN contacts used as input for each of the simulations are shown in Figures S1 and S2 of the supplementary information.

2.2 Coevolutionary contact model

Knowledge of native contacts can be incorporated into a perfectly funneled landscape using a native-centric model. The native-centric model originally developed by Eastwood and Wolynes[34] relies on the same coarse-grained description of the protein used by AWSEM[28] in which only the C_α, C_β, and O atoms of each residue are explicitly represented. The locations of the other backbone atoms are inferred based on ideal amino acid geometry. In these models, protein-like conformations of the backbone are maintained using terms that dictate excluded volume and proper dihedral angle distributions. Predicted secondary structural information from PSIpred[35] is also provided as input for the Ramachandran portion of the backbone term and hydrogen bonding terms. Our version of the native-centric model can either have an additive or nonadditive contact term depending on the value of the nonadditivity exponent (p). For this study, we set p=1, which results in a pairwise additive contact term, which stabilizes contacts specified as input. When we use contacts predicted via coevolutionary methods as input, we refer to this contact term as V_ER to make it clear that no explicit structural information from the protein has been included. The full form of the coevolutionary contact potential is given in Equation 1.

Typically, when perfect funnel models (often called structure-based[36, 37, 38] or Gō models[39, 40]) are used for studying proteins of known structure, the native contacts included in the model are obtained from complete three-dimensional structures and thus the interaction wells can be centered precisely based on the pairwise separation distances in the experimentally determined structure. The exact distances of contacts predicted using coevolutionary information are uncertain. When using predicted contacts as input for the coevolutionary contact model, we then need to address where each of the interaction wells should be centered for each contact. We chose to locate the well centers for each contact pair by using the identities of the interacting amino acids to specify the expected contact length. The distance for each possible pair of amino acid types was set to the median separation distance found from a survey of thousands of PDB structures (full details are given in the supplementary information and the well centers used are given in Figure S3).

$$V_{\mathit{CoEv}-\mathit{contact}=}{V}_{\mathit{backbone}}+V_{\mathit{ER}}$$ (1)

2.3 AM-ER

A variation on the coevolutionary contact model involves adding an associative memory term to the Hamiltonian, resulting in the associative memory model with evolutionary restraints (AM-ER). The full AM-ER potential is given in Equation 2. The fragment memory term, V_FM, is a purely knowledge based term, which guides local-in-sequence structure formation. The fragment memories are obtained by searching sequences of proteins in the PDB for matches to short (approximately 9 amino acid) “fragments” from the target protein. Local interactions are then biased toward these fragment memories using an associative memory term. Associative memory terms, originally motivated by spin models of neural networks developed by Hopfield and Little, have been a key aspect of the protein folding models developed in our group.[41, 42] The details of these models have evolved over the decades.[43, 44, 45]

$$V_{\mathit{AM}-\mathit{ER}}=V_{\mathit{backbone}}+V_{\mathit{ER}}+V_{\mathit{FM}}$$ (2)

2.4 AWSEM

In close harmony with the native-contact-based models outlined above, AWSEM (Associative memory, Water mediated, Structure and Energy Model) employs a coarse-grained protein model consisting of three atoms per residue (C_α, C_β, and O). The total energy function for AWSEM is given in Equation 3. The backbone terms are the same for both AWSEM and the coevolutionary contact models. The V_contact, V_burial, and V_HB terms in AWSEM are all physically motivated. V_contact is an optimized, transferable tertiary interaction that acts between all pairs of residues beyond a minimum sequence separation. Unlike those used in a structure-based model, these interactions are not restricted to pairs of residues that are close together in the native state. Furthermore, V_contact includes both direct and mediated interactions, which are active over different spatial separation ranges. The direct contact term is a pairwise additive term for residues having a separation distance between 4.5 to 6.5 Å. Mediated pair interactions occur when residues are separated between 6.5 and 9.5 Å. These interactions are classified as either water- or protein-mediated depending on the local coordination number of each of the interacting amino acids, which makes the mediated interaction non-pairwise additive. V_burial is another nonadditive term that accounts for the propensity of an amino acid to be buried in the core of the protein or to be exposed on the surface. Its strength is correlated with amino acid hydrophobicity. V_HB is responsible for hydrogen bonding and aids in the formation of α-helices and β-sheets. As outlined for AM-ER, the fragment memory term, V_FM, is a bioinformatically informed term used to aid local-in-sequence structure formation. A more thorough description of all of the terms in the model is given in the supplementary information of an earlier paper.[28]

$$V_{\mathit{AWSEM}}=V_{\mathit{backbone}}+V_{\mathit{contact}}+V_{\mathit{burial}}+V_{\mathit{HB}}+V_{\mathit{FM}}$$ (3)

For this study, in order to examine the power of the method on de novo structure prediction problems, we chose to exclude homologues from the fragment memory search, although they are sometimes available. Excluding homologues allows us to approximate the situation that would be faced when predicting a new fold for which no structure homologues are available. For reference, we show results in the supplementary information when homologue information is also included for the fragment memory term (Figures S4 and S5).

2.5 AWSEM-ER

The AWSEM-ER model, given in Equation 4, combines terms from the models outlined above. When creating a hybrid algorithm or adding any additional term to an existing model, one must ensure the individual terms are weighted appropriately. As a general guideline, we have found that setting approximately one third of the stabilization energy in proteins to come from local-in-sequence interactions (i.e. the fragment terms and local biases) and the other two thirds to come from other nativizing interactions including tertiary interactions turns out to be quite effective and is also in harmony with physicochemical arguments.[46] To maintain this approximate balance, the strength of V_contact, which is the primary tertiary interaction term in AWSEM, is cut in half. Similarly, the strength of V_ER is cut in half from the standard value ordinarily used for structure-based models. We found that the quality of predictions using the hybrid model is fairly robust to changing the relative strength of different terms in the potential. For example, doubling the strength of V_ER does not significantly affect the quality of prediction. Likewise, adjusting the strength of V_contact, V_burial, or V_FM by 50 percent did not result in an appreciable difference in the structure prediction results.

$$V_{\mathit{AWSEM}-\mathit{ER}}=V_{\mathit{AWSEM}}+V_{\mathit{ER}}$$ (4)

The source code for AWSEM along with tutorials on how to setup and run AWSEM and AWSEM-ER simulations are available on the AWSEM-MD Github repository page (https://github.com/adavtyan/awsemmd).

2.6 Structure prediction

To test how the models compare in their quality of protein structure prediction, we carry out simulated annealing molecular dynamics simulations starting from random-coil-like chain configurations. All of the force fields in this study were implemented in the LAMMPS molecular dynamics package.[47] The annealing schedule used was fairly wide, starting at a temperature of 1000 K (well above the folding temperature) and annealing to 200 K (well below the folding temperature for most proteins in the model). Annealing runs were carried out over 8 million time steps using Langevin dynamics.

2.7 Free energy profile analysis

Free energy calculations were carried out using pyMBAR, an implementation of the multistate Bennet acceptance ratio method in Python.[48] The simulation data for pyMBAR calculations were obtained via umbrella sampling using Q, a measure of foldedness, as the biasing coordinate. The harmonic biasing potential shown in Equation 7 was used for the umbrella sampling calculations. The definition of Q is given in Equation 5, where N is the number of amino acids in the protein, r_ij is the separation between amino acids i and j in a given structure, and σ_ij = (1 + |i – j|)^0.15. As an additional order parameter for the free energy analyses, we introduce an alternative measure, Q_CoEv, to measure how well the GREMLIN contact predictions are sampled in the simulation (Equation 6). The function sums over all pairs of correctly predicted contacts from GREMLIN, and r_estimate depends on the residue types of the predicted amino acid pairs. The values of r_estimate for each possible pair of amino acids are given in Figure S3.

$$Q=\frac{2}{(N-2)(N-3)}\sum _{i-j>2}\exp \left(-\frac{{(r_{\mathit{ij}}-r_{\mathit{ij}}^{\mathit{native}})}^2}{2{\sigma }_{\mathit{ij}}^2}\right)$$ (5)

$$\begin{array}{c}{Q}_{\mathit{CoEv}}=\frac{1}{N}{\sum }_{|i-j|>3}\mathit{exp}\left[-\frac{{(r_{\mathit{ij}}-r_{\mathit{ij}}^{\mathit{estimate}})}^2)}{2{\sigma }_{\mathit{ij}}^2}\right]\\ {\sigma }_{\mathit{ij}}=|i-j{|}^{0.15}\AA \end{array}$$ (6)

$$V_{\mathit{bias}}=\frac{1}{2}{k}_{\mathit{bias}}{(Q-Q^0)}^2$$ (7)

It is also useful to measure how well the native contacts are predicted, both as input and as output. One such measure is the precision, sometimes referred to as the positive predictive value (PPV), defined by:

$$\mathit{Precision}=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FP}}$$ (8)

Here, TP are the true positives, the contacts present in the experimental structure that are predicted by GREMLIN. FP are the false positives, the contacts that are predicted by GREMLIN that are not present in the crystallographic structure of the protein.

2.8 Proteins studied

We tested the structure prediction abilities of the methods described above on two distinct test panels of proteins. The first panel of proteins was selected to compare results from the AWSEM-ER model to results from earlier variations of AWSEM developed by the group. This panel of proteins was taken directly from those proteins that also have been studied using AAWSEM, the AWSEM code that uses only atomistic simulations as input to the fragment memory term. All the members of the first panel of proteins have a large number of sequences available for the coevolutionary analysis, so their contact predictions are very good. To test then what happens when fewer sequences are available, leading to fewer and less precise contact predictions, we also selected another panel of proteins with fewer than 5L sequences in their multiple sequence alignments. The number of sequences of family members used for the coevolutionary analysis for each of the proteins is shown in Table 1. The PDB IDs of the proteins in panel 1 are: 1r69, 3icb, 1n2x (residues 115-215), 4cpv, 1mba, and 2eb8. The PDB IDs of the proteins in panel 2 are: 1ljp, T251 (residues 1-102 from PDB 1xg8), 2ea9, 256b, T0766 (PDB 4q53), T120 (residues 1-117 from PDB 1fu1), and 2z15. We note here that proteins 1mba, 1r69, 256b, 3icb, and 4cpv were originally included in the training set during the optimization of the contact term for AWSEM.[49]

Table 1.

A List of the proteins studied along with the numbers of amino acids in each of them (L), the number of sequences (N) available for the coevolutionary analysis in each of them, the sequence to length ratio (N/L), and the precision (P) of the contact prediction for each of them, as defined in Equation 8. N/L = 5 is often used as a guideline for the minimum number of sequences required to carry out an accurate coevolutionary analysis. The list is sorted in descending order of N/L. The fold of the protein is given along with its full name and function, if known.

Name	L	N	N/L	P	Fold	Full name (Function)
1r69	63	46,684	753.0	0.96	α	amino-terminal of phage 434 repressor (DNA binding)
3icb	75	24,116	354.6	0.90	α	Vit. D-dependent Calcium-binding protein (Calcium binding)
4cpv	108	7533	73.1	0.83	α	Calcium-liganded Carp Parvalbumin (Calcium binding)
1n2x	101	3670	37.4	0.94	α	TM0872 (SAM-dependent methyltransferase)
1mba	146	3975	27.8	0.82	α	Myoglobin (Oxygen storage)
2eb8	154	3828	25.9	0.85	α	apo-Myoglobin (Oxygen storage)
2z15	119	395	3.4	0.49	α/β	Tob1 (Signaling protein)
T251	99	265	2.8	0.60	α/β	SA0789 (unknown)
2ea9	103	242	2.4	0.37	α/β	JW2626 (unknown)
256b	106	244	2.3	0.76	α	Cytochrome b562 (electron transport)
1ljp	98	181	1.9	0.38	α	beta-Cinnamomin Elicitin (toxin)
T0766	108	184	1.5	0.47	α/β	BACUNI 04292 (unknown)
T120	117	151	1.3	0.32	α/β	XRCC4 (gene regulation)

3 Results and discussion

3.1 Prediction results

The results from the structure prediction runs are summarized in Figures 1 and 2. Figure 1 highlights the maximum Q values achieved during the 20 simulated annealing runs for each of the different models. These high values are typically sampled around the folding temperature and are a bit larger than the final value. The results showing the predictions corresponding to the lowest energy structures, which is a useful metric in evaluating structure prediction schemes for truly blind prediction without human intervention, can be found in the supplementary information (Figures S6 and S7). Larger Q values indicate more native-like structures based on the experimentally determined crystal structure of the protein. We find that the combined AWSEM-ER potential yields the highest quality predictions compared to predictions from the AWSEM, the pure coevolutionary contact model, or the AM-ER models on their own. The worst prediction from the combined AWSEM-ER model on this panel of proteins led to a Q value of ~0.6, which is still quite an accurate prediction. We see that adding evolutionary information significantly improves the structure prediction capabilities of the physically based AWSEM model.

Figure 1.

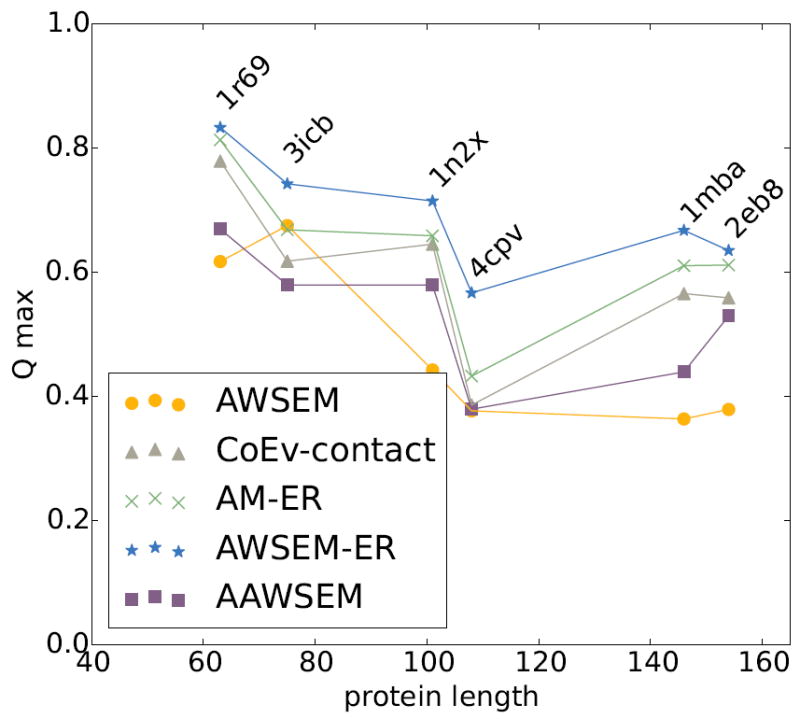
Comparison of the top predictions from each of the potentials in the study for panel 1 proteins, which have a large number of sequences available as input to coevolutionary analysis (N>5L). The maximum Q prediction out of 20 simulated annealing runs for each of the proteins in panel 1 is plotted for the AWSEM model (amber circles), the coevolutionary contact model (grey triangles), the AM-ER model (green Xs), the combined AWSEM-ER model (blue stars), and AAWSEM (purple squares). We see that in all cases the combined AWSEM-ER model yields the best prediction. The coevolutionary contact and AM-ER models also yield quite good predictions, aided by the abundance of homologous sequences available for these proteins.

Figure 2.

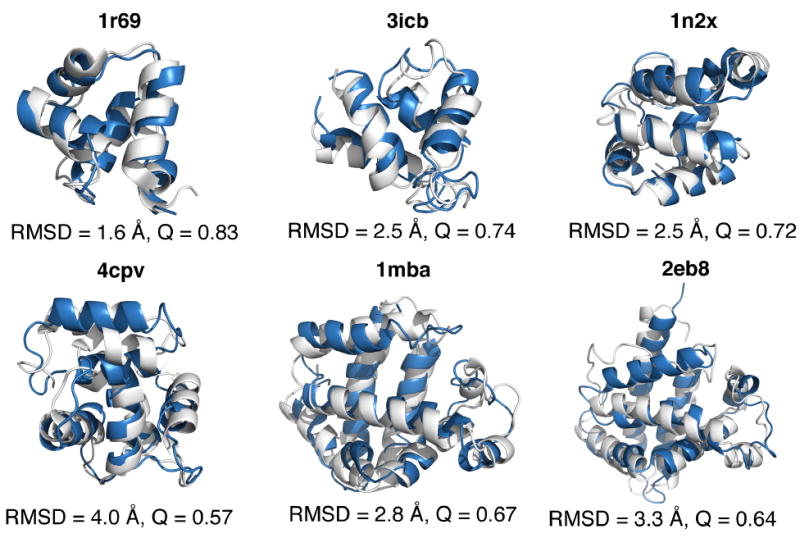
Structural comparison of experimental and predicted structures. The experimentally crystallized structures, shown in white, are aligned with the top predicted structures from the AWSEM-ER potential. The proteins contained in this panel all have a large number of homologous sequences available for the inference of coevolutionary information. Structural alignment was carried out using the TM-score algorithm and PyMOL[53] was used to visualize the structures.

For each of the proteins in the first panel, there is a large amount of sequence information available for the GREMLIN calculation (see Table 1). Figure 1 shows that the coevolutionary contact model by itself typically yields quite good tertiary structure predictions when many sequences are available. This is a testament to the accuracy of the inferred contacts from coevolution. For all of the proteins, the AM-ER model yields predictions better than does the pure coevolutionary contact model without the memory term, but these are worse than the predictions from the combined AWSEM-ER model. Of the proteins in panel 1, the coevolutionary contact potential performs the worst on 4cpv, with a best predicted structure that has Q~0.4. 4cpv happens to be a calcium-binding protein. The presence of the metal could have an effect on the prediction quality. We will discuss this point in detail later in the paper. As an additional measure of the structure prediction quality, we also applied the commonly used global distance test (GDT) and TM-Score measures to each of the top predictions (see supplementary information Figures S8, Figure S9, and Table S2).[50]

We compare the known structures and the predicted structures for each of the proteins in panel 1 in Figure 2. Figure 2 shows the top structure prediction result obtained by the AWSEM-ER potential (colored blue) aligned using with the crystal structure (shown in white). The structures in Figure 1 were aligned using the TM-score algorithm developed by Zhang.[50] For these α-helical proteins, we see the predictions from the AWSEM-ER potential are all quite good, yielding the correct topology and secondary structure for each protein. The proteins 3icb, 4cpv, and 1mba each contain ligands in the experimentally determined structure, which are lacking in our simulations. Some of the discrepancies between the predicted and crystal structures are doubtless caused by the lack of explicit ligands in the AWSEM-ER model, an issue that we will discuss in more detail in the Results section.

To get an idea of the consistency of the structure prediction quality, we plot the maximum Q value that is achieved during each of the 20 annealing runs for each of the potentials in Figure S10. We find that all four potentials yield consistent predictions for this panel of proteins. It appears that adding evolutionary information to AWSEM does help improve the consistency of the predicted structures for some proteins, as in the case of 3icb.

Figure 3 summarizes the structure prediction results for the second panel of proteins where there are less sequence input data than was available for the first panel of proteins. This second panel of proteins all have fewer than 5L sequences available as input for the GREMLIN calculation, where L is the length of the protein in amino acids. When there are fewer sequences available for the coevolutionary inference, the predictions of contacts become less reliable. For this second panel of proteins, the coevolutionary contact model by itself yields the worst predictions of the different algorithms, with the best Q value across all proteins being only 0.45. This is still a useful level of prediction. It is clear, however, that the accuracy of the coevolutionary contact prediction directly affects the structure prediction capability of both the coevolutionary contact and AM-ER potentials. To quantify the prediction quality of the GREMLIN predicted contacts, we compute their precision relative to the contacts of experimentally determined structure. The precision values for each of the contact predictions are shown in Table 1. The consistency of the predictions for proteins in panel 2 can be observed in Figure S11.

Figure 3.

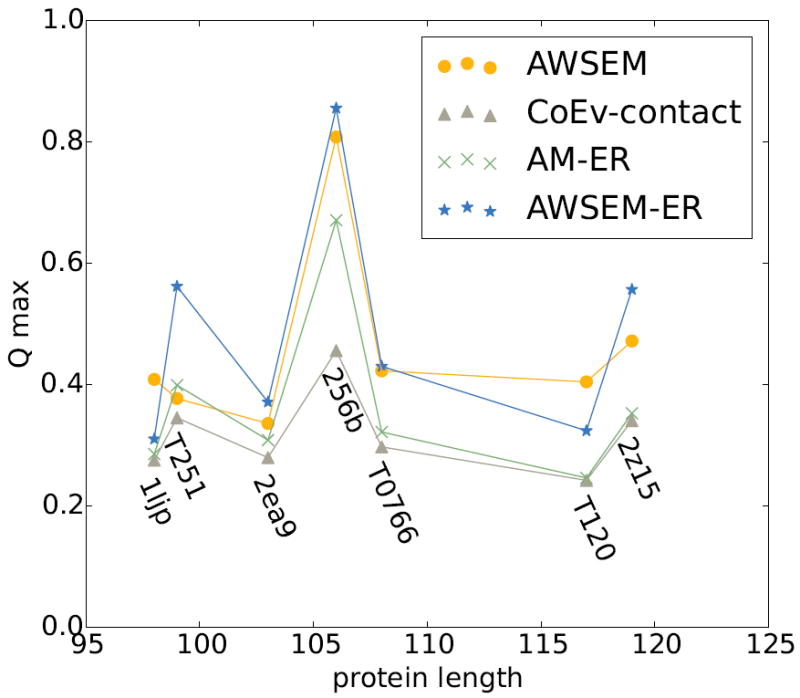
Comparison of the top predictions from each of the potentials in the study for panel 2 proteins, which have a lower number of sequences available as input to coevolutionary analysis (N<5L). The maximum Q prediction out of 20 simulated annealing runs for each of the proteins in panel 2 is plotted for the AWSEM model (amber circles), the coevolutionary contact model (grey triangles), the AM-ER model (green Xs), the combined AWSEM-ER model (blue stars). The coevolutionary contact model yields the worst predictions when there are not a sufficient number of homologous sequences. Using AWSEM-ER improves upon the coevolutionary contact model predictions for each of the proteins. We note that, unlike the situation for the targets where a large number of sequences are available as input to the coevolutionary contact inference, in a few of these cases (1ljp and T120), the performance of the AWSEM-ER model is slightly worse than that for the pure AWSEM model.

Nevertheless, we might ask, “Does including coevolutionary information in the combined AWSEM-ER model help even when the predicted contacts are more sparse and less reliable on their own?” For this second panel of proteins, where there are fewer sequences available for contact prediction, the combined AWSEM-ER potential still yields the best predictions for many proteins. For proteins T251, 2ea9, 256b, and 2z15, adding the coevolutionary information to the pure AWSEM homologues excluded prediction makes the structures more native-like, improving the Q value by about ~0.1 for T251 and 2z15. There are, however, two examples where adding coevolutionary information to AWSEM actually hurts the predictions slightly. These are 1ljp and T120. For 1ljp and T120, the AWSEM potential by itself yields the best predictions, but the inclusion of coevolutionary information into AWSEM only decreases the structure prediction quality, Q, by about 0.05. Of the proteins in this study, T120 and 1ljp have the least reliable evolutionary information. Therefore, the poor prediction quality from the purely evolutionarily based model may not be surprising.

We visualize the prediction quality of the top structures obtained from the AWSEM-ER potential for the proteins from panel 2 in Figure 4 by aligning (via TM-score) the top predicted structure (shown in blue) with the experimentally determined structure (shown in white). The predictions of T251, 256b, and 2z15 are topologically correct, although there are some deviations in the secondary structure relative to the experimental structure. Adding evolutionary information to AWSEM yields a much better prediction for T251 than AWSEM or AAWSEM.[26] The structure for T0766 is largely correct except for the fact that one of the α-helices is not fully formed and one of the β-strands is not fully formed. For 1ljp, 2ea9, and T120, clear deviations from the experimental structures can be observed. T120 exists naturally as an oligomer and it is possible that it is unstable as an individual monomer, as we have simulated them in this study. Experiments also suggest that 1ljp can form a homodimeric interface, which could have an effect on the structure prediction quality.[51]

Figure 4.

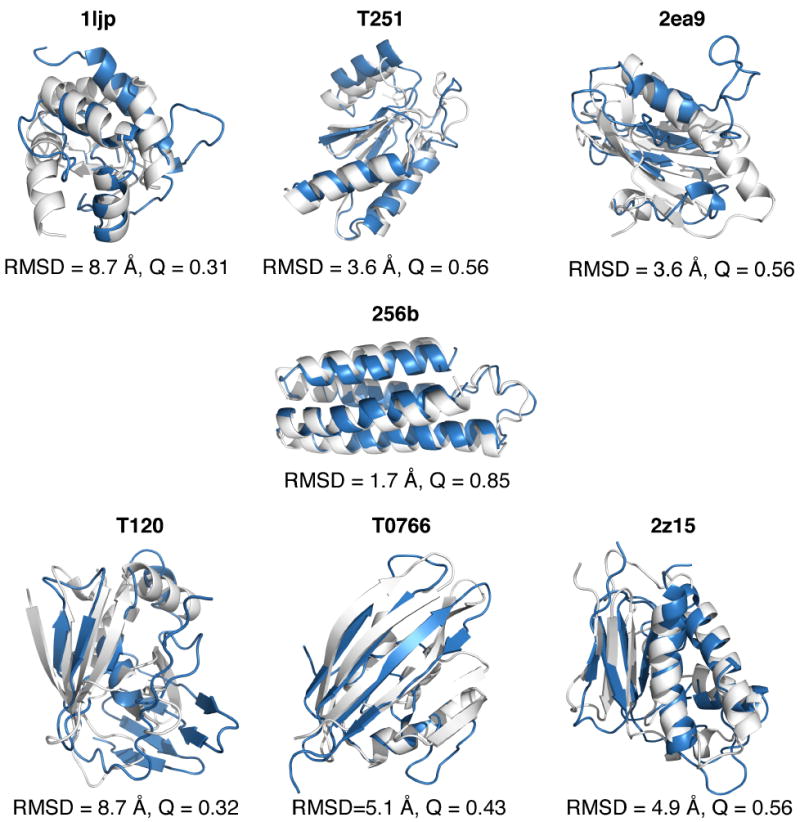
Structural comparison of experimental and predicted structures for panel 2 proteins. The experimentally determined structures, shown in white, are aligned with the top predicted structures from the AWSEM-ER potential, shown in blue. The predictions for this panel of proteins are less native-like than those of panel 1, partly due to the lack of homologous sequences available for the proteins. Structural alignment was carried out using the TM-score algorithm and PyMOL[53] was used to visualize the structures.

From the point of view of someone who is trying to use coevolutionary information alone to predict structures of proteins in the “coevolutionary twilight zone”, the AWSEM-ER results in Figure 3 results are quite encouraging. Without exception, mixing AWSEM with the coevolutionary contact term improves the results of the structure prediction compared to using the coevolutionary contact term alone. In other words, supplementing coevolutionary contact-based structure prediction methods with a physically-motivated transferrable potential seems to be a robust way of improving prediction for targets with relatively few sequences available. Recently, deep learning has been used to combine coevolutionary predictions with other protein features to yield accurate protein contact predictions. Figures S12 and S13 show the result of leveraging contact predictions provided by “ultra-deep learning”[52] as input for the V_ER term of the AWSEM-ER model. The structure prediction results on the second panel of proteins using AWSEM-ER are dramatically improved when using contacts predicted from a method that combines multiple inputs, compared to using contacts inferred from purely coevolutionary methods such as GREMLIN.

3.2 Free energy analysis

As shown in Figures 1-4, adding evolutionary information to AWSEM generally results in more accurate structure prediction. To gain a better understanding of the way in which the coevolutionary information enhances the quality of prediction, we carried out free energy profile analyses for several of the proteins (Figure 5). We chose to carry out free energy analyses on four proteins, each from a different regime of performances: (1) 1r69 for which the coevolutionary contact model by itself yields a somewhat better prediction than the usual AWSEM, (2) 256b, for which AWSEM yields a better prediction than the coevolutionary contact model, (3) 4cpv for which AWSEM and the pure coevolutionary contact model yield about the same prediction quality, and (4) 1ljp which is one of the few cases where adding coevolutionary information results in a worse prediction than was obtained by AWSEM alone. The free energy analyses show that adding coevolutionary information to AWSEM typically shifts the minimum in the free energy to more properly folded (higher Q) structures. For 1r69, 256b, and 4cpv, the combined AWSEM-ER potential is funneled to higher Q values than is seen for the AWSEM and coevolutionary contact potentials used by themselves. Interestingly, the landscape of the AM-ER model is funneled to the most native-like structure for 1r69 and 1ljp, although only slightly more than other models in both cases. In the case of 1ljp, for which adding coevolutionary information does not result in more accurate structure prediction, the free energy minimum of the AWSEM-ER potential occurs at a value of Q=0.27, while the minimum in the AWSEM potential occurs at a value of Q=0.3, and the minimum for the AM-ER model occurs at a value of Q=0.31.

Figure 5.

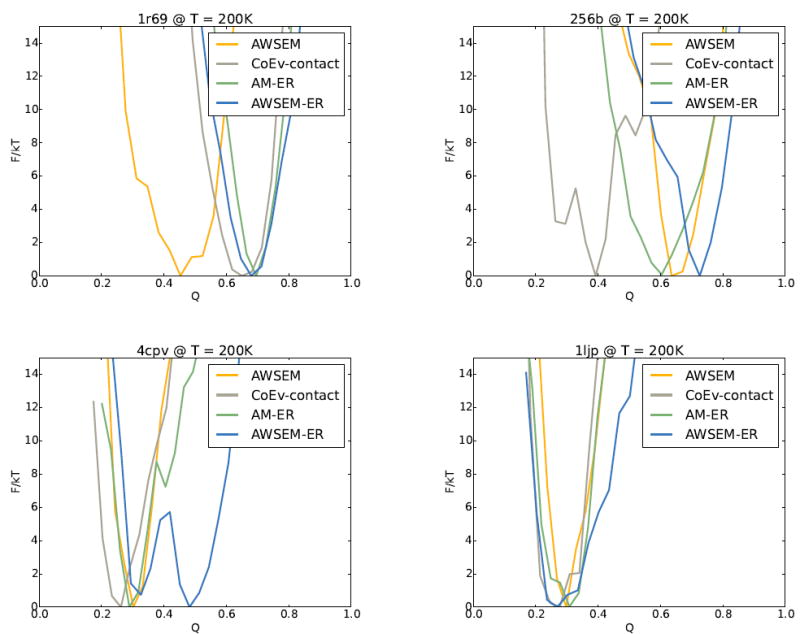
The free energy profiles for AWSEM, the coevolutionary contact model, the AM-ER model, and the combined AWSEM-ER models are shown for four different proteins. (a) For 1r69 the coevolutionary contact model, AM-ER, and AWSEM-ER yield better predictions than AWSEM alone due to being funneled to higher Q. (b) For 256b, AWSEM and AWSEM-ER yield better predictions than AM-ER and the coevolutionary contact model as the landscapes for AWSEM and AWSEM-ER are funneled to higher Q than those of AM-ER and the coevolutionary contact model. (c) For 4cpv, the profiles of AWSEM, AM-ER, and the coevolutionary contact model are funneled to a similar Q, while the combined AWSEM-ER potential contains an additional free energy basin at higher Q, leading to better predictions. (d) 1ljp is one of the few scenarios in which the AWSEM-ER model does not yield the best predictions. For 1ljp, none of the potentials do particularly well at predicting the structure.

To better understand the contribution of the evolutionary restraint term, V_ER, to the AWSEM-ER potential, we compute the expectation value of V_ER as a function of the nativeness of the protein, Q, as shown in Figure 6. When all the contacts included in the coevolutionary contact term turn out to be perfectly predicted native contacts, the landscape, not surprisingly, is perfectly funneled to the native structure. Several measures of the accuracy of the contact predictions from GREMLIN are given in Table 1. For 1r69, V_ER is strongly funneled to the folded state, which is expected due to the accurate prediction of contacts obtained from coevolution. The V_ER term for 256b also yields the lowest energy for the most folded structures, although it is not funneled as smoothly as the V_ER is for 1r69. The profile for 4cpv and 1ljp are funneled to Q values of 0.6 and 0.5, respectively, which is lower than for 1r69 due to GREMLIN incorrectly predicting some of the contacts. Note that for 1ljp the native-like structures (Q>0.6) are not well sampled, which is why the corresponding expected energy values are omitted from the plot.

Figure 6.

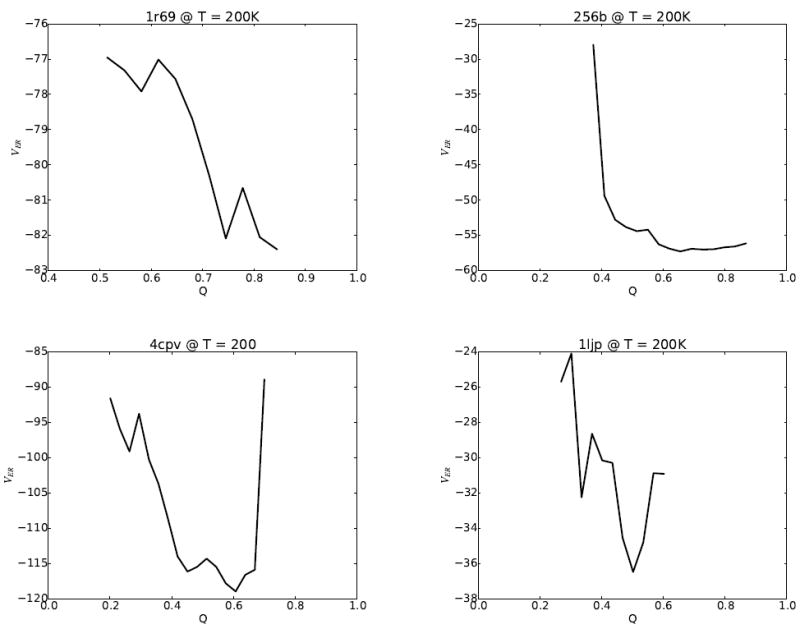
The expectation values of V_ER from the AWSEM-ER potential for (a) 1r69, (b) 256b, (c) 4cpv, and (d) 1ljp. The V_ER term is well funneled to native-like (high Q) structures for 1r69 and 256b. For 4cpv, V_ER has a minimum at a Q of 0.6. 1ljp, the worst predicted protein, has a minimum at Q=0.5 for the V_ER term, whereas the highest sampled Q during simulated annealing using the coevolutionary contact model is Q=0.3. A trap around Q=0.3 is evident in the expectation value of V_ER for 1ljp, which suggests that the relatively poor results achieved using simulated annealing may be due in part to poor sampling on a rugged energy landscape.

3.3 Correlation of potentials

The principle of minimal frustration predicts that native contacts are significantly stronger than random contacts that are formed in non-native collapsed states.[2] Optimizing a minimally frustrated transferable potential[43] and using native contacts predicted using information about residue covariation as input to a coevolutionary contact model are thus two complementary ways of approximating the energy function under which the sequences of natural proteins have been selected to fold and function. Therefore, despite the seemingly disparate philosophies of these approaches, we expect that the energies of these two models evaluated on the same set of structures should be correlated. A previous study showed a high degree of correlation between the energies obtained using the AWSEM potential and a coevolutionary potential for the case of 1r69.[27] We measured the correlation between the coevolutionary contact energy and the AWSEM potential for each of the proteins that was studied via free energy analysis. Both V_AWSEM and V_{CoEv–contact} were computed on the same set of thermally sampled structures. This set of structures was originally obtained via umbrella sampling at 350 K using the AWSEM-ER model. Figure 7 shows that the coevolutionary contact and AWSEM potentials are indeed highly correlated, particularly for proteins 1r69 and 256b, with correlation coefficients of r=0.800 and r=0.875, respectively. The correlation between the two potentials turns out not to be as strong for the protein 4cpv, where there is a correlation coefficient of only 0.449 between the potentials. It appears that a significant part of the discrepancy between the AWSEM and coevolutionary contact potentials for 4cpv arises from a cluster of low Q structures that has a much higher coevolutionary contact energy than do the other structures sampled. We tested this hypothesis by recomputing the correlation coefficient without the cluster of low Q data and found the r-value for 4cpv increased to 0.612 (Figure S14 in the supplementary information). To better understand the origins of the lack of strong correlation between AWSEM and coevolutionary contact potentials for 4cpv, we carried out a more detailed structural analysis.

Figure 7.

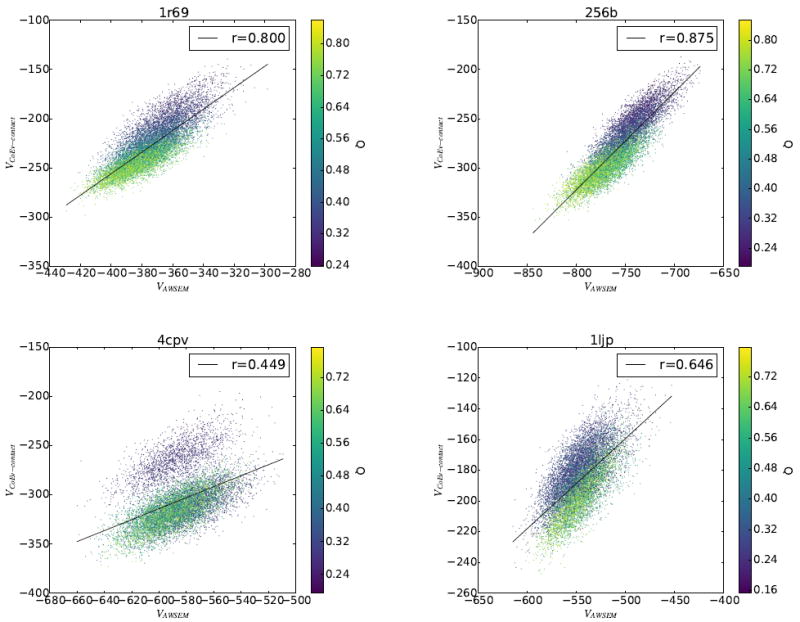
Correlation between V_AWSEM and V_{CoEv–contact} was measured for 1r69, 256b, 4cpv, and 1ljp. The set of structures on which the energies were calculated was generated using umbrella sampling of the combined AWSEM-ER potential.

3.4 Structural analysis of Calcium-liganded Carp Parvalbumin (4cpv) predictions

Figure 8 shows the top predicted structures for the protein 4cpv along with the corresponding contact maps that result from using the AWSEM and coevolutionary contact potentials individually. The top predicted structures from AWSEM by itself and the coevolutionary contact model look quite different. The structure obtained by using AWSEM is a compact structure with several of the helices out of place compared to the experimentally solved structure. The pure coevolutionary contact algorithm, on the other hand, predicts properly the region of the protein that surrounds the bound calcium ions, but misses nearly all of the contacts on the N-terminal end. The best predicted structure from the combined AWSEM-ER potential combines the best aspects of both of these predictions to yield the correct topology and secondary structure, with only minor deviations from the crystal structure. Free energy landscape analysis (shown in Figure 9) reveals there are two free energy basins at a Q of ~0.33, one that is more AWSEM-like at Q_CoEv = 0.53, and one that resembles the pure coevolutionary contact ensemble at Q_CoEv = 0.65. This suggests the two potentials combine in a complementary manner for 4cpv to yield the best overall prediction. Many proteins that bind ligands have different apo- and holo- forms of the protein, as we discuss for myoglobin below. Though the apo- form of 4cpv is currently unknown, it is possible that one of the basins resembles its apo- form. Representative structures from each of the basins of the free energy surface are shown in Figure 9. The coevolutionary contact ensemble is folded on the C-terminal end of the protein while remaining fairly extended on the N-terminal end of the protein. Looking at the predicted contacts for 4cpv shows that almost no contacts are predicted from the coevolutionary inference on the N-terminal half of the protein other than some that are local in sequence.

Figure 8.

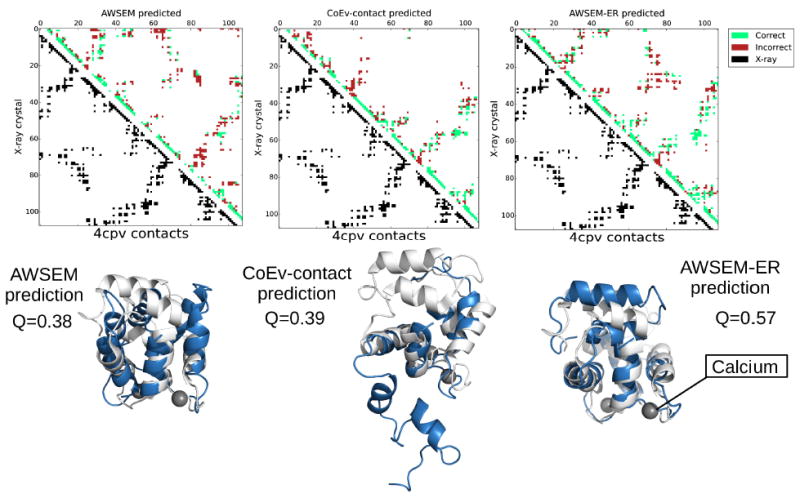
Contact maps and the corresponding structures for the max Q predictions for 4cpv from AWSEM, the coevolutionary contact model, and AWSEM-ER potentials. The best predicted structures are shown in blue, while the experimentally determined structures are overlaid in white. The calcium ions present in the experimental structure are shown as grey spheres. The contact maps show the contacts present in the experimental structure in the lower left triangle in black and the contacts in the maximum Q structure obtained via simulated annealing in the upper right. Predicted contacts that are present in the crystal structure are shown in green, whereas predicted contacts that are not present in the experimental structure are shown in red. PyMOL[53] was employed to generate the structure images.

Figure 9.

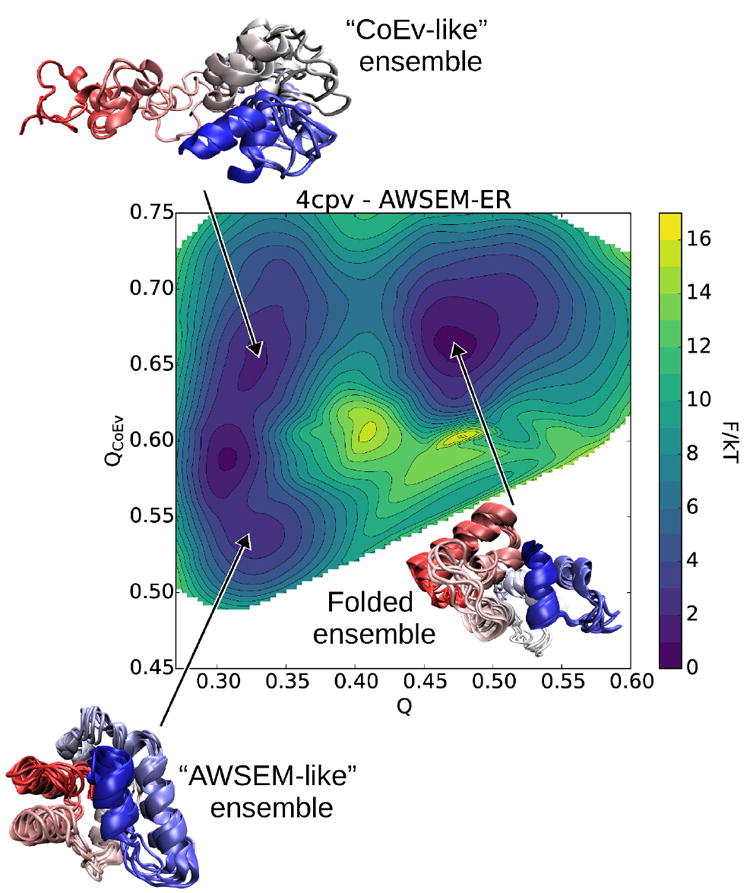
Two-dimensional free energy calculation for 4cpv using the AWSEM-ER potential. We see three basins: one ensemble contains structures more energetically favored by AWSEM, another ensemble of structures favored by the coevolutionary contact model, and the third basin corresponds to an ensemble of native-like folded structures predicted by AWSEM-ER. VMD[54] was employed to generate the structure images.

3.5 Structural analysis of myoglobin predictions

Like 4cpv, several other proteins in the present study have ligands bound in their experimentally determined structures. 3icb is a calcium binding protein. 256b and 1mba both have hemes bound within the natively folded protein. Neither the AWSEM nor the coevolutionary contact predicted potentials explicitly represent these bound ligands in the simulations used to find the structures. The lack of explicit ligand representation results in forming some additional contacts that are not found in the experimental holo structures. This over-collapse is especially clear for myoglobin (1mba). Figure 10 shows the top predictions from each of the protocols for myoglobin. In all cases, the top predictions for myoglobin are more compact than are the experimentally determined structures due to the absence of the heme, which sits between several hydrophobic helices in the crystal structure. For the AWSEM-ER prediction, the only real defects in the predicted structure are precisely these extra contacts that form which would be prevented by the intervening heme if it were in the model explicitly. These additional contacts are labeled as heme-mediated contacts in the contact maps in Figure 10. We also ran predictions on 2eb8, a Cu(II)(Sal-Phe) bound apo form of myoglobin for comparison. Because the sequence of 2eb8 is identical to holo forms of myoglobin, many of the family members that inform the contact prediction have hemes even though 2eb8 does not have a heme. The performance of AWSEM-ER for apo-myoglobin is similar to that for 1mba and, again, the deviation occurs in the area where the heme would be, as shown in Figure 11. In the apo-form, the helix that makes contact with the heme in myoglobin, however, becomes unstructured. The unstructured portion of apo-myoglobin is predicted to be helical both in the results from the pure coevolutionary contact model and from AWSEM-ER, presumably because most of the sequences used as input to the contact prediction contain a heme.

Figure 10.

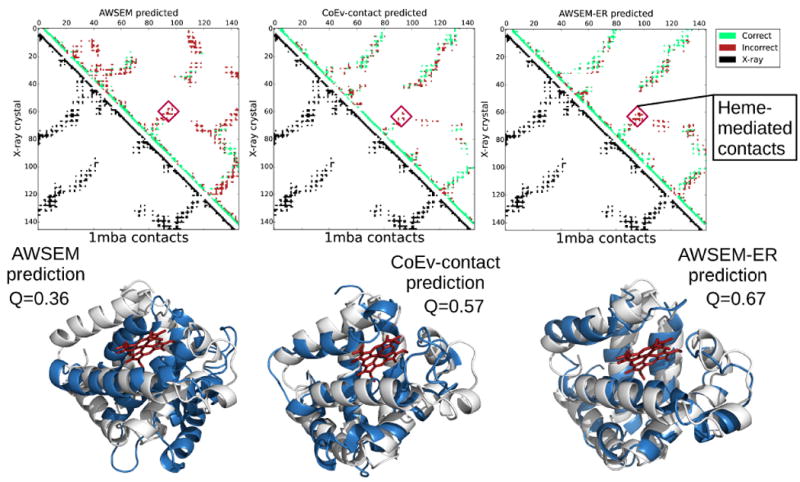
Contact maps and the corresponding structures for the max Q prediction of 1mba from AWSEM, the coevolutionary contact model, and AWSEM-ER potentials. The best predicted structures are shown in blue, while the experimentally determined structures are overlaid in white. The heme present in the experimental structure is shown in red. The contact maps show the contacts present in the experimental structure in the lower left triangle in black and the contacts in the maximum Q structure obtained via simulated annealing in the upper right. Predicted contacts that are present in the crystal structure are shown in green, whereas predicted contacts that are not present in the experimental structure are shown in red. Additional contacts that are formed due to the absence of heme in the simulations are labeled as heme-mediated contacts. PyMOL[53] was employed to generate the structure images.

Figure 11.

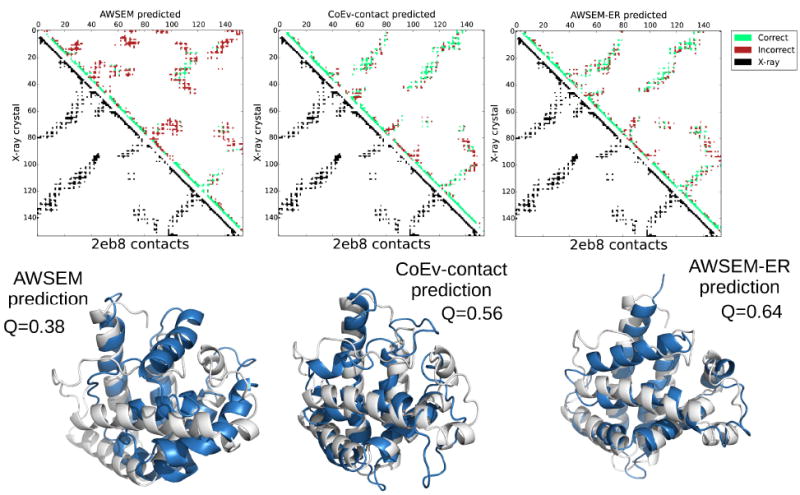
Contact maps and the corresponding structures for the max Q prediction of 2eb8 from AWSEM, the coevolutionary contact model, and AWSEM-ER potentials. The best predicted structures are shown in blue, while the experimentally determined structures are overlaid in white. The contact maps show the contacts present in the experimental structure in the lower left triangle in black and the contacts in the maximum Q structure obtained via simulated annealing in the upper right. Predicted contacts that are present in the crystal structure are shown in green, whereas predicted contacts that are not present in the experimental structure are shown in red. PyMOL[53] was employed to generate the structure images.

4 Conclusions

Adding coevolutionary information from families of proteins can strongly improve the structure prediction capabilities of AWSEM, which ordinarily only uses a single target sequence as input. It is important to emphasize that none of the algorithms surveyed in this study were in a mode that used any structural information from homologous proteins. (The only exception to this is in the supplementary information where we show results of including homologue input explicitly, for comparison. Using structural homologues in the fragment memory term gives results comparable to other schemes of homology modeling.[28]) Including evolutionary information in structure prediction is a powerful part of the protein structure prediction toolkit, especially when no structurally solved homologues can be recognized. The incorporation of coevolutionary information into the AWSEM model now opens the door to mechanistic studies of functional proteins that do not have experimentally solved structures and are too large to simulate on biological timescales with all-atom models.