Endocytosis as a stabilizing mechanism for tissue homeostasis

Significance

Many tissues in the body constantly turn over as cells divide and are replaced within weeks. Despite this turnover, tissues are able to keep proper ratios of their different cell types. How tissues attain this balance, called homeostasis, is unclear. Here we show that homeostasis can be achieved by circuits of cells that signal to each other using diffusible signals. A key negative feedback loop that stabilizes these circuits is endocytosis, a common feature of biological signaling in which a cell takes up and degrades the signal molecule that makes it divide and survive. Thus, the more of that cell type the less its numbers increase.

Abstract

Cells in tissues communicate by secreted growth factors (GF) and other signals. An important function of cell circuits is tissue homeostasis: maintaining proper balance between the amounts of different cell types. Homeostasis requires negative feedback on the GFs, to avoid a runaway situation in which cells stimulate each other and grow without control. Feedback can be obtained in at least two ways: endocytosis in which a cell removes its cognate GF by internalization and cross-inhibition in which a GF down-regulates the production of another GF. Here we ask whether there are design principles for cell circuits to achieve tissue homeostasis. We develop an analytically solvable framework for circuits with multiple cell types and find that feedback by endocytosis is far more robust to parameter variation and has faster responses than cross-inhibition. Endocytosis, which is found ubiquitously across tissues, can even provide homeostasis to three and four communicating cell types. These design principles form a conceptual basis for how tissues maintain a healthy balance of cell types and how balance may be disrupted in diseases such as degeneration and fibrosis.

Tissues are made of several types of cells, including organ-specific parenchymal cells, fibroblasts, macrophages, and endothelial cells. For optimal function, tissues must maintain proper ratios of these component cell types (1–3). In many tissues, cell-type proportions are kept constant despite the fact that cells continually turn over. This feature is called tissue homeostasis. In tissues such as liver and lung, homeostasis is often restored even after damage or perturbation (4–11). Loss of homeostasis is a basis for diseases: Loss of a cell type characterizes degenerative diseases, whereas hyperactivity of a cell type occurs in fibrosis.

Maintaining tissue homeostasis is challenging, because cells must control their proliferation rates and death/removal rates. If removal exceeds proliferation, cell numbers decline to zero. If proliferation exceeds removal, cell numbers increase until they reach a limiting factor (carrying capacity) which is defined either by extrinsic factors such as oxygen and nutrients or within tissues by spatial constrains (12–16). Therefore, cells must use control circuits to adjust their proliferation and removal to reach a constant concentration (17), especially for cell types such as macrophages that need to be maintained far below their carrying capacity in the tissue (Fig. 1 A and B). What these control circuits are and what design principles guide their structure are currently unclear.

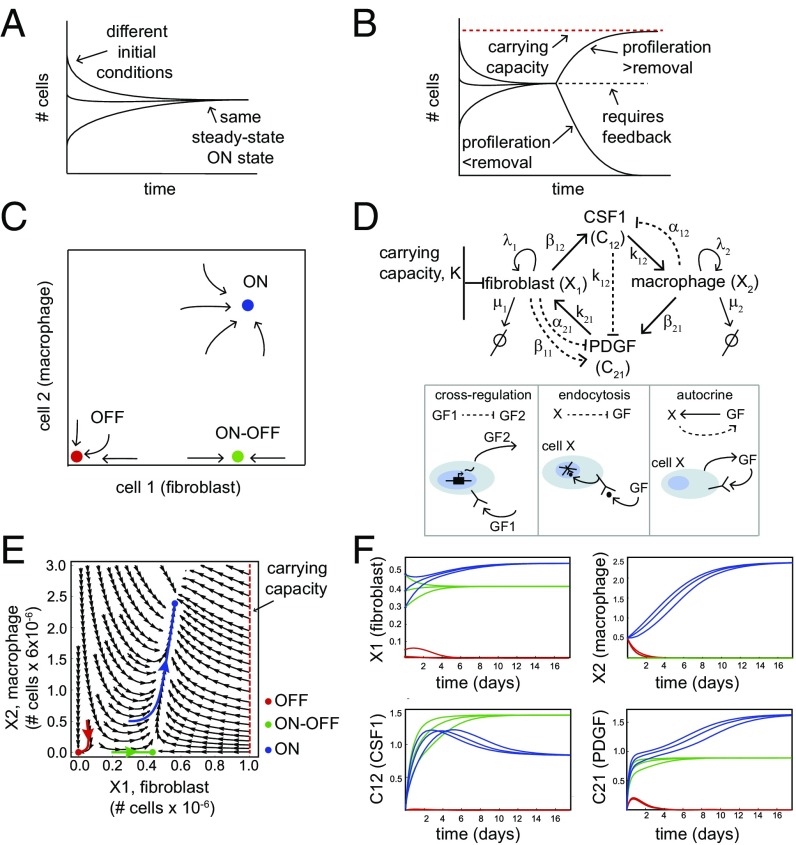
Fig. 1.

Homeostasis of cell numbers through circuits of communicating cells. (A) An ON state exists when cell numbers converge to the same steady-state concentration starting from a range of different initial conditions. (B) The ON state requires careful regulation, because if proliferation and removal rates are unequal cells rise to a high carrying capacity or decline to zero. (C) A schematic phase portrait of the FB–MP coculture experiment, showing its three fixed points: a stable OFF state (red), a stable ON state (blue), and an ON–OFF state (green). (D) The FB–MP circuit topology: CSF1 cross-inhibits PDGF gene expression, FB and MP endocytose their GFs, and FB secrete PDGF. (Lower) Description of the interactions in the circuits. (E) The phase portrait of the FB–MP circuit provided by the model of Eqs. 1–4, using the biologically plausible parameter values ${\stackrel{\sim }{\lambda }}_1=3.7,\hspace{0.17em}{\stackrel{\sim }{\lambda }}_2=2.2,\hspace{0.17em}\stackrel{\sim }{\mu }=1,\hspace{0.17em}{\stackrel{\sim }{\beta }}_{12}=3.4,\hspace{0.17em}{\stackrel{\sim }{\beta }}_{11}=6.8,\hspace{0.17em}\hspace{0.5em}\text{and}\hspace{0.17em}{\stackrel{\sim }{\alpha }}_{12}=10,\hspace{0.17em}{\stackrel{\sim }{\alpha }}_{21}=1$. The axes are dimensionless cell numbers, with conversion factors to cell numbers shown. Examples of trajectories that go to each fixed point are shown in color. (F) Dynamics of the cell and GF concentrations for the trajectories highlighted in E as well as two other trajectories for each fixed point.

Principles for cell number homeostasis were recently elucidated for a one-cell-type case, for CD4+ T cells (14, 18). The T cells show autocrine feedback control in which they secrete and sense the cytokine IL-2. Secrete-and-sense is a common signaling motif found also in bacteria and yeast (19–21). The effects of IL-2 are paradoxical, because it enhances both proliferation and death of the T cells. This control leads to a stable situation where a 30-fold range of initial T-cell concentrations converges over time to a steady-state concentration that varies less than twofold and lies far below the carrying capacity of the system. This fixed point is called a stable ON state [see also homeostasis in vivo (22, 23)]. The stable ON state is due to a dynamic balance between proliferation and death. The system also has another fixed point: Below a certain initial concentration of T cells the population decays to zero cells, converging to a stable OFF state (14, 18). A stable OFF state in addition to a stable ON state is a form of bistability (24–28). The OFF state may help to avoid unwanted fluctuations in which a small group of cells expands to give rise to a new tissue.

To approach the complexity of a multicell-type tissue there is need to explore circuits of more than one cell type. Unlike T cells, which secrete their own growth factors (GFs), in many tissues the GFs for each cell type are supplied by other cell types. To address this complexity in a controlled situation Zhou et al. (29) studied in detail an in vitro coculture of two cell types, fibroblasts (primary mouse embryonic fibroblasts, FB) and macrophages (bone-marrow-derived macrophages, MP) (29). Three key features were found by tracking cell dynamics at high resolution (Fig. 1C): (i) an ON state: A 2,500-fold range of initial FB and MP concentrations all converge within 14 d to steady-state concentrations that vary less than fourfold and maintain this steady state in a dynamic balance of proliferation and death, (ii) an OFF state: There is a range of low concentrations of MP and FB which decay to zero cells, and (iii) an ON–OFF state: FB above a certain concentration can grow without MP, indicating a third fixed point with only one cell type.

The coculture system defines a two-cell circuit in which cells communicate by GF secretion. The interactions in this circuit were mapped (29) (Fig. 1D). Each cell type secretes a GF required by the other cell type (FB require PDGF and MP require CSF1). Furthermore, CSF1 inhibits PDGF production in FB (cross-regulation), and both GFs are primarily removed by receptor binding and internalization (endocytosis). Finally, FB also have an autocrine loop where they secrete PDGF, thus allowing growth without MP (29).

These findings raise several questions. What is the feedback loop that leads to homeostasis? What other circuits are possible? Are there principles that can tell us which circuits and types of feedback are more functional than others? Given that real tissues are typically made of at least four cell types (parenchymal cells, macrophages, fibroblasts, and endothelial cells), can two-cell circuits be scaled up to provide homeostasis to more than two cell types?

To address these questions we study cell circuits theoretically by introducing an analytically solvable framework for a wide class of circuits, aiming to use the coculture circuit as a starting point to define principles for homeostatic circuits. We prove a design principle which is necessary for robust tissue homeostasis within our framework of circuits, namely that the GF for the cell far from carrying capacity must be down-regulated in a negative feedback loop. There are two possible mechanisms for this feedback. The first is by cross-inhibition through gene regulation, and the second is by receptor binding of the GF and internalization. The latter mechanism, known as endocytosis, occurs when cells internalize and degrade their cognate GFs by well-understood molecular mechanisms (30–34).

Endocytosis is ubiquitous in tissues and provides systems-level function to intracellular pathways (33, 35–38). There have been fewer studies addressing its computational/circuit role on the level of tissues. An elegant exception is a recent study on cytokine endocytosis that showed that the balance between diffusion and endocytosis-based consumption defines local cell neighborhoods of a specific size (39). We find here a key regulatory role for endocytosis: Feedback by endocytosis can provide tissue homeostasis and is faster and more robust than the alternative feedback mechanism of cross-inhibition by the other GF. We finally demonstrate that endocytosis in modular cell circuits can provide homeostasis to three and four cell types simultaneously.

Results

Model for the FB–MP Coculture Circuit Explains Observed Dynamics.

We begin by developing a model of the FB–MP circuit of Zhou et al. (29) to describe the in vitro dynamics of the two cell types. Each cell type secretes a GF that enhances the proliferation rate of the other cell type: FB cells ($X_1$) secrete CSF1 ($C_{12}$), and MP cells ($X_2$) secrete PDGF ($C_{21}$) (Fig. 1D). We exclude spatial distributions and instead use a well-mixed (or mean-field) approximation in which all cells see the same concentration of GFs. The model also neglects cell contact and chemotaxis effects.

The dynamics of the cells are therefore defined by equations in which cells can divide and are removed (e.g., by apoptosis) according to rates that are affected by the concentration of the secreted factors (Eqs. 1 and 2) (40, 41):

$$\frac{d{X}_1}{dt}=X_1\left({\lambda }_{1}h\left(C_{21}\right)\left(1-\frac{X_1}{K}\right)-{\mu }_1\right)$$ [1]

$$\frac{d{X}_2}{dt}=X_2\left({\lambda }_{2}h\left(C_{12}\right)-{\mu }_2\right).$$ [2]

Here ${\lambda }_i\hspace{0.5em}\text{and}\hspace{0.5em}{\mu }_i$ are the proliferation and removal rates of cell type $X_i$, respectively. $K$ is the carrying capacity at which proliferation rate of FB ($X_1$) drops to zero. We assume that $X_2<<K$, because macrophages were shown to be far below their carrying capacity in the coculture experiments (29). The effect of each GF on its target cell occurs by binding of the GF to its cognate receptor on the target cells, as described by Michaelis–Menten-like functions $h\left(C_{ij}\right)=C_{ij}/(C_{ij}+k_{ij})$ with halfway effect at $k_{ij}$.

The equations for the concentration of the GFs depend on their secretion rates by cells and on their removal rates (endocytosis, diffusion, and degradation). The equation for CSF1 ($C_{12}$) includes secretion by $X_1$ cells at rate ${\beta }_{12}$, endocytosis by $X_2$ cells at rate ${\alpha }_{12}$, and degradation/diffusion at rate $\gamma$:

$$\frac{d{C}_{12}}{dt}={\beta }_{12}{X}_1-{\alpha }_{12}{X}_{2}h\left(C_{12}\right)-\gamma C_{12}.$$ [3]

We assume here that endocytosis works with Michaelis–Menten kinetics with the same halfway point, $h\left(C_{ij}\right)$, as does the effect of $C_{ij}$ on their target cells in Eqs. 1 and 2. We use the same halfway point because both signaling and endocytosis depend on ligand binding to the cognate receptor. This use of the same function $h\left(C_{ij}\right)$ makes the analysis simpler. Relaxing this assumption, by using a different halfway point for internalization than for signaling, does not affect the conclusions (SI Methods).

The equation for the second GF, PDGF ($C_{21}$), is slightly more complicated because PDGF expression is inhibited by CSF1, and it is also produced by $X_1$ cells in an autocrine signaling loop at rate ${\beta }_{11}$ (Fig. 1D):

$$\frac{d{C}_{21}}{dt}={\beta }_{21}{X}_2\frac{k_{12}}{k_{12}+C_{12}}+{\beta }_{11}{X}_1-{\alpha }_{21}{X}_{1}h\left(C_{21}\right)-\gamma C_{21}.$$ [4]

Again, we use the same $k_{12}$ as for signaling and endocytosis, assuming that cross-regulation works through the same receptor signaling pathway.

These equations, together with the parameter values, define the dynamics of the FB–MP circuit (Fig. 1D). The equations have 13 parameters. We reduced this down to eight dimensionless parameter groups (Methods) using dimensional analysis. Biologically plausible values for the parameters are given in Tables 1 and 2.

Table 1.

Model parameters

Parameter	Biological meaning	Biologically plausible value	Source
${\lambda }_i$	Maximal proliferation rate of $X_i$ cells	$\sim$0.1 h−1	BNID 111159, 101560
${\mu }_i$	Removal rate of $X_i$ cells	10−2 to 5 × 10−2 h−1	BNID 101940 (40)
$K$	Carrying capacity of $X_1$ cells	∼10−3 cells per μm3	77
$k_{ij}$	Binding affinity ($K_{\text{d}}$) of growth factor $C_{ij}$	3 × 10−2 to 3 × 10−1 molecules per μm3	78, 79
${\beta }_{ij}$	Maximal secretion rate of growth factor $C_{ij}$ by $X_i$ cells	10 to 102 molecules per cell per minute	BNID 112718
${\alpha }_{ij}$	Maximal endocytosis rate of growth factor $C_{ij}$ by $X_j$ cells	102 to 103 molecules per cell per minute	(80) BNID 112725
$\gamma$	Degradation rate of growth factors	0.01 to 1 h−1	(29)

BNID, BioNumbers ID number.

Table 2.

Dimensionless model parameters

Dimensionless parameter	Definition	Biologically plausible range
${\stackrel{\sim }{\lambda }}_i$	${\lambda }_i/{\mu }_i$	$2\text{to}10$
$\stackrel{\sim }{\mu }$	${\mu }_2/{\mu }_1$	$\sim 1$
${\stackrel{\sim }{\beta }}_{12}$	${\beta }_{12}K/\gamma k_{12}$	${10}^{-1}\text{to}10$
${\stackrel{\sim }{\beta }}_{22}$	${\beta }_{22}{k}_{21}/{\beta }_{12}{k}_{12}$	${10}^{-2}\text{to}1$
${\stackrel{\sim }{\beta }}_{11}$	${\beta }_{11}K/\gamma k_{21}$	${10}^{-1}\text{to}10$
${\stackrel{\sim }{\alpha }}_{12}$	${\alpha }_{12}{k}_{21}/{\beta }_{21}{k}_{12}$	$1\text{to}{10}^2$
${\stackrel{\sim }{\alpha }}_{21}$	${\alpha }_{21}K/\gamma k_{21}$	$1\text{to}{10}^2$

We next asked whether the interactions captured by this model are sufficient for a stable steady state of cell numbers. To answer this, we use the fact that GF dynamics are faster (time scale of minutes to tens of minutes) than the dynamics of cell populations (time scale of days). We hence set GF equations (Eqs. 3 and 4) to quasi steady state by setting the temporal derivative to zero (we tested numerically that this is a good approximation for the dynamics; Fig. S1). As a result, GF concentrations are described by algebraic equations. Solving for the steady state of the GFs we end up with two rate equations for the cells.

We find that these equations describe the experimentally observed dynamics well with biologically plausible parameters (Tables 1 and 2). The phase portrait of the equations shows three fixed points (ON, OFF, and ON–OFF) (Fig. 1E). A wide range of initial cell concentrations converge to the same steady-state level—the ON state. There is also a basin of attraction to the OFF state, defined as the set of initial conditions that flow to zero cell concentrations. The green curves show that even without MP ($X_2$) FB ($X_1$) still reach a high steady-state level, the ON–OFF state (Fig. 1F).

The existence of three fixed points occurs for a wide range of model parameters. One can vary GF production rates ($\beta$) by 10-fold, endocytosis rates ($\alpha$) by 100-fold, and proliferation to removal ratios $\lambda /\mu$ by 10-fold without losing the ON state. At other values of the parameters one or two of the fixed points can be lost, leading to loss of one or both cell types regardless of initial conditions. These altered parameter sets thus provide phenotypes similar to degenerative diseases (42, 43).

An Analytical Framework for Two-Cell Circuit Topologies with Endocytosis and Cross-Regulation.

We next asked how unique the observed FB–MP circuit is in terms of its ability to maintain ON and OFF fixed points. To address this, we consider all possible two-cell circuit topologies which include the types of interactions seen in the coculture circuit. We use a mathematical screening approach that was pioneered in other contexts, such as to discover circuits for robust morphogenesis (44–50), exact adaptation (51, 52), ultrasensitivity (53), bistability (54), cell polarization (55, 56), and fold-change detection (57, 58). An advantage of the present analytically solvable framework is that we need not numerically scan different parameters, which would entail millions of numerical runs per topology; instead, we deduce the fixed point structure of the phase portrait analytically (58).

We considered all circuit topologies that differ from the circuit depicted in Fig. 1D by including or lacking the following interactions. (i) Each GF can be removed by endocytosis by the target cell type, or instead be removed primarily by degradation/diffusion. (ii) Each cell can secrete its own GF, forming an autocrine loop, or have no autocrine loop. (iii) Each GF can up- or down-regulate the production of the other GF, by activating or inhibiting gene expression, or have no such cross-regulation. Together, these possibilities make up 144 different topologies (Fig. S2) (Fig. 1D). The FB–MP circuit described above is one of these 144 possibilities.

The dynamics of each circuit are therefore defined by equations for cell dynamics which are the same as Eqs. 1 and 2. The equations for the concentration of the GFs are the same as Eqs. 3 and 4 except for allowing the cross-regulation terms to include up-regulation, down-regulation, or no interaction in any combination. All of these possibilities can be written in a single set of equations:

$$\frac{d{C}_{12}}{dt}={\beta }_{12}{X}_1\left(1-\frac{1}{2}\theta \left(1+\theta \right)+\theta h\left(C_{21}\right)\right)+{\beta }_{22}{X}_2-{\alpha }_{12}{X}_{2}h\left(C_{12}\right)-\gamma C_{12}$$ [5]

$$\frac{d{C}_{21}}{dt}={\beta }_{21}{X}_2\left(1-\frac{1}{2}\omega \left(1+\omega \right)+\omega h\left(C_{12}\right)\right)+{\beta }_{11}{X}_1-{\alpha }_{21}{X}_{1}h\left(C_{21}\right)-\gamma C_{21},$$ [6]

where the numbers $\theta \hspace{0.5em}\text{and}\hspace{0.5em}\omega$ are equal to 1, −1, or 0 to represent the sign of the interactions. $\theta \hspace{0.5em}\text{and}\hspace{0.5em}\omega =1$ represent activation [that is, $C_{ij}/(k_{ij}+C_{ij})$], $\theta \hspace{0.5em}\text{and}\hspace{0.5em}\omega =-1$ represent inhibition [namely, $k_{ij}/(k_{ij}+C_{ij})$], and $\theta \hspace{0.5em}\text{and}\hspace{0.5em}\omega =0$ correspond to no interaction. Each topology can further have ${\alpha }_{12}=0$ or ${\alpha }_{21}=0$, meaning that endocytosis of that GF is negligible compared with the removal by degradation/diffusion. Finally, circuits can have ${\beta }_{11}=0$ or ${\beta }_{22}=0$ representing no autocrine secretion. The FB–MP circuit, for example, has $\theta =0$, $\omega =-1$, ${\alpha }_{12},{\alpha }_{21}>0$, and ${\beta }_{22}=0$, ${\beta }_{11}>0$. Each of the 144 topologies has the same eight dimensionless parameter groups (Table 2) as the FB–MP circuit of Eqs. 1–4 (the FB–MP circuit has one of these groups equal to zero because ${\beta }_{22}=0$).

A Stable ON State Requires Down-Regulating the GF for the Cell That Is Far from Carrying Capacity.

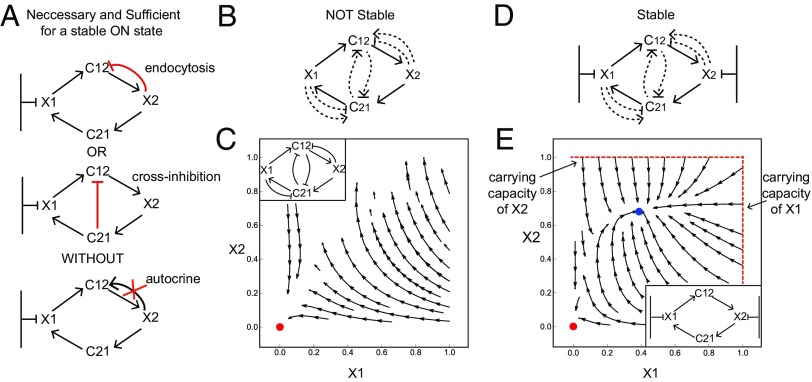
We asked which circuit topologies among the 144 can reach a robust steady state with a defined ratio of the two cell types (an ON state). We computed the steady states of the circuits by solving for the nullclines (${\dot{X}}_1,{\dot{X}}_2=0$) (59). By analytically solving the shape of the nullclines in each of the 144 circuits we find a necessary and sufficient condition for a circuit to have a stable ON state (at least for some parameter values; see SI Methods). This condition is that the GF ($C_{12}$) that drives the cell that is far from carrying capacity ($X_2$) must be down-regulated. Without this condition, the level of $X_2$ cells grows without bound (until reaching a high carrying capacity not specified in the model).

There are two ways that this down-regulation can occur. The first is endocytosis of $C_{12}$ by $X_2$ cells. The second is by cross-inhibition of $C_{12}$ production in $X_1$ cells by $C_{21}$. Furthermore, there must not be autocrine secretion of $C_{12}$ by $X_2$ cells, otherwise the ON state is unstable (in the case of $C_{21}$ cross-inhibiting $C_{12}$) or has a very small basin of attraction (in the case of endocytosis of $C_{12}$; see SI Methods) (Fig. 2A). This necessary and sufficient condition on the circuit topology is found in 48 of the 144 topologies.

Fig. 2.

A necessary and sufficient condition for a stable ON state in cell circuits. (A) The GF for the cell that is far from carrying capacity ($C_{12}$) must be inhibited either by endocytosis or by cross-regulation and must have no autocrine loop. (B) Circuits in which neither cell type is close to carrying capacity do not have a stable ON state. (C) Stream plot of one of the circuits in B shows that cell numbers either degenerate to zero (marked in red) or grow without bound. (D) Circuits in which both cells are close to carrying capacity are stable with no need for cross-regulation or feedback. (E) Stream plot of one of the circuits in D shows that even without regulation on the GFs cells reach either an OFF state (marked in red) or an ON state (marked in blue).

Importantly, we also screened two-cell circuits in which both cell types are far from carrying capacity (Fig. 2B). We find that none of the 144 possible circuits can show a stable ON state: Such circuits, modeled by deleting the carrying capacity term $K$ in Eq. 1, either degenerate to zero cells or show cell numbers that climb to infinity (and eventually reach some high, nonmodeled, limiting factor) (Fig. 2C). This statement, proved in SI Methods, will become relevant when we consider three- and four-cell circuits below. We also tested the case in which both cells have a carrying capacity (by different limiting factors); in this case regulation makes little difference, and both cell types can reach a stable ON state close to their carrying capacity even without down-regulating the GFs (Fig. 2 D and E).

Endocytosis Is Important for Resilient Circuits That Recover Quickly and Are Robust to Parameter Fluctuations.

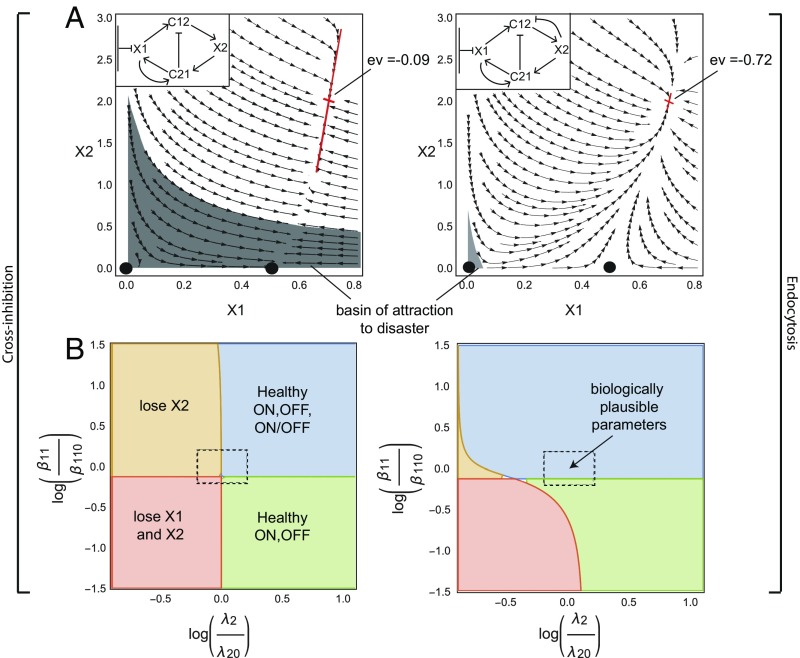
According to our design principle, homeostasis depends on negative feedback on $C_{12}$, either by endocytosis or cross-regulation. In the experimental FB–MP circuit, endocytosis seems to be the dominant mode of GF removal (29). One may ask why endocytosis is used to stabilize the circuit instead of cross-inhibition of $C_{12}$ by $C_{21}$.

To address this, we compare two circuits: the first has endocytosis of $C_{12}$ by $X_2$ (without cross-regulation between the GFs) and the second has no endocytosis but has cross-regulation in which $C_{21}$ down-regulates $C_{12}$ (Fig. 3A). To compare the circuits on equal footing we use mathematically controlled comparison (60). In this approach, one keeps equal as many internal parameters and external dynamical features of the circuits as possible.

Fig. 3.

Endocytosis is a more robust and rapid mechanism than cross-regulation for cell circuits to stabilize their ON state. (A) A mathematically controlled comparison of endocytosis and cross-inhibition mechanisms shows that endocytosis (Right) provides a smaller basin of attraction for losing one or both cell types (gray region). The endocytosis circuit also reaches the stable ON state eightfold faster, as indicated by its more negative Jacobian eigenvalue (ev) at the fixed point. (B) The circuit with endocytosis is more robust with respect to parameter variation than the circuit with cross-inhibition, in the sense that it is less prone to lose one or both cell types. The center of the dashed rectangle corresponds to parameter values of ${\stackrel{\sim }{\lambda }}_1=8,\hspace{0.17em}{\stackrel{\sim }{\lambda }}_2=8,\hspace{0.17em}\stackrel{\sim }{\mu }=1,\hspace{0.17em}{\stackrel{\sim }{\beta }}_{11}=4.4,\hspace{0.5em}\text{and}\hspace{0.17em}{\stackrel{\sim }{\alpha }}_{21}=15.0$. For the circuit with cross-inhibition (Left) ${\stackrel{\sim }{\beta }}_{12}=0.35\hspace{0.5em}\text{and}\hspace{0.17em}{\stackrel{\sim }{\alpha }}_{12}=0.001$. For the circuit with endocytosis (Right) ${\stackrel{\sim }{\beta }}_{12}=1.99\hspace{0.5em}\text{and}\hspace{0.17em}{\stackrel{\sim }{\alpha }}_{12}=5$. Axes are log relative variation from these parameters.

For a fair comparison we therefore demand that the concentrations of cells $X_1$ and $X_2$ and GFs $C_{12}$ and $C_{21}$ in the ON and ON–OFF states be the same between the two circuits. This equality can be achieved while demanding equal values of six out of the eight dimensionless parameters. The remaining two parameters must vary between the circuits, the endocytosis rate of $C_{12}$ ($a_{12}$) and the production rate of $C_{12}$ (${\beta }_{12}$), because these rates define the essential topological difference between the two circuits (Methods).

We plot the phase diagram for the two circuits for biologically plausible parameters (Tables 1 and 2) in Fig. 3A. We find that the circuit with cross-inhibition has a much larger basin of attraction for losing $X_2$ cells or both $X_1$ and $X_2$ cells (gray region in Fig. 3A). The circuit with endocytosis has a very small basin of attraction to the OFF state and a basin of attraction of area zero to the ON–OFF state, since adding even a small number of $X_2$ cells leads to the ON state.

In addition, we compared the response time of the two circuits to reach the ON state by computing the eigenvalues of the Jacobian at the ON state (Fig. 3A). We find that the circuit with endocytosis reaches the ON state about eightfold faster than the circuit with cross-inhibition.

We also tested the impact of changing the parameters on the existence of fixed points in the two circuits. Changing the biochemical parameters in the model can lead to losing either the ON state or the ON–OFF state, or both. Losing the ON state means that for every initial condition of $X_2$ we end up losing this cell type. We find that the circuit with endocytosis is more robust to fluctuation in parameters, whereas the circuit with cross-inhibition is closer in parameter space to losing $X_2$ or losing both cells (Fig. 3B and Fig. S4).

We conclude that endocytosis is a more robust and rapid regulatory mechanism than cross-inhibition for attaining a stable ON state.

Effects of Receptor Internalization, Down-Regulation, and Sensory Adaptation.

The model described so far (Eqs. 1–6) did not explicitly include the GF receptor dynamics. In this section we analyze the effects of considering the receptors explicitly.

We begin with the effect of negative feedback in which signal through the receptor causes a down-regulation of receptor expression (by transcriptional or posttranscriptional effects). Such negative feedback can in principle occur in GF signaling (61, 62). To model down-regulation we explicitly add an equation for the receptor in cell type $i$: $d{R}_i/dt={\beta }_{Ri}f\left(S\right)–{\alpha }_{Ri}{R}_i$, where the signal $S$ is due to Michaelis–Menten binding of the GF: $S=R_i{C}_{ji}/(k_{ji}+C_{ji})$ and $f\left(S\right)=k_S/(k_S+S)$ is a decreasing function causing the down-regulation. At large signal ($S>>k_S$), we find at steady state that $R_{i,st}$ decreases with GF as $R_{i,st}=\sqrt{{\beta }_{Ri}/({\alpha }_{Ri}{C}_{ji}/(k_{ji}+C_{ji}))}$. Plugging $R_{i,st}$ into the model equations, we find that all terms with $C_{ji}/(k_{ji}+C_{ji})$ need to be replaced with $\sqrt{C_{ji}/(k_{ji}+C_{ji})}$. The receptor parameters ${\beta }_{Ri}$ and ${\alpha }_{Ri}$ can be collapsed into the model parameters.

Simulating the dynamics results in very similar phase portraits of the original model (Fig. S5A). We conclude that negative feedback that works on receptor level does not make a significant difference, at least in the simple framework we consider here.

Next, we study the impact of endocytosis on receptor levels. Endocytosis, with receptor internalization and degradation, acts to reduce both GF and receptor levels. We model receptor dynamics in cell type $i$ as a balance between production, removal by endocytosis, and nonendocytosis removal:

$$\frac{d{R}_i}{dt}={\beta }_{Ri}-{\alpha }_{ji}\frac{C_{ji}}{k_{ji}+C_{ji}}{R}_i-{\alpha }_{Ri}{R}_i.$$ [7]

At steady state, receptor numbers decrease due to endocytosis: $R_{i,st}={\beta }_{Ri}/({\alpha }_{ji}\left(C_{ji}/k_{ji}+C_{ji}\right)+{\alpha }_{Ri})$. We next used this steady-state receptor level term in the equations for cell and GF dynamics. Thus, endocytosis rates of $C_{ji}$ and signaling rates due to $C_{ji}$ are multiplied by $R_{i,st}$ (SI Methods). This results in the same equations as before, but with renormalized parameters: Halfway binding coefficients $k_{ij}$ change to $k_{ij}{\alpha }_{Ri}/({\alpha }_{Ri}+{\alpha }_{ij})$ and secretion, endocytosis, and proliferation rates are multiplied by ${\beta }_{Ri}/({\alpha }_{Ri}+{\alpha }_{ij})$. Thus, the fixed-point structure of the model remains invariant (Fig. S5B). The renormalized parameter values, using typical receptor production and removal rates, result in minor changes to the biologically plausible parameter set (SI Methods).

We also considered the effect of exact sensory adaptation on the receptor (e.g., by covalent modification). We analyzed two models for sensory adaptation (52, 63), an incoherent feedforward loop (I1FFL) (64) and an integral feedback loop (65). In these models, the receptor signaling output $S\left(t\right)$ adapts precisely to a set-point $S_0$ for any constant level of input GF, $C_{st}$. At first sight, exact adaptation abrogates the effect of the circuit (within our separation of timescale approach in which cell dynamics is much slower than GF dynamics) because the GF concentration is at steady state and its level no longer affects the cell’s proliferation rates.

However, analysis shows that these adaptation circuits cannot adapt exactly when the input $C_{ij}\left(t\right)$ rises exponentially (exponential ramp) (66). This exponential rise occurs when the cells that secrete $C_{ij}$ grow exponentially, $X_i\sim e^{r_{i}t}$. The result is a steady-state level of signaling that depends on the exponential growth rate of the cells, $S=f\left(r_i\right)$.

Analyzing this situation shows that exact adaptation cannot support an ON stable state when one cell is far from carrying capacity. The reason is that the cell with carrying capacity stops growing when it reaches its carrying capacity. Hence, its growth rate $r_i$ drops to zero and can no longer pull the adapting circuit away from its steady-state output. As a result, there is no feedback on the cell far from carrying capacity to avoid instability. Thus, we predict that the cell away from carrying capacity must not have exact adaptation in the receptor signaling for its cognate GF.

The Two-Cell Circuits Can Scale Up to Form a Modular Circuit for Homeostasis of a Tissue with Three and Four Cell Types.

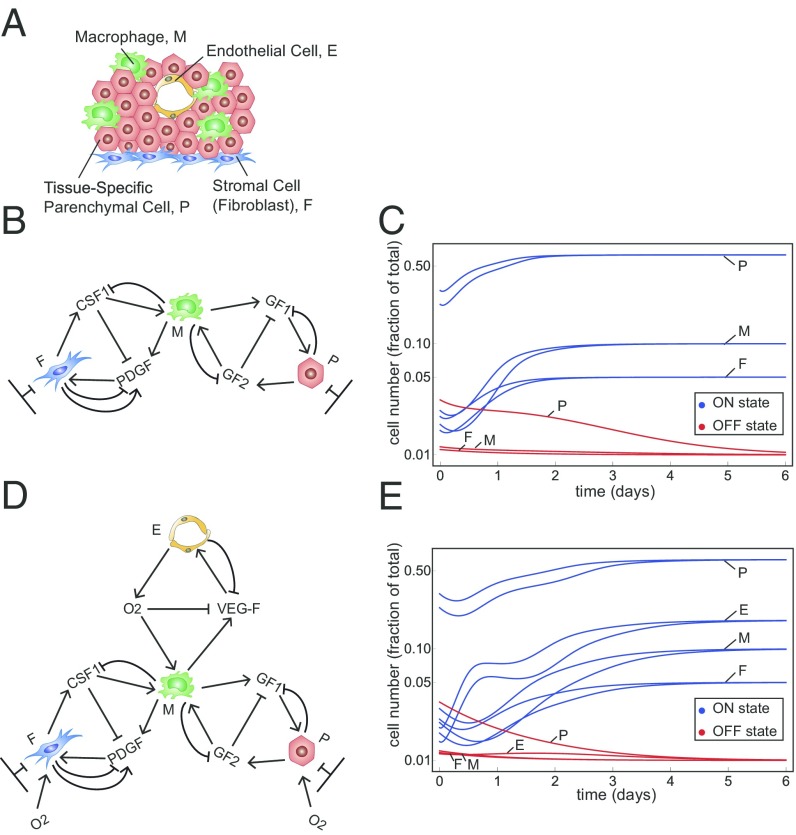
We finally consider a tissue made of more than two cell types. We consider, for example, a tissue made of four types of cells: parenchymal cells, macrophages, fibroblasts, and endothelial cells (Fig. 4A) or a set of three of these cell types (Fig. 4 B and D). These cells communicate by secreted GFs (or, in the case of endothelium, by oxygen). The number of possible circuit topologies increases rapidly with the number of cell types. There are $\sim {10}^{12}$ ways to connect three cell types using the present class of circuit topologies, and $\sim {10}^{24}$ different ways for four cell types (Methods). An exhaustive screen is therefore unfeasible. Even counting only cell circuits made of modules, each with a two-cell circuit topology, results in $\sim {10}^6$ different circuit topologies for three cells types and $\sim {10}^{12}$ for four cell types (Methods).

Fig. 4.

The two-cell circuits can scale up to form a modular, bistable circuit made of three and four cell types. (A) A typical tissue unit made of parenchymal cells, macrophages, fibroblasts, and endothelial cells. (B) A three-cell circuit topology made of modules of the observed two-cell circuit topology. Fibroblasts (F) and parenchymal cells (P) have a carrying capacity, whereas macrophages (M) are far from carrying capacity. In this circuit, macrophages integrate the responses of the other two cell types. (C) Dynamics of cell numbers show that all cell types converge to an ON steady state from a wide range of initial conditions (blue curves). For initial cell numbers below a threshold cells decline to zero (OFF state, red lines). The parameters used are ${\stackrel{\sim }{\beta }}_{12}={\stackrel{\sim }{\beta }}_{23}={\stackrel{\sim }{\beta }}_{32}=10,\hspace{0.17em}{\stackrel{\sim }{\beta }}_{11}=5,\hspace{0.17em}{\stackrel{\sim }{\alpha }}_{12}={\stackrel{\sim }{\alpha }}_{21}={\stackrel{\sim }{\alpha }}_{23}={\stackrel{\sim }{\alpha }}_{32}=10,\text{and}\hspace{0.17em}{\lambda }_1={\lambda }_2={\lambda }_3=10$. (D) A four-cell circuit topology made of modules of the observed two-cell circuit topology with endothelial cells (E) that are far from carrying capacity. (E) The same as in C with the parameters ${\stackrel{\sim }{\beta }}_{12}={\stackrel{\sim }{\beta }}_{23}={\stackrel{\sim }{\beta }}_{32}={\stackrel{\sim }{\beta }}_{24}={\stackrel{\sim }{\beta }}_4=10,\hspace{0.17em}{\stackrel{\sim }{\beta }}_{11}=5,\hspace{0.17em}{\stackrel{\sim }{\alpha }}_{12}={\stackrel{\sim }{\alpha }}_{21}={\stackrel{\sim }{\alpha }}_{23}={\stackrel{\sim }{\alpha }}_{32}={\stackrel{\sim }{\alpha }}_{24}={\stackrel{\sim }{\alpha }}_4=10,\hspace{0.17em}\text{and}{\lambda }_1={\lambda }_2={\lambda }_3={\lambda }_4=10$.

As an alternative to a full screen we take the more modest aim of providing a proof of principle for the possibility of homeostasis by plausible three- and four-cell circuits. For this purpose we study a three-cell circuit made of modules, each with the two-cell circuit topology analyzed above (Fig. 4B).

In this three-cell circuit model (Methods) fibroblasts and parenchymal cells are close to their carrying capacity, whereas macrophages are far below carrying capacity. Macrophages secrete GFs for the other two cell types. Fibroblasts and parenchymal cells communicate with macrophages using the same two-cell circuit design observed in the FB–MP circuit (Fig. 4B). We find that this three-cell circuit shows a stable ON state, in which cells converge to steady-state cell numbers from a wide range of initial conditions. Below a threshold number of cells, the circuit reaches an OFF state, in which all cells flow to zero (Fig. 4C). The ON state has a large basin of attraction and a wide range of feasible parameters (each parameter can be changed by at least 10-fold around a reference set of plausible parameters and still maintain stability).

We next study a four-cell circuit with endothelial cells which are far below carrying capacity (Methods). Endothelial cells supply oxygen to all other cell types which down-regulates the production rate of VEGF by macrophages (67) (Fig. 4D). We find that this four-cell circuit is also stable, showing stable ON and OFF states (Fig. 4E).

Interestingly, the present four-cell circuit has one module that is inherently unstable on its own. This is the module made of two cell types that are both far from carrying capacity—endothelial cells and macrophages. Such a circuit cannot show an ON state in isolation: Cell numbers either degenerate to zero or increase to infinity. This module, however, is stabilized and shows a stable ON state in the presence of the other two cell types.

In Fig. S6 we show several other three-cell and four-cell circuit topologies that have robust homeostasis. For example, homeostasis can be achieved by a minimal circuit with only two endocytosis interactions (Fig. S6 A, B, and D). This raises interesting questions about design principles for three-cell and four-cell circuits. Based on a numerical test of several hundred three-cell and four-cell circuits we hypothesize the following generalization of the present two-cell circuit principle: A necessary condition of a stable ON state is that for each cell type far from carrying capacity at least one of its GFs must be down-regulated (by endocytosis or cross-regulation).

Discussion

We present a mathematical framework for cell circuits that robustly reach homeostasis by means of communication by secreted GFs. When both cells are close to carrying capacity, an ON steady state can be reached without regulation. When neither has a carrying capacity regulation cannot achieve an ON steady state. When one cell type has a carrying capacity we find a necessary condition for reaching homeostasis in this class of circuits: The GF for the cell type that is far from carrying capacity must be down-regulated. There are two ways of implementing this condition: endocytosis or inhibitory cross-regulation by the other GF. We find that endocytosis is a more robust and rapid mechanism than cross-regulation for cell circuits to stabilize their ON state. Finally, we show that endocytosis can provide robust homeostasis to more than two cell types and we model a tissue made of four types of cells: parenchymal cells, fibroblasts, macrophages, and endothelial cells.

Endocytosis in cell circuits provides negative feedback control because a cell removes its own GF. If endocytosis is the dominant mode of GF removal, compared with GF degradation, it can provide robust homeostasis. Endocytosis enables circuits to recover faster from perturbations and be more robust to parameter fluctuations than cross-regulation. An intuitive reason for the advantages of endocytosis is that endocytosis allows cells to directly control the level of their own GFs, without being dependent on other cell types to sense the GFs they secrete. If there is a fluctuation of too many $X_2$ cells they endocytose and remove more $C_{12}$, leading to lower $X_2$ proliferation and to stabilization back to the fixed point.

The need to provide homeostasis and at the same time to avoid disease leads to an interesting tradeoff. Cell circuits with both ON and OFF states show a tradeoff between the sizes of the basin of attraction to these fixed points. A large basin of attraction for the ON state of the tissue is important to ensure recovery from injury or inflammation, whereas a large basin of attraction to the OFF state is important for the prevention of spurious tissue growth from a few cells. Here, we showed that endocytosis provides a large basin of attraction for the ON state compared with cross-inhibition.

We also analyzed additional modes of receptor-based negative feedback. We find that receptor down-regulation and receptor internalization by endocytosis do not have a sizable effect on the dynamics. Exact sensory adaptation can abolish the circuit function, because it makes the cells insensitive to the level of GF. We predict therefore that the cell far from carrying capacity must not have exact adaptation for its cognate GF.

One may ask why cells in tissues secrete GFs for the other cell types, instead of a design in which cells do not cross-communicate but instead have autocrine circuits that keep each cell type in homeostasis as in the T-cell/IL2 system, or fibroblasts in the Zhou et al. (29) system. We believe that communication via GFs across cell types may offer advantages: Macrophages cannot proliferate on their own but require the other cell type (fibroblasts), preventing unwanted growth of a single cell type outside of a tissue context. Moreover, GFs can signal the need for function from other cell types, as when macrophages (as well as other cell types) sense a lack of oxygen and signal this to endothelial cells using VEGF (67).

The cell circuits presented here may be useful in recovery from situations that perturb cell number ratios, such as inflammation. During inflammation, macrophage number rises significantly (68), thus disrupting the balance between cell types in the tissue. Homeostatic cell circuits may help cells to restore balance after inflammation. The present approach may also help to understand certain disease states, such as degeneration and fibrosis, as states of “bad” parameters or initial conditions, or loss of a necessary regulation. For example, the OFF state can result in loss of all cell types reminiscent of degeneration. In addition, changing the biochemical parameters in our model can lead to a state in which one of the cell types is lost (e.g., macrophages), leading to an excess of the other cell type (fibroblasts), which may lead to overactive ECM production characteristic of fibrosis.

We also considered homeostasis of three and four cell types, which is a model for typical tissues. We find that negative feedback by endocytosis in a modular circuit can provide homeostasis to three and four cell types. Future work can scan additional multicell circuits, although a complete survey is challenging due to their very large number. One possible way forward is to use the assumption that natural circuits can show the property of modularity. Scanning three- and four-cell circuits made from modules of two cell types may make the computational scan more feasible. Such modularity seems to commonly occur on different levels of biological organization and can arise based on natural selection for modular goals (69–72).

Future work can address issues of spatial heterogeneity, chemotaxis, cell contact, and other interactions found in natural tissues. It would be interesting to test whether endocytosis feedback mechanisms are important for homeostasis in stable tissues (tissues where parenchymal cells self-renew) such as liver, kidney, and pancreas in vivo. The role of endocytosis in keeping homeostasis of cell numbers can be tested using synthetic cell circuits or bioengineered tissues, which may demonstrate the differences between cross-inhibition and endocytosis (73–75). Future work can also address tissues in which stem cells renew some of the cell types. As molecular information accumulates on cell communication in tissues we hope that the present framework can help to provide meaning to molecular interactions such as endocytosis within a systems-level context.

Methods

Dimensional Analysis of the Two-Cell Circuit Model.

We start with the model for the two-cell circuits in our screen:

$$\dot{X_1}=X_1\left({\lambda }_{1}h\left(C_{21}\right)\left(1-\frac{X_1}{K}\right)-{\mu }_1\right)$$ [8]

$$\dot{X_2}=X_2\left({\lambda }_{2}h\left(C_{12}\right)-{\mu }_2\right)$$ [9]

$$\dot{C_{12}}={\beta }_{12}{X}_1\left(1-\frac{1}{2}\theta \left(1+\theta \right)+\theta h\left(C_{21}\right)\right)+{\beta }_{22}{X}_2-{\alpha }_{12}{X}_{2}h\left(C_{12}\right)-\gamma C_{12}$$ [10]

$$\dot{C_{21}}={\beta }_{21}{X}_2\left(1-\frac{1}{2}\omega \left(1+\omega \right)+\omega h\left(C_{12}\right)\right)+{\beta }_{11}{X}_1-{\alpha }_{21}{X}_{1}h\left(C_{21}\right)-\gamma C_{21}.$$ [11]

According to Buckingham’s pi theorem (76), there should be eight dimensionless parameter groups for these equations. We accordingly define dimensionless variables ${\stackrel{\sim }{X}}_1=X_1/K,\hspace{0.17em}{\stackrel{\sim }{X}}_2={\beta }_{21}/\gamma k_{21}{X}_2,\hspace{0.17em}{\stackrel{\sim }{C}}_{12}=C_{12}/k_{12},\hspace{0.17em}{\stackrel{\sim }{C}}_{21}=C_{21}/k_{21},\hspace{0.5em}\text{and}\hspace{0.5em}\hspace{0.17em}\stackrel{\sim }{t}={\mu }_{1}t$ and obtain differential equations for the dimensionless variables (for convenience we do not keep the ∼ sign):

$$\dot{X_1}=X_1\left(\frac{{\lambda }_1}{{\mu }_1}h\left(C_{21}\right)\left(1-X_1\right)-1\right)$$ [12]

$$\dot{X_2}=X_2\frac{{\mu }_2}{{\mu }_1}\left(\frac{{\lambda }_2}{{\mu }_2}h\left(C_{12}\right)-1\right)$$ [13]

$$\frac{{\mu }_1}{\gamma }\dot{C_{12}}=\frac{{\beta }_{12}K}{\gamma k_{12}}{X}_1\left(1-\frac{1}{2}\theta \left(1+\theta \right)+\theta h\left(C_{21}\right)\right)+\frac{{\beta }_{22}{k}_{21}}{{\beta }_{21}{k}_{12}}{X}_2-\frac{{\alpha }_{12}{k}_{21}}{k_{12}{\beta }_{21}}{X}_{2}h\left(C_{12}\right)-C_{12}$$ [14]

$$\frac{{\mu }_1}{\gamma }\dot{C_{21}}=X_2\left(1-\frac{1}{2}\omega \left(1+\omega \right)+\omega h\left(C_{12}\right)\right)+\frac{{\beta }_{11}K}{\gamma k_{21}}{X}_1-\frac{{\alpha }_{21}K}{\gamma k_{21}}{X}_{1}h\left(C_{21}\right)-C_{21}.$$ [15]

Here $h\left(C_{ij}\right)=C_{ij}/1+C_{ij}$. Since ${\mu }_1\ll \gamma$, we can set time derivatives in Eqs. 14 and 15 to zero. Defining dimensionless parameters, ${\stackrel{\sim }{\lambda }}_1={\lambda }_1/{\mu }_1,\hspace{0.17em}{\stackrel{\sim }{\lambda }}_2={\lambda }_2/{\mu }_2,\hspace{0.17em}\stackrel{\sim }{\mu }={\mu }_2/{\mu }_1,\hspace{0.17em}{\stackrel{\sim }{\beta }}_{12}={\beta }_{12}K/\gamma k_{12},\hspace{0.17em}{\stackrel{\sim }{\beta }}_{22}={\beta }_{22}{k}_{21}/{\beta }_{21}{k}_{12},\hspace{0.17em}{\stackrel{\sim }{\beta }}_{11}={\beta }_{11}K/\gamma k_{21},\hspace{0.17em}{\stackrel{\sim }{\alpha }}_{12}={\alpha }_{12}{k}_{21}/{\beta }_{21}{k}_{12},\text{and}\hspace{0.17em}{\stackrel{\sim }{\alpha }}_{21}={\alpha }_{21}K/\gamma k_{21}$, we obtain the dimensionless model (for convenience we do not keep the ∼ sign):

$$\dot{X_1}=X_1\left({\lambda }_{1}h\left(C_{21}\right)\left(1-X_1\right)-1\right)$$ [16]

$$\dot{X_2}=\mu \hspace{0.17em}{X}_2\left({\lambda }_{2}h\left(C_{12}\right)-1\right)$$ [17]

$$0={\beta }_{12}{X}_1\left(1-\frac{1}{2}\theta \left(1+\theta \right)+\theta h\left(C_{21}\right)\right)+{\beta }_{22}{X}_2-{\alpha }_{12}{X}_{2}h\left(C_{12}\right)-C_{12}$$ [18]

$$0=X_2\left(1-\frac{1}{2}\omega \left(1+\omega \right)+\omega h\left(C_{12}\right)\right)+{\beta }_{11}{X}_1-{\alpha }_{21}{X}_{1}h\left(C_{21}\right)-C_{21}.$$ [19]

The dimensionless model (Eqs. 16–19) has eight dimensionless parameters. Note that the proliferation to removal ratios obey ${\lambda }_1,{\lambda }_2>1$, otherwise there is no solution for a positive fixed point for the cells, and they only decay to zero. The FB–MP circuit is given by setting $\theta =0,\omega =-1,{\beta }_{22}=0$.

Derivation of the Nullclines.

The steady states of Eqs. 16 and 17 are (assuming positive cell numbers $X_1,X_2>0$)

$$C_{12,st}=\frac{1}{{\lambda }_2-1}$$ [20]

$$C_{21,st}=\frac{1}{{\lambda }_1\left(1-X_1\right)-1}.$$ [21]

Note that for the steady state of $C_{21}$to be positive (Eq. 21), $X_1$ must be below its carrying capacity: $X_1<1-1/{\lambda }_1$. When ${\lambda }_1>>1$, $X_1$ is bounded by its carrying capacity.

Substituting these GF steady states (Eqs. 20 and 21) in Eqs. 18 and 19 yields equations for the cell nullclines:

$$0={\beta }_{12}{X}_1\left(1-\frac{1}{2}\theta \left(1+\theta \right)+\frac{\theta }{{\lambda }_1\left(1-X_1\right)}\right)+{\beta }_{22}{X}_2-\frac{{\alpha }_{12}}{{\lambda }_2}{X}_2-\frac{1}{{\lambda }_2-1}$$ [22]

$$0=X_2\left(1-\frac{\omega }{2{\lambda }_2}({\lambda }_2\left(\omega +1\right)-2)\right)+{\beta }_{11}{X}_1-\frac{{\alpha }_{21}{X}_1}{{\lambda }_1(1-X_1)}-\frac{1}{{\lambda }_1\left(1-X_1\right)-1}.$$ [23]

Solving each of Eqs. 22 and 23 for $X_2\left(X_1\right)$ yields the two nullclines:

$$X_2=\frac{{\lambda }_2}{{\alpha }_{12}-{\lambda }_2{\beta }_{22}}(\frac{1}{1-{\lambda }_2}+X_1(1-\frac{\theta }{2}\left(1+\theta \right)+\frac{\theta }{{\lambda }_1\left(1-X_1\right)}){\beta }_{12})$$ [24]

$$X_2=\frac{2{\lambda }_2(X_1{\alpha }_{21}+{\lambda }_1^2{\left(-1+X_1\right)}^2{X}_1{\beta }_{11}+{\lambda }_1(-1+X_1)(1+X_1({\alpha }_{21}+{\beta }_{11})))}{{\lambda }_1(-2\omega +{\lambda }_2(-2+\omega +{\omega }^2))(1+{\lambda }_1(-1+X_1))(-1+X_1)}.$$ [25]

The points $(X_1,X_2)$ that solve Eqs. 24 and 25 (intersection of the nullclines) are the fixed points of the system. Note that also the lines $X_1=0,X_2=0$ are nullclines that intersect at the zero fixed point, $X_1,X_2=0$.

Mathematically Controlled Comparison Between Two Circuits.

To compare the two circuits in a mathematically controlled way, we assume the two circuits have the same fixed points, and we solve the steady-state equations (Eqs. 16–19) for the parameters instead of the cells and GFs. We denote the ON-state level of cells and GFs by $X_{i,h},C_{ij,h}$. Substituting this steady state in Eqs. 16–19, we get

$$0={\lambda }_{1}h\left(C_{21,h}\right)\left(1-X_{1,h}\right)-1$$ [26]

$$0={\lambda }_{2}h\left(C_{12,h}\right)-1$$ [27]

$$0={\beta }_{12}{X}_{1,h}\left(1-\frac{1}{2}\theta \left(1+\theta \right)+\theta h\left(C_{21,h}\right)\right)+{\beta }_{22}{X}_{2,h}-{\alpha }_{12}{X}_{2,h}h\left(C_{12,h}\right)-C_{12,h}$$ [28]

$$0=X_{2,h}\left(1-\frac{1}{2}\omega \left(1+\omega \right)+\omega h\left(C_{12,h}\right)\right)+{\beta }_{11}{X}_{1,h}-{\alpha }_{21}{X}_{1,h}h\left(C_{21,h}\right)-C_{21,h}.$$ [29]

For the ON–OFF we have $X_1=X_{1,l},X_2=0,C_{ij}=C_{ij,l}$. Since the ON–OFF state is also a fixed point, we can use it as well in the steady-state equations:

$$0={\lambda }_{1}h\left(C_{21,l}\right)\left(1-X_{1,l}\right)-1$$ [30]

$$0={\beta }_{12}{X}_{1,l}\left(1-\frac{1}{2}\theta \left(1+\theta \right)+\theta h\left(C_{21,l}\right)\right)-C_{12,l}$$ [31]

$$0={\beta }_{11}{X}_{1,l}-{\alpha }_{21}{X}_{1,l}h\left(C_{21,l}\right)-C_{21,l}.$$ [32]

Solving Eqs. 26, 27, and 30 for the GF fixed points and substituting them in Eqs. 28, 29, 31, and 32 we end up with four equations that depend on the parameters and $C_{12,l}$. We can solve these four equations for four different parameters. We chose to solve for ${\beta }_{11},{\beta }_{12},{\alpha }_{21},c_{12,l}$:

$${\beta }_{11}=\frac{1}{2X_{1,h}}\left(\frac{-2+2\left(-1+X_{1,h}\right)\left(-1+X_{1,l}\right){\lambda }_1}{X_{1,l}\left(1+\left(-1+X_{1,h}\right){\lambda }_1\right)\left(1+\left(-1+X_{1,l}\right){\lambda }_1\right)}+\frac{\left(-1+X_{1,h}\right)X_{2,h}\left(-2\omega +{\lambda }_2\left(-2+\omega +{\omega }^2\right)\right)}{\left(X_{1,h}-X_{1,l}\right){\lambda }_2}\right)$$ [33]

$${\beta }_{12}=\frac{2\left(1-X_{1,h}\right){\lambda }_1({\lambda }_2+X_{2,h}(-1+{\lambda }_2)({\alpha }_{12}-{\beta }_{22}{\lambda }_2))}{X_{1,h}\left(2\theta +\left(-1+X_{1,h}\right)\left(-2+\theta +{\theta }^2\right){\lambda }_1\right)\left(-1+{\lambda }_2\right){\lambda }_2}$$ [34]

$${\alpha }_{21}=\frac{\left(-1+X_{1,h}\right)\left(-1+X_{1,l}\right){\lambda }_1(-\frac{X_{1,h}}{1+\left(-1+X_{1,l}\right){\lambda }_1}+X_{1,l}(\frac{1}{1+\left(-1+X_{1,h}\right){\lambda }_1}+X_{2,h}(1-\frac{\omega (-2+{\lambda }_2+{\lambda }_2\omega )}{2{\lambda }_2})))}{X_{1,h}(X_{1,h}-X_{1,l})X_{1,l}}$$ [35]

$$C_{12,l}=\frac{(-1+X_{1,h})X_{1,l}(2\theta +\left(-1+X_{1,l}\right)\left(-2+\theta +{\theta }^2\right){\lambda }_1)({\lambda }_2+X_{2,h}(-1+{\lambda }_2)({\alpha }_{12}-{\beta }_{22}{\lambda }_2))}{X_{1,h}\left(-1+X_{1,l}\right)\left(2\theta +\left(-1+X_{1,h}\right)\left(-2+\theta +{\theta }^2\right){\lambda }_1\right)\left(-1+{\lambda }_2\right){\lambda }_2}.$$ [36]

Note that the only parameters that depend on the endocytosis rate of $C_{12}$, ${\alpha }_{12}$, are $C_{12,l}$ and ${\beta }_{12}$. Therefore, for comparing a circuit with negative regulation of $C_{12}$ but no endocytosis to a circuit with endocytosis, we can keep six of the parameters (${\lambda }_1,{\lambda }_2,\mu ,{\beta }_{11},{\beta }_{22},\text{and}{\alpha }_{21}$) and the fixed points ($x_{i,h},x_{i,l},c_{ij,h},\text{and}{c}_{21,l}$) the same between the two circuits and change only two parameters (${\alpha }_{12}\text{and}{\beta }_{12}$), and the ON–OFF fixed point of $C_{12}$ ($C_{12,l}$).

Counting More than Two Cell Circuits.

To estimate the amount of different three-cell circuits and four-cell circuits we count circuits with the maximal number of secreted GFs. For three cells, each cell can secrete at most two GFs for all two other cell types. Therefore, there are at most six GFs. Each GF can either be secreted in an autocrine signaling by its target cell or not ($2^6$), and can be either endocytosed by its target cell or not ($2^6$). In addition, each GF can be up- or down-regulated by all other two GFs for the cell type that secretes it or not [${\left(3^3\right)}^6$]. Together, all combination of these interactions results in $\sim {10}^{12}$. Following the same calculation for four cells, there are $2^{12}{2}^{12}{\left(3^3\right)}^{12}\sim {10}^{24}$ possible four-cell circuits.

In modular three-cell circuits each GF can be affected only by the GF secreted in the same two-cell circuit module. Therefore, for a three-cell circuit with six GFs (composed of three two-cell modules) there are ${144}^3\sim {10}^6$ different circuit topologies. For four-cell circuits there are ${144}^6\sim {10}^{12}$ different modular circuit topologies.

Model for a Stable Three-Cell Circuit.

The following Eqs. 37–43 describe the three-cell circuit (Fig. 4B):

$$\dot{C_{12}}={\beta }_{12}{X}_1-{\alpha }_{12}{X}_2\frac{C_{12}}{1+C_{12}}-C_{12}$$ [37]

$$\dot{C_{21}}=\frac{1}{1+C_{12}}{X}_2+{\beta }_{11}{X}_1-{\alpha }_{21}{X}_1\frac{C_{21}}{1+C_{21}}-C_{21}$$ [38]

$$\dot{C_{23}}={\beta }_{23}\frac{1}{1+C_{32}}{X}_2-{\alpha }_{23}{X}_3\frac{C_{23}}{1+C_{23}}-C_{23}$$ [39]

$$\dot{C_{32}}={\beta }_{32}{X}_3-{\alpha }_{32}{X}_2\frac{C_{32}}{1+C_{32}}-C_{32}$$ [40]

$$\dot{X_1}=X_1\left({\lambda }_1\frac{C_{21}}{1+C_{21}}\left(1-X_1\right)-1\right)$$ [41]

$$\dot{X_2}=X_2\left({\lambda }_2\frac{C_{12}}{1+C_{12}}\frac{C_{32}}{1+C_{32}}-1\right)$$ [42]

$$\dot{X_3}=X_3\left({\lambda }_3\frac{C_{23}}{1+C_{23}}\left(1-X_3\right)-1\right).$$ [43]

Model for a Stable Four-Cell Circuit.

The following Eqs. 44–53 describe the four-cell circuit (Fig. 4D):

$$\dot{C_{12}}={\beta }_{12}{X}_1-{\alpha }_{12}{X}_2\frac{C_{12}}{1+C_{12}}-C_{12}$$ [44]

$$\dot{C_{21}}=\frac{1}{1+C_{12}}{X}_2+{\beta }_{11}{X}_1-{\alpha }_{21}{X}_1\frac{C_{21}}{1+C_{21}}-C_{21}$$ [45]

$$\dot{C_{23}}={\beta }_{23}\frac{1}{1+C_{32}}{X}_2-{\alpha }_{23}{X}_3\frac{C_{23}}{1+C_{23}}-C_{23}$$ [46]

$$\dot{C_{32}}={\beta }_{32}{X}_3-{\alpha }_{32}{X}_2\frac{C_{32}}{1+C_{32}}-C_{32}$$ [47]

$$\dot{C_4}={\beta }_4{X}_4-{\alpha }_4\left(X_1+X_2+X_3\right)\frac{C_4}{1+C_4}-C_4$$ [48]

$$\dot{C_{24}}={\beta }_{24}\frac{1}{1+C_4}{X}_2-{\alpha }_{24}{X}_4\frac{C_{24}}{1+C_{24}}-C_{24}$$ [49]

$$\dot{X_1}=X_1\left({\lambda }_1\frac{C_{21}}{1+C_{21}}\frac{C_4}{1+C_4}\left(1-X_1\right)-1\right)$$ [50]

$$\dot{X_2}=X_2\left({\lambda }_2\frac{C_{12}}{1+C_{12}}\frac{C_{32}}{1+C_{32}}\frac{C_4}{1+C_4}-1\right)$$ [51]

$$\dot{X_3}=X_3\left({\lambda }_3\frac{C_{23}}{1+C_{23}}\frac{C_4}{1+C_4}\left(1-X_3\right)-1\right)$$ [52]

$$\dot{X_4}=X_4\left({\lambda }_4\frac{C_{24}}{1+C_{24}}-1\right).$$ [53]