Diverse Sensitivity Thresholds in Dynamic Signaling Responses by Social Amoebae

Abstract

The complex transition from a single-cell to a multicellular life form during the formation of a fruiting body by the amoeba Dictyostelium discoideum is accompanied by a pulsatile collective signaling process that instigates chemotaxis of the constituent cells. Although the cells used for the analysis of this phenomenon are normally genetically identical (isogenic), it is not clear whether they are equally responsive to the waves of the signaling stimulus, nor is it clear how responses across the population influence collective cell behavior. Here, we found that isogenic Dictyostelium cells displayed differing sensitivities to the chemoattractant cyclic adenosine monophosphate (cAMP). Furthermore, the resulting signaling responses could be explained by a model in which cells are refractory to further stimulation for 5 to 6 min after the initial input and the signaling output is amplified, with the amplification threshold varying across the cells in the population. This pathway structure could explain intracellular amplification of the chemoattractant gradient during cell migration. The new model predicts that diverse cell responsiveness can facilitate collective cell behavior, specifically due to the presence of a small number of cells in the population with increased responsiveness that aid in propagating the initial cAMP signaling wave across the cell population.

INTRODUCTION

Changes in environmental conditions, such as nutrient limitation, can trigger complex responses in living cells, including self-organization of individual cells into multicellular ensembles and organisms (1). Cell-cell communication that takes place during the conversion from individual to collective cell behavior frequently relies on chemotactic responses, as exemplified by the social amoeba Dictyostelium discoideum, which undergo a complex process of slug and fruiting body formation involving the creation of dynamically and spatially complex waves of the chemoattractant cyclic adenosine monophosphate (cAMP). Individual cells can both respond to and secrete cAMP in an oscillatory fashion, resulting in behaviors characterized by considerable complexity and spatial and temporal variability, even if the population consists of isogenic cells. Several decades of research have revealed many aspects of cell signaling correlated with chemotactic responses in D. discoideum and the similarity of these responses to those displayed by mammalian cells in many physiological (2, 3) and pathological (4–7) conditions. However, the research into chemotactic cell responses and the associated signaling has for the most part focused on representative cell behavior characteristic of the population average rather than the individual cell responses. It is still therefore largely unknown whether D. discoideum cells exposed to the same, albeit complex and quickly changing external inputs, would react in unison or display diversity in signaling and whether any such diversity would be of functional importance. Furthermore, given simple cAMP stimulation protocols (for example, step-like concentration increases) frequently used in the analysis of cell responses, our understanding of the dynamic response regulation remains incomplete, allowing for the existence of many alternative models of dynamics signaling responses that are consistent with the known behavior of this organism (8). We therefore set out to explore the dynamics and diversity of cell responses to a series of complex, time-varying inputs under well-controlled conditions.

RESULTS

To conveniently query cell responses to diverse signaling inputs, we developed and used a microfluidic function generator (fig. S1A). This device enables controlled, complex perturbations of the cellular microenvironment. In D. discoideum, the first step in activating the multiple signaling pathways involved in chemotaxis is the binding of cAMP to corresponding heterotrimeric guanosine triphosphate–binding protein (G protein)–coupled receptors (GPCRs) on the cell surface (9). The GPCRs remain uniformly distributed over the cell surface, and receptor occupancy mirrors the concentration of chemoattractant, displaying little amplification (10). However, various signaling processes downstream of GPCRs, notably activation of PI3K (phosphoinositide 3-kinase), can undergo transient activation followed by adaptation to persistent spatially homogeneous cAMP stimuli while displaying sharp persistent intracellular activity gradients in the presence of extracellular cAMP gradients, even if the gradients are very shallow. Although numerous studies have shown that cAMP induces PI3K activity, the kinetic response of individual cells to cAMP doses has rarely been measured (11, 12). In the initial analysis, we stimulated populations of developed D. discoideum cells with a spatially homogeneous step increase in cAMP and measured the resulting time course of PI3K activity, using the phosphatidylinositol 3,4,5-trisphosphate (PIP₃)–specific biosensor PHcrac- GFP [pleckstrin homology (PH) domain of the cytosolic regulator of adenylyl cyclase (crac) fused to green fluorescent protein (GFP)]. We specifically monitored the kinetics of the sensor translocation to the plasma membrane (determining the ratio, σ, of the membrane and cytosol GFP fluorescence intensities, normalized to the initial value) in response to cAMP stimuli spanning seven orders of magnitude, from 1 pM to 10 µM at 10°C (Fig. 1A and movies S1 to S4).

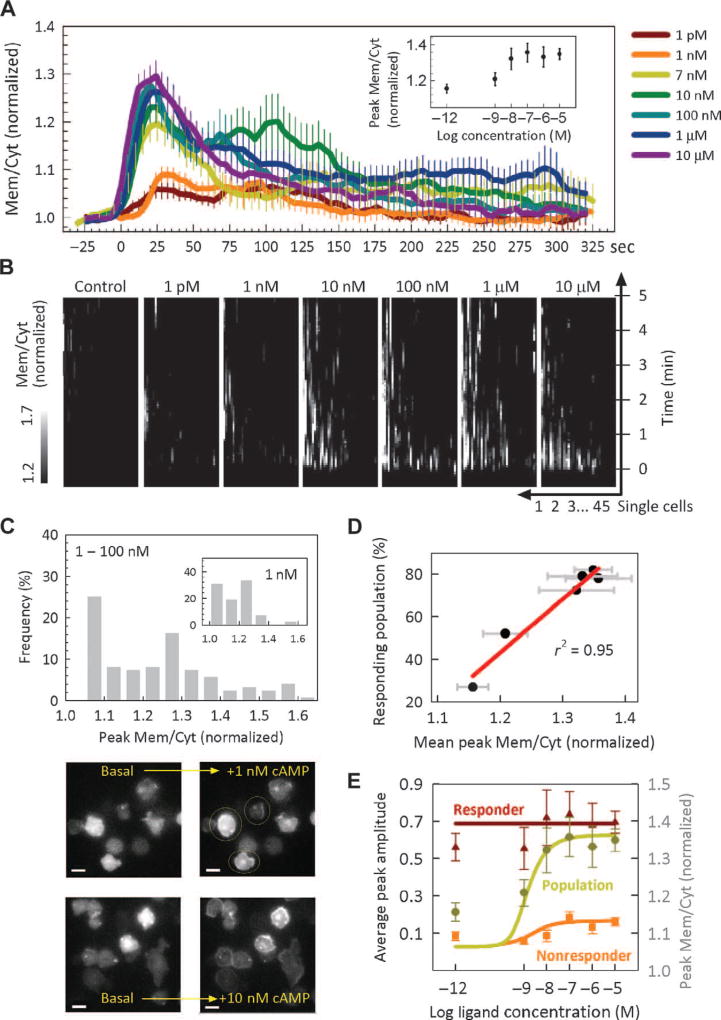
Fig. 1.

Translocation kinetics of PHcrac-GFP in response to single-step inputs of cAMP of various doses. (A) Population-averaged kinetics of PIP₃ translocation [expressed as the normalized ratio of the membrane (Mem) and cytosolic (Cyt) fluorescence signals, σ] in response to a step input of the indicated doses of cAMP. Inset: Dose-response curve of PIP₃ translocation. Error bars denote SEM. (B) Kymographs of 315 individual cell responses versus time for six different cAMP doses and unstimulated control (45 cells per condition). The intensity of cell responses is indicated by grayscale color variations. The x axes denote arbitrary numberings of the individual cells. (C) Top: histogram of the peak responses to a step input of cAMP for the indicated doses, with the histogram for 1 nM shown in the inset. Bottom: sample images of PHcrac-GFP– expressing cells taken before and after their exposure to a step input of cAMP (examples of responders are designated with yellow circles in the 1 nM stimulation case). Scale bars, 10 µm. (D) Percentage of responding cells in the analyzed population at the various cAMP doses plotted against the corresponding mean σ value, with the error bars denoting SEM. A linear regression to the data points is shown in red. (E) Dose-response curves of peak translocation for the entire population, responders, and nonresponders. A responder cell is defined by having a peak σ value greater than 1.15, whereas a nonresponder has a peak σ value not exceeding 1.15. Simulated population average of the dose response is fitted to the experimental data (shown in symbols) for the entire population (yellow line), responders (red line), and nonresponders (orange line). Error bars denote SEM.

On average, consistent with previous observations, we found that the probe transiently translocated to the membrane over the first minute of the stimulation (9) followed by secondary activity (13, 14) present most prominently for 10 nM cAMP (Fig. 1A). The dose response of the peak amplitude was half-saturated between 1 and 10 nM (Fig. 1A, inset), in line with the receptor’s estimated dissociation constant (K_D) of 30 nM (15). When examined on the single-cell level, however, there was a marked diversity of cell responses (Fig. 1B). In particular, the fraction of cells that showed a detectable response varied widely with the dose, with the number of responding cells progressively increasing with increasing signaling input (Fig. 1C, lower panels, and D). When sampled at doses in the 1 to 100 nM range (which is the range in which the peak response changes about linearly with the log cAMP concentration), the combined distribution of responses was bimodal (Fig. 1C). Bimodality was also evident for individual dose responses in this stimulation range (for example, for 1 nM of cAMP) (Fig. 1C, inset).We found that, for all doses examined, the responder cell outputs clustered around the maximal response values achieved for σ (varying from 1.3 to 1.4, a narrow range), whereas the nonresponder cell outputs similarly clustered around the minimal response value for σ, which was ≈1.1 (Fig. 1E), essentially indistinguishable from the value found in unstimulated cells (σ = 1). Fitting techniques revealed that the threshold best separating the two responding subpopulations was about σ = 1.15 (text S1). The average population responses correlated well with the proportion of responder cells (Fig. 1D). These observations suggested that D. discoideum cells had variable, stochastically distributed sensitivity thresholds in their responsiveness to extracellular cAMP, with both response types confined in a relatively narrow range, resulting in response bimodality. This interpretation of bimodality is based on the analysis of peak cell responses, although it may be related to the bimodality suggested to exist in correlation with the cell’s ability to form long-lived patches of PIP₃ in response to step-like inputs (11).

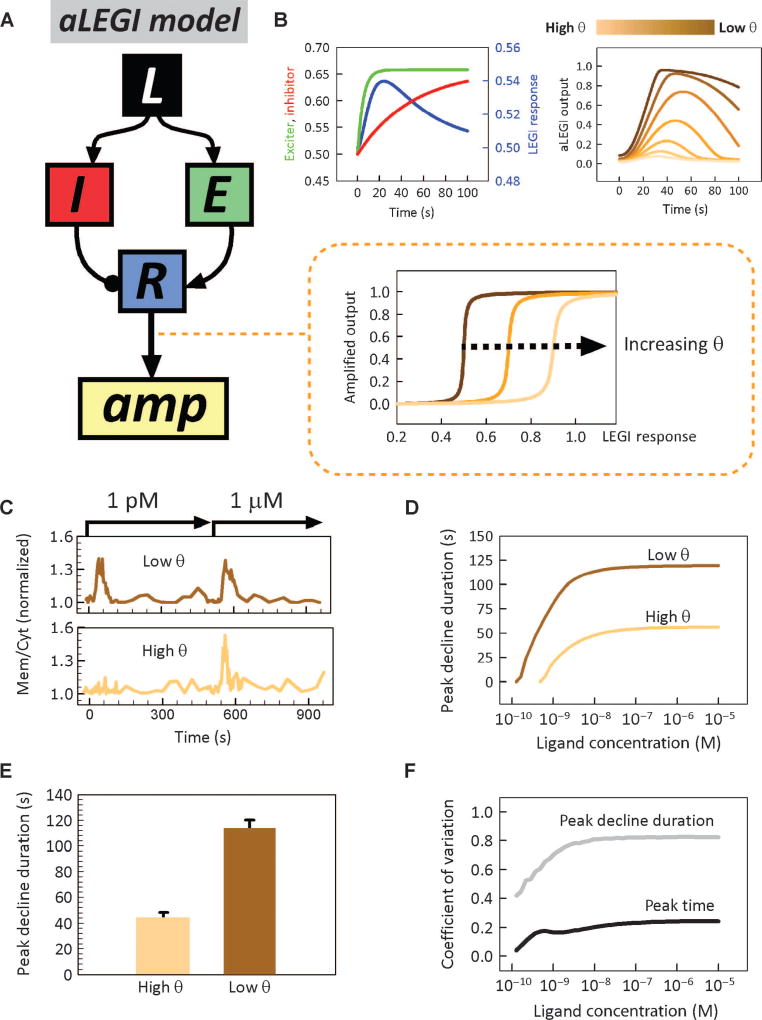
Various conceptual and computational models have been proposed to account for the response of PI3K and other signaling processes activated by cAMP, including the so-called local excitation, global inhibition (LEGI) model that postulates parallel excitatory and inhibitory signaling processes that are initiated by the same cAMP input (16–18). Although the LEGI model and its derivatives are consistent with many experimentally observed cell responses, it is still poorly characterized quantitatively and is unable to account for the diversity of cell responses shown in Fig. 1. We therefore sought to modify and further refine the model on the basis of a more detailed analysis of cell behavior. Because the average population activation of PI3K was consistent with a graded, rheostat-like response to variation in the dose of cAMP, which in turn could be well explained, along with many previously reported results, by the LEGI model, we made the simplest assumption needed for model modification: that within the signaling pathway, the LEGI signaling module is followed downstream by an additional signaling module that could amplify the output of the LEGI module, if this output exceeds a certain threshold value, θ (Fig. 2A). The threshold variability across cell population determines whether the output from the LEGI module leads to a cell becoming a responder or a nonresponder, given a certain value of input (Fig. 2B). This assumption, simpler and distinct from other signal amplification mechanisms proposed recently (19, 20), is analyzed further below. When coupled with the assumption of a uniform distribution of the threshold values across the cell population, the altered model indeed resulted in the prediction of a bimodal response distribution (fig. S2A). Sequential stimulation of single cells with two distinct doses of cAMP revealed that although virtually all cells responded at higher dose (1 µM), only a subset of these cells responded to the lower dose (1 pM), consistent with the variable response threshold model (Fig. 2C and movie S5). Numerical simulations suggested that this “amplified LEGI” (aLEGI) model was successful in explaining the average dose responses of the whole population and the responder and nonresponder subpopulations (Fig. 1E; see Materials and Methods and text S5 for further details on the model). In contrast to models postulating excitability of responses (19, 20), which are expected to yield the same response duration for the excitable response kinetics, the aLEGI model also predicted that the duration of the decline phase of the PI3K response (the time for the peak σ value to decline to the prestimulation value) would be shorter for cells with a high value of the amplification threshold θ compared to low- θ cells (Fig. 2D). This was confirmed experimentally (Fig. 2E). Furthermore, the model suggested that the variability in timing of the peak of PI3K activation would be lower for all cAMP doses than the variation in timing of the response decline (Fig. 2F), which was also confirmed experimentally (Table 1). These tests provided the initial evidence of the validity of the aLEGI model, but it was still not clear whether this simple extended model could explain cell responses to more complex and dynamically variable stimuli. We therefore used the microfluidic function generator to examine individual and population cell responses to a diverse set of time-varying stimuli.

Fig. 2.

The amplified LEGI model. (A) A schematic of the aLEGI model. Inset: the normalized amplified output value as a function of the constant LEGI response for three different θ values. (B) Simulation of the LEGI model (left) and the responses of aLEGI model (right) at various θ values. (C) The responses of two representative cells stimulated with 1 pM cAMP for 5 min and then 1 µM cAMP for another 5 min. The high- θ cell did not respond to the 1 pM stimuli but responded to the 1 µM stimuli. The low-θ cell responded to both stimuli with equal degrees of translocation. (D) Simulated peak decline time (time for the response to return to baseline from peak translocation) as a function of input dose, for a high (θ = 0.7) and low (θ = 0.6) amplifier threshold. (E) Experimentally measured peak decline time in response to 1 µM cAMP step stimulation [stimulation protocol and sample response are shown in (C)] in a population of 20 cells. Cells were classified as having a high θ value if they did not respond to 1 pM stimulation and a low θ value if they did. Error bars denote SEM. (F) The coefficient of variation of the peak time (black) and duration of peak decline (gray) in the response of simulated cell populations as a function of the stimulus dose. The corresponding experimental data are in Table 1.

Table 1.

System properties of PIP3 production. Values of means and SD of time to peak, peak amplitude, duration of decline, and degree of decline to baseline of the responder cells in response to step stimuli of different doses. Coefficients of variation, defined as SD/mean, are indicated in parentheses.

	1 pM	1 nM	10 nM	100 nM	1 µM	10 µM
Time to peak (s)	34.8 ± 18.4 (0.528)	38.7 ± 16.9 (0.436)	37.8 ± 18.3 (0.483)	31.8 ± 8.7 (0.282)	34.7 ± 14.3 (0.412)	35. ± 11.4 (0.326)
Peak amplitude (membrane/cytosol ratio)	1.33 ± 0.118 (0.089)	1.33 ± 0.258 (0.194)	1.41 ± 0.206 (0.146)	1.42 ± 0.212 (0.150)	1.39 ± 0.228 (0.164)	1.40 ± 0.163 (0.117)
Duration of decline (s)	90.2 ± 82.8 (0.92)	73.3 ± 52.1 (0.71)	121 ± 85.5 (0.71)	91.1 ± 79.2 (0.87)	114 ± 86.7 (0.76)	111 ± 83.7 (0.75)
Degree of decline*	0.93 ± 0.13 (0.14)	0.99 ± 0.12 (0.12)	0.94 ± 0.19 (0.20)	0.93 ± 0.17 (0.19)	0.90 ± 0.34 (0.38)	0.99 ± 0.16 (0.16)

^*Degree of decline to baseline is defined as (peak value − decline value)/(peak value − baseline value).

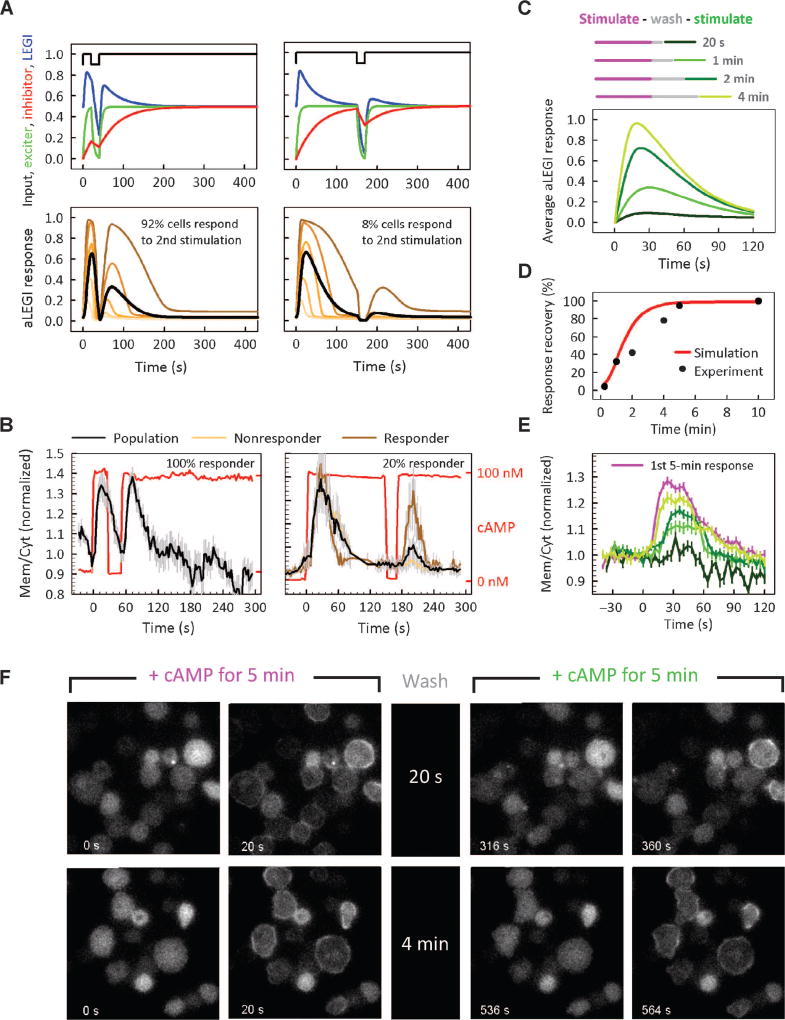
The original LEGI model postulates that the kinetics of the inhibitory process defines two different features of cell responses. The activation rate of the inhibitor controls the timing of the decline of the response, whereas the inactivation rate of the inhibitor after the removal of the stimulus defines how fast cells reset their sensitivity to the input (17). Therefore, cells stimulated with a transient pulse that was shorter than the characteristic response decline time are predicted to have incomplete activation of the inhibitor and thus be more sensitive to ensuing secondary stimulation, provided that a relatively short time period elapses between the stimulation pulses.

Furthermore, the aLEGI model predicted that this increase in the average cell responsiveness would be primarily due to the number of responsive cells, rather than the amplitude of the response of individual cells (Fig. 3A). We sought to validate both predictions while also obtaining a more quantitative parameterization of the LEGI response. The experimental analysis revealed that, consistent with the model predictions, the average population response to the second stimulation pulse declined as the duration of initial stimulation pulse increased, and this decrease in the average population response was due to a lower fraction of responder cells rather than decreases in the amplitude of the signaling response (Fig. 3B). The aLEGI model further suggested that even if the initial pulse was sufficiently long to fully trigger activation of the inhibitor, the increase in the time interval between the stimulation pulses could allow the cells to effectively reset their signaling sensitivity. The timing of this process would be defined by the time scale of the inactivation of the inhibitory process, an additional parameter whose direct determination has not been reported. Again, the model predicted that the response would be defined by the fraction of responding cells rather than the amplitude of the individual cell responses (Fig. 3C and D). This prediction was confirmed experimentally, and the resetting time of sensitivity to prestimulation values was about 5 min (Fig. 3D to F, and movies S6 to S9). This value essentially defines the cellular memory of each transient signal exposure (for example, during the naturally occurring pulsatile chemoattractant secretion). It is also close to the “optimal” cAMP oscillation period postulated to mediate the cell responses during aggregation phase (21, 22), suggesting that this period is determined by the cellular memory, which in turn is defined by the kinetics of the inhibitory process in the LEGI response framework.

Fig. 3.

Simulation and experimental measurement of cell responses to two-step stimuli of variable durations separated by a wash period of variable length. (A) Top: input stimulation profile of variable initial stimulation times followed by fixed wash and restimulation periods and corresponding LEGI responses. Bottom: simulated aLEGI responses for the population average (black) and for single cells with values of θ ranging from 0.55 to 0.85 (orange to brown curves). (B) Experimental verification of the model predictions in (A). Cells (n = 26) were stimulated with an initial 100 nM cAMP step input of variable duration (30 s or 2.5 min) and then washed for a short time interval (23 s) followed by a 5-min prolonged restimulation. (C) Model predictions for responses of cells stimulated with 100 nM cAMP for 5 min, washed with buffer for the indicated time periods, and restimulated with 100 nM cAMP for 5 min. (D) Percentage of the cells (n = 116) responding to the second step stimulation as a function of washing period in the model simulations (red line) and experiment (black circles). (E) Experimentally measured recovery of the average population response to the second stimulation step [cells stimulated as in (C)]. The pink curve denotes the cell response to the initial stimulation, and the green curves represent responses to the restimulation. Error bars denote SEM. (F) Sample images of PHcrac-GFP–expressing cells before and after their exposure to the first and second step stimulations with the indicated intermediate wash times. Scale bar, 10 µm.

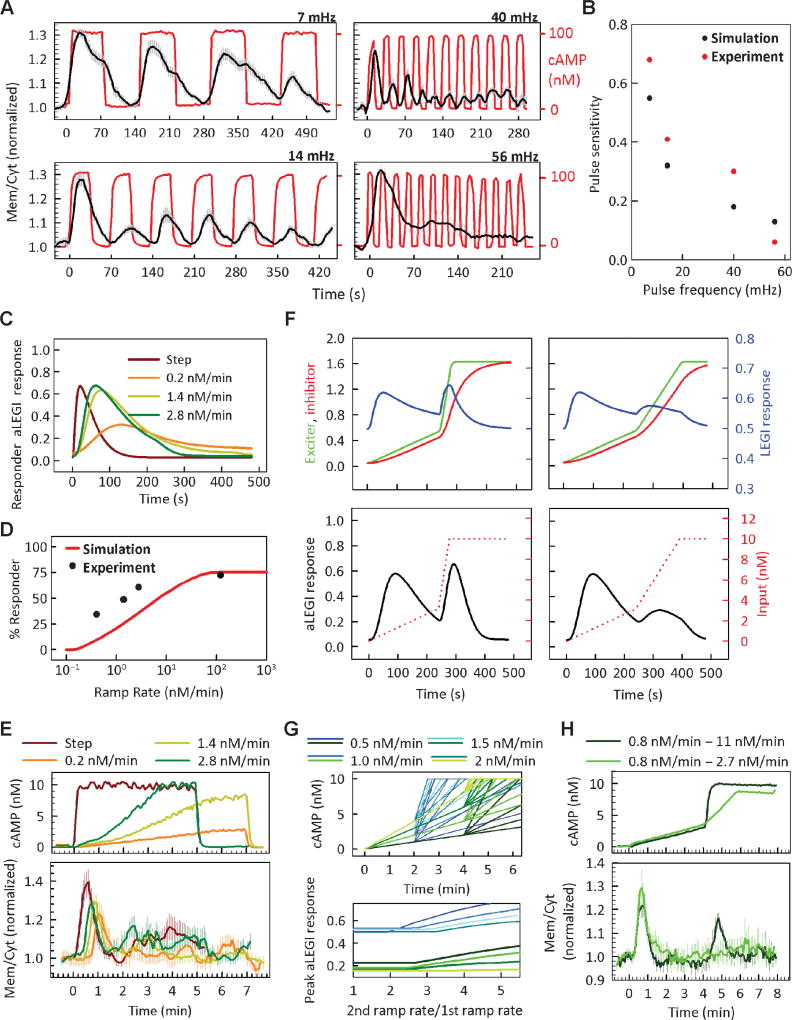
The analysis of the dynamics of the onset and decline of PI3K activation and recovery of sensitivity to the cAMP signal allowed us to predict the response of the signaling events to the periodic stimulation protocols, similar to those used recently to query the bandwidth of diverse cellular processes (23, 24). This analysis is particularly relevant because D. discoideum cells are naturally exposed to and are responsive to fluctuating signaling inputs as a result of the pulsatile nature of the chemoattractant secretion. In agreement with the model predictions (fig. S2B), we found that the average cell responses displayed the property of band-pass filtering of the input fluctuations so that at or above the stimulation frequency of about 50 mHz (or a period of 20 s), the oscillatory input becomes unrecognized as a series of pulses by the signaling system and is instead perceived as a constant stimulus (Fig. 4A and movies S10 to S13). The results of modeling and experimental analysis further suggested that the variation in the average response amplitude with stimulus frequency was primarily due to the variation in the fraction of responsive cells (Fig. 4B). In this stimulation regime, the response “bandwidth” is defined by the LEGI excitation kinetics, and thus this analysis constrains the time scale of this part of the model to be on the order of 10 to 20 s or slower for 100 nM pulses of cAMP. Examination of responsiveness to lower input frequencies (Fig. 4B) further suggested that responses to each pulse are maximized when the frequency reaches about 3 mHz, corresponding to a period of 6 min, which agrees with the cellular memory estimate above. This analysis suggests that the ability of the cells to recognize oscillations is defined by the faster, activator kinetics–defined process (10 to 20 s), whereas the ability of the cells to respond maximally to each pulse is defined by the longer, inhibitor kinetics–defined process (5 to 6 min). Thus, molecular kinetics values can place upper and lower limits on the oscillatory response dynamics during cell responses to natural cAMP oscillations.

Fig. 4.

Cell responses to pulsatile and ramp cAMP stimulation. (A) Kinetic responses of PHcrac-GFP (black) in cells (n = 100) stimulated with pulse trains of 100 nM cAMP of the indicated frequency (red). Plotted values are means ± SEM of the cells that responded to the first stimulation pulse, although not necessarily re-responding to subsequent stimulation pulses. (B) Pulse sensitivity quantified by normalizing the average peak amplitude of the responses to all pulses except the first one versus the peak amplitude of the response to the first stimulation pulse. The aLEGI model predictions for a heterogeneous population of simulated cells are compared to the corresponding experimental results. (C) Predicted aLEGI model responses for a heterogeneous cell population to stimulations with increasing ramp rates. (D) Percentage of cells classified as responders as a function of stimulation ramp rate in the model simulations (red line) and experiment (black circles, n = 113 cells). (E) Cell responses to ramp stimuli of different rates (experimentally measured stimulation profiles are shown in the upper panel). Plotted values are means ± SEM of the responding cells. (F) Predicted cell responses to a change in ramp rate. Top: step-like second ramp. Bottom: second ramp rate with rate twice as high as the first ramp rate. (G) Simulation studies of the parameters determining the sensitivity of cell responses to the changes in stimulation ramp rate. Top: cAMP input profiles. Bottom: Peak aLEGI response of a simulated heterogeneous cell population to the change in the ramp rate and initial ramp duration. (H) Experimental analysis of cell responses to two sequential ramp stimuli of different rates and one shallow ramp followed by a step stimulus. About 25 responding cells were quantified for each experiment. Plotted values are means ± SEM of the responding cells.

An important property of the LEGI model is its ability to account for the adaptive PI3K activation displayed by D. discoideum cell populations during exposure to spatially homogeneous stimuli. However, this property can also be accounted for by other types of adaptive signaling models, particularly those relying on the integral negative feedback (25, 26). It is therefore of interest to determine whether other types of signaling inputs might help distinguish between these two general models of adaptive responses. One such input is a “ramp” stimulation, with the cAMP concentration increasing linearly in time. Common, simple integral feedback models predict persistent responses (lack of perfect adaptation) to this class of stimuli (text S2), as was also observed experimentally for an example of a negative feedback–based adaptive signaling process (27). The LEGI-type incoherent feed-forward loop, on the other hand, can adapt perfectly to ramp stimuli, with the aLEGI model further suggesting that the timing of the peak is progressively delayed with a decreasing rate of cAMP ramping (Fig. 4C and text S2). The aLEGI model also predicted that the decreasing ramp rates would lead to a decreasing fraction of responding cells (Fig. 4D), resulting in a decrease in the average response amplitude. The experimental analysis confirmed the aLEGI model predictions, supporting the notion that the underlying signaling circuit is of the incoherent feed-forward loop type (Fig. 4D and E, and movie S14). The aLEGI model further suggested that the signaling system adapting to a ramp stimulus could become insensitive to the subsequent change in the ramp rate unless the rate of the second ramp stimulation exceeded a certain threshold value (Fig. 4F). This threshold value depended only on the duration of the initial ramp stimulation, with the amplitude of the average second response peak inversely related to the initial ramp rate (Fig. 4G). This was confirmed by experimentally stimulating cells with ramps of cAMP concentrations of different rates with the microfluidic function generator (Fig. 4H). This result might have implications for the ability of cells to respond to the initially disorganized cAMP waves occurring during the early stages of the colony self-organization. If a cell is exposed to a series of cAMP waves in a close succession, experienced as sequential ramp-like increases in the cAMP concentration, the cell’s responsiveness to a secondary wave might be depressed in proportion to the duration and strength of the primary cAMP wave, thus increasing the persistence of the initial response.

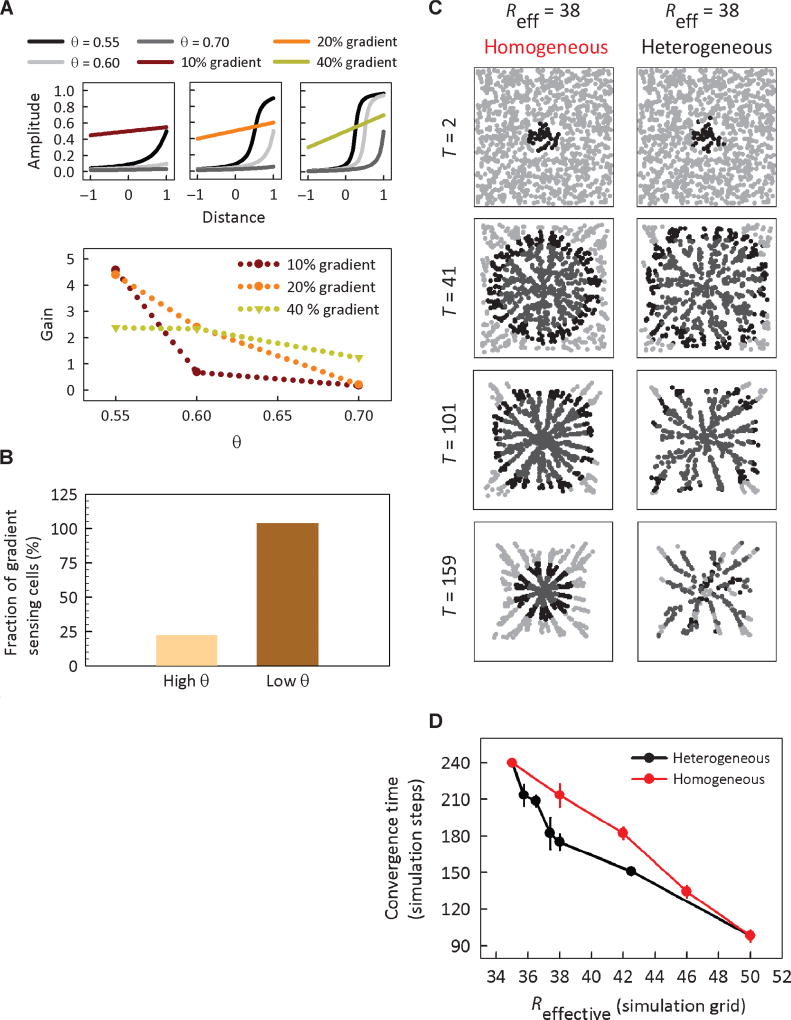
The results presented so far argue that the aLEGI model predicts both the population and the single-cell responses of D. discoideum cells to various cAMP inputs. However, the potential functional consequences of aLEGI signaling for single-cell and population responses within the physiological context of gradient sensing and chemotaxis are not immediately clear. One of the more obvious implications of the amplification process in the aLEGI framework is the possibility of the amplification of the intracellular gradient of the signaling response given an extracellular stimulus gradient. The existence of some type of a gradient amplification process downstream of an adaptation molecular circuit was previously hypothesized on the basis of the imaging of cell signaling in spatial cAMP gradients (8), but this amplification process has not been well characterized. Here, the response amplification is suggested on different grounds: to explain the sharp diversification of signaling events in spatially homogeneous cAMP fields. We therefore explored, in a simple model of gradient sensing, the degree of gradient amplification suggested by aLEGI and its dependence on both the amplification threshold θ and the fractional stimulus gradient value (text S3). We found that although the predicted amplification gain was relatively insensitive to θ at sharp gradient values, both the gain value and the gain sensitivity to θ increased at low gradient values (Fig. 5A). These results suggested that aLEGI can indeed engender intracellular gradient amplification in the regime in which improved sensitivity may be needed to detect the gradient. The model predicted, furthermore, that at low cAMP gradient values, only the low- θ responder cells might be effectively sensing the cAMP gradient. These predictions were supported by experimental observations that cell polarization and ensuing cell migration up the gradient of cAMP was a direct function of cell responsiveness threshold (Fig. 5B).

Fig. 5.

Functional consequences of diversification of the signal amplification threshold. (A) Simulated aLEGI intracellular responses distributed across the cell length induced by linear extracellular cAMP gradients. Top: aLEGI responses resulting from nine combinations of θ values and gradient slopes. Bottom: gain of the cells with various θ values at the applied gradients (see text S3 for the definition of gain). (B) Fraction of cells that exhibit motility in response to a linear cAMP gradient, with the cAMP concentrations varying from 0 to 100 nM. Cells that exhibit PHcrac translocation were classified as low θ and vice versa. All of the motile cells migrated in the direction of higher concentration. (C) Time series of the simulated aggregation of cells displaying heterogeneous versus homogeneous θ threshold values. The two populations have identical effective excitation radius: the cAMP sensing distance R₁ for 80% of the cells in the heterogeneous population is 35 grid units and R₂ = 50 grid units for the remaining 20%, whereas the homogeneous population has a uniform cAMP sensing distance R of 38 grid units. The grayscale intensity of the cell denotes its corresponding state: light gray, unstimulated and responsive; black, responsive; dark gray, refractive. (D) Quantification of the convergence time compared to the effective excitation radius for the two populations. The convergence time is defined as the time at which 90% of the cells have stopped streaming toward the pulsing source. Plotted values are means ± SEM from five simulations, with cells seeded randomly in space at the start of each simulation.

The higher sensitivity of responder cells to the dose of the stimulating signal also suggests that these cells might be more poised to respond during the initial stages of the cAMP-mediated self-organization of an aggregating cell colony, increasing the initial percolation of the cAMP waves through the cell population and serving as the local attractors of less responsive cells. Thus, the presence of even a relatively small fraction of highly sensitive cells could increase the rate of the pattern formation in self-organizing cell colonies. A simple model of a multicellular colony was used to explore this effect. The model incorporated the essential properties of aLEGI, including threshold-dependent response amplification, cellular memory–dependent refractory period, and diversification of the input responsiveness across the population of randomly distributed cells. We made an additional simple assumption that responding cells would be able to translate their response into generating a cAMP wave, thus postulating that binary cell responsiveness translates into binary secretion of cAMP. The simulation results indeed confirmed the initial intuitive predictions (Fig. 5C, text S4, and fig. S3), suggesting that heterogeneous cell populations could converge faster upon self-organized multicellular patterns than homogeneous populations (Fig. 5D).

Although the mechanism for achieving diversity of responsiveness thresholds across the cell population remains uncertain, it is of interest that over the developmental time, the fraction of cells responding to low cAMP concentration increased considerably, resulting in an essentially unimodal response by 7 hours of exposure to cAMP (fig. S6). At this developmental time, cells lose the ability to secrete cAMP in an oscillatory fashion and are generally committed to moving within well-organized, self-assembling streams. Thus, the diversification of cell responsiveness is likely of importance at the initial phases of colony self-organization and associated cell decision-making, as discussed above. Inhibition of actin polymerization did not abolish bimodality in cell responsiveness (fig. S7) but decreased the fraction of responsive cells and lowered the overall sensitivity of the cell population to cAMP, thus implicating the actin cytoskeleton in setting the threshold for cellular responsiveness.

DISCUSSION

Together, the results presented here argue that D. discoideum cells use a combination of sensory and population diversification strategies (28, 29), enabling a cell population to respond over a wide range of stimuli while also permitting single cells to display individuality in the sensitivity thresholds. The diverse range of complex, dynamic stimuli used in this study served to both increase the stringency of the model validation and unmask the kinetic responses usually not evident in simple step-like stimulation protocols. We found that the average cell responses fitted the previously proposed LEGI model in various contexts, both providing further support for the existence of a LEGI-like signaling module within the signaling network and enabling further characterization of this module. For instance, both the activation and the inactivation kinetics of regulation of the excitatory process were about an order of magnitude faster than those of the inhibitory process, setting the limits on the speed of the adaptive and de-adaptive responses and on the overall responsiveness of the cell population to the frequency of the naturally pulsatile stimulation. In particular, the upper threshold of the frequency responsiveness, or the limit at which cells can still recognize the input as being oscillatory (10- to 20-s time scale), is predicted to be defined by the kinetics of the activator. In contrast, the lower threshold, or when the response amplitude to each oscillation phase is maximized (5- to 6-min time scale), is defined by the kinetics of the inhibitor, constituting a previously unknown value that characterizes cell memory of the previous inputs and possibly the optimal cAMP oscillation period in vivo.

The use of microfluidic control of cell microenvironment allowed the delivery of more complex stimuli, including ramp stimulation. Naturally, during responses to sequential pulses of cAMP, cells are expected to experience them as ramp-like stimuli, both rising and ebbing in time. We found that the responsiveness to an increasing slope of the ramp was defined by the previous ramp slope value, suggesting that cell responsiveness was greater to inputs with gradually rising rather than gradually decreasing ramp rates. The ability of cells to adapt to ramp stimulation, as predicted by the model and supported experimentally, further suggested that the dynamics of concentration changes in the wave-like inputs experienced by cells is less important than the oscillatory dynamics leading to wave generation.

The faithfulness with which the average cell responses were explained by the LEGI model, coupled with the switch-like responses of individual cells, suggested that the LEGI module is followed by a downstream amplification process. This combination of a complex and adaptive upstream sensory mechanism with a downstream amplification “filter” differs from simpler on-off switches suggested previously for some processes involving cell diversification (30, 31) and are more akin to the adaptation-amplification architecture found in a bacterial chemotaxis network (32). We surmise that this similarity might be more than superficial because of the similar tasks of chemotactic responses performed by both systems. In particular, we find that the amplification module in the aLEGI model can amplify the cell sensitivity to shallow gradients, a function also proposed for amplification processes in bacterial chemotaxis (32). This network architecture is simpler and distinct from that of models usually proposed for excitable molecular circuits, usually containing a combination of negative and positive feedback interactions. Although our results are more consistent with ultrasensitive responses not requiring positive feedback, we cannot exclude the existence of such a feedback, particularly for responses after the initial peak response considered in our analysis.

Previously, cell individuality in D. discoideum cell populations has been suggested on the basis of a differential cell responsiveness to the direction of the cAMP gradients (29) or the ability to generate or respond to cAMP oscillations (21). Our results suggest that the cell individuality extends further, with the amoebae having a population of more responsive cells that provide the initial “skeleton” of the network of cell responses because they are more sensitive than their peers to the input gradient and that transmit the signal from the center(s) of high cell density. This differential sensitivity property can help enhance self-organization of the colony while avoiding potentially inappropriate activation of most of the colony cells by weak extracellular cAMP fluctuations. We thus conclude that variability in the local cell density (21, 33) is not the only determinant of the colony self-organization process, but that this process is also controlled by the fraction of hypersensitive cells that can naturally serve to enhance and nucleate the initial stages of colony response. It will be of interest to explore whether similar phenomena are also present in other eukaryotic cell systems displaying chemotactic behaviors by means of homologous signaling processes.

MATERIALS AND METHODS

Microfluidic function generator operation principles

We custom-designed and built a microfluidics device, designated microfluidic function generator, that can uniformly expose cells to arbitrary waveforms of soluble chemicals. The device is a compact monolithic two-layer polydimethylsiloxane (PDMS) chip reversibly sealed to a glass coverslip (fig. S1A). The PDMS chip has two layers (fig. S1B): the bottom fluidic layer (channels filled with a red dye in the figure) contains a cell culture chamber connected by a mixing channel to two inlets, one filled with washing buffer and the other with the stimulus. The culture chambers (large red dots in the figure) are also connected to a separate set of channels (0.03 mm in height) for waste output and cell introduction. The cell culture chambers (0.8 mm in diameter) have higher “ceilings” (0.3 mm) for locally reducing shear stress on the cells. Fluid flow in the device is controlled by pushdown pneumatic valves in the top layer (green in the figure). Three valves marked “partitioning valves” in fig. S1B divide the cell culture chambers into independent compartments, allowing separate experimentation in the subset of the chamber. The remaining valves control fluid flow entry and exit. The stimulation profile is generated by sequentially turning on and off the control valves gating the stimuli and the washing buffer inlets (fig. S1C). The pressurized valve (green in fig. S1C) stops the fluidic flow beneath, whereas the inactive valve is not shown in the diagram. When both inlets are flowing into the mixing channel, changing their relative volumetric flow rates can result in dynamically changing stimuli concentrations. Ligand concentrations in the chamber housing the cells can be linear or pulsatile in time on the basis of this principle (fig. S1D).

PDMS device fabrication

The device design was laid out in FreeHand 10 (Macromedia) and then printed as a high-resolution Mylar transparency mask (in Tandem). The dual-layer microfluidic device was made with standard soft lithography (34). The master mold for fabrication of the bottom, fluidic layer had a 30-µm-thick SPR-220 (Shipley) relief with rounded edges. The mold was spin-coated with a ~150-µm-thick layer of PDMS prepolymer (GE RTV 615; 20:1 monomer/curing agent ratio), which was cured in the standard prebonding condition. The master mold for fabrication of the top, control layer had a 40-µm-thick SU-8 relief. It was used to make a ~5-mm-thick PDMS (5:1 monomer/curing agent ratio) cast that was cut into individual chips. The inlets on this layer were drilled with a syringe tip. The chips were then aligned and placed on top of the partially cured PDMS layer on the bottom fluidic layer wafer. After another partial curing, monolithic two-layer PDMS chips were peeled off the master mold, the remaining inlets were drilled, and the membrane above the observation chamber was excised. Then, the chips were aligned and placed on top of glass coverslips. After the bond was reinforced by heating in an 85°C oven overnight, PDMS chips were ready for experimentation. After use, the PDMS chips were either disposed of or recycled by the following procedure. The PDMS chips were separated from the coverslips and rinsed with Alconox solution, water, and, finally, 70% ethanol. Chips were then dried with sterile filtered compressed air and bond to new coverslips. After the bond was reinforced overnight in an oven, the chips were ready for reuse.

Cell culture

Cells of the D. discoideum wild-type strain AX3 expressing PHcrac were axenically cultured in HL5 medium containing G418 (50 µg/ml) at 22°C. Before a chip experiment, cells grown in HL5 were washed twice and developed for 4 hours in development buffer [DB: 5 mM Na₂HPO4, 5 mM NaH₂PO₄ (pH 6.5), 2 mM MgSO₄and 0.2 mM CaCl₂] as previously described (9). To assess the viability and behavior of Dictyostelium cells cultured under continuous flow inside the device, we used time lapse imaging of a field of differentiated cells for a period of time, contrasting the motility exhibited by the cells cultured inside the microfluidic chip to that of the cells in a standard open culture chamber (LabTech). We found no significant difference in motility between the two culture environments, suggesting that the cells are not compromised by the flow or other properties of the device.

Dynamic stimulus generation and response measurement

Control channels were filled with water and pressurized with in-house compressed air to 20 psi to prevent air from being forced from the control channel into the test chambers when valves were actuated during normal operation. Valve actuation was controlled by a set of miniature three-way solenoid valves (The Lee Company) that toggled between 0 and 20 psi. The sequence of valve actuation for the various stimulation profiles was controlled by custom JAVA-implemented programs through a digital input / output computer card (PCI-6517, National Instruments). Real-time modulation of fluidic flow rate for linear and parabolic ramp stimulations was achieved by changing the hydraulic pressure by altering the heights of the media reservoirs feeding the inlets and outlets. The media reservoirs were mounted onto a linear slider (Velmex) with a motorized shaft (Anaheim Automation). Slider movement was controlled by custom JAVA programs regulating the motor operation through an EZ 17 stepper driver (AllMotion). After dead-volume priming of the device channels with DB, differentiated cells were introduced into the device at the concentration of 8 million cells/ml. Cells adhered to the glass surface within minutes after perfusion was stopped. The perfusion rate used throughout the whole study was ~250 nl/min. cAMP profile was measured through a surrogate tracer dye, Alexa Fluor 594 hydrazide (Molecular Probes). Images of living cell responses were observed with a motorized Zeiss Axiovert 200 M epifluorescence microscope equipped with a Lambda DG-5 300-W light source and wavelength switching excitation system (Sutter) and a Cascade 512B charge-coupled device (CCD) camera (Photometrics) and driven by Slidebook (Intelligent Imaging Innovations). The Semrock filters used to visualize the GFP and the Alexa tracer dye are the following: single fluorescein isothiocyanate (FITC) band-pass filter 494 ± 20; triple dich 4′,6-diamidino-2-phenylindole (DAPI)/FITC/TXRed; triple DAPI/FITC/TXRed emitter. Temperatures were held at 11°C during imaging by means of a custom-made on-stage incubator to provide stable focus and prevent overheating the cells.

Response quantification

The custom algorithms for background correction and quantification of the ratio, σ, of the membrane/cytosol GFP fluorescence intensities were implemented in Mathematica (Wolfram) as follows. For a single cell, fluorescence intensities were measured along 16 four-pixel-wide lines drawn through the membrane portion and ending at the central portion of the cell. The pixels around the periphery and cytosolic regions were extracted by segmentation and normalized against the local background value. The pixels of each region on the multiple lines for each cell at each time frame were averaged together to produce the membrane and the cytosol signal values. The signaling output was estimated as the ratio of the membrane and the cytosolic fluorescence signal that was normalized to the prestimulation values. The cell responses have no dependence on PHcrac-GFP expression (fig. S5).

aLEGI model setup and development

The frequently used step stimuli response data shown in Fig. 1 present an initial opportunity to investigate whether the previously published LEGI model (17) can successfully approximate the observed results. Upon comparing the predictions made by the model with the experimental measurements, we found that the model failed to account for the following: (i) switch-like dose response for single cells but graded dose response for the population average and (ii) diverse response decline times for the first response phase (first peak) in single cells responding to the same input (Fig. 1). Instead, the LEGI model predicted that each cell should uniformly exhibit a graded change in response to increasing doses of step inputs and nonvariable response decline time. Despite its inability to account for the heterogeneous single-cell behavior, LEGI was able to predict the ensemble average responses observed in all the experiments. We therefore hypothesized that the LEGI model should be modified rather than discarded. Arguably, the simplest assumption needed for model modification was that within the signaling pathway, the LEGI signaling module would be followed downstream by an amplification signaling module, capable of strong amplification of the LEGI module output if this output exceeded a certain threshold value, θ. A similar scheme was earlier proposed by us before on the grounds of the need for gene amplification (8). We further assumed that the distribution of the values of θ would be uniform across a range of parameters, as discussed below, again aiming to see whether this simple assumption would be consistent with the experimental results. Although the amplification module could be implemented in different ways, we have adopted a simple description based on zero-order ultrasensitivity, with the LEGI output further “filtered” through two coupled saturated reactions (35). Thus, the overall response is positively regulated by the output from the LEGI module and negatively regulated by a second unknown inhibitor defining the threshold θ. For the same LEGI response, higher values for θ will cause the cells to be classified as nonresponders, whereas in a cell with a low value for θ, the cell’s response would be maximal because of the ultrasensitive nature of the amplifier (fig. S2A). Except for the θ values, all other parameters of the model have been assumed to exhibit no cell-to-cell variation. This model has been referred to in the main text as the aLEGI model. It was implemented in Mathematica, and 200 cells were simulated for each condition.

The model equations and the assumed parameter values are shown in text S5. Below we discuss how the model was “trained” by initial experimental data to arrive at the assumed model parameters and how its predictions were tested in further experimentation.

Experimental dose-response results are consistent with uniform θ population distribution

The equations (1 to 4) (text S5) represent the simple embodiment of the aLEGI model discussed above. The dependencies of the exciter (activator) a and inhibitor i and stimulation by the input L are assumed to be distinct only in the kinetics of activation and inactivation represented by the corresponding rate constants ρ_a and ρ_i. These constants are estimated experimentally as described below. The constitutive synthesis constant, k_cis introduced so that the baseline response value would be nonzero. Furthermore, we assume that at the steady state, the ratio of the exciter and inhibitor amounts would be equal to unity, which implies that the steady-state amounts of these two components are equal to each other and equal to k_c/k_d. The normalization of the ratio of the steady states of the exciter and inhibitor to unity does not affect the results other than in defining the steady state of the response element r, which is then normalized to r_tot/2. Again, this normalization does not affect the generality of the conclusions other than in defining the steady state of the amplified response (Eq. 4), which is forced in the model to be below 20% of the peak response for any of the concentrations of L, therefore preventing amplification of the LEGI output at the steady-state amounts. Overall, therefore, the response element can vary in the simulations between r_tot /2 and r_tot values, which is expected to lead to amplified responses only given the input stimulation, with the degree of response determined by the particular value of the amplification threshold in a particular cell. The higher the input L, the higher the chances that the corresponding output r(t) can, at least transiently, exceed the threshold for amplification in a given cell. To illustrate this dependence of response amplification on the values of the threshold θ and the input L, we plotted the maximum amplified response value as a function of these two parameters (fig. S2A). The average population response to a specific dose is thus a function of the distribution of the values of θ across the cell population, allowing us to examine whether the assumption of a uniform distribution of θ is consistent with the experimental data, and determining in the process the approximate limits of this distribution. We indeed found that the experimental data were well explained by the assumption of the uniform distribution with the values of θ ranging within the interval given in text S5. The lower limit of this interval is determined by the condition stipulated above (in that the absence of response amplification at the steady-state LEGI response value of r = r_tot /2). The upper limit is determined by the appropriate weighing of the fraction of poorly responsive cells within the population to fit the experimental average dose-response data. The exact value of K_mthe constant defining the degree of saturation of the ultrasensitive reactions determining the amplifier output, was also not consequential to the outcome of the simulations as long as the conditions of ultrasensitivity were satisfied, thus demanding that this value was low compared to both modified amp θ and unmodified (amp_tot − ampθ) amplifier states.

Constraining the kinetic constants

The degree of response amplification is not sensitive to the exact values of many of the model parameters and depends primarily on the distribution of the amplification threshold values across the cell population. However, the ability of the model to describe kinetic responses observed experimentally does require further constraining of the model parameters, particularly the characteristic reactions rates ρ_i. Within the context of the LEGI model, during observation of a pronounced peak in response, the activation rate of the exciter should exceed the activation rate of the inhibitor. Furthermore, the initial rise in the response is primarily determined by the activation rate of the exciter ρ_aallowing one to constrain this rate with experimental data. Likewise, the subsequent fall of the response to the baseline steady-state values is primarily determined by the activation rate of the inhibitor ρ_i and thus can also be constrained.

To constrain the rates ρ_a and ρ_i, we therefore contrasted the modeling output (fig. S4) with the dynamic average dose-response data shown in Fig. 1. We aimed to reproduce both the kinetics of the responses and the dose response of the response amplitudes. We found that there was a close agreement between model predictions and experimental measurements for the values of the parameters given in text S5 for all the doses analyzed, suggesting an order of magnitude difference in the parameter values. These estimates agreed well with both the LEGI module output and the average output of the aLEGI model, provided that the response rates of the response element r and the amplifier module were faster than either of the rates ρ_a and ρ_i, which therefore constituted an important additional assumption of the model, and led to the assumed values of parameters ρ_r and ρ_m shown in text S5.

The simple step-like input profile used to obtain the data in Fig. 1 was not sufficient to reveal the rate constants of inactivation of the exciter and inhibitor because the step-like input leads only to activation of these two model species within the context of the LEGI model. Using a different experimental protocol, which was also used to validate the more basic assumption of the LEGI model itself, we therefore tested whether the simplifying assumption was supported by the data. We analyzed cell responses to two pulse-like stimuli of variable durations separated by wash periods of variable periods (Fig. 3). The duration of zero input separating two stimulation pulses can allow the cells to “reset” their sensitivity to the input or adapt, which is determined by how fast the exciter and inhibitor species return to their baselines. Furthermore, given sufficient duration of the first pulse, which would allow the adaptive return of the cell response to the baseline, the response to input removal is expected to show no detectable change if the inactivation rate of the exciter is much faster than that of the inhibitor. In fact, the rate of the response decrease after the onset of the zero input defines the exciter inactivation rate, yielding a value similar to the exciter activation rate, thus allowing us to use the same value for both, as shown in text S5. Finally, shorter durations of the initial stimulation might not allow full inhibitor activation, facilitating its inactivation during the adaptive, zero input periods, whereas shorter durations of zero input periods might not allow full inhibitor inactivation, limiting the response during the secondary stimulation pulse. These experiments thus allow the inhibitor activation and inactivation kinetics to be further constrained. We have particularly focused on determining the approximate value of the inhibitor inactivation rate, obtaining the value close to that of the activation rate, allowing us to use the same value for both in the model shown in text S5.

The considerations above and the corresponding experiments finalized the model training, with the rest of the analysis using the model to predict the outcomes, in terms of both the response kinetics and the variable fractions of cells responding to a given input. The details are provided in the Results section and the main figure legends.