Efficiency of Two Sample Tests via the Restricted Mean Survival Time for Analyzing Event Time Observations

Summary

In comparing two treatments with the event time observations, the hazard ratio (HR) estimate is routinely used to quantify the treatment difference. However, this model dependent estimate may be difficult to interpret clinically especially when the proportional hazards (PH) assumption is violated. An alternative estimation procedure for treatment efficacy based on the restricted means survival time or t-year mean survival time (t-MST) has been discussed extensively in the statistical and clinical literature. On the other hand, a statistical test via the HR or its asymptotically equivalent counterpart, the logrank test, is asymptotically distribution-free. In this paper, we assess the relative efficiency of the hazard ratio and t-MST tests with respect to the statistical power under various PH and non-PH models theoretically and empirically. When the PH assumption is valid, the t-MST test performs almost as well as the HR test. For non-PH models, the t-MST test can substantially outperform its HR counterpart. On the other hand, the HR test can be powerful when the true difference of two survival functions is quite large at end but not the beginning of the study. Unfortunately, for this case, the HR estimate may not have a simple clinical interpretation for the treatment effect due to the violation of the PH assumption.

1. Introduction

In a randomized, comparative clinical trial with an event time as the study end point, treatment difference is often summarized by the hazard ratio (HR) by assuming a proportional hazards (PH) model, namely, the ratios of two hazard functions between two treatment groups, labeled as 1 and 0, are approximately constant over time (Cox, 1972). Under the PH assumption, the HR can be consistently estimated by maximizing a partial likelihood function from the Cox model. However, a HR of, for instance, 0.7 for treatment 1 versus treatment 0 cannot be interpreted as a 30% event rate reduction in favor of treatment 1 since the hazard is not a simple probability of event occurrence. The clinical interpretation of a HR depends on the temporal profile of the hazard function for the reference group. For example, it is not clear whether a HR of 0.7 alone is clinically meaningful: a 30% reduction of hazard in treatment group 1 may not be clinically important for a “low” hazard function in treatment group 0, while quite meaningful for a “high” hazard function in the treatment group 0. However, there is a lack of a simple nonparametric estimator for the hazard function as the Kaplan-Meier (KM) estimator for the survival function. Oftentimes the HR is interpreted as the inverse ratio of the median event times in practice assuming an exponential distribution for the survival outcome and thus provides an informative summary for the treatment effect when coupled with the median survival time in group 0. However, such an interpretation may be problematic when the exponential assumption does not hold. Furthermore, when the PH assumption is violated, the HR estimator from the Cox model converges to a parameter which is difficult to interpret (Kalbeisch and Prentice, 1981; Lin and Wei, 1989). For this case, one often considers the estimated HR as an approximation to a weighted average of the HR’s over time. Unfortunately, the weights depend on the censoring distributions. This adds another complexity of translating HR for effective clinical decision making. Other model-based summary measures for the group difference have similar issues as the HR (Wei, 1992).

There are several alternatives to summarize a survival distribution. For example, the median survival time, the t-year event rate and the t-year mean survival time, t-MST. The t-year mean survival time is also coined as the restricted mean survival time. In this paper we are interested in studying properties of using a summary measure as a group contrast based on the t-MST. The inference procedures for t-MST and the function thereof have been studied extensively, for example, by Karrison (1987); Zucker (1998); Royston and Parmar (2011); Zhao et al. (2012); Tian et al. (2014) and Uno et al. (2014). The t-MST has a clear physical and clinical interpretation. For example, an observed 2.5 year of the 3-year mean survival time indicates if a patient is followed up to 3 years, on average, he or she would survive 2.5 years. The t-MST can be readily estimated via the area under the corresponding Kaplan-Meier (KM) curve up to t year. Contrary to the model-dependent nature of the HR, the treatment effect can be quantified by, for example, the difference in t-MST between two treatment groups, which is purely nonparametric without requiring any model assumption. This group difference measure with a reference value of t-MST from the control arm in a comparative study is more informative than the HR.

Since the HR estimate is routinely used for making inference about the treatment effect, it would be interesting to compare it with the t-MST based inference procedure. However, since these two estimation procedures empirically quantify different parameters, it seems difficult, if not impossible, to study their relative merits from an estimation point of view. On the other hand, under the testing hypothesis paradigm, the HR based test is asymptotically distribution-free. Therefore, it is possible to compare the t-MST and HR based tests with respect to, for example, their conventional statistical power profiles. It is interesting to note that recently Trinquart et al. (2016) utilized the data from a large number of clinical trials to show empirically these two types of tests are quite concordant in terms of the conventional statistical significance interpretation.

In this paper, we formally compare these two types of tests under a more theoretical setting. To be specific, we first present the testing procedures based on HR and t-MST in Section 2. The asymptotic relative efficiency (ARE) of these two tests is derived in Section 3. In Section 4, the performance of the two tests are studied theoretically and compared empirically via extensive numerical study. We also use the data from a recent clinical trial to illustrate our findings in the same section. In general, we find that the test based on t-MST performs well compared with its HR counterpart when the PH assumption is valid. For certain non-PH models, for instance, when the two survival functions are quite large at the end but not the beginning of the study followup time, the HR test is quite powerful. Unfortunately, the corresponding HR estimate is difficult to interpret clinically. With this additional finding, the robust, easily interpretable t-MST based inference procedure provides a useful alternative tool to the HR based counterpart in survival analysis.

2. The HR and t-MST based tests for the equivalence of two survival functions

Let T₁ and T₀ be the event times in treatment groups 1 and 0, respectively. The group difference in t-MST up to the time point t is defined as

$$D=E(T_1\wedge t)-E(T_0\wedge t),$$

which is the area between two survival curves over the time interval [0, t] :

$${\int }_0^t\{S_1(u)-S_0(u)\}\mathit{\text{du}},$$

where S_j(·) is the survival function of the failure time T_j in arm j, j = 0, 1. In order to make D identifiable based on observed data, π_j(t) = pr (T_j ∧ C_j ≥ t) needs to be bounded away from zero, where C_j denotes the censoring time in treatment group j, j = 0, 1, i.e., min{π₀(t), π₁(t)} > 0. In practice, t can be chosen, for example, as the minimum of the 95th percentiles of observed T_j ∧ C_j from two treatment groups. The difference in t-MST can then be estimated by

$$\hat{D}={\int }_0^t\{{\hat{S}}_1(u)-{\hat{S}}_0(u)\}\mathit{\text{du}},$$

where Ŝ_j(t) is the KM estimator for S_j(t). As the sample size n → ∞, $\sqrt{n}(\hat{D}-D)$ converges weakly to a mean zero Gaussian distribution whose variance can be consistently estimated by

$${\hat{\sigma }}_D^2={\int }_0^t{\{{\int }_{\upsilon }^t{\hat{S}}_0(u)\mathit{\text{du}}\}}^2\frac{d{\hat{\mathrm{\Lambda }}}_0(\upsilon )}{p_0{\hat{\pi }}_0(\upsilon )}+{\int }_0^t{\{{\int }_{\upsilon }^t{\hat{S}}_1(u)\mathit{\text{du}}\}}^2\frac{d{\hat{\mathrm{\Lambda }}}_1(\upsilon )}{p_1{\hat{\pi }}_1(\upsilon )},$$ (1)

where p_j is the proportion of patients randomized into group j, π̂_j(υ) is the empirical counterpart of π_j(υ) and Λ̂_j(t) is the Nelsen-Aalan estimator for the cumulative hazard function in group j, j = 0, 1 (Pepe and Fleming, 1989, 1991; Zhao et al., 2012). Under the null hypothesis that there is no difference between two survival functions, the distribution of $\sqrt{n}\hat{D}/{\hat{\sigma }}_D$ is approximately the standard normal for large n.

Similarly, let θ̂ be the estimator of θ =log(HR) by maximizing the partial likelihood function over the time interval [0, t_H]. Under the PH model, as n → ∞, $\sqrt{n}(\hat{\theta }-\theta )$ converges weakly to a mean zero Gaussian distribution, whose variance can be consistently estimated by

$${\hat{\sigma }}_{\theta }^2={\{{\int }_0^{t_H}\frac{e^{\hat{\theta }}{p}_0{p}_1{\hat{\pi }}_0(u){\hat{\pi }}_1(u)}{p_0{\hat{\pi }}_0(u)+e^{\hat{\theta }}{p}_1{\hat{\pi }}_1(u)}d{\stackrel{\sim }{\mathrm{\Lambda }}}_0(u)\}}^{-1},$$ (2)

where Λ̃₀(u) is the Breslow estimator for the cumulative hazard function at the treatment group 0 (Cox, 1972; Fleming and Harrington, 2011). Under the null hypothesis, θ = 0 and the distribution of $\sqrt{n}\hat{\theta }/{\hat{\sigma }}_{\theta }$ is approximately standard normal for large n. Therefore, tests based on both D̂ and θ̂ are asymptotical valid in retaining the appropriate type I error rate.

Note that similar to t-MST, in theory the large sample normal approximation to the distribution of HR estimator is only valid with observations within a finite time interval, say [0, t_H], where max{π₀(t_H), π₁(t_H)} > 0 (p289–290, Chapter 8, Fleming and Harrington (2011)). There is a misconception that the exp(θ̂) approximates the HR at all time points. In practice, the interpretation of this estimated HR should be restricted to the finite time interval [0, t_H], where t_H is smaller than the maximum the followup time. Compared with t in t-MST, t_H and t can be identical under the condition that sup{u | π₁(u) > 0} = sup{u | π₀(u) > 0}. Otherwise, without loss of generality assume that sup{u | π₀(u) > 0} < sup{u | π₁(u) > 0}. In such a case, one may choose t_H = sup{u | π₀(u) > 0}, which is greater than t = sup{u | π₀(u) > ε} for some positive ε. However, in theory, the difference between t and t_H can be made small by choosing ε close to zero.

3. Asymptotical efficiency of the test based on D̂ and θ̂

In this section, we derive the asymptotic efficiencies of the tests based on D̂ and θ̂ under a sequence of contiguous alternatives (Hoeffding and Rosenblatt, 1955; Hodges and Lehmann, 1956). Specifically, for the current case, these alternatives are defined as

$$\text{log}\left\{\frac{{\lambda }_{1n}(u)}{{\lambda }_0(u)}\right\}=\frac{\alpha (u)}{\sqrt{n}},$$

where λ₀(t) and λ_1n(t) are the hazard functions of the failure time T₀ from the treatment 0 and T_1n from the treatment 1, whose distribution depends on the sample size n, respectively (Lagakos, 1988; Slud, 1991). Here, α(·) is a deterministic function over time providing a specific alternative hypothesis of interest. For any given α(·), we can derive the asymptotic efficiency of the test under the mild regularity conditions given in p230–232, Chapter 6, Fleming and Harrington (2011).

For study size n, it follows from similar arguments in Schoenfeld (1981) and Harrington and Fleming (1982) that under the above contiguous alternatives $\sqrt{n}\hat{D}$ is asymptotic normal with mean

$${\int }_0^t\{{\int }_0^{\upsilon }\alpha (u){\lambda }_0(u)\mathit{\text{du}}\}{S}_0(\upsilon )d\upsilon$$

and variance

$${\sigma }_D^2={\int }_0^t{\{{\int }_{\upsilon }^t{S}_0(u)\mathit{\text{du}}\}}^2\frac{{\lambda }_0(\upsilon )}{w(\upsilon )}d\upsilon ,$$ (3)

which is the limit of ${\hat{\sigma }}_D^2$ defined in (1), where

$$w(\upsilon )=\frac{p_0{p}_1{\pi }_0(\upsilon ){\pi }_1(\upsilon )}{p_0{\pi }_0(\upsilon )+p_1{\pi }_1(\upsilon )}.$$

Thus, the asymptotic efficiency of the test based D̂ is

$${\xi }_1=\frac{{[{\int }_0^t\{{\int }_{\upsilon }^t{S}_0(u)\mathit{\text{du}}\}\alpha (\upsilon ){\lambda }_0(\upsilon )d\upsilon ]}^2}{{\int }_0^t{\{{\int }_{\upsilon }^t{S}_0(u)\mathit{\text{du}}\}}^{2}w{(\upsilon )}^{-1}{\lambda }_0(\upsilon )d\upsilon }.$$

Similarly, it follows from Lin and Wei (1989) that under above contiguous alternatives the test statistic $\sqrt{n}\hat{\theta }$ is also asymptotic normal with mean

$$\frac{{\int }_0^{t_H}w(u)\alpha (u){\lambda }_0(u)\mathit{\text{du}}}{{\int }_0^{t}w(u){\lambda }_0(u)\mathit{\text{du}}}$$

and variance

$${\sigma }_{\theta }^2={\{{\int }_0^{t_H}w(u){\lambda }_0(u)\mathit{\text{dt}}\}}^{-1},$$ (4)

which is the limit of ${\hat{\sigma }}_{\theta }^2$ in (2). The asymptotic efficiency for this test is

$${\xi }_2=\frac{{\{{\int }_0^{t_H}w(u)\alpha (u){\lambda }_0(u)\mathit{\text{du}}\}}^2}{{\int }_0^{t_H}w(u){\lambda }_0(u)\mathit{\text{du}}}.$$

It follows that the ARE of the t-MST based test relative to the HR-based test is ξ₁/ξ₂, which can be interpreted approximately as the inverse of the ratio of the sample sizes needed for two tests to have the same power to detect the alternative ${\lambda }_{1n}(u)=\text{exp}\{\alpha (u)/\sqrt{n}\}{\lambda }_0(u)$.

Note that the standard logrank test, a score test based on the Cox partial likelihood function for testing the equivalence of two survival functions, is asymptotically equivalent to the Wald-type of test based on the HR and therefore ξ₁/ξ₂ is also the ARE of the t-MST based test relative to the logrank test.

Since ARE is approximately a ratio of the sample size of two tests to have similar power for testing the same alternative hypothesis, this connection provides a clear practical interpretation of ARE (Schoenfeld and Richter, 1982; Zhang and Quan, 2009). Specifically, assuming that the alternative hypothesis consists of two fixed unequal hazard functions, say, λ₀(u) and λ₁(u), the sample size needed for the t-MST based test can be approximated by (z_1−α/2 + z_1−β)²/ξ₁, if this alternative is “close” to the null hypothesis, where z_q is qth quantile of the standard normal and α and β are the Type I and II error rates, respectively. More generally, a more accurate sample size estimator for 100(1 − β)% power at the two-sided significance level of α is

$${(z_{1-\alpha /2}+z_{1-\beta })}^2\frac{{\int }_0^t[{\{{\int }_{\upsilon }^t{S}_0(u)\mathit{\text{du}}\}}^2\frac{{\lambda }_0(\upsilon )}{p_0{\pi }_0(\upsilon )}+{\{{\int }_{\upsilon }^t{S}_1(u)\mathit{\text{du}}\}}^2\frac{{\lambda }_1(\upsilon )}{p_1{\pi }_1(\upsilon )}]d\upsilon }{{[{\int }_0^t\{S_1(u)-S_0(u)\}\mathit{\text{du}}]}^2},$$ (5)

for any pair of {λ₀(u), λ₁(u)}. Similarly, the corresponding sample size estimate analogy for HR based test is

$${(z_{1-\alpha /2}+z_{1-\beta })}^2\frac{{\int }_0^{t}w{(u)}^2\{\frac{{\lambda }_0(u)}{p_0{\pi }_0(u)}+\frac{{\lambda }_1(u)}{p_1{\pi }_1(u)}\}\mathit{\text{du}}}{{[{\int }_0^{t}w(u)\{{\lambda }_1(u)-{\lambda }_0(u)\}\mathit{\text{du}}]}^2}.$$ (6)

When λ₁(u) for the treated arm is close to λ₀(u) for the control arm, the ratio of the two sample size estimates is approximately equal to the inverse of ARE. The ARE, coupled with these two sample size estimates, may provide a meaningful comparison of these two tests. However, when λ₁(u) is quite different from λ₀(u), ARE may not be a good approximation to such a ratio of the sample sizes. In this case, one may consider the empirical relative efficiency (ERE), $E_D^2/E_{\theta }^2$, where

$$E_D=\frac{E(\hat{D})}{\mathit{\text{se}}(\hat{D})}\text{ and }{E}_{\theta }=\frac{E(\hat{\theta })}{\mathit{\text{se}}(\hat{\theta })}$$

are the effect sizes standardized by their standard errors for tests based on D̂ and θ̂, respectively. While ERE in general can only be approximated numerically, a close-form expression for ARE can often be obtained via a series of first order approximations under the contiguous alternative. For example, the approximation

$$E(\hat{D})\approx {\int }_0^t\{S_1(u)-S_0(u)\}\mathit{\text{du}}={\int }_0^t{S}_0(\upsilon )[e^{-{\int }_0^{\upsilon }\{{\lambda }_1(u)-{\lambda }_0(u)\}\mathit{\text{du}}}-1]d\upsilon \approx {\int }_0^t[{\int }_0^{\upsilon }{\lambda }_0(u)\text{ log}\{{\lambda }_0(u)/{\lambda }_1(u)\}\mathit{\text{du}}]S_0(\upsilon )d\upsilon ,$$

may be used to compute the asymptotic efficiency of the test based on t-MST. While the first approximation above is fairly accurate in general, the second approximation is sensitive to the distance between λ₁(u) and λ₀(u). Similar approximation has been employed to derive ${\sigma }_D^2$ in (3). Consequently, the asymptotic efficiency ξ₁ may not be a good approximation to the ratio {E(D̂)}²/var(D̂), which ultimately dictates the actual power of the test based on t-MST, especially when λ₁(u) and λ₀(u) are markedly different at some time points. On the other hand, for any given sample size, we may simulate a large number of D̂s according to the postulated survival and censoring distributions under the alternative and directly approximate E(D̂) and var(D̂) by the empirical average and variance of simulated D̂s, respectively, without relying on any assumption on the difference between λ₁(u) and λ₀(u). This approach is even more appealing in estimating the expectation and variance of the HR estimator, which is the solution of a complex nonlinear estimating equation and does not have an exact close-form expression. In summary, although estimating ERE is more computational intensive, the power calculation based on ERE is more robust and the approximations to (5) and (6) can be used to evaluate the relative merits of two tests under any alternative. An example is given in the next section to illustrate this point.

4. Example and Numerical Study

In this section, we will evaluate the empirical performance of these two tests. To gain insights for the numerical results to be presented, we first note that under the contiguous alternative, the t-MST based test is asymptotically equivalent to the test based on

$${\int }_0^t\frac{{\int }_{\upsilon }^t{S}_0(u)\mathit{\text{du}}}{{\int }_0^t{S}_0(u)\mathit{\text{du}}}d\{{\hat{\mathrm{\Lambda }}}_1(\upsilon )-{\hat{\mathrm{\Lambda }}}_0(\upsilon )\},$$

while the HR-based test is equivalent to the test based on

$${\int }_0^{t_H}{S}_C(\upsilon )S_0(\upsilon )d\{{\hat{\mathrm{\Lambda }}}_1(\upsilon )-{\hat{\mathrm{\Lambda }}}_0(\upsilon )\}.$$

Here we assume that the survival functions of the censoring distributions at two groups are identical and denoted by S_C(·). If t = t_H, the difference between these two tests thus only depends on the choice of weight function. To be specific, let

$$w_D(\upsilon )=\frac{{\int }_{\upsilon }^t{S}_0(u)\mathit{\text{du}}}{{\int }_0^t{S}_0(\upsilon )d\upsilon }\text{ and }{w}_{\theta }(\upsilon )=S_C(\upsilon )S_0(\upsilon )$$

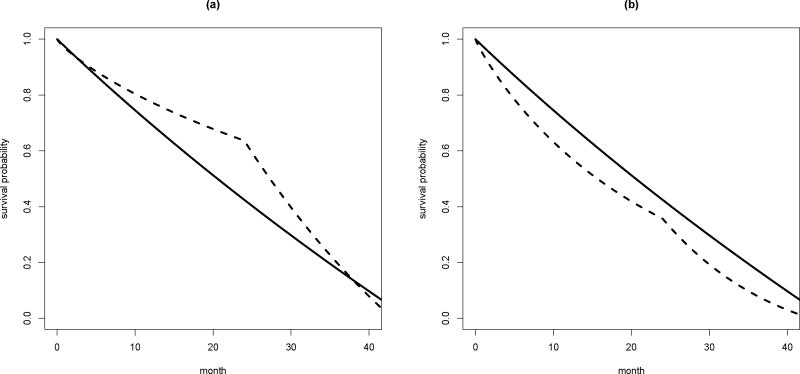
be the weight functions of the t-MST and HR based tests, respectively. w_D(υ) is independent of the censoring distribution and monotone decreasing from 1 to 0, while w_θ(υ) depends on the censoring distribution and monotone decreasing from 1 to S_C(t)S₀(t) > 0. In Figure 2, we plot the weight functions for both tests with following survival functions for the failure and censoring time distributions:

$$S_0(\upsilon )=\text{exp}(-0.016{\upsilon }^{0.826})\text{ and }{S}_C(\upsilon )=e^{-{\lambda }_c\upsilon }\frac{\{{\tau }_u-\text{max}(\upsilon ,{\tau }_l)\}}{({\tau }_u-{\tau }_l)}I(\upsilon \le {\tau }_u),$$

where λ_c = 0.06% or 2.5% and [τ_l, τ_u] = [24, 43]. Those model parameters are selected to mimic the ECOG-ACRIN study described in the next subsection. It is clear that w_D(υ) assigns less weights to later difference in hazard function compared with w_θ(υ) when the censoring is light. In such a case, the relative performance of t-MST and HR based tests should depend on the temporal profile of the difference between two hazard functions. For example, when the treatment difference is anticipated at later study time points, the t-MST based test tends to be less powerful than the HR based test. On the other hand, when the drop-out rate is high, w_D(υ) can be very similar to w_θ(υ), suggesting similar performance of these two tests. In the next two subsections, we will present detailed results from numerical study, which confirms the aforementioned expectation.

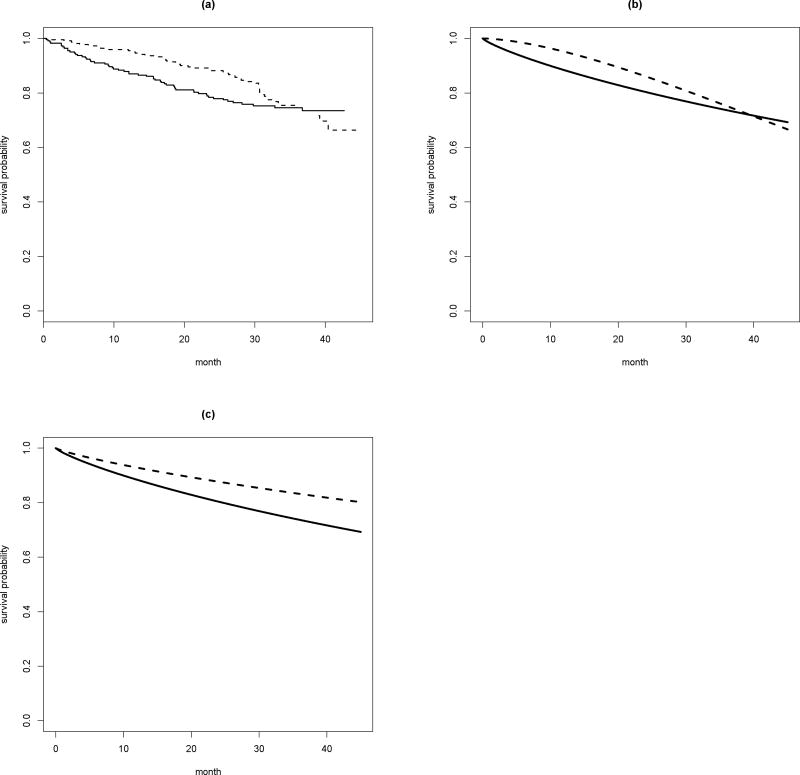
Figure 2.

(a) The KM curves in two arms of the ECOG-ACRIN study; (b) The survival curves based on the Weibull model in two arms of the ECOG-ACRIN study without assuming the PH assumption; (c) The survival curves based on the Weibull model in the high dose arm of the ECOG-ACRIN study assuming the PH assumption with a HR of 0.7; solid: high dose arm; dotted: low dose arm.

4.1 Real Data Example

We first use a study recently conducted by the ECOG-ACRIN Cancer Research Group to compare low- and high-dose dexamethasone for treating newly diagnosed multiple myeloma (Rajkumar et al., 2010) to illustrate how to interpret the ARE (t-MST vs. HR based tests). This study randomized 222 patients to the low-dose group and 223 patients to the high-dose group. Figure 1a shows the resulting KM curves of overall survival by treatment groups. Visually it seems that the patients in the low-dose group survived longer than those in the high dose group. The p-values from the tests based on HR and t-MST are 0.47 and 0.04, respectively. The discrepancy is likely due to the presence of crossing hazards. In this study, the nonparametric KM curves are fairly similar to their parametric counterparts based on a Weibull model (Figure 1b). Now, suppose that we are interested in designing a new study using the results from this ECOG-ACRIN study. That is, assume that the observed pattern of the two observed hazard functions from this study is the alternative hypothesis for a new study. The question is how the t-MST test would perform compared with the HR based test with respect to the ARE and how to interpret this ratio measuring the relative merit of these two tests. To this end, we assume that the event time follows Weibull distributions as shown in Figure 1b. Furthermore, we assume this new study would have similar patient’s accrual and follow up time patterns, that is the entire study duration is about 43 months with a 19-month enrollment period. Furthermore, we let the time of loss of follow-up follows an exponential distribution with an annual drop-off rate of 1% for both arms without accounting for the administrative censoring due to the staggered entry of study patients. We also let t = 40 and t_H = 43 months for defining the follow-up period of interest for t-MST and HR, respectively. Under these assumptions, the required sample size for 80% power at the significance level of 0.05 is n_θ = 2532 per arm for the HR-based test and n_D = 564 per arm for the t-MST based test. The ARE is 2.23, which also strongly favors t-MST based test but quantitatively different n_θ/n_D. In this case, we also can use simulation to directly estimate the ERE, the finite sample analogy of ARE. To this end, we simulate 5000 sets of data consisting of 1000 patients each under the assumed alternatives and obtain the corresponding D̂ and θ̂ from each simulated data set. We then approximate the expectation and variance of D̂ (and θ̂) by their empirical counterparts. The resulting ERE is 4.41, which is pretty close to n_θ/n_D. It suggests that the “alternative” of interest is not adequately close to null and ARE may not accurately reflect the ratio of the needed sample sizes of the two tests in this case. With the above sample size estimates, one still can assess the practical gain from the t-MST test over the HR test. We have performed the additional simulation studies to empirically estimate the true power of HR and t-MST based tests with the estimated sample sizes. The empirical powers based on 5000 simulations are 80.1% and 80.9% for t-MST and HR based tests, respectively, which confirms the adequacy of the estimated sample sizes based on (5) and (6). The required sample size is much greater than that in actual study, since more patients are needed to ensure 80% chance of obtaining a p-value smaller than 0.05.

Figure 1.

The weight functions for t-MST and HR based tests; solid: weight function for t-MST based test; dotted: weight function for HR based test; (a) light drop-out rate with λ_c = 0.06% and (b) high drop-out rate with λ_c = 2.5%

Now, we use the above setting, but modify the underlying Weibull distribution of the low dose group to follow the PH assumption with a true HR of 0.70 against the high-dose arm. The survival curves of this alternative are plotted in Figure 1c. With this specific PH alternative, the required sample sizes are n_D = 641 for t-MST based test and n_θ = 591 for HR based test. Both ARE and ERE are 0.96 and 0.91, respectively, which are pretty close to n_θ/n_D. This example suggests that even when the PH assumption is valid, the t-MST test is essentially as powerful as the HR test.

4.2 Simulation Study

In this subsection, we further explore extensively the relative merits between the two tests under various scenarios. We focus on the settings, where the survival functions are ordered without crossing during the followup and we can claim patients from one arm live longer than those from another during the time interval of interest without any ambiguity. When two KM curves cross during the study followup period, one may explore whether there is a subgroup of patients who may not benefit from the new therapy based on the patients baseline covariates. Note that the hazard functions may still cross during the followup even if the survival curves don’t. Now, for our study, firstly, we consider the case where t_H ≥ t and the PH assumption holds true, i.e., α(u) = 1. For this case, the ARE

$$\le \frac{{[{\int }_0^t\{{\int }_{\upsilon }^t{S}_0(u)\mathit{\text{du}}\}{\lambda }_0(\upsilon )d\upsilon ]}^2}{{\int }_0^t{\{{\int }_{\upsilon }^t{S}_0(u)\mathit{\text{du}}\}}^{2}w{(\upsilon )}^{-1}{\lambda }_0(\upsilon )d\upsilon \times {\int }_0^{t}w(u){\lambda }_0(u)\mathit{\text{du}}},$$

which is always ≤ 1 by Cauchy inequality, suggesting that the HR-based test is more powerful under the PH assumption. To quantify the efficiency loss of the t-MST based test under practical settings, we assume that the study has a recruitment period of 19 months and additional follow-up of 24 months after the last patient entered the trial as in the aforementioned ECOG-ACRIN study. Specifically, the censoring time is assumed to be the minimum of C_L ~ EXP(λ_c) and C_A ~ U(τ_L, τ_U), reflecting the loss of follow-up and administrative censoring due to staggered entry, respectively. It follows that the survival function for the censoring time is

$$S_C(u)=e^{-{\lambda }_{c}u}\frac{\{{\tau }_U-\text{max}(u,{\tau }_L)\}}{({\tau }_U-{\tau }_L)}I(u\le {\tau }_U),$$

where [τ_L, τ_U] = [24, 43]. Here, we let t = 40 and t_H = 42.5 months. Furthermore, we set λ_c = 0.06% matching the annual loss of follow-up rate observed in the ECOG-ACRIN study and λ_c = 2.5%, an annual loss of follow-up rate of 26%, to represent heavier censoring caused by, for example, drop-out. Lastly, we also assume that the survival time in the treatment group 0 follows a Weibull distribution with the shape parameter being the maximum likelihood estimator in the high-dose group of the ECOG-ACRIN study, that is, having a decreasing hazard function λ₀(u) = a₀u^−0.174. With this setup, ARE is determined by a0, the scale parameter of the Weibull distribution in the treatment group 0. We adjusted the scale parameter so that S₀(t) = 0.1, ⋯, 0.9. The detailed results on ARE are summarized in Table 1. Under the PH assumption, the HR-based test is slightly more powerful as anticipated. Furthermore, when the cumulative event rate is relatively high, for example, pr(T₀ < t) ≥ 0.5, as for studies of serious diseases with high event rates, the efficiency loss of t-MST based test relative to the HR based optimal test is almost negligible.

Table 1.

Asymptotical relative efficiency ARE) and empirical relative efficiency (ERE) under PH alternatives with a HR of 0.7; EREs are estimated based on 5000 sets simulated data.

	ARE(ERE)
Censoring	light	heavy
S0(t) = 0.90	0.95(0.94)	1.05(1.03)
S0(t) = 0.80	0.96(0.96)	1.05(1.03)
S0(t) = 0.70	0.97(0.93)	1.05(1.01)
S0(t) = 0.60	0.98(0.96)	1.06(1.03)
S0(t) = 0.50	0.99(0.96)	1.06(1.02)
S0(t) = 0.40	1.01(0.97)	1.06(1.02)
S0(t) = 0.30	1.02(0.97)	1.06(1.02)
S0(t) = 0.20	1.04(0.99)	1.05(1.02)
S0(t) = 0.10	1.05(1.01)	1.04(1.01)

To confirm these theoretical AREs, we have also performed numerical simulations to obtain the ERE by estimating E_D and E_R based on results from 5000 simulated data sets. The true HR for two treatment groups (treatment group 1 vs. 0) is 0.70. The resulting EREs are all very close to their asymptotical counterparts (Table 1). For example, when λ_c = 0.06% and S₀(t) = 0.60, the ARE and ERE are 0.98 and 0.96, respectively.

Next, we consider three non-PH settings:

1. HR is monotone increasing from < 1 at time 0 to > 1 at time t;

2. HR is monotone increasing from < 1 at time 0 to 1 at time t;

3. HR is monotone decreasing from 1 at time 0 to < 1 at time t.

The first setting corresponds to the worst violation of the PH assumption: crossing hazards. In this case, we let α(u) = log(0.46) + (u/t_M)^s, i.e., the HR is 0.46 at time zero, crosses 1 and eventually increases to 1.25 at time t_M. Here t_M is the longest follow-up time, which is greater than both t in t-MST and t_H in estimating the HR. In this case, the parameter s dictates how fast the HR increases with time and ARE. Although HR crosses one, two survival functions here don’t cross within the interval [0, t_M]. The second setting corresponds to the case where the treatment benefit is large at time 0 but gradually diminishes. To characterize this pattern, we let α(u) = −c(t_M − u)^s, where the constant c is chosen such that the average HR, $t_M^{-1}{\int }_0^{t_M}\text{exp}\{\alpha (u)\}\mathit{\text{du}}$, is approximately 0.7. The last setting corresponds to the case, where the treatment benefit is small at the beginning but grows gradually during the follow-up. Specifically, we let α(u) = −cu^s, where c is a constant such that the average HR is approximately 0.7. For all three settings, both the analytic ARE and ERE based on 5000 simulations are evaluated for all combinations of s ∈ {0.5, 1, 2}, λc ∈ {0.06%, 2.5%} and survival rates S₀(t) ∈ {0.30, 0.50, 0.70} and reported in Table 2. In the simulation, we let (t, t_H, t_M) = (40, 42.5, 43) to reflect the fact that HR often can be estimated over a larger time interval than t-MST.

Table 2.

Asymptotical relative efficiency (ARE) and empirical relative efficiency (ERE) under nonproportional hazards alternatives; EREs are estimated based on 5000 sets simulated data.

	S0(t) = 0.30		S0(t) = 0.50		S0(t) = 0.70
	ARE(ERE)		ARE(ERE)		ARE(ERE)
Censoring	light	heavy	light	heavy	light	heavy
			α(u) = log(0.46) + (u/t)s
s = 0.5	1.76(1.77)	1.16(1.13)	2.02(2.05)	1.24(1.22)	2.30(2.37)	1.34(1.31)
s = 1.0	1.34(1.33)	1.11(1.08)	1.42(1.41)	1.15(1.13)	1.49(1.47)	1.20(1.17)
s = 2.0	1.18(1.17)	1.09(1.07)	1.21(1.19)	1.11(1.10)	1.23(1.23)	1.13(1.12)
			α(u) = −c(α)(t − u)s
s = 0.5	1.10(1.05)	1.07(1.05)	1.10(1.06)	1.09(1.06)	1.10(1.07)	1.10(1.06)
s = 1.0	1.20(1.17)	1.09(1.06)	1.22(1.19)	1.11(1.09)	1.24(1.21)	1.13(1.11)
s = 2.0	1.37(1.34)	1.11(1.09)	1.43(1.38)	1.16(1.13)	1.48(1.45)	1.19(1.17)
			α(u) = −c(α)us
s = 0.5	0.84(0.80)	1.02(0.99)	0.81(0.77)	1.00(0.96)	0.78(0.76)	0.98(0.94)
s = 1.0	0.74(0.70)	1.00(0.96)	0.70(0.67)	0.96(0.92)	0.67(0.64)	0.92(0.90)
s = 2.0	0.61(0.58)	0.96(0.93)	0.56(0.54)	0.89(0.86)	0.53(0.52)	0.84(0.82)

When HR is monotone increasing and crosses one during the follow-up (Case 1), the t-MST based test can be substantially more efficient than the HR-based test; when the HR is less than one at time 0 and increases to 1 at the end the study (Case 2), the t-MST based test is also more efficient than the HR-based test but the difference is modest; and when the HR is 1 at time 0 and decreases over time (Case 3), the t-MST based test can be less efficient than the HR-based test. Similar to the case where the PH assumption holds, the EREs are in general consistent with their asymptotical counterparts in all settings, supporting the use of EREs for evaluating the finite sample performances of two tests.

5. Conclusions

In this paper, we compared the inference procedures based on HR and the t-MST difference under a hypothesis testing paradigm. Through an extensive numerical study with various treatment difference profiles, the AREs for the t-MST and HR tests are similar under the PH-models. For the non-PH models, unless the true difference of two survival functions is quite large near the end of the study and the censoring is light during the study follow-up, the t-MST test generally outperforms the HR test. The employed technique is analogous to those used for comparing the nonparametric tests for shift in location with the t-test when the normality assumption is violated (Ruberg, 1986). In summary, the t-MST based test is preferred if we are expecting an early benefit, for example, caused by less invasive treatment such as a low dose option. On the other hand, HR-based test is more powerful for detecting the delayed treatment effect encountered in recent oncology trials testing the efficacy of immunotherapy.

Perhaps a line of future research is to construct more powerful tests adaptive to the deviation from PH assumption. There are quite a few novel statistical tests for non-proportional hazards alternatives proposed and discussed in the literature (Fleming et al., 1987; Pepe and Fleming, 1989; Kosorok and Lin, 1999; Feng and Wahed, 2008; Yang and Prentice, 2010; Uno et al., 2015; Garès et al., 2015). However, there are no coherent corresponding estimation procedures to quantify the treatment difference. A more powerful test than the HR test for a non-PH case without a companion estimation procedure would have limited value clinically. To make coherent evaluation on the group difference, we suggest to first define a clinically meaningful measure summarizing the treatment benefit and employ the corresponding estimation and hypothesis testing procedure to conduct the statistical analysis. There are very few two-sample model-free estimating procedures for treatment effect, which can also be used for testing the equivalence of two survival functions in survival analysis. For example, one may use the difference or ratio of two t-year event rates, median survival times, and t-MSTs. Often the median event time is not estimable due to a short study followup time. Using the t-year event rate difference as the primary parameter of interest would ignore the temporal profile of the treatment effect before and after the time point t. The estimate for the t-MST difference or ratio appears to be a useful tool for analyzing event time observations for both its interpretability and the power of the associated hypothesis testing procedure.