Comprehensive computational design of ordered peptide macrocycles

Abstract

Mixed-chirality peptide macrocycles such as cyclosporine are among the most potent therapeutics identified to date, but there is currently no way to systematically search the structural space spanned by such compounds. Natural proteins do not provide a useful guide: Peptide macrocycles lack regular secondary structures and hydrophobic cores, and can contain local structures not accessible with L-amino acids. Here, we enumerate the stable structures that can be adopted by macrocyclic peptides composed of L- and D-amino acids by near-exhaustive backbone sampling followed by sequence design and energy landscape calculations. We identify more than 200 designs predicted to fold into single stable structures, many times more than the number of currently available unbound peptide macrocycle structures. Nuclear magnetic resonance structures of 9 of 12 designed 7- to 10-residue macrocycles, and three 11- to 14-residue bicyclic designs, are close to the computational models. Our results provide a nearly complete coverage of the rich space of structures possible for short peptide macrocycles and vastly increase the available starting scaffolds for both rational drug design and library selection methods.

The high stability, diverse functionality, and favorable pharmacokinetic properties of macrocyclic peptides make them promising starting points for targeted therapeutics (1–4). However, there are few well-characterized natural macrocycles, and they are difficult to repurpose for new functions. Thus, most current approaches focus on random library selection methods, which, although powerful (5–7), only cover a small fraction of the vast sequence space that can be accessed by even short sequences of L- and D-amino acids (8,9) and often yield peptides that are not structured in the absence of target. Methods are needed for designing ordered macrocycles with shapes precisely crafted to bind their targets and with functionalities common in medicinal chemistry, but absent in the natural 20 amino acids, positioned at critical interaction sites. Despite the progress in computational design of proteins (10–14) and constrained peptides as small as 18 residues (15), designing shorter peptide macrocycles had remained an unsolved challenge. The driving force for the folding of larger peptides and proteins is the sequestration of hydrophobic residues in a nonpolar core, enabled by regular secondary structures in which buried backbone polar groups can make hydrogen bonds. This principle has been the basis of almost all previous peptide and protein design work. However, the balance of forces is considerably different for 7- to 10-residue peptides: They are too small to have either a solvent-excluded hydrophobic core or α-helical and β-sheet (other than β-hairpin) secondary structures. Beyond these differences in the physics of folding, protein design methods often use the PDB (Protein Data Bank) as a source of local structural information, but native structures provide a poor guide for local structures that include noncanonical D-amino acids. On the other hand, short cyclic peptides are an attractive target for computational design because unlike larger systems, there is the possibility of obtaining a completeness of conformational sampling rare in any molecular design endeavor.

The local structure space relevant for cyclic peptides is quite different from that of proteins, so they cannot be systematically generated by assembling protein fragments. Instead, we used generalized kinematic closure (genKIC) (15–17) drawing from achiral flat-bottom backbone torsional distributions (fig. S1, A and B) to generate closed backbone structures starting from a polyglycine chain. For each structure, we used Monte Carlo simulated annealing to search for the lowest-energy amino acid sequence, restricting positions with negative values of the backbone torsion angle phi to L-amino acids (and rotamers) and those with positive values to D-amino acids, and disallowing glycine to maximize local sequence encoding of the structure. In preliminary calculations, we found that energy gaps greater than ~10 k_BT (~6 kcal/mol), where k_B is the Bolzmann constant and T is temperature, could only be obtained for N-residue macrocycles if they contained at least N/3 backbone hydrogen bonds; hence, in subsequent calculations, back-bones with fewer hydrogen bonds were discarded. We carried out large-scale backbone generation and sequence design calculations for 7- to 10-residue backbone cyclized peptides, obtaining 50, 596,12,374, and 49,571 distinct backbones for lengths 7, 8, 9, and 10, respectively, after clustering based on backbone torsion angle bins (ABXY, where torsion bin A is the helical region of Ramachandran space, B is the extended strand region, X is mirror of A, and Y is mirror of B) (Fig. 1A) and backbone hydrogen bond patterns (fig. S1, C to E). Because the sampling method is stochastic, there is no guarantee of completeness, but the symmetry of the system enables a convergence test: For each distinct peptide backbone conformation identified, the mirror image should also be observed (figs. S2 and S3). As the amount of sampling increases, the number of clusters identified for which the mirror image is observed initially increases, as does the number of clusters with no mirror. The former then plateaus, whereas the latter decreases to near zero (Fig. 1B). Such convergence suggests near-complete coverage of the combined D- and L-space compatible with peptide closure with backbone hydrogen bonds and no steric clashes. We also sampled and designed structures for 11- to 14-residue macrocycles, but did not seek completeness owing to combinatorial explosion in the number of states.

Fig. 1. Expanding the repertoire of ordered macrocycles by comprehensive sampling.

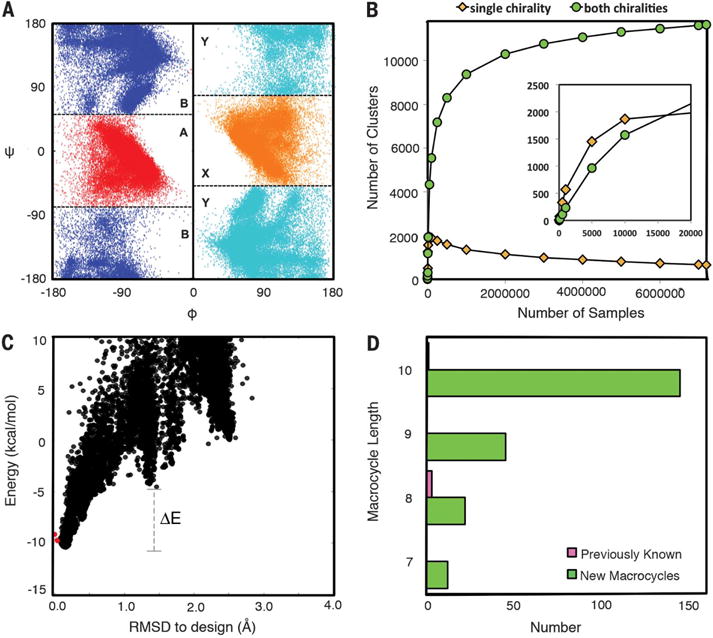
(A) Torsion bin definitions (bin B = blue; A = red; Y = mirror of bin B, cyan; X = mirror of bin A, orange) overlaid on the generated nine-residue macrocycle backbone torsion angle distributions. The inversion symmetry is evident. (B) Convergence test. The number of clusters (torsion bin strings) observed for which the mirror image is not observed (yellow) or for which the mirror image is observed (cyan) was determined both for the complete set of 7,500,000 samples for nine-residue macrocycles and for randomly selected subsets of different sizes (x axis). For comparison, the less converged results obtained starting from a 20,000-sample subset and then down-sampling are shown in the inset: The fraction of single-chirality clusters is higher, and the number of both-chirality clusters does not plateau. (C) Energy landscape analysis using large-scale genKIC backbone generation followed by all-atom energy minimization. Each point is the result of an independent calculation; the energy is shown on the y axis and the root mean square deviation (RMSD) from the design model on the x axis. The extent of funneling (or convergence) of the energy landscape is quantified through the energy gap between conformations generated by stochastic sampling around the design model (red points) and high-RMSD structures, and the Boltzmann weight of the near–design model population. (D) Number of designed macrocycle clusters with distinct torsion bin strings and backbone hydrogen bond patterns with energy gaps less than −0.1 and Boltzmann weights greater than 0.85; the number of unbound peptide macrocycles in the PDB and CSD, consisting of only 20 canonical amino acids and their D-enantiomers, is indicated in pink.

The Monte Carlo simulated annealing sequence design calculations seek a sequence that minimizes the energy of the target backbone conformation, but there is no guarantee that the sequence found maximizes the energy gap between the target backbone conformation and alternative conformations. To assess the energy landscape for low-energy designs (from 21 designs for length 7 to 673 designs for length 10), 10⁴ to 10⁵ conformations were generated for each sequence, and the energy was minimized with respect to the backbone and side-chain torsion angles. The energy gap and Boltzmann-weighted probability of finding the peptide in or close to the designed main-chain conformation (P_Near) were estimated from the resulting energy landscapes (Fig. 1C). A total of 12, 22, 45, and 145 designs with distinct backbone structures had energy landscapes strongly funneled into the design target structure for 7-, 8-, 9, and 10-residue macrocycles, respectively (Fig. 1D and figs. S4 and S5). For comparison, in the PDB and CSD (Cambridge Structure Database), we only found four 7- to 10-residue macrocycle structures not bound to a target and composed only of the 20 canonical amino acids and their mirror images without cross-links or backbone modifications such as N-methylation (Fig. 1D and fig. S6).

Because of the constraints imposed by the cyclic backbone, the small size, and the presence of D-amino acids, the designs span a local structural space inaccessible or underexplored in native proteins. Recurrent features include hydrogen-bonded turnlike structures and proline-stabilized kinks, some of which are observed rarely or not at all in native proteins (Fig. 2 and fig. S7A), that can be viewed as macrocycle-generating building blocks (fig. S7B and table S1). Stepwise residue insertion preserves some of the building blocks and alters others, resulting in a complex propagation of features from the shorter macrocycles to the longer ones (Fig. 2).

Fig. 2. Recurrent local structural motifs in designed macrocycles.

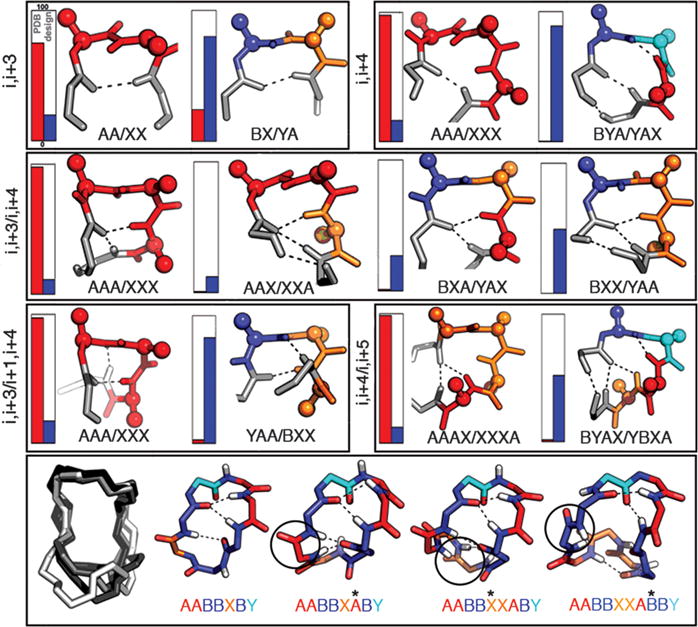
Top three rows: frequencies in native proteins in the PDB (red) and in the designed macrocycles (blue) indicated by vertical bars (including both enantiomers); structures on the right are colored by torsion bin as in Fig. 1A. Bottom row: example of structure propagation with residue insertion for a 7- to 10-residue macrocycle series.

It was not feasible to characterize each of the >200 macrocycle designs (database S1) experimentally. Instead, we chemically synthesized (fig. S8) a subset of 12 peptides [four 7-residue peptides (7mers), two 8mers, three 9mers, and three 10mers; tables S2 to S4] and experimentally characterized their structures by nuclear magnetic resonance (NMR) spectroscopy (table S5 and figs. S9 to S11). Ten of the 12 peptides had well-dispersed one-dimensional NMR spectra, with the number of backbone HN peaks expected for a single conformation (tables S2 to S5). We collected extensive nuclear Overhauser effect (NOE) data (fig. S11) for these peptides and solved their structures using XPLOR-NIH (18,19) followed by NOE-restrained molecular dynamics (MD) simulations [similar structures were obtained with an independent large-scale enumeration approach (fig. S12)]. As shown in Figs. 3 and 4 and described below, the experimental NMR structures closely matched the design models for nine of these peptides, and in unrestrained MD simulations, eight out of the nine peptides are within 1 Å of the designed structure more than 75% of the time (figs. S13 to S15 and table S6). These data suggest that a large fraction of our >200 macrocycles are structured as designed.

Fig. 3. Seven- to eight-residue macrocycle NMR structures are very close to design models.

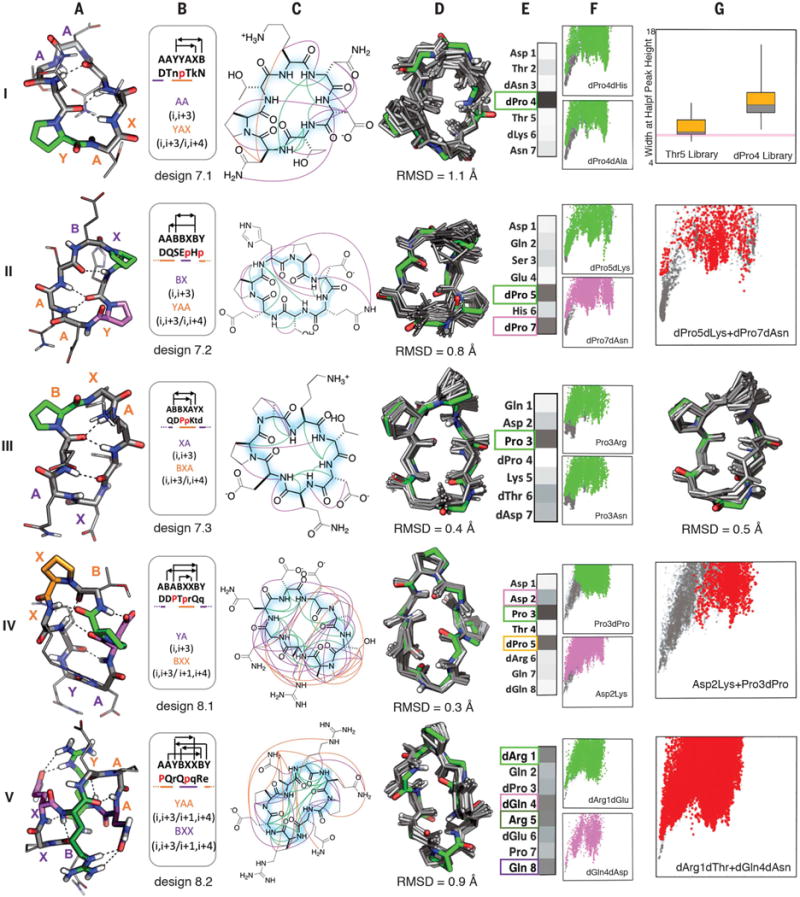
Columns A: Design model. B: Amino acid sequence, torsion bin string, hydrogen bond pattern, and building block composition. C: Observed backbone-backbone (green), backbone–side-chain (purple), and side-chain–side-chain (orange) NOEs. D: Overlay of design model (green) on MD-refined NMR ensemble (gray; the average backbone RMSD to the NMR ensemble is indicated). E: Average decrease in the propensity to favor the designed state (P_Near, see methods) over all mutations at each position. Darker gray indicates larger decreases (P_Near values for each substitution at each position are in fig. S16); positions particularly sensitive to mutation are boxed and indicated by color in the design model in column A. F: Representative energy funnels for mutations at key positions (colored points) as compared to the design sequence (gray points). Row I, column G: Experimental SLIM data. Distribution of peak width at half height for peptide libraries with all amino substitutions at positions 4 and 5; the position 4 library has a broader distribution consistent with the computed energy landscape in column F. Rows II, IV, V, column G: Representative energy landscapes for double substitutions (red) of critical residues overlaid on the original design landscape (gray). Row III, column G: Overlay of design model on alternative structure NMR ensemble (turn flip at bottom right).

Fig. 4. Nine- to 14-residue macrocycle NMR structures are very close to design models.

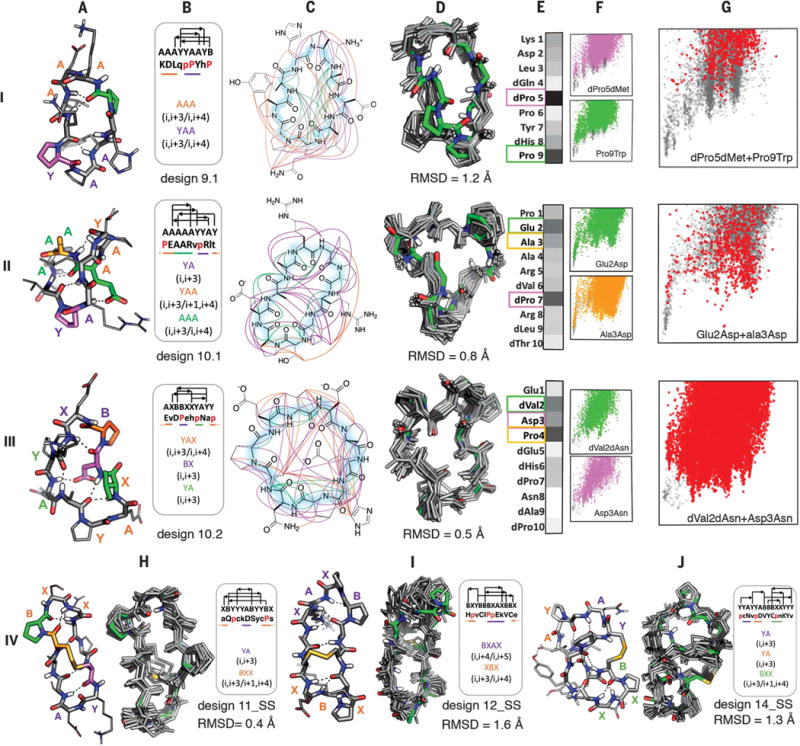
Rows I to III: 9- and 10-residue designs. Columns A to G are as in Fig. 3 rows II, IV, and V. Row IV: Comparison of bicyclic design models and NMR structures.

Unlike proteins, macrocycles cannot be stabilized primarily by the hydrophobic effect as they are too small to form a core that can exclude solvent (20). How, then, do the sequences of the designs specify their structures? To address this question, we computed the effect on folding of every single substitution to a different amino acid with the same chirality, and to an alanine with opposite chirality, at each position, for all the designs with NMR-confirmed structures. For each of the 20xNres variants, full energy landscape calculations were carried out through large-scale backbone enumeration (Figs. 3 and 4; details in fig. S16). These computationally intensive calculations were carried out by using cellular phones and tablets of volunteers participating in the Rosetta@Home distributed computing project (http://boinc.bakerlab.org/rosetta). To evaluate the computed sequence-energy landscape experimentally, we used SLIM (structures for lossless ion manipulations), an ion-mobility mass spectrometry technique that can distinguish different conformations in small molecular structures (21). This technique requires only a small amount of unpurified sample and enables parallel evaluation of the effects of amino acid substitutions on folding. SLIM results from a set of variants with point mutations of design 7.1 at either the dPro⁴ or Thr⁵ position (Fig. 3 and fig. S17) were consistent with the sequence-energy landscape calculations: The structure was perturbed more by mutations at the dPro⁴ position than at the Thr⁵ position, consistent with the computed P_Near values.

Several general principles emerge from the comprehensive landscape calculations and from folding calculations on permuted sequences (fig. S18). First, L- and D-proline residues play a key role in structure specification: 52% of the positions in which substitutions disrupt the structure are proline residues in the design, and in almost all of the cases, the most destabilizing mutant of a nonproline residue is a substitution to proline (fig. S19). Proline is the most torsionally constrained amino acid, and placement of L- and D-proline residues favors specific turn and kink structures. Second, side-chain–to–backbone hydrogen bonds that either stabilize a local structural motif, such as Asp² in design 8.1, or connect two sides of the structure, such as Glu² in design 10.1 or Asp³ in design 10.2, are important for structural specification as removal of these interactions substantially reduces the energy gaps. Third, chirality in many cases plays a greater role in structure specification than side-chain identity: Replacing an amino acid residue with its mirror-image isomer is usually more disruptive than changing to a different amino acid with the same chirality. Fourth, for each design, usually fewer than three residues (often proline) are critical to defining the fold, leaving the remainder largely free for future functionalization (figs. S16 and S19). Even after mutation of the remaining residues to Ala (retaining chirality), a number of the sequences still encode the designed structure (fig. S20). Overall, this global analysis of the effect of substitutions on energy landscape topography defines the sequence determinants of the folding-energy landscape in exceptional detail.

It is instructive to consider these data in the context of the structures and sequences of the individual designs. The seven-residue macrocycles exhibit several recurrent backbone hydrogen-bonding patterns, often featuring a proline-nucleated i, i + 3/i, i + 4 motif (Fig. 2, second row, and fig. S21). Of the four seven-residue designs experimentally tested, three had structures nearly identical to the design models (Fig. 3 and table S7), and MD and Rosetta calculations on the fourth (design 7.4) suggest that it also is close to the design model despite overlap of backbone NH-group NOEs (figs. S12 and S15). The energy landscape calculations show that the proline nucleating the i, i + 3/i, i + 4 turn is essential (Fig. 3, A and E). The remainder of the structure is largely specified by the designed amino acid chirality with the exception of dPro⁵ in design 7.2, which packs on the turn-nucleating dPro⁷. The eight-residue macrocycles (fig. S22) are dominated by two major classes, one featuring two i, i + 3/i, i + 4 motifs (Fig. 2, second row) and the other, two criss-cross i, i + 3/i + 1, i + 4 motifs (Fig. 2, third row). The two eight-residue macrocycles that were experimentally characterized both had NMR structures within 1 Å of the design model. Design 8.1 has multiple slow-exchanging (fig. S23) side-chain–side–chain and side-chain–backbone hydrogen bonds, with a structurally critical (Fig. 3, panels IV. A and E) hydrogen bond from Asp² to the backbone of Thr⁴, which along with Pro³ stabilizes a sharp kink in the chain. Adjacent to the kink is a BXX (i, i + 3/i + 1, i + 4) motif rare in proteins, anchored by the structurally critical dPro⁵. Design 8.2 has near-perfect sequence inversion symmetry; the sequence-symmetric version of this design with sequence Pro-Gln-dArg-Glu-dPro-dGln-Arg-dGlu and torsion string AAYBXXBY has half the number of NMR resonances (three backbone HN instead of six), consistent with structural S₂ symmetry (fig. S24). In contrast to the other seven- to eight-residue designs characterized, all residues in design 8.2 are important for structure specification (fig. S16 and Fig. 3, panel V. E), with residues involved in multiple side-chain–side-chain hydrogen bonds more essential than the two prolines.

As the macrocycle length increases (9 and 10 residues, Fig. 4), so does the entropic cost of folding, and more hydrogen bonds in increasingly diverse patterns (fig. S25) are required to stabilize the peptide in the folded state. Three of six experimentally characterized designs had structures close to computational models, one was disordered, and two had well-dispersed spectra, but the NOE data did not uniquely define the structures (table S5). Design 9.1 contains a YAA i, i + 3/i, i + 4 building block similar to those in the seven-residue macrocycles in which dPro⁵ plays a critical role (as in the L-Pro/D-Pro in design 7.3, the second proline plays a less critical role). The structure is expanded by insertion of a kink stabilized by Pro⁹; the remainder of the structure is completed by a tight AAA i, i +3/i, i + 4 turn. Design 10.1 contains a five-residue distorted helix terminated by the critical dPro⁷. On one face, the structurally critical Glu² in the middle of the helix makes a long-range side-chain–backbone hydrogen bond to Arg⁸, and on the other, Ala³, dVal⁶, and dLeu⁹ form a nonpolar cluster. Design 10.2 contains BX, YA, and the rare YAX building blocks, each beginning with a proline residue; of these, Pro⁴ in the BX motif is the most critical. As with 10.1, the building blocks are held together by nonpolar interactions (between dVal² and dAla⁸) on one face, and a long-range side-chainðbackbone hydrogen bond (from Asp³ to Asn⁸) on the other; both dVal² and Asp³ are critical for specifying the structure (Fig. 4, panel IV.E).

The entropic cost of folding continues to increase with increasing number of residues, and for 11- to 14-residue macrocycles, additional crosslinks to form bicyclic structures were required to obtain single states amenable to NMR structure determination (table S5). We solved the structures of three such designs (Fig. 4, row IV) that feature long-range backbone-backbone hydrogen bonds. Design 11_SS has a i, i + 3/i + 1, i + 4 building block (Fig. 2, third row) with a critical proline (fig. S16) in the first position preceded by a cysteine that forms a critical disulfide to a cysteine preceding a YA turn. Design 12_SS has a rare BXAX i, i + 4/i, i + 5 turn, which exhibits higher flexibility in the NMR structure, and a disulfide between non-hydrogen-bonding residues. The more compact and complex 14_SS design has a network of interleaved local and nonlocal backbone hydrogen bonds (22), and a D-Cys to L-Cys disulfide bond.

The wide variety of shapes spanned by our macrocycle designs, together with their high stability (fig. S26) and high predicted tolerance for sequence mutations (figs. S16 and S20), makes them attractive starting points for developing new therapeutics. One approach to inhibitor design is scaffolding loops at binding interfaces in the PDB; such scaffolding can increase binding affinity by preorganizing the loops in the binding-competent conformation, enable additional interactions with the target, and improve cell permeability and oral bioavailability (23). We found that 907 of the 1017 “hot loops” identified at protein-protein interfaces by Kritzer and co-workers (24) (database S2) could be scaffolded by one or more of our designs (see fig. S27 for some examples).

The finding that 70% of the experimentally tested 7- to 10-residue macrocycle designs adopt single unique structures close to the computationally designed models suggests that most of the 200+ new macrocycle designs with high computed Boltzmann weights fold as designed, increasing the known repertoire of possible macrocycle structures by more than two orders of magnitude. Our results demonstrate that the principles and energy functions developed in recent years to design proteins have quite broad applicability, transferring over to much smaller systems even though (i) the factors dominating the folding of proteins (for example, the hydrophobic effect) differ considerably from those that stabilize conformations of small peptide macrocycles (local hydrogen bonding patterns and intrinsic conformational preferences of amino acid building blocks), and (ii) all designed proteins to date contain regular α-helix or β-sheet structures, whereas small peptide macrocycles lack these and instead contain a wide range of local structures, some of which are rarely or never observed in proteins.

There are two clear paths forward for engineering new macrocyclic therapeutics by exploiting the rigidity and stability of the designs together with the freedom to choose the identities of the nonstructure-specifying positions. The first is experimental: Libraries can be constructed in which, at each position, all residues compatible with the structure are allowed (identified as described above by using large-scale energy landscape calculations) and screened for target binding with current library selection methodologies. The second is computational: Each macrocycle can be docked against the target (using, for example, rigid body docking or “hot loop” superposition), and the interface residues designed to maximize binding affinity. Unnatural amino acids can be incorporated in either approach, but the second has the advantage that new functionalities—such as known active site binding groups—can be strategically placed to maximize binding affinity. Beyond binding, the control over geometry and chemistry provided by our approach should contribute to understanding the structural correlates of membrane permeability and other desirable pharmacological properties.