Abstract
The Ebola forecasting challenge organized by the Research and Policy for Infectious Disease Dynamics (RAPIDD) program of the Fogarty International Center relies on synthetic disease datasets generated by numerical simulations of a highly detailed spatially-structured agent-based model. We discuss here the architecture and technical steps of the challenge, leading to data sets that mimic as much as possible the data collection, reporting, and communication process experienced in the 2014–2015 West African Ebola outbreak. We provide a detailed discussion of the model’s definition, the epidemiological scenarios’ construction, synthetic patient database generation and the data communication platform used during the challenge. Finally we offer a number of considerations and takeaways concerning the extension and scalability of synthetic challenges to other infectious diseases.
Keywords: Ebola, Forecast, Computational modeling
1. Introduction
The RAPIDD Ebola forecasting challenge arose from an Ebola Modeling workshop organized in March 2015 as part of the Research and Policy for Infectious Disease Dynamics (RAPIDD) program of the Fogarty International Center, US National Institutes of Health (NIH). The workshop convened the major academic teams that were involved in generating disease forecasts during the 2014–2015 West Africa Ebola outbreak to explore the successes and failures of disease forecasting in relation to this particular emergency. At the conclusion of the workshop, the participants agreed that a disease forecasting challenge relying on well-defined and ground-truth synthetic datasets would provide unique assessment of the performance of multiple models in real-time.
Accordingly, we launched an Ebola forecasting challenge in August–December 2015 that relied on synthetic epidemic datasets derived from an agent-based “mother model”. We considered four scenarios involving different levels of data accuracy, availability, and interventions, and were reminiscent of the epidemic in West Africa. These synthetic datasets were used as a basis to assess forecasting performance of 8 competing teams during the course of the Ebola challenge. In this paper, we describe the technical architecture of the RAPIDD Ebola Forecasting Challenge, including generation of synthetic disease datasets, development of a web interface to support data visualization and exchange with the challenge participants, and generation of contextual information.
Synthetic datasets for the Ebola forecasting challenge were derived from a highly detailed spatially-structured agent-based model (Ajelli et al., 2016; Merler et al., 2015) in order to achieve the level of resolution necessary to mimic realistic epidemic scenarios. The model was previously used in the context of the 2014 West Africa Ebola outbreak to assess the effect of control interventions and the probability of elimination (Merler et al., 2015; Ajelli et al., 2016). The epidemic model integrated detailed data on local demography, case isolation, Ebola treatment units, contact tracing, and safe burial interventions - factors that were taken into account in several other modeling studies (Merler et al., 2016; Ajelli et al., 2015; Lewnard et al., 2014; Meltzer et al., 2014; Kucharski et al., 2015; Pandey et al., 2014; Rivers et al., 2014; Weitz and Dushoff, 2015; Fang et al., 2016). Individual level information, spatial context, and health-care related transmission characteristics derived from model runs could be summarized in synthetic patient line lists and aggregated epidemiological time series.
Real-world situations are always affected by the so-called “fog of war” that arises from the data reporting process. For instance, data are not communicated in real time and a variable degree of under-reporting is always present. Moreover, patient records may contain errors and missing data (WHO Ebola Response Team, 2014). For this reason, the challenge accounted for the “noise” introduced during collection and reporting of epidemiological data. Further more each synthetic scenario was accompanied by contextual information (in the form of situation reports), which was not necessarily precise and was often qualitative in nature, but was nevertheless relevant for challenge participants to define modeling assumptions.
The performance of the different models participating in the RAPIDD Ebola challenge are described in an accompanying article (Viboud et al., 2017); here we aim to provide a detailed account of the process used for generating the synthetic data and displaying information in the challenge. First, we describe the mother model and the assumptions underlying the generation of the synthetic datasets associated with each of the four challenge scenarios. Second, we describe the “fog of war” rules applied to data generated by the agent-based model to introduce different levels of data precision. Finally, we provide a detailed description of the databases and the contextual information provided to participating teams during the course of the Ebola challenge.
2. Methods
The data provided for the Challenge were derived from the output of a mother agent-based model, which is a variant of the ones presented in (Merler et al., 2015; Ajelli et al., 2016) for Liberia and Guinea. The original models were specifically calibrated for the 2014 Ebola epidemic in West Africa and were able to reproduce the spreading patterns and trends observed in the actual epidemic. In order to generate the synthetic data used in the challenge, key parameters defining the natural history of the disease in the model were varied. Furthermore, interventions and containment policies were implemented with plausible timelines but differently from the historical case of 2014 epidemic. Moreover, differently from (Merler et al., 2015) but according to (Ajelli et al., 2016), the model took into account two important features observed in the 2014–15 Ebola epidemic: the heterogeneity in transmission potential among individuals (with the presence of superspreaders), and the different susceptibility to infection in children and adults. The model differed from (Merler et al., 2015; Ajelli et al., 2016) also in terms of the distributions of key time periods and of the implemented interventions. Simulations were computationally intensive; thus the model was coded in C language. In this section we detail the model’s definition, the intervention strategies and the selection of the stochastic runs used to generate the challenge data. How the model’s output has has been filtered and communicated to the teams participating to the challenge is reported in Sec. 3. All the data and materials generated for the challenge are publicly available at the web page: http://www.ebola-challenge.org/.
2.1. Model definition
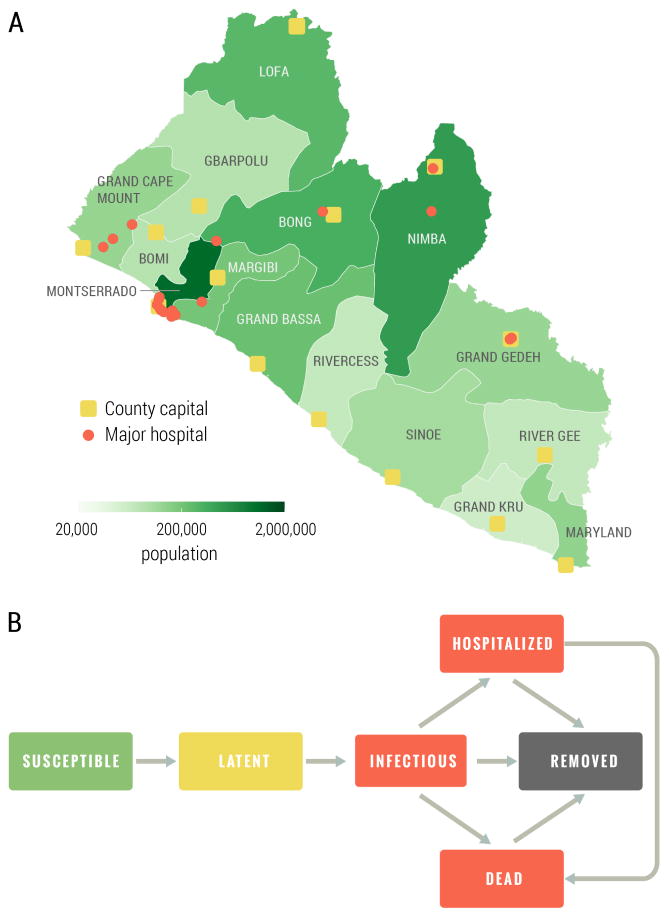
As in (Merler et al., 2015; Ajelli et al., 2016), the population was grouped in households and hospitals, and health care workers were explicitly represented. Infection transmission was stochastic and specific interventions were simulated. The model accounted for three routes of transmission: transmission in households and to the extended family, transmission in hospitals, and transmission during funerals (to household and extended family members). The population of Liberia was subdivided into 15 administrative counties; for each county we placed the corresponding capital in the exact location given by GPS coordinates and with the exact number of inhabitants as obtained from census data. Simulated individuals were grouped into households and assigned to villages and capital city by preserving the population density at the level of county, and in order to match demographic information derived from the 2007 Demographic Health Surveys (Program, 2007) on household size and demographics for Liberia (see the Supplementary information for details). Hospitals were located on the territory according to their actual location as reported in the Humanitarian Data Exchange database (United Nations Office for the Coordination of Humanitarian Affairs, 2015). Each hospital was characterized by number of beds and number of health care workers (HCW), which were determined in order to match statistics available from the WHO Regional Office for Africa (WHO Regional Office for Africa, 2014). The counties considered, the population density, and the location of hospitals is shown in Fig. 1A.
Figure 1.
A Map of Liberia with county capitals, major hospitals and population. B Ebola transmission dynamic scheme. The values and the distribution of the transition times are reported in the Supplementary Information.
Each individual in the population was explicitly simulated as an agent of the individual based model, with an associated epidemiological status. The natural history of the disease followed the one used in (Merler et al., 2015), as outlined in Figure 1 B. Specifically, susceptible individuals could acquire infection after contact with an infectious individual and become latent (asymptomatic). At the end of the latent period, assumed to be equal to the incubation period for Ebola as there is no evidence of Ebola transmission before symptom onset, latent individuals became infectious (symptomatic). Infectious individuals could transmit the infection, to both household members and members of the extended family. Ebola infections would either lead to hospitalization, death or recovery. Hospitalized individuals could transmit the infection to HCW and inpatients; afterwards, they would either die or recover. However, after recovery, a hospitalized individual remained in the hospital (though no longer infectious) for an additional period of time before being discharged. Deceased individuals could transmit infection to household and extended family members during funerals, and were then removed from the model. As in the West African Ebola outbreak, we accounted for contact tracing, an important aspect of disease control. In the Ebola forecasting challenge model, individuals belonging to the contact tracing pool were constantly checked and admitted to a hospital/ETU at the onset of symptoms.
The progression of infection is characterized by seven key time periods defining the natural history of the disease: the incubation period (which is the time between infection and the onset of symptoms); the interval from symptom onset to hospital admission; the interval from hospital admission to death; the interval from hospital admission to the end of infectivity; the interval from hospital admission to discharge; the interval from symptom onset to death; the interval from symptom onset to the end of the infectivity. Each key time period in the infection process was randomly sampled for every individual. In particular, time from death to burial was assumed to follow a truncated exponential distribution with mean 2 days and maximum 3 days, while all other key time periods (such as the incubation period, the time from symptom onset to admission, etc.) were assumed to be gamma distributed, in agreement with (WHO Ebola Response Team, 2014). Values for these parameters were chosen in such a way as to obtain plausible scenarios for an Ebola epidemic similar to the one experienced in West Africa (see Supplementary Information for a full list of parameters). In the early transmission phase the reproduction number was calibrated to be around 1.5–1.6, in agreement with early estimates in West Africa (WHO Ebola Response Team, 2014; Chowell and Nishiura, 2014; Nishiura and Chowell, 2014; Fisman et al., 2014; Merler et al., 2015; Gomes et al., 2014).
As in (Ajelli et al., 2016), the Ebola Forecasting Challenge model included two important features observed in the 2014–15 Ebola epidemic: heterogeneity in transmission rates among individuals, and differences in susceptibility to infection between children and adults. This choice was supported by modeling studies of the2014–15 Ebola epidemic in West Africa, which highlighted that a small fraction of infected individuals were responsible for a large majority of secondary cases (presence of superspreaders) (Ajelli et al., 2015; Althaus, 2015; Faye et al., 2015; WHO Ebola Response Team, 2016a), recently confirmed in (WHO Ebola Response Team, 2016b; Lau et al., 2017). In the model we assumed that each infectious individual had a different infection transmission potential, which was sampled from a gamma distribution of mean 1 and a given shape. This is equivalent to using a negative binomial distribution for the distribution of secondary cases, with dispersion equal to the shape of the gamma distribution. Further, in line with previous studies of the 2014–15 West African outbreak (Ajelli et al., 2015; WHO Ebola Response Team, 2015), we assumed an age-dependent risk of infection, with children being less susceptible to infection with the Ebola virus than adults. Accordingly, we introduced a parameter accounting for the relative susceptibility of 0–14 years old, equal to one-fourth of that of adults (Ajelli et al., 2015). Lastly, the Challenge model differed from that in (Merler et al., 2015) in terms of the distributions of key time periods and implemented interventions. More details on the computational implementation of the transmission mechanisms are provided in the Supplementary Information.
2.2. Modeling of intervention strategies
The challenge model was used to explore four different epidemic scenarios, each characterized by different disease parameters and intensity of interventions aimed at controlling the epidemic. In particular the challenge model accounted for the following interventions:
Hospitals and ETUs. ETUs were put in place and opened according to the spatio-temporal spread of the epidemic in particular simulations. Each Ebola case was assigned a hospitalization probability, based on bed availability in hospitals/ETUs. If an ETU with available beds was located in the same county as the case, the Ebola patient was directly admitted to that ETU; otherwise, the patient first went to the hospital that was closest to his/her place of residence and had space. Then, for the three days following hospital admission, if there was an available bed in any of the ETUs of the county, the patient was transferred to the closest one; otherwise he/she remained in the hospital where he/she was first admitted. If all hospitals and ETUs were at maximum capacity, the patient remained at home. We assumed that ETUs were exclusively used to treat Ebola patients. In contrast, general hospitals could admit individuals presenting different pathologies (and thus susceptible to Ebola infection) as well as true Ebola patients. Non-Ebola patients were hospitalized for 7 days on average. We assumed that when a hospital had availability, Ebola cases were prioritized, and then non-Ebola patients were admitted until the hospital reached full capacity. In other words, an Ebola case that was hospitalized in an ETU could transmit the infection to the HCWs of that ETU only; while an Ebola case hospitalized in a general hospital could transmit to HCWs and to non-Ebola patients hospitalized in the same facility and at the same time.
Contact tracing. Once an individual was admitted to the hospital/ETU, a number of his/her contacts, chosen among members of his/her extended family (including his/her own household), were monitored starting at time t after admission; this parameter varied over time and by scenario. Traced contacts could then either remain in their original status (e.g., susceptible, recovered) or become infected. If a traced contact became infected, the contact was admitted to the hospital/ETU (if there were available beds) on the first day that he/she experienced symptoms. In contrast, for Ebola cases arising outside of the contact tracing process, we assumed a time delay between symptom onset and admission to the hospital/ETU (i.e., the time interval from symptom onset to hospitalization).
Safe burials. Once an Ebola patient died, he/she could be buried either safely (i.e., no onward transmission could occur) or unsafely (i.e., there was a non-zero probability of transmission). Specifically, three possibilities were considered: 1) the individual died in the community (i.e., he was not previously admitted to hospital/ETU) and was safely or unsafely buried depending on a daily scenario-dependent probability; 2) the individual died in an ETU, in which case, he was buried safely; 3) the individual died in a hospital. In this case, in the first three months of the epidemic (that is, up to 89 days the first Ebola case report) the body was released to the family and buried in the community (as described in point 1). Later in the course of the outbreak, all patients dying in the hospital were buried safely.
Behavioral changes. We accounted for reactive behavioral changes in the population such as avoiding or limiting contacts with bodily fluids of Ebola cases (e.g., in the family setting or when visiting patients in hospitals), mirroring increased awareness in the general population during the course of the epidemic. We modeled this phenomenon by scaling the three baseline Ebola transmission rates (family, hospital/ETU, funeral) by the same factor, for each day of the simulation. These time-dependent scaling factors were specific to each scenario.
We considered four different epidemiological scenarios, each one defined by a different set of interventions. In Supplementary Information, we report graphically a summary of the interventions used in each scenario by visualizing the evolution in the cumulative number of ETUs beds, the daily number of traced contacts, the rate of safe burial, and the reduction in transmission due to behavioral changes. The timeline of interventions dictated the course of the epidemic and thus controlled peak timing and the magnitude of the outbreak. Interventions could fluctuate in time, mirroring changes in intervention efficacy due to resource constraints, as observed in the 2014–2015 West Africa Ebola outbreak.
In addition to differences in the timing and intensity of control interventions, we used different natural history parameters for each scenario, which contributed to generate different epidemic trajectories. A table summarizing scenario-specific disease parameters is provided in the Supplementary Information. Overall, there was less variability in the choice of disease parameters than in the definition of interventions because we aimed to reproduce a natural disease history compatible with the Ebola patterns observed in the West African and historical outbreaks.
2.3. Stochastic variability and selected realizations
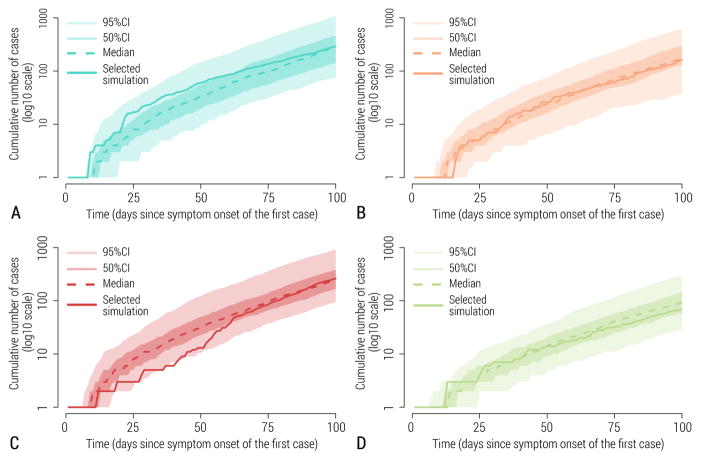
As we used a stochastic model, repeat runs of the model with the same set of initial conditions, disease parameters, and interventions, could result in different epidemic realizations that are all plausible. While some runs may substantially deviate from the ensemble of stochastic realizations (e.g., some runs led to early epidemic extinction), we selected epidemic realizations that fell within the 50% interquartile range of the ensemble. That is, for each scenario we selected a single realization lying asymptotically close to the median of curves of cumulative cases, for realizations that did not go extinct (see Figure 2). Therefore, each synthetic dataset shared with challenge participants corresponded to a unique stochastic realization of the epidemic and included all fluctuations and stochastic variability associated with a single realization under a given epidemiological scenario, as would a real outbreak. The resulting synthetic epidemic curves representing the number of cases or deaths over time exhibited substantial fluctuations; in contrast, averaging over the ensemble of stochastic realizations would have resulted in unrealistically smooth curves.
Figure 2.
Stochastic simulation output. 95% CI, 50% CI, median simulation and the simulation selected as representative for the scenario are depicted. A Scenario 1. B Scenario 2. C Scenario 3. D Scenario 4.
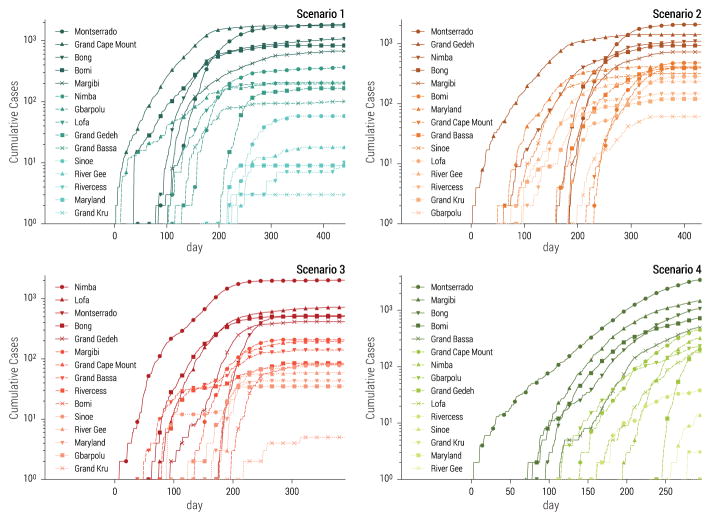
Our selected set of stochastic realizations also allowed for unequivocal spatio-temporal assignation of individual cases and a complete line-list of patients comprising detailed individual-level information, similar in spirit to the one obtained during the 2014–15 Ebola epidemic in West Africa (WHO Ebola Response Team, 2014). In addition, the spatial structure of the model reproduced heterogeneity in the timing and impact of the epidemic across different counties of Liberia. Each selected stochastic realization of the model had a particular spatial and temporal evolution captured by county-level incidence data. In Fig. 3 we report the cumulative number of infections as a function of time for each county in the four selected realizations before the application of the additional noise use to simulate the “fog of war” (see Sec.3.3). The figure shows that the most affected counties and the timing of the epidemic in each county depend on the initial conditions and the level of intervention strategies in each scenario.
Figure 3.
Cumulative number of cases as a function of time in each county of Liberia for the four scenarios considered in the challenge. Each epidemic is based on the stochastic simulation selected in Fig. 2.
3. Results
The performances of the various models used by the 8 participating teams in the RAPIDD Ebola Forecasting challenge, and ensemble predictions, are described elsewhere (Viboud et al., 2017). Here, the results of this particular article concentrate on the preparation of the synthetic epidemiological data and the contextual information shared with challenge participants during the course of the competition. In particular synthetic data generated for each epidemiological scenario with the methodology described above were organized in a database format and shared with the teams through a dedicated password-protected website. Synthetic epidemiological time series and patient line lists were supplemented with additional information contextualizing the data in the form of situation reports. Data access and communication with the challenge participants was processed through the web interface (see Fig. 4). The teams were presented with outbreak data corresponding to five different times of the 4 synthetic scenarios. Typically for each scenario, we chose two time points in the ascending phase of the epidemic, a time point near the peak, and two time points in the descending phase (with the exception of Scenario 4, characterized by a prolonged ascending phase). At each of the five data release time points, challenge participants were given access to an incrementally larger database containing information up to that point of the epidemic. All files are accessible upon request. For each of the 5 prediction time points, the teams were asked to provide forecasts for a number of target estimates, including 1 to 4-week ahead weekly incidences, peak timing, peak magnitude, case fatality rate estimate and reproduction number estimates. Separate forecasts were requested for each of the 4 scenarios.
Figure 4.
Snapshot of the landing web page providing the challenge participants access to the database and the Supplementary Information regarding each scenario.
3.1. Scenarios’ overview
The Ebola Challenge database included the four scenarios described in the previous sections. A different level of data quantity/quality applied to each scenario. In addition, the “difficulty” level offered by each scenario was also determined by the choice of the intervention strategies and/or selected realization of the epidemic.
Scenario 1. With this scenario, the participating teams were offered a “Data Rich” situation in which from Day 1 of reporting the modelers had access to the full patient database, with a staggered ramp up of interventions that ultimately controlled the outbreak. Although affected by the “fog of war”, all timelines and individual-level patient databases were available along with fairly detailed situation reports. Age statistics were provided for each data release as well. Data were available at the national and county level. In addition, a large branch of the transmission tree was provided for the teams.
Scenario 2. This was a “data poor” scenario in which individual-level patient data was unavailable to participating teams throughout the challenge. Only timelines and national age statistics were released, along with situation reports providing contextual information. Two small branches of transmission trees were provided; this was a controlled outbreak as well.
Scenario 3. Like Scenario 2, this was a “data poor” situation, with additional complications. The scenario was based on a far from typical stochastic realization for the first two months of the outbreak. In addition the implementation of intervention strategies was characterized by an abrupt change within the time span of a single week. The situation reports were not detailed nor reliable. National ETU occupancy rate was provided after the 3rd data release, while individual-level patient data were provided for the 5th and final data release. Two small branches of transmission trees were provided; the outbreak was ultimately controlled.
Scenario 4. This scenario was complicated by the fact that the outbreak is uncontrolled; i.e. does not present a clear inflection point, with no true declining phase, during the entire challenge. This scenario was also “data poor” as timelines and age statistics only were available throughout the challenge. Additionally, two small partial transmission trees were also provided to the teams in the same fashion as Scenario 3.
In summary, each scenario represented a different level of difficulty for the modeling teams. In particular, scenario 1 was an idealized case, with timely availability of data, but without neglecting the presence of a fog of war that would be unreasonable to rule out in any real world situation.
3.2. Data format
In order to provide consistent data query capabilities to all teams, we set up a dedicated challenge database offering a number of query masks according to the type of data available under each scenario. The most granular data were available for scenario 1, while data availability and noise gradually increased with scenarios 2–4. The data explorer interface ran as a Python Flask application with a MySQL database, served through the Apache web service. For each scenario, the interface provided daily/weekly and national/county-level timelines for the following outcomes:
New confirmed and probable EVD cases.
New EVD cases among Health Care Workers.
New EVD deaths in the population.
New EVD deaths among Health Care Workers.
Number of new contacts traced.
ETU occupancy – number of beds occupied, counting each bed each day.
New suspected EVD cases.
For most scenarios, the above data were not available at all times nor at the county level. For some scenarios, a number of timelines were not available at all as discussed in Sec. 3.1. Further, the timelines made available to the participating teams were post-processed with the addition of noise in order to simulate problems in data reporting as detailed in Sec. 3.3.
A second type of data file generated from the model contained individual-level records for all hospitalized patients with a complete medical record (patients who were discharged, dead or buried). A full list of the information provided in the patient record database is provided in the supplementary information file. Similarly to the timelines, the patient databases were released after the addition of noise simulating missing or incomplete records as detailed in Sec. 3.3. Dates were expressed in number of days. The outbreak day (week) noted as Day=1 (Week=1) was not necessarily the first day (week) of the epidemic. On Day (Week) 1 several cases could be reported at once and in some cases from different locations. Hence Day 1 should be considered as the first day of reporting. From the patient databases, it was in principle possible to reconstruct infection trees and generate statistics for key natural history parameters such as the length of the incubation period, the time from symptom onset to admission, the time from admission to death, etc. The patient records however were restricted to a subset of the epidemic and were limited to EVD cases admitted to the ETU/hospital and discharged with a final outcome, and traced contacts. Thus the patient database missed EVD cases that were not admitted to the health care system. In addition, patient records could contain missing information and errors. Similarly, the epidemic timelines could include cases for whom the full patient record was not yet released. In summary, disease timelines and patient records were handled as separate datasets.
3.3. Fog of war
In real world situations, data are not communicated in real time, and a variable degree of under-reporting is always present. Furthermore, patient records contain errors and, even more often, missing data, which all contribute to the “fog of war”. Therefore, it would have been highly unrealistic to provide participating teams the direct output of the Ebola model without addition of noise. The synthetic epidemic curves and patient-level data shared with the challenge participants thus included stochastic noise added by post-processing the model outputs according to filters that mirrored real-world problems in data collection, including underreporting and reporting delays. As a result, the postprocessed synthetic data became the actual ground truth for the assessment of the teams’ performances. Although measurement errors and data collection issues are widely known to the community of epidemiologists and disease modelers, the data collected through epidemiological surveillance is always used as the benchmark for modeling predictions.
In defining the “fog of war” we introduced the following sources of noise. We assumed that all cases arising from the pool of contact traced patients were reported. For patients admitted to the hospital or ETU outside of contact-tracing efforts, we assumed a 90% probability of reporting. For the remaining cases who had neither been admitted to medical units nor contact-traced, we assumed a 30% reporting probability. The level of noise applied to the data is informed by the literature on underreporting and missing data during the West Africa outbreak (WHO Ebola Response Team, 2014; Scarpino et al., 2014; Atkins et al., 2015). The latter simulates a large amount of under-reporting typically occurring when the health care system breaks down and cases are not admitted to the health care system. All timelines provided to the Challenge’s teams were based on reported cases and thus had an intrinsic under-reporting factor. The level of under-reporting fluctuated in time, reflecting both the changing situation on the ground during the epidemic (variable number of ETUs, contact tracing capacity, etc.) and the intrinsic binomial noise associated with the reporting probability. The latter was more pronounced when the number of cases was small. Finally, suspected cases were drawn from the subset of EVD cases without medical treatment. To further mimic the issue of missing or inaccurate data arising in real-world situations, we also added noise to the patient-level records, as detailed in the supplementary information file.
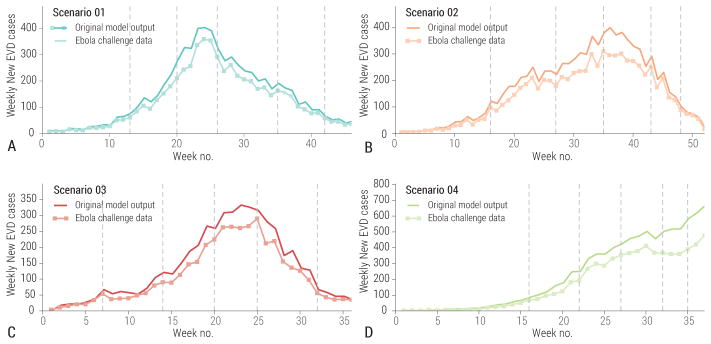
In Fig. 5 we report the difference between the challenge model’s timeline before and after the addition of the noise filter. Fluctuations in the epidemic curves tended to emphasize or attenuate natural fluctuations inherent to the stochastic model depending on the phase of the outbreak and the specific scenario. While we used plausible arguments in defining the level of under-reporting and noise in the Ebola challenge data, we did not want to mimic specific and well-known data issues associated with the 2014–2015 West Africa Ebola outbreak. The aim was to build in uncertainties that the participating teams could not easily extrapolate from the literature, as was initially the case for the 2014–2015 Ebola epidemic.
Figure 5.
Weely number of cases in the original model output and as provided for the challenge after adding noise and underreporting. A Scenario 1. B Scenario 2. C Scenario 3. D Scenario 4. Vertical lines indicate the 5 data release dates of each scenario, corresponding to 5 prediction times points.
3.4. Situation reports
In real world situations, quantitative epidemiological data are generally integrated in situation reports that also provides qualitative descriptions of the situation on the ground. Situation reports also contain information about the planning of control interventions and other news that although not quantitative can guide interpretation of the trends observed in numerical data. In order to provide context to the teams participating in the challenge, we issued a scenario-specific narrative with each data release, akin to a situation report, typically providing the following information:
Approximate geographical distribution of cases and health care workers infections (when not provided explicitly in a timeline).
Opening of new Ebola treatment units.
Level of contact tracing.
Compliance to safe burial protocol.
A typical situation report for the Ebola Forecasting Challenge is included in the Supplementary Information file. The level and accuracy of the situation report differed across scenarios, in the same way that data availability differed. The information contained in the situation report was purposely not always accurate, simulating uncertainty and misreporting due to the fog of war.
3.5. Infection trees
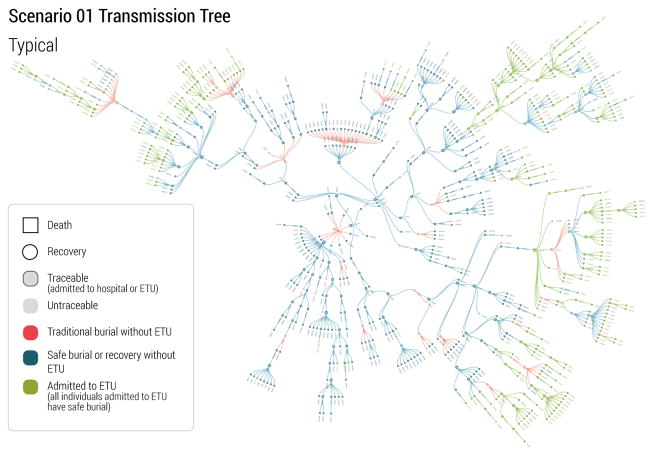
In real-world situations, the quality and richness of data provided to the research community improves with time. This is because with time an increasing number of cases can be analyzed, more efficient data collection strategies and databases are put in place, and knowledge about the disease and the transmission mechanisms improves. During the 2014–2015 Ebola epidemic, a turning point for the modeling community was the publication of transmission tree data. Those data allowed a detailed understanding of heterogeneity in Ebola transmission, and the contribution of different settings to Ebola transmission and behavioral practices (Faye et al., 2015; Ajelli et al., 2015; Nyenswah et al., 2015; Fasina et al., 2014; Coltart et al., 2015). Accordingly, at the time of the set of forecast for the last set of target dates from the participating teams, we provided transmission trees for three scenarios of the challenge. For Scenario 1, we provided one large branch of the transmission tree, covering a typical transmission period associated with weak intervention (safe burial only was carried out), followed by strong control (ETU units in place). For Scenario 3 and Scenario 4, we provided two relative small branches representing weak and strong interventions. The transmission trees were provided in the same format as the line lists of patients as detailed in Sec. 3.2. The patient records used for the transmission trees were supposed to be documented with accuracy, and were provided without missing entries. Fig. 6 displays the visualization of the rich transmission tree branch provided for Scenario 1. It is important to stress that these supplementary data could not be used by the team to revise past forecasts. The aim of the infection trees release was to simulate what happened during the real world West African outbreak when at a later stage of the outbreak more detailed data were made available, and to see if the participating teams would use those data to improve parameters? estimation in the final part of the challenge.
Figure 6.
A visualization of a branch of the EVD transmission tree in Scenario 1. Nodes of various colors and shapes denote different type of EVD patients. Links denote the transmission routes among cases.
4. Discussion
The possibility of using synthetic data in defining modeling challenges is a new framework that allows to overcome some of the issues encountered in forecast of actual data. First, it is possible to conduct synthetic challenges for infectious diseases for which outbreak data are scarce. Furthermore synthetic challenges make it possible to control the amount and quality of data released to the teams to provide different degree of complications in the modeling effort. The synthetic challenge framework thus allows for the practice of modeling approaches, forecasting methodologies and integrative schemes on a wide range of diseases and contextual situations that would not otherwise be available if constrained to retrospective analysis of historical outbreaks.
While the analysis of the forecast and analysis produced by the teams participating in the RAPIDD Ebola Forecasting challenge are reported in a separate paper (Viboud et al., 2017), here we aimed to provide a detailed description of the model used to generate synthetic Ebola epidemic curve and patient-level data, the post-processing steps taken to make the data more realistic, and the synthetic situation reports developed to provide contextual information to the challenge participants.
Below we summarize some of the lessons learned about the preparation of the challenge. A first takeaway is that the data format and the database setup have to be clearly documented and tested by the participating teams. We released a dummy database a few weeks before of the start of the challenge so that the teams could prepare their data mining tools and software. We also prepared “Read Me” documents and a FAQ section of the database. We realize that this level of preparation is not generally possible in real-world situations.
The procedure used to simulate fog of war in the Ebola Challenge was only one of a virtually infinite set of procedures that could be possibly devised to mimic real-world scenarios. Furthermore, one has to consider that the fog of war could be of a very different kind if the synthetic challenge were to focus on a different disease or a different country. In the preparation of a synthetic challenge, the choice of the quality and reliability of the data made available to the participants should be carefully gauged against historical experience and current practices in data collection and sharing. It is also important that the modeling teams are not aware of the changes applied to the model and/or the kind of fog of war applied to the model’s output. It would also relevant to systematically investigate what level of noise in the data comprises the ability of the modeling teams to recover epidemiological information consistent with the underlying outbreak.
It is worth remarking that synthetic challenges depends on a clever choice of epidemic scenarios. The aim is to have the modelers group facing situations that can be useful for future events and fall into a broad range of plausible situations. At the same time the synthetic data should challenge the competing teams with patterns and data that cannot be easily matched against past events. If this is not the case, the modeling teams could just leverage on the past experience, voiding the learning process aimed at by synthetic challenges. In our case the competing teams did not know what kind of fog of war was in the data, what kind of interventions were implemented in the different scenarios and where the natural history of the disease was set in the range of plausible parameters. While this certainly provides a lot of uncertainty to modeling teams, more severe situations in which even the kind of pathogen is unknown can be devised. We believe the this flexibility on the prior knowledge of modeling teams, is one more added value to synthetic challenges that cannot be replicated by using real world data.
Although the Ebola challenge considered four synthetic scenarios of Ebola-like outbreaks in a relatively small country such as Liberia, resulting in a small number of cases (< 10,000 reported EVD cases), data generation and database preparation required considerable computational resources. Extending synthetic challenges to pandemic threat scenarios, such as a flu pandemic for instance, would have to consider the potential for quick international spread. This would imply running large scale global epidemic simulations and handling databases spanning multiple countries, raising the issue of scalability. Synthetic challenges could provide useful drills for the disease modeling community and guide preparedness for major emerging health threats across the world. However commitment of adequate resources is required to allow for a proper level of realism to be built-in, and is key to successfully inform disease forecasting in real-world emergencies.
Supplementary Material
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ajelli M, Merler S, Fumanelli L, y Piontti AP, Dean NE, Longini IM, Halloran ME, Vespignani A. Spatiotemporal dynamics of the Ebola epidemic in Guinea and implications for vaccination and disease elimination: a computational modeling analysis. BMC Med. 2016;14:130. doi: 10.1186/s12916-016-0678-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ajelli M, Parlamento S, Bome D, Kebbi A, Atzori A, Frasson C, Putoto G, Carraro D, Merler S. The 2014 Ebola virus disease outbreak in Pujehun Sierra Leone: epidemiology and impact of interventions. BMC Med. 2015;13:281. doi: 10.1186/s12916-015-0524-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Althaus CL. Ebola superspreading. Lancet Infect Dis. 2015;15:507–508. doi: 10.1016/s1473-3099(15)70135-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkins KE, Wenzel NS, Ndeffo-Mbah M, Altice FL, Townsend JP, Galvani AP. Under-reporting and case fatality estimates for emerging epidemics. bmj. 2015;350:h1115. doi: 10.1136/bmj.h1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowell G, Nishiura H. Transmission dynamics and control of Ebola virus disease (EVD): a review. BMC Med. 2014;12:196. doi: 10.1186/s12916-014-0196-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coltart CE, Johnson AM, Whitty CJ. Role of healthcare workers in early epidemic spread of ebola: policy implications of prophylactic compared to reactive vaccination policy in outbreak prevention and control. BMC Med. 2015;13:271. doi: 10.1186/s12916-015-0477-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang LQ, Yang Y, Jiang JF, Yao HW, Kargbo D, Li XL, Jiang BG, Kargbo B, Tong YG, Wang YW, et al. Transmission dynamics of Ebola virus disease and intervention effectiveness in Sierra Leone. Proc Natl Acad Sci USA. 2016;113:4488–4493. doi: 10.1073/pnas.1518587113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fasina F, Shittu A, Lazarus D, Tomori O, Simonsen L, Viboud C, Chowell G. Transmission dynamics and control of Ebola virus disease outbreak in Nigeria July to September 2014. Eurosurveill. 2014;19:20920. doi: 10.2807/1560-7917.es2014.19.40.20920. [DOI] [PubMed] [Google Scholar]
- Faye O, Boëlle PY, Heleze E, Faye O, Loucoubar C, Magassouba N, Soropogui B, Keita S, Gakou T, Bah EHI, Koivogui L, Sall AA, Cauchemez S. Chains of transmission and control of Ebola virus disease in Conakry Guinea, in 2014: an observational study. Lancet Infect Dis. 2015;15:320–326. doi: 10.1016/s1473-3099(14)71075-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisman D, Khoo E, Tuite A. Early epidemic dynamics of the West African 2014 Ebola outbreak: estimates derived with a simple two-parameter model. PLOS currents outbreaks. 2014 doi: 10.1371/currents.outbreaks.89c0d3783f36958d96ebbae97348d571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomes MF, Pastore y Piontti A, Rossi L, Chao D, Longini I, Halloran ME, Vespignani A. Assessing the international spreading risk associated with the 2014 west african ebola outbreak. PLOS Currents Outbreaks. 2014 doi: 10.1371/currents.outbreaks.cd818f63d40e24aef769dda7df9e0da5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucharski AJ, Camacho A, Flasche S, Glover RE, Edmunds WJ, Funk S. Measuring the impact of Ebola control measures in Sierra Leone. Proc Natl Acad Sci USA. 2015;112:14366–14371. doi: 10.1073/pnas.1508814112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau MS, Dalziel BD, Funk S, McClelland A, Tiffany A, Riley S, Metcalf CJE, Grenfell BT. Spatial and temporal dynamics of superspreading events in the 2014–2015 west africa ebola epidemic. Proc Natl Acad Sci USA. 2017;114:2337–2342. doi: 10.1073/pnas.1614595114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewnard JA, Mbah MLN, Alfaro-Murillo JA, Altice FL, Bawo L, Nyenswah TG, Galvani AP. Dynamics and control of Ebola virus transmission in Montserrado, Liberia: a mathematical modelling analysis. Lancet Infect Dis. 2014;14:1189–1195. doi: 10.1016/S1473-3099(14)70995-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meltzer MI, Atkins CY, Santibanez S, Knust B, Petersen BW, Ervin ED, Nichol ST, Damon IK, Washington ML, et al. Estimating the future number of cases in the Ebola epidemic—Liberia and Sierra Leone, 2014–2015. Mort Mort Weekly Rep. 2014;63:1–14. [PubMed] [Google Scholar]
- Merler S, Ajelli M, Fumanelli L, Gomes MFC, y Piontti AP, Rossi L, Chao DL, Longini IM, Halloran ME, Vespignani A. Spatiotemporal spread of the 2014 outbreak of Ebola virus disease in Liberia and the effectiveness of non-pharmaceutical interventions: a computational modeling analysis. Lancet Infect Dis. 2015;15:204–211. doi: 10.1016/s1473-3099(14)71074-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merler S, Ajelli M, Fumanelli L, Parlamento S, y Piontti AP, Dean NE, Putoto G, Carraro D, Longini IM, Halloran ME, Vespignani A. Containing Ebola at the Source with Ring Vaccination. PLOS Neglect Trop Dis. 2016;10:e0005093. doi: 10.1371/journal.pntd.0005093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiura H, Chowell G. Early transmission dynamics of Ebola virus disease (EVD), West Africa, March to August 2014. Eurosurveill. 2014;19:20894. doi: 10.2807/1560-7917.es2014.19.36.20894. [DOI] [PubMed] [Google Scholar]
- Nyenswah T, Fallah M, Sieh S, Kollie K, Badio M, Gray A, Dilah P, Shannon M, Duwor S, Ihekweazu C, et al. Controlling the last known cluster of Ebola virus disease—Liberia, January–February 2015. Mort Morb Weekly Rep. 2015;64:500–504. [PMC free article] [PubMed] [Google Scholar]
- Pandey A, Atkins KE, Medlock J, Wenzel N, Townsend JP, Childs JE, Nyenswah TG, Ndeffo-Mbah ML, Galvani AP. Strategies for containing Ebola in west Africa. Science. 2014;346:991–995. doi: 10.1126/science.1260612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Program TD. Demographic and Health Survey. 2007 URL: http://www.dhsprogram.com.
- Rivers CM, Lofgren ET, Marathe M, Eubank S, Lewis BL. Modeling the impact of interventions on an epidemic of ebola in sierra leone and liberia. PLOS Currents Outbreaks. 2014 doi: 10.1371/currents.outbreaks.4d41fe5d6c05e9df30ddce33c66d084c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scarpino SV, Iamarino A, Wells C, Yamin D, Ndeffo-Mbah M, Wenzel NS, Fox SJ, Nyenswah T, Altice FL, Galvani AP, et al. Epidemiological and viral genomic sequence analysis of the 2014 ebola outbreak reveals clustered transmission. Clinical Infectious Diseases. 2014;60:1079–1082. doi: 10.1093/cid/ciu1131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- United Nations Office for the Coordination of Humanitarian Affairs. The Humanitarian Data Exchange Project. 2015 URL: https://data.hdx.rwlabs.org/
- Viboud C, Gaffey R, Sun K, Ajelli M, Fumanelli L, Merler S, Zhang Q, Chowell G, Simonsen L, Vespignani A the RAPIDD Ebola Forecasting Challenge Group. The RAPIDD Ebola Forecasting Challenge: Synthesis and Lessons Learnt. Epidemics. 2017 doi: 10.1016/j.epidem.2017.08.002. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weitz JS, Dushoff J. Modeling post-death transmission of Ebola: challenges for inference and opportunities for control. Sci Rep. 2015;5:8751. doi: 10.1038/srep08751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO Ebola Response Team. Ebola Virus Disease in West Africa — The First 9 Months of the Epidemic and Forward Projections. N Eng J Med. 2014;371:1481–1495. doi: 10.1056/nejmoa1411100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO Ebola Response Team. Ebola Virus Disease among Children in West Africa. N Eng J Med. 2015;372:1274–1277. doi: 10.1056/nejmc1415318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO Ebola Response Team. After ebola in west africa—unpredictable risks, preventable epidemics. N Engl J Med. 2016a;2016:587–596. doi: 10.1056/NEJMsr1513109. [DOI] [PubMed] [Google Scholar]
- WHO Ebola Response Team. Exposure patterns driving ebola transmission in west africa: A retrospective observational study. PLoS Med. 2016b;13:e1002170. doi: 10.1371/journal.pmed.1002170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO Regional Office for Africa. Country Health Profile - Liberia Factsheets of Health Statistics. 2014 URL: http://www.aho.afro.who.int/profiles_information/images/c/cd/Liberia-Statistical_Factsheet.pdf.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.