Abstract
Motivation
When proteins mutate or bind to ligands, their backbones often move significantly, especially in loop regions. Computational protein design algorithms must model these motions in order to accurately optimize protein stability and binding affinity. However, methods for backbone conformational search in design have been much more limited than for sidechain conformational search. This is especially true for combinatorial protein design algorithms, which aim to search a large sequence space efficiently and thus cannot rely on temporal simulation of each candidate sequence.
Results
We alleviate this difficulty with a new parameterization of backbone conformational space, which represents all degrees of freedom of a specified segment of protein chain that maintain valid bonding geometry (by maintaining the original bond lengths and angles and ω dihedrals). In order to search this space, we present an efficient algorithm, CATS, for computing atomic coordinates as a function of our new continuous backbone internal coordinates. CATS generalizes the iMinDEE and EPIC protein design algorithms, which model continuous flexibility in sidechain dihedrals, to model continuous, appropriately localized flexibility in the backbone dihedrals and ψ as well. We show using 81 test cases based on 29 different protein structures that CATS finds sequences and conformations that are significantly lower in energy than methods with less or no backbone flexibility do. In particular, we show that CATS can model the viability of an antibody mutation known experimentally to increase affinity, but that appears sterically infeasible when modeled with less or no backbone flexibility.
Availability and implementation
Our code is available as free software at https://github.com/donaldlab/OSPREY_refactor.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Protein design algorithms (Donald, 2011; Lippow and Tidor, 2007; Regan, 1999) address the following problem: given a protein system and a set of possible localized changes in chemical composition, choose the combination of changes that will optimize a desired functional property. Typically the chemical changes are mutations in sequence or modification of a ligand, while the functional requirement is ligand binding affinity (Floudas et al., 1999; Georgiev et al., 2008b; Karanicolas and Kuhlman, 2009; Lilien et al., 2005), protein stability (Desmet et al., 1992; Donald, 2011; Gainza et al., 2012; Georgiev et al., 2014; Kuhlman and Baker, 2000), or some combination thereof (Hallen and Donald, 2016; Lewis et al., 2014). Solving this problem requires the ability to accurately model protein structure, as binding affinity is sensitive to small changes in the conformation of the protein and ligand.
Two approaches are currently employed for protein structure modeling and coupling it to sequence optimization. First, molecular dynamics can be used to simulate the behavior of a candidate design over time (Rapaport, 2004). This approach has the advantage that it can explore all conformational degrees of freedom. However, these simulations are time consuming and must be run separately for each candidate, making them prohibitively expensive for large sequence spaces. For example, a molecular dynamics-based design considering all 20 amino-acid types for each of 10 residues will require 2010=10 trillion simulations, which is clearly intractable. Indeed, accurately computing the binding constant for a single sequence is relatively time-consuming, since the timesteps are on the order of femtoseconds while the timescale of ligand binding is many orders of magnitude greater. Other loop modeling methods, such as POOL (Tripathy et al., 2012), that search extensively over the backbone conformational space of a protein loop also limit their search to a single sequence (Donald, 2011).
This brings us to the second approach, consisting of combinatorial algorithms that search a much larger sequence space without considering each sequence separately—the time cost scales sublinearly in the number of candidate sequences. This is important because the number of sequences is exponential in the number of mutable residues. Several classes of methods fall under this approach, as reviewed extensively in Donald (2011) and Gainza et al. (2016). Methods based on the DEE/A* algorithm (Desmet et al., 1992; Gainza et al., 2012; Georgiev et al., 2008b; Gordon et al., 2003; Hallen et al., 2013; Leach and Lemon, 1998; Pierce et al., 2000), on branch- (Jou et al., 2016) and tree decompositions (Xu and Berger, 2006), and on algorithms from integer linear programming (Kingsford et al., 2005; Roberts et al., 2015) and weighted constraint satisfaction (Roberts et al., 2015; Traoré et al., 2013, 2016) offer provable guarantees of accuracy, while methods based on simulated annealing (Das and Baker, 2008; Kuhlman and Baker, 2000; Wang et al., 2005) and genetic algorithms (Desjarlais and Handel, 1995; Lewis et al., 2014; Leaver-Fay et al., 2011) do not. Although the technique we present in this work could be used with most of these methods in principle, we have implemented it in a framework based on the DEE/A* algorithm, which we will now explain further. Using a provable algorithm with our new model ensures that empirical observations of accuracy precisely reflect the accuracy of the model, rather than a convolution of modeling and algorithm accuracy.
DEE/A* was first presented as a method to optimize protein stability while modeling only sidechain flexibility (Leach and Lemon, 1998). Protein sidechain flexibility is known empirically to consist almost entirely of flexibility in sidechain dihedral angles, which are restricted to certain regions of dihedral space. These regions, termed rotamers, have been characterized for each natural amino-acid type, (Lovell et al., 2000) by clustering of sidechain dihedral values for many residues of each type across many different high-resolution crystal structures. DEE/A* provided an efficient way to assign an amino acid type and rotamer to each residue in a protein to minimize energy.
Initially, DEE/A* assumed every residue would only be found at the ‘ideal’ dihedral values for its rotamer (the modal values for that rotamer in crystal structure data). Later work helped to relax this assumption. The minDEE algorithm (Georgiev et al., 2008b; Roberts et al., 2012) enabled search over sequence and conformational space with each sidechain dihedral restricted to a continuous range (an ideal rotameric value ), instead of to an ideal rotameric value exactly. The energy minima over this larger, more realistic sidechain conformational space have been shown to be significantly lower (Gainza et al., 2012). The iMinDEE (Gainza et al., 2012) and EPIC (Hallen et al., 2015) algorithms sped up minDEE substantially while using the same modeling assumptions, and other extensions added the capability to model sidechain conformational entropy (Chen et al., 2009; Donald, 2011; Georgiev et al., 2008b; Lilien et al., 2005; Roberts et al., 2012) and backbone motions (Georgiev and Donald, 2007; Georgiev et al., 2008a; Hallen et al., 2013), while still exploiting the speedups iMinDEE and EPIC offer.
Previous combinatorial protein design algorithms have also incorporated backbone flexibility, albeit to a limited extent. The BD algorithm (Georgiev and Donald, 2007) can allow motions in all backbone dihedrals ( and ψ), but these motions are propagated down the entire backbone chain, which severely limits the extent to which the backbone in the region of interest (e.g. active-site loop) can move without unfolding the protein (generally to 1 Å). Modeling larger changes would require either handling dramatic backbone movement elsewhere in the protein or facing the ill-conditioned problem of making dihedral changes in subsequent residues cancel each other’s downstream effects. The new parameterization we present here makes the latter problem well-conditioned, by using an intrinsically local set of internal coordinates.
Another previous model for backbone flexibility in protein design is the use of a restricted repertoire of motions that may move the backbone more, but do not search all biophysically feasible motions even locally. These can be ad hoc, discrete backbone changes specific to a particular protein system (e.g. from antibody loop libraries (Al-Lazikani et al., 1997)), transplantations of fragments of other proteins’ backbones (Jacobs et al., 2016; Zhou and Grigoryan, 2015), or backbones generated by molecular dynamics simulations (Fung et al., 2008). Alternately, the repertoire can contain motions like the backrub (Davis et al., 2006) and shear (Hallen et al., 2013) that have been observed repeatedly in crystallographic alternates. The backrub (Davis et al., 2006) in particular has been used in both DEE/A*-based (Georgiev et al., 2008a; Hallen et al., 2013) and simulated annealing-based (Smith and Kortemme, 2008) protein design algorithms. The DEEPer algorithm (Hallen et al., 2013) performs a provably complete search over the space defined by a set of possible mutations and a predefined repertoire of backrubs, shears and/or local discrete backbone perturbations.
Indeed, some restriction on backbone flexibility is acceptable in the protein design context, because we know from X-ray crystallography that backbone conformational changes due to mutations or ligand binding are usually fairly local (Al-Lazikani et al., 1997; Wong et al., 1999). We also know that backbone motions are mostly limited to changes in the two dihedral angles and ψ of each residue, and that these dihedrals are restricted to a small subset of their possible values (Lovell et al., 2003). This subset is known as the Ramachandran-allowed region and is well-characterized for each amino acid type (Lovell et al., 2003), analogously to how sidechains are generally restricted to rotamers. Thus, the set of feasible backbone conformational changes can be characterized in the space of and ψ changes in the flexible region by imposing both inequality (Ramachandran) constraints, and holonomic (i.e. equality) constraints that ensure the non-flexible regions of the backbone do not move. Without the latter, significant and ψ changes would unfold the protein, because the amount of atomic motion due to a backbone dihedral change increases for atoms that are further from the axis of the dihedral rotation. Nevertheless, previous combinatorial protein design algorithms restrict the backbone substantially more than these empirical limits on flexibility would require.
In the present work, we use a new parameterization of backbone conformational space to obtain a much more systematic search over the continuous space of local conformational changes. Any differential motion in a specified region of the backbone that is accessible by changing the backbone dihedrals and ψ can be accessed via our parameterization (Fig. 1). Our parameterization is designed for use in continuous energy minimization with box constraints on all degrees of freedom (Gainza et al., 2012; Hallen et al., 2013). Thus, we need not explicitly include holonomic constraints when using our parameterization; our parameterization intrinsically does not move the regions of protein backbone that need to be kept fixed. This parameterization allows us to use polynomial approximations (Taylor series) to efficiently evaluate the continuous backbone movements around a reference backbone. We thus provide a fast method to compute all atomic coordinates as a function of our novel degrees of freedom, by calculating Coordinates of Atoms by Taylor Series (CATS). We have integrated CATS with the iMinDEE (Gainza et al., 2012) and EPIC (Hallen et al., 2015) protein design algorithms, which call such continuous minimization as a subroutine. CATS casts the modeling of localized, continuous backbone dihedral flexibility into a form that supports all operations required by iMinDEE and EPIC.
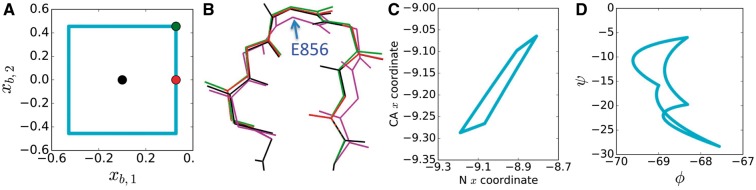
Fig. 1.
Backbone degrees of freedom used by CATS. (A) A voxel used in CATS for a 7-residue loop in ponsin (PDB id 2O9S (Gehmlich et al., 2007)), projected into the 2-D space of two of our new continuous degrees of freedom, denoted by and . Voxel border, blue; central conformation, black. (B) Conformations in the voxel: black, central conformation; red and green, conformations shown as dots in A; purple, a conformation for which all 8 degrees of freedom are at the voxel edge. (C, D) The boundary of the 2-D-projected voxel shown in A, graphed in the space of atomic Cartesian x coordinates (in Å) for the N and Cα atoms of E856 (C) and in the space of that residue’s backbone dihedrals (in degrees, D). For this 7-residue loop, the voxel has 8 dimensions and thus forms an 8-dimensional hypersurface in the 14-dimensional backbone dihedral space. The distorted parallelogram in (C) would be exactly a parallelogram if the constraints were linear
We have implemented CATS in the OSPREY (Gainza et al., 2013; Georgiev et al., 2008b, 2009; Ojewole et al., 2017) open-source protein design package. OSPREY has yielded many designs that performed well experimentally—in vitro (Chen et al., 2009; Frey et al., 2010; Georgiev et al., 2012; Gorczynski et al., 2007; Roberts et al., 2012; Rudicell et al., 2014; Stevens et al., 2006) and in vivo (Frey et al., 2010; Gorczynski et al., 2007; Roberts et al., 2012; Rudicell et al., 2014) as well as in non-human primates (Rudicell et al., 2014)—and contains a wide array of flexibility modeling options and provably accurate design algorithms (Gainza et al., 2013; Georgiev et al., 2009). These features will allow CATS to be used for many different types of designs.
By presenting CATS, this paper makes the following contributions:
A new, continuous parameterization of backbone conformational space that includes all degrees of freedom that respect the backbone’s natural geometric constraints.
An efficient algorithm, CATS, for using this parameterization in protein design.
An implementation of CATS in our laboratory’s open-source OSPREY protein-design software package (Chen et al., 2009; Frey et al., 2010; Georgiev et al., 2008b, 2009; Gainza et al., 2013), configured for use with any of the protein design algorithms in OSPREY (Georgiev et al., 2008b; Gainza et al., 2012; Hallen et al., 2013, 2015, 2016; Hallen and Donald, 2016; Lilien et al., 2005; Roberts and Donald, 2015), available for download upon publication as free software.
Experimental results of computational design calculations that demonstrate CATS finds sequences and conformations that are significantly lower in energy than previous algorithms, across 81 test cases using 29 different crystal structures, including an antibody mutant that resisted modeling by previous algorithms. In the antibody study, CATS models a loop backbone motion that is sterically crucial to the binding activity of a mutant that improves both gp120 binding and HIV-1 neutralization.
2 Materials and methods
2.1 Protein design with continuous flexibility in closed loops
2.1.1 Framework
CATS builds on previous protein design algorithms that model continuous flexibility: iMinDEE (Gainza et al., 2012) and its variants DEEPer (Hallen et al., 2013) and EPIC (Hallen et al., 2015). In this section, we will review some aspects of the mathematical framework underlying these algorithms, which will also serve as the foundation for CATS.
We assume that the conformation of the protein is a function of the sequence and n internal coordinates . We then define the conformational space of our system as the union of voxels (Georgiev et al., 2008b; Gainza et al., 2012; Hallen et al., 2013). Each voxel v is defined by a protein sequence and the inequality constraints
| (1) |
for , where and are voxel-specific constants defined per our modeling assumptions. If , coordinate xi is said to have continuous flexibility in v.
The conformation of each residue j will be a function of only that residue’s amino-acid type and a subset of the degree-of-freedom values where . Thus, we can construct a very large voxel space combinatorially. The conformation space of each residue j consists of a limited number (usually <100) of ‘residue-specific’ voxels that bound only the degrees of freedom in . Thus, the conformation space of the entire system consists of all possible combinations of residue-specific voxels, where v1 is a voxel specific to residue 1, v2 to residue 2, etc. and thus all degrees of freedom of the system are bounded in their finite intersection v. These residue-specific voxels are called residue conformations (RCs) (Hallen et al., 2013). As discussed by Hallen et al. (2013), any continuous degrees of freedom can be used in this framework, as long as we can perform efficient and accurate energy minimizations of the form
| (2) |
where is the energy as a function of the conformational degrees of freedom. We must be able to evaluate Eq. (2) for the entire system and for subsets of it. In the former case, the voxel v will bound all the system’s degrees of freedom and will be the energy of the entire system. In the latter case, v will only restrict degrees of freedom for a subset A of the residues: v will be of the form . Likewise, the energy will consist only of interactions among those residues, and thus only will depend on the degrees of freedom .
Following Georgiev et al. (2008b), Gainza et al. (2012) and Hallen et al. (2013), we assume local minimization to be sufficient to find the minimum within a voxel, and we perform this minimization with the cyclic coordinate descent algorithm implemented in OSPREY (Chen et al., 2009; Frey et al., 2010; Georgiev et al., 2008b, 2009; Gainza et al., 2013). We also assume the availability of an energy function that maps the coordinates of the m atoms in the system to an energy. We use the implementation of AMBER (Cornell et al., 1995; Weiner and Kollman, 1981) with EEF1 (Lazaridis and Karplus, 1999) solvation in OSPREY for this for purposes of this work, but the iMinDEE framework supports a wide range of energy functions (Georgiev et al., 2009; Hallen et al., 2015), and adding CATS to this framework introduces no additional restrictions on the energy function. Having chosen Ec, we define , where maps internal coordinates to all-atom coordinates.
As discussed by Hallen et al. (2013), the iMinDEE framework is actually agnostic to the geometric meaning of the degrees of freedom x, as long as (i) each voxel is defined by box constraints, of the form in Eq. (1), and (ii) we know how to compute the kinematic map . The reason iMinDEE and its previously described variants have limited or no backbone flexibility is that holonomic constraints on the backbone dihedrals and ψ which restrict backbone motion to a specified region of protein backbone—e.g. a flexible loop region—are not box constraints. Our contribution in this paper is a parameterization of backbone conformational space that is equivalent to varying and ψ subject to these holonomic constraints, but satisfies the conditions (i) and (ii) above.
2.1.2 Open and closed loops
For internal coordinates that are sidechain dihedrals, the kinematic map a is well known: the sidechains are just rotated to the correct angles. This is because there is no restriction on the termini of the sidechains. Likewise, defining the voxel in sidechain dihedral space is fairly straightforward: we assume as in Georgiev et al. (2008b), Gainza et al. (2012) and Hallen et al. (2013) that each voxel corresponds to the assignment of a sidechain rotamer (Janin et al., 1978; Lovell et al., 2000) to each residue, and each dihedral is allowed to vary by about the ideal dihedral for the rotamer, which is empirically derived from a database of high-resolution crystal structures (Lovell et al., 2000). Using sidechain dihedrals as continuous degrees of freedom allows sidechain motions in all directions that keep the bond lengths and angles and backbone conformation fixed.
However, as mentioned in Section 1, backbone conformational changes associated with mutations or binding are generally fairly local—and indeed, complex, non-local changes are likely outside the scope of what protein design algorithms can accurately predict. This effectively imposes holonomic equality constraints: we vary and ψ subject to the constraint that the (user-designated) flexible section of backbone matches the starting structure at both ends of the flexible section. Such equality constraints are incompatible with the iMinDEE framework (Gainza et al., 2012; Hallen et al., 2013). To resolve this incompatibility, we reparameterize the backbone conformational space. Moving our new backbone degrees of freedom will allow backbone motions in all directions that do not change the bond lengths, angles and ω dihedrals, while keeping the non-flexible parts of the backbone fixed.
We will now describe the assumptions about peptide plane geometry underlying CATS (Section 2.2). We will then use these assumptions to define the new degrees of freedom x and explain how all-atom coordinates are computed from them (Section 2.3).
2.2 Peptide-plane geometry assumptions
The starting point for CATS is a set of assumptions about which backbone degrees of freedom are free to move and which are not. We will assume (iii) that peptide planes are rigid bodies, and (iv) that the N-Cα-C′ bond angle in each residue is fixed. We encode these assumptions as equality constraints in the form
| (3) |
where denotes the nitrogen and alpha-carbon coordinates of the flexible residues, the elements of c are quantities constrained by our geometry assumptions (iii–iv), and the corresponding elements of are the values of those quantities in the starting crystal structure. There are four constrained quantities per residue, and each component of c is a multivariate quadratic function. A detailed description of these constraints and a justification of the assumptions are provided in Supplementary Material (SM) 1. The coordinates of all backbone atoms besides the nitrogens and alpha carbons can be computed from and the assumption that peptide planes are rigid bodies, as described in SM 1 as well. Once the backbone conformation is determined, the sidechains and alpha hydrogens are placed onto the backbone as in Hallen et al. (2013). These observations greatly simplify the calculation of from our backbone degrees of freedom x: we need only calculate , and then the other components of can be computed from .
2.3 New backbone parameterization
To define a voxel in backbone conformational space, we will choose a central conformation and allow backbone motions away from this conformation in all directions that maintain the peptide plane geometry (Fig. 1). For a flexible backbone segment of k contiguous residues with , this space of motions has dimensions: 2k for the and ψ dihedrals of each residue, and 6 constraints to ensure that the residue at the end of the segment is continuous with the non-flexible residues after it (since the position and orientation of a rigid body each have 3 degrees of freedom). In the computational experiments described in this work, the central conformation for each voxel will be the crystal structure conformation, since we know it to be favorable and expect that local backbone adjustments around it can be scored energetically more accurately than arbitrary backbone motions can. However, in principle other central conformations could be used, to cover as much of backbone conformational space as desired (albeit at increased computational cost, which could scale up to linearly in the number of voxels in backbone conformational space).
Let y be the vector of nitrogen and alpha-carbon coordinates for the k flexible residues. Let be the value of y at the central conformation. Consider a vector function such that the first components of are the constrained quantities (see Section 2.2), and the remaining components are affine functions of y, which we will call . In other words, . The components z parameterize the ()-dimensional hypersurface of constraint-satisfying backbone conformations, and are chosen to be affine for simplicity. As long as is nonsingular, any direction of motion b of the nitrogen and alpha-carbon atoms that keeps the constrained quantities c constant corresponds to a direction of motion of the affine components. To put this more formally,
Theorem 1.
Let denote the directional derivative in direction b. If is an affine function and c satisfies , then there exists an affine bijection between and .
A proof of Theorem 1 is provided in SM 3.
Thus we can use the affine components z as our continuous backbone degrees of freedom. We will choose the constant terms of the affine functions so that . We can choose the linear coefficients defining z somewhat arbitrarily as long as is nonsingular; we will choose the (constant) gradient of each component of z to have norm 1 and to be orthogonal to all other gradients of components of f (evaluated at in the case of the constrained components c, which have non-constant gradient). In other words, we let
| (4) |
where Mz is a matrix whose rows are orthonormal, and also are orthogonal to the rows of the matrix . In this sense the components resemble ‘normal modes’ of backbone flexibility (Bahar and Rader, 2005) in the vicinity of the central conformation (though whether they are actual normal modes depends on the energy landscape; our definition of z is intended to be agnostic to the energy function). They are also analogous to the user-controllable degrees of freedom in computer graphics systems that allow image manipulation while maintaining satisfaction of a set of constraints (Gleicher, 1992; Ngo et al., 2000; Ngo and Donald, 1999).
Now, let denote the vector of backbone degrees of freedom. To evaluate , as is required by the iMinDEE framework, we must evaluate the inverse mapping of f at the correct constrained values: . We compute this inverse function efficiently in the form of a Taylor series, whose coefficients we can derive analytically because we can compute all derivatives of f. The Taylor series is valid within a certain neighborhood around the central conformation , and we verify its accuracy within that neighborhood by sampling. In the case where there are multiple possible values of a given values of , we are interested in the branch defined by the Taylor series. This way, a is a well-defined function mapping values of our new backbone degrees of freedom to constraint-satisfying atomic Cartesian coordinates (Fig. 1). A summary of the algorithm for computing a is given in SM 2 and details of the Taylor series computation are given in SM 5.
Thus, we can use these as a set of continuous degrees of freedom to parameterize our backbone conformational space for use in the iMinDEE framework. Finally, we can impose bounds on to define a voxel, allowing motion away from the central conformation in any direction that satisfies the peptide-plane geometry constraints (Eq. 3).
3 Results
3.1 Energy differences and backbone shifts
80 test cases using 28 different crystal structures showed CATS can make a big difference in protein energetics (Fig. 2). Three types of test cases were used: (a) design cases searching a large sequence space, (b) conformational searches for the wild-type sequence and (c) single-voxel minimizations starting from the wild-type backbone and sidechain conformations. In each case, CATS was compared to rigid-backbone design and to DEEPer backbone flexibility (Hallen et al., 2013). The iMinDEE (Gainza et al., 2012) and EPIC (Hallen et al., 2015) search algorithms were used throughout, which have guarantees of accuracy, thus ensuring that energy improvements between the different models of conformational space are actually due to changes in the backbone flexibility model and not to error in the search algorithm. The five to nine flexible residues in each test case were chosen to be a contiguous segment of protein backbone.
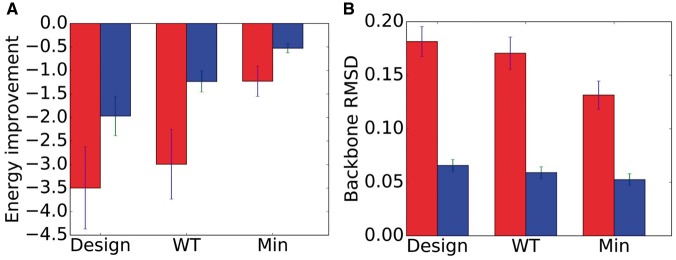
Fig. 2.
Seventy-nine computational experiments comparing CATS, DEEPer and rigid-backbone design. (A) Average improvement in energy (kcal/mol) in CATS (red) and DEEPer (blue) calculations compared to rigid-backbone calculations. Averages with standard error bars shown for designs, wild-type (WT) conformational searches, and single-voxel minimizations starting from the wild-type conformation. (B) RMSD (Å) between crystal-structure backbones and optimal backbones computed by CATS (red) and DEEPer (blue) for the same test cases as (A). CATS is able to model larger backbone changes, and the greater RMSD for designs compared to minimizations indicates CATS is modeling the backbone shifts induced by mutations
In 87% of designs, 86% of wild-type conformational searches, and 54% of minimizations, the minimum-energy conformation found using CATS was lower than the minimum rigid-backbone energy by at least the thermal energy at room temperature (0.592 kcal/mol, calculated as the universal gas constant times a room temperature of 298 K). This is a rough measure for functional significance (Hallen et al., 2013). Indeed, in 73% of designs the gap between the CATS and DEEPer minima exceeded this thermal energy. The gap between DEEPer and rigid-backbone minima in designs exceeded thermal energy in 67% of designs, closely matching the result in Hallen et al. (2013). On average, designs had 3.5 kcal/mol better energies with CATS than without backbone flexibility (Fig. 2A).
Moreover, designs with CATS often differed in optimal sequence from the corresponding rigid-backbone designs, with CATS favoring larger amino acids in all but one case. Some of these amino acids were dramatically larger: for example, tryptophan replaced methionine 31 in a redesign of high-potential iron-sulfur protein (PDB id 3A38). This reflects CATS’ ability to find space in a protein for larger amino acids that would be sterically infeasible with the original backbone conformation. Thus, CATS greatly improves the modeling of major sequence changes.
Ironically, the design with the largest backbone motion identified by CATS was in an 8-residue loop in the Dachshund regulatory protein (PDB id 1L8R (Kim et al., 2002)), which had backbone RMSD 0.31 Å RMSD and improved the energy by 17.1 kcal/mol compared to the original backbone.
As discussed in SM 5, voxel sizes were selected by starting with a 2-Å range (-1 to 1) for each CATS degree of freedom, and then scaling down this range (for all degrees of freedom at once) by a factor of 1.3 repeatedly until RMS constraint violations sank below 0.01 Å. Despite this strict threshold, a ∼1-Å range for each CATS degree of freedom was usually chosen (Supplementary Fig. S2). These voxels are thus centered at the original (crystal structure) backbone conformation, which by construction has a value of 0 for each CATS degree of freedom. Sidechain dihedrals were allowed 9 degrees of motion in either direction from ideal rotameric values, as described previously (Georgiev et al., 2008b; Gainza et al., 2012; Hallen et al., 2015). Conformational search over the space defined by these voxels was performed using the EPIC algorithm (Hallen et al., 2015). Computation times for the CATS designs reported here ranged from less than a minute to eleven days, with a median of 17.6 hours; for wild-type conformational searches the median was 7.9 hours.
Further details of all the test cases described in this section are provided in SM 6.
3.2 Modeling of Trp 54 mutation in VRC07
The homologous antibodies NIH45-46 and VRC07 both bind with high potency to the HIV surface glycoprotein gp120, and neutralize a broad range of strains of the virus. However, HIV is notorious for mutating to resist the immune system, and thus modified antibodies with increased potency and breadth are of great biomedical interest—both for passive immunization and as a guide for vaccine development. A mutation from glycine to tryptophan at position 54 of NIH45-46 was found to increase breadth and potency significantly (Diskin et al., 2011). In a previous study, one of us (BRD) and colleagues showed that this mutation increases the breadth and potency of VRC07 as well (Rudicell et al., 2014). Since then, the question of whether this mutation can be modeled in computational design has been an open problem of considerable interest. Large changes in sizes of sidechains, as in this mutation, are more likely to induce backbone motions and thus more difficult to model computationally.
Indeed, modeling this mutation has presented a challenge for previous protein design algorithms. A rigid-backbone conformation search (starting from a VRC07-gp120 complex structure with leucine at position 54 and PDB id 4OLX (Rudicell et al., 2014)) shows extensive clashes with two nearby backbone segments (Fig. 3A). Backrub perturbations (Davis et al., 2006) to the backbone, which are often used to model previously unobserved backbone changes in extended conformations such at this loop (Georgiev et al., 2008a; Hallen et al., 2013; Smith and Kortemme, 2008), could not resolve these clashes (Fig. 3B). The provably complete DEEPer algorithm was used to search the space of backrubs, ensuring that a feasible conformation was not missed in the search. Backbone conformational changes can also be modeled using loops transplanted from other structures, and indeed antibody loops have been classified into a list of canonical structures (Al-Lazikani et al., 1997). But the crucial backbone motion here is far more subtle than the shifts between canonical structures, and thus is best handled with a continuous approach. Although molecular dynamics techniques can search over all degrees of freedom in a protein, they are unsuitable for large design spaces because a separate simulation would be needed for each sequence. Thus, modeling this sort of backbone motion in the combinatorial protein design context requires a technique for continuous and systematic search of backbone conformations that is compatible with combinatorial protein design algorithms.
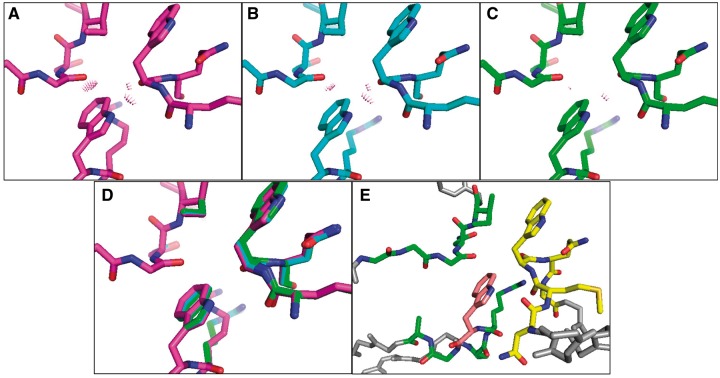
Fig. 3.
The CATS conformational space for a mutant of the antibody VRC07 includes non-clashing conformations inaccessible to rigid-backbone design. The backbone was either held rigid (A) or allowed DEEPer (Hallen et al., 2013) (B) or CATS (C) flexibility for five residues. (A–C) Steric clashes between atoms indicated in pink. (D) The three designs overlaid (rigid backbone in magenta, DEEPer in cyan, CATS in green). (E) Broader view: 15 residues (green, yellow, pink) were allowed continuous sidechain flexibility, of which ten were restrained in an -continuous rotamer voxel centered on the original rotamer (n = number of sidechain dihedrals); the segment with backbone flexibility is shown in yellow, and Trp 54 in pink. Designs were run starting from PDB id 4OLX (Rudicell et al., 2014)
Indeed, CATS resolves this problem, as its conformational space includes a conformation with favorable contacts all around the mutation. Allowing one of the backbone segments that clashes heavily with Trp 54 in rigid-backbone search to relax by CATS resolves the clashes (Fig. 3C), causing a 16 kcal/mol improvement in energy relative to the rigid-backbone search (this is a 9 kcal/mol improvement relative to the DEEPer search). This improvement results from a fairly modest backbone shift: 0.28 Å backbone RMSD for the flexible segment, with per-residue backbone RMSDs up to 0.46 Å (Fig. 3D). The backbone motion modeled by CATS reduces the backbone RMSD of the modeled structure compared to a crystal structure with Trp 54 (PDB id 4OLZ (Rudicell et al., 2014)), from 0.61 Å to 0.46 Å, calculated using the method of Kromann and Bratholm (2013) and Kabsch (1976) for Trp 54 and the two gp120 residues it clashes with in the rigid-backbone model (Trp 427 and Gly 473). However, the RMSD change is somewhat difficult to interpret because independent crystal structures of the same protein would also be likely to exhibit RMSDs around this level.
These results show the key role that local backbone flexibility, as modeled by CATS, can play in identifying favorable conformations and sequences. They also show that CATS can perform designs that could not be modeled using previous algorithms. In particular, they show that the level of backbone flexibility modeled by CATS is functionally significant, resulting in a qualitatively different conformational space. In particular, CATS reveals how a mutant that rigid-backbone computations dismiss as sterically infeasible can actually bind its target well.
4 Conclusions
CATS is a novel and systematic method to search substantial, continuous regions of backbone conformational space during protein design calculations. By moving away from fixed repertoires of motions and into comprehensive search of conformations with valid bonding geometry, it moves closer to fully realistic modeling of backbone conformational changes.
A key challenge as we move into these larger spaces is ensuring that the energetic cost of the backbone conformational changes is estimated accurately enough by the energy function to yield useful results. But CATS can play an important role in addressing this challenge as well. CATS enables provably accurate algorithms, which introduce no new error beyond the error in the model, in contrast to stochastic, heuristic approaches that have been shown to drastically undersample the conformational space specified by the model (Gainza et al., 2016; Simoncini et al., 2015). As a result, CATS can be used to validate energy functions in the highly backbone-flexible designs it enables, with the guarantee that error in design predictions is due only to error in the energetic and geometric modeling and not to error in the algorithm (aside from CATS’ negligible and well-controlled Taylor series error). In addition, because CATS is agnostic to the energy function, it will be useful for performing conformational searches with the more accurate energy functions of the future (Hallen et al., 2015, 2016).
CATS is also easily generalizable to non-protein systems—whether other macromolecules or small molecules. It is applicable in any context where local conformational perturbations are needed subject to bonding geometry constraints. One need only construct the appropriate multivariate quadratic to reflect these constraints.
We believe these capabilities will make CATS useful in many kinds of designs.
Supplementary Material
Acknowledgements
We thank Dr Kyle Roberts for molecular structures and helpful comments on the VRC07 system; and Dr Pablo Gainza, Hunter Nisonoff, Jonathan Jou, Adegoke Ojewole, Marcel Frenkel, Anna Lowegard, Siyu Wang and Graham Holt for helpful comments on the manuscript.
Funding
This work was supported by the Liebmann Foundation [to M.A.H.]; and National Institutes of Health [R01-GM-78031 to B.R.D.].
Conflict of Interest: none declared.
References
- Al-Lazikani B. et al. (1997) Standard conformations for the canonical structures of immunoglobulins. J. Mol. Biol., 273, 927–948. [DOI] [PubMed] [Google Scholar]
- Bahar I., Rader A.J. (2005) Coarse-grained normal mode analysis in structural biology. Curr. Opin. Struct. Biol., 15, 586–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chazelle B. et al. (2004) A semidefinite programming approach to side chain positioning with new rounding strategies. INFORMS J. Comput. Comput. Biol. Special Issue, 16, 380–392. [Google Scholar]
- Chen C.-Y. et al. (2009) Computational structure-based redesign of enzyme activity. Proc. Natl. Acad. Sci. U. S. A., 106, 3764–3769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornell W.D. et al. (1995) A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc., 117, 5179–5197. [Google Scholar]
- Das R., Baker D. (2008) Macromolecular modeling with Rosetta. Annu. Rev. Biochem., 77, 363–382. [DOI] [PubMed] [Google Scholar]
- Davis I.W. et al. (2006) The backrub motion: how protein backbone shrugs when a sidechain dances. Structure, 14, 265–274. [DOI] [PubMed] [Google Scholar]
- Desjarlais J.R., Handel T.M. (1995) De novo design of the hydrophobic cores of proteins. Protein Sci., 4, 2006–2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmet J. et al. (1992) The dead-end elimination theorem and its use in protein side-chain positioning. Nature, 356, 539–542. [DOI] [PubMed] [Google Scholar]
- Desmet J. et al. (2002) Fast and accurate side-chain topology and energy refinement (FASTER) as a new method for protein structure optimization. Proteins Struct. Funct. Bioinf., 48, 31–43. [DOI] [PubMed] [Google Scholar]
- Diskin R. et al. (2011) Increasing the potency and breadth of an HIV antibody by using structure-based rational design. Science, 334, 1289–1293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donald B.R. (2011). Algorithms in Structural Molecular Biology. MIT Press, Cambridge, MA. [Google Scholar]
- Floudas C.A. et al. (1999) Global optimization approaches in protein folding and peptide docking In: Farach-Colton M. (ed.) Mathematical Support for Molecular Biology, Volume 47 of DIMACS Series in Discrete Mathematics and Theoretical Computer Science, pp. 141–172. American Mathematical Society, Providence, RI. [Google Scholar]
- Frey K.M. et al. (2010) Predicting resistance mutations using protein design algorithms. Proc. Natl. Acad. Sci. U. S. A., 107, 13707–13712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fung H.K. et al. (2008) Toward full-sequence de novo protein design with flexible templates for human β-defensin-2. Biophys. J., 94, 584–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gainza P. et al. (2012) Protein design using continuous rotamers. PLoS Comput. Biol., 8, e1002335.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gainza P. et al. (2013) OSPREY: Protein design with ensembles, flexibility, and provable algorithms. Methods Enzymol., 523, 87–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gainza P. et al. (2016) Algorithms for protein design. Curr. Opin. Struct. Biol., 39, 16–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gehmlich K. et al. (2007) Paxillin and ponsin interact in nascent costameres of muscle cells. J. Mol. Biol., 369, 665–682. [DOI] [PubMed] [Google Scholar]
- Georgiev I., Donald B.R. (2007) Dead-end elimination with backbone flexibility. Bioinformatics, 23, i185–i194. [DOI] [PubMed] [Google Scholar]
- Georgiev I. et al. (2008a) Algorithm for backrub motions in protein design. Bioinformatics, 24, i196–i204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgiev I. et al. (2008b) The minimized dead-end elimination criterion and its application to protein redesign in a hybrid scoring and search algorithm for computing partition functions over molecular ensembles. J. Comput. Chem., 29, 1527–1542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgiev I. et al. (2009). OSPREY (Open Source Protein Redesign for You) user manual. Available online: www.cs.duke.edu/donaldlab/software.php Updated, 2015. 94 pages.
- Georgiev I. et al. (2012) Design of epitope-specific probes for sera analysis and antibody isolation. Retrovirology, 9, P50. [Google Scholar]
- Georgiev I.S. et al. (2014) Antibodies VRC01 and 10E8 neutralize HIV-1 with high breadth and potency even with Ig-framework regions substantially reverted to germline. J. Immunol., 192, 1100–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gleicher M. (1992). Integrating constraints and direct manipulation. In: Proceedings of the 1992 symposium on Interactive 3D graphics. ACM, pp. 171–174.
- Gorczynski M.J. et al. (2007) Allosteric inhibition of the protein-protein interaction between the leukemia-associated proteins Runx1 and CBFβ. Chem. Biol., 14, 1186–1197. [DOI] [PubMed] [Google Scholar]
- Gordon D.B. et al. (2003) Exact rotamer optimization for protein design. J. Comput. Chem., 24, 232–243. [DOI] [PubMed] [Google Scholar]
- Hallen M.A., Donald B.R. (2016) COMETS (Constrained Optimization of Multistate Energies by Tree Search): a provable and efficient protein design algorithm to optimize binding affinity and specificity with respect to sequence. J. Comput. Biol., 23, 311–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallen M.A. et al. (2013) Dead-end elimination with perturbations (DEEPer): A provable protein design algorithm with continuous sidechain and backbone flexibility. Proteins Struct. Funct. Bioinf., 81, 18–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallen M.A. et al. (2015) Compact representation of continuous energy surfaces for more efficient protein design. J. Chem. Theory Comput., 11, 2292–2306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallen M.A. et al. (2016). LUTE (Local Unpruned Tuple Expansion): Accurate continuously flexible protein design with general energy functions and rigid-rotamer-like efficiency. In: International Conference on Research in Computational Molecular Biology. Springer, pp. 122–136. [DOI] [PMC free article] [PubMed]
- Jacobs T.M. et al. (2016) Design of structurally distinct proteins using strategies inspired by evolution. Science, 352, 687–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janin J. et al. (1978) Conformation of amino acid side-chains in proteins. J. Mol. Biol., 125, 357–386. [DOI] [PubMed] [Google Scholar]
- Jou J.D. et al. (2016) BWM*: A novel, provable, ensemble-based dynamic programming algorithm for sparse approximations of computational protein design. J. Comput. Biol., 23, 413–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabsch W. (1976) A solution for the best rotation to relate two sets of vectors. Acta Crystallogr. Sect. A Cryst. Phys. Diffract. Theor. Gen. Crystallogr., 32, 922–923. [Google Scholar]
- Karanicolas J., Kuhlman B. (2009) Computational design of affinity and specificity at protein-protein interfaces. Curr. Opin. Struct. Biol., 19, 458–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S.-S. et al. (2002) Structure of the retinal determination protein Dachshund reveals a DNA binding motif. Structure, 10, 787–795. [DOI] [PubMed] [Google Scholar]
- Kingsford C.L. et al. (2005) Solving and analyzing side-chain positioning problems using linear and integer programming. Bioinformatics, 21, 1028–1039. [DOI] [PubMed] [Google Scholar]
- Kromann J.C., Bratholm L.A. (2013). Calculate RMSD for two XYZ structures. Available online: http://github.com/charnley/rmsd. Updated, 2017.
- Kuhlman B., Baker D. (2000) Native protein sequences are close to optimal for their structures. Proc. Natl. Acad. Sci. U. S. A., 97, 10383–10388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazaridis T., Karplus M. (1999) Effective energy function for proteins in solution. Proteins Struct. Funct. Bioinf., 35, 133–152. [DOI] [PubMed] [Google Scholar]
- Leach A.R., Lemon A.P. (1998) Exploring the conformational space of protein side chains using dead-end elimination and the A* algorithm. Proteins Struct. Funct. Bioinf., 33, 227–239. [DOI] [PubMed] [Google Scholar]
- Leaver-Fay A. et al. (2011) A generic program for multistate protein design. PLoS One, 6, e20937.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis S.M. et al. (2014) Generation of bispecific IgG antibodies by structure-based design of an orthogonal Fab interface. Nat. Biotechnol., 32, 191–198. [DOI] [PubMed] [Google Scholar]
- Lilien R.H. et al. (2005) A novel ensemble-based scoring and search algorithm for protein redesign and its application to modify the substrate specificity of the gramicidin synthetase A phenylalanine adenylation enzyme. J. Comput. Biol., 12, 740–761. [DOI] [PubMed] [Google Scholar]
- Lippow S.M., Tidor B. (2007) Progress in computational protein design. Curr. Opin. Biotechnol., 18, 305–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lovell S.C. et al. (2000) The penultimate rotamer library. Proteins Struct. Funct. Genet., 40, 389–408. [PubMed] [Google Scholar]
- Lovell S.C. et al. (2003) Structure validation by Cα geometry: ϕ, ψ, and Cβ deviation. Proteins Struct. Funct. Bioinf., 50, 437–450. [DOI] [PubMed] [Google Scholar]
- Ngo J.T., Donald B.R. (1999). System for image manipulation and animation using embedded constraint graphics. US Patent 5,933,150.
- Ngo T. et al. (2000). Accessible animation and customizable graphics via simplicial configuration modeling. In: Proceedings of the 27th annual conference on Computer graphics and interactive techniques. ACM Press/Addison-Wesley Publishing Co., pp. 403–410.
- Ojewole A. et al. (2017) OSPREY predicts resistance mutations using positive and negative computational protein design Methods Mol. Biol., 1529, 291–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierce N.A., Winfree E. (2002) Protein design is NP-hard. Protein Eng., 15, 779–782. [DOI] [PubMed] [Google Scholar]
- Pierce N.A. et al. (2000) Conformational splitting: A more powerful criterion for dead-end elimination. J. Comput. Chem., 21, 999–1009. [Google Scholar]
- Rapaport D.C. (2004). The Art of Molecular Dynamics Simulation, 2nd edn Cambridge University Press, Cambridge, England. [Google Scholar]
- Regan L. (1999) Protein redesign. Curr. Opin. Struct. Biol., 9, 494–499. [DOI] [PubMed] [Google Scholar]
- Roberts K.E., Donald B.R. (2015) Improved energy bound accuracy enhances the efficiency of continuous protein design. Proteins Struct. Funct. Bioinf., 83, 1151–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts K.E. et al. (2012) Computational design of a PDZ domain peptide inhibitor that rescues CFTR activity. PLoS Comput. Biol., 8, e1002477.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts K.E. et al. (2015) Fast gap-free enumeration of conformations and sequences for protein design. Proteins Struct. Funct. Bioinf., 83, 1859–1877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudicell R.S. et al. (2014) Enhanced potency of a broadly neutralizing HIV-1 antibody in vitro improves protection against lentiviral infection in vivo. J. Virol., 88, 12669–12682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simoncini D. et al. (2015) Guaranteed discrete energy optimization on large protein design problems. J. Chem. Theory Comput., 11, 5980–5989. [DOI] [PubMed] [Google Scholar]
- Smith C., Kortemme T. (2008) Backrub-like backbone simulation recapitulates natural protein conformational variability and improves mutant side-chain prediction. J. Mol. Biol., 380, 742–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevens B.W. et al. (2006) Redesigning the PheA domain of gramicidin synthetase leads to a new understanding of the enzyme’s mechanism and selectivity. Biochemistry, 45, 15495–15504. [DOI] [PubMed] [Google Scholar]
- Traoré S. et al. (2013) A new framework for computational protein design through cost function network optimization. Bioinformatics, 29, 2129–2136. [DOI] [PubMed] [Google Scholar]
- Traoré S. et al. (2016) Fast search algorithms for computational protein design. J. Comput. Chem., 37, 1048–1058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tripathy C. et al. (2012) Protein loop closure using orientational restraints from NMR data. Proteins Struct. Funct. Bioinf., 80, 433–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C. et al. (2005) Improved side-chain modeling for protein-protein docking. Protein Sci., 14, 1328–1339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner P.K., Kollman P.A. (1981) AMBER: Assisted model building and energy refinement. A general program for modeling molecules and their interactions. J. Comput. Chem., 2, 287–303. [Google Scholar]
- Wong K.-B. et al. (1999) Hot-spot mutants of p53 core domain evince characteristic local structural changes. Proc. Natl. Acad. Sci. U. S. A., 96, 8438–8442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J., Berger B. (2006) Fast and accurate algorithms for protein side-chain packing. J. ACM, 53, 533–557. [Google Scholar]
- Zhou J., Grigoryan G. (2015) Rapid search for tertiary fragments reveals protein sequence–structure relationships. Protein Sci., 24, 508–524. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.