A computational analysis of sequence features involved in recognition of short introns

Abstract

Splicing of short introns by the nuclear pre-mRNA splicing machinery is thought to proceed via an “intron definition” mechanism, in which the 5′ and 3′ splice sites (5′ss, 3′ss, respectively) are initially recognized and paired across the intron. Here, we describe a computational analysis of sequence features involved in recognition of short introns by using available transcript data from five eukaryotes with complete or nearly complete genomic sequences. The information content of five different transcript features was measured by using methods from information theory, and Monte Carlo simulations were used to determine the amount of information required for accurate recognition of short introns in each organism. We conclude: (i) that short introns in Drosophila melanogaster and Caenorhabditis elegans contain essentially all of the information for their recognition by the splicing machinery, and computer programs that simulate splicing specificity can predict the exact boundaries of ≈95% of short introns in both organisms; (ii) that in yeast, the 5′ss, branch signal, and 3′ss can accurately identify intron locations but do not precisely determine the location of 3′ cleavage in every intron; and (iii) that the 5′ss, branch signal, and 3′ss are not sufficient to accurately identify short introns in plant and human transcripts, but that specific subsets of candidate intronic enhancer motifs can be identified in both human and Arabidopsis that contribute dramatically to the accuracy of splicing simulators.

RNA splicing is an essential step in the expression of most eukaryotic genes. An important goal of research on this process is to determine a set of rules that accurately predicts the splicing pattern of primary transcripts. Unlike the process of mRNA translation by the ribosome, which follows a set of rules that is essentially invariant in all known organisms, the rules governing RNA splicing clearly differ between different groups of eukaryotes. Therefore, there is not one but several variants of the “splicing code” that remain to be worked out. In addition, the rules for splicing appear to be significantly more complex than those for translation, involving presence of multiple degenerate motifs occurring with appropriate spacing in the transcript. Development of computer algorithms that directly model recognition by the splicing machinery is recognized as an important challenge (1).

In human transcripts, the exons are usually short (typically 100–200 bases) and the introns are much longer, averaging about 3 kb (2). The realization that the splicing machinery would face great difficulty in locating splice sites across such long introns led to the exon definition model in which splice sites are paired first across the exons, with spliceosome assembly proceeding through subsequent pairing of exon units (3). The alternative intron definition model derives from the observation that introns in some transcripts (especially in invertebrates) are quite short relative to exons, and so the splicing machinery may initially pair splice sites across introns rather than exons in these cases. As expected from this model, mutation of the 5′ splice site (5′ss) of a short intron leads to intron retention rather than exon skipping, and expansion of short introns inhibits their splicing in vitro and in vivo (4). Short introns inserted into intronless transcripts can be properly spliced, suggesting that the information for splicing of short introns may be contained entirely within the intron (5).

Here, we analyze transcript features involved in recognition of short introns by using a computational approach that takes advantage of the recent availability of large sets of transcripts from five organisms with essentially complete genome sequences. Our analysis had three goals. First, to define and measure the amount of information usable for intron recognition that is present in the three classical splice signal motifs [5′ss, 3′ splice site (3′ss), and branch signal] in each organism. Second, to determine how much information is required to accurately identify short introns in transcripts from each organism, and therefore how much additional information must be present in other transcript features besides the classical splice signals. And, finally, to identify other transcript features that are likely to provide the additional information needed for accurate intron recognition.

Methods

Splicing Simulators.

The pairscan algorithm assigns scores, defined as the sum of the 5′ and 3′ splice signal log-odds scores, to all possible 5′, 3′ splice signal pairs that have appropriate short intron separation in the transcript (e.g., 40–81 bases apart for Drosophila transcripts). All such pairs whose scores exceed a predetermined cutoff C and do not overlap with more highly scored pairs are predicted to be short introns. The score cutoff C is chosen empirically for each organism to maximize accuracy, defined as the average of sensitivity (Sn) and specificity (Sp). The definitions of these quantities are: Sn = TP/(TP + FN) and Sp = TP/(TP + FP), where TP is the number of true positives (correctly predicted introns), FN is the number of false negatives (introns not predicted), and FP is the number of false positives (predicted introns which are incorrect). In triplescan, a branch score is added to the score of each splice signal pair. The branch score is defined as the log-odds score of the highest-scoring potential branch site located between 15 and 45 bases upstream of the 3′ss (15–200 upstream for yeast), using the weight matrix model (WMM) branch model derived from Fig. 2B, less the logarithm of the width of the window searched, i.e., subtracting log₂185 for yeast or log₂30 for other organisms. The possibility that the branch point may not be present in this window was accounted for by using the formula S′ = log₂(2^SP_B + 1 − P_B), where S is the WMM branch score and P_B is an estimate of the probability that the branch site occurs in the given window. intronscan is similar to triplescan, except that an intron length score and an intron composition score (see below) are added to the score of each potential intron. pairscan, triplescan, and intronscan were implemented in the c programming language.

Figure 2.

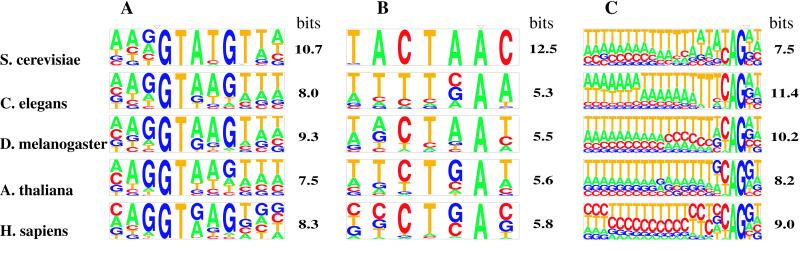
Splice signal motifs. Sequence motifs for the 5′ss (A), branch site (B), and 3′ss (C) are displayed by using the pictogram program (http://genes.mit.edu/pictogram.html). The height of each letter is proportional to the frequency of the corresponding base at the given position, and bases are listed in descending order of frequency from top to bottom. The RelEnt (in bits) of the motif model used in our analyses (I1M or WMM) relative to the background transcript base composition is also shown. The splice junctions and branch point are marked by inverted triangles.

Scores for Intron Length and Composition.

For any length l between the minimum and maximum short intron lengths in an organism (L_min and L_max), the intron length preference score was defined as s(l) = log₂(f_l/g_l), where f_l is the frequency of length l in the empirical distribution of short intron lengths (smoothed by using the r statistical package with default kernel), and g_l = (L_max + 1 − L_min)⁻¹ is a uniform density. The intron pentamer score for an intron was defined as s(I) = log₂[P(I)/q(I)] where P(I) is the probability of generating the given intron sequence (excluding the splice signals and branch signal) under the intron composition model and q(I) is the corresponding probability under the transcript composition model. By default, homogeneous fourth-order Markov chain models were used for both introns and transcripts, with parameters estimated from the data listed in Table 1. Such models capture pentanucleotide composition. Similar models have been used previously for exon-intron discrimination (6). For the experiment shown in Fig. 5, the pentamer score was calculated by using specific subsets of pentamers as described in the supporting information, which is published on the PNAS web site, www.pnas.org.

Table 1.

Accuracy of splicing simulators

Organism	No. of transcripts	No. of introns	% Short introns	pairscan		triplescan		intronscan
				DAc	EAc	DAc	EAc	DAc	EAc
S. cerevisiae	152	152	46	90	43	98	83	98	86
C. elegans	691	3,577	46	95	92	95	92	97	95
D. melanogaster	1,310	3,737	54	92	88	93	90	96	94
A. thaliana	1,121	5,265	63	82	68	83	69	96	92
H. sapiens	8,165	33,666	10	76	65	78	66	88	85

The numbers of transcripts and introns derived from cDNA/genomic alignments are listed, as well as the percentage of introns classified as short according to the cutoffs given in the text. The percent DAc and EAc are cross-validated values as described in Methods. 

Figure 5.

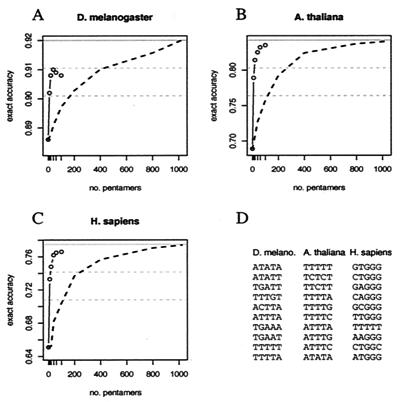
Contribution of subsets of pentamers to intron prediction. Exact prediction accuracies are shown for intronscan by using the 5′ss and 3′ss signals and specialized intron composition models that score particular subsets of pentamers (see the supporting information) as a function of the number of pentamers used. Circles represent accuracy calculated by using 0, 10, 20, 40, 60, and 100 pentamers, with pentamers chosen in order from high values of flog(f/g) to low, where f and g are the pentamer frequency in introns and exons, respectively, using a protocol that avoids choosing overlapping pentamers (see the supporting information). (A) Drosophila, (B) Arabidopsis, (C) human. (D). The first ten intron-biased pentamers chosen from each organism. The dashed black line represents average accuracy for 25 random orderings of pentamers. The solid gray line represents accuracy by using all 1,024 pentamers—dashed gray lines are described in text.

Cross-Validation.

The data in Table 1 were 5-fold cross-validated by randomly dividing the transcript data into five subsets and measuring the accuracies of pairscan, triplescan, and intronscan on each subset, with splice site and intron composition parameters derived from the other four subsets, and taking the average of the five accuracy values obtained. Two-fold cross-validation was used for yeast because of the limited number of transcripts.

Measuring Contributions to Intron Detection.

The contribution of each transcript feature to intron detection (see Fig. 4) was measured by tabulating the accuracy of “mutant” versions of intronscan that scored different subsets of transcript features: 5′ss + 3′ss, 5′ss + 3′ss + branch, 5′ss + 3′ss + intron composition, etc. All combinations of features involving both splice signals were used. In addition, the ability of the 5′ss and 3′ss alone to detect introns was measured. Intron detection accuracy (DAc) was converted to log error, defined as log₂(1 − DAc), and linear regression was then used to estimate the relative contribution of each signal to reduction of the log error.

Figure 4.

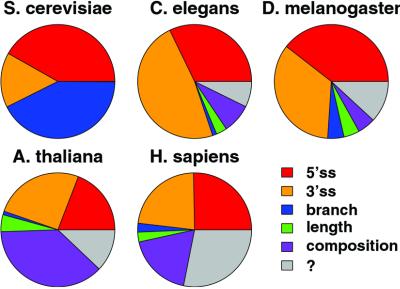
Relative contributions of five transcript features to intron detection. The area of each wedge represents the relative contribution to intron detection accuracy of the corresponding transcript feature, calculated as described in Methods. The sizes of the wedges are scaled so that the complete circle represents the RelEnt per intron required to achieve 98% detection accuracy in each organism, derived from Fig. 3.

Results

Construction of Transcript Datasets.

Five eukaryotes for which complete or nearly complete genomic sequences are currently available were chosen: the yeast Saccharomyces cerevisiae, the nematode worm Caenorhabditis elegans, the fruit fly Drosophila melanogaster, the mustard weed Arabidopsis thaliana, and human. To avoid using computationally predicted genes, available cDNAs from each organism were systematically aligned to their respective genomic loci by using a gene annotation script called genoa (unpublished work) (see the supporting information). Genes identified by this script as alternatively spliced were excluded. The total number of verified gene structures determined by this procedure is listed in Table 1. All analyses described here used transcripts whose exon-intron structure was confirmed by cDNA alignment.

Intron Length Distributions.

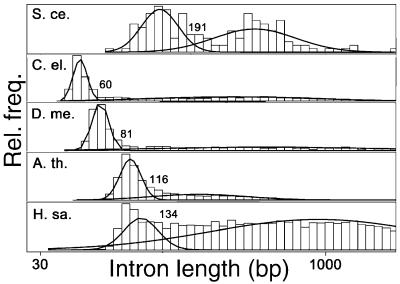
Histograms of intron lengths from these transcripts revealed the presence of a distinct population of short introns in all five organisms (Fig. 1). Fitting the observed length distribution as a sum of two lognormal distributions determined a natural cutoff length for short introns in each organism as described in the legend to Fig. 1. This criterion defines short introns as those not longer than 60 bases in C. elegans, ≤81 bp in Drosophila, ≤116 bp in A. thaliana, ≤134 bp in human, and ≤191 bp in S. cerevisiae. For our purposes, introns longer than these cutoff lengths are considered long introns. The fraction of introns classified as short was between 45% and 65% in each organism except human, where it was only about 10%. Here, our goal was to study short introns, which are thought to be recognized primarily through intron definition. Therefore, in each organism all long introns were removed from the set of transcripts, as if they had already been processed by a separate mechanism, leaving only exons and short introns. The remainder of our analyses focused on these modified transcript sequences. In yeast, where transcripts generally contain at most one intron and intron definition is the rule, we did not remove long introns, effectively treating all introns as short.

Figure 1.

Intron length distributions. Histograms of the lengths of introns from each organism are plotted, using a log scale for the abscissa. Each histogram was fitted as a mixture of two lognormal distributions by using the r statistical package (curved lines). The position of the point of intersection of these distributions is indicated. S. ce., S. cerevisiae; C. el., C. elegans; D. me., D. melanogaster; A. th., A. thaliana; H. sa., Homo sapiens.

Splice Signal Models.

Next, we analyzed the classical splice signal motifs in the set of short introns from each organism. The results, displayed in Fig. 2, reveal well-known motifs. Using these data, statistical models of the 5′ and 3′ splice signals were created that can be used to score potential splice sites. First, WMMs were constructed that capture the position-specific base composition of the signals, assuming independence between positions. Although WMMs have been widely used in sequence analysis, the assumption of independence between positions made by WMMs is not warranted in the case of the 5′ and 3′ splice signals (7). In fact, we confirmed the presence of significant statistical dependencies between positions in the 5′ss and 3′ss of all four multicellular organisms studied (see the supporting information). To account for these potentially significant statistical interactions, inhomogeneous first-order Markov models (I1Ms) were developed for the 5′ss and 3′ss signals from each organism, as described (8). I1Ms account both for position-specific nucleotide composition and dependencies between adjacent positions in a sequence motif. Because too few introns were available from yeast to construct I1M splice site models, WMMs were used instead for this organism. Both WMMs and I1Ms can be used to assign log-odds scores to potential splice sites in a transcript that approximate the log likelihood that the site is used as a splice site.

Given the complex and somewhat variable motifs shown in Fig. 2, it is natural to ask how much information these motifs provide for identifying introns and splice sites in primary transcripts. From information theory, the answer to this question is that the amount of information useful for identifying occurrences of a given motif is directly related to the relative entropy (RelEnt) or Kullback–Liebler distance between the motif sequence distribution and a suitable background distribution (9, 10). The RelEnt of a distribution f relative to the background distribution g is defined as

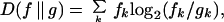where f_k is the probability of observing sequence k under the motif distribution, g_k is the probability of observing sequence k under the background sequence distribution, and the sum is taken over all possible nucleotide sequences of appropriate length. When base 2 logarithms are used, RelEnt is measured in binary digits or bits. RelEnt has a number of desirable statistical properties and in an important sense measures the amount of “information for discrimination” that is present in a distribution (9). In general, the higher the RelEnt of a motif, the more rarely similar sequences will occur in random sequences with composition g, and each extra bit of RelEnt corresponds to approximately a 50% reduction in the frequency of chance occurrences of motif-like sequences. The RelEnt of the 5′ and 3′ splice signal sequences for each organism are listed in Fig. 2 (see also ref. 11).

Information Required for Identification of Introns.

The above data raise a fundamental question in RNA splicing specificity: how much information is required to accurately identify the locations of introns in primary transcript sequences? This issue was addressed by using Monte Carlo simulations in which the accuracy of intron identification was measured in randomized sequences as a function of the information content (RelEnt) of artificial splice signal motifs. The ability of these motifs to specify short intron locations was assessed by measuring the accuracy of intron identification using a procedure called pairscan, which implements a simple splice site pairing model of intron recognition. In pairscan, all potential 5′ss and 3′ss in a transcript are assigned log-odds scores by using the appropriate motif models and introns are recognized as pairs of potential 5′ss and 3′ss, which are located with appropriate spacing for a short intron in the given organism and have sufficiently high score, as described in Methods.

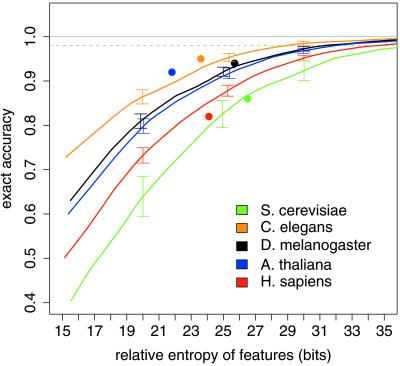
The accuracy of pairscan in identifying short introns in the randomized transcripts (defined below) was then plotted as a function of the sum of the RelEnts of the 5′ and 3′ splice signal models used (Fig. 3). As expected, accuracy improves monotonically as the information content of the splice signal motifs is increased. However, the increase is not linear, but levels off when the information content becomes high. To achieve high accuracy of precise intron identification, say 98% of introns identified exactly, requires ≈30 bits of information in each organism (Fig. 3). However, the precise amount needed varies somewhat depending on transcript geometry—about 29 bits per intron in C. elegans, 31 bits in Drosophila, and 32, 34 and 37 bits in Arabidopsis, human, and yeast, respectively (see the supporting information). Comparing these values with the RelEnt data from Fig. 2 indicates that the classical splice signals do not appear to provide enough information to exactly identify 98% of short introns in any organism, with the amount of the information deficit varying from 10 bits in C. elegans and 11 bits in Drosophila to 16, 17, and 19 bits in Arabidopsis, human, and yeast, respectively.

Figure 3.

Monte Carlo estimation of information required for short intron recognition. EAc of prediction of short introns by pairscan in randomized transcripts is plotted versus the sum of the RelEnts of the splice signal motifs used. Dotted gray line indicates 98% EAc. Each curve is the best-fit from 130 simulations. Brackets indicate 1 SD above and below the best-fit curve for three chosen RelEnt values. Solid circles represent EAc for intronscan in real transcripts versus the sum of the RelEnts of the transcript features used.

Accuracy of Splice Site Pair Model of Intron Recognition.

To clarify this matter, the pairscan algorithm was then applied to the set of real transcripts from each organism by using the splice signal motifs from Fig. 2. The results are summarized by using two different measures of accuracy: (i) DAc defined in terms of the fraction of true introns detected (at least one splice site correct); and (ii) exact accuracy (EAc), defined in terms of the fraction of true introns predicted exactly (both splice sites correct)—see Methods for precise definitions. In yeast, using the 5′ss and 3′ss alone gave a detection accuracy of 90%, but an exact accuracy of only about 40% (Table 1), underscoring the usefulness of distinguishing these two measures. This difference reflects the ability of the strong yeast 5′ splice signal to indicate the existence of an intron but the inability of the weak yeast 3′ splice signal motif to accurately specify the precise location of the 3′ss (12). The 5′ and 3′ splice signals alone are sufficient to achieve relatively high (>90%) accuracy in fly and worm transcripts. By contrast, these motifs by themselves cannot accurately identify short introns in human or Arabidopsis (Table 1). This analysis implies that other transcript features must play a large role in recognition of short introns in both human and plant transcripts and must play at least some role in splicing in yeast, fly, and worm. Below, we review three such features and describe how their possible contribution to intron recognition was assessed.

Branch Signals, Intron Length, and Intron Composition.

Unlike the 5′ss and 3′ss, the position of the branch site cannot be directly determined from cDNA/genomic alignments alone. To assess the contribution of this signal to splicing specificity, the region immediately upstream of the 3′ss was extracted from the set of short introns available from each organism, and potential branch sites were identified by using the Gibbs sampling algorithm (13), as described in the supporting information. The branch motifs identified in this way are shown in Fig. 2B. This procedure easily identifies the canonical TACTAAC sequence in S. cerevisiae and identifies consensus patterns CTAAT, CTGAT, and CTGAC, in fly, mustard weed and human, respectively, all of which have significant complementarity to U2 small nuclear RNA. These patterns are similar to consensus branch signals described in the literature for these organisms (14, 15). The consensus pattern TTT(C/G)AA identified by the Gibbs sampler in C. elegans introns differs substantially from the other branch motifs, exhibiting only weak complementarity to U2 small nuclear RNA, consistent with previous observations that nematode introns lack a recognizable branch motif (16). Incorporation of this motif into splicing simulators does not increase accuracy (Table 1), suggesting that this pattern is not critically involved in intron recognition.

Another possible source of information for intron recognition is a preference on the part of the splicing machinery for short introns of particular lengths. For example, the Drosophila intron length histogram (Fig. 1) has a sharp peak at around 60 nt, with over 40 times as many introns in the range of 60 to 65 bp than in the range of 40 to 45 bp, and seven times as many introns in the range of 60 to 65 than in the range of 75 to 80 bases. There is some evidence of natural selection for short intron lengths (17), and it is possible that selection favors introns with lengths very close to 60–65 bases over shorter or longer introns because they are spliced more efficiently. Consistent with this idea, expanding the length of a 68-base Drosophila intron to 84 bp greatly decreased its splicing in vitro (18), and expansion of other short Drosophila introns led to activation of weak cryptic splice sites within the expansion cassette (4).

Other sequences in the intron besides the classical splice signals also may play a role in recognition of short introns. In many cases, oligonucleotide motifs 3–7 bases in length appear to play a role in splicing (19, 20). Here, we analyzed the possible role of intron pentanucleotide composition. Pentamer composition implicitly includes composition of 3- and 4-nt patterns and will capture some of the information in longer patterns. Pentamers were chosen because too few intron sequences were available from some organisms to reliably estimate frequencies of longer oligomers.

Log-odds scores were derived for each of the three features described above: the branch signal, intron length preference, and intron pentamer composition, as described in Methods. To assess the importance of these features for intron recognition, two algorithms were developed that simulate somewhat more complex models of intron recognition than pairscan. triplescan implements a model in which the 5′ss, branch site, and 3′ss are recognized as a unit. intronscan implements a model of intron recognition in which intron length preference and intron pentamer composition also play a role (see Methods for details). Too few confirmed intron sequences were available from yeast to effectively model intron pentamer composition in this organism. The accuracies of triplescan and intronscan are listed in Table 1, and the intronscan results are also displayed in Fig. 3. As expected, inclusion of the strong yeast branch signal in triplescan allows a very high rate of intron detection in yeast transcripts (98%). However, the weak yeast 3′ss signal is not sufficient to determine the 3′ss location with comparable accuracy (EAc only 83% for triplescan and 86% for intronscan). In Drosophila and C. elegans, intronscan has very high detection accuracy and comparable exact accuracy, demonstrating that short introns contain essentially all of the information necessary for their recognition by the splicing machinery in these two invertebrates. In human introns, the branch signal is relatively weak, and triplescan is only slightly more accurate than pairscan. However, intron composition contributes significantly, and intronscan is much more accurate than pairscan (85% EAc versus 65% for pairscan). The results for Arabidopsis are similar, except that accuracy is even more dramatically improved in intronscan versus pairscan (92% EAc versus 68%).

Relative Contributions of Intron Features to Intron Detection.

Given the significant improvements in accuracy achieved by intronscan, it is natural to ask which intron features contribute most. To assess the contribution of each feature to accuracy, a method based on linear regression was used (see Methods). The results (Fig. 4) show that the relative contributions of different transcript features differ dramatically between yeast, invertebrates, vertebrates, and plants (Fig. 4). The branch signal provides close to half of the information required to detect introns in yeast, whereas the 3′ss is relatively insignificant. As expected, the 5′ and 3′ splice signals contribute at least 75% of the information in Drosophila and C. elegans. However, in Arabidopsis and human these signals provide only 50% or less of the necessary information. A very large contribution from intron pentamer composition is particularly notable in Arabidopsis and human. Calibrating the proportional contributions represented in Fig. 4 to the RelEnt data from Fig. 2 allows estimation of the information content (RelEnt) that must be present in other (unknown) transcript features to achieve 98% detection accuracy in each organism (gray wedges in Fig. 4), found to be about 9 bits per intron in human, 3–4 bits in fly and mustard weed, 2 bits in worm, and 0 bits in yeast.

The very large contribution to intron recognition derivable from intron pentamer composition in Arabidopsis and human is striking. It is natural to ask whether this effect can be attributed to a small subset of pentamers, which might function as intronic splicing enhancers. To address this question, the ability of intronscan to predict introns was analyzed in these organisms by using simpler models of intron composition that consider only particular subsets of pentamers. The results (Fig. 5) show clearly that when only intron-biased pentamers are included, sorted by their contribution to the relative entropy of intron- vs. exon pentamer composition, a large contribution to intron recognition can be derived from a very small subset of pentamers. Strikingly, a subset of only 10 pentamers (less than 1% of the total) gives more than 50% of the total contribution to accuracy that can be derived from considering all possible pentamers in all three organisms (lower dashed gray lines indicate 50% level in Fig. 5). These “top 10” pentamers are listed in Fig. 5D. Approximately 75% of the contribution to accuracy derivable from all pentamers in each organism (upper dashed gray lines in Fig. 5) can be derived from only 40 pentamers, still less than 4% of the total.

Discussion

This study presents a large-scale computational analysis of pre-mRNA splicing that has been able to take advantage of sequence data from five essentially complete eukaryotic genomes. We present a systematic approach for assessing the contributions of different transcript features to intron recognition and for estimating the amount of information required to achieve any desired level of accuracy of intron identification. This approach has been applied to analyze recognition of short introns in five different eukaryotes: yeast, C. elegans, Drosophila, Arabidopsis, and human. Short introns may represent a distinct class of introns that are spliced by an intron definition mechanism (3, 21).

Our results highlight significant similarities and differences between the organization of splicing information in transcripts from different organisms. In yeast, the 5′ss, 3′ss, and branch signal motifs contain sufficient information to detect the locations of introns in transcripts with very high accuracy (98%; see also ref. 22), but the low information content of the yeast 3′ss motif is sufficient to determine the precise 3′ splice junction for only about 86% of yeast introns (Table 1). Some additional transcript feature(s) not included in our models must play a role in specifying the 3′ splice junction of at least some yeast introns. Plausible candidates for this feature include RNA secondary structure (23, 24) or presence of additional enhancer or repressor elements in the 3′ ends of some yeast introns.

In Drosophila and C. elegans, the 5′ and 3′ splice signal motifs are sufficient to detect more than 90% of short introns. Our analysis suggests that the branch signal motif plays a minor but appreciable role in Drosophila splicing. Intron length preference and intron pentamer composition also may play a small role in intron recognition in both invertebrates (Table 1 and Fig. 4). The intronscan model is able to predict the locations and exact splice junctions of short introns in both Drosophila and C. elegans with high accuracy (94% and 95%, respectively), implying that invertebrate introns contain essentially all of the information necessary for their recognition.

The 5′ and 3′ splice signal motifs of Arabidopsis introns are not sufficient to accurately specify short intron locations, and the branch signal motif could contribute only marginally. However, the pentamer composition of Arabidopsis introns can contribute enormously to the recognition of short intron locations (Table 1). This effect can be attributed to a relatively small number of pentanucleotides, most quite U-rich (Fig. 5D), consistent with previous results implicating U-rich sequences in splicing of plant introns (25, 26). Thus, splicing of short Arabidopsis introns can largely be explained by a model involving recognition of the classical splice signals and a handful of U-rich intronic enhancer motifs. Interestingly, the accuracy observed for intronscan in Arabidopsis transcripts is significantly higher than that predicted on the basis of the Monte Carlo data (Fig. 3). Preliminary analysis suggests that this discrepancy results from a “compensation” effect in which introns with weak splice sites are more likely to contain U-rich pentamers (data not shown).

As in Arabidopsis, the 5′ and 3′ splice signals of human introns are far too weak to reliably determine the locations of even short introns in human transcripts, and the human branch signal can contribute only marginally to intron recognition. Our analysis also implicates a small subset of intron-biased pentamers in recognition of short human introns (Fig. 5). These pentamers appear to be dominated by the presence of G triples (GGG), a well-established splicing enhancer motif in human introns (19, 27, 28). However, these motifs do not appear to provide all of the information necessary for accurate determination of short intron locations in human transcripts. Some additional transcript feature(s) must play a role in recognition of at least some short human introns. It could be that some intronic enhancers are longer than five bases or require precise spacing that we have not effectively modeled. The separation between long and short introns is much less pronounced in human than in the other organisms (Fig. 1). This observation might indicate that some human introns we have classified as short may functionally act as long introns and be spliced by exon definition mechanisms, which we have not modeled.

Interestingly, short introns show a statistically significant tendency to cluster together in C. elegans, D. melanogaster, A. thaliana, and human (data not shown). This observation suggests that simply scanning the genome for clusters of predicted short introns by using intronscan could help to identify genes. This method, because it does not rely on ORFs, could potentially identify nonprotein coding genes (which are effectively invisible to most gene prediction algorithms) as well as protein coding genes. To test this approach, intronscan was applied to a sample of Drosophila genomic contigs, identifying a number of statistically significant clusters of predicted short introns. Most of these clusters overlapped annotated genes. At least one novel gene also was detected (see supporting information and Fig. 6, which is published on the PNAS web site).

Here, we have focused on the constitutive splicing of short introns, ignoring genes known to be alternatively spliced. Further progress in modeling and understanding splicing specificity will require development of models of the exon definition process to complement our initial efforts to model intron definition and will eventually require consideration of alternative splicing. It will also be important to more precisely define the nature of the enhancers and repressors that function in splicing. It is interesting that many of the top 10 intron-biased pentamers identified in Fig. 5D match well-known intronic enhancer motifs in human and Arabidopsis. The top 10 intron-biased pentamers in Drosophila appear to fall into two classes: AU-rich motifs and sequences containing UGA (Fig. 5D). A previous study showed that AU-rich sequences from plant introns could function as intronic splicing enhancers in Drosophila (29). Our analysis supports a role for naturally occurring AU-rich and/or UGA-containing sequences in recognition of fly introns.

Abbreviations

5′ss

5′ splice site

3′ss

3′ splice site

RelEnt

relative entropy

DAc

detection accuracy

EAc

exact accuracy

WMM

weight matrix model