Faucet: streaming de novo assembly graph construction

Abstract

Motivation

We present Faucet, a two-pass streaming algorithm for assembly graph construction. Faucet builds an assembly graph incrementally as each read is processed. Thus, reads need not be stored locally, as they can be processed while downloading data and then discarded. We demonstrate this functionality by performing streaming graph assembly of publicly available data, and observe that the ratio of disk use to raw data size decreases as coverage is increased.

Results

Faucet pairs the de Bruijn graph obtained from the reads with additional meta-data derived from them. We show these metadata—coverage counts collected at junction k-mers and connections bridging between junction pairs—contain most salient information needed for assembly, and demonstrate they enable cleaning of metagenome assembly graphs, greatly improving contiguity while maintaining accuracy. We compared Fauceted resource use and assembly quality to state of the art metagenome assemblers, as well as leading resource-efficient genome assemblers. Faucet used orders of magnitude less time and disk space than the specialized metagenome assemblers MetaSPAdes and Megahit, while also improving on their memory use; this broadly matched performance of other assemblers optimizing resource efficiency—namely, Minia and LightAssembler. However, on metagenomes tested, Faucet,o outputs had 14–110% higher mean NGA50 lengths compared with Minia, and 2- to 11-fold higher mean NGA50 lengths compared with LightAssembler, the only other streaming assembler available.

Availability and implementation

Faucet is available at https://github.com/Shamir-Lab/Faucet

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Assembly graphs encode relationships among sequences from a common source: they capture sequences as well as the overlaps observed among them. When assembly graphs are indexed, their sequence contents can be queried without iterating over every sequence in the input. This functionality makes graph and index construction a prerequisite for many applications. Among these are different types of assembly—e.g. de novo assembly of whole genomes, transcripts, plasmids etc. (Pertea et al., 2015; Rozov et al., 2017)—and downstream applications—e.g. mapping reads to the graphs, variant calling, pangenome analysis etc. (Iqbal et al., 2012; Novak et al., 2017).

In recent years, much effort has been expended to reduce the amount of memory used for constructing assembly graphs and indexing them. Major advances often relied on index structures that saved memory by enabling subsets of possible queries: e.g. one could query what extensions a given substring s has, but not how many times s was seen in the input data. A great deal of success ensued in reducing the amount of memory needed to efficiently construct the central data structures used by most de novo assembly algorithms, namely, the de Bruijn and string graphs (Chikhi and Rizk, 2012; Pell et al., 2012; Simpson and Durbin, 2010; Ye et al., 2012). Furthermore, efficient conversion of de Bruijn graphs to their compacted form (essentially string graphs with fixed overlap size) has been demonstrated Chikhi et al., 2014, 2016; Minkin et al., 2016).

In parallel to these efforts, streaming approaches were demonstrated as alternative resource-efficient means of performing analyses that had typically relied on static indices. Although appealing in terms of speed and low memory use, these approaches were initially demonstrated primarily for counting-centered applications such as estimating k-mer frequencies, error-correction of reads, and quantification of transcripts (Melsted and Halldorsson, 2014; Mohamadi et al., 2017; Roberts and Pachter, 2012; Song et al., 2014; Zhang et al., 2014).

Recently, a first step towards bridging the gap between streaming approaches and those based on static index construction was taken, hinting at the potential benefits of combining the two. El-Metwally et al. (2016) demonstrated a streaming approach to assembly by making two passes on a set of reads. The first pass subsamples k-mers in the de Bruijn graph and inserts them into a Bloom filter, and the second uses this Bloom filter to identify ‘solid’ (likely correct) k-mers, which are then inserted into a second Bloom filter. This streaming approach resulted in very high resource efficiency in terms of memory and disk use. However, LightAssembler finds solid k-mers while disregarding paired-end and coverage information, and thus is limited in its ability to resolve repeats and to differentiate between different possible extensions in order to improve contiguity.

In this work, we extend this approach with the aim of providing a more complete alternative to downloading and storing reads for the sake of de novo assembly. We show this is achievable via online graph and index construction. We describe the Faucet algorithm, composed of an online phase and an offline phase. During the online phase, two passes are made on the reads without storing them locally to first load their k-mers into a Bloom filter, and then identify and record structural characteristics of the graph and associated metadata essential for achieving high contiguity in assembly. The offline phase uses all of this information together to iteratively clean and refine the graph structure.

We show that Faucet requires less disk space than the input data, in contrast with extant assemblers that require storing reads and often produce intermediate files that are larger than the input. We also show that the ratio of disk space Faucet uses to the input data improves with higher coverage levels by streaming successively larger subsets of a high coverage human genome sample. Furthermore, we introduce a new cleaning step called disentanglement enabled by storage of paired junction extensions in two Bloom filters—one meant for pairings inside a read, and one meant for junctions on separate paired end mates. We show the benefit of disentanglement via extensive experiments. Finally, we compared Faucet’s resource use and assembly quality to state of the art metagenome assemblers, as well as leading resource-efficient genome assemblers. Faucet used orders of magnitude less time and disk space than the specialized metagenome assemblers MetaSPAdes and Megahit, while also improving on their memory use; this broadly matched performance of other assemblers optimizing resource efficiency—namely, Minia and LightAssembler. However, on metagenomes tested, Faucet’s outputs had 14–110% higher mean NGA50 lengths compared with Minia, and 2- to 11-fold higher mean NGA50 lengths compared with LightAssembler, the only other streaming assembler available.

2 Preliminaries

For a string s, we denote by s[i] the character at position i, s[i: j] the substring of s from position i to j (inclusive of both ends), and |s| the length of s. Let pref(s, j) be the prefix comprised of the first j characters of s and suff(s,j) be the suffix comprised of the last j characters of s. We denote concatenation of strings s and t by $s°t$, and the reverse complement of a string s by $s\prime$.

A k-mer is a string of length k drawn from the DNA alphabet $\Sigma =\{A,C,G,T\}$. The de Bruijn graph G(S,k) = (V,E) of a set of sequences S has nodes defined by consecutive k-mers in the sequences, $V={\cup }_{s\in S}{\cup }_{i=0}^{\left|s\right|-k+1}s[i:i+k-1]$; E is the set of arcs defined by (k−1)−mer overlaps between nodes in V. Namely, identifying vertices with their k-mers, $(u,v)\in E\iff suff(u,k-1)=pref(v,k-1)$. Each node v is identified with its reverse complement $v\prime$, making the graph G bidirected, in that edges may represent overlaps between either orientation of each node (Medvedev et al., 2007). When necessary, our explicit representation of nodes will use canonical node naming, i.e. the name of node $(v,v\prime )$ will be the lexicographically lesser of v and $v\prime$. Junction nodes are defined as k-mers having in-degree or out-degree > 1. Terminal nodes are k-mers having out-degree 1 and in-degree 0 or in-degree 1 and out-degree 0. Terminals and junctions are collectively referred to as special nodes. The compacted de Bruijn graph is obtained from a de Bruijn graph by merging all adjacent non-branching nodes (i.e. those having in-degree and out-degree of exactly 1). The string associated with merged adjacent nodes is the first k-mer, concatenated with the single character extensions of all following non-branching k-mers. Such merged non-branching paths are called unitigs.

Since a junction v having in-degree > 1 and out-degree 1 is identified with $v\prime$ having out-degree > 1 and in-degree 1, we speak of junction directions relative to the reading direction of the junction’s k-mer. Therefore, a forward junction has out-degree > 1, and a back junction has in-degree > 1. We refer to outbound k-mers beginning paths in the direction having out-degree > 1 as heads, and the sole outbound k-mer in the opposite direction as the junction’s tail. It is possible that a junction may have no tail.

A Bloom filter B is a space-efficient probabilistic hash table enabling insertion and approximate membership query operations (Bloom, 1970). The filter consists of a bit array of size m, and an element x is inserted to B by applying h hash functions, f₀, … ,f_h−1 such that ${\forall }_{i\in [0,h-1]}{f}_i(x)\in [0,m-1]$, and setting values of the filter to 1 at the positions returned. For a Bloom filter B and string s, by $s\in B$ or the term ’s in B’ we refer to B[s] = 1, i.e. when the h hash functions used to load B are applied to s, only 1 values are returned. Similarly, $s\notin B$ or ‘s not in B’ means that at least one of the h hash functions of B returned 0 when applied to s. For any s that has been inserted to B, B[s] = 1 by definition (i.e. there are no false negatives). However, false positives are possible, with a probability that can tuned by adjusting m or h appropriately.

3 Materials and methods

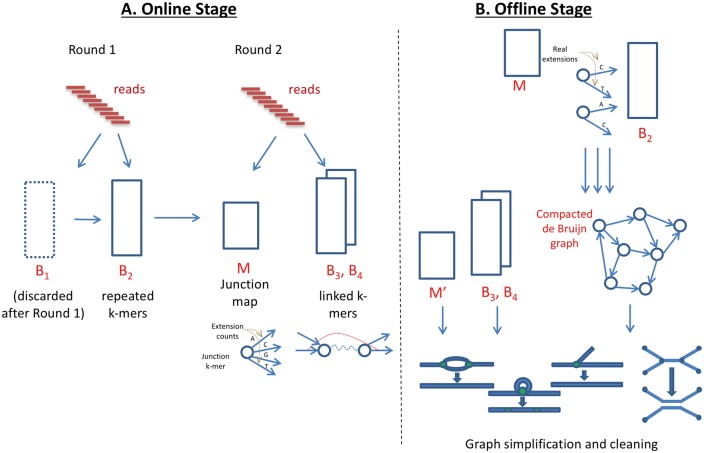
We developed an algorithm called Faucet for streaming de novo assembly graph construction. A bird’s eye view of its entire work-flow is provided in Figure 1. Below we detail individual steps.

Fig. 1.

Faucet work-flow. (A) The online stage involves a first round of processing all reads in order to load Bloom filters B₁ and B₂, and a second round in order to build the junction map M and load additional Bloom filters B₃ and B₄. M stores the set of all junctions and extension counts for each junction, while B₃ and B₄ capture connections between junction pairs. The two online rounds capture information from and perform processing on each read, and the processing performed always depends on the current state of data structures being loaded. (B) The offline stage uses B₂ and M, constructed during the online stage, in order to build the compacted de Bruijn graph by extending between special nodes using Bloom filter queries. ContigNodes (not shown) take the place of junctions and are stored in $M\prime$, allowing access (via stored pointers) to Contigs out of each junction, and coverage information. An additional vector of coverage values at fake or past junctions is also maintained for each Contig. Then, B₃, B₄, and this coverage information are used together to perform simplifications on and cleaning of the graph

3.1 Online Bloom filter loading

Faucet begins by loading two Bloom filters, B₁ and B₂, as it iterates through the reads, using the following procedure: all k-mers are inserted to B₁, and only k-mers already in B₁ (i.e. those for which all hash queries return 1 from B₁) are inserted to B₂. Namely, for each k-mer s, if B₁[s] = 1 then we insert s into B₂, otherwise we insert into B₁. After iterating through all reads, B₁ is discarded and only B₂ is used for later stages. This procedure imposes a coverage threshold on the vast majority of k-mers so that primarily ‘solid k-mers’ (Pevzner et al., 2001) observed at least twice are kept. This process is depicted in Round 1 of Figure 1A. We note that a small proportion of singleton or false positive k-mers may evade this filtration. No count information is associated with k-mers at this round.

3.2 Online graph construction

B ₂, loaded at the first round, enables Faucet to query possible forward extensions of each k-mer. Faucet iterates through all reads a second time to collect information necessary for avoiding false positive extensions, building the compacted de Bruijn graph, and later, cleaning the graph. The second round consists of finding junctions and terminal k-mers, recording their true extension counts, and recording k-mer pairs (Round 2 of Fig. 1A).

Faucet’s Online stage has one main routine—Algorithm 1—that calls upon two subroutines—Algorithms 2 and 3. First, junction k-mers and their start positions are derived from a call to Algorithm 2. To find junctions, Algorithm 2 makes all possible alternate extension queries (Lines 3–5) to B₂ for each k-mer in the read sequence r. A junction k-mer j may have multiple extensions in B₂—either because there are multiple extensions of j in G that are all real (i.e. present on some read), or because there is at least one real extension in G and some others in B₂ that are false positives. Accordingly, each k-mer possessing at least one extension that differs from the next base on the read is identified as a junction. Whenever one is found, its sequence along with its start position are recorded (Line 4), and the list of such tuples is returned. We note that each k-mer in the read is also queried for junctions in the reverse complement direction, but this is not shown in Algorithm 2.

Algorithm 1.

scanReads(R, B₂)

Input: read set R, Bloom filter B₂ loaded from round 1, an empty Bloom filter B₃

Output: 1. a junction Map M comprised of (key, value) pairs. Each key is a junction k-mer, and each $value\in {\mathbb{N}}^4$ is a vector $[c_A,c_C,c_G,c_T]$ of counts representing the number of times each possible extension of key was observed in R; 2. B₃ is loaded with linked k-mer pairs (i.e. specific 2k-mers—see text—are hashed in).

1: $M\leftarrow \varnothing$

2: for$r\in R$do

3:  $juncs\leftarrow findJunctions(r,B_2)$ ▹ call to Algorithm 2

4:  for$(junc,pos)\in juncs$do

5:   if$junc\notin M$then

6:    $M[junc]\leftarrow [0,0,0,0]$

7:   increment counter in$M for r[pos+k]\hspace{0.17em}\hspace{0.17em}recordPairs(r,juncs,B_3)$ ▹ call to Algorithm 3

8: returnM,B₃

Algorithm 1 then uses this set of junctions to perform accounting (Lines 4–8). All junctions are inserted into a hash map M that maps junction k-mers to vectors maintaining counts for each extension. For each junction of r, a count of 0 is initialized for each possible extension. These counters are only incremented based on extensions observed on reads—i.e. extensions due to Bloom filter outputs alone are not counted. As every real extension out of each junction must be observed on some read, and we scan the entire set of reads, an extension will have non-zero count only if it is real. This mechanism allows Faucet to maintain coverage counts for all real extensions out of junctions. In later stages, only extensions having non-zero counts will be visited, but counts are stored for real extensions of false junctions as well. These latter counts are used to sample coverage distributions on unitig sequences at more points than just their ends. Proportions of real junctions versus the totals stored after accounting are described in the section ‘Solid junction counts’ in the Supplementary Appendix.

Algorithm 2.

findJunctions(r, B₂)

Input: read r and Bloom filter B₂

Output: juncTuples, a list of tuples (seq, p), where p is the start position of junction k-mer seq in r, in order of appearance on r

1: $juncTuples\leftarrow \varnothing$

2: for$i\in [0,|r|-k]$do$kmer\leftarrow r[i:i+k-1]$

3:  for$c\in \Sigma \mathrm{\setminus }\{r[i+k]$} do

4:   if$(suff(kmer,k-1)°c\in B_2)$then   $juncTuples\leftarrow juncTuples\cup (kmer,i)$

5: returnjuncTuples

Following the accounting performed on observed junctions, Faucet records adjacencies between pairs of junctions using additional Bloom filters—B₃ and B₄. These adjacencies are needed for disentanglement—a cleaning step applied in Faucet’s offline stage. Disentanglement, depicted in Figure 2, is a means of repeat resolution. Its purpose is to split paths that have been merged due to the presence of a shared segment—the repeat—in both paths. In order to ‘disentangle’, or resolve the tangled region into its underlying latent paths, we seek to store sequences that flank opposite ends of the repeat. Pairs of heads observed on reads provide a means of ‘reading out’ such latent paths by indicating which heads co-occur on sequenced DNA fragments. The application of disentanglement is presented in the section ‘Offline graph simplification and cleaning’, while we now focus on the mechanism of pair collection and its rationale. To capture short and long range information separately, Bloom filter B₃ holds head pairs on the same read, while B₄ holds heads chosen such that each head is on a different mate of a paired-end read. Algorithm 3 is the process by which pairs are inserted into B₃, and insertion into B₄ is described in the Supplementary Appendix.

Fig. 2.

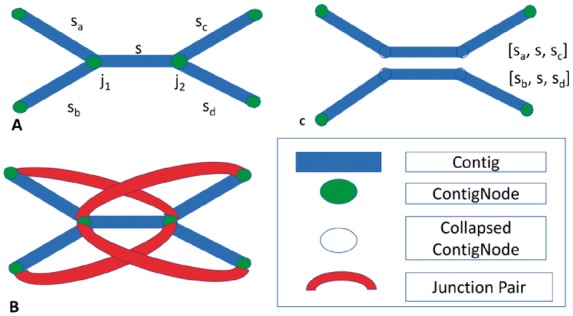
Disentanglement. (A) A tangle characterized by two opposite facing junctions j₁ and j₂, each with out-degree 2. (B) Junction pairs linking extensions on s_a with s_c and s_b with s_d. Since no pairs link extensions on s_a with s_d or s_b with s_c, only one orientation is supported. (C) the result of disentanglement: paths [s_a,s,s_c] and [s_b,s,s_d] are each merged into individual sequences, and junctions j₁ and j₂ are removed from M

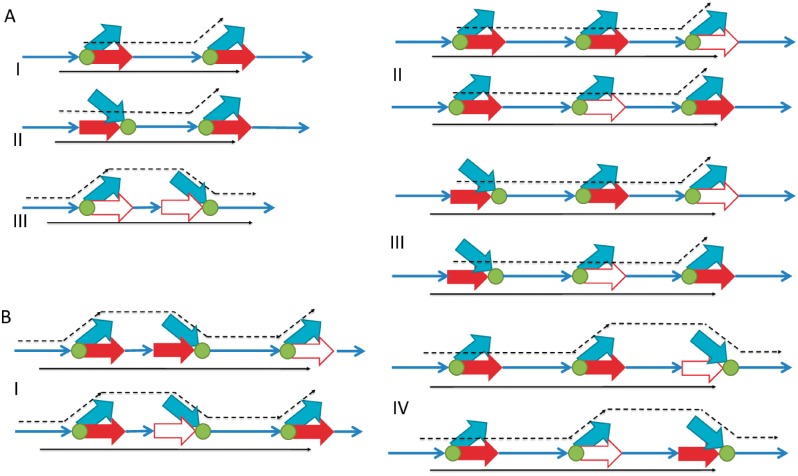
In Algorithm 3, we aim to pair heads that are maximally informative. Informative pairs are those that allow us to ‘read out’ pairs of unitigs that belong to the same latent path. We specifically choose to insert heads because during the offline stage when disentanglement takes place, adjacencies between each unitig starting at an edge to a head and the unitig starting at the edge from the junction to its tail of are known and accessible via pointers to their sequences. Therefore, extension pairs capturing information of direct adjacencies provide no new information. The closest indirect adjacency that may be informative when captured from a read is that between two junctions that either face in the same direction, or when the first faces back and the second faces forward, as shown in Figure 3A. Thus, when there are only two junctions on a read, their pair of heads is inserted as long as the two junctions are not facing each other. When there are at least three junctions on a read, every other junction out of every consecutive triplet is paired, as shown for a single triplet in Figure 3B. This figure demonstrates that selecting every other head is preferable to selecting consecutive heads out of a triplet. This type of insertion is executed in Lines 1–6 of Algorithm 3 and ensures all unitigs flanking some triplet are potentially inferable. For reads having more than three junctions, applying the triplet rule for every consecutive window of size 3 similarly allows for all unitigs on the read to be included in some hashed pair.

Fig. 3.

Rationale for B₃ insertions. Narrow blue arrows indicate unitigs observed on a read, green circles are junctions and thick arrows are junction heads. Among red arrows, solids are those inserted to B₃. For simplicity, we provide a direction to each arrow. The opposite direction is equally valid, hence in this view heads can also enter a junction and not only exit from it. In each case, a pair of red heads is inserted from a read. They will be inserted if they provide additional information to infer a path on the graph. Black lines indicate a subset of possible paths; out of these the solid path is that observed on a read. (A) Two junctions observed on a read. I, II: The two heads together imply the solid paths and rule out alternatives, so the pair is inserted to B3. III: The two heads lie on the ends of the same unitig and thus add no information. (B) Three junctions observed on a read, comparing insertions of consecutive heads against non-consecutive heads. Four possible arrangements are shown; there are four more that are symmetrical reflections and are not shown to save space. In each case, we compare the unitigs covered (i.e. either having a head on them or being a sole extension at a junctionve heads against non-consecconsecutive (top) and non-consecutive (bottom) junctions are chosen. Note that in Cases I–III the right-most unitig is not covered under consecutive heads (Color version of this figure is available at Bioinformatics online.)

Algorithm 3.

recordPairs(r, juncs, B₃)

Input: read r, juncs—a list of pairs (j, p), where p is the start position of junction j in r, and Bloom filter B₃. We also make use of a subroutine getOutExt(j_i,p_i,r) that for a junction j_i returns $pref(j_i,k-1)°r[p_i-k]$ if j_i is a back junction, and $suff(j_i,k-1)°r[p_i+k]$ otherwise.

Output: Bloom filter B₃, loaded with select linked k-mer pairs

1: iflen(juncs) > 2 then

2:  for$i\in [0,len(juncs)-2]$do

3:   $back\leftarrow getOutExt(j_i,p_i,r)$

4:   $front\leftarrow getOutExt(j_{i+2},p_{i+2},r)$

5:   $insert(back°front,B_3)$ ▹ insert the concatenation into B₃

6: else if ($len(juncs)=2)\wedge (\neg (j_0 \text{is} \mathrm{a} \text{forward} \text{junction}\wedge j_1 \text{is} \mathrm{a} \text{back} \text{junction})$) then

7:  $back\leftarrow getOutExt(j_0,p_0,r)$

8:  $front\leftarrow getOutExt(j_1,p_1,r)$

9:  $insert(back°front,B_3)$

10: returnB₃

3.3 Offline graph simplification and cleaning

Given B₂, B₃, B₄ and M resulting from the online stage, the compacted de Bruijn graph is generated by traversing each forward extension out of every special k-mer, as well as traversing backwards in the reverse complement direction when the node has not been reached before by a traversal starting from another node. This is done by querying B₂ for extensions and continuing until the next special node is reached. During each such traversal from special node u to special node v, a unitig sequence s_uv is constructed. s_uv is initialized to the sequence of u, and a base is added at each extension until v is reached.

New data structures are constructed in the course of traversals in order to aid later queries and updates. A ContigNode structure is used to represent a junction that points to Contigs. ContigNodes are structures possessing a pointer to a Contig at each forward extension, as well as one backwards pointer. This backwards pointer connects the junction to the sequence beginning with the reverse complement of the junction’s k-mer. Contigs initially store unitig sequences, but these may later be concatenated or duplicated. They also point to one ContigNode at each end. To efficiently query Contigs and ContigNodes, a new hashmap $M\prime$ is constructed having junction k-mers as keys, and ContigNodes that represent those junctions as values. Isolated contigs formed by unitigs that extend between terminal nodes are stored in a separate set data structure.

Once the raw graph is obtained, cleaning steps commence, incorporating tip removal, chimera removal, collapsing of bulges, and disentanglement. Coverage information and paired-junction links are crucial to these steps. Briefly, tip removal involves deletion of Contigs shorter than the input read length that lead to a terminal node. Chimera and bulge removal steps involve heuristics designed to remove low coverage Contigs when a more credible alternative (higher coverage, or involved in more sub-paths) is identified. These first three steps proceed as described in (Bankevich et al., 2012), thus we omit their full description here.

Disentanglement relies on paired junction links inserted into B₃ and B₄. We iterate through the set of ContigNodes to look for ‘tangles’—pairs of opposite-facing junctions joined by a repeat sequence—as shown in Figure 2. Tangles are characterized by tuples (j₁,j₂,s) where j₁ is a back junction, j₂ is a forward junction (or vice-versa), and there is a common Contig s pointed to by the back pointers of both j₁ and j₂. Junctions j₁ and j₂ each have at least two outward extensions. We restrict cleaning to tangles having exactly two extensions at each end. Let s_a and s_b be the Contigs starting at heads of j₁, and s_c and s_d be the Contigs starting at heads of j₂. By disentangling, we seek to pair extensions at each side of s to form two paths. The possible outputs are paths [s_a,s,s_c] together with [s_b,s,s_d] or [s_a,s,s_d] together with [s_b,s,s_c].

Thus, each such pair straddling the tangle—e.g. having one head on s_a and the other on s_c—lends some support to the hypothesis that the correct split is that which pairs the two. To decide between the two possible split orientations, we count the number of pairs supporting each by querying B₃ or B₄ for all possible junction pairings that are separated by a characteristic length associated with the pairs inserted to each. For example, B₃ stores heads out of non-consecutive junction pairs on the same read. Therefore, for each junction on s_a we count each pairing accepted by B₃ with a junction on s_c that is at most one read length away. Specifically for B₃, we also know that inserted pairs are always one or two junctions away from the starting junction, based on the scheme presented in Figure 3. To decide when a tangle should be split, we apply XOR logic to arrive at a decision: if the count of pairs supporting both paths in one orientation is > 0, and the count of both paths in the other orientation is 0, we disentangle according to the first, as shown in Figure 2. Similar yet more involved reasoning is used for junction links in B₄, using the insert size between read pairs (see Supplementary Appendix). Once we arrive at a decision, we add a new sequence to the set of Contigs that is the concatenation of the sequences involved in the original paths. We note one of the consequences of this simplification step is that the graph no longer represents a de Bruijn graph, in that each k-mer is no longer guaranteed to appear at most once in the graph. Furthermore, the XOR case presented is the most frequently applied form of disentanglement out of a few alternatives. We discuss these alternatives in the Supplementary Appendix.

3.4 Optimizations and technical details

Here we discuss some details omitted from the above descriptions for the sake of completeness. Based on the description of Algorithms 1 and 2, it is possible that false positive extensions out of terminal nodes will ensue. This is possible because the mechanism described for removing false positive junctions can differentiate between one or multiple extensions existing in G for a given node, but cannot differentiate between one or none. This may lead to assembly errors at sink nodes.

To overcome such effects, we store distances between junctions seen on the same read with the distance recorded being assigned to the extension of each junction observed on the read. When an outermost junction on a read has not been previously linked to another junction, we record its distance from the nearest read end—this solves the problem mentioned previously as long as paths to sinks are shorter than read length. To obtain accurate measurements of distances on longer non-branching paths, we also introduce artificial ‘dummy’ junctions whenever a pre-defined length threshold is surpassed. In effect, this means that reads with no real junctions are assigned dummy junctions.

Once distances and dummy junctions are introduced, an additional benefit is gained: the speed of the read-scan can be improved by skipping between junctions that have been seen before. Once distances are known, if we see a particular extension out of a junction, and then a sequence of length ℓ without any junctions, then, wherever else we see that junction and extension, it must be followed by the exact same ℓ next bases. Otherwise, there would be a junction earlier. So we store ℓ when we see it, and skip subsequent occurrences.

Finally, we note that Faucet can benefit from precise Bloom filter sizing. When a good estimate of dataset parameters is known, the algorithm can do the two-pass process above. Otherwise, to determine the numbers of distinct k-mers and the number of singletons in the dataset in a streaming manner, we have used the tool ntCard (Mohamadi et al., 2017). This requires an additional pass over the reads (for a total of three passes). The added pass does not increase RAM or disk use. In fact, in tests on locally stored data, we found it only adds negligible time.

4 Results

4.1 Assembling while downloading

As a demonstration of streaming assembly, we ran Faucet on publicly available human data, SRR034939, used for benchmarking in (Chikhi and Rizk, 2012). To assess resource use at different data volumes, we ran Faucet on 10, 20 and 37 paired-end files out of 37 total. Streaming was enabled using standard Linux command line tools: wget was used for commencing a download from a supplied URL, and streamed reading from the compressed data was enabled by the bzip2 utility. Downloads were initiated separately for each run. The streaming results are shown in Table 1.

Table 1.

Resource use and data compression observed as data volume increases

No. of files	Time (h)	RAM (GB)	Disk (GB)	Data size (GB)	Comp. ratio
10	26.3	48.3	19.0	29.6	0.64
20	47.7	84.3	34.3	59.2	0.58
37	98.2	144.7	50.0	108.4	0.46

We emphasize that Faucet required less space than the size of the input data in order to assemble it, while most assemblers generate files during the course of their processing that are larger than the input data. Also, the ratio of input data to disk used by Faucet decreased as data volume increased, reflecting the tendency of sequences to be seen repeatedly with high coverage. We also note that Faucet’s outputs effectively create a lossy compression of the read data, in that the choice of k value inherently creates some ambiguity for read substrings larger than k. This compression format is also queryable, in that given a k-mer in the graph, its extensions can be found: indeed, this is the basis of Faucet’s graph construction and cleaning.

4.2 Disentanglement assessment

To gauge the benefits of disentanglement on assembly quality, we compared Faucet’s outputs with and without each of short- and long-range pairing information, provided by Bloom filters B₃ and B₄, on SYN 64—a synthetic metagenome produced to provide a dataset for which the ground truth is known comprised of 64 species (dataset sizes and additional characteristics are provided in the Supplementary Appendix). The results of this assessment are presented in Table 2. We measured assembly contiguity by the NGA50 measure. NG50 is defined as ‘the contig length such that using equal or longer length contigs produces x% of the length of the reference genome, rather than x% of the assembly length’ in (Gurevich et al., 2013). NGA50 is an adjustment of the NG50 measure designed to penalize contigs composed of misassembled parts by breaking contigs into aligned blocks after alignment to the reference. We found that disentanglement more than doubled contiguity measured by mean NGA50 values, with greater gains as more kinds of disentanglement were enabled. This was also reflected by corresponding gains in the genome fractions, and in the number of species for which at least 50% of the genome was aligned to, allowing NGA50 scores to be reported. More applications of disentanglement also increased the number of misassemblies reported and the duplication ratio; however, two-thirds of the maximum misassembly count is already seen without any disentanglement applied.

Table 2.

The effect of increasing levels of disentanglement on contiguity and accuracy

Measure	No disent.	B3 only	B4 only	both B3, B4
Genome fraction (%)	76.4	79.9	80.3	82.3
Dup. ratio	1.00	1.01	1.02	1.02
Mean NGA50	13048	21703	26356	29066
Misassemblies	388	480	521	572
Species reported	54	56	56	56

4.3 Tools comparison

We sought to assess Faucet’s effectiveness in assembling metagenomes, and its resource efficiency. For the former, we compared Faucet to MetaSPAdes (Nurk et al., 2017) and Megahit (Li et al., 2014), state of the art metagenome assemblers in terms of contiguity and accuracy that require substantial resources. To address resource efficiency, we also compared Faucet to two leading resource efficient assemblers, Minia 3 (Beta) (Chikhi and Rizk, 2012) and LightAssembler (El-Metwally et al., 2016). We note these last two were not designed as metagenome assemblers, but they perform operations similar to what Faucet does—both in the course of their graph construction steps, and in their cleaning steps. They differ from Faucet in that neither is capable of disentanglement, as they do not utilize paired-end information, but counter this advantage with more sophisticated traversal schemes. All tools were run on two metagenome datasets—SYN64 and HMP—a female tongue dorsum sample sequenced as part of the Human Microbiome Project. Both datasets were used for testing in (Nurk et al., 2017). To achieve a fair comparison, runs were performed with a single thread on the same machine, as Faucet does not currently support multi-threaded execution. Full details of the comparison, including versions, parameters, and data accessions, are presented in the Supplementary Appendix.

Table 3 presents the full results for the tools comparison. There was a strong advantage to Megahit and MetaSPAdes over the three lightweight assemblers (Minia, LightAssembler, and Faucet) in terms of contiguity achieved (shown by NGA50 statistics), but this came at a large cost in terms of memory, disk space, and time, particularly in the case of MetaSPAdes. Among the lightweight assemblers, Minia used by far the most disk space, and differences in other resource measures were less pronounced. Among these three, Faucet had a large advantage in NGA50 statistics relative to the other two. This is highlighted by the trend of Table 3, and shown by its 14–110% advantage in the mean of NGA50 relative to Minia, and 2- to 11-fold advantage relative to LightAssembler.

Table 3.

Tool comparison on two metagenomes

	SYN64					HMP
Measure	Metaspades	Megahit	LightAssembler	Minia	Faucet	Metaspades	Megahit	LightAssembler	Minia	Faucet
Genome fraction (%)	89.1	90.1	75.6	76.5	82.3	46.9	48.6	23.4	27.8	27.9
Duplication ratio	1.02	1.02	1.01	1.00	1.02	1.05	1.12	1.02	1.01	1.05
Mean NGA50 (kb)	167	99.0	2.60	14.6	30.7	28.3	36.8	3.18	6.25	7.12
Median NGA50 (kb)	71.1	57.6	2.30	10.5	23.7	28.3	36.8	3.18	6.25	7.12
Misassemblies	785	949	314	395	572	504	602	100	184	202
Species reported	59	61	55	52	56	12	12	5	3	6
Time (h)	41.2	10.9	1.63	0.97	2.61	30.5	13.0	3.35	0.99	2.30
Memory (GB)	26	9.1	2.7	4.8	6.0	14	8.3	3.4	3.7	7.3
Disk (GB)	43.1	14.3	1.84	28.2	1.59	53.2	11.5	1.30	23.5	1.61

Top values in each cell are for SYN 64 data, and bottom values are for HMP. Duplication ratio is the ratio between the total aligned length to the combined length of all references aligned to. The mean and median NGA50 values are calculated on based on species sufficiently covered by all assemblers to yield an NGA50 value (i.e. 50% of the genome is covered). Species reported are those for which an NGA50 value is reported. In the HMP data, only two species were reported for all, making the mean and median NGA50 values equal. Disk and memory use are those reported by the Linux time utility, and Disk use is the total amount written to disk during the course of a run.

5 Discussion

Streaming de novo assembly presents an opportunity to significantly ease some of the burdens introduced by the recent deluge of second generation sequencing data. We posit the main applications of streaming assembly will be de novo assembly of very large individual datasets (e.g. metagenomes from highly diverse environments) and re-assembly of pangenomes derived from many samples. In both cases, very large volumes of data must be digested in order to address the relevant biological questions behind these assays. Therefore, streaming graph assembly presents an attractive alternative to data compression: instead of attempting to reduce the size of data, the aim is to keep locally only relevant information in a manner that is queryable and that allows for future re-analysis.

Here, we have demonstrated a mechanism for performing streaming graph assembly and described some of its characteristics. First, we showed that assembly can be achieved without ever storing raw reads locally. By assembling the graph, an intermediate by-product of many assemblers, we show this technique is generally applicable. By refining the graph and showing better assembly contiguity than competing resource efficient tools on metagenome assembly, we showed this method can also be applied in the setting when sensitive recovery of rare sequences is crucial.

In future work, we aim to expand the capabilities of Faucet in a number of ways. Multi-threaded processing will reduce run times and make the tool more applicable to large data volumes. We believe further refinements of cleaning and contig generation can be achieved by adopting a statistical approach to making assembly decisions. In addition, beyond graph cleaning, we aim to apply Faucet’s data structures to path generation, as done with paired end reads in (Nihalani and Aluru, 2016; Prjibelski et al., 2014; Shi et al., 2017). Both have the potential to greatly improve contiguity and accuracy.

Beyond this, this work raises several remaining challenges pertaining to what one may expect of streaming assembly. For instance, it is immediately appealing to ask if streaming assembly can be achieved with a just a single pass on the reads, and if so, what inherent limitations exist. In Song et al. (2014), a simple solution is proposed wherein the first 1 M reads are processed to provide a succinct summary for the rest, but such an approach is more suited to high coverage or low entropy data, and thus unlikely to perform well on diverse metagenomes or when rare events are of particular interest. Another issue raised by the performance comparison herein is that of capturing the added value that iterative (multi-k value) graph generation provides. We have given a partial solution by capturing subsets of junction pairs within each read, and between mates of paired-end reads. Although it is possible to iteratively refine the graph with more passes on the reads, each time for the collection of k-mers at different lengths, this becomes unwieldy with large data volumes. Identifying the contexts for which such information would be useful in the graph and indexing the reads to allow for querying of such contexts may provide more efficient means of extracting such information.

Funding

This work was supported in part by the Israel Science Foundation as part of the ISF-NSFC joint program to R.S. R.S. was supported in part by the Raymond and Beverley Chair in Bioinformatics at Tel Aviv University. E.H. was supported in part by the USA–Israel Binational Science Foundation [Grant 2012304] and E.H. and R.R. were supported in part by the Israel Science Foundation [Grant 1425/13]. R.R. was supported in part by a fellowship from the Edmond J. Safra Center for Bioinformatics at Tel Aviv University, an IBM PhD fellowship, and by the Center for Absorption in Science, the Israel Ministry of Immigrant Absorption. E.H. is a Faculty Fellow of the Edmond J. Safra Center for Bioinformatics at Tel Aviv University. G.G. was supported by the MISTI MIT-Israel program at MIT and Tel Aviv University.

Conflict of Interest: none declared.