Erratic overdispersion of three molecular clocks: GPDH, SOD, and XDH

Abstract

The neutrality theory predicts that the rate of neutral molecular evolution is constant over time, and thus that there is a molecular clock for timing evolutionary events. It has been observed that the variance of the rate of evolution is generally larger than expected according to the neutrality theory, which has raised the question of how reliable the molecular clock is or, indeed, whether there is a molecular clock at all. We have carried out an extensive investigation of three proteins, glycerol-3-phosphate dehydrogenase (GPDH), superoxide dismutase (SOD), and xanthine dehydrogenase (XDH). We have observed that (i) the three proteins evolve erratically through time and across lineages and (ii) the erratic patterns of acceleration and deceleration differ from locus to locus, so that one locus may evolve faster in one than another lineage, whereas the opposite may be the case for another locus. The observations are inconsistent with the predictions made by various subsidiary hypotheses proposed to account for the overdispersion of the molecular clock.

The hypothesis of the molecular clock of evolution emerged from early observations that the number of amino acid replacements in a given protein appeared to change linearly with time (1). Indeed, if proteins (and genes) evolve at constant rates they could serve as molecular clocks for timing evolutionary events and reconstructing the evolutionary history of extant species; and for delimiting the choices among mechanistic descriptions of the amino acid (and nucleotide) substitution process. A notable feature of the hypothesis of the molecular evolutionary clock is empirical multiplicity: every one of the thousands of proteins or genes of an organism would be an independent clock, each ticking at a different rate but all measuring the same events. Kimura's neutrality theory of molecular evolution provides a mathematical foundation for the clock (2, 3). The theory states that the rate of substitution, k, of adaptively neutral alleles is precisely the rate of mutation, u, of neutral alleles, k = u. The neutrality theory predicts that molecular evolution behaves like a stochastic clock, such as radioactive decay, with the properties of a Poisson process; therefore, the variance of the number of substitutions, V, should be equal to the mean, M, so that the “index of dispersion” R = V/M = 1. A common observation, however, is that genes and proteins evolve more erratically than allowed by the neutral theory (the so-called overdispersed molecular clock; refs. 4 and 5), which casts doubts on the validity of the molecular clock model (5, 6). Several subsidiary hypotheses have been proposed that modify the predictions of the neutrality theory, allowing for greater variance in evolutionary rates (6).

Here we present an analysis of the rates of evolution of three genes: glycerol-3-phosphate dehydrogenase (GPDH; EC 1.1.1.8), Cu,Zn superoxide dismutase (SOD; EC 1.15.1.1), and xanthine dehydrogenase (XDH; 1.1.1.204). We have previously analyzed the evolutionary rates of GPDH and SOD (6–8), but we now include another protein (XDH) and expand the number and range of taxa investigated; moreover, we take into account two variables that were not previously considered: the phylogenetic structure of the data (i.e., that sequences have not independent evolutionary histories) in the calculation of average evolutionary rates for lineages, and heterogeneity of rates from site to site within each protein. We study a total of 78 species (30–61 per gene) that include representatives of the three multicellular kingdoms, plants, fungi, and animals.

Materials and Methods

Genes.

The three enzymes encoded by Gpdh, Sod, and Xdh are globular, soluble, homodimeric oxidoreductases (9–11). The subunit molecular mass is for XDH ≈145 kDa, for GPDH ≈40 kDa, and for SOD ≈15 kDa. The nicotinamide-adenine dinucleotide (NAD)-dependent cytoplasmic GPDH plays a crucial role in metabolism through its keystone position in the glycerophosphate cycle, which in Drosophila and other dipterans provides energy for flight in the thoracic muscles (12). In Drosophila melanogaster, GPDH consists of eight exons and is encoded by a gene located on chromosome arm 2L. The gene can produce three different isoforms of the enzyme by differential splicing of the last three exons (9). We analyze most of the coding sequence of exons 3–6 (750 of 831 bp) corresponding to the whole catalytic domain plus 45 codons of the NAD-binding domain (13). Cu,Zn SOD is a ubiquitous metalloprotein that forms part of an organism's defense against the toxicity of oxygen by removing the superoxide anion (O₂⁻). In D. melanogaster, the Sod gene is located on chromosome arm 3L, consists of two exons, and is translated into a polypeptide consisting of 151 aa. We investigate the complete Sod sequence in all species. XDH is a complex metalloflavoprotein that plays an important role in nucleic acid degradation in all organisms: it catalyzes the oxidation of hypoxanthine to xanthine and xanthine to uric acid with concomitant reduction of NAD to NADH. XDH protects the cell against damage induced by free oxygen radicals through the antioxidant action of uric acid (14). In D. melanogaster, Xdh is located on chromosome arm 3R. We analyze ≈52% of the Xdh coding sequence (≈2085 bp) corresponding to 24 codons of the flavine adenine dinucleotide (FAD) domain, 45–54 codons of interdomain, and most of the C-terminal Molybdenum Cofactor (MoCo) domain (≈95%; 613–618 codons) (15).

Taxa and Sequences.

The 78 species studied and the GenBank accession numbers are given in the Fig. 1. For Gpdh (30 sequences) and Sod (61 sequences) we use the alignments from refs. 8 and 16, slightly modified to fit additional sequences. For Xdh (34 sequences) we use the alignment from ref. 15. The GPDH, SOD, and XDH alignments consist of 241, 107, and 599 aa residues, respectively. We treat Dorsilopha, Hirtodrosophila, and Zaprionus as Drosophila subgenera, following refs. 17 and 18, but Scaptodrosophila as a genus according to refs. 17–19.

Figure 1.

Tree topology for the species used in this study. Labels and numbers on the branches represent taxonomic categories and divergence times, respectively.

The 78 species encompass four orders of insects (dipterans for all of the three genes; plus hymenoptherans and orthoptherans for Gpdh, and lepidopterans for Xdh), six orders of mammals (lagomorpha, rodents, and primates; plus artiodactyla for Sod and Xdh, and carnivora and perissodactyla for Sod), six classes of vertebrates (mammals; plus birds for Sod and Xdh, bony fishes for Gpdh and Sod, and turtle, frog, and shark for Sod), three metazoan phyla (arthropods, chordates, and nematodes; plus platyhelminthes for Sod), one phylum of fungi (ascomycetes), and three multicellular kingdoms (animal, plants, and fungi).

Models of Sequence Evolution.

We follow a model-based maximum likelihood framework of statistical inference. We first model the substitution processes of the genes by using a tree topology that is approximately correct; then, we use the model to generate maximum likelihood distances between pairs of sequences. For model fitting, we use the phylogenetic hypothesis shown in Fig. 1. Relationships that are not well established (e.g., the branching order of animal phyla) are set as polytomies. Use of other reasonable topologies does not affect parameter estimates (see also ref. 20).

The amino acid substitution models used in this study are all special forms of the model of ref. 21, which is based on the empirical matrix of ref. 22, with amino acid frequencies set as free parameters (referred to as JTT-F). Substitution rate variation from site to site is accommodated by using the discrete gamma approximation of ref. 23, with eight equally probable categories of rates, to approximate the continuous gamma distribution (dG models). Several hypotheses of interest are tested with likelihood ratio tests using the CODEML programs from the PAML 3.0b package (24).

Results

Evolution of GPDH, SOD, and XDH in Dipterans.

The best description of the substitution process of GPDH, SOD, and XDH is provided by the JTT-F + dG model, which treats amino acid frequencies as free parameters and allows variable replacement rates among sites. The discrete gamma distribution that better accommodates the variation of the replacement rate from site to site along GPDH is extremely L-shaped (α = 0.06; i.e., α ≪ 1), reflecting that most (216/241; i.e., ≈90%) of the aligned residues are conserved in dipterans; the number of conserved sites is ≈95% when the comparisons are confined to the genus Drosophila. Among-site rate variation is somewhat less pronounced in SOD (α = 0.22), and lowest in XDH (α = 0.45), indicating that it is least constrained.

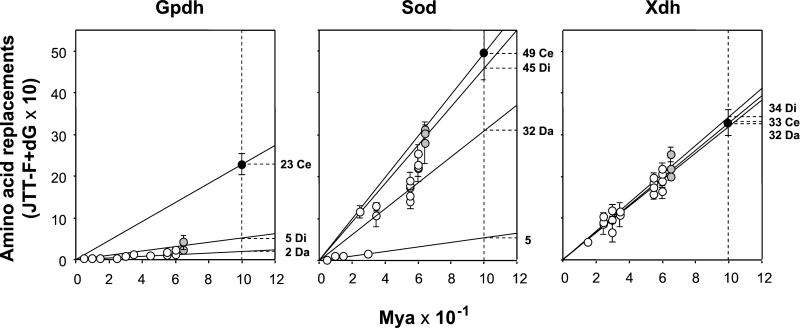
Table 1 shows the rates of amino acid evolution expressed in units of 10⁻¹⁰ replacements per site per year, normalized to give lineage values. Fig. 2 displays the number of replacements against time. Each gene follows its own dynamics. Consider GPDH. The rate of replacement is ≈2 × 10⁻¹⁰ per site per year between Drosophila species; 2.5 times greater (≈5 × 10⁻¹⁰) between species of different genera; and more than 10 times greater (≈23 × 10⁻¹⁰) between species of different families. The SOD rate also increases as less related dipterans are compared, but the slope of the increase is much less steep: the rate between Drosophila species is ≈20 × 10⁻¹⁰, twice as fast when the taxonomic window is enlarged to drosophilids (≈40 × 10⁻¹⁰), and 2.5 times faster when drosophilids are compared with Ceratitis (≈50 × 10⁻¹⁰). The average rate of replacement between Drosophila species in SOD conceals important differences among species groups. Thus, the mean rate between species of the obscura group (4.3 × 10⁻¹⁰) is about half the rate in the melanogaster group (9.4) or between the two Chymomyza species (8.8), and 10 times slower than the rate between species of the willistoni group (44.8).

Table 1.

Normalized rates of evolution of Gpdh, Sod, and Xdh for increasingly remote lineages of dipterans, inferred by using α estimates

Comparison	Myr	Amino acid replacements × 100 Myr
		Gpdh	Sod	Xdh
Within Drosophila groups*	25–30	0.0–2.0	4.3–44.8	20.9–38.7
Between Drosophila groups	55  ± 10	1.7	30.7	32.6
Between Drosophila subgenera	60  ± 10	2.7	38.2	31.6
Between drosophilid genera	65  ± 10	5.2	45.3	34.2
Between dipteran families	120  ± 20	22.6	49.4	32.8

The species compared are listed in Fig. 1. The ± values are crude estimates of error for Myr. Rate values are expressed in units of 10⁻¹⁰ amino acid replacements per site per year. 

^*Comparisons between species of the same or different subgroups. Considerable rate of heterogeneity exists, particularly at SOD, with the lowest value (4.3) occurring between species of the obscura group and the largest (44.8) between species of the willistoni group. 

Figure 2.

Rates of amino acid replacement for GPDH, SOD, and XDH in dipterans. Time (abscissa) is in million years × 10⁻¹. White dots indicate comparisons made between Drosophila species, gray dots between the drosophilid genera, and black dots between dipteran families. Averages (with their standard errors) are calculated to minimize the impact of the phylogenetic structure shown in Fig. 1. Thus, for example, for the D. melanogaster species-group, the average amino acid distance used for XDH is 0.0855 ± 0.0243, the arithmetic mean of the pair-wise distances Drosophila ananassae to D. melanogaster (0.0971) and D. ananassae to Drosophila erecta (0.0723). The rates on the right are for replacements × 10⁻¹⁰ per site per year. Da is the rate for comparisons between Drosophila species (2, 32, and 32), Di for drosophilid genera (5, 45, and 34), and Ce for dipteran families (23, 49, and 33) for GPDH, SOD, and XDH, respectively. These rates are obtained by linear regression with the intercept constrained to be the origin. The rate 5 to the right of the SOD graphic corresponds to the comparisons within the melanogaster and obscura groups.

The rate of amino acid replacement is fairly regular in XDH. The rates are 32.6 × 10⁻¹⁰ per site per year between Drosophila groups, 31.6 between Drosophila subgenera, and 34.2 between drosophilid genera, acceptable as sample variation of the same stochastic clock. The average of these three rates is ≈32.8 × 10⁻¹⁰, similar to the rate between dipteran families (see Table 1 and Fig. 2).

Global Rates of GPDH, SOD, and XDH Evolution.

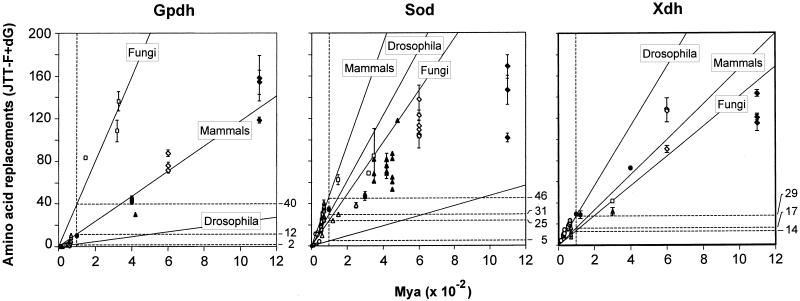
The best description of the amino acid substitution process of GPDH, SOD, and XDH is again provided by the JTT-F + dG model. However, the among-site rate variation is much less than for the dipterans (i.e., α values are larger). Amino acid rate variation from site to site decreases least for SOD, with α = 0.57 (0.22 for dipterans), and most for GPDH, α = 0.82 (0.06 for dipterans), nearly equal to that of XDH, α = 0.84 (0.45 for dipterans). The shape of the discrete gamma distribution for the genes remains basically the same when only the lineages included for all three genes are analyzed (0.59, 0.80, and 0.84, for SOD, GPDH, and XDH, respectively). The increase in α from Dipterans to global is expected because the proportion of invariable positions decreases with the enlarged time scale (i.e., 1100 million years (Myr) vs. 100 Myr since the split of the three dipteran families); but also because the variable positions of one lineage are not the same as those of another (i.e., the proteins evolve in nonstationary fashion with regard to the among-site rate variation; see refs. 25–27). Fungi show significantly larger α (0.94 ± 0.20) than dipterans (0.06 ± 0.02) and mammals (0.21 ± 0.14) for GPDH, and than dipterans (0.22 ± 0.05) for SOD; and dipterans show a greater α (0.45 ± 0.04) than mammals (0.34 ± 0.09) for XDH (normal deviate tests with standard errors computed by the curvature method of ref. 24).

Table 2 (see also Fig. 3) gives the rate of amino acid evolution, which changes erratically from one to another level of evolutionary divergence, and in different directions from gene to gene. Coincidentally, the rate of evolution is nearly the same for all three genes when comparisons are made between species from different kingdoms. This rate is 13.0 for GPDH, roughly similar to the average rates of amino acid replacement between animal phyla (13.2), which are ≈600 Myr old, and between orders of mammals (11.6), which evolved independently over the last 70 Myr. But this is not so for the other two genes, where the corresponding rates are 12.6, 19.2, and 46.0 for SOD and 11.5, 19.2, and 17.1 for XDH. The rates change erratically among lineages. The rates between drosophilid genera and between fungi are 4.4 and 40.0 for GPDH, 34.9 and 24.9 for SOD, and 31.7 and 13.7 for XDH. These rates assume that the drosophilid genera diverged 65 Myr ago and the ascomycetes 300 Myr ago (28, 29), but changing these divergence times does not eliminate the erratic behavior of the rates.

Table 2.

Normalized rates of evolution of Gpdh, Sod, and Xdh for increasingly remote lineages, inferred by using α estimates obtained from the full data sets, with estimates of divergence time derived from the Drosophila subgenera rate

Comparison	Myr	Amino acid replacements × 100 Myr				Clock estimates, Myr
		Gpdh	Sod	Xdh	Average	Gpdh	Sod	Xdh	Average
Within Drosophila groups	25–30	0.0–1.9	4.8–40.6	20.3–36.7	13.3–28.1	0–28	3–33	19–35	12–33
Between Drosophila groups	55  ± 10	1.5	25.7	30.4	22.4	41	46	53	49
Between Drosophila subgenera	60  ± 10	2.0	30.7	29.2	22.3	60	60	60	60
Between drosophilid genera	65  ± 10	4.4	34.9	31.7	24.9	142	74	65	85
Between dipteran families	120  ± 20	9.25	33.7	25.3	22.0	455	110	90	183
Between mammalian orders	70  ± 10	11.6	46.0	17.1	18.7	400	105	38	135
Between animal phyla	600  ± 100	13.2	19.2	19.2	17.5	3890	374	364	1243
Between fungi	300  ± 50	40.0	24.9	13.7	21.4	6699	276	130	1787
Between kingdoms	1100  ± 200	13.0	12.6	11.5	11.9	7045	451	398	2062

The species compared are listed in Fig. 1. The ± values are crude estimates of error for Myr. Rate values are expressed in units of 10⁻¹⁰ per site per year. Averages across loci are obtained by weighing the rate of each gene by the length of its sequence. The clock estimates of divergence time are extrapolated under the assumption that the Drosophila subgenera rate applies to other organisms. 

Figure 3.

Global rates of amino acid replacement for GPDH, SOD, and XDH. Time (abscissa) is in million years × 10⁻². The rates on the right are for replacements × 10⁻¹⁰ per site per year. The rates correspond to comparisons between drosophilid subgenera, mammal orders, or fungi. Other points in the figures are for other comparisons, such as between kingdoms (1,100 Myr) or animal phyla (600 Myr; see also Table 2).

The rate variations displayed in Table 2 (and Fig. 3) mask a much greater variation between lineages at different times because the rates given apply to largely overlapping lineages. Consider XDH. The average number of replacements between birds and mammals is 10.5 × 10⁻¹⁰ per site per year. If we accept that the lineage of mammals has evolved at an average rate of 17.1 (the mammal rate in Table 2) since they became separated from birds, to attain an average of 10.5 between mammals and birds, the bird lineage must have evolved at a rate of only 3.9, ≈8 times slower than the Drosophila rate. The rate between vertebrates (as inferred from the divergence between birds and mammals) and nematodes, which diverged some 600 Myr ago, is 21.4 × 10⁻¹⁰ per site per year. But the rate between vertebrates and arthropods is 15.1; because arthropods evolve at a slightly greater rate (18.1), the rate of evolution of XDH in vertebrates during the 600 Myr since they split from nematodes would be 10.5. This means that to attain an average of 21.4 between vertebrates and nematodes, XDH must have evolved at a prevailing rate three times larger in nematodes (32.3 × 10⁻¹⁰) than in vertebrates. Similarly, lepidopterans must have evolved at a rate of 5.6 × 10⁻¹⁰, one-sixth slower than dipterans to yield a rate of 18.1 in arthropods.

Estimated rates of amino acid replacement shown in Table 1 (i.e., between dipteran families and successively lower categories within it) differ from their correlates in Table 2, because they assume different degrees of among-site rate variation: the rates in Table 1 use α values obtained from dipterans, which are substantially smaller (see above) than the values used in Table 2, derived from the entire data set. Which of the two sets of α values is more nearly correct is not easily decided (30). In the absence of sampling bias, for a substitution process with stationary among-site rate variation (i.e., sites retain the same relative rates of change throughout the tree), the estimates obtained from closely related species should be closer to the true value of α (31). If the process is nonstationary, however, using closely related species to estimate α can be misleading, because different lineages can have disparate α values (see refs. 25 and 27). In the present case, it is apparent that the GPDH α value obtained from diptera is very low because this gene is extremely conserved in Drosophila; therefore, the rate of GPDH amino acid replacement between Ceratitis and the drosophilids obtained with this value of α is likely to be unduly large (i.e., the variation introduced by Ceratitis is outweighed).

Discussion

The neutral theory of molecular evolution predicts that the rate of substitution of neutral alleles equals the rate of neutral mutation, k = u. However, the index of dispersion, R = V/M, is often significantly greater than 1 (5, 32). Rate heterogeneity occurs between lineages, but also at different times along a given lineage, both factors having significant effects (5, 30, 32–39).

Subsidiary hypotheses have been proposed to account for the rate heterogeneity, while still retaining the hypotheses of neutral evolution and the molecular clock, even though this would be somewhat constrained. Some proposed explanations include the following (6).

(i) Generation Time.

Organisms with shorter generation time will evolve faster because the time to fix new mutations will be shortened. This hypothesis accounts for the observation that various genes evolve faster in rodents than in cows or primates, with much longer generations (40, 41). The prediction follows that all genes will be similarly accelerated or decelerated. If the hypothesis accounts for the faster rate of evolution of gene a in lineage A (say, rodents) than in lineage B (say, primates), it follows that a proportionally similar acceleration will occur for genes b and c.

(ii) Population Size.

Organisms with larger effective population size have slower rates of evolution than organisms with small population size, because larger populations increase the time required to fix new mutations. It has been suggested that population size and generation time are often inversely related, which thus might partially cancel out, yielding more nearly constant rates than if only i or ii were significant factors (3, 42). This inverse relationship can hardly be very general, because organisms with short generation times may range several orders of magnitude in population size. Some Proechimys spiny rats and Spalax moles have narrow ecological niches and much smaller population sizes than the cosmopolitan house mice and common rats; the population size of the widespread tropical Drosophila willistoni is surely more than six orders of magnitude greater than that of Drosophila insularis, which is confined to two small Caribbean islands. Population sizes may, however, have been very different in the past. In any case, demographic parameters impact all genes in a similar manner, so that hypothesis ii leads to the same prediction as i: evolutionary rate differences between lineages should equally apply to all genes.

(iii) Mutation Rate.

Species-characteristic differences may exist in polymerases or biological processes that affect the fidelity of DNA replication, and hence the incidence of mutations. Without any specific knowledge, this hypothesis simply says that mutation rates may differ from one lineage to another, or from time to time in a given lineage. Evolutionary rates will consonantly vary. Distinctive evolutionary rates have been observed in rodents vs. primates, as previously noted, as well as between the slower evolving birds vs. the faster mammals (43), a difference which is difficult to relate to either population size or generation time. This hypothesis again predicts that differences between lineages will be consistent across genes.

(iv) Functional Change.

A protein's function may change through time and become less (or more) constrained, so that the number of amino acid sites that can vary becomes greater (or smaller). These changes could differently affect different genes and different lineages, as well as the same lineage at different times. Thus formulated, this hypothesis is similar to iii in that the rate of neutral mutation will increase when there are fewer constrained amino acids, but differs from iii in that not all genes will be similarly impacted within a given lineage. This hypothesis, then, becomes a special case of hypothesis v, which allows for all sorts of variations across lineages and across genes as a consequence of the vagaries of natural selection. It ultimately implies that there is no molecular clock of evolution. Even if k = u, the rate would not be constant because the neutral mutation rate u varies in an unpredictable manner owing to functional changes. A particular case of this hypothesis says that, following gene duplication, selective constraints may change for one or both duplicates, as they evolve new functions. Accelerated evolution after duplication has been observed, for example, in the globin genes (44, 45). This version of the hypothesis predicts that comparisons between orthologous duplicates in different lineages would yield similar rates of evolution. This prediction has been falsified in various groups of organisms, such as for duplicated albumins in mammals (46), globins in Artemia shrimp (47), and for a set of 19 genes, of which 6 are duplicated in mammals and 14 in teleost fish (39).

(v) Natural Selection.

Organisms are continually adapting to the physical and biotic environments, which change endlessly in patterns that are unpredictable and differently significant from gene to gene and from species to species. This hypothesis amounts to a denial of predictable rates of molecular evolution. All that remains is the consideration that evolution is a time-dependent process, and thus the longer the time elapsed, the larger the number of changes, on the average.

We have observed (Tables 1 and 2; Figs. 2 and 3) that (i) rates of evolution change erratically between and within lineages, and that (ii) the patterns of change for different genes are discordant. Thus (Table 2), the GPDH rate of evolution is much slower between species of Drosophila than between species of mammals (2.0 for Drosophila subgenera vs. 11.6 × 10⁻¹⁰ replacements per site per year), whereas the rate is much faster in Drosophila than in mammals for XDH (31.7 vs. 17.1). The rate of evolution (Table 2) ranges from <2 (between Drosophila species) to 40 (between fungi species) for GPDH; from 12.6 (between kingdoms) to 46.0 (between mammalian orders) for SOD; and from 11.5 (between kingdoms) to >30 (between Drosophila species) for XDH.

Fitch and Ayala (16) showed that the reduction in rate of evolution that occurs in SOD when the species compared become increasingly remote conforms to a molecular clock process where the replacements follow a constrained covarion model (i.e., all lineages evolve at a constant rate, but the set of variable sites changes across lineages). The covarion-clock model postulates that (i) sites belong to, at least, two rate categories: those that vary and those that do not; (ii) the number of variable sites is fixed throughout the tree; and (iii) variable sites change at an equal rate. Under the covarion-clock model, the extent of among-site rate variation should remain constant throughout the tree. But we have shown that different lineages display disparate α values (i.e., either the proportion of variable positions, or their relative rates, or both change from one to another lineage) for all of the three genes, which invalidates the covarion-clock as a model accounting for rate variation over time.

Our analyses corroborate previous conclusions concerning the irregular and contrasting patterns of evolution of GPDH and SOD (6–8). These previous studies did not take into account the phylogenetic inertia of the data in the calculation of average evolutionary rates for lineages; also, backward and parallel amino acid replacements were corrected by using the PAM algorithm of ref. 48, instead of the updated matrix of ref. 22 used herein, which sets amino acid frequencies as free parameters (JTT-F model; ref. 21). In addition, we have taken into account variation in the rate of amino acid replacement from site to site by using the discrete gamma approach of ref. 20. Ignoring the among-site rate variation leads to a greater underestimation of distances as the distance increases; specifically, failure to accommodate among-site rate variation can account for consistently lower rates in previous than in the present study (e.g., the average rates for comparisons between kingdoms for GPDH are 4.0 vs. 13.0 in ref. 8 vs. this study; 3.3 vs. 12.6 for SOD). But the overall picture that GPDH and SOD change erratically, in patterns inconsistent across the two loci, remains in both investigations. It could be argued that the estimates of the among-site rate variation that we use to correct for multiple replacements in Fig. 3 (also Table 2) are underestimates, because they are derived without accounting for the nonstationarity of α (see ref. 27). Using lower α's, supposedly closer to their parametric values, would amplify the rate differences between slowly and rapidly evolving lineages, for example, in Fig. 3.

The extent to which the erratic patterns of evolution of GPDH and SOD are an aberration rather than representative of prevailing modes of protein evolution was left in abeyance (8). We now show that XDH also evolves erratically and following an evolutionary path that is different from those of either GPDH or SOD (see Figs. 2 and 3). Compared with GPDH and SOD, the extent of variation of the XDH rate of evolution appears to be lower (see Table 2 and Figs. 2 and 3). This might be expected because of the larger number of residues analyzed for XDH (599 vs. 241 and 107 for GPDH and SOD, respectively), so that the dispersion due to sampling variance would be larger for the last two loci. Note, however, that the number of residues analyzed for GPDH (241 sites) is more than twice that for SOD (107), yet the rate variation of GPDH is not smaller than that of SOD.

All three proteins are globular, soluble homodimeric oxidoreductases, but GPDH and SOD are relatively small proteins [subunit molecular weight is 15 K_d for SOD (10) and 40 K_d for GPDH (9)]. Comparatively, XDH is a huge protein [145 K_d (11)]. It would be hard to attribute to GPDH or SOD more important functions than to XDH. The three enzymes are involved in primary metabolism: GPDH participates in the glycerophosphate cycle, catalyzing the reversible reduction of dihydroxyacetone phosphate to sn-glycerol-3-phosphate; SOD catalyzes the dismutation of superoxide anion O₂⁻; and XDH takes part in the catabolism of purines, acting on a variety of purines and aldehydes. XDH may be the enzyme showing affinity for the broadest spectrum of physiological substrates of the three enzymes. This circumstance would entail that functional constraints are lesser for XDH than for GPDH and SOD, because the probability of a mutational change not being harmful is smaller for substrate-specific enzymes than for substrate-nonspecific enzymes (3).

It has, indeed, been suggested that larger enzymes may tolerate more amino acid replacements that are effectively neutral than smaller proteins. Large molecular size has been posed to account for the high levels of amino acid polymorphism at Xdh in natural populations of Drosophila (49). In almost all proteins where positive Darwinian selection has been demonstrated, only a few amino acid sites have been responsible for the adaptive evolution (see ref. 50). In the case of XDH, it seems unlikely that adaptive selection on a few sites would have a large effect on estimates of the evolutionary rate of the average site of the protein. It seems, therefore, reasonable to assume that the evolutionary path of XDH stands closer to the expectation for a neutral molecule than those of GPDH and SOD. Because the last two are encoded by much shorter genes, with presumably a larger fraction of sites as possible targets for positive selection, the evolutionary dynamics of GPDH and SOD might reflect to a greater extent the influence of adaptation.

Whichever may be the explanation for the lower variation of evolutionary rates in XDH, our observations for all three genes are inconsistent not only with the molecular clock predicted by the neutrality theory, but also with subsidiary hypotheses, such as i, ii, and iii, that predict that patterns of evolution will be consistent across genes even if variable between lineages for any given gene. We are left with hypotheses that attribute rate variation to the vagaries of natural selection, whether as a consequence of functional shifts that change rates of neutral mutation through time differently for different genes in different organisms (hypothesis iv) or in response to phenotypic evolution and environmental heterogeneities (hypothesis v). These two hypotheses amount to a denial of there being a molecular clock, although there would be an overall correlation between amount of change and time elapsed, expected from any time-dependent process such as evolution.

The erroneous inferences that could be reached by assuming a molecular clock for any of the three genes investigated are dramatically illustrated in Table 2 (last four columns). If we use the average rate of evolution of Drosophila over the last 60 Myr for estimating the time of divergence for other organisms, the divergence of the three multicellular kingdoms is estimated at 7,045 Myr by GPDH, a gross overestimate, but at 451 Myr and 398 Myr, which are blatant underestimates, by SOD and XDH, respectively. Similarly, erroneous and disparate divergence times would be inferred for other groups of organisms.

Abbreviations

GPDH

glycerol-3-phosphate dehydrogenase

SOD

superoxide dismutase

XDH

xanthine dehydrogenase

Myr

million years