Eco-evolutionary feedbacks promote fluctuating selection and long-term stability of antagonistic networks

Abstract

Studies have shown the potential for rapid adaptation in coevolving populations and that the structure of species interaction networks can modulate the vulnerability of ecological systems to perturbations. Although the feedback loop between population dynamics and coevolution of traits is crucial for understanding long-term stability in ecological assemblages, modelling eco-evolutionary dynamics in species-rich assemblages is still a challenge. We explore how eco-evolutionary feedbacks influence trait evolution and species abundances in 23 empirical antagonistic networks. We show that, if selection due to antagonistic interactions is stronger than other selective pressures, eco-evolutionary feedbacks lead to higher mean species abundances and lower temporal variation in abundances. By contrast, strong selection of antagonistic interactions leads to higher temporal variation of traits and on interaction strengths. Our results present a theoretical link between the study of the species persistence and coevolution in networks of interacting species, pointing out the ways by which coevolution may decrease the vulnerability of species within antagonistic networks to demographic fluctuation.

1. Introduction

Natural selection is one of the mechanisms that bridge ecological and evolutionary processes in biological systems [1]. Ecological interactions among species may cause selection that drives many evolutionary processes, such as phenotypic evolution [2], coevolution [3–5] and speciation [6]. Similarly, evolutionary processes are important for understanding population dynamics [7–9], community composition [10,11] and metacommunity dynamics [12]. Eco-evolutionary dynamics occur when ecology and evolution affect each other [1], potentially resulting in feedback loops between ecological and evolutionary processes [13]. Feedbacks between evolutionary processes and ecological dynamics can alter both adaptive evolution and species coexistence [13–15]. Empirical and theoretical studies support the notion that eco-evolutionary feedbacks are expected when evolution is rapid. In this scenario, ecological and evolutionary changes occur at similar temporal scales [1,16–18]. Rapid evolutionary changes are especially common in antagonistic interactions, such as predator–prey and host–parasite systems, because species are constantly responding to a coevolving selective pressure [7,19–22]. A classic example is the rapid evolution of beak and body size on Galápagos ground finches that prey upon seeds in response to changes in ecological conditions and seed size distributions [23]. Therefore, antagonistic interactions represent a useful model to explore the ecological and evolutionary consequences of eco-evolutionary feedbacks.

Phenotypic evolution may influence population dynamics of victims and their natural enemies by affecting interaction strengths [7,24–27]. For instance, in parasite–host interactions the infection dynamics are driven through eco-evolutionary feedback loops and parasites interact only with hosts they have evolved to overcome the defences of [28]. Evolution of host and/or parasite traits can occur within the course of an epidemic, shaping the host and parasite densities [29]. Many studies have documented rapid evolutionary change that affects the structure of interspecific interactions and genotypic patterns within natural communities (reviews in [16,30,31]). Environmental cues associated with changing levels of predation risk can trigger phenotypic changes in resource organisms. For example, Johnson & Agrawal [32] experimentally generated selection on biomass, life history and herbivore resistance of the primrose Oenothera biennis (Onagraceae), and the resulting evolutionary changes affected abundance and diversity of the associated arthropods. The evolution of traits shaping interaction strengths can significantly decrease or increase the strength and rate of consumption, and therefore is likely to alter the structure and dynamics of trophically interacting populations [33], which may impact community stability and persistence [15,34].

Evolving traits such as body size may reorganize the interaction strengths of ecological networks, affecting structural attributes such as the fraction of all possible links that are realized in a network (connectance) or the number of trophic levels of a food web [11]. These ecological changes may, in turn, modulate the strength of selection and drive subsequent evolution in the system. These predictions indicate that rapid trait evolution could contribute significantly to the short-term dynamics of community interaction structure. Hence, considering the effects of the structure of species interactions to adaptive evolution would increase the predictive potential of evolutionary models [16]. In the same way, models of ecological networks assuming that adaptive evolution can contribute to the temporal change of interspecific interactions over short periods may lead to new insights about the mechanisms that promote and maintain biological diversity [35–37].

In diverse communities, pairwise reciprocal evolution might be altered by the network of multiple interactions. Theory on mutualistic networks predicts that coevolution might occur among multiple interactions [38,39] and evolutionary responses may propagate through the network [40]. Previous approaches also studied the consequences of adaptive foraging in food webs [41–45] and found that fitness-enhancing changes in individuals' feeding-related traits may increase the stability of food web dynamics. However, trait evolution may be rapid, and feedbacks between ecology and evolution may occur at the same time scale [46]. To understand the long-term persistence of ecological communities formed by coevolving species, it is crucial to develop theoretical predictions about the interplay of trait coevolution and population dynamics in species-rich networks. Here, we model population dynamics and trait evolution of networks formed by several interacting victim and exploiter species to investigate how rapid evolution of coevolving interactions affects the long-term stability of interacting assemblages [30]. For that, we model eco-evolutionary dynamics in 23 empirical antagonistic networks. We measure network and species structural characteristics to explore how network structure affects eco-evolutionary dynamics and how species interaction patterns within the networks may drive population and trait dynamics.

Several processes can promote long-term stability of ecological communities. Most of these processes can be summarized in environmental and interaction selection processes, such as climate conditions or predator–prey interactions [30]. Here we evaluate the effect of eco-evolutionary feedbacks on long-term ecological network stability. Our main questions were (i) how environmental and interaction selection strength affect population and trait dynamics, and (ii) how eco-evolutionary feedbacks affect the long-term stability of antagonistic networks. Our results show that rapid coevolution significantly increases the demographic stability of antagonistic networks, defined as reduced vulnerability to demographic stochasticity. Our results also indicate that feedback loops between ecological and evolutionary processes lead to specific patterns of species specialization and abundance distribution.

2. Material and methods

(a). The model

We model the eco-evolutionary dynamics of victim and exploiter species interacting within antagonistic networks. We assume that interactions between species are mediated by matching of defence and attack traits, such as antigen and antibody in parasite–host interactions [47], or secondary compounds and detoxifying enzymes in herbivore–plant interactions [48]. Trait matching assumes that the probability of interaction depends on the similarity between victims' and exploiters’ traits [49]. Trait matching has been shown to be important in antagonistic coevolving interactions, such as among brood parasites and their hosts [50], and wild parsnip and parsnip webworms [51]. Each network is composed of N_V + N_E species (1 < i ≤ N_V and 1 < j ≤ N_E), and each victim species i and exploiter species j is characterized by their abundance, V_i and E_j, and a mean trait value, z_i and y_j, respectively. We focus our work on assemblages that are characterized by two trophic levels and interactions only occur between species in different trophic levels, such as parasite–host or plant–herbivore interactions.

(b). Population dynamics

We model species’ population dynamics (equation (2.1)) as a victim–exploiter discrete time model [52] in order to estimate the effect of species interactions on mean population fitness per generation. Initial V_i and E_j values are sampled from normal distributions (mean ± s.d., V_i: 0.5 ± 0.1; E_j: 0.1 ± 0.1). Other initial distributions did not affect the eco-evolutionary dynamics. We assumed the victims' populations are, on average, higher than exploiters’ populations, to emulate differences in abundances (or biomass) between trophic levels [52].

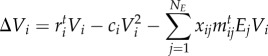2.1a

and

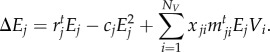2.1b

We model the strength of species interactions 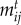as a function of species' traits to connect ecological dynamics with phenotypic evolution. The 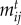values represent the degree of trait matching between species, 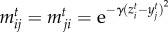, where γ determines the interaction sensitivity to deviations from trait matching. The 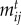follows a Gaussian distribution where γ defines the variance and maximal 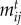(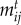) = 1 occurs with maximal trait matching, 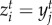. The intraspecific competition term of both species is defined as c_i = c_j = 1, which is an assumption made without loss of generality [53]. We assume that interspecific competition has a weaker impact on population dynamics because we model births and deaths depending on environment and victim–exploiter interactions. Population growth rates are defined as 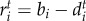and 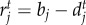, where b_i and b_j are species intrinsic birth rates, an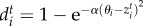d and 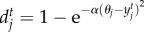are death rates affected by the degree of mismatch between population mean trait value and the optimum trait favoured by environmental selection, θ_i and θ_j. The scaling parameter α controls the sensitivity to deviations from the optimum trait favoured by the environment. We assume that 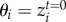and 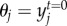. The matrix X = [x_ij] is the squared empirical matrix of species interactions, where x_ij = x_ji = 1 if species i interacts with j and x_ij = x_ji = 0 otherwise (i.e. when the link has not been observed in the empirical network). We use empirical networks of different antagonistic interactions to designate which interactions occur and which do not, but we allow interaction strengths to evolve in response to trait evolution [54]. Thus, the absence of interactions (x_ij = 0) is treated as a forbidden link in our simulations. High trait mismatch (low 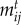) also leads to a functional forbidden link. We explore a broad range of birth rates, b, and in our simulations we use b parameter values that allow an average of 89% of species to persist per network (electronic supplementary material, table S1). Because we are interested in the effects of network structure on eco-evolutionary dynamics, we avoid local extinctions by fixing population sizes smaller that 10⁻¹³ as equal to 10⁻¹³. This implies we assume that rare species are maintained in the community in low abundance.

(c). Phenotypic evolution

We explore how selection affects trait evolution in order to investigate the eco-evolutionary feedbacks in antagonistic networks. Time-dependent mean fitness at population level for the victims (W^t_i) and exploiters (W_j) can be approximated as the population per capita rate of increase [55]:

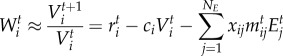2.2a

and

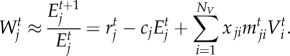2.2b

Fitness-gradient-based models can provide great insight into the combined adaptive change and population dynamics in biological communities [56]. Thus, we model species mean trait evolution as discrete events of change caused by selective pressures imposed by the environment and antagonistic partners. We assume that the evolving traits z_i and y_j result from the additive genetic effects of many loci [57]. A major consequence of this assumption is that traits tend to be normally distributed in the species populations and can be approximated by the population mean trait value. We made the simplifying assumption that the genetic variance is constant [57]. We estimate the trait values that maximize mean population fitness at each time step by numerically calculating the fitness gradients for victims (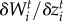) and exploiters (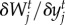). The traits favoured by selection, 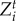and 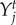, are the traits that maximize the mean population fitness function for each species. The fitness gradients can have many local maxima, and we selecte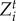d and 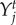as the local maxima nearest to the trait value at time t.

As a first approximation to understand the complexity of eco-evolutionary feedbacks in ecological networks, we focus our analysis on species mean trait dynamics. Initial values of z_i and y_j are sampled from a normal distribution (0 ± 0.1). We update the species mean trait in one generation according to an equation for phenotypic evolution [40]:

2.3a

and

2.3b

where φ is a constant proportional to the slope of the selection gradient and the additive genetic variance of the trait, and describes the potential to evolve in traits modulated by selective pressures (see [40] for further details). For sake of simplicity, we assume φ is fixed and identical for all species (φ = 0.25).

The dynamics expressed by equation (2.3) reflect adaptive changes in species traits resulting from the combined effect of environmental and interaction selection. To study the effect of eco-evolutionary feedbacks on species coevolution and long-term stability, we contrast scenarios varying in the intensity of environmental and interaction selection. The first scenario describes the situation of eco-evolutionary feedbacks with weak environmental selection and strong interaction selection (α = 0.001, γ = 0.1). This scenario describes an asymmetric selection regime with strong coevolution leading trait changes and population dynamics. Our second scenario considers strong environmental and strong interaction selection (α = γ = 0.1). In this scenario, the probability to survive and to interact depend strongly on trait values. The third scenario is the quasi-neutral scenario with weak environmental and interaction selection (α = γ = 0.001). Weak environmental selection may arise when the probability to survive depends weakly on matching the environmental optimum trait. In the same way, weak interaction selection occurs when the probability of interaction depends only weakly on victim and exploiter trait matching. Our last scenario describes another asymmetric selection regime, where environmental selection is strong and interaction selection is weak (α = 0.1, γ = 0.001). The variables and parameters used in the simulations are listed in the electronic supplementary material, table S1. To explore the sensitivity of these four scenarios to interaction and environmental selection, we use Latin hypercube sampling to explore multiple values of α and γ.

(d). Empirical antagonistic networks and network structure

We use 23 empirical antagonistic networks to define the matrix X (see equation (2.1)), which encompass a broad range of antagonisms, including parasitism, herbivory, predation and grazing (electronic supplementary material, table S2). To explore the effects of network structure on eco-evolutionary dynamics, we describe the structure of empirical networks using four network metrics: (i) species richness, (ii) connectance, (iii) nestedness and (iv) modularity (electronic supplementary material). To investigate if a species's degree of generalization or specialization within the network determines its abundance and trait dynamics, we characterized each species according to two descriptors: (i) normalized degree and (ii) standardized Kullback–Leibler distance (d′) (electronic supplementary material).

(e). Ecological and coevolutionary dynamics

We run each replicate for 3000 time steps, which was sufficient time to reach convergence. We run 100 replicates with different initial conditions of species abundances and mean traits per network and scenario, totalling 9200 simulations. To characterize species ecological dynamics, we compute each species mean abundance and abundance temporal variance since t = 0. We calculate the average values across all the species in a network to describe the ecological dynamics on each network. We define demographic stability as low vulnerability of that community to stochastic extinctions [58–60]. This was inferred by assuming that higher abundances and lower temporal variance in abundances increase the community demographic stability [58–60]. Similarly, we characterize each species's trait dynamics by its mean trait and temporal variance of the mean trait. We describe trait dynamics on each network as the average values across species in that network. A higher temporal variation in mean trait values indicates a stronger and faster evolutionary response to selective pressures.

We characterize the temporal fluctuation in the interaction strength among species pairs, s_ij, as the cumulative change in pairwise matching, following 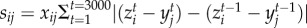. The cumulative change in pairwise matching for each victim is calculated as 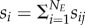(a similar definition holds for exploiters). The mean cumulative change in pairwise matching across all species in a network is calculated as 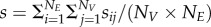and the variance as 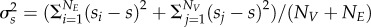. A high s-value indicates high temporal variation in interaction strength among species, which we use as a proxy for interaction fluctuating selection.

We investigate the relationship between (i) abundances, (ii) traits and (iii) the mean (s) and variance (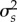) of interaction fluctuating selection across the selection scenarios. We use log values for trait values and s to reduce the skewness in data. We performed path analysis [61] to investigate the effects of network structure on ecological and coevolutionary dynamics. Because structural descriptors of networks often affect each other, we estimate the direct effects of richness and connectance on nestedness and modularity, and their effects on dynamics. We test the entire causal structure of the path model simultaneously by estimating model parameters via maximum likelihood [61]. We investigate the effects of species metrics on ecological and coevolutionary dynamics by using general linear mixed models considering scenario and species trophic group as fixed-effect factors, and network identity as a random factor. We did not report p-values because statistical significance is not useful to determine the relative importance or presence/absence of effects of the various predictors in simulation studies [62]. We rather use the effect sizes for investigating the importance of different predictors [62]. We calculate R² statistics for fixed effects according to Nakagawa & Schielzeth [63].

3. Results

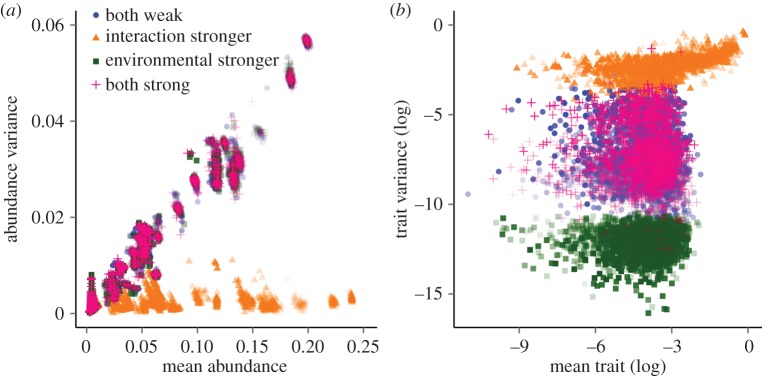
Our results show that reciprocal antagonistic selection stronger than environmental selection (i) increases species abundance, (ii) promotes temporal stability of population sizes and (iii) results in large fluctuations in trait values due to selection exerted by a particular partner species. In the scenarios where the strength of environmental and interaction selection are equal or where environmental selection is higher than interaction selection, there is a positive correlation between species' mean abundances and their temporal variation (coefficient ± standard error; β = 0.25 ± 0.002, R² = 0.96; figure 1a). By contrast, if interaction selection is stronger than environmental selection, species’ mean abundances are, on average, higher and less variable (figure 1a; electronic supplementary material, table S3). There are no differences in the mean abundances and temporal variance among the other scenarios with stronger environmental selection or environmental selection equal to interaction selection (figure 1a). Victims have higher abundances than exploiters in all scenarios (β_victim = 0.14 ± 0.016, β_exploiter = −0.01 ± 0.016; figure 3; electronic supplementary material, figures S13–S15). Accordingly, abundances of victims are more variable in time than abundances of exploiters in all scenarios (β_victim = 0.03 ± 0.003, β_exploiter = 0.001 ± 0.003, figure 3; electronic supplementary material, figure S13–S15).

Figure 1.

Relationship between species' mean abundance and temporal variance in abundance (a) and mean trait (log of absolute values) and temporal variance in trait (log) (b). Each dot represents the mean value and temporal variance, in average for a network on each replicate. Results shown for the scenarios with both environmental and interaction selection weak (blue), both strong (pink), stronger interaction than environmental selection (orange) and stronger environmental than interaction selection (green). Colours are transparent such that darker colours represent a high overlay of points.

Figure 3.

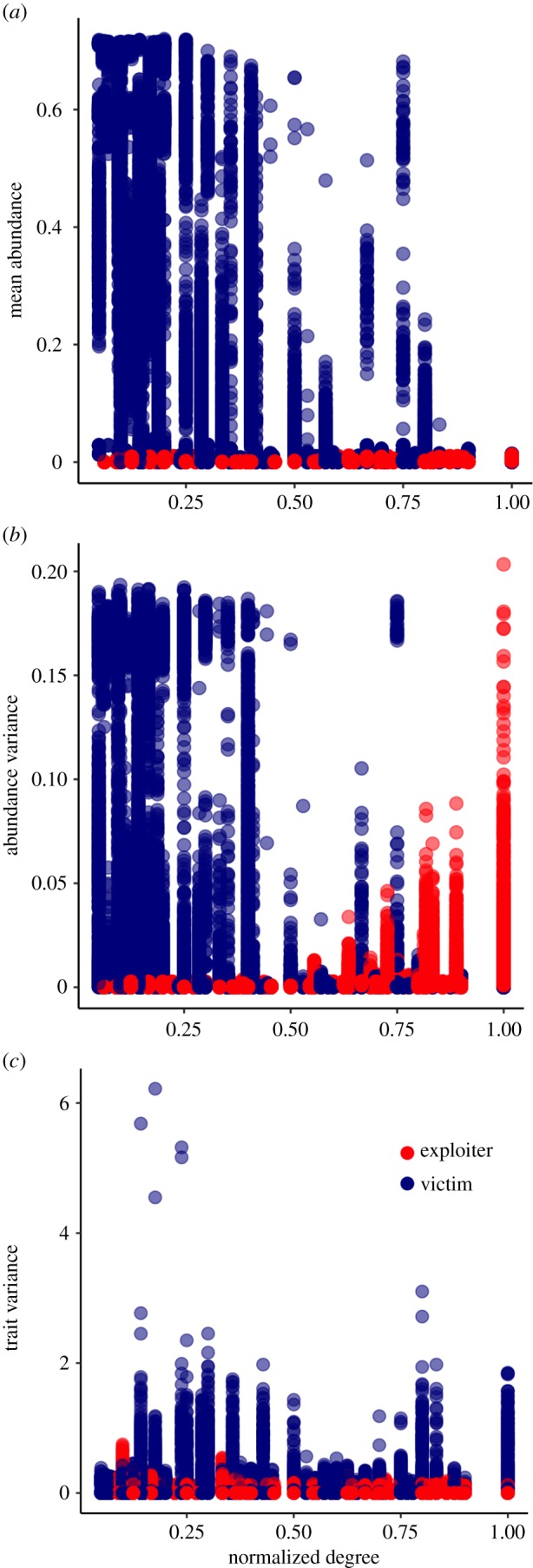
Effect of species normalized degree on exploiter (red) and victim (blue) mean abundance (a), abundance coefficient of variation (b) and trait coefficient of variation (c) in the four scenarios. Each dot represents the value of a single species in a replicate. Colours are transparent such that darker colours represent a high overlay of points.

Species’ trait dynamics differ from abundance dynamics (figure 1a,b). Temporal variance in species' traits is weakly related to species' mean trait (β = −0.006 ± 0.02, R² = 0.89, figure 1b). Attack and defence mean traits reach higher magnitude of change when interaction selection is stronger than environmental selection (electronic supplementary material, table S3). Interaction selection stronger than environmental selection also increases the temporal variance of species’ traits (electronic supplementary material, table S3). However, there is no difference in temporal trait variance when interaction and environmental selection are both either weak or strong (figure 1b). Eco-evolutionary feedbacks result from interaction selection stronger than environmental selection. This asymmetry reduces abundance fluctuations and increases attack and defensive traits as well as the temporal variation in these traits (orange triangles in figure 1). By contrast, when interaction and environmental selection strengths are similar, abundances fluctuate but species' traits almost do not change (figure 1). Finally, strong environmental selection associated with weak interaction selection restricts even more the temporal variance in attack and defence traits. A deeper evaluation of multiple strengths of environmental and interaction selection with a two-species system corroborates the role of stronger interaction selection and weaker environmental selection in generating fluctuations on traits and buffering variations in abundances (electronic supplementary material). Thus, asymmetry associated with strong interaction selection and weak environmental selection is the main driver of low variation in abundances associated with high variation in traits.

The average temporal fluctuation in the interaction strength among species pairs (s) is positively related to its variance, 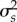(β = 1.26 ± 0.05, R² = 0.87; figure 2). The fluctuation of interaction strength among species is lower when environmental selection is stronger than or equal to interaction selection (electronic supplementary material, table S3). Similarly to species abundance and trait results, there is no difference in the temporal fluctuation in interaction strength among species pairs between the scenarios with both strong and both weak interaction and environmental selection, respectively (figure 2). Our result suggests that the higher the interaction fluctuating selection, s, the lower is the fluctuation in species abundances (β =−110.3 ± 3.56, R² = 0.71).

Figure 2.

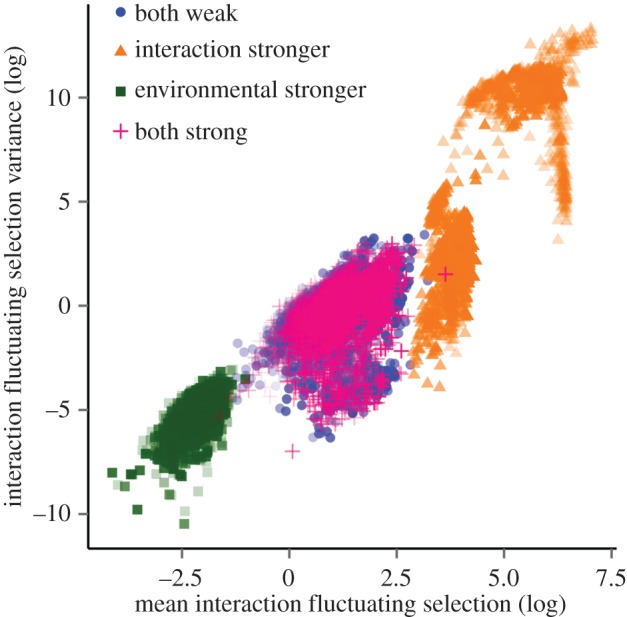
Relationship between mean interaction fluctuating selection (s, log values) and variance (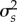, log values). Each dot represents the mean value and variance among species, in average for a network on each replicate Results shown for the scenarios with both environmental and interaction selection weak (blue), both strong (pink), stronger interaction than environmental selection (orange) and stronger environmental than interaction selection (green). Colours are transparent such that darker colours represent a high overlay of points.

Network structure affects demography in a consistent way across different scenarios. Richness, connectance and nestedness decrease species’ mean abundance (electronic supplementary material, figures S1 and S2) and temporal variance in abundances (electronic supplementary material, figures S3 and S4). By contrast, network modularity increases species' mean abundance (electronic supplementary material, figures S1 and S2) and temporal variance in abundances (electronic supplementary material, figures S3 and S4). However, network structural patterns have weaker effects on trait dynamics. Richness, connectance, nestedness and modularity have negligible effects on attack and defence mean traits (electronic supplementary material, figures S5 and S6) and weak effects on species’ trait temporal variance (electronic supplementary material, figures S7 and S8). Network structural patterns also have negligible effects on mean fluctuating interaction strengths, s (electronic supplementary material, figures S9 and S10), and on fluctuating interaction strength variance, 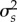(electronic supplementary material, figures S11 and S12).

Finally, species’ specialization metrics within the networks are related to their abundance and trait dynamics and differ between exploiters and victims (figure 3; electronic supplementary material, figures S13–S15). Victims attacked by a smaller number of exploiter species often have higher mean abundances while specialized exploiters are less abundant (normalized degree: β_victim = −0.31 ± 0.001, β_exploiter = 0.08 ± 0.002, R² = 0.35; specialization (d′): β_victim = 0.28 ± 0.001, β_exploiter = −0.12 ± 0.001, R² = 0.38; figure 3a; electronic supplementary material, figure S13a). Specialized victims also show higher temporal variance in abundance while specialized exploiters' abundance varies less in time (normalized degree: β_victim = −0.06 ± 0.0004, β_exploiter = 0.02 ± 0.0004, R² = 0.25; specialization (d′): β_victim = 0.05 ± 0.0003, β_exploiter = −0.03 ± 0.0003, R² = 0.28; figure 3b; electronic supplementary material, figure S13b). Temporal variance in trait values is highly variable among species and weakly affected by species interaction patterns (figure 3c; electronic supplementary material, figure S13c). Generalist victims and exploiters tend to show higher temporal variation in trait values (normalized degree: β_victim = 0.015 ± 0.001, β_exploiter = 0.017 ± 0.001, R² = 0.33; specialization (d′): β_victim = −0.02 ± 0.0008, β_exploiter = −0.02 ± 0.008, R² = 0.33). However, effects of species interaction patterns on trait temporal variances are weak (figure 3c; electronic supplementary material, figure S13c).

4. Discussion

In this study, we integrate approaches derived from ecological and evolutionary theory with network-based modelling and empirical data to investigate the consequences of rapid coevolution and eco-evolutionary feedbacks on the stability of antagonistic networks. Previous theoretical approaches already investigated patterns of trait coevolution in mutualistic networks [38,39] and adaptive foraging in food webs [42], but we still lack predictions about the interplay of coevolution and demography for community dynamics when evolution is rapid (but see [15]). Here we have merged trait and demographic dynamics to move forward our understanding of long-term stability in species-rich antagonistic networks. Our results show that eco-evolutionary feedbacks significantly increase species mean abundances and decrease temporal variation in abundances compared with the scenario without feedbacks (i.e. weak interaction selection). We also found that the interaction strength between exploiters and victims was on average two orders of magnitude more variable when interaction selection was stronger than environmental selection. Our results illustrate how ecological and evolutionary processes may represent alternative routes to how populations respond to changes in interacting species-rich assemblages [64].

We identify three points related to the mechanism by which coevolution decreases the vulnerability of antagonistic networks to stochastic processes. First, strong selection between victims and exploiters creates eco-evolutionary feedbacks that disrupt the positive correlation between mean abundance and temporal variance in abundances. Previous models and experiments using two or few interacting species/strains found contrasting results, with trait evolution triggering fluctuations [7,20,46,65] or stabilizing predator–prey population dynamics [66–69]. Our model predicts that when ecological interactions are the main evolutionary force, rapid coevolution in attack and defence traits stabilizes abundance oscillations in antagonistic networks. Rapid coevolution temporally changes the interaction strength between interacting partners, which dampens the temporal variability in species abundances. This indicates that interaction selection driving trait fluctuations can stabilize population dynamics in species-rich antagonistic interactions. When other selective pressures have similar or greater importance on species fitness, network structure is the main driver of the eco-evolutionary dynamics (electronic supplementary material, figure S1).

Second, our results predict correlated trends between network structure and eco-evolutionary dynamics. There is a long-standing debate on whether ecological community complexity increases its stability [70–73], with ecosystems often supporting large numbers of species interacting in highly complex networks [74,75]. More specifically, the analysis of local stability to small perturbations in eco-evolutionary models led to the prediction that evolution decreased the resilience of highly diverse random communities when populations are at equilibrium [15]. By contrast, it was hypothesized that fluctuating selection on interaction strengths among species increases the persistence of interactions and promotes stability in complex antagonistic communities [18,30]. Fluctuating selection may arise from adaptive foraging and behaviour or evolutionary trait changes [7,41,46,76–78]. Our results support that interaction fluctuating selection resulting from eco-evolutionary feedback loops positively affects the stability of antagonistic networks. In fact, the fluctuating selections arising from eco-evolutionary dynamics promote the stability (low abundance oscillations) of populations connected by strong interaction strengths. Strong interaction strengths are often associated with unstable dynamics (or at least unstable fixed points to small perturbations [70]). Our results indicate that if rapid evolution is operating, strong interaction strengths and fluctuating selection might favour stability of interacting populations.

Our results also predict correlated trends between network structure and eco-evolutionary dynamics. Network richness, connectance and nestedness decrease abundance mean and temporal variance while modularity increases overall species mean abundances and also abundance temporal fluctuations in the absence of strong coevolution. Modular structures reduce the sharing of interacting partners, which may reduce the negative indirect effects of apparent competition and thereby the propagation of direct and indirect negative effects across the network [53,79]. Our results also suggest that modularity and the fluctuating selection mechanism have a synergistic effect on long-term stability of antagonistic networks, especially when interaction selection is stronger than environmental selection (figure 3; electronic supplementary material, figure S1). This happens because modularity restricts the number of possible partners with which a species interacts, which reduces the amount of trait change required to adaptively adjust the strength of interaction with its partners. In addition, the amount of trait change is reduced in highly modular networks because species outside modules will seldom trigger adaptive evolution in species within modules [54]. In contrast to studies where high modularity has been related to high ecological stability in the absence of adaptive evolution [53], our results show that population fluctuations increase with network modularity. Thus, we show that eco-evolutionary feedbacks affect the dynamics of antagonistic networks and that different predictions may be related to the relative importance of eco-evolutionary feedbacks on community dynamics.

Third, species dynamics within networks are not homogeneous but highly variable across species. The degree of species generalization partially predicts their population patterns but has almost no effect on trait dynamics. If species are ecologically equivalent, abundances would determine the probability of interactions and it is predicted that generalists would be the most abundant species [80,81]. Contrary to the neutral expectation [80–82], we found that specialized victim species tended to have higher mean abundances than generalists. Exploiters always show smaller abundances independent of their number of interactions, but this can be a consequence of parameter choice. However, when attack and defence trait constraints are more important than species abundance in determining species interactions, we would not expect a positive association between abundance and degree of generalization. Our results indicate that when the strength of interactions changes in time because of species coevolution, the feedbacks between ecological and evolutionary dynamics create a trade-off between the number of interacting partners and abundance. This trade-off has already been found in parasite–host and parasitoid–host interactions [83–85], and has been related to the high cost of adaptations to multiple victim defences (or exploiter attack) mechanisms [84] (but see [86]). Experiments have also found evidence for a trade-off driven by fluctuating selection when there is rapid coevolution between antagonistic species [87]. In this case, coevolution stabilized population dynamics after the evolution of a diversity of strains with different levels of resistance and virulence ranges [87]. These results support our findings that rapid coevolution among multiple species increases the temporal variation in interaction strength, which is the basic mechanism that increases community stability in our model. In addition, we found that species abundances tend to be smaller when environmental selection is stronger or equal to interaction selection. Contrasting selection pressures often reduce species abundances because of trade-offs effects on the mechanisms that contribute to species fitness [67,88,89]. For instance, selection for a trait that increases an exploiter's attack or a victim's defence may decrease its ability to deal with environmental conditions. These secondary effects of trait evolution explain why species achieved smaller mean abundances and larger temporal variation when environmental selection has a stronger effect on fitness.

Our results highlight the importance of eco-evolutionary feedbacks for community stability. By using an eco-evolutionary framework to study coevolution in species-rich networks, we found support for the notion that fluctuating selection would lead to long-term community stability (the fluctuating selection hypothesis of community stability [30]). However, network structure also constrains adaptive change in interaction strengths, therefore affecting community dynamics. Different approaches pointed out that modularity increases antagonistic network stability, whereas connectance and nestedness reduce it [41,53,79]. Our results corroborate this pattern and indicate that modularity can enhance the fluctuating selection mechanism by driving modules to a coevolutionary stable unit when interaction selection is stronger than environmental selection. Eco-evolutionary feedbacks also generate a trade-off between the number of interacting partners and abundance, which is not expected if the strength of interaction between exploiter and victim is determined uniquely by species abundances. In this way, the study of eco-evolutionary feedbacks unifies ecological and evolutionary processes, and may provide a mechanistic understanding of how communities respond to disturbances and fragmentation, how diseases evolve and reshape communities, how introduced species spread across landscapes, and how links among species change even amid normal environmental fluctuations [30,90,91]. In our model, the eco-evolutionary feedbacks occur through direct effects only (i.e. species trait changes do not alter the environment). Given that many eco-evolutionary interactions probably occur through indirect effects, future approaches should investigate how linking changes in traits to changes in environmental selection affect community stability.

Data accessibility

This article has no additional data.

Authors' contributions

C.S.d.A., P.R.G. and C.J.M. designed research. C.S.d.A. performed research and analysed data. C.S.d.A., P.R.G. and C.J.M. wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

Financial support was provided by CNPq (Ciência sem fronteiras) to C.S.d.A. and FAPESP 2017/08406-7 to C.S.d.A. and P.R.G. C.J.M. and (partially) C.S.d.A. were supported by the Swiss National Science Foundation (SNSF-project 31003A-144162).