A Nonquiescent “Idling” Population State in Drug-Treated, BRAF-Mutated Melanoma

Abstract

Targeted therapy is an effective standard of care in BRAF-mutated malignant melanoma. However, the duration of tumor remission varies unpredictably among patients, and relapse is almost inevitable. Here, we examine the responses of several BRAF-mutated melanoma cell lines (including isogenic subclones) to BRAF inhibitors. We observe complex response dynamics across cell lines, with short-term responses (<100 h) varying from cell line to cell line. In the long term, however, we observe equilibration of all drug-treated populations into a nonquiescent state characterized by a balanced rate of death and division, which we term the “idling” state, and to our knowledge, this state has not been previously reported. Using mathematical modeling, we propose that the observed population-level dynamics are the result of cells transitioning between basins of attraction within a drug-modified phenotypic landscape. Each basin is associated with a drug-induced proliferation rate, a recently introduced metric of an antiproliferative drug effect. The idling population state represents a new dynamic equilibrium in which cells are distributed across the landscape such that the population achieves zero net growth. By fitting our model to experimental drug-response data, we infer the phenotypic landscapes of all considered melanoma cell lines and provide a unifying view of how BRAF-mutated melanomas respond to BRAF inhibition. We hypothesize that the residual disease observed in patients after targeted therapy is composed of a significant number of idling cells. Thus, defining molecular determinants of the phenotypic landscape that idling populations occupy may lead to “targeted landscaping” therapies based on rational modification of the landscape to favor basins with greater drug susceptibility.

Introduction

Targeted small-molecule inhibitors of BRAF (1) show remarkable short-term efficacy in melanoma patients with tumors harboring BRAF^V600 mutations (2, 3). However, clinical responses are variable: tumor recurrence is nearly universal within a few months of therapy initiation (3, 4), although a number of patients have prolonged periods of disease control over many months or years before actual progression. Analyses of postresistant tumors or cells provide most of our current knowledge of tumor recurrence in melanoma (5), usually attributed to rare, resistance-conferring genetic alterations that either preexist (6, 7, 8) or develop during therapy (9, 10). However, accumulating evidence suggests nongenetic processes play a significant role in the response of cancer cells to drugs (11, 12, 13, 14). For example, there is preclinical and clinical evidence that cancer cells can become resensitized to therapy after a brief “drug holiday” (15, 16, 17, 18). It has also been suggested that cancer cells employ a dynamic survival strategy governed by epigenetic alterations to survive lethal drug exposure (19, 20), similar to strategies seen in bacterial cell populations (21, 22).

Recently, the idea that networks of genes can give rise to multiple metastable cellular phenotypes has received considerable interest (23, 24, 25, 26, 27). The idea dates back to Waddington (28), who posited that cellular differentiation can be conceptualized as a dynamical trajectory through an “epigenetic landscape.” Borrowing concepts from physical chemistry (29), researchers have defined the epigenetic landscape mathematically in terms of a quasi-potential-energy surface (30). Local minima, or basins of attraction, within this surface represent cell types, and the relative stability of cell types depends on the depths of the basins. Cells can transition between basins, with rates dependent on the heights of local maxima, or energy barriers, separating basins. Within this framework, a cellular differentiation hierarchy is a special type of epigenetic landscape where transitions down a series of basins are more probable than up, although reverse transitions, or dedifferentiation, are theoretically possible, as has been confirmed experimentally (31). The concept of the epigenetic landscape has recently been extended to understanding cancer cells’ fates (23, 24, 32). In contrast to normal cellular development, a clear hierarchy of cell types is not generally believed to exist for many cancers (7, 33). Rather, multiple metastable phenotypes of comparable stability can coexist, and a population of cancer cells—driven by both intrinsic (e.g., gene expression) (11) and extrinsic (13) stochastic forces—will tend to spread out across these available phenotypes (34, 35). This phenotypic “drift” is postulated to be the source of nongenetic heterogeneity in cancer, which is known to influence therapeutic response (25, 36).

Here, we experimentally quantify drug-induced proliferation dynamics in BRAF-mutated melanoma cell lines at the population level. We show that in all cases examined, treatment with BRAF inhibitors induces entry of the cell population into a previously unrecognized nonquiescent state of balanced death and division, which we refer to as an “idling” population state. To understand the nature of an idling population, we build a simple three-state model of drug-response dynamics in terms of our recently proposed drug-induced proliferation (DIP) rate metric (37, 38). The model posits that the addition of a drug alters the epigenetic landscape melanoma cells inhabit. As a result, the cell population begins to re-equilibrate within the new drug-modified landscape. The complex population dynamics observed immediately after drug addition reflect the re-equilibration process, whereas idling represents the final equilibrated state of the population. In this state, cells are distributed across the landscape such that the population exhibits zero net growth. By calibrating the model to time-lapse imaging data, we infer the topography of the drug-modified landscapes for multiple BRAF-mutated melanoma cell lines. We show that the differential, short-term dynamics between cell lines can be explained in terms of slight topographical variations in the drug-induced epigenetic landscapes, which we attribute to slight differences in genetic backgrounds. Our analysis thus provides a simple theoretical explanation for the wide range of responses observed for BRAF inhibition of different BRAF-mutated melanomas. We discuss the potential clinical relevance of idling populations of cancer cells as well as the possibility for novel therapies based on rational modification of the epigenetic landscape (“targeted landscaping”).

Materials and Methods

Reagents

PLX4720 (Cat No. S1152) and vemurafenib (Cat No. S1267) were obtained from Selleckchem (Houston, TX). Dabrafenib (Cat No. HY-14660) was obtained from MedChem Express (Monmouth Junction, NJ) and solubilized in dimethyl sulfoxide (DMSO) at a stock concentration of 10 mM. BKM120 (Cat No. S2247, buparlisib) was obtained from Selleckchem and solubilized in DMSO at a stock concentration of 10 mM. Trametinib (Cat No. T-8123) and BEZ235 (Cat No. N-4288) were obtained from LC Laboratories (Woburn, MA) and solubilized in DMSO at stock concentrations of 1 mM. Cisplatin (Cat No. 479306, cis-Diamineplatinum(II) dichlorine) was obtained from Sigma-Aldrich (St. Louis, MO) and solubilized in phosphate-buffered saline at a stock concentration of 12.5 mM. All drugs were aliquoted and stored at −20°C until use except for cisplatin, which was stored at −80°C. Phospho-MEK1/2 antibody (Cat No.9121) was obtained from Cell Signaling Technology (Danvers, MA).

Cell culture

BRAF-mutated melanoma cells (SKMEL5, A375, WM793, SKMEL19, SKMEL28, WM164, WM88, and A2058) were grown and cultured in Dulbecco’s modified Eagle’s medium and Ham’s F-12 medium (DMEM:F12, 1:1, Cat No. 11330-032). Media were obtained from Gibco (Grand Island, NY) and supplemented with 10% fetal bovine serum. All cells were cultured in humidified incubators that were CO₂ and temperature controlled (37°C). Cells were tested for mycoplasma before use and were confirmed negative. Cells were passaged 1–2 times per week and were maintained as exponentially growing cultures for a maximum of less than 20 passages. Unless otherwise indicated, cells were seeded ∼16–24 h before treatment to allow cells to adhere to culture plates. Reagents and/or drugs were prepared in complete medium immediately before adding to cells by replacement.

Fluorescent imaging

To facilitate automated image processing, cells were engineered to express the fluorescent fusion proteins histone 2B monomeric red fluorescent protein (H2BmRFP (monomeric red fluorescent protein); Addgene plasmid No. 18982) and geminin1–110 monomeric Azami-Green (39) using replication-incompetent recombinant lentiviral particles, as previously described (40, 41). Cells were seeded at 1000–5000 cells per well in 96-well culture imaging plates (product No. 353219; BD Biosciences, San Jose, CA). DMSO and phosphate-buffered saline were used as vehicle controls, as appropriate. Images were acquired through a 10× or 20× objective with a Cellavista HighEnd Bioimager (SynenTec Bio Services, Münster, Germany) every 6–12 h as 3 × 3 or 5 × 5 montages for approximately 2 weeks. Media containing matching concentrations of a drug or vehicle in each well were replaced every 3 days. Image processing to obtain counts of cell nuclei at each time point was performed as previously described (38, 40). SKMEL5 (including all clonal derivatives), A375, WM88, SKMEL19, and A2058 were all treated with 8 μM BRAF inhibitor (BRAFi; PLX4720 unless otherwise stated); SKMEL28 was treated with 16 μM BRAFi; WM164 and WM793 were treated with 32 μM BRAFi. Drug-naïve and post-idling (pretreated with 8 μΜ BRAFi for 2 weeks followed by a brief 24 h drug holiday) cell populations of the SKMEL5 subclones SC01, SC07, and SC10 were treated with 1 μΜ trametinib, 5 μΜ cisplatin, 1 μΜ BKM120, and 2 μΜ BEZ-235 for 100 h. In all cases, population growth curves were plotted as the ratio of cell counts to the initial cell counts (at the time of drug addition) in log₂ scale (i.e., population doublings).

Clonal Fractional Proliferation assay

Clonal Fractional Proliferation (cFP) was done as previously described (37). Briefly, subconfluent cells were seeded at low density (∼10–20 cells per well) in 96-well culture imaging plates. Plates were kept in humidified and CO₂-controlled incubators for approximately 1 week, with medium replacement every 3 days to allow single cells to expand into colonies of ∼50 cells. The medium was then replaced with a drug- or vehicle-containing medium, and cells were imaged every ∼8–12 h until the end of the experiment, with drug replacement every 3 days. Images were processed as previously described (37). Raw images were sequentially organized into spatially registered montages and temporally assembled into image stacks. Cell counts per colony were obtained using the freely available ImageJ software (https://imagej.nih.gov/ij/) with a custom-written macro, as described previously (37). The colony drug response was quantified in terms of DIP rate, obtained as the slope of a linear fit to the log₂-scaled growth curve (37, 38).

Single-cell-derived subclones

Sixteen SKMEL5 subclones were derived from single cells by serial dilution. Briefly, cells were serially diluted to less than one cell per well in 96-well imaging plates and imaged to identify wells containing a single cell. Cells were expanded in complete growth medium (in the absence of BRAFi) and sequentially transferred to 48-, 24-, and 6-well plates until sufficient numbers of cells were available for cryopreservation. All subclones were tested for their sensitivity to BRAFi before cryopreservation.

Time-lapse single-cell tracking

Fluorescence images of cellular nuclei were obtained as previously described (41). Briefly, images were acquired using a BD Pathway 855 in (spinning disk) confocal mode with a 20× (0.75 NA) objective in a CO₂- and temperature-controlled environment every 20 min for 260 h from the time of the first drug addition. The medium was replaced with a freshly prepared drug every 3 days. Images from each well were organized into stacks of a time series. Fluorescent nuclei were manually tracked across sequential images to obtain cell life spans and resultant cell fates (death or division), as previously described (40). “Birth time” denotes the time at which a mitotic event occurred, resulting in two sister cells. “Lifetime” denotes the duration of single-cell viability until the cell either died or underwent another mitosis. End of the experiment (EOE) represents the cells that were born in a drug but did not exhibit any cell fate during the remaining observation time. Data are displayed as two-dimensional plots of birth time versus lifetime, with death, division, and EOE signified with different markers.

Mathematical modeling and parameter calibration

We consider three cell subpopulations, defined in terms of their net proliferation rates: R (regressing), S (stationary), and E (expanding). Cells within each subpopulation can divide, die, or transition into “adjacent” subpopulations. The ordinary differential equations describing the temporal dynamics of the system are

$$\frac{d{N}_R}{dt}=\left(k_{pR}-k_{rs}\right)N_R+k_{sr}{N}_S,$$ (1)

$$\frac{d{N}_S}{dt}=\left(k_{pS}-k_{sr}-k_{se}\right)N_S+k_{rs}{N}_R+k_{es}{N}_E,\text{and}$$ (2)

$$\frac{d{N}_E}{dt}=\left(k_{pE}-k_{es}\right)N_E+k_{se}{N}_S,$$ (3)

where N_R, N_S, and N_E are the numbers of cells in subpopulations R, S, and E, respectively; k_pR, k_pS, and k_pE are the DIP (net proliferation) rates of subpopulations R, S, and E, respectively; k_rs and k_sr are the forward and reverse transition rate constants between subpopulations R and S, respectively; and k_se and k_es are the forward and reverse transition rate constants between subpopulations S and E, respectively. DIP rates were set to $k_{pR}=-0.055h^{-1}$, $k_{pS}=0h^{-1}$, and $k_{pE}=0.015h^{-1}$, and a total initial cell population of 10,000 was assumed (see Supporting Material). The remaining six parameters (k_rs, k_sr, k_se, k_es, and the initial cell proportions R₀ and S₀ (≥0 and ≤1)) were calibrated to experimental data (see below). The model was encoded in R (https://www.r-project.org/), and ordinary differential equation simulations were performed using the “ode” function of the R package “deSolve” (42).

Parameter calibration was performed using Markov chain Monte Carlo (MCMC) sampling (43, 44) (1.5 × 10⁵ iterations) using the “modMCMC” function of the R package “FME” (45). Goodness of fit was quantified using the cost function

$$Cost=\sum _{i=1}^n\frac{{\left(M_i-O_i\right)}^2}{{\sigma }_i},$$ (4)

where n is the number of measured time points and M_i, O_i, and σ_i are the model prediction, experimentally observed value, and standard experimental error (automatically determined by “modMCMC”) at the time point i, respectively. For the SKMEL5 cell line, the model was calibrated against an experimental time course for a 1:1:1 clonal mixture of three single-cell-derived subclones (SC01, SC07, and SC10). Predictions for the dynamics of the SKMEL5 parental line and subclones were then made by selecting 1000 random parameter sets from the last 50% of iterations (accounting for burn-in) in the MCMC-generated parameter ensemble. Specifically, for each of the 1000 parameter sets, we recalibrated the model using MCMC, keeping the transition rate constants (k_rs, k_sr, k_se, k_es) fixed at the values for that particular iteration and allowing the initial cell proportions (R₀ and S₀) to vary as free variables. For other BRAF-mutated melanoma cell lines (WM88, WM164, SKMEL28, SKMEL19, A375, and WM793), model calibration was performed against experimental time courses for the parental lines. In all cases, we plotted simulated time courses as one-standard-deviation envelopes around the mean from 1000 random samples of the MCMC-generated parameter ensemble. Additional details of the model and the MCMC calibration procedure, including MCMC-generated parameter distributions, are provided in the Supporting Material.

Inferring quasi-potential-energy landscapes

We assumed the probability that a cell transitions from subpopulation X to Y follows Arrhenius’ equation (46, 47). Within this view, each subpopulation constitutes a basin of attraction within a quasi-potential-energy landscape, and transitions between subpopulations require traversal of an energy barrier separating adjacent basins. The height of this barrier, ΔU_xy, is proportional to the negative logarithm of the transition rate constant: i.e.,

$$\Delta U_{xy}\sim -ln{k}_{xy}.$$ (5)

Intuitively, the higher the barrier, the less probable the transition. For each cell line considered, we randomly selected 2000 parameter sets from the MCMC-generated parameter ensemble (see above) and estimated barrier heights between basins for each set using Eq. 5. A pictorial representation of the inferred quasi-potential-energy landscape was then generated as a one-standard-deviation envelope around the mean barrier heights from the 2000 sampled parameter sets.

Results

BRAF-mutated melanoma cell populations exhibit balanced death and division upon long-term exposure to BRAF inhibition

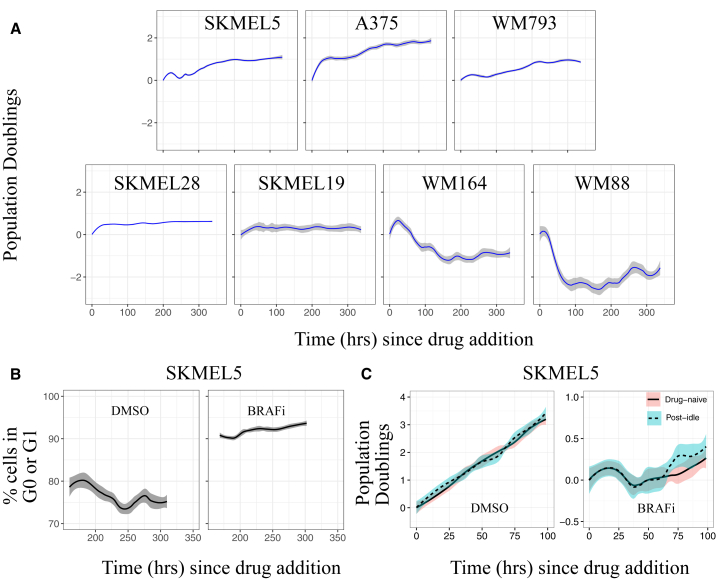
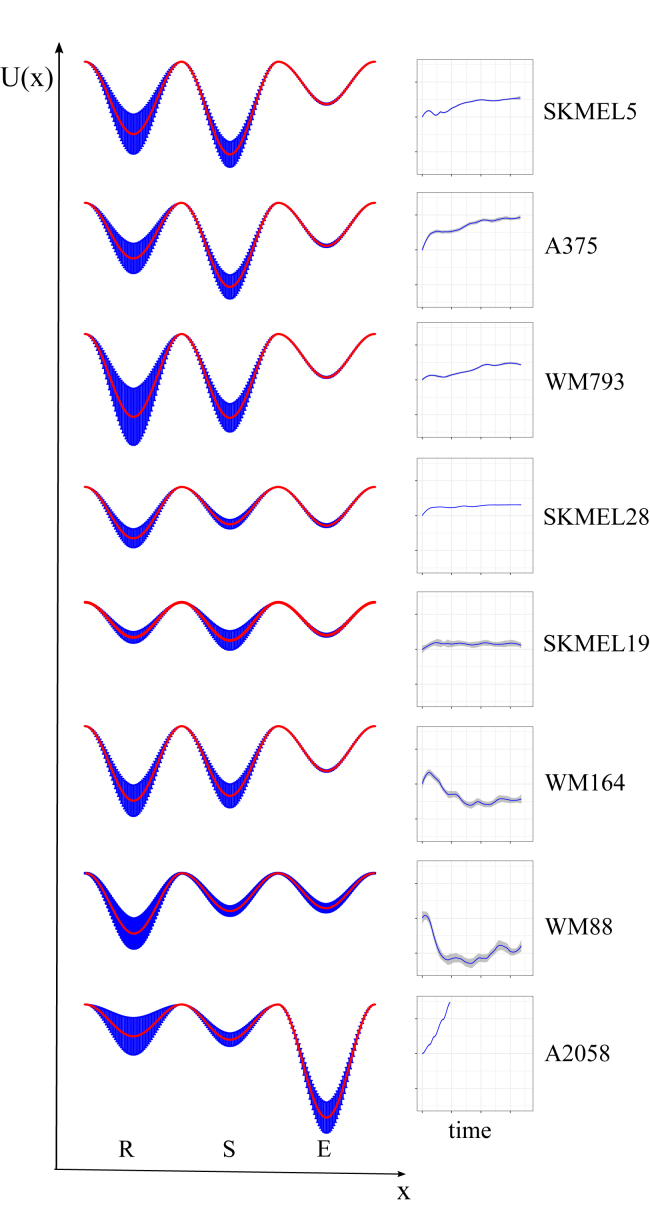
To investigate the effects of BRAF inhibition on BRAF-mutated melanoma, we subjected populations of seven BRAF-mutated human melanoma cell lines to the small-molecule BRAFi PLX4720 for a period of approximately 2 weeks (∼350 h; Figs. 1 A and S1 A). The proliferation dynamics immediately after drug addition (<100 h) varied between cell lines, with some populations continuing to slowly expand and others experiencing significant cell death (Fig. 1 A). Over longer time periods, however, all cell populations settled into a state of zero net growth (Fig. 1 A). For the initially expanding cell populations, we confirmed that entry into the zero-net-growth state was not trivially due to confluency (Fig. S1 B). Moreover, we observed that ∼5–15% of cells continued to divide during this period, as indicated by an exogenous marker of the S, G2, and M cell cycle phases (39) (Figs. 1 B and S1 C). Cell death was also observed, as indicated by early nuclear morphological changes associated with apoptosis (48) (Fig. S1 D). Because cells continue to turn over (divide and die) during this period of drug exposure, but with balanced rates of division and death such that the cell population maintains a constant level, we refer to the state of this population as “idling.” Importantly, idling is not a state of individual cells but of the population as a whole. Other BRAFis (dabrafenib and vemurafenib) also caused idling, as did the combination of BRAFi and trametinib, an inhibitor of MEK (a downstream target of BRAF in the MAPK signaling cascade; Fig. S1 E). Interestingly, we also observed that idling populations resume normal exponential proliferation when switched to drug-free media and exhibit similar drug-response dynamics when rechallenged with BRAFi (Fig. 1 C). This reversibility suggests the idling population state is nongenetic in nature (24). Taken together, these results demonstrate that the idling population state is drug-induced, reversible, and a common response of BRAF-mutated melanoma cell populations to prolonged MAPK pathway inhibition.

Figure 1.

BRAF-mutated melanoma cell populations idle under continued BRAF inhibition. (A) Shown are population growth curves (log₂ normalized; 3+ technical replicates) for seven BRAF-mutated melanoma cell lines treated with saturating concentrations of BRAFi. (B) The percentage of cells in G0 or G1 phase of cell cycle during 168–350 h of DMSO control and BRAFi treatment for two BRAF-mutated melanoma cell lines is shown. (C) Idling cell populations (1 week of BRAFi treatment) return to normal predrug function after a 24 h drug holiday: (left) drug-naïve and post-idling cells expand at equal rates in complete-growth media; (right) drug-naïve and post-idling cells respond almost identically to the BRAFi (mean responses are shown as solid or dashed lines, and 95% confidence intervals are shown as shaded regions). To see this figure in color, go online.

Short-term drug response reflects preexisting clonal heterogeneity

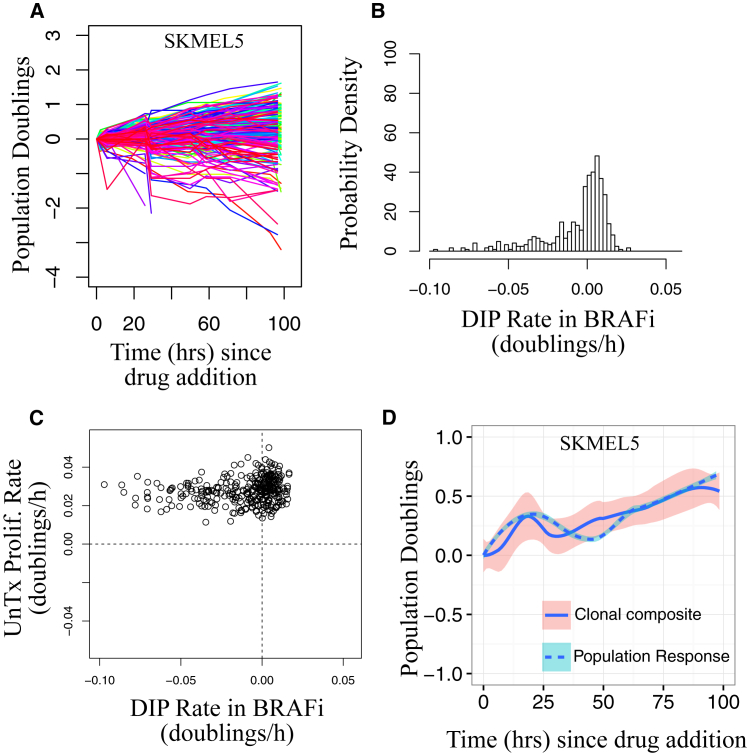
We investigated more closely the short-term drug response dynamics in the SKMEL5 cell line by tracking ∼200 single-cell-derived colonies, or “subclones” (∼110 cells per clone), treated with BRAFi using the cFP assay (see Materials and Methods) (37). Because of the reversibility of the idling phenotype (Fig. 1 C), we assumed that differences in response to a drug across these subclones originate from nongenetic processes—i.e., are not based on genetic alterations (this differs from a more conventional use of the term “clone,” e.g., (49)). Drug responses were quantified in terms of DIP rate (38) and varied from clone to clone, encompassing a broad range of behaviors, from expanding to regressing (Fig. 2, A and B). Similar results were obtained for other drug concentrations (Fig. S2 A) and other BRAF-mutated melanoma cell lines (Fig. S2 B). We observed that the proliferation rate of a clonal lineage before treatment did not correlate to its DIP rate in BRAFi (Fig. 2 C), indicating a nontrivial relationship between drug-free and DIP (i.e., “fast” proliferators in the absence of a drug are not necessarily fast proliferators in a drug, and vice versa). Furthermore, the aggregate of clonal responses qualitatively matches the short-term population-level response (Fig. 2 D). This suggests that the short-term dynamics are due to clonal competition (8) (i.e., clones with negative DIP rates die out, whereas clones with positive DIP rates expand and ultimately drive the population-level response). Thus, these results indicate that BRAF-mutated melanoma cell lines contain preexisting, hidden, nongenetic clonal heterogeneity that is revealed upon drug exposure, which drives the short-term drug response.

Figure 2.

Short-term drug response dynamics reveal preexisting clonal heterogeneity. (A) Population growth curves (log₂ normalized) for BRAFi-treated SKMEL5 single-cell-derived colonies (n = 203) obtained using the cFP assay are shown. (B) Shown is the distribution of clonal drug-induced proliferation (DIP) rates (doublings per hour) obtained by linear fits to the growth curves. (C) Colony DIP rates do not correlate with untreated proliferation rates. (D) The clonal composite (sum of cell counts from all colonies at each time point) closely corresponds to the short-term population-level response (same data as in Fig. 1A; means are shown as solid or dashed lines, and 95% confidence intervals are shown as shaded regions). Prolif., proliferation; UnTx, untreated. To see this figure in color, go online.

Idling occurs for populations of single-cell-derived subclones with varying short-term drug sensitivities

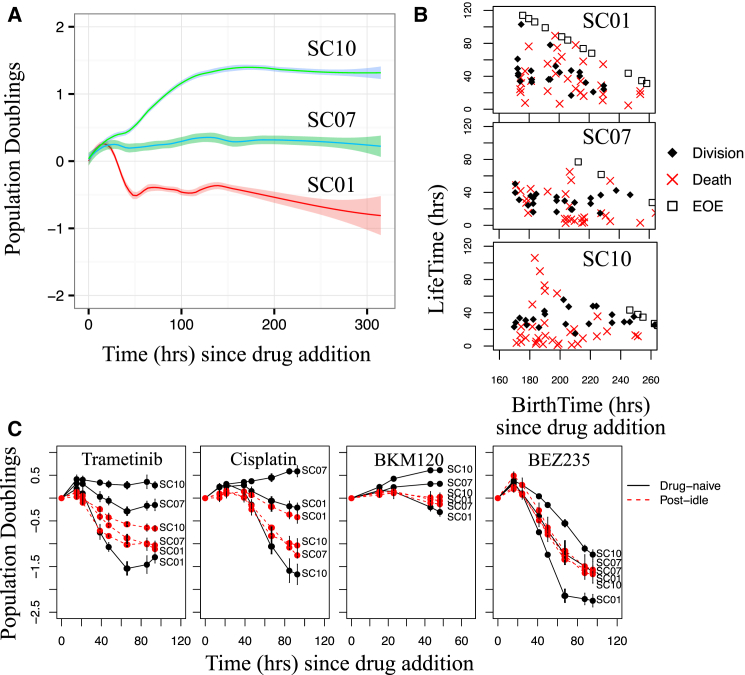
To reconcile the long-term population-level idling response (Fig. 1) with the observed clonal heterogeneity (Fig. 2), we sought to determine whether each clonal lineage enters an idling population state independently or if the phenomenon is limited to select clones. To distinguish between these possibilities, we isolated 16 single-cell-derived subclones from the SKMEL5 cell line (Fig. S3 A; Materials and Methods). As in the cFP assay (Fig. 2 A), upon exposure to BRAFi the short-term dynamics (<100 h) varied significantly across the subclones, with some expanding, some regressing, and some maintaining a stationary population size (Fig. S3 B; Table S1). We selected three subclones representative of the range of observed short-term responses for further experimentation: SC01 (regressing), SC07 (stationary), and SC10 (expanding). Upon prolonged exposure to BRAFi, despite their initial divergent responses, both SC01 and SC10 converged to near-zero DIP rates, whereas SC07 maintained its initial zero-net-growth response (Fig. 3 A). Similar results were obtained for three other SKMEL5 subclones (Fig. S3 C). As before, we confirmed that entry into the idling population state is not due to confluence (Fig. S3 D). Furthermore, by manually tracking the fates of multiple individual cells over time, we determined that all three subclone populations exhibit death and division while in the idling state (Fig. 3 B). Thus, although we cannot exclude the possibility that some cells might be quiescent, these results confirm that balanced rates of death and division are largely responsible for idling cell populations. This suggests, therefore, that the idling population state is a characteristic feature of BRAF-mutated melanoma, which is achieved by all subclonal populations in the continued presence of BRAF inhibition regardless of their initial responses.

Figure 3.

Single-cell-derived subclone populations idle independent of short-term drug sensitivity. (A) Shown are population growth curves (log₂ normalized) for three single-cell-derived SKMEL5 subclones treated with a BRAFi (3+ technical replicates; means are shown as solid lines, and 95% confidence intervals are shown as shaded regions). (B) Shown are single-cell life spans versus birth times (time of first mitotic event) for the three subclones after a week in a BRAFi (cells born during the experiment but that reached the end of the experiment (EOE) without a second mitotic event are plotted along the diagonal). (C) Shown are population growth curves (log₂ normalized) for drug-naïve and post-idling (1 week of BRAFi treatment; the BRAFi was removed overnight (16–24 h) before subsequent drug addition) single-cell-derived SKMEL5 subclones treated with saturating concentrations of trametinib, cisplatin, BKM120, and BEZ235 (error bars represent one standard deviation). To see this figure in color, go online.

BRAFi-induced idling cell populations are not multidrug resistant

Multidrug resistance is the ability of cancer cells to withstand the effects of anticancer drugs and compounds that are structurally and/or functionally unrelated (50, 51, 52). Recently, it was reported that when exposed to sublethal drug concentrations for multiple weeks, melanoma cells display multidrug resistance (53). To determine whether our BRAFi-induced idling populations were multidrug resistant, we rechallenged idling populations (“post-idling”) of three SKMEL5 subclones (SC01, SC07, and SC10) with trametinib (a MEK inhibitor), cisplatin (a platinum-based chemotherapeutic), BKM120 (a PI3K inhibitor), and BEZ235 (a PI3K/mTOR dual inhibitor; see Materials and Methods) and compared their responses to those of BRAFi-naïve populations of the same subclones. In all cases, the post-idling populations exhibited significantly altered sensitivities relative to the drug-naïve populations (Fig. 3 C). In particular, the least sensitive drug-naïve subclones (SC10 for trametinib, BKM120, and BEZ235; SC07 for cisplatin) were significantly more drug sensitive after prolonged BRAF inhibition. Furthermore, the responses of the post-idling populations were more uniform across subclones (almost identical in BKM120 and BEZ235) than in the drug-naïve case (Fig. 3 C, red curves), suggesting that all three subclones enter the same idling population state under continued BRAFi exposure. Moreover, the least sensitive subclone to three of the drugs (SC10 to trametinib, BKM120, and BEZ234) was the most sensitive to cisplatin, eliminating the possibility that this subclone is intrinsically multidrug resistant. Taken together, these results demonstrate that the short-term drug-response dynamics of single-cell-derived clonal melanoma populations are drug- and subclone-specific for drug-naïve populations and largely independent of initial clonal identity after entry into idling.

Mathematical modeling qualitatively reproduces complex, population-level drug-response dynamics

Our experimental observations can be summarized as follows: 1) BRAF-mutated melanoma cell populations are nongenetically clonally heterogeneous, with initial clonal responses to BRAF inhibition varying over a wide range, from expanding to regressing (Fig. 2, A and B); 2) the short-term population-level response is a composite of clonal responses (Fig. 2 D); 3) all cell line and subclonal populations eventually exhibit a state of balanced death and division, termed idling, in the continued presence of BRAFi (Figs. 1 A and 3 A); 4) the idling population state is reversible, with cell populations resuming normal exponential growth upon drug removal and responding like drug-naïve populations when rechallenged (Fig. 1 C); and 5) idling populations are not multidrug resistant and exhibit near-uniform sensitivities to secondary drug treatment, regardless of any initial drug-free response (Fig. 3 C).

To mathematically formalize these observations, we constructed a simple kinetic model of cell proliferation that qualitatively captures the treatment responses of all BRAF-mutated melanoma cell lines considered here. Briefly, we defined three cell subpopulations: regressing (R), stationary (S), and expanding (E), with negative, zero, and positive DIP rates, respectively (Fig. 4 A). A negative DIP rate results from the rate of cell death exceeding the rate of cell division, a zero DIP rate is due to balanced rates of cell death and division, and a positive DIP rate is due to the rate of cell division exceeding death. We assume that cells in each subpopulation can (reversibly) transition into “adjacent” subpopulations, thus changing the proportion of cells in each subpopulation over time (see Materials and Methods and Supporting Material for further details). A similar formalism has been proposed to study cancer cell population dynamics (54). With cells distributed across the three subpopulations, we expect a period of short-term, nonlinear dynamics driven by differences in rates of death and division of each subpopulation (i.e., clonal competition), followed by phenotypic transitions of cells between subpopulations, resulting in the population achieving idling. Intuitively, the nature of the short-term dynamics and the timescale for transition into idling will depend upon the initial proportions of cells in each subpopulation and the values of the transition rate constants (Table S2).

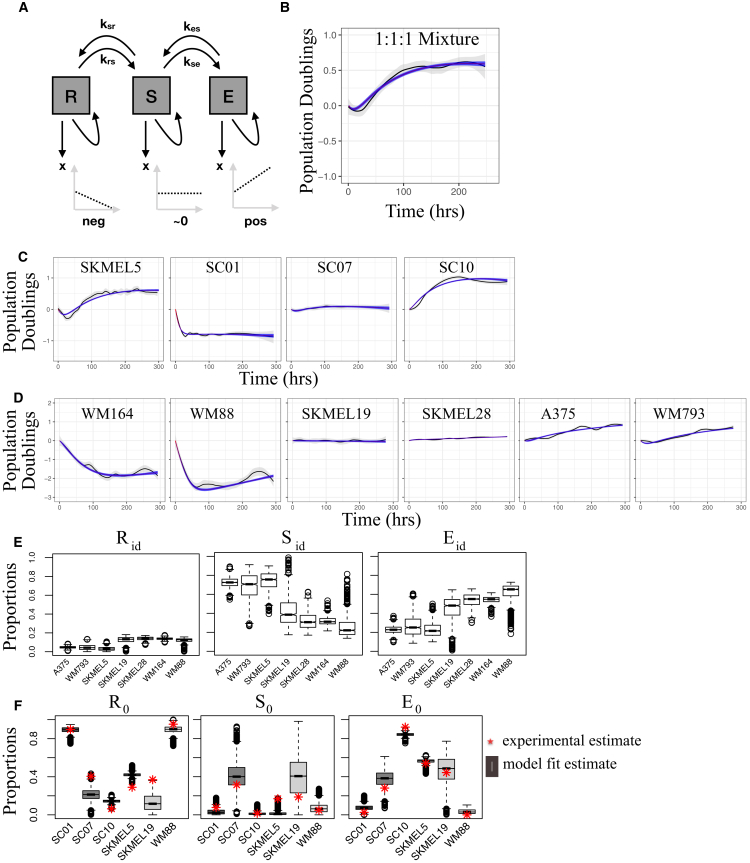
Figure 4.

A three-state kinetic model qualitatively captures complex drug-response dynamics for numerous BRAF-mutated melanoma cell lines and subclones. (A) Shown is a graphical representation of the three-state model (arrows represent cell fates—i.e., death, division, and state transitions; growth dynamics for each subpopulation are illustrated in the lower plots). (B) Shown is a BRAFi-induced response of a 1:1:1 clonal mixture of SKMEL5 subclones SC01, SC07, and SC10 used for model fitting (fit shown as a dark blue shaded region). (C) Shown are the model fits to the BRAFi-induced responses of the SKMEL5 SC01, SC07, and SC10 subclones (Fig. 3A) and the parental line (Fig. 1A) using the rate constants inferred from the fit to the 1:1:1 clonal mixture. (D) Shown are the model fits to the BRAFi-induced responses of six additional BRAF-mutated melanoma cell lines (Fig. 1A). (E) Shown are model-predicted proportions of cells in the regressing (R_id), stationary (S_id), and expanding (E_id) subpopulations in the idling state. (F) Shown is a comparison of model-predicted and experimentally derived proportions of cells in the regressing (R₀), stationary (S₀), and expanding (E₀) subpopulations at the time of drug addition (experimental estimates, based on cFP, are shown as red stars). In (B), (C), and (D), the initial time (0 h) corresponds to 24 h after drug addition, a period of drug-action delay not considered in the model. For the box plots in (E) and (F) the solid line is the median, the box spans the first and third quartiles, the whiskers extend to 1.5× the interquartile range, and outliers are shown as black circles. neg, negative; pos, positive. To see this figure in color, go online.

For the SKMEL5 cell line, we estimated model parameters by fitting the mathematical model to experimental data for a 1:1:1 clonal mixture of the SC01, SC07, and SC10 subclones (Fig. 4 B) using MCMC sampling (see Materials and Methods). We then used the estimated transition rate constants (Fig. S4 A) to predict drug-response dynamics for individual SKMEL5 subclones as well as the parental line (allowing the initial cell proportions to vary). In each case, the model predictions matched closely with the experimental time courses, capturing both the short-term dynamics and the transition into the idling population state (Fig. 4 C). Importantly, the model cannot explain the observed dynamics if the transition rate constants are set to zero (Fig. S4 B), demonstrating that the nonlinear growth curves cannot simply be explained by clonal selection. We also fitted the model to experimental time courses for six additional melanoma cell lines (Fig. 4 D). In all cases, the model predicted that the idling state is composed of very few cells in the R subpopulation but significant proportions of cells in both the S and E subpopulations, ranging between ∼20 and 80% (Figs. 4 E and S4 C). This is a significant result because it demonstrates that the idling state is not characteristic of an individual cell but is rather an emergent state of the population as a whole.

To further validate the model, we compared the predicted initial cell proportions (R₀, S₀, and E₀ = 1−R₀−S₀) for the SKMEL5 parental line, subclones, and two additional BRAF-mutated melanoma cell lines to results of cFP assays (Fig. S4 D; see Materials and Methods). The cFP assay quantifies the short-term drug response and, therefore, reflects the initial distribution of state occupancy across subpopulations before drug exposure. In each case, the predicted proportions qualitatively matched the experimental results (Fig. 4 F). In summary, our model, incorporating both clonal competition and phenotypic state transitions, captured the key features of the drug-response dynamics of several BRAF-mutated melanoma cell populations, which differ significantly in the shape and duration of their short-term response but eventually converge into an idling population state.

Drug-response dynamics as a re-equilibration over a drug-modified quasi-potential-energy landscape

Using the values of the transition rate constants from the MCMC-generated parameter ensembles (Figs. S5 and S6), we inferred BRAFi-induced quasi-potential-energy landscapes for all BRAF-mutated melanoma cell lines considered (Fig. 5; see Materials and Methods). Within a quasi-potential-energy landscape, each subpopulation is associated with a basin of attraction, and transitions between subpopulations amount to traversals of energy barriers separating basins (54). Our results showed that the basin associated with the expanding subpopulation (E) was consistently the shallowest across cell lines (i.e., had the smallest exit barrier (k_es; Fig. S5 A)). This makes intuitive sense, since for the cell population to reach the idling state (zero net growth), cells must rapidly evacuate the basin for the E state, otherwise the cell population would continue expanding. However, at equilibrium, a proportion of cells remained in this basin (Figs. 4 E and S4 C), providing a source to counterbalance the cell depletion occurring in the regressing subpopulation. The depths of the basins associated with the regressing (k_rs) and stationary (k_sr, k_se) subpopulations were more variable than the basin for the expanding state (across the MCMC-generated parameter ensemble), but they generally showed the basin for the S state to be deeper than the basin for the R state (Fig. S5 A). Notable exceptions were the WM164 and WM88 cell lines, which exhibited significant short-term cell loss. Again, this makes intuitive sense because for this to occur, the exit barrier from the basins for the R to the S state has to be large enough to reduce the flux into the basin for the S state after drug exposure.

Figure 5.

Inferred drug-modified epigenetic landscapes provide insight into the drug-response dynamics. Landscapes are shown for eight BRAF-mutated melanoma cell lines (seven from Fig. 1A, plus the largely BRAFi-insensitive A2058 cell line) and were inferred from model fits to the drug-response dynamics (shown to the right). U(x) is the quasi-potential-energy, and x is the “reaction coordinate.” Landscapes are based on 2000 random samples of the MCMC-generated parameter ensemble. Mean basin depths and barrier heights are shown as red lines; the blue shaded regions correspond to one standard deviation around the mean. E, expanding; R, regressing; S, stationary. To see this figure in color, go online.

For comparison, we also inferred the BRAFi-induced epigenetic landscape for the A2058 cell line, which is known to be largely, but not entirely, insensitive to BRAF inhibition (Fig. S7) (55). Unsurprisingly, in this case the basin for the E state was significantly deeper than the other basins, and simulations showed that the system cannot achieve a long-term dynamic equilibrium. Hence, we did not observe idling in this cell line within the time frame of our experiment and do not expect it to ever idle regardless of duration of drug exposure. Overall, the inferred epigenetic landscapes are powerful theoretical tools for understanding the basis of the complex population-level dynamics observed in BRAF-mutated melanoma cell populations and for reconciling differences in drug response seen across cell lines in terms of variations in an epigenetic landscape’s topography.

Discussion

We report here that sustained BRAF inhibition (>100 h in vitro) induces entry of BRAF-mutated melanoma cell populations into a nonquiescent idling state of balanced death and division, characterized by a near-zero proliferation rate. Idling occurs in both parental and clonal populations, independent of differences in initial short-term responses, and is both drug induced and reversible, consistent with nongenetic drug tolerance described in earlier reports (14, 56, 57). Cells in the idling population state are also not multidrug resistant and respond to secondary drug treatments (nearly) uniformly, independent of initial variation. Although a balanced state of cell proliferation and apoptosis has been described as tumor dormancy (58), the idling population state is distinct because it occurs in the context of drug response. Idling was not previously described, possibly because drug-response assays tend to be performed over short observation times (72−96 h), and proliferation rates are not usually measured (37, 38, 40, 59), as we do in this work. Taken together, our findings are not easily explained within the existing paradigms of drug resistance or tolerance (7, 19, 33, 53, 60, 61, 62). In particular, cell populations that initially expand but then transition into the idling state (SKMEL5 and A375 in Fig. 1 A; SC10 in Fig. 3 A) can neither be the result of selection of rare, preexisting resistant clones nor of the acquisition of resistance-conferring genetic mutations. Furthermore, idling populations are not due to confluence (Figs. S1 B and S3 D) or quiescence alone (Figs. 1 B, 3 B, and S1 C). This begs the question as to why an apparently thriving cell population would cease expanding and enter a less proliferative state of balanced death and division.

To garner insights into these complex dynamics, we propose a kinetic model (Fig. 4 A) in which a cell population is composed of multiple discrete, interconverting subpopulations, each of which is characterized by a DIP rate (38) quantifying its net proliferation in a drug. The model is most easily understood within the framework of epigenetic landscapes, where cell subpopulations are associated with basins of attraction and phenotypic state transitions with traversals of quasi-potential-energy barriers. An implicit assumption of the model is that an epigenetic landscape exists in the absence of drug, defined by the genetic background of the cell (24). Over time, cells within an isogenic population (e.g., a cell line) stochastically diffuse across basins in this landscape. This drug-naïve “phenotypic drift” sets the initial cellular occupancies of each basin. Upon drug addition, the epigenetic landscape is modified in a drug- and dose-dependent manner. With the cFP assay (37), we have an experimental platform for quantifying initial cell occupancies in the drug-naïve landscape based on measured DIP rate distributions (Figs. 2 B and S4 D).

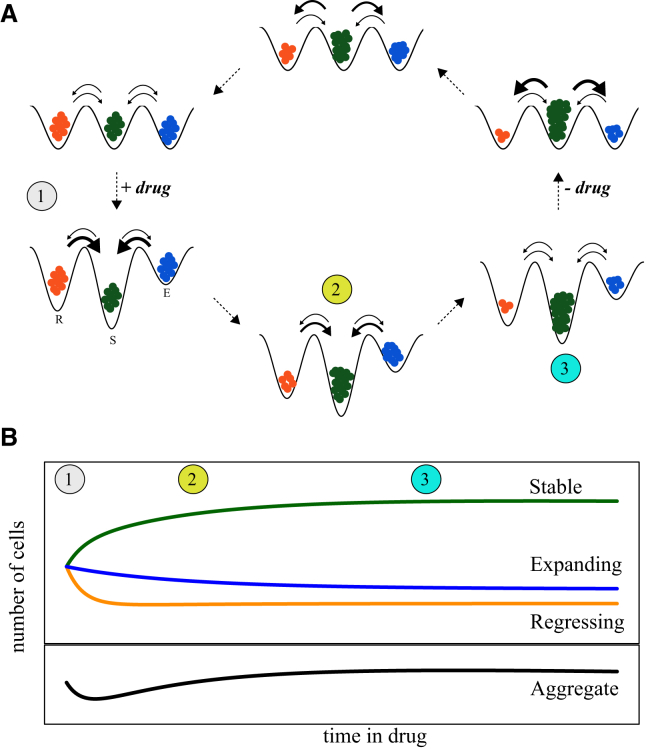
The central hypothesis of this work is that drug-treated cell populations re-equilibrate over this new drug-modified landscape; the short-term population-level drug response is a reflection of this re-equilibration process, and the idling state constitutes the final equilibrated state of the population (Fig. 6). This theoretical framework explains why populations of single-cell-derived subclones respond differently to a drug in the short term (different initial numbers of cells in each basin) but identically in the long term (exposure to the same landscape topography), as we report here (Fig. 3 A). Convergence to a common drug-induced equilibrium state also explains the near-uniform drug responses of post-idling populations to subsequent drug treatments (Fig. 3 C). The reversibility of the idling phenotype for parental cell populations (Fig. 1 C) is explained by a return to the drug-naïve epigenetic landscape upon drug removal and re-equilibration back to the original cell occupancies (Fig. 6). This is consistent with recent work showing that intermittent addition and withdrawal of vemurafenib leads to sequential periods of tumor shrinkage and growth, which forestalls development of drug resistance in BRAF-mutated melanoma cell populations (16). Differential dynamics across cell lines are explained in terms of variations in the topography of drug-modified landscapes (Fig. 5) that are set by the genetic backgrounds of the cell lines. An important consequence is that each cell line (with one exception, i.e., A2058) achieves idling in a slightly different way—with varying proportions of regressing, stationary, and expanding subpopulations (Fig. 4 F)—despite harboring a common BRAF-activating mutation (i.e., the driving addicting oncogene). Differences in the sizes of idling cell populations may explain the extreme diversity of durability, or lack thereof, in individual patients’ clinical responses (i.e., the probability of acquiring resistance mutations depends on the number of cells surviving treatment). For instance, tumors that show significant early regression (e.g., WM88, WM164; Fig. 1 A) would be expected to take longer, perhaps significantly longer, to acquire secondary mutations than those that either show no initial change or expand (e.g., SKMEL5, A375; Fig. 1 A).

Figure 6.

Drug-induced and drug-free population dynamics are explained as re-equilibrations over epigenetic landscapes. (A) Schematic representation of a drug-addition and drug-removal cycle for a cancer cell population: (top left) cells begin in complete growth medium and are in a dynamic equilibrium across basins of a drug-free epigenetic landscape; (top left to bottom left) exposure to a drug modifies the landscape, taking the system out of equilibrium; (bottom left to bottom right) the population re-equilibrates over the new drug-induced landscape by reducing cell proportions in the regressing (R) and expanding (E) basins and increasing the proportion in the stationary (S) basin; (bottom right) the idling state corresponds to the newly achieved dynamic equilibrium; (bottom right to top right) removal of the drug reestablishes the drug-free epigenetic landscape and, again, takes the system out of equilibrium; (top right to top left) the population re-equilibrates over the drug-free landscape, returning the system to the original dynamic equilibrium. Arrow thicknesses represent relative transition rates at each stage of the re-equilibration process. (B) Clonal (top) and parental (bottom) drug-response population dynamics illustrating the connection to the different stages of the drug-induced re-equilibration process. Numbers and colors (orange, regressing; green, stationary; blue, expanding) correspond to those in the schematic above. To see this figure in color, go online.

Cellular resistance to anticancer therapies is a complex, multifaceted problem (50). Genetic mutations obviously play a major role in the acquisition of irreversible drug resistance and ultimate treatment failure, but it is becoming increasingly clear that genetics is not the whole story (63). Indeed, several recent studies highlight the role of nongenetic, drug-induced phenotypic state transitions into a stem-cell-like state or induction of epithelial-mesenchymal transitions to evade an initial drug stress (64, 65). Consistent with these reports, we believe that the idling population presented here, and the relatively simple theoretical framework describing it, has potentially far-reaching implications for patient therapies. In particular, even in tumors with high therapeutic sensitivity, a minority of cells often survive and can persist for months or even years (63). This “residual disease” is suspected to act as a reservoir from which resistance-conferring genetic mutations, and ultimately tumor recurrence, arise (19, 53, 60, 61, 66). We speculate that idling cancer populations may, in fact, constitute the bulk of the residual disease. Indeed, by continuing active progression through the cell cycle, idling populations are more prone to accumulate deleterious mutations and, hence, are a more fertile ground for acquiring resistance mutations than quiescent (18, 19, 67, 68) or senescent (69) populations. Recently described “drug-addicted” cells, which can arise by either genetic (16) or epigenetic (70) mechanisms, may also emerge from idling cell populations. These cells are dependent upon a drug for continued proliferation such that drug withdrawal leads to initial tumor shrinkage followed by regrowth. Within our modeling framework, drug addiction due to genetic changes would correspond to a change in the epigenetic landscape relative to that for drug-sensitive cells. Alternatively, if drug addiction is nongenetic in nature, this implies that additional basins exist within the drug-modified epigenetic landscape that are not easily accessible. In either case, idling cell populations are clearly distinct from drug-addicted populations. Applying the methods presented here to drug-addicted cells is a possible area of future investigation.

In summary, we have shown that the idling state is not a property of individual cells but rather a property of a BRAF-mutated melanoma population as a whole under prolonged BRAF-inhibition. As such, idling populations cannot be eradicated by targeting one particular subpopulation (i.e., a basin). Rather, the landscape itself must be altered (e.g., using drugs) to favor basins for regressing states over stationary and expanding states. This is a significant departure from recent approaches that aimed to identify and eliminate rare cell subtypes (e.g., cancer stem cells, drug-tolerant persisters) thought to be responsible for tumor progression and recurrence (19, 50, 62, 71). This type of cellular reprogramming will require deep knowledge of the molecular factors that shape and define the epigenetic landscapes cancer cells inhabit (72, 73). Future work should aim to identify the molecular actors that define basins in the BRAF-mutated melanoma epigenetic landscape using (e.g., single-cell RNA sequencing technologies (74, 75, 76)). “Targeted landscaping” (i.e., therapeutic approaches that rationally modify the epigenetic landscape to suppress or eliminate the nonquiescent reservoir of idling cancer cells) could delay, perhaps indefinitely, tumor recurrence.

Author Contributions

B.B.P., L.A.H., and V.Q. conceived and designed the study. B.B.P. and L.A.H. built the mathematical model and performed simulations. B.B.P., K.N.H., A.A.A., and C.E.H. acquired experimental data. B.B.P., L.A.H., D.R.T., and V.Q. analyzed and interpreted the experimental data. B.B.P., L.A.H., and V.Q. wrote, reviewed, and revised the manuscript. V.Q. supervised the study.

Editor: Nathalie Balaban.