Distinct thermodynamic signature of oligomer generation in the aggregation of the amyloid-β peptide

Abstract

Mapping energy landscapes has proved to be a powerful tool for studying reaction mechanisms. Many complex biomolecular assembly processes, however, have remained challenging to access using this approach, including the aggregation of peptides and proteins into amyloid fibrils implicated in various disorders. Here we generalize the strategy used to probe energy landscapes in protein folding to determine the activation energies and entropies that characterise each of the molecular steps in the aggregation of the amyloid-β peptide (Aβ42), which is associated with Alzheimer’s disease. Our results reveal that interactions between monomeric Aβ and amyloid fibrils during fibril-dependent nucleation fundamentally reverse the thermodynamic signature of this process relative to primary nucleation, even though both processes generate aggregates from soluble peptides. By mapping the energetic and entropic contributions along the reactive trajectories, we show that the catalytic efficiency of Aβ42 fibril surfaces results from the enthalpic stabilisation of adsorbing peptides in conformations amenable to nucleation, driving a dramatic lowering of the activation energy barrier for nucleation.

The aberrant self-assembly of proteins and peptides into amyloid fibrils is implicated in the pathology of over 30 clinical disorders, including Alzheimer’s and Parkinson’s diseases^1–3. Although it is a priority of both fundamental and translational research to characterise the molecular-level processes involved in amyloid formation^4–7, this has proved challenging to achieve in practice^7–9. Recently, however, advances in both experimental^{7, 10} and theoretical^{7, 11} methods have made it possible to acquire highly reproducible kinetic data in solution^{7, 10} under a wide range of experimental conditions, and to connect these measurements with the underlying microscopic processes through chemical kinetic rate laws^{5, 11}. In the case of the 42-residue amyloid-β peptide (Aβ42), the aggregation of which is associated with Alzheimer’s disease, the key molecular steps in amyloid formation have been identified⁷ as the primary nucleation of new aggregates from monomers^{4, 6, 12}, the addition of monomers to fibril ends resulting in their elongation^13–15, and secondary nucleation of monomers involving the fibril surface^{7, 16}.

This latter secondary nucleation process is a defining feature of Aβ42 aggregation^{7, 16}, and several other amyloid systems^{8, 17, 18}, and plays a key role in generating the high levels of toxicity associated with this peptide^19–22, as well as potentially playing an important role in the spreading of the pathology in the brain^23–25. The secondary nucleation process involves the surfaces of existing amyloid fibrils catalysing the formation of new pre-fibrillar aggregates from the soluble peptide²⁶. Since the aggregates generated in this manner can grow into fibrils and subsequently catalyse additional nucleation events, the secondary nucleation step results in positive feedback and a chain reaction which underlies the autocatalytic nature of amyloid formation^{7, 9, 16}. Furthermore, although the pre-fibrillar aggregates, also called oligomers, which are generated by both the primary and secondary nucleation processes are likely to be toxic to cells^{7, 19–22}, once a small but critical concentration of Aβ42 fibrils is present, the concentration of toxic oligomers generated through the secondary nucleation process rapidly exceeds that generated by primary nucleation⁷.

Although the fundamental steps involved in Aβ amyloid formation have been identified, the molecular mechanisms underlying these nucleation and growth processes remain poorly understood. In the study of protein folding dynamics, the key to overcoming this same challenge has been to probe the energy landscape associated with the folding process, in practice by establishing the activation free energy, and the component enthalpic and entropic contributions from thermodynamic analysis of experimental data acquired across a range of temperatures. Here, we generalize this approach to describe complex protein self-assembly processes that involve multiple molecular events occurring simultaneously across heterogeneous size distributions of aggregates. We achieve this goal through advances in experimental and theoretical chemical kinetics that make it possible to decouple from measurements of the overall aggregation reaction the characteristic signatures of the individual steps in amyloid formation, each of which can then be analysed using the same approach used in protein folding dynamics.

Using this strategy, we determine the activation free energies of fibril elongation, primary nucleation and secondary nucleation in Aβ42 amyloid formation, and the enthalpic and entropic contributions to these barriers. The results uncover striking similarities between the interactions driving the elongation of fibrils and primary nucleation, but expose the secondary nucleation process as having an entirely different thermodyamic character from primary nucleation. This contrast in the thermodynamic signatures of the two nucleation processes occurs despite the fact that both processes generate new aggregates from monomers, indicating that the molecular nature of the fibril surface and its interactions with monomers plays a critical role in secondary nucleation. By probing directly the interactions between monomeric peptides and fibrils, we map the energy landscape that characterises secondary nucleation, revealing how the interactions between monomers and the surfaces of amyloid fibrils drive a dramatic reduction in the activation energy for nucleation.

Results

Global analysis of Aβ42 aggregation at different temperatures

We explored the kinetics of aggregation of the amyloid-β (M1–42) peptide, referred to here as Aβ42, across a range of concentrations and temperatures. In order to establish well-defined initial conditions for the kinetic experiments, and hence to obtain reproducible data, it is crucial to use highly purified sequence homogeneous recombinant Aβ42 together with repeated isolation of monomers through size-exclusion chromatography, and to control carefully the inertness of surfaces with which the peptide makes contact^{7, 10}. Furthermore, to accurately decouple the temperature and concentration dependence of the individual reaction rates, the relative initial concentrations of monomeric peptide used at each temperature must be known to a very high degree of accuracy, since the reaction rates for this peptide are highly sensitive to the concentration of monomers in addition to the temperature⁷. To address this challenge, we arranged to carry out our experiments in parallel, using monomer solutions prepared simultaneously by dilution from a single master stock of Aβ42 and loaded in parallel into an array of fluorescence plate readers with the temperature of each device held constant at a different temperature.

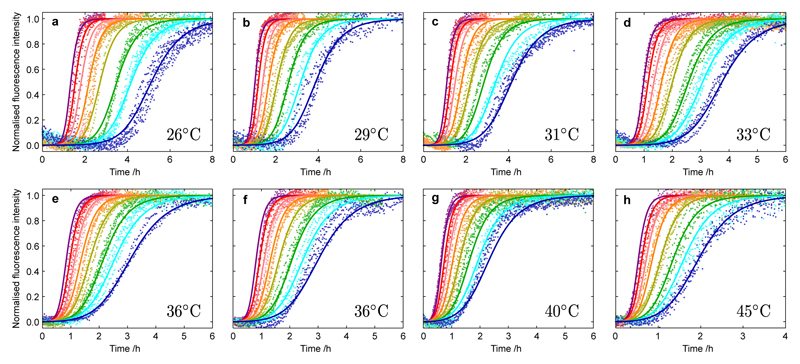
We first monitored the concentration-dependent kinetics of the aggregation of Aβ42 under quiescent condition for reactions beginning from purely monomeric peptide at seven different temperatures (Fig. 1). We carried out two sets of experiments, each involving four different temperatures, and included measurements at 36°C in both data sets to verify the high level of reproducibility across the two sets of data. At higher reaction temperatures, we observed an increase in the overall rate of formation of fibrils and characteristic changes in the time course of the reaction. At all temperatures and monomer concentrations we observe sigmoidal-like kinetic traces with a noticeable decrease in the sharpness of the transition as the temperature increases (Supplementary Fig. 2). To connect these macroscopic observations with the underlying microscopic processes, we applied an analytical approach, based on the integrated rate law that describes the aggregation of Aβ42, to determine the values of the rate constants controlling the reaction at each temperature^{5, 7, 27}. Specifically, although there are distinct microscopic rate constants for fibril elongation (k₊), primary nucleation (k_n) and secondary nucleation (k₂), the integrated rate law for Aβ aggregation^{7, 27} shows that the macroscopic reaction profiles, for reactions beginning from purely monomeric peptide, are controlled by just two combinations of these rate constants, k₊k_n and k₊k₂. Remarkably, at each temperature, we are able to fit essentially perfectly all of the data across multiple concentrations (Fig. 1a–g) using just these two kinetic parameters fixed globally across the entire data set, providing values for these combined rate parameters at each temperature (Fig. 3b,c).

Figure 1. Kinetics of Aβ42 aggregation from purely monomeric peptide at different temperatures and initial monomer concentrations.

Normalized experimental reaction profiles, monitored by ThT fluorescence, for Aβ42 aggregation from purely monomeric peptide for different initial concentrations of monomeric peptide and at different temperatures (a) 26°C, (b) 29°C, (c) 31°C, (d) 33°C, (e-f) 36°C, (g) 40°C and (h) 45°C in 20 mM sodium phosphate, 0.2 mM EDTA, 0.02% sodium azide, pH 8.0, with 6 µM ThT. The initial concentrations of monomers were 5.0 µM (purple), 4.5 µM (red), 4.0 µM (pink), 3.5 µM (orange), 3.0 µM (yellow), 2.5 µM (green), 2.2 µM (cyan) and 1.9 µM (blue). Note the different scales on the time axes; Supplementary Fig. 1 shows the data with the same scale for each panel. The data were recorded in two sets of four temperatures with measurements at 36°C included in both sets to act as a reference condition. The solid lines are global fits at each temperature using the analytical integrated rate law for Aβ42 aggregation. Two combinations of the microscopic rate constants, k₊k_n and k₊k₂, are used to globally fit the entire data set in each panel, in terms of rate constants for elongation (k₊), primary nucleation (k_n) and secondary nucleation (k₂). The rate parameters determined at each temperature from the global fitting are plotted in Fig. 3a,b.

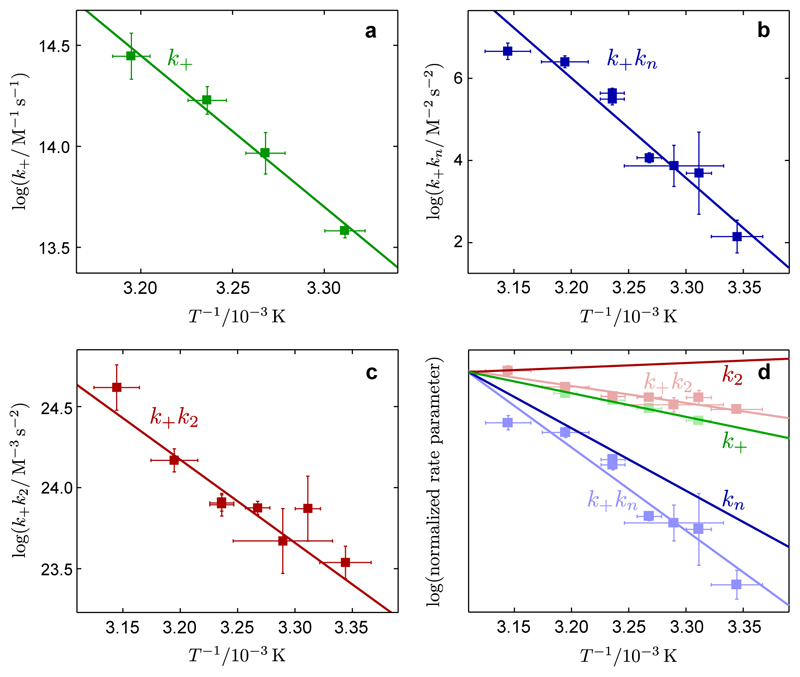
Figure 3. Arrhenius behavior of the microscopic rate constants for Aβ42 aggregation.

Arrhenius plots showing the temperature dependence of the rate parameters determined from the analytical fitting in Figs. 1, 2: (a) for k₊, (b) for the combined rate parameter k₊k_n, (c) for the combined rate parameter k₊k₂, in terms of rate constants for elongation (k₊), primary nucleation (k_n) and secondary nucleation (k₂). (d) shows how the data from (a-c), which is plotted as the faded data points and lines, are combined to give the temperature dependencies of the individual rate constants. Interestingly, while k₊ and k_n increase at higher temperatures, k₂ has a weak temperature dependence with the opposite trend. The error bars for the rate parameters represent standard errors from the global fits shown in Figs. 1-2 and for the temperatures indicate the ranges of fluctuations recorded during each experiment.

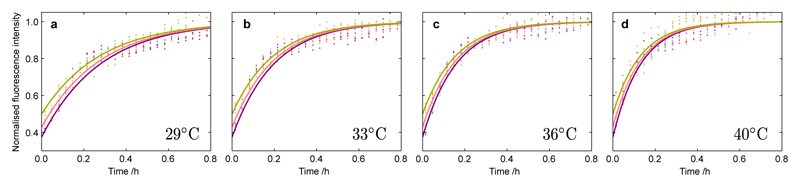
In order to decouple the values of the individual rate constants from the combined parameters k₊k_n and k₊k₂, it is necessary to determine one of the rate constants in isolation. To achieve this goal we measured reaction profiles from solutions containing not only monomeric peptide but also pre-formed fibrils (Fig. 2). At sufficiently high concentrations of pre-formed fibrils¹¹ (here ca. 40% or greater of the total peptide concentration), the rate equations indicate that the elongation of fibrils is the dominant process and that the nucleation processes can be neglected, allowing determination of the elongation rate constant in isolation¹¹. More precisely, the reaction profiles under these conditions depend primarily on the value k₊/L(0)¹¹, where L(0) is the mean length of the pre-formed fibrils present at the start of the reaction, which can be estimated independently using cryogenic transmission electron microscopy (Supplementary Fig. 3). In order to ensure that L(0) was consistent across all of our experiments, we used pre-formed fibrils generated at a single temperature (36°C). We also observed that the temperature at which pre-formed fibrils were generated did not significantly impact their ability to act as reactive fibril ends (Supplementary Fig. 3), and analyses by TEM and differential centrifugal sedimentation (Supplementary Fig. 4) were consistent with the prediction from the kinetic analysis⁷ that the mean length of fibrils, μ, generated in the aggregation reaction increases at higher temperatues, since $\mu \sim \sqrt{k_{+}/k_2}.$ Interestingly, by contrast to aggregation from purely monomeric peptide, the integrated rate law in the case of heavily pre-seeded reactions indicates that the normalized reaction profiles will be only weakly sensitive to the initial concentration of peptides¹¹. The global fits to the data (Fig. 2a–d) in this case provide a direct estimate of the elongation rate constant k₊ at each temperature. We find that k₊ increases with temperature, which is reflected in our measurements (Fig. 2) by a steeper initial slope at higher temperatures.

Figure 2. Kinetics of pre-seeded Aβ42 aggregation at different temperatures and initial monomer concentrations.

Normalized experimental reaction profiles, monitored by ThT fluorescence, for Aβ42 aggregation in the presence of pre-formed fibrils for different initial concentrations of monomeric peptide and at different temperatures (a) 29°C, (b) 33°C, (c) 36°C and (d) 40°C. The initial concentrations of monomers were 5.0 µM (yellow), 4.0 µM (pink) and 3.0 µM (purple). The solid lines are global fits at each temperature using the analytical integrated rate law for Aβ42 aggregation. The data in each panel is fitted globally with a single parameter, k₊/L(0), where L(0) is the average length of the pre-formed fibrils. The rate parameters determined at each temperature from the global fitting are plotted in Fig. 3c.

Arrhenius behaviour for combined rate constants

The global analyses in Figs. 1 and 2 provide values for the combined rate parameters k₊k_n and k₊k₂, and the elongation rate constant k₊ at a variety of temperatures. These measurements together make it possible to decouple the values and temperature dependences of the individual rate constants k₊, k_n and k₂, which describe transitions from well-defined initial to final states^{7, 11} on a free energy landscape. By analogy with protein folding^{28, 29}, we extract the essential features of the free energy landscapes that are associated with the elongation of fibrils and the nucleation events by describing each of these processes as diffusive motions along one-dimensional free energy surfaces. Kramers theory^28–31 provides the temperature dependence of the rate constants (k₊, k_n and k₂) in the form of an Arrhenius equation which directly links a kinetic rate constant to the corresponding highest energy barrier along the potential landscape measured relative to the starting point: $k=A\text{exp}(-\frac{\Delta G^{‡ϴ}}{RT})$ for a rate constant k, highest free energy barrier ΔG^‡ϴ, and temperature T. It is important to note that, although the energy landscape may include multiple intermediate barriers, only the highest free energy barrier measured relative to the starting point enters the various rate constants and hence is directly probed by these experiments (see the Supplementary Note for a detailed discussion of the application of Kramers theory to biomolecular reactions). Where the rate laws contain products of the individual rate constants (i.e. k₊k_n or k₊k₂), the same temperature dependence is maintained with the component activation energies appearing summed in the exponent: $k_1{k}_2=A_1{A}_2\text{exp}(-\frac{\Delta G_1^{‡ϴ}+\Delta G_2^{‡ϴ}}{RT}).$

We first checked whether or not plots of the logarithms of the reaction rates against the inverse absolute temperatures were linear over the temperature range used (Fig. 3). Interestingly, we observed linearity of the Arrhenius plots in all three cases, indicating that well-defined activation energies characterize the distinct microscopic processes of fibril elongation, primary nucleation and secondary nucleation, and that any changes in heat capacity, ΔC_p = ∂ΔH^‡ϴ/∂T, between the starting states and transition states of the three processes were small over the temperature range studied. Since the free energy barrier ΔG^‡ϴ associated with each process is related to the enthalpy ΔH^‡ϴ and entropy ΔS^‡ϴ of activation through the relationship ΔG^‡ϴ = ΔH^‡ϴ−TΔS^‡ϴ, the enthalpies of the microscopic processes can be directly determined from the gradient of each plot according to ∂(log k)/∂(1/T) = −ΔH^‡ϴ/R (Fig. 3a) or $\partial (\text{log}{k}_1{k}_2)/\partial (1/T)=-(\Delta H_1^{‡ϴ}+\Delta H_2^{‡ϴ})/R$ (Fig. 3b–c).

As a means to determine the free energy barrier ΔG^‡ϴ, and hence also the entropy of activation using −TΔS^‡ϴ = ΔG^‡ϴ−ΔH^‡ϴ, an independent estimate of the prefactor A is needed, although ΔG^‡ϴ has only a logarithmic dependence on this value. The prefactor A can be thought of as the frequency of attempts at a given reaction, which is multiplied by $\text{exp}(-\frac{\Delta G^{‡ϴ}}{RT})$ to obtain the rate of successful (i.e. barrier-crossing) attempts at the reaction. We have in the past reported an estimate of the prefactor for amyloid fibril elongation, based on modeling the elongating monomer as a Gaussian chain that diffusively crosses the energy barrier and escapes from the metastable soluble state³². Given the fundamentally limited information about diffusion along the reaction coordinates for the nucleation processes, we partition all of the missing information into the free energy barrier in the rate equation. Other choices for the pre-factors are possible (for example, incorporating the process of monomer adsorption), and as such the free energy barrier is only meaningful if stated together with the corresponding pre-factor. The prefactor can be expressed as A ~ Dr_eff with a characteristic diffusion constant D ~ 10⁻⁹m²s⁻¹ and the radius of the effective reaction volume r_eff ~ 3·10⁻¹¹m in the case of the Aβ peptide^{32, 33}. An analogous approach can be applied for the nucleation processes (see the Supplementary Note for the derivation), accounting for the different species involved in each process. Overall, the pre-factors for the nucleation processes are likely to involve characteric diffusion constants and effective length scales of the same order of magnitude as fibril elongation³², although the concentration dependence of the pre-factor must be scaled to account for the reaction order of each process.

Hence, the measurements of the molecular rate constants together with the Arrhenius plots provide values for the free energy, enthalpy and entropy of activation for fibril elongation (Fig. 3a), and the sums of these barriers for elongation and primary nucleation (Fig. 3b), and elongation and secondary nucleation (Fig. 3c). Moreover, using the temperature dependence of the elongation rate constant k₊, we are able to resolve the temperature dependence of the nucleation rate constants k_n and k₂ from the combined rate parameters k₊k_n and k₊k₂ (Fig. 3d). We note that while the rates of both fibril elongation and primary nucleation increase strongly as temperature rises, the secondary nucleation rate is observed to have a much weaker dependence on temperature. These data explain the observed increase in the sharpness of the transition of the reaction profiles at lower temperatures (Supplementary Fig. 2), since the ratio of the rates of secondary to primary pathways increases⁷ at lower temperatures. We verified the continuation of this trend by monitoring aggregation reactions at temperatures as low as 10°C (Supplementary Fig. 2).

Activation energies of distinct molecular steps

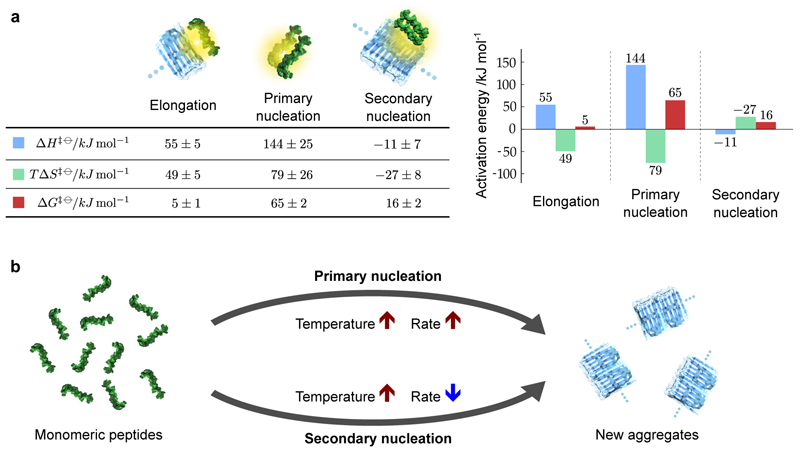
The values determined from Fig. 3 for the barriers in free energy, and the enthalpic and entropic contributions, reveal the individual energy barriers associated with the three key molecular steps in the aggregation of Aβ42 to form amyloid fibrils (Fig. 4). The results for elongation reveal a small free energy barrier $\Delta G_{+}^{‡ϴ}=5\pm 1kJ{\text{mol}}^{-1},$ with an enthalpic barrier $(\Delta H_{+}^{‡ϴ}>0)$ and a favourable entropy of activation $(\Delta S_{+}^{‡ϴ}>0).$ The enthalpic barrier for the addition of a monomeric peptide to a fibril, measured here for Aβ42 as $\Delta H_{+}^{‡ϴ}=55\pm 5kJ{\text{mol}}^{-1},$ is likely to represent the breakage of hydrogen bonds (and other interactions) associated with solvation and with the ensemble of internal structures of the Aβ peptide. By contrast, the favorable entropy of the transition state, $T\Delta S_{+}^{‡ϴ}=49\pm 5kJ{\text{mol}}^{-1}$ (at 298K), can be attributed to the desolvation of hydrophobic segments of the incoming polypeptide and the fibril end. Remarkably, these values for the energy barriers associated with fibril elongation in solution are in agreement with previous two-state measurements of the elongation of surface-immobilized Aβ42 fibrils^{33, 35}.

Figure 4. Activation energies of fibril elongation, primary nucleation and secondary nucleation in Aβ42 amyloid formation.

(a) The free energies of activation, and the enthalpic and entropic contributions, determined from our measurements. The activation energies for elongation and primary nucleation and primary nucleation consist of enthalpic barriers and favorable entropies of activation, whereas the enthalpic and entropic contributions to the free energy are reversed in sign for secondary nucleation. The values and standard errors shown were calculated by fitting the data shown in Fig. 3 with ΔH^‡ϴ = −R ∂(log k)/∂(1/T) and ΔG^‡ϴ = −RT log(k/A), which were combined to give TΔS^‡ϴ = ΔH^‡ϴ −ΔG^‡ϴ. The entropic term is shown at T = 298K. The values are given per mole of reaction at a standard state of 1M. (b) Schematic showing the different temperature dependencies of the two nucleation processes that both generate aggregates from monomeric peptides. The structures used in the visual representations of each process are adapted from Refs. ⁴⁵ and ⁴⁶.

Moreover, the present strategy, which makes it possible to decouple and characterise the activation energies of complex processes in solution, also reveals the energy barriers for primary nucleation and secondary nucleation. The values determined for the barriers to primary nucleation (Fig. 4) follow the same overall trend to the elongation process $(\Delta H_n^{‡ϴ}>0\text{and}\Delta S_n^{‡ϴ}>0),$ indicating that fibril elongation and primary nucleation share fundamental qualitative similarities. The high activation energy for primary nucleation $(\Delta G_n^{‡ϴ}=65\pm 2kJ{\text{mol}}^{-1})$ consists of an enthalpic barrier $(\Delta H_n^{‡ϴ}=144\pm 25kJ{\text{mol}}^{-1})$ and a favorable entropy of activation $(T\Delta S_n^{‡ϴ}=79\pm 26kJ{\text{mol}}^{-1}).$ These values have the same signs as the barriers for the elongation process, but have larger magnitudes, as would be expected for this slow nucleation process. Indeed, the free energy of activation determined here for primary nucleation is approximately 10 times larger than for fibril elongation. This increase occurs in spite of a more favourable entropy of activation and is driven by the much larger enthalpic barrier observed for primary nucleation relative to elongation.

The qualitative similarity in the data obtained for primary nucleation and fibril elongation implies that the hydrophobic effect also plays a dominant role in primary nucleation, and that the rate-limiting step in this process can be understood as an overall transition similar to fibril elongation, albeit requiring more extensive bond breaking. Specifically, the data show that the magnitude of the enthalpic barrier for primary nucleation is more than two times greater than the equivalent barrier for elongation, whereas the magnitude of the favourable entropic contributions are similar. The increase in the enthalpic barrier can be rationalised by noting that in forming a nucleus, the relevant hydrogen bonds associated with solvation must be broken in two monomers⁷, in contrast to the elongation process where the penalty corresponds to a single monomer being added to a partially desolvated existing fibril end ^{15, 32}. Conversely, the rough similarity between the favourable entropies of activation measured for fibril elongation and primary nucleation is likely a consequence of the fact that in both processes an interface of similar size is desolvated. Interestingly, the data reveal a slightly less favourable entropy of activation for the elongation process, which may be explained by the fact that the terminal monomer at the fibril end in the elongation process is already partially desolvated relative to a free monomer. It is also interesting to note that the different magnitudes of the enthalpic barriers measured here for nucleation and elongation are in contrast to simple colloidal models of one-dimensional growth, where the energy barriers to nucleation and elongation are identical³⁶. The increased enthalpic barrier for primary nucleation observed here thus reflects the large number of internal and solvent degrees of freedom associated with the peptide.

The results for secondary nucleation are in quantitative and qualitative contrast to those for fibril elongation and primary nucleation. The secondary nucleation process involves existing fibrils catalysing the nucleation of new aggregates from monomeric peptide. By definition, as a catalysed reaction, the energy barrier of secondary nucleation must be reduced relative to primary nucleation. This prediction is verified by the measurement of the activation energy of secondary nucleation as $\Delta G_2^{‡ϴ}=16\pm 2kJ{\text{mol}}^{-1},$ which represents a four-fold reduction in the energy barrier relative to primary nucleation, demonstrating the remarkably effective manner in which amyloid fibrils catalyse the nucleation of new aggregates from monomers. Strikingly, in addition to this dramatic lowering of the activation energy relative to primary nucleation, the enthalpic and entropic contributions to the free energy barrier are reversed in sign $(\Delta H_2^{‡ϴ}<0\text{and}\Delta S_2^{‡ϴ}<0).$ By contrast to the enthalpic barriers and favorable changes in entropy observed for primary nucleation and fibril elongation, the energy barrier for secondary nucleation is entirely entropic $(T\Delta S_2^{‡ϴ}=-27\pm 8kJ{\text{mol}}^{-1})$ with a small negative enthalpic barrier $(\Delta H_2^{‡ϴ}=-11\pm 7kJ{\text{mol}}^{-1}).$ In what follows we analyse in detail the energy landscape of secondary nucleation.

Mapping the energy landscape for secondary nucleation

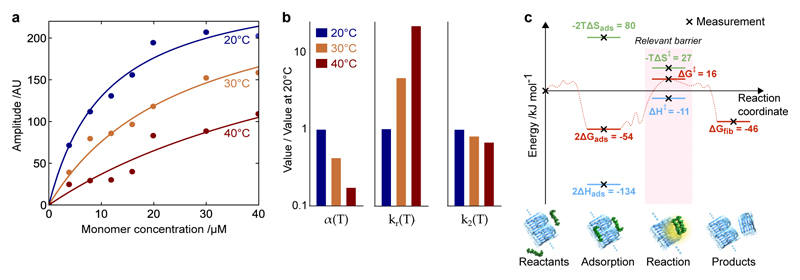
Elementary chemical reactions are typically associated with positive enthalpies of activation, while the data obtained here for secondary nucleation, which is a multimolecular reaction governed by diffusion dynamics, reveal a negative value. In order to gain additional mechanistic insight into the secondary nucleation process, we therefore mapped the reactive trajectory to construct a more complete picture of the energy landscape. To achieve this goal, we measured directly the interactions between monomeric peptides and the surfaces of fibrils as a function of concentration and temperature using surface plasmon resonance (SPR). The results (Fig. 5a) reveal strikingly that the surface coverage of monomers on the fibril surfaces decreases with increasing temperature.

Figure 5. Mapping the energy landscape for secondary nucleation.

(a) SPR measurements of the adsorption of monomers onto fibrils as a function of concentration and temperature. The data are fitted to the Langmuir isotherm to determine K_D fitted at each temperature. (b) The variation in the surface coverage α(T) = 1/K_D(T), the rate constant of the subsequent nucleation reaction k_r(T), and the overall rate of secondary nucleation k₂(T) = α(T)²k_r(T). The corresponding values of K_D are K_D(20°C) = 11μM, K_D(30°C) = 26μM, K_D(40°C) = 64μM. (c) The energy landscape for secondary nucleation assuming a standard state of 1M, showing the trajectory from starting materials, through adsorption and reaction, to products. Since our experiments are typically at micromolar concentrations, the same landscape is shown assuming a standard state of 1μM in Supplementary Fig. 6, where ΔG_ads > 0. Note that, according to Kramers theory of diffusive reactions, the activation parameters determined from the temperature dependence of the rate constants correspond to the highest free energy barrier measured relative to the reactants.

In general, the rate of secondary nucleation can be written as r₂(T, c) = k_r(T)θ(T, c)^n₂, where θ(T, c) is the fibril surface coverage determined directly via SPR measurements³⁹, c is the monomer concentration, n₂ is the reaction order⁷, and k_r(T) is the rate constant of the surface catalysed reaction. In the limit of low surface coverage, θ(T, c) = α(T)c, where α(T) is the inverse of the peptide-fibril equilibrium dissociation constant, α(T) = 1/K_D(T) (see the Supplementary Note for a detailed derivation). In this case the rate of secondary nucleation reduces to r₂(T, c) = k₂(T)c^n₂, with k₂(T) = k_r(T)α(T)^n₂. The data reveal (Fig. 5b) that the surface occupancy of monomers on the fibril surface α(T) decreases with temperature, ∂α(T)/∂T < 0 (i.e. the adsorption is exothermic), while the rate of the subsequent surface catalysed reaction k_r(T) increases with temperature, ∂k_r/∂T > 0. At higher temperatures, the decrease in the concentration of monomers on the fibril surface α(T) is sufficient to outweigh the increase in the rate constant controlling the subsequent reaction k_r(T), so that the overall rate constant of the secondary nucleation process k₂(T) decreases as temperature increases (Fig. 5b).

Although the major role of the fibril, as the catalytic surface, is to provide a stabilisation of the transition state prior to nucleus formation, in this case driven by a favourable enthalpy of activation, it is interesting to note that the thermodynamic features uncovered here for surface-catalyzed secondary nucleation are reminiscent to those of classical heterogeneous catalysis of a reaction at a solid surface⁴⁰.

This data for the adsorption of monomers onto the fibril surface also directly provides access to the change with adsorption in free energy through $\Delta G_{\text{ads}}^{ϴ}=-RT\text{log}(\alpha (T)c^{ϴ}).$ Furthermore, the corresponding change in enthalpy is given by the Clausius Clapeyron equation $\Delta H_{\text{ads}}^{ϴ}=-R\partial \alpha /\partial (1/T)$ and the change in entropy may be calculated since $T\Delta S_{\text{ads}}^{ϴ}=\Delta H_{\text{ads}}^{ϴ}-\Delta G_{\text{ads}}^{ϴ}$ (see the Supplementary Note for detailed calculations). By combining these direct measurements of the adsorption process with the results from bulk solution, we are able to map out the energy landscape for secondary nucleation (Fig. 5c) that characterises the transition from the initial reactants, through the adsorbed monomers on the fibril and the subsequent nucleation reaction, to the final products. Note that the free energy of the final products is known via equilibrium measurements of the critical concentration c_crit¹⁰, which gives $\Delta G_{\text{flb}}^{ϴ}=RT\ln (c_{\text{crit}}/c^{ϴ})\approx -46\text{kJ}{\text{mol}}^{-1}$ at protein concentration c^ϴ = 1 M. Since our experiments are typically at micromolar concentrations, which are significantly closer to physiologically relevant conditions than a standard state of 1M, the energy landscape for secondary nucleation can also be calculated assuming a standard state of 1μM (Supplementary Fig. 6).

It is interesting to note from the energy landscape that the difference in enthalpy between the adsorbed state and the highest point on the energy landscape is given by $\Delta H_2^{‡}-2\Delta H_{\text{ads}}=123\text{kJ}{\text{mol}}^{-1},$ which is similar to the enthalpic barrier determined for primary nucleation, $\Delta H_n^{‡}.$ We can speculate, therefore, that the secondary nucleation reaction that occurs after the adsoroption of monomers onto the fibril surface may share similar characteristics with primary nucleation in solution.

Discussion

The results presented here are the first determination of the thermodynamic signatures of the key microscopic steps in Aβ amyloid formation. The activation energies determined for primary nucleation and fibril elongation reveal that these processes are controlled by enthalpic barriers and favourable entropies of activation (ΔH^‡ϴ > 0, ΔS^‡ϴ > 0). By contrast, the results for secondary nucleation reveal remarkably that this process has a fundamentally different signature, with the relevant barrier being entropic rather than enthalpic in nature (ΔH^‡ϴ < 0, ΔS^‡ϴ < 0).

Although the primary and secondary nucleation processes both generate new aggregates from monomeric peptides, the results here show that these two processes have opposite temperature dependencies (Fig. 4b). These observations reveal that the interactions between monomeric Aβ and amyloid fibrils are not only able to change the rate constant characterising nucleation, but also to fundamentally reverse the thermodynamic signature of this process relative to primary nucleation. Moreover, our results show that Aβ42 monomers have an intermediate affinity for the surface of amyloid fibrils (K_D ≈ 10μM), and indicate a mechanism involving the rapid adsorption (and desorption) of monomers prior to a rate-limiting reaction step on the fibril surface, a process analogous to classical heterogeneous catalysis. Indeed, the Sabatier principle states in qualitative terms that for efficient catalysis, the affinity between the catalyst and substrate should neither be too strong nor too weak, but rather intermediate to allow the substrate to bind and the products to dissociate. This classical concept was recently evaluated using DFT calculations leading to predictors of catalytic efficiency based on the interactions between surfaces and reactants⁴¹. In thermodynamic terms, the catalytic efficiency of Aβ42 fibril surfaces can therefore be explained through enthalpic stabilisation of conformations amenable to nucleation, resulting in a significant lowering of the activation energy barrier. Indeed, the surface-binding of monomers is likely to induce a significant structural change in the peptide, consistent with the very high specificity that has been observed for the secondary nucleation reaction, as demonstrated by the fact that fibrils constructed from other proteins and peptides, including Aβ40, are not able to efficiently catalyse nucleation of Aβ42 monomers^{7, 42}.

Through mapping the energy landscapes that characterise the distinct molecular steps in the aggregation of Aβ42 into amyloid fibrils, the present study provides foundational insights into the molecular mechanism of secondary nucleation, which has been identified as a critical step in generating the high levels of toxicity associated with Aβ42 amyloid formation. Our results suggest that strategies that seek to interfere with the interactions between monomers and fibril surfaces, which drive the unique thermodynamic signature of secondary nucleation, may therefore be effective approaches to reducing the toxicity of Aβ aggregation. Indeed, we have recently shown that nature has designed molecular chaperones capable of binding to Aβ42 fibrils in competition with monomeric peptides, resulting in a lower population of surface bound Aβ42 monomers, inhibition of the overall rate of secondary nucleation, and the abolition of toxicity in living brain tissue⁹. Furthermore, the secondary nucleation of new aggregates on fibril surfaces is increasingly recognised as a central feature in several amyloid disorders beyond Alzheimer’s disease, ranging from Parkinson’s disease to type-II diabetes. It is likely that interactions between monomeric peptides and fibril surfaces will become a common target in the development of therapeutics which seek to ablate the toxicity associated with amyloid formation. Interestingly, the present work indicates that stabilisation of surface-bound monomers on the fibril surface could be a complementary approach.

More generally, the approach developed in this study extends the methods commonly used to probe the energy landscapes of two-state systems in protein folding to investigations of complex protein self-assembly, which involve a multitude of processes occurring simultaneously across heterogeneous populations. Probing energy landscapes has for decades proved a powerful tool to study reaction mechanisms. With our increasing ability to decouple and probe the rates of the individual processes driving self-assembly reactions, we expect this approach to have direct applicability across a diverse range of complex biochemical phenomena for which mechanistic information is currently challenging to achieve, including the more than thirty disease-related amyloid systems and a wide range of functional bio-molecular assembly processes involved in cellular structure and molecular trafficking.

Methods

Materials

We expressed the Aβ(M1-42) peptide (MDAEFRHDSGYEVHHQKLVFFAEDVGSNKGAIIGLMVGGVVIA) in Escherichia coli and purified the peptide as described previously⁴⁴. Aliquots of purified Aβ42 were thawed and dissolved in 6 M GuHCl, and the monomer was isolated by two rounds of gel filtration on a Superdex 75 column in 20 mM sodium phosphate buffer, pH 8, with 200 μM EDTA and 0.02% NaN₃. The centre of the monomer peak was collected on ice and lyophilized. The sample was again dissolved in 6 M GuHCl, and the monomer isolated by gel filtration on a Superdex 75 column in 20 mM sodium phosphate buffer, pH 8, with 200 μM EDTA and 0.02% NaN₃ was typically found to have a concentration (determined by quantitative amino acid analysis purchased from BMC Uppsala) of 5-12 μM. The gel filtration step removes traces of pre-existing aggregates and exchanges the buffer to the one used in the fibril formation experiments.

Kinetic assays

The monomer was supplemented with 6 μM ThioflavinT (ThT) and was used to prepare a series of samples of Aβ42 with concentrations between 0.5 and 6 μM. All samples were prepared in low-bind Eppendorf tubes (Axygen, California, USA) on ice. Samples were pipetted into multiple wells of a 96 well half-area plate of black polystyrene with a clear bottom and PEG coating (Corning 3881, Massachusetts, USA), 100 μL per well. Assays were initiated by placing the 96-well plate at the designated temperature in a plate reader (Fluostar Omega, Fluostar Optima or Fluostar Galaxy, BMGLabtech, Offenburg, Germany). A series of control experiments^{7, 10} demonstrated that under the conditions used, the fluorescence from ThT is linearly related to the Aβ42 aggregate mass concentration.

Pre-formed fibrils

Kinetic experiments were set up as above for multiple samples of Aβ42 at 36°C. The fluorescence of added ThT was monitored for 1.5 h to verify the formation of fibrils. The samples were then collected from the wells into low-bind Eppendorf tubes (Axygen, California, USA) and sonicated for 2 min in a sonicator bath at room temperature to disrupt any fibril clusters. The previously established rate constants⁷ for elongation and secondary nucleation in Aβ42 aggregation show that at the concentrations of pre-formed fibrils applied here, the accelerating effect on the reaction is due primarily to elongation processes induced by the added reactive fibril ends.

Surface plasmon resonance studies

The SPR experiments were performed with a Biacore 3000 instrument (GE Healthcare), using C3 sensors, essentially as described previously³⁹. The flow rate was 10 μl/min throughout using 20 mM phosphate, 0.2 mM EDTA, pH 8.0 with 0.005% Tween20 as the flow buffer. The central fraction of Aβ42 peptide monomer from gel filtration in 20 mM phosphate, 0.2 mM EDTA, pH 8.0, was collected and stored on ice for up to 8h until use. A solution of 10 μM of monomeric peptide was incubated for 2 h at 37°C to form fibrils, followed by tip sonication to produce short (ca. 50 nm) fibrils for immobilization. For the attachment of the fibrils to the surface of the sensor, the fibrils were diluted 10-fold into 10 mM sodium acetate buffer at pH 3.0. The carboxylic acid groups on the CM3 sensor surface were activated with a mixture of EDC and NHS to enable standard amine coupling chemistry. The injection of fibrils led to an increase of ca. 3000 RU. The subsequent incubation with monomer in 20 mM phosphate, 0.2 mM EDTA, pH 8.0 added ca. 9000 RU. Injection of monomers was followed by buffer flow. The linear parts of the dissociation curves were fitted to a linear function which was extrapolated to the beginning of the dissociation phase. The difference amplitude relative to baseline was taken to correspond to the monomer binding to the fibril surface. The amplitudes, A, were plotted as a function of monomer concentration, and fitted to A = A(∞)Kc/(1 + Kc), with K being the binding constant and c the monomer concentration.

Kinetic rate laws

Following our previous analysis^{7, 27}, the generation of fibril mass, M, when both primary and secondary nucleation events occur is described by the integrated rate law:

$$\frac{M(t)}{M(\infty )}=1-{\left(\frac{B_{+}+C_{+}}{B_{+}+C_{+}{e}^{\kappa t}}\frac{B_{-}+C_{+}{e}^{\kappa t}}{B_{-}+C_{+}}\right)}^{\frac{k_{\infty }^2}{\kappa {\tilde{k}}_{\infty }}}{e}^{-k_{\infty }t}$$ (1)

where two particular combinations of the rate constants for primary nucleation (k_n), elongation (k₊) and fibril-catalysed secondary nucleation (k₂) define much of the macroscopic behaviour; these parameters are related to the rate of formation of new aggregates through primary pathways $\lambda =\sqrt{2k_{+}{k}_{n}m{(0)}^{n_c}}$ and through secondary pathways $\kappa =\sqrt{2k_{+}{k}_{2}m{(0)}^{n_2+1}},$ where k₂ = k₋ when n₂ = 0. Indeed, Eq. 1 depends on the rate constants through these two parameters, λ and κ, alone since B_± = (k_∞ ± k̃_∞)/(2κ), C_± = ±λ²/(2κ²), $k_{\infty }=\sqrt{2{\kappa }^2/[n_2(n_2+1)]+2{\lambda }^2/n_c}$ and ${\tilde{k}}_{\infty }=\sqrt{k_{\infty }^2-4C_{+}{C}_{-}{\kappa }^2}.$ The initial concentration of soluble monomers is denoted m(0) and the exponents describing the dependencies of the primary and secondary pathways on the monomer concentration are given as n_c and n₂ respectively.

Kramers rate theory for multi-well potentials

Kramers rate theory for a double-well potential states that the rate at which the system diffuses from one minimum x₁ to the other x₂ is given by a prefactor A (which depends on the curvatures of the potential landscape at x₁ and at the barrier x*) multiplied by the negative exponential of the highest free energy point measured relative to the starting point. When the potential landscape has greater than two local minima, the escape rate is still described by an equation of the same form provided that the local minima satisfy certain ordering conditions; in particular, for a multi-well potential landscape having local minima at x₁, x₂, … , x_n there exists an ordering ≺ of these local minima (obtained by ordering the minima from deepest to shallowest) so that the expectation value for the average escape time from x_k to the set ℳ_k = {x_j|x_j ≺ x_k} satisfies Kramers formula. The Supplementary Note provides a detailed analysis of the temperature dependence of the individual microscopic steps involved in secondary nucleation.

Supplementary Material

Supplementary information accompanies this paper.