Extracting neuronal functional network dynamics via adaptive Granger causality analysis

Significance

Probing functional interactions among the nodes in a network is crucial to understanding how complex systems work. Existing methodologies widely assume static network structures or Gaussian statistics or do not take account of likely sparse interactions. They are therefore not well-suited to neuronal spiking data with rapid task-dependent dynamics, binary statistics, and sparse functional dependencies. We develop an inference framework for extracting functional network dynamics from neuronal data by integrating techniques from adaptive filtering, compressed sensing, point processes, and high-dimensional statistics. We derive efficient estimation algorithms and precise statistical inference procedures. We apply our proposed techniques to experimentally recorded neuronal data to probe the neuronal functional networks underlying attentive behavior. Our techniques provide substantial gains in computation, resolution, and statistical robustness.

Abstract

Quantifying the functional relations between the nodes in a network based on local observations is a key challenge in studying complex systems. Most existing time series analysis techniques for this purpose provide static estimates of the network properties, pertain to stationary Gaussian data, or do not take into account the ubiquitous sparsity in the underlying functional networks. When applied to spike recordings from neuronal ensembles undergoing rapid task-dependent dynamics, they thus hinder a precise statistical characterization of the dynamic neuronal functional networks underlying adaptive behavior. We develop a dynamic estimation and inference paradigm for extracting functional neuronal network dynamics in the sense of Granger, by integrating techniques from adaptive filtering, compressed sensing, point process theory, and high-dimensional statistics. We demonstrate the utility of our proposed paradigm through theoretical analysis, algorithm development, and application to synthetic and real data. Application of our techniques to two-photon Ca²⁺ imaging experiments from the mouse auditory cortex reveals unique features of the functional neuronal network structures underlying spontaneous activity at unprecedented spatiotemporal resolution. Our analysis of simultaneous recordings from the ferret auditory and prefrontal cortical areas suggests evidence for the role of rapid top-down and bottom-up functional dynamics across these areas involved in robust attentive behavior.

Converging lines of evidence in neuroscience, from neuronal network models and neurophysiology (1–8) to resting-state imaging (9–11), suggest that sophisticated brain function results from the emergence of distributed, dynamic, and sparse functional networks underlying the brain activity. These networks are highly dynamic and task-dependent, which allows the brain to rapidly adapt to abrupt changes in the environment, resulting in robust function. To exploit modern-day neuronal recordings to gain insight into the mechanisms of these complex dynamic functional networks, computationally efficient time series analysis techniques capable of simultaneously capturing their dynamicity, sparsity, and statistical characteristics are required.

Historically, various techniques such as cross-correlogram (12) and joint peristimulus time histogram (13) analyses have been used for inferring the statistical relationship between pairs of spike trains (12–14). Despite being widely used, these methods are unable to provide reliable estimates of the underlying directional patterns of causal interactions among an ensemble of interacting neurons due to the intrinsic deficiencies in identification of directionality, low sensitivity to inhibitory interactions (15), and susceptibility to the indirect interactions and latent common inputs.

Methods based on Granger causality (GC) analysis have shown promise in addressing these shortcomings and have thus been used for inferring functional interactions from neural data of different modalities (16–19). The rationale behind GC analysis is based on two principles: the temporal precedence of cause over effect and the unique information of cause about the effect. Given two time series ${\{X_t,Y_t\}}_{t=1}^T$, if including the history of $Y_t$ can improve the prediction of $X_{t+1}$, it is implied that the history of $Y_t$ contains unique information about $X_t$, not captured by other covariates. In this case, we say that $Y_t$ has a G-causal link to $X_t$.

Numerous efforts have been dedicated to extending the bivariate GC measure to more general settings, such as the conditional form of GC in ref. 20 for multivariate setting, and several frequency-domain variants of GC (21–23). Despite significant advances in time series analysis using GC and its variants, when applied to neuronal data, the existing methods exhibit several drawbacks.

First, most existing methods for causality inference provide static estimates of the causal influences associated with the entire data duration. Although suitable for the analysis of stationary neural data, they are not able to capture the rapid task-dependent changes in the underlying neural dynamics. To address this challenge, several time-varying measures of causality have been proposed in the literature based on Bayesian filtering and wavelets (24–30). Second, there are very few causal inference approaches to take into account the sparsity of the functional networks (31–33). As an example, authors in ref. 31 introduced a method for sparse identification of functional connectivity patterns from large-scale functional imaging data. Despite their success in inferring sparse connectivity patterns, these techniques assume static connectivity structures.

Third, most existing approaches are tailored for continuous-time data, such as electroencephalography (EEG) and local field potential recordings, which limits their utility when applied to binary neuronal spike recordings. These methods are generally based on multivariate autoregressive (MVAR) modeling, with a few nonparametric exceptions (30, 34). Some efforts have been made to adapt the MVAR modeling to neuronal spike trains (17, 35, 36). For instance, the binary spikes were preprocessed in refs. 17 and 35 via a smoothing kernel, which significantly distorts the temporal details of the neuronal dynamics. In addition, the frequency-domain GC analysis techniques implicitly assume that the data have rich oscillatory dynamics. Although this assumption is valid for steady-state EEG responses or resting-state recordings, spike trains recorded from cortical neuronal ensembles often do not exhibit any oscillatory behavior.

To address the third challenge, point process modeling and estimation have been successfully used in capturing the stochastic dynamics of binary neuronal spiking data (37, 38). This framework has been particularly used for inferring functional interactions in neuronal ensembles from spike recordings (32, 38–42). A maximum likelihood (ML)-based approach was introduced in ref. 38 based on a network likelihood formulation of the point process model; a model-based Bayesian approach based on point process likelihood models with sparse priors on the connectivity pattern was introduced in ref. 32. Among the more recent results, an information-theoretic measure of causality is proposed in ref. 41; a static GC measure based on point process likelihoods is proposed in ref. 40. However, a modeling and estimation framework to simultaneously take into account the dynamicity and sparsity of the G-causal influences as well as the statistical properties of binary neuronal spiking data is lacking.

In this paper, we close this gap by developing a dynamic measure of GC by integrating the forgetting-factor mechanism of recursive least squares (RLS), point process modeling, and sparse estimation. To this end, we first exploit the prevalent parsimony of neurophysiological time constants manifested in neuronal spiking dynamics, such as those in sensory neurons with sharp tunings, as well as the potential low-dimensional structure of the underlying functional networks. These features can be captured by point process models in which the cross-history dependence of the neurons is described by sparse vectors. We then use an exponentially weighted log-likelihood framework (43) to recursively estimate the model parameters via sparse adaptive filtering, thereby defining a dynamic measure of GC, which we call the adaptive GC (AGC) measure.

The significance of sparsity in our approach is twofold. First, while the functional networks may not be truly sparse, they can often be parsimoniously described by a sparse set of significant functional links. Our models can indeed capture these significant links through sparse cross-history dependence. Second, sparsity enables stable estimation in the face of limited data. This is particularly important for adaptive estimation, where the goal is to reliably estimate a large number of cross-history parameters using short, effective observation windows.

We next develop a statistical inference framework for the proposed AGC measure by extending classical results on the analysis of deviance to our sparse dynamic point process setting. We provide simulation studies to evaluate the identification and tracking capabilities of our proposed methodology, which reveal remarkable performance gains compared with existing techniques, in both detecting the existing G-causal links and avoiding false alarms, while capturing the dynamics of the G-causal interactions in a neuronal ensemble. We finally apply our techniques to two experimentally recorded datasets: two-photon imaging data from the mouse auditory cortex under spontaneous activity and simultaneous single-unit recordings from the ferret primary auditory (A1) and prefrontal cortices (PFC) under a tone-detection task. Our analyses reveal the temporal details of the functional interactions between A1 and PFC under attentive behavior as well as among the auditory neurons under spontaneous activity at unprecedented spatiotemporal resolutions. In addition to their utility in analyzing neuronal data, our techniques have potential application in extracting functional network dynamics in other domains beyond neuroscience, such as social networks or gene regulatory networks, thanks to the plug-and-play nature of the algorithms used in our inference framework.

Theory and Algorithms

Preliminaries and Notations.

We use point process modeling to capture neuronal spiking statistics. A point process is a stochastic sequence of discrete events occurring at random points in continuous time. When adapted to the discrete time domain, point process models have proven to be successful in capturing the statistics of neuronal spiking (37, 44–46). Our analysis in this paper is based on discrete point process models, in which the observation interval $\mathcal{T}$ is discretized to $T≔\lceil \mathcal{T}/\mathrm{\Delta }\rceil$ bins of length $\mathrm{\Delta }$. By choosing $\mathrm{\Delta }$ small enough, the resulting neuronal data transform into a binary sequence ${\{n_t\}}_{t=1}^T$. The statistics of this sequence can be fully characterized by its conditional intensity function (CIF) denoted by ${\lambda }_t$, representing the neuron’s instantaneous firing rate at time bin $t$ conditional on all of the data and covariates up to time $t$. The binary spiking sequence can be modeled by a conditionally independent Bernoulli process with success probability of ${\lambda }_t\mathrm{\Delta }$.

Suppose that at time bin $t$ the effective neural covariates are collected in a vector ${𝐱}_t\in {ℝ}^M$. Such covariates include the neuron’s spiking history, the history of the activity of other neurons, and extrinsic stimuli. A dynamic generalized linear model (GLM) with logistic link function for this neuron’s CIF (43) is given by

$${\lambda }_t\mathrm{\Delta }≔{\text{logit}}^{-1}\left({𝝎}_t^{\prime }{𝐱}_t\right),$$ [1]

where ${\text{logit}}^{-1}(z)≔\frac{1}{1+\exp (-z)}$, for $z\in ℝ$, is the logistic function, and ${𝝎}_t$ denotes the time-varying parameter vector of length $M$ at time $t$, characterizing the dynamics of the underlying neuronal encoding process. We consider a multiscale window-based model for ${𝝎}_t$ with piecewise constant dynamics within windows of length $W\ge \mathrm{\hspace{0.17em}1}$ samples. To this end, we segment the spiking activity ${\{n_t\}}_{t=1}^T$ to $K≔\lceil T/W\rceil$ windows of length $W$ bins and assume that ${𝝎}_t={𝝎}_k$ for all $t\in [(k-1)W+1,\dots ,kW]$, where $k=1,\dots ,K$. For notational convenience, we denote the spiking activity associated with time window $k$ by a vector ${𝐧}_k≔{[n_{(k-1)W+1},n_{(k-1)W+2},\dots ,n_{kW}]}^{\prime }$, the CIF vector by ${𝝀}_k≔{[{\lambda }_{(k-1)W+1},{\lambda }_{(k-1)W+2},\dots ,{\lambda }_{kW}]}^{\prime }$, and the matrix of covariates by ${𝐗}_k≔{[{𝐱}_{(k-1)W+1},{𝐱}_{(k-1)W+2},\dots ,{𝐱}_{kW}]}^{\prime }$ with rows corresponding to the covariate vectors. We assume that the parameter vectors ${\{{𝝎}_k\}}_{k=1}^K$ are sparse.

To capture the adaptivity manifested in the spiking dynamics, we use the forgetting factor mechanism of RLS algorithms (47) and combine the data log-likelihoods up to time $k$ using an exponential weighting scheme (43):

$${\mathrm{\ell }}_k^{\beta }(𝝎)≔(1-\beta )\sum _{i=1}^k{\beta }^{k-i}({𝐧\prime }_i{𝐗}_i𝝎-{\mathbf{\hspace{0.17em}1}}_W^{\prime }\log ({\mathrm{𝟏}}_W+\exp ({𝐗}_i𝝎))),$$ [2]

where $𝝎$ denotes a generic parameter vector, $0<\beta \le 1$ is the forgetting factor parameter, and ${\mathrm{𝟏}}_W$ is the vector of all-ones of length $W$. When applied to vectors, the functions $\log (\cdot )$ and $\exp (\cdot )$ are understood to act in an elementwise fashion.

The parameter vectors ${𝝎}_k$ for $k=\mathrm{1,2},\dots ,K$ can be efficiently estimated from the data using a sparse adaptive point process filter, referred to as ${\mathrm{\ell }}_1{\text{–PPF}}_1$ (43). The ${\mathrm{\ell }}_1{\text{–PPF}}_1$ algorithm estimates the sparse time-varying parameter vectors from point process observations in an online fashion by recursively maximizing a sequence of ${\mathrm{\ell }}_1$-regularized exponentially weighted log-likelihoods via a proximal algorithm:

$${\widehat{𝝎}}_k=\underset{{𝝎}_k}{\text{argmax}}\{{\mathrm{\ell }}_k^{\beta }({𝝎}_k)-\gamma \parallel {𝝎}_k\parallel 1\},$$ [3]

where $\gamma \ge 0$ is a regularization parameter and can be selected analytically or through cross-validation (43). Statistical confidence regions for the estimates ${\widehat{𝝎}}_k$ can be computed using a recursive nodewise regression procedure (43). Throughout the rest of paper, we use the ${\mathrm{\ell }}_1{\text{–PPF}}_1$ algorithm for adaptive parameter estimation.

The AGC Measure.

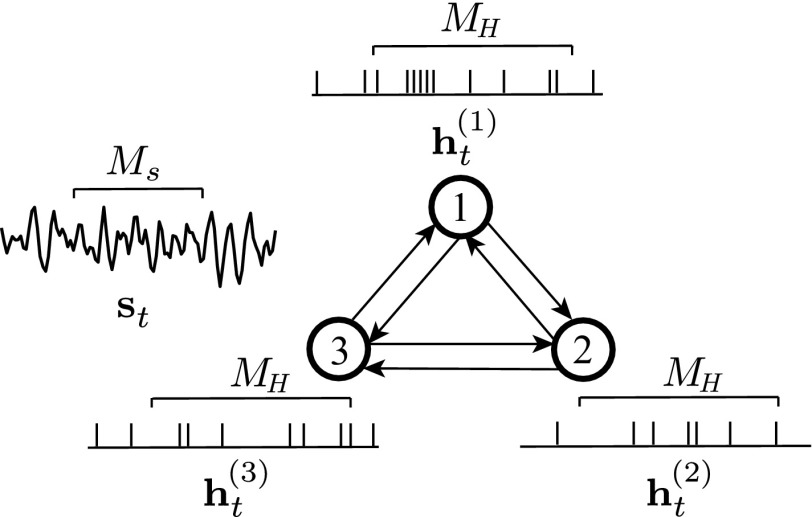
Consider simultaneous spike recordings from an ensemble of $C$ neurons indexed by $c=\mathrm{1,2},\mathrm{\cdots },C$, denoted by ${\{{\{n_t^{(c)}\}}_{t=1}^T\}}_{c=1}^C$ over the time bins $t=1,\mathrm{\cdots },T$. At time $t$, the spiking statistics of each neuron $(c)$ are modeled via the CIF formulation of Eq. 1 using a sparse modulation parameter vector ${𝝎}_t^{(c)}={[{\mu }_t^{(c)},{𝝎}_t^{{(c,1)}^{\prime }},{𝝎}_t^{{(c,2)}^{\prime }},\mathrm{\cdots },{𝝎}_t^{{(c,C)}^{\prime }},{𝜽}_t^{(c)}]}^{\prime }$ consisting of a scalar baseline firing parameter ${\mu }_t^{(c)}$, a collection of sparse history dependence parameter vectors ${\{{𝝎}_t^{(c,\stackrel{\sim }{c})}\}}_{\stackrel{\sim }{c}=1}^C$ of size $M_H$, in which ${𝝎}_t^{(c,\stackrel{\sim }{c})}$ represents the contribution of the spiking history of neuron $(\stackrel{\sim }{c})$ to the CIF of neuron $(c)$, and ${𝜽}_t^{(c)}$ accounts for the stimulus modulation vector (e.g., receptive field). Let $h_{t,i}^{(c)}≔{\sum }_{j=t-1-b_i}^{t-1-b_{i-1}}{n}_j^{(c)}$ be the spike count of neuron $(c)$ within the $i$-th spike counting window of length $W_{H,i}$, where $b_i≔{\sum }_{j=1}^i{W}_{H,j}$ for $i=\mathrm{1,2},\mathrm{\cdots },M_H$ and $b_0=0$. The covariates associated with the ensemble activity are given by ${𝐱}_t≔{[1,{𝐡}_t^{{(1)}^{\prime }},{𝐡}_t^{{(2)}^{\prime }},\mathrm{\cdots },{𝐡}_t^{{(C)}^{\prime }},{𝐬}_t^{\prime }]}^{\prime }$, where ${𝐡}_t^{(c)}≔{[h_{t,1}^{(c)},h_{t,2}^{(c)},\mathrm{\cdots },h_{t,M_H}^{(c)}]}^{\prime }$ denotes the history of spike counts of neuron $(c)$ within nonoverlapping windows of $W_H=[W_{H,1},\dots ,W_{H,M_H}]$ up to a lag of $L_H≔{\sum }_{i=1}^{M_H}{W}_{H,i}$, and ${𝐬}_t\in {ℝ}^{M_s}$ is the vector of neural stimuli in effect at bin $t$. We refer to this model, where the history of all of the neurons in the ensemble is taken into account, as the full model. Fig. 1 shows an example of the neuronal ensemble and the corresponding covariates for $C=3$.

Fig. 1.

An example of the neuronal ensemble model for $C=3$ neurons and $W_{H,i}=1,\forall i$. The CIF of neuron (2) can be expressed as ${\lambda }_t^{(2)}\mathrm{\Delta }={\text{logit}}^{-1}({\mu }_t^{(2)}+{𝝎}_t^{{(\mathrm{2,1})}^{\prime }}{𝐡}_t^{(1)}+{𝝎}_t^{{(\mathrm{2,2})}^{\prime }}{𝐡}_t^{(2)}+{𝝎}_t^{{(\mathrm{2,3})}^{\prime }}{𝐡}_t^{(3)}+{𝜽}_t^{{(2)}^{\prime }}{𝐬}_t)$.

To assess the G-causal influences, a likelihood-based GC measure has been proposed in ref. 40 for point process models. Consider neuron $(c)$ as the target neuron with an observation vector ${𝐧}^{(c)}≔{[n_1^{(c)},n_2^{(c)},\mathrm{\cdots },nT(c)]}^{\prime }$. Let ${\mathcal{H}}^{(c)}$ denote the history of the covariates of neuron $(c)$. The parameter vector and covariate history of neuron $(c)$ after excluding the effect of neuron $(\stackrel{\sim }{c})$ are denoted by ${𝝎}^{(c\setminus \stackrel{\sim }{c})}$ and ${\mathcal{H}}^{(c\setminus \stackrel{\sim }{c})}$, respectively, and compose the so-called reduced model. The log-likelihood ratio statistic associated with the G-causal influence of neuron $(\stackrel{\sim }{c})$ on neuron $(c)$ can be defined as

$${\mathcal{F}}^{(\stackrel{\sim }{c}\mapsto c)}≔s({\widehat{𝝎}}^{(c,\stackrel{\sim }{c})})\log \frac{\mathcal{L}({\widehat{𝝎}}^{(c)}|{𝐧}^{(c)},{\mathcal{H}}^{(c)})}{\mathcal{L}({\widehat{𝝎}}^{(c\setminus \stackrel{\sim }{c})}|{𝐧}^{(c)},{\mathcal{H}}^{(c\setminus \stackrel{\sim }{c})})},$$ [4]

where $\mathcal{L}(\widehat{𝝎}|𝐧,\mathcal{H})$ denotes the likelihood of estimated parameter vector $\widehat{𝝎}$ given the observation sequence $𝐧$ and the history of the covariates $\mathcal{H}$, and $s(𝝎)≔\text{sign}({\sum }_l{\omega }_l)$. Based on this formulation, the GC effect from neuron $(\stackrel{\sim }{c})$ to neuron $(c)$ can be measured as the reduction in the point process log-likelihood of neuron $(c)$ in the reduced model as compared with the full model. Note that the signum function determines the effective excitatory or inhibitory nature of this influence.

Most existing formulations of GC leverage the MVAR modeling framework (20–29, 31, 35), which pertains to data with linear Gaussian statistics. The GC measure in Eq. 4, however, benefits from the likelihood-based inference methodology and covers a wide range of complex statistical models. Both the MVAR-based GC measure and its log-likelihood-based point process variant of ref. 40 assume that the underlying time series are stationary (i.e., the modulation parameters are all static). In many scenarios of interest, however, the underlying dynamics exhibit nonstationarity. An example of such a scenario is the task-dependent receptive field plasticity phenomenon (43, 48, 49). In addition, ML estimation used by these techniques does not capture the underlying sparsity of the parameters and often exhibits poor performance, when the data length is short or the number of neurons $C$ is large.

To account for possible changes in the ensemble parameters and their underlying sparsity, we introduce the AGC measure, which is capable of capturing the dynamics of G-causal influences in the ensemble. To this end, we make two major modifications to the classical GC measure. First, we leverage the exponentially weighted log-likelihood formulation of Eq. 2 to induce adaptivity into the GC measure. Second, we exploit the possible sparsity of the ensemble parameters. Replacing the standard data log-likelihoods in Eq. 4 by their sparse adaptive counterparts given in Eqs. 2 and 3, we define the AGC measure from neuron $(\stackrel{\sim }{c})$ to neuron $(c)$ at time window $k$ as

$${\mathcal{F}}_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}≔s_k({\widehat{𝝎}}_k^{(c,\stackrel{\sim }{c})})({\mathrm{\ell }}_k^{\beta }({\widehat{𝝎}}_k^{(c)})-{\mathrm{\ell }}_k^{\beta }({\widehat{𝝎}}_k^{(c\setminus \stackrel{\sim }{c})})).$$ [5]

Although these modifications bring about crucial advantages in capturing the functional network dynamics in a robust fashion, they require construction of a statistical inference framework in order for the proposed AGC measure to be useful. We address these issues in the forthcoming section.

Statistical Inference of the AGC Measure.

Due to the stochastic and often biased nature of GC estimates, nonzero values of GC do not necessarily imply existence of G-causal influences. Hence, a statistical inference framework is required to assess the significance of the extracted G-causal interactions.

Consider two nested GLM models, referred to as full and reduced models, with parameters ${𝝎}^{(F)}≔{𝝎}^{(c)}$ and ${𝝎}^{(R)}={𝝎}^{(c\setminus \stackrel{\sim }{c})}$, respectively, in which the latter is a special case of the former. To assess the significance of a GC link, one can test for the null hypothesis $H_0:𝝎={𝝎}^{(R)}$ against the alternative $H_1:𝝎={𝝎}^{(F)}$. The commonly used test statistic is referred to as the deviance difference of the two models and is defined as $D({\widehat{𝝎}}^{(F)};{\widehat{𝝎}}^{(R)})≔\mathrm{\hspace{0.17em}2}(\mathrm{\ell }({\widehat{𝝎}}^{(F)})-\mathrm{\ell }({\widehat{𝝎}}^{(R)}))$, where $\mathrm{\ell }(\cdot )$ is the log-likelihood and ${\widehat{𝝎}}^{(F)}$ and ${\widehat{𝝎}}^{(R)}$ denote the parameter estimates under the full and reduced models, respectively. The deviance difference for the likelihood-based GC is twice the right-hand side of Eq. 4, modulo the signum function.

To perform the foregoing hypothesis test, the distributions of the deviance difference under the two hypotheses need to be characterized. Although these distributions are known for the classical GC measure (50–52), they cannot be readily extended to our AGC measure for two main reasons. First, the log-likelihoods are replaced by their exponentially weighted counterparts, which suppresses their dependence on the data length $N$ due to the forgetting factor mechanism. Second, unlike ML estimates, which are asymptotically unbiased, the ${\mathrm{\ell }}_1$-regularized ML estimates are biased and hence violate the common asymptotic normality assumptions.

To address these challenges, inspired by recent results in high-dimensional regression (53, 54), we define the adaptive de-biased deviance as

$$D_{k,\beta }({\widehat{𝝎}}_k;{𝝎}_k)≔\frac{1+\beta }{1-\beta }(\mathrm{\hspace{0.17em}2}({\mathrm{\ell }}_k^{\beta }({\widehat{𝝎}}_k)-{\mathrm{\ell }}_k^{\beta }({𝝎}_k))-{\dot{\mathbf{\ell }}}_k^{\beta }{({\widehat{𝝎}}_k)}^{\prime }{\ddot{\mathbf{\ell }}}_k^{\beta }{({\widehat{𝝎}}_k)}^{-1}{\dot{\mathbf{\ell }}}_k^{\beta }({\widehat{𝝎}}_k)),$$ [6]

where ${\dot{\mathbf{\ell }}}_k^{\beta }(\cdot )$ and ${\ddot{\mathbf{\ell }}}_k^{\beta }(\cdot )$ are the gradient vector and Hessian matrix of the exponentially weighted log-likelihood function ${\mathrm{\ell }}_k^{\beta }(\cdot )$, and ${𝝎}_k$ and ${\widehat{𝝎}}_k$ denote the true and estimated parameter vector at time window $k$, respectively. The adaptive de-biased deviance is composed of two main terms: The first term is twice the exponentially weighted log-likelihood ratio statistic, which is analogous to the standard deviance difference, whereas the second is a bias correction term. The bias correction term compensates for the effect of the ${\mathrm{\ell }}_1$-regularization bias imposed in favor of enforcing sparsity in the estimate ${\widehat{𝝎}}_k$. The effect of forgetting factor mechanism appears in the form of the scaling $(1+\beta )/(1-\beta )$. Finally, we define a test statistic referred to as adaptive de-biased deviance difference:

$$D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}≔D_{k,\beta }({\widehat{𝝎}}_k^{(c)};{𝝎}_k^{(c)})-D_{k,\beta }({\widehat{𝝎}}_k^{(c\setminus \stackrel{\sim }{c})};{𝝎}_k^{(c\setminus \stackrel{\sim }{c})}).$$ [7]

In what follows, we will mainly work with $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}$, as opposed to its biased version given by ${\mathcal{F}}_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}$ in Eq. 5. Note that ${\mathcal{F}}_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}=\frac{1}{2}{s}_k({\widehat{𝝎}}_k^{(c,\stackrel{\sim }{c})})(\frac{D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}}{1+\beta }+B_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)})$, where $B_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}$ is the difference of the bias terms of the full and reduced models.

There are four major challenges in inferring a GC influence from $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}$: (i) efficient computation of $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}$ from the data, (ii) determining the distribution of $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}$ under the absence and presence of a GC link, (iii) controlling the false discovery rate (FDR), and (iv) assessing the significance of the detected GC links. We will address these challenges in the remainder of this section. Fig. 2 shows a schematic depiction of the overall inference procedure, which we will discuss next.

Fig. 2.

Schematic depiction of the inference procedure for the AGC measure.

(i) Recursive computation of the AGC.

The computation of the adaptive de-biased deviance differences $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}$ for all of the possible $|\mathcal{C}|$ links and at all times $k$ is required for our statistical analysis. Therefore, in order for the analysis to scale favorably with the network size $C$ and the data length $K$, it is crucial to develop an efficient framework for the computation of the AGC measure. The RLS-inspired exponential weighting of the log-likelihoods in Eq. 2 indeed paves the way for the recursive computation of the AGC measure. The recursive procedure for computing ${\mathrm{\ell }}_k^{\beta }({\widehat{𝝎}}_k)$ for a generic estimate ${\widehat{𝝎}}_k$ is given in Algorithm S3 in SI Appendix, section 3, from which the AGC measure of Eq. 5 can be computed. This step comprises the recursive AGC computation block in Fig. 2.

(ii) Asymptotic distributional analysis of the AGC.

Let $M^{(F)}$ and $M^{(R)}$ denote the dimensions of ${𝝎}^{(c)}$ and ${𝝎}^{(c\setminus \stackrel{\sim }{c})}$, respectively. In Theorem S1 in SI Appendix, section 1 we establish the following result under mild technical conditions: As $\beta \to 1$,

• i)in the absence of a GC link from $(\stackrel{\sim }{c})$ to $(c)$, $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}\to {\chi }^2(M^{(d)})$, and
• ii)in the presence of a GC link from $(\stackrel{\sim }{c})$ to $(c)$, if the corresponding cross-history coefficients scale at least as $\mathcal{O}\left(\sqrt{\frac{1-\beta }{1+\beta }}\right)$, then $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}\to {\chi }^2(M^{(d)},{\nu }_k^{(\stackrel{\sim }{c}\mapsto c)})$,

where $M^{(d)}≔M^{(F)}-M^{(R)}$ is the dimensionality difference of the two nested models, and ${\nu }_k^{(\stackrel{\sim }{c}\mapsto c)}>0$ is the corresponding noncentrality parameter at time window $k$.

Theorem S1 has two main implications. First, it establishes that our proposed adaptive de-biased deviance difference statistic admits simple asymptotic distributional characterization. Given that these asymptotic distributions form the main ingredients of the forthcoming inference procedure, the second block in Fig. 2 serves to highlight the significance of adaptive de-biasing. As shown in SI Appendix, section 3, the bias $B_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}$ can also be computed in a recursive fashion.

Second, given that for ${\nu }_k^{(\stackrel{\sim }{c}\mapsto c)}=\mathrm{\hspace{0.17em}0}$ the noncentral chi-squared distribution coincides with the chi-squared distribution, the noncentrality parameter plays a key role in separating the distributions under the null and alternative hypotheses: When the deviance difference is close to zero, the null hypothesis $H_0$ is likely to be true (i.e., no GC link). When the deviance difference is large, the alternative $H_1$ is likely to be true (i.e., a GC link exists) (See Remark 2 in SI Appendix, section 1, for further discussion.) The noncentrality parameter ${\nu }_k^{(\stackrel{\sim }{c}\mapsto c)}$, however, is a complicated function of the true values of the parameters and cannot be directly observed. In the next two subsections, we initially assume that an estimate ${\widehat{\nu }}_k^{(\stackrel{\sim }{c}\mapsto c)}$ is at hand, and later on derive an algorithm for its estimation.

The output of the second block in Fig. 2 is the de-biased deviance differences corresponding to all pairs of neurons (shown in 2D as deviance difference maps). In the next two subsections we will show how to translate the deviance differences to statistically interpretable AGC links.

(iii) FDR control.

First, we use part i of the result of Theorem S1 to control the FDR in a multiple hypothesis testing framework. To this end, we use the Benjamini–Yekutieli (BY) procedure (55). The BY procedure aims at controlling the FDR, which is the expected ratio of incorrectly rejected null hypotheses, or namely “false discoveries,” at a desired significance level $\alpha$.

To identify significant GC interactions while avoiding spurious false positives, we conduct multiple hypothesis tests on the set of $|\mathcal{C}|≔C\times (C-1)$ pairwise possible GC interactions $\mathcal{C}≔\{(\stackrel{\sim }{c}\mapsto c)|\stackrel{\sim }{c},c=1,\dots ,C,c\ne \stackrel{\sim }{c}\}$ among the $C$ neurons at each time step $k$. The null hypothesis $H_{0,k}^{(\stackrel{\sim }{c}\mapsto c)}$ corresponds to lack of a GC link from neuron $(\stackrel{\sim }{c})$ to $(c)$ at time step $k$. Thus, rejection of the null hypothesis amounts to discovering a GC link $(\stackrel{\sim }{c}\mapsto c)$ at time step $k$. We first compute $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}$ for all possible links in $\mathcal{C}$. Based on Theorem S1, under null hypothesis $H_{0,k}^{(\stackrel{\sim }{c}\mapsto c)}$ we have $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}\to {\chi }^2(M^{(d)})$ as $\beta \to 1$. Hence, by virtue of convergence in distribution, for $\beta$ close to $1$, thresholding the test statistic results in a consistent approximation to limiting the false positive rate: $H_{0,k}^{(\stackrel{\sim }{c}\mapsto c)}$ is rejected at a confidence level of $1-\alpha$, if $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}>{\text{F}}_{{\chi }^2(M^{(d)})}^{-1}(1-\alpha )$, where ${\text{F}}_{{\chi }^2(M^{(d)})}^{-1}(\cdot )$ is the inverse CDF of a ${\chi }^2$ distribution with $M^{(d)}$ degrees of freedom. Using the BY procedure, we can thus control the mean FDR at a rate of $\overline{\alpha }≔\frac{(|\mathcal{C}|+1)\alpha }{2|\mathcal{C}|\log |\mathcal{C}|}$ for all tests (Fig. 2, third block). Algorithm S1 in SI Appendix, section 2, summarizes this procedure.

(iv) Test strength characterization via noncentral ${\chi }^2$ filtering and smoothing algorithm.

Next, we use part ii of the result of Theorem S1 to assess the significance of the tests for the detected GC links. Under the alternative hypothesis, Theorem S1 implies that $H_{1,k}^{(\stackrel{\sim }{c}\mapsto c)}:D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}\to {\chi }^2(M^{(d)},{\nu }_k^{(\stackrel{\sim }{c}\mapsto c)})$ as $\beta \to 1$. Hence, by virtue of convergence in distribution, the false negative rate can be estimated by ${\eta }_k^{(\stackrel{\sim }{c}\mapsto c)}≔{\text{F}}_{{\chi }^2(M^{(d)},{\widehat{\nu }}_k)}({\text{F}}_{{\chi }^2(M^{(d)})}^{-1}(1-\alpha ))$, at a confidence level of $1-\alpha$, where ${\text{F}}_{{\chi }^2(M^{(d)},{\widehat{\nu }}_k)}(\cdot )$ represents the CDF of a noncentral ${\chi }^2$ distribution with $M^{(d)}$ degrees of freedom and the estimate ${\widehat{\nu }}_k$ of the noncentrality parameter ${\nu }_k^{(\stackrel{\sim }{c}\mapsto c)}$. To quantify the significance of an estimated GC link, we use the Youden’s $J$-statistic, which is an effective measure often used for summarizing the overall performance of a diagnostic test. The J-statistic in our setting is given by

$$J_k^{(\stackrel{\sim }{c}\mapsto c)}≔\mathrm{\hspace{0.17em}1}-\alpha -{\text{F}}_{{\chi }^2(M^{(d)},{\widehat{\nu }}_k)}({\text{F}}_{{\chi }^2(M^{(d)})}^{-1}(1-\alpha )),$$ [8]

for a fixed significance level $\alpha$. Note that the J-statistic can take values in $[\mathrm{0,1}]$. The case of $J_k^{(\stackrel{\sim }{c}\mapsto c)}$ being close to one represents high sensitivity and specificity of the test statistic, which coincides with large values of noncentrality. One advantage of the J-statistic over the conventional P value is that it accounts for both type I and type II errors. In the context of GC analysis, the J-statistic for each possible link can serve as a normalized indicator of how reliable the detected link is. For consistency, we assign a value of $J_k^{(\stackrel{\sim }{c}\mapsto c)}=0$, when the null hypothesis is not rejected.

It remains to estimate the unknown noncentrality parameters ${\nu }_k^{(\stackrel{\sim }{c}\mapsto c)}$ given the observed deviance differences $D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}$. Under the assumption that ${\nu }_k^{(\stackrel{\sim }{c}\mapsto c)}$ changes smoothly in time, this can be carried out efficiently by a noncentral ${\chi }^2$ filtering and smoothing algorithm, which is given by Algorithm S2 in SI Appendix, section 2. Given these estimates, the J-statistics for the rejected nulls can be computed at $\overline{\alpha }$ (Fig. 2, fourth block), as summarized in Algorithm S1 in SI Appendix, section 2.

Algorithm 1: AGC Inference from Ensemble Neuronal Spiking

Input: Spike trains ${\{{\{n_t^{(c)}\}}_{t=1}^T\}}_{c=1}^C$ and parameters $\mathrm{\Theta }$.

• 1.for $c,\stackrel{\sim }{c}=1,\mathrm{\dots },C$,$\stackrel{\sim }{c}\ne c$ do
• 2.Recursively estimate the sparse time-varying modulation parameter vectors ${\{{\widehat{𝝎}}_k^{(c)}\}}_{k=1}^K$ and ${\{{\widehat{𝝎}}_k^{(c\setminus \stackrel{\sim }{c})}\}}_{k=1}^K$ corresponding to full and reduced GLMs using ${\mathrm{\ell }}_1{\text{–PPF}}_1$ (43),
• 3.Recursively compute the adaptive de-biased deviance differences ${\{D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}\}}_{k=1}^K$ (Algorithm S3),
• 4.Perform noncentral ${\chi }^2$-squared filtering and smoothing to estimate the noncentrality parameters ${\{{\widehat{\nu }}_k^{(\stackrel{\sim }{c}\mapsto c)}\}}_{k=1}^K$ from ${\{D_{k,\beta }^{(\stackrel{\sim }{c}\mapsto c)}\}}_{k=1}^K$ (Algorithm S2),
• 5.$\text{𝐟𝐨𝐫}$ k = 1, $\mathrm{\dots }$, K $\text{𝐝𝐨}$
• 6.Apply BY rejection rule to the ensemble set of GC tests to control FDR at rate $\alpha$ (Algorithm S1),
• 7.Compute AGC maps ${\widehat{𝚽}}_k\in {[-1,1]}^{C\times C}$ based on the $J$-statistics as ${({\widehat{𝚽}}_k)}_{c,\stackrel{\sim }{c}}≔s_k({\widehat{𝝎}}_k^{(c,\stackrel{\sim }{c})})J_k^{(\stackrel{\sim }{c}\mapsto c)}$ (Algorithm S1).

Output: AGC maps${\{{\widehat{𝚽}}_k\}}_{k=1}^K$.

Summary of Advantages over Existing Work.

Algorithm 1 summarizes the overall AGC inference procedure. Choices of the parameters $\mathrm{\Theta }$ involved in Algorithm 1 and its computational complexity are discussed in SI Appendix, sections 4–6. Before presenting applications to synthetic and real data, we summarize the advantages of our methodology over existing work:

• i)Sparse dynamic GLM modeling provides more accurate estimates of the parameters (43), and hence more reliable detection of the GC links, as compared with existing static methods based on ML. We examine this aspect of our methodology in SI Appendix, section 8, using an illustrative simulation study;
• ii)Relating the noncentrality parameters to the test strengths of the detected GC links is not used by existing techniques. In light of Theorem S1 and the need for estimating the noncentrality parameters, we devised a noncentral ${\chi }^2$ filtering and smoothing algorithm to exploit the entire observed data for obtaining reliable estimates;
• iii)Exponential weighting of the log-likelihoods admits construction of adaptive filters for estimating the network parameters in a recursive fashion, which significantly reduces the computational complexity of our inference procedure; and
• iv)Characterization of AGC via the J-statistic as a normalized measure of hypothesis test strength for each detected GC link can be further used for graph-theoretic analysis of the inferred functional networks. By viewing the J-statistic as a surrogate for link strength, the AGC networks can be refined by thresholding the J-statistics, and access to the distribution of the J-statistics in a network allows one to perform further hypothesis tests regarding the network function (56).

In the next section, we illustrate these advantages by comparing our methodology with two representative techniques for inferring functional network dynamics.

Applications

A Simulated Example.

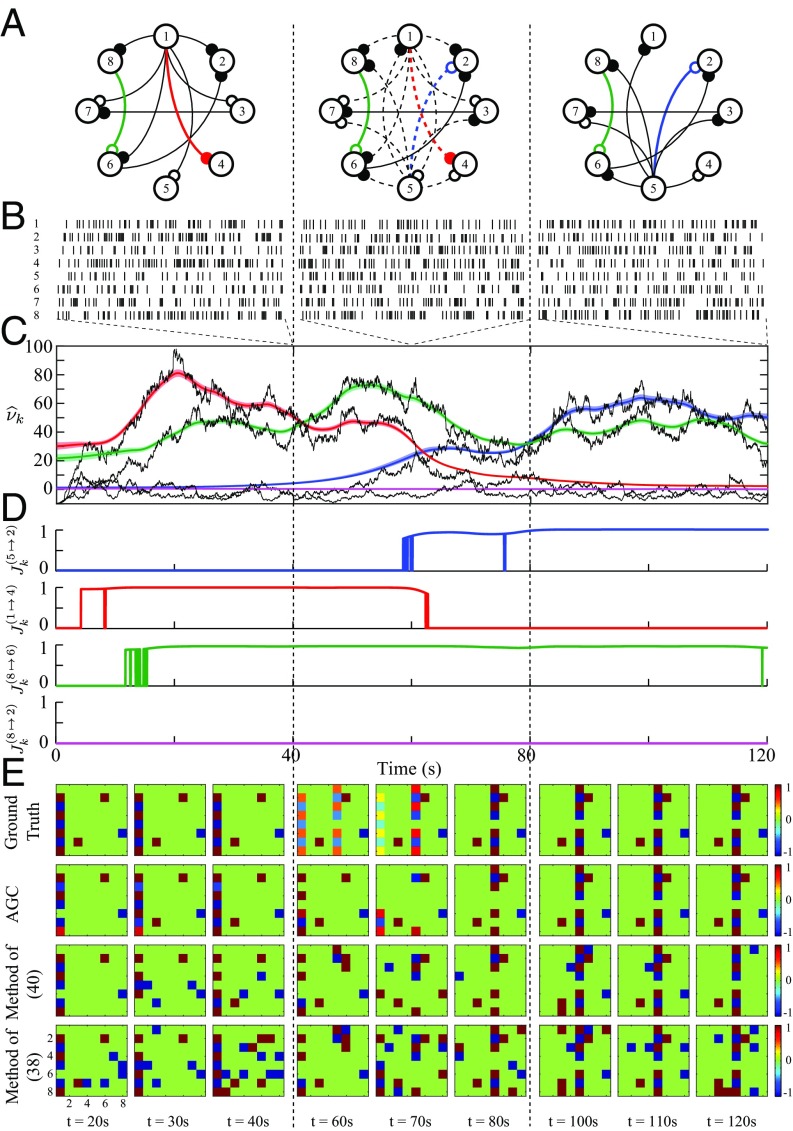
We consider a network of $C=8$ functionally interconnected neurons whose connectivity pattern evolves in time. As illustrated in Fig. 3A, the network dynamics undergo three main states, each covering one-third ($40$ s) of the simulation period: (i) the first static state, where neuron $(1)$ plays a dominant role, causally influencing all other neurons; (ii) the intermediate dynamic state, where neuron $(1)$ loses the dominant role to neuron $(5)$, as its causal influences smoothly decay, while a new set of causal interactions from neuron $(5)$ to all of the other neurons emerge; and (iii) the final static state, where all of the causal links from neuron $(1)$ are completely vanished and the links from neuron $(5)$ are stabilized. The network also comprises three static causal links, for example, $(3\mapsto 7)$, which remain constant throughout.

Fig. 3.

Functional network dynamics inference from simulated spikes. (A) Three states of the functional network evolution, where neurons (vertices) are interacting through static (solid edges) or dynamic (dashed edges) causal links of inhibitory (open circles) or excitatory (filled circles) nature. (B) One realization of simulated spikes within windows of $1$ s selected at $\{\mathrm{40,60,120}\}$ s. (C) Estimated noncentrality ${\widehat{\nu }}_k$ across time corresponding to four selected GC links (color-coded in network map), along with the shifted deviance differences $D_k-M^{(d)}$ (black traces) and the $95\%$ confidence regions for each estimated trace ${\widehat{\nu }}_k$ (colored traces). (D) Four panels of estimated $J$-statistics $J_k$ corresponding to the selected GC links. (E) Performance comparison of the causal inference methods: (i) the proposed AGC method (second row), (ii) the static GC method in ref. 40 (third row), and (iii) the functional connectivity method in ref. 38 (last row), along with the true causality maps (first row). Each panel represents the estimated $8\times 8$ causality map at a specific time.

An observation period of $\mathcal{T}=120\text{s}$ is discretized to $K=120\text{k}$ bins of length $\mathrm{\Delta }=1\text{ms}$. We use a point process model with Bernoulli spiking statistics to generate the binary spike trains for all neurons, where the CIF is modeled given the dynamic GLM of Eq. 1. The details of the parameter selection and estimation are given in SI Appendix, section 5. Fig. 3B shows a realization of the simulated spike trains indicated by black vertical lines for all eight neurons within three sample windows of length $1$ s, with end points at $\{\mathrm{40,60,120}\}\text{s}$, selected from the three segments of the simulation. Note that the G-causal pattern of Fig. 3A is unknown to the estimator, and is to be inferred from the simulated spike trains. Fig. 3C shows the time course of the estimated noncentrality parameters ${\widehat{\nu }}_k$ and their $95\%$ confidence intervals obtained by the noncentral ${\chi }^2$ filtering and smoothing algorithm associated with four selected GC links: (i) $(1\mapsto \mathrm{\hspace{0.17em}4})$ a dynamic weakening GC link (red), (ii) $(5\mapsto \mathrm{\hspace{0.17em}2})$ a dynamic strengthening GC link (blue), (iii) $(8\mapsto \mathrm{\hspace{0.17em}6})$ a static link (green), and (iv) $(8\mapsto \mathrm{\hspace{0.17em}2})$ a nonexisting GC link (magenta). Black traces show the shifted observed deviances $D_k-M^{(d)}$. Fig. 3D represents the time course of the estimated $J$-statistics plotted in four separate panels, where the FDR is controlled at a rate $\alpha =0.1$.

In Fig. 3C, the estimates of ${\widehat{\nu }}_k$ corresponding to the three existing GC links take significant values, correctly identifying the G-causal interactions, while ${\widehat{\nu }}_k$ takes values close to zero for the nonexisting link, implying no significant G-causal interaction. The time course of changes for both dynamic links and the static link is closely tracked by the noncentrality parameters, albeit with an apparent delay. This delay is due to the choice of the effective window length and highlights the trade-off between estimation accuracy and delay. While it is possible to reduce this delay by choosing smaller effective windows, for the sake of accuracy of parameter estimation, and thereby robust detection of the AGC links, we have chosen the effective window length to be $10$ s (a fraction of the $40$-s transition period) to incur a tolerable delay. The aforementioned performance is echoed in the test strengths quantified by the $J$-statistics shown in Fig. 3D. Even though the noncentrality parameters in Fig. 3C track the changes of the network parameters much faster, the J-statistics may lag behind due to the conservative statistical thresholds set by the FDR control procedure. By choosing a higher FDR level, the J-statistics will capture the changes much faster, but at the expense of possibly more false discoveries. It is noteworthy that our proposed method distinguishes the direct GC links from the indirect ones, as it correctly detects the direct GC links $(8\mapsto \mathrm{\hspace{0.17em}6})$ and $(6\mapsto \mathrm{\hspace{0.17em}2})$ but rejects the existence of the corresponding indirect link $(8\mapsto \mathrm{\hspace{0.17em}2})$.

The top row in Fig. 3E shows the ground truth G-causal maps plotted at nine time instances (three per segment). Each map $\mathrm{\Phi }$ represents an $8\times 8$ color-coded array showing the excitatory, inhibitory, and no-GC links in red, blue, and green, respectively. The AGC maps estimated by our method are shown in the second row, where each entry ${({\widehat{𝚽}}_k)}_{c,\stackrel{\sim }{c}}$ represents the $J$-statistic $J_k^{(\stackrel{\sim }{c}\mapsto c)}$ of the estimated GC link $(\stackrel{\sim }{c}\mapsto c)$, where the excitatory or inhibitory nature of the links is determined by the sign of the AGC measure, accounting for the aggregate cross-history contribution, and is not indicative of the morphological identity of the connections.

We compare the AGC maps with two other methods: the static GC method of ref. 40 (third row), and the functional connectivity analysis of ref. 38 (final row). To adapt these methods to the time-varying setting, we used nonoverlapping window segments whose length is chosen to match the effective window length $N_{eff}≔\frac{W}{1-\beta }$ of our method. Within each window, the signed binary functional connectivity is estimated using the methods outlined in refs. 38 and 40. The true model order and the same significance level are used for all methods (see SI Appendix, section 5, for more details). Fig. 3E (last two rows) shows the connectivity maps obtained by refs. 38 and 40. On a qualitative level, Fig. 3E reveals the favorable performance of our proposed framework in terms of both identification and tracking of the GC influences. The method of ref. 40 results in both high false positive and false negative errors and fails to track the GC dynamics due to highly variable parameter estimates. Similarly, the method of ref. 38 shows poor false positive rejection and tracking performance.

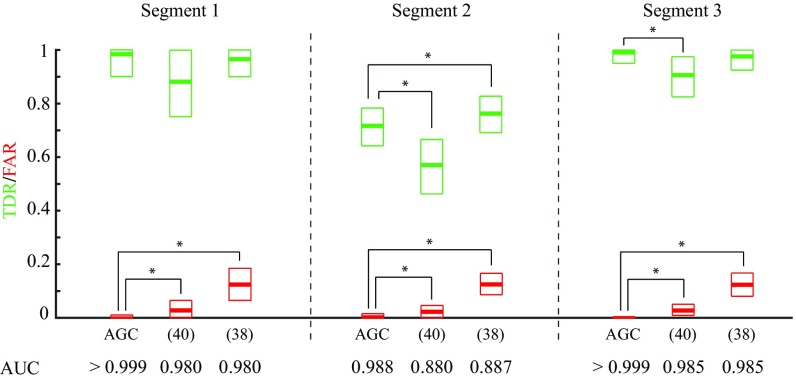
To quantify the foregoing performance comparison, we repeated the simulation for $R=500$ realizations of spike trains randomly generated based on the network dynamics in Fig. 3A. Fig. 4 represents the performance results in terms of true detection rate (TDR) and false alarm rate (FAR), which are shown in green and red, respectively. Boxes represent the mean and $90\%$ confidence intervals. Based on the Wilcoxon signed-rank test with $P<0.001$, our method has a significantly lower FAR compared with both ref. 38 (effect sizes of $r=1$ for all segments) and ref. 40 ($r=0.8,0.86$ and $0.98$ for the three segments, respectively). Our achieved TDRs are also significantly higher than those of ref. 40 ($r=0.73,0.996$ and $0.94$ for the three segments, respectively) and are only outperformed by ref. 38 in the middle segment ($r=0.19,0.86$ and $0.27$ for the three segments, respectively). By varying the significance levels for all of the algorithms, we also evaluated their receiver operating characteristic (ROC) performance, whose area under the curve (AUC) values for the three segments are indicated in Fig. 4. Further details on the comparison procedure as well as assessing the robustness of our method to the choice of parameters are given in SI Appendix, section 7. It is noteworthy that our method is the only one with consistently low FAR ($<1\%$), while maintaining high TDR. Finally, both methods in refs. 38 and 40 output binary connectivity maps, as opposed to AGC, which provides normalized continuous-valued test strengths of the detected GC links. In the spirit of easing reproducibility, we have archived a MATLAB implementation that fully generates Fig. 3 on GitHub (https://github.com/Arsha89/AGC_Analysis).

Fig. 4.

Performance comparison of AGC inference with the methods of refs. 40 and 38 in terms of TDR (green) and FAR (red) for the three segments of the simulation period. Boxes represent the mean and $90\%$ confidence intervals. Asterisks indicate significant difference with effect size of $r\ge 0.8$ (Wilcoxon signed-rank test, $P<0.001$). AUC values corresponding to the ROC performance of the three algorithms are reported at the bottom (see SI Appendix, section 7 for more details).

Application to Real Data: Spontaneous Activity in the Mouse Auditory Cortex.

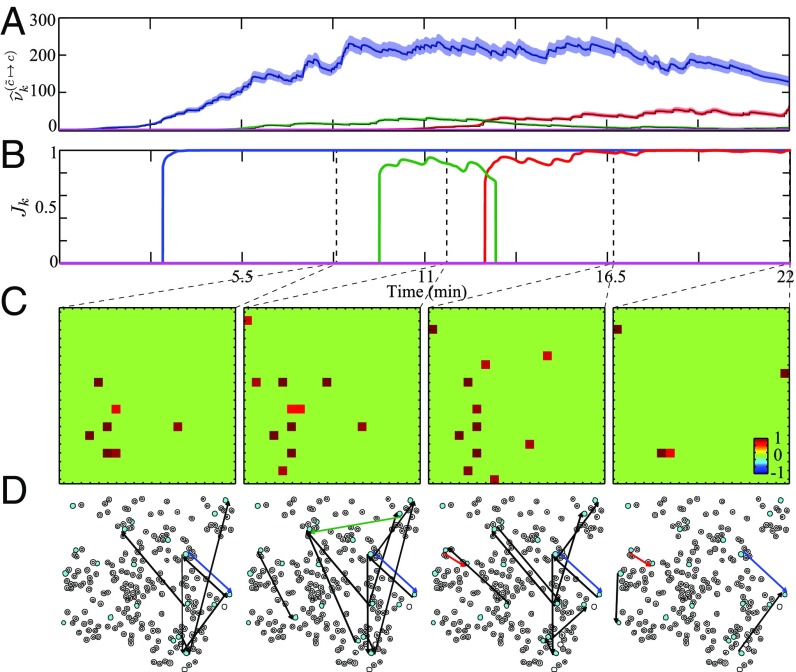
In this section, we apply our proposed method to experimentally recorded neuronal population data from the mouse auditory cortex. We imaged the spontaneous activity in the auditory cortex of an awake mouse with in vivo two-photon calcium imaging (see SI Appendix, section 13 for details of the experimental procedures). Within an imaged field of view, the activity of $N_{\text{cells}}=219$ neurons is recorded at a sampling rate of $f_s\approx 30\text{Hz}$ for a total duration of $T\approx 22\text{min}$. Spike trains are inferred from the fluorescence traces using the constrained-foopsi technique (57). For GC inference, a subset of $C=20$ neurons exhibiting high spiking activity were selected, as many of the neurons in the ensemble are relatively silent. The FDR is controlled at a rate of $\alpha =0.005$ for testing the $|\mathcal{C}|=380$ possible GC links. Fig. 5 A and B show the time course of the noncentrality estimates and $J$-statistics for four selected candidate GC links, respectively. These representative GC links consist of a persistent link $(6\mapsto 4)$ (blue), two transient links $(1\mapsto 18)$ (red) and $(2\mapsto \mathrm{\hspace{0.17em}12})$ (green), and an insignificant link $(8\mapsto 9)$ (magenta). Fig. 5 C and D show four snapshots of the AGC map estimates, respectively in the matrix form and as a network overlaid on the slice, at time-stamps $\{8.33,11.66,16.66,22.22\}\text{min}$. Other than the three color-coded significant links, the rest of the detected G-causal links are indicated by black arrows.

Fig. 5.

Adaptive G-causal interactions among ensemble of neurons in mouse auditory cortex under spontaneous activity. The time course of estimated GC changes for four selected GC links obtained through (A) noncentrality parameter ${\widehat{\nu }}_k$ and (B) J-statistics $J_k$. (C) AGC map estimates ${\widehat{\mathrm{\Phi }}}_k$ at four selected points in time, marked by the dashed vertical lines in the top panel. (D) network maps overlaid on the slice, showing cells with black circles and the selected cells highlighted in cyan. The detected GC links are depicted in black directed arrows and colored for the selected links.

The detected G-causal maps are considerably sparse (maximum $\sim 16$ out of $380$ possible links), with a few persistent GC links and a multitude of transient links emerging and vanishing over time (Movies S1 and S2). The sparsity of the AGC maps is consistent with sparse activity in auditory cortex (58). A careful inspection of the spatial pattern of the AGC links reveals that the detected links correspond to distances in the range of $[\mathrm{150,200}]\mu \text{m}$. These distances are consistent with in vitro measurements of the spatial patterns of intralaminar connectivity within the mouse auditory cortex (59), showing a significant peak in the connection probability within the mean radial range of $[\mathrm{120,200}]\mu \text{m}$. These results indicate that the proposed AGC method is able to detect underlying connectivity patterns among neurons.

Application to Real Data: Ferret Cortical Activity During Active Behavior.

Studies of the PFC have revealed its association with high-level executive functions such as decision making and attention (60–62). In particular, recent findings suggest that PFC is engaged in cognitive control of auditory behavior (62), through a top-down feedback to sensory cortical areas, resulting in enhancement of goal-directed behavior. It is conjectured in ref. 63 that the top-down feedback from PFC triggers adaptive changes in the receptive field properties of A1 neurons during active attentive behavior, to facilitate the processing of task-specific stimulus features. This conjecture has been examined in the context of visual processing, where top-down influences exerted on the visual cortical pathways have been shown to alter the functional properties of cortical neurons (64, 65).

To examine this conjecture at a single-unit level, we apply our proposed AGC inference method to single-unit spiking activities from an ensemble of neurons simultaneously recorded from two cortical regions of A1 and PFC in ferrets during a series of passive listening and active auditory task conditions. In this application, we sought to reveal the significant task-specific changes in the G-causal interactions within or between PFC and A1 regions at the single-unit level during active behavior. We used the spike data recordings from a large set of experiments (more than $35$) conducted on three ferrets for GC inference analysis (data from the Neural Systems Laboratory, Institute for Systems Research, University of Maryland, College Park, MD). During each trial in an auditory discrimination task, the ferrets were presented with a random sequence of broadband noise-like acoustic stimuli known as temporally orthogonal ripple combinations (TORCs) along with randomized presentations of the target tone. Ferrets were trained to attend to the spectrotemporal features of the presented sounds and discriminate the tonal target from the background reference stimuli (see ref. 63 for details of the experimental procedures). Due to their broadband noise-like features, the TORCs and the corresponding neural responses admit efficient estimation of the spectrotemporal tuning of the primary auditory neurons via sparse regression (43, 66).

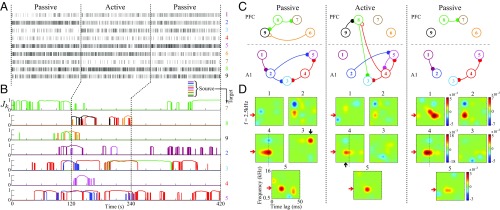
Fig. 6 shows our results on a selected experiment in which a total number of $C=9$ single units were detected through spike sorting (five units in A1 and four units in PFC). The selected experiment consists of three main blocks: passive listening pretask, active task, and passive listening post-task, composed of $R=\mathrm{4,4},$ and $6$ repetitions, respectively. Within each repetition, a complete set of $30$ randomly permuted TORCs were presented along with a randomized presentation of the target tone at $f=2.5\text{kHz}$. Fig. 6A shows the activity of all of the units during the first repetition of each block, separated by vertical dashed lines. Fig. 6B shows the time courses of the inferred $J$-statistics, where each row represents the significant incoming GC links from all of the other units. Each unit and its significant outgoing GC links are color-coded uniquely as labeled on the right side of each panel. For brevity, the significant GC links that show a degree of persistence during at least one block of the experiment are plotted. Fig. 6C depicts the representative network maps of the GC links among the nine units during the three main blocks, where each significant GC link from panel Fig. 6B is indicated by a directional link. Finally, Fig. 6D exhibits snapshots of the STRFs of all of the five A1 units, taken at the end point of each block. The red arrow marks the tonal target.

Fig. 6.

Dynamic inference of G-causal influences between single-units in ferret PFC and A1 during auditory task. (A) Spike trains corresponding to the first repetition of each block. (B) Time course of significant GC changes through $J$-statistics for selected single-units (FDR controlled at $\alpha =0.1$). (C) Detected patterns of network AGC maps during three main blocks of experiment. (D) Spectrotemporal receptive field (STRF) snapshots of A1 units at the end points of three blocks of experiment.

Three major task-specific dynamic effects can be inferred from Fig. 6: (i) a significant bottom-up GC link from the target-tuned A1 unit during active behavior, (ii) a persistent task-relevant top-down GC link, and (iii) task-relevant plasticity and rapid tuning changes within A1. First, unit $4$ in A1 shows strong frequency selectivity to the target around $f=2.5$ kHz during the whole experiment (vertical dashed lines, Fig. 6D). Moreover, its STRF dynamics reveal a plastic shift of the target-tuned facilitative regions to shorter latencies following the active attentive behavior (upward arrow, middle panel; see also Movie S3). Strikingly, a bottom-up GC link from the very same strongly target-tuned unit to PFC (red link, $4\mapsto 8$) emerges during the active task (second row, Fig. 6B), temporally preceding any top-down significant GC link.

The second effect appears as a strong top-down GC link (green link, $8\mapsto 3$) which builds up during the active auditory behavior and even persists during a few repetitions of the post-active condition (fifth row, Fig. 6B). The onset of this top-down GC link coincides with a dramatic and rapid change in the STRF of the A1 unit $3$, which was initially tuned to $\sim 8$ kHz (downward arrow, Fig. 6D, Left) but eventually gets suppressed at this nontarget frequency (Fig. 6D, Middle) by getting G-causally influenced by the PFC unit $8$. This effect reveals the relationship between the top-down network dynamics and the changes in the tuning of the A1 units. We examine the dynamics of the parameters of the foregoing bottom-up and top-down links in detail in SI Appendix, section 10, for further clarification. The third effect concerns the emergence and strengthening of frequency selectivity in some of the A1 units (e.g., units $1$ and $2$, Fig. 6D, Right) to the target tone, which alludes to a salient synaptic reinforcement effect within A1 during and after the active task.

In addition to these interregion GC links, multiple instances of GC links within A1 (e.g., $5\mapsto 4$) or within PFC (e.g., $9\mapsto 8$) emerge or vanish during the active block, which accounts for the task-specific network-level changes within the cortical regions that are involved in active listening. A salient instance of this phenomenon can be observed in the dynamics of unit $8$, whose GC links within PFC significantly change during the active behavior: As it gets G-causally linked to the lower-level A1 region, its GC links to the other PFC units fade away (rows 1, 3 and 5, Fig. 6B). It is noteworthy that the fluctuating instances of the J-statistics (e.g., Fig. 6B, fourth row, third segment) are due to the FDR control procedure, and there is no evidence to believe that they have a neurophysiological basis. To reduce these fluctuations, one can choose a higher FDR rate. If these effects persist at high FDR rates, further inspection of the cross-history coefficients is needed to assess their possible neurophysiological basis (see SI Appendix, section 10 for further discussion).

To validate our results in the absence of ground truth, we assess their reliability using surrogate data obtained by random shuffling and network subsampling in SI Appendix, section 11 and verify the robustness of the inferred task-dependent functional network dynamics against the aforementioned adversarial perturbations. In conclusion, our methodology enabled the extraction of the top-down and bottom-up network-level dynamics that were previously conjectured in ref. 63 to be involved in active attentive behavior, at the neuronal scale with high spatiotemporal resolution. In SI Appendix, section 12 we present our analysis of another experiment, which further corroborates our findings.

Discussion and Concluding Remarks

Summary and Extensions of Our Contributions.

Most widely adopted time series analysis techniques for quantifying functional causal relations among the nodes in a network assume static functional structures or otherwise enforce dynamics using sliding windows. While they have proven successful in analyzing stationary Gaussian time series, when applied to spike recordings from neuronal ensembles undergoing rapid task-dependent dynamics they hinder a precise statistical characterization of the sparse dynamic neuronal functional networks underlying adaptive behavior.

To address these shortcomings, we developed a dynamic inference paradigm for extracting functional neuronal network dynamics in the sense of Granger, by integrating techniques from adaptive filtering, compressed sensing, point process theory, and high-dimensional statistics. We proposed a measure of time-varying GC, namely AGC, and demonstrated its utility through theoretical analysis, algorithm development, and application to synthetic and real data. Our analysis of the mouse auditory cortical data revealed unique features of the functional neuronal network structures underlying spontaneous activity at unprecedented spatial resolution. Application of our techniques to simultaneous recordings from the ferret auditory and prefrontal cortical areas suggested evidence for the role of rapid top-down and bottom-up functional dynamics across these areas involved in robust attentive behavior.

The plug-and-play nature of the algorithms used in our framework enables it to be generalized for application to various other domains beyond neuroscience, such as the analysis of social networks or gene regulatory networks. As an example, the GLM models can be generalized to account for $m$-ary data, the forgetting factor mechanism for inducing adaptivity can be extended to state-space models governing the coefficient dynamics, and the FDR correction can be replaced by more recent techniques such as knockoff filters (67). To ease reproducibility and aid the adoption of our method, we have archived a MATLAB implementation on GitHub (https://github.com/Arsha89/AGC_Analysis).

Limitations of Our Approach.

In closing, it is worth discussing two potential limitations of our proposed paradigm.

Confounding effects due to network subsampling.

A common criticism of statistical causality measures, such as the GC, directed information, or transfer entropy, is susceptibility to latent confounding causal effects arising from network subsampling. In practice, these methods are typically applied to a small subnetwork of the circuits involved in neuronal processing. Given that each neuron may receive thousands of synaptic inputs, lack of access to a large number of latent confounding inputs can affect the validity of the causal inference results obtained by these methods.

We have evaluated the robustness of our method against such confounding effects using comprehensive numerical studies in SI Appendix, section 9. These studies involve scenarios with deterministic and stochastic latent common inputs as well as confounding effects due to network subsampling and suggest that our techniques indeed exhibit a degree of immunity to such confounding effects. We argue that this performance is due to explicit modeling of the dynamics of the Granger causal effects in the GLM framework, invoking the sparsity hypothesis, and using sharp statistical inference procedures (see SI Appendix, section 9 for further discussion).

Biological interpretation.

The functional network characterization provided by our framework must not be readily interpreted as direct or synaptic connections that result in causal effects. Our analysis results in a sparse number of GC interactions between neurons that can appear and vanish over time in a task-specific fashion. While it is possible that these connections reflect synaptic contacts between neurons, as changes in synaptic strengths can be induced rapidly within minutes (68), the observed GC dynamics could also be due to other underlying mechanisms such as desynchronization of inputs, altered shunting, or dendritic filtering. Thus, these plasticity effects remain to be tested with ground truth experiments. An alternative and inclusive view is that these links reflect a measure of information transferred from one neuron to another.

The relatively rapid switching of these links, however, must be interpreted with caution: While some of the rapid fluctuations are due to the use of the FDR control procedure (as discussed in the Applications), sudden emergence or disappearance of a link does not necessarily imply sudden changes in the causal structure or information transfer in the network. A sudden disappearance of a steady link most likely reflects the fact that given the amount of currently available data, there is not enough evidence to maintain the existence of the link at the group level with the desired statistical confidence; similarly, a sudden emergence of a link most likely implies that enough evidence has just been accumulated to justify its presence with statistical confidence. The gradual effects of these interactions are indeed reflected in the dynamics of the noncentrality parameters estimated by our methods.

As demonstrated by the applications of our inference procedures, our framework provides a robust characterization of the dynamic statistical dependencies in the network in the sense of Granger at high temporal resolution. This characterization can be readily used at a phenomenological level to describe the dynamic network-level functional correlates of behavior, as demonstrated by our real data applications. More importantly, this characterization can serve as a guideline in forming hypotheses for further testing of the direct causal effects using experimental procedures such as lesion studies, microstimulation, or optogenetics in animal models.