Peptide Level Turnover Measurements Enable the Study of Proteoform Dynamics

Abstract

The coordination of protein synthesis and degradation regulating protein abundance is a fundamental process in cellular homeostasis. Today, mass spectrometry-based technologies allow determination of endogenous protein turnover on a proteome-wide scale. However, standard dynamic SILAC (Stable Isotope Labeling in Cell Culture) approaches can suffer from missing data across pulse time-points limiting the accuracy of such analysis. This issue is of particular relevance when studying protein stability at the level of proteoforms because often only single peptides distinguish between different protein products of the same gene. To address this shortcoming, we evaluated the merits of combining dynamic SILAC and tandem mass tag (TMT)-labeling of ten pulse time-points in a single experiment. Although the comparison to the standard dynamic SILAC method showed a high concordance of protein turnover rates, the pulsed SILAC-TMT approach yielded more comprehensive data (6000 proteins on average) without missing values. Replicate analysis further established that the same reproducibility of turnover rate determination can be obtained for peptides and proteins facilitating proteoform resolved investigation of protein stability. We provide several examples of differentially turned over splice variants and show that post-translational modifications can affect cellular protein half-lives. For example, N-terminally processed peptides exhibited both faster and slower turnover behavior compared with other peptides of the same protein. In addition, the suspected proteolytic processing of the fusion protein FAU was substantiated by measuring vastly different stabilities of the cleavage products. Furthermore, differential peptide turnover suggested a previously unknown mechanism of activity regulation by post-translational destabilization of cathepsin D as well as the DNA helicase BLM. Finally, our comprehensive data set facilitated a detailed evaluation of the impact of protein properties and functions on protein stability in steady-state cells and uncovered that the high turnover of respiratory chain complex I proteins might be explained by oxidative stress.

Proteins participate in the control as well as the execution of virtually every process that is involved in the perpetuation of cellular homeostasis thereby defining the functional state of a cell. Despite a common genetic basis, cells and tissues of organisms feature a wide range of physiological diversity not least determined and regulated by underlying differences in protein expression patterns (1). Even though the abundance of cellular proteins remains constant over time under steady-state conditions, they exist in a dynamic state in which they are continuously destructed and reconstructed (2). This “default” protein turnover contributes to a cell's capability to rapidly respond to external stimuli by dynamically altering protein abundance to establish an appropriate new equilibrium. To expand the understanding of the concerted action of protein synthesis and degradation for the control and adjustment of protein abundance, protein turnover has been studied for decades (3). Traditional approaches have made use of a multitude of methodologies notably pulse-chase radiolabeling (4, 5), inhibition of protein synthesis (6), or tagging of endogenous proteins with fluorescent dyes (7, 8). However, radioactive labeling only allows for the analysis of bulk protein turnover or the determination of the stability of single proteins. Treatment of cells with translation inhibitors disrupts cell homeostasis and half-lives determined in this way might not fully reflect the actual endogenous degradation process. Similarly, measuring the stability of fluorescently tagged and overexpressed proteins might also not equate physiological protein half-lives.

In recent years, advances in mass spectrometry (MS) based technologies in conjunction with Stable Isotope Labeling in Cell Culture (SILAC)¹ (9) have dramatically improved protein turnover measurements. Today, protein replacement rates can be determined on a global scale by measuring the incorporation of “heavy” isotope labeled amino acids into newly synthesized proteins in a time dependent manner. Likewise, the loss of the residual “light” amino acids reflecting the degradation of proteins can be determined in each pulse time point. Such a dynamic SILAC setup has enabled the parallel measurement of turnover characteristics of thousands of endogenous proteins expressed at physiological levels (10–16). However, despite ongoing efforts, technical issues still exist and important cellular mechanisms affecting protein stability at the molecular level still remain elusive. For example, comparison of different studies often show limited correlation of protein turnover rates and sometimes arrive at contrasting conclusions about which protein properties might affect half-lives (7, 11, 14, 16–18). In addition, different cellular stabilities have been reported for the same protein depending on its localization (14), the cellular condition (16), protein interactions (19), or its post-translational modification state (17). Moreover, differences in turnover rates have also been detected for splice variants of the same gene (20). Considering that more than 200 different types of protein modifications have been described to exist (21) and that nearly all multi-exon genes have been shown to be alternatively spliced (22), proteoform level turnover measurements are important but have largely been neglected in the past.

Studying proteoform dynamics is not trivial. First, a robust and accurate method for quantification of pulsed SILAC labeled peptides across multiple time points is needed because, in proteomic datasets, often only single peptide sequences distinguish noncanonical from canonical isoforms or modified from nonmodified proteins. However, the standard dynamic SILAC approach suffers from substantial missing quantitative values across pulse time-points. This issue is amplified when increasing the number of measured pulse time-points and matters a lot when analyzing data at the peptide level. Although protein level quantification can make use of averaging several peptide measurements thereby increasing the robustness of turnover estimation, every missing value may severely lower accuracy at the peptide level. Multiplexing of pulsed SILAC samples derived from different time-points might overcome this issue and the general feasibility of combining pulsed SILAC with iTRAQ (isobaric Tags for Relative and Absolute Quantification) 4-plex labeling has previously been demonstrated in Streptomyces coelicolor (23) albeit with low proteome coverage. Subsequently, TMT (tandem mass tag) labeling of pulsed SILAC samples has been proposed in a review by Hughes and Krijgsveld (24) and recently demonstrated by Welle et al. (25) who determined turnover dynamics for 1,276 human proteins in a single MS3 based experiment. However, none of the above studies have specifically addressed turnover at the level of proteoforms.

In the present study, we combined the standard dynamic SILAC approach with TMT labeling of 10 pulse time-points to perform proteome-wide analysis of proteoform resolved turnover. We report a robust normalization method for multiplexed turnover data and describe a new approach to compute absolute protein copy numbers per cell from TMT data. We demonstrate high concordance of pulsed SILAC-TMT and standard dynamic SILAC data. Moreover, we show that SILAC-TMT hyperplexing enabled high proteome coverage (6,000 proteins) within reasonable time (2 days) of LC-MS measurements. Systematic evaluation of replicates showed that robust single peptide level turnover measurements are possible if experiments are conducted carefully. Following this approach and facilitated by the deep proteome coverage, we highlight several examples of post-transcriptional and post-translational processing leading to differential protein stabilities. Our dataset also enabled a reevaluation of molecular determinants of proteome stability and showed that oxidative stress contributes to the high turnover of proteins in the respiratory chain complex I. To enable further research on the topic, all raw data obtained in this study is available in PRIDE (26) and protein stability data will be made available in ProteomicsDB (27).

EXPERIMENTAL PROCEDURES

Experimental Design and Statistical Rationale

The rationale of the experimental design, data normalization and curve fitting of time-resolved SILAC pulse data is described in detail in the results section and the supplementary methods. Briefly, four HeLa cell culture replicates and a MS measurement duplicate of SILAC pulse experiments were performed to assess the reproducibility of the pulsed SILAC-TMT approach and enable statistical evaluation of differences in peptide turnover rates measured as rates of SILAC label incorporation or loss. Two cell batches were switched from light (K0/R0) to heavy (K8/R10) label and two replicates were switched from heavy to light label and lysed after different time-points. After digestion, peptides were labeled using TMT, combined, fractionated, and analyzed employing a MS2 or MS3 method for TMT quantification. In addition, for one replicate, fractional SILAC labeling was directly analyzed on MS1 level omitting the TMT labeling step to enable a comparison of the three different quantification approaches. To obtain labeling rate constants, TMT data were normalized based on steady-state assumptions and equations following first-order kinetics were fitted to peptide data. After filtering for high quality curve fits, data condensed at the peptide and protein level were analyzed regarding determinants of protein turnover and splice variant and proteoform-specific turnover behavior. For the investigation of the turnover of proteins assembled in respiratory chain complex I on induction of oxidative stress, HeLa cells were treated with the complex I inhibitor rotenone and the complex I specific substrates glutamate and malate. After a 3 or 8 h pulse with heavy medium, ratios of newly synthesized to formerly existing proteins (heavy-to-light ratios) were evaluated in a parallel reaction monitoring (PRM) assay and compared with control cells either treated with glutamate and malate or with DMSO. All cell culture conditions were evaluated as triplicates to enable statistical analysis of turnover differences. Detailed information on the procedures of the cell culture experiment, sample processing, PRM assay setup (Tier level 3), data normalization and analysis can be found in the supplementary methods section.

Cell Culture and Lysis

HeLa cells were cultured in SILAC DMEM (Thermo Fisher Scientific, Waltham, MA) supplemented with 10% dialyzed FBS (Gibco^TM via Thermo Fisher Scientific), 1% antibiotic antimycotic solution (Sigma, Munich, Germany) and 1.74 mm l-proline (≥ 99%, Sigma). l-lysine and l-arginine were added in either light (Lys-¹²C₆¹⁴N₂/K0, isotope purity ≥ 99%; Arg-¹²C₆¹⁴N₄/R0 ≥ 98%, Sigma) or heavy (Lys-¹³C₆¹⁵N₂/K8, isotope purity ≥ 99%; Arg-¹³C₆¹⁵N₄/R10, isotope purity ≥ 99%, Cambridge Isotope Laboratories, Tewksbury, MA) form to a final concentration of 0.798 mm and 0.398 mm, respectively. For time-resolved pulse experiments, HeLa cells were seeded at 5.7e3 cells/cm² and the pulse was started after 40 h of cultivation. Old medium was removed, light (or heavy) labeled cells were washed twice using PBS with MgCl₂/CaCl₂ (Sigma), and heavy (or light) medium was added. Cells were lysed in urea lysis buffer (8 m urea, 40 mm Tris-HCl (pH 7.6), 1 × EDTA-free protease inhibitor (cOmplete^TM, Mini, Roche via Sigma) and 1× phosphatase inhibitor mixture) directly before medium exchange (0 h time point) and 1, 3, 6, 10, 16, 24, 34, and 48 h (0, 1, 3, 6, 10, 16, 24, 32, 40, and 50 h for the comparison of MS2 and MS3 based quantification) after medium exchange. For the “infinite” time point, cells grown in heavy (or light) medium for ≥ 10 cell doublings (checked for >99.9% label incorporation) were seeded in heavy (or light) medium concurrently to light (or heavy) labeled cells and lysed in urea lysis buffer at the same time as the cells of the 48 h time point. For determination of cell doubling times, HeLa cells were seeded in 96 well plates at the same density as for the pulse experiments. After medium exchange, cells were counted in six replicates every 12 h.

Protein Digestion, TMT Labeling and Peptide Fractionation

Lysates were cleared by centrifugation for 20 min at 20,000 × g and 4 °C, protein concentration was determined by the Bradford method (Coomassie (Bradford) Protein Assay Kit, Thermo Fisher Scientific), and 200 and 30 μg of protein per sample were further processed for the pulsed SILAC-TMT and the pulsed SILAC workflow, respectively. After reduction (10 mm DTT, 30 °C, 30 min) and alkylation (50 mm chloroacetamide, room temperature, 30 min, in the dark), lysates were diluted to 1.6 m urea using 40 mm Tris-HCl (pH 7.6). Digestion was performed by adding trypsin (Promega, Mannheim, Germany, 1:50 enzyme-to-substrate ratio) and incubating overnight at 37 °C at 700 rpm. Digests were acidified by addition of neat formic acid (FA) to 1% and desalted using 50 mg tC18, reversed-phase (RP) solid-phase extraction cartridges (Waters Corp., Eschborn, Germany; wash solvent: 0.1% FA; elution solvent: 0.1% FA in 50% ACN). Peptide solutions were frozen at −80 °C and dried in a SpeedVac.

TMT labeling and high pH RP tip fractionation were performed as previously described (28). Briefly, digests (200 μg per time point) were reconstituted in 20 μl of 50 mm HEPES (pH 8.5), and 5 μl of a 11.6 mm TMT stock (Thermo Fisher) in 100% anhydrous ACN were added to each sample. After incubation for 1 h at 25 °C and 500 rpm, the labeling reaction was stopped by adding 2 μl of 5% hydroxylamine. Peptide solutions were pooled and acidified using 20 μl of 10% FA. Reaction vessels in which the labeling took place were rinsed with 20 μl of 10% FA in 10% ACN, and the solvent was added to the pooled sample. The pools were frozen at −80 °C and dried down in a SpeedVac. Subsequently, pooled samples were desalted using 50 mg tC18, RP solid-phase extraction cartridges (Waters Corp.; wash solvent: 0.1% FA; elution solvent: 0.1% FA in 50% ACN). Peptide solutions were frozen at −80 °C and dried in a SpeedVac.

For high pH RP tip fractionation, self-packed StageTips (five disks, Ø 1.5 mm, C18 material, 3 m Empore^TM via Sigma) were activated and equilibrated using 50 μl of 100% ACN, followed by 50 μl of 25 mm NH₄COOH (pH 10) in 50% ACN and 100 μl of 25 mm NH₄COOH (pH 10). Dried digests (30 μg) were reconstituted in 50 μl of 25 mm NH₄COOH (pH 10) and loaded onto the C18 material. Peptides were sequentially eluted using 40 μl of 25 mm NH₄COOH (pH 10) containing increasing concentrations of ACN (5, 7.5, 10, 12.5, 15, 17.5, and 50% ACN for TMT labeled digests for comparison of MS2 and MS3 based quantification and 5, 10, 15, 17.5, and 50% ACN for untagged SILAC labeled digests for comparison of MS1 and MS3 based quantification). The sample flow through was combined with the 17.5% ACN eluate and the 5% ACN fraction with the 50% ACN fraction, resulting in a total of six or four fractions, respectively, which were dried down in a SpeedVac and stored at −20 °C until LC-MS measurement.

For the final experimental setup conducted in 4 replicates, TMT labeled sample pools were fractionated via hydrophilic strong anion exchange (hSAX) chromatography as previously described (29). Briefly, samples were reconstituted in hSAX solvent A (5 mm Tris-HCl, pH 8.5) and separated using a Dionex Ultimate 3000 HPLC system (Dionex Corp., Idstein, Germany) equipped with an IonPac AG24 guard column (2 × 50 mm) and an IonPac AS24 strong anion exchange column (2 × 250 mm, Thermo Fisher) at a flow rate of 250 μl/min. The equivalent of 180 μg protein digest was loaded onto the column using 100% hSAX solvent A for 2 min and subsequently separated by increasing hSAX solvent B (5 mm Tris-HCl, pH 8.5, 1 m NaCl) from 0 to 40% in 16 min. After washing the column for 10 min at 100% hSAX solvent B, it was equilibrated with 100% hSAX solvent A. During separation, 40 fractions (1 min each) were collected. Afterward, fractions were acidified with 5 μl neat FA and less complex, early and late fractions were pooled as follows: 1–4, 5–7, 8–9, 26–27, 28–30, 31–33, 34–35, 36–40. The resulting 24 fractions were desalted using self-packed StageTips (three disks, Ø 1.5 mm, C18 material, 3 m Empore^TM; wash solvent: 0.1% FA; elution solvent: 0.1% FA in 50% ACN). Eluted fractions were frozen, dried down in a SpeedVac and stored at −20 °C until LC-MS analysis.

LC-MS Measurements

Nano flow LC-ESI-MS measurements were performed using a Dionex Ultimate 3000 UHPLC+ system coupled to a Fusion Lumos Tribrid mass spectrometer (Thermo Fisher Scientific). After reconstitution in 0.1% FA, an amount corresponding to 1.2–1.5 μg peptides was injected. Peptides were delivered to a trap column (75 μm x 2 cm, packed in-house with 5 μm C18 resin; Reprosil PUR AQ, Dr. Maisch, Ammerbruch-Entringen, Germany) and washed using 0.1% FA at a flow rate of 5 μl/min for 10 min. Subsequently, peptides were transferred to an analytical column (75 μm × 45 cm, packed in-house with 3 μm C18 resin; Reprosil Gold, Dr. Maisch) applying a flow rate of 300 nL/min and separated using a 100 min linear gradient from 4% to 32% LC solvent B (0.1% FA, 5% DMSO in ACN) in LC solvent A (0.1% FA in 5% DMSO). The Fusion Lumos was operated in data dependent acquisition (DDA) and positive ionization mode. Full scan MS1 spectra were recorded in the orbitrap from 360 to 1300 m/z at a resolution of 60K (automatic gain control (AGC) target value of 4e5 charges, maximum injection time (maxIT) of 50 ms). For MS analysis of SILAC samples without TMT label, MS2 spectra were recorded in the orbitrap at 15K resolution after HCD (higher energy collisional dissociation) fragmentation using an isolation window 1.6 m/z, an AGC target value of 1e5, a maxIT of 50 ms, 28% normalized collision energy (NCE), and a fixed first mass of 100 m/z. In the MS2-based TMT method, the isolation window was set to 1.2 m/z, the AGC target value to 1.2e5, the maxIT to 100 ms, the NCE to 33%, and the fixed first mass to 120 m/z. For both methods, cycle time and dynamic exclusion were set to 2 and 60 s, respectively. In the MS3-based TMT method, MS2 spectra for peptide identification were recorded in the ion trap in rapid scan mode via sequential isolation of up to 10 precursors (isolation window 0.7 m/z, AGC target value of 2e4, maxIT of 100 ms, dynamic exclusion of 90 s) and fragmentation via CID (NCE of 35%, activation Q of 0.25). Then, for each peptide precursor, an additional MS3 spectrum for TMT quantification was obtained in the orbitrap at 60K resolution (scan range 100–1000 m/z, charge dependent isolation window from 1.3 (2+) to 0.7 (5–6+) m/z, AGC of 1.2e5 charges, maxIT of 110 ms). For this, the precursor was again fragmented as for MS2 analysis, followed by synchronous selection of the 10 most intense peptide fragments in the ion trap and further fragmentation via HCD using a NCE of 55%.

Database Searching

Peptide and protein identification and quantification for DDA type of experiments was performed using MaxQuant (v1.5.5.1) with its built in search engine Andromeda (30, 31). Tandem mass spectra were searched against the Swissprot database (human, 42,145 entries, including splice variants, downloaded on 01.02.2016) supplemented with common contaminants. Carbamidomethylated cysteine was set as fixed modification and oxidation of methionine, and N-terminal protein acetylation as variable modifications. For pulsed SILAC samples without TMT label, Lys0/Arg0 and Lys8/Arg10 were specified as metabolic labels, whereas for pulsed SILAC-TMT samples, TMT10 was specified as label within a reporter ion MS3 experiment type and K8 and R10 were set as additional variable modifications. Isotope impurities of the TMT batch were specified in the configuration of TMT modifications to allow MaxQuant the automated correction of TMT intensities. Trypsin/P was specified as the proteolytic enzyme, with up to two missed cleavage sites allowed. Precursor tolerance was set to ±5 ppm, and fragment ion tolerance to ±20 ppm. Results were adjusted to 1% peptide spectrum match (PSM) and 1% protein false discovery rate (FDR) employing a target-decoy approach using reversed protein sequences.

Pulsed SILAC-TMT Data Normalization, Curve Fitting and Half-life Determination

Reverse database hits, nonhuman contaminants and missed cleavage peptides that contained both a light and a heavy version of lysine or arginine were removed from the pulsed SILAC-TMT dataset. Data normalization was conducted under the assumption that the total protein amount (light plus heavy labeled protein) is equal across time-points (see supplementary methods for detailed information). Subsequently, curves were fitted to TMT intensities using a nonlinear least square (NLS) optimization in R (version 3.3.3) (32) adopting first order labeling kinetics. Data were filtered according to following criteria: labeling (turnover) rate K: 0–5; offset B: 0–0.3; curve maximum A: 0.67–1.5; coefficient of determination R²≥0.8. To determine protein and peptide half-lives (T1/2), cell doubling rates were estimated via fitting an exponential growth equation to counted cell numbers and subtracted from labeling rates to obtain protein degradation rates (k). Half-life was then calculated as ln(2)/k (see supplementary methods for details).

Bioinformatic Analysis

For comparisons to previously published data (11, 12, 14, 25, 33–35), proteins were first matched based on the first IPI/UniProt identifier and, second, on the first gene name entry in each protein group. For integration of turnover data with protein properties and functions, the median of log transformed data from all four replicates was utilized. Functional annotations (36–41) were always based on the leading UniProt identifier in each group. Protein copy numbers were estimated by harnessing the fractional MS1 intensity assigned to the intensity of the first (for degradation curves) or last (for synthesis curves) TMT-channel and approximating the mass of a protein as a fraction of the total protein mass by the proportion of the protein's MS signal intensity to the total MS signal (42). Secondary structure prediction was performed employing the s2d method (43). Expected linear relationships were analyzed using Pearson's correlation coefficients (R). Otherwise Spearman rank correlation coefficients (ρ) were computed. The Perseus software suite (v.1.5.6.0) (44) was used to perform correlation analysis, functional 1D enrichment analyses (45) and two-sided t-tests using log-transformed, normal-distributed peptide and protein turnover rates or heavy-to-light ratios obtained in the PRM assay and corrected for multiple testing applying a permutation based FDR calculation. S0, a constant which accounts for differing variances across the range of measured values and accordingly adapts the significance cutoff of statistical analyses (46), was calculated in R (version 3.4.1, function “samr”) for each dataset separately. Crystal structures of respiratory chain complex I were obtained from the RCSB protein data bank website (http://www.rcsb.org (47); PDB ID: 5XTD (48)) and visualized using PyMOL. More detailed information on specific data analyses can be found in the supplementary methods.

RESULTS

Experimental Design for the Measurement of Protein Turnover on a Proteome-wide Scale

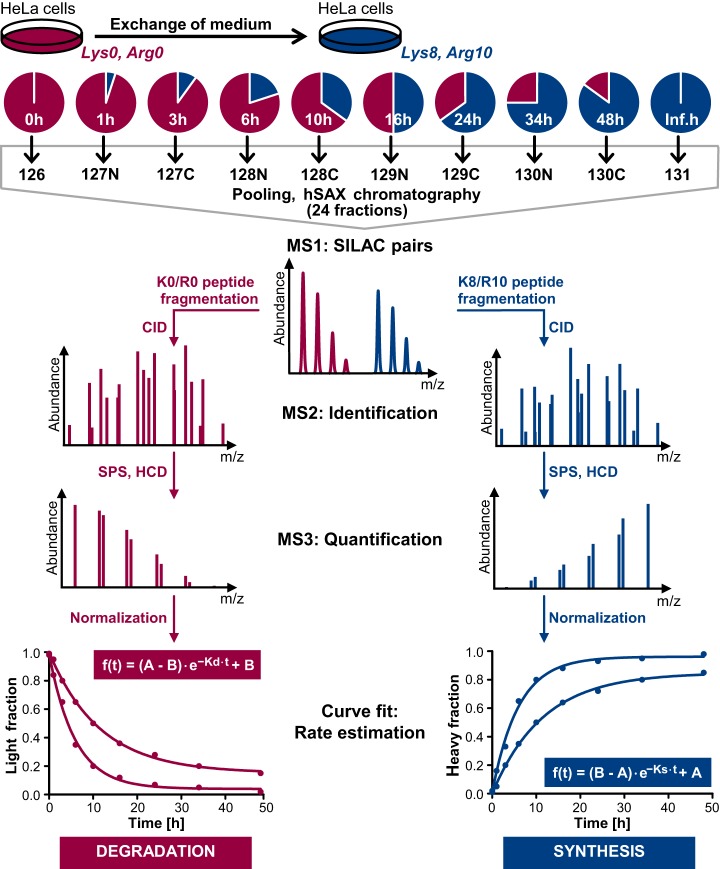
We aimed to design an experimental workflow which facilitates systematic determination of protein turnover measured as SILAC label incorporation or loss on a proteome-wide scale ideally providing proteoform resolution. This demanded (1) a deep proteome profiling method to ensure good protein and peptide coverage, (2) an adequate number of pulse time-points enabling high accuracy of turnover estimation, (3) a robust quantification method for single peptides across all time-points, and (4) high reproducibility of (peptide) rate estimations. To meet these requirements, an approach combining TMT labeling of ten different pulsed SILAC time-points together with peptide fractionation by hydrophilic strong anion exchange chromatography was employed (see Fig. 1). For calculation of meaningful peptide ratios for curve fitting, a maximum value corresponding to the total abundance of a peptide for both, increasing (synthesis) and decreasing (degradation) label, was required. This was achieved by allocating the first TMT channel to cells lysed directly before the pulse start (0 h) and reserving the last TMT channel for cells that were already completely labeled with the SILAC amino acids that were provided during the pulse (inf. h, in practice > 200 h, see Fig. 1). This experimental design also allowed for estimation of ratio compression in the first/last TMT channel resulting from coisolation of oppositely labeled peptides which can negatively influence turnover rate estimations. In addition, this enabled us to calculate protein abundances as copies per cell from TMT intensities by utilizing the fraction of the MS1 intensity that was linked to the first or the last TMT channel of peptides showing degradation or synthesis, respectively (see supplementary Methods for details).

Fig. 1.

Schematic representation of the multiplexed pulsed SILAC-TMT strategy for estimation of protein synthesis and degradation employed in this study. Cells grown in K0/R0 containing medium were pulsed labeled with medium supplemented with K8/R10 and lysed after 10 different time-points (inf. h corresponds to ≥ 10 cell doublings). After digestion, peptides derived from different time-points were labeled with TMT, pooled, and fractionated using hydrophilic strong anion exchange (hSAX) chromatography. Peptides were identified by MS2 spectra and quantified using MS3 scans. Decreasing and increasing labels represent protein degradation and synthesis. Assuming exponential protein degradation, one-phase decay and association functions were applied for estimation of the rates of K0/R0 label decrease and K8/R10 label increase (A: curve maximum; B: curve offset; K: turnover rate; see supplementary methods for a detailed explanation of the curve fitting).

Intermittent time-points were chosen based on three requirements: (1) High temporal resolution for early time-points to facilitate accurate quantification based on the assumed first order kinetics; (2) Exponential growth of HeLa cells during the entire pulse period to maintain the steady-state assumption which required avoiding growth inhibition because of high cell densities at later time-points; (3) Given the DDA mode for MS analysis, a comparable MS1 intensity of SILAC pairs to increase the probability of fragmentation and thus quantification of fractional SILAC labeling of both, the K0/R0 and the K8/R10 labeled peptides. Based on these considerations, HeLa cells were lysed 1, 3, 6, 10, 16, 24, 34, and 48 h after medium exchange (see Fig. 1). It should be noted that optimal time-points may differ for different cell lines depending on the respective cell doubling rates.

To correct for mixing errors of TMT labeled digests, data were normalized based on the premise that the sum of K0/R0 and the K8/R10 peptide intensities should be constant across different time-points (i.e. TMT channels), as equal protein amounts were employed for each time point (for detailed information see supplementary methods). After normalization, curves for estimation of turnover rates, determined from the kinetics of SILAC label incorporation or loss, were fitted to quantitative data of all peptide evidence, based on the assumption of exponential protein degradation (see Fig. 1, see supplemental Table S1). The normalization procedure improved the overall quality of the curve fitting as indicated by an overall shift of the R² distribution to higher values (see supplemental Fig. S1A). In addition, the number of successful curve fits after filtering also increased (in total 210,704 before and 238,489 after normalization in all four cell culture replicates). We systematically evaluated several criteria to remove poor quality peptide curve fits, for example, because of low TMT intensities or high ratio compression (see supplemental Fig. S1A) and provide a graphical user interface implemented in the R package “proturn” (“https://github.com/mengchen18/proturn”) for curve fitting visualization and assessment of filter criteria.

For calculation of half-life times (T1/2), labeling rates indicative of protein or peptide turnover were corrected for cell doubling rates to obtain rates of protein synthesis and degradation. To account for minor differences in growth behavior and thus to improve accuracy of half-life time calculations, cell doubling rates were determined for each cell culture replicate separately. Using the identical cell batch and applying the same conditions (e.g. cell medium exchange) as for the corresponding, simultaneously conducted pulse experiment, cell doubling times for the four cell culture replicates ranged from 26.3 h to 30.9 h (see supplemental Fig. S1B).

Comparison to Other SILAC Based Protein Turnover Measurement Approaches

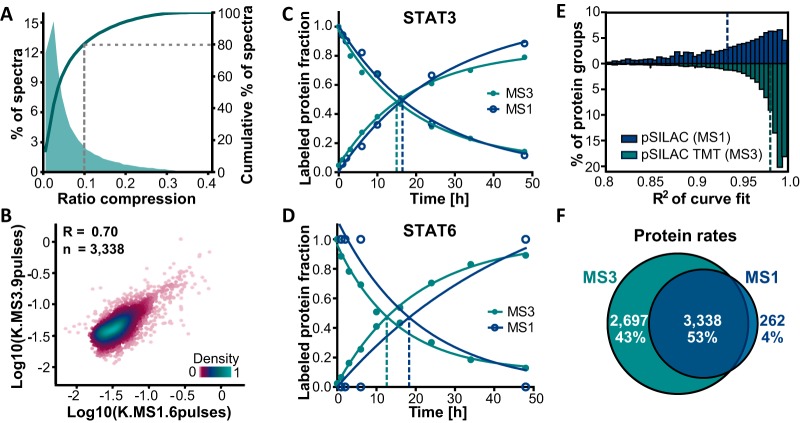
It is well known that isobaric tagging circumvents missing values occurring in data dependent MS1 based quantification approaches. However, quantification based on fragment ions of isobaric tags can suffer from ratio compression resulting from coisolation of peptides featuring differing quantitative behavior. Hence, it was of interest to assess and minimize such ratio compression as much as possible to avoid an adulteration of labeling rate estimations. Our experimental design enabled estimation of ratio distortion in either the first or last TMT channel. Indeed, a median residual intensity of 28.0% in the 0 h time point of synthesis curves indicated that severe ratio compression was present for SILAC-TMT samples that were measured in 6 high pH RP fractions using a MS2 readout (see supplemental Fig. S2A). In contrast, the MS3 based quantification method using the same sample and fractionation reduced the median residual intensity to 1.8%. In addition, a more extensive fractionation scheme was employed in following experiments to further minimize ratio distortion and concomitantly increase proteome coverage. In this final setup, residual intensities in the outermost TMT channels were still detectable, but data filtering based on curve fitting parameters (see above) resulted in less than 10% ratio compression for more than 80% of all used peptide evidence (see Fig 2A).

Fig. 2.

Comparison of MS1 (pulsed SILAC) and MS3 (pulsed SILAC-TMT) based quantification. A, The fraction of MS3 spectra as a function of the detected ratio compression (from measuring the residual intensities in outermost TMT channels) illustrates that ratio distortion was still present, but that >80% of all fitted and filtered spectra showed less than 10% residual intensities. B, Correlation analysis of log transformed labeling rates showed good agreement between the MS1 and MS3 based quantification approaches (R: Pearson's correlation coefficient). C, Labeling characteristics measured for the protein STAT3 either using the MS1 or MS3 strategy yielded consistent data. D, Fractional labeling determined for the protein STAT6 in which MS1 data points were missing (one SILAC isotope pair signal missing for 1, 3, 6, and 48 h time points and no data for the 10 and 24 h time points) led to substantial differences in curve fits between MS1 and MS3 data. E, Distributions of coefficients of determination (R²) of curve fits display consistently higher values for the MS3 compared with the MS1 approach (dotted lines: medians). F, Comparison of the number of proteins with determined turnover parameters shows a higher number for the MS3 strategy.

In order to address if our TMT multiplexed, pulsed SILAC approach using MS3 based quantification provided results like the standard dynamic SILAC workflow, aliquots of lysates from pulsed HeLa cells were processed in either way. Resulting samples were analyzed expending equal amounts of LC-MS measurement time, using the same function for curve fitting, and applying identical filtering criteria after curve fitting. Hence, TMT labeled and pooled samples derived from 10 pulse time-points (see Fig. 1, measured in 24 fractions) were compared with 6 nontagged pulsed SILAC samples (1, 3, 6, 10, 24, 48 h, each measured in 4 fractions). MS3 based ratios of labels across time-points and derived turnover rates were in good agreement with those calculated from the classical MS1 based pulsed SILAC method as indicated by an overall correlation of R = 0.70 (see Fig. 2B and supplemental Table S2) and exemplified by the virtually identical labeling curves of the protein STAT3 (see Fig. 2C). Importantly, rates determined by either of both approaches also correlated as well with already published protein rates as these literature data correlated among each other (R = 0.51–0.53, see supplemental Fig. S2B). However, for 41% of filtered synthesis and degradation curve fits in the MS1 based approach, intensities were not detectable for all 6 time-points. A head-to-head comparison of MS1 and MS3 measurements disclosed that these missing intensity values across SILAC isotope pairs or time-points can decrease accuracy of rate estimations as exemplified by the protein STAT6 (see Fig. 2D) resulting in half-lives of 31.3 and 23.6 h for MS1 and MS3, respectively. More generally, it became apparent that the precision of MS3 based quantification of reporter ions devoid of missing values enhanced the overall goodness of the curve fits in the multiplexing strategy to a median R² of 0.98 compared with 0.94 in the MS1 based approach (see Fig 2E). As a result, turnover dynamics could be determined for 83% of proteins identified with the multiplexing strategy, whereas only 58% of protein identifications in the MS1 based quantification approach passed filter criteria after curve fitting. Also facilitated by a deeper fractionation, the pulsed SILAC-TMT strategy yielded 6035 proteins with quantified turnover compared with 3,600 proteins in the classical pulsed SILAC approach using the same amount of measurement time yet covering ten instead of six pulse time-points (see Fig 2F).

Reproducibility of Protein and Peptide Turnover Rate Estimations

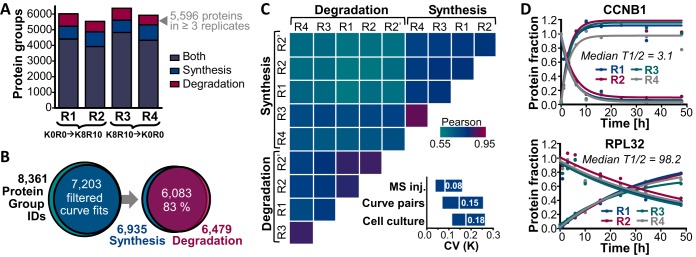
Next, we assessed the reproducibility of the pulsed SILAC-TMT approach. To do so, a total of four pulsed SILAC experiments using different HeLa cell batches were performed, two of which were subjected to a SILAC label swap. In addition, fractions of one replicate were measured twice providing a technical MS replicate. After data processing and filtering, turnover rates were computed for on average 5,957 protein groups per cell culture replicate (see Fig. 3A and supplemental Table S1). For 71–76% of all proteins, information on both protein label increase and decrease was available providing an internal duplicate measurement of protein turnover rates for each sample in a steady-state system. In all four cell culture replicates combined, synthesis and/or degradation curves were obtained for 55,067 protein group unique peptides (59,586 peptides when also counting oxidized forms) assigned to 7203 proteins (see Fig 3B) with a median sequence coverage of 17.4%. In total, turnover rates were computed for more than 86% of all identified proteins groups and for 6083 proteins, rates from both label increase and decrease were obtained. Labeling rate pairs showed a median Pearson's correlation coefficient (R) of 0.64 and a median coefficient of variation (CV) of 15% (see Fig. 3C). When rates of label decrease and increase were treated separately, the technical MS duplicate and the cell culture quadruplicates exhibited a median R of 0.80 and 0.77 and a median CV of 8 and 18%, respectively (see Fig. 3C), demonstrating good precision of the pulsed SILAC-TMT approach. Interestingly, turnover rate determinations on peptide level were as reproducible as for proteins (median R of 0.84 and 0.72 and median CV of 8 and 18%, see supplemental Fig. S3A). Notably, for technical replicates more than 82% of both estimated protein and peptides rates showed a CV of less than 20%. However, when correlating rates obtained from label increase and decrease within a sample, the level of concordance dropped on peptide level (median R of 0.51 and CV of 0.16, see supplemental Fig. S3A). This observation was attributable to residual ratio distortion which still affected some peptides and adulterated turnover rate determination in opposite ways, eventually more strongly deteriorating correlation analysis on peptide than on protein level. Likewise, a weak correlation (R of 0.36) of peptide labeling rates with CVs computed from increasing and decreasing curve pairs was identified suggesting that ratio compression more severely affects rate determinations of high turnover peptides (see supplemental Fig. S3B) as one might expect. However, we point out that there was generally no correlation of turnover rates and replicate CVs (exemplified for peptide rates across technical replicates in supplemental Fig. S3C, R = 0.04). This encouragingly implies the absence of an overall precision bias depending on the turnover rate, meaning that rate determination is reliable across the measured range of fast and slow turnover peptides or proteins (for examples see Fig. 3D and supplemental Fig. S3D).

Fig. 3.

Reproducibility of protein turnover rate determination by pulsed SILAC-TMT labeling. A, Turnover rates were determined for between 5528 and 6367 protein groups per cell culture replicate (R1-R4). B, In total, rates were obtained for 7203 proteins, and for 83% of these turnover information was available from both label increase and decrease. C, Correlation matrix depicts color-coded Pearson's correlation coefficients for log transformed protein turnover rates determined from synthesis and degradation curves for cell culture (R1-R4) and MS injection (R2 and R2′) replicates. The boxplots (10th–90th percentile) show the coefficients of variation of turnover rates across replicate MS injections, synthesis and degradation curve pairs within a sample and cell culture replicates. D, Examples of the reproducibility of turnover determination across cell culture replicates are displayed for the high turnover protein G2/mitotic-specific cyclin-B1 (CCNB1) and the stable 60S ribosomal protein L32 (RPL32).

Evaluation of Intrinsic Determinants of Protein Turnover

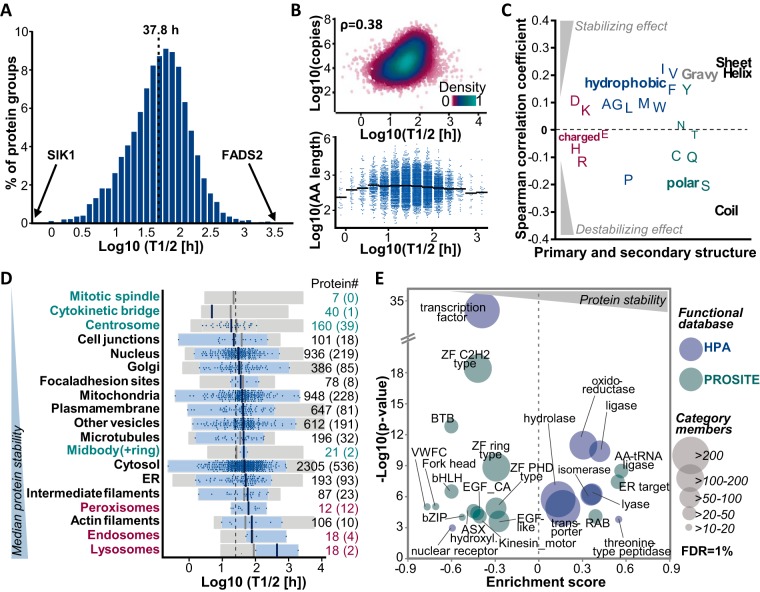
Estimated protein turnover rates spanned three orders of magnitude resulting in calculated half-lives ranging from minutes (exemplified by serine/threonine-protein kinase SIK1) to thousands of hours (for fatty acid desaturase 2 (FADS2), see Fig 4A and supplemental Table S3). The median half-life of all proteins was 37.8 h. Apart from an expected slight underrepresentation of the membrane and the extracellular subproteomes, our set of proteins proved to be functionally representative for the entire human proteome (see supplemental Fig. S4A). In addition, protein copy numbers per cell determined from the SILAC-TMT data were in good agreement with published data (33, 34) (R = 0.72 and 0.85, see supplemental Fig. S4B) and covered several orders of magnitude substantiating the highly representative character of the data at hand (see supplemental Fig. S4C). Hence, the current compilation of protein turnover data provided a good opportunity to investigate the influence of protein properties and functions on protein stability.

Fig. 4.

Analysis of protein half-lives relating to intrinsic protein properties and functions. A, The distribution of protein half-lives in HeLa cells is displayed. The median protein half-life of all proteins is 37.8 h. B, Correlations of protein half-lives and copy numbers per cell (upper panel, ρ: Spearman rank correlation coefficient) and protein length (bottom panel) are shown. Solid black lines indicate the median length of all proteins in the half-life bin. C, Spearman rank correlation coefficients are depicted for the correlation of protein half-lives and amino acid composition, amino acid properties, and protein secondary structure elements. D, Floating bar charts illustrate the range of protein half-lives as a function of cellular localization (according to the Human Protein Atlas (HPA) and MitoCharta project). Proteins which are part of cell structures involved in cell division are shown in green, endo-, lyso- and peroxisome associated proteins are shown in red. Gray boxes display all proteins associated with the respective subcellular location, blue boxes refer to proteins (blue dots) which were reported to be exclusively found in this cell compartment or structure. Numbers on the right indicate how many proteins are in each category and numbers in brackets refer to proteins with exclusive localization. E, The scatter plot shows significantly enriched categories after a one-dimensional functional enrichment analysis (1% FDR) using protein domain and family information provided by the PROSITE and HPA databases. The size of each circular shape indicates the number of proteins in each category.

Two factors that might affect protein turnover could be protein size and cellular abundance, as these codetermine the energy costs caused by resynthesis of a certain protein species after its degradation in a steady-state system. Indeed, protein half-lives were positively (albeit not strongly) correlated with protein abundance (ρ = 0.38, see Fig. 4B). In contrast, and perhaps surprisingly, protein size did not show any consistent or global effect on protein stability. Other protein properties that potentially influence turnover are the primary and secondary structure as well as the hydrophobicity of a protein. We observed overall weak correlations of protein half-lives and amino acid content or predicted proportion of α-helix, β-sheet and coil structures (ρ between −0.28 and 0.23). For example, a high percentage of hydrophobic amino acids and an ordered secondary structure were associated with longer half-lives, whereas polar amino acids and a disordered structure (often showing high proline content) seemed to rather destabilize proteins (see Fig. 4C and supplemental Fig. S4D). It is noteworthy that all examined protein features correlated with each other to some extent, i.e. for instance, the more abundant a protein was, the smaller (ρ = −0.40) and the less polar (ρ = −0.30) and disordered (ρ = −0.22) it tended to be (see supplemental Fig. S4E). In order to investigate whether susceptibility to aggregation might be associated with cellular protein turnover, protein half-lives were compared with corresponding melting points that have recently been reported for HeLa proteins (35). However, no general dependence of cellular protein turnover on thermal stability could be determined (see supplemental Fig. S4F).

The localization of proteins might also affect their stability. To examine a potential spatial regulation of turnover, proteins were grouped according to their subcellular location reported by the human protein atlas (HPA) (40) and the MitoCharta 2.0 (38) project. Again, proteins in these categories spanned a wide range of stability even when only assessing proteins which were exclusively found at a single location (see Fig. 4D). However, endo-, lyso-, and peroxisomal proteins (median T1/2 of 80.2 h) appeared to be more stable compared with the overall cellular proteome. We note that the small number of data points limits the generalizability of this observation. Conversely, proteins which constitute members of mitotic cell structures (centrosome, mitotic spindle, cytokinetic bridge, and midbody, median T1/2 of 24.9 h) exhibited shorter median half-lives potentially reflecting the need for rapid regulation of abundance during different phases of the cell cycle. In contrast, actin and intermediate filaments and proteins exclusively located in the endoplasmic reticulum (ER) were on average slightly more stable compared with nuclear and cell junction proteins (median T1/2 of 77.8, 58.7 and 50.5 versus 30.3 and 22.4 h). Other localizations did not show any considerable trend toward an overall stabilization or destabilization of associated proteins.

We next investigated the relation of protein half-lives to annotated functions using protein domain and family information provided by the PROSITE (37) and HPA (39) databases. A functional 1D enrichment analysis illustrated the significantly shorter half-lives of transcription factors containing zinc finger (ZF), fork head, basic helix-loop-helix (bHLH) and leucine zipper domains (bZIP), as well as nuclear receptors (see Fig. 4E). Examples included, members of the STAT (Signal transducer and activator of transcription) family, the transcriptional regulators MAX and MYC as well as retinoic acid and androgen receptors. In contrast, several families of enzymes, notably oxidoreductases, ligases, lyases, isomerases, and hydrolases were significantly overrepresented in more stable proteins (see Fig. 4E). Interestingly, the aforementioned transcription factors and enzymes also clearly differed in the biochemical features assessed above. Enzymes did not only possess longer half-lives compared with transcription factors (55.4 h versus 17.6 h), but were also more abundant (50,000 versus 9,000 copies per cell) and more hydrophobic (44% versus 37% hydrophobic amino acids) and exhibited much less disordered secondary structures (54% versus 84% coil structure, see supplemental Fig. S4G). Other distinctively more stable functional protein groups included cell and organelle membrane associated transporters and, interestingly, proteins with a C-terminal KDEL motif, which targets proteins to the ER. The latter indicates that proteins which permanently and exclusively reside in the ER lumen, like for instance protein disulfide isomerases, are indeed more stable as already suggested by the HPA subcellular location annotations (see Fig. 4D). Furthermore, the Rab family of GTPases, which regulate vesicular trafficking, exhibited significantly longer half-lives. On the contrary, kinesin like proteins, which are involved in mitosis via the control of chromosome segregation, were enriched in high turnover proteins. Likewise, proteins bearing ASX hydroxyl and EGF like domains appeared to be rather short-lived. We note that these domains often cooccur on extracellular proteins (e.g. fibrillins and fibulins), and the detected comparably short half-lives might therefore rather reflect the intracellular transit time before these secreted proteins are lost from the pool of analyzed proteins than their overall stability. The same argument applies for proteins featuring von Willebrand factor type C (VWFC) repeats which include among others fibrillar collagens. Taken together, the collective turnover data set facilitated the analysis of protein properties and functions affecting protein stability, but no universal protein immanent factors strongly influencing half-lives were identified.

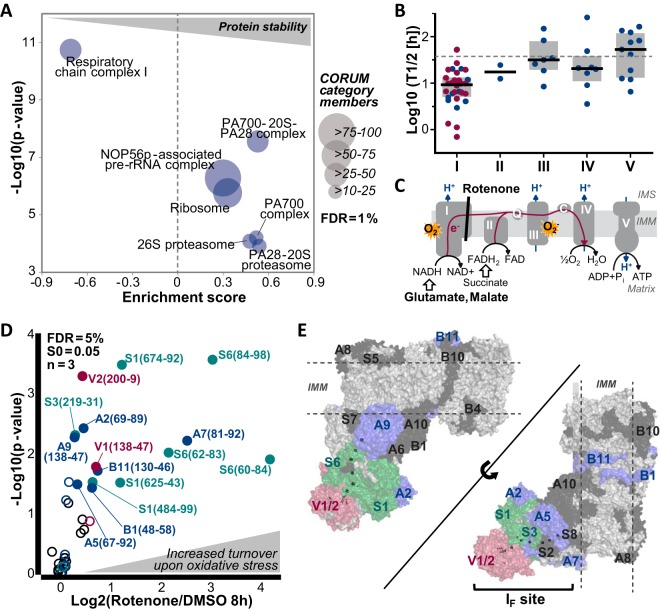
Oxidative Stress as a Regulating Factor for NADH Dehydrogenase Stability

Besides protein intrinsic factors such as structure and function, protein half-lives might also be regulated by molecular interactions. To this end, we evaluated the stability of CORUM complex members (36) and found that proteins reported to be part of a protein complex exhibited overall longer half-lives (median 51.9 h) compared with proteins which are not listed in the CORUM database (median 44.1 h) suggesting a stabilizing effect of protein interactions and complex formation. In particular, the proteasome and ribosome (and their precursors) were significantly enriched in more stable proteins (see Fig. 5A). Interestingly, respiratory chain complex I (NADH dehydrogenase) members were the only proteins participating in complexes and the electron transport chain that showed overall significantly shorter half-lives (median 9.5 h, p value = 1.84e-11, see Fig. 5A and 5B). Together with the ubiquinol cytochrome C oxidoreductase (respiratory chain complex III), the NADH dehydrogenase is the main site of superoxide radical formation caused by electron leakage in the respiratory chain (see Fig. 5C). Therefore, we hypothesized that the high turnover of complex I proteins may be an adaptive mechanism to compensate oxidative stress by replacing damaged complex members and thus to maintain the functionality of the electron transport chain which is needed for energy generation by oxidative phosphorylation. Following this assumption, the turnover of NADH dehydrogenase proteins should be accelerated on enhanced oxidative stress. In order to test this hypothesis, HeLa cells were treated with the complex I inhibitor rotenone in combination with glutamate and malate to increase oxidative stress specifically at complex I (49) (see supplemental Fig. S5A). By inhibiting electron transfer from iron-sulfur centers to ubiquinone, rotenone treatment should lead to a backload of electrons which should be further amplified by the increased electron supply provided by the NADH dehydrogenase substrates glutamate and malate (see Fig. 5C). The rotenone and control treatments (either DMSO or solely glutamate and malate) were followed by a 3 or 8 h pulse in K8/R10 SILAC medium (see supplemental Fig. S5A). To overcome missing quantitative data across treatment conditions and replicates in a DDA type of experiment, a parallel reaction monitoring assay was developed to quantify heavy-to-light ratios, which reflected the fraction of newly synthesized to the total protein amount. In total, 43 peptides representing 27 complex I proteins were monitored in their K0/R0 and K8/R10 labeled states (see supplemental Table S4). For both pulse time-points, rotenone treated cells showed a clear shift toward higher heavy-to-light (H/L) ratios compared with control cells implying that the overall fraction of newly synthesized complex I members and thus their turnover increased (see Fig. 5D and supplemental Fig. S5B–S5D). Proteins featuring peptides with a significantly different H/L ratio were mainly located at the so-called I_F site where electrons are transferred from NADH to FMN (flavin mononucleotide) and further passed down the chain of iron-sulfur centers (see Fig. 5E). Taken together, these results indicate that the turnover of many respiratory chain complex I members is accelerated on the blockade of electron transfer to ubiquinone suggesting that a general regulation of their half-lives by oxidative stress could exist.

Fig. 5.

Analysis of turnover of respiratory chain complex I proteins in response to rotenone induced, oxidative stress. A, One-dimensional enrichment analysis (1% FDR) using CORUM database annotations revealed that respiratory chain complex I (NADH dehydrogenase) was significantly enriched in high turnover proteins. The size of each circular shape indicates the number of proteins in each complex. B, Scatter dot plots show protein half-lives of members of the different respiratory chain complexes. Black lines indicate the median half-life of proteins within each complex and proteins marked in red were followed up by rotenone and/or glutamate and malate treatment in the subsequent PRM assays. C, The schematic representation of the different complexes of the respiratory chain (I-V) illustrates sites of metabolic reactions and superoxide production (IMM: Inner mitochondrial membrane; IMS: Intermembrane space; Q: Ubiquinone; C: Cytochrome C). D, The Volcano plot shows the results of triplicate PRM assays monitoring the turnover of 22 members of the respiratory chain complex I in response to rotenone (1 μm), glutamate and malate (5 mm) treatment. Peptides exhibiting a significantly higher turnover on treatment (5% FDR, S0 = 0.05) are illustrated by filled circles and labeled with the subunit, peptide start and end positions. Colors refer to proteins shown in panel E. E, Crystal structures of respiratory chain complex I proteins are displayed. NADH dehydrogenase proteins with significantly increased turnover on rotenone treatment are colored in red, blue and green. Iron sulfur clusters are shown as sticks. Subunits colored in black were detected in the PRM assay but did not show a significant change in turnover on treatment after an 8 h pulse. Subunits in light gray could not be robustly monitored in the PRM assay.

Proteoform Resolved Protein Turnover

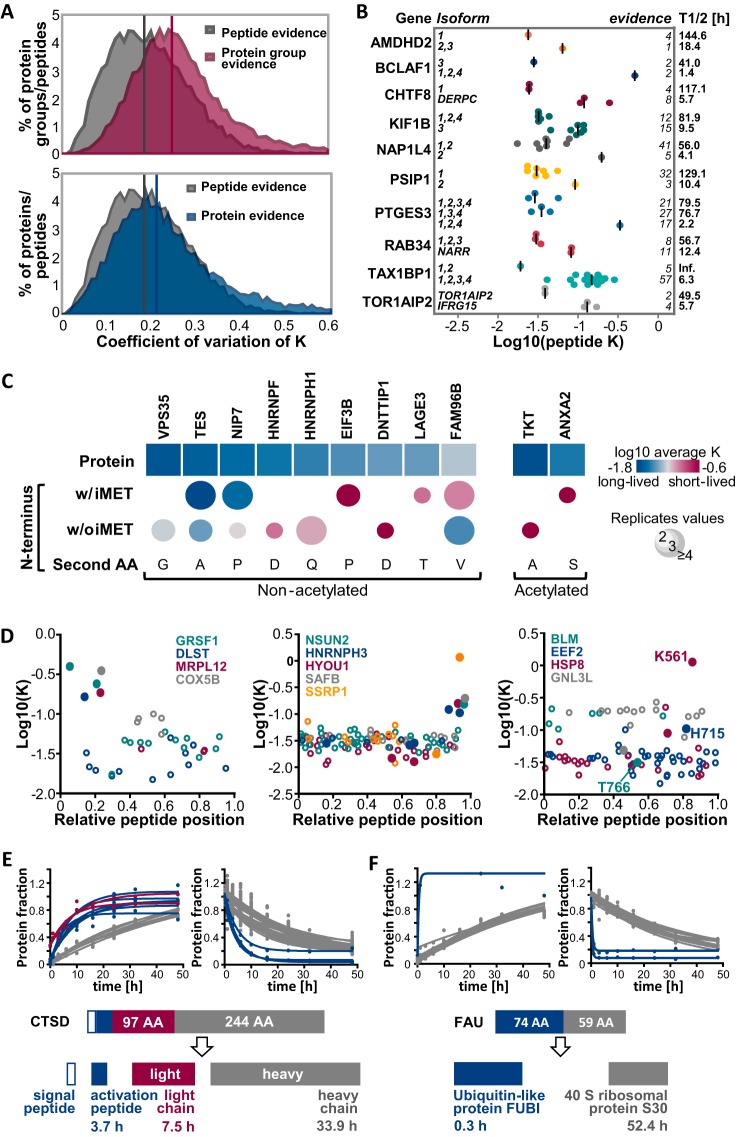
Expecting a cell to be able to respond quickly to cellular stimuli such as rotenone induced, oxidative stress as shown above, inevitably leads to the hypothesis that protein turnover could be dynamically regulated by post-translational protein modifications. For the above example on the turnover of respiratory chain proteins, it was unfortunately not possible to test this hypothesis directly because information on methionine oxidized respiratory chain peptides and their nonoxidized counterparts was not available. In general, the comparison of oxidized and nonmodified counterpart peptides did not show any global shift in turnover because of oxidation (see supplemental Fig. S6A). This is not surprising assuming that protein and peptide oxidation largely also occurs during sample processing and, hence, would not alter the measured, cellular turnover. Moreover, a Student's t-Test did not reveal any significant differences of individual oxidized and nonmodified peptide pairs (FDR = 5%, S0 = 0.05). However, we generally, and quite unexpectedly, observed that turnover rates determined from all spectrum evidences for a certain peptide sequence showed less variation (median CV of 18%) than rates derived from all spectrum evidences for a protein group (median CV of 25%, see Fig. 6A upper panel). A protein group can contain peptides which originated from different, expressed protein isoforms, if unique peptide(s) are identified solely for one of these isoforms and only shared peptides have been identified for the other isoform(s). Thus, the global difference in CV values of protein groups compared with peptides suggested that protein isoforms (that are unavoidably included in a protein group) might indeed often differ in their turnover behavior. Given the availability of four cell culture replicates, statistical testing was feasible to prioritize protein groups consistently containing peptides with considerably varying stabilities. To do so, only peptides for which a turnover rate was determined at least 3 times (from synthesis or degradation curves or different replicates) and which belong to protein groups containing at least three of these peptides were included (25,313 peptides assigned to 3130 protein groups). A two-sided, 5% FDR corrected t-Test (S0 = 0.048) yielded 425 peptides from 305 protein groups for which turnover rates significantly differed (see supplemental Fig. S6B and supplemental Table S5). Among these, several protein groups containing different splice variants were identified. For example, the only peptide which was exclusively assigned to isoform 2 of nucleosome assembly protein 1-like 4 (NAP1L4) was much less stable (T1/2 = 4.1 h) compared with peptides occurring in both isoforms 1 and 2 (T1/2 = 56.0 h, see Fig. 6B). It must be pointed out that these differences might also be caused by a putative stabilizing modification which happens to occur in the identified isoform 1 specific sequence stretch, hence making the unmodified counterpart peptide appear less stable compared with the other peptides of the protein. However, the occurrence of different half-lives for different isoforms was also observed in cases where isoforms were unambiguously identified via several unique peptides and which thus were assigned to different protein groups as exemplified by chromosome transmission fidelity protein 8 homolog (CHTF8, 5.7 versus 117.1 h for isoform 1 versus splice variant DERPC, see Fig. 6B). Notably, most of these protein group separated isoforms featuring significantly different turnover rates also possessed considerably different primary sequences and thus physicochemical properties.

Fig. 6.

Analysis of proteoform resolved protein turnover. A, Distributions of coefficients of variation of turnover rates across spectra are displayed for peptides and proteins. The upper panel shows the distribution of CVs of all spectra for the same protein group (irrespective of the number of proteins or protein isoforms in each group). The bottom panel shows the CV distribution of all spectra for protein groups that only contain a single protein. Medians are indicated by vertical lines in the corresponding color. B, Scatter dot plots depict the distributions of turnover rate constants for peptides of different protein isoforms. Peptides corresponding to a gene share the same color. Median peptide rates across replicates are shown as vertical lines. C, Turnover rates are shown for different modified N-terminal peptides and corresponding proteins. Only N termini and proteins with statistically significantly different rates are displayed (see also supplemental Fig. S6C). D, Scatter plots illustrate peptide turnover rates as a function of the relative position within the protein sequence. Zero denotes the N terminus and 1 denotes the C terminus of a protein. Peptides from each protein are denoted by the same color whereas closed circles denote peptides that exhibit significantly different turnover compared with the rate of the whole protein (see also supplemental Fig. S6B). The left panel shows examples for mitochondrial proteins in which the N-terminal transit peptides shows a higher turnover than other peptides of the same protein. The middle panel shows a similar analysis but for proteins with higher turnover C-terminal peptides. The right panel shows examples for proteins in which one peptide displayed a strong difference in turnover compared with other peptides of the same protein which often but not always encompass known modification sites. E, Fractional peptide labeling is depicted for cathepsin D (CTSD), a protein that is proteolytically processed into a signal peptide, an activation peptide (blue circles), a light chain (red circles) and a heavy chain (gray circles). F, Fractional peptide labeling is depicted for the fusion protein FAU. Peptides representing the Ubiquitin-like protein FUBI are shown in blue, peptides from the 40S ribosomal protein S30 are shown in gray.

After the removal of all protein groups that contained more than one protein (isoform), turnover rates of all peptide evidences belonging to a single protein still showed overall higher CVs (median CV of 22%) than rates derived from all evidences for single peptides (median CV of 18%, see Fig. 6A, lower panel). This demonstrates that alternative splicing alone is not sufficient to explain the variation in turnover across peptides assigned to the same gene. In fact, many peptides located at the protein N terminus were found to exhibit significantly different turnover rates. To further explore this, rates of differently modified N-terminal peptides of the same protein were compared among each other in addition to the comparison to the overall protein turnover rate. Even without enrichment of N-terminal peptides, rates were obtained for 343 N-terminal peptides from 306 proteins. About half of these peptides (53%) neither contained the initiator Met residue nor were they acetylated. After filtering, differences were statistically evaluated for 287 proteins (see supplemental Fig. S6C). Eleven N termini significantly differed in their turnover rates, but the effect was not consistent for the type of modification (see Fig. 6C). Although, for instance, the N-terminal peptide without the initiator methionine of HNRNPH1 appeared to be turned over more quickly compared with the whole protein, it was the other way around for the mitotic spindle-associated MMXD complex subunit MIP18 (FAM96B).

Higher turnover rates for peptides located near the N terminus were also identified for mitochondrial proteins like the G-rich sequence factor 1 (GRSF1, see Fig. 6D, left panel). As a matter of fact, these peptides were part of or spanned cleavage sites of transit peptides which target nuclear encoded proteins to mitochondria. This suggests that these localization signals are in general rapidly cleaved off and degraded leading to mature, more stable proteins. Likewise, propeptides often appeared to be less stable compared with mature proteins as exemplified by prosaposin which is cleaved into four different saposins, a signal peptide, and several propeptides (see supplemental Fig. S6D). Another case where proteolytic processing led to products with different apparent cellular stability is illustrated by cathepsin D (CTSD), a protease that consists of a light and a heavy chain which are encoded by the same gene and is post-translationally cleaved (50) (see Fig. 6E). Interestingly, not only did the activation peptide of CTSD exhibit a higher turnover (T1/2 = 3.7 h), but also its light chain showed a shorter half-life (7.5 h) compared with the heavy chain (33.9 h). Moreover, we provide, to our knowledge, the first experimental evidence for the post-translational cleavage of the protein produced by the fusion gene FAU. This is demonstrated by the considerably different stabilities of peptides corresponding to the Ubiquitin-like protein FUBI and the 40S ribosomal protein S30 part of the fusion protein (T1/2 = 0.3h versus 52.4 h, see Fig. 6F).

Apart from these rather intuitively explicable examples, mechanistic explanations for discrepancies between peptide and corresponding protein turnover rates were often less apparent. A group of proteins, for instance, exhibited a distinctively higher turnover for the most C-terminal located peptides (examples are shown in Fig. 6D, middle panel). This might hint to a C-terminal modification which stabilizes these proteins and thus would lead to a seemingly shorter half-life of the unmodified C terminus. In fact, many peptides showing significantly different turnover rates encompassed reported modification sites. Among others, for example the only peptide of elongation factor 2 (EEF2) showing a substantially higher turnover rate contained His715 which is believed to be the only histidine in eukaryotes that is converted into diphthamide (51) (see Fig. 6D, right panel). Furthermore, for the heat shock cognate 71 kDA protein (HSPA8), the peptide showing the by far highest turnover rate included a lysine (position 561) that was demonstrated to be trimethylated by the methyltransferase METTL21A, thereby modulating its chaperone activity (52). In addition, the most stable peptide of the bloom syndrome protein (BLM) comprises Thr766 which has been shown to be phosphorylated by cyclin dependent kinase 1 (CDK1) potentially regulating its helicase activity during mitosis (48). In contrast to these examples, many peptides also featuring significantly different rates did not encompass any known modification site (exemplified by GNL3L in Fig. 6D, right panel). Still, all the cases described above clearly demonstrate differential turnover rates for different proteoforms suggesting an association of post-transcriptional and post-translational processing with protein stability.

DISCUSSION

Technical and Data Analysis Considerations

Enabled by the introduction of the SILAC technology and advances in MS based proteomic technologies in general, several attempts have been made in recent years to investigate endogenous proteome turnover (10–15). Still, generating such data at high quality is far from trivial and many factors must be carefully considered when planning and executing such experiments. At the technical level, the accuracy of the commonly applied standard dynamic SILAC method employing MS1 based quantification can be impaired by missing data across different pulse time-points. When considering the combined use of quantitative information of multiple peptides, this shortcoming might be tolerable at the protein level, but, especially for single peptides, such rate estimations can be unreliable. Therefore, we established a method that combines the quantitative precision of TMT-10plex labeling with pulsed SILAC labeling of cells and evaluated the merits of this approach. Direct comparisons illustrated the extent of the missing value issue in the MS1 based quantification method. Absent intensities across SILAC pairs and time-points reduced the number of successfully determined protein labeling rate constants and concomitantly decreased the quality of curve fits. This was the case even though missing values were already minimized by utilizing the automatic SILAC pair identification and the match between runs function implemented in the MaxQuant software (53) and even though less stringent criteria regarding missing values were applied for the curve fitting of MS1 quantified label accumulation and clearance. Even though TMT labeling effectively overcomes the issue of missing values and thus facilitates determination of turnover rates at single peptide level, it is well known that quantification using isobaric tags suffers from ratio distortion caused by coisolated peptides. This drawback can have massive consequences for rate determinations in particular if a light and a heavy peptide are cofragmented because they would in general show the exact opposite TMT intensity behavior. Indeed, when applying MS2 based quantification of reporter ions, severe ratio compression was detected often rendering determined labeling rates plain invalid. This was also underlined by the fact that, after correction of these turnover rates for cell doubling, almost 50% of all quantified proteins had negative half-lives which typically result either from an underestimation of labeling rates or an overestimation of cell doubling rates. By contrast, using a more extensive fractionation scheme and a MS3 based TMT quantification strategy, ratio distortion was minimized, and negative values were obtained for less than 3% of all proteins which is a very small fraction compared with other published turnover studies. Moreover, turnover rates obtained from this experimental workflow were in good agreement with rates determined via the classical approach based on MS1 quantification. Overall, we conclude that a MS3 based measurement is required for proper estimation of protein turnover when using a pulsed SILAC-TMT format.

In contrast to the standard pulsed SILAC approach, the SILAC-TMT hyperplexing strategy provided a duplicate measurement of turnover rates for all cases where both peptides of a SILAC pair were fragmented. This helped to assess the quality of rate estimations offering an additional level of confidence within the same experiment. In fact, a comparison of rates calculated from label increase and decay exposed those, mainly high turnover peptides for which residual TMT ratio compression affected determined rates. Although not investigated in this study, this internal duplicate may be particularly helpful for the evaluation of turnover rates in nonsteady state dynamic or disturbed systems such as cell differentiation or on cell treatments. The data normalization and curve fitting functions used assumed that the average abundance of all proteins does not change during the course of the experiment (steady state) and, therefore, that the synthesis rate of a protein equals its degradation rate. For this reason, cell seeding densities and culture conditions were carefully elaborated to assure that HeLa cells were no longer in lag phase or not yet entering the stationary growth phase during all SILAC pulses. Still, cells were cultured under somewhat noncontinuous conditions as nutrients were depleted and metabolites accumulated over the course of the experiment. These factors can potentially cause cells to respond with a change in abundance of certain proteins. Consequently, we cannot preclude the possibility that the applied curve fitting algorithms might not perfectly describe the detected labeling behavior for all proteins.

In light of the above, an even greater challenge might be posed when aiming to establish an appropriately adopted model for labeling kinetics under nonsteady-state circumstances which would account for changes in protein abundance during an experiment. In addition, when studying dynamic systems, one would typically compare different conditions eventually obtaining absolute quantitative information about protein stabilities. In this regard, measured labeling kinetics are not only dependent on protein degradation and resynthesis, but are also critically influenced by sheer cell doubling. However, cell doubling rates are likely to change during cell treatments and might even be changing during a pulse experiment under nonsteady-state conditions. This illustrates the difficulties of such comparative experiments and emphasizes the need for an accurate method to measure temporally resolved labeling kinetics and the correct determination of cell doubling times which must be conducted under the same culture conditions using identical cell batches.

In addition to steady-state assumptions, the applied exponential synthesis and degradation models also presume that the probability of a protein being degraded stays constant over its life-time. This alone might not hold true for all proteins. In fact, newly synthesized proteins have previously been reported to show shorter half-lives before they enter a second, more stable state (4). Recently, McShane et al. found that about 10% of all proteins detected in their study show such nonlinear degradation behavior (19). Many of these proteins were members of protein complexes that were produced in super-stoichiometric amounts substantiating the assumption of protein stabilization because of complex formation which has been termed cooperative stability (54). Besides, cotranslational ubiquitination and rapid degradation of misfolded proteins immediately after synthesis have also been demonstrated (55, 56) suggesting that a biphasic degradation behavior could also be a result of cellular quality control mechanisms. For evaluation of nonlinear degradation kinetics, an initial discrimination of newly and aged proteins would be needed, for example via a combination of different pulse and chase time-points (4) or a second metabolic label (19). Our present study, as most other published turnover surveys, does not provide such resolution. Instead, our data describes an average behavior of the different states of a protein likely dominated by the turnover characteristics of the most abundant one.

The systematic evaluation of replicate analyses, followed by the assessment of the reproducibility for turnover estimations attested a reliable precision of the SILAC-TMTM approach on the protein as well as the peptide level. Moreover, the four cell culture replicates did not only allow for testing of statistically significant differences but should also increase the robustness of combined turnover information from replicates. To the best of our knowledge, the present study provides the most comprehensive dataset on endogenous protein turnover. Still, we point out that very quickly turned over proteins, particularly those which are completely turned over within 1 h, will be missing or underrepresented in the dataset simply because of the choice of time-points and curve fitting constraints. Nevertheless, the representative proteome coverage and high quality of the data allowed us to reassess potential determinants of protein stability which are inherent to the protein itself.

Biological Implications

We observed a positive correlation between protein abundance and turnover, but a negative correlation between protein abundance and length which corroborates findings by others (13, 14, 57). Making highly abundant proteins stable and small might offer a route for cells to avoid excessive energy consumption considering the costs for resynthesis of degraded proteins. It should be noted though that for high abundant proteins, even slow degradation rates will lead to degradation of many molecules. For the 60S ribosomal protein L18, for example, only 0.13% of all molecules were determined to be degraded per hour (corrected for cell doubling). But at a cellular abundance of on average more than 1 Mio copies per cell, this still results in the degradation and subsequent resynthesis of about one RPL18 molecule every 3 s illustrating the energy efforts for the maintenance of the default turnover of very stable, but high abundant proteins. Protein size (length) has also been reported to be associated with protein stability based on measurements using fluorescently tagged proteins in mammalian cells and yeast (7, 18). Although perhaps intuitive, as making longer proteins should contribute to energy consumption during translation, others subsequently argued that this is not the case for endogenous proteins (11, 14) and our data confirms that there is no global correlation of protein length with protein stability.

However, we did observe a weak correlation of protein half-lives with features of primary and secondary protein structure in that polar amino acids, proline (which is known to disrupt ordered structures), and random coils were associated with short-lived proteins, the latter confirming earlier reports (11, 18). In addition, overall sequence and structure differences appeared to explain, at least in part, the significantly different stabilities of functionally distinct proteins. It has been known for a long time that the hydrophobic effect drives protein folding thereby reducing the surface area of proteins and the solvent accessibility of hydrophobic amino acids and leading to more ordered structures (58, 59). Conversely, a more polar and random protein structure with relatively larger surface areas could possibly lead to a higher accessibility for modifications and interactions which could potentially induce protein degradation. This assumption would be in line with the hypothesis of cooperative protein stability because surfaces of proteins in complexes are also less solvent exposed (54, 60). Indeed, it has been hypothesized that disordered proteins with larger surface areas tend to engage in more promiscuous interactions and are also more likely to have pathological effects when overexpressed (61). This higher dosage sensitivity of disordered proteins would provide a conceptual explanation for the inverse correlation of the content of random coils with protein abundance which was observed in the present study. Overall, the observed higher turnover rate of rather disordered proteins could be a regulatory mechanism that protects cells from toxic protein aggregates.

In terms of single amino acids, serine had the strongest association with protein stability. One might speculate that its destabilizing effect might in part be related to its involvement in the formation of phosphodegrons, amino acid motifs that are recognized by E3 ligases which ubiquitinylate and thus mark respective proteins for degradation (62). In contrast, charged amino acids did not appear to have any consistent effect on endogenous protein turnover in our data. This is somewhat contradictory to results of a fluorescence-based genomic tagging study, which found glutamate, aspartate, lysine and arginine to be enriched in stable proteins (7). This again suggests that protein stabilities derived from genomic tagging approaches investigating overexpressed proteins might not be readily transferable to endogenous protein half-lives.

Another factor that has been described to influence turnover rates is the localization of proteins. In the present study only minor differences in half-lives of proteins assigned to different cell locations were observed. However, we note that potentially different turnover rates for the same protein species localizing to various cell compartments could not be distinguished in our work because whole cell extracts were analyzed. A spatially resolved study would provide further insights, especially considering recent observations that proteins frequently localize to multiple cell compartments (40). Indeed, after subcellular fractionation, Boisvert et al., detected differing stabilities of the same proteins depending on their localization (14). They detected complex subunits to exhibit longer half-lives after complex assembly which has recently been further supported by McShane et al. (19).

As mentioned earlier, the present study does not provide the resolution to discriminate between free and assembled complex units. However, a generally longer half-life of proteins that are part of complexes was detected supporting the overall notion of a stabilizing effect of protein interactions. The only significant exception to this rule was the NADH dehydrogenase, complex I of the electron transport chain. Despite of being highly abundant, members of this complex exhibited rather short half-lives. We suspected that this may be related to damage inflicted by oxidative stress, which was corroborated by experiments performed under rotenone induced, oxidative stress conditions. Within the scope of this work, only NADH dehydrogenase proteins were investigated, thus further studies are required to clarify whether the turnover of other respiratory chain proteins can also be regulated by other forms of oxidative stress. This might be of interest for members of complex III, as this is the second site of superoxide formation in the electron transport chain. Surprisingly, not all assayed subunits of respiratory chain complex I showed the same significant increase in turnover on rotenone treatment indicating that single subunits mainly located around the iron-sulfur centers were substituted in the complex. Although a selective exchange of single subunits has been described before in other complexes (63, 64), the process and mechanisms by which this occurs still remain to be determined. Notably, half-lives of proteins within some complexes (also including the respiratory chain complexes) showed major variations which might further support the principle of a selective degradation of single complex subunits. However, another explanation might be that measured turnover rates represent an average of the degradation behavior of free and assembled subunits. As already stated, these two states might possess different stabilities and, in addition, not exhibit the same frequencies for all complex members. Indeed, for NADH dehydrogenase, this presumption was substantiated by an observed negative correlation of copies and half-lives (ρ = −0.34) attesting a higher turnover for those subunits which must feature a higher proportion of the free protein state.

Not only proteins within the same complex varied in their stabilities, but even peptides assigned to the same protein group differed more in their turnover rates than what could be simply explained by technical variation. It has been stated before that isoforms and differentially modified proteins can exhibit different stabilities (12, 17, 20), but because of the restricted quantification accuracy at the peptide level, these kinds of analyses have hitherto largely been limited to comparisons of turnover dynamics of groups of peptides or the simple comparison of proteins included in a modification database to those not registered in this database. As we demonstrated, using the pulsed SILAC-TMT multiplexing approach, an evaluation of turnover rates at the level of single peptides is feasible. Among the peptides with significantly different turnover times, several were constituents of distinct splice variants potentially representing isoform specific protein turnover. For most of these examples, physicochemical properties of annotated splice variants considerably differed which further reinforces the notion that structure, hydrophobicity and abundance play a fundamental role in regulating protein stability. How this is controlled at a molecular level, however, remains largely elusive.

As noted above, certain sequence motifs termed degrons have been found to serve as recognitions signals for E3 ubiquitin ligases and are therefore connected to protein stability (65–67). In addition to the aforementioned phosphodegrons, it has been demonstrated that the identity of N-terminal residues following the initiator methionine and N-terminal processing are associated with different protein stabilities (17, 68). We also found that proteins possessing an N-terminal alanine were significantly enriched in long-lived proteins, whereas lysine and glutamate appeared to have a rather destabilizing effect (1D enrichment analysis at 1% FDR employing protein half-life data). However, the overall effect was small (enrichment scores between −0.14 and 0.09) indicating a high variation in the half-lives of proteins featuring the same N-terminal residue. Regarding N-terminal processing, Gawron et al. also detected a generally higher stability for peptides that retained the initiator Met residue (iMet) before valine and proline residues compared with those without it (17). Consistent with this, the proline containing N terminus of 60S ribosome subunit biogenesis protein NIP7 was detected to be less stable after iMet cleavage in our data. Conversely, the eukaryotic translation initiation factor 3 subunit B (EIF3B) protein and the mitotic spindle-associated MMXD complex subunit MIP18 (FAM96B), which contain an N-terminal Pro and Val residue respectively, displayed the opposite behavior with iMet containing peptides featuring a much higher turnover. Overall, this indicates that effects of N-degrons do not necessarily need to be consistent across proteins and that additional, and so far unknown, factors might be involved in N-terminal regulation of protein stability.

With regard to potentially modified peptides, it needs to be emphasized that the disappearance of SILAC labeled peptides can either be caused by actual degradation of the proteoform related to this detected peptide or by the peptide entering another (modification) state. In other words, a higher turnover rate of iMet containing peptides could also be related to the rate of N-terminal proteolytic processing. The same applies to other irreversible post-translational modifications and in general to all cases where the detected peptide or protein is lost from the pool of analyzed species as it is the case, for example, for secreted proteins. Accordingly, it is conceivable that the high turnover rate of the peptide encompassing His715 in EEF2 might also reflect the rate of diphthamide modification (51). Similarly, the turnover of peptides comprising cleavage sites in CTSD and PSAP, might as well illustrate the proteolytic process itself. In contrast, peptides that are completely contained in a cleavage product should represent its actual stability as observed for mitochondrial transit peptides, the ubiquitin-like part of FAU and also the light chain of CTSD. Two different products of CTSD which are likely to be related to the full length protein and the product resulting from the cleavage of the secretion signal peptide have previously been shown to differ in their turnover rates (20). However, it has never been demonstrated that the amino-terminal light chain of CTSD is less stable than the carboxyl-terminal heavy chain. Because both chains are associated via hydrophobic interactions to form the active site of CTSD (69), this potentially hints to a hitherto unknown control mechanism of CTSD activity by regulation of the abundance of the light chain via its higher turnover. Consequently, a stabilization of the light chain alone would rapidly increase the abundance of active CTSD.

A similar principle might underlie the regulation of BLM activity. This helicase has been proposed to be involved in DNA double strand repair (70) and described to be phosphorylated at Thr766 by the cell cycle regulating kinase CDK1 (48) which in turn has been demonstrated to be degraded on genotoxic stress (71). Together with our observation of a much higher stability of the Thr766 nonphosphorylated state, this suggests that BLM half-life can be increased via diminished phosphorylation on Thr766 because of reduced CDK1 activity following DNA damage, providing a rapid means to enhanced helicase activity for DNA repair. This illustrates that a high “default” protein turnover, which at first sight might appear to be disadvantageous from an energy efficiency point of view, can enable a cell to respond more flexibly and rapidly to altered cellular conditions via a post-translationally regulated stabilization of required proteins and without the need to induce transcription and translation. With respect to the further identification of differentially turned over proteoforms, it generally needs to be considered that, in bottom-up proteomics, every peptide that is analyzed might include molecules derived from various proteoforms. As a result, when comparing single peptides to the whole protein, only modifications which either very potently alter protein stability and/or exhibit an overall high occupancy can be identified as turnover regulating PTMs. To overcome the limitation of proteoform-shared peptides, a direct comparison of modified peptides to their unmodified counterparts would prove beneficial in the future.

In general, the transferability of turnover data obtained from different biological systems remains a subject of debate. Although a high species conservation of protein stability has been claimed for mammalian proteins (12), we and others (14, 17) have also detected considerable discrepancies across published turnover datasets. This might to some extent be of technical nature and for example be related to different measurement strategies, detection of different peptides for the same protein which display distinct turnover rates, data quality or analysis approaches further underscoring the challenge to reproducibly determine protein turnover. However, the present study found turnover rates published from different labs but for the same cell line to correlate better among each other than across different cell lines which indicates some cell line specific component affecting turnover. This might not be surprising considering the reported relationships of protein abundance, localization or interactions with protein stability. Although features such as amino acid content and structure will not differ for the same protein between various cell lines, expression patterns, main splice variants and complex partners might vary considerably and thus influence measured protein stability. Moreover, it has to be noted that the HeLa cells used in this study are highly aneuploid. It has already been shown that proteins derived from amplified gene regions often feature a higher degradation rate (19), which might provide a further explanation for the observed discrepancies across cell lines. In addition, we and others studied the dynamic state of the proteome in proliferating cells which might not resemble protein stability in whole organisms where most cells reside in a nondividing state. Nevertheless, our turnover rates correlated well with data derived from arrested HeLa cells (12). Overall, the degree of conservation of protein stability still needs to be determined more systematically. This should also help to further illuminate how protein turnover is regulated and even if protein turnover may differ to a great extent across biological systems, some principles of protein stability control via, for instance, post-translational modifications might still universally apply.

In summary, our pulsed SILAC-TMT proof-of-concept study provides, to our knowledge, the most comprehensive turnover dataset to date with high temporal resolution of endogenously expressed, untagged proteins in a steady-state cell system. Observed protein degradation rates spanned more than four orders of magnitude demonstrating that protein turnover must be a highly regulated process. Although multiple protein features were associated with turnover on the protein level, correlations were often only weak which diminishes their overall predictive value and underscores the intricacies of the regulatory processes. This is illustrated by an even higher variation of degradation rates at the peptide level (more than five orders of magnitude) demonstrating that post-transcriptional and post-translational processing plays an essential role in the dynamic regulation of protein stability and thus revealing a new dimension in the functional control of life. Future efforts should be directed toward the identification of particularly fast turnover proteins in steady state-systems, though these might be difficult to study not least because of their presumed low abundance. However, these proteins might be of interest considering that short-lived proteins are enriched in molecules that regulate primary cell functions (like transcription factors) and that quickly turned over proteins bear a high chance of being effectively regulated in abundance via post-translational stabilization. Finally, accurate measurements of protein turnover on disturbing the steady-state condition of a cell pose a challenge for the future, but also holds tremendous potential for broadening our understanding of how cellular functions are regulated by adaptive proteostasis.

DATA AVAILABILITY

The MS proteomics data and complete Max-Quant search results have been deposited to the ProteomeXchange Consortium (http://www.proteomexchange.org/) via the PRIDE (26) partner repository with the data set identifier PXD008579. Spectra identifying post-translational modified peptides and proteins on the basis of single peptide matches can be viewed in the MaxQuant Viewer included in MaxQuant (v1.5.5.1) software which has also been deposited in the same location.