Abstract
Motivation: Advances in high-throughput technologies have led to the acquisition of various types of -omic data on the same biological samples. Each data type gives independent and complementary information that can explain the biological mechanisms of interest. While several studies performing independent analyses of each dataset have led to significant results, a better understanding of complex biological mechanisms requires an integrative analysis of different sources of data.
Results: Flexible modeling approaches, based on penalized likelihood methods and expectation-maximization (EM) algorithms, are studied and tested under various biological relationship scenarios between the different molecular features and their effects on a clinical outcome. The models are applied to genomic datasets from two cancer types in the Cancer Genome Atlas project: glioblastoma multiforme and ovarian serous cystadenocarcinoma. The integrative models lead to improved model fit and predictive performance. They also provide a better understanding of the biological mechanisms underlying patients’ survival.
Availability and implementation: Source code implementing the integrative models is freely available at https://github.com/mgt000/IntegrativeAnalysis along with example datasets and sample R script applying the models to these data. The TCGA datasets used for analysis are publicly available at https://tcga-data.nci.nih.gov/tcga/tcgaDownload.jsp.
Contact: marie.denis@cirad.fr or mgt26@georgetown.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Advances in high throughput technologies have led to the acquisition of various types of -omic data, including whole-genome sequencing, methylation, transcriptomic, glycomic, proteomic and metabolomic. Each data type provides a snapshot of the molecular processes involved in a particular phenotype. While studies focused on one type of -omic data have led to significant results (Civelek and Lusis, 2014), an integrative -omic analysis can provide a better understanding of the complex biological mechanisms involved in the etiology or progression of a disease by combining the complementary information from each data type. Consequently, there has been a growing effort in recent years to collect multiple -omic data types on the same sampling units. Initially, the efforts had focused on the integration of two types of data, as in expression quantitative trait loci (eQTL) analysis which explores the association between DNA sequence variations and gene expression phenotypes (Morley etal., 2004; van Nas etal., 2010), or copy number variants (CNV)-gene expression associations (Pollack etal., 2002; Stranger etal., 2007; Tyekucheva etal., 2011). There are now several studies that collect various -omic data on the same samples. The NCI-60 project, for example, provides various -omic data for a panel of 60 cancer cell lines collected from diverse tissues (http://discover.nci.nih.gov/cellminer). The Cancer Genome Atlas (TCGA) project (http://cancergenome.nih.gov/) is another great public resource for integrative genomic analysis that collects multiple -omic data types on the same samples for different cancers. The availability of these data has led to the development of statistical methods and bioinformatics tools to explore the associations between different -omic datasets and evaluate their relationships with phenotypic outcomes (see Hamid etal. (2009) for a review). Various studies have demonstrated that integrative approaches are more effective in identifying subtle effects that would have been missed in single dataset analysis, thus providing improved statistical power while reducing the detection of false positives (Dvorkin et al., 2013; Tyekucheva etal., 2011).
A commonly used approach for integrative analysis remains the application of univariate tests evaluating the association between pairs of elements from two -omic data types (Morley etal., 2004; Stranger etal., 2007). This, however, raises a problem of multiplicity making it practically impossible to identify significant links after correcting for multiple testing. In addition, it ignores the fact that genomic markers do not work independently but in coordination. Monni and Tadesse (2009) developed a Bayesian stochastic partitioning method that overcomes this by combining ideas of mixtures of regression models and variable selection to uncover cluster structures in gene expression profiles and simultaneously identify subsets of CNVs associated to the correlated expression profiles. Shen etal. (2009) proposed iCluster, which uncovers tumor subtypes by integrating various -omic datasets using latent allocation indicators and specifying a variance–covariance structure that accounts for the dependence across data types. Wang etal. (2013) proposed an integrative Bayesian analysis of genomic data (iBAG), which specifies a hierarchical model that considers links between markers from different -omic sources at the gene level and identifies their association with a clinical outcome using Bayesian lasso. In a similar approach, Jennings etal. (2013) used a hierarchical Bayesian model to incorporate relationships between biological features and introduced latent scores to explain the clinical outcome.
In this paper, our main objective is to identify significant associations between markers across -omic datasets and elucidate the complementary information that explain the clinical outcome. Similarly to Wang etal. (2013) and Jennings etal. (2013), we will focus on -omic features at the gene-level but we also explore different modeling approaches that allow dependencies between features within a gene, within a functional network, or across all genes in the datasets. In addition, we do not introduce latent scores that summarize the information of several markers, as our primary interest is in identifying relevant markers and their interrelationships in order to gain a better understanding of the biological mechanisms underlying a phenotype. The remainder of the paper is organized as follows: Section 2 describes the TCGA datasets used to demonstrate the performance of the models. Section 3 presents the biological considerations and the different statistical models investigated. Section 4 presents the results of the analyses and Section 5 concludes the paper with a summary of the main findings.
2 Data
2.1 TCGA data
The TCGA Research Network has generated multiple -omic data for various types of cancers. These data are publicly available along with clinical information on the tissue samples. In this paper we focus on two cancer types: glioblastoma multiforme (GBM), the most common and aggressive form of malignant brain cancer in adults, and ovarian serous cystadenocarcinoma (OSC), the most prevalent form of ovarian cancer. For each cancer type, we consider data on genomic characterizations at three biological levels: The downloaded data are already pre-processed and converted into a common format for all platforms. We use the survival time after diagnosis as clinical outcome and consider for analysis patients with survival information and measurements for all three data sources. This resulted in 277 patients for GBM and 560 patients for OSC.
Gene expression profiles from Affymetrix Human Genome U133A array summarized at the gene level (level 3 data);
DNA methylations from Human Methylation 27 K arrays from methylated sites along a gene (level 3 data);
Copy number data based on normalized signal for copy number alterations of regions aggregated per probe (level 2 data)—we used the HG_CGH_244A and the CGH-1x1M_G4447A platforms respectively for GBM and OSC.
2.2 Data subsets for analysis
Integrative analysis is commonly performed by narrowing down the data to a subset of markers. Two widely used approaches consist of focusing on target pathways known to be implicated in the phenotype of interest or focusing on markers with significant effects in univariate analyses. We considered three different data subsets based on these criteria to investigate the performance of the models under varying amount of information.
Data1 focuses on genes that belong to pathways known to be relevant for the particular disease under investigation.
For GBM the three signaling pathways described in Jennings etal. (2013), namely RTK/PIK3, P53 and RB pathways, are considered. There are 49 genes with mRNA abundance, 166 methylation markers, and 524 CNVs in the datasets that belong to one of these pathways. 96% of the genes have information for all data types. There is a maximum of 18 methylation sites per gene and an average of 3.53 methylations per gene.
For OSC, the four signaling pathways known to be deregulated in ovarian cancer, PI3K/RAS, RB, NOTCH and FOXM1, are considered (The Cancer Genome Atlas Research Network, 2011). There are 29 genes with mRNA abundance, 85 methylation markers, and 229 CNV probes in the datasets that belong to one of these pathways. 72.4% of the genes have information on all three data sources. The maximum number of methylations per gene is 16 and the average is 3.85 methylations per gene.
Data2 is obtained by considering the top 100 gene expressions from univariate Cox survival models, along with the methylation sites and CNV probes mapping to these genes. The genes are then mapped to unique function/disease networks using the Ingenuity Pathway Analysis (IPA) software (www.ingenuity.com).
For GBM, this resulted in 131 methylation sites and 382 CNVs, with 71% of genes having both methylation and CNV information. There was a maximum of 2 methylations per gene and an average of 1.64 methylations per gene.
For OSC, this resulted in 125 methylation sites and 329 CNV probes, with 62% of genes having both information. There were one or two methylations per gene with an average of 1.74 methylations per gene.
Data3 consists of 200 genes obtained by taking the union of Data2 and an additional set of 100 genes. The latter are selected by taking the top ranking copy number probes in univariate CNV-survival model fits, mapping them to their corresponding genes and ensuring that they have gene expression data available.
For GBM, this led to 234 methylation sites and 2023 CNV probes, with 68% of genes having both methylation and CNV information. There was a maximum of 11 methylations per gene and an average of 1.63 methylations per gene.
For OSC, this led to 303 methylation sites and 1963 CNV probes, with 71% of genes having both methylation and CNV information. There was a maximum of 4 methylations per gene and an average of 1.83 methylations per gene.
3 Methods
We first discuss the biological considerations that motivated the different modeling approaches then formulate the models.
3.1 Biological considerations
Integrative approaches are challenging for several reasons. One difficulty is the complex and often unknown dependencies that exist between and within datasets. Direct or indirect links may exist between genomic features from different biological sources, and between these features and the phenotypic outcome. For example, DNA sequence variations can influence a phenotypic outcome by modulating the expression level of genes or by modifying other molecular features. Figure 1a shows an example of possible links between the three data types and the clinical outcome considered in this study. In this model, methylation markers can only act on mRNA abundance, while CNVs can modulate methylation as well as gene expression and the clinical outcome. CNVs that have already been found to be related to a particular biological feature, and thus have their effects already captured, are not considered for downstream associations. For example, a CNV that is found to be associated with a methylation marker is not considered for association with mRNA transcript level, since the effect of the CNV on the methylation is accounted for and the association between the methylation and the gene expression level is assessed subsequently. As for gene expression levels, they can be affected by both methylation and CNV, and they can in turn influence the outcome. Figure 1b shows a similar model but with CNVs not allowed to act directly on the clinical outcome. An alternative model we investigate does not allow CNVs to act on methylations but have them operate at the same level in their modulation of gene expression levels (Fig. 2).
Fig. 1.
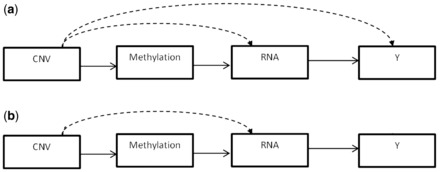
Models allowing CNVs to be associated with all other biological features. The solid arrows indicate that all markers in the set can potentially act on the next level while dotted lines indicate that only markers that have not already been shown to be associated with the next level can modulate subsequent levels. In (a) CNVs may act directly on the clinical outcome, but not in (b)
Fig. 2.
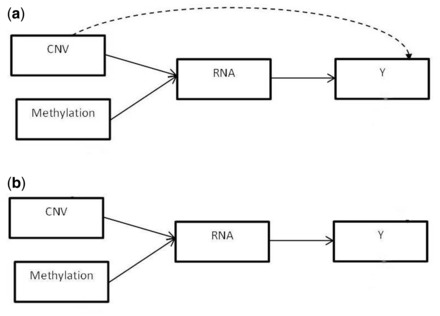
Model with no direct association between CNV and methylation. Both biological features can potentially act on gene expression. In (a) CNVs may also act directly on the clinical outcome, but not in (b)
In addition to the different possible links between molecular features, the level at which these relationships occur can vary. Some biological features may act locally on the same gene while others can influence markers located anywhere in the genome. For example, DNA sequence variations can be associated to expression levels of transcripts located on the same or nearby gene (cis-acting) or can modulate the transcript abundance of genes mapping to a different chromosome (trans-acting) (Civelek and Lusis, 2014; Morley et al., 2004). These biological considerations guided us to explore and compare different integrative models. Methylation effects are expected to occur only near the gene of interest (±250 kb) (Wagner etal., 2014). Thus, we allowed associations between methylation markers and other biological features to occur only within the same gene. That is, CNVs can act on methylation within the same gene and methylation markers can influence the mRNA abundance of the gene they map to. On the other hand, relationships between CNVs and gene expression levels were investigated at three different levels: one model allows CNVs to act on the expression level of the gene in which they are found, another model lets CNVs affect the mRNA abundance of any gene that is in the same disease/function network, and a third model lets CNVs potentially influence the expression levels of genes anywhere in the genome. We refer to these as Integrative-gene, Integrative-network and Integrative-genome, respectively.
3.2 Model formulation
Let be the observed data for N subjects with Y denoting the survival times, Gk the expression levels for gene k (), Mj the methylation levels for site j () and Cl the copy numbers for probe l (. Age is related to cancer survival and is therefore included as a covariate in the Cox model.
The proposed integrative model displayed in Figure 1a can be formulated as a hierarchical model similarly to Wang etal. (2013):
| (1) |
where the mechanistic submodels relate features among the different biological data types and the clinical submodel relates the linear predictor of the clinical outcome, η, to genomic and non-genomic variables. The mechanistic submodel is decomposed into two components: one capturing the association between methylation and CNV markers, and another linking gene expression with methylation and CNV data. The subscripts γ identify the features selected in the association between pairs of data types. Let γC be the set of CNVs considered for analysis, which can be decomposed into four disjoint subsets
where indicates the subset of CNVs associated with methylation markers, the subset of CNVs associated with gene expression levels but not methylations, the subset of CNVs associated to the clinical outcome among those not already selected for methylation or gene expression, and corresponds to the remaining subset of CNVs not found to be associated with any of the features. Similar subsets are defined for the methylations and gene expressions: is the subset of methylations associated to gene expressions and is the subset of gene expressions associated with the clinical outcome. The relevant subset of markers at each level are selected using penalized regression methods (Tibshirani, 1996).
The hierarchical model in (1) can be written more explicitly. For methylation site in a particular gene, its expression can be modeled in terms of CNVs mapping to the same gene:
| (2) |
where denotes the part of the methylation accounted for by CNVs and is the remaining part explained by other unmeasured factors.
The expression level of gene can be decomposed into three parts corresponding to epigenetic effects of DNA methylation, , CNV modulation by markers not already linked to methylation in (2), , and residual effects, :
| (3) |
The methylation effect on mRNA abundance, , is in turn decomposed into the effects of CNVs and other factors modulating methylation levels as formulated in Eq. (2). The levels at which CNV-gene expression relationships are considered determine the set of CNV probes considered in estimating . For the Integrative-gene scenario, we restrict our attention to CNV probes mapping to gene k that are not associated to methylation sites in the same gene, i.e.
where we use and to denote respectively association and no association. For the Integrative-network setting, let be the disease/function network in which gene k falls. In this case, we consider CNV probes mapping to genes that belong to , after removing CNVs in gene k associated to methylations in that gene, i.e.
For the Integrative-genome setting, all CNVs in the dataset (denoted by C) are considered after removing those in gene k associated to methylations in that gene, i.e.
For the last level of the hierarchical model in Figure 1a, the linear predictor of the Cox regression is modeled in terms of the gene expression effects and the CNV effects on survival. The former can be decomposed into parts corresponding to modulations via methylation, CNV and other factors:
| (4) |
For the model in Figure 1b, no direct relationship between CNVs and the survival outcome is allowed, thus the linear predictor in the Cox model reduces to the gene expression effects:
| (5) |
For the models in Figure 2 in which CNVs do not affect methylation patterns, the gene expression model in (3) is modified such that the methylation and CNV markers are both directly associated to the transcription levels:
| (6) |
In this model, the set for the different CNV-gene expression integrations considered becomes for the Integrative-gene setting, for the Integrative-network relationship, and simply all CNVs in the dataset for the Integrative-genome scenario.
These formulations not only allow us to identify markers associated to the survival outcome but also to understand the underlying biological relationships between different molecular processes.
3.3 Model fitting
For the association between methylation sites and CNVs, univariate and multivariate models are considered. In a first approach, the methylation outcomes () are analyzed one at a time using lasso penalized linear regression models (Tibshirani, 1996). In a second approach, to account for the high dependence among methylation sites within the same gene, a block-wise descent algorithm for group-penalized multi-response regression is investigated (Simon etal., 2013). In this approach, the same set of CNVs are selected for methylations corresponding to the same gene but separate regression coefficients are estimated for each methylation site within the gene. We refer to these as uni- and multi-methylation models. For the association between gene expression levels and the other biological data sources, a penalized lasso linear regression model is used. Finally, a lasso penalized Cox regression model is used to relate the survival outcome to the biological features (Friedman etal., 2010).
Studies investigating the relationship of epigenetic data with other biological features are starting to emerge, but these relationships are not yet well established. To incorporate this lack of information and to account for the uncertainty in the submodels assessing the dependence between CNVs and methylations within a gene , we implement an expectation–maximization (EM) algorithm by specifying a mixture of two Gaussian densities corresponding to the methylation profiles being modulated by CNV effects or not:
| (7) |
where is a univariate or multivariate Gaussian density function depending on whether there is a single or multiple methylations mapping to gene k, are the mixing proportions, and are the component mean and covariance parameters such that
where corresponds to the subset of CNVs in gene k identified to be associated to the methylations in the same gene. For component 2, the parameter does not depend on the CNVs and is estimated directly from the methylation data. CNVs are deemed to be associated to the methylation patterns only if there is more support for component 1. Details of the EM algorithm are provided in the online Appendix.
3.4 Model performance criteria
The objectives of the analysis are (i) to model survival time using relevant features from the different biological data types and (ii) to capture the relationships between these features in order to better understand the underlying biological mechanisms. To assess the performance of the various models considered, we need to define reasonable criteria. In the presence of censoring, defining measures of goodness-of-fit and predictive performance is complicated (van Wieringen etal., 2009). The coefficient of determination, which is the traditional linear regression measure for quantifying the proportion of total variation in the outcome accounted for by the model, is not valid in the context of Cox model with censored data. We consider a general measure developed by Nagelkerke (1991) for Cox proportional hazard models:
| (8) |
where N is the number of subjects, corresponds to the partial log-likelihood of the null model (without predictors), and ) is the partial log-likelihood for the model using the selected predictors. We use an adjusted-R2 to take into account the number of estimated parameters, p, and penalize for the complexity of the model:
| (9) |
We also examine the predictive performance using cross-validation by considering the concordance index (c-index), which captures the proportion of pairs of subjects whose predicted survival times are correctly ordered (Harrell, 2001):
| (10) |
where corresponds to the set of all pairs of subjects (i, j) with survival times ti > tj and if the predicted survival times satisfy , 0 otherwise. The closer the c-index is to 1, the better the ordinal predictive power of the model. Since predictive evaluations on training data give optimistic results, we performed repeated 10-fold cross validations to evaluate the c-index. This consists of partitioning the data into 10 subsamples, using 9 of the subsamples for training and the left-out set for validation, with each subsample being used in turn as a test set. The predictive survival times from the test sets are used to calculate the c-index. This is repeated multiple times to account for the variability in randomly partitioning the data into subsamples, and the mean and standard deviation of the c-index are reported.
4 Discussion
Tables 1 and 2 present the mean and standard deviation of the adjusted-R2 over repeated cross-validation fits for the various integrative models in each of the three data subsets (Data1, Data2, Data3) for the GBM and OSC datasets, respectively. As a reference comparison model, we fit a penalized Cox model on the gene expression data only, adjusting for age:
| (11) |
We also report the Cox model with only age effect.
Table 1.
GBM—Adjusted-R2 (SD) for various models and integration levels
| Model | no CNV- | Uni-methylation | Multi-methylation | ||
|---|---|---|---|---|---|
| methylation | with EM | without EM | with EM | without EM | |
| Models allowing direct CNV-survival association (models in Figs 1a and 2a) | |||||
| Data1 | |||||
| Integrative-gene | 0.385 (1.99E-02) | 0.374 (1.56E-02) | 0.355 (1.48E-02) | 0.330 (8.08E-02) | 0.357 (7.98E-03) |
| Integrative-network | 0.296 (3.19E-02) | 0.343 (4.11E-02) | 0.282 (1.60E-02) | 0.311 (2.87E-02) | 0.280 (3.68E-02) |
| Integrative-genome | 0.331 (9.42E-03) | 0.300 (4.85E-02) | 0.262 (3.85E-03) | 0.315 (1.88E-02) | 0.286 (7.30E-02) |
| Reference model | 0.237 (2.94E-17) | ||||
| Age model | 0.168 (0.00E + 00) | ||||
| Data2 | |||||
| Integrative-gene | 0.578 (3.90E-03) | 0.524 (2.76E-03) | 0.533 (8.78E-03) | 0.522 (4.02E-03) | 0.537 (7.22E-03) |
| Integrative-network | 0.571 (1.07E-02) | 0.539 (3.33E-02) | 0.519 (4.03E-02) | 0.531 (2.88E-02) | 0.504 (6.37E-02) |
| Integrative-genome | 0.517 (2.86E-02) | 0.479 (2.39E-02) | 0.474 (4.82E-02) | 0.486 (6.32E-02) | 0.454 (1.10E-02) |
| Reference model | 0.407 (0.00E + 00) | ||||
| Age model | 0.168 (0.00E + 00) | ||||
| Data3 | |||||
| Integrative-gene | 0.593 (1.42E-02) | 0.605 (1.09E-02) | 0.607 (9.51E-03) | 0.594 (7.81E-03) | 0.600 (1.40E-02) |
| Integrative-network | 0.574 (1.29E-02) | 0.554 (8.69E-02) | 0.584 (6.82E-03) | 0.587 (3.71E-02) | 0.454 (2.88E-02) |
| Integrative-genome | 0.415 (3.89E-02) | 0.458 (3.35E-02) | 0.547 (3.50E-02) | 0.530 (6.07E-02) | 0.550 (4.95E-02) |
| Reference model | 0.464 (3.12E-02) | ||||
| Age model | 0.168 (0.00E + 00) | ||||
| Models allowing no direct CNV-survival association (models in Fig. 1b and 2b) | |||||
| Data1 | |||||
| Integrative-gene | 0.253 (5.90E-02) | 0.297 (1.60E-02) | 0.279 (3.80E-02) | 0.271 (3.80E-02) | 0.296 (9.60E-03) |
| Integrative-network | 0.259 (1.30E-02) | 0.314 (2.60E-02) | 0.290 (3.00E-02) | 0.277 (4.20E-02) | 0.299 (3.70E-02) |
| Integrative-genome | 0.287 (1.20E-02) | 0.291 (2.40E-02) | 0.307 (3.20E-02) | 0.299 (2.80E-02) | 0.283 (1.80E-02) |
| Reference model | 0.237 (2.94E-17) | ||||
| Age model | 0.168 (2.90E-17) | ||||
| Data2 | |||||
| Integrative-gene | 0.487 (6.81E-03) | 0.454 (6.50E-02) | 0.478 (5.00E-02) | 0.482 (6.00E-02) | 0.472 (4.70E-02) |
| Integrative-network | 0.538 (1.44E-02) | 0.538 (3.40E-02) | 0.519 (2.80E-02) | 0.511 (2.60E-02) | 0.536 (2.60E-02) |
| Integrative-genome | 0.494 (3.32E-02) | 0.520 (7.00E-02) | 0.460 (1.00E-02) | 0.483 (3.30E-02) | 0.453 (1.30E-02) |
| Reference model | 0.407 (0.00E + 00) | ||||
| Age model | 0.168 (3.04E-17) | ||||
| Data3 | |||||
| Integrative-gene | 0.536 (8.23E-03) | 0.575 (9.75E-03) | 0.567 (1.36E-02) | 0.572 (2.83E-02) | 0.568 (1.85E-02) |
| Integrative-network | 0.554 (8.68E-03) | 0.506 (1.12E-01) | 0.569 (1.66E-02) | 0.580 (4.12E-02) | 0.500 (8.01E-02) |
| Integrative-genome | 0.433 (4.69E-02) | 0.483 (5.17E-02) | 0.537 (5.10E-02) | 0.517 (6.24E-02) | 0.547 (4.64E-02) |
| Reference model | 0.464 (3.12E-02) | ||||
| Age model | 0.168 (0.00E + 00) | ||||
Table 2.
OSC—Adjusted-R2 (SD) for various models and integration levels
| Model |
no CNV- | Uni-methylation | Multi-methylation | ||
|---|---|---|---|---|---|
| methylation | with EM | without EM | with EM | without EM | |
| Models allowing direct CNV-survival association (models in Figs 1a and 2a) | |||||
| Data1 | |||||
| Integrative-gene | 0.039 (0.00E + 00) | 0.045 (8.64E-03) | 0.044 (4.48E-03) | 0.047 (7.95E-03) | 0.043 (2.51E-03) |
| Integrative-network | 0.055 (1.31E-03) | 0.055 (2.47E-03) | 0.042 (3.14E-03) | 0.044 (2.79E-03) | 0.044 (3.61E-03) |
| Integrative-genome | 0.066 (4.50E-03) | 0.050 (2.11E-02) | 0.055 (1.70E-02) | 0.060 (1.74E-02) | 0.068 (4.95E-03) |
| Reference model | 0.029 (2.96E-04) | ||||
| Age model | 0.022 (0.00E + 00) | ||||
| Data2 | |||||
| Integrative-gene | 0.394 (4.50E-03) | 0.390 (9.22E-03) | 0.389 (6.19E-03) | 0.395 (5.02E-03) | 0.398 (5.39E-03) |
| Integrative-network | 0.373 (7.01E-03) | 0.387 (8.86E-03) | 0.381 (5.29E-03) | 0.383 (5.11E-03) | 0.388 (6.22E-03) |
| Integrative-genome | 0.354 (3.90E-03) | 0.361 (1.68E-02) | 0.373 (1.67E-02) | 0.395 (9.59E-03) | 0.387 (9.13E-03) |
| Reference model | 0.324 (2.62E-03) | ||||
| Age model | 0.022 (0.00E + 00) | ||||
| Data3 | |||||
| Integrative-gene | 0.407 (7.86E-03) | 0.406 (7.31E-03) | 0.418 (1.90E-02) | 0.421 (1.25E-02) | 0.413 (2.42E-02) |
| Integrative-network | 0.420 (6.91E-03) | 0.456 (1.31E-02) | 0.451 (6.79E-03) | 0.449 (1.56E-02) | 0.450 (1.23E-02) |
| Integrative-genome | 0.415 (1.39E-02) | 0.429 (1.29E-02) | 0.418 (2.44E-02) | 0.397 (1.85E-02) | 0.398 (7.43E-03) |
| Reference model | 0.421 (4.41E-04) | ||||
| Age model | 0.022 (0.00E + 00) | ||||
|
| |||||
| Models allowing no direct CNV-survival association (models in Figs 1b and 2b) | |||||
| Data1 | |||||
| Integrative-gene | 0.043 (0.00E + 00) | 0.051 (6.55E-03) | 0.045 (4.51E-03) | 0.041 (5.83E-03) | 0.042 (3.85E-03) |
| Integrative-network | 0.054 (2.41E-04) | 0.069 (1.76E-02) | 0.048 (6.21E-03) | 0.044 (2.91E-03) | 0.044 (3.61E-03) |
| Integrative-genome | 0.067 (4.71E-03) | 0.057 (4.07E-03) | 0.051 (1.71E-02) | 0.060 (1.76E-02) | 0.068 (6.13E-03) |
| Reference model | 0.029 (2.96E-04) | ||||
| Age model | 0.022 (0.00E + 00) | ||||
| Data2 | |||||
| Integrative-gene | 0.381 (4.59E-03) | 0.384 (9.78E-03) | 0.388 (3.63E-03) | 0.389 (3.16E-03) | 0.390 (6.73E-03) |
| Integrative-network | 0.363 (4.82E-03) | 0.380 (1.09E-02) | 0.377 (3.62E-03) | 0.382 (5.84E-03) | 0.382 (7.40E-03) |
| Integrative-genome | 0.354 (3.60E-03) | 0.371 (1.73E-02) | 0.359 (9.74E-03) | 0.396 (7.98E-03) | 0.386 (1.26E-02) |
| Reference model | 0.324 (2.62E-03) | ||||
| Age model | 0.022 (0.00E + 00) | ||||
| Data3 | |||||
| Integrative-gene | 0.440 (1.41E-02) | 0.438 (3.87E-03) | 0.450 (1.95E-02) | 0.433 (1.01E-02) | 0.434 (8.83E-03) |
| Integrative-network | 0.417 (3.00E-02) | 0.456 (4.15E-03) | 0.455 (5.08E-03) | 0.448 (1.47E-02) | 0.455 (5.55E-03) |
| Integrative-genome | 0.430 (1.76E-02) | 0.422 (1.71E-02) | 0.418 (2.42E-02) | 0.399 (1.93E-02) | 0.405 (1.62E-02) |
| Reference model | 0.421 (4.41E-04) | ||||
| Age model | 0.022 (0.00E + 00) | ||||
We considered integrative models investigating association between CNVs and gene expression levels at the gene level (Integrative-gene), within the same disease/function network (Integrative-network), and throughout the genome (Integrative-genome). When CNV-methylation relationships are considered as in Figure 1, the methylation sites within the gene are viewed as independent outcomes (uni-methylation) or as a multivariate correlated outcome (multi-methylation). We also assessed the impact of incorporating the uncertainty in the CNV-methylation relationship using the EM algorithm outlined in Section 3.3. These comparisons are performed allowing CNVs to directly affect or not the survival outcome as depicted in Figures 1 and 2.
For all the datasets, the integrative models provide better fit to the data compared to the reference model or the model with only age effect. With regards to the subsets of features considered for integration, focusing on markers selected based on the relevance of pathways for the phenotype under investigation, as in Data1, has the worst performance compared to using features selected based on univariate scans; we obtain the largest adjusted-R2 with Data3.
In terms of CNV-methylation relationships, the performance depends on the data subsets considered and the subsequent CNV-gene expression or CNV-survival associations allowed. For example, for GBM Data2, the integrative model that considers CNVs and methylations not to be related to each other but to each act directly on gene expressions (no CNV-methylation) gave the largest adjusted-R2 when CNV-survival association is allowed. Instead for GBM Data3, the no CNV-methylation model did not necessarily have the best performance and had the lowest adjusted-R2 when allowing all CNVs to act on gene expression changes (Integrative-genome). When allowing for CNV-methylation association, the multi-methylation model that accounts for the dependence between methylation sites in the same gene and the uni-methylation model have similar performance. This may be due to two factors: (i) in most cases, there are only one or two methylation sites that map to the same gene; (ii) the multivariate regression group-penalization procedure of Simon etal. (2013) we used is designed to select the same covariates for all outcomes but with varying regression coefficients. Thus, in a situation where a CNV may affect only one of the methylation sites mapping to a gene, all sites would be related to the CNV thereby introducing noise. When a CNV-methylation relationship is allowed, accounting for the uncertainty in the association using the EM algorithm appears to help in some of the models.
With respect to CNV-gene expression association, the model that lets CNVs act on expression levels of genes they map to (Integrative-gene) performs significantly better for all GBM data subsets when CNV-survival association is allowed. When copy numbers are not allowed to be directly associated with the survival outcome, the integrative-genome setting, which lets all CNVs potentially act on a gene expression level, provides, in general, the best performance. For OSC, although the integrative-gene model is the best for Data2, for the other data subsets, the integrative-network or the integrative-genome scenarios give better model fits.
With regard to CNV-survival association, allowing copy numbers to act directly on survival rather than just through their effect on gene expression levels, provides improved model fit. This is most obvious in GBM Data1 and Data2. For the other data subsets, the performance slightly varied depending on the CNV-methylation and CNV-gene expression associations considered, although the results were relatively comparable.
Finding models with good predictive performance is more challenging than determining good explanatory models. In particular, survival prediction in cancer is a difficult task because of the intrinsic high variability that exists in patients’ survival outcome (Henderson and Keiding, 2005). Another challenge is the lack of a good criterion to assess the predictive performance of survival models. Here, we used repeated 10-fold cross-validations to assess the performance of the various models using the c-index measure as described in Section 3.3. We present in Table 3 the results for GBM and OSC in the larger data subset, Data3, which gave the best model fit. Considering methylation sites mapping to the same gene as a multivariate outcome or incorporating the EM algorithm in the CNV-methylation relationships gave similar results as the uni-methylation models, so only the latter and the models assuming no CNV-methylation link are reported. We note that the integrative models give improved predictive performance. For example, for GBM, the integrative-gene models give the highest cross-validated c-indices. When considering CNV-gene expression associations across the whole genome (integrative-genome), the model with no CNV-methylation appears not to perform as well as the reference model (relating only gene expression data to survival outcomes). However, when allowing for CNV-methylation associations, this model’s predictive performance is comparable to that of the integrative-gene. Similarly, for OSC, the integrative-gene models and the models that allow for CNV-methylation association have the highest c-index values. We note concordant results between goodness-of-fit and predictive performance; the better explanatory models with higher adjusted-R2 values also give better prediction with higher cross-validated c-indices.
Table 3.
Cross-validated c-index (SD)
| Model | no CNV-methylation | Uni-methylation | no CNV-methylation | Uni-methylation |
|---|---|---|---|---|
| GBM Data3 | OSC Data3 | |||
| Models with direct CNV-survival association | Models with direct CNV-survival association | |||
| Integrative-gene | 0.747 (3.50E-02) | 0.756 (4.59E-02) | 0.743 (3.90E-02) | 0.737 (2.86E-02) |
| Integrative-network | 0.733 (4.20E-02) | 0.728 (5.73E-02) | 0.737 (4.01E-02) | 0.747 (2.72E-02) |
| Integrative-genome | 0.701 (5.24E-02) | 0.745 (4.78E-02) | 0.723 (4.12E-02) | 0.746 (3.09E-02) |
| Reference model | 0.713 (4.89E-02) | 0.728 (3.60E-02) | ||
| Age model | 0.657 (5.04E-02) | 0.604 (4.43E-02) | ||
| Models allowing no direct CNV-survival association | Models allowing no direct CNV-survival association | |||
| Integrative-gene | 0.732 (3.25E-02) | 0.737 (5.15E-02) | 0.743 (3.61E-02) | 0.746 (2.55E-02) |
| Integrative-network | 0.722 (3.47E-02) | 0.727 (4.57E-02) | 0.723 (3.96E-02) | 0.755 (2.74E-02) |
| Integrative-genome | 0.695 (3.96E-02) | 0.735 (4.58E-02) | 0.720 (3.33E-02) | 0.747 (3.01E-02) |
| Reference model | 0.713 (4.89E-02) | 0.728 (3.60E-02) | ||
| Age model | 0.657 (5.04E-02) | 0.604 (4.43E-02) | ||
Table 4.
Genes to which CNVs acting directly on survival in Figure 3 map to
| CNV marker | Gene symbol | CNV Marker | Gene symbol |
|---|---|---|---|
| A_14_P110633 | NDUFB11 | A_14_P125987 | EPHA7 |
| A_14_P127637 | MRPL2 | A_16_P01527635 | BACH2 |
| A_16_P02571038 | BCL2L14 | A_16_P03481569 | PLCB4 |
| A_16_P03680093 | IL1RAPL1 | A_16_P15125260 | ACOT11 |
| A_16_P20477498 | NUP93 | A_16_P20582406 | STX8 |
| A_16_P21053212 | PTPRA | A_16_P37686619 | SNAP91 |
Besides providing improved model fit and better predictive performance, an advantage of the integrative approach is that it gives insights into the biological mechanisms underlying the clinical outcome by identifying relationships between molecular features and their effects on the outcome. Figure 3 provides a graphical summary of these relationships for the best performing integrative model in GBM (adjusted-R2 = 0.605, cross-validated c-index = 0.756). This corresponds to the model depicted in Figure 1a allowing for CNV-methylation and direct CNV-survival association in Data3. Overall 33 mRNA transcripts are found to be associated with survival. Among these, 2 genes have transcript levels that are modulated by methylation markers, which themselves are influenced by CNV markers mapping to the same genes; 3 gene expression levels are associated to copy number changes, while 4 other genes have their mRNA abundance modulated by methylation markers. There are also another set of 12 CNVs found to be directly associated to survival. Many of the identified markers are known to be implicated in cancer. We found p21 protein-activated kinase 7 (PAK7), which is predominantly expressed in brain, to have a couple of methylation markers modulating its transcription levels, which in turn, are related to survival in GBM. Previous studies have determined this gene to be highly expressed in tumor tissues of glioma patients and have suggested that inhibition of this gene by RNA interference might efficiently suppress tumor development in glioma cells (Gu etal., 2015). Another study examining the underlying molecular mechanism of PAK7 found that suppression of this gene in glioma cells significantly inhibited cell growth, cell migration and invasion, and that PAK7 could inhibit cell apoptosis, suggesting that it could have a potential role in prevention and treatment of glioma tumors (Han etal., 2015). Among the CNV markers directly associated to survival is EPH receptor A7 (EPHA7), which is known to be overexpressed in different tumors, including GBM, and shows an inverse association with survival in GBM. EPHA7 has been put forward as a prognostic marker and a potential therapeutic marker for primary and recurrent GBM (Wang etal., 2008). Other CNV markers we identified, like protein tyrosine phosphatase, receptor type, A (PTPRA) and BCL2-like 14 (BCL2L14) have respectively been shown to be implicated in oncogenic transformation and to play an important role in inducing apoptosis. Among the mRNA transcripts identified to be associated to survival is fibroblast growth factor 7 (FGF7), a gene known to be involved in cell survival activities, tumor growth and invasion. Other gene expression changes found to be related to GBM survival include eukaryotic translation initiation factor 5A (EIF5A), which has two isoforms both carrying unfavorable prognostics for various cancers, glutathione S-transferase mu 3 (GSTM3), which has been linked to adult brain tumors, and TNF receptor-associated factor 1 (TRAF1) known to mediate anti-apoptotic signals from TNF receptors.
Fig. 3.
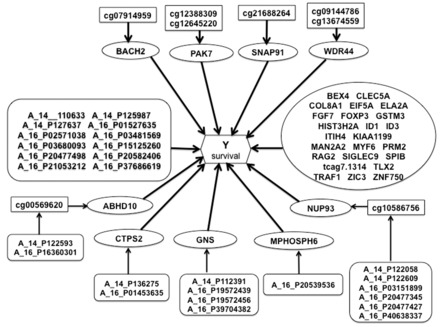
Result of integrative genomic analysis for GBM Data 3. Methylation markers are represented with rectangles; CNV markers with soft-edged rectangles; mRNA transcripts with ellipses. For CNVs acting directly on survival, the names of the genes they map to are provided in Table 4
5 Conclusion
The integrative models we considered are designed to identify significant relationships between molecular markers at different biological levels, as well as their association to a clinical outcome. We therefore use variable selection methods rather than a latent variable formulation or dimension reduction techniques. The proposed models can provide a better understanding of the biological mechanisms underlying the phenotypic outcome. Our analyses using different subsets of a meta-data including CNV, methylation, gene expression, and survival outcome collected on the same set of tissues show that integrative models lead to improved results. In addition to providing better model fits, they also yield better out-of-sample predictions. There are, however, differences in performance between the various integrative models considered. The subset of features considered for analysis, whether CNVs are allowed to act or not on methylation, whether direct CNV-survival associations are allowed or not, and the level at which CNV-gene expression relationships are allowed (within the same gene, within the same disease/function network, or across the whole genome) affect the goodness-of-fit and predictive performance of the integrative models. That is, the results depend on the type of information available in the data considered for analysis. Thus, when fitting integrative models, care is needed in defining the relationships between biological features. A systematic integration that allows for all possible links between biological features is not necessarily the best approach.
Funding
This work was supported by National Institutes of Health Grant R01HD059827 to M.D.
Conflict of Interest: none declared.
Supplementary Material
References
- Civelek M., Lusis A.J. (2014) Systems genetics approaches to understand complex traits. Nat. Rev. Genet., 15, 34–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dvorkin D., et al. (2013) A graphical model method for integrating multiple sources of genome-scale data. Stat. Appl. Genet. Mol. Biol., 12, 469–487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J., et al. (2010) Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw., 33, 1–22. [PMC free article] [PubMed] [Google Scholar]
- Gu X., et al. (2015) Efficient inhibition of human glioma development by RNA interference-mediated silencing of PAK5. Int. J. Biol. Sci., 12, 230–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamid J.S., et al. (2009) Data integration in genetics and genomics: methods and challenges. Hum. Genomics Proteomics., 2009, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han Z., et al. (2015) Downregulation of PAK5 inhibits glioma cell migration and invasion potentially through the PAK5-Egr1-MMP2 signaling pathway. Brain Tumor Pathol., 31, 234–241. [DOI] [PubMed] [Google Scholar]
- Harrell F.E. (2001) Regression Modeling Strategies, With Applications to Linear Models, Logistic Regression, and Survival Analysis. Springer, New York. [Google Scholar]
- Henderson R., Keiding N. (2005) Individual survival time prediction using statistical models. Clin. Ethics, 31, 703–706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jennings E., et al. (2013) Bayesian methods for expression-based integration of various types of genomics data. EURASIP J. Bioinf. Syst. Biol., 13, doi: 10.1186/1687–4153–2013–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monni S., Tadesse M. (2009) A stochastic partitioning method to associate high-dimensional responses and covariates (with discussion). Bayesian Anal., 4, 413–436. [Google Scholar]
- Morley M., et al. (2004) Genetic analysis of genome-wide variation in human gene expression. Nature, 430, 743–747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagelkerke N.J.D. (1991) A note on a general definition of the coefficient of determination. Biometrika, 78, 691–692. [Google Scholar]
- Pollack J.R., et al. (2002) Microarray analysis reveals a major direct role of DNA copy number alteration in the transcriptional program of human breast tumors. Proc. Natl. Acad. Sci. USA, 99, 12963–12968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen R., et al. (2009) Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics, 25, 2906–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simon N., et al. (2013) A blockwise descent algorithm for group-penalized multiresponse and multinomial regression. arXiv. [Google Scholar]
- Stranger B., et al. (2007) Relative impact of nucleotide and copy number variation on gene expression phenotypes. Science, 315, 848–853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Research Network (2011) Integrated genomic analyses of ovarian carcinoma. Nature, 474, 609–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. (1996) Regression shrinkage and selection via the lasso. J. R. Statist. Soc. Ser. B, 58, 267–288. [Google Scholar]
- Tyekucheva S., et al. (2011) Integrating diverse genomic data using gene sets. Genome Biol., 12, R105+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Nas A., et al. (2010) Expression quantitative trait loci: replication, tissue- and sex-specificity in mice. Genetics, 185, 1059–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Wieringen W.N., et al. (2009) Survival prediction using gene expression data: a review and comparison. Comput. Stat. Data Anal., 53, 1590–1603. [Google Scholar]
- Wagner J., et al. (2014) The relationship between DNA methylation, genetic and expression inter-individual variation in untransformed human fibroblasts. Genome Biol., 15, R37+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., et al. (2008) Increased expression of epha7 correlates with adverse outcome in primary and recurrent glioblastoma multiforme patients. BMC Cancer, 8, 79–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang W., et al. (2013) iBAG: integrative Bayesian analysis of high-dimensional multiplatform genomics data. Bioinformatics (Oxford, England), 29, 149–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


