Comparing Two Algorithms for Calibrating the Restricted Non-Compensatory Multidimensional IRT Model

Abstract

The non-compensatory class of multidimensional item response theory (MIRT) models frequently represents the cognitive processes underlying a series of test items better than the compensatory class of MIRT models. Nevertheless, few researchers have used non-compensatory MIRT in modeling psychological data. One reason for this lack of use is because non-compensatory MIRT item parameters are notoriously difficult to accurately estimate. In this article, we propose methods to improve the estimability of a specific non-compensatory model. To initiate the discussion, we address the non-identifiability of the explored non-compensatory MIRT model by suggesting that practitioners use an item-dimension constraint matrix (namely, a Q-matrix) that results in model identifiability. We then compare two promising algorithms for high-dimensional model calibration, Markov chain Monte Carlo (MCMC) and Metropolis–Hastings Robbins–Monro (MH-RM), and discuss, via analytical demonstrations, the challenges in estimating model parameters. Based on simulation studies, we show that when the dimensions are not highly correlated, and when the Q-matrix displays appropriate structure, the non-compensatory MIRT model can be accurately calibrated (using the aforementioned methods) with as few as 1,000 people. Based on the simulations, we conclude that the MCMC algorithm is better able to estimate model parameters across a variety of conditions, whereas the MH-RM algorithm should be used with caution when a test displays complex structure and when the latent dimensions are highly correlated.

Diagnostic assessments are increasingly used to measure educational outcomes and psychological constructs (Rupp, Templin, & Henson, 2010). Recent psychometric, statistical, and computational advances have improved the performance and widened the availability of these models in measuring complex psychological phenomena (Roussos, Templin, & Henson, 2007). In particular, successfully integrating diagnostic models in large-scale, standardized testing can better direct feedback on student strengths and weakness to significantly improve instruction and learning (Chang, 2012).

In psychometrics, two distinct classes of models have been proposed for cognitive diagnostic purposes, namely, multidimensional item response theory (MIRT) models and diagnostic classification models (DCMs). The major difference between MIRT and DCM is how they conceptualize the latent space. In DCMs, the latent space is assumed to consist of dichotomous skills that combine to form K-dimensional, discrete cognitive states. Conversely, MIRT models (i.e., latent trait models) consist of continuous skills that comprise a K-dimensional, continuous latent trait vector. Whether to use a particular type of model depends on whether practitioners should treat skills as discrete or continuous (Stout, 2007). One rule of thumb in deciding between models is that if the attributes measured by a test, questionnaire, or inventory are broadly defined, such as general math ability, then a continuous latent trait is typically more informative. Otherwise, if the attributes are finer grained, such as mastering the chain rule in calculus, then a discrete constellation of latent traits should be assumed.

A fundamental restriction common to either set of multidimensional models is specifying whether the traits or states combine in a compensatory or non-compensatory fashion. In compensatory latent trait models, examinees with high ability on one dimension can compensate for lower abilities on the other dimensions. Compensatory tasks often assume that examinees use one of several, alternative strategies for solving each problem (Embretson & Yang, 2013). Conversely, non-compensatory models (also called conjunctive models) assume that examinees must possess all skills comprising an item to obtain a correct response to that item. Conjunctive approaches tend to be popular when modeling cognitive traits because the process of solving a cognitive problem is often seen as successfully executing a series of steps, in order, each of which depends on a different skill.

Unfortunately, the multiplicative structure of conjunctive MIRT (C-MIRT) presents severe estimation challenges. Unlike compensatory models, non-compensatory models often necessitate separate difficulty parameters for each item on each dimension. As Bolt and Lall (2003) noticed, estimating these parameters “requires sufficient variability in the relative difficulties of components across items to identify the dimensions” (p. 396). Therefore, despite a non-compensatory structure potentially modeling cognitive processes better than a compensatory structure, few authors have proposed methods for estimating non-compensatory MIRT model parameters or advocated using non-compensatory MIRT models in practical applications. The aim of this article is, therefore, to present a restricted and estimable version of the C-MIRT model and compare several methods of estimating its parameters. The organization of the article is as follows. First, the original C-MIRT model is introduced, and a restricted version that is the focus of this article is proposed. We then present two algorithms used in model calibration (the details of which are outlined in Appendices A and B of the online version of this article) then, using analytical and graphical methods, the properties of conjunctive models and corresponding reasons for the simulation results are discussed. Finally, the performance of each algorithm is explored via an extensive simulation study.

C-MIRT Models

The simplest (Rasch) version of the C-MIRT model (Bolt & Lall, 2003; Embretson, 1984; Whitely, 1980) defines the probability of a correct response to item j by examinee i as

$$P(X_{\mathrm{ij}}=1|{\text{θ}}_{i1},\dots ,{\text{θ}}_{\mathrm{iK}})=\underset{k=1}{\overset{K}{\Pi }}\frac{\text{exp}({\text{θ}}_{\mathrm{ik}}-b_{\mathrm{jk}})}{1+\text{exp}({\text{θ}}_{\mathrm{ik}}-b_{\mathrm{jk}})},$$

where $b_{i1},\dots ,b_{\mathrm{iK}}$ are the K component-specific difficulty parameters of item i. Unlike compensatory IRT models, non-compensatory models include separate item-specific difficulty parameter for each ability dimension. A simple explanation of Model 1 is that a correct response to item i requires the successful completion of a sequence of K task components, and $b_{i1},\dots ,b_{\mathrm{iK}}$ correspond to the difficulty of successfully executing each component.

One extension of the C-MIRT model, the multi-component latent trait model (MLTM; Embretson, 1984, 1997), links being able to apply the necessary attributes with being able to correctly answer an item. The item response function (IRF) for the ith examinee and the jth item in MLTM is defined as

$$P(X_{\mathrm{ij}}=1)=a\underset{k}{\Pi }P(X_{\mathrm{ijk}}=1)+g(1-\underset{k}{\Pi }P(X_{\mathrm{ijk}}=1)),$$

where P(X_ijk = 1) is the probability that examinee i has applied attribute k to item j, a is the probability that item j is correctly solved when all of the necessary components are successfully applied to the item, and g is the probability that item j is correctly solved when at least one of the necessary components are not successfully applied to the item. The a-parameter of Equation 2 can be interpreted as the probability of using a meta-component, such as executive functioning (Embretson, 1984), to correctly answer an item, whereas the g-parameter can be interpreted as the probability of using an alternative method, such as guessing, to correctly answer an item. According to the MLTM, the probability of person i correctly applying attribute k to item i depends on the ability of person i on skill k (θ_ik) and the difficulty of item j on skill k (b_ik):

$$P(x_{\mathrm{ijk}}=1)=\frac{\text{exp}({\text{θ}}_{\mathrm{ik}}-b_{\mathrm{jk}})}{1+\text{exp}({\text{θ}}_{\mathrm{ik}}-b_{\mathrm{jk}})}.$$

MLTM uses the same unidimensional IRFs as C-MIRT to model both the probability of successfully applying each skill and the probability of successfully executing all of the necessary skills.

Although MLTM and C-MIRT are similar in structure, they differ in how their model parameters are usually estimated. Bolt and Lall (2003) and Babcock (2011) estimated both item and examinee parameters of the C-MIRT model via Markov chain Monte Carlo (MCMC). Conversely, Maris (1999) proposed estimating the MLTM by treating attribute-specific responses, the x_ijks, as missing data and using the EM algorithm. Maris's method improved over Embretson, who originally assumed that both the item and attribute within item responses, x_ij and x_ijk, were observed. Observing x_ijk greatly simplifies estimation but is nearly impossible to obtain in practice. In this article, we present two algorithms in detail, MCMC and Metropolis–Hastings Robbins–Monro (MH-RM), which should capably estimate parameters of the MLTM without requiring observable attribute-specific item responses. Unlike previous attempts at estimation, we add an additional term to the model—the Q-matrix—which removes indeterminacy inherent in the original MLTM and also simplifies parameter estimation. Before detailing the model estimation methods, we explain the purpose of restricting item loadings by means of a Q-matrix.

Restricted C-MIRT (RC-MIRT) Model

Without sufficient restrictions on the item parameter or person parameter matrices, multidimensional IRT models manifest both metric and rotational indeterminacy. Metric indeterminacy can be resolved by setting b_1k = 0 $\forall k\in \{1,2,\dots ,K\}$, a specification recommended by both Maris (1995) and Bolt and Lall (2003). However, arbitrary restrictions on the item parameter matrix require post-equating the $\hat{b}$s and $\widehat{\text{θ}}$s back to the original metric of the generating parameters. Instead, we fix the mean of estimated ability to be a vector of zeros. Anchoring θ = 0 is a common method of mitigating indeterminacy in unidimensional IRT models and does not require post-equating the item parameters.

After setting a metric, one must also ensure that the ability estimates measure the appropriate latent traits. Bolt and Lall (2003) observed dimension switching over stages of a Markov chain and suggested inspecting the history of a chain for inadvertent switching. If switching occurs, they advised imposing an ordinal constraint across a single item’s difficulty parameter and restarting the chain. In contrast to previous suggestions, we recommend establishing a Q-matrix to force particular items to load on particular attributes (see Embretson & Yang, 2008, 2009, 2013, who recently proposed a similar matrix, the C-matrix of Embretson & Yang, 2012, to ensure model identification). Q-matrices have been implemented in DCM (Tatsuoka, 1995) to link individual items with the attributes that those items measure. Specifically, a Q-matrix contains J rows (representing items) and K columns (representing dimensions or attributes) of 1s and 0s. If the jth item loads on the kth attribute, then the element in row j and column k should be 1. Otherwise, the (j, k)th element should be 0. DCM researchers generally assume that Q-matrices are constructed by subject matter experts and/or test developers (McGlohen & Chang, 2008; Roussos, DiBello, Henson, Jang, & Templin, 2008) and are known prior to model calibration. Recently, though, Q-matrix construction by means of a priori knowledge is proving to be time-consuming (e.g., Roussos et al., 2007), and several authors (e.g., de la Torre, 2008; Liu, Xu, & Ying, 2012) have proposed statistical methods designed to empirically estimate the Q-matrix.

Statistically, McDonald (2000) provided the rationale for an item-restriction matrix by showing that a sufficient condition for identifying within-item dimensional structure for a compensatory multidimensional model is for at least two items (if Cov (θ) is not a diagonal matrix) or three items (if Cov (θ) is a diagonal matrix) measuring a specific θ_k to load only on the kth dimension. Therefore, if each trait has several “unidimensional” items, then the compensatory MIRT model is properly identified, and estimation will occur in the proper orientation. With regard to non-compensatory models, Babcock (2011) found that at least six items were needed to load separately on each dimension for accurate estimation of the C-MIRT model. Assuming that an appropriate Q-matrix is specified, estimation is ready to proceed.

Hereafter, we assume that practitioners have a priori knowledge of the Q-matrix structure for any set of MLTM items. Imposing a Q-matrix on MLTM estimation aligns MLTM test development theory with cognitive diagnosis theory and helps avoid dimensional indeterminacy inherent in the original MLTM. Given an appropriate Q-matrix, let q_jk = 1 if item j loads onto dimension k and q_jk = 0 otherwise. Then, the RC-MIRT model becomes

$$P(Y_{\mathrm{ij}}=1|{\text{θ}}_{i1},\dots ,{\text{θ}}_{\mathrm{ik}})=p_{\mathrm{ij}}=(a-g)\underset{k=1}{\overset{K}{\Pi }}{\left(\frac{\text{exp}({\text{θ}}_{\mathrm{ik}}-b_{\mathrm{jk}})}{1+\text{exp}({\text{θ}}_{\mathrm{ik}}-b_{\mathrm{jk}})}\right)}^{q_{\mathrm{jk}}}+g.$$

For the purposes of this article, we restrict the a-parameter to be 1 and the g-parameter to be 0. These constraints are necessary due to one of the proposed algorithms, MH-RM, requiring inversion of a sizable matrix. Setting a = 1 and g = 0 simplifies this matrix to block-diagonal form and allows inversion to proceed while avoiding potential numeric difficulty. If a and g must be estimated (either due to theory or model fit), then one could easily estimate these parameters using MCMC (see Appendix B of the online supplementary material for additional estimation details).

Model Calibration

In this section, two algorithms—MCMC and MH-RM—that might adequately calibrate the RC-MIRT model are considered. MCMC is especially flexible in estimating model parameters when response data come from an (sparse data) adaptive testing design. Unlike MCMC, the MH-RM algorithm, which combines elements from MCMC with stochastic approximation, has a strict convergence criterion reminiscent of conventional maximization routines. MH-RM was proposed by Cai (2008) and successfully implemented in several commercial programs (e.g., IRTPRO, Cai, du Toit, & Thissen, 2011, and FlexMIRT, Cai, 2012) for calibrating multigroup, multilevel, and multidimensional IRT models. Unfortunately, all previous applications have used MH-RM to estimate parameters of models with linear (compensatory) structure. Little research has compared MH-RM with MCMC in a more difficult maximization problem, such as that found in estimating parameters of a nonlinear (conjunctive) IRT model.

MCMC Versus MH-RM

The technical details of both the MCMC and MH-RM algorithms, as applied to the RC-MIRT model, are outlined in Appendices A and B, respectively, of the online version of this article. MH-RM is an alternative algorithm to MCMC that, as the name suggests, synthesizes elements from MCMC with stochastic approximation. At a general level, MH-RM is a data-augmented Robbins–Monro algorithm driven by the random imputations produced by a Metropolis–Hastings sampler (see Cai, 2010a, 2010b, for details of the general algorithm). Due to its stochastic component, the MH-RM algorithm supplies a flexible and efficient mechanism for handling complex parametric structures, such as those of the C-MIRT model. MH-RM consists of three basic steps: stochastic imputation, stochastic approximation, and a Robbins–Monro update. In every iteration of the algorithm, these three steps are sequentially executed, and the algorithm terminates after satisfying a particular convergence criterion. With regard to the RC-MIRT model, the known Q-matrix restricts certain b-parameters to be zero, which affects the MH-RM equations, and, ultimately, identifiability.

To facilitate a fair comparison between the MH-RM and the MCMC algorithms, we adopt a Bayesian version of the MH-RM algorithm, which is also described in Appendix B of the online version of this article. Note that the idea behind MH-RM is to let simple, stochastic imputation approximate the expectation step of EM in lieu of high-dimensional integration (over the space of θ). Unsurprisingly, one can adopt EM to maximize a posterior distribution instead of a likelihood function, and therefore, we consider this approach (MH-RM with a prior distribution) as an additional experimental condition.

Usually, the objective of marginal maximum likelihood estimation (and thus MH-RM estimation) is to accurately estimate the item parameters. The examinee parameters, by contrast, are usually treated as nuisance parameters in model calibration. However, if one does need to estimate both item and examinee parameters, then a simple solution would be to estimate item parameters using MH-RM, then treat item parameters as known, and then estimate examinee parameters using a standard (e.g., maximum likelihood, Bayesian modal, expected-a-posteriori) method. In the next section, we discuss additional challenges in estimating MLTM model parameters. We then compare the performance of MCMC and MH-RM (as well as Bayesian MH-RM) in estimating parameters of the MLTM model in a comprehensive simulation study.

Analytical Discussions

Non-compensatory models have been shown to be much more difficult to calibrate than compensatory models under similar conditions (Bolt & Lall, 2003). Therefore, before detailing the simulation studies, we first discuss analytical properties of the RC-MIRT model that lead to challenges in model calibration. These analytical properties include the Q-matrix structure and the ultimate form of the likelihood function. (An additional difficulty arises for large correlations between ability dimensions. Due to space constraints, we include a description of this phenomenon in Appendix D of the online supplement.)

The role of Q-matrix: complex versus simple structure

We had earlier claimed that the Q-matrix must be of a particular form for estimation to proceed. Previous authors noticed that a certain number of items must load on only one dimension for the C-MIRT model to be accurately calibrated (Babcock, 2011). In this subsection, we analytically show why items loading on a single dimension are typically preferred. For simplicity, assume a = 1, g = 0, and K = 2. If an item loads on both dimensions, then the asymptotic variance of ${\hat{b}}_{j1}$, $\text{var}({\hat{b}}_{j1})$, is

$$\text{var}\left({\hat{b}}_{j1}\right)=\frac{1}{\left[\sum _{i=1}^N\frac{p_{i1}{p}_{i2}{(1-p_{i1})}^2}{1-p_{i1}{p}_{i2}}\right]\left[\sum _{i=1}^N\frac{p_{i1}{p}_{i2}{(1-p_{i2})}^2}{1-p_{i1}{p}_{i2}}\right]-{\left[\sum _{i=1}^N\frac{p_{i1}{p}_{i2}(1-p_{i1})(1-p_{i2})}{1-p_{i1}{p}_{i2}}\right]}^2},$$

where $p_{i1}=\frac{\text{exp}({\text{θ}}_{i1}-b_{j1})}{1+\text{exp}({\text{θ}}_{i1}-b_{j1})}$ and p_i2 is defined in the similar fashion. But if item j loads on only the first dimension, then the asymptotic variance of ${\hat{b}}_{j1}$ becomes

$$\text{va}{\text{r}}^{*}\left({\hat{b}}_{j1}\right)=\frac{1}{\sum _{i=1}^N{p}_{i1}(1-p_{i1})}.$$

One can easily verify that $\text{va}{\text{r}}^{*}({\hat{b}}_{j1})\le \text{var}({\hat{b}}_{j1})$. Therefore, MLTM items loading on a single dimension tend to have smaller sample to sample variability than items loading on multiple dimensions and, thus, have parameters that are easier to accurately estimate.

Estimation errors contained in θ estimates will likely to carry along and affect item param-eter recovery ultimately. Thus, one could also estimate the effect of Q-matrix structure on the precision in θ estimates. To do this, write the likelihood function for a single examinee, θ_i, given a set of J items as

$$L\left(X|{\text{θ}}_i,b\right)={\displaystyle \prod _{j=1}^J{\left[{\displaystyle \prod _{k=1}^2{\left(\frac{\text{exp}\left({\text{θ}}_{ik}-b_{jk}\right)}{1+\text{exp}\left({\text{θ}}_{ik}-b_{jk}\right)}\right)}^{q_{jk}}}\right]}^{x_{ij}}}{\left[1-{\displaystyle \prod _{k=1}^2{\left(\frac{\text{exp}\left({\text{θ}}_{ik}-b_{jk}\right)}{1+\text{exp}\left({\text{θ}}_{ik}-b_{jk}\right)}\right)}^{q_{jk}}}\right]}^{1-x_{ij}}.$$

Define $p_{\mathrm{ijk}}=\frac{\exp ({\text{θ}}_{\mathrm{ik}}-b_{\mathrm{jk}})}{1+\exp ({\text{θ}}_{\mathrm{ik}}-b_{\mathrm{jk}})}$ for clarity, and partition the Fisher information matrix into $ℐ({\mathbf{\text{θ}}}_i)=\left(\begin{array}{c}\hfill {ℐ}_{11}({\mathbf{\text{θ}}}_i){ℐ}_{12}({\mathbf{\text{θ}}}_i)\hfill \\ \multicolumn{1}{c}{{ℐ}_{21}({\mathbf{\text{θ}}}_i){ℐ}_{22}({\mathbf{\text{θ}}}_i)}\end{array}\right)$. Then, elements of the top row of the information matrix become

$${ℐ}_{11}\left({\text{θ}}_i\right)={\displaystyle \sum _{j=1}^J{\left[\frac{p_{ij1}{p}_{ij2}{\left(1-p_{ij1}\right)}^2}{1-p_{ij1}{p}_{ij2}}\right]}^{q_{j1}{q}_{j2}}{\left[p_{ij1}\left(1-p_{ij1}\right)\right]}^{q_{j1}(1-q_{j2})}}{\left(0\right)}^{(1-q_{j1})(1-q_{j2})}$$

and

$${ℐ}_{12}\left({\text{θ}}_i\right)={\displaystyle \sum _{j=1}^J{\left[\frac{p_{ij1}{p}_{ij2}\left(1-p_{ij1}\right)\left(1-p_{ij2}\right)}{1-p_{ij1}{p}_{ij2}}\right]}^{q_{j1}{q}_{j2}}}{\left(0\right)}^{1-q_{j1}{q}_{j2}}.$$

To find elements of the bottom row of $ℐ({\text{θ}}_i)$, simply switch p_ij1 and p_ij2 in ${ℐ}_{11}({\text{θ}}_i)$ and ${ℐ}_{12}({\text{θ}}_i)$. If all items load on both dimensions, then the information matrix obviously becomes

$$ℐ\left({\text{θ}}_i\right)=\left(\begin{array}{cc}{\displaystyle \sum _{j=1}^J\frac{p_{ij1}{p}_{ij2}{\left(1-p_{ij1}\right)}^2}{1-p_{ij1}{p}_{ij2}}}& {\displaystyle \sum _{j=1}^J\frac{p_{ij1}{p}_{ij2}\left(1-p_{ij1}\right)\left(1-p_{ij2}\right)}{1-p_{ij1}{p}_{ij2}}}\\ {\displaystyle \sum _{j=1}^J\frac{p_{ij1}{p}_{ij2}\left(1-p_{ij1}\right)\left(1-p_{ij2}\right)}{1-p_{ij1}{p}_{ij2}}}& {\displaystyle \sum _{j=1}^J\frac{p_{ij1}{p}_{ij2}{\left(1-p_{ij2}\right)}^2}{1-p_{ij1}{p}_{ij2}}}\end{array}\right).$$

But if t₂ items load exclusively on the first dimension, t₃ items load exclusively on the second dimension, and the remaining t₁ items load on both dimensions (so that J = t₁+t₂+t₃), then the information matrix changes to

$${ℐ}^{\ast }\left({\text{θ}}_i\right)=\left(\begin{array}{cc}{\displaystyle \sum _{j=1}^{t_1}\frac{p_{ij1}{p}_{ij2}{\left(1-p_{ij1}\right)}^2}{1-p_{ij1}{p}_{ij2}}}+{\displaystyle \sum _{j=t_1+1}^{t_1+t_2}{p}_{ij1}^{\ast }\left(1-p_{ij1}^{\ast }\right)}& {\displaystyle \sum _{j=1}^{t_1}\frac{p_{ij1}{p}_{ij2}\left(1-p_{ij1}\right)\left(1-p_{ij2}\right)}{1-p_{ij1}{p}_{ij2}}}\\ {\displaystyle \sum _{j=1}^{t_1}\frac{p_{ij1}{p}_{ij2}\left(1-p_{ij1}\right)\left(1-p_{ij2}\right)}{1-p_{ij1}{p}_{ij2}}}& {\displaystyle \sum _{j=1}^{t_1}\frac{p_{ij1}{p}_{ij2}{\left(1-p_{ij2}\right)}^2}{1-p_{ij1}{p}_{ij2}}}+{\displaystyle \sum _{j=t_1+t_2+1}^{t_1+t_2+t_3}{p}_{ij2}^{\ast }\left(1-p_{ij2}^{\ast }\right)}\end{array}\right),$$

where $p_{\mathrm{ij}1}^{*}$ might be smaller than p_ij1 for $j=t_1+1,\dots ,t_1+t_2$ because a single dimension must now account for the earlier multiplicative structure across two dimensions. If θ_i is estimated by means of maximum likelihood estimation, then $\text{var}({\widehat{\text{θ}}}_i)={ℐ}^{-1}({\text{θ}}_i)$, so that $\text{var}({\widehat{\text{θ}}}_{i1})={[{ℐ}^{-1}({\text{θ}}_i)]}_{11}$. Although we could not find any explicit analytical condition under which ${[{ℐ}^{\ast -1}({\text{θ}}_i)]}_{11}\le {[{ℐ}^{-1}({\text{θ}}_i)]}_{11}$, we found that this inequality is often satisfied for a majority of examinees.

To illustrate this idea, we selected 3,721 θ_is on a two-dimensional grid, such that Θ₁ = Θ₂ = $\{-3.0,-2.9,-2.8,\dots ,+2.8,+2.9,+3.0\}$, Θ² = Θ₁×Θ₂, and θ_i∈Θ². We then chose a test length of J = t₁+t₂+t₃ = 60, and we sampled b-parameters from either $N(0,1)$ or $N(-1,1)$. The latter density was selected because the difficulty of each item-by-attribute should be low for the probability of a correct response to be sufficiently high due to the multiplicative structure of a non-compensatory model (Bolt & Lall, 2003). Using randomly generated b-parameters, we considered tests conforming to four Q-matrix structures: t₂ = t₃ = 0, 10, 20, and 30. Then the number of cases (out of 3,721) that the inequality ${[{ℐ}^{\ast -1}({\text{θ}}_i)]}_{11}\le {[{ℐ}^{-1}({\text{θ}}_i)]}_{11}$ was satisfied was found, and this number was averaged over 50 replications.

The results are displayed in Table 1 and can be explained pretty succinctly: $\text{var}({\widehat{\text{θ}}}_{i1})$ is generally smaller when at least some items load only on a single dimension (n₂ = n₃≥ 10) than when all items load on both dimensions. An additional discussion about the role that the Q-matrix plays in facilitating parameter estimation of tests displaying hierarchical structure (Rupp & Templin, 2008) is provided in Appendix C of the online version of this article.

Table 1.

Number of Examinees (Out of 3,721) That Satisfy the Inequality ${\mathbf{I}}_{11}^{*-1}\le {\mathbf{I}}_{11}^{-1}$.

	n2 = n3 = 10	n2 = n3 = 20	n2 = n3 = 30
$b~N(-1,1)$	3,682	3,634	3,346
$b~N(0,1)$	3,716	3,715	3,661

The challenge of optimization-based method

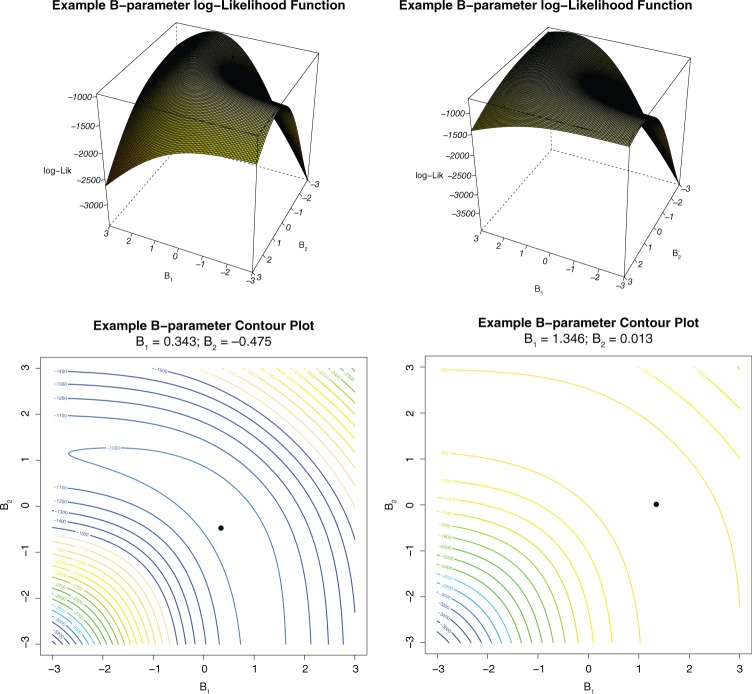
As opposed to MCMC, the MH-RM algorithm must implicitly maximize a likelihood function through Robbins–Monro updates. The precision of MH-RM thus depends on the concavity of this function. As an illustration, Figure 1 shows a log-likelihood surface as well as the corresponding contours of equal density for two items measuring two dimensions. As is easily seen in the plot, both items include a relatively large region near the maximum with nearly indistinguishable log-likelihood values. Due to the relatively flat likelihood function, the standard MH-RM algorithm should have trouble finding the maximum and result in parameter estimates with excessive error. To overcome instability in likelihood estimates, two corrections to the standard MH-RM algorithm were considered. First a version of the MH-RM algorithm that maximizes the posterior distribution rather than the likelihood function was attempted. Due to a moderately informative prior, the posterior distribution should be more peaked and, thus, easier for an algorithm to maximize. Also the stochastic imputation step of the MH-RM algorithm was tweaked to depend on the degree of correlation between latent ability. Specifically, the “burn-in” size of the imputation sampler (i.e., m_r) was increased given increased correlations between true ability dimensions.

Figure 1.

Log-likelihood function surface and contour of b for two items.

Note. The black dot in the contour plot denotes the position of the true parameter.

Simulation Study

A simulation study was conducted to determine the performance of both the MCMC and MH-RM algorithms on the accuracy of item parameter estimates. To keep things simple, RC-MIRT models with three dimensions and three levels of correlation among pairs of dimensions, ρ = .2, ρ = .5, and ρ = .75, were considered. Higher correlations among the dimensions should create difficulties in model estimation (e.g., Babcock, 2011). The sample consisted of either n = 1,000 or n = 2,000 simulees, with ability vectors generated from a multivariate normal distribution where µ = 0 and ${\text{Σ}}_2\text{θ}=\left(\begin{array}{lll}1\hfill & \rho \hfill & \rho \hfill \\ \rho \hfill & 1\hfill & \rho \hfill \\ \rho \hfill & \rho \hfill & 1\hfill \end{array}\right)$. We simulated responses of examinees to tests of length J = 30 or J = 45 with either a simple or complex Q-matrix structure. If the Q-matrix was “simple” in structure, then one third of the items loaded exclusively on each of the three dimensions. Conversely, if the Q-matrix was “complex” in structure, then one sixth of the items loaded exclusively on each of the three dimensions, and the remaining items randomly loaded on either two or three dimensions (see Table E1 in Appendix E of the online supplement for an example of complex Q-matrix that was used in one of the simulation conditions). Items that loaded on a single dimension had difficulty parameters generated from a normal distribution with a mean of 0 and a variance of 1.5. Otherwise, difficulty parameters were generated from a normal distribution with a mean of −1.0 and a variance of 1.5 (see Bolt & Lall, 2003, who found that difficulty parameters generated from the latter distribution most closely matched those observed in Embretson, 1983). The design therefore has 3 (correlations) × 2 (sample sizes) × 2 (test lengths) × 2 (Q-matrix structures) = 24 conditions. For each condition, results across 50 replications were averaged (using the median rather than the mean). Most of the code was written in R (R Core Team, 2012) with some of the heavy computations wrapped in a C loop.

The purpose of this study was to compare three parameter estimation algorithms: MCMC, MH-RM, and a Bayesian version of MH-RM. The MCMC algorithm differs from Babcock’s (2011) in two important ways: (a) Initial values were obtained using an informative method; see Appendix A of the online supplement, and (b) the inverse-Wishart distribution was used as the prior for the unknown covariance matrix, Σ_θ. For both of the MH-RM algorithms, the item parameters were assumed to be targets of calibration, so that the Metropolis–Hastings portion of the algorithm sampled person parameters and the ability covariance matrix. As discussed in Appendix B of the online supplement, the degree of imputation “burn-in” (i.e., m_r) was increased as ρ increased. Specifically, the number of “burn-in” iterations given true correlations of ρ = .25, .50, and .75 were m_r = 20, 40, and 60, respectively. As in any maximization algorithm, the convergence of MH-RM depends on the proximity of the initial values to the maximum of the function. For each iteration of the MH-RM algorithm, the behavior of parameter updates were closely monitored and were (rarely) restarted the algorithm if a divergence were detected. Simulation results and computation times were recorded only in the case of successfully converged runs (at ε < .001). The eventual calibration accuracy of each algorithm for a given condition was determined via the mean-squared error (MSE; that is, $\text{MSE}(b_k)=\frac{1}{J}\sum _{j=1}^J{({\hat{b}}_{\mathrm{jk}}-b_{\mathrm{jk}})}^2{q}_{\mathrm{jk}}$), average bias (i.e., $\text{bias}({\text{θ}}_k)=\frac{1}{N}\sum _{j=1}^j({\hat{b}}_{\mathrm{jk}}-b_{\mathrm{jk}})q_{\mathrm{jk}}$), and correlation coefficient between the true and estimated parameters. Results are presented in Table 2.¹ Note that the results were aggregated over the three b-parameters due to the space limit in Table 2, and the full results are presented in Appendix E in the online supplement.

Table 2.

Bias, MSE, Correlation, Computation Time (in seconds), and Number of Iterations (for both MH-RM algorithm and B MH-RM algorithm) for the Item Parameter b_jk Estimates.

				J = 30					J = 45
	ρ	n		Bias	MSE	Correlation	Time	No. of iterations	Bias	MSE	Correlation	Time	No. of iterations
Simple Q	.2	1,000	MCMC	0.000	0.010	1.000	492.02	NA	0.003	0.010	1.000	717.87	NA
			MH-RM	0.000	0.010	1.000	79.5	84	0.000	0.010	1.000	108.22	78
			B MH-RM	0.003	0.010	1.000	80.83	84	0.000	0.010	1.000	106.09	76
		2,000	MCMC	0.000	0.000	1.000	966.64	NA	0.000	0.000	1.000	1,420.63	NA
			MH-RM	−0.007	0.003	1.000	163.95	94	0.000	0.000	1.000	210.95	87
			B MH-RM	−0.003	0.007	1.000	161.49	94	0.000	0.000	1.000	205.53	85
	.5	1,000	MCMC	0.003	0.010	1.000	491.95	NA	0.003	0.010	1.000	718.08	NA
			MH-RM	0.007	0.010	1.000	89.05	60	0.007	0.010	1.000	115.78	55
			B MH-RM	0.003	0.010	1.000	91.08	62	0.007	0.010	1.000	119.23	56
		2,000	MCMC	−0.007	0.000	1.000	965.69	NA	0.000	0.000	1.000	1,419.71	NA
			MH-RM	−0.003	0.000	1.000	179.5	66	0.003	0.000	1.000	236.57	60
			B MH-RM	−0.003	0.000	1.000	180.77	66	0.003	0.000	1.000	236	60
	.75	1,000	MCMC	0.000	0.010	1.000	491.98	NA	0.000	0.010	1.000	717.28	NA
			MH-RM	−0.007	0.010	1.000	97.03	48	0.003	0.010	1.000	122.24	42
			B MH-RM	−0.003	0.010	1.000	87.21	44	0.000	0.010	1.000	118.53	41
		2,000	MCMC	−0.007	0.000	1.000	965.7	NA	0.010	0.000	1.000	1,420.27	NA
			MH-RM	−0.007	0.000	1.000	179.8	48	0.010	0.000	1.000	252.04	47
			B MH-RM	−0.007	0.000	1.000	177.71	47	0.000	0.000	1.000	245.56	46
Complex Q	.2	1,000	MCMC	−0.067	0.117	.967	552.77	NA	−0.060	0.123	.967	815.87	NA
			MH-RM	−0.130	0.177	.953	557.12	550	−0.130	0.180	.953	915.15	611
			B MH-RM	−0.150	0.180	.953	440.81	436	−0.167	0.203	.950	705.39	471
		2,000	MCMC	−0.030	0.077	.977	1,087.74	NA	−0.037	0.067	.980	1,618.52	NA
			MH-RM	−0.140	0.187	.957	891.39	476	−0.133	0.133	.973	1,397.23	527
			B MH-RM	−0.147	0.207	.957	812.32	442	−0.167	0.157	.970	1,225.45	463
	.5	1,000	MCMC	−0.077	0.210	.943	551.44	NA	−0.090	0.180	.953	815.59	NA
			MH-RM	−0.123	0.270	.923	913.78	571	−0.140	0.223	.943	1,526.35	654
			B MH-RM	−0.170	0.313	.917	752.88	468	−0.193	0.270	.937	1,203.88	515
		2,000	MCMC	−0.073	0.127	.967	1,088.72	NA	−0.050	0.093	.970	1,612.69	NA
			MH-RM	−0.163	0.250	.943	1,439.1	482	−0.137	0.167	.957	2,355.77	547
			B MH-RM	−0.183	0.293	.927	1,305.82	440	−0.157	0.187	.947	2,028.03	469
	.75	1,000	MCMC	−0.110	0.363	.907	554.18	NA	−0.123	0.363	.900	816.04	NA
			MH-RM	−0.153	0.453	.870	1,497.51	682	−0.150	0.417	.877	2,551.96	799
			B MH-RM	−0.180	0.450	.877	1,164.89	531	−0.210	0.480	.877	2,000.09	626
		2,000	MCMC	−0.053	0.227	.933	1,091.4	NA	−0.083	0.210	.937	1,620.53	NA
			MH-RM	−0.150	0.403	.883	2,274.41	555	−0.137	0.387	.897	3,992.68	668
			B MH-RM	−0.170	0.387	.883	2,123.96	514	−0.170	0.403	.900	3,361.92	565

Note. MSE = mean-squared error; MH-RM = Metropolis–Hastings Robbins–Monro; B MH-RM = Bayesian Metropolis–Hastings Robbins–Monro; MCMC = Markov chain Monte Carlo.

Consider the accuracy of the parameter estimates first, as shown in Table 2. When every items loads on only one dimension, then all three algorithms tend to accurately recover the item difficulty parameters. Notice that for those conditions with a simple Q-matrix, the bias is nearly zero, the MSE is very small, and the correlation between the estimated and true parameters is close to 1 irrespective of the value of ρ. Moreover, for these conditions, the MH-RM and Bayesian MH-RM algorithms are much faster than MCMC. When items are allowed to load on multiple dimensions, then, as predicted, MH-RM results in less accurate parameter estimates than MCMC. Adding a prior to the MH-RM algorithm helps stabilize the estimation process. Notice that Bayesian MH-RM yields fewer required iterations and a shorter average computation time than standard MH-RM. Moreover, despite the Bayesian MH-RM estimates often resulting in reduced sample to sample variability as compared with standard MH-RM, the Bayesian MH-RM estimates are often much more biased. Interestingly, the relative estimation accuracy of MCMC over alternative estimation methods increases as the correlation between the dimensions is increased. Therefore, MCMC appears less affected by any underlying correlation between latent ability dimensions than the MH-RM algorithms.

As shown in Table 2, the MH-RM algorithm also results in a highly variable running time compared with MCMC. It was decided to run MCMC the same number of iterations regardless of condition, so the corresponding computation times only depend on the size of the item and person parameter matrices. Conversely, MH-RM relies on a convergence criterion for terminating each estimation loop. With a Q-matrix that displays simple structure, MH-RM quickly finds the maximum and is, therefore, a much more efficient algorithm than is MCMC. However, when a test exhibits complex structure, then the number of iterations required for convergence dramatically increases, and MH-RM is no longer more computationally efficient than MCMC. Not surprisingly, holding everything else constant, the MH-RM algorithm terminates in fewer iterations for n = 2,000 as compared with n = 1,000.

Table 3 presents the median standard errors corresponding to each of the conditions and algorithms. Again, the results were aggregated over b₁, b₂, and b₃. For the MCMC algorithm, the “standard error” is defined as the standard deviation of the marginal posterior distribution and estimated from 5,000 post burn-in draws of the MCMC sampler. Conversely, the estimated standard error for both MH-RM algorithms is simply the square-rooted diagonal elements of the negative, inverse Hessian matrix (Cai, 2008). As shown in Table 3, the standard errors obtained using the MH-RM algorithm are uniformly larger than those obtained using either the MCMC algorithm or the Bayesian MH-RM algorithm (excepting very few cases with a complex Q-matrix and a correlation of ρ = .75 between the dimensions). Because an informative, multivariate normal we used prior on the item difficulty parameters in MCMC and Bayesian MH-RM, the resulting posterior variance of $\widehat{b}$ should be smaller than likelihood-based, asymptotic variance estimated from MH-RM. Oddly, when a test displays complex structure and when ρ = .75, then MH-RM algorithms perform worse (as evidenced by increased MSE, average bias, and/or standard error of the item parameters in a few cells) for the larger sample size condition. This result is unexpected, and further analyses and simulations will be to pinpoint its underlying reasons.

Table 3.

Standard Error of Parameter Estimates.

			J = 30			J = 45
	ρ	n	MCMC	MH-RM	B MH-RM	MCMC	MH-RM	B MH-RM
Simple Q	.2	1,000	0.076	0.149	0.149	0.080	0.154	0.152
		2,000	0.057	0.109	0.111	0.059	0.101	0.102
	.5	1,000	0.082	0.190	0.184	0.084	0.183	0.182
		2,000	0.057	0.143	0.141	0.056	0.133	0.129
	.75	1,000	0.081	0.276	0.269	0.081	0.236	0.230
		2,000	0.061	0.207	0.189	0.057	0.200	0.187
Complex Q	.2	1,000	0.227	0.248	0.237	0.269	0.248	0.237
		2,000	0.178	0.198	0.194	0.194	0.202	0.196
	.5	1,000	0.319	0.294	0.292	0.259	0.283	0.264
		2,000	0.184	0.241	0.238	0.201	0.227	0.219
	.75	1,000	0.429	0.405	0.422	0.354	0.371	0.338
		2,000	0.369	0.439	0.500	0.300	0.410	0.363

Note. MCMC = Markov chain Monte Carlo; MH-RM = Metropolis–Hastings Robbins–Monro; B MH-RM = Bayesian Metropolis–Hastings Robbins–Monro.

Discussion and Conclusion

For researchers who study MIRT, a distinction is often made between compensatory and non-compensatory models (see, e.g. Ackerman, 1989; Embretson & Reise, 2000). Both classes of models make assumptions about the process underlying examinee responses to items. Compensatory models are appropriate for items with disjunctive component processes (Maris, 1999) such as examinees being able to use multiple strategies to arrive at the solution (Reckase, 1997). On items with many routes to an answer, one ability can naturally compensate for deficiencies in other abilities. Contrarily, non-compensatory models, such as those discussed in this article, would better represent items with conjunctive component processes (Embretson & Yang, 2013; Maris, 1999) such as a mathematical word problem requiring both reading and math ability (Bolt & Lall, 2003). Unlike the compensatory MIRT models, which are relatively easy to calibrate, non-compensatory models include component-specific difficulty parameters that add complexity to model calibration. Accurate estimation of non-compensatory model parameters requires sufficient variability in the relative difficulties of components across items (Bolt & Lall, 2003).

Examined were the relative strengths and weaknesses of calibrating a restricted version of a one-parameter non-compensatory MIRT model using two promising algorithms: MCMC and MH-RM. Unlike previous simulation studies by Bolt and Lall (2003) or Babcock (2011), restrictions to constrain certain items to load on specific dimensions were explicitly imposed and, as a consequence, increased the estimability of model parameters (Embretson & Yang, 2013). Based on preliminary simulations, when the correlation between true ability was small, both MCMC and MH-RM resulted in similar and accurate parameter estimates. But as the correlation between true ability increased, both MH-RM algorithms were much less precise than MCMC at recovering true item parameters. It was predicted that the worsen parameter estimates under high correlation scenario would be offset by more items, and future studies could certainly extend the current test length of 45 to a longer length. Given the comparable running times of all three algorithms, the authors would caution against estimating RC-MIRT item parameters via a MH-RM algorithm except in the simplest cases. The study supported both Bolt and Lall (2003) and Babcock (2011), who found that high correlations between ability dimensions lead to poorer item parameter estimation. With high correlations between ability, a wide variety of item parameters could accurately fit the data, which implies large standard errors and difficult estimation. And as shown in this article, items loading on multiple dimensions resulted in increased variability (and, therefore, decreased information) with respect to the difficulty parameters on each dimension. Even so, the MCMC algorithm appears to be relatively robust with respect to the magnitude of correlation between different abilities. However, for tests displaying simple structure, all three algorithms generated nearly indistinguishable, accurate results.

Recently, Embretson and Yang (2013) proposed a new model based on the logic underlying the RC-MIRT model examined in this article. The multicomponent latent trait model for diagnosis (MLTM-D) assumes that responses to test items depend on both a global, continuous competency trait (θ) and local, finer grained, dichotomous attributes (α). One might apply the MLTM-D model to tests constructed from a heterogeneous item pool where items differ in the specific, cognitive operations needed for finding a solution (Embretson & Yang, 2013). Examples of tests potentially fitting a MLTM-D model include accountability tests and licensure exams. Yet, as emphasized by Embretson and Yang (2013), the estimation of the MLTM-D model also requires powerful estimation algorithms. The current article is one of the first few attempts at applying a newly developed algorithm, MH-RM, to an IRT model with multiplicative structure. The resulting discussion of the pros and cons of MH-RM (and MCMC) should also apply to models with a more complicated structural form, such as the MLTM-D model.

As calibration is generally considered the first step toward applying any model to a set of real data, the focus of this article was primarily on the relative strengths and weaknesses of different estimation algorithms. However, we bolstered findings from the simulation by examining some structural aspects of the model, such as briefly showing that items loading on a single dimension yield more informative ability estimates. If applying any model in practice, practitioners must also select items to be on an exam. One might wonder how he or she could select the most informative items in estimating ability. Recall that in a unidimensional Rasch model, ability Fisher information is maximized when θ = b. And in a multidimensional compensatory model (e.g., Mulder & van der Linden, 2009; Wang, Chang, & Boughton, 2011), Fisher information is maximized when item difficulty is equal to a weighted linear combination of the abilities. To demonstrate what happens in a non-compensatory model, consider a two-dimensional item with q₁ = q₂ = 1 (so the item is non-trivial), and a = 1 and g = 0 (for simplicity). Then, the Fisher information for ability θ₁ can be easily expressed as $ℐ({\text{θ}}_1)=\frac{p_1{p}_2}{1-p_1{p}_2}{(1-p_1)}^2$, where p₁ and p₂ are both between 0 and 1. For fixed p₂, one can easily verify that $ℐ({\text{θ}}_1)$ is maximized when $p_1=\frac{3-\sqrt{9-8p_2}}{4p_2}$, which evaluates to a maximum value of $I({\text{θ}}_1|p_2)=\frac{3-\sqrt{9-8p_2}}{1+\sqrt{9-8p_2}}{(1-\frac{3-\sqrt{9-8p_2}}{4p_2})}^2$. In this equation, $ℐ({\text{θ}}_1|p_2)$ is monotonically increasing with respect to p₂, so that when p₂ = 1, then p₁ = .5 and $ℐ({\text{θ}}_1|p_2)$ is at a maximum. Therefore, an item will result in maximum information for a given ability (or, alternatively, an ability vector will result in maximum information for a given item dimension) if the item is moderately difficult on that dimension and extremely easy on the other. Generalizing to the K-dimensional case, an item will result in maximum information for a given ability if the corresponding component probability is close to .5 and the product of the remaining component probabilities is close to 1. Of course, a more rigorous derivation will be needed to consider the change in information across multiple dimensions simultaneously. Yet, the main argument in this article holds that items loading on a single dimension tend to be more informative at measuring that dimension. Although writing purely unidimensional items is rather difficult, especially in the context of a non-compensatory, multidimensional test, these results can provide useful guidelines for item pool construction and test assembly.