Efficient Interpolation of Computationally Expensive Posterior Densities With Variable Parameter Costs

Abstract

Markov chain Monte Carlo (MCMC) is nowadays a standard approach to numerical computation of integrals of the posterior density π of the parameter vector η. Unfortunately, Bayesian inference using MCMC is computationally intractable when the posterior density π is expensive to evaluate. In many such problems, it is possible to identify a minimal subvector β of η responsible for the expensive computation in the evaluation of π. We propose two approaches, DOSKA and INDA, that approximate π by interpolation in ways that exploit this computational structure to mitigate the curse of dimensionality. DOSKA interpolates π directly while INDA interpolates π indirectly by interpolating functions, for example, a regression function, upon which π depends. Our primary contribution is derivation of a Gaussian processes interpolant that provably improves over some of the existing approaches by reducing the effective dimension of the interpolation problem from dim(η) to dim(β). This allows a dramatic reduction of the number of expensive evaluations necessary to construct an accurate approximation of π when dim(η) is high but dim(β) is low.

We illustrate the proposed approaches in a case study for a spatio-temporal linear model for air pollution data in the greater Boston area.

Supplemental materials include proofs, details, and software implementation of the proposed procedures.

1. INTRODUCTION

The core of Bayesian inference is formalization of beliefs about model parameters η given the observed data Y using the posterior density π of η. For most nontrivial problems, analytical derivation of characteristics of individual components η_i, such as posterior moments, quantiles, or other functionals of the marginal density of η_i, is intractable and one has to resort to Markov chain Monte Carlo (MCMC) to sample from π in order to estimate the desired quantities from the sample. Each transition of the Markov chain typically requires an evaluation of the target density π at a candidate state drawn from a proposal density. Therefore, when π is computationally expensive to evaluate, only short MCMC runs are feasible, which is not sufficient for accurate estimation.

The focus of our work is reduction of computational burden of MCMC via efficient construction of approximate posterior densities in settings where η is high-dimensional but there is structure in the computation to evaluate the exact posterior density π or its logarithm l. In many such problems, it is possible to identify in η the minimal subset of variables, β, that is responsible for the expensive computation, and thereby to partition η as η = [β, ζ]. Consequently, l can be evaluated at a new parameter value η* = [β*, ζ*] in two steps: (i) a computationally expensive step υ = G_E(β*), followed by (ii) a cheap calculation G_C(υ, β*, ζ*) or sometimes even G_C(υ, ζ*), so that l([β*, ζ*]) = G_C[G_E(β*), β*, ζ*].

For example, consider the linear model Y = Xw + e, where e has a multivariate normal (MVN) distribution with a zero mean and a covariance matrix V ≔ V(γ) parameterized by γ. If the dimension of the vector of observations Y is large, V⁻¹ is not available in closed form and V does not have exploitable sparsity structure; as is often the case in spatio-temporal models, the cost of evaluation of the posterior density of [w, γ] is dominated by the factorization of V, which constitutes the major cost in G_E, while the cost to complete the rest of the computations G_C is of smaller magnitude.

Another class of examples comes from the field of computationally expensive inverse problems, discussed in the article by Kennedy and O’Hagan (2001) and references therein. In the simplest case, the vector of observed data Y is modeled as Y = f(β) + e, where f is the vector-valued computationally expensive “black-box” nonlinear regression function (known as simulator) and e is the vector of errors that has a multivariate normal density. Evaluation of f at β* often presents the main computational challenge which we associate with G_E, and once the value f(β*) is known, the remaining computation G_C to evaluate l is cheap.

In this article, we are concerned with systematic examination of computationally tractable approaches to approximate l when its argument η separates into the “expensive” and “cheap” blocks. Consequently we assume that l([β*, ζ*]) = G_C[G_E(β*), β*, ζ*], with G_E and G_C well-defined, and omit the details of actual identification of the expensive and cheap computations, which are specific to an application area and to an implementation of l. The main idea is simple: evaluate G_E at a set of points on a high-probability region for β and use the values G_E(β⁽ⁱ⁾) to approximate l by an interpolant l̃. The resulting cheap-to-evaluate surrogate surface l̃ can be used to define a proposal density for MCMC sampling from π that produces candidate states with a high probability of being accepted (Rasmussen 2003; Christen and Fox 2005), or as a substitute for l if the approximation is accurate enough (Bliznyuk et al. 2008).

Reduction of the computational burden for such models via approximations to π (or its logarithm l) attracted considerable attention in recent years. To improve the efficiency of MCMC, Rasmussen (2003) used best linear unbiased prediction (BLUP, known in geostatistics as kriging) to interpolate l directly, that is, at the knots chosen on the η-space, under the assumption that l is a realization of a Gaussian process (GP). As a consequence, his heuristic approach is sensitive to the “curse of dimensionality” and only posterior densities with dim(η) around 15 are conjectured to be tractable (Rasmussen 2003, p. 659).

The main contribution of our article is extension of Rasmussen’s interpolant to high-dimensional models where only a subvector β of η is “expensive.” In the class of zeromean GPs with separable covariance functions (as defined in Section 3), we derive a direct optimal interpolant ( DOSKA), for which the interpolation error is controlled only by the placement of knots in the β-space, rather than in the η-space. This causes the effective dimension of the interpolation problem to drop from dim(η) to dim(β), and is capable of reducing the number of expensive computations G_E necessary to construct a direct interpolant by orders of magnitude when dim(β) is low and dim(η) is high. As we illustrate in the case study of Section 5 for the above linear model with dim(η) = 70 and dim(β) = 6, fewer than 300 β-knots are sufficient for construction of a very accurate approximation to l. To address situations in which these assumptions on the GP may be overly restrictive, we discuss generalizations in Section 6.

Our second contribution is development of the idea of indirect approximation ( INDA) in the context of general computationally expensive statistical problems with variable parameter costs. We propose to use the indirect interpolants of l of the form $\stackrel{\sim }{l}([{\beta }^{\ast },{\zeta }^{\ast }])=G_C[\stackrel{\sim }{G_E}({\beta }^{\ast }),{\beta }^{\ast },{\zeta }^{\ast }]$, where the ith component of $\stackrel{\sim }{G_E}$ interpolates the ith component of the “output” of G_E. To the best of our knowledge, this simple idea has not attracted attention outside of the literature on analysis of computer experiments, where considerable research effort was devoted to emulation of an expensive computer model using a GP model (e.g., Kennedy and O’Hagan 2001). The dimension of each subproblem of interpolating a component of G_E is dim(β). We recommend and use interpolation under a radial basis function (RBF) model, which is much cheaper to fit than kriging models when the dimension of the “output” of G_E is very large (Sections 2 and 6.2).

The article is structured as follows: Necessary notation and definitions for the direct and indirect interpolants are introduced in Section 2. Section 3 is devoted to derivation and analysis of properties of the optimal direct interpolant DOSKA. The impact of the dimensionality and of dependence between the “expensive” and “cheap” blocks of η is studied in the simulation studies of Section 4. Application of both of the proposed methods, direct and indirect, is illustrated in Section 5 on a spatio-temporal linear model for a real air pollution dataset. Possible extensions of the proposed direct interpolant and relative merits of direct and indirect approximations are discussed in Section 6. Technical details, such as proofs and discussion of fitting, are gathered in the Appendix.

2. NOTATION AND DEFINITIONS OF INTERPOLANTS

In this section, we introduce relevant notation and define the RBF and kriging interpolants that are used in this article for direct and indirect approximation.

2.1 Notation

All variables are assumed to be (column) vectors or matrices of size specified in the appropriate definition; this will not be emphasized by boldface notation. We define the distance between a point x and a set 𝒮 as dist(x, 𝒮) = inf_{x′∈ 𝒮} ‖x − x′‖₂. Only when applied to a vector, a single subscript notation is used to “extract” components, for example, x_i is the ith component of x. For sets 𝒮₁ and 𝒮₂, 𝒮₁ \ 𝒮₂ will denote the set of elements of 𝒮₁ that are not in 𝒮₂ and |𝒮₁| will give the number of elements in 𝒮₁. We represent sets as lists with lexicographic ordering of elements. The direct (Cartesian) product operator ⊕ is used to “merge” elements from lists 𝒮₁ and 𝒮₂ as

$${𝒮}_1\oplus {𝒮}_2≔\left\{\right[x^{(i)},y^{(1)}],\dots ,[x^{(i)},y^{(|{𝒮}_2|)}]:i=1,\dots ,|{𝒮}_1|\}.$$

(To emphasize the ordering of elements in the list 𝒮₁ ⊕ 𝒮₂ necessary for the proof of Proposition A.2 of Appendix A.1, we did not use the conventional notation, ×, for the Cartesian product of two sets.)

For a scalar-valued function g : (x, y) ↦ g(x, y), we extend its definition to finite sets as g : (𝒮₁, 𝒮₂) ↦ g(𝒮₁, 𝒮₂), where g(𝒮₁, 𝒮₂) is a |𝒮₁| × |𝒮₂| matrix whose ijth element is g(x⁽ⁱ⁾, y^(j)) for x⁽ⁱ⁾ ∈ 𝒮₁ and y^(j) ∈ 𝒮₂. We use an analogous extension for functions of a single vector argument.

2.2 General Form of Interpolants

In the most general form, an RBF or a kriging interpolant of a scalar-valued function g at a set of points 𝒟 = {x⁽¹⁾,…, x^(K)} is given by

$$\stackrel{\sim }{g}(x)=\sum _{i=1}^K{a}_i\varphi (x,x^{(i)};\theta )+q(x;c),$$ (2.1)

where ϕ is a basis function parameterized by θ and q is a “model” for the systematic variation in g. We restrict attention to “tails” q that are linear in c such as low-degree polynomials in x with coefficients c. The basis function parameters θ enter into Equation (2.1) in a nonlinear way, whereas the interpolant is linear in the coefficients a = [a₁, …, a_K]^⊤ and c. In the case of kriging, ϕ(·, ·; θ) is a positive definite function. Merits of kriging and RBF interpolation were discussed by Cressie (1991, section 4.4) and Bliznyuk et al. (2008).

For a given vector θ of basis function parameters, the vectors of coefficients a = [a₁, …, a_K]^⊤ and c can be obtained by solving the system of dual kriging equations given in the work of Cressie (1991, section 4.4.5), which requires 𝒪(K³) floating point operations (flops). The right side of this system—determined by the values that g takes at 𝒟 and by the linear constraints on a and c to ensure existence and uniqueness of the solution—does not depend on θ, while the (interpolation) matrix on the left side is typically a function of θ.

2.3 (Specifics of) Interpolants of Densities

Our focus is interpolation of the log-posterior l that can be represented as l(β, ζ) = G_C[G_E(β), β, ζ], where evaluation of G_E is expensive, but that of G_C is cheap.

As we noted in the Introduction, knots for our direct ( DOSKA) and indirect ( INDA) interpolants (specified below) are chosen on β-space rather than η-space. It is crucial that these be selected on a high probability density (HPD) region for β. The true HPD region for β is unknown but can be approximated using a local quadratic fit or a more general nonparametric approximation of l as discussed in the work of Bliznyuk et al. (2008) and Bliznyuk et al. (2011), respectively. Here we follow fitting recommendations outlined in these articles. In particular, to reduce the sensitivity of the interpolants to scaling of variables, we fit the interpolants upon a “sphering” (Scott 1992, section 7.3) transformation β ↦ H⁻¹ β, where H is any square matrix satisfying HH^⊤ ≈ var(β).

If l̃ is a direct or an indirect interpolant of l, the approximate posterior density π̃ is defined as

$$\stackrel{\sim }{\pi }([{\beta }^{\ast },{\zeta }^{\ast }])=\text{exp}\{\stackrel{\sim }{l}([{\beta }^{\ast },{\zeta }^{\ast }])\}·𝕀\{{\beta }^{\ast }\in 𝒩,{\zeta }^{\ast }\in ℨ\},$$ (2.2)

where 𝕀 is the indicator function, 𝒩 is some neighborhood of the β-knots ℬ used for interpolation, and ℨ is the parameter space for ζ. Thus we restrict the support of π̃ to the region where l̃ is well-approximated. To ensure that π̃ is a valid unnormalized density, that is, is integrable, we assume that the interpolant l̃ is continuous as a function of η, and that 𝒩 and ℨ are closed and bounded. A more extensive discussion of the knot selection and fitting issues can be found in the work of Bliznyuk et al. (2008, 2011). The steps to construction and use of the posterior density interpolants are outlined in Appendix A.2.

2.4 Indirect Approximation ( INDA)

The indirect approximation ( INDA) that we consider has the form l̃(β, ζ) = G_C[G̃_E(β), β, ζ], where the ith component of G̃_E is a function that interpolates the ith component of G_E at the set of knots ℬ.

If kriging is used, the vector of covariance function parameters θ ideally needs to be estimated individually for every component of G_E. However, several popular RBFs (most notably, cubic and thin-plate spline) do not require estimation of θ (particularly, after “sphering” β; Section 2.3), yet are quite robust in practice. In this case, the linear systems of equations to interpolate components of G_E have the same interpolation matrices, and, consequently, only a single matrix factorization is required to simultaneously solve the interpolating equations for multiple right sides determined by values of components of G_E at the knots ℬ; see Appendix A.2.3 for details.

In our work, we use RBF interpolation with a cubic basis function $\varphi (x,y;\theta )≔{\Vert x-y\Vert }_2^3$ and a linear tail q(x; c) ≔ [1, x^⊤] · c for indirect approximation.

2.5 Direct Approximation

Direct interpolants such as those using RBFs or by kriging, approximate l by treating it as a “black box,” without an attempt to identify computationally expensive blocks in the evaluation of l (Rasmussen 2003).

Our direct optimal interpolant of l by (separable) simple kriging ( DOSKA)—the main focus of this work—will be derived in Section 3.1 and fitting issues will be discussed in Appendix A.2.2. Simple kriging assumes that the mean function of the GP is known (Cressie 1991) and the BLUP is computed after the mean has been subtracted from the GP. Following Rasmussen (2003), we “recenter” l to have roughly a zero mean over the (estimated) high-probability region of π. Likewise, we use a Gaussian basis function defined as

$$\varphi (x,y;\theta )=\text{exp}\{-\sum _{j=1}^{\text{dim}(x)}{\theta }_j{(x_j-y_j)}^2\}.$$ (2.3)

RBF-based direct interpolants similar to DOSKA can also be used as discussed in Section 6.1. However, because the basis functions are typically neither separable nor positive definite, theoretical optimality (like in the case of simple kriging) of these generalizations of DOSKA cannot be established.

3. DOSKA—DIRECT OPTIMAL SEPARABLE (SIMPLE) KRIGING APPROXIMATION

The focus of this section is derivation and study of the properties of the direct interpolant of l that distinguishes between expensive and cheap computations in the evaluation of l. We proceed under the assumption that l is a realization of a GP with mean 0, constant variance σ², and a correlation function satisfying the separability condition

$$C_{\eta }\left(\right[{\beta }^{(1)},{\zeta }^{(1)}],[{\beta }^{(2)},{\zeta }^{(2)}\left]\right)=C_{\beta }({\beta }^{(1)},{\beta }^{(2)})·C_{\zeta }({\zeta }^{(1)},{\zeta }^{(2)}).$$ (3.1)

The implications and possible relaxations of this assumption are discussed in Sections 3.2 and 6. In Section 3.1, we derive an optimal interpolant as a solution to the following adaptive design problem: given a finite set ℬ of β-knots, construct a set of knots

$$𝒟([{\beta }^{\ast },{\zeta }^{\ast }])=\left\{\right[{\beta }^{(j)},{\zeta }^{(i,j)}]:1\le i\le K_j,{\beta }^{(j)}\in ℬ\},$$ (3.2)

of arbitrary size, to minimize the error of prediction of l([β*, ζ*]) with the best linear unbiased predictor (BLUP) E{l([β*, ζ*])|l(𝒟)}. Notice the set ℬ is held fixed and the “expensive” subvector of each element of 𝒟([β*, ζ*]) is an element of ℬ. In Section 3.2 we study the properties of the proposed interpolant. Fitting issues are addressed in Appendix A.2.2.

3.1 Derivation of DOSKA

Let 𝒟 = {[β^(j), ζ^(i,j)] : 1 ≤ i ≤ K_j, β^(j) ∈ ℬ} be any finite set of η-knots that can be created using β-knots from ℬ. Define 𝒵* ≔ {ζ*} ∪ {ζ^(i,j) : [β^(j), ζ^(i,j)] ∈ 𝒟 for some j}.

By Proposition A.2 proved in Appendix A.1,

$$\text{var}\{l([{\beta }^{\ast },{\zeta }^{\ast }])|l(𝒟)\}\ge \text{var}\{l([{\beta }^{\ast },{\zeta }^{\ast }])|l(ℬ\oplus {𝒵}^{\ast })\},$$

as 𝒟 ⊂ ℬ ⊕ 𝒵*. Since E{l([β*, ζ*])|l(𝒟)} and E{l([β*, ζ*])|l(ℬ ⊕ 𝒵*)} are both unbiased, the latter predictor improves over the former.

From Proposition A.2 proved in Appendix A.1 it follows that, under separability of C_η of Equation (3.1), var{l([β*, ζ*])|l(ℬ ⊕ 𝒵*)} = var{l([β*, ζ*])|l(ℬ ⊕ ζ*)}. Hence E{l([β*, ζ*])|l(ℬ ⊕ ζ*)} improves over E{l([β*, ζ*])|l(𝒟)} and cannot be improved upon no matter what 𝒟 is constructed using the knots in ℬ. The resulting Direct Optimal Separable (Simple) Kriging Approximant ( DOSKA) has the form

$${\stackrel{\sim }{l}}_D([{\beta }^{\ast },{\zeta }^{\ast }])≔E\{l([{\beta }^{\ast },{\zeta }^{\ast }])|l(ℬ\oplus {\zeta }^{\ast })\}=C_{\beta }({\beta }^{\ast },ℬ)·C_{\beta }{(ℬ,ℬ)}^{-1}·l(ℬ\oplus {\zeta }^{\ast }).$$ (3.3)

To simplify notation, here we suppressed dependence of C_β on the correlation function parameters θ, which will be examined in Appendix A.2.2 when we discuss fitting.

A reader may wonder how the predictor in Equation (3.3) is different from the usual kriging equations. Clearly, the best predictor of l([β*, ζ*]) based on ℬ is E{l([β*, ζ*])|l(ℬ ⊕ ℨ)}, where ℨ is the entire parameter space for ζ. Using a limiting argument, a naïve evaluation of the best predictor would require an inversion of an infinite covariance matrix of l(ℬ ⊕ ℨ). Equation (3.3) gives the expression for the best predictor in the form that can be evaluated in practice.

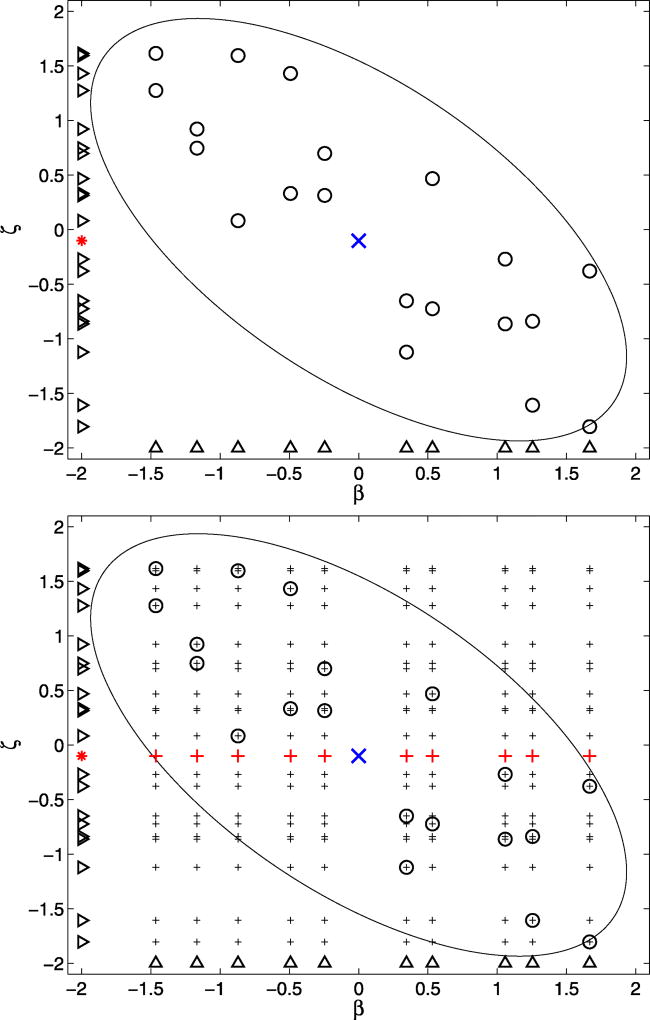
In Figure 1, we illustrate the derivation of DOSKA graphically when dim(η) = 2 and dim(β) = 1. One is given the set ℬ of 10 β-knots, denoted by Δ. The goal is to predict l(η*) at a new site η*= [β*, ζ*], marked by x. A reasonable strategy for creation of the set 𝒟 of η-knots (marked by o) attempts to cover the (elliptical) HPD region for η. To improve the prediction error of the BLUP given 𝒟, one (i) projects {η*} ∪ 𝒟 onto the ζ -space to obtain 𝒵* = {ζ*}∪𝒵 (with ζ* marked by * and 𝒵 marked by ▹) and (ii) constructs ℬ ⊕ 𝒵* (marked by +, large and small). Under the above assumptions on l, the BLUP given the knots ℬ ⊕ 𝒵* is the same as the BLUP given the knots ℬ ⊕ ζ* (marked by large +).

Figure 1.

Illustration of derivation of DOSKA: The goal is to obtain a prediction of l at η* = [β*, ζ*] ( x) using the set ℬ of β knots (△). Top: the knots 𝒟 (○) are selected to cover the elliptical HPD region. {η*} ∪ 𝒟 is projected onto the ζ -space to produce 𝒵* (▹ and *). Bottom: ℬ ⊕ 𝒵* is marked by large and small +; ℬ ⊕ ζ* is marked by large +. The online version of this figure is in color.

3.2 Analysis

In this section we make several important observations about DOSKA.

1. The predictor of Equation (3.3) does not assume that either C_β or C_ζ is separable, although this assumption is often made out of convenience in applications of kriging (Rasmussen 2003). Remarkably, under the above assumptions on the GP, DOSKA does not depend on the choice of C_ζ at all, as can be seen from Equation (3.3).

2. It follows by Taylor’s expansion of l̃_D of Equation (3.3) in the neighborhood of its maximizer [β̂, ζ̂] that, under the assumed separability of the correlation function of Equation (3.1), the unnormalized approximate posterior density exp(l̃_D) implies neither the independence of β and ζ, nor the separability of the covariance matrix of β and ζ.

3. If β* ∈ ℬ, then l̃_D([β*, ζ*]) = l([β*, ζ*]). In this case, the gradients with respect to ζ of the left and right sides are equal, but the gradients with respect to β are not.

4. The derivatives of DOSKA are available analytically so long as C_β is differentiable and l is differentiable in ζ. They can be used for efficient sampling from the approximate posterior density using gradient-based MCMC samplers such as Langevin diffusions (Robert and Casella 1999).

5. Given a compact set S and a set of n knots 𝒟_n ⊂ S ⊂ ℝ^d, define m(𝒟_n, S) = max_x∈S dist(x, 𝒟_n). This is the minimum value of the coverage “radius” r that ensures that every point in S is within distance r from 𝒟_n. Convergence of interpolants to the underlying function g (over S) is governed by m(𝒟_n, S), and often the rate is 𝒪(m(𝒟_n, S)^α), where α > 0 is determined by the smoothness g, by the choice of the interpolant, and by the L_p norm used to measure distance between g and the interpolant. It is possible to show that the fastest rate at which m(𝒟_n, S) shrinks is 𝒪(n^−1/d). For example, if S = [0, 1] ⊂ ℝ, m(𝒟_n, S) ≥ 1/(2n).

If the full direct approximation to a continuous l is used (like in Rasmussen 2003) and the set 𝒟_n of η-knots is chosen on some subset S of ℝ^dim(η) to minimize m(𝒟_n, S), the point-wise convergence rate of the kriging interpolant to l is (bounded above by) 𝒪(n^−1/dim(η)), where dim(η) = dim(β) + dim(ζ). On the other hand, the corresponding convergence rate for DOSKA is not influenced by dim(ζ), and is 𝒪(n^−1/dim(β)). Stated differently, DOSKA interpolates each element of the family of functions {l([·, ζ]) : ζ ∈ ℨ} using the same set of knots 𝒟_n chosen in ℝ^dim(β), and is optimal within the rich class of kriging interpolants under the assumptions of this section. (Of course, direct interpolants other than DOSKA are possible for this family of functions and we discuss extensions in Section 6.)

We are not aware of the results about L_p convergence rates for interpolation by kriging, but we conjecture that results similar to those for RBFs (Buhmann 2003, chapter 5) may be possible.

4. SIMULATION STUDY: A MULTIVARIATE NORMAL (MVN) DENSITY WITH CORRELATION

In this section, we conduct a large simulation study using a collection of cheap-to-evaluate densities from which a long sample can be obtained efficiently for reference purposes. We examine the impact of dimensionality and of dependence in the components of the argument of the posterior density on the performance of DOSKA. In order to speed up the construction of interpolants, we make use of the known shape and location of the high-probability region to select β-knots. (Even so, the experiments reported here required well over 100 hours of computer time to run, with estimation of the parameters of DOSKA by the KfCV being the dominant cost.)

Our first set of experiments was inspired by the work of Rasmussen (2003) that chose knots on the η-space for his GP interpolant under the Gaussian correlation function. We adopt his “equicorrelation” test problem 2 that assumes that l is the logarithm of a 10-dimensional MVN(0, Σ) density, with the entries of Σ on the main diagonal equal to 1 and all off-diagonal entries equal to 0.908. (One eigenvalue of Σ is roughly 100 times greater than the rest.) This MVN density is treated as a “black-box” posterior density for a 10- dimensional parameter vector η. We investigate the impact of partitioning of the argument η = [β, ζ] of l into the “expensive” and “cheap” blocks on the number of knots required to ensure an accurate approximation of l by DOSKA. In this experiment, dim(η) = 10 and dim(β) ranges from 1 to 10. The distinction between “expensive” and “cheap” parameters is artificial in this synthetic test problem.

The β-knots are chosen to cover the exact 0.99 HPD region for β after “sphering” (see Section 2.2). The exact covariance matrix for β is used to define the transformation matrix. (In a real application, the “sphering” matrix can be estimated from an MCMC sample from an approximate posterior density as discussed by Bliznyuk et al. (2011).) To select the knots for interpolation we use the “greedy” maximin heuristic from appendix A.2 of the article by Bliznyuk et al. (2008). For each value of dim(β) studied, we start with a modest number of knots K and add extra knots in 20% increments until a discrepancy measure between the exact and approximate marginal posterior densities for the ith component of η falls below a specified threshold δ for every i. As the discrepancy measure, we use an estimate of the total variation (TV) norm for each component of η under the exact and approximate posterior densities

$$\text{TV}({\pi }_i,{\stackrel{\sim }{\pi }}_i)=\frac{1}{2}\int |{\pi }_i(x)-{\stackrel{\sim }{\pi }}_i(x)|\mathit{\text{dx}}$$

(see Appendix A.4). Thus, if K knots are used and the TV norm between the “exact” and “approximate” samples for some η_i exceeds δ, we augment the set of K knots with additional K₀ ≈ 0.2K knots, set K ← K + K₀, and refit DOSKA so that a new MCMC sample can be collected from the updated approximate density for estimation of the approximate marginal densities.

We note that K(d, δ)—the number of knots used to achieve the approximation of “quality” δ when the dimension of β is d—is a random variable because the knot selection procedure is stochastic. For this reason, we repeated the knot selection 150 times with different placements of knots for every d from 1 to 9.

The parameters θ of the Gaussian correlation function [Equation (2.3)] used in DOSKA were estimated by KfCV as discussed in Appendix A.2.2 using four restarts of a gradient-based optimization algorithm (a quasi-Newton method).

We estimate the component-wise TV norms as outlined in Appendix A.4. For that purpose, we use an i.i.d. sample from the exact posterior density exp(l) and a sample from the approximate posterior density exp(l̃_D) obtained using a Metropolis–Hastings independence sampler (Tierney 1994) with exp(l) as the proposal. If DOSKA is accurate, exp(l) ≈ exp(l̃_D) and an MCMC sample from exp(l̃_D) is essentially an i.i.d. sample. Each sample is of size 10⁴. The value δ = 0.05 was used as an upper bound on the maximum component-wise TV norm, which corresponds to a fairly accurate approximation.

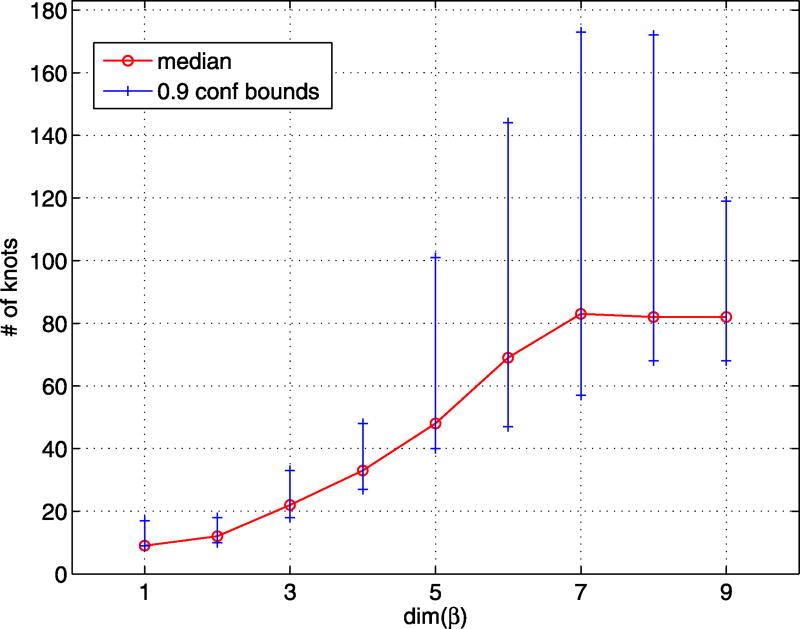
The results of our study are summarized in Figure 2, where we plot against dim(β) the sample median and confidence bounds of level 0.9 for K(dim(β), δ). Based on a separate experiment with 200 replications (below), the median of K(10, 0.05) is about 84 with little variability about this value. Comparison of values of K(dim(β), 0.05) on this plot with K(10, 0.05) allows one to appreciate the potential computational savings of exploiting the separation of η into the “expensive” and “cheap” blocks. For example, the median number of required knots for DOSKA was 22 when dim(β) = 3, whereas 84 knots are necessary if separation is ignored.

Figure 2.

MVN problem of Section 4: Sample median and quantiles of level 0.05 and 0.95 for the estimated minimum number of β-knots required to achieve maximum component-wise TV norm less than δ = 0.05. The plot is based on 150 replications (trials). KfCV is used to estimate DOSKA parameters. The online version of this figure is in color.

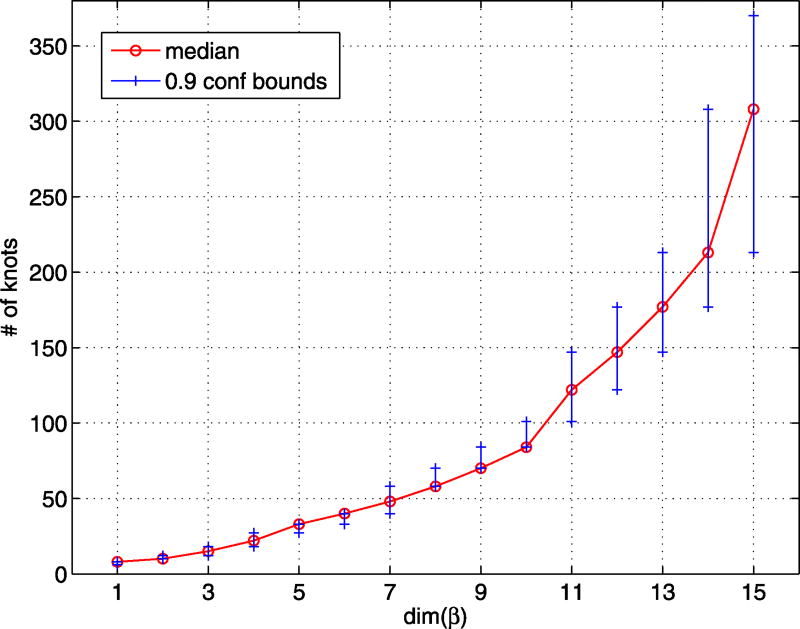
Figure 3 summarizes results of a different set of 200 independent approximation trials on MVN densities, in which dim(ζ) = 0 and dim(β) = dim(η) varies from 1 to 15. Because of “sphering” and joint normality, the components of transformed η are independent. As expected, the median K(d, δ) is an increasing function of d, as is the width of the confidence interval.

Figure 3.

DOSKA interpolation on MVN problems of dimensions 1, …, 15 without “cheap” parameters: Sample median and quantiles of level 0.05 and 0.95 for the estimated minimum number of β-knots required to achieve maximum component-wise TV norm less than δ = 0.05. The plot is based on 200 (design) replications for each value of dim(β). KfCV is used to estimate DOSKA parameters. The online version of this figure is in color.

Comparison of Figure 3 with Figure 2 allows one to examine the impact of dependence and of “sphering” on the performance of DOSKA. “Sphering” removes dependence in the components of β, but can actually increase the dependence between the transformed β (H⁻¹ β) and the untransformed ζ. (For example, the maximum component-wise correlation can increase from 0.908 up to about 0.95 after the transformation in our first experiment.) The non-monotonic behavior of the 0.95th sample quantile in the first experiment appears to be influenced by two factors: (i) the growth of dim(β), which calls for higher numbers of knots to approximate the posterior of β, as was seen from Figure 3 and (ii) non-monotonic behavior of the condition number of the covariance matrix of the transformed η, which increases from about 100 at d = 1 to about 187 at d = 4, and then slowly decreases to about 37 at d = 9. The condition number reflects the considerably different directional variability in the joint density of H⁻¹ β and ζ, which is conjectured to be the cause of non-monotonicity.

Performance of DOSKA without “sphering” is considerably worse than with it. For example, on the above test problem with dim(β) = 3 and dim(η) = 10, without sphering over 200 knots were needed to produce an accurate approximation. For this reason, we did not follow this path deeply.

5. CASE STUDY: SPATIO-TEMPORAL MODELING OF BLACK CARBON POLLUTION IN THE GREATER BOSTON AREA

The primary goal of this section is illustration and comparison of the direct and the indirect approximation frameworks on a large spatio-temporal model for air pollution data. Descriptive and predictive inferences from such models are of interest to environmental epidemiologists and have a profound impact on public policy making. From the computational standpoint, our focus is on linear models that are “large enough” to be statistically and practically meaningful, whose computational structure is similar to that of bigger problems. However, doing exact Bayesian inference in order to evaluate the quality of approximations should still be possible.

In what follows, we discuss the data, the statistical model, and the considerations for drawing exact Bayesian inference under our model. We then go over the practicalities of building the direct and the indirect approximations and assess their quality.

5.1 Background

Concentrations of traffic particles such as black carbon are well-known markers of overall air pollution in metropolitan areas. Multiple health effects studies have revealed association between the elevated air pollution levels and increased rates of mortality and morbidity (Gryparis et al. 2007). In spite of the individual risks being small, the impact of the air pollution on public health is immense because it affects large groups of people. Considerable research effort at the Harvard School of Public Health focused on monitoring and spatio-temporal modeling of concentrations of elemental and black carbon in the greater Boston area. Inferences and predictions from these models, while interesting in their own right, are also often used as exposure variables in environmental epidemiology models.

We obtained the data on daily average concentrations of black carbon used in the work of Gryparis et al. (2007) from the authors. These data come from two studies where the measurements were taken by outdoor monitors at 49 spatial locations in Boston and its suburbs over the period from mid October, 1999, until the end of September, 2004. One of the studies had roughly 30 monitors that worked over shorter periods of time (on the order of 2 weeks, with only several monitors overlapping in time). The rest of the monitors (coming from the other study) worked much longer, up to the whole period of the study. More details are provided in the article by Gryparis et al. (2007).

The dataset we use consists of 5943 measurements on a daily scale. In the next section, we propose a model for spatio-temporal smoothing for these data.

5.2 Statistical Model

For our analysis, we use a modification of the statistical model used by Gryparis et al. (2007). The additive model for the logarithm of daily average concentration of black carbon at spatial location s at time t is

$$Y(s,t)=w_0+g_S(s)+g_T(t)+\epsilon (s,t),$$ (5.1)

where g_S and g_T are smooth functions of spatial coordinates and of time, respectively, while ε(·, ·) is a Gaussian (error) process indexed by space and time. Here, g_T is the annual (cyclic) temporal trend, so that g_T(t) = g_T (d_t), where d_t = mod(t, 365) is the day of the year if leap years are ignored. Each of g_S and g_T has a form similar to Equation (2.1). (To avoid confusion, we should point out that Equation (2.1) is used here in two distinct ways, as part of a statistical model—to define smooth spatial and temporal trends—and for interpolation of the log-posterior.) In particular, the spatial smooth term is modeled using a thin-plate spline with 49 knots, one at each monitoring station, whereas a cubic spline with 13 equally spaced knots is used to model g_T (Wood 2006). Linear constraints were placed on the coefficients of g_T to ensure that g_T is periodic, that is, continuous and differentiable at t = 0. Thus, the model of Equation (5.1) can be written as a linear model

$$Y(s,t)=x(s,t)·w+\epsilon (s,t),\text{ where}$$ (5.2)

$$x(s,t)=[1,s^{\top },\varphi (s,s^{(1)}),\dots ,\varphi (s,s^{(n_S)}),d_t,\psi (d_t,d_t^{(1)}),\dots ,\psi (d_t,d_t^{(n_T)}\left)\right]$$

is a row vector of “predictors” and $w{[w_0,w_S^{\top },w_T^{\top }]}^{\top }$ is a column vector of coefficients. Here, ϕ(·, s⁽ⁱ⁾) is the ith spatial basis function and $\psi (·,d_t^{(j)})$ is the j th basis function for the smooth temporal trend. Following Wood (2006), we penalize the square of the second derivative of the nonparametric smooth terms to prevent overfitting. This approach is attractive because the penalty matrices for g_S and g_T can be written as positive semidefinite (psd) quadratic forms in w_S and w_T. For example, the penalty for g_T is

$${\wp }_t=\int {\{g_T^{″}(t)\}}^2\mathit{\text{ dt}}=w_T^{\top }·M_t·w_T$$ (5.3)

for some symmetric psd matrix M_t. These penalty matrices are subsequently used to define a precision matrix for the multivariate normal prior on w to mimic the penalized log-likelihood criterion with penalty matrices M_s and M_t, which is used in frequentist statistics. This prior has a zero mean and a precision matrix

$${\sum }_w=\mathrm{\Delta }·I_{\text{dim}(w)}+\text{blkdiag}\{0,M_s/{\sigma }_S^2,M_t/{\sigma }_T^2\},$$ (5.4)

where a small multiple Δ of the identity matrix is used to ensure that the prior is proper, and where blkdiag is a block-diagonal matrix with blocks listed as arguments. Connections between penalized splines and Bayesian models, as well as alternative penalties, were discussed by Ruppert, Wand, and Carroll (2003).

Preliminary investigations using residuals from a frequentist model fit with i.i.d. errors indicate the presence of unexplained spatio-temporal dependence. In particular, examination of the plots of autocorrelation and partial autocorrelation functions for residuals from a monitoring station with a long series of daily measurements revealed that temporal dependence can be explained well by an order-1 autoregressive process with moderate lag-1 correlation (of less than 0.5). The implications of this observation on computational aspects of the inference will be discussed in the next section.

To model spatial dependence, we use the Matern family of correlation functions

$$C_S(s,s+h)={(2\sqrt{\nu }{\theta }_S{\Vert h\Vert }_2)}^{\nu }·K_{\nu }(2\sqrt{\nu }{\theta }_S{\Vert h\Vert }_2)/\{2^{\nu -1}\mathrm{\Gamma }(\nu )\},$$ (5.5)

where ν, θ_S > 0, Γ(·) is the gamma function, and K_ν(·) is the modified Bessel function of order ν (Banerjee, Carlin, and Gelfand 2004). The smoothness parameter ν is difficult to estimate accurately unless the spatial resolution of the data is very fine. Due to the spatial sparsity of the set of monitors, we hold ν fixed at 2.

To account for the instrument measurement error and data aggregation errors, we need to allow for a nugget effect (Banerjee, Carlin, and Gelfand 2004). The covariance function for ε has the form

$$\text{cov}\{\epsilon (s,t),\epsilon (s\prime ,t\prime )\}={\sigma }_1^2·𝕀\{s=s\prime ,t=t\prime \}+{\sigma }_2^2·C_S(s,s\prime |{\theta }_S)·C_T(t,t\prime |{\theta }_T),$$ (5.6)

where C_S is the Matern spatial correlation function, C_T is the temporal correlation function (specified below), and 𝕀 is the indicator function.

5.3 Computational Considerations for Exact Bayesian Inference

5.3.1 Evaluation of the Likelihood

Under the plausible assumption that the rates of decay of the temporal autocorrelation are similar across all monitoring stations, it can be seen that the components of ε that are 15 days or more apart are practically uncorrelated since the correlation is less than 10⁻⁴. However, the covariance matrix of the errors for the space–time indices for which black carbon observations are available is numerically dense. It can take on the order of 20 seconds on a modern computer to form and factorize this matrix. Even though this does not impact the costs to fit and evaluate the proposed interpolants, it makes comparisons of the approximation quality based on the samples from the approximate and exact posterior densities problematic since a sufficiently long exact MCMC sample is very expensive to obtain. Consequently, we introduce structure into the covariance matrix via covariance tapering. As a temporal correlation function we use the product of the exponential and the (compactly supported) spherical correlation functions (Furrer, Genton, and Nychka 2006)

$$C_T(t,t+h)=\text{exp}(-{\theta }_T·h)·\text{max}{\{(1-h/r),0\}}^2(1+h/(2r))$$

for r = 15, which behaves similarly to the exponential correlation function when h is small, and is exactly zero when h ≥ 15. This reduces the proportion of nonzero entries (the fill) of Σ to less than 2%. In addition, we reorder the observed data lexicographically with respect to the temporal index, which makes unnecessary the element reordering approaches discussed in the article by Furrer, Genton, and Nychka (2006). This brings the nonzeros closer to the main diagonal, which, by dramatically reducing the bandwidth of Σ_Y, allows a very efficient sparse Cholesky factorization. As a result, the cost to evaluate the likelihood drops to about 2 seconds, in which the computational bottleneck is construction of Σ_Y using its sparsity pattern (precomputed).

5.3.2 Reparameterization

Our work with later versions of these air pollution data revealed sensitivity of computational effort required by the maximization of the log-posterior and by MCMC sampling to the parameterization of some of the variance components.

Define $\gamma =\{{\sigma }_1^2,{\sigma }_S^2,{\sigma }_T^2,{\sigma }_2^2,{\theta }_S,{\theta }_T\}$ and let β = log(γ). If [w, γ |Y]_γ is the joint posterior density of w and γ, then

$$[w,\beta |Y]={[w,\gamma (\beta )|Y]}_{\gamma }·\text{exp}(\sum _i{\beta }_i),$$ (5.7)

where γ(β) = exp(β). For simplicity, we work with the whole log-transformed γ.

The parameter space for γ was taken to be a hyper-rectangle with lower bounds 10⁻⁴ for the variance components (σ²’s) and 10⁻³ for the parameters of the correlation functions (θ ’s), and with the respective upper bounds equal to 30 and 10. The parameter space for β is also a hyper-rectangle obtained by taking the logarithms.

5.3.3 MCMC Sampling of the Exact Joint Posterior

Even though the computational burden to evaluate [w, β|Y] has been considerably reduced by tapering, the random walk Metropolis–Hastings (RWMH; Robert and Casella 1999) sampler mixes very poorly due to the high dimensionality of w and β even when adaptive sampling (Haario, Saksman, and Tamminen 2001) is used, with typical lag-1 autocorrelations routinely exceeding 0.995. However, a long informative sample from this density can be obtained by proceeding as follows.

Since [Y|w, β] is a multivariate normal density and [w|β] is a conjugate normal prior, [w|β, Y] is also multivariate normal and is available in closed form. Consequently, one can analytically integrate w out of [w, β, Y] as [β, Y] = [β, w, Y]/[w|β, Y]. We sample from [β|Y] using RWMH since the normalizing constant is not important and, for each state β* of β, we simulate w exactly from [w|β*, Y]. The convergence of this Markov chain is governed entirely by the properties of [β|Y]. It is also seen that if β* is a sample from [β|Y], then {w*, β*} is a sample from [w, β|Y] if w* is a sample from [w|β*, Y]. The lag-1 autocorrelation in the components of β that we obtained in the actual sampling was below 0.9; mixing for w was considerably better.

This approach is considerably more attractive than a Gibbs sampler that “metropolizes” simulation from [β|w, Y] since (i) the convergence is not influenced by the dependence between w and β, and (ii) recalibration of the proposal density for each new (fixed) w* when sampling β from [β|w*, Y] is not required (since we are sampling from [β|Y]).

The actual expressions for [β|Y] and [w|β, Y] are provided in Appendix A.3.

5.3.4 Definition of the Expensive Computation

Even if tapering is used, the major part of the expensive computation is evaluation and factorization of Σ_Y. The exact expressions of the components of the expensive computation G_E are given in Appendix A.3.

The expensive computation G_E in the evaluation of [β, w|Y] is incurred entirely in the evaluation of [β|Y]. Once this is done for a given value of β, evaluation of [w, β|Y] = [w|β, Y] · [β|Y] is computationally cheap. Therefore, we associate w with the cheap parameter ζ from the earlier discussion.

The definition of the “expensive” parameter β in this problem was influenced by our ability to evaluate [β|Y] (up to a multiplicative constant), which is instrumental for generation of the knots over a HPD region of [β|Y] (in next section). If analytical integration is not possible, one can use approximations to [β|Y] reviewed in the work of Bliznyuk et al. (2008).

5.4 Generation of β-knots for DOSKA and INDA

Unlike in Section 4, the β-knots for interpolation are not available. We need to produce them on the unknown HPD region of the true marginal posterior density of β. We do this using our recent approximation procedure GRIMA that performs robustly on “irregular” densities (those having non-elliptical high-probability regions and modes occurring on the boundary of the parameter space), on which existing approaches, such as that of Bliznyuk et al. (2008), can fail. GRIMA reuses the points from the optimization trajectory to build an initial response surface, which is used to select those sites for new expensive evaluations that are likely to belong to the true HPD region. The response surface is updated after each new expensive evaluation, thereby becoming more accurate. The approximate HPD region is being refined until an accurate approximation to the exact HPD region and to the true posterior density over it are obtained. (Details are available in the supplied version of the article by Bliznyuk, Ruppert, and Shoemaker (2011).)

The marginal posterior density of β is used in GRIMA to generate β-knots for DOSKA and INDA. These approximants are fitted to interpolate the exact joint posterior density of η as was discussed in Sections 2.2 and 3.

To reach the HPD region of β, we used a derivative-free optimization algorithm CONDOR (Vanden Berghen and Bersini 2005) started in the center of the parameter space for β. Optimization took 155 evaluations of log[β|Y], out of which 45 values were retained to build the initial approximation for [β|Y]. GRIMA was allowed to add new β-knots sequentially until the improvement in the response surface approximation of the log[β|Y] from adding new knots became negligible. More precisely, we monitored the component-wise TV norms between samples from the “current” approximate density and the preceding ones that used fewer knots. For example, judging from Figure 4 in the online supplementary materials, it is seen that the extra reduction in the TV norms from using more than 105 knots is negligible, and we terminate GRIMA after it has added 140 new knots to the 45 that came from optimization.

5.5 Comparisons

DOSKA and INDA were fitted to the logarithm l of the full joint posterior density of η = {β, ζ } using the same set of 185 β-knots that were supplied by GRIMA. The “sphering” matrix as well as the approximate HPD region, to which the direct and indirect interpolants are restricted (see the end of Section 2.2), were also produced by GRIMA.

For the purpose of reference, an MCMC sample ℳ of size 10⁵ from the exact [β, w|Y] was collected as discussed in Section 5.3.3. We obtained samples of size 10⁵ from the approximate densities by (i) taking a mildly correlated subsample of size 10⁴ from the “exact” correlated sample and then (ii) resampling the available “exact” subsample and the corresponding values of l(ℳ). The resulting independence M-H sampler reduced the maximum component-wise lag-1 autocorrelation in the Markov chain from 0.9 to 0.2. The same set of 10⁵ candidate states from ℳ was used for both INDA and DOSKA. This reduces the MCMC variability of the component-wise TV norms between the “exact” and “approximate” samples for the two approximations. The use of the same resample can be viewed as an application of the common random numbers technique (e.g., see Asmussen and Glynn 2007).

From the plot of component-wise TV norms for the two approximations in Figure 5 in the online supplementary materials it is seen that either of them is very accurate, with typical TV norm values (between the exact and approximate marginal densities) of about 0.015.

To conclude the case study, only 155 − 45 + 185 = 295 evaluations of G_E were sufficient for very accurate fully Bayesian inference using MCMC when dim(η) = 70 and dim(β) = 6.

6. EXTENSIONS AND COMPUTATIONAL ISSUES

6.1 Extensions

Recall that, to ensure optimality, DOSKA uses all of the knots ℬ at which the expensive computation G_E has been performed. Therefore, fitting of the model is infeasible if the size of ℬ measures in tens or hundreds of thousands, as is the case in some applications (Taddy, Lee, and Sanso 2009). Also, separability of the basis function assumed by Equation (3.1) may be unappealing for the models with very high degree of dependence between β and ζ, especially when the number of allowed β-knots is small. These concerns can be resolved by using the following generalization by localization: Instead of constructing 𝒟 of Equation (2.1) from the full set of knots ℬ as was done in Section 3, 𝒟 can be chosen adaptively depending on the new prediction site η* = [β*, ζ*] as

$$𝒟([{\beta }^{\ast },{\zeta }^{\ast }])=\left\{\right[{\beta }^{(j)},{\zeta }^{(i,j)}]:1\le i\le K_j,{\beta }^{(j)}\in ℬ({\beta }^{\ast })\},$$ (6.1)

where ℬ(β*) ⊂ ℬ are knots in some neighborhood of β*, and ζ^(i,j)’s are knots in a neighborhood of ζ*. Of course, if some components of ζ are “more expensive” than the rest, it is beneficial to use multiple values of the “cheaper” block for each value of the “more expensive” block of ζ. Notice that fitting is now done on the η-space, rather than β-space, and a general interpolant of Equation (2.1) with a nonseparable basis function and a nonzero tail q may be used. This local interpolant can arise naturally when one uses basis or covariance functions with bounded supports discussed by Buhmann (2003, chapter 6) and Gneiting (2002a), respectively, since the influence of the knots whose supports do not include [β*, ζ*] is expected to be negligible on prediction of l([β*, ζ*]). (More precisely, the estimated coefficients a and c of Equation (2.1) depend on all knots but the basis functions are nonzero only for neighbors of η*.) The cost to estimate parameters of the local interpolant using the knots 𝒟([β*, ζ*]) is low if the size of 𝒟([β*, ζ*]) is modest. However, this cost is incurred every time the evaluation of the approximation at a new site is required.

It is expected that if 𝒟([β*, ζ*]) includes the knots ℬ(β*) ⊕ ζ*, the local direct interpolant will behave similarly to DOSKA. In the simplest case when 𝒟([β*, ζ*]) ≡ ℬ(β*)⊕ ζ*, this local approximation amounts to interpolating the function l(·, ζ*) at the knots ℬ(β*) as we remarked near the end of Section 3.2. Because of the loose assumptions on the form of this local interpolant, it is unlikely that any kind of optimality can be proved.

6.2 Computational Considerations

We conclude this section with an account of the relative computational advantages of direct and indirect interpolants under the assumption of ideal practical implementation of each method. A more refined analysis of the computational costs that makes use of the cost structure in the evaluation of G_C is possible, but is application-specific and is beyond the scope of this work. Computationally, the choice only matters if very large MCMC samples from the surrogate density are required, since neither approximation evaluates G_E. As far as the quality of the interpolation is concerned, we doubt that a definitive recommendation can be given as to when to use each type of approximation.

Let dim(G_E) be the dimension of the “output” of G_E and cost(G_C) be the flop count of the cheap computation. If K is the number of β-knots and c is the cost to evaluate a basis function once, the cost to evaluate an interpolant of a one-dimensional function is cK. Each evaluation of DOSKA costs K · cost(G_C) flops to compute l[ℬ(β*) ⊕ ζ*] plus K² flops to solve the dual kriging system (Section 2) with the right side l[ℬ(β*) ⊕ ζ*] using a precomputed factorization of the interpolation matrix. The cost of evaluation of INDA is cK · dim(G_E) flops to obtain G̃_E(β*) plus cost(G_C) flops to compute G_C[G̃_E(β*), β*, ζ*]. Therefore, the “global” version of DOSKA is less attractive than INDA when K and cost(G_C) are high and is more attractive when K and cost(G_C) are low but dim(G_E) is large. As an illustration, consider the inverse problem example from Section 1. If n = dim(f) is large and the covariance matrix for e is unstructured so that cost(G_C) = 𝒪(n³), then DOSKA is roughly K times more “expensive” than INDA. On the other hand, if the covariance matrix for e is diagonal, DOSKA may be preferable (depending on the magnitude of c).

When “local” direct and indirect interpolants are used with the same basis function and tail [recall Equation (2.1)], DOSKA becomes more attractive because of the lower cost to refit the interpolant for each new evaluation. If F is the cost to fit a local interpolant with K knots, the refitting cost for DOSKA is F flops. However, INDA costs F + K² · dim(G_E) flops under some RBF models (if factorization of interpolation matrix can be reused—see end of Section 2) and F · dim(G_E) under most kriging models, since a separate interpolant needs to be fitted for each component of the “output” of G_E. Because F = 𝒪(K³), the difference in overall fitting and evaluation cost can be quite considerable for the two “local” interpolants.

7. CONCLUSIONS

In this article we presented two classes of interpolants, direct and indirect, that allow one to carry out fully Bayesian inference with the help of the approximate density when the exact posterior density π of the parameter vector η is computationally expensive to evaluate. The key to success is identification of the subvector β of η that is responsible for the dominant computational cost in the evaluation of π. This identification can be done in a host of practical problems such as large-scale inverse problems and high-dimensional linear models with parametric spatio-temporal dependence.

The primary contribution of this article is derivation of the optimal direct interpolant DOSKA (in Section 3) that provably improves over the existing direct GP interpolants of the logarithm l of π such as that of Rasmussen (2003). Since the quality of approximation by our interpolant of l is governed by dim(β) rather than by dim(η), a gain of several orders of magnitude over the naïve approaches that interpolate l on the η-space is expected when dim(η) is high but dim(β) is low.

We supported our analytical findings by simulation experiments of Section 4. There we showed that intelligent exploitation of separation of η into the “expensive” and “cheap” subvectors allows reduction of the number of expensive evaluations G_E by roughly an order of magnitude relative to the already very efficient approach of Rasmussen’s if dim(β) is low and dim(η) is moderate. In the case study of Section 5, we provided an example of accurate fully Bayesian inference with the proposed direct ( DOSKA) and indirect ( INDA) interpolants for a large-scale spatio-temporal model that has dim(η) = 70 and dim(β) = 6 using fewer than 300 (expensive) evaluations of G_E.

The answer to the question “Which interpolant is ‘better,’ direct or indirect?” is very problem- and implementation-specific, in our opinion. Unless only one interpolant can be used due to the computational costs of fitting and evaluation (discussed in Section 6), we recommend that both be used using the same set of β-knots. There is hardly a better guarantee that both approximations of π are accurate than the agreement of summaries of the approximate posterior densities produced by these two distinct methods.

These very encouraging results support application of the proposed approximations to high-dimensional structured statistical problems for which there currently do not exist computationally tractable alternatives.

Supplementary Material

supp materials

Appendix: Proofs, details of implementation, and additional plots provided in the Appendix. (appendix.pdf)

Matlab code: A zip file with Matlab implementation of the proposed procedures (see the !readme.txt for details). (Supplements.zip)