Abstract
Asthma is fundamentally a disease of airway constriction. Due to a variety of experimental challenges, the dynamics of airways are poorly understood. Of specific interest is the narrowing of the airway due to forces produced by the airway smooth muscle wrapped around each airway. The interaction between the muscle and the airway wall is crucial for the airway constriction that occurs during an asthma attack. Although cross-bridge theory is a well-studied representation of complex smooth muscle dynamics, and these dynamics can be coupled to the airway wall, this comes at significant computational cost—even for isolated airways. Because many phenomena of interest in pulmonary physiology cannot be adequately understood by studying isolated airways, this presents a significant limitation. We present a distribution-moment approximation of this coupled system and study the validity of the approximation throughout the physiological range. We show that the distribution-moment approximation is valid in most conditions, and we explore the region of breakdown. These results show that in many situations, the distribution-moment approximation is a viable option that provides an orders-of-magnitude reduction in computational complexity; not only is this valuable for isolated airway studies, but it moreover offers the prospect that rich ASM dynamics might be incorporated into interacting airway models where previously this was precluded by computational cost.
Introduction
Asthma is characterized by bronchospasm and reversible airway obstruction, along with persistent inflammatory changes on a longer timescale. The former is driven by the activation and subsequent constriction of airway smooth muscle (ASM), which surrounds each airway. As such, ASM has been the focus of much research into the underlying pathophysiology of asthma, both experimentally (e.g., (1, 2, 3, 4)) and theoretically (5, 6, 7, 8, 9, 10). Often this is done on ASM strips that have been excised from the surrounding tissue; this has many benefits in terms of experimental control, but it raises questions about the nature of the interactions between the ASM and other tissues that occur in vivo. Recently, several studies using methods that preserve some of this interaction have highlighted the importance of considering these interactions when attempting to extrapolate from in vitro results to in vivo (11, 12, 13, 14, 15, 16).
Theoretical models have been developed in parallel with these experimental findings in an attempt to understand the complex interaction mechanisms between ASM and the airway wall (17, 18, 19). These efforts are heavily influenced by extensive efforts to model ASM in isolation: specifically, the rich dynamics of ASM are arguably best described by cross-bridge theory, originating with Huxley (20) for striated muscle, adapted to smooth muscle by Hai and Murphy (5, 6), and reaching its modern form for ASM with Mijailovich et al. (7) and subsequent variants (e.g., (8, 9); see (21) for more details on cross-bridge theory and its evolution). Although cross-bridge theory offers much insight into the rich dynamics of ASM, it also presents a significant challenge, namely, that ASM cross-bridge models are typically coupled systems of hyperbolic partial differential equations (PDEs). These equations submit to analytic solution in very few situations, and typically they must be solved numerically. Even then, the computational cost is significant, and even more so when coupling with the airway wall is introduced.
Several groups have successfully combined cross-bridge PDEs with coupled airway wall models in investigations of key phenomena (17, 18, 19), but thus far only in isolated airways. Unfortunately it is increasingly clear that whole-lung behavior often cannot be easily inferred from isolated-airway behavior (22) and that inter-airway interactions, via both flow coupling and parenchymal interdependence, must be considered. (Direct mechanical effects through the parenchyma are also possible, but likely minimal unless the airways are very close together (23, 24).) These inter-airway interactions, and their role in asthma, have also been the subject of extensive theoretical investigation (25, 26, 27, 28, 29), but typically using only vastly simplified models for ASM. Thus, existing models exhibit a dichotomy: incorporate rich cross-bridge ASM dynamics on an isolated-airway basis, or explore inter-airway interactions and abandon cross-bridge theory. At present, this is dictated by computational complexity.
The obvious approach is to construct ASM models of lesser complexity—typically ordinary, rather than partial, differential equations (ODEs). Often this is done via circuit analog (e.g., (10)) or other phenomenological basis (30). In this article, we derive a systematic reduction of the cross-bridge PDEs to ODEs using the distribution-moment (DM) approximation method due to Zahalak (31). The central idea is that because the system of hyperbolic PDEs describes probability distribution functions (PDFs) of the bonds, by making an ansatz regarding the form of these distributions, one can reduce the governing PDEs to a system of ODEs in terms of the DMs. Although the DM method has been used for other types of muscle (e.g., (32, 33)), it is not widely used for ASM. In terms of computational cost, the savings of such an approach is potentially two orders of magnitude (or more). If appropriate, then, a DM approximation to the ASM-airway coupled system would result in vast computational savings for isolated airways, but, perhaps more importantly, it will open up the prospect of incorporating appropriately rich ASM dynamics into lung-scale interacting-airway models.
We thus proceed as follows: starting from a coupled cross-bridge-airway model (19), we derive the appropriate DM approximation according to Zahalak’s approach (31). (Zahalak’s original article pre-dates application of cross-bridge theory to ASM theory; it describes a detailed application of the DM approximation approach to the original Huxley model, consisting of a single PDE. Although the general principles are applicable to an ASM cross-bridge system of PDEs, several adjustments are necessary to accommodate such a system.) We then proceed to test the validity of the approximation by making appropriate comparisons between solutions to the DM approximation model and solutions to the full cross-bridge PDE-based model. In making this comparison, we are aided by several aspects of the problem: first, that airways are typically subject to an oscillatory pressure environment (viz. breathing), and second, that airway bistability (19, 34, 35) can provide a natural metric by discriminating between “open” and “closed” (or effectively closed) airway states. In this way, we are able to establish regions of validity for the DM approximation to the coupled airway-ASM system. We show that most parameter space exhibits good quantitative agreement between the DM approximation model and its full PDE-based counterpart. Furthermore, although significant quantitative deviations do begin to appear when the airway is subjected to high-amplitude, high-frequency oscillations near airway closure, it is important to note that the qualitative behavior is maintained, suggesting that a relatively simple correction factor might render the DM approximation acceptable throughout parameter space. Thus, the DM approximation to cross-bridge dynamics within a coupled ASM-airway system provides a viable alternative to the solution of the explicit cross-bridge PDEs and an avenue for future inclusion of (systemically reduced) ASM dynamics in lung-scale interacting airway models.
Methods
Model
In this section, we describe two approaches to modeling the same system. The first is to use an isolated, intact airway segment, with ASM and airway wall intact but shorn of parenchymal attachments and with explicit pressure control. By design, this mimics experimental apparatus (e.g., (13, 14)). The fundamental model elements are the cross-bridge ASM model of Mijailovich et al. (7) and the airway-wall model of Lambert et al. (36), appropriately coupled together (19, 37). This system will be both solved directly and then reduced using the DM approximation. Here, we briefly review key model elements before proceeding to the DM derivation.
ASM cross-bridge model
At its most basic, cross-bridge theory involves the binding, unbinding, and sliding of the so-called thick and thin filaments, myosin (M), and actin (A). Binding and unbinding is governed not just by Ca2+ but by the position of the actin and myosin filaments (21). The model proposed by Mijialovich et al. (7) includes position-dependent rate transitions between the phosphorylated populations and (unbound and bound, respectively) and also between the unphosphorylated myosin populations M and AM, analogous to that originally defined by Huxley (20). This model can be represented as a system of four coupled PDEs that express conservation for each myosin species and are written as
| (1) |
where the vector, , corresponds to each of the myosin states (, , , and ) which are all functions of space and time . The operator represents the material derivative, , where is the velocity of the actin filament relative to the myosin filament. The rate transition matrix represents the transitions between these states and how these rates vary with the position of the myosin head relative to the actin filament. These rates then depend on the binding-site positioning and hence the filament movement, as represented by
| (2) |
Briefly, and are (spatially independent) phosphorylation and de-phosphorylation rates; is the binding rate (phosphorylated), whereas and are the unbinding rates (phosphorylated and unphosphorylated, respectively). Specific forms , , and are from Mijailovich et al. (7) (see the Supporting Material). This system of PDEs is also subject to the conservation equation
| (3) |
The relative myosin filament velocity, v, is related to the muscle length, L, by , and the force produced by the ASM is considered as being proportional to the sum of the first moment of the bound states and (37) and is given as
| (4) |
The γ proportionality constant relates the macroscopic scaling factor for the relative change in cross-bridge velocity to the smooth muscle cell velocity.
Airway-wall model
The radius of the airway lumen is determined by the transmural pressure, , and is given by the static model of Lambert et al. (36) as
| (5) |
where the maximal radius, , the radius (at ), and the parameters , , and are all dependent on the airway order and is calculated explicitly from , , , , and . (see Table S1). Using the notation r for the time-dependent airway radius, we then impose first-order relaxation dynamics toward the static equilibria,
| (6) |
which has stable fixed points at open and closed states for the time constant (19, 29).
ASM-airway model coupling
The ASM and the airway wall can be coupled by considering relationships between the ASM length, the radius of the airway lumen, and the contribution of the tension of the ASM to the pressure balance. We assume that any change in length of the ASM directly affects the radius of the airway , which can be modeled via the relationship , for which . Additionally, the force produced by the ASM (37) to constrict the airway is modeled as
| (7) |
which affects the transmural pressure via
| (8) |
The dependence arises from the Laplace law approximation for a thin-walled cylinder and refers to the effective transmural pressure, arising as a combination between the imposed transmural pressure, , and the constricting pressure of the ASM. Here, we see the coupling of the force produced by the tension of the ASM to the airway wall, where we introduce the force scaling parameter, λ, which controls the magnitude of the force. Additionally, for the coupling mechanism we use the length-radius relationship, . Finally, substituting the relationship to adjust for the airway size of differing airway orders, we obtain
| (9) |
which relates the relative filament velocity of the muscle contractile units to the rate of change of the radius of the airway lumen.
The DM approximation
The fundamental idea behind the DM approximation (31) is that the cross-bridge equations describe solutions that are distributions. Thus, by assuming a form for those distributions, under certain conditions (see the Conclusions for more details regarding the conditions), the original system of equations (PDEs) can be reduced to ODEs, which describe the evolution of the moments of the distribution(s). Consider the following equations representing the change in distribution populations of the attached phosphorylated myosin and the attached dephosphorylated myosin during the cross-bridge cycle:
| (10) |
| (11) |
If we multiply both sides of Eq. 10 by and integrate over the domain of x, we obtain
Defining to be the moment of the bond distribution, Eq. 10 further reduces to the ODE
| (12) |
After this process, Eq. 11 can be reduced to
| (13) |
Here, as in (31), we assume a Gaussian shape; hence, three moments are required to define the distribution—the usual mean (first moment) and variance (second moment), but also normalization by the zeroth moment. The right-hand-side terms to depend on the assumed form of the distribution and are computed in terms of the moments—explicit derivation is given in the Supporting Material.
In the original DM method (31), only one bound species was considered; here, our ASM cross-bridge system has two bound species and two unbound species. Above, we have described the equations that govern the moments of the bound species. In addition, we have the conservation law (Eq. 3), which allows us to express one unbound species. To close the system, we require one additional constraint; fortunately, the balance between phosphorylated and de-phosphorylated species can provide that closure. Specifically, we write the dephosphorylated fraction, c, which is then governed by
| (14) |
where , the sum of the zeroth moments of and (see Supporting Material). This then allows us to close the system for the unbound species and (see the Supporting Material). Thus, the DM system of ODEs consists of Eqs. 12, 13 (for ), 14, and 6.
Numerical methods
The DM system of ODEs is solved numerically using the standard fourth-order Runge-Kutta method (RK4). The PDE-based cross-bridge system is solved by first reducing to a larger system of ODEs using the method of characteristics (MoC; e.g., (19)), which is then also integrated using the RK4 method. In both models, the initial conditions were chosen as the steady-state solution without ASM activation. Parameter values are given in Table S1.
Inter-model comparison
Comparison between the full model (the PDE cross-bridge-based system) and its DM-based approximation is complicated by the conditions imposed on the system. For example, the accuracy of the DM approximation might be very different in an iso-pressure contraction of a large, cartilaginous central airway, as opposed to contraction of a small, peripheral airway under periodic breathing. If one allows an arbitrary external pressure waveform, the space over which a comparison must be made is, in fact, of infinite dimension.
To simplify this comparison to workable form, we make two key reductions:
-
1.
We assume a three-parameter external pressure waveform consisting of triangular waves; thus, the frequency, amplitude, and minimum pressure (three parameters) are sufficient to define this space. This is designed to mimic both common experimental protocols and also in vivo considerations.
-
2.
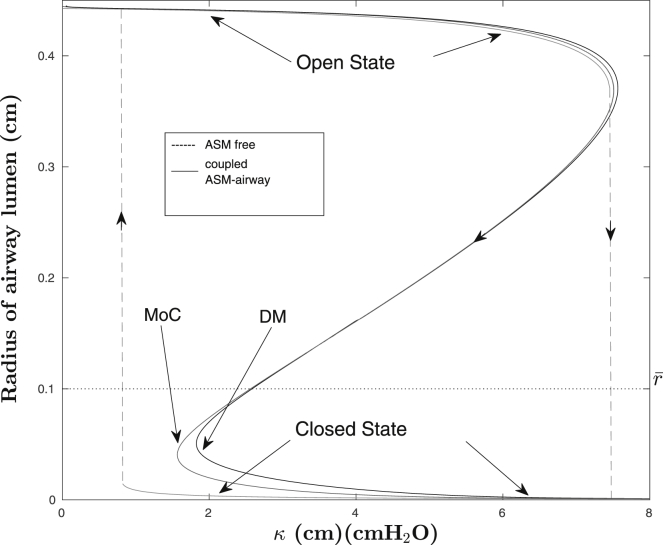
Rather than attempting to quantify the entire time-series solutions to the system, we define a key measure based on the relevant physiological concerns. These are that, first, the airway luminal radius is the primary quantity of interest, and second, the existence of airway bistability can be exploited. Namely, for a given airway size, degree of activation, and fixed external pressure waveform, an airway can respond in only three qualitatively distinct ways: a) remain in the open state; b) close, and remain in the closed state; or c) switch between open and closed states indefinitely. The basic idea is illustrated in Fig. 1, showing the underlying bistability (gray), as well as sample trajectories for each model (black).
Figure 1.
Underlying bistability response of a (static-force) peripheral airway to an increase in force (dashed gray line), as well as sample trajectories for each model (black lines) in the absence and presence of activated (dynamic) ASM.
Using this latter idea, we define as the degree of activation (e.g., the value of the parameter λ) at which the transition occurs (e.g., airway closure). This critical transition value then is itself a function of the external pressure waveform, e.g., it is a function of the external pressure frequency, amplitude, and minimal external pressure. We then define a range of these parameters of physiological interest and compute over this parameter space for both the full model and the DM approximation; by then comparing these, we are able to understand the situations under which the DM approximation is most accurate, and those in which deviations are larger.
To determine , we consider a threshold radius (denoted ) within the unstable region of the open-to-closed transition (see Fig. 1) and then use the bisection method to determine the value of λ required to constrict the airway lumen past , within the set integration time.
Indefinite switching between open and closed states occurs when the airway is subject to large-amplitude, slow-frequency oscillations and minimal λ. At these values, the radius of the airway lumen is reduced past , but the force provided by the ASM is not sufficient to keep the airway at the closed state and it thus returns to the open state. Because this occurs in only a very small portion of the physiological parameter space, we concentrate here on the transition.
Results and Discussion
Static pressure conditions
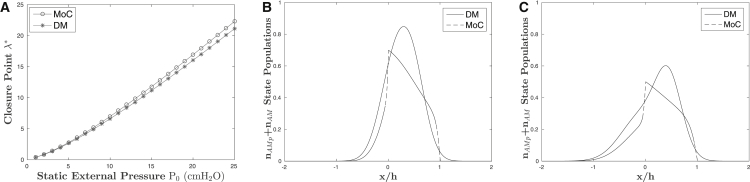
The simplest case for comparison between the DM approximation model and its full cross-bridge counterpart is simply to narrow the airway against a static external pressure. As described in the previous section, we compute as a function of this imposed pressure for both models and compare these critical closure values; the results are given in Fig. 2, with given for DM and MoC (). In this simplest case, both models show good agreement both with expectations and with one another. Specifically, one would qualitatively expect a monotonic increase in as the external pressure increases, as shown by both models. Furthermore, DM shows excellent quantitative agreement with the full model, with a 2–5 difference, as well as having absolute differences in the range 0–1.2. This suggests that the DM approximation is suitable at least for this simplest, static case; however, as the entire protocol is quasi-isometric, one might have expected that accurate estimation of the first bond moment is all that is necessary here. Further comparison of the bound-state distributions is given in Fig. 2, B and C, for both low and high static external pressure, respectively. In (31), although the distributions themselves showed significant departures, the moments agreed rather better; here, a similar observation can be made regarding the relatively large deviation in the distributions versus the rather better performance of the coupled system (in terms of ).
Figure 2.
(A) Predicted monotonic increase in closure points for both models due to increasing static external pressure. The DM shows great quantitative and qualitative agreement to the full MoC model for this static case, with a 2 to 5% difference, as well as having absolute differences in the range 0–1.2. (B and C) Comparison of the sum of the attached myosin populations for both models at P0 = 5 cmH2O and P0 = 25 cmH2O, respectively. These distribution plots were taken at the first instant after the closure threshold, , was passed. At low external pressure, the moment matching of the DM is a good approximation to the exact distribution of the MoC (B), but it deviates as the external pressure is increased, as seen in (C), which leads to qualitative differences in .
External-pressure oscillations
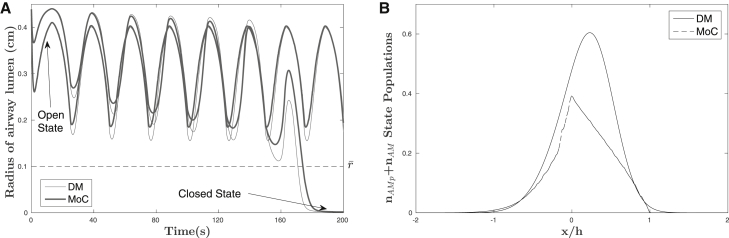
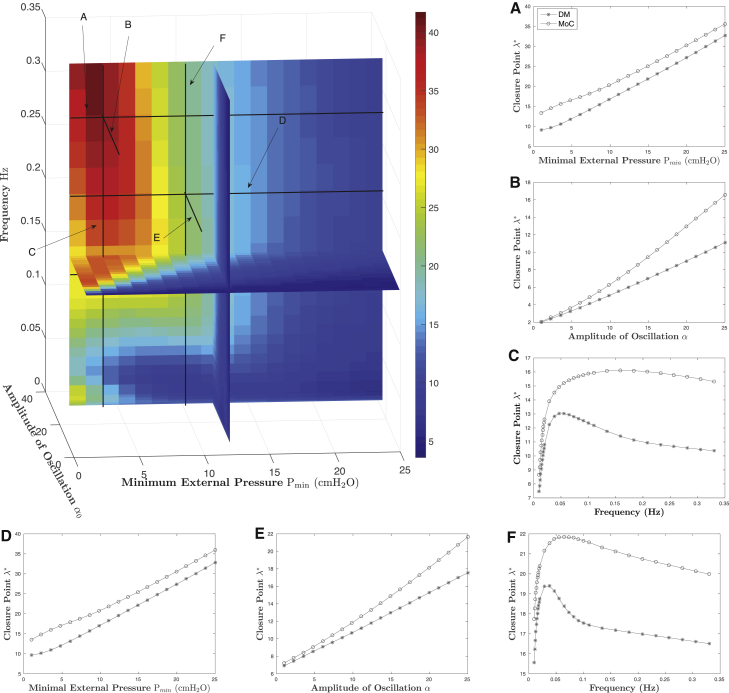
A more realistic and challenging scenario is to impose external-pressure oscillations, mimicking either the breathing environment or common experimental protocols. Hence we impose triangular pressure oscillations determined by three parameters: amplitude, frequency, and minimal external pressure. For fixed-pressure oscillations, then, the critical value can be found in that environment, for each model, and again compared. The central idea is illustrated in Fig. 3, which shows individual radius trajectories for each model for fixed external-pressure oscillations; the transition from trajectories that remain in the open state to those that transition to closed occurs at . To characterize this relationship for not just one fixed-pressure waveform but more generally, we compute for a range of pressure waveforms within the three-parameter space, amplitude × frequency × minimal external pressure, throughout the physiological range. The percentage difference between the values (DM versus MoC) is given in Fig. 4, chosen at an amplitude of 25 to illustrate maximumal percentage differences. Broadly speaking, there is good qualitative agreement between the DM and MoC models for much of this parameter space, with differences of <10% existing for broad regions, in particular for larger minimal pressures, lower amplitudes, and lower frequencies. On the other hand, differences of ∼40% appear for high-frequency, large-amplitude oscillations with low minimal pressures. To better illustrate the behavior of these differences, we also show selected “slices” of the parameter space in Fig. 4, A–F; the location of each “slice” is also noted in the main figure.
Figure 3.
(A) Individual radius trajectories for each model for fixed-external-pressure oscillations; the transition from trajectories that remain in the open state to those that transition to closed state occurs at . (B) Comparison of the sum of the attached myosin populations for both models at frequency f = 0.33 Hz, amplitude α = 25 cmH2O, and minimal external pressure Pmin = 2 cmH2O. The distribution plot was also taken at the first instant the closure threshold, , was passed.
Figure 4.
Percentage error in closure points ( versus ) for a range of external-pressure waveforms within the three-parameter space, amplitude × frequency × minimal external pressure. (A–F) Selected slices of the parameter space. The locations of these slices are noted in the main figure. To see this figure in color, go online.
Several observations are apparent. First, parametric dependence on minimal external pressure (Fig. 4, A and D) and oscillation amplitude (Fig. 4, B and E) are relatively simple and in good qualitative agreement, even within the region of relatively large quantitative departure (25–40 relative error). On the other hand, the frequency response (Fig. 4, C and F) is more complex, being both non-linear and non-monotonic, with relative percentage differences ranging from 5–40 in Fig. 4 C and 5–25 in Fig. 4 F. It is worth a mention that although the percentage differences are relatively large, the absolute error between predicted values at the largest deviation is ≈5 and that at the lowest percentage differences is ≈0.5. Even so, because of the persistent qualitative agreement through parameter space, these differences can be reduced to <15% everywhere with a relatively simple second-order polynomial correction factor.
ASM without airway-wall coupling
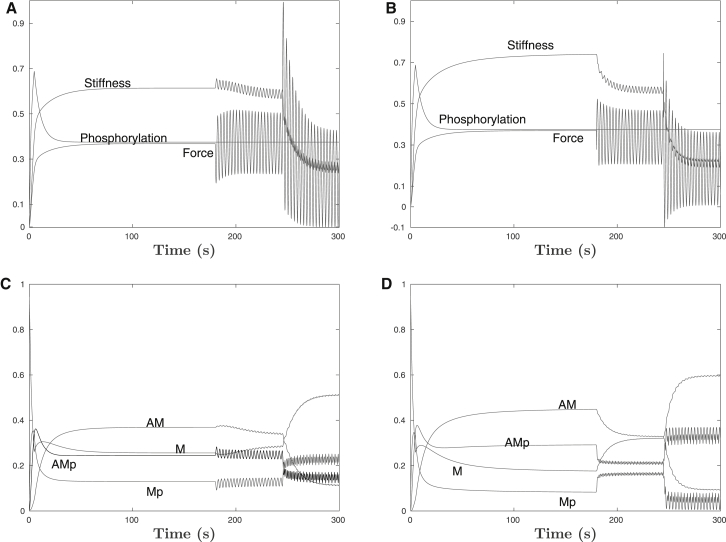
For completeness, we also show a more explicit comparison between the Mijailovich cross-bridge PDE model, without the airway attached, and the DM approximation. These results are given in Fig. 5 for the length-controlled protocol used in (7); specifically, isometric contraction was followed by a period of 1% length oscillation at 0.33 Hz, then increased to 4% length oscillation. Fig. 5, A and B, show the bulk observables of force, stiffness, and phosphorylation for each model. Fig. 5, C and D, give a more detailed breakdown by cross-bridge state. Although differences are certainly in evidence, broadly speaking, the ASM-only model agreement suggests that relatively modest differences in ASM during forced oscillations, particularly in the form and structure of the myosin bond populations, as well as the macroscopic muscle behavior, are amplifed by non-linear interactions with the airway wall into more complex differences, especially in terms of frequency dependence (and at higher oscillation frequencies/amplitudes).
Figure 5.
ASM-only solutions, without the airway wall. A length-controlled protocol of isometric contraction was followed by a period of 1% length oscillations at 0.33 Hz, and then increased length oscillations at 4%. (A and B) Shown are the bulk observables of force, stiffness, and phosphorylation for DM and MoC, respectively. (C and D) Breakdown of the state-population transitions for the DM and MoC models, respectively.
Numerical efficiency
We quantified the numerical efficiency of the DM approach relative to MoC in terms of the number of (ordinary) differential equations that must be solved in each. For DM, this is fixed at 7, whereas for MoC, a spatial discretization (consisting of points) must be chosen. Because applies to three PDEs (the fourth can be obtained by conservation), the overall numerical efficiency can be estimated as . Our “gold-standard” MoC uses and so, naively, the efficiency ratio is . However, this does not account for the reduction in numerical accuracy. To do so, we estimate an equivalent MoC discretization for which the error is equivalent to the DM approximation (for details, see the Supporting Material). This varies across parameter space, but on average the efficiency ratio is . Thus, the DM provides a reduction in computational cost by nearly two orders of magnitude relative to an MoC approach of equivalent accuracy.
Conclusions
In this study, we have derived a DM approximation method for a coupled cross-bridge-airway-wall system. The goal was to find a reduced model that retains a rich set of cross-bridge dynamics coupled to the airway-wall model, at the same time substantially reducing the computational complexity of numerical solution. This is motivated not just by studies of isolated airway dynamics, but with an eye toward incorporation of such a reduction into whole-lung models with coupled (interacting) airways.
By making suitable comparisons between the DM model and the full coupled cross-bridge-airway model, we show that 1) the DM approximation is accurate when static external pressures are imposed; 2) for much of the oscillatory waveform parameter space, with the possible exception of high-frequency, large-amplitude oscillations with low minimal pressures, the DM approximation again provides a satisfactory approximation; and 3) even within this region of relatively large quantitative departure, persistent qualitative agreement allows a relatively simple correction factor to reduce relative errors to <15% throughout the physiological range. Taken together, this suggests that the DM approximation provides a viable method for vast reduction in computational complexity while retaining key ASM dynamics through a systematic reduction. Because of this, it provides a plausible route forward toward inclusion of such ASM dynamics in coupled airway systems. It is also conceivable that a hybrid approach might be adopted in which DM approximation dynamics in a coupled airway system might be selectively validated using MoC methods.
Several more subtle points deserve additional analysis. First, throughout this analysis, we have treated the crossbridge-airway coupled model as an appropriate standard of comparison. Because of the systematic-reduction approach, this is the most valid comparison; however, one should be aware that aspects of this model are known to depart from observations, for example, in terms of thin-walled assumptions (17, 18), the validity of the Huxley model for ASM (9), and also more complex phenomena, potentially involving length-tension characteristics, which are not yet fully understood (15, 19). Although in principle the same comparison might be made with experimental data, at this time, the authors unfortunately are not aware of any such data set.
Second, the relatively complex frequency dependence of the coupled model suggests that care should be taken within the high-frequency, large-amplitude oscillation regime. This is consistent with observations about the product of frequency and amplitude setting key behavior in ASM (38). Despite the fact that empirical correction is possible in this regime, the complexity of frequency-dependent behavior suggests that this regime should be treated carefully.
Third, although the bistability airway model used in this study allowed for direct comparison between the MoC and DM methods within a space of tractable size, there are situations in which such a comparison may be less relevant, for example, when the region of bistability is reduced or eliminated, perhaps due to airway size or parenchymal tethering (23, 39). However, the bistable regime is arguably the most challenging because of the sensitivity of airway behavior to relatively small changes in ASM behavior near the transition; thus, an approximation that performs well in the bistable regime might reasonably be expected to do well in a simpler monostable regime.
Finally, it is worth discussing some aspects of the DM approximation that affect its extensibility to other systems. In the model derivation, we noted that there were conditions imposed on the DM reduction method; here, we outline the restrictions. First, observe that the DM approximation technique is not restricted to assuming a Gaussian form of the bond distribution. In principle, one could assume any distribution, so long as both the moment integrals and the product of the rate functions with the assumed distribution can be written in closed form. (If the rate functions are piecewise polynomial, as is usual, then the product-form terms are expressible in terms of higher-order moments.) The size of the reduced system would then be determined by the number of moments required to identify the distribution. It is also worth noting that the approach we used here for expressing the unbound species in terms of both conservation and phosphorylation balance depends on the facts that 1) the phosphorylation and de-phosphorylation rates and are spatially independent, and 2) the phosphorylation and de-phosphorylation rates are the same for both bound and unbound species. Both assumptions are typical of this family of models, but variants for which this is not true would require a modified approach.
Author Contributions
A.K.R. and G.M.D. designed the study. A.K.R. performed the model derivation and computations. A.K.R. and G.M.D. prepared and finalized the manuscript.
Acknowledgments
The authors gratefully acknowledge the support of the Royal Society of New Zealand via the Marsden Fund grant (14-UOA-145).
Editor: Jeffrey Fredberg.
Footnotes
Supporting Materials and Methods, one figure, and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(17)31252-3.
Supporting Material
References
- 1.Fredberg J.J., Inouye D., Shore S.A. Airway smooth muscle, tidal stretches, and dynamically determined contractile states. Am. J. Respir. Crit. Care Med. 1997;156:1752–1759. doi: 10.1164/ajrccm.156.6.9611016. [DOI] [PubMed] [Google Scholar]
- 2.Gunst S.J. Contractile force of canine airway smooth muscle during cyclical length changes. J. Appl. Physiol. 1983;55:759–769. doi: 10.1152/jappl.1983.55.3.759. [DOI] [PubMed] [Google Scholar]
- 3.Wang L., Paré P.D., Seow C.Y. Effects of length oscillation on the subsequent force development in swine tracheal smooth muscle. J. Appl. Physiol. 2000;88:2246–2250. doi: 10.1152/jappl.2000.88.6.2246. [DOI] [PubMed] [Google Scholar]
- 4.Chin L.Y., Bossé Y., Paré P.D. Mechanical properties of asthmatic airway smooth muscle. Eur. Respir. J. 2012;40:45–54. doi: 10.1183/09031936.00065411. [DOI] [PubMed] [Google Scholar]
- 5.Hai C.-M., Murphy R.A. Regulation of shortening velocity by cross-bridge phosphorylation in smooth muscle. Am. J. Physiol. 1988;255:C86–C94. doi: 10.1152/ajpcell.1988.255.1.C86. [DOI] [PubMed] [Google Scholar]
- 6.Hai C.-M., Murphy R.A. Cross-bridge phosphorylation and regulation of latch state in smooth muscle. Am. J. Physiol. 1988;254:C99–C106. doi: 10.1152/ajpcell.1988.254.1.C99. [DOI] [PubMed] [Google Scholar]
- 7.Mijailovich S.M., Butler J.P., Fredberg J.J. Perturbed equilibria of myosin binding in airway smooth muscle: bond-length distributions, mechanics, and ATP metabolism. Biophys. J. 2000;79:2667–2681. doi: 10.1016/S0006-3495(00)76505-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Donovan G.M. Modelling airway smooth muscle passive length adaptation via thick filament length distributions. J. Theor. Biol. 2013;333:102–108. doi: 10.1016/j.jtbi.2013.05.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bates J.H. Modeling the impairment of airway smooth muscle force by stretch. J. Appl. Physiol. 2015;118:684–691. doi: 10.1152/japplphysiol.00938.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bates J.H., Bullimore S.R., Lauzon A.-M. Transient oscillatory force-length behavior of activated airway smooth muscle. Am. J. Physiol. Lung Cell. Mol. Physiol. 2009;297:L362–L372. doi: 10.1152/ajplung.00095.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ansell T.K., McFawn P.K., Noble P.B. Bronchodilatory response to deep inspiration in bronchial segments: the effects of stress vs. strain. J. Appl. Physiol. 2013;115:505–513. doi: 10.1152/japplphysiol.01286.2012. [DOI] [PubMed] [Google Scholar]
- 12.Ansell T.K., McFawn P.K., Noble P.B. Does smooth muscle in an intact airway undergo length adaptation during a sustained change in transmural pressure? J. Appl. Physiol. 2015;118:533–543. doi: 10.1152/japplphysiol.00724.2014. [DOI] [PubMed] [Google Scholar]
- 13.LaPrad A.S., Szabo T.L., Lutchen K.R. Tidal stretches do not modulate responsiveness of intact airways in vitro. J. Appl. Physiol. 2010;109:295–304. doi: 10.1152/japplphysiol.00107.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Noble P.B., Jones R.L., McFawn P.K. Responsiveness of the human airway in vitro during deep inspiration and tidal oscillation. J. Appl. Physiol. 2011;110:1510–1518. doi: 10.1152/japplphysiol.01226.2010. [DOI] [PubMed] [Google Scholar]
- 15.Gazzola M., Henry C., Bossé Y. Smooth muscle in human bronchi is disposed to resist airway distension. Respir. Physiol. Neurobiol. 2016;229:51–58. doi: 10.1016/j.resp.2016.04.005. [DOI] [PubMed] [Google Scholar]
- 16.Mailhot-Larouche S., Lortie K., Bossé Y. An in vitro study examining the duration between deep inspirations on the rate of renarrowing. Respir. Physiol. Neurobiol. 2017;243:13–19. doi: 10.1016/j.resp.2017.04.013. [DOI] [PubMed] [Google Scholar]
- 17.Hiorns J.E., Jensen O.E., Brook B.S. Nonlinear compliance modulates dynamic bronchoconstriction in a multiscale airway model. Biophys. J. 2014;107:3030–3042. doi: 10.1016/j.bpj.2014.10.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hiorns J.E., Jensen O.E., Brook B.S. Static and dynamic stress heterogeneity in a multiscale model of the asthmatic airway wall. J. Appl. Physiol. 2016;121:233–247. doi: 10.1152/japplphysiol.00715.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Donovan G.M. Airway bistability is modulated by smooth muscle dynamics and length-tension characteristics. Biophys. J. 2016;111:2327–2335. doi: 10.1016/j.bpj.2016.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Huxley H.E. The double array of filaments in cross-striated muscle. J. Biophys. Biochem. Cytol. 1957;3:631–648. doi: 10.1083/jcb.3.5.631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Keener J.P., Sneyd J. Volume 1. Springer; New York: 1998. Mathematical Physiology. [Google Scholar]
- 22.Dubsky S., Zosky G.R., Fouras A. Assessment of airway response distribution and paradoxical airway dilation in mice during methacholine challenge. J. Appl. Physiol. 2017;122:503–510. doi: 10.1152/japplphysiol.00476.2016. [DOI] [PubMed] [Google Scholar]
- 23.Ma B., Bates J.H. Mechanical interactions between adjacent airways in the lung. J. Appl. Physiol. 2014;116:628–634. doi: 10.1152/japplphysiol.01180.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ma B., Smith B.J., Bates J.H. Resistance to alveolar shape change limits range of force propagation in lung parenchyma. Respir. Physiol. Neurobiol. 2015;211:22–28. doi: 10.1016/j.resp.2015.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Venegas J.G., Winkler T., Harris R.S. Self-organized patchiness in asthma as a prelude to catastrophic shifts. Nature. 2005;434:777–782. doi: 10.1038/nature03490. [DOI] [PubMed] [Google Scholar]
- 26.Donovan G.M. Clustered ventilation defects and bilinear respiratory reactance in asthma. J. Theor. Biol. 2016;406:166–175. doi: 10.1016/j.jtbi.2016.06.035. [DOI] [PubMed] [Google Scholar]
- 27.Stewart P.S., Jensen O.E. Patterns of recruitment and injury in a heterogeneous airway network model. J. R. Soc. Interface. 2015;12:20150523. doi: 10.1098/rsif.2015.0523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Leary D., Winkler T., Maksym G.N. Effects of airway tree asymmetry on the emergence and spatial persistence of ventilation defects. J. Appl. Physiol. 2014;117:353–362. doi: 10.1152/japplphysiol.00881.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Donovan G.M., Kritter T. Spatial pattern formation in the lung. J. Math. Biol. 2015;70:1119–1149. doi: 10.1007/s00285-014-0792-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dowie J., Ansell T.K., Donovan G.M. Airway compliance and dynamics explain the apparent discrepancy in length adaptation between intact airways and smooth muscle strips. Respir. Physiol. Neurobiol. 2016;220:25–32. doi: 10.1016/j.resp.2015.09.006. [DOI] [PubMed] [Google Scholar]
- 31.Zahalak G.I. A distribution-moment approximation for kinetic theories of muscular contraction. Math. Biosci. 1981;55:89–114. doi: 10.1016/j.mbs.2020.108455. [DOI] [PubMed] [Google Scholar]
- 32.Gielen A.W., Oomens C.W., Janssen J.D. A finite element approach for skeletal muscle using a distributed moment model of contraction. Comput. Methods Biomech. Biomed. Engin. 2000;3:231–244. doi: 10.1080/10255840008915267. [DOI] [PubMed] [Google Scholar]
- 33.Wu J.Z., Herzog W., Cole G.K. Modeling dynamic contraction of muscle using the cross-bridge theory. Math. Biosci. 1997;139:69–78. doi: 10.1016/s0025-5564(96)00115-0. [DOI] [PubMed] [Google Scholar]
- 34.Affonce D.A., Lutchen K.R. New perspectives on the mechanical basis for airway hyperreactivity and airway hypersensitivity in asthma. J. Appl. Physiol. 2006;101:1710–1719. doi: 10.1152/japplphysiol.00344.2006. [DOI] [PubMed] [Google Scholar]
- 35.Anafi R.C., Wilson T.A. Airway stability and heterogeneity in the constricted lung. J. Appl. Physiol. 2001;91:1185–1192. doi: 10.1152/jappl.2001.91.3.1185. [DOI] [PubMed] [Google Scholar]
- 36.Lambert R.K., Wilson T.A., Rodarte J.R. A computational model for expiratory flow. J. Appl. Physiol. 1982;52:44–56. doi: 10.1152/jappl.1982.52.1.44. [DOI] [PubMed] [Google Scholar]
- 37.Politi A.Z., Donovan G.M., Sneyd J. A multiscale, spatially distributed model of asthmatic airway hyper-responsiveness. J. Theor. Biol. 2010;266:614–624. doi: 10.1016/j.jtbi.2010.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Oliver M., Kováts T., Lenormand G. Remodeling of integrated contractile tissues and its dependence on strain-rate amplitude. Phys. Rev. Lett. 2010;105:158102. doi: 10.1103/PhysRevLett.105.158102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bates J.H., Lauzon A.-M. Parenchymal tethering, airway wall stiffness, and the dynamics of bronchoconstriction. J. Appl. Physiol. 2007;102:1912–1920. doi: 10.1152/japplphysiol.00980.2006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.