Simulating Genetic Circuits in Bacterial Populations with Growth Heterogeneity

Abstract

We computationally study genetic circuits in bacterial populations with heterogeneities in the growth rate. To that end, we present a stochastic simulation method for gene circuits in populations of cells and propose an efficient implementation that we call the “Next Family Method”. Within this approach, we implement different population setups, specifically Chemostat-type growth and growth in an ideal Mother Machine and show that the population structure and its statistics are different for the different setups whenever there is growth heterogeneity. Such dependence on the population setup is demonstrated, in the case of bistable systems with different growth rates in the stable states, to have distinctive signatures on quantities including the distributions of protein concentration and growth rates, and hysteresis curves. Applying this method to a bistable antibiotic resistance circuit, we find that as a result of the different statistics in different population setups, the estimated minimal inhibitory concentration of the antibiotic becomes dependent on the population setup in which it is measured.

Introduction

Cellular functions and their adaptation to environmental conditions are to a large extent encoded in the regulatory connections of genetic circuits. Therefore, a quantitative understanding of the dynamics and the function of genetic circuits, combining predictive mathematical models with quantitative experiments and with the design of engineered circuits, is one of the key goals of systems biology (1, 2, 3, 4, 5, 6). Specifically, a large body of work has addressed multistability (7, 8, 9, 10) and stochastic effects (11, 12, 13, 14, 15), both of which result in heterogeneous gene expression in a genetically homogeneous population of cells.

One complication in the quantitative study of genetic circuits is that genetic circuits are usually coupled to the physiological state of the cell (16). The latter, for example, affects the availability of gene expression machinery and thereby influences the level of gene expression. In many cases, however, the expression status of a gene also has an effect on the cellular physiology; for example, in the case of essential enzymes limiting cell growth. This coupling has mostly been studied in bacteria in exponential growth phase, where the physiological state of the cell can often be characterized by the growth rate (17, 18). In the last 10 years such coupling has been demonstrated for a variety of genetic circuits (19, 20, 21, 22, 23, 24, 25). In these cases, heterogeneity in gene expression is accompanied by heterogeneity in cell growth with part of the population growing faster than the rest. For some genetic circuits, growth heterogeneity is a crucial part of their biological function; for example, bet hedging for survival in varying environments as proposed for the formation of bacterial persister cells (8, 26), or for the heterogeneous expression of genes conveying resistance to antibiotics (23, 27). In other cases, specifically in synthetic genetic circuits, growth heterogeneity may arise as an unavoidable and possibly unintended side effect of the desired function, but also allows for the implementation of more complex functions (22, 28, 29).

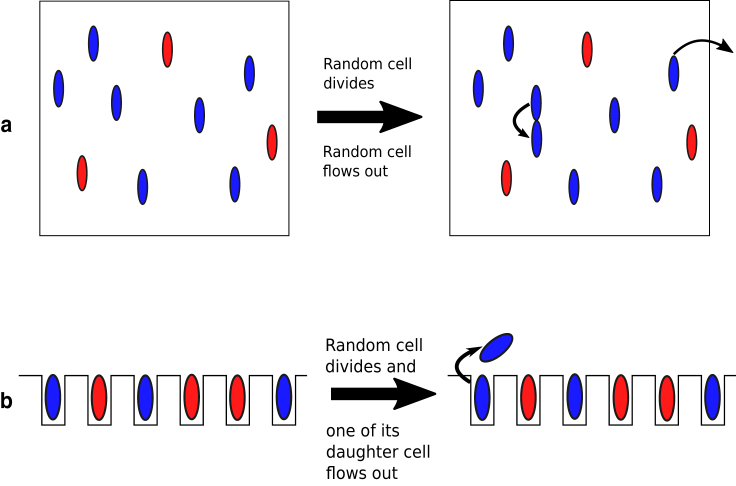
To study the growth and the heterogeneity of populations of cells, various setups have been used. Traditionally, bacterial growth has been studied in batch cultures, where bacteria grow exponentially until the medium gets depleted (20, 30), and in continuous cultures or the Chemostat, where exponential growth is maintained by continuously diluting the population by washing out cells with fresh medium (17, 31, 32) (Fig. 1 a). More recently, microfluidic devices have been developed to observe cell growth at the single cell level (33, 34, 35, 36). These devices include a microfluidic version of a Chemostat (34) and the so-called Mother Machine, in which a cell is trapped in a dead-end channel whereas its daughter cells are flushed away upon cell division, enabling the long-time study of individual cells (35) (Fig. 1 b).

Figure 1.

Schematic representation of the two population setups. The blue and red ellipsoids represent the two types of cells, fast and slow growing. (a) Chemostat-type growth. Dilution of the population is implemented by replacing a randomly chosen cell in the population with the newly formed daughter cell, whenever a cell divides. (b) Ideal Mother-Machine. Upon division, one of its daughter cells is flushed away whereas the other is kept. To see this figure in color, go online.

By contrast, simulations of gene circuits have typically been carried out for single cells and analyzed with statistics over time using long trajectories rather than statistics over a population (37, 38). These two types of statistical ensembles are usually equivalent, given sufficiently long trajectories and in the absence of growth heterogeneity. Growth heterogeneity, however, can be expected to result in the accumulation of the faster proliferating cells within a population, an effect not seen in the time statistics of a typical simulation. Indeed, the accumulation effect will in general depend on the type of experimental setup used, so that the statistical results for populations heterogeneous in growth may be different in different experimental setups. Recently, such an effect has been shown experimentally and discussed analytically for growth heterogeneity in a monostable system (39).

Here we present a method for stochastic simulations of genetic circuits in populations of growing cells, specifically populations that are heterogeneous in growth. The method is based on Gillespie’s stochastic simulation algorithm (40, 41), for which we propose a computationally efficient implementation, the Next Family Method; this is particularly suitable for a scenario with many cells. Within this approach, we implement Chemostat-type and Mother Machine-type population setups. We use a bistable mutual repression system with growth inhibited in one of the two states to demonstrate explicitly how growth heterogeneity results in different statistics in these two setups for commonly measured quantities such as subpopulation fractions, growth rates, and hysteresis curves. We then apply the method to study growth bistability in an antibiotic resistance system (23). In that case, we find a dependence of the minimal inhibitory concentration (MIC) of the antibiotic, a parameter commonly used to quantify the effect of an antibiotic on bacterial populations, on the experimental setup.

Methods

Simulating gene circuits in populations of growing cells

To simulate the dynamics of a genetic circuit in a population of growing cells, allowing also for the possibility of phenotype switching, we adapt Gillespie’s stochastic simulation algorithm for a set of chemical reactions or other stochastic processes (40, 41). In the Gillespie algorithm, each reaction (protein synthesis/degradation/dilution) is characterized by a propensity a_j corresponding to its reaction rate in the deterministic rate equation. These propensities determine the probabilities of the time, τ, when the next reaction will take place, and the type of reaction, j, which will take place at that time. There are multiple ways to generate τ and j. In the Direct Method, two random numbers are drawn in each step to determine the time and index of the next reaction, the simulation time is advanced to τ, the reaction j is carried out, and the reaction rates are updated for the next reaction to reflect changes in the copy number of relevant reactants.

This method can be applied directly to a population of cells, by considering reactions that occur in different cells as parallel reaction channels. Thus, for simulating a set of s reactions in a population of N cells, one has to evaluate sN propensities in total, and use them to calculate τ and j as before. This will give the time and the index of the next reaction happening in any of the N cells. However, to apply this method to a population of proliferating cells, we also need to account for cell division and to that end implement the different population setups. Implementing a growing population also means that the computational effort grows with increasing cell number. The implementation of the different population setups that we propose here also limits the increase of the cell number. Several different methods for limiting that increase are possible, and those correspond to different population setups and as we will show below, result in different predictions for experiments. Here, we specifically consider two setups of populations of proliferating cells that correspond to the ideal Mother Machine and the Chemostat. In both cases, we simulate a fixed population size N. In the first case, corresponding to an ideal Mother Machine, every time a cell divides, we keep only one of its daughter cells. This is very similar to how simulations are done for a single cell (which corresponds to the special case N = 1). To implement this scenario, we do not need to describe the formation of the daughter cells through cell division explicitly, but only a dilution term for the proteins. In the second case, the Chemostat, we keep the population size constant by removing a random cell whenever a cell divides, mimicking the continuous dilution. This scenario corresponds to a variant of the Moran process (42), a stochastic model in evolution, with continuous time and a population with heterogeneous growth rates. In this case, an explicit description of the formation of daughter cells is required, because typically both cells remain in the population. We implement this production of daughter cells by introducing an additional propensity function a_s+1 = λ for each of the cells, with λ being the growth rate of that cell. This gives the probability that a cell divides into two daughter cells, both of which are in the same expression state and follow the original model for the dynamics of protein numbers. Whenever this reaction is selected, we produce an identical copy of the cell and replace a randomly selected member of the population with this copy, thereby mimicking the flushing out of cells and keeping the total number of cells (N) constant. We note that our method is not restricted to this Poissonian description of cell division. More detailed descriptions of cell division (with more realistic distributions of the division times) have been implemented in stochastic simulation of single cells (38), and can be implemented in our method for populations. One such case will be considered below.

Efficient implementation: the Next Family Method

The Gillespie algorithm using the Direct Method becomes quite slow when the number of reaction channels is large, as it spends a lot of computational time in determining the reaction channel j. Therefore, alternative but mathematically equivalent implementations have been developed. For example, in the First Reaction Method (41, 43), the expected times are calculated for all individual reactions rather than just one, and the reaction to occur, i.e., the reaction number j, is determined by searching for the minimum among them. The reaction j is carried out and then the new time for that reaction is calculated. The Next Reaction Method (44) improves upon it by using an indexed heap data structure in which the reaction times are stored. This data structure generally speeds up sorting and finding a minimum (45), which is used here to determine the next reaction that occurs. However, the method loses this advantage when many of the reactions are coupled, so that the heap structure needs to be repaired for each of the coupled reactions when their corresponding reaction times are modified. A generalization, the First Family Method (43), partitions the reactions into families and then considers these families as pseudo-reactions. The First Reaction Method is then applied to determine which of these families or pseudoreactions occur next and the Direct Method to determine the actual reaction within that family.

Even though the First Family Method was originally introduced mainly as a book-keeping method, in our case a natural classification of reactions into families is provided by the different cells. Moreover, as there is no interaction between the cells, these pseudoreactions given by the grouped reactions in each cell are decoupled. We, therefore, calculate the expected time of next reaction for each of the N families (cells), heapify these reaction times so that any node has reaction times larger than its parent node (45), and identify the cell at the top of the heap as the one in which reaction will take place next. Once this reacting cell is identified, we can then use the Direct Method to find the actual reaction that occurs in that cell. A heap repair step is only required for this one cell in which reaction takes place. We note that if the reaction chosen is cell division and results in the production of a daughter cell in the case of Chemostat growth, one needs to perform an additional heap repair step on this new cell, which randomly replaces one of the existing cells (see the Supporting Material for more details). However, as long as there is no cross talk between different cells, this method, which may be called the Next Family Method, will be more efficient than any of the previous methods. Even under cross talk, it may be possible to group the cells into modules that interact more among themselves than with cells of other modules, thereby making this current method quite powerful. In principle, this method can be generalized to any system where there are clustered reactions.

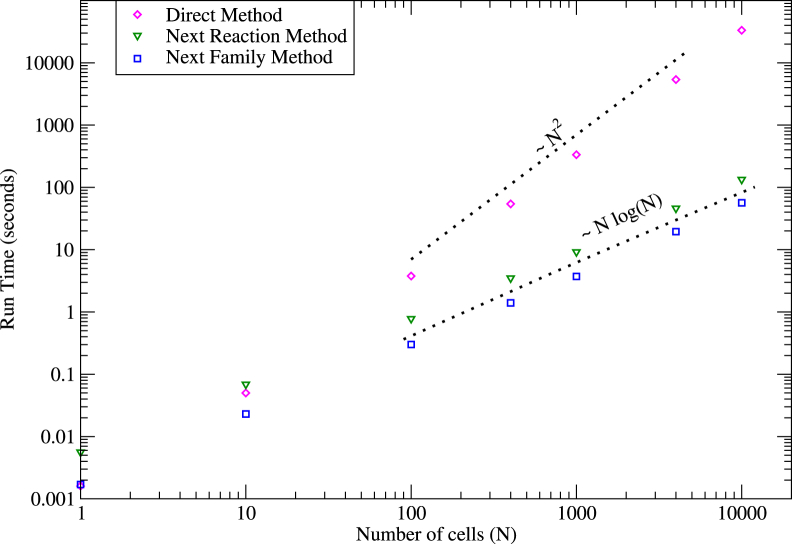
In Fig. 2, we demonstrate the significant speedup of simulations using the Next Family Method as compared to the Direct Method and the Next Reaction Method. Although the runtime scales as N² for the Direct Method, it scales as Nlog(N) for the Next Reaction Method as well as for the Next Family Method. Here, the first factor comes from the number of reactions occurring in a given time, which scales as N irrespective of the method used. The second factor comes from the time it takes to find j for each of the reaction steps. This scales as N for the Direct Method, which is the timescale required to scan through the propensities, and as log(N) for the Next Reaction and the Next Family Methods, which is the timescale required to repair the heap (45). As expected, there is a difference of a multiplicative factor between the runtimes of the Next Reaction and Next Family Methods. This difference corresponds to the extra heap repair steps needed for each of the coupled reactions and it will linearly increase with increasing number of coupled reactions. In Fig. S1, we show that the results obtained from these methods are statistically identical. We mention that other methods for implementing Gillespie’s algorithm can also speed up the simulations. However, they either assume that some of the reactions can be introduced later (46) or that the reactions have widely different rates (47, 48), neither of which is applicable in the situation we consider here.

Figure 2.

Speedup of simulations by the Next Family Method. Shown here are runtimes for a simulation of the toggle switch (see next section) in a Chemostat population of N cells, using the proposed Next Family Method (blue squares) as compared to that using the Direct Method (magenta diamonds) and the Next Reaction Method (green triangles), with all parameters being the same (in all these cases the system is evolved for 6000 min in total). To see this figure in color, go online.

Results and Discussion

Test system: a toxic genetic toggle switch

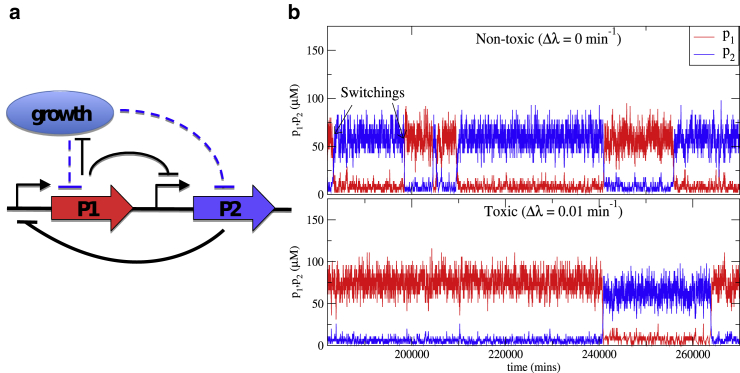
To study the effect of the different growth setups on the observed behavior of growth heterogeneous systems, we first consider a bistable system with different growth rates in the two states. Specifically, we study a mutual repressor system or toggle switch with one toxic protein (Fig. 3 a). In a simple mutual repressor system, two proteins P₁ and P₂ repress the transcription of each other. This system is known to exhibit bistability: For sufficiently strong repression, there are two stable states. In one of them, the concentration of P₁ (denoted by p₁) is high and the concentration of P₂ (denoted by p₂) is low; in the other, the roles are reversed (1). In simulations, a single cell switches stochastically between these two states (Fig. 3 b, upper panel). We modify this simple toggle switch by assuming that one of the proteins (say P₁) inhibits the growth of the cell, such that the growth rate of the cell is different in the two stable states. To keep the analysis simple, we describe the dependence of the growth rate on the concentration of P₁ by a simple interpolation between a maximal growth rate λ_max for small p₁ and a minimal growth rate λ_min for large p₁. The strength of the growth inhibition is modulated by varying Δλ = λ_max – λ_min. Furthermore, we make the following simplifications: we consider the symmetric case, where both genes/proteins are characterized by the same parameters except for the growth inhibition, and growth is taken to affect gene expression only through dilution, neglecting a growth rate dependence of the protein synthesis rate (19) (see the Supporting Material for details). A scenario with more realistic assumptions is studied below. As a consequence of the symmetry of the parameters, a cell spends equal amounts of time in the high p₁ and high p₂ states in the absence of growth inhibition (Fig. 3 b, top panel). With increasing toxicity of P₁, the reduction in growth rate in the high p₁ state leads to reduced dilution (reduced effective degradation rate of the proteins) and thereby increases the concentration of P₁ in the high p₁ state. As a consequence, the symmetry between the high p₁ and high p₂ states is broken. This in turn affects the rates of stochastic switching between the two states: a larger fluctuation is needed to switch from high p₁ to low p₁ than from high p₂ (low p₁) to low p₂, making the cell spend more and more time in the slower growing (high p₁) state (Fig. 3 b, bottom panel).

Figure 3.

Toxic toggle switch. (a) Shown here is a schematic representation of the mutual repression circuit with growth inhibition by one of the two proteins (P₁). The black arrows represent specific gene regulation (here transcriptional repression), whereas the blue dashed arrows represent effects of the global state of the cell (pointed arrowheads are for positive regulation and flat arrowheads for negative). (b) Dynamics of the protein concentrations from simulations of a single cell without growth inhibition (top, Δλ = 0 min⁻¹) and with growth inhibition by protein P₁ (bottom, Δλ = 0.01 min⁻¹). Here we show a small segment of the whole temporal dynamics to clearly see the switching events. For the used parameters, see the Supporting Material. To see this figure in color, go online.

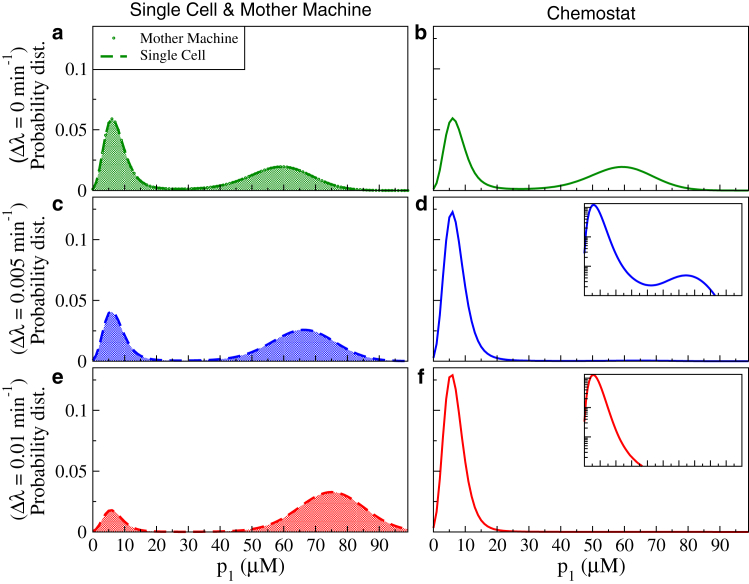
We then simulated the dynamics of this genetic circuit for the two population setups with 1000 cells each, varying the growth rate difference Δλ between the high p₂ and high p₁ states. The distribution of the concentration of protein P₁ obtained from the simulations for the three scenarios are shown in Fig. 4. Due to the bistability of the genetic circuit, the distributions typically exhibit two (broad, but well-separated) peaks corresponding to the subpopulations with high and low p₁ (and low and high p₂). In the absence of a growth difference (Δλ = 0), the distributions are exactly the same for all three simulation scenarios. In addition, due to the symmetry of the parameters, the system spends an equal amount of time in the two states. This is reflected in the population fractions of the two states (obtained as the areas under the two peaks) being equal.

Figure 4.

Distribution of the concentration of protein P₁ of the toxic toggle switch. Results are shown for three levels of growth inhibition by P₁ and three population scenarios. (a, c, and e) Single cell (dashed curves) and Mother Machine (shaded down curves). (b, d, and f) Chemostat (solid curves). The insets in (d) and (f) plot the same data on a log-linear scale to show the existence or absence of the small second peak. Sampling is done over 10⁸ time steps of 5 min each for the Single cell, and over N = 1000 cells and 10⁷ time steps of 5 min for the two populations. The parameters are given in the Supporting Material. It can be seen that the distribution is identical for the Single cell and the Mother Machine (see text). To see this figure in color, go online.

The distributions for a single cell show that with increasing growth difference, the population with high p₁ is shifted to even higher p₁, and at the same time the probability of that subpopulation is increased. This reflects the observations made in Fig. 3 b above about the breaking of symmetry between the two states due to growth rate modulation.

The distribution obtained for the two population setups, which both coincided with the distribution for a single cell in the case Δλ = 0, are in general different from each other for Δλ > 0. As expected, the results for the population in an ideal Mother Machine is identical to those for a single cell for all values of Δλ. This is because the ideal Mother Machine is essentially an array of many individual cells and studying it is equivalent to taking an ensemble average over the individual cells (possibly in addition to a time average). The choice of one over the other is mostly a question of practicalities, e.g., if dynamics is observed over times in which no steady state is reached because of rare switchings, one might prefer statistics over a population. Note that even if sampling is done over all cells in a real Mother Machine with 10–20 cells per channel (most of which are flushed out after some time) rather than the one cell in our ideal Mother Machine (which is not flushed out), the results are very similar (Fig. S2). Therefore, in the rest of this study we will be referring to our ideal Mother Machine simply as the Mother Machine.

For the Chemostat, the results are quantitatively and qualitatively different. In the presence of a growth rate difference, the dominant population is not the slow growing high p₁ subpopulation as in the single cell and the Mother Machine scenarios, but the fast growing low p₁ subpopulation. This can also be seen in Fig. S3 where we plot the distribution of the growth rates explicitly. This could be either because of the low p₁ state suddenly becoming more stable, which should not be the case as individual cells are still the same, or because there are more of these fast growing low p₁ cells. Indeed, unlike the Mother Machine where the daughter cells are washed away, a Chemostat has both daughter and mother cells in the population. As a result, a Chemostat population will contain more offspring of the fast growing cells than of the slow growing ones.

The distribution of switching times between the two states, defined as the time interval between two instances of p₁ and p₂ crossing each other in one cell, is plotted in Fig. S4. The switching times are seen to be exponentially distributed and symmetric between the two states for the nontoxic case. In the toxic case, as expected, the switching times from the slow to fast growing state gets increased. Again, we see that the results are identical for the single cell and the Mother Machine, apart from the noise.

In Fig. S5, we plot the hysteresis curves when the synthesis rate α₁ is modulated. Here, the switching to and from the low p₁ state happens at larger values of α₁ in the Chemostat than in the Mother Machine/Single cell, because in the low p₁ state the fast growing cells accumulate more by replacing the slow growing ones.

The subpopulation fractions for a bistable system with growth differences can be estimated with a two-state model originally used in the context of persister cells (8, 49). This model describes the population as consisting of two subpopulations (which in our case correspond to the high p₁ and high p₂ states) with different growth rates (λ₁ and λ₂) and with stochastic switching between the two subpopulations, but in contrast to our full model assumes the growth rate to have a unique sharp value in each state. In that case, the population fraction of the slow growing state (λ₂) is given by (49)

$$\frac{N_2}{N_1+N_2}\approx \frac{k}{{\lambda }_1-{\lambda }_2},$$ (1)

where k is the switching rate from the fast growing to the slow growing state. The rate for switching in the opposite direction does not affect the population fractions. A simple interpretation of this relation is that the population fractions are determined by a balance between two processes: slow growing cells are outgrown by the fast growing cells, but the slow growing population does not disappear because it is continuously restored by switching of fast growing cells to the slow growing state. Simulating this two-state model with our method, we find excellent agreement between the population fractions obtained from the simulation and the prediction of this relation, as shown in Table 1. (We note that this agreement also provides a quantitative test of our simulation method.) In our full model, the distribution of the growth rate is not sharp, but we can extract the average single cell growth rates (λ₁ and λ₂) as well as the size of the two subpopulations (N₁ and N₂) from the Chemostat simulations shown in Fig. S3. The switching rates are estimated as the inverse of the average switching times in the Single cell or Mother Machine simulations (Fig. S4). Doing so, we still find agreement with Eq. 1 within a factor 2 (Table 1), which appears to result from the broad distribution of growth rates within the subpopulations.

Table 1.

Subpopulation Fraction of the Slow Growing State

Case	k	λ1	λ2	N2/(N1 + N2)	k/(λ1−λ2)
Two-state model	0.001	0.04	0.03	0.0983	0.1
Toggle switch with Δλ = 0.01	4.36 × 10−5	0.03746	0.03268	4.2 × 10−3	9.12 × 10−3
Toggle switch with Δλ = 0.005	7.58 × 10−5	0.03863	0.03623	1.7 × 10−2	3.16 × 10−2

Subpopulation fraction obtained directly from Chemostat simulation (N₂/(N₁ + N₂)) of the two-state system matches almost exactly with that estimated from the ratio of switching rate to the slow growing state (k) and relative growth rate of fast growing state (λ₁−λ₂). For the toggle switch, the agreement is within a factor of 2.

So far, we have presented results for a highly simplified model with a very particular type of growth rate modulation. However, these qualitative results are generally expected whenever there is heterogeneity in the growth rate. As a test that the results are not dependent on the specific assumptions we have made, we also considered a more realistic model, in which the growth rate depends on the concentration p₁ through a Hill function. In that case, the toxicity of the protein P₁ is modulated by changing the threshold concentration (K_λ) of that Hill function. We also included a growth rate dependence of the protein synthesis rates (50) (see the Supporting Material for details). The results for this model are qualitatively the same as for the simplified model, as shown in Fig. S6. In particular, we observe again that growth heterogeneity (finite threshold K_λ) results in an increase of the slow growing (high p₁) subpopulation in the Mother Machine, but to an increase in the fast growing (low p₁) subpopulation in the Chemostat.

Another aspect of our current model that is highly simplified is the description of cell division as a Poissonian process. More detailed descriptions can be implemented within our method. As an example, we have used a Gaussian distribution of division times, without correlations between subsequent generations. Fig. S7 compares the results in the Chemostat scenario for the two descriptions of division and shows that the differences between them are very small in this case. In general, however, the mechanism of division can affect the results. For example, in a recent study, Hashimoto et al. (39) concluded that for a system with a monomodal distribution of growth rates, the measured population doubling time is smaller than the mean doubling time of the constituent single cells, indicating a dominance of the faster growing cells. This conclusion was reversed in another recent study by Lin and Amir (51) by including correlations between the division times of mother and daughter cells that result from the underlying size homeostasis mechanism. In that case, the population growth rate was found to be lower than the average growth rate of the cells rather than higher. In the bistable systems we consider here, however, the growth heterogeneity is dominated by the difference in growth rate between the phenotypes, which exceeds the more subtle growth heterogeneity due to stochastic cell division control and size homeostasis in the monostable systems discussed in (39, 51). As a result, the impact of the mechanism of division can be expected to be weaker than in those systems.

A bistable antibiotic-resistant system

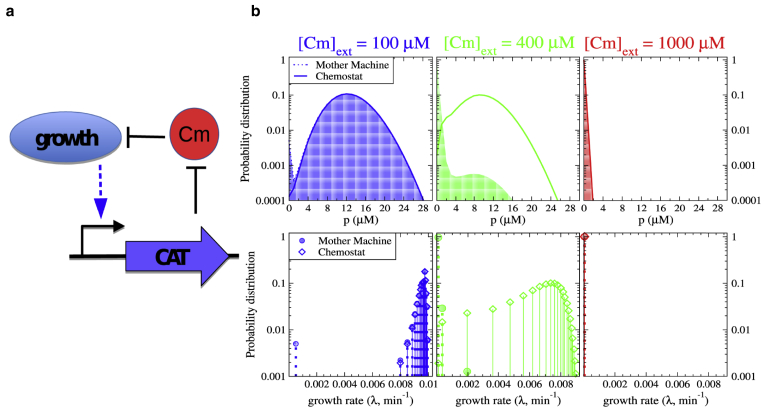
Next, we apply our approach to growth bistability in an antibiotic resistance circuit, which has been demonstrated recently (23): for translation-targeting antibiotics, a positive feedback results from the growth modulation by a resistance gene and the growth-rate-dependent expression of that resistance gene. Specifically, we consider the constitutive expression of chloramphenicol acetyltransferase (CAT), which modifies and deactivates the translation-targeting antibiotic chloramphenicol (Cm). Under growth modulation by translation-inhibiting antibiotics, constitutively expressed genes display a linearly increasing dependence of the concentration of their protein product on the growth rate (20). Increased expression of CAT results in a reduced intracellular concentration of Cm and thereby to an increased growth rate, establishing the positive feedback (Fig. 5 a) (see the Supporting Material for details of the model).

Figure 5.

Growth bistability in an antibiotic resistance circuit. (a) Given here is the schematic representation of the growth-modulating antibiotic resistance system. (b) Shown here is the distribution of concentration of the resistance protein CAT (top) and of the growth rates of cells (bottom), as obtained from Chemostat and Mother Machine simulations for three different antibiotic concentrations. The solid curves and the diamonds with solid dropdown lines are for the Chemostat and the shaded down-curves and the shaded circles with dotted dropdown lines are for the Mother Machine. For parameter values, see the Supporting Material. The sampling is done over 1000 cells and for 10⁶ time steps of 60 min each. To see this figure in color, go online.

In Fig. 5 b, we plot distributions of the CAT concentration and of the growth rate for three different extracellular antibiotic concentrations, as obtained from simulations with the Mother Machine and Chemostat setups. For the highest of the three Cm concentrations, all cells are slow growing; for the lowest concentration, (almost) all cells are fast growing. For the intermediate concentration, the circuit is bistable, with fast growing and slow growing subpopulations. In the two monomodal situations (high and low Cm concentrations), the two population setups result in almost the same distributions, in agreement with the general picture obtained for the toggle switch example discussed above. In the bistable regime (intermediate Cm concentration), however, we see again that the results are different for the two setups: the Mother Machine has more of the slower growing cells, whereas the Chemostat has more of the faster growing cells.

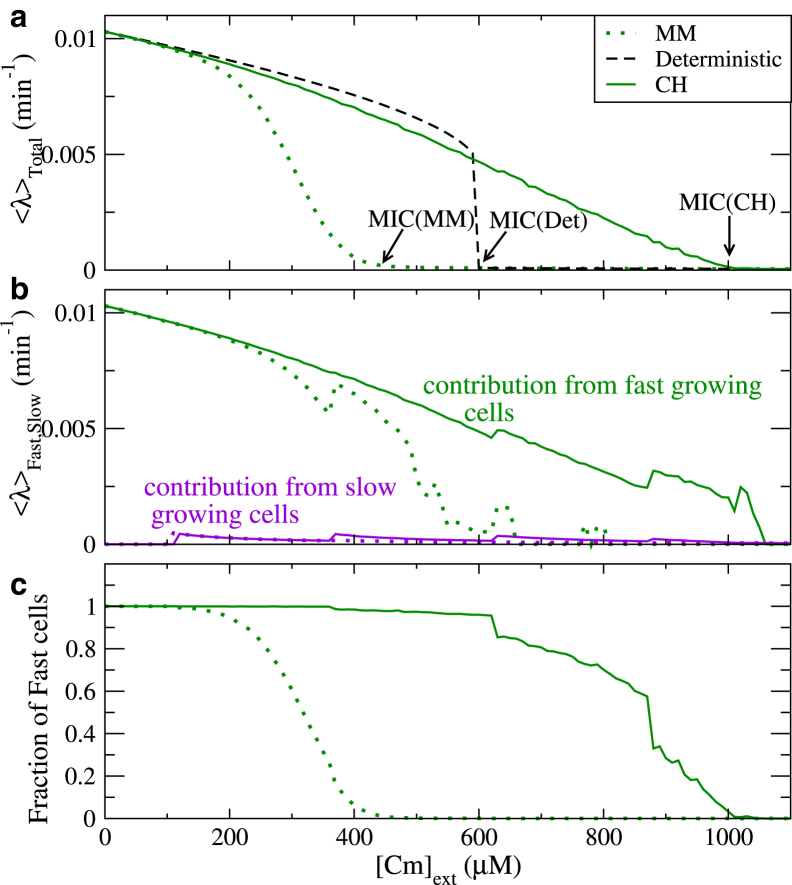
The impact of the growth setup on the population structure has an important consequence for the measurement of MIC. The MIC is often determined as the concentration, where the growth rate drops abruptly to a very low value. Because, in our model, the drop is gradual rather than abrupt, we determine an MIC as the antibiotic concentration, for which the growth rate drops below 2% of the growth rate in absence of the antibiotic. As can be seen in Fig. 6 a, the MICs obtained in the two scenarios differ substantially (1000 μM for the Chemostat simulations and 450 μM for the Mother Machine). This difference reflects again that the cells in the Mother Machine population preferentially stay in the more long-lived slow growing state, whereas in the Chemostat, fast growing cells will dominate the population, whenever some of them appear (Fig. 6 c).

Figure 6.

Dependence of the MIC on the population setup. (a) Shown here is the average growth rate of the population as a function of the (increasing) Cm concentration in the Chemostat (solid lines) and the Mother Machine (dotted lines). The dashed black line shows the corresponding result from the deterministic model. (b) Shown here are growth rate averages within the two subpopulations of fast growing (green) and slow growing cells (magenta). (c) Shown here are fractions of fast growing and slow growing cells in the two setups. Cells with λ > 0.0005 min⁻¹ are taken as fast cells (we note that the jumps in b and c arise when the discrete values of the growth rate cross this cutoff upon increase of the antibiotic concentration). The averaging is done over 10,000 cells and over 10 time steps of 30 min each, after equilibrating for 1000 min in the corresponding antibiotic concentration. To see this figure in color, go online.

Conversely, the measured MIC has been used to determine parameters of the circuit (23). In doing so, one will get different results based on which growth scenario is used in the simulation one fits the experimental data with, and care has to be taken to use the growth setup matching the experimental conditions.

Experimentally, MICs are usually measured in growing populations, either in batch cultures or petri dishes rather than in a system with a fixed number of cells. We emphasize that our Chemostat simulation is designed to reflect the properties of such a growing population, despite the fact that the number of cells is constant. To check this explicitly, we also simulated a population with a growing number of cells and determined growth rates from the growth curves. The results, including the resulting MIC, are in excellent agreement with the results from the Chemostat simulation (Fig. S8). We note that in the experiments of (23), the drop in growth rate at the MIC is sharper than in our simulations. This discrepancy is likely due to the stochastic description, possibly the relatively wide distribution of growth rates it generates (Fig. 5 b, bottom panel), as a sharp drop is also seen in the deterministic version of the same model (Fig. 6 a). However, because the dependence of the MIC on the population setup is a consequence of the different population statistics, this would also be seen in modifications of the stochastic description. We reiterate that the presence of growing cells above the MIC of the deterministic model is a result of fast growing cells replacing slow growing ones, rather than transient resistance due to stochastic gene expression (27).

Concluding remarks

In summary, we developed a computational formalism to simulate a set of reactions in a population of growing cells, implementing two types of experimental setups, the Mother Machine and the Chemostat. We also developed a modified version of Gillespie’s stochastic simulation algorithm, which is extremely efficient in simulating a set of reactions that are clustered, in our case, into the different cells. With the help of two test genetic circuits, a mutual repressor with growth reduction in one state and a bistable antibiotic-resistant system, we then showed how various measurable quantities can have the distinct signature of the experimental setup being studied. This was seen to be a result of the different subpopulation structures in the different setups whenever there is heterogeneity in growth, such as the growth bistability in the two cases we studied. Specifically, we showed for the resistance circuit that the MIC of the antibiotic may depend on the experimental setup.

We expect that our method, which may be extended to other population setups, will provide a basis for future studies of any genetic circuit where growth heterogeneity has the potential to modify the subpopulation structures. With the broad current interest in microbial communities, from single-species biofilms to the diversity of the microbiome, we expect that there will be many other applications for our approach.

Author Contributions

A.R. and S.K. designed the research. A.R. performed the research. A.R. and S.K. wrote the manuscript.

Editor: Nathalie Balaban.