Steady-State Differential Dose Response in Biological Systems

Abstract

In pharmacology and systems biology, it is a fundamental problem to determine how biological systems change their dose-response behavior upon perturbations. In particular, it is unclear how topologies, reactions, and parameters (differentially) affect the dose response. Because parameters are often unknown, systematic approaches should directly relate network structure and function. Here, we outline a procedure to compare general non-monotone dose-response curves and subsequently develop a comprehensive theory for differential dose responses of biochemical networks captured by non-equilibrium steady-state linear framework models. Although these models are amenable to analytical derivations of non-equilibrium steady states in principle, their size frequently increases (super) exponentially with model size. We extract general principles of differential responses based on a model’s graph structure and thereby alleviate the combinatorial explosion. This allows us, for example, to determine reactions that affect differential responses, to identify classes of networks with equivalent differential, and to reject hypothetical models reliably without needing to know parameter values. We exemplify such applications for models of insulin signaling.

Introduction

Dose-response curves are a classical tool for relating the dose of a biochemically active agent, such as a ligand, enzyme, drug, or toxicant, to its biochemical (e.g., receptor activation in a cell), physiological (concentration of a chemical in a body compartment), or even population-level (mortality) effect (1). Experimentally obtained dose-response curves frequently associate a given dose with its time-independent, steady-state effect and they often have a sigmoid shape when the dose is plotted in log scale (see Fig. 1). Their standard analysis aims to retrieve important characteristics such as the baseline and maximal responses as well as the dose that produces a response halfway between baseline and maximum as a measure of the agent’s potency, alternatively denoted as effective concentration $\left({\text{EC}}_{50}\right)$, inhibitory concentration $\left({\text{IC}}_{50}\right)$, or infectious dose $\left({\text{ID}}_{50}\right)$. Such measures allow one to analyze relative differences between a reference and a perturbed dose-response curve, which we call a “differential response” (or “differential” for short). One can, for example, compare how dose affects different system responses to find an optimal trade-off between therapeutic efficiency and toxicity via the therapeutic index (2). Natural systems also exploit differential responses. For example, insulin receptors recognize various natural ligands, such as insulin and insulin-like growth factor 1 (IGF-1), that have different binding affinities to the receptor to trigger appropriate differential (metabolic or mitogenic) responses (3).

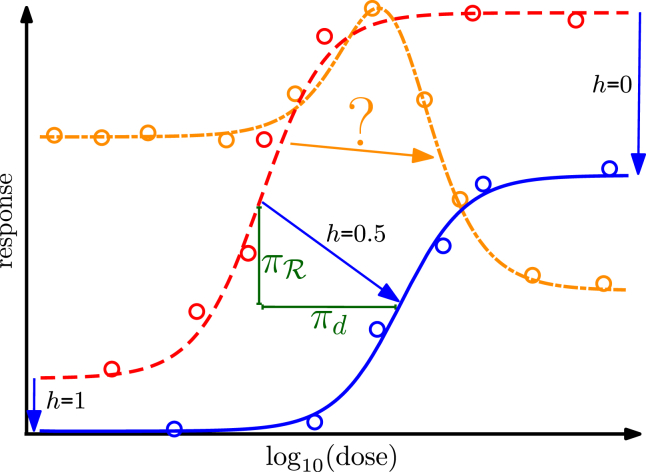
Figure 1.

Relations between sigmoid reference (red, dashed line), perturbed sigmoid (blue, solid line), and hormetic (orange, dash-dotted line) dose-response curves and hypothetical experimental data (circles) and fitted empirical models (lines). When perturbations preserve the shape of the dose-response curve (blue, solid line versus red, dashed line), the effect of a perturbation can be quantified by the shifts in baseline response and maximal response, and by the difference in the dose required for half-maximal response, as indicated by blue arrows. Analogously, we quantify the differential in the dose (${\pi }_d$, green) and the response $\left({\pi }_{\mathcal{R}}\right)$ components via the distance between points on a reference curve and points on a perturbed curve that have the same proportion of response between the minimum $\left(h=1\right)$ and maximum ($h=0$; correspondence indicated by blue arrows). As indicated by the question mark, such a quantification is not straightforward for dose-response curves with different shapes. To see this figure in color, go online.

More generally, it is often of interest to understand how perturbations such as mutations, drugs, or natural variations affect dose-response relations. Shifts in quantities such as the ${\text{EC}}_{50}$ easily capture the differential between sigmoid dose-response curves. However, biphasic dose-response curves with low-dose stimulation and high-dose inhibition, so-called hormetic curves, have received renewed attention (4, 5, 6), and non-monotonic dose-response curves with several peaks have been experimentally obtained (7). A recent study of drug responses in cancer cells illustrates that “non-standard” dose-response relations occur in substantial numbers: among 11,650 experimental dose-response curves, 28% were best described by a non-monotonic model, and 12% required two inflection points (6). However, it is unclear how to compare dose-response curves of (potentially) any shape with each other (see Fig. 1).

Like any perturbation experiment, differential analysis can probe the functioning of a biological system to identify the underlying mechanisms of the system’s (steady-state) behavior. However, relating the observed effects to biochemical mechanisms is a key open challenge. Mathematical models in dose-response analysis are frequently empirical (for data interpolation to estimate the characteristics described above), and not mechanistic in the sense of incorporating (hypothesized) relationships between biochemical entities that give rise to the experimental data. There exists no comprehensive mechanistic model-based theory to describe differential responses, despite their fundamental nature and importance in all fields of biology. This is not surprising: many relevant biological network models are non-linear and cannot be analyzed symbolically for non-trivial network sizes to derive design principles. Thus, the characterization of differential responses has to resort to numerical simulations that depend on often unknown network structures and parameter values. Current parameter-free methods such as chemical reaction network theory, which uses the network (model) structure to obtain a qualitative understanding of biological systems by determining their capabilities in terms of number of steady states (8, 9), are not directly applicable to differential responses, because we are interested in quantitative features (e.g., shifts in ${\text{EC}}_{50}$).

To tackle such limitations, and to extract general principles of biological systems, we concentrate on models in the graph-theoretical “linear framework” introduced in (10), which we call “linear framework models”. These models represent linear molecular-state transitions but can also explicitly account for certain non-linear kinetics (10). They can be interpreted as deterministic (linear ordinary differential equation (ODE), or linear algebraic for the steady state) or stochastic (master equations of Markov processes) models of biochemical systems (11). The “linear framework” has provided multiple promising applications (12, 13, 14) and it unifies results across many biological areas such as enzyme kinetics, G-protein-coupled receptors, and gene regulation (10). Importantly, the framework connects the symbolic derivation of steady-state expressions to combinatorial objects on graphs (10). This relation between network function and structure makes the framework appealing to analyze principles of differential responses.

Linear framework models result from demonstrated or, more frequently, assumed timescale separation, where a part of a biochemical system reaches a steady state because it operates much faster than the rest of the system (15). Dose-response analysis with mechanistic models, for instance in pharmacology, often assumes that the system is at thermodynamic equilibrium (1). There, the principle of detailed balance imposes structural (all reactions must be microscopically reversible) and parametric (the so-called “cycle condition”) constraints on linear framework models. It leads to simple “history-independent” equilibrium derivations that contain only products of equilibrium constants along any path in the model graph (10). However, for systems that dissipate energy, such as cell signaling pathways and eukaryotic gene regulation, this formalism does not apply. Energy dissipation keeps systems away from equilibrium, thus abolishing detailed balance. As a result, non-equilibrium steady states become “history dependent” and algebraically substantially more complex (14). A paramount challenge in working with non-equilibrium steady states of linear framework models symbolically is their frequently (super)exponentially growing size with model size—making even apparently “small” systems practically intractable.

Here, we develop a comprehensive theory and practically scalable computational methods for studying non-equilibrium steady-state differential dose-response relationships to pinpoint the mechanisms leading to experimentally observed behaviors. We extend the classic comparison of sigmoid dose-response curves and formally define a general notion of the differential. We then exploit connectivity properties of directed graphs representing linear framework models to address challenges such as determining the reactions that affect differential responses, identifying equivalence classes of networks according to their differential, and reliably rejecting hypothetical models without needing to know parameter values. Specifically, the theory helps determine which reactions take part in the differential and how perturbations such as variation of parameter values, deletions and additions of states and reactions affect the differential. In our approach, realistic practical applications are possible, because we do not actually need to derive complete steady-state expressions for quantitative and qualitative symbolic analysis. Our computationally efficient graph algorithms (16; unpublished data) yield compact, factorized steady-state expressions. We illustrate the application of the framework for insulin signaling, covering aspects such as model building and analysis, model rejection, experimental design, and (numerical) bounds on differential dose-response relations.

Materials and Methods

Linear framework models

We focus on the deterministic interpretation of linear framework models, that is, on biochemical reaction networks governed by Laplacian dynamics and modeled by systems of linear ODEs. Consider the example network in Fig. 2 A, in which all reactions follow first-order mass-action kinetics. It comprises three species and four reactions: a receptor, R, can transition to (from) its ligand-bound state, $\text{RL}$, with rate constant $r_1$ $\left(r_2\right)$, or the receptor can become irreversibly phosphorylated as $\text{RLp}$ with rate constant $r_3$, and $\text{RLp}$ can transition to R with rate constant $r_4$. This system is a simple model of insulin receptor activation, and its dynamics can be expressed as the ODE system

$$\frac{d}{dt}\left(\begin{array}{c}{x}_{\text{R}}\\ x_{\text{RL}}\\ x_{\text{RLp}}\end{array}\right)=\underset{\mathcal{L}}{\underbrace{\left(\begin{array}{ccc}-r_1& r_2& r_4\\ r_1& -\left(r_2+r_3\right)& 0\\ 0& r_3& -r_4\end{array}\right)}}\left(\begin{array}{c}{x}_{\text{R}}\\ x_{\text{RL}}\\ x_{\text{RLp}}\end{array}\right),$$ (1)

where x denotes the concentration of the respective species in the subscript and $\mathcal{L}$ is called the Laplacian matrix of the system.

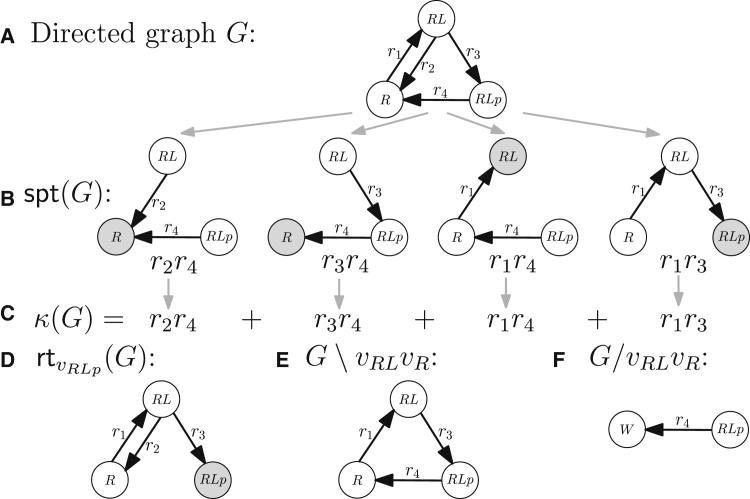
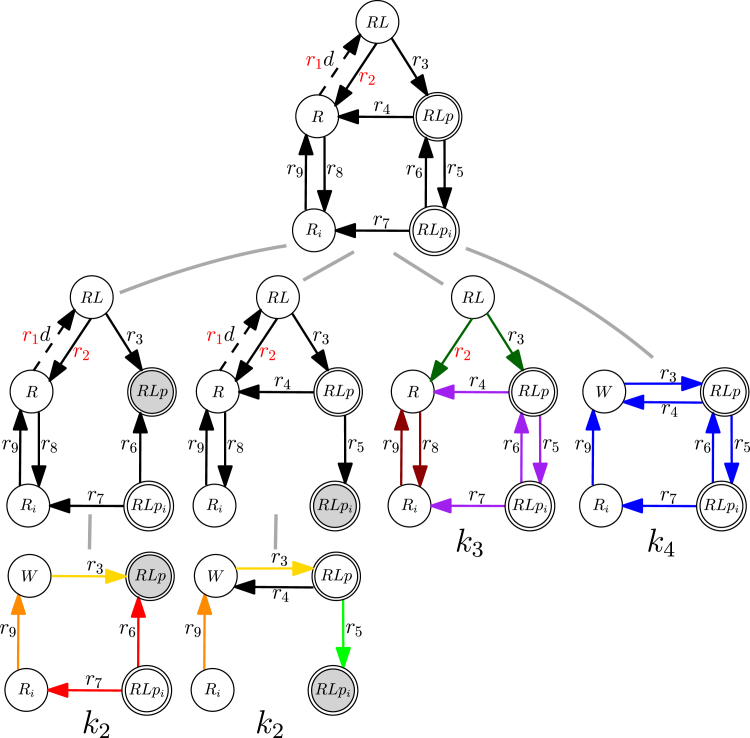
Figure 2.

Example model of insulin receptor activation. (A) Graph (kinetic scheme) G. (B) All spanning trees of graph G rooted at each vertex. (C) The corresponding Kirchhoff polynomial. (D) The graph obtained by rooting G at $v_{\text{RLp}}$. (E) The edge-deleted graph, $G⧹v_{\text{RL}}{v}_{\text{R}}$. (F) The edge-contracted graph, $G\text{/}{v}_{\text{RL}}{v}_{\text{R}}$. Labels on vertices denote names of species represented by them and W denotes a vertex obtained after the application of graph operations. Gray vertices are roots of the corresponding spanning tree and of all spanning trees when rooting a graph, respectively.

The dynamics of linear framework models can be represented as a diffusion process on directed graphs corresponding to their reaction schemes. Formally, a simple directed graph, $G=\left(V,E\right)$, consists of a set of vertices, $V\left(G\right)$, and a set of edges (ordered pairs of distinct vertices), $E\left(G\right)$; it has no self loops and no multiple parallel edges. For conciseness, we use “graph” as shorthand for “directed graph” throughout. Here, we concentrate on linear framework models of biological networks corresponding to “strongly connected” graphs, that is, graphs G in which, for any two distinct vertices $u,v\in V\left(G\right)$, there exists a directed path from u to v and from v to u. For example, the graph in Fig. 2 A is strongly connected (whereas the graph in Fig. 2 D is not). Strong connectivity is not a restrictive assumption for our theory, but rather mirrors the cell signaling models we consider. Note that non-strongly-connected graphs could emerge during the analysis procedures, but these are not linear framework models.

We consider the reaction scheme in Fig. 2 A as a labeled graph, G, with $V\left(G\right)=\left\{v_{\text{R}},v_{\text{RL}},v_{\text{RLp}}\right\}$, where v denotes the vertex corresponding to the species in the subscript, and $E\left(G\right)=\left\{v_{\text{R}}{v}_{\text{RL}},v_{\text{RL}}{v}_{\text{RLp}},v_{\text{RL}}{v}_{\text{R}},v_{\text{RLp}}{v}_{\text{R}}\right\}$. The reaction rate constants are labels of the corresponding edges in G. In such a labeled graph G, we can associate each vertex, $v_i\in V\left(G\right)$, to a non-negative species concentration $x_i$ and each edge to a mass-action reaction. Hence, we obtain a dynamical system in which species concentrations hosted on the vertices of G flow in the direction of the edges at rates proportional to the concentrations on the edges’ source vertices.

Proportionality of reaction rates is defined by edge labels, which have units of inverse time. We denote the label of an edge $uv\in E\left(G\right)$ by $\ell \left(uv\right)$. For example, $\ell \left(v_{\text{R}}{v}_{\text{RL}}\right)=r_1$. Edge labels can also host complex algebraic expressions of species concentrations and kinetic parameters. They can exactly account for non-linearities, for example, by containing concentrations of slow species resulting from timescale separation, provided that the uncoupling condition holds that prohibits concentrations corresponding to species from $V\left(G\right)$ in the edge labels (10). Note that here we mostly take the labels $\ell \left(e\right)$ as uninterpreted symbols, that is, we ignore the algebraic expressions to which they correspond and regard them as unique edge names. The only exceptions are edges affected by the dose (of a ligand), because we need explicit dose dependencies to determine differentials.

Linear framework models can be “closed,” not exchanging matter with the environment (as in the illustrative example), or “open,” when synthesis and degradation reactions are present. In general, the dynamics of closed models can be expressed in the form:

$$\frac{dx}{dt}=\mathcal{L}\left(G\right)x,$$ (2)

where $x={\left(x_1,\dots ,x_n\right)}^T$ is the vector of species concentrations corresponding to each vertex $v_1,\dots ,v_n\in V\left(G\right)$ and $\mathcal{L}\left(G\right)$ is the Laplacian matrix of G, defined as

$$\mathcal{L}{\left(G\right)}_{ij}=\{\begin{array}{cc}\ell \left(v_j{v}_i\right)& \text{if }i\ne j,\\ -{\sum }_{r\ne j}\ell \left(v_j{v}_r\right)& \text{if }i=j,\end{array}$$ (3)

and $\ell \left(v_j{v}_i\right)=0$ when $v_j{v}_i\notin E\left(G\right)$. In closed models, the total amount of material $x_t$ is conserved and there is a single conservation law, $x_1+\cdots +x_n=x_t$. The system reaches a unique stable steady state that can be derived symbolically for any species from $x_t$ and the kernel of the Laplacian matrix. Analogous definitions for open models can be found in the Supporting Material, and for more details, proofs, and derivations, see (10, 11, 17).

Spanning trees

Non-equilibrium steady states of linear framework models can always be derived in symbolic form, but, in practice, the length of the symbolic steady-state expressions grows (super) exponentially with the size of graph G. To cope with this growth, we introduce concepts intimately connected to both the structure of linear framework models and their steady states. Namely, a certain class of subgraphs, so-called “rooted directed spanning trees,” can be used to generate Kirchhoff polynomials (see next section).

Formally, a graph H is a subgraph of a graph G if $V\left(H\right)\subseteq V\left(G\right)$ and $E\left(H\right)\subseteq E\left(G\right)$, where every edge in G between vertices in H is also an edge in H. A strongly connected component (SCC) of G is any largest (w.r.t. vertex inclusion) strongly connected induced subgraph of G. It can be shown that no two distinct SCCs can share a vertex, and thus, the SCCs $G_1,\dots ,G_k$ of a graph G induce a unique partition, $V\left(G_1\right),\dots ,V\left(G_k\right)$ of $V\left(G\right)$. Additionally, for two distinct SCCs $G_i$ and $G_j$, there can be a directed path from $G_i$ to $G_j$, or from $G_j$ to $G_i$, but not both. The existence of such paths between SCCs naturally induces a unique partial order on the SCCs $G_1,\dots ,G_k$.

A rooted directed spanning tree (spanning tree, for short) A is a subgraph of G spanning its vertex set such that a root vertex is reachable from all vertices along a unique directed path. By $\mathsf{spt}\left(G\right)$ we denote the set of all spanning trees of G, and by $\mathsf{sp}{\mathsf{t}}_{\upsilon }\left(G\right)$ the set of all spanning trees rooted at vertex v. All spanning trees of the example graph are shown in Fig. 2 B: two spanning trees are rooted at $v_{\text{R}}$, one is rooted at $v_{\text{RL}}$, and another is rooted at $v_{\text{RLp}}$. Let $\mathsf{rt}$ be the graph rooting operation such that $\mathsf{r}{\mathsf{t}}_{\upsilon }\left(G\right)$ is the graph constructed from G by removing all edges outgoing from v (see Fig. 2 D). All spanning trees of $\mathsf{r}{\mathsf{t}}_{\upsilon }\left(G\right)$ are necessarily rooted at v. We will say that a graph G is rooted at a vertex v if v has no outgoing edges and v is reachable from every other vertex in G. Observe that $\mathsf{sp}{\mathsf{t}}_{\upsilon }\left(G\right)=\mathsf{spt}\left(\mathsf{r}{\mathsf{t}}_{\upsilon }\left(G\right)\right)$. Note also that a spanning tree of G exists iff the partial order of the SCCs has exactly one maximal element (no other SCC is reachable from a maximal SCC). Such an SCC is called a terminal SCC.

Kirchhoff polynomials and steady states of linear framework models

A spanning tree A of a graph G with n vertices has $n-1$ edges, $e_1,\dots ,e_{n-1}\in E\left(G\right)$ (for a concise notation, we denote edges with the symbol e when not referring to the pairs of vertices defining them). A spanning tree can also be represented as a monomial $\ell \left(e_1\right)\ell \left(e_2\right)\cdots \ell \left(e_{n-1}\right)$ in the edge labels $\ell \left(e_1\right),\ell \left(e_2\right),\dots ,\ell \left(e_{n-1}\right)$, when the edge labels are taken as uninterpreted symbols denoting unique edge names. Correspondingly, one can represent the set of all spanning trees in G by a homogeneous multivariate polynomial over the variables $\ell \left(e_i\right)$, $e_i\in E\left(G\right)$. This polynomial is called the Kirchhoff polynomial, $\kappa \left(G\right)$:

$$\kappa \left(G\right)=\sum _{A\in \mathsf{spt}\left(G\right)}\prod _{e_i\in E\left(A\right)}\ell \left(e_i\right).$$

The Kirchhoff polynomial of the example graph is shown in Fig. 2 C. Observe that if G is disconnected or has more than one terminal SCC, then $\kappa \left(G\right)=0$, and if G consists of a single vertex, then $\kappa \left(G\right)=1$.

Kirchhoff polynomials establish a direct connection between model structure, in terms of spanning trees, and function, in terms of steady-state expressions. Briefly, the steady state of a linear framework model can be symbolically obtained from initial conditions and the kernel of the Laplacian matrix by employing Tutte’s Matrix-Tree Theorem (18), which links the minors of the Laplacian matrix to the spanning trees in the model’s graph and their representation as Kirchhoff polynomials (see (10, 11, 17) for details and proofs).

Here, we are interested in the final results, namely that the steady-state concentration $x_i^{\text{SS}}$ of species i in a closed system associated to a vertex $v_i$ can be expressed as a fraction of Kirchhoff polynomials:

$$x_i^{\text{SS}}=\frac{{\kappa }_{v_i}\left(G\right)}{\kappa \left(G\right)}{x}_t,$$ (4)

where we denote the Kirchhoff polynomial of all spanning trees rooted at vertex v by ${\kappa }_v\left(G\right)$ $({\kappa }_v\left(G\right)$ is a shorter notation for $\kappa \left(\mathsf{r}{\mathsf{t}}_{\upsilon }\left(G\right)\right))$. Thus, the steady-state concentration of species $\text{RLp}$ associated to vertex $v_{\text{RLp}}$ in our example system is (see Fig. 2, B–D)

$$x_{\text{RLp}}^{\text{SS}}=\frac{{\kappa }_{v_{\text{RLp}}}\left(G\right)}{\kappa \left(G\right)}{x}_t=\frac{r_1{r}_3}{r_3{r}_4+r_2{r}_4+r_1{r}_4+r_1{r}_3}{x}_t.$$

Although these expressions look simple, the number of spanning trees in a graph G often grows (super) exponentially with the size of G (19). Symbolic steady-state expressions of linear framework models as expressed by Kirchhoff polynomials, therefore, face the problem of combinatorial explosion, which makes manipulation and generation of such expressions challenging.

Manipulation of Kirchhoff polynomials

The manipulation of combinatorially complex Kirchhoff polynomials is facilitated by establishing a relation between procedures for their algebraic simplification and operations on their corresponding graphs (unpublished data). Graph operations such as edge deletion-contraction and prime decomposition (16) allow a Kirchhoff polynomial to be written as a sum and a product, respectively, of other Kirchhoff polynomials without the need of explicit Kirchhoff polynomial generation.

For a graph G with $e\in E\left(G\right)$ and $v\in V\left(G\right)$ we denote edge deletion by $G⧹e$, i.e., the graph obtained from G by deleting e (see Fig. 2 E for an application to the example graph). Further, for a graph G and an edge $e=v_i{v}_j\in E\left(G\right)$, we denote by $G/e$ the edge-contracted graph that is constructed from G by 1) removing the edge $v_j{v}_i$, if it exists, and all outgoing edges from $v_i$, i.e., $v_{i}u\in E\left(G\right)$, and 2) fusing vertices $v_i$ and $v_j$ into a single new vertex, w (see Fig. 2 F). Edge contractions may yield graphs with multiple parallel edges between two vertices. We resolve this by replacing m multiple parallel directed edges $e_1,e_2,\dots ,e_{\text{m}}$ going from u to v with a single edge $e=uv$ such that $\ell \left(e\right)=\ell \left(e_1\right)+\ell \left(e_2\right)+\dots +\ell \left(e_{\text{m}}\right)$.

The classic deletion-contraction formula for an edge $e\in E\left(G\right)$ partitions $\mathsf{spt}\left(G\right)$ into two sets, one in which e participates in no spanning trees and one in which e participates in all spanning trees. Equivalently, it decomposes $\kappa \left(G\right)$ into a sum of Kirchhoff polynomials (20):

$$\kappa \left(G\right)=\kappa \left(G⧹e\right)+\ell \left(e\right)\kappa \left(G/e\right).$$ (5)

We call a Kirchhoff polynomial, P, a “factor” of another Kirchhoff polynomial, Q, if there exists a Kirchhoff polynomial R such that $Q=PR$. A Kirchhoff polynomial P that cannot be factorized into non-trivial factors is called “prime”. We extend these definitions to graphs by calling $G^{\mathit{\prime }}$ a component (a prime component) of G if $\kappa \left(G^{\mathit{\prime }}\right)$ is a factor (a prime factor) of $\kappa \left(G\right)$. The work in (16) provides graph decomposition rules that correspond to factorization steps of the Kirchhoff polynomial and also gives necessary and sufficient primality conditions of the resulting factors expressed by connectivity properties of the corresponding decomposed components. In particular, the exhaustive application of two decomposition rules to a graph G yields in linear time graphs whose Kirchhoff polynomials are prime factors of the Kirchhoff polynomial of the original G:

$$\kappa \left(G\right)=\prod _{i=1}^n\kappa \left(P_i\right),$$

where $P_i$ are the prime components of G. A prime component $P_i$ can be either 1) strongly connected or 2) rooted at v such that $P_i⧹v$ is strongly connected and $P_i$ does not have any non-trivial vertex dominators (using the definition that a vertex u dominates a vertex w if every path from w to v goes through u). Note that the prime factorization is conditional on label uniqueness—when the labels are not unique or contain expressions, the factorization is not guaranteed to be prime. This is why we regard edge labels as unique uninterpreted symbols when defining Kirchhoff polynomials on linear framework models. Further, we call an edge $e\in E\left(G\right)$ a “prime bridge” if the edge deleted graph $G⧹e$ has more non-trivial prime components than the original graph G. To efficiently manipulate and generate Kirchhoff polynomials we used the Python package KirchPy (unpublished data).

Results

Formalizing differential responses

Differentials describe how a perturbation transforms a reference dose-response curve. For monotone curves, we can simply quantify this transformation by the difference between points on the reference and the perturbed curve with identical percentage of response between baseline and maximum, such as the distance between $E{C}_{50}$ values. However, there exists no established approach for comparing dose-response curves of different functional form (sigmoid or multiphasic). Comparisons are particularly ambiguous when they involve non-monotone curves (see Fig. 1), but they are essential, because non-monotone curves have been experimentally observed and receive increasing attention (4, 7).

To provide a general formal procedure for comparison, let ${\mathcal{R}}^{\alpha }\left(d\right)$ and ${\mathcal{R}}^{\beta }\left(d\right)$ be the functions generating the reference and the perturbed dose-response curves, respectively. Here and in the following, the superscripts α and β denote the specific dissimilar (parametric and structural) features of the systems generating the two curves. Without explicitly specifying α or β, we refer to both identifiers at the same time. To quantify the differential, we propose the following procedure (see the Supporting Material for details):

• 1)Subdivide the curves into monotone segments. To obtain monotone segments, we subdivide the dose-response curves along the dose coordinate at their critical points, that is, at the doses for which $\mathcal{R}\left(d\right)$’s first derivative is zero.
• 2)Decide which segments to compare. If the curves have equal numbers of segments, it is reasonable to assume that the perturbation shifts and scales the segments such that they can be compared in the order defined by the critical points: the first segment of ${\mathcal{R}}^{\alpha }\left(d\right)$ maps to the first segment in ${\mathcal{R}}^{\beta }\left(d\right)$, and so on. When the perturbed curve has more or fewer segments than the reference curve, and without information about which segments fuse or split, we compare the segments in all possible ways while preserving their order. For example, comparing a sigmoid and a biphasic curve amounts to mapping the sigmoid to each of the two monotone segments of the biphasic curve.
• 3)Determine corresponding points in compared pairs of segments. As for monotone dose-response curves, we relate the doses that have the same proportion h, $h\in \left[\mathrm{0,1}\right]$, of response between the minimal and maximal response in each pair of segments.
• 4)Quantify the displacement of corresponding points. We quantify the displacement between points with identical proportion of response h for all pairs of mapped segments. In particular, we calculate the dose differential, ${\pi }_d\left(h\right)$, and the response differential, ${\pi }_{\mathcal{R}}\left(h\right)$, as the difference in the dose and the response components of corresponding points:

$${\pi }_d\left(h\right):={\text{log}}_{10}\frac{{\mathtt{d}}_h^{\alpha }}{{\mathtt{d}}_h^{\beta }}\text{and}{\pi }_{\mathcal{R}}\left(h\right):={\mathtt{R}}_h^{\alpha }-{\mathtt{R}}_h^{\beta },$$

with doses d and responses R. The dose differential is expressed in log scale to easily identify fold differences. These quantities have clear biological interpretations. For example, for corresponding segments, ${\pi }_d\left(h=0.5\right)$ is the difference between ${\text{EC}}_{50}$ log values and ${\pi }_d\left(h=0\right)$ is the difference between maximal responses.

Differentials cannot be obtained in closed form in general, but we will show next that one can often determine differentials analytically when functional relations between dose and response originate from steady-state expressions of linear framework models.

Differential systems

To derive general expressions for the dose $\left({\pi }_d\right)$ and response $\left({\pi }_{\mathcal{R}}\right)$ differentials, we need to define dose, response, and perturbation in linear framework models (see Materials and Methods for formal concepts), leading to the notion of differential linear framework models.

Here, we assume that the dose variable affects one or more reactions proportionally, which can be interpreted as an input changing the rate constant gradually, or as an input species with constant concentration binding to the educt of the reaction; for example, the effect of a ligand with constant external concentration that binds to a receptor incorporated in this way via the law of mass action. Formally, the input dose variable, d, partakes in the mathematical expressions labeling w edges in the model’s graph G, $I\left(G\right):=\left\{e_{d,1},\dots ,e_{d,w}\right\}$. We call members of the set $I\left(G\right)$ “dose edges” of G and their labels are expressions proportional to the input dose variable, d:

$$\ell \left(e_{d,i}\right)=g_i\left(p\right)d,$$

where $g_i\left(p\right)$ are functions that do not contain d (see Fig. 3 A for the insulin receptor example in which we assume that the dose affects receptor-ligand binding).

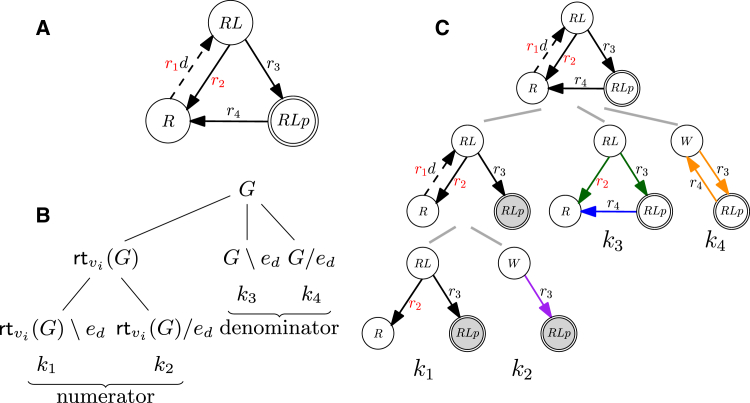
Figure 3.

Differential analysis for the simple insulin receptor activation model. (A) Graph for the differential system. The dose edge is marked by a dashed arrow, red symbols correspond to differential parameters (those with different values in the reference and perturbed model), and doubly encircled vertices mark the output vertices. (B) Tree scheme for a general graph G, showing how to obtain the relevant graphs participating in the coefficients $k_i$ of the dose-response relationship in closed systems (for reference and perturbed models through the graph operations rooting, deletion, and contraction). Note that there are also additional terms contained in the steady-state coefficients. (C) The tree scheme for decomposition of the insulin receptor activation model. Gray-shaded vertices denote that the graphs are rooted at them; different edge colors in the leaves of the tree mark the prime components (same color means same prime component also among different graph leaves), and black edges (when present) are not part of any prime component. To see this figure in color, go online.

In our analysis, the response $\mathcal{R}$ is a linear combination of the steady-state concentrations at chosen output vertices (such as the phosphorylated receptor-ligand complex, $\text{R}{\text{L}}_{\text{p}}$, in Fig. 3 A). The q species eliciting the response are associated with a set of output vertices $O\left(G\right):=\left\{v_1,\dots ,v_q\right\}$ in closed systems. Then, if we use Eq. 4 to derive a general expression for the steady-state response of closed models using Kirchhoff polynomials, $\kappa \left(G\right)$, we obtain

$${\mathcal{R}}_{O\left(G\right)}=\frac{{\sum }_{v_i\in O\left(G\right)}{a}_i{\kappa }_{v_i}\left(G\right)}{\kappa \left(G\right)}{x}_t,$$

where $a_i\ge 0$ designates the weight given to the steady-state concentration associated with vertex $v_i$. The response function for open models is similar (see the Supporting Material). This implies that steady-state dose-response curves of linear framework models are rational functions of the dose variable, for example, ${\mathcal{R}}_{O\left(G\right)}\left(d\right)$.

Perturbations are any changes in the model structure (additions and deletions of species and reactions), parameters (having different values in the reference and perturbed model; such parameters we call “differential parameters”), number and position of the edges affected by the input variable, number and position of the output vertices, and parametrization of the output function. We capture these perturbations by defining two linear framework models for a reference (α) and a perturbed (β) condition, each of which consists of a graph, G, a set of parameters, p (from G’s labels and $x_t$ for closed models), a set of dose edges, I (whose labels contain the dose variable, d), and a set of output vertices, O, the concentrations associated to which are weighted by a to obtain the observed response $\mathcal{R}$. Formally, a differential system is then an ordered pair, $\mathcal{D}=\left(\left(G^{\alpha },p^{\alpha },I^{\alpha },O^{\alpha },a^{\alpha }\right),\left(G^{\beta },p^{\beta },I^{\beta },O^{\beta },a^{\beta }\right)\right)$.

We use our example insulin receptor model from Fig. 2 A to define a first differential system, $\mathcal{D}$ (Fig. 3 A). Let the receptor, R, transition to its ligand-bound state, RL, upon activation by a ligand with constant concentration d. We account for the dose variable d in the transition rate by changing the label of edge $v_{\text{R}}{v}_{\text{RL}}$ to $r_{1}d$. To construct a differential Laplacian system, we consider a reference model with graph topology as the example graph, G, dose edge $e_d=v_{\text{R}}{v}_{\text{RL}}$, i.e., $I=\left\{e_d\right\}$ with $\ell \left(e_d\right)=r_{1}d$, a single output vertex, $O=\left\{v_{\text{RLp}}\right\}$, weighted by 1, and parameters $p=\left\{r_1,r_2,r_3,r_4,x_t\right\}$. The perturbed model is identical to the reference one, with the exception of the values of parameters $r_1$ and $r_2$, which we will denote as $r_1^{\alpha }$, $r_2^{\alpha }$ ($r_1^{\beta }$ and $r_2^{\beta }$) in the reference (perturbed) system. These differential parameters correspond to stimulation of the system with two different ligands that have different affinities to the receptor R, such as insulin and IGF-1. Since reference and perturbed model are identical except for their differential parameters, we can illustrate the differential system by a single graph and highlight the differential parameters as shown in Fig. 3 A.

Symbolic derivation of the differential and its properties

For tractability, we are first interested in deriving analytical expressions for the differential of systems with a constant input that influences exactly one edge proportionally in both reference and perturbed models, $(I\left(G\right)=\left\{e_d\right\}$ and $\ell \left(e_d\right)=g\left(p\right)d)$, to model, for example, a ligand binding once to a receptor.

To express the steady-state response, $\mathcal{R}$, explicitly as a function of the dose variable, d, we apply the deletion-contraction property from Eq. 5 to partition the set of spanning trees from the numerator and denominator of the corresponding rational function into two categories—those that contain the dose d in one of their labels and those that do not. This is equivalent to factoring out the edge labels from the monomials in the corresponding Kirchhoff polynomial that contain the dose variable d. After simplification, we obtain the general form of dose-response expressions for models with a graph G:

$${\mathcal{R}}_O\left(d\right)=\frac{k_1+k_{2}d}{k_3+k_{4}d},$$ (6)

where for closed models (see the Supporting Material for open models),

$$\begin{array}{l}{k}_1=x_t\sum _{v_i\in O\left(G\right)}{a}_{v_i}{\kappa }_{v_i}\left(G\setminus e_d\right),\\ k_2=x_{t}g\left(p\right)\sum _{v_i\in O\left(G\right)}{a}_{v_i}{\kappa }_{v_i}\left(G/e_d\right),\\ k_3=\kappa \left(G\setminus e_d\right),\\ k_4=g\left(p\right)\kappa \left(G/e_d\right).\end{array}$$

We call the $k_i$ terms “steady-state coefficients,” although they are symbolic expressions involving parameters and Kirchhoff polynomials of specific graphs obtained from G. The coefficients k might be zero if spanning trees do not exist in the respective graphs.

How to obtain the relevant graphs participating in the coefficients for closed models can be seen in the tree scheme from Fig. 3 B (see the tree scheme for open models in Fig. S1), and an application to the example differential system can be found in Fig. 3 C. With only one edge containing the dose d, the numerator and denominator are at most first degree in d, and thus, the tree schemes in Fig. 3, B and C, have four leaves. Note that the tree scheme is the same for the reference and perturbed systems, except for the differential parameters. The coefficients for the example are $k_1=x_t\kappa$(rt_RLp(G)\e_d), $k_2=x_t{r}_1\kappa$(rt_RLp(G)/e_d), $k_3=\kappa$(G\e_d), and $k_4=r_1\kappa \left(G/e_d\right)$. By generating the Kirchhoff polynomials in the respective graphs, we obtain

$$k_1=0,k_2=x_t{r}_1{r}_3,k_3=r_4\left(r_2+r_3\right),\text{and }{k}_4=r_1\left(r_3+r_4\right).$$

Following the procedure for deriving the differential expressions ${\pi }_d$ and ${\pi }_{\mathcal{R}}$ (for details, see the Supporting Material), we obtain

$${\pi }_d={\text{log}}_{10}\frac{k_3^{\alpha }{k}_4^{\beta }}{k_3^{\beta }{k}_4^{\alpha }}\text{and}{\pi }_{\mathcal{R}}\left(h\right)=h\left(\frac{k_1^{\alpha }}{k_3^{\alpha }}-\frac{k_1^{\beta }}{k_3^{\beta }}\right)+\left(1-h\right)\left(\frac{k_2^{\alpha }}{k_4^{\alpha }}-\frac{k_2^{\beta }}{k_4^{\beta }}\right).$$ (7)

When either $k_1$ or $k_2$ is zero, the response differential ${\pi }_{\mathcal{R}}$ has a simpler form but the dose differential ${\pi }_d$ is not affected. The differential can be degenerate, e.g., when $\mathcal{R}\left(d\right)$ is always zero, implying that $k_1=k_2=0$, or undefined, e.g., when $\mathcal{R}\left(d\right)$ is either constant or unbounded, leading to $k_3=0$ or $k_4=0$.

The dose differential ${\pi }_d$ in Eq. 7 depends not on h, $k_1$, and $k_2$ but on the Kirchhoff polynomials contained in the coefficients $k_3$ and $k_4$. It is therefore independent of the choice of output vertices in O, of the vertex weights, a, and of the total conserved amount, $x_t$, in closed systems (the synthesis reactions, $s_i$, in open systems) for the reference and perturbed models. The dose differential can be simplified to the logarithm of an irreducible fraction by obtaining the prime factorizations of the numerator and denominator and dividing them by the greatest common divisor, $\text{gcd}\left(k_3^{\alpha }{k}_4^{\beta },k_3^{\beta }{k}_4^{\alpha }\right)$. Then, the necessary and sufficient condition for a reaction to participate in ${\pi }_d$ is to be part of a prime component of the relevant graphs that is different in the reference and perturbed models, and not the same in the dose-edge-deleted and dose-edge-contracted graphs of the same condition. To illustrate these points, consider ${\pi }_d$ for closed differential systems:

$${\pi }_d={\text{log}}_{10}\frac{\kappa \left(G^{\alpha }\setminus e_d^{\alpha }\right)g^{\beta }\left(p^{\beta }\right)\kappa \left(G^{\beta }/e_d^{\beta }\right)}{\kappa \left(G^{\beta }\setminus e_d^{\beta }\right)g^{\alpha }\left(p^{\alpha }\right)\kappa \left(G^{\alpha }/e_d^{\alpha }\right)}.$$

The polynomials $\kappa$(G\e_d) are factorizable if and only if $e_d$ is a prime bridge. Edge contraction for $\kappa \left(G/e_d\right)$ could also lead to a factorizable Kirchhoff polynomial if any of the deleted edges during the procedure is a prime bridge. The factor $g\left(p\right)$ we assume to be prime as part of the label of a single edge. Overall, thus, whether the dose differential is reducible depends exclusively on the perturbation, the connectivity of the dose edge, $e_d$ (in $G^{\alpha }$ and $G^{\beta }$), and the connectivity of the edges in the immediate neighborhood of e_d. Note that the reducibility characterization of ${\pi }_d$ for open differential systems is analogous but includes an additional dependency on the location and connectivity of the synthesis edges in $G^{\alpha }$ and $G^{\beta }$.

The response differential, ${\pi }_{\mathcal{R}}$, in Eq. 7 is a sum of ratios dependent on all coefficients $k_i$ and includes the conserved $x_t$ in each ratio for closed systems, the synthesis reactions in open systems, and the mapping variable h. However, it does not depend on the dose-edge label function, $g\left(p\right)$, because $g\left(p\right)$ always cancels in the fraction $k_2/k_4$ (for both reference and perturbed coefficients). To illustrate, let us focus on the response differential, ${\pi }_{\mathcal{R}}$ (see Eq. 7), for closed systems when $h=0$. To simplify the expression, first, the common factors between $k_2$ and $k_4$ are canceled (keeping in mind that $k_2$ is a linear combination of prime factorized Kirchhoff polynomials) to obtain $\overline{k_2}$ and $\overline{k_4}$. The response differential can be further reduced if $\text{gcd}\left({\overline{k_4}}^{\alpha },{\overline{k_4}}^{\beta }\right)\ne 1$ by combining the fractions under a common denominator. Note that the response differential could be zero due to the minus sign. The characterization of the response differential in the general case for h not fixed and for open systems is analogous.

For the example differential system, we find that ${\pi }_d={\text{log}}_{10}\left(r_1^{\beta }/r_1^{\alpha }\right)\left(r_2^{\alpha }+r_3)/(r_2^{\beta }+r_3\right)$ and ${\pi }_{\mathcal{R}}=0,$ where the response component of the differential vanishes because $k_1=0$ and because the differential parameters $r_1$ in $k_2$ and $k_4$ cancel each other. Also, the dose differential is independent of the rate constant $r_4$.The example illustrates that by deriving the general form of the differentials ${\pi }_d$ and ${\pi }_{\mathcal{R}}$, which are algebraic expressions of Kirchhoff polynomials in linear framework models, we establish a direct connection between the structure of the differential system and its function.

Analyzing the insulin receptor life-cycle

Insulin signaling in response to various ligands determines differential cellular responses through complex and incompletely understood mechanisms (3, 21). To unravel the processes at play, it is important to comprehend the role of reactions and species in the observed cellular functions. To illustrate applicability of our theory to such an investigation, we extend the example insulin model stepwise to a model incorporating insulin receptor binding, recycling, and phosphorylation. The resulting model is a subsystem of a more comprehensive insulin receptor signaling model from (22). This subsystem is appropriate for our analysis, because it is a linear framework model, it is away from equilibrium since receptor recycling and phosphorylation dissipate energy (as indicated by irreversible reactions), and the steady state of phosphorylated insulin receptors determines insulin signal transduction (23).

Here, we do not explicitly consider the molecular details of all reactions of this model but adopt a more general structural analysis approach by equating each reaction rate constant to a unique symbol. Specifically, we take the reaction rate constants $r_4$, $r_7$, and $r_{16}$ (see Fig. 6 A) as unique symbols, although they actually depend on the concentration of protein tyrosine phosphatase (PTP) and are thus coupled. This still allows us to analyze the role of each reaction in the differential, but it precludes algebraic simplifications for the concentration of PTP; if more molecular details are of interest, they have to be explicitly included. Again, we define the differential system by assuming that the reference and the perturbed model differ only in the values of a subset of parameters—the differential parameters corresponding to ligands with different affinity toward the insulin receptor—and that all other elements are identical.

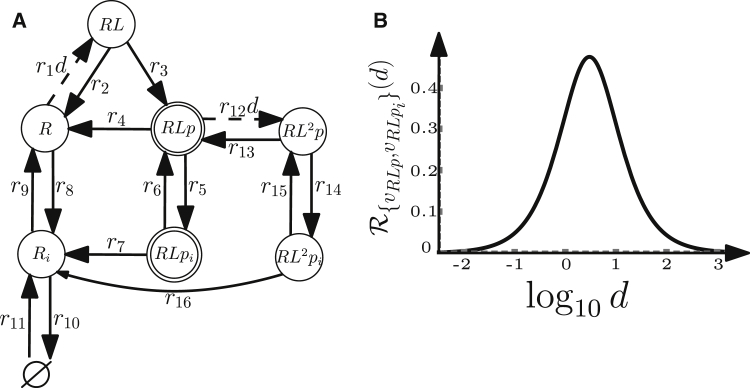
Figure 6.

Extended insulin model with two dose edges. (A) Model of insulin receptor binding, recycling, and phosphorylation with notation as in Fig. 3A. (B) A hormetic dose-response curve generated by the model for output vertices $O=\left\{v_{\text{RLp}},v_{\text{RLpi}}\right\}$ and all parameters fixed to 0.5.

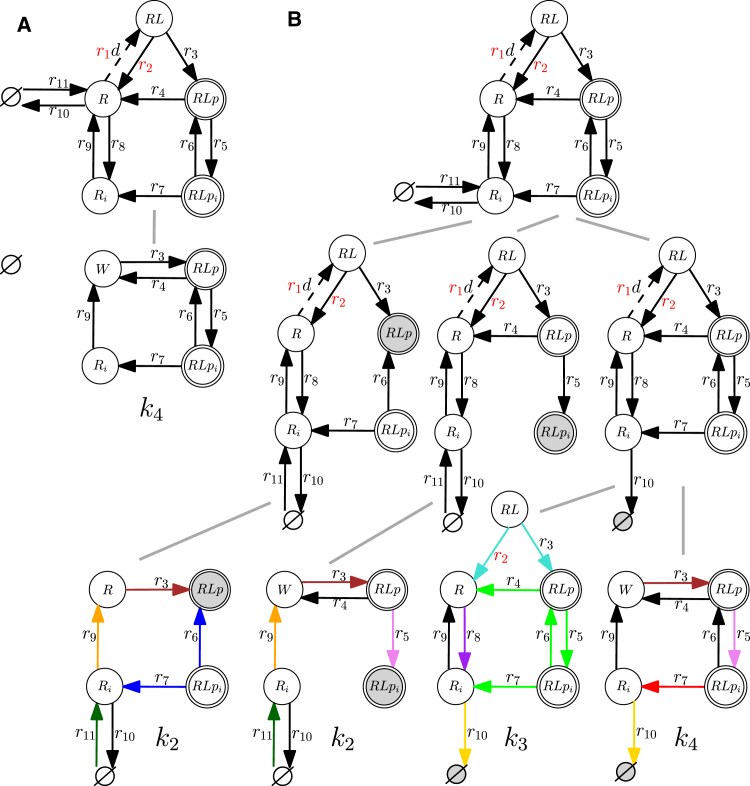
We extend the example model (Fig. 2) with two states, an internalized phosphorylated ligand-bound receptor, ${\text{RL}}_{\text{pi}}$, and an internalized receptor, ${\text{R}}_{\text{i}}$ (Fig. 4). These states can be reached by reversible reactions from their non-internalized (membrane) counterparts, $\text{RLp}$ and R, to represent endocytosis and receptor recycling, and ${\text{RLp}}_{\text{i}}$ can be dephosphorylated to R by an irreversible reaction. We regard the phosphorylated ligand-bound receptors as output species, such that $O\left(G\right)=\left\{v_{\text{RLp}},v_{\text{RLpi}}\right\}$, with unit weights $\left(a_{\text{RLp}}=a_{{\text{RLp}}_{\text{i}}}=1\right)$.

Figure 4.

Tree scheme for the differential system in Fig. 3 extended with internalized species ${\text{RLp}}_{\text{i}}$ and ${\text{R}}_{\text{i}}$. Note that only graphs belonging to non-zero coefficients are shown. To see this figure in color, go online.

The resulting differential system is what we call a “basic signaling system.” It is a differential system with a closed graph that contains a reversible reaction for which the forward and reverse rates differ between the reference and perturbed model, and for which the forward rate is affected by the dose variable, d. More precisely, we have a graph G with $I\left(G\right)=\left\{e_{\text{on}}\right\}$, $\ell \left(e_{\text{on}}\right)=g_{\text{on}}\left(p\right)d$, and $\ell \left(e_{\text{off}}\right)=g_{\text{off}}\left(p\right)$. Also, the reference and perturbed models have no structural differences; they differ only by the functions $g_{\text{on}}\left(p\right)$ and $g_{\text{off}}\left(p\right)$ (and the parameters contained in them). In such basic signaling models, the dose-edge-contracted graph $G/e_{\text{on}}$ is the same for the reference and perturbed systems; therefore, its Kirchhoff polynomial always cancels in the dose-differential fraction. The dose differential for closed systems (results and definitions are analogous for open systems) is

$${\pi }_d={\text{log}}_{10}\frac{\kappa \left(G^{\alpha }\setminus e_{\text{on}}\right)}{\kappa \left(G^{\beta }\setminus e_{\text{on}}\right)}\frac{g_{\text{on}}^{\beta }\left(p^{\beta }\right)}{g_{\text{on}}^{\alpha }\left(p^{\alpha }\right)}.$$

The response component of the differential for $h=0$ will always be zero under the stated assumptions, since $\left(k_2^{\alpha }/k_4^{\alpha }\right)=\left(k_2^{\beta }/k_4^{\beta }\right)$. When $h=1$, the response component is not affected by the assumptions for basic signaling systems.

Although the graph of the extended system contains more states and reactions and the steady-state expression is more complicated (see the Supporting Material), the differential is identical to that of our initial example without endocytosis, because the newly added reactions take part in prime components that do not contain differential parameters and therefore cancel out (see Fig. 4). We can formally describe such differential systems giving rise to identical differential expressions by employing the mathematical concept of “equivalence classes.” Let $\mathfrak{D}$ be a set of differential systems and define the equivalence relation, ${\sim }_{\pi }$, on $\mathfrak{D}$ such that ${\mathcal{D}}_1{\sim }_{\pi }{\mathcal{D}}_2$, ${\mathcal{D}}_1,{\mathcal{D}}_2\in \mathfrak{D}$, iff ${\pi }_d\left({\mathcal{D}}_1\right)={\pi }_d\left({\mathcal{D}}_2\right)$ and ${\pi }_{\mathcal{R}}\left({\mathcal{D}}_1\right)={\pi }_{\mathcal{R}}\left({\mathcal{D}}_2\right)$. Thus, the initial and extended models of insulin signaling belong to the same equivalence class with respect to their differential. The concept of equivalence classes has direct applications for model selection and experimental design. For example, assume that we have experimental evidence that changes in the rate constant of a reaction such as $r_4$, in both the reference and perturbed models, affect the dose differential. If this reaction does not take part in the dose-differential expression of the equivalence class of models we are studying (as for the equivalence class for insulin signaling defined above), we can directly reject all members of the equivalence class, because they are incompatible with the experimental observation. Similarly, we can use the analytic framework to answer questions such as what second perturbation to design (or how to change the first perturbation) to differentiate between models in the same equivalence class (see the Supporting Material).

Next, to analyze long-term effects of insulin receptor trafficking, we need to account for receptor synthesis and degradation. This converts the model from a closed system to an open system. Let us consider a model extension in which the non-internalized free receptor, R, is synthesized and degraded. Then, however, the differential is not defined because the steady-state coefficient $k_4$ is zero. Fig. 5 A shows that the contraction of the dose edge eliminates the degradation edge $e_{r_{10}}$ and, additionally, that the rooting at the environment vertex $v_{\varnothing }$ eliminates the synthesis edge $e_{r_{11}}$; this results in a disconnected graph with no spanning trees in $k_4$. Hence, we can reject this extension just based on structural considerations. We therefore add synthesis and degradation reactions for $R_i$ as a more biologically plausible way to capture receptor trafficking (Fig. 5 B). The steady-state expression changes in this case (see the Supporting Material), but the differential is still identical to that of the initial example model from Fig. 2; the extended model belongs to the same equivalence class due to cancellation of prime factors that do not contain differential parameters in both reference and perturbed models (see Fig. 5 B). Overall, our structural analysis predicts that differential responses for ligands with different affinities always exhibit a zero response differential and a dose differential dependent on the ligand affinities. This result is corroborated by the observation that most natural and modified insulin receptor ligands shift sigmoid dose-response curves leftward or rightward (relative to insulin) but have an identical maximal response (24).

Figure 5.

Extended insulin model with receptor degradation (open system). (A) The dose and response differential for the system with synthesis and degradation of membrane-bound receptor R (for reference and perturbed graph) is not defined, since the steady-state coefficient $k_4=0$ (the contained graph is disconnected and therefore does not contain any spanning trees). (B) Tree scheme for a differential system containing synthesis and degradation of the internalized receptor, ${\text{R}}_{\text{i}}$. Graphs without spanning trees are not shown. To see this figure in color, go online.

Extension: two dose edges

To extend the framework to cases in which hormesis is possible, we consider that the input dose acts proportionally and simultaneously on two edges, i.e., $I\left(G\right)=\left\{e_{d,1},e_{d,2}\right\}$, $\ell \left(e_{d,1}\right)=g_1\left(p\right)d$, and $\ell \left(e_{d,2}\right)=g_2\left(p\right)d$. To derive the general form of dose-response expressions for closed and open systems, we apply the deletion-contraction formula to partition the set of spanning trees from the numerator and denominator of the response function, $\mathcal{R}$, into four categories—those containing no input edges, those containing $e_{d,1}$ but not $e_{d,2}$, those containing $e_{d,2}$ but not $e_{d,1}$, and those containing both $e_{d,1}$ and $e_{d,2}$. After simplification, we obtain

$${\mathcal{R}}_O\left(d\right)=\frac{k_1+k_{23}d+k_4{d}^2}{k_5+k_{67}d+k_8{d}^2},$$ (8)

where $k_{23}:=k_2+k_3$ and $k_{67}:=k_6+k_7$ (see the Supporting Material for all details). For two dose edges, the numerator and denominator polynomials in the dose d can be at most of degree two; for an input acting on w edges simultaneously, the maximal degree is w. However, the spanning tree partitioning determines the graphs contained in the coefficients k (see, for definitions, the tree scheme in Fig. S3). The exponential increase of the number of relevant graphs with number of dose edges ($2^w$ graphs) makes systems with multiple inputs complex.

Depending on the coefficients $k_i$, two or three critical points define a sigmoid or a biphasic/hormetic dose-response relationship, respectively. A necessary and sufficient condition for a biphasic dose-response function, which we call the “Hormesis condition,” is

$$\left(k_{67}=0\wedge k_{23}\ne 0\right)\vee \left(k_{67}\ne 0\wedge \left(\frac{k_{23}}{k_{67}}<\frac{k_4}{k_8}\le \frac{k_1}{k_5}\vee \frac{k_{23}}{k_{67}}<\frac{k_1}{k_5}<\frac{k_4}{k_8}\vee \frac{k_4}{k_8}\le \frac{k_1}{k_5}<\frac{k_{23}}{k_{67}}\vee \frac{k_1}{k_5}<\frac{k_4}{k_8}<\frac{k_{23}}{k_{67}}\right)\right).$$

Because the values of the coefficients $k_i$ are not known in general, the number of critical points cannot be determined unambiguously, and we need to distinguish cases depending on the number of segments in the reference and perturbed curves that are mapped to each other to derive the differential ${\pi }_d$ and ${\pi }_{\mathcal{R}}$ (see the Supporting Material for details).

The differential expressions have a more complicated form (for example, they may involve square roots), and multiple conditions have to be considered, but the expressions are symbolic and (more involved) symbolic analysis with efficient methods for the generation and manipulation of Kirchhoff polynomials is applicable. For example, general properties of the differentials in systems with two dose edges are 1) in contrast to systems with a single dose edge, the dose differential, ${\pi }_d$, depends on the choice of output vertices and their weights; 2) ${\pi }_d$ depends on the proportion variable, h, and the synthesis reactions in open systems, but not on the conserved $x_t$ in closed systems; 3) the response differential, ${\pi }_{\mathcal{R}}$, depends on all eight partitions of the set of spanning trees of G, and it includes $x_t$ in closed systems; and 4) the differential can also be degenerate or undefined.

To apply the theory to insulin signaling, we consider a more detailed model for receptor trafficking that includes binding of a second ligand molecule to the receptor, as well as the relevant reactions and internalized species shown in Fig. 6 A. It is a receptor-level subsystem of the more comprehensive model of insulin signaling from (22). The motivation for the analysis is twofold. First, designed insulin analogs that trigger hormetic responses could potentially influence insulin differential signaling, for example, by alleviating mitogenic effects at high ligand doses. Second, biphasic dose-response behaviors of insulin receptor phosphorylation were experimentally observed in cells stimulated with an insulin analog, the peptide S961 (24). We therefore asked if there exist sets of species that need to be active to achieve a robust hormetic response in the model. We derived the steady-state coefficients for all 127 combinations of output vertices in O and used the hormesis condition to classify the resulting models into four groups. The first three groups contain models with robust dose-responses (same qualitative shape irrespective of parameter values), namely, 1) constant response for models with output vertex $\left\{v_{\text{Ri}}\right\}$; 2) sigmoid for models with output vertices $\left\{v_{\text{RLLp}}\right\}$, $\left\{v_{\text{RLLpi}}\right\}$, and $\left\{v_{\text{RLLp}},v_{\text{RLLpi}}\right\}$; and 3) hormetic for models with output vertices $\left\{v_{\text{RLp}}\right\}$, $\left\{v_{\text{RLpi}}\right\}$, and $\left\{v_{\text{RLp}},v_{\text{RLpi}}\right\}$ (see Fig. 6 B). The fourth group contains the remaining 120 combinations of output vertices; the shapes of dose-response curves generated by these models depend on parameter values (see the Supporting Material for examples of analysis results that account for parameter dependencies). In particular, outputs producing robust hormetic responses comprise only phosphorylated receptors bound to a single ligand molecule, implying that doubly bound phosphorylated receptors should not signal if we are to obtain a robust hormetic dose response. This is consistent with the proposed mechanism of action of S961 in (24), namely, that the first binding of S961 cross-links the receptor, leading to agonist activity, and the second binding results in receptor inactivation.

Extension: numerical analysis

Numerical methods can augment the symbolic analysis when quantitative prior knowledge or experimental data are available. For example, we can directly incorporate known parameter values (or their ratios) to simplify symbolic expressions. We may also account for prior knowledge by defining plausible intervals of parameter values and determining whether the model’s thus bounded differential is consistent with an experimentally observed differential, thereby assessing whether the model agrees with the observations.

Formally, we denote the range of the differential as the interval $\mathbb{D}=\{\pi (p^{\alpha },p^{\beta })\in \mathbb{R}|p^{\alpha },p^{\beta }\in \mathcal{I}\}$, where $\mathcal{I}\subseteq {\left({\mathbb{R}}_{\ge 0}\right)}^N$ is a box in parameter space. Let a and b be the infimum and supremum of $\mathbb{D}$. We want to determine tight outer bounds of the differential, finding $\hat{a}$ and $\hat{b}$ of $\mathbb{D}$ over the parameter box $\mathcal{I}$, where $\hat{a}\le a$ and $\hat{b}\ge b$. In systems with a single dose edge, with edge labels that contain rational expressions, and regarding all parameters as variables, bounding the differential translates to finding the global extrema of a multivariate rational function. This is an NP-hard problem (25), but several numerical methods give certificates for global optimality or find bounds based on polynomial optimization. Here, we focus on Bernstein enclosures of rational functions (26) whose implementation in the Kodiak package, for example, was shown to produce tighter outer bounds for a dose differential expression with 12 free variables compared to the established method of interval arithmetic (27).

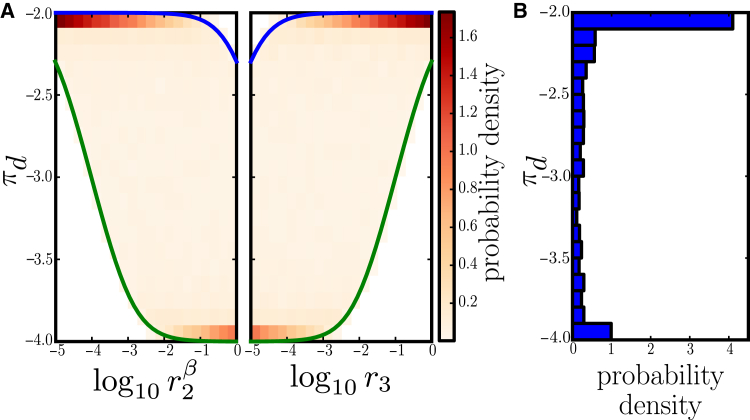
To illustrate the approach for the example model from Fig. 3 A (for a two-dose-edge example, see the Supporting Material), we analyze how the bounds of the dose differential change when a parameter is altered; we call the resulting plots “profile differential bounds”. Specifically, we fix each of the free parameters taking part in the differential, $r_2^{\beta }$ and $r_3$, for every value in their interval of definition, and calculate the bounds of the dose differential (Fig. 7 A). This analysis shows the capacity of individual parameters to control and constrain the possible magnitude of the differential: independent of the value of the other free parameter, $r_2^{\beta }$ can significantly change the lower bound of the differential for values smaller than ∼${10}^{-2}$, and for higher values it starts decreasing the upper bound. If the observed differential is outside the calculated bounds, one can reliably reject the model (and the parameter box $\mathcal{I}$), because no parametrization (in $\mathcal{I}$) can reproduce the observed differential. Conversely, this analysis can help confine $\mathcal{I}$ such that all considered parameter values are consistent with the experimental observations.

Figure 7.

Numerical analysis of the example single-dose-edge model from Fig. 3A. (A) Profile bounds (blue, upper outer bound; green, lower outer bound) superimposed on the profile differential distribution (density) for the free parameters $r_2^{\beta }$ and $r_3$. (B) Marginal probability distribution of the dose differential magnitude. Densities were obtained from uniform samples of the parameter box $\mathcal{I}$ defined by $r_1,r_2,r_3,r_4\in \left[{10}^{-5},1\right]s^{-1}$, assuming $x_t=1\text{nM}$, $r_1^{\alpha }/r_1^{\beta }=100$, and $r_2^{\alpha }/r_2^{\beta }=0.01$. To see this figure in color, go online.

The non-linear differential expressions’ algebraic structures also imply that not every differential value is equally likely when we sample parameter values uniformly from $\mathcal{I}$. The non-uniformity of the differential can be interpreted as parametric robustness, because random changes of parameters may not lead to random magnitudes of the differential. For our simple model from Fig. 3 A, uniform sampling of the dose differential yields a few magnitudes of variability $\left(\widehat{{\mathbb{D}}_{{\pi }_d}}=\left[-4,-2\right]\right)$ but two small regions of most probable values with a marginal density peaked at $-2$ and $-4$ (Fig. 7 B). The profile differential distributions in Fig. 7 A show how the free parameters $r_2^{\beta }$ (ligand dissociation rate in the perturbed model) and $r_3$ (receptor phosphorylation) affect not only the bounds but also the peak of the marginal distribution, revealing their potential to control the differential. Hence, the differential system induces an important structural prior on the behavior—system structures (and parameter intervals) define what magnitude of the differential can be expected. This information could be exploited for more detailed model selection against experimental data.

Discussion

Here, we aimed to develop a theory for steady-state dose-response relationships in linear framework models of biochemical reaction networks that is analytic, and therefore also applicable when parameter values are largely unknown. We formalized the concept of differential responses to establish a comprehensive parameter-free framework for analyzing relative responses. It helps to study system behaviors upon perturbations of many features of reaction networks, such as network topology, parameters, and choice and number of inputs and outputs. In particular, the algebraic and numerical methods allow us to explore possible network topologies and perturbations to arrive efficiently at a set of candidate models that are consistent with prior knowledge and experimental data. For example, if it is known from experiments that a particular perturbation leads to a significant dose differential, we can reliably reject all potential models for which the differential expression does not depend on the perturbed variable. Numerical bounding over a predefined region in parameter space provides us with limits for all possible differential magnitudes—which we can use as a certificate to reliably reject models that can never reproduce quantitative experimental data. Another application of our methodology is in experimental design, namely, to determine (optimal) perturbations of a reference system that lead to a desired differential, to invalidate a model, to discriminate between equivalence classes of networks, or for applications such as finding optimal (combinations of) drug targets. Note also that the differential analysis framework extends to applications beyond the ones we covered: in general, every element of the differential system can be perturbed and labels for dose edges can be formulated in a more general form.

The most obvious limitation of our framework is the restriction to systems with Laplacian dynamics; it has to rely on prior, often parameter- and state-dependent simplifications from higher-order kinetics, such as those obtained via timescale separation. In terms of scalability, the exponential growth of the number of graphs to be considered for the analysis and the resulting high-degree polynomials with increasing number of reactions influenced by the dose is a challenge. Our examples demonstrate that systems with up to two dose edges can be analyzed efficiently due to the linear scaling of the prime factorization algorithm and the few relevant graphs. General algebraic solutions for the roots of polynomial equations of degree five or higher with arbitrary coefficients—corresponding to the dose acting proportionally on five or more edges—do not exist. However, depending on the particular graph structure and form of the label expressions, such cases, or cases with labels that are non-linear functions of the dose, could be analytically tractable if the polynomials simplify to a lower degree. Similarly, obtaining exact bounds might only be feasible for simple differential expressions with few variables and convex properties. In practice, therefore, bounding methods provide us with inner bounds, which do not guarantee reliable model rejection. Because bounding approaches are often employed in control theory (28) and methods are being continuously improved (27, 29), these limitations may be less pertinent.

Extensions of the framework could further build on the central insight that prime factors and components (and their similarity in perturbed graphs) are the units, the very characterization, of the differential response function in steady-state linear framework models. For example, additions and deletions of vertices and edges in certain parts of both the reference and perturbed graph may never have an effect on the differential if they belong to a prime component that always cancels in the differential expression. In general, the positions (connectivity) of additions and deletions within the graph and the size distribution of the induced prime components play an important role in the change of the differential upon structural perturbations. This could be exploited to develop a notion of “structural robustness” of the differential to random changes of the network topology. Finally, many of our graph theoretical notions subsume graph theoretical concepts such as distributions of sizes of SCCs, strong bridges, and strong articulation points that are actively researched in computer science; efficient algorithms for their characterization (30, 31, 32, 33, 34) could help to extend the scope of our framework.

In terms of applications, our analysis of the insulin signaling network demonstrates first steps in a direction we believe will become increasingly important: a systematic analysis of differential dose responses in biochemical reaction networks despite prevailing uncertainties as to the networks’ quantitative features. In particular, we showed how to characterize the dose responses of natural ligands, such as insulin and IGF-1, where different affinities influence the dose but not the maximal response component, and we recovered previously hypothesized modes of action of the insulin analog S961. We envisage that our framework will be most useful for the systematic study of mechanisms underlying hormesis, a phenomenon in toxicology and cell signaling that is receiving increasing attention. For example, empirical evidence favored hormetic over threshold models for dose-response relationships in a large-scale yeast anticancer drug screen (35), and hormetic phenomena are frequently observed in stress responses and their relations to aging (36). Corresponding theoretical work has only (re-)started very recently, showing, for example, that non-monotonic dose-response relationships can arise through non-obvious pathway interactions, and that network structures impose fundamental constraints on options for pharmacological treatment (37).

Author Contributions

P.Y. and J.S. designed research, P.Y. performed research, and P.Y. and J.S. wrote the manuscript.

Editor: Stanislav Shvartsman.