NON-LOCAL PRIORS FOR HIGH-DIMENSIONAL ESTIMATION

Abstract

Jointly achieving parsimony and good predictive power in high dimensions is a main challenge in statistics. Non-local priors (NLPs) possess appealing properties for model choice, but their use for estimation has not been studied in detail. We show that for regular models NLP-based Bayesian model averaging (BMA) shrink spurious parameters either at fast polynomial or quasi-exponential rates as the sample size n increases, while non-spurious parameter estimates are not shrunk. We extend some results to linear models with dimension p growing with n. Coupled with our theoretical investigations, we outline the constructive representation of NLPs as mixtures of truncated distributions that enables simple posterior sampling and extending NLPs beyond previous proposals. Our results show notable high-dimensional estimation for linear models with p ≫ n at low computational cost. NLPs provided lower estimation error than benchmark and hyper-g priors, SCAD and LASSO in simulations, and in gene expression data achieved higher cross-validated R² with less predictors. Remarkably, these results were obtained without pre-screening variables. Our findings contribute to the debate of whether different priors should be used for estimation and model selection, showing that selection priors may actually be desirable for high-dimensional estimation.

1. Introduction

Developing high-dimensional methods to balance parsimony and predictive power is a main challenge in statistics. Non-local priors (NLPs) are appealing for Bayesian model selection. Relative to local priors (LPs), NLPs discard spurious covariates faster as the sample size n grows, but preserve exponential rates to detect non-zero coefficients (Johnson and Rossell, 2010). When combined with Bayesian model averaging (BMA), this regularization has important consequences for estimation.

Denote the observations by ${\mathbf{y}}_n\in {\mathcal{Y}}_n$, where ${\mathcal{Y}}_n$ is the sample space. We entertain a collection of models M_k for k = 1, …, K with densities f_k(y_n | θ_k, ϕ_k), where θ_k ∈ Θ_k ⊆ Θ are parameters of interest and ϕ_k ∈ Φ is a fixed-dimension nuisance parameter. Let p_k = dim(Θ_k) and without loss of generality let M_K be the full model within which M₁, …, M_K−1 are nested (Θ_k ⊂ Θ_K = Θ). To ease notation let (θ, ϕ) = (θ_K, ϕ_K) ∈ Θ×Φ be the parameters under M_K and p = p_K = dim(Θ). A prior density π(θ_k | M_k) for θ_k ∈ Θ_k under M_k is a NLP if it converges to 0 as θ_k approaches any value θ₀ consistent with a sub-model M_k′ (and a LP otherwise).

Definition 1

Let θ_k ∈ Θ_k, an absolutely continuous measure with density π(θ_k | M_k) is a non-local prior if $\underset{{\mathit{\theta }}_k\to {\mathit{\theta }}_0}{\lim }\pi ({\mathit{\theta }}_k|M_k)=0$ for any θ₀ ∈ Θ_k, ⊂ Θ_k, k′ ≠ k.

For precision we assume that intersections Θ_k ∩ Θ_k′ have 0 Lebesgue measure and are included in some M_k″, k^″ ∈ {1, …, K}. As an example consider a Normal linear model y_n ~ N(X_nθ, ϕI) where X_n is an n × p matrix with p predictors, θ ∈ Θ = ℝ^p and ϕ ∈ Φ = ℝ⁺. As we do not know which columns in X_n truly predict y_n we consider K = 2^p models by setting elements in θ to 0, i.e. f_k(y_n | θ_k, ϕ_k) = N(y_n; X_k,nθ_k, ϕ_kI) where X_k,n is a subset of columns of X_n. We develop our analysis considering the following NLPs

$${\pi }_M(\mathit{\theta }|{\varphi }_k,M_k)={\displaystyle \prod _{i\in M_k}\frac{{\theta }_i^2}{\tau {\varphi }_k}}N({\theta }_i;0,\tau {\varphi }_k)$$ (1)

$${\pi }_I(\mathit{\theta }|{\varphi }_k,M_k)={\displaystyle \prod _{i\in M_k}\frac{{(\tau {\varphi }_k)}^{\frac{1}{2}}}{\sqrt{\pi }{\theta }_i^2}}\exp \left\{-\frac{\tau {\varphi }_k}{{\theta }_i^2}\right\}$$ (2)

$${\pi }_E(\mathit{\theta }|{\varphi }_k,M_k)={\displaystyle \prod _{i\in M_k}\exp \left\{\sqrt{2}-\frac{\tau {\varphi }_k}{{\theta }_i^2}\right\}N({\theta }_i;0,\tau {\varphi }_k)},$$ (3)

where i ∈ M_k are the non-zero coefficients and π_M, π_I and π_E are called the product MOM, iMOM and eMOM priors (pMOM, piMOM and peMOM).

A motivation for considering K models is to learn which parameters are truly needed to improve estimation. Consider the usual BMA estimate

$$E(\mathit{\theta }|{\mathbf{y}}_n)={\displaystyle \sum _{k=1}^{K}E(\mathit{\theta }|M_k,{\mathbf{y}}_n)P(M_k|{\mathbf{y}}_n)}$$ (4)

where P (M_k | y_n) ∝ m_k(y_n)P (M_k) and m_k(y_n) = ∫ ∫ f_k(y_n | θ_k, ϕ_k)π(θ | ϕ_k, M_k)π(ϕ_k | M_k)dθ_kdϕ_k is the integrated likelihood under M_k. BMA shrinks estimates by assigning small P (M_k | y_n) to unnecessarily complex models. The intuition is that NLPs assign even smaller weights. Let M_t be the smallest model such that f_t(y_n | θ_t, ϕ_t) minimizes Kullback-Leibler divergence (KL) to the data-generating density f*(y_n) amongst all (θ, ϕ) ∈ Θ × Φ. For instance, in Normal linear regression this means minimizing the expected quadratic error E((y_n − X_nθ)′(y_n − X_nθ)) with respect to f*(y_n) (which may not be a linear model and include X_n when it is random). Under regular models with fixed P (M_k) and p, if π(θ_k | M_k) is a LP and M_t ⊂ M_k then $P(M_k|{\mathbf{y}}_n)=O_p(n^{-\frac{1}{2}(p_k-p_t)})$ (Dawid, 1999). Models with spurious parameters are hence regularized at a slow polynomial rate, which we shall see implies E(θ_i | y_n) = O_p(n⁻¹)r (Section 2), where r depends on model prior probabilities. Any LP can be transformed into a NLP to achieve faster shrinkage, e.g. E(θ_i | y_n) = O_p(n⁻²)r (pMOM) or $E({\theta }_i|{\mathbf{y}}_n)=O_p(e^{-\sqrt{n}})r$ (peMOM, piMOM). We note that another strategy is to shrink via r, e.g. Castillo and Van der Vaart (2012) and Castillo et al. (2014) show that P (M_k) decreasing fast enough with p_k achieve good posterior concentration. Martin and Walker (2013) propose a related empirical Bayes strategy. Yet another option is to consider the single model M_K and specify absolutely continuous shrinkage priors that induce posterior concentration (Bhattacharya et al., 2012). For a related review on penalized-likelihood strategies see Fan and Lv (2010).

In contrast our strategy is based upon faster m_k(y_n) rates, a data-dependent quantity. For Normal linear models with bounded P (M_k)/P (M_t) Johnson and Rossell (2012) and Shin et al. (2015) showed that when p = O(n^α) or $p=O(e^{n^{\alpha }})$ (respectively) with α < 1 and certain regularity conditions pertain one obtains $P(M_t|{\mathbf{y}}_n)\stackrel{P}{\to }1$ when using certain NLPs and to 0 when using any LP, which from (4) implies the strong oracle property $E(\mathit{\theta }|{\mathbf{y}}_n)\stackrel{P}{\to }E(\mathit{\theta }|{\mathbf{y}}_n,M_t)$. We note that when sparse unbounded P (M_k)/P (M_t) are used, consistency of P (M_t | y_n) may still be achieved with LPs, e.g. setting prior inclusion probabilities $O(p_K^{-\gamma })$ for γ > 0 as in Liang et al. (2013) or Narisetty and He (2014).

Our main contribution is considering parameter estimation under NLPs, as previous work focused on model selection. We characterize complexity penalties and BMA shrinkage for certain linear and asymptotically Normal models (Section 2). We also provide a fully general NLP representation from latent truncations (Section 3) that justifies NLPs intuitively and adds flexibility in prior choice. Suppose we wish to both estimate θ ∈ ℝ and test M₁ : θ = 0 vs. M₂ : θ ≠ 0. Figure 1 (grey) shows a Cauchy(0, 0.25) prior expressing confidence that θ is close to 0, e.g. P (|θ| > 0.25) = 0.5. Under this prior P (θ = 0 | y_n) = 0 and hence there is no BMA shrinkage. Instead we set P (θ = 0) = 0.5 and, conditional on θ ≠ 0, a Cauchy(0,0.25) truncated to exclude (−λ, λ), where λ is a practical significance threshold (Figure 1(top)). Truncated priors have been discussed before, e.g. Verdinelli and Wasserman (1996), Rousseau (2007). They encourage coherence between estimation and testing, but they cannot detect small but non-zero coefficients. Suppose that we set λ ~ G(2.5, 10) to express our uncertainty about λ. Figure 1 (bottom) shows the marginal prior on θ after integrating out λ. It is a smooth version of the truncated Cauchy that goes to 0 as θ → 0, i.e. a NLP. Section 4 exploits this construction for posterior sampling. Finally, Section 5 studies finite-sample performance in simulations and gene expression data, in particular finding that BMA achieves lower quadratic error than the posterior modes used in Johnson and Rossell (2012).

Figure 1.

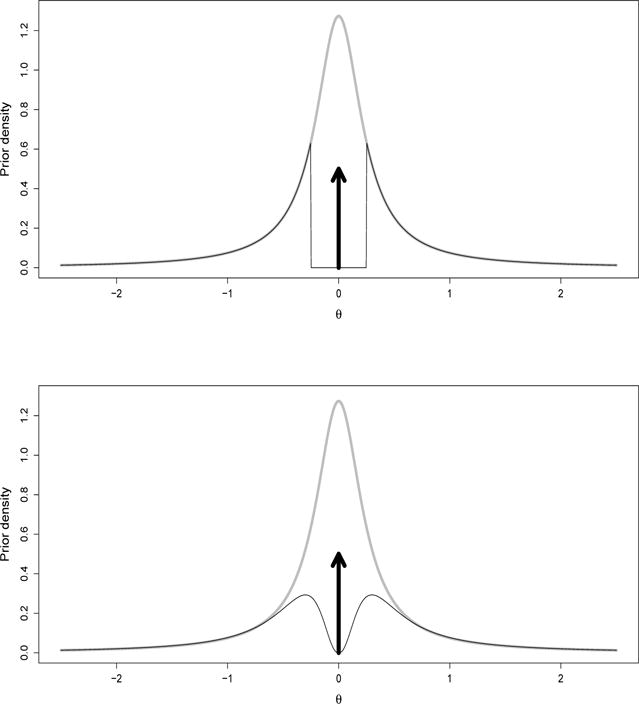
Marginal priors for θ ∈ ℝ (estimation prior Cauchy(0, 0.0625) shown in grey). Top: mixture of point mass at 0 and Cauchy(0, 0.0625) truncated at λ = 0.25; Bottom: same as top with λ ~ IG(3, 10)

2. Data-dependent shrinkage

We now show that NLPs induce a strong data-dependent shrinkage. To see why, note that any NLP can be written as π(θ_k, ϕ_k | M_k) ∝ d_k(θ_k, ϕ_k)π^L(θ_k, ϕ_k | M_k), where d_k(θ_k, ϕ_k) → 0 as θ_k → θ₀ for any θ₀ ∈ Θ_k′ ⊂ Θ_k and π^L(θ_k, ϕ_k) is LP. NLPs are often expressed in this form but the representation is always possible since $\pi ({\mathit{\theta }}_k,{\varphi }_k|M_k)=\frac{\pi ({\mathit{\theta }}_k,{\varphi }_k|M_k)}{{\pi }^L({\mathit{\theta }}_k,{\varphi }_k|M_k)}{\pi }^L({\mathit{\theta }}_k,{\varphi }_k|M_k)=d_k({\mathit{\theta }}_k,{\varphi }_k){\pi }^L({\mathit{\theta }}_k,{\varphi }_k|M_k)$. Intuitively, d_k(θ_k, ϕ_k) adds a penalty term that improves both selection and shrinkage via (4). The theorems below make the intuition rigorous. Proposition 1 shows that NLPs modify the marginal likelihood by a data-dependent term that converges to 0 for certain models containing spurious parameters. The result does not provide precise rates, but shows that under very general situations NLPs improve Bayesian regularization. Proposition 2 gives rates for posterior means and modes under a given M_k for finite p asymptotically Normal models and growing p linear models, whereas gives Proposition 3 Bayes factor and BMA rates.

We first discuss the needed regularity assumptions. Throughout we assume that π(θ_k, ϕ_k | M_k) is proper, π(ϕ_k | M_k) is continuous and bounded for all ϕ_k ∈ Φ, denote by m_k(y_n) the integrated likelihood under π(θ_k | ϕ_k, M_k) = d_k(θ_k, ϕ_k)π^L(θ_k, ϕ_k) and by $m_k^L({\mathbf{y}}_n)={\displaystyle \iint f_k({\mathbf{y}}_n|{\mathit{\theta }}_k,{\varphi }_k)}{\pi }^L({\mathit{\theta }}_k,{\varphi }_k|M_k)d{\mathit{\theta }}_{k}d{\varphi }_k$ that under the corresponding LP. Assumptions A1–A5, B1–B4 are from Walker (1969) (W69, Supplementary Section 1) and guarantee asymptotic MLE normality and validity of second order log-likelihood expansions, e.g. including generalized linear models with finite p. A second set of assumptions for finite p models follows.

Conditions on finite-dimensional models

• C1
  Let A ⊂ Θ_k × Φ be such that $f_k({\mathbf{y}}_n|{\mathit{\theta }}_k^{\ast },{\varphi }_k^{\ast })$ for any $({\mathit{\theta }}_k^{\ast },{\varphi }_k^{\ast })\in A$ minimizes KL to f*(y_n). For any $({\stackrel{\sim }{\mathit{\theta }}}_k,{\stackrel{\sim }{\varphi }}_k)\notin A$ as n → ∞

  $$\frac{f_k({\mathbf{y}}_n|{\mathit{\theta }}_k^{\ast },{\varphi }_k^{\ast })}{f_k({\mathbf{y}}_n|{\stackrel{\sim }{\mathit{\theta }}}_k,{\stackrel{\sim }{\varphi }}_k)}\stackrel{\mathrm{a}.\mathrm{s}.}{\to }\mathrm{\infty }.$$
• C2Let ${\pi }_{k,\tau }^L({\mathit{\theta }}_k,{\varphi }_k)=N(\mathbf{0};\tau {\varphi }_{k}I)$. The ratio of marginal likelihoods $m_{k,\tau (1+\epsilon )}^L({\mathbf{y}}_n)/m_{k,\tau }^L({\mathbf{y}}_n)\stackrel{\mathrm{a}.\mathrm{s}.}{\to }c\in (0,\mathrm{\infty })$ as n → ∞, ε ∈ (0, 1).
• C3Let (θ*, ϕ*) minimize KL(f*(y_n), f_K(θ, ϕ) for (θ, ϕ) ∈ (Θ, Φ). There is a unique M_t with smallest p_t such that $f_t({\mathbf{y}}_n|{\mathit{\theta }}_t^{\ast },{\varphi }_t^{\ast })=f_K({\mathbf{y}}_n|{\mathit{\theta }}^{\ast },{\varphi }^{\ast })$ and $\text{KL}(f_t({\mathbf{y}}_n|{\mathit{\theta }}_t^{\ast },{\varphi }_t^{\ast }),f_k({\mathbf{y}}_n|{\mathit{\theta }}_k,{\varphi }_k))>0$, for any k such that M_k ⊄ M_t.
• C4In C3 ϕ* is fixed and ${\theta }_i^{\ast }={\theta }_{0i}^{\ast }{a}_n$ for fixed ${\theta }_{0i}^{\ast }$ where either a_n = 1 or $\underset{n\to \mathrm{\infty }}{\lim }{a}_n=0$ with a_n ≫ n^−1/2 (pMOM) or a_n ≫ n^−1/4 (peMOM, piMOM).

C1 essentially gives MLE consistency and C2 a boundedness condition that guarantees $P({\mathit{\theta }}_k\in N(A)|{\mathbf{y}}_n.M_k)\stackrel{P}{\to }1$ under a pMOM for a certain neighbourhood N(A) of the KL-optimal parameter values, the key to ensure that d_k(θ_k, ϕ_k) acts as a penalty term. Redner (1981) gives general conditions for C1 that include even certain non-identifiable models. C2 is equivalent to the ratio of posterior densities under τ and τ(1 + ε) at an arbitrary (θ_k, ϕ_k) and converging to a constant, which holds under W69 or Conditions D1–D2 below (see proof of Proposition 1 for details). C3 assumes a unique smallest model $f_t({\mathbf{y}}_n|{\mathit{\theta }}_t^{\ast },{\varphi }_t^{\ast })$ minimizing KL to f*(y_n) and that there is no equivalent model M_k ⊅ M_t, e.g. for linear models no M_k ⊅ M_t can have p_k = p_t variables being perfectly collinear with X_t,n. C4 allows θ* to be either fixed or to vanishes at rates slower than n^−1/2 (pMOM) or n^−1/4 (peMOM, piMOM), to characterize the ability to estimate small signals. Finally, for linear models we consider the following.

Conditions on linear models of growing dimension

• D1Suppose f_k(y_n | θ_k, ϕ_k) = N(y_n; X_k,nθ_k, ϕ_kI), θ_k ∈ Θ_k, p_k = dim(θ_k) = O(n^α) and α < 1.
• D2There are fixed a, b, n₀ > 0 such that $a<\frac{1}{n}{l}_1\left(X_{k,n}^{\prime }{X}_{k,n}\right)<\frac{1}{n}{l}_k\left(X_{k,n}^{\prime }{X}_{k,n}\right)<b$ for all n > n₀, where l₁, l_k are the smallest and largest eigenvalues of $X_{k,n}^{\prime }{X}_{k,n}$.

D1 reflects the common practice that although p ≫ n one does not consider models with p_k ≥ n, which lead to data interpolation. D2 guarantees strong MLE consistency (Lai et al., 1979) and implies that no considered model has perfectly collinear covariates, aligning with applied practice. For further discussion on eigenvalues see Chen and Chen (2008) and Narisetty and He (2014). We now state our first result. All proofs are in the Supplementary Material.

Proposition 1

Let m_k(y_n), $m_k^L({\mathbf{y}}_n)$ be as above.

1. We have: $m_k({\mathbf{y}}_n)=m_k^L({\mathbf{y}}_n)g_k({\mathbf{y}}_n)$, where

   $$g_k({\mathbf{y}}_n)={\displaystyle \iint d_k({\mathit{\theta }}_k,{\varphi }_k)}{\pi }^L({\mathit{\theta }}_k,{\varphi }_k|{\mathbf{y}}_n)d{\mathit{\theta }}_{k}d{\varphi }_k$$
2. Assume f_k(y_n | θ_k, ϕ_k) with finite p_k satisfies C1 under a peMOM or piMOM prior or C2 under a pMOM prior for some A. If $A=\{({\mathit{\theta }}_k^{\ast },{\varphi }_k^{\ast })\}$ is a singleton (identifiable models), then $g_k({\mathbf{y}}_n)\stackrel{P}{\to }{d}_k({\mathit{\theta }}_k^{\ast },{\varphi }_k^{\ast })$. For any A, if

   $$f^{\ast }({\mathbf{y}}_n)=f_t({\mathbf{y}}_n|{\mathit{\theta }}_t^{\ast },{\varphi }_t^{\ast })$$

   for some t ∈ {1, …, K}, then $g_k({\mathbf{y}}_n)\stackrel{P}{\to }0$ when M_t ⊂ M_k, k ≠ t and

   $$g_k({\mathbf{y}}_n)\stackrel{P}{\to }c>0$$

   when M_k ⊆ M_t.

3. Let f_k(y_n | θ_k, ϕ_k) = N(y_n; X_n,kθ_k, ϕ_kI), with growing p_k, satisfy D1–D2. Let $({\mathit{\theta }}_k^{\ast },{\varphi }_k^{\ast })$ minimize KL to f*(y_n) with $\mathit{Var}({\mathbf{y}}_n-X_{k,n}{\mathit{\theta }}_k^{\ast })={\varphi }_k^{\ast }<\mathrm{\infty }$ and $\pi ({\varphi }_k^{\ast }|M_k)>0$. Then $g_k({\mathbf{y}}_n)\stackrel{P}{\to }{d}_k({\mathit{\theta }}_k^{\ast },{\varphi }_k^{\ast })$ and $d_k({\mathbf{m}}_{k,n},{\varphi }_k^{\ast })\stackrel{\mathrm{a}.\mathrm{s}.}{\to }{d}_k({\mathit{\theta }}_k^{\ast },{\varphi }_k^{\ast })$, where ${\mathbf{m}}_{k,n}=S_{k,n}^{-1}{X}_{k,n}^{\prime }{\mathbf{y}}_n$, $S_{k,n}=X_{k,n}^{\prime }{X}_{k,n}+{\tau }^{-1}I$. Further, if $f^{\ast }({\mathbf{y}}_n)=N({\mathbf{y}}_n;X_{t,n}{\mathit{\theta }}_t^{\ast },{\varphi }_t^{\ast })$ then $g_k({\mathbf{y}}_n)\stackrel{P}{\to }c$ with c = 0 when either M_t ⊂ M_k or M_t ⊄ M_k but a column in ${(X_{k,n}^{\prime },X_{k,n})}^{-1}{X}_{k,n}^{\prime }{X}_{t,n}$ converges to zero. Else, c > 0.

That is, even when the data-generating f*(y_n) does not belong to the set of considered models, g_k(y_n) converges to 0 for certain M_k containing spurious parameters, e.g. for linear models when either M_t ⊂ M_k or M_t ⊄ M_k but some columns in X_k,n are uncorrelated with X_t,n given X_k,n ∩ X_t,n. Propositions 2–3 give rates for the case when $f^{\ast }({\mathbf{y}}_n)=f_t({\mathbf{y}}_n|{\mathit{\theta }}_t^{\ast },{\varphi }_t^{\ast })$.

Proposition 2

Let $({\widehat{\mathit{\theta }}}_k,{\widehat{\varphi }}_k)$ be the unique MLE and $f_k({\mathbf{y}}_n|{\mathit{\theta }}_k^{\ast },{\varphi }_k^{\ast })$ minimize KL to the data-generating $f_t({\mathbf{y}}_n|{\mathit{\theta }}_t^{\ast },{\varphi }_t^{\ast })$ for $({\mathit{\theta }}_k^{\ast },{\varphi }_k^{\ast })\in {\mathrm{\Theta }}_k\times \mathrm{\Phi }$. Assume C3–C4 are satisfied.

1. Let f_k(y | θ_k, ϕ_k) with fixed p_k satisfy W69 and ${\stackrel{\sim }{\mathit{\theta }}}_k$ be the posterior mode, with $\mathit{sign}({\stackrel{\sim }{\theta }}_{ki})=\mathit{sign}({\widehat{\theta }}_{ki})$ for i = 1, …, p_k under a pMOM, peMOM or piMOM prior. If ${\theta }_{ki}^{\ast }\ne 0$ is fixed then $n({\stackrel{\sim }{\theta }}_{ki}-{\widehat{\theta }}_{ki})\stackrel{P}{\to }c$ for some 0 < c < ∞. If ${\theta }_{ki}^{\ast }={\theta }_{0i}^{\ast }{a}_n\ne 0$ with a_n → 0 as in C4 then ${\stackrel{\sim }{\theta }}_i-{\widehat{\theta }}_{ki}=O_p(1/n{a}_n))$ for pMOM and ${\stackrel{\sim }{\theta }}_i-{\widehat{\theta }}_{ki}=O_p(1/n{a}_n^3))$ for peMOM, piMOM. If ${\theta }_{ki}^{\ast }=0$ then $n^2{({\stackrel{\sim }{\theta }}_{ki}-{\widehat{\theta }}_{ki})}^2\stackrel{P}{\to }c$ for pMOM and $n{\stackrel{\sim }{\theta }}_{ki}^4\stackrel{P}{\to }c$ for peMOM, piMOM with 0 < c < ∞. Further, any other posterior mode is O_p(n^−1/2) (pMOM) or O_p(n^−1/4) (peMOM, piMOM).

2. Under the conditions in (i) $E({\theta }_{ki}|M_k,{\mathbf{y}}_n)={\widehat{\theta }}_{ki}+O_p(n^{-1/2})={\theta }_{ki}^{\ast }+O_p(n^{-1/2})$ for pMOM and ${\widehat{\theta }}_{ki}+O_p(n^{-1/4})={\theta }_{ki}^{\ast }+O_p(n^{-1/4})$ for peMOM/piMOM.

3. Let f_k(y_n | θ_k, ϕ_k) = N(y_n; X_n,kθ_k, ϕ_kI) satisfy D1–D2 with diagonal $X_{n,k}^{\prime }{X}_{n,k}$. Then the rates in (i)–(ii) remain valid.

We note that given that there is a prior mode in each of the 2^pk quadrants (combination of signs of θ_ki) there always exists a posterior mode ${\stackrel{\sim }{\mathit{\theta }}}_k$ satisfying the sign conditions in (i). Further, for elliptical log-likelihoods given that the pMOM, peMOM and piMOM priors have independent symmetric components the global posterior mode is guaranteed to occur in the same quadrant as ${\widehat{\mathit{\theta }}}_k$. Part (i) first characterizes the behaviour of this dominant mode and subsequently the behaviour of all other modes. Conditional on M_k, spurious parameter estimates converge to 0 at n^−1/2 (pMOM) or n^−1/4 (peMOM,piMOM). Vanishing ${\theta }_i^{\ast }\ne 0$ are captured as long as ${\theta }_i^{\ast }\gg n^{-1/2}$ (pMOM) or ${\theta }_i^{\ast }\gg n^{-1/4}$ (peMOM, piMOM). This holds for fixed p_k or linear models with growing p_k and diagonal $X_{n,k}^{\prime }{X}_{n,k}$. We leave further extensions as future work.

Proposition 3 shows that weighting these estimates with P (M_k | y_n) gives a strong selective shrinkage. We denote $SS{R}_0={\displaystyle {\sum }_{{\theta }_i^{\ast }=0}{(E({\theta }_i|{\mathbf{y}}_n)-{\theta }_i^{\ast })}^2}$, $SS{R}_1={\displaystyle {\sum }_{{\theta }_i^{\ast }\ne 0}{(E({\mathit{\theta }}_i|{\mathbf{y}}_n)-{\theta }_i^{\ast })}^2}$, $p_0={\displaystyle {\sum }_{i=1}^{p}I({\theta }_i^{\ast }=0)}$, p₁ = p − p₀ and let $E_{{\mathit{\theta }}^{\ast }}(SS{R}_0)={\displaystyle \int SS{R}_{0}f({\mathbf{y}}_n|{\mathit{\theta }}^{\ast },{\varphi }^{\ast })}d{\mathbf{y}}_n$ be the mean under the data-generating f(y_n | θ*, ϕ*).

Proposition 3

Let E(θ_i | y_n) be as in (4), M_t the data-generating model, BF_kt = m_k(y)/m_t(y) and a_n as in C4. Assume that P (M_k)/P(M_t) = o(n^(pk−pt)) for M_t ⊂ M_k.

1. Let all M_k satisfy W69, C3 and p be fixed. If M_t ⊄ M_k, then BF_kt = O_p(e⁻ⁿ) under a pMOM, peMOM or piMOM prior if ${\theta }_{ti}^{\ast }\ne 0$ are fixed and $B{F}_{kt}=O_p(e^{-a_n^{2}n})$ if ${\theta }_{ti}^{\ast }={\theta }_{0i}^{\ast }{a}_n$. If M_t ⊂ M_k then $B{F}_{kt}=O_p(n^{-\frac{3}{2}(p_k-p_t)})$ under a pMOM prior and $B{F}_{kt}=O_p(e^{-\sqrt{n}})$ under peMOM or piMOM.

2. Under the conditions in (i) let a_n be as in C4 and r = max_kP(M_k)/P(M_t) where p_k = p_t + 1, M_t ⊂ M_k. Then the posterior means and sums of squared errors satisfy

   	pMOM		peMOM-piMOM
   	E(θi | yn)	SSR	E(θi | yn)	SSR
   ${\theta }_i^{\ast }\ne 0$	${\theta }_i^{\ast }+O_p(n^{-1/2})$	Op(p1n−1)	${\theta }_i^{\ast }+O_p(n^{-1/2})$	Op(p1n−1)
   ${\theta }_i^{\ast }={\theta }_{0i}^{\ast }{a}_n$	${\theta }_i^{\ast }+O_p(n^{-1/2})$	Op(p1n−1)	${\theta }_i^{\ast }+O_p(n^{-1/4})$	Op(p1n−1/2)
   ${\theta }_i^{\ast }=0$	rOp(n−2)	Op(p0r2n−4)	$r{O}_p(e^{-\sqrt{n}})$	$O_p(p_0{r}^2{e}^{-\sqrt{n}})$

3. Let y_n ~ N(X_n,kθ_k, ϕ_kI) satisfy D1–D2 with diagonal $X_n^{\prime }{X}_n$ and known ϕ. Let ε, $\stackrel{\sim }{\epsilon }>0$ be arbitrarily small constants and assume that P (θ₁ ≠ 0, …, θ_p ≠ 0) is exchangeable with r = P (δ_i = 1)/P (δ_i = 0). Then

   	pMOM		peMOM-piMOM
   	E(θi | yn, ϕ)	$E_{{\mathit{\theta }}^{\ast }}(\mathit{SSR})$	E(θi | yn, ϕ)	$E_{{\mathit{\theta }}^{\ast }}(\mathit{SSR})$
   ${\theta }_i^{\ast }\ne 0$	${\theta }_i^{\ast }+O_p(n^{-1/2})$	O(p1/n1−ε)	${\theta }_i^{\ast }+O_p(n^{-1/2})$	Op(p1/n1−ε)
   ${\theta }_i^{\ast }={\theta }_{0i}^{\ast }{a}_n$	${\theta }_i^{\ast }+O_p(n^{-1/2})$	O(p1/n1−ε)	${\theta }_i^{\ast }+O_p(n^{-1/4})$	$O(p_1/n^{\frac{1}{2}-\epsilon })$
   ${\theta }_i^{\ast }=0$	rOp(n−2)	Op(p0r2/n4−ε)	$r{O}_p(e^{-\sqrt{n}})$	$O(p_0{r}^2{e}^{-n^{1/2-\epsilon }})$

   where the results for ${\theta }_i^{\ast }\ne 0$ and ${\theta }_i^{\ast }={\theta }_{0i}^{\ast }{a}_n$ hold as long as $r\gg e^{-n^{\stackrel{\sim }{\epsilon }}}$ and the result for ${\theta }_i^{\ast }=0$ holds for any r.

BMA estimates for active coefficients are $O_p(1/\sqrt{n})$ of their true value (O_p(n^−1/4) for vanishing ${\theta }_i^{\ast }$ under peMOM or piMOM), but inactive coefficients estimates are shrunk at rO_p(n⁻²) or $r{O}_p(e^{-\sqrt{n}})$ (to be compared with rO_p(n⁻¹) under the corresponding LPs) where r are the prior inclusion odds. The condition $P(M_k)/P(M_t)=o(n^{pk-pt})$ for M_t ⊂ M_k ensures that complex models are not favoured a priori (usually P (M_k)/P (M_t) = O(1)). The condition $r\gg e^{-n^{\stackrel{\sim }{\epsilon }}}$ in Part (iii) prevents the prior from favouring overly sparse solutions. For instance, a Beta-Binomial(1, l) prior on the model size gives r = 1/l, hence any fixed finite l satisfies $r\gg e^{-n^{\stackrel{\sim }{\epsilon }}}$. Suppose that we set l = p, then $r\gg e^{-n^{\stackrel{\sim }{\epsilon }}}$ is satisfied as long as $p=O(e^{n^{\alpha }})$ for some α < 1.

3. Non-local priors as truncation mixtures

We establish a correspondence between NLPs and truncation mixtures. Our discussion is conditional on M_k, hence for simplicity we omit ϕ and denote π(θ) = π(θ | M_k), p = dim(Θ_k).

3.1. Equivalence between NLPs and truncation mixtures

We show that truncation mixtures define valid NLPs, and subsequently that any NLP may be represented in this manner. Given that the representation is not unique, we give two constructions and discuss their merits. Let π^L(θ) be an arbitrary LP and λ ∈ ℝ⁺ a latent truncation.

Proposition 4

Define π(θ | λ) ∝ π^L(θ)I(d(θ) > λ), where $\underset{\mathit{\theta }\to {\mathit{\theta }}_0}{\lim }d(\mathit{\theta })=0$ for any θ₀ ∈ Θ_k′⊂ Θ_k, and π^L (θ) is bounded in a neighborhood of θ₀. Let π(λ) be a marginal prior for λ placing no probability mass at λ = 0. Then π(θ) = ∫π(θ | λ)π(λ)dλ defines a NLP.

Corollary 5

Assume that $d(\mathit{\theta })={\displaystyle {\prod }_{i=1}^p{d}_i({\theta }_i)}$. Let $\pi (\mathit{\theta }|\mathbf{\lambda })\propto {\pi }^L(\mathit{\theta }){\displaystyle {\prod }_{i=1}^{p}I(d_i({\theta }_i)>{\mathrm{\lambda }}_i})$ where λ = (λ₁, …, λ_p)′ have an absolutely continuous prior π(λ). Then ∫π(θ | λ)π(λ)dλ is a NLP.

Example 1

Consider y_n ~ N(Xθ, ϕI), where θ ∈ ℝ^p, ϕ is known and I is the n×n identity matrix. We define a NLP for θ with a single truncation point with $\pi (\mathit{\theta }|\mathrm{\lambda })\propto N(\mathit{\theta };\mathbf{0},\tau I)I({\displaystyle {\prod }_{i=1}^p{\theta }_i^2>\mathrm{\lambda }})$ and some π(λ), e.g. Gamma or Inverse Gamma. Obviously, the choice of π(λ) affects π(θ) (Section 3.2). An alternative prior is

$$\pi (\mathit{\theta }|{\mathrm{\lambda }}_1,\dots ,{\mathrm{\lambda }}_p)\propto N(\mathit{\theta };\mathbf{0},\tau I){\displaystyle \prod _{i=1}^{p}I({\theta }_i^2>{\mathrm{\lambda }}_i)},$$

giving marginal independence when π(λ₁, …, λ_p) has independent components.

We address the reverse question: given any NLP, a truncation representation is always possible.

Proposition 6

Let π(θ) ∝ d(θ)π^L(θ) be a NLP and denote h(λ) = P_u (d(θ) > λ), where P_u(·) is the probability under π^L(θ). Then π(θ) is the marginal prior associated to π(θ | λ) ∝ π^L(θ)I(d(θ) > λ) and π(λ) = h(λ)/E_u (d(θ)) ∝ h(λ), where E_u (·) is the expectation with respect to π^L(θ).

Corollary 7

Let $\pi (\mathit{\theta })\propto {\pi }^L(\mathit{\theta }){\displaystyle {\prod }_{i=1}^p{d}_i({\theta }_i)}$ be a NLP,

$$h(\mathbf{\lambda })=P_u(d_1({\theta }_1)>{\mathrm{\lambda }}_1,\dots ,d_p({\theta }_p)>{\mathrm{\lambda }}_p)$$

and assume that ∫h(λ)dλ < ∞. Then π(θ) is the marginal prior associated to $\pi (\mathit{\theta }|\mathbf{\lambda })\propto {\pi }^L(\mathit{\theta }){\displaystyle {\prod }_{i=1}^{p}I({\theta }_i>{\mathrm{\lambda }}_i)}$ and π(λ) ∝ h(λ).

Corollary 7 adds latent variables but greatly facilitates sampling. The condition ∫h(λ)dλ < ∞ is guaranteed when π^L(θ) has independent components (apply Proposition 6 to each θ_i).

Example 2

The pMOM prior with $d(\mathit{\theta })={\displaystyle {\prod }_{i=1}^p{\theta }_i^2}$, π^L(θ) = N(θ, 0, τI) can be represented as $\pi (\mathit{\theta }|\mathrm{\lambda })\propto N(\mathit{\theta };\mathbf{0},\tau I)I({\displaystyle {\prod }_{i=1}^p{\theta }_i^2>\mathrm{\lambda }})$ and

$$\pi (\mathrm{\lambda })=\frac{P({\displaystyle {\prod }_{i=1}^p{\theta }_i^2/\tau }>\mathrm{\lambda }/{\tau }^p)}{E_u({\displaystyle {\prod }_{i=1}^p{\theta }_i^2})}=\frac{h(\mathrm{\lambda }/{\tau }^p)}{{\tau }^p},$$

where h(·) is the survival function for a product of independent chi-square random variables with 1 degree of freedom (Springer and Thompson, 1970). Prior draws are obtained by

1. Draw u ~ Unif(0, 1). Set λ = P ⁻¹(u), where P(u) = P_π(λ ≤ u) is the cdf associated to π(λ).

2. Draw θ ~ N(0, τI)I(d(θ) > λ).

As drawbacks, P(u) requires Meijer G-functions and is cumbersome to evaluate for large p and sampling from a multivariate Normal with truncation region ${\displaystyle {\prod }_{i=1}^p{\theta }_i^2>\mathrm{\lambda }}$ is nontrivial. Corollary 7 gives an alternative. Let P (u) = P (λ < u) be the cdf associated to $\pi (\mathrm{\lambda })=\frac{h(\mathrm{\lambda }/\tau )}{\tau }$ where h(·) is the survival of a ${\chi }_1^2$. For i = 1, …, p, draw u_i ~ Unif(0, 1), set λ_i = P⁻¹ (u_i) and draw θ_i ~ N(0, τ)I(θ_i > |λ_i|). The function P⁻¹(·) can be tabulated and quickly evaluated, rendering efficient computations. Supplementary Figure 1 shows 100,000 draws from pMOM priors with τ = 5.

3.2. Deriving NLP properties for a given mixture

We show how two important characteristics of a NLP functional form, the penalty and tails, depend on the chosen truncation. We distinguish whether a single or multiple truncation variables are used.

Proposition 8

Let π(θ) be the marginal of $\pi (\mathit{\theta },\mathrm{\lambda })=\frac{{\pi }^L(\mathit{\theta })}{h(\mathrm{\lambda })}\pi (\mathrm{\lambda }){\displaystyle {\prod }_{i=1}^{p}I(d({\theta }_i)>\mathrm{\lambda })}$, where h(λ) = P_u(d(θ₁) > λ, …, d(θ_p) > λ) and λ ∊ ℝ⁺ with P (λ = 0) = 0. Let d_min(θ) = min{d(θ₁), …, d(θ_p)}.

1. Consider any sequence {θ^(m)}m≥1 such that $\underset{m\to \mathrm{\infty }}{\lim }{d}_{\mathit{min}}({\mathit{\theta }}^{(m)})=0$ Then

   $$\underset{m\to \mathrm{\infty }}{\lim }\frac{\pi ({\mathit{\theta }}^{(m)})}{{\pi }^L({\mathit{\theta }}^{(m)})d_{\mathit{min}}({\mathit{\theta }}^{(m)})\pi ({\mathrm{\lambda }}^{(m)})}=1,$$

   for some λ^(m) ∊ (0, d_min(θ^(m)). If π(λ) = ch(λ) then $\underset{m\to \mathrm{\infty }}{\lim }\pi ({\mathrm{\lambda }}^{(m)})=c\in (0,\mathrm{\infty })$.

2. Let {θ^(m)}_m≥1 be any sequence such that $\underset{m\to \mathrm{\infty }}{\lim }d({\mathit{\theta }}^{(m)})=\mathrm{\infty }$. Then $\underset{m\to \mathrm{\infty }}{\lim }\pi ({\mathit{\theta }}^{(m)})/{\pi }^L({\mathit{\theta }}^{(m)})=c,$ where c > 0 is either a positive constant or ∞. In particular, if ${\displaystyle \int \frac{\pi (\mathrm{\lambda })}{h(\mathrm{\lambda })}d\mathrm{\lambda }<\mathrm{\infty }}$ then c < ∞.

Property (i) is important as Bayes factor rates depend on the penalty, which we see is given by the smallest d(θ₁), …, d(θ_p). Property (ii) shows that π(θ) inherits its tail behavior from π^L(θ). Corollary 9 is an extension to multiple truncations.

Corollary 9

Let π(θ) be the marginal NLP for $\pi (\mathit{\theta },\mathbf{\lambda })=\frac{{\pi }^L(\mathit{\theta })}{h(\mathrm{\lambda })}{\displaystyle {\prod }_{i=1}^{p}I(d_i({\theta }_i)>{\mathrm{\lambda }}_i){\pi }_i({\mathrm{\lambda }}_i)}$, where h(λ) = P_u (d₁(θ₁) > λ₁,…,d_p(θ_p) > λ_p) under π^L(θ) and π(λ) is absolutely continuous.

1. Let {θ^(m)}_m≥1 such that $\underset{m\to \mathrm{\infty }}{\lim }{d}_i({\theta }_i^{(m)})=0$ for i = 1, …, p. Then for some ${\mathrm{\lambda }}_i^{(m)}\in (0,d({\theta }_i))$, $\underset{m\to \mathrm{\infty }}{\lim }\pi ({\mathit{\theta }}^{(m)})/({\pi }^L({\mathit{\theta }}^{(m)})\pi ({\mathbf{\lambda }}^{(m)}){\displaystyle {\prod }_{i=1}^p{d}_i({\theta }_i^{(m)})})=1$.

2. Let {θ^(m)}_m≥1 such that $\underset{m\to \mathrm{\infty }}{\lim }{d}_i({\theta }_i^{(m)})=\mathrm{\infty }$ for i = 1, …p. Then $\underset{m\to \mathrm{\infty }}{\lim }\pi ({\mathit{\theta }}^{(m)})/{\pi }^L({\mathit{\theta }}^{(m)})=c>0$ where c ∈ ℝ⁺ ∪ {∞}. In particular, if E (h(λ)⁻¹) < ∞ under π(λ), then c < ∞.

That is, multiple independent truncation variables give a multiplicative penalty ${\displaystyle {\prod }_{i=1}^p{d}_i({\theta }_i)}$ and tails are at least as thick as those of π^L(θ). Once a functional form for π(θ) is chosen, we need to set its parameters. Although the asymptotic rates (Section 2) hold for any fixed parameters, their value can be relevant in finite samples. Given that posterior inference depends solely on the marginal prior π(θ), whenever possible we recommend eliciting π(θ) directly. For instance, Johnson and Rossell (2010) defined practical significance in linear regression as signal-to-noise ratios $|{\theta }_i|/\sqrt{\varphi }>0.2$, and gave default τ assigning $P(|{\theta }_i|/\sqrt{\varphi }>0.2)=0.99$. Rossell et al. (2013) found analogous τ for probit regression, and also considered learning τ either via a hyper-prior or minimizing posterior predictive loss (Gelfand and Ghosh, 1998). Consonni and La Rocca (2010) devised objective Bayes strategies. Yet another possibility is to match the unit information prior e.g. setting $V({\theta }_i/\sqrt{\varphi })=1$ which can be regarded as minimally informative (in fact prior e.g. $V({\theta }_i/\sqrt{\varphi })=1.074$ for the MOM default τ = 0.358). When π(θ) is not in closed-form prior elicitation depends both on τ and π(λ), but prior draws can be used to estimate $P(|{\theta }_i|/\sqrt{\varphi }>t)$ for any t. An analytical alternative is to set π(λ) so that E(λ) = d(θ_i, ϕ)when ${\theta }_i/\sqrt{\varphi }=t$, i.e. E(λ) matches a practical relevance threshold. For instance, for t = 0.2 and π(λ) ~ IG(a, b) under the MOM prior we would set E(λ) = b/(a−1) = 0.2²/τ, and under the eMOM prior $b/(a-1)=e^{\sqrt{2}-\tau /{0.2}^2}$. Both expressions illustrate the dependence between τ and π (λ). Here we use default τ (Section 5), but as discussed other strategies are possible.

4. Posterior sampling

We use the latent truncation characterization to derive posterior sampling algorithms. Section 4.1 provides two Gibbs algorithms to sample from arbitrary posteriors, and Section 4.2 adapts them to linear models. Sampling is conditional on a given M_k, hence we drop M_k to keep notation simple.

4.1. General algorithm

First consider a NLP defined by a single latent truncation, i.e. $\pi (\mathit{\theta }|\mathrm{\lambda })={\pi }^L(\mathit{\theta })\mathrm{I}(d(\mathit{\theta })>\mathrm{\lambda })/h(\mathrm{\lambda })$, where h(λ) = P_u (d(θ) > λ) and π (λ) a prior on λ ∊ ℝ⁺. The joint posterior is

$$\pi (\mathit{\theta },\mathrm{\lambda }|{\mathbf{y}}_n)\propto f({\mathbf{y}}_n|\mathit{\theta })\frac{{\pi }^L(\mathit{\theta })\mathrm{I}(d(\mathit{\theta })>\mathrm{\lambda })}{h(\mathrm{\lambda })}\pi (\mathrm{\lambda }).$$ (5)

Sampling from π(θ | y_n) directly is challenging as it is highly multi-modal, but straightforward algebra gives the following k^th Gibbs iteration to sample from π(θ, λ | y_n).

Algorithm 1. Gibbs sampling with a single truncation

1. Draw λ^(k) ~ π(λ | y_n, θ^(k−1)) ∝ I(d(θ) > λ)π(λ)/h(λ). When π(λ) ∝ h(λ) as in Proposition 6, λ^(k) ~ Unif(0, d(θ^(k−1))).

2. Draw θ^(k) ~ π(θ | y_n, λ^(k)) ∝ π^L(θ | y_n)I(d(θ) > λ^(k)).

That is, λ^(k) is sampled from a univariate distribution that reduces to a uniform when setting π(λ) ∝ h(λ), and θ^(k) from a truncated version of π^L(), which may be a LP that allows posterior sampling. As a difficulty, the truncation region {θ : d(θ) > λ^(k)} is non-linear and non-convex so that jointly sampling θ = (θ₁, …, θ_p) may be challenging. One may apply a Gibbs step to each element in θ₁, …, θ_p sequentially, which only requires univariate truncated draws from π^L(·), but the mixing of the chain may suffer. The multiple truncation representation in Corollary 7 provides a convenient alternative. Consider $\pi (\mathit{\theta }|\mathbf{\lambda })={\pi }^L(\mathit{\theta }){\displaystyle {\prod }_{i=1}^p\mathrm{I}(d_i({\theta }_i)>{\mathrm{\lambda }}_i)\pi (\mathbf{\lambda })/h(\mathbf{\lambda })}$, where h(λ) = P_u(d₁(θ₁) > λ₁, … d_p(θ_p) > λ_p). The following steps define the k Gibbs iteration:

Algorithm 2. Gibbs sampling with multiple truncations

1. Draw ${\mathbf{\lambda }}^{(k)}~\pi (\mathbf{\lambda }|{\mathbf{y}}_n,{\mathit{\theta }}^{(k-1)})={\displaystyle {\prod }_{i=1}^p\text{Unif}({\mathrm{\lambda }}_i;0,d_i({\theta }_i))\frac{\pi (\mathbf{\lambda })}{h(\mathbf{\lambda })}}.$ If π(λ) ∝ h(λ) as in Corollary 7, ${\mathrm{\lambda }}_i^{(k)}~\text{Unif}(0,d_i({\theta }_i))$.

2. Draw ${\mathit{\theta }}^{(k)}~\pi (\mathit{\theta }|{\mathbf{y}}_n,{\mathbf{\lambda }}^{(k)})\propto {\pi }^L(\mathit{\theta }|{\mathbf{y}}_n){\displaystyle {\prod }_{i=1}^p\mathrm{I}}(d_i({\theta }_i)>{\mathrm{\lambda }}_i^{(k)}).$

Now the truncation region in Step 2 is defined by hyper-rectangles, which facilitates sampling. As in Algorithm 1, by setting the prior conveniently Step 1 avoids evaluating π(λ) and h(λ).

4.2. Linear models

We adapt Algorithm 2 to a linear regression y_n ~ N(Xθ, ϕI) with the three priors in (1)-(3). We set the prior ϕ ~ IG(a_ϕ/2, b_ϕ/2). For all three priors, Step 2 in Algorithm 2 samples from a multivariate Normal with rectangular truncation around 0, for which we developed an efficient algorithm. Kotecha and Djuric (1999) and Rodriguez-Yam et al. (2004) proposed Gibbs after orthogonalization strategies that result in low serial correlation, which Wilhelm and Manjunath (2010) implemented in the R package tmvtnorm for restrictions l ≤ θ_i ≤ u. Here we require sampling under d_i(θ_i) ≥ l, a non-convex region. Our adapted algorithm is in Supplementary Section 3 and implemented in R package mombf. An important property is that the algorithm produces independent samples when the posterior probability of the truncation region becomes negligible. Since NLPs only assign high posterior probability to a model when the posterior for non-zero coefficients is well shifted from the origin, the truncation region is indeed often negligible. We outline the algorithm separately for each prior.

4.2.1. pMOM prior

Straightforward algebra gives the full conditional posteriors

$$\begin{gathered} \pi (\mathit{\theta }|\varphi ,{\mathbf{y}}_n)\propto \left({\displaystyle \prod _{i=1}^p{\theta }_i^2}\right)N(\mathit{\theta };\mathbf{m},\varphi S^{-1}) \\ \pi (\varphi |\mathit{\theta },{\mathbf{y}}_n)=\text{IG}\left(\frac{a_{\varphi }+n+3p}{2},\frac{b_{\varphi }+s_R^2+{\mathit{\theta }}^{\prime }\mathit{\theta }/\tau }{2}\right), \end{gathered}$$ (6)

where S = X′X + τ⁻¹I, m = S⁻¹X′y_n and $s_R^2={({\mathbf{y}}_n-X\mathit{\theta })}^{\prime }({\mathbf{y}}_n-X\mathit{\theta })$ is the sum of squared residuals. Corollary 7 represents the pMOM prior in (1) as

$$\pi (\mathit{\theta }|\varphi ,\mathbf{\lambda })=N(\mathit{\theta };\mathbf{0},\tau \varphi I){\displaystyle \prod _{i=1}^p\mathrm{I}\left(\frac{{\theta }_i^2}{\tau \varphi }>{\mathrm{\lambda }}_i\right)}\frac{1}{h({\mathrm{\lambda }}_i)}$$ (7)

marginalized with respect to $\pi ({\mathrm{\lambda }}_i)=h({\mathrm{\lambda }}_i)=P\left(\frac{{\theta }_i^2}{\tau \varphi }>{\mathrm{\lambda }}_i|\varphi \right)$, where h(·) is the survival of a chi-square with 1 degree of freedom. Algorithm 2 and simple algebra give the k^th Gibbs iteration

1. ${\varphi }^{(k)}~\text{IG}\left(\frac{a_{\varphi }+n+3p}{2},\frac{b_{\varphi }+s_R^2+{({\mathit{\theta }}^{(k-1)})}^{\prime }{\mathit{\theta }}^{(k-1)}/\tau }{2}\right)$

2. ${\mathbf{\lambda }}^{(k)}~\pi (\mathbf{\lambda }|{\mathit{\theta }}^{(k-1)},{\varphi }^{(k)},{\mathbf{y}}_n)={\displaystyle {\prod }_{i=1}^p\mathrm{I}\left(\frac{{({\theta }_i^{(k-1)})}^2}{\tau {\varphi }^{(k)}}>{\mathrm{\lambda }}_i\right)}$

3. ${\mathit{\theta }}^{(k)}~\pi (\mathit{\theta }|{\mathbf{\lambda }}^{(k)},{\varphi }^{(k)},{\mathbf{y}}_n)=N(\mathit{\theta };\mathbf{m},{\varphi }^{(k)}{S}^{-1}){\displaystyle {\prod }_{i=1}^{p}I\left(\frac{{\theta }_i^2}{\tau {\varphi }^{(k)}}>{\mathrm{\lambda }}_i\right)}.$

Step 1 samples unconditionally on λ, so that no efficiency is lost for introducing these latent variables. Step 3 requires truncated multivariate Normal draws.

4.2.2. piMOM prior

We assume dim(Θ) < n. The full conditional posteriors are

$$\begin{gathered} \pi \left(\mathit{\theta }|\varphi ,{\mathbf{y}}_n\right)\propto \left({\displaystyle \prod _{i=1}^p\frac{\sqrt{\tau \varphi }}{{\theta }_i^2}{e}^{-\frac{\tau \varphi }{{\theta }_i^2}}}\right)N\left(\mathit{\theta };\mathbf{m},\varphi S^{-1}\right) \\ \pi \left(\varphi |\mathit{\theta },{\mathbf{y}}_n\right)=e^{-\tau \varphi {\displaystyle {\sum }_{i=1}^p{\theta }_i^{-2}}}\text{IG}\left(\varphi ;\frac{a_{\varphi }+n-p}{2},\frac{b_{\varphi }+s_R^2}{2}\right), \end{gathered}$$ (8)

where S = X′X, m = S⁻¹X′y_n and $s_R^2={\left({\mathbf{y}}_n-X\mathit{\theta }\right)}^{\prime }\left({\mathbf{y}}_n-X\mathit{\theta }\right)$. Now, the piMOM prior is π_I(θ | ϕ) =

$$N\left(\mathit{\theta };\mathbf{0};{\tau }_N\varphi \mathrm{I}\right){\displaystyle \prod _{i=1}^p\frac{\frac{\sqrt{\tau \varphi }}{\sqrt{\pi {\theta }_i^2}}{e}^{-\frac{\varphi \tau }{{\theta }_i^2}}}{N\left({\theta }_i;0,{\tau }_N\varphi \right)}}=N\left(\mathit{\theta };\mathbf{0};{\tau }_N\varphi \mathrm{I}\right){\displaystyle \prod _{i=1}^p{d}_i\left({\theta }_i,\varphi \right)}.$$ (9)

In principle any τ_N may be used, but τ_N ≥ 2τ guarantees d(θ_i, ϕ) to be monotone increasing in ${\theta }_i^2$, so that its inverse exists (Supplementary Section 4). By default we set τ_N = 2τ. Corollary 7 gives

$$\pi \left(\mathit{\theta }|\varphi ,\mathbf{\lambda }\right)=N\left(\mathit{\theta };\mathbf{0},{\tau }_N\varphi \mathrm{I}\right){\displaystyle \prod _{i=1}^p\mathrm{I}\left(d\left({\theta }_i,\varphi \right)>{\mathrm{\lambda }}_i\right)\frac{1}{h\left({\mathrm{\lambda }}_i\right)}}$$ (10)

and $\pi \left(\mathbf{\lambda }\right)={\displaystyle {\prod }_{i=1}^{p}h\left({\mathrm{\lambda }}_i\right)}$, where h(λ_i) = P(d(θ_i, ϕ) > λ_i) which we need not evaluate. Algorithm 2 gives the following MH within Gibbs procedure.

1. MH step

   1. Propose ${\varphi }^{\ast }\sim \text{IG}\left(\varphi ;\frac{a_{\varphi }+n-p}{2},\frac{b_{\varphi }+s_R^2}{2}\right)$
   2. Set ϕ^(k) = ϕ* with probability $min\left\{1,e^{\left({\varphi }^{\left(k-1\right)}-{\varphi }^{\ast }\right)\tau {\displaystyle {\sum }_{i=1}^p{\theta }_i^{-2}}}\right\}$, else ϕ^(k) = ϕ^(k−1).

2. ${\mathbf{\lambda }}^{\left(k\right)}~{\displaystyle {\prod }_{i=1}^p\text{Unif}\left({\mathrm{\lambda }}_i;0,d\left({\theta }_i^{\left(k-1\right)},{\varphi }^{\left(k\right)}\right)\right)}$

3. ${\mathit{\theta }}^{\left(k\right)}~N\left(\mathit{\theta };\mathbf{m},{\varphi }^{\left(k\right)}{S}^{-1}\right){\displaystyle {\prod }_{i=1}^p\mathrm{I}\left(d\left({\theta }_i,{\varphi }^{\left(k\right)}\right)>{\mathrm{\lambda }}_i^{\left(k\right)}\right)}.$

Step 3 requires the inverse d⁻¹(·), which can be evaluated efficiently combining an asymptotic approximation with a linear interpolation search (Supplementary Section 4). As a token, 10,000 draws for p = 2 variables required 0.58 seconds on a 2.8 GHz processor running OS X 10.6.8.

4.2.3. peMOM prior

The full conditional posteriors are

$$\pi \left(\mathit{\theta }|\varphi ,{\mathbf{y}}_n\right)\propto \left({\displaystyle \prod _{i=1}^p{e}^{-\frac{\tau \varphi }{{\theta }_i^2}}}\right)N\left(\mathit{\theta };\mathbf{m},\varphi S^{-1}\right);\pi \left(\varphi |\mathit{\theta },{\mathbf{y}}_n\right)\propto e^{-{\displaystyle {\sum }_{i=1}^p\frac{\tau \varphi }{{\theta }_i^2}}}\text{IG}\left(\varphi ;\frac{a^{\ast }}{2},\frac{b^{\ast }}{2}\right),$$ (11)

where S = X′X + τ⁻¹I, m = S⁻¹X′y_n, a* = a_ϕ + n + p, $b^{\ast }=b_{\varphi }+s_R^2+{\mathit{\theta }}^{\prime }\mathit{\theta }/\tau$. Corollary 7 gives

$$\pi \left(\mathit{\theta }|\varphi ,\mathbf{\lambda }\right)=N\left(\mathit{\theta };\mathbf{0},\tau \varphi I\right){\displaystyle \prod _{i=1}^p\mathrm{I}\left(e^{\sqrt{2}-\frac{\tau \varphi }{{\theta }_i^2}}>{\mathrm{\lambda }}_i\right)\frac{1}{h\left({\mathrm{\lambda }}_i\right)}}$$ (12)

and $\pi \left({\mathrm{\lambda }}_i\right)=h({\mathrm{\lambda }}_i)=P\left(e^{\sqrt{2}-\frac{\tau \varphi }{{\theta }_i^2}}>{\mathrm{\lambda }}_i|\varphi \right)$. Again h(λ_i) has no simple form but is not required by Algorithm 2, which gives the k^th Gibbs iteration

1. ${\varphi }^{(k)}~e^{-{\displaystyle {\sum }_{i=1}^p\frac{\tau \varphi }{{\theta }_i^2}}}\text{IG}\left(\varphi ;\frac{a^{\ast }}{2},\frac{b^{\ast }}{2}\right)$

   1. Propose ${\varphi }^{\ast }~\text{IG}\left(\varphi ;\frac{a^{\ast }}{2},\frac{b^{\ast }}{2}\right)$
   2. Set ϕ^(k) = ϕ* with probability $min\left\{1,e^{({\varphi }^{(k-1)}-{\varphi }^{\ast })\tau {\displaystyle {\sum }_{i=1}^p{({\theta }_i^{(k-1)})}^{-2}}}\right\}$, else ϕ^(k) = ϕ^(k−1).

2. ${\mathbf{\lambda }}^{(k)}{\displaystyle {\prod }_{i=1}^p\text{Unif}\left({\mathrm{\lambda }}_i;0,e^{\sqrt{2}-\tau \varphi /{({\theta }_i^{(k-1)})}^2}\right)}$

3. ${\mathit{\theta }}^{(k)}~N(\mathit{\theta };\mathbf{m},{\varphi }^{(k)}{S}^{-1}){\displaystyle {\prod }_{i=1}^p\mathrm{I}\left({\theta }_i^2>|\frac{\varphi \tau }{\log ({\mathrm{\lambda }}_i^{(k)})-\sqrt{2}}|\right)}$

5. Examples

We assess our posterior sampling algorithms and the use of NLPs for high-dimensional estimation. Section 5.1 shows a simple yet illustrative multi-modal example. Section 5.2 studies p ≥ n cases and compares the BMA estimators induced by NLPs with benchmark priors (BP, Fernández et al. (2001)), hyper-g priors (HG, Liang et al. (2008)), SCAD (Fan and Li, 2001), LASSO (Tibshirani, 1996) and Adaptive LASSO (ALASSO, Zhou (2006)). For NLPs and BP we used R package mombf 1.6.0 with default prior dispersions τ = 0.358, 0.133, 0.119 for pMOM, piMOM and peMOM (respectively), which assign 0.01 prior probability to $|{\theta }_i/\sqrt{\varphi }|<0.2$ (Johnson and Rossell, 2010), and ϕ ~ IG(0.01/2, 0.01/2). The model search and posterior sampling algorithms are described in Supplementary Section 5. Briefly, we performed 5,000 Gibbs iterations to sample from P(M_k|y_n) and subsequently sampled θ_k given M_k, y_n as outlined in Section 4.2. For HG we used R package BMS 0.3.3 with default alpha=3 and 10⁵ MCMC iterations in Section 5.2, for the larger example in Section 5.3 we used package BAS with 3 × 10⁶ iterations as it provided higher accuracy at lower running times. For LASSO, ALASSO and SCAD we set the penalization parameter with 10-fold cross-validation using functions mylars and ncvreg in R packages parcor 0.2.6 and ncvreg 3.2.0 (respectively) with default parameters. The R code is in the supplementary material. For all Bayesian methods we set a Beta-Binomial(1,1) prior on the model space. This is an interesting sparsity-inducing prior, e.g. for M_k with p_k = p_t + 1 it assigns P(M_k)/P(M_t) = 1/(p − p_t). From Proposition 3 if p > n this penalty more than doubles the shrinkage of E(θ_i|y_n) under LPs, i.e. they should perform closer to NLPs. Also note that BP sets θ_k|ϕ_k, $M_k~N(\mathbf{0};g\varphi X_{k,n}^{\prime }{X}_{k,n})$ with g = max{n, p²}, which in our p ≥ n simulations induces extra sparsity and thus shrinkage. We assess the relative merits of each method without any covariate pre-screening procedures.

5.1. Posterior samples for a given model

We simulated n = 1, 000 realizations from y_i ~ N(θ₁x_1i + θ₂x_2i, 1), where (x_1i, x_2i) are drawn from a bivariate Normal with E(x_1i) = E(x_2i) = 0, V(x_1i) = V(x_2i) = 2, Cov(x_1i, x_2i) = 1. We first consider θ₁ = 0.5, θ₂ = 1, and compute posterior probabilities for the four possible models. We assign equal a priori probabilities and obtain exact m_k(y_n) using pmomMarginalU, pimomMarginalU and pemomMarginalU in mombf (the former has closed-form, for the latter two we used 10⁶ importance samples). The posterior probability assigned to the full model under all three priors is 1 (up to rounding) (Supplementary Table 1). Figure 2 (left) shows 900 Gibbs draws (100 burn-in) obtained under the full model. The posterior mass is well-shifted away from 0 and resembles an elliptical shape for the three priors. Supplementary Table 2 gives the first-order auto-correlations, which are very small. This example reflects the advantages of the orthogonalization strategy, which is particularly efficient as the latent truncation becomes negligible.

Figure 2.

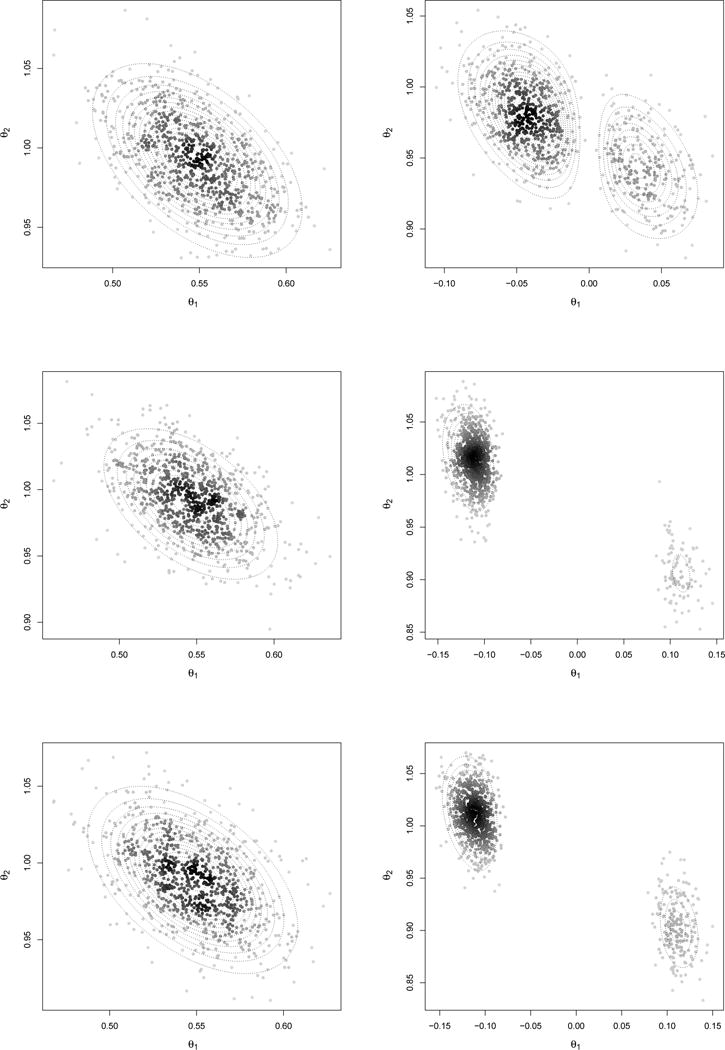
900 Gibbs draws when θ = (0.5, 1)′ (left) and θ = (0, 1)′ (right) and posterior density contours. Top: MOM (τ = 0.358); Middle: iMOM (τ = 0.133); Bottom: eMOM (τ = 0.119)

We now set θ₁ = 0, θ₂ = 1 and keep n = 1000 and (x_1i, x_2i) as before. We simulated several data sets and in most cases did not observe a noticeable posterior multi-modality. We portray a specific simulation that did exhibit multi-modality, as this poses a greater challenge from a sampling perspective. Table 1 shows that the data-generating model has highest posterior probability. Although the full model was clearly dismissed in light of the data, as an exercise we drew from its posterior. Figure 2 (right) shows 900 Gibbs draws after a 100 burn-in, and Supplementary Table 2 shows a low auto-correlation. The samples adequately captured the multiple modes.

Table 1.

Expression data with p = 172 or 10, 172 genes. $\overline{p}$: mean (MOM, iMOM, BP, HG) or selected number of predictors (SCAD, LASSO, ALASSO). R² coefficient is between (y_i, ŷ_i) (leave-one-out cross-validation). CPU time on Linux OpenSUSE 13.1, 64 bits, 2.6GHz processor, 31.4Gb RAM for 1,000 Gibbs iterations (MOM,iMOM,BP) or 3×10⁶ model updates (HG)

	p = 172		p = 10, 172
	$\overline{p}$	R2	$\overline{p}$	R2	CPU time
MOM	4.3	0.566	6.5	0.617	1m 52s
iMOM	5.3	0.560	10.3	0.620	59m
BP	4.2	0.562	3.0	0.586	1m 23s
HG	11.3	0.562	26.4	0.522	11m 49s
SCAD	29	0.565	81	0.535	16.7s
LASSO	42	0.586	159	0.570	23.7s
ALASSO	24	0.569	10	0.536	2m 49s

5.2. High-dimensional estimation

5.2.1. Growing p, fixed n and θ

We perform a simulation study with n = 100 and growing p = 100, 500, 1000. We set θ_i = 0 for i = 1, …, p − 5, the remaining 5 coefficients to (0.6, 1.2, 1.8, 2.4, 3) and residual variances ϕ = 1, 4, 8. Covariates were sampled from x ~ N(0, Σ), where Σ_ii = 1 and all correlations set to ρ = 0 or ρ = 0.25. We remark that ρ are population correlations, the maximum sample correlations when ρ = 0 were 0.37, 0.44, 0.47 for p = 100, 500, 1000 (respectively), and 0.54, 0.60, 0.62 when ρ = 0.25. We simulated 1,000 data sets under each setup.

Figure 3 shows sum of squared errors (SSE) averaged across simulations for ϕ = 1, 4, 8, ρ = 0, 0.25. pMOM and piMOM perform similarly and present a lower SSE as p grows than other methods in all scenarios. To obtain more insight on how the lower SSE is achieved, Supplementary Figures 2–3 show SSE separately for θ_i = 0 (left) and θ_i ≠ 0 (right). The largest differences between methods were observed for θ_i = 0, the performance of pMOM and piMOM coming closer for smaller signal-to-noise ratios $|{\theta }_i|/\sqrt{{\varphi }_i}$. For θ_i ≠ 0 differences in SSE are smaller, iMOM slightly outperforming MOM. For all methods as $|{\theta }_i|/\sqrt{{\varphi }_i}$ decrease the SSE worsens relative to the oracle least squares (Supplementary Figures 2–3, right panels, black horizontal segments).

Figure 3.

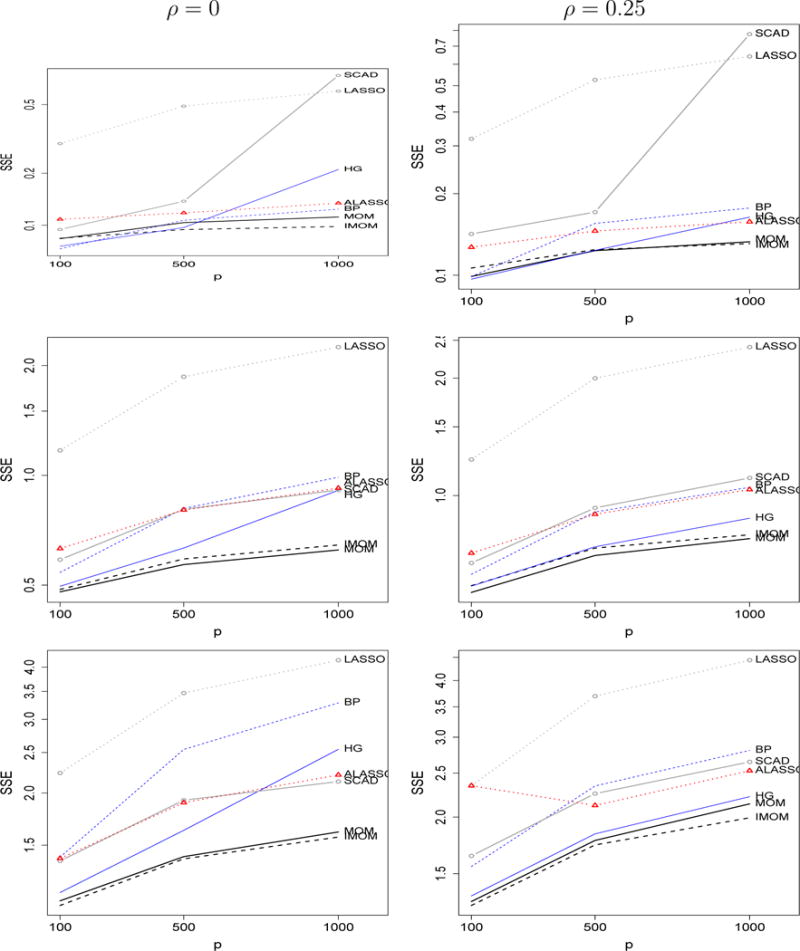
Mean SSE when ϕ = 1, 4, 8 (top, middle, bottom), ρ = 0, 0.25 (left, right). Simulation settings: n = 100, p = 100, 500, 1000 and 5 non-zero coefficients 0.6, 1.2, 1.8, 2.4, 3.0.

5.2.2. Growing p, θ = O(n^−1/4)

We extend the simulations by considering p = 100, 500, 1000 and ρ = 0, 0.25 as before in a setting with vanishing θ = O(n^−1/4). Specifically, we set n = 100, 250, 500 for p = 100, 500, 1000 (respectively), θ_i = 0 for i = 1, …, p − 5 as before and the remaining 5 coefficients to n^−1/4(0.6, 1.2, 1.8, 2.4, 3) and ϕ = 1. The goal is to investigate if NLP shrinkage rate comes at a cost of reduced precision when the coefficients are truly small. Note that n^−1/4 is only slightly larger than the n^−1/2 error of the MLE, and hence represents fairly small coefficients.

Figure 4 shows the total SSE and Supplementary Figure 4 that for zero (left) and non-zero (right) coefficients. MOM and iMOM present the lowest overall SSE in most situations but HG and ALASSO achieve similar performance, certainly closer than the earlier sparser scenario with fixed θ, n = 100 and growing p.

Figure 4.

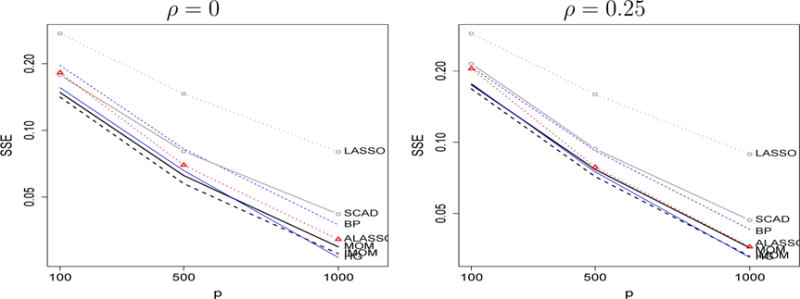
Mean SSE when non-zero θ = n^−1/4 (0.6, 1.2, 1.8, 2.4, 3.0), ρ = 0, 0.25 (left, right), ϕ = 1. Simulation settings: (n = 100, p = 100), (n = 250, p = 500), (n = 500, p = 1000)

Because NLPs assign high prior density to a certain range of $|{\theta }_i|/\sqrt{\varphi }$ values, we conducted a further study when θ contains an ample range of non-zero coefficients (i.e. both large and small). To this end, we set n = 100, 250, 500 for p = 100, 500, 1000 with ϕ = 1 as before, θ_i = 0 for i = 1, …, p − 11, vanishing (θ_p−10, …, θ_p−6) = n^−1/4 (0.6, 1.2, 1.8, 2.4, 3) and fixed (θ_p−5, …, θ_p) = (0.6, 1.2, 1.8, 2.4, 3). Figure 5 shows the overall MSE and Supplementary Figure 5 that for θ_i = 0 and θ_i ≠ 0 separately. The lowest overall MSE is achieved by iMOM and MOM, followed by HG and BP, whereas ALASSO is less competitive than in the earlier simulations where all θ_i = O(n^−1/4). Overall, these results support that NLPs remain competitive even with small signals and that their performance relative to competing methods is best in sparse situations, agreeing with our theoretical findings.

Figure 5.

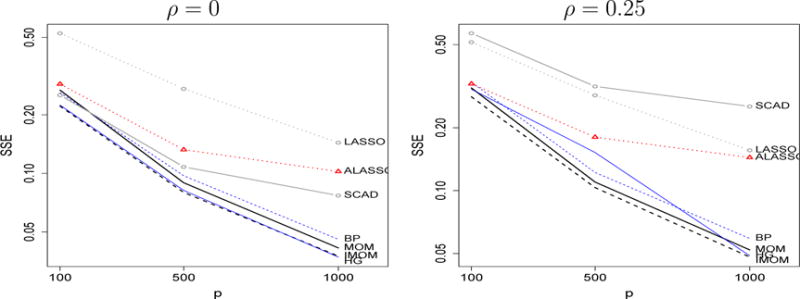
Mean SSE when non-zero (θ_p−10, …, θ_p−6) = n^−1/4(0.6, 1.2, 1.8, 2.4, 3), (θ_p−5, …, θ_p) = (0.6, 1.2, 1.8.2.4, 3) and ρ = 0, 0.25 (left, right), ϕ = 1. Simulation settings: (n = 100, p = 100), (n = 250, p = 500), (n = 500, p = 1000)

5.3. Gene expression data

We assess predictive performance in high-dimensional gene expression data. (Calon et al., 2012) used mice experiments to identify 172 genes potentially related to the gene TGFB, and showed that these were related to colon cancer progression in an independent data set with n = 262 human patients. TGFB plays a crucial role in colon cancer and it is important to understand its relation to other genes. Our goal is to predict TGFB in the human data, first using only the p = 172 genes and then adding 10,000 extra genes that we selected randomly from the 18,178 genes with distinct Entrez identifier contained in the experiment. Their absolute Pearson correlations with the 172 genes ranged from 0 to 0.892 with 95% of them being in (0.003,0.309). Both response and predictors were standardized to zero mean and unit variance (data and R code in Supplementary Material). We assessed predictive performance via the leave-one-out cross-validated R² coefficient between predictions and observations. For Bayesian methods we report the posterior expected number of variables in the model (i.e. the mean number of predictors used by BMA), and for SCAD and LASSO the number of selected variables.

Table 1 shows the results. For p = 172 all methods achieve similar R², that for LASSO being slightly higher, although pMOM, piMOM and BP used substantially less predictors. These results appear reasonable in a moderately dimensional setting where genes are expected to be related to TGFB. However, when using p = 10, 172 predictors important differences between methods are observed. The BMA estimates based on pMOM and piMOM remain parsimonious (6.5 and 10.3 predictors, respectively) and the cross-validated R² increases roughly to 0.62. The BP prior dispersion parameter g = 172² induces strong parsimony, though relative to NLPs the non-selectiveness of this penalty causes some loss of prediction power (R² = 0.586). For the remaining methods the number of predictors increased sharply and R² did not improve relative to the p = 172 case. Predictors with large marginal inclusion probabilities in pMOM/piMOM included genes related to various cancer types (ESM1, GAS1, HIC1, CILP, ARL4C, PCGF2), TGFB regulators (FAM89B) or AOC3 which is used to alleviate certain cancer symptoms. These findings suggest that NLPs effectively detected a parsimonious subset of predictors in this high-dimensional example. We also note that computation times were highly competitive. BP and NLPs are programmed in mombf in an identical manner (piMOM has no closed-form expressions, hence the higher time) whereas HG is implemented in BAS with a slightly more advanced MCMC model search algorithm (e.g. pre-ranking variables and considering swaps). NLPs focus P (M_k | y_n) on smaller models, which alleviates the cost required by matrix inversions (non-linear in the model size). NLPs also concentrate P (M_k | y_n) on a smaller subset of models, which tend to be revisited and hence the marginal likelihood need not be recomputed. Regarding the efficiency of our posterior sampler for (θ, ϕ), we ran 10 independent chains with 1,000 iterations each and obtained mean serial correlations of 0.32 (pMOM) and 0.26 (piMOM) across all non-zero coefficients. The mean correlation between Ê(θ | y_n) across all chain pairs was > 0.99 (pMOM and piMOM). Supplementary Section 5 contains further convergence assessments.

6. Discussion

We showed how combining BMA with NLPs gives a coherent joint framework encouraging model selection parsimony and selective shrinkage for spurious coefficients. Beyond theory, the latent truncation construction motivates NLPs from first principles, adds flexibility in prior choice and enables effective posterior sampling even under strong multi-modalities. We obtained strong results when p ≫ n in simulations and gene expression data, with parsimonious models achieving accurate cross-validated predictions and good computation times. Note that these did not require procedures to pre-screen covariates, which can cause a loss of detection power. Interestingly, NLPs achieved low estimation error even in settings with vanishing coefficients: their slightly higher SSE for active coefficients was compensated by a lower SSE for inactive coefficients. That is, NLPs can be advantageous even with sparse vanishing θ, although of course they may be less competitive in non-sparse situations. An important point is that inducing sparsity via P (M_k) (e.g. Beta-Binomial) or vague π(θ_k | M_k) (e.g. the BP) also performed reasonably well, although relative to the NLP data-adaptive sparsity there can be a loss of detection power.

Our results show that it is not only possible to use the same prior for estimation and selection, but may indeed be desirable. We remark that we used default informative priors, which are relatively popular for testing, but perhaps less readily adopted for estimation. Developing objective Bayes strategies to set the prior parameters is an interesting venue for future research, as well as determining shrinkage rates in more general p ≫ n cases, and adapting the latent truncation construction beyond linear regression, e.g. generalized linear, graphical or mixture models.