A fine-scale functional logic to convergence from retina to thalamus

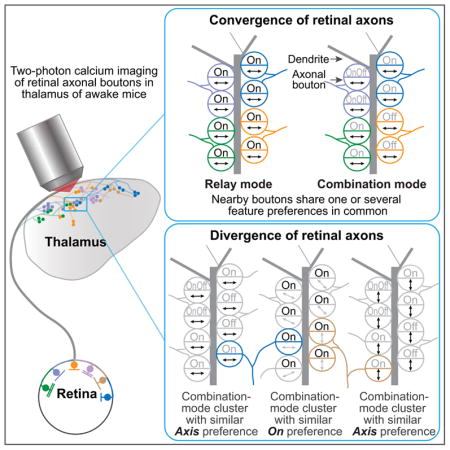
Summary

Numerous well-defined classes of retinal ganglion cells innervate the thalamus to guide image-forming vision, yet the rules governing their convergence and divergence remain unknown. Using two-photon calcium imaging in awake mouse thalamus, we observed a functional arrangement of retinal ganglion cell axonal boutons in which coarse-scale retinotopic ordering gives way to fine-scale organization based on shared preferences for other visual features. Specifically, at the ~6 μm scale, clusters of boutons from different axons often showed similar preferences for either one or multiple features, including axis and direction of motion, spatial frequency, and changes in luminance. Conversely, individual axons could “de-multiplex” information channels by participating in multiple, functionally-distinct bouton clusters. Finally, ultrastructural analyses demonstrated that retinal axonal boutons in a local cluster often target the same dendritic domain. These data suggest that functionally-specific convergence and divergence of retinal axons may impart diverse, robust and often novel feature selectivity to visual thalamus.

In brief

Functional arrangement of retinal ganglion cell axonal boutons may help explain how visual tuning in thalamic neurons can be sharp despite dense convergence of many retinal axons onto a single thalamic neuron.

Introduction

Axons of sensory neurons converge on target cells to combine information, and diverge to share information among targets. Using these simple operations, a limited number of neurons can give rise to robust and parallel representations of key aspects of the sensory world. For example, diverse visual information is relayed from retina to primary visual cortex (V1) via the visual thalamus (dorsolateral geniculate nucleus, dLGN). Compared with downstream nodes in this pathway, a relatively small number of retinal ganglion cell (RGC) inputs converge on a target dLGN neuron to efficiently drive postsynaptic spiking responses (Cleland et al., 1971; Usrey et al., 1998; Litvina and Chen, 2017a). This provides a unique opportunity to infer the anatomical and functional rules underlying ‘feedforward’ transformations of sensory inputs.

In the mouse, RGCs are sensitive to a rich array of visual features, such as stimulus location, direction and/or axis of motion, changes in luminance, and spatial frequency (Baden et al., 2016). This information is carried by at least 15 distinct types of dLGN-projecting RGCs that each tile the retina (Dhande et al., 2015). Mouse dLGN cell bodies exhibit similarly diverse and sharp tuning for a wide range of visual features (Grubb and Thompson, 2003; Marshel et al., 2012; Scholl et al., 2013; Zhao et al., 2013; Piscopo et al., 2013; Suresh et al., 2016).

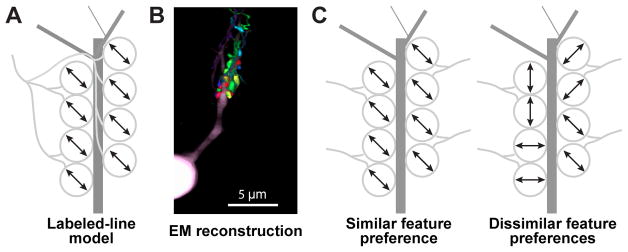
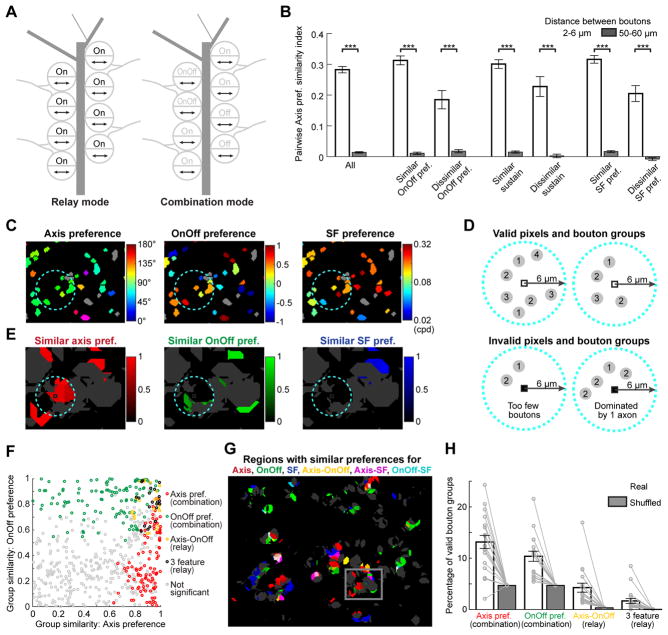
Early studies across a number of species suggested that dLGN neurons often inherit their tuning from one or a few RGC inputs of the same type, consistent with a labeled-line model of transmission (Figure 1A; Kaplan and Shapley, 1984; Cleland et al., 1971; Litvina and Chen, 2017a). However, recent studies in mice using genetic tools (Hammer et al., 2015), electron microscopy (EM, Morgan et al., 2016), rabies tracing (Rompani et al., 2017), and optogenetics (Litvina and Chen, 2017b) suggest that up to tens of RGC axons – including inputs from morphologically-distinct RGC types – can converge on a dLGN neuron. Moreover, at a scale of ~10 μm, boutons from multiple RGCs often form synaptic clusters on individual dLGN dendrites (Figures 1B and 5; Morgan et al., 2016). To understand the functional implications of this fine-scale convergence for the transmission and integration of visual information, we asked whether or not nearby boutons from different RGCs share similar tuning preferences (Figure 1C).

Figure 1. Models for convergence of retinal axons in dLGN thalamus.

A. Labeled-line model: all or most retinal boutons contacting a dLGN neuron proximal dendrite (dark gray) arise from a single RGC axon (light gray).

B. Electron microscopy reconstruction demonstrates boutons from multiple RGC axons (different colors) contacting the same dLGN neuron dendritic domain. Adapted from Morgan et al., 2016.

C. Different axons contacting the same dLGN neuron could exhibit the same visual feature preference (left; arrows indicate common preference for axis of motion) or random preferences (right).

We addressed this question using a combination of methods. First, we mapped visual responses of hundreds of individual RGC boutons in the dorsal ‘shell’ region of dLGN (Grubb and Thompson, 2004; Cruz-Martín et al., 2014), using high-resolution, chronic two-photon calcium imaging in awake mice. We ensured that comparisons of visual tuning preferences were restricted to boutons from different RGC axons by axon classification based on inter-bouton correlations in spontaneous activity. At the scale of ~2–6 μm, pairs of boutons from different RGCs often exhibited similar feature preferences. In particular, groups of nearby boutons could exhibit similar preferences for either a single feature or for multiple features, suggesting the presence of ‘combination-mode’ or ‘relay-mode’ convergence, respectively (Rompani et al., 2017). New analyses of a large-scale EM dataset confirmed that RGC boutons spaced 2–6 μm apart frequently synapse onto a common target dendritic domain. Together, these data suggest rules by which thalamic dendrites may integrate information from within and across specific classes of RGCs.

Results

Retinotopic mapping of dLGN cell bodies and retinal axons in awake mice

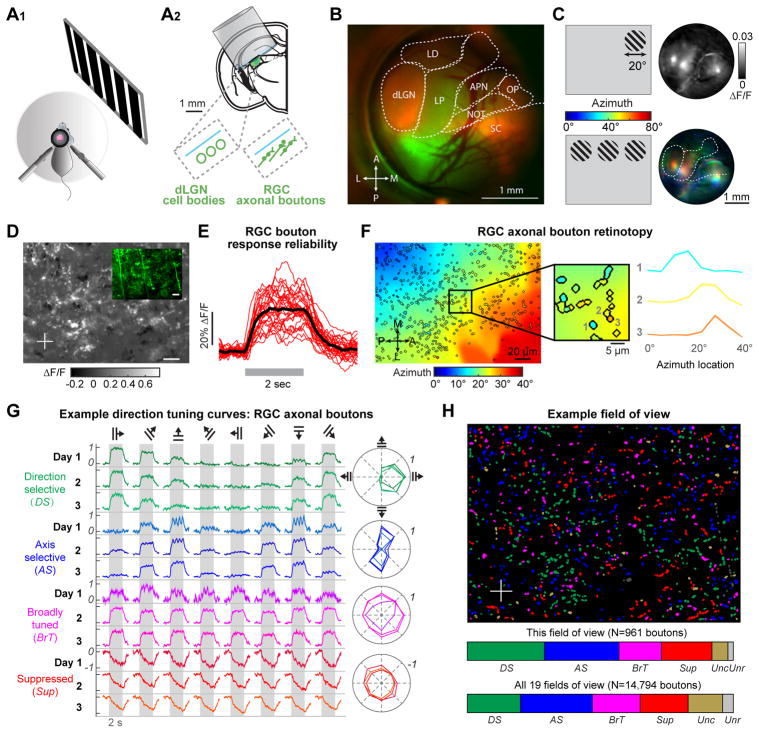
To visualize the organization of tuning properties in dLGN, we developed methods for chronic implantation of a cranial window and cannula over dorsal thalamus (Figure 2A). The benefits of this approach as compared to acute imaging studies (Marshel et al., 2012; Hillier et al., 2017) include improved image quality and an absence of anesthesia, which can affect visual responses (Durand et al., 2016). We first mapped visually-evoked bulk epifluorescence responses from GCaMP6f-expressing cell bodies. We observed retinotopic maps in dLGN, lateral posterior thalamus, superior colliculus, and other areas (Figure 2B–C). Injection of an anterograde tracer into the contralateral eye near the end of an experiment further confirmed dLGN location (Figure 2B, red).

Figure 2. Retinotopic scatter and diverse feature tuning of retinal axons in dLGN of awake mice.

A. A₁: schematic of imaging setup. A₂: schematic of mouse brain coronal section and implanted cannula for high-resolution imaging of cell bodies or RGC axonal boutons.

B. Epifluorescence image through the cranial window. Green: AAV-GCaMP6f infection of thalamus. Red: CTB-Alexa594 fluorescence in RGC axons following contralateral eye injection. Outlined thalamic nuclei: LD, lateral dorsal nucleus; dLGN, dorsal lateral geniculate nucleus; LP, lateral posterior nucleus; APN, anterior pretectal nucleus; NOT, nucleus of the optic tract; OP, olivary pretectal nucleus; SC, superior colliculus.

C. Top: Bulk GCaMP6f response of different thalamic nuclei (right) to presentation of a focal visual stimulus (left). Bottom: Pseudocolored image of retinotopic azimuth preferences (right) for stimuli presented at three horizontal locations (left).

D. Two-photon image of visually-evoked responses across RGC boutons in dLGN (sum of maximum- and minimum-response projections across multiple stimulus conditions). ΔF/F: fractional change in fluorescence. Inset: image of raw fluorescence from the same FOV, 135 μm below the surface of the optic tract.

E. Reliable single-trial responses of an individual RGC bouton to repeated presentations of the same visual stimulus.

F. Left: map of bouton retinotopic preferences. Colors within bouton masks indicate preferred azimuth location. All other pixels contain a smoothed estimate of neuropil retinotopic preferences. Middle: zoom-in illustrating substantial scatter of retinotopic preference in neighboring boutons. Right: normalized azimuth tuning curves of neighboring boutons (mean ± s.e.m.).

G. Boutons were classified into functional categories according to their responses to 2-sec presentation of drifting gratings (gray bars). Left: example mean response timecourse for one bouton in each category. Right: normalized mean response tuning curves. Tuning was stable across 3 consecutive days.

H. Example FOV with bouton masks labeled by category (STAR Methods). Lower colorbar: proportion of boutons in each category across 19 FOV from 5 mice (N = 14,794 boutons; DS: 20%; AS: 27%; BrT: 18%; Sup: 18%). Rarely, masks were responsive but not classified (Unc: 13%) or were not significantly responsive to any stimuli (Unr: 4%).

See also Figures S1, S2, and Videos S1, S2.

We then mapped retinotopic preferences at cellular resolution using two-photon calcium imaging of dLGN shell neurons. We presented a vertical or horizontal bar containing band-passed spatiotemporal noise (bar width: 5°; Video S1; Niell and Stryker, 2008) at several locations in visual space. In 3 fields of view (FOV) from 2 mice, we observed large-scale maps of retinotopy across visual axes of elevation (ventral-to-dorsal) and azimuth (nasal-to-temporal; Figure S1B).

While previous studies showed that dLGN inherits a coarse topographic map of visual space from retina (Pfeiffenberger et al., 2006), the fine-scale limit of retinotopic organization across RGC boutons is unknown. We recorded the calcium activity of hundreds of RGC boutons in the upper 20–90 μm of the dLGN (80–150 μm below the surface of the optic tract; STAR Methods). We used a similar imaging approach as for cell body recordings, except that AAV-GCaMP6f was injected into the contralateral eye (Figure 2A₂, D). Single-trial evoked responses from individual boutons were robust across multiple presentations of the same stimulus (e.g. Figure 2E). RGC boutons exhibited a coarse-scale retinotopic organization (Figures 2F and S1D; background pixels indicate smoothed population retinotopic preference; Video S2; N=15 FOV from 3 mice). We observed an approximately two-fold expansion in the spatial representation of retinotopic locations along the visual axis of elevation vs. azimuth, similar to dLGN cell bodies (Figure S1E–F). However, the retinotopic map was disordered at the level of neighboring boutons (Figure 2F, right), indicating fine-scale retinotopic ‘scatter’ (Figure S1G). Notably, this scatter of ~20 μm in azimuth and ~40 μm in elevation corresponded to average retinotopic displacements of only ~2° — less than the size of most RGC receptive fields (Baden et al., 2016).

Diverse yet sharp feature tuning across cell bodies and retinal axons in dorsal dLGN

Given that RGC boutons are not arranged according to retinotopic preferences at the 20 μm spatial scale, we asked whether nearby RGC boutons were organized according to preferences for other visual features (Figure 1C). A first clue came from imaging of cell bodies in dLGN shell, a region known to process visual motion and other features (Grubb and Thompson, 2003; Marshel et al., 2012; Piscopo et al., 2013; Suresh et al., 2016). Locally broad or homogeneous feature tuning of dLGN neurons might imply random retinal convergence onto dLGN targets. In contrast, we found that feature tuning (e.g. for axis of motion, Figure S1H) could be diverse yet sharp across nearby dLGN neurons.

RGC inputs to the same region of dLGN shell exhibited a high degree of functional diversity, sufficient to give rise to this diverse tuning of nearby dLGN neurons. Visual response profiles of individual RGC boutons, and their stability across recording sessions, are illustrated in Figure 2G. Boutons were categorized (Figure S2A–C and STAR Methods) as either responsive to one direction of motion (direction selective, ‘DS’), responsive to opposite directions of motion along the same axis (axis selective, ‘AS’, also known as ‘orientation selective’, Dhande et al., 2015), broadly responsive across all directions (broadly tuned, ‘BrT’), or suppressed (‘Sup’; Rodieck, 1967; Tien et al., 2015). We observed relatively similar proportions of boutons in each of these categories in a map of 961 boutons from one FOV, and across 19 FOV from 5 mice (Figure 2H). Further, boutons within each category exhibited diverse feature preferences (e.g. for different directions or axes of motion, Figure S2B), and thus belonged to distinct RGC types (Sanes and Masland, 2015). In addition, responses to luminance increments/decrements (‘OnOff’), to gratings of different spatial frequencies (‘SF’), and to different stimulation locations revealed diverse preferences and receptive field sizes across boutons in each category (Figure S2D–H). Together, these data revealed sharp and diverse visual feature tuning across neighboring RGC boutons in dorsal dLGN.

Identifying RGC boutons from the same axon

To assess whether nearby bouton pairs exhibit similar visual feature preferences (Figure 1C), it was critical that we avoid analyzing pairs belonging to the same axon. Bouton pairs were assigned to the same axon if they showed high correlations in spontaneous activity during long periods of uniform luminance (Petreanu et al., 2012). As illustrated in Figure 3A, the spontaneous activity of neighboring bouton pairs could be uncorrelated, while pairs of boutons spaced far apart could be highly correlated. We assigned correlated groups of boutons to the same axon by selecting a very conservative threshold based on hierarchical clustering, thereby restricting subsequent analyses to bouton pairs clearly belonging to different axons (Figures 3B, S3A–B and STAR Methods, Axon identification). Analyses of stimulus-evoked responses – epochs not used for classification – confirmed highly similar visual tuning of boutons assigned to the same axon (Figure 3B). This approach yielded ~100 distinct axons per FOV, with 1–79 imaged boutons per axon (median: 4 boutons/axon; Figure S3F).

Figure 3. Assignment of RGC boutons to the same axon.

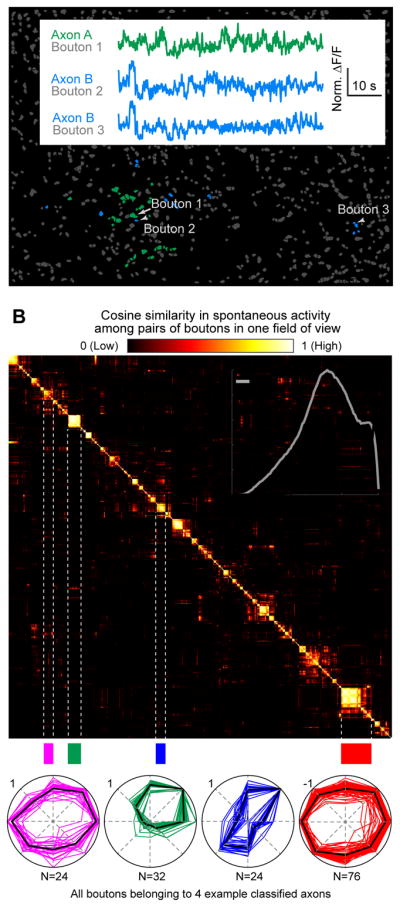
A. Boutons with high correlations in spontaneous activity were assigned to the same axon (e.g. Axon A, green, or Axon B, blue). Inset: an example pair of boutons assigned to the same axon (Bouton 2 vs. 3) had highly correlated spontaneous activity (Pearson correlation coefficient: 0.62) despite being ~100 μm apart, while nearby or distant boutons assigned to different axons showed lower pairwise correlations (Bouton 1 vs. 2: 0.07; 1 vs. 3: 0.04).

B. Top: matrix of pairwise cosine similarity in spontaneous activity (a measure of similarity in correlation coefficients between each bouton in a pair and all other boutons in the FOV; STAR Methods) for boutons imaged in A, sorted using hierarchical clustering. Four distinct blocks of boutons assigned to four different axons are highlighted. Bottom: peak-normalized direction tuning curves for all boutons from these four axons. Red: polar plots of boutons from a suppressed axon. Inset: increased similarity in evoked response tuning curves (including all 26 stimulus types, Figure S2D) for pairs of boutons from the same axon (black) or different axons (gray). N = 19 FOV, 5 mice.

See also Figure S3.

Nearby RGC boutons prefer a similar axis of visual motion

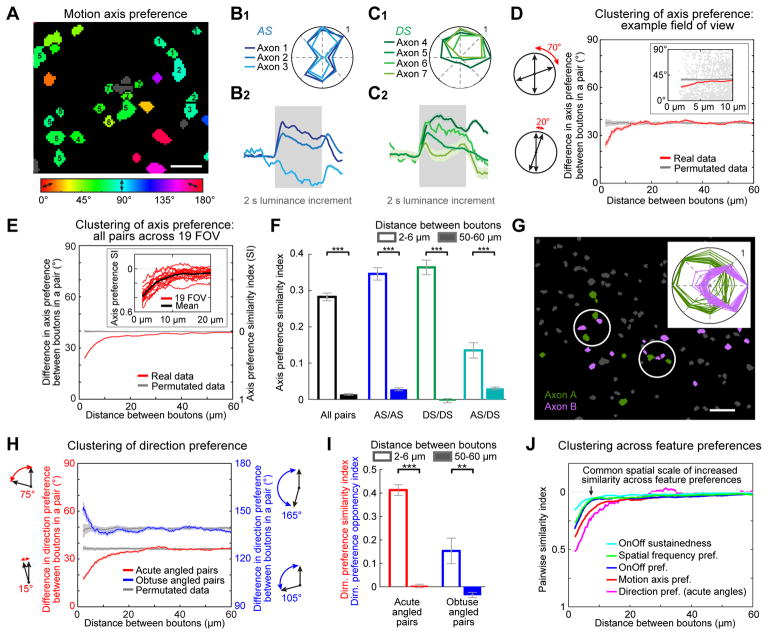
We tested if nearby RGC bouton pairs exhibit similar or random preferences for axis of motion (Figure 1C). Figure 4A shows neighboring boutons from three different axis-selective (AS) axons with similar preferences for gratings drifting either upward or downward along the vertical axis (Axons 1–3; Figure 4B₁). Each of these axons exhibited distinct OnOff responses (Figure 4B₂), further confirming that these responses originated from distinct axons. Similarly, neighboring boutons from four different direction-selective (DS) axons also preferred a similar axis of motion (Axons 4–7; Figure 4C₁), despite exhibiting distinct OnOff responses (Figure 4C₂).

Figure 4. Fine-scale functional organization of visual feature preferences in RGC boutons.

A. RGC boutons from a subregion of an example FOV, each colored according to its preferred motion axis (gray: no preference).

B–C. Average direction tuning curves (top) and normalized response timecourses during full-field luminance increments (bottom) for AS (B) and DS (C) axons numbered in panel A. These nearby axons preferred similar directions of motion (Axons 4–7) and/or similar axes of motion (Axons 1–7). Nevertheless, Axons 1 and 5–7 had ‘On’ responses at stimulus onset, while Axon 3 had an ‘Off’ response at stimulus offset and Axons 2 and 4 had both On and Off responses. Timecourses are mean ± s.e.m. across boutons from each axon.

D. Left: schematics illustrating calculation of difference in axis preference for a pair of boutons. Right: average absolute difference in motion axis preference vs. inter-bouton spacing (red, mean ± s.e.m., 4 μm sliding window) for an example FOV (generated from 87,827 pairs for which both boutons had well-defined axis preferences and belonged to different axons). Gray: same analysis following random permutation of differences in axis preference across all bouton pairs spaced 2–150 μm apart. Inset: zoomed-in scatter plot of pairs spaced 2–10 μm apart.

E. Same as D, but including all bouton pairs (from 19 FOV, 5 mice). Inset: functional clustering of axis preference for nearby boutons was evident in every FOV. SI: axis preference similarity index (1: perfect similarity; 0: chance similarity).

F. Mean axis preference similarity index for pairs of boutons spaced 2–6 μm apart (hollow bars; # of pairs: all pairs: 3258; AS/AS: 1383; DS/DS: 1066; AS/DS: 809) and 50–60 μm apart (solid bars; all pairs: 70,522; AS/AS: 28,736; DS/DS: 18,525; AS/DS: 23,261). AS/DS pairs are composed of one AS and one DS bouton. ***p < 0.001; Mann-Whitney-Wilcoxon test.

G. Example FOV and direction tuning curves (inset) for boutons from two DS axons (green and purple) with opposite direction preferences. Inter-axonal bouton pairs were often in close proximity (white circles).

H. Two forms of clustering of DS/DS bouton pairs. For pairs with preferences differing by <90° (i.e. by acute angles: N=159,282 pairs, 19 FOV, 5 mice), nearby pairs tended to prefer similar directions (red: mean absolute difference in direction preference). For pairs with preferences differing by >90° (i.e. by obtuse angles: N=64,487 pairs), nearby pairs tended to prefer opposite directions (blue). Gray: same analysis following permutation of differences in direction preference across pairs spaced 2–150 μm apart. Error bars, s.e.m.

I. Mean direction preference similarity index for all DS/DS bouton pairs with preferences differing by <90° (red; 1: identical direction preferences; # pairs 2–6 μm apart: 884; 50–60 μm apart: 13,241) and by >90° (blue; 1: opposite direction preferences; # pairs 2–6 μm apart: 182; 50–60 μm apart: 5,284). **p < 0.01; ***p < 0.001; Mann-Whitney-Wilcoxon test.

J. Direct comparison of pairwise similarity indices across feature preferences.

See also Figure S4.

We quantified the absolute difference in axis preference between pairs of boutons belonging to distinct axons (including AS and DS boutons, all of which had a well-defined axis preference; Figure S2A–B). Figure 4D shows the difference in axis preference between two boutons as a function of inter-bouton distance, for one FOV. The mean absolute difference in axis preference of boutons spaced ~2–6 μm apart was substantially less than chance (STAR Methods, Functional clustering of bouton pairs), indicating that they preferred similar axes of motion. In contrast, similar effects were not observed for boutons spaced farther apart (e.g. 50–60 μm apart).

We obtained similar results when combining data from all 1,024,626 eligible bouton pairs imaged across 19 FOV from 5 mice (Figure 4E). Similar axis preferences (<10° apart) were especially common for nearby pairs spaced 2–6 μm apart (Figure S4B). To evaluate the consistency of this functional clustering across experiments, we converted differences in axis preference into a pairwise similarity index (0: chance similarity; 1: identical feature preference; STAR Methods). We found that the increased similarity in axis preference for nearby bouton pairs was remarkably robust, as it was evident in each of 19 FOV from 5 mice (Figure 4E, inset; Figure 4F). Importantly, this fine-scale increase in similarity of axis preference was not strongly sensitive to the threshold used to assign two boutons to the same axon (Figure S4C).

The observed increase in pairwise similarity in axis preference persisted when restricting analysis either to pairs of AS boutons or to pairs of DS boutons (Figure 4F), suggesting that a similar clustering rule exists for functionally-distinct categories of boutons. Interestingly, we also observed above-chance similarity in axis preference for across-category pairs consisting of one AS and one DS bouton (Figure 4F). As elaborated below, these results have important functional implications for selective convergence of inputs within and across RGC types.

Functional clustering of RGC boutons preferring similar or opposite directions of motion

The similarity in axis preference in nearby pairs of DS boutons could be driven by boutons with near-identical direction preferences (thereby reinforcing direction tuning in a target dendrite), and/or by pairs with near-opposite direction preferences (thereby creating motion axis or orientation tuning). Examples of nearby pairs of DS boutons with similar or opposite direction preferences are shown in Figures 4C, G and S4D. When considering all pairs of DS boutons with preferences differing by less than 90° (i.e. by acute angles), we observed functional clustering of similar direction preferences for pairs spaced ~2–6 μm but not for those spaced 50–60 μm apart (Figure 4H–I, red). Next, we considered all pairs of DS boutons with preferences differing by greater than 90° (i.e. by obtuse angle s). We observed significant fine-scale functional clustering of pairs with near-opposite direction preferences (Figures 4H–I, blue, and S4E). Thus, a judicious arrangement exists whereby neighboring DS boutons demonstrate functional clustering for similar or opposite direction preferences, possibly contributing to direction tuning or axis tuning of target dLGN neurons, respectively (Marshel et al., 2012; Zhao et al., 2013; Scholl et al., 2013; Dhande et al., 2015; Suresh et al., 2016).

Generality of fine-scale functional clustering across multiple visual features

Next, we asked whether similar functional clustering also existed for OnOff or SF preference, and for OnOff response sustainedness. We first characterized sensitivity to full-field changes in luminance. Most boutons, regardless of functional category, were also responsive to luminance increments, decrements, or both (corresponding to OnOff preference index values of 1, −1, or 0, respectively; Figures 4B₂, C₂ and S2E). Figure S5A–C shows a group of nearby boutons from different axons, all ‘On’ sensitive and broadly tuned for motion direction. As with axis preference and direction preference, we observed a sharp increase in similarity of OnOff preference for bouton pairs spaced 2–6 μm apart that was evident in every FOV (Figure S5D–E). This functional clustering persisted even when restricting analyses to pairs of boutons both belonging to a specific functional category (Figure S5F). In addition, we observed fine-scale functional clustering of bouton pairs with similar response dynamics (i.e. transient or sustained responses) during changes in luminance (Figures S5A–C, S2F and S5G), and of bouton pairs with similar SF preferences (Figures S2G and S5H–J). Thus, a similar spatial scale of functional clustering of RGC boutons in dLGN exists across multiple visual feature preferences (Figure 4J).

Nearby RGC boutons often target the same dLGN neuron dendritic domain

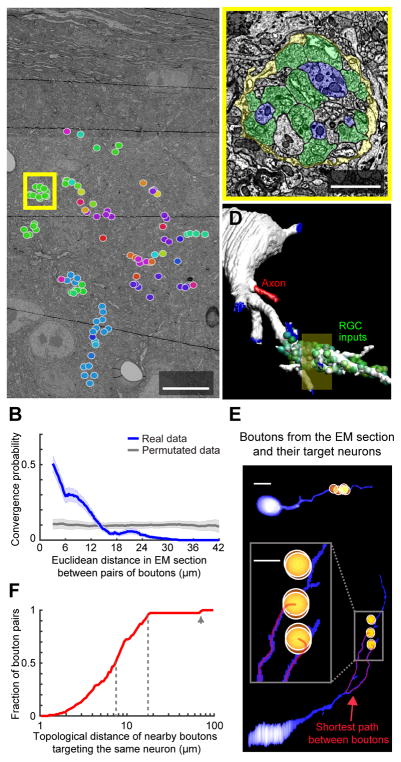
What is the likelihood that pairs of RGC boutons spaced ~2–6 μm apart converge on the same dLGN neuron, and specifically onto the same dendritic domain (e.g. Figure 1B)? To address this question, we analyzed an existing EM volume of dLGN (Morgan et al., 2016), focusing on a 30 μm × 40 μm region in dLGN shell, roughly matching the region imaged in vivo. We identified all RGC boutons in this region (N=100) and labeled them according to the thalamocortical cells they innervated. Critically, we found that 52.3% (182/348) of all bouton pairs spaced less than 6 μm apart targeted the same dLGN neuron. This percentage was much higher than expected by chance, and dropped rapidly with increasing inter-bouton distance (Figures 5B and S6A–B). These tight local clusters of converging RGC boutons often reflect glia-encapsulated structures referred to as synaptic glomeruli (Figure 5C; Famiglietti and Peters, 1972). A 3D reconstruction of a dLGN neuron dendrite illustrates how RGC boutons densely cluster and extend along the dendritic shaft and protrusions (Figure 5D; Video S3). Analysis of the EM plane in Figure 5A revealed that, for all pairs of boutons spaced 2–6 μm apart that shared a common target neuron, over 95% contacted the same dendritic domain (topological distances along the dendrite were <18 μm; Figures 5E–F and S6C). Rarely, however, two boutons spaced ≤6 μm apart (Euclidean distance) could each target a different dendrite of the same neuron (and were therefore separated by a large topological distance, Figure 5E, bottom).

Figure 5. Nearby RGC boutons often target the same dLGN neuron dendritic domain.

A. New analysis of a 3D EM volume of mouse dLGN (Morgan et al., 2016), focusing on a dorsal subregion of a coronal section through dLGN shell. All 100 RGC boutons in this subregion were identified, and those targeting the same dLGN neuron were assigned the same color.

B. The fraction of bouton pairs sharing a common target dLGN neuron (blue) decreased with increasing distance between boutons, with a falloff similar to Figure 4J. Gray: permutated data. Errorbars: 95% confidence intervals.

C. Zoom-in of yellow box in A, illustrating many RGC boutons (green) decorating the same postsynaptic dendritic shaft or protrusions (violet), with all RGC boutons in this ‘glomerulus’ surrounded by common glial ensheathment (yellow). See Video S3.

D. The dLGN dendrite from the zoomed-in area in C (yellow shaded square in D) was traced back to its cell body, together with all apposing RGC boutons (green). Blue regions: terminations of reconstruction.

E. Projection images of two additional example neurons contacted by RGC boutons (semitransparent orange balls) contained in the EM subregion in A. Most nearby pairs of boutons in A targeted the same dendritic domain (e.g., top neuron, contacted by a cluster of 5 RGC boutons from A; see also Figure S6D). However, in 1/32 neurons (bottom) contacted by RGC boutons from A, boutons that were nearby in space sometimes targeted different dendrites. To distinguish between these distinct bouton arrangements, we quantified the shortest trajectory (red line) along the dendrite(s) between any pair of boutons (topological distance).

F. Cumulative distribution of topological distances between all boutons pairs (N = 182) that were 2–6 μm apart in space (Euclidian distance in the EM subregion in A) and that contacted the same target neuron. Most pairs had short topological distances (dashed lines: median: 7.49 μm; 95%: 17.53 μm), and nearby boutons only rarely targeted different dendrites (arrow).

See also Figure S6.

We also analyzed a large number of RGC axon segments from the dLGN core region of the EM volume, the majority of which likely originated from distinct RGCs (Morgan et al., 2016). We found a similarly high level of pairwise synaptic convergence for bouton pairs spaced ≤6 μm apart, even when restricting to pairs in which each bouton belonged to a distinct RGC axon. Specifically, 51% of these bouton pairs (1278/2528 pairs from 84 different axons) shared a common target neuron (Figure S6D). Together, these data support the hypothesis that bouton pairs spaced ≤6 μm apart and with similar functional preferences typically converge onto a common dLGN neuron dendritic domain.

Convergence of groups of nearby boutons

The above results demonstrate that nearby RGC bouton pairs often possess similar feature preferences when each feature is considered separately. In practice, however, the same RGC can be tuned for multiple features (e.g. axis and OnOff preference), thereby multiplexing distinct channels of visual information. Local similarity of individual feature preferences may reflect a ‘relay mode’ of axonal convergence (Figure 6A), in which nearby boutons from different RGC axons are mostly of the same functional type, thus sharing multiple feature preferences in common. Alternatively, a ‘combination mode’ of convergence may exist in which some preferences are matched while others are not (Figure 6A). The names of these two modes are adopted from a recent anatomical study (Rompani et al., 2017) suggesting that some dLGN neurons receive inputs from one or two morphologically similar RGC types, while others receive inputs from many distinct types which may nevertheless share some feature preferences in common.

Figure 6. Relay-mode and combination-mode convergence of nearby RGC boutons.

A. RGC axons often multiplex information (e.g. motion axis and OnOff). Nearby boutons from different axons could exhibit similar preferences for all features (‘relay mode’, left) or for a single feature (‘combination mode’, right).

B. Bouton pairs 2–6 μm apart with either similar or dissimilar preferences for OnOff, OnOff sustainedness, or SF all exhibit similar motion axis preference. N’s, from left to right: 3,258; 70,522; 2,004; 32,916; 391; 13,075; 2,042; 39,071; 422; 12,639; 2,635; 49,163; 578; 18,498. All bar plots: mean ± s.e.m. ***p < 0.001; Mann-Whitney-Wilcoxon test.

C. Left to right: maps of boutons in an example subregion, colored by bouton preferences for motion axis, OnOff or SF, respectively. Gray boutons lack well-defined preference estimates.

D. Schematic illustrating analyses of ‘groupwise’ functional similarity. Analyses were restricted to pixels (black squares) that contained groups of 3 or more boutons (gray discs) within a concentric circle of 6 μm radius (blue dotted circles). In addition, we required that these boutons have well-defined preference estimates for motion axis, OnOff and SF, and that <67% of boutons in the group belong to any single axon (see also Figure S7B). Bouton numbering denotes axon identity.

E. Pixel maps of groupwise similarity index for motion axis (left), OnOff (middle), and SF preferences (right), for the subregion in C. Pixels with significant similarity index values (exceeding 95% of shuffled estimates) are colored, while other valid pixels are gray and invalid pixels are black. Dashed cyan circles in C and E illustrate an example of a pixel surrounded by a local group of boutons with similar preferences for axis (left) but not for other features (middle and right).

F. Groupwise similarity indices for motion axis preference and OnOff preference (as in Figure 6E), plotted for valid pixels (same FOV as C, E). Bouton groups could exhibit similar preferences for motion axis only (‘Axis preference combination mode’, red), for OnOff only (‘OnOff preference combination mode’, green) or for both features (‘Axis-OnOff relay mode’, yellow). Other groups additionally demonstrated significant groupwise similarity for SF preference (‘3 feature relay’, black). Gray circles indicate groups that did not exhibit significant groupwise similarity (i.e. greater than 95% of shuffled estimates) for either feature preference.

G. Pseudocolor image illustrating various modes of convergence for groups of boutons in an example FOV (gray square, subregion shown in E). Red, green and blue: combination-mode groups with similar preference for only one feature (motion axis, OnOff, or SF, respectively). Yellow, purple, cyan, white: relay-mode bouton groups with similar preferences for two or more features.

H. Percentages of valid groups of nearby boutons with significant similarity in preference for only axis or OnOff preference (combination mode), for axis and OnOff preference (relay mode), or for all three feature preferences (3 feature relay mode), for each of 19 FOV. The percentages of unique bouton groups of each mode were consistently higher than expected by chance (shuffled data, gray bars).

See also Figure S7A–E.

Further analyses provided evidence for the existence of both modes. For example, consistent with combination-mode convergence, we observed functional clustering of axis preference even when analysis was restricted to bouton pairs with dissimilar OnOff preferences (Figure 6B; see also Figure 4A–C). Consistent with relay-mode convergence, we also observed functional clustering of axis preference when restricting analyses to pairs of boutons with similar OnOff preferences. This was also evident when separately analyzing bouton pairs with either similar or dissimilar OnOff sustainedness, or with similar or dissimilar SF preferences. Analysis of local pairwise similarity in OnOff preferences yielded similar results (Figures S7A and S5A–C), suggesting the presence of distinct combination-mode bouton clusters for either axis or OnOff preference.

Thus far, we have focused on analyses of pairs of RGC boutons. We next assessed whether larger groups of nearby boutons (Figures 1B and 5A, C–E) share similar preferences for one or multiple features. Examples of nearby groups of boutons with similar preferences for motion axis, OnOff preference, or SF preference are illustrated for a subregion of one FOV (Figure 6C). To directly assess groupwise similarity in feature preferences of nearby boutons, we first selected all pixels in the FOV that were located within 6 μm of a group of boutons (typically 3–7 boutons) that mostly belonged to distinct axons (Figures 6D and S7B; for full criteria, see STAR Methods, Functional clustering of local groups of boutons). In order to assess similarity in feature preferences of nearby groups of boutons, we generated a normalized groupwise similarity index for each valid pixel (index of 1: identical feature preference in all boutons in the group; 0: chance level of similarity, estimated after shuffling bouton preferences). Maps of groupwise similarity index for the group of nearby boutons surrounding each pixel in Figure 6C are shown in Figure 6E. A scatter plot of the degree of similarity in axis preference vs. OnOff preference for valid pixels revealed local groups of boutons with significant groupwise similarity in preferences for only one visual feature, corresponding to ‘combination-mode’ clusters (Figure 6F). We also observed groups of boutons with significant similarity in preferences across multiple visual features, corresponding to ‘relay-mode’ clusters, possibly consisting of boutons from RGC cells of the same type (Rompani et al., 2017). This finding was further illustrated by combining data from the three maps in Figure 6E into a single pseudocolor map (Figures 6G and S7C).

Combination-mode bouton groups with similar axis or OnOff preference, and relay-mode groups with similar axis and OnOff preferences, were present in nearly all fields of view across 5 mice (Figures 6H and S7D; we also observed extreme ‘relay-mode’ groups with above-chance similarity in axis, OnOff and SF preference). The presence of groupwise similarity did not depend strongly on the number of boutons in the group (Figure S7E). Finally, we did not observe a bimodal distribution of groupwise similarity for any tuning preferences (e.g. Figure 6F), suggesting that convergence across groups of RGC boutons may lie on a continuum between combination and relay modes.

Divergent boutons from the same RGC axon may ‘de-multiplex’ visual information channels

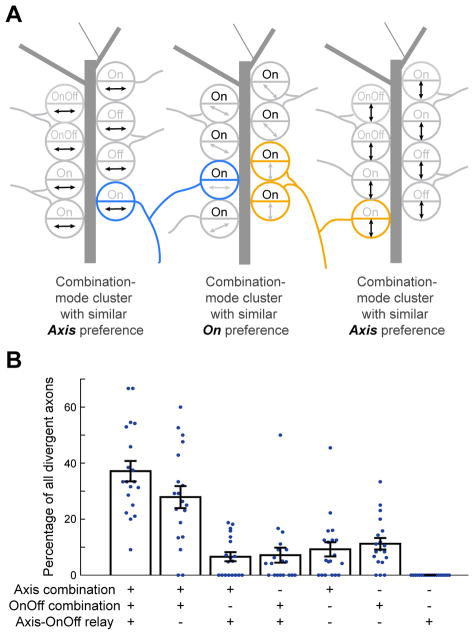
RGC axonal arbors often diverge to participate in several bouton clusters targeting different dLGN neurons (Morgan et al., 2016). We wondered whether the same RGC axon could contribute different boutons to functionally distinct clusters. Figure 7A illustrates a hypothetical situation involving one axon (blue) selective for motion along the horizontal axis and for luminance increments. Different boutons from this axon might participate either in a cluster of similarly On-responsive boutons or in a cluster with similar motion axis preference. Indeed, the majority of imaged axons contained multiple boutons that each participated in distinct combination-mode clusters exhibiting preferences for different visual features (Figure 7B, left two bars; Figure S7F; STAR Methods). We also observed cases where different boutons from the same axon participated in either combination-mode or relay-mode clusters. As discussed below, such axonal divergence may provide an efficient means by which the same RGC can contribute to the creation and robustness of distinct tuning properties across different target neurons.

Figure 7. Different RGC boutons from the same axon often participate in distinct functional clusters.

A. Schematic illustrating three combination-mode bouton clusters that exhibit similar preferences for either horizontal motion (left), On (middle), or vertical motion (right). An axon selective for horizontal motion and On (blue) could participate in the first two clusters, while an axon selective for vertical motion and On (orange) could participate in the last two clusters.

B. Percentage of divergent axons in each FOV (blue dots) that contain boutons innervating different types of functional clusters (combination-mode clusters with common axis preference or OnOff preference, or relay-mode clusters that share both preferences). Mean ± s.e.m.

See also Figure S7F.

Discussion

We have discovered a fine-scale organization of RGC axonal boutons, revealing a functional logic underlying bouton clusters that typically converge onto the same thalamic dendrite. Our findings suggest a set of rules underlying dendritic pooling of visual information from within and across specific subsets of RGC cell types. Below, we discuss the potential benefits of this pooling for promoting high sensitivity, functional diversity, and context-invariant feature tuning of dLGN neurons.

A common spatial scale for convergence of axons with similar visual feature preferences

The spatial scale of functional bouton clustering (~6 μm) was surprisingly similar across visual feature preferences (Figure 4J). This scale is comparable to the local clustering of functionally-similar synapses, identified by imaging nearby dendritic spines of neurons in visual cortex (Wilson et al., 2016; Iacaruso et al., 2017). Synaptic clustering on a local region of dendrite may facilitate transmission of sensory information, including via nonlinear dendritic integration (Wilson et al., 2016; Gökçe et al., 2016). Notably, the relative synaptic strengths of individual boutons in a cluster will also influence dendritic integration (Litvina and Chen, 2017b).

Convergence of inputs within and across RGC functional categories and cell types

Electrophysiology (Grubb and Thompson, 2003; Piscopo et al., 2013; Tang et al., 2016) and imaging (Marshel et al., 2012; Figure S1H) studies suggest that dLGN neurons – even neighboring neurons – can show sharp yet diverse tuning for distinct visual features. Our findings suggest that sharp feature tuning may arise, in part, via selective presynaptic convergence of clusters of axonal boutons from one or multiple RGC types that all share a common preference for at least one visual feature (Figure 6A, right). Notably, we found that bouton clusters can integrate across RGC types belonging to different categories (e.g. DS and AS) or to the same category (e.g. for RGC boutons with opposite direction preferences but with a common preference for axis of motion, reviewed by Dhande et al., 2015).

Our definition of ‘relay mode’ is based on the presence of at least two shared feature preferences. Interestingly, we even found a subset of groups of RGC boutons with similar preferences for AS, OnOff and SF, suggesting the presence of ‘extreme relay-mode’ tuning, consistent with a labeled-line model. We speculate that relay-mode convergence may allow target neurons to inherit RGC type-specific feature tuning with increased signal-to-noise (Martinez et al., 2014; Jeanne and Wilson, 2015) and/or increased contrast sensitivity (Rathbun et al., 2016). Indeed, both relay- and combination-mode convergence may decrease the effects of trial-to-trial variability and/or adaptation in the responses of individual RGC inputs, and could increase the efficacy of weaker RGCs that might not drive postsynaptic responses when activated in isolation.

Combination-mode convergence may bestow dLGN neurons with the property of invariance, more commonly studied in cortical neurons. For example, complex cells in cat visual cortex show phase-insensitive responses to a sinusoidal grating, likely due to integration of inputs from many phase-sensitive ‘simple cells’ (Hubel and Wiesel, 1962). We propose that a similar logic applies to combination-mode RGC bouton clusters targeting individual dLGN dendrites, which could pool information from shared bouton preferences for one feature while integrating diverse preferences for other features. As the shared feature preference will differ across combination-mode clusters, the thalamus is poised to create robust, ‘all-purpose’ feature detectors of local luminance changes, motion direction, motion axis, or other visual features. For example, a cluster of ‘On’ RGC boutons synapsing on a dLGN neuron could promote tuning for local luminance increments irrespective of the axis of motion or spatial frequency of the stimulus (Figure 7A, middle). Future studies could assess whether this logic underlying pre-synaptic functional clustering of different information channels in the mouse dLGN shell is generalizable to other mouse thalamic regions (e.g. dLGN core), to other species (e.g. the C laminae of cat dLGN, Stanford et al., 1981), and to brain regions beyond the thalamus.

Technical considerations

Caveats involving calcium imaging in axons are unlikely to alter our main findings. First, the relationship between spiking and calcium activity in axons, while not necessarily linear, is nevertheless monotonic, and thus unlikely to affect estimates of peak response preferences (e.g. preferred direction of motion). Second, tuning estimates in nearby boutons could suffer from common contamination from surrounding neuropil. However, GCaMP6 expression was sparse, surrounding neuropil response magnitudes were relatively small, and neighboring boutons often showed completely non-overlapping tuning curves.

We were unable to record from deeper RGC boutons in the dLGN ‘core’ region. Interestingly, bouton clusters are larger and more common in dLGN shell than core (Hammer et al., 2015), and dLGN neurons in shell may receive inputs from a morphologically more diverse set of RGC types than in core (Rompani et al., 2017). Future studies could use advanced imaging approaches (e.g. Sun et al., 2016) to assess whether functional clustering of RGC boutons is more common and/or more biased to combination mode in dLGN shell vs. core. Answers to this question could help clarify the contributions of dLGN shell vs. core to the emergence of cortical selectivity for features including motion direction, which has been shown to involve both retinal and extra-retinal contributions (Hillier et al., 2017). It is possible that direction-tuned dLGN shell neurons projecting to superficial layers of V1 (Cruz-Martín et al., 2014) mainly receive combination-mode RGC input (and thus more invariance to stimulus context). In contrast, direction-tuned dLGN projections to layer 4 of V1 (Sun et al., 2016) may receive heavier relay-mode RGC input, thereby transmitting information primarily from a single RGC type.

Functional organization of boutons can explain the ‘fuzzy’ logic of anatomical connections

A large-scale EM study of dLGN showed that morphologically distinct sets of RGC axons made specific connections on different sets of target neurons (Morgan et al., 2016). At the same time, these distinct sets of RGC axons all converged onto an additional set of mixed-input thalamocortical neurons. Our findings provide a functional explanation for this ‘fuzzy’ anatomical logic: we commonly observed different boutons from the same axon participating in functionally-distinct clusters. As illustrated in Figure 7A, two RGC axons might each participate in separate bouton clusters that matched each axon’s distinct preference for motion axis, while both axons might also participate in a third combination-mode cluster of boutons that matched their common preference for luminance increments. This selective divergence provides an elegant and efficient means for single RGC axons in dLGN to ‘de-multiplex’ information regarding different visual features, thereby enhancing parallel information channels across different target neurons (Alonso et al., 2006) via feature-specific functional clustering.

Perspectives and future directions

Fine-scale functional clustering of presynaptic axons has been described in fly visual projection neurons (e.g. Keleş and Frye, 2017), and in mouse and fly olfactory receptor neurons, where developmental guidance cues and activity-dependent refinement both play key roles (Imai et al., 2010; Wu et al., 2017). In contrast, functional clustering of presynaptic axons has received relatively little attention in studies of mammalian visual circuitry (but see Kremkow et al., 2016). Our demonstration of fine-scale organization of retinotopy and other features in adult mouse RGC axonal boutons points to a profound role for developmental refinement. Future studies can delineate the role of molecular mechanisms and of activity (e.g. correlated firing of similarly-tuned RGC inputs, Meister et al., 1995) in sculpting this exquisite axonal organization (Huberman et al., 2008; Hong and Chen, 2011).

Our results involving ‘combination-mode’ organization of certain bouton clusters suggest the existence of rich subthreshold receptive fields in dLGN neurons. Additional richness could arise from integration of functionally similar or distinct bouton clusters targeting separate dendrites or dendritic domains of the same dLGN neuron (Figures 5E and S6C; Morgan et al., 2016). Such richness could support both rapid, context-dependent dynamics and longer-term synaptic plasticity. For example, changes in the weights of different inputs could rapidly alter the tuning of relay neurons (Moore et al., 2011). Our chronic imaging approach in awake mice should facilitate studies of functional organization, behavioral modulation and experience-dependent plasticity of local bouton clusters in the dLGN and other hitherto inaccessible thalamic areas.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to, and will be fulfilled by, the Lead Contact, Mark L. Andermann (manderma@bidmc.harvard.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All animal care and experimental procedures were approved by the Beth Israel Deaconess Medical Center Institutional Animal Care and Use Committee. Animals were housed with standard mouse chow and water provided ad libitum. Male C57BL/6 adult mice (2–6 months old) were used in this study.

METHOD DETAILS

Viral injections

To label retinal ganglion cell axons, 1.2 μl of AAV2/2.CAG.GCaMP6f.WPRE.SV40 (Chen et al., 2013; Boston Children’s Hospital Viral Core) was gently injected intravitreally into the right eye after the mice were anesthetized by isoflurane in 100% O₂ (induction, 3%–5%; maintenance, 1%–2%). Care was taken to minimize bleeding and to prevent cataract formation during the injection procedure, and infection of RGCs was confirmed histologically. To label neurons in the dLGN, mice were anesthetized with isoflurane in 100% O₂ (induction, 3%–5%; maintenance, 1%–2%), and 100 nl of AAV2/1.CAG.GCaMP6f.WPRE.SV40 (Penn Vector Core) was stereotaxically injected into the left dLGN, at 2.25–2.3 mm lateral and 2.3–2.75 mm posterior to Bregma, and 2.55–2.85 mm ventral to the dura, respectively. In a subset of experiments, we instead injected 75 nl of AAV2/retro.hSyn.Flex.GCaMP6s (BCH Viral Core; Tervo et al., 2016) into the left V1, at 2.5–3.1 mm lateral and 3.8 mm posterior to Bregma, and 0.2 mm below the dura, respectively, and 100 nl of AAV2/1.hSyn.Cre.WPRE.hGH was stereotaxically injected into the left dLGN in the same animal, at 2.25–2.3 mm lateral and 2.3–2.75 mm posterior to Bregma, and 2.55–2.85 mm ventral to the dura. As we did not observe a difference in the labeling of dLGN neurons using the two viral injection methods, we pooled these datasets together.

Headpost and cranial window implantation

A headpost and cranial window were implanted 2–3 weeks after viral injection. Mice were given 0.03 ml of dexamethasone sodium phosphate (4 mg/ml, i.m.) roughly 3 hours prior to surgery in order to reduce brain edema. Mice were anesthetized using isoflurane in 100% O₂ (induction, 3%–5%; maintenance, 1%–2%) and placed on a heating pad (CWE) in a stereotaxic apparatus (KOPF). Ophthalmic ointment (Vetropolycin) was applied to the eyes. Using procedures similar to those described previously (Goldey et al., 2014), a two-pronged headpost was affixed to the skull, centered roughly 2.7 mm lateral and 1.9 mm posterior to Bregma over the left hemisphere, tangential to the curved skull surface. The head was then tilted to secure the headpost in custom clamps (Thorlabs, Standa) that aligned the headpost precisely parallel to the platform of the stereotaxic apparatus. A 3-mm diameter craniotomy was performed at the center of the headpost. The underlying cortical and hippocampal tissue was carefully aspirated until reaching the surface of the thalamus. The thalamic surface and optic tract was kept intact. A 3 mm × 3.4 mm (diameter × height) stainless steel cylindrical cannula (MicroGroup) was inserted stereotaxically into the craniotomy, perpendicular to the plane of the headpost. A 3-mm diameter coverslip (glued to the bottom of the cannula prior to surgery using UV-cured Norland Optical Adhesive 71) was lowered approximately 2.75 mm below the skull where it pressed slightly on the surface of the thalamus. The cannula was affixed to the skull with Vetbond (3M) followed by C&B Metabond (Parkell), to form a permanent seal. To create a low-profile adaptor to accommodate the water-immersion objective and light shielding, a neodymium ring magnet (Indigo® Instruments, outer diameter, inner diameter, height: 7.5 mm, 5 mm, 1 mm) was positioned around the cannula and glued to the skull. During two-photon imaging sessions, this ring magnet held the light shielding in place by contact with a 8 mm × 0.3 mm (diameter × height) spring steel round shim (McMaster) attached to the blackout fabric (Thorlabs). Meloxicam (0.5 mg/kg, s.c.) was administered and the mouse was allowed to recover.

Epifluorescence and two-photon calcium imaging

To initially map thalamic areas, we used epifluorescence calcium imaging to measure changes in calcium signals in response to visual stimulation in awake mice. Epifluorescence calcium videos were acquired using a custom microscope with a 4×, 0.28 NA objective (Olympus). A blue LED light source (470 nm center, 40 nm band, Chroma) was used for excitation, and the green fluorescence was passed through a 500 nm long-pass emission filter and collected using an EMCCD camera (Rolera). Images (251 × 250 pixels) were recorded using the Image Acquisition Toolbox (MATLAB) at 4 Hz.

Two-photon calcium imaging was performed using a resonant-scanning two-photon microscope (Neurolabware). All images were acquired using a 20×, 1.0 NA, 5.6 mm WD objective (Zeiss) at 4.7× (~160 × 210 μm²) digital zoom. Light shielding around the objective was used to block light emitted from the LCD screen We concentrated on imaging fields of view (FOV) at depths of 80–150 μm below the surface of the optic tract (roughly corresponding to the upper 20–90 μm of the dLGN shell; high-quality images could be obtained throughout the upper ~140–150 μm of the dLGN, data not shown), using a Ti:Sapphire laser (80 MHz; MaiTai HP DeepSee, prechirped) at 960 nm. The functional clustering in Figure 4E and the distribution of boutons belonging to each functional categories was not sensitive to imaging depth within this range (not shown). Laser power measured at the front aperture of the objective was 30–65 mW, likely a substantial overestimate of actual power reaching the sample via the cannula. Images were collected at 15.5 frames/s, 686 × 512 pixels/frame, using ScanBox (Neurolabware). Each imaging run lasted approximately 30 min, and 4–5 runs were performed during each imaging session. Occasionally, the imaging depth in between runs was adjusted slightly to account for slow drifts in the z-plane. For a given mouse, each FOV imaged in a given session was at least 20 μm above or below any FOV imaged in another session. Epifluorescence and two-photon imaging experiments were typically performed between one week and one month after headpost and cranial window implantation.

Visual Stimulation

Visual stimuli were generated using Psychtoolbox (Brainard, 1997), and displayed on a luminance-calibrated LCD monitor (Dell, 17″,1280 × 1024 pixels, 60 Hz refresh rate) placed 22 cm from the mouse’s right eye and spanning 80° × 70° of visual space (azimuth: 5° – 8 5°; elevation: −13° – 57°).

To measure large-scale retinotopic organization using epifluorescence imaging, local 20° Gabor-like circular patches containing square-wave drifting gratings (80% contrast) were presented at 9 retinotopic locations for 2 seconds (180°, 0.08 cycles/degree, 2 Hz), followed by 4 seconds of uniform mean luminance, with 30 repeats per stimulus location. To measure retinotopy with high spatial resolution during two-photon imaging, we used a binarized version of a bandpass-filtered noise stimulus with a spatial frequency corner of 0.05 cycles per degree, a cutoff of 0.32 cycles per degree and a temporal frequency cutoff of 4 Hz (Niell and Stryker, 2008). The noise stimulus was presented within 5° × 40° bars, presented vertically at one of 8 azimuth locations and horizontally at one of 8 elevations. For imaging of retinal ganglion cell axons or of dLGN cells, stimuli were presented for 2 seconds each, with a 2-second inter-stimulus interval (mean luminance) for retinal ganglion cell axons, and a 6-second inter-stimulus interval for dLGN cells. Visual stimulation also included a blank condition (mean luminance). Stimulus order was randomized within a single repeat (consisting of a single presentation of each stimulus condition), and 30 repeats (for RGC axons) or 15 repeats (for dLGN cells) were presented during one run. We performed 1–2 runs of retinotopic mapping per imaging session.

To measure visual tuning properties during two-photon imaging, we presented full screen sine-wave drifting gratings (80% contrast) at one of eight directions of motion spaced 45° apart, at spatial frequencies of 0.02, 0.08 and 0.32 cycles per degree and a temporal frequency of 2 Hz. The visual stimulation paradigm also included periods of full-screen mean luminance (gray, blank trials) or periods of luminance increments or decrements (‘On’ or ‘Off’ trials, respectively, 80% contrast). All stimuli were displayed for a 2-second duration. The inter-stimulus interval (mean luminance gray) lasted 2 seconds (for retinal ganglion cell axons) or 6 seconds (for dLGN cells). A single repeat involved presentation of the set of all of the above stimuli (one presentation of each direction/spatial frequency, three presentations of ‘On’, ‘Off’, and three or six presentations of ‘blank’ stimuli, in random order). A single run usually consisted of 10–14 repeats (for retinal ganglion cell axons) or 6–8 repeats (for dLGN cells). We recorded 3–5 runs per imaging session, each with a different randomization of trial order.

Image processing

Image preprocessing

To correct for x–y motion along the imaged plane, a series of image registration and data cleaning steps were applied. The movies taken on each imaging day were first registered to a common average field-of-view using efficient subpixel registration methods (Bonin et al., 2011). The registered movies were then spatially downsampled by 2, temporally downsampled by 5, and denoised using principal component analyses (PCA). PCA was computed from the concatenated movies across the entire imaging session. The spatial principal components with highest eigenvalues typically contained pixels with signal variations across time beyond those due to photon shot noise. Each image could be characterized by a weighted sum of these principle components. We used only the first 400 principle components (highest eigenvalues) out of ~30,000 total to reconstruct the registered and downsampled movie while removing shot noise (Burgess et al., 2016). Note that this PCA de-noising was employed only for purposes of improving the image warping coregistration steps, below. A local image normalization method (http://bigwww.epfl.ch/sage/soft/localnormalization/) was applied to each frame to normalize the fluorescence intensity across boutons and to increase the contrast between boutons and neuropil. After normalization, image warping using the imregdemons.m function (MATLAB) was implemented to align all images to a new common average field of view. The pixel-wise displacement resulting from the imregdemons function was spatially upsampled by 2 and then applied to the original, subpixel-registered movies (in the absence of PCA de-noising). A second round of image de-noising, local normalization and warping was then applied to the full-size processed movies. The newly computed pixel-wise displacement was then applied to the aligned movies from the first round of image warping. After these image registration and warping steps, no obvious x-y motion was observed. As a final step, PCA de-noising was performed a third time. Importantly, while the PCA de-noising did increase signal-to-noise and therefore yield of usable boutons or cells, the observed results did not depend on use of this operation (data not shown).

Bouton mask identification

To identify boutons and extract masks for further signal processing, we established an automated image segmentation algorithm. First, an average image of absolute ΔF/F was calculated for each trial type by averaging single condition evoked response maps across all N repetitions of that trial type (|mean((F_i−F_i0)/F_i0)|, i=1..N, where F_i is the mean fluorescence during the stimulus presentation and F_i0 is the average baseline fluorescence during the 1 second prior to each stimulus onset). We used the absolute value of ΔF/F in order to include boutons that were strongly suppressed by visual stimuli, corresponding to negative values of ΔF/F. A bouton identification procedure was then independently applied to each of these projection images. First, local normalization was applied (subtraction of local mean and division by local variance across pixels), with the local mean estimated by isotropic filtering of the image using a Gaussian kernel (with standard deviation, sigma = 3 μm). The local variance was estimated using a larger Gaussian filter (sigma = 50 μm).

Morphological filters were then applied to identify connected sets of pixels that together resembled the size and shape of a typical RGC bouton, as follows: first, small pixel gaps were filled by interpolation using a square-shaped structuring element of 1.3-by-1.3 μm. We then removed all small unconnected structures via an ‘opening’ operation using the same structuring element. To obtain candidate masks, we first binarized the above images by setting to ‘1’ all pixels with values above 10% to 15% of the maximal pixel amplitude after filtering, and setting all other pixels to ‘0’. A Euclidian distance transform was then applied to these binary images (MATLAB function ‘bwdist.m’). The built-in MATLAB watershed transform (Meyer, 1994) was used to finalize the segmentation. The results from the distance transform and the watershed transform from the individual ΔF/F images were combined by summing the distance transform across conditions and normalizing this value by the bouton count obtained by the watershed transformation. A final watershed transformation was applied to this normalized distance image to increase the accuracy of the procedure and to reduce the risk of false positives in the bouton identification procedure. In addition, to remove residual calcium signals not originating from the bouton itself, we estimated neuropil masks as circular annuli of 3 μm width, with the inner edge located 2 μm beyond the edge of a corresponding bouton mask. Pixels from adjacent bouton masks were excluded from these neuropil masks.

dLGN cell mask identification

Masks for dLGN cell bodies were automatically extracted using custom implementation of a previously developed cell sorting procedure that combines independent component analysis and image segmentation (Mukamel et al., 2009; Burgess et al., 2016). To avoid signal contamination in a minority of cases involving dendrites situated proximal to a cell body, masks for dendritic segments were also extracted using the same custom procedure, and the overlapping areas were subtracted from the masks for dLGN cell bodies. In addition, to remove background calcium signals not originating from the cell body, we estimated neuropil masks as circular annuli of 9 μm width, with the inner edge located 7 μm beyond the outermost edge of a corresponding cell body mask. Pixels from adjacent cell body masks and from dendritic segment masks were excluded from these neuropil masks. Calcium activity timecourse extraction and visual response analysis of the dLGN cells were carried out using the same methods as for RGC boutons, as described below.

Timecourse extraction and correction

To obtain raw fluorescence traces for bouton masks and neuropil masks, the fluorescence intensity value of a bouton at each time point was defined as the average fluorescence across the pixels belonging to the mask.

To account for photobleaching during imaging sessions, a bleaching correction method was established. Raw bouton and neuropil traces were first smoothed using a sliding filter (30^th percentile of a 5-minute sliding window). Then, the filtered traces were fitted using a decaying exponential, where the amplitude and the offset were independently estimated for each bouton and each neuropil ring, while the time constant was fixed to an experimentally defined constant value of 75 minutes, which was in agreement with time constants other groups have determined for the photobleaching of GCaMP6f using two-photon imaging at similar excitation wavelengths and laser power (Harris lab/Photophysics, https://www.janelia.org/lab/harris-lab-apig/research/photophysics/two-photon-fluorescent-probes). To correct for photobleaching in each trace, the fitted offset value was first subtracted from the raw trace, then the resulting trace was multiplied by the inverse of the exponential of the fixed decay time constant before adding back the offset value.

To account for neuropil signals which may contaminate signals in the bouton trace, neuropil correction was applied by subtracting a scaled version of the corresponding neuropil trace (0.6 × neuropil trace) from each bouton trace before adding back the mean neuropil fluorescence (temporally-averaged across the neuropil trace) (Kerlin et al., 2010).

We also corrected baseline fluorescence F₀ to remove the decay in fluorescence from activity evoked during the previous visual stimulus presentation. Due to slow decay dynamics in vivo (as a result of calcium buffering and GCaMP6f buffering) after stimulus-evoked calcium activity, the bouton fluorescence did sometimes not fully return to baseline during the 1 second after the offset of a previous stimulus presentation and persisted in the 1 second used to calculate F₀ for the following stimulus period. Therefore, a baseline correction was introduced that modeled this exponential decay of previously evoked GCaMP6f calcium activity, using an experimentally determined fixed time constant of 1 second (in agreement with previously determined GCaMP6f dynamics in vivo; Storace et al., 2015). This fitting procedure was independently carried out for each bouton and each single trial.

To assess the fractional change in fluorescence, ΔF/F(t), following each visual stimulus presentation, the fitted, exponentially decaying contribution from the previous trial was first subtracted from F(t) during the 1-second interval prior to and the 2-second interval during visual stimulus presentation. Then, the corrected baseline was used as the new baseline F₀ to compute ΔF/F(t). Single response values during a given trial were obtained by averaging the ΔF/F(t) response during the 2-second stimulus window.

Estimation of visual tuning preferences in RGC boutons

Estimation of boutons with significant visual responses

We define single condition response as the average from all the trials of a given stimulus condition. Visually-evoked responses were corrected by subtracting the average response across blank trials. There were approximately 30 repeats for each of the retinotopic conditions, 60 trials for each combination of direction and spatial frequency (SF), 180 trials of luminance increments and decrements (‘On’ and ‘Off’) and 360 blank trials. Different boutons had differing response dynamics, and we attempted to minimize bias in which boutons were deemed significantly visually responsive. Thus, we assessed, for each bouton and each stimulus condition, if the evoked response was significantly different from noise, by requiring the amplitude of ΔF/F(t) during the response window to exceed 2.5 standard deviations above or below the mean baseline activity (computed using the 1-second window prior to stimulus onset) for at least 10 out of the 31 time points (15.5 Hz frame rate × 2 sec stimulus presentation). For assessment of significant On and Off responses, we only required the ΔF/F(t) amplitude to exceed this threshold for at least 5 of the 31 time points, as a substantial proportion of boutons exhibited transient On and/or Off responses. These criteria were confirmed to be highly conservative, thereby including only highly robustly visually responsive boutons.

To assess if a given bouton exhibited a significantly positive response at a particular spatial frequency, we required that at least 3 out of the 8 directions at this spatial frequency evoked significantly positive responses according to the criteria described above. A similar approach was used to determine if a bouton exhibited a significantly negative response to a particular spatial frequency. Note that all boutons contributing to the main results (e.g. clustering of direction and axis selectivity) underwent additional quality controls (see below), further protecting against inclusion of any noisy boutons in our analyses.

Direction tuning curve fitting

For each bouton showing a significantly positive response at a given spatial frequency, a direction tuning curve was computed. The direction tuning curves were initially sampled in steps of 45°. In order to obtain a more precise estimate of the preferred axis and direction, a fitting approach was used to estimate the preferred direction. Tuning curves were fitted with a two-peaked Gaussian with offset (Sun et al., 2016):

$$R(\theta )=R_1{e}^{-\frac{{\left(\theta -{\theta }_{\mathit{pref}}\right)}^2}{2{\sigma }^2}}+R_2{e}^{-\frac{{\left(\theta -{\theta }_{\mathit{pref}}-180°\right)}^2}{2{\sigma }^2}}+R_{\mathit{off}}$$

R(θ) was the ΔF/F response for stimulus direction θ. This model assumed that the peaks of the two Gaussians were 180° apart. θ_pref was defined as the preferred direction evoking the strongest ΔF/F response, R₁. R₂ was the amplitude of the second peak located at θ_pref + 180°. It was also assumed that both Gaussians shared a common standard deviation, σ. The fifth fitted parameter was a constant amplitude offset, R_off.

Several steps were taken to improve the reliability of the fitting of direction tuning curves and to optimize the accuracy of estimation of preferred direction of motion. To increase the number of input points for the fitting procedure from 8 to 25, a heuristic method of interpolation and extrapolation was implemented. First, a ninth point was added at 360°, which was identical to the one at 0°. Then, the number of input point s was doubled from 9 to 17 by linear interpolation of the 9-point direction tuning curve. For the interpolated data point between the two most strongly driven initial directions (out of 9), we further adjusted the interpolated amplitude so that its value became a close approximation of that predicted point from a Gaussian curve fit through the rest of the points, thus reducing the error introduced by linear interpolation given the expected continuity of the curves. To this end, we applied a following empirical formula as described below. Note that our results were largely unchanged if this additional adjustment to the linear interpolation was omitted (mean difference in preferred direction: 2°, median difference: 1.2°). However, this additional peak adjustment resulted in significantly smaller residual values between the fitted curve and the initial 8-direction tuning curve.

The interpolated amplitude between the two most strongly driven initial directions was calculated as follows. R_S1 was defined as the strongest response out of all 8 directions and R_S2 as the stronger of the two responses for directions ± 45° adjacent to R_S1. R_S3 was defined as the weaker of the two responses adjacent to R_S1. R_S4 was defined as the response adjacent to R_S2, at 90° from R_S1. The interpolated ΔF/F response R_S12 between R_S1 and R_S2 was defined as: $R_{S12}=\frac{R_{S1}+R_{S2}}{2}+\frac{1}{6}\left(1-\frac{R_{S1}-R_{S2}}{R_{S1}-R_{S3}}\right)\left((R_{S1}-R_{S3})+\left(R_{S2}-R_{S4}\right)\right)$. This method compared the slope between R_S1 and R_S2 with the slope between R_S1 and R_S3. If the peak was flat, a maximum amount of $\frac{1}{6}\left(\left(R_{S1}-R_{S3}\right)+\left(R_{S2}-R_{S4}\right)\right)$ was added, corresponding roughly to the expected value of a Gaussian peak. If the absolute values of the slopes between R_S1 and R_S2 and between R_S1 and R_S3 were identical (and therefore R_S1 was the real peak of the Gaussian), this corresponds to $\left(1-\frac{R_{S1}-R_{S2}}{R_{S1}-R_{S3}}\right)=0$ in the above equation, therefore resulting in no additional value added to the interpolation method. A similar method was used to interpolate negative peaks.

To further improve the stability of the fitting procedure and to better approximate the direction tuning curve, we added two shadow-copies of the two-peaked Gaussian function, circularly shifted by +360° and −360°:

$$R_{\mathit{fit}}(\theta )=R_1\left(e^{-\frac{{\left(\theta -{\theta }_{\mathit{pref}}\right)}^2}{2{\sigma }^2}}+e^{-\frac{{\left(\theta -{\theta }_{\mathit{pref}}-360°\right)}^2}{2{\sigma }^2}}+e^{-\frac{{\left(\theta -{\theta }_{\mathit{pref}}+360°\right)}^2}{2{\sigma }^2}}\right)+R_2\left(e^{-\frac{{\left(\theta -{\theta }_{\mathit{pref}}-180°\right)}^2}{2{\sigma }^2}}+e^{-\frac{{\left(\theta -{\theta }_{\mathit{pref}}-540°\right)}^2}{2{\sigma }^2}}+e^{-\frac{{\left(\theta -{\theta }_{\mathit{pref}}+180°\right)}^2}{2{\sigma }^2}}\right)+R_{\mathit{off}}$$

This addition of the shadow-copies increased the range to [−90°, 450°], and thus extended the fitted tuning curve by 4 additional directions (at 22.5° spacing) on either end. While the adjusted linear interpolation and the addition of the shadow copies improved the fitting procedure, similar results were obtained using the basic 17-point linearly interpolated tuning curve (data not shown).

A bootstrapping method involving random sampling of trials from each condition was then implemented to fit the tuning curves. Specifically, for each of 100 iterations, the tuning curve was initially computed by randomly sampling (with replacement) and averaging responses from 60 trials sampled from each of the 8 directions. These 8-point tuning curves were then interpolated, extended and finally fitted using the method described above. The final parameters used were the mean of the fitted parameters across the 100 sampling iterations.

To determine if the fitting procedure yielded a high-quality fit, a combination of criteria was used. Each iteration of the fitting procedure yielded a coefficient of determination, r², defined as the explained variance using least-squares regression to fit the data. As a second control step, a combined coefficient of determination, $r_{\mathit{comb}}^2$, was computed by comparing the original direction tuning curve with the fitted curve derived using the average of each fitting parameter (across 100 iterations). To assess both the quality and the reliability of the fitting procedure, we introduced a heuristic goodness of fit, G_fit: $G_{\mathit{fit}}=\overline{\sqrt{r^2}}\left(1-\mathit{IQR}\left(\sqrt{r^2}\right)\right)\sqrt{r_{\mathit{comb}}^2}$ where IQR was defined as the interquartile range – the difference between the 75^th-percentile and the 25^th-percentile (of $\sqrt{r^2}$ values across iterations). A bouton was considered to have a well-fit direction tuning curve at a given spatial frequency if the goodness of fit, G_fit, was greater than 0.66. The threshold was chosen based on examination of a large proportion of example boutons, and values in the range of 0.5 to 0.9 yielded similar results. The complete direction curve fitting procedure was separately run for each of the three spatial frequencies employed, and therefore each bouton was attributed up to three sets of fitting parameters.

Axis and direction selectivity

For each bouton, we calculated a ‘vector sum’ axis selectivity index (ASI; i.e., selectivity for a motion along a given axis) on each interpolated direction tuning curve (Kerlin et al., 2010). This index was calculated by projecting the ΔF/F response for each of the 16 directions in the range between 0° and 360° onto a circle with 2i progression and estimating the magnitude of the normalized vector sum, which ranged from 0 to 1 (maximum selectivity): $\mathit{ASI}=\frac{\mid {\displaystyle \sum _{n=1}^{16}}R\left({\theta }_n\right)e^{\frac{2i\ast 2\pi {\theta }_n}{360°}}\mid }{{\displaystyle \sum _{n=1}^{16}}\mid R\left({\theta }_n\right)\mid }$. Opposite directions contributed in an additive fashion, while orthogonal directions canceled each other out. The ASI computation was iterated 100 times by bootstrapping and averaged for each spatial frequency. To obtain a final ASI estimate for a given bouton (Figure S2C₂), the mean ASI was computed across all spatial frequencies for which we observed a significantly positive evoked response.

In a similar manner, we computed a ‘vector sum’ direction selectivity index (DSI), by projecting the 16 directions onto a circle with 1i progression: $\mathit{DSI}=\frac{\left|{\displaystyle \sum _{n=1}^{16}}R\left({\theta }_n\right)e^{\frac{1i\ast 2\pi {\theta }_n}{360°}}\right|}{{\displaystyle \sum _{n=1}^{16}}\left|R\left({\theta }_n\right)\right|}$. As with ASI, the DSI estimate was repeated with the bootstrapping method and a final DSI estimate was computed as the mean DSI across all spatial frequencies for which we observed a significantly positive evoked response.

Preferred direction of motion and preferred axis of motion

The preferred direction was defined for direction selective boutons (see Section 8, ‘Bouton type classification’) by taking the circular average of the fitted θ_pref values across spatial frequencies with significant responses, and for which goodness of fit exceeded the defined threshold and DSI exceeded the defined threshold. Estimates of preferred direction ranged from 0° and 360°.

The preferred axis of motion was defined in a similar fashion, for both axis selective and direction selective boutons, by averaging the fitted estimate of preferred axis across spatial frequencies with significant responses. Estimates of preferred axis of motion ranged from 0° and 180°.

Preferred spatial frequency

For simplicity of presentation, we converted relative spatial frequency of stimulation to integer numbers (with two-octave spacing between integers) using the formula ${SF}_n={log}_4\left(\frac{\omega }{0.02}\right)+1$, with ω being defined as the spatial frequency in cycles per degree. SF₁, SF₂ and SF₃ respectively corresponded to actual stimulus spatial frequencies of 0.02, 0.08 and 0.32 cycles/degree. For a given bouton, we estimated the preferred spatial frequency evoking the strongest ΔF/F response, using a modified version of the center of mass method:

$${SF}_{\mathit{pref}}=\frac{\left(R\left({SF}_1\right)-min\left(R\left({SF}_n\right)\right)\right)+2\left(R\left({SF}_2\right)-min\left(R\left({SF}_n\right)\right)\right)+3\left(R\left({SF}_3\right)-min\left(R\left({SF}_n\right)\right)\right)}{\left(R\left({SF}_1\right)-min\left(R\left({SF}_n\right)\right)\right)+\left(R\left({SF}_2\right)-min\left(R\left({SF}_n\right)\right)\right)+\left(R\left({SF}_3\right)-min\left(R\left({SF}_n\right)\right)\right)}$$

R(SF₁), R(SF₂) and R(SF₃) correspond to the average ΔF/F responses across all eight directions at 0.02 cycles/degree, 0.08 cycles/degree and 0.32 cycles/degree, respectively. Note that, in the above equation, the minimal ΔF/F response across spatial frequencies, min(R(SF_n)), was subtracted from each of the three responses before computing the center of mass. SF_pref ranges from 1 to 3 and was converted back to cycles/degree by ω_pref = 0.02 × 4^SF_pref−1.

For boutons with suppressed responses to stimulation in all directions of motion (see below), the preferred spatial frequency was defined as the frequency with the strongest suppression and therefore a slightly modified formula was used for consistency. Specifically, the mean ΔF/F response at a given spatial frequency was calculated as R_supp(SF_n) = −R(SF_n), n=1,2,3.

OnOff preference index

An OnOff preference index was calculated using the averaged response traces to luminance increments (On stimulus) and to luminance decrements (Off stimulus). A positive response to On only, to Off only, or a positive response of equal magnitude to On and Off corresponded to index values of 1, −1 or 0, respectively. Boutons lacking both a significant On response and a significant Off response (see Subsection 6.1, ‘Estimation of boutons with significant visual responses’) were not considered. In addition, boutons that were significantly suppressed by an On stimulus were defined as Off-responsive, while boutons that were significantly suppressed by an Off stimulus were defined as On-responsive.

In order to take into account the dynamics of the evoked On and Off responses, a weighted OnOff preference index was introduced as follows:

$${\mathit{OnOff}}_{\mathit{pref}}=\frac{\left(O{n}_t-{\mathit{Off}}_t\right)·\left({\left|On\right|}_t+{\left|\mathit{Off}\right|}_t\right)}{{\Vert {\left|On\right|}_t+{\left|\mathit{Off}\right|}_t\Vert }^2}$$

On_t and Off_t were defined as the On and Off response timecourses during the 2-second response window. In this equation, the term (On_t − Off_t) determines the sign of the index at each timepoint. The dot product of this term with (|On|_t + |Off|_t) was used to assign a relative weight to each timepoint according to its summed response magnitude. Then the numerator was normalized to obtain a single preference index between −1 and 1.

For suppressed boutons, the same formula was used. As suppressed boutons sometimes exhibited a positive rebound after a transient suppression (Mastronarde, 1985; Tien et al., 2015), the positive values in On and Off response traces from those boutons were set to zero prior to estimating OnOff preference.

OnOff sustain index

An OnOff sustain index, ranging from 0 for transient responses to 1 for sustained responses (e.g. responses that do not attenuate over time during the 2-second stimulus presentation), was calculated from the average trace across trials as follows:

$${\mathit{OnOff}}_{\mathit{sustain}}=\frac{\langle {\left|On\right|}_t+{\left|\mathit{Off}\right|}_t\rangle }{{\mathit{prc}}_t\left({\left|On\right|}_t+{\left|\mathit{Off}\right|}_t,95\right)}$$

In this equation, the mean value across the 2-second stimulus period of the sum of the absolute On and Off traces, 〈|On|_t + |Off|_t〉, is divided by the 95^th percentile value (prc_t)of the sum of these rectified traces (Piscopo et al., 2013). In suppressed boutons, any positive response values were set to zero before calculating the index.

Estimation of retinotopic preferences in RGC boutons

Retinotopic tuning curve fitting

Two retinotopic tuning curves, which were independently fitted for each bouton, were established, respectively, for tuning along the azimuth and along the elevation axes. Both curves consisted of eight evenly spaced values, each consisting of the average response across trials for a given location in visual space of the oriented bar containing binarized spatiotemporal noise (see above). Tuning curves were approximated using a Gaussian function:

$$R(x)=R_1{e}^{-\frac{{\left(x-x_{\mathit{pref}}\right)}^2}{2{\sigma }^2}}+R_{\mathit{off}}$$

The ΔF/F response, R(x) varied as a function of the retinotopic stimulus location, x. The maximum response, R₁ + R_off, was evoked at x_pref, the preferred retinotopic location. The standard deviation σ of the Gaussian was proportional to the receptive field size along this axis. To increase the number of points for fitting from 8 to 15, an interpolation method similar to the one used for direction tuning curves was implemented. As responses were very reliable and well fit, no bootstrapping method was implemented. Fitting was considered significant if 2 out of the 8 directions showed a significant response (see Subsection 6.1, ‘Estimation of boutons with significant visual responses’), if the absolute correlation coefficient $\sqrt{r^2}$ exceeded 0.8, and if the fitted peak amplitude was confirmed to be positive or negative for non-suppressed and for suppressed boutons, respectively.

Retinotopic responses of neuropil surrounding RGC axonal boutons

Retinotopic tuning curve fitting was also implemented for the neuropil rings surrounding each bouton, to estimate the local retinotopic preference in the field of view. Each pixel in the field of view was attributed a preferred retinotopic location by first assigning the center of each neuropil ring with a value corresponding to the preferred retinotopic location of that neuropil ring, then dilating by a disk of 10 μm radius from each neuropil center respectively and averaging the preferred retinotopy across overlapping disks. The final pixel-wise estimates of retinotopic preference were obtained by spatial smoothing using an isotropic two-dimensional Gaussian filter with a standard deviation of 3 μm.

The rate of change of retinotopy along the field of view (which was tangential to the surface of dLGN) was measured along the axis for which the retinotopic map changed the fastest. To compute this spatial axis, we first calculated the two-dimensional pixel-wise gradient: $\nabla \mathit{Ret}\left(x,y\right)=\frac{\partial \mathit{Ret}\left(x,y\right)}{\partial x}\widehat{i}+\frac{\partial \mathit{Ret}\left(x,y\right)}{\partial y}\widehat{j}$. The spatial axis was defined as the normalized mean gradient vector across pixels, $\frac{\overline{\nabla \mathit{Ret}}}{\Vert \overline{\nabla \mathit{Ret}}\Vert }$. The smoothed retinotopic map was then projected onto the normalized mean gradient vector (i.e., onto the unit vector along the direction of maximal change in retinotopic preference). For each pixel, we derived its projected location along this new spatial axis as: $\stackrel{\sim }{x}=\left(x,y\right)·\frac{\overline{\nabla \mathit{Ret}}}{\Vert \overline{\nabla \mathit{Ret}}\Vert }$. The relationship between the preferred retinotopic location and x̃ was modeled according to a linear function with offset: Ret_fit(x̃) = ax̃ + b. The fitted parameter a (units: deg/μm) indicated the progression rate of the smoothed retinotopic map. We computed the normalized mean gradient axis and the scale factor, a, both for maps of azimuth and for maps of elevation.

Fine-scale retinotopic scatter

Fine-scale retinotopic scatter (‘deg scatter’, Figure S1F) was estimated as the absolute retinotopic deviation, S_ret (units: degrees of visual space): S_ret = |Ret_pref(x̃_B) − (ax̃_B + b)|. Here, Ret_pref(x̃_B) denoted the preferred retinotopic location of a given bouton, while (ax̃_B + b) gave the predicted receptive field center based on the neuropil estimate, according to the projected location x̃_B along the mean gradient axis. We also calculated the absolute deviation in spatial distance from the fitted spatial progression in the field, S_spa (‘distance scatter’, Figure S1F; units: μm): $S_{\mathit{spa}}=\left|{\stackrel{\sim }{x}}_B-\frac{{\mathit{Ret}}_{\mathit{pref}}\left({\stackrel{\sim }{x}}_B\right)-b}{a}\right|$. This value is equivalent to the distance that a bouton would need to be moved along azimuth or elevation in order to obtain a perfectly smooth map.

Bouton type classification

A bouton was classified as direction selective if, for at least one of the three spatial frequencies used, (i) it had a significant positive response, (ii) the tuning curve was successfully fit (as estimated by goodness of fit criteria), (iii) the direction selectivity index (DSI) exceeded 0.2 (a value equivalent to 0.33 if direction selectivity was calculated as $\mathit{DSI}=\frac{R_{\mathit{pref}}-R_{\mathit{opp}}}{R_{\mathit{pref}}+R_{\mathit{opp}}}$, where R _pref was the response at the preferred direction and R_opp was the response at the opposite direction). Additionally, for all spatial frequencies which showed a significant positive response, we also required the DSI at each of these spatial frequencies to exceed 0.15 (to ensure that group assignment was not sensitive to the vagaries of which spatial frequencies were used). Finally, we verified that boutons in this group did not show any significantly negative responses for any spatial frequency.

A bouton was defined as axis selective (i.e., most strongly responsive to motion along two opposite directions constituting a single axis of motion) if (i) it had at least one significantly positive response for at least one of the three spatial frequencies, (ii) the fitting procedure was reliable, and (iii) the axis selectivity index (ASI) exceeded 0.15 (a value equivalent to 0.33 if axis selectivity was calculated as $\mathit{ASI}=\frac{R_{\mathit{pref}}-R_{\mathit{orth}}}{R_{\mathit{pref}}+R_{\mathit{orth}}}$, where R_pref was the response at the preferred direction and R_orth was the mean response at the two directions orthogonal to the preferred one). We distinguish the term axis selectivity from orientation selectivity, as the latter is often used even for responses to stationary (i.e., non-drifting) oriented gratings – a stimulus not examined in this study. It is possible that certain axis selective boutons may not be strongly driven by stationary gratings. For all spatial frequencies for which we observed a significant positive response, we further required that the DSI was less than 0.2 and that the ASI was greater than 0.1. If these conditions were not met or if the bouton showed any significant negative response at any spatial frequency, the bouton was removed from this group.

A bouton was defined as ‘broadly tuned’ if (i) it exhibited a significant positive response for at least one of the three spatial frequencies and (ii) the ASI and DSI were below 0.15 and 0.2, respectively, for all significant spatial frequencies. We also removed boutons that exhibited any significant negative responses at any spatial frequency.

Boutons having significant negative responses for at least one spatial frequency and no significant positive response at any spatial frequency were defined as ‘suppressed’. Two subpopulations of suppressed boutons were included in this group: (i) ‘suppressed-by-contrast’ (SBC) boutons, defined as those boutons generally suppressed by all types of visual stimuli, including horizontal and vertical bars containing spatiotemporal noise (used for retinotopic mapping). To be defined as SBC, a bouton needed to be significantly suppressed by at least 2 out of the 8 retinotopic conditions in at least one of the two stimulation axes. If no retinotopic mapping stimulus evoked a significant response, or if the response to one or both retinotopic stimulation axes was significantly positive, the bouton was classified as ‘suppressed’, but not as part of the subcategory of ‘SBC’ boutons. For analyses involving boutons’ preferred spatial frequency, OnOff preference index and the preferred retinotopic location, only the SBC subcategory of suppressed boutons was considered.

Boutons which showed a significant visually-evoked response but were not classified into any of the above conservatively-defined categories, were labeled as ‘unclassified’ boutons and were not included in subsequent analyses.

Finally, a small proportion of candidate bouton masks were not significantly driven by any of the presented visual stimuli. These were classified as ‘unresponsive’ and not considered further.

Axon identification

Axon identification – the process of assigning boutons imaged in a field of view to the same axon – was carried out on data from blank trials (up to 360 trials per session) to avoid assessment of pairwise correlations during periods of visual stimulus presentation. We made the assumption that boutons from the same axon would share spontaneous calcium events with substantially higher frequency than pairs of boutons not belonging to a common axon. To identify spontaneous calcium events, the activity timecourses of all blank trials were first concatenated to obtain a single ‘spontaneous’ activity trace for each bouton (15–30 minute duration). We focused on periods containing significant spontaneous events for each bouton, as these periods were robust to sources of noise. To this end, we thresholded each spontaneous trace by 3 standard deviations above and below the mean activity. To identify entire events including the baseline before event onset, time points in an interval of 700 milliseconds before and 700 milliseconds after each thresholded event were included. Finally, for each bouton, we concatenated these peri-event timecourses of spontaneous activity. All boutons exhibited some significant spontaneous activity and were thus included in the axon classification procedure.

The concatenated timecourse of spontaneous events for a given bouton were then cross-correlated with the timecourse of all other boutons during the same epochs. In this way, we created a matrix of Pearson correlation coefficients between all pairs of boutons in the field of view. To obtain a sparse matrix only populated by large values, the original matrix was further thresholded: the correlation coefficients for a given bouton were maintained if the coefficients were larger than 0.7 or if they exceeded 2.5 standard deviations above the mean value of all the coefficients between this bouton and all others. If neither of these conditions were met for a given bouton pair, the associated correlation coefficient was set to 0. The cosine similarity between every pair of boutons was then computed from the thresholded matrix of Pearson correlation coefficients. Each bouton in a pair has an associated vector of rectified spontaneous activity pairwise correlation coefficients with all other boutons in the field of view, and the cosine similarity between two boutons reflected the cosine of the angle between these two vectors of correlation coefficients (Figure 3B). This step is important: if a small minority of pairwise correlation coefficients are low due to noise, while most other coefficients are high for other pairs of boutons belonging to the same axon, this procedure will help ensure that all boutons are nevertheless properly assigned to the same axon. We next classified bouton clusters using agglomerative hierarchical clustering based on the pairwise distance, computed as ‘1 – cosine similarity’. We defined ‘correlation similarity’ as ‘1 - cluster distance’, where the cluster distance is the distance between two groups, each consisting of one or more bouton. This distance was calculated using the weighted-pair group method with arithmetic means (WPGMA) algorithm. We chose a cutoff threshold of correlation similarity to classify two groups of boutons as belonging to a common axon. Specifically, two groups of boutons with a correlation similarity exceeding a threshold of 0.15 were assigned to the same axon. This threshold was highly conservative, as it erred on the side of combining groups together. Thus, this procedure minimized the likelihood that pairs of boutons that actually belong to the same axon would be assigned to two different axons, and would thereby be included in subsequent pairwise analyses in Figures 4, 6 and 7. On average, the mean Pearson correlation coefficient increased monotonically with correlation similarity as defined above, and the correlation similarity threshold of 0.15 corresponded to a mean Pearson pairwise correlation coefficient of 0.34. The choice of correlation similarity threshold did not affect the main results: when the correlation similarity threshold was varied from 0.05 to 0.95 for clustering boutons into different axons, the axis preference similarity index for nearby boutons changed smoothly, subtly, and without any obvious inflection point (Figure S4C).

Inter-bouton feature comparison

The absolute preferred difference in axis preference ranged from 0° and 90° and was computed for pairs of boutons from the same categories (AS/AS and DS/DS pairs) and across categories (AS/DS pairs).

The absolute difference in preferred direction of motion ranged between 0° and 180° and was only computed for DS/DS pairs.

The absolute difference in the logarithm (base 4) of preferred spatial frequency ranged from 0 to 2 (i.e. from 0 to ${log}_4\left(\frac{0.32\mathit{cpd}}{0.02\mathit{cpd}}\right)$), and was computed for all bouton pairs, within and across categories, if both boutons had a well-defined preferred spatial frequency.

The absolute difference in OnOff preference index ranged from 0 to 2 and was computed for all bouton pairs, within and across categories, if both boutons had significant On and/or Off responses.

The absolute difference in OnOff sustain index ranged from 0 to 1 and was computed for all bouton pairs, within and across categories, if both boutons had significant On and/or Off responses.

Functional clustering

Functional clustering of bouton pairs

Functional clustering of bouton pairs was assessed by plotting the inter-bouton feature differences versus spatial distance between boutons, and considering only pairs of boutons for which each bouton belonged to a different axon. A 4 μm sliding average was applied at 0.25 μm steps to these plots. The standard error of the mean was calculated by considering all pairs in a given 4 μm bin. We also computed the chance level, estimated after randomly permutating the feature differences across all bouton pairs spaced from 2 μm to 150 μm in the field of view while maintaining their spatial distances. This randomization was repeated 10 times. The standard error of the mean estimate for the permutated data was calculated for each randomization and then averaged across the 10 randomizations.

To normalize the above curves for comparison across different fields of view, we used a pairwise similarity index (SI) that compared the degree of actual similarity to the ‘null’ estimate of similarity using the above permutation procedure, as follows: $SI=-\frac{\left({FD}_{\mathit{True}}-{FD}_{\mathit{Null}}\right)}{{FD}_{\mathit{Null}}}$. Here, the null functional distance (FD_Null, the average absolute difference in feature preference across all pairs between 2 μm and 150 μm) was subtracted from the true functional distance (FD_True, the average absolute difference in feature preference across all pairs with inter-bouton distances in a defined range), followed by normalization. A similarity index value of 0 corresponded to similarity at chance levels, while an index value of 1 indicated identical feature preferences. Negative clustering indices were obtained if pairs were less similar than expected by chance. Clustering effects on a short spatial scale were assessed for pairs spaced 2 μm to 6 μm apart, while pairs spaced 50 μm to 60 μm apart served as a control for any large-scale similarity or global bias.

Functional clustering of local groups of boutons

To quantify functional clustering of nearby groups of boutons for each visual tuning feature, we computed a group similarity index for each visual feature, and included all boutons within a vicinity of each given pixel in the image, assuming the local group of boutons met certain topological and other criteria: (i) the group of boutons within a 6 μm radius of the pixel must contain at least 3 AS or DS boutons which exhibited well-defined motion axis preferences, OnOff preferences, and spatial frequency (SF) preferences; (ii) the group of boutons must belong to at least two axons, with no more than 67% of the boutons belonging to any given axon. Pixels satisfying these topological criteria usually contained 3 to 12 acceptable boutons within the 6 μm radius. We then computed the group similarity index for motion axis preference, OnOff preference and SF preference, respectively, among well-defined boutons near each pixel. To compute this group similarity index (SI), we first calculated (1 - standard deviation of OnOff preference indices), (1 - standard deviation of SF preference indices), or the magnitude of the mean of polar unit vectors along preferred axes – a measure of groupwise circular variance in axis preference. We then normalized these values with the corresponding averages from 1000 shuffles according to (real SI - shuffled SI)/(1 - shuffled SI), where we shuffled triplets of preference values (motion axis preference, OnOff preference, and SF preference) among axons across all fields of view that contained the same number of boutons. A normalized similarity index was defined to be significant if it was larger than 95% of indices derived from shuffled data. For a group of boutons surrounding a given pixel to be considered as part of a combination- or relay-mode cluster, the similarity index for the corresponding visual feature (or features, for relay mode) had to be significant. For example, a group of boutons surrounding a given pixel was considered to be in an Axis-OnOff relay mode cluster if both of its Axis similarity index and OnOff similarity index were significant. A group of boutons surrounding a given pixel was considered to be in an Axis combination mode cluster if the axis similarity index was significant but the OnOff similarity index was not. A group of boutons surrounding a given pixel was considered to be in a 3-feature relay cluster if Axis, OnOff and SF similarity indices were all significant.

To compute the frequency of each type of functional cluster, we calculated the number of unique pixels (i.e. number of unique groups of boutons within a circle of 6 μm radius) belonging to each type of cluster, and divided by the total number of unique pixels satisfying the aforementioned topological criteria. Quantification of these percentages for each type of cluster used the number of unique groups of boutons, as neighboring pixels could ‘double-count’ the same unique group of boutons.

To quantify divergence of axons with boutons participating in more than one distinct, functionally-similar bouton cluster, we implemented a conservative approach, as described below. First, we only considered different boutons from the same axon that participated in distinct bouton clusters. We accomplished this by excluding from this analysis all boutons from a divergent axon that were less than 12 um apart (i.e. within a common group of boutons, defined above as within a circle of 6 μm radius). To this end, for each axon, we created a list of usable boutons, by sequentially adding additional boutons (from top left to bottom right of the FOV) to the list only if those boutons were not within 12 μm of any previous bouton already added to the list. The boutons in this subselected list were also required to be within a 6 μm radius of a pixel that had significant groupwise similarity indices for at least one of the 3 visual features (axis preference, OnOff preference, and SF preference). An axon was considered to be ‘divergent’ if it contained at least two boutons in this subselected list. Results in Figure 7B were qualitatively similar if we randomly permuted this bouton order for every axon. The diverging boutons were classified into those participating in an Axis combination mode cluster, an OnOff combination mode cluster, or an Axis-OnOff relay mode cluster, according to the criteria defined above. We then classified each divergent axon into subcategories according to whether it was involved in at least one combination-mode and/or relay-mode cluster of each type, and quantified the percentage of divergent axons in the same FOV that were part of each of these subcategories.

Electron microscopy methods and analyses

The EM images were taken from a publicly available postnatal day 32 mouse LGN EM image volume published in (Morgan et al., 2016; https://software.rc.fas.harvard.edu/lichtman/LGN/). This EM volume spans a 600 × 400 × 300 μm³ region of LGN. Sections are 30 nm thick and were imaged at 4 nm pixel size.

The current bouton convergence analysis (Figure 5) was performed on a 4× downsampled (x,y) version of the LGN dataset using VAST (Kasthuri et al., 2015; https://software.rc.fas.harvard.edu/lichtman/vast/) manual segmentation software. To calculate the probability of nearby boutons converging on the same thalamocortical cell, we first identified all the RGC boutons (N = 100) that intersected a single ~45 μm × 45 μm region of a single coronal section from the dLGN shell. The presynaptic boutons were confirmed to be RGC boutons by identifying their characteristic pale mitochondria within the three-dimensional volume of the bouton. We then identified the target dendrite innervated by each bouton and traced the dendrite back to the cell body. A pair of boutons had a convergence probability of ‘1’ if they both targeted to the same neuron, or ‘0’ if they targeted different neurons. The mean convergence probability in Figure 5B was calculated using a running bin (6 μm width, 0.25 μm steps) across inter-bouton spatial distances. This way of calculating the mean convergence probability was similar to the calculation, for a given range of inter-bouton distances, of the fraction of bouton pairs targeting the same neuron (of all possible pairs; see in Figure S6B–C). We also randomly permutated the convergence probability across bouton pairs while maintaining a constant distribution of spatial distances between pairs of boutons, and calculated the mean convergence probability for the permutated data set. We repeated this procedure 10 times to obtain the mean distribution of the permutated data. The 95% confidence intervals of both the real data and permutated data were estimated according to simple asymptotic method with continuity correction.

Cell renderings were performed in Matlab (Mathworks). Distances between boutons were measured in two ways: (i) Euclidian distance, and (ii) a topological measure of distance along the dendrite. The topological distance between two boutons was measured as the shortest path along the postsynaptic dendritic arbor that connected the two boutons (Figure 5E, red overlay). To find this path, volume tracings were first skeletonized into a node-edge representation as previously described (Morgan et al., 2016). Paths through the skeleton were simplified into a series of ~1.1 μm line segments to prevent overestimation of length due to small kinks in the dendrite.

Similar analyses of convergence were performed in Figure S6D by estimating convergence fractions for a second set of boutons from different reconstructed RGC axons within the same 3D EM volume. While these axons could only be reconstructed back to the edge of the EM volume, the vast majority of these likely belong to distinct RGCs (Morgan et al., 2016). This set of traced axons constitute the set of all axons that synapsed onto one of 4 ‘seed’ neurons previously selected for analysis from within the 3D EM volume (Morgan et al., 2016); located in dLGN core). All pairs of boutons belonging to distinct RGC axons from this set were included in Figure S6D (other than boutons directly targeting seed dLGN neurons, which were excluded from this analysis to avoid biasing the results; see Morgan et al., 2016). These data demonstrated a similar relationship of probability of pairwise convergence onto a common target vs. inter-bouton distance as that observed in the analysis in Figure 5B (which was generated from RGC boutons within a single EM section in dLGN shell in Figure 5A, and which included all pairs of RGC boutons from that section, regardless of their axon of origin).

QUANTIFICATION AND STATISTICAL ANALYSIS

Statistical tests were conducted using MATLAB. Non-parametric tests were used for comparing two independent groups (Mann-Whitney-Wilcoxon test), two related groups (Wilcoxon signed-rank test), and multiple groups (Kruskal-Wallis test with Bonferroni correction). p<0.05 was considered significant. Additional details on sample sizes, statistical test, significant levels for each experiment can be found in figure legends, Results and METHOD DETAILS. All acquired data were included for analyses.

DATA AND SOFTWARE AVAILABILITY

Requests for analyses and raw data on calcium imaging results may be made to the Lead Contact, Mark L. Andermann, manderma@bidmc.harvard.edu

Supplementary Material

1. Figure S1. Retinotopic properties of cell bodies and RGC boutons in dorsal dLGN, Related to Figure 2.

A. We used two-photon calcium imaging to estimate retinotopic preferences for individual dLGN cell bodies and RGC boutons, by presenting a horizontal or vertical bar (5° width) at various levels of visual elevation or azimuth (for 2 s). Bars contained band-pass filtered spatiotemporal noise to elicit robust responses (see Videos S1 and S2). Average evoked responses (changes in GCaMP6 fluorescence from baseline, ΔF/F) are plotted as a function of bar location along elevation or azimuth, for an example RGC bouton (top panels, black). We also measured evoked responses in neuropil rings surrounding each bouton (and excluding other bouton masks; bottom panels, black). Responses of the bouton and of background neuropil were fit by a Gaussian function. We used the fit to each bouton’s responses (following subtraction of the neuropil contribution) to estimate retinotopic response preferences and as a rough estimate of receptive field size. The same procedure was used for recordings from dLGN cell bodies.

B. Maps of retinotopic preference of dLGN cell bodies, for fields of view from two mice. Cell body masks (black outlines) were color-coded according to preferred stimulus elevation (left) or azimuth (right). All other pixels were color-coded according to a smoothed estimate of neuropil retinotopic preference.

C. RGC bouton masks identified by morphological filters are outlined (orange) on top of the intensity projection image across average evoked response maps for each stimulus condition (30 repeats per condition), for the example field of view in Figure 2D. This projection image was computed as the sum of maximum-intensity and minimum-intensity projections (STAR Methods).

D. Maps of retinotopic preference of RGC axonal boutons, for example fields of view from 2 mice. Bouton masks (black outlines) were color-coded according to preferred stimulus elevation (left) or azimuth (right). All other pixels were color-coded according to a smoothed estimate of the RGC bouton neuropil retinotopic preference. Note the slower, more gradual rate of change in elevation preference than azimuth preference across the image.

E. On a coarse scale, the rates of change in retinotopic preference across the image were similar for dLGN cell bodies and for RGC boutons (cell bodies: N = 3 fields of view from 2 mice; RGC boutons: N = 15 fields of view from 3 mice). Mean ± s.e.m.

F. Scatter plot of RGC bouton retinotopic preferences vs. location in dLGN along elevation (left) and azimuth (right) axes of retinotopic progression, for an example field of view. Black line: linear fit to retinotopic gradient. Blue dots: individual boutons in the field of view. Vertical orange line indicates deviation in preference of a given bouton from the mean retinotopic gradient (‘deg scatter’). Horizontal orange line indicates distance of a bouton from its expected location in the dLGN in the absence of scatter (‘distance scatter’).

G. Retinotopy was disordered below the spatial scale of ~40 μm (elevation) or ~20 μm (azimuth) (p<0.001; Wilcoxon signed-rank test; N = 15 fields of view from 3 mice), corresponding to an approximately 2° of scatter in retinotopic preference in both elevation and in azimuth (not significant; Wilcoxon signed-rank test; N = 15 fields of view from 3 mice). Note that only boutons yielding high-confidence estimates of retinotopic preference were included (e.g. Figure 2F, right; Figure S1A), thereby minimizing any contribution of noise to the estimation of local scatter (see also STAR Methods).

H. Left: zoom-in within one field of view containing three nearby dLGN cell bodies with different preferences for stimulus direction or axis of motion, as assessed using visual responses to high contrast, full-field sinusoidal gratings drifting in one of eight different directions. Right: direction tuning curves for the three neighboring neurons numbered in the leftmost panel – one direction-selective (DS) neuron and two axis-selective (AS) neurons. Similar results were also evident in 5 other fields of view from 5 mice (data not shown).

10. Video S1: Stimulus protocol for retinotopic mapping of RGC axonal boutons in dLGN, Related to Figure 2.

This movie illustrates the visual stimulus protocol used for mapping retinotopic organization of RGC axonal boutons in dLGN. We presented 5° bars containing bandpass-filtered spatiotemporal noise, for a duration of 2 seconds each (with 2 second inter-trial intervals). Bars were presented in pseudorandom order. First, the geometry of a stimulus bar is shown. Subsequently, two example stimuli are shown. See also STAR Methods.

2. Figure S2. Visual tuning feature preferences of RGC boutons in dLGN shell, Related to Figure 2.

A. To estimate preferred direction and preferred axis of motion of RGC boutons, we fit direction tuning curves (e.g. Figure 2G) using a sum-of-two-Gaussians model (STAR Methods; Gaussians were forced to be 180° apart). Model fits for an axis-selective RGC bouton (AS; top) and for a direction-selective RGC bouton (DS; bottom) are shown. Only boutons with high goodness-of-fit were included in subsequent analyses.

B. Top left: polar distribution of preferred axis of motion for all RGC boutons categorized as axis-selective (AS; N=3,935 boutons across 19 fields of view from 5 mice) or direction-selective (DS; N=3,013 boutons across 19 fields of view from 5 mice). See also C, below. Data from 180°–360° is the same as for 0°–180°. Top right: interestingly, we observed a non-uniform distribution of axis preferences for AS boutons in this region of dLGN, possibly reflecting at least two distinct types of RGC boutons. Bottom left: similarly, we observed a non-uniform distribution of axis preference in DS boutons. Bottom right: distribution of direction preferences for DS boutons (ranging from 0°– 360°). Note that while many DS boutons preferred motion along one of two axes with a motion component in the temporal direction, smaller subsets preferred motion with a motion component in the nasal direction (temporal: ~−15°; nasal: ~165°; dorsal: ~75°; ventral: ~255°; see also panel D).

C. (C₁) Direction selectivity index (DSI; 0: non-selective; 1: responsive to only one direction of motion; N = 9,614 boutons across 19 fields of view from 5 mice), across all direction selective (DS), axis selective (AS), and broadly tuned boutons (see below). DS boutons were defined as having a DSI ≥0.2. (C₂) Axis selectivity index (0: non-selective; 1: responsive to only one or to two opposite directions of motion along a single axis; N = 9,614 boutons across 19 fields of view from 5 mice) across all DS, AS and broadly tuned boutons. AS boutons were defined as having an ASI ≥0.15. See also Figure S2A.

D. Full stimulus protocol. Direction tuning curves were calculated for each bouton using average responses to full-field sinusoidal gratings (2 s duration) presented at 8 different directions and 3 separate spatial frequencies. In addition, we estimated response timecourses to presentation of a full-field luminance increment or decrement (2 s duration). Blank trials were also included.

E. Distribution of OnOff preferences across RGC bouton categories in dLGN shell. Boutons in each group had a broad range of OnOff preferences (1: ‘On’, responds to luminance increments only; −1: ‘Off’, responds to luminance decrements only; 0: ‘On-Off’, responds to both luminance increments and decrements). SBC: suppressed-by-contrast.

F. Distribution of OnOff response sustainedness (1: entirely sustained response; 0: entirely transient response; STAR Methods).

G. Distribution of spatial frequency preferences across RGC bouton categories. Despite the coarse sampling in our study (3 spatial frequencies: 0.02, 0.08 and 0.32 cycles/degree), boutons in each group exhibited a broad range of spatial frequency preferences (STAR Methods), with a bias towards higher spatial frequencies (possibly related to the role of dLGN in image-forming vision) for DS, AS and broadly tuned boutons. Note that spatial frequency preference for suppressed boutons indicates estimated frequency driving maximal suppression of activity. Thus, the majority of boutons in all categories showed relatively higher peri-stimulus activity at higher spatial frequencies.

H. Distribution of receptive field sizes across RGC bouton categories. Estimation of receptive field size (sigma, from the Gaussian fit) using the retinotopic mapping stimulus protocol (Figure S1A) for elevation (left) and azimuth (right). Note that this procedure likely overestimates some receptive field sizes due to coarse sampling (5° bar width, 5° spacing). Note also that suppressed (SBC) boutons show larger receptive fields, consistent with their lower spatial frequency preferences (panel G) and with the relatively large receptive fields of SBC neurons in the dLGN (Piscopo et al., 2013).

3. Figure S3. Properties of axons classified using in vivo imaging data, Related to Figure 3.

A. Distribution of pairwise correlation coefficients of spontaneous activity for inter- and intra-axonal bouton pairs. Note that a small subset of bouton pairs lacking strongly correlated activity were still classified as belonging to the same axon. This is because the overall pattern of correlations in spontaneous activity of each bouton in this pair with all boutons in the field of view was highly similar (as determined by estimation of ‘cosine similarity’, see STAR Methods). Pairs of boutons with similar spontaneous activity were then assigned to the same axon if a metric of pairwise similarity, ’correlation similarity’ (derived from cosine similarity, see STAR Methods), exceeded a threshold of 0.15. This threshold was highly conservative, as it erred on the side of combining groups together. Thus, this procedure minimized the likelihood that pairs of boutons that actually belong to the same axon would be assigned to two different axons, and would thereby be included in subsequent pairwise analyses in Figure 4.

B. Average number of axons per field of view as a function of threshold level of ‘correlation similarity’ in spontaneous activity timecourses between pairs of boutons (mean ± s.e.m., n=19 fields of view from 5 mice).

C. Fraction of all boutons belonging to axons associated with a given number of boutons in the field of view, across all 19 fields of view.

D. Cumulative distribution of number of boutons belonging to axons associated with a given number of boutons, across all 19 fields of view.

E. Fraction of all imaged axons containing a given number of boutons.

F. Cumulative distribution of number of axons with a given number of boutons, across all imaged axons (axons contained between 1 and 79 boutons).

4. Figure S4. Additional analyses of fine-scale similarity in axis preference and in direction preference across pairs of RGC boutons, Related to Figure 4.

A. Cumulative distribution of pairs of boutons as a function of difference in axis preference, for bouton pairs from different axons (gray) or from the same axon (black). Analysis was restricted to AS and DS boutons within each field of view. We assume that boutons belonging to the same axon would share similar feature preferences (as confirmed for the examples in Figure 3B). Thus, intra-axon differences in estimated feature preference are likely to be due to insufficient sampling of feature space and other sources of measurement error. Using model-fitting procedures, estimates of preferred axis were far more precise than 45°, but nevertheless imperfect. Thus, the observed degree of fine-scale clustering of pairs of boutons with similar axis preference (Figure 4) is a conservative estimate of the actual enhancement in similarity of feature preferences for nearby boutons from different axons. This is illustrated by the distribution of differences in axis preference estimated for pairs of boutons from the same axon (i.e. ‘intra-axon pairs’, black line; median difference: ~8°; 90^th percentile: ~45°).

B. Distribution (red bars) of axis preference difference for pairs of boutons spaced 2–6 μm apart (left) or spaced 50–60 μm apart (right), pooled across all 5 mice. Short black horizontal lines indicate the global distribution using all bouton pairs spaced 2–150 μm apart. The excess number of pairs with small differences in axis preference for pairs spaced 2–6 μm apart was not observed for pairs spaced 50–60 μm apart.

C. We observed a robust and roughly constant pairwise similarity index for motion axis preference (indicative of functional clustering) for pairs of boutons spaced 2–6 μm apart, across axon classification thresholds ranging from 0.05 to 0.95 (compare with Figure S3B). We only included pairs of boutons each belonging to different axons in the estimates of axis preference similarity index.

D. Example subregion of a field of view with three example axons highlighted (different colors), all of which exhibited similar axis preferences (D₁). The blue axon contains AS boutons preferring motion along a given axis (D_2, blue), and the other two nearby axons contain DS boutons preferring opposite directions of motion while sharing the same axis preference as the blue axon (D_2, green and red).

E. Frequency of pairs of boutons spaced 2–6 μm apart with a given inter-bouton difference in direction preference, pooled across mice (N=5), and analyzed separately for bouton pairs with differences in preferred direction between 0° and 90° (left) and between 90° and 180° (right). Note the difference in y-axis labeling. Black horizontal lines indicate the global distribution using all bouton pairs spaced 2 – 150 μm apart. Bouton pairs with direction preferences between 90° and 180° were substantially less common, due to the non-uniform distribution of direction preferences of RGC axons in the dLGN shell area examined (Figure S2B; Sabbah et al., 2017).

5. Figure S5. Additional evidence for functional clustering of OnOff preference, OnOff response sustainedness, and spatial frequency preference, Related to Figure 4J.

A. Example subregion of a field of view. (left) Boutons are colored according to their OnOff preference (−1: pure Off responsive; 0: On and Off responsive; 1: pure On responsive).

B. Normalized direction tuning curves for the four axons numbered in A. Normalization was performed across average responses to all stimulus conditions (Figure S2D).

C. Normalized average response timecourses during presentation of a full-field luminance increment (gray shaded region), for the same four axons as in B (mean ± s.e.m.). These nearby axons all had similar OnOff preference (i.e., all were On-preferring), but their temporal dynamics differed, further confirming that the boutons belonged to distinct axons.

D. Mean difference in OnOff preference across bouton pairs vs. distance between boutons, for real data (red) and shuffled data (gray), pooled across 3,825,696 eligible bouton pairs from 19 fields of view, 5 mice. Normalized OnOff preference similarity index is also depicted on right y-axis. Shaded error, s.e.m.

E. Enhancement in similarity of OnOff preferences at the scale of 2–6 μm was observed in all 19 fields of view.

F. Bouton pairs within each functional category (number of bouton pairs 2–6 μm apart vs. 50–60 μm apart: all pairs: N=12,126 vs. 308,583; AS: N=1202 vs. 24,608; DS: N=862 vs. 14,262; broadly tuned: N=705 vs. 11,596; suppressed by contrast: N=240 vs. 4478) showed significantly higher similarity indices for OnOff preference at a small spatial scale (2–6 μm) than at a longer spatial scale (50–60 μm). ***p < 0.001; Mann-Whitney-Wilcoxon test. Note that an intermediate level of pairwise similarity in OnOff preference also existed at a larger spatial scale for SBC boutons, possibly reflecting additional, larger-scale functional organization. DS: direction selective; AS: axis selective; BrT: broadly tuned; SBC: suppressed-by-contrast. All bar plots show mean ± s.e.m.

G. Bouton pairs within each functional category (number of bouton pairs 2–6 μm apart vs. 50–60 μm apart: all pairs: N=12,126 vs. 308,583; AS: N=1202 vs. 24,608; DS: N=862 vs. 14,262; broadly tuned: N=705 vs. 11,596; suppressed by contrast: N=240 vs. 4,478) showed significantly higher similarity indices for OnOff response sustainedness at a small spatial scale (2–6 μm) than at a larger spatial scale (50–60 μm). *p<0.05, ***p < 0.001; Mann-Whitney-Wilcoxon test. All bar plots show mean ± s.e.m.

H. Mean difference in spatial frequency preference across bouton pairs vs. distance between boutons, for real data (red) and shuffled data (black), pooled across 19 fields of view from 5 mice. Normalized spatial frequency preference similarity index also depicted on right y-axis. Shaded error, s.e.m.

I. A similar enhancement in similarity of spatial frequency preferences at the spatial scale of 2–6 μm was observed in all 19 fields of view.

J. Bouton pairs within each functional category (number of bouton pairs 2–6 μm apart vs. 50–60 μm apart): all pairs: N=11,972 vs. 301,432; AS: N=1,383 vs. 28,736; DS: N=1,066 vs. 18,525; broadly tuned: N=845 vs. 13,805; suppressed by contrast: N=244 vs. 4,566) showed significantly higher similarity indices for spatial frequency preference at a small spatial scale (2–6 μm) than at a larger spatial scale (50–60 μm). ***p < 0.001; Mann-Whitney-Wilcoxon test. Note, however, an intermediate level of pairwise similarity in spatial frequency preference at the larger scale for certain categories of boutons. All bar plots show mean ± s.e.m.

6. Figure S6. Ultrastructural convergence as a function of distance between boutons, Related to Figure 5.

A. To quantify the probability that nearby RGC boutons target a common dLGN neuron, we first considered the numbers of RGC bouton pairs within the EM section in A that contacted (blue) or did not contact (black) a common dLGN neuron, as a function of inter-bouton Euclidean distance. Bars include data from all pairs with inter-bouton distances that fall within the interval specified on the x-axis.

B. Using the data in Figure S6A, we estimated the probability that two boutons contacted at least one common target neuron: (# pairs of boutons both targeting the same neuron) / (# pairs of boutons targeting either the same neuron or different neurons). We then plotted this probability as a function of the Euclidean distance between boutons.

C. Side-view of each dLGN cell body targeted by one or more RGC boutons from the EM section in Figure 5A. The portion of postsynaptic dendrite contacting each of these RGC bouton synapses is shown, along with reconstruction of this dendrite back to the cell body. RGC boutons were colored translucent orange if they were ≤6 μm from at least one other RGC bouton detected in Figure 5A, and otherwise green. Regions with superposition of multiple nearby boutons are indicated by increasingly yellow color. Most, but not all, nearby RGC boutons contacting the same neuron were found to target the same local domain of a proximal dendrite. Rarely, multiple nearby dendrites from the same neuron were contacted by different RGC boutons or clusters of boutons from the same EM plane (e.g. right column, 9^th and 10^th neurons from the top).

D. By analyzing a separate dataset of reconstructed axons, we could plot the probability that two boutons from different axons target the same postsynaptic neuron, as a function of inter-bouton spacing. These data were estimated using all RGC boutons (N = 1,627) belonging to RGC axons that also targeted at least one of four ‘seed’ dLGN neurons selected from the EM volume (boutons directly targeting seed dLGN neurons were excluded from this analysis to avoid biasing the results; STAR Methods and Morgan et al., 2016). Note that the majority of pairs of RGC boutons from different axons and spaced ≤6 μm apart converged on a common dLGN target neuron.

7. Figure S7. Additional analyses of pairwise and groupwise clustering of RGC boutons, Related to Figures 6 and 7.

A. Pairs of boutons spaced 2–6 μm apart showed increased similarity in OnOff preference, when separately considering pairs with similar or dissimilar preferences for other visual features including axis preference, OnOff sustainedness, and spatial frequency preference (SF). N’s, from left to right: 12,126; 308,583; 1,599; 27,683; 788; 13,075; 391; 7497; 172,593; 2,054; 65,034; 5,672; 116,358; 2,986; 96,862. All bar plots: mean ± s.e.m. ***p < 0.001; Mann-Whitney-Wilcoxon test.

B. Image of the number of boutons within a radius of 6 μm surrounding each pixel (gray outlined area is from the same example field of view as in Figures 4A and 6C, E). Invalid pixels not meeting topological criteria are black. Valid pixels that satisfy the topological criteria (Figure 6D) but that do not have a significant groupwise similarity index for either motion axis, OnOff, or spatial frequency are shaded gray (significant similarity indices exceed 95% of those obtained following shuffling; STAR Methods).

C. Schematic illustrating groups of boutons determined to be ‘combination mode’, ‘relay mode’, or neither.

D. Same data as in Figure 6H, but plotted as fold-increase in incidence of groups of boutons exhibiting combination or relay mode, relative to chance incidence. Data are plotted on a logarithmic scale. Note that while the fold-change above chance in relay-mode clustering appears higher than for combination-mode clustering, this is largely accounted for by the fact that each type of combination-mode clustering (in which a single feature preference is shared by the group of boutons) occurs at above-chance levels (not shown). Specifically, there is an above-chance likelihood that clusters sharing two feature preferences will occur.

E. Groupwise bouton similarity was not strongly dependent on the number of boutons in a local group. For pixels surrounded by a varying number of eligible boutons within a 6 μm radius (3, 4, 5, or ≥6 boutons; cf. Figures 6D and S7B), we plotted the percentage of unique pixels classified as combination mode or relay mode, pooling data across 19 fields of view. Both modes of convergence were observed in local groups containing few boutons as well as those containing more boutons (in each mode, similarity indices for groups containing 3, 4, 5, or ≥6 boutons were not significantly different; Kruskal-Wallis test with Bonferroni correction for multiple comparisons).

F. On average, boutons from divergent axons that innervated combination-mode and relay-mode groups of boutons did not differ from other boutons in these groups, in that they exhibited feature preferences close to the mean feature preference of the associated group (cf. Figure 7A). This is evident from a comparison of the groupwise similarity index for (i) all boutons in a group, (ii) all boutons in a group after removing a bouton from a ‘divergent’ axon, and (iii) all boutons in a group after removing a bouton not belonging to a ‘divergent’ axon. These three cases were not significantly different when assessing mean similarity across the 19 fields of view (Kruskal-Wallis test with Bonferroni correction for multiple comparisons). In other words, divergent axons participate in functionally similar clusters of boutons in a manner that matches, on average, the shared feature preference(s) of the target cluster.

All bar plots show mean ± s.e.m.

8. Video S2: Retinotopic responses of RGC axonal boutons in dLGN, Related to Figure 2.

This movie illustrates the average evoked responses of RGC axonal boutons in the dLGN shell region (right) to 2-s presentations of 5° bars containing bandpass-filtered spatiotemporal noise (left; bars are presented in pseudorandom order but sorted for presentation purposes). Averaged evoked responses (fraction change in fluorescence; white dots: increased bouton activity, black: decreased bouton activity) are shown for stimuli presented at various retinotopic locations varying in azimuth and in elevation. See also Figures 2F, S1 and S2H.

9. Video S3: Electron microscopy data illustrating concentrated inputs from many RGC axonal boutons surrounding a dLGN neuron dendrite, Related to Figure 5.

This movie shows a traced dLGN dendrite (white) and all RGC boutons that contact it (green spheres), derived from a 3D ultrastructural dataset in the dLGN shell region. Note the presence of small dendritic protrusions targeted by a subset of RGC boutons. Blue: limits of traced region of dendrite and soma. Red: axon. See also Figure 5C–D.

Highlights.

• Chronic imaging reveals diverse visual tuning of mouse retinothalamic boutons

• Clusters of boutons can share one or several visual feature preferences in common

• Functional clustering of boutons occurs at a canonical spatial scale of ~6 μm

• One axon can innervate multiple clusters specialized for different visual features