Two-way mixed-effects methods for joint association analysis using both host and pathogen genomes

Significance

Genome-wide association (GWA) mapping is a powerful tool for identification of genetic variants underlying complex traits. However, existing methods typically perform GWA mapping within a single species; methods allowing the description of the genomic landscape of interspecies interactions are only beginning to be developed. Here, we present a method to simultaneously perform GWA mapping on two interacting species. We applied our approach to the Arabidopsis thaliana–Xanthomonas arboricola pathosystem and identified candidate genes conferring host–pathogen specificity. By integrating the whole-genome sequence data available for pairs of interacting species, we can decipher the genetic architecture of complex traits in finer detail than has previously been possible.

Abstract

Infectious diseases are often affected by specific pairings of hosts and pathogens and therefore by both of their genomes. The integration of a pair of genomes into genome-wide association mapping can provide an exquisitely detailed view of the genetic landscape of complex traits. We present a statistical method, ATOMM (Analysis with a Two-Organism Mixed Model), that maps a trait of interest to a pair of genomes simultaneously; this method makes use of whole-genome sequence data for both host and pathogen organisms. ATOMM uses a two-way mixed-effect model to test for genetic associations and cross-species genetic interactions while accounting for sample structure including interactions between the genetic backgrounds of the two organisms. We demonstrate the applicability of ATOMM to a joint association study of quantitative disease resistance (QDR) in the Arabidopsis thaliana–Xanthomonas arboricola pathosystem. Our method uncovers a clear host–strain specificity in QDR and provides a powerful approach to identify genetic variants on both genomes that contribute to phenotypic variation.

Genome-wide association studies (GWASs) can provide insight into the genetic basis of complex traits. A standard paradigm in genome-wide association (GWA) mapping (1–3) is to genotype a sample of individuals of a single species and then measure the statistical association between each genetic variant (such as single-nucleotide polymorphism, SNP) on the genome and the trait of interest. Owing to advances in genotyping and sequencing technology, the GWA mapping approach has become a powerful tool of trait analysis for a number of species, including humans, Drosophila, Arabidopsis, and maize (3–6).

Despite the widespread popularity of GWASs, GWA mapping has rarely been performed on two interacting species simultaneously (7). Integration of genomes from a pair of organisms into GWA mapping will allow the elucidation of genomic regions that are likely to carry evidence of co-evolution between species. Pathosystems, in which a pathogen and host adapt to each other and jointly determine infectious disease status (8, 9), constitute an important class of examples. Interactions between host and pathogen can include G $\times$ G interactions between pairs of causal variants as well as interactions between population membership indicators representing genetic backgrounds of host and pathogen. To our knowledge, existing GWA methods (2, 10) performed on disease phenotypes either exclusively focus on the host genome (6) or stratify the mapping by pathogen strain (11), leaving the pathogen genome unexplored (12). With advances in sequencing, both host and pathogen genome data are becoming readily available. Identifying genetic associations on both genomes can provide insight into the genetic basis of host–pathogen specificity, thereby shedding light on the molecular landscape of host–pathogen interactions. Therefore, statistical methods that integrate genomes from a pair of organisms into GWA mapping could enable important advances.

In this paper, we present the ATOMM method (for Analysis with a Two-Organism Mixed Model) designed to simultaneously detect genetic variants on a pair of genomes that are associated with a trait of interest. We develop both Gaussian and binomial-like, two-way, mixed-effects models whose features include random and fixed effects for the two organisms and interactions between them. ATOMM offers three main advantages over previous methods (1–3). First, ATOMM takes advantage of the genome sequence data from both partners in the pathosystem, with effects of variants in the two genomes jointly incorporated in the model. In addition to including main effects of both host and pathogen variants, ATOMM explicitly models interaction between variants on the host and pathogen genomes. This can enable identification of, for example, host variants whose effects are specific to certain strains of pathogen, which might be expected to occur due to co-evolution, but could be overlooked by existing GWA methods (2, 10). Second, ATOMM addresses the challenges of confounding due to host and pathogen population structure by using a two-way, mixed-effects model with three types of genetic relatedness matrices (GRMs): one each for the host and pathogen additive polygenic random effects individually, and the third for the additive-by-additive polygenic interaction random effects between the two genomes. The inclusion of GRMs in the model for background correlation of the trait can improve both power and type 1 error when mapping in structured samples. Third, ATOMM integrates different types of genetic variants, including both mutation and deletion polymorphisms, into the association mapping, and we develop a generalized GRM that allows multiallelic variants. While available methods can be directly applied to marginal analysis of most common host species, there is a lack of association methods appropriate for bacterial pathogens, whose genomes typically include a large number of insertion–deletion polymorphisms in addition to the usual allelic polymorphisms (13). Our method takes into account both the core genome (i.e., regions shared by all strains) and the dispensable genome (i.e., regions shared by a subset of strains) in bacterial pathogens, thus making better use of the wealth of genomic data provided by whole-genome sequencing of the pathogen.

We demonstrate the applicability of ATOMM in a pathosystem in which the model plant Arabidopsis thaliana interacts with the bacterial pathogen Xanthomonas arboricola in natural settings (see SI Appendix). A. thaliana is known to harbor a considerable number of genetic variants for many adaptively important traits, and a GWAS approach appears to be productive even with low sample size (3).

With some modification, our framework can be extended as well to association studies involving human participants, provided that the infectious agent also has an available genome sequence (Discussion). We believe that the development of ATOMM is timely, as several consortium efforts have emerged to sequence the genomes of a variety of organisms (4, 5, 12, 14).

ATOMM for Joint GWA Mapping

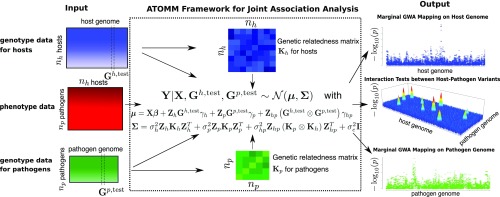
Fig. 1 illustrates the schematic diagram of ATOMM in a host–pathogen association study. ATOMM takes as input (i) phenotype data consisting of a trait measured on host–pathogen pairs and (ii) genotype data consisting of genome-wide variants in host and pathogen samples. Our goal is to identify genomic regions associated with the trait in both host and pathogen genomes simultaneously and to detect gene–gene interaction between host and pathogen.

Fig. 1.

Schematic diagram of the ATOMM framework for joint association analysis. ATOMM takes as input (i) phenotypic values obtained from host–pathogen pairs and (ii) whole-genome sequencing data for both host and pathogen samples and outputs results from (i) marginal GWA mapping on host and pathogen genomes and (ii) G $\times$ G interactions between host and pathogen variants. In this schematic, a (conditionally) multivariate normal trait is assumed, but we have also developed a version of ATOMM for binomial-like count data.

In genetic association studies, failure to adequately account for population structure can lead to inflated type 1 error and loss of power (2, 15). This issue requires particular attention in our context because both host and pathogen samples may exhibit population structure, though not necessarily of the same type. Furthermore, host and pathogen subpopulations may undergo co-adaptation in a natural biotic system, resulting in a systematically heterogeneous genetic background across samples. This introduces further complexity into association analysis because differences in phenotype may be due to the pairing of the genetic backgrounds or population memberships of the organisms rather than to the pair of variants being tested. This population-level interaction must be accounted for to avoid confounding in the association analysis. We tackled these challenges via a mixed-model approach, which we describe below.

Two-Way Mixed-Effects Model Underlying ATOMM.

We first consider association analysis with a quantitative trait, meaning that the response is multivariate Gaussian (conditional on the predictors). The extension to a binomial-like trait is given in Materials and Methods. Suppose there are $n$ observations, and for $1\le k\le n$, let $Y_k$ denote the trait value for the $k$th observation. Suppose the $k$th observation is for host–pathogen pair $\left(i,j\right)$, where $i=1,\dots ,n_h$ indexes the host line, and $j=1,\dots ,n_p$ indexes the pathogen strain. We propose to model $Y_k$ as

$$\begin{array}{ll}\hfill Y_k=& X_k\mathit{\beta }+G_i^{h,\text{test}}{\gamma }_h+G_j^{p,\text{test}}{\gamma }_p+G_i^{h,\text{test}}{G}_j^{p,\text{test}}{\gamma }_{hp}\hfill \\ \hfill & +{\eta }_i^h+{\eta }_j^p+{\eta }_{ij}^{hp}+{\epsilon }_k,\hfill \end{array}$$ [1]

where $X_k$ is a row vector of observed covariate values (with first entry 1, to represent an intercept term) for pair observation $k$; $\mathit{\beta }$ is a column vector of unknown coefficients; $G_i^{h,\text{test}}$ and $G_j^{p,\text{test}}$ are the observed genotype of, respectively, host $i$ at the host genetic variant currently being tested and pathogen $j$ at the pathogen genetic variant currently being tested; ${\gamma }_h$, ${\gamma }_p$, and ${\gamma }_{hp}$ are unknown parameters of interest representing the effects of the host genetic variant being tested, the pathogen genetic variant being tested, and the interaction of these, respectively; ${\eta }_i^h$ is the additive polygenic random effect of other host genomic variants not currently being tested; ${\eta }_j^p$ is the additive polygenic random effect of other pathogen genomic variants not currently being tested; ${\eta }_{ij}^{hp}$ is a random effect representing additive-by-additive polygenic interactions between host and pathogen variants not currently being tested; and ${\epsilon }_k$ is assumed to be independent and identically distributed (i.i.d.) $\mathcal{N}\left(0,{\sigma }_e^2\right)$. Note that if, for example, the pathogen variant currently being tested is not binary, then the model specification changes somewhat (see SI Appendix).

We use Fisher’s infinitesimal approach (16) to model the polygenic random effects ${\eta }_i^h$, ${\eta }_j^p$, and ${\eta }_{ij}^{hp}$, which arise as the result of many variants, assumed to be of small effect, throughout the genomes. Specifically, let ${\mathit{\eta }}^h={\left({\eta }_1^h,\dots ,{\eta }_{n_h}^h\right)}^T$, ${\mathit{\eta }}^p={\left({\eta }_1^p,\dots ,{\eta }_{n_p}^p\right)}^T$, and ${\mathit{\eta }}^{hp}={\left({\eta }_{11}^{hp},\dots ,{\eta }_{1n_p}^{hp},\dots ,{\eta }_{n_{h}1}^{hp},\dots ,{\eta }_{n_h{n}_p}^{hp}\right)}^T$. Then, under certain infinitesimal model assumptions (SI Appendix), we have

$${\mathit{\eta }}^h\sim \mathcal{N}\left(\mathbf{0},{\sigma }_h^2{\mathit{K}}_h\right),\hspace{0.17em}{\mathit{\eta }}^p\sim \mathcal{N}\left(\mathbf{0},{\sigma }_p^2{\mathit{K}}_p\right),\hspace{0.17em}{\mathit{\eta }}^{hp}\sim \mathcal{N}\left(\mathbf{0},{\sigma }_{hp}^2{\mathit{K}}_{hp}\right),$$ [2]

where ${\mathit{K}}_h{\in \mathbb{R}}^{n_h\times n_h}$ and ${\mathit{K}}_p{\in \mathbb{R}}^{n_p\times n_p}$ are, respectively, the GRMs (to be specified in the next section) for the hosts and for the pathogens; ${\mathit{K}}_{hp}{\in \mathbb{R}}^{\left(n_h{n}_p\right)\times \left(n_h{n}_p\right)}$ is the covariance matrix for the host–pathogen intergenome polygenic random effects; and ${\sigma }_h^2$, ${\sigma }_p^2$, and ${\sigma }_{hp}^2$ are unknown scalar parameters. We assume ${\mathit{K}}_{hp}={\mathit{K}}_h\otimes {\mathit{K}}_p$, where $\otimes$ denotes the Kronecker product. The derivation of this modeling assumption using Fisher’s infinitesimal approach is detailed in SI Appendix, Section 1.2.

Combining Eqs. 1 and 2 yields the vectorized version of the full model,

$$\begin{array}{ll}\hfill \mathit{Y}& |\mathit{X},{\mathit{G}}^{h,\text{test}},{\mathit{G}}^{p,\text{test}}\sim \mathcal{N}\left(\mathit{\mu },\mathbf{\Sigma }\right),\hspace{1em}\text{with}\hfill \\ \hfill \mathit{\mu }& =\mathit{X}\mathit{\beta }+{\mathit{Z}}_h{\mathit{G}}^{h,\text{test}}{\gamma }_h+{\mathit{Z}}_p{\mathit{G}}^{p,\text{test}}{\gamma }_p\hfill \\ \hfill & +{\mathit{Z}}_{hp}\left({\mathit{G}}^{h,\text{test}}\otimes {\mathit{G}}^{p,\text{test}}\right){\gamma }_{hp},\hfill \\ \hfill \mathbf{\Sigma }& ={\sigma }_h^2{\mathit{Z}}_h{\mathit{K}}_h{\mathit{Z}}_h^T+{\sigma }_p^2{\mathit{Z}}_p{\mathit{K}}_p{\mathit{Z}}_p^T+{\sigma }_{hp}^2{\mathit{Z}}_{hp}\left({\mathit{K}}_h\otimes {\mathit{K}}_p\right){\mathit{Z}}_{hp}^T\hfill \\ \hfill & +{\sigma }_e^2\mathit{I},\hfill \end{array}$$ [3]

where $\mathit{Y}={\left(Y_1,\dots ,Y_n\right)}^T$; $\mathit{X}\mathit{\beta }$ represents the intercept and the covariate effects; ${\mathit{G}}^{h,\text{test}}={\left(G_1^{h,\text{test}},\dots ,G_{n_h}^{h,\text{test}}\right)}^T$; ${\mathit{G}}^{p,\text{test}}={\left(G_1^{p,\text{test}},\dots ,G_{n_p}^{p,\text{test}}\right)}^T$; ${\mathit{Z}}_h{\in \mathbb{R}}^{n\times n_h}$, ${\mathit{Z}}_p{\in \mathbb{R}}^{n\times n_p}$, and ${\mathit{Z}}_{hp}{\in \mathbb{R}}^{n\times n_{hp}}$ are the incidence matrices that map the trait value to host lines, to pathogen strains, and to host–pathogen pairs, respectively; and $\mathit{I}$ denotes an $n$-by-$n$ identity matrix.

The parameters of interest in the model in Eq. 3 are the association parameters $\left({\gamma }_h,{\gamma }_p,{\gamma }_{hp}\right)$, while the nuisance parameters are $\mathit{\beta }$ and the variance components (VCs) $\left({\sigma }_h^2,{\sigma }_p^2,{\sigma }_{hp}^2,{\sigma }_e^2\right)$. We find it convenient to represent the VCs in terms of $\left({\sigma }_t^2,{\xi }_h,{\xi }_p,{\xi }_{hp}\right)$, where ${\sigma }_t^2={\sigma }_h^2+{\sigma }_p^2+{\sigma }_{hp}^2+{\sigma }_e^2$ represents the total residual variance of the trait, and ${\xi }_h={\sigma }_h^2/{\sigma }_t^2$, ${\xi }_p={\sigma }_p^2/{\sigma }_t^2$, and ${\xi }_{hp}={\sigma }_{hp}^2/{\sigma }_t^2$ represent the (narrow-sense) heritability due to host, pathogen, and host–pathogen additive-by-additive polygenic effects, respectively. In our analysis of the A. thaliana–X. arboricola pathosystem, we include an additional VC in the model to represent a plant random effect (see ATOMM with an Additional VC).

General Formulation for Haploid GRM Estimation.

ATOMM uses whole-genome sequence data to estimate the GRMs ${\mathit{K}}_h$ and ${\mathit{K}}_p$. For ease of presentation, we consider only the case of a haploid organism or inbred lines of a diploid organism and drop the subscript/superscript $h$ or $p$ in this section.

GRM estimation with mutation polymorphisms.

Let $G_{il}$ be the genotype of individual $i$ at genetic variant $l$, for $i=1,\dots ,n$ and $l=1,\dots ,m$. Suppose each variant $l$ has only two possible states (e.g., variant could be a SNP), $G_{il}\in \left\{\mathrm{0,1}\right\}$, and let $f_l$ be the allele frequency at variant $l$. A standard model (2, 17, 18) for ${\eta }_i$, the additive polygenic effect of background variants in the genome for individual $i$, is expressed as

$${\eta }_i=\sum _{l=1}^m{\alpha }_l\frac{G_{il}-f_l}{\sqrt{f_l\left(1-f_l\right)}},\hspace{1em}i=1,\dots ,n,$$ [4]

where, conditional on $\mathit{G}=\left[\left[G_{il}\right]\right]{\in \mathbb{R}}^{n\times m}$, the ${\alpha }_l$s are i.i.d. with

$$\mathbb{E}\left({\alpha }_l\mathit{G}\right)=0,\hspace{0.17em}\text{Var}\left({\alpha }_l\mathit{G}\right)=\frac{{\sigma }^2}{m},\hspace{1em}l=1,\dots ,m.$$ [5]

Let $\mathit{\eta }={\left({\eta }_1,\dots ,{\eta }_n\right)}^T$. Then, Eqs. 4 and 5 lead to the asymptotic approximation $\mathit{\eta }\mathit{G}\sim \mathcal{N}\left(\mathbf{0},{\sigma }^2\mathit{K}\right)$ for large $m$, where $\mathit{K}{\in \mathbb{R}}^{n\times n}$ is the GRM with $\left(i,j\right)$th entry

$$K_{ij}=\frac{1}{m}\sum _{l=1}^m\frac{\left(G_{il}-f_l\right)\left(G_{il}-f_l\right)}{f_l\left(1-f_l\right)}.$$ [6]

When whole-genome sequence data are available, $\mathit{K}$ can be estimated by Eq. 6, using the set of typed bi-allelic variants, with their sample frequencies ${\widehat{f}}_l$s used in place of the $f_l$s.

GRM estimation with both mutation and deletion polymorphisms.

Now suppose that each variant $l$ has three possible states, $G_{il}\in \left\{0,1,D\right\}$. The particular type of tri-allelic variant we consider is what we will call a “deletion variant,” where “0” and “1” represent two alleles of a SNP, and “D” represents “deletion.” This encoding is motivated by a genomic feature of pathogens such as X. arboricola, in which many SNP sites (known as dispensable SNP sites) are present in only a subset of the sampled strains. We consider ${\eta }_i$, the additive polygenic effect due to all such dispensable SNP sites in the genome (i.e., summed over all such sites), for individual $i$. We propose to decompose ${\eta }_i$ into two orthogonal parts: ${\eta }_i={\eta }_{i1}+{\eta }_{i2}$, where ${\eta }_{i1}$ represents the random effect due to the SNP alleles at the variants and ${\eta }_{i2}$ represents the random effect due to the presence or absence of sites. We model these two effects similarly as in Eq. 4 and assume that they contribute approximately equally to the variance (SI Appendix). The resulting model for the additive polygenic effect, $\mathit{\eta }={\mathit{\eta }}_1+{\mathit{\eta }}_2$, where $\mathit{\eta }={\left({\eta }_1,\dots ,{\eta }_n\right)}^T$, ${\mathit{\eta }}_1={\left({\eta }_{11},\dots ,{\eta }_{n1}\right)}^T$, and ${\mathit{\eta }}_2={\left({\eta }_{12},\dots ,{\eta }_{n2}\right)}^T$, can be written as $\mathit{\eta }|\mathit{G}\sim \mathcal{N}\left(\mathbf{0},{\sigma }^2\mathit{K}\right)$, where $\mathit{K}{\in \mathbb{R}}^{n\times n}$ is the GRM with $\left(i,j\right)$th entry

$$\begin{array}{ccc}\hfill K_{ij}=\frac{1}{2m}\sum _{l=1}^m\left(-{\mathbb{1}}_{\left\{G_{il}\hspace{0.17em}\ne \hspace{0.17em}{G}_{jl}\right\}}\sum _{s\in \left\{D,\mathrm{0,1}\right\}}\frac{1-f_{ls}}{f_{ls}}{\mathbb{1}}_{\left\{G_{il}=G_{jl}=s\right\}}\right),& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ [7]

where $m$ is the number of tri-allelic variants, $f_{ls}$ is the frequency of state $s$ at variant $l$, and $f_{l1}+f_{l0}+f_{lD}=1$. The scale factor 2 in Eq. 7 is to ensure $\mathbb{E}\left(K_{ii}\right)=1$ assuming $G_{il}$ follows a three-class categorical distribution.

Our approach essentially treats the deletion as a third allelic type and can be generalized to variants with $\delta$ alleles, where $\delta \ge 3$. SI Appendix, Eq. 13 gives the formula for general $\delta$, which reduces to Eq. 6 when $\delta =2$ and to Eq. 7 when $\delta =3$.

Finally, in the general case when the genome consists of both bi-allelic and tri-allelic variants, we construct the empirical GRM $\mathit{K}$ using the weighted average of Eqs. 6 and 7, where the weight is proportional to the number of corresponding variants and the sample frequencies are used in place of the true allele frequencies in each $\mathit{K}$.

Association Mapping with ATOMM.

We may wish to estimate the parameters of the full ATOMM model, or for the purpose of hypothesis testing, we may wish to estimate the parameters under a submodel in which some or all of ${\gamma }_h$, ${\gamma }_p$, and ${\gamma }_{hp}$ are set to 0, as we describe in the following paragraphs. The method of parameter estimation is essentially the same in either case. In the conditionally Gaussian model, the unknown parameters are estimated by maximum likelihood. For the binomial-like version of the ATOMM model, which is described in Materials and Methods, we perform parameter estimation by extending a previously described quasi-likelihood approach (19, 20) to construct and solve a set of estimating equations (SI Appendix).

In the joint association analysis, there may be several hypothesis tests of interest depending on the goal. Given a pair of genetic variants, one from the host genome (call this variant H) and the other from the pathogen genome (call this variant P), we derive here two kinds of hypothesis tests that were examined in the A. thaliana–X. arboricola pathosystem. Other forms of hypothesis tests are also possible and are provided in SI Appendix.

Marginal Test of H or P.

In the model in Eq. 3, the genetic effect of an individual host or pathogen variant can be assessed marginally by testing, for example, in the case of a host SNP

$${\mathcal{H}}_0:{\gamma }_h=0\hspace{1em}\text{vs}.{\hspace{1em}\mathcal{H}}_A:{\gamma }_h\ne 0,$$

with the constraint that ${\gamma }_p={\gamma }_{hp}=0$. ATOMM uses a score statistic for this hypothesis test:

$$\begin{array}{cc}\hfill T=& \frac{1}{{\widehat{\sigma }}_{t,0}^2}{\left(\mathit{Y}-\mathit{W}{\widehat{\mathit{\beta }}}_0\right)}^T{\widehat{\mathbf{\Sigma }}}_0^{-1}\mathit{G}[{\mathit{G}}^T{\widehat{\mathbf{\Sigma }}}_0^{-1}\mathit{G}-{\mathit{G}}^T{\widehat{\mathbf{\Sigma }}}_0^{-1}\mathit{W}\hfill \\ \hfill & {\left({\mathit{W}}^T{\widehat{\mathbf{\Sigma }}}_0^{-1}\mathit{W}\right)}^{-1}{\mathit{W}}^T{\widehat{\mathbf{\Sigma }}}_0^{-1}\mathit{G}{]}^{-1}{\mathit{G}}^T{\widehat{\mathbf{\Sigma }}}_0^{-1}\left(\mathit{Y}-\mathit{W}{\widehat{\mathit{\beta }}}_0\right),\hfill \end{array}$$ [8]

where in Eq. 8 we set $\mathit{G}={\mathit{Z}}_h{\mathit{G}}^{h,\text{test}}$, $\mathit{W}=\mathit{X}$, and the quantities with subscript 0 denote the estimates under the global null ${\gamma }_h={\gamma }_p={\gamma }_{hp}=0$. Under ${\mathcal{H}}_0$, $T$ follows a ${\chi }_1^2$ distribution. The marginal association of a pathogen variant can be assessed similarly, in which we test the null ${\mathcal{H}}_0:{\gamma }_p=0$ against ${\mathcal{H}}_A:{\gamma }_p\hspace{0.17em}\ne \hspace{0.17em}0$ with constraint ${\gamma }_h={\gamma }_{hp}=0$.

Gene $\times$ Gene interaction between H and P.

For a given pair (H, P) consisting of a host variant and a pathogen variant, the interaction test, defined to test

$${\mathcal{H}}_0:{\gamma }_{hp}=0\hspace{1em}\text{vs}.{\hspace{1em}\mathcal{H}}_A:{\gamma }_{hp}\hspace{0.17em}\ne \hspace{0.17em}0,$$

can be carried out to assess whether the combined effects of the genetic variant pair are modified by additional interaction. The ability to test the G $\times$ G effect separately from the marginal effects can be particularly useful for identifying host variants that respond differently for different pathogen variants. The test statistic is the same as in Eq. 8, except that we set $\mathit{G}={\mathit{Z}}_{hp}\left({\mathit{G}}^{h,\text{test}}\otimes {\mathit{G}}^{p,\text{test}}\right)$, $\mathit{W}=(\mathit{X},\hspace{0.17em}{\mathit{Z}}_h{\mathit{G}}^{h,\text{test}}$, ${\mathit{Z}}_p{\mathit{G}}^{p,\text{test}})$, and the estimates, ${\widehat{\mathit{\beta }}}_0$ and ${\widehat{\sigma }}_{t,0}^2$, are recalculated under ${\mathcal{H}}_0:{\gamma }_{hp}=0$, instead of ${\gamma }_h={\gamma }_p={\gamma }_{hp}=0$. The resulting test statistic has a ${\chi }_1^2$ or ${\chi }_2^2$ null distribution depending on whether the variant $P$ is bi-allelic or tri-allelic (assuming the variant $H$ is bi-allelic).

The association mapping can be performed on a genome-wide scale over the two genomes, with one pair of host–pathogen variants being tested at a time (see Fig. 1). The testing procedure is parallelizable in a very straightforward way, which makes ATOMM computationally feasible for large-scale studies through parallel implementation. In practice, since most host–pathogen variant pairs have only small effects, we follow the common approach in GWASs (2, 10, 21, 22) and choose to compute the VC ratios, $\left({\xi }_h,{\xi }_p,{\xi }_{hp}\right)$, under the global null, ${\gamma }_h={\gamma }_p={\gamma }_{hp}=0$, only once per genome-wide scan (at least at the initial stage of analysis). The fixed effects $\mathit{\beta }$ and total residual variance ${\sigma }_t^2$ are refit for every host–pathogen variant pair.

Application of Joint Association Study to the A. thaliana–X. arboricola Pathosystem

To investigate the capability of ATOMM to reveal the genetic landscape of complex traits, we carried out a joint association study (Materials and Methods) of quantitative disease resistance (QDR) in a plant pathosystem of 130 A. thaliana inbred lines (host) and 22 bacteria X. arboricola strains (pathogen). Briefly, we paired each of the 130 A. thaliana lines with each of the 22 X. arboricola strains, using three biological replicates for each A. thaliana–X. arboricola pair. These combinations resulted in a total of $130\times 22\times 3$ plants. One of three researchers then infected 2 to 4 leaves (median = 4) on each plant. The QDR score for each leaf was measured by one of the three researchers 11 d after inoculation. As described in ref. 23, the QDR was defined using a disease index from 0 (resistant) to 4 (susceptible). We took the individual leaf as the experimental unit with $\mathit{Y}\in {\left\{\mathrm{0,1,2,3,4}\right\}}^n$, $n$ = 32,960.

We also collected the whole-genome sequence data for both A. thaliana and X. arboricola samples (Materials and Methods). In particular, the 130 A. thaliana lines in our study are a subset of the 1001 Genomes Project (14), which contains the most complete whole-genome sequencing to date for 1,135 natural A. thaliana lines.

Population Structure and Effects.

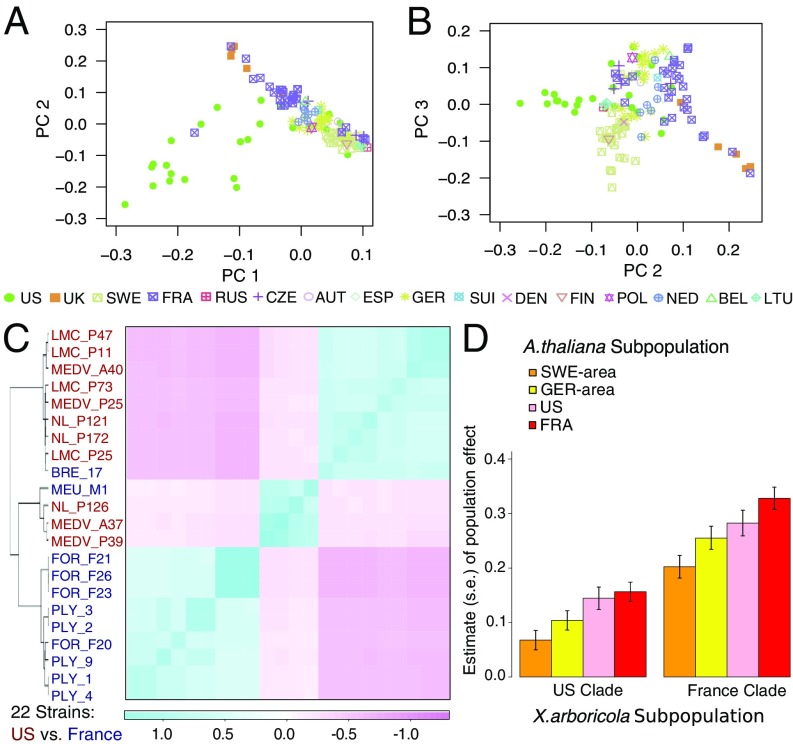
A well-recognized challenge in association studies is to account for various forms of sample structure, including population stratification, admixture, family relatedness, and cryptic relatedness. We found that our proposed GRMs captured the latent structure present in the host and pathogen samples well (Fig. 2 A–C). Hierarchical clustering based on the host GRM demonstrated that the 130 sampled A. thaliana lines had multiple levels of population structure, ranging from continental and regional clusters of lines to closely related pairs of lines (SI Appendix, Fig. S1). We found that the first three principal components (PCs) of the GRM captured the geographical origins of A. thaliana (Fig. 2 A and B): The first two PCs distinguished US lines from European lines, while the combination of the three top PCs were effective at separating some of the countries of Europe from one another. On the basis of these PCs, the 130 A. thaliana lines cluster into four subpopulations: Sweden area (36 lines), Germany area (33 lines), US (25 lines), and France area (36 lines). On the pathogen side, several X. arboricola strains exhibited remarkable closeness, with seven strain pairs having genomic correlations larger than 0.9: {MEDV_A37, MEDV_A39}, {LMC_P11, LMC_P47}, {PLY_1, PLY_4}, {PLY_2, PLY_3}, and {FOR_F21, FOR_F23, FOR_F26}, where 1 is the genomic correlation for a pair of identical strains. The top two PCs of the GRM (SI Appendix, Fig. S2) result in a clustering of the 22 X. arboricola strains into two subpopulations: US clade (13 strains) and France clade (9 strains). These clusters matched the geographic origin of strains, except that BRE_17 and MEU_M1 originated in France but were genetically more similar to US than French strains (Fig. 2C).

Fig. 2.

Population structure and effects in the A. thaliana–X. arboricola pathosystem. A and B depict the top three PCs extracted from the A. thaliana GRM, which cluster the 130 A. thaliana lines into four subpopulations as described in the text. C is the level plot for the X. arboricola GRM, which clusters the 22 strains into two subpopulations as described in the text. The hierarchical clustering overlaid on Left is obtained using the unweighted pair group method with arithmetic mean (UPGMA) (25), where for the dissimilarity measure, we use $\left[1-\widehat{\rho }\left(i,j\right)\right]/2$ with $\widehat{\rho }\left(i,j\right)$ being the genomic correlation between strains $i$ and $j$. D plots the joint effects of host and pathogen population membership on QDR. Each bar represents the effect on QDR of a particular pairing of host subpopulation and pathogen clade, where these effects were estimated from a linear model that includes indicators for each of the $4\times 2=8$ possible pairings of subpopulations (one host and one pathogen) as predictors, with correction for additional covariates.

To assess the extent to which the variation in QDR is attributable to the particular geographic areas from which the host and pathogen are drawn, we fit an ordinary linear model to QDR, in which we included indicators for each of the 4 $\times$ 2 = 8 possible pairings of subpopulations (one host and one pathogen, inferred from the PCs) as predictors, with correction for additional covariates (see ATOMM with an Additional VC). We found no strong evidence of population-level interaction indicative of local adaptation or maladaptation between host and pathogen (Fig. 2D and Materials and Methods). Nevertheless, the pathogen clade was highly predictive of QDR ($p=9.89\times 10^{-33}$), with the France clade being more virulent than the US clade (Fig. 2D). To investigate which strains drove the differentiation, we estimated the strain effects by fitting a linear model but with strain indicators as predictors. Among the 22 strains, FOR_F21 and PLY_1, both of French origin, were found to be the most virulent (SI Appendix, Fig. S3). Interestingly, their respective genetically closest strains (i.e., strains with genomic covariance $>$ 0.9), FOR_F26 and PLY_4, were not as virulent. As previously observed with the bacterial pathogen Pseudomonas syringae sampled in natural populations of A. thaliana (24), strains of X. arboricola that differ in virulence can co-inhabit populations of A. thaliana. Results of fitting additional models to the data can be found in SI Appendix, where we also address the issues of model selection and assessment of goodness of fit of the models to the observed data.

Heritability Estimation.

We applied the null ATOMM model to QDR and estimated the contribution of the genomic variation to the phenotypic variation. We found that the X. arboricola polygenic effects explained a large proportion (44%) of the residual variance of QDR, whereas A. thaliana and A. thaliana–X. arboricola polygenic effects explained 2% and 5% of the residual variance, respectively (Table 1). The results under the binomial-like ATOMM (Materials and Methods) were similar (Table 1). A similar phenomenon was previously found in the human-HIV pathosystem where a larger proportion of viral load was explained by virus genetic diversity (29%) than by host factors (8.4%) (26). Because each pathogen strain had a number of replicates in our design, we were able to further investigate whether the phenotypic variance explained by X. arboricola was attributable to additive polygenic effects of genome-wide variants, so that related strains would have similar phenotypic values, or whether the interactions among variants in each X. arboricola strain led each strain to have its own distinctive effect, with little similarity among closely related strains. To examine this, we fit a model that includes a fixed effect for each host line, each pathogen strain, and each line–strain pair (SI Appendix, Eq. 41). In that model, the strain fixed effects explain 52% of the phenotypic variance. This can be interpreted as the proportion of phenotypic variance explained by pathogen genetic effects, including both additive and epistatic pathogen genetic effects (note that there is no dominance effect because the organism is haploid). Comparison of this value of 52% to the estimate of 44% for the proportion of phenotypic variance explained by pathogen additive genetic effects in the ATOMM model showed that QDR was highly heritable with respect to the pathogen and that nearly all of the strain effect was attributable to additive polygenic effects of variants in the X. arboricola genome, so that the responses to related strains tended to be similar.

Table 1.

Parameter estimates under the Gaussian and binomial-like ATOMM models for the A. thaliana–X. arboricola pathosystem

Parameter estimate under the null	Gaussian ATOMM estimate (SE)	Binomial-like ATOMM estimate (SE)
Intercept, ${\beta }_0$	0.19 (0.011)	-0.75 (0.013)
Person 1, ${\beta }_1$	0.15 (0.015)	0.16 (0.015)
Person 2, ${\beta }_2$	0.20 (0.015)	0.19 (0.015)
Total residual variance, ${\sigma }_t^2$	1.23	1.45
Proportion of residual variance due to
A. thaliana, ${\xi }_h$	0.021	0.011
X. arboricola, ${\xi }_p$	0.441	0.581
A. thaliana–X. arboricola interaction, ${\xi }_{hp}$	0.048	0.011
Plant/block effect, ${\xi }_J$	0.093	0.069

We included in ATOMM the person effects (i.e., effects due to which lab researcher scored the QDR) as covariates. There were three persons measuring the trait scores. One person effect is subsumed into the intercept, leaving us to estimate effects of person 1 and person 2 only. In addition to the four genetic VC_s described in Eq. 3, we also included the plant effect as arandom effect (see Materials and Methods). The parameters were estimated under the global null hypothesis ${\mathcal{H}}_0:{\gamma }_h={\gamma }_p={\gamma }_{hp}=0$.

Marginal GWA Mapping.

To identify genetic variants that were associated with QDR, we used ATOMM to perform a score test for the effect of each A. thaliana variant and a score test for the effect of each X. arboricola variant. The marginal GWA mapping on the A. thaliana genome was well calibrated; that is, the type 1 error was well controlled (SI Appendix, Fig. S10A, genomic control coefficient $\lambda =1.07$), suggesting that our method does a good job of correcting for confounding due to population structure. Nevertheless, we observed few strong association signals from the marginal analysis (SI Appendix, Fig. S4). This indicated that most host genes were unlikely to confer broad-spectrum resistance to the full range of 22 X. arboricola strains. For the top associated pathogen variants, we found that their genotype patterns (see Genotyping Experiment) tended to differentiate strain PLY_1 from PLY_4 and to differentiate strain FOR_21 from FOR_26. In particular, among the top 100 genotype patterns tested, all of them differentiated FOR_21 from FOR_F26 and 84% of them differentiated PLY_1 from PLY_4. This result was in agreement with the noticeable difference in QDR between FOR_21/PLY_1, on the one hand, and their genetically closest strains FOR_26/PLY_4, on the other (SI Appendix, Fig. S3).

Gene $\times$ Gene Interaction.

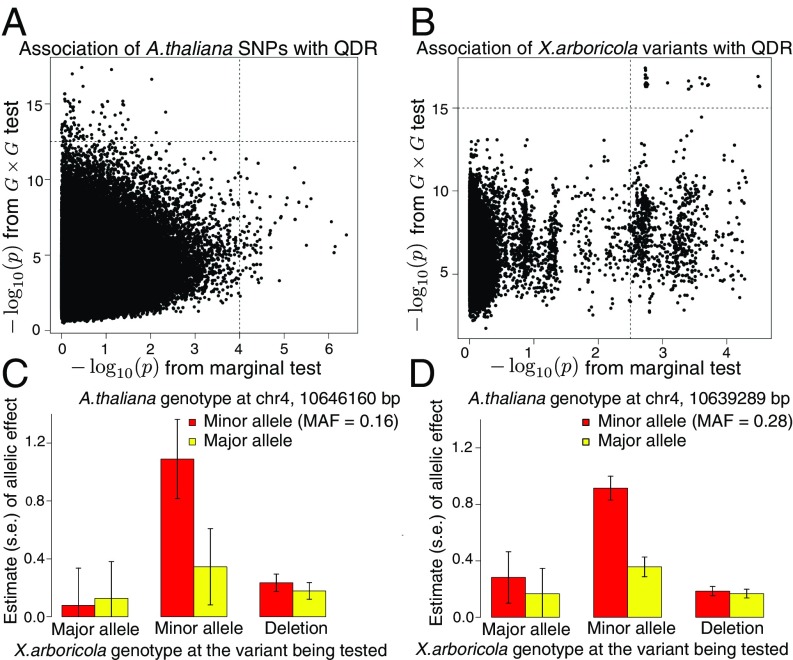
We applied ATOMM to test for interaction between each SNP on the A. thaliana genome and each variant on the X. arboricola genome. We ranked the A. thaliana–X. arboricola SNP pairs in ascending order of interaction $p$ value and formed a list of the A. thaliana SNPs that appeared among the top interaction results. Similarly, we ranked the A. thaliana SNPs in ascending order of marginal $p$ value and formed a list of those that appeared among the top marginal results. By comparing the A. thaliana SNPs that appeared among the top interaction results with those that appeared among the top marginal results, we found that the two analyses prioritized different sets of SNPs (Fig. 3A). This suggested pathogen-specific host defense genes; that is, certain A. thaliana SNPs exhibited genetic effects only when paired with certain X. arboricola variants. For example, the SNP (MAF = 0.16) at location base pair 10646160 of chromosome 4 at the gene AT4G19520 (SI Appendix, Fig. S5) was not among the SNPs with the top marginal effects (marginal $p$ value = 0.0757) but was prioritized second in the interaction analysis (G $\times$ G $p$ value = $5.28\times 10^{-18}$) (Fig. 3C). In fact, the gene AT4G19520 encodes a disease resistance protein (TIR-NBS-LRR class). Several other SNPs at this gene (base pairs 10639269 to 10647079 of chromosome 4) also appeared among the top interaction results for association with QDR (Fig. 3D), whereas those SNPs were not prioritized in the marginal analysis (SI Appendix, Fig. S4).

Fig. 3.

ATOMM analysis in the A. thaliana–X. arboricola pathosystem. A and B are scatterplots of the association $p$ value from the G $\times$ G test vs. association $p$ value from the marginal test. A plots 1,220,413 A. thaliana SNPs, and B plots 33,610 distinct observed X. arboricola genotype patterns. For each A. thaliana SNP or X. arboricola variant, the reported G $\times$ G $p$ value is the minimum $p$ value taken across all host–pathogen interaction tests in which this SNP or variant is included, where the minimum is taken so that each variant will appear only once in the plot. C shows the joint effects of the A. thaliana SNP located at base pair 10646160 of chromosome 4 (gene AT4G19520) and the X. arboricola variant at which the strongest interaction occurs (marginal A. thaliana $p$ value = 0.0757; marginal X. arboricola $p$ value = 0.00183; G $\times$ G $p$ value = $5.28\times 10^{-18}$). D shows the joint effects of the A. thaliana SNP located at base pair 10639289 of chromosome 4 and the X. arboricola variant at which the strongest interaction occurs (marginal A. thaliana $p$ value = 0.0401; marginal X. arboricola $p$ value = 0.00185; G $\times$ G $p$ value = $1.20\times 10^{-15}$). Each bar represents the effect on QDR of a particular pairing of host and pathogen genotypes, where these effects were estimated from Gaussian ATOMM.

To better understand the genomic regions detected by ATOMM, we performed a gene ontology (GO) enrichment analysis for the A. thaliana SNPs that appeared among the top interaction results, where we took the top 0.01% of distinct SNPs. Based on a permutation procedure that takes into account the linkage disequilibrium (LD) among SNPs (Materials and Methods), the three most highly enriched Biological Process (BP) terms were retrograde transport from endosome to Golgi, cellular response to hypoxia, and cellular calcium ion homeostatis (Table 2). Though these results do not reach significance after correction for multiple comparisons ($p$ value = 0.097), they do prioritize genes related to host defense. The gene underlying enrichment of “cellular response to hypoxia” is located at locus AT4G19520, which, as we have noted earlier, encodes a disease resistance protein. The AT2G24710/AT2G24720 genes underlying enrichment “cellular calcium ion homeostatis” correspond to plant glutamate receptor homologs that, like their animal counterparts, are intimately associated with C${\text{a}}^{2+}$ influx through plasma membrane. Recent reports have shed light on their role in wound response and disease resistance (27). Since the enrichments were based on interaction tests, our results suggested the presence of strain specificity to X. arboricola in these host defense genes. In contrast, enrichment analysis based on marginal testing identified only basic plant function BPs. Many of the identified BPs are involved in primary metabolism and correspond to genes in a 37 kb genomic region on chromosome 5 (SI Appendix, Table S1). Such functions include carbon accumulation during photosynthesis, regulation of cell growth, or DNA recombination, for example. Thus, FUMARASE 2, which encodes a cytosolic enzyme, is involved in carbon accumulation into fumarate as a result of photosynthesis, required for rapid nitrogen assimilation and growth (28). ARR10 is a type-B response regulator involved in cytokinin sensitivity, affecting cell expansion and division during development (29). Finally, MHF1 is a DNA-binding co-factor limiting crossover formation at meiosis (30).

Table 2.

Enrichment of BP in the 0.01% tail of the top interactive A. thaliana SNPs

BP	Enrichment	Nominal P value	ATG number	Locus name	Molecular function	No. of hits
Retrograde transport endosome to golgi	78.3	0.001	AT4G19490	VPS54	Putative homolog of yeast Vps54	14
Cellular response to hypoxia	39.6	0.002	AT4G19520		Disease resistance protein (TIR-NBS-LRR class)	11
				GLUTAMATE	Member of Putative ligand-gated ion channel subunit family	12
Cellular calcium ion homeostasis	28.7	0.005	AT2G24710,	RECEPTOR 2.3
			AT2G24720	GLUTAMATE	Member of Putative ligand-gated ion channel subunit family
				RECEPTOR 2.3

The nominal significance of the observed enrichment was assessed using a null distribution based on 10,000 permutations from a procedure that takesinto account LD patterns (see Materials and Methods).

In addition, if we compare the ranked lists of X. arboricola variants from the marginal and interaction analyses, then the interaction analysis in ATOMM pinpoints a subset of the X. arboricola variants from among the top marginal variants (Fig. 3B). These interactive X. arboricola variants exhibited both mutation and deletion polymorphisms, and their genotype patterns tended to differentiate strain FOR_21 from both FOR_23 and FOR_26 (Fig. 3 C and D). Further investigation revealed two very short regions on the X. arboricola genomes that had highly significant interactions with the aforementioned A. thaliana disease resistance gene AT4G19520. The first region ($\sim$1.7 kb) contains two genetic variants, including one leading to an amino acid change in a D-serine/D-alanine/glycine transporter. The second region ($\sim$20 bp) contains four genetic variants located between a glutathione peroxidase and a multidrug ABC transporter ATP binding protein.

Discussion

We present a statistical method, ATOMM, for detecting association between a complex trait, such as an infectious disease, and genetic variants on the genomes of two organisms that contribute to the trait. ATOMM takes advantage of the genome sequence data from both partners in a two-organism pathosystem and enables the identification of interaction between variants on the host and pathogen genomes, in addition to the marginal effects of individual host and pathogen variants.

Usefulness of ATOMM for Uncovering Genomic Regions with Biological Significance in the A. thaliana–X. arboricola Pathosystem.

Our marginal analysis suggested a lack of genes conferring broad-spectrum QDR to X. arboricola in A. thaliana. Instead, we observed clear strain specificity in our interaction analysis (Fig. 3). In particular, the interaction analysis identified three main biological functions on the A. thaliana genome that contribute to QDR to X. arboricola (Table 2). Of particular interest is the AT4G19520 gene that corresponds to a typical immune receptor located near two other TIR-NB-LRR genes known to confer disease resistance to specific races of the oomycete Hyaloperonospora parasitica (9). Although most QDR genes identified to date do not correspond to typical immune receptors, few studies have reported the cloning of NB-LRR genes underlying resistance QTLs, leading to the hypothesis that QDR can be mediated by weak alleles of R genes (31).

Interestingly, the genomic architecture underlying QDR in A. thaliana differs substantially between X. arboricola and another phylogenetically close phytopathogenic Xanthomonas species. Indeed, previous GWASs on the A. thaliana–Xanthomonas campestris pathosystem revealed that QDR to X. campestris involves four A. thaliana genes with strikingly different ranges of specificity. While the gene RKS1 encoding an atypical kinase confers broad-spectrum QDR to X. campestris (32), a gene of unknown function (AT5G22540) and a well-known immune receptor pair, RRS1/RPS4, contribute to QDR to a limited number of X. campestris races (33). Furthermore, the four A. thaliana genes conferring QDR to X. campestris do not overlap with the A. thaliana genomic regions identified in this study of X. arboricola, suggesting differential resistance determinants to these closely related pathogen species. Why the host genetic architecture underlying QDR differs between X. campestris and X. arboricola remains an open question.

On the pathogen side, in agreement with the reduced effector repertoire composition in X. arboricola (SI Appendix, Tables S2 and S3), the three candidate X. arboricola genes we identified do not correspond to typical effectors in the type III secretion system (T3SS). Instead, they encode a broad range of molecular functions that can be critical for pathogenesis. For example, GSTs are known to counter oxidative stress generated by the host in response to microbial attack (34).

The candidate genes identified in both interacting partners undoubtedly constitute key candidate genes for functional analysis, thereby providing an exciting opportunity to dissect the molecular landscape of A. thaliana–X. arboricola interactions.

Methodological Considerations.

As an association mapping tool, the analysis of cross-species gene–gene interaction can, in some cases, lead to increased flexibility and power when the variant pair under consideration has negligible marginal effects but strong joint effect. On the other hand, when the most important effects are marginal effects, power could be severely compromised by the multiple comparison penalty for a large number of hypothesis tests if all interactions are tested. To reduce both the burden of the multiple-testing correction and computation time, gene–gene interaction tests can be applied to a focused subset of variants that is likely to be enriched for interaction effects, for example, those achieving a certain significance threshold from marginal GWA mapping. However, in the A. thaliana–X. arboricola dataset, the interaction analysis identified several important loci associated with QDR that were not identified in the marginal analysis. We note that the G $\times$ G $p$ values from the interaction analysis should be interpreted with caution because of multiple testing. Nevertheless, they can be used to provide a ranked priority list of variants that can be compared with the corresponding ranked list from the marginal analysis. We thus recommend using gene–gene interaction as a complement to, rather than replacement for, marginal GWA mapping.

To correct for possible population confounding in association testing, ATOMM considers multiple VCs based on three types of GRMs: one each for the host and pathogen marginally and the third for the interaction between the two. Recent work (35) has demonstrated that including a Hadamard-type matrix to account for background interaction, as in ATOMM, can reduce inflation when the interaction effect is of primary interest. An alternative approach to correct for population confounding is to use top PCs as fixed effects (17). In our context, we can extend such an approach by including as fixed effects the top PCs of both GRMs as well as the top PCs of their Hadamard product. The choice as to which approach to take involves similar considerations as in single-organism association mapping (15, 17, 35). We chose to take the mixed-model approach in our application because it enforces a less stringent correction on the X. arboricola clade-specific variants.

In the ATOMM analysis, we partition the pathogen VC into the variance attributable to pathogen deletion polymorphisms and that attributable to pathogen mutation polymorphisms, assuming that they contribute equally to the variance. Other forms of partition may also be beneficial, such as using separate GRMs for common and rare variants (36). For parsimony, we choose to include only a single GRM for the host, one for the pathogen and one for their interaction, although the ATOMM method is able to accommodate other choices. Several studies have also pointed out that the SNP being tested, and those nearby that tag it, should be excluded from the GRM to avoid “dilution” (37). The same strategy can be incorporated in the ATOMM method.

In the ATOMM model, we have included both fixed and random effects of genetic variants that are assumed to act additively both within and between variants, with additional additive-by-additive interaction effects allowed between host and pathogen variants. We note that in the A. thaliana–X. arboricola study, the host is a diploid inbred organism, and the pathogen is a haploid organism. Therefore, the assumption of additivity within a variant is in fact fully general in this case (there is no other choice), and the assumption that the interaction effect between a host variant and a pathogen variant is additive-by-additive is also fully general. In the case of noninbred diploid organisms, dominance effects and additive-by-dominant or dominant-by-dominant interactions could in principle be included if desired. We note that a linear mixed model with interaction terms for both fixed and random effects has previously been proposed (38) in a somewhat different genetic context of maize breeding in which the fixed effects represent the haplotypes to be tested and sets of i.i.d. random effects represent general and specific combining abilities of different heterotic groups. This approach to the random effects is closely related to that in the model of SI Appendix, Eq. 42. It differs somewhat from the approach we take in ATOMM, in that ATOMM includes sets of i.i.d. random effects for host variants, pathogen variants, and their interactions, as opposed to sets of i.i.d. random effects for host inbred lines, pathogen strains, and their interactions.

By incorporating the whole-genome sequence data from a pair of organisms, ATOMM provides a powerful approach to detecting crucial host–pathogen gene–gene interactions and to uncovering genomic regions that are likely to carry evidence of co-evolution between hosts and pathogens. Although the A. thaliana–X. arboricola dataset we analyze has a fully crossed factorial design, note that our formulation of ATOMM is fully general in that it does not place any particular requirements on the design, beyond that the effects of interest be estimable from the data (e.g., we would obviously require that host and pathogen variant effects of interest not be completely confounded). As a result of this generality, our joint mapping framework can easily be extended to more complex study designs, including observational studies involving human participants, provided that the infectious agent also has an available genome sequence. We believe that our approach provides an opportunity to integrate the whole-genome sequence data available for a variety of organisms and to uncover the genetic architecture of complex traits in finer detail than has previously been possible.

Materials and Methods

We provide here the details on the A. thaliana–X. arboricola joint association study that were not fully described earlier.

Phenotyping Experiment.

The A. thaliana–X. arboricola joint association study initially consisted of 176 different inbred lines of A. thaliana (host) and 24 different strains of X. arboricola (pathogen). Each of the 176 A. thaliana lines was paired with each of the 24 X. arboricola strains, with three biological replicates for each A. thaliana–X. arboricola pair. These combinations resulted in a total of 176 $\times$ 24 $\times$ 3 plants, and they were all put into arrays of mini-greenhouses. For each strain and each biological replicate, the 176 A. thaliana lines were divided into 11 groups of equal size and put into 11 mini-greenhouses. We found that the mini-greenhouse explains only 4% of the phenotypic variation, so we decided not to include this batch effect in the association model. Plants were grown on Jiffy pots under controlled conditions (39).

Three researchers infected two to four leaves (median = 4) on each plant by piercing three holes in the primary vein of each leaf with a needle dipped in a bacterial solution of $2.10^8$ cfu/mL. Eleven days after inoculation, a QDR score for each leaf was measured by one of three researchers. As described in ref. 23, the resistance score was defined using a disease index of 0, 1, 2, 3, or 4, which corresponds to the number of holes among the three prepierced holes on a leaf showing infection symptoms, while disease index “4” stands for completely dead (no resistance).

Among the 176 A. thaliana lines, genotype information was not available for 46 lines as of the date when the analysis was performed, reducing the total number of host lines to 130. In addition, a greenhouse temperature failure in the experiment was observed for two X. arboricola strains—that is, FOR_F24 and ME_P9. Thus, we removed these two strains from the data analysis. The final dataset we analyzed consisted of $n$ = 32,960 sampling units (leaves) resulting from multiple combinations of the 130 A. thaliana lines and the 22 X. arboricola strains.

Genotyping Experiment.

We collected whole-genome sequencing data for both the 130 A. thaliana lines and the 22 X. arboricola strains. The A. thaliana sequencing data were obtained from the 1001 Genomes project (14). After quality control and genotype imputation, we included in the analysis 1,220,413 A. thaliana SNPs (MAF $\ge 0.1$). The genome annotation was obtained from TAIR10 (https://www.arabidopsis.org). In addition to the genotypes, we also retrieved the geographical information, such as origin countries, site names, latitudes, longitudes, and so forth, for each A. thaliana line.

On the pathogen side, we included in the analysis 3,709,869 X. arboricola variants (MAF$\hspace{0.17em}\ge \hspace{0.17em}.045$). The bioinformatics pipeline for sequencing, assembling, and aligning X. arboricola genomes is described in SI Appendix. Because we focused on only 22 (based on 24; see Phenotyping Experiment) X. arboricola strains and because of the relatedness among the strains, there were only 33,610 distinct genotype patterns observed, so, from a computational point of view, there were effectively only 33,610 distinct X. arboricola variants to be tested for association.

Effects of A. thaliana–X. arboricola Population Membership on QDR.

To assess the extent to which the variation in QDR is attributable to the particular geographical areas from which the host and pathogen are drawn, we fit the following linear model:

$$\begin{array}{ccc}\hfill & \hfill & \hspace{1em}\mathit{Y}|\mathit{X},\text{Subpopulation}\sim \mathcal{N}\left(\mathit{\mu },\mathbf{\Sigma }\right),\hspace{1em}\text{where}\hfill \\ \hfill \mathit{\mu }& =\hfill & \mathit{X}\mathit{\beta }+\sum _{i=1}^4\sum _{j=1}^2{\gamma }_{ij}{\mathbb{1}}_{\left\{\text{host population}i\text{and pathogen population}j\right\}},\hfill \\ \hfill \mathbf{\Sigma }& =\hfill & {\sigma }_a^2\mathit{J}+{\sigma }_e^2\mathit{I},\hfill \end{array}$$

where the individual leaf is the experimental unit, with $\mathit{Y}{\in \mathbb{R}}^n$, $n$ = 32,960, $\mathit{X}\mathit{\beta }$ represents the person effect (i.e., the effect due to which lab member scored the QDR), ${\gamma }_{ij}$ represents the effect on QDR of pairing a host from A. thaliana subpopulation $i$ with a pathogen from X. arboricola subpopulation $j$, $\mathit{J}$ is a covariance matrix with ${\mathit{J}}_{ij}=1$ if $i$ and $j$ represent two leaves from the same plant and 0 otherwise, ${\sigma }_a^2$ is the variance of the plant random effect, and ${\sigma }_e^2$ is the variance of i.i.d. environmental noise. Note that in this model, the intercept is subsumed into the second term of the mean. We used the R function lmer for parameter estimation and hypothesis testing.

ATOMM with an Additional VC.

The simplest version of the ATOMM model is given in Eq. 3. Here we give the extension of the model in Eq. 3 to allow for inclusion of the plant random effect. We took the individual leaf as the experimental unit with $\mathit{Y}{\in \mathbb{R}}^n$, $n$ = 32,960. We included the person effect (i.e., the effect due to which lab member scored the QDR) as a covariate. In the model for the variance, we added a random effect to represent the plant or block effect, in addition to the four random effects specified in Eq. 3. The plant/block random effect was designated to reflect the correlation among observations on leaves from the same plant. The final Gaussian model we fit is

$$\mathit{Y}|\mathit{X},{\mathit{G}}^{h,\text{test}},{\mathit{G}}^{p,\text{test}}\sim \mathcal{N}\left(\mathit{\mu },{\sigma }_t^2\mathbf{\Sigma }\right),\hspace{1em}\text{where}$$

$$\begin{array}{cc}\hfill \mathit{\mu }& =\mathit{X}\mathit{\beta }+{\mathit{Z}}_h{\mathit{G}}^{h,\text{test}}{\gamma }_h+{\mathit{Z}}_p{\mathit{G}}^{p,\text{test}}{\gamma }_p\hfill \\ \hfill & +{\mathit{Z}}_{hp}\left({\mathit{G}}^{h,\text{test}}\otimes {\mathit{G}}^{p,\text{test}}\right){\gamma }_{hp},\hfill \\ \hfill \mathbf{\Sigma }& ={\xi }_h{\mathit{Z}}_h{\mathit{K}}_h{\mathit{Z}}_h^T+{\xi }_p{\mathit{Z}}_p{\mathit{K}}_p{\mathit{Z}}_p^T+{\xi }_{hp}{\mathit{Z}}_{hp}\left({\mathit{K}}_h\otimes {\mathit{K}}_p\right){\mathit{Z}}_{hp}^T\hfill \\ \hfill & \hspace{1em}+{\xi }_J\mathit{J}+\left(1-{\xi }_h-{\xi }_p-{\xi }_{hp}-{\xi }_J\right)\mathit{I},\hfill \end{array}$$ [9]

where ${\sigma }_t^2$ is the total residual variance; $\mathit{X}\mathit{\beta }$ represents the intercept and the person effect; $\mathit{J}$ is an $n$-by-$n$ matrix with ${\mathit{J}}_{i,j}=1$ if $i$ and $j$ represent two leaves on the same plant, and 0 otherwise; and ${\mathit{Z}}_h{\in \mathbb{R}}^{n\times n_h}$, ${\mathit{Z}}_p{\in \mathbb{R}}^{n\times n_p}$, and ${\mathit{Z}}_{hp}{\in \mathbb{R}}^{n\times n_{hp}}$ are the incidence matrices that map the observed QDR score to A. thaliana lines, to X. arboricola strains, and to A. thaliana–X. arboricola pairs, respectively. The procedure for parameter estimation and association analysis is similar to that for the original ATOMM model (SI Appendix).

Extension to a Binomial-Like Trait.

Binomial-like traits are a natural generalization of binary traits and are encountered commonly in GWAS. In the A. thaliana–X. arboricola phenotyping experiment, the QDR score could be considered a count measurement taking values in $\left\{0,1,2,3,4\right\}$. For a binomial-like count trait, one could still apply the Gaussian model, though one might expect the mean to be related to variance (SI Appendix, Fig. S9). Here we provide an alternative approach by extending our model to a binomial-like trait.

Let $Y_{ij}\in \left\{0,1,2,\dots ,k\right\}$ be a binomial-like trait. We propose the following model for the mean

$$\begin{array}{cc}\hfill & \mathbb{E}\left(\mathit{Y}|\mathit{X},{\mathit{G}}^{h,\text{test}},{\mathit{G}}^{p,\text{test}}\right)=k\mathit{\mu },\hfill \\ \hfill \text{logit}\left(\mathit{\mu }\right)& =\mathit{X}\mathit{\beta }+{\mathit{Z}}_h{\mathit{G}}^{h,\text{test}}{\gamma }_h+{\mathit{Z}}_p{\mathit{G}}^{p,\text{test}}{\gamma }_p\hfill \\ \hfill & \hspace{1em}+{\mathit{Z}}_{hp}\left({\mathit{G}}^{h,\text{test}}\otimes {\mathit{G}}^{p,\text{test}}\right){\gamma }_{hp},\hfill \end{array}$$ [10]

and for the variance

$$\begin{array}{cc}\hfill & \text{Var}\left(\mathit{Y}|\mathit{X},{\mathit{G}}^{h,\text{test}},{\mathit{G}}^{p,\text{test}}\right)={\sigma }_t^2\mathit{M}\mathbf{\Sigma }\mathit{M},\hfill \end{array}$$ [11]

where $\mathit{M}$ is a diagonal matrix with $i$th diagonal element $\sqrt{k{\mu }_i\left(1-{\mu }_i\right)}$, $\mathbf{\Sigma }$ is the same as in the model in Eq. 9, and ${\sigma }_t^2$ is an additional unknown dispersion parameter. Note that $\mathbf{\Sigma }$ is pre- and postmultiplied by the diagonal matrix $\mathit{M}$ to respect the binomial-like variance. In particular, the conditional variance of the $i$th unit is $k{\mu }_i\left(1-{\mu }_i\right){\sigma }_t^2$.

The model given in Eqs. 10 and 11 is an extension of the linear mixed model in Eq. 9 (in which the link is an identity function and $\mathit{M}=\mathit{I}$) to a generalized linear mixed model (GLMM). In practice, fitting a GLMM can be computationally costly. To overcome this challenge, we extended previous work (19, 20) for a binary trait that uses a quasi-likelihood and estimating equation approach. This approach (see SI Appendix) ensures the method is efficient for large-scale studies. We constructed prospective score statistics for both the marginal and interaction hypothesis tests. In the case of the marginal hypothesis tests, we were able to construct retrospective score tests, in which significance was assessed conditional on $\mathit{Y}$ and $\mathit{X}$ and treating ${\mathit{G}}^{\text{test}}$ as random (19). In our data analysis, we found that the retrospective approach better controls the genome-wide inflation than the prospective approach for the binomial-like model (SI Appendix, Fig. S10).

GO Analysis.

To determine which BPs were enriched among SNPs associated with the response of A. thaliana to X. arboricola, we tested whether or not the top 0.01% of associated A. thaliana SNPs were overrepresented in each of 736 GO BPs from the GOslim set [The Gene Ontology Consortium, 2008 (40)]. We adopted the procedures in ref. 41 to take into account the LD patterns among the SNPs. Specifically, we defined a 10 kb window around each top SNP (5 kb on each side of the SNP) and let $T$ denote the set of SNPs covered by the union of these windows. Now consider a BP term of interest. Let $S$ denote the set of SNPs covered by the genes belonging to this BP term. Define the observed enrichment score by

$${\text{Enrichment}}_o\stackrel{\text{def}}{=}|S\cap T|,$$

where $|\cdot |$ denotes the cardinality of the set. In each permutation, we shifted the location of the SNPs in $T$ by a random number $k$, where $k\sim \text{Unif}\left\{1,\dots ,(\text{total number of SNPs}-\text{1})\right\}$, and let $T^{\prime }$ denote the resulting SNP set. Then the enrichment score for the given BP term in the permutation set is

$${\text{Enrichment}}_p\stackrel{\text{def}}{=}|S\cap T^{\prime }|.$$

To assess the nominal significance of the enrichment of the given BP term, we generated 10,000 permutation replicates and compared ${\text{Enrichment}}_o$ with the empirical distribution of ${\text{Enrichment}}_p$ for the given BP term. For each significantly enriched BP, we reported the (relative) enrichment score as ${\text{Enrichment}}_o/\text{Mean}\left({\text{Enrichment}}_p\right)$, and we retrieved the identity of all of the genes containing the top 0.01% of associated SNPs. Our procedure for assessing significance taking into account multiple comparisons is given in SI Appendix.

Availability.

ATOMM is implemented in C using the LAPACK linear algebra library. Our software, including source code, will be publicly available at https://www.stat.uchicago.edu/∼mcpeek/software/.