In two C4 species, mesophyll conductance increases with short-term exposure to decreasing pCO2 and limits photosynthetic capacity below ambient levels, whilst carbonic anhydrase imposes a further limitation only at very low pCO2.
Keywords: A-Ci curves, carbonic anhydrase, CO2, C4 photosynthesis, diffusional limitations, in-vitro Vpmax, leakiness, mesophyll conductance, Setaria viridis, Zea mays
Abstract
Mesophyll conductance (gm) limits rates of C3 photosynthesis but little is known about its role in C4 photosynthesis. If gm were to limit C4 photosynthesis, it would likely be at low CO2 concentrations (pCO2). However, data on C4-gm across ranges of pCO2 are scarce. We describe the response of C4-gm to short-term variation in pCO2, at three temperatures in Setaria viridis, and at 25 °C in Zea mays. Additionally, we quantified the effect of finite gm calculations of leakiness (ϕ) and the potential limitations to photosynthesis imposed by stomata, mesophyll, and carbonic anhydrase (CA) across pCO2. In both species, gm increased with decreasing pCO2. Including a finite gm resulted in either no change or increased ϕ compared with values calculated with infinite gm depending on whether the observed 13C discrimination was high (Setaria) or low (Zea). Post-transitional regulation of the maximal PEP carboxylation rate and PEP regeneration limitation could influence estimates of gm and ϕ. At pCO2 below ambient, the photosynthetic rate was limited by CO2 availability. In this case, the limitation imposed by the mesophyll was similar or slightly lower than stomata limitation. At very low pCO2, CA further constrained photosynthesis. High gm could increase CO2 assimilation at low pCO2 and improve photosynthetic efficiency under situations when CO2 is limited, such as drought.
Introduction
In C4 plants photorespiration is reduced by concentrating CO2 around Rubisco (ribulose 1,5-bisphosphate carboxylase/oxygenase) (Edwards and Walker, 1983; Hatch, 1987; Sage, 2004). In Kranz-type C4 plants this is achieved with a compartmentalized two-carboxylation process: (1) in the cytosol of mesophyll cells, bicarbonate (HCO3–) and phosphoenolpyruvate are fixed into four-carbon acids by phosphoenolpyruvate carboxylase (PEPC) (Hatch et al., 1967); and (2) in chloroplasts of the bundle-sheath cells the concentrated CO2 released from the decarboxylation of these acids is fixed by Rubisco.
Mesophyll conductance (gm) describes the movement of CO2 from stomata across the intercellular spaces to the sites of first carboxylation, which are the chloroplast stroma or mesophyll cytosol in C3 and C4 species, respectively (Evans and von Caemmerer, 1996). There is extensive research describing gm in C3 species; however, C4-gm is poorly understood because it is difficult to estimate. Traditionally gm was assumed to be larger in C4 compared to C3 species, but most recent studies suggest that values for C4-gm correspond to higher-end C3-gm reports, and that C4-gm reacts similarly to C3-gm with regards to variation in factors such as leaf age and temperature (Barbour et al., 2016; Osborn et al., 2017; Ubierna et al., 2017). If C4-gm is lower than previously thought, that could affect derivations of other key parameters such as leakiness (ϕ, the proportion of C fixed by PEPC that subsequently leaks out the bundle-sheath cells). Leakiness cannot be directly measured and is commonly estimated from observations and models of 13C discrimination (Δ13C) (Farquhar, 1983; Farquhar and Cernusak, 2012). Historically, gm is generally assumed to be infinite when solving for ϕ from Δ13C; however, this simplification and estimates of ϕ would be compromised if gm is finite and low.
Mesophyll conductance has long been recognized as a significant limitation for C3 photosynthesis (Evans, 1983; Evans et al., 1986; Evans and Terashima, 1988), limiting photosynthesis as much as stomatal conductance (Warren, 2008). It is unclear if gm limits C4 photosynthesis as the reduction of photorespiration achieved by the CO2-concentrating mechanism saturates C4 photosynthesis at ambient pCO2. If gm were to limit C4 photosynthesis, it would likely only be at very low pCO2. However, not much is known about the variation of C4-gm with pCO2. In the C4 grass Setaria viridis, gm derived with the 18O discrimination (Δ18O) method increased as pCO2 decreased, although the variation was not significant (Osborn et al., 2017). Some reports have shown that in C3 species gm increases with short-term exposure to decreasing pCO2 (Bongi and Loreto, 1989; Loreto et al., 1992; Flexas et al., 2007, 2008; Hassiotou et al., 2009; Bunce, 2010; Douthe et al., 2011; Tazoe et al., 2011). However, others have suggested that C3-gm is insensitive to changes in pCO2 (Loreto et al., 1992; Tazoe et al., 2009). It has been hypothesized that the observed C3-gm response to pCO2 might result from a significant chloroplast resistance (Tholen and Zhu, 2011; Tholen et al., 2012) or artifacts in the calculations (Gu and Sun, 2014).
In C4 plants, gm has been estimated with the Δ18O method (Gillon and Yakir, 2000a, 2000b; Barbour et al., 2016; Osborn et al., 2017; Ubierna et al., 2017) and the in vitro maximal PEP carboxylation rate (Vpmax) method (Ubierna et al., 2017). The latter method solves for the pCO2 in the mesophyll cells (Cm) needed to simultaneously match modeled and measured rates of CO2 assimilation and Δ13C when the models are parameterized with in vitro Vpmax, as determined in a crude leaf extract. Values derived for gm with the Δ18O and in vitro Vpmax methods were similar in two C4 species measured over a range of temperatures (Ubierna et al., 2017). The in vitro Vpmax method also allows the implementation of two modeling alternatives: carbonic anhydrase (CA)-saturated and CA-limited. They differ in the calculation of PEP carboxylation rate as a function of CO2 or HCO3– for the CA-saturated and -limited scenarios, respectively. Ubierna et al. (2017) found no difference between CA-limited and CA-saturated estimates of gm at ambient pCO2, but CA limitation is expected at low pCO2.
In this study, we calculated gm using the in vitro Vpmax method across a range of pCO2 in two C4 grasses, one economically important (Zea mays) and the other the adopted model system for studying C4 photosynthesis (S. viridis). Measurements were performed at three temperatures (10, 25, and 40 °C) in Setaria and at 25 °C in Zea. Our objectives were to: (1) describe the response of C4-gm to short-term variation in pCO2; (2) evaluate the impact of disequilibrium between CO2 and HCO3– at a range of pCO2 and temperatures; (3) investigate if gm represents a limitation to C4 photosynthesis across pCO2; and (4) assess the impact of finite gm on ϕ calculations.
Materials and methods
Plant material
Seeds of Z. mays (var. Trucker’s Favorite, Victory Seed Company, Oregon, USA) were grown in a greenhouse supplemented with artificial lighting at the School of Biological Sciences at Washington State University, Pullman, WA (USA) during August to October 2011. Seeds of S. viridis (A-010) were grown in a controlled environment growth chamber (Enconair Ecological GC-16) in 2013. Plants used for measurements were 4 and 6 weeks old for Zea and Setaria, respectively. Zea was fertilized with 17-3-6 NPK and weekly additions of 4 g l–1 solution of 10% Fe-DPTA (Sprint 330, Becker Underwood, IA, USA). Setaria was treated weekly with Peters 20-20-20 (J. R. Peters, Inc., Allentown, PA, USA). For all plants, the photon flux density was ≥500 μmol m–2 s–1, the day length was 14 h, and the temperature was 25–28/20–25 °C for day/night.
Coupled gas exchange and isoflux measurements
The system used for measurements has been described in detail in Ubierna et al. (2013, 2017). Briefly, a LI-6400XT open gas exchange system assembled with a 6400-22L conifer chamber fitted with a LI-6400–18 RGB light source (Li-Cor, Lincoln, NE, USA) was coupled with a tunable-diode laser absorption spectroscope (TDLAS, TGA 200A, Campbell Scientific, Inc. Logan, UT, USA). The entire gas exchange system was placed in a growing cabinet (Percival Scientific, Perry, IA), where the temperature was varied to match leaf temperature (TL) settings. The TDLAS data were calibrated with the concentration series method (Tazoe et al., 2011; Ubierna et al., 2013) using two calibration gases, one measured at different [CO2] that spanned the gas exchange reference and sample lines. Each measurement cycle included five to seven TDLAS sequences of zero air, calibration gases, reference, and sample lines measured for 40 s each. Data from the last three sequences were averaged and used for calculations.
Young fully-expanded leaves of Setaria and Zea were acclimated for ~1 h with chamber conditions of Ca (ambient CO2 supply to the chamber) ≈ 35 Pa, 21% O2, and photosynthetically active radiation (PAR) =2000 μmol m–2 s–1. Then, Ca was varied in steps, and gas and 13C isotopic exchange were measured simultaneously. In Setaria (n=4) Ca was set at 5, 7, 10, 12, 14, 19, 28, 38, 56, and 93 Pa, and measurements were performed at TL=10, 25 and 40 °C. In Zea (n=3), Ca was set at 9, 14, 19, 35, 56, 84, and 112 Pa, and TL=25 °C. In both species the measurements were performed in the sequence ambient – low – ambient – high pCO2.
Enzyme-limited C4 photosynthesis model for CA-limited or CA-saturated conditions
The enzyme-limited C4 photosynthesis rate is (von Caemmerer, 2000):
| Eqn 1 |
where:
| Eqn 2 |
| Eqn 3 |
| Eqn 4 |
where α (= 0) is the fraction of PSII activity in the bundle-sheath cells (von Caemmerer, 2000); uoc is the ratio of O2 and CO2 diffusivities and solubilities, 0.047 at 25 °C but variable with temperature (Yin et al., 2016); gbs is the bundle-sheath conductance, 0.0164 μmol m–2 s–1 Pa-1 (Ubierna et al., 2013) or variable; Om is the O2 partial pressure in the mesophyll (19.5 kPa, which corresponds to 21%); Rd is the non-photorespiratory CO2 released in the dark, assumed to equal measured rates of dark respiration after 30 min of dark adaptation, which at 25 °C were 1.89 and 1.06 μmol m–2 s–1 in Zea and Setaria, respectively, but were also measured at each temperature; Rm is the mesophyll mitochondrial respiration rate, Rm=0.5Rd (von Caemmerer, 2000); γ* is half of the reciprocal of Rubisco specificity, and equals 0.5/SC/O (von Caemmerer, 2000), where SC/O is the Rubisco CO2/O2 specificity. KC and KO are the Michaelis–Menten constants of Rubisco for CO2 and O2, respectively. SC/O, KC, and KO were determined in vitro at 25 °C in Zea (SC/O=2147 Pa Pa–1, KC=96 Pa, KO=49 683 Pa; R.A. Boyd, Washington State University, pers. comm.) and Setaria (SC/O=1310 Pa Pa–1, KC=121 Pa, KO=29 200 Pa; Boyd et al., 2015). Their values at different temperatures were obtained using the temperature functions of Boyd et al. (2015). For Vcmax (maximal Rubisco carboxylation rate) we used in vivo values calculated as described in Ubierna et al. (2017) or as specified otherwise. The calculation of Cm (pCO2 in the mesophyll cells) will be discussed subsequently.
CA-saturated and CA-limited models differ as follows.
(1) The calculation of PEP carboxylation rate (Vp):
| Eqn 5 |
where the maximal PEP carboxylation rate (Vpmax) was measured in vitro at 25 °C in Zea (184 μmol m–2 s–1, R. A. Boyd, pers. comm.) and in Setaria (450 μmol m–2 s–1, Boyd et al. 2015) and varied with temperature as described in Boyd et al. (2015). For all species, the Michaelis–Menten constant of PEPC for CO2 (KP) was modeled with the temperature response and value at 25 °C (60.5 μM HCO3–) from Boyd et al. (2015). The [HCO3–] was calculated as previously discussed (Jenkins et al., 1989; Hatch and Burnell, 1990; Boyd et al., 2015): for details see Ubierna et al. (2017).
If the rate of PEP regeneration is limiting, then Vp is (von Caemmerer, 2000):
| Eqn 6 |
where Vpr is the PEP regeneration rate (Peisker, 1986; Peisker and Henderson, 1992). We arbitrarily set Vpr to 64 and 59 μmol m–2 s–1 in Setaria and Zea, respectively, which corresponded to twice the maximum measured net assimilation rate, A.
(2) The calculation of the ratio Vp/Vh, where Vh is hydration rate:
| Eqn 7 |
where KCA is the rate constant of CA for CO2, that at 25 °C was 65.5 and 124 μmol m–2 s–1 Pa–1 in Zea and Setaria, respectively (R.A. Boyd pers. comm., Boyd et al., 2015), varying with temperature as described in Boyd et al. (2015).
Measurements and models of discrimination
The observed photosynthetic discrimination against 13C () is calculated as (Evans et al., 1986):
| Eqn 8 |
where C and δ are the 12CO2 mol fraction and the δ13C of the CO2, respectively, in dry air in and out the chamber.
The theoretical model for Δ13C is (Farquhar and Cernusak, 2012):
| Eqn 9 |
Values and calculations of the variables included in this equation have been discussed before (i.e. Ubierna et al., 2017) and can also be found in Supplementary Methods S1 at JXB online.
Calculation of mesophyll conductance (gm)
Following Fick’s law of diffusion:
| Eqn 10 |
where the Cm is calculated for two case scenarios, CA-saturated and CA–limited, resulting in CA-sat gm and CA-lim gm values. In both cases, Cm is derived with the in vitro Vpmax method as the Cm that needs to be combined with in vitro Vpmax to match measurements and predictions of A and Δ13C (Eqns 1, 9); details on these calculations have been provided in Ubierna et al. (2017). The CA-sat and CA-lim options are introduced through the calculation of Vp and Vp/Vh (Eqns 5–7).
Limitations to photosynthesis
To calculate the limitation on CO2 assimilation by either finite stomatal conductance (Ls), by mesophyll conductance (Lm), or by carbonic anhydrase (LCA), we adapted to C4 photosynthesis an approach previously used for C3 photosynthesis. This compares A when all conductances are finite with the A estimated assuming that the conductance related with the limitation of interest is infinite (Farquhar and Sharkey, 1982; Warren et al., 2003). In all cases A was calculated with Eqn 1 and assuming:
(a) Aall (expected A with all limitations, ≈ measured photosynthetic rate): finite gs and gm, CA-lim model.
(b) As (expected A if there were no stomatal limitations): infinite gs (Ci=Ca), finite gm, CA-lim model.
(c) Am (expected A if there were no mesophyll limitations): infinite gm (Cm=Ci), gs as measured, CA-lim model.
(d) ACA (expected A if there were no CA limitations): gs as measured, gm finite, CA-sat model.
Then Ls, Lm, and LCA were calculated as:
| Eqn 11 |
| Eqn 12 |
| Eqn 13 |
Calculation of leakiness (ϕ)
The C4 photosynthesis model (von Caemmerer, 2000) calculates ϕ as:
| Eqn 14 |
where Cbs, the pCO2 in the bundle-sheath cells, is (von Caemmerer, 2000):
| Eqn 15 |
where Os is the O2 partial pressure in the bundle-sheath cells.
From Δ13C (Eqn 9), ϕ is solved as:
| Eqn 16 |
where b3 (combined effects of Rubisco fractionation, and fractionations associated with respiration and photorespiration) and b4 (combined fractionation during PEP carboxylation, hydration, and respiration) are calculated as (Farquhar, 1983; Cousins et al., 2006):
| Eqn 17 |
| Eqn 18 |
A description of other variables included in Eqns 16–19 can be found in Supplementary Methods S1.
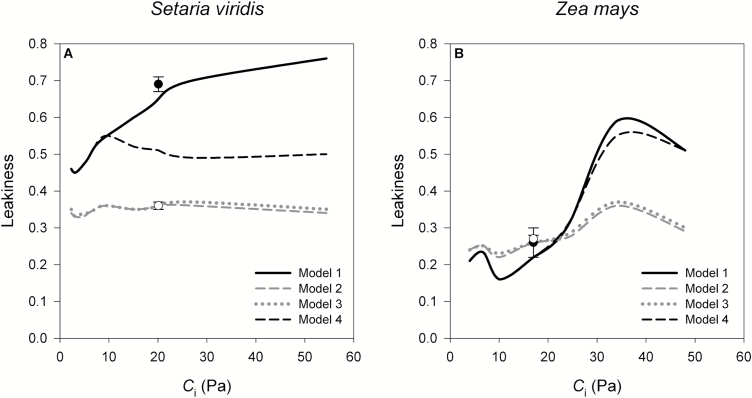
To evaluate the effect of gm on calculations of ϕ we implemented four model scenarios, which differed in values for gm, calculation of Vp, or constrains imposed. Model 1 used in vitro Vpmax and gm finite and equal to the values for CA-lim gm presented in the Results; Model 2 used in vivo Vpmax and gm infinite; Model 3 was the same as Model 1 but the solution was only constrained by A and not Δ13C; and Model 4 was the same as Model 1 but with Vp calculated with Eqn 6, which introduces a PEP regeneration limitation. The in vitro Vpmax method calculates gm by solving the system of two equations formed by the models of A and Δ13C. Therefore, once a solution is found, ϕ values calculated with either Eqn 14 or 16 are identical. This is the case for Models 1, 2, and 4; however, in Model 3, which is constrained only by A, ϕ was obtained only with Eqn 14. All four modeling scenarios described above used the CA-limited calculations (Eqns 5–7).
At ambient pCO2, ϕ was also calculated with a simplified equation derived from Δ13C assuming that Cbs is much larger than Cm and that hydration and assimilation fluxes are large (Vp/Vh≈0, and Vo≈0, where Vo is oxygenation rate):
| Eqn 19 |
where and are (von Caemmerer et al., 2014):
| Eqn 20 |
| Eqn 21 |
Statistical analyses
Statistical analyses were performed using SAS v9.4 (SAS Institute Inc., Cary, NC, USA). Differences between CA-lim gm and CA-sat gm were investigated using t-tests (Ho: CA-lim gm/CA-sat gm=1). The effect of CO2 supply on CA-lim gm was analysed using repeated measurements ANOVA. Data were log-transformed to meet normality criteria. In Setaria we used PROC MIXED with: plant as the repeated measurement; pCO2, temperature, and their interaction as fixed effects; a covariance structure of compound symmetry; and we applied Kenward–Roger’s approximation to correct the denominator degrees of freedom (Arnau et al., 2009). In Zea, we used PROC ANOVA with the statement REPEAT.
Results
A-Ci curves and observed 13C photosynthetic discrimination
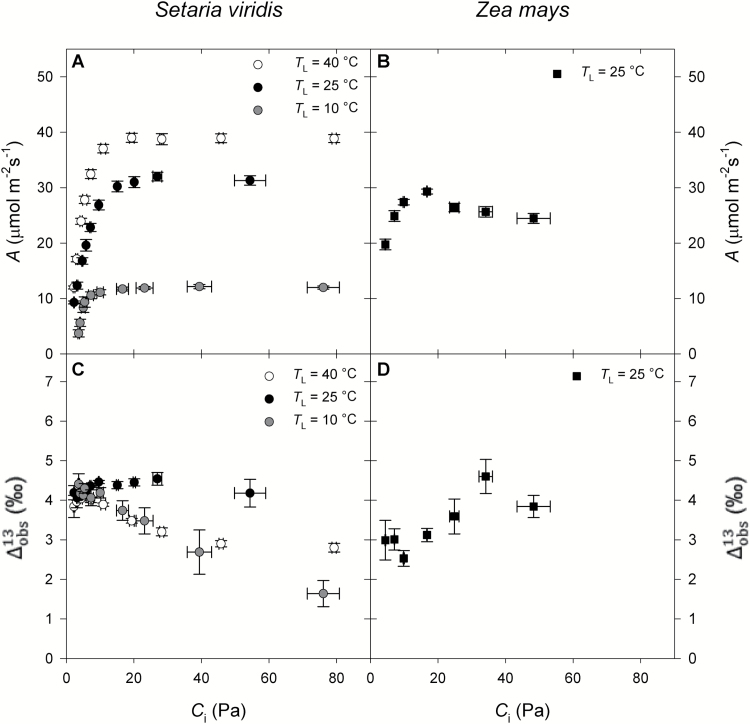
Under all leaf measurement temperatures (TL), the rate of net photosynthesis (A) in Setaria increased with Ci as the pCO2 supplied increased from ~5 Pa to ambient air values (~35 Pa) and then leveled off (Fig. 1A). At all pCO2, increasing TL resulted in larger A (Fig. 1A). In Zea, A also increased with increasing Ci and reached a maximum at ambient air pCO2 before decreasing at higher pCO2 (Fig. 1B).
Fig. 1.
Responses of (A, B) photosynthetic rate (A) and (C, D) observed 13C photosynthetic discrimination () to variation in the CO2 partial pressure inside the leaf (Ci) in Setaria viridis (circles) and Zea mays (squares). In Setaria, three leaf temperatures (TL) were measured: 40, 25, and 10 °C, as indicated in the key. Measurements in Zea were at TL=25 °C. Values are means ±SE; n=4 in Setaria and n=3 in Zea.
At ambient air pCO2 and 25 °C, was larger in Setaria (4.5 ± 0.1‰) than in Zea (3.1 ± 0.2‰) (Fig. 1C, D). In Zea, the was low at ambient air pCO2 and increased at lower or higher Ci (Fig. 1D). However, in Setaria, remained constant with Ci when TL=25 °C, but decreased as Ci increased both at 40 and 10 °C (Fig. 1C).
Mesophyll conductance calculated assuming CA-saturated or CA-limited conditions
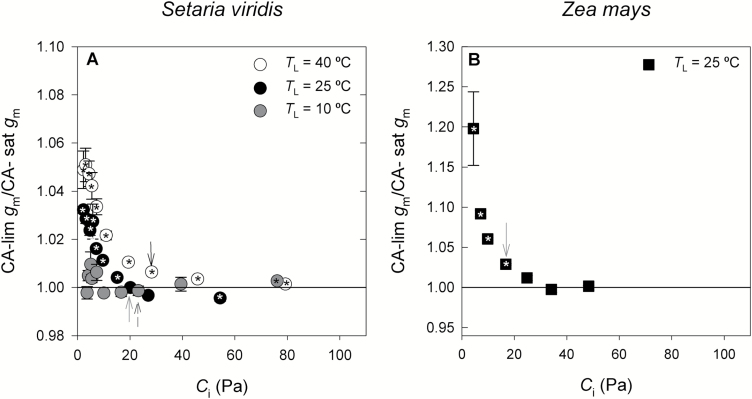
For both species and at all temperatures, the ratio CA-lim gm/CA-sat gm ≈ 1 when pCO2 was above ambient (Fig. 2). As pCO2 decreased, CA-lim gm became larger than CA-sat gm; the differences increased with temperature and were larger in Zea than in Setaria. In Setaria, CA-lim gm and CA-sat gm were significantly different (P<0.05) at all pCO2 at 40 °C, at all pCO2 except at ambient and the measurement just above ambient at 25 °C, and at the largest pCO2 at 10 °C (Fig. 2A). In Zea, CA-lim gm and CA-sat gm were significantly different (P<0.05) at all pCO2≤ambient air (Fig. 2B).
Fig. 2.
The ratio of carbonic anhydrase-limited mesophyll conductance (CA-lim gm) to CA-saturated gm (CA-sat gm) at different pCO2 inside the leaf (Ci) in (A) Setaria viridis (circles) and (B) Zea mays (squares). Setaria was measured at three leaf temperatures (TL): 40, 25, and 10 °C, as indicated in the key. Zea was measured at TL=25 °C. Values are means ±SE; n=4 in Setaria and n=3 in Zea. An asterisk inside a symbol indicates CA-lim gm/CA-sat gm ≠ 1 with P<0.05. The arrows indicate the values at ambient pCO2 and at 40 °C (black arrow), 25 °C (grey arrow), and 10 °C (dashed arrow).
In Setaria, the under-estimation of gm by ignoring the CA limitation was very small (maximum of 5%, CA-lim gm/CA-sat gm<1.1; Fig. 2A). However, in Zea, the CA-lim gm calculated at the lowest pCO2 was 20 ± 8% larger than CA-sat gm at 25 °C. Because CA limitation was relevant at low pCO2, for subsequent analyses we use the CA-lim gm values for all species, temperatures, and pCO2.
CO2 response of mesophyll conductance
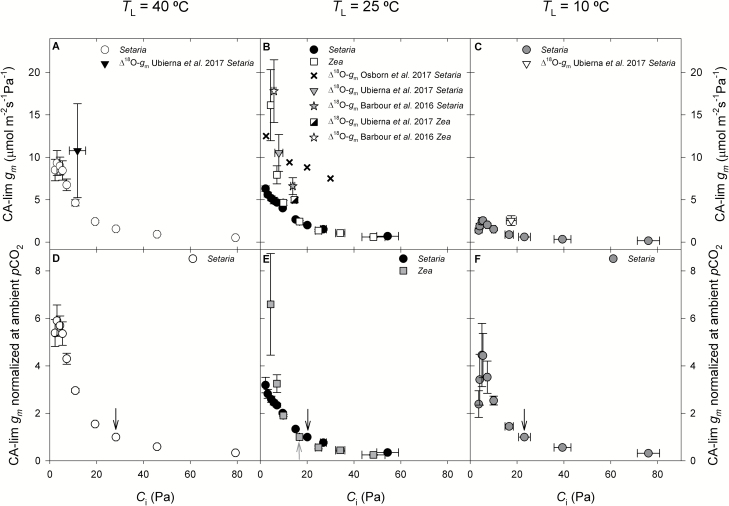
The CA-lim gm significantly increased as pCO2 decreased in Setaria at all temperatures (P<0.0001) and in Zea at 25 °C (P<0.0004) (Fig. 3). At ambient pCO2 and 25 °C, CA-lim gm values (mean±SE) were 2.00 ± 0.10 μmol m–2 s–1 Pa–1 in Setaria, and 2.43 ± 0.13 μmol m–2 s–1 Pa–1 in Zea. At the lowest pCO2 measured (~5–9 Pa) and 25 °C, the CA-lim gm increased to 6.30 ± 0.32 and 16.20 ± 5.74 μmol m–2 s–1 Pa–1 in Setaria and Zea, respectively. Values for Cm across Ci can be found in Supplementary Fig. S1.
Fig. 3.
The response of carbonic anhydrase-limited mesophyll conductance (CA-lim gm) to changes in pCO2 inside the leaf (Ci) in (A, C) Setaria viridis (circles) and (B) Zea mays (white squares). Setaria was measured at three leaf temperatures, as indicated at the top of the figure. Zea was measured at TL=25 °C. For comparison, the available literature reports for Δ18O-gm for different species and temperatures are included, as indicated in the keys: Ubierna et al. (2017)Setaria measured at TL=40 °C, TL=25 °C, and TL=10 °C; Osborn et al. (2017)Setaria measured at TL=25 °C; Barbour et al. (2016)Setaria measured with block temperature of 30 °C; Ubierna et al. (2017)Zea measured at TL=25 °C; Barbour et al. (2016)Zea measured with block temperature of 30 °C. For all species and temperatures CA-lim gm significantly varied with pCO2. (D–F) The CO2 response of normalized gm, calculated by dividing individual values by the gm at ambient pCO2 at each temperature. Values are means ±SE; n=4 in Setaria, n=3 in Zea. The arrows indicate the values at ambient pCO2: black, Setaria; grey, Zea.
To compare the magnitude of the change in CA-lim gm across species and temperatures, CA-lim gm was normalized by dividing each value at a given temperature and pCO2 by CA-lim gm at ambient pCO2 at that temperature (Fig. 3D–F). At 25 °C, the increase in CA-lim gm with decreasing pCO2 was steeper in Zea than in Setaria (Fig. 3E). In Setaria, the gmpCO2 response was greatest at 40 °C and there was little difference between the 25 and 10 °C curves.
Limitations to photosynthesis
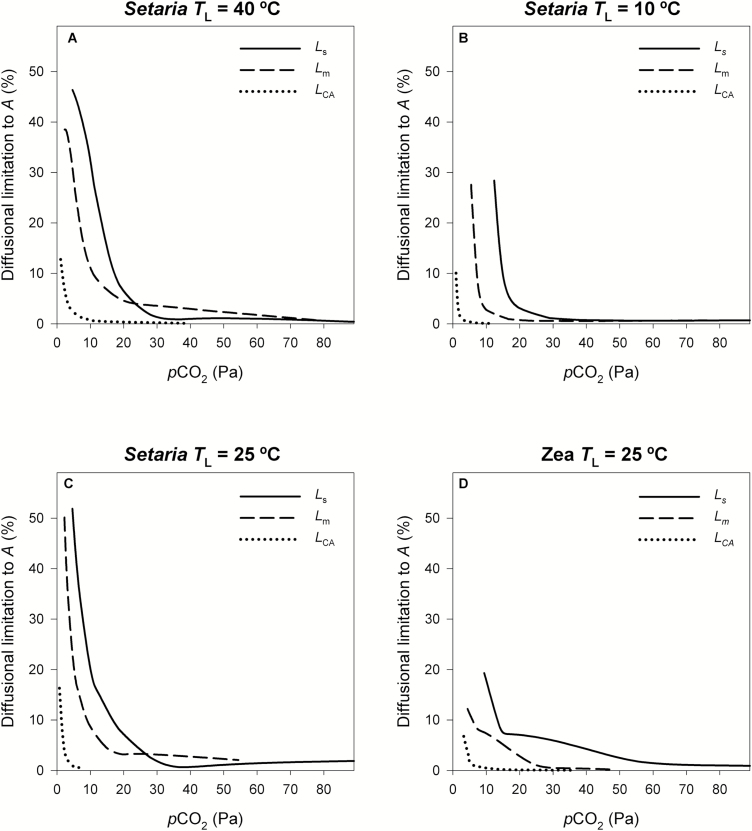
At elevated pCO2 assimilation rate was not limited by diffusion or substrate availability, as indicated by Ls, Lm, and LCA ≈ 0% for both species and all temperatures (Fig. 4). However, below ambient pCO2, the diffusional limitation to A increased exponentially with decreasing pCO2. The data in Fig. 4 show the different limitations as a function of the amount of substrate available: Ca, Ci, and Cm for Ls, Lm, and LCA, respectively. In Setaria, diffusional limitations were lower at 10 °C than at any other temperature. Comparing Zea and Setaria at 25 °C, they had similar Ls but Lm was larger in Setaria than in Zea. For example, when Ca=9 Pa, Ls=23% and 19% in Setaria and Zea, respectively. The corresponding Ci at this Ca was 5 Pa for both species, whereas Lm was almost double in Setaria (23%) compared to Zea (12%) (Fig. 4C, D). In both species, LCA was small in comparison with Ls and Lm, and rapidly decreased below 5% as pCO2 increased.
Fig. 4.
Diffusional limitation to photosynthetic rate (A) imposed by stomatal resistance (Ls, Eqn 11, solid line), mesophyll resistance (Lm, Eqn 12, dashed line), and carbonic anhydrase (LCA, Eqn 13, dotted line) as a function of the CO2 supply (pCO2) available for each (Ca, Ci, and Cm for Ls, Lm, and LCA, respectively). (A) Setaria viridis at TL=40 °C, (B) Setaria viridis at TL=10 °C, (C) Setaria viridis at TL=25 °C, and (D) Zea mays at TL=25 °C.
Leakiness (ϕ)
Values of ϕ across pCO2 for Setaria and Zea at 25 °C calculated under different modeling assumptions are shown in Fig. 5. When gm was finite and variable with pCO2 (Model 1), ϕ increased from low to high pCO2, with a range of 0.16–0.59 in Zea and 0.45–0.76 in Setaria. Assuming that gm was infinite and Vpmax variable with pCO2 (Model 2) removed the pCO2 response of ϕ and generally decreased ϕ at all pCO2 in Setaria, but only at large pCO2 in Zea. Model 3 resulted in nearly identical ϕ to Model 2 using the same finite gm as Model 1 but with the solution constrained by only the photosynthesis model. However, this scenario failed to predict (see Supplementary Fig. S2). Imposing a PEP regeneration rate (Vpr) limitation of 64 and 59 μmol m–2 s–1 in Setaria and Zea, respectively (Model 4), decreased ϕ compared to the results with Model 1 in Setaria but resulted in no change in Zea. Interestingly, at pCO2 ≤ambient air, values for ϕ were similar across models in Zea, but they differed in Setaria. The values of Vpmax, Vcmax, Vp, Vc, Cbs, and gbs used in these four models are reported in Supplementary Fig. S2.
Fig. 5.
Effect of different parameterizations of models of photosynthesis in the calculation of leakiness (ϕ) in (A) Setaria virids and (B) Zea mays at 25 °C and over a range of pCO2 inside the leaf intercellular spaces (Ci). Model 1 (solid black line) uses in vitro Vpmax and gm finite and equal to the values presented in Fig. 3; Model 2 (dashed grey line) uses in vivo Vpmax (which is variable with pCO2, see Supplementary Fig. S2) and gm infinite; Model 3 (dotted grey line) uses the same as Model 1 but the solution was only constrained by A and not Δ13C; Model 4 (dashed black line) uses the same as Model 1 but introducing Vpr (= 64 and 59 μmol m–2 s–1 in Setaria and Zea, respectively) in the calculation of Vp (Eqn 6). The rest of the variables included in these models were calculated as explained in the Methods section: values for some of them can be found in Supplementary Fig. S2. In Models 1, 2, and 4, ϕ was calculated with Eqns 14 or 16 (same result) and in Model 3, ϕ was calculated with Eqn 14. The symbols indicate the value of ϕ at ambient air pCO2 calculated with the simplified Eqn 19 assuming either gm finite (solid symbols) or infinite (clear symbols). Values are means ±SE; n=4 in Setaria, n=3 in Zea.
For comparison we also present ϕ at ambient pCO2 calculated with the simplified Eqn 19 and assuming either gm finite or infinite. For both species, ϕ calculated with Eqn 19 was not different to values obtained with the complete Eqn 16 when gm was finite (compare black lines and black symbols in Fig. 5) and when gm was infinite (compare grey dashed line and clear symbols).
Discussion
Calculation of mesophyll conductance and model parameterization
Mesophyll conductance (gm) was derived with the in vitro Vpmax method (Ubierna et al., 2017). Estimations of gm with this method were similar to Δ18O-gm across temperatures (Ubierna et al., 2017) and across pCO2 (Kolbe and Cousins, 2018). Potential errors in gm originating from inaccurate model parameterization of the in vitro Vpmax method were tested with a sensitivity analysis using Setaria data at three temperatures and across pCO2 (see Supplementary Fig. S3). Halving in vitro Vpmax increased gm by <20% at large pCO2 and almost doubled it at low pCO2 and high temperature. Alternatively, doubling in vitro Vpmax decreased gm by <15% at all pCO2 and temperatures ( Supplementary Fig. S3J–L). This demonstrates that uncertainties in in vitro Vpmax affect absolute values of gm, but not the trend of increasing gm with decreasing pCO2. The sensitivity analysis also demonstrated that variations up to ±50% in KP, KC, or KCA resulted in negligible (when pCO2 ≥ambient) or small (at low pCO2) errors in gm calculations at any temperature (Supplementary Fig. S3A–I) and did not affect the observed trend of gm with pCO2.
In C3 plants, it has been suggested that large gm values reported for low pCO2 might be an artifact of uncertainties in parameters such as Rd, Γ*, and b′3 (Gu and Sun, 2014). The simulations with different values for Rd (see Supplementary Fig. S4A, B) or b′3 (Supplementary Fig. S4C, D) resulted in variations in gm of <6% and did not affect the trend of increasing gm with decreasing pCO2. Ubierna et al. (2017) demonstrated that gm is largely independent of values of gbs or Vcmax and this is also illustrated in Supplementary Fig. S2.
CA-limited versus CA-saturated models to estimate gm
The substrate for the initial carboxylation by PEPC is HCO3– and not CO2. However, Vp is often calculated in terms of CO2, because the hydration of CO2 (Vh) generally happens very fast when catalysed by CA (Stryer, 1988). We refer to this case as the CA-saturated model. In contrast, the CA-limited model calculates Vp as a function of HCO3–. The value of HCO3– is calculated with Cm, Vh, Vpmax, and a series of rate constants (see Ubierna et al., 2017, for details). Producing the same Vp with the CA-limited and the CA-saturated calculations requires larger Cm for the former than the latter, and the difference could potentially be large if Vh is low. Subsequently, neglecting the hydration step, as in the CA-saturated calculations, can result in under-estimation of Cm and gm. The terminology CA-saturated or -limited refers to the modeling of Vp and how this affects the calculated Cm value, but it does not imply different roles of CA in the photosynthetic process. Ubierna et al. (2017) found no difference between CA-sat gm and CA-lim gm at ambient pCO2; however, the aim here is to compare these calculations for a range of pCO2.
In both species and at all temperatures, the difference between CA-sat gm and CA-lim gm was negligible for pCO2 >ambient (Fig. 2). However, as pCO2 decreased, CA-lim gm became larger than CA-sat gm, especially at high temperatures and in Zea. In this species ignoring the hydration step resulted in under-estimating gm by as much as 20%, whereas in Setaria the under-estimation was <5%.
The larger differences at high temperatures can be explained by the temperature response of KCA, which increases from 10 to 30 °C but plateaus above that (Boyd et al., 2015). Species differences can be explained by different KCA values and CO2 availability to CA. Firstly, KCA in Setaria (124 μmol m–2 s–1 Pa–1) was double the value for Zea (65.5 μmol m–2 s–1 Pa–1). Below ambient pCO2, Setaria and Zea had similar A, gs, and Ci. Sustaining similar A in these two species requires larger Cm in Zea than in Setaria because of the lower in vitro Vpmax value in the former (184 μmol m–2 s–1) versus the latter (450 μmol m–2 s–1). Therefore, in Zea the lower KCA and in vitro Vpmax was counterbalanced by increased CO2 availability to CA through higher gm. Osborn et al. (2017) also suggested large gm as a mechanism to increase CO2 assimilation rate at low pCO2.
At low pCO2 or in species with low KCA, ignoring the hydration step results in under-estimation of gm. However, the error is insignificant at pCO2 above ambient or in species with large KCA, such as Setaria. The hydration step should be included for accurate determination of gm at low pCO2 in species with low KCA and/or high A, such as C4 grasses (Cousins et al., 2008), especially at high temperatures.
Values for CA-lim gm and variation with pCO2
Across pCO2 and temperatures, CA-lim gm ranged from 0.6 ± 0.1 to 9.3 ± 1.5 μmol m–2 s–1 Pa–1 in Setaria, and 0.6 ± 0.1 to 16.2 ± 5.7 μmol m–2 s–1 Pa–1 in Zea (Fig. 3). In Zea, photosynthetic rate declined above ambient pCO2, indicating deactivation at low Ci that did not fully recover when pCO2 supply was returned to ambient levels (Fig. 1B). This could have introduced some bias in the CA-lim gm values calculated at high pCO2. Nevertheless, the CA-lim gm values were used at pCO2 ≤ambient, because above ambient, photosynthesis was not restricted by diffusional limitations (Fig. 4).
To validate CA-lim gm values, they were compared with literature reports for the same species obtained with the alternative Δ18O method (Barbour et al., 2016; Osborn et al., 2017; Ubierna et al., 2017; Fig. 3). In Zea, there was a good agreement between Δ18O-gm (Barbour et al., 2016; Ubierna et al., 2017) and CA-lim gm (Fig. 3B). A recent study in Zea by Kolbe and Cousins (2018) also found agreement between Δ18O-gm and in vitro Vpmaxgm across a range of pCO2, although both estimations of gm deviated at very low pCO2. In Setaria, Δ18O-gm (Barbour et al., 2016; Osborn et al., 2017; Ubierna et al., 2017) was larger than our CA-lim gm results (Fig. 3A–C). This discrepancy could have originated if in vitro Vpmax was over-estimated, and more studies exploring gm variation and assessing the impacts of the method are needed.
In Zea at 25 °C and in Setaria at three temperatures, the CA lim-gm increased with short-term exposure to decreasing pCO2. Increasing gm with decreasing pCO2 has also been observed in C3 species (Bongi and Loreto, 1989; Loreto et al., 1992; Flexas et al., 2007, 2008; Hassiotou et al., 2009; Bunce, 2010; Douthe et al., 2011; Tazoe et al., 2011), although there are also a few studies that have concluded there is no change (Loreto et al., 1992; Tazoe et al., 2009). There are only two studies that have presented C4-gm across pCO2. In Osborn et al. (2017), Δ18O-gm values for Setaria increased with decreasing pCO2 but the trend was not significant. In Zea, Kolbe and Cousins (2018) found a significant increase in Δ18O-gm with decreasing pCO2.
The initial slope of an A-Ci curve can be modified with either Cm (gm) or Vpmax (see Supplementary Fig. S5). Therefore, there may be a value for Vpmax that would cancel out the trend in CA-lim gm. However, this is not the case if Vpmax is independent of pCO2, and cancelling the observed trend in CA-lim gm would require Vpmax to decrease with increasing pCO2 (Supplementary Fig. S6). There is evidence showing that CO2 levels affect the phosphorylation state of PEPC and PEPCK, and therefore variation of in vivo Vpmax across pCO2 could be expected (Bailey et al., 2007). However, the CO2 response of photosynthetic rate was found to be no different between wild-type and transgenic plants with low PEPC phosphorylation (Furumoto et al., 2007). Much of the post-translational modifications that presumably lower Vpmax would probably occur when CO2 is saturating and some other factor limits C4 photosynthesis. At ambient pCO2 and below it is generally thought, although not known, that PEPC is operating at Vpmax. The fact that Δ18O-gm data have demonstrated a similar trend of increasing gm with decreasing pCO2 (Kolbe and Cousins, 2018) points to a constant Vpmax value. Nevertheless, if fast in vivo regulation of Vpmax occurs it could alter values and trends in gm. In reality, there might be a combination of both fluctuations in gm and Vpmax in response to short-term variation in pCO2. Future work should investigate in vivo regulation of Vpmax and its impact on gm calculations.
Limitation to photosynthesis at low pCO2
C4 photosynthesis saturates at ambient pCO2 and A was not limited by diffusion, as indicated by Ls, Lm, and LCA ≈ 0% for both species and all temperatures (Fig. 4). However, below ambient air pCO2, diffusional limitations constrained CO2 assimilation and increased exponentially with decreasing pCO2. As shown in Fig. 1 and Supplementary Fig. S5, in both species the CO2 responsive part of the A-Ci curve corresponded to Ci below ~10 Pa. This raises the question of whether C4 plants operate below this threshold. In laboratory experiments, high irradiance and N fertilization shifted the operational Ci down to the CO2 responsive part of the A-Ci curve (Ghannoum et al., 1997; Ghannoum and Conroy, 1998). Additionally, moderate water stress decreased Ci in several C4 species, although under severe drought declines in A precluded Ci from getting very low (Ghannoum, 2009, and references herein). Under ambient air pCO2, Ci<11 Pa were reported for Zea grown in FACE-type experiments (Leakey et al., 2004; Markelz et al., 2011), and Sorghum bicolor grown in an open field reached Ci/Ca=0.2 after two consecutive water-stress cycles (Steduto et al., 1997). Therefore, under certain growth conditions, CO2 availability may limit C4 photosynthesis.
Interestingly, Setaria and Zea displayed different behavior at low pCO2. At low pCO2, Zea was more efficient because it achieved high A despite lower Vpmax and KCA by decreasing diffusional limitations and sustaining greater Cm with high gm. The high gm at low pCO2 could increase or maintain photosynthesis at low Ci and could improve photosynthetic rates under situations that result in low CO2 availability, such as drought.
In both species, the conversion of CO2 into bicarbonate as catalysed by CA was fast enough that the hydration rate only limited A at low pCO2 (LCA=6–16% for Cm<4 Pa, Fig. 4). Such low Cm is unlikely to occur, even under drought conditions. At these very low pCO2, the hydration rate (Vh) was comparable to rates in CA-depleted transgenic plants (Supplementary Fig. S7). For example, in Setaria at 25 °C, Vh decreased from 581 μmol m–2 s–1 at ambient pCO2 to 100 μmol m–2 s–1 at the lowest pCO2 measured. Using values from Osborn et al. (2017) at 25 °C and ambient pCO2 to calculate Vh as Cm×KCA resulted in 1215 and 142 μmol m–2 s–1 for the wild type and CA-depleted transgenic, respectively. Osborn et al. (2017) concluded that in Setaria at low pCO2, gm posed a greater limitation than CA activity. Our study confirms that gm is a major determinant of photosynthetic capacity at low pCO2 and CA further constrains assimilation rates only at very low pCO2. However, the CA limitation at low pCO2 will be exacerbated at higher temperatures as the hydration rate is less able to keep up with the increase in PEPC activity (Boyd et al., 2015).
Leakiness (ϕ)
Leakiness is often estimated from comparing models and measurements of Δ13C assuming gm is infinite (Pengelly et al., 2010; Ubierna et al., 2011, 2013) or large (Kromdijk et al., 2010). Values of ϕ vary by as much as 0.04–0.9 (for a compilation of values and review of methods see Kromdijk et al., 2014), although for most species under most conditions ϕ=0.2–0.3 (Cousins et al., 2006; Kromdijk et al., 2010; Pengelly et al., 2010; Ubierna et al., 2013; Bellasio and Griffiths, 2014).
In our study, considering gm to be finite had a different effect on the calculation of ϕ for Setaria and Zea. At ambient air pCO2 and 25 °C, both Setaria and Zea had similar gm (2.00 and 2.43 μmol m–2 s–1 Pa–1, respectively). However, while ϕ in Zea was the same whether gm was finite or infinite, in Setaria, accounting for a finite gm doubled ϕ (Fig. 5, compare Models 1 and 2). This high ϕ in Setaria was driven by constrains imposed by the Δ13C model rather than the photosynthesis model. This is illustrated by the comparison of Models 2 and 3 (Fig 5). Both models predicted the same A and ϕ, but Model 2 used gm finite (and in vitro Vpmax) and Model 3 assumed gm infinite (and in vivo Vpmax). However, Model 3 failed to predict (see Supplementary Fig. S2). Forcing the solution to satisfy both models of A and resulted in increases in ϕ in Setaria, but not in Zea.
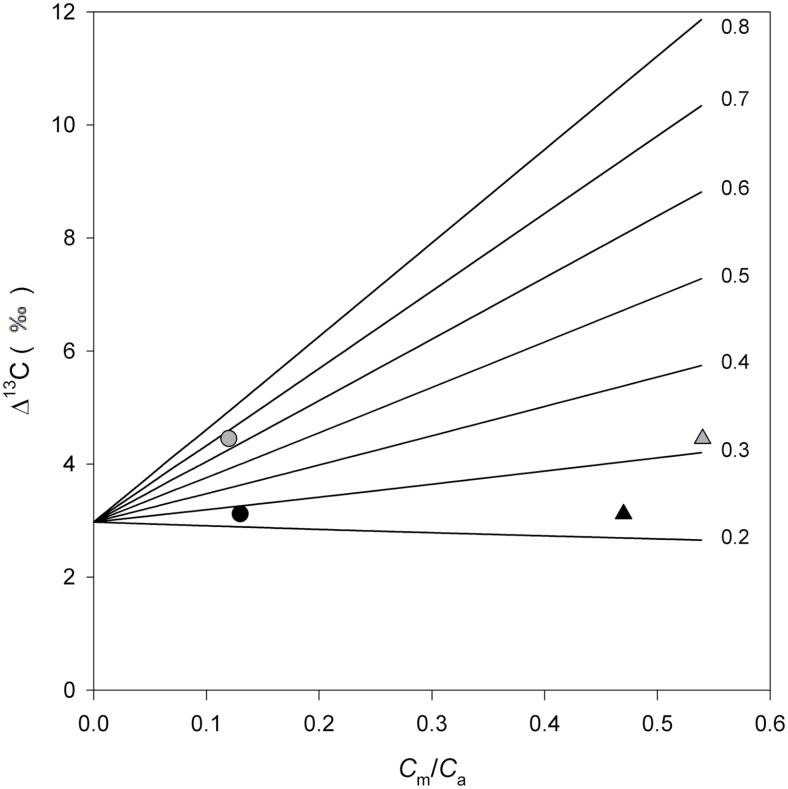
This can be explained through the relationship between Δ13C and Cm/Ca, which is illustrated in Fig. 6 for different values of ϕ. Increasing Cm/Ca results in either increased or decreased Δ13C depending on whether ϕ is low (≤0.3) or high (Henderson et al., 1992; von Caemmerer et al., 2014). When > as + (am – as)(Ci/Ca) ( = 4.4–2.6 Ci/Ca ≈ 2.9‰ in our data set at 25 ºC and ambient pCO2) increasing Cm/Ca results in decreased ϕ; meanwhile the opposite is true when The value as + (am – as)(Ci/Ca) represents the intercept of the line Δ13C versus Cm/Ca when Cbs and boundary layer conductance are large and ternary effects are ignored. At ambient air pCO2 and 25 °C, =3.1‰ in Zea. Therefore, varying Cm/Ca resulted in minimal changes in ϕ (compare black triangle and circle in Fig. 6). However, in Setaria, =4.5‰ and therefore low Cm/Ca translated into large ϕ (compare grey triangle and circle in Fig. 6). The photosynthesis model demonstrated that this increase in ϕ was achieved by increased Vp and gbs (see Supplementary Fig. S2).
Fig. 6.
Δ13C (Eqn 9) as a function of Cm/Ca for different ϕ values (indicated by the numbers at the end of each line). For calculations we used values of 37, 36, 20, and 1364 Pa for Ca, CL, Ci, and Cbs, respectively; t=0.0058, b4=–4.49‰, and b3=29.87‰. These values correspond to the mean values measured or calculated in Setaria at 25 °C and ambient pCO2. Black symbols represent data for Zea and grey symbols for Setaria. For both species, ϕ was calculated assuming either gm infinite (triangles) or gm=2.00 and 2.43 μmol m–2 s–1 Pa–1 in Setaria and Zea, respectively (circles).
It is questionable that Setaria operates with ϕ=0.7, and it is seemly unreasonable that it does. Because Δ13C is mostly determined by Cm/Ca and ϕ, low Cm/Ca forces the increase in ϕ. But are there any other parameters in the discrimination equation that could be manipulated in order to predict large Δ13C with low Cm/Ca without large ϕ? Calculations of ϕ with the complete (Eqn 16) and simplified (Eqn 19) models suggest that, at least at ambient pCO2, this was not the case. The simplified calculation of ϕ produced values similar to the complete model, suggesting that at ambient air pCO2 or above, modifying parameters such as Cbs, b3, or b4 within their current definition did not result in large changes in Δ13C.
In addition to the possible post-translational regulation of Vpmax, PEP regeneration (Vpr) may also influence Vp (Eqn 6) and estimates of ϕ. In our calculations, Vpr=64 μmol m–2 s–1 decreased ϕ in Setaria by 0.3 and resulted in slightly larger gm values at high pCO2 but no change at low pCO2 (compare Models 1 and 4 in Fig. 5 and Supplementary Fig. S2). In fact, at low pCO2 it is expected that Vpr would not limit Vp and would have no effect on estimates of gm or ϕ under these conditions. Changes in ϕ in response to pCO2 or other conditions are possible if Vpr is allowed to vary, although at present Vpr variation across species, temperatures, or pCO2 is unknown. The Vpr values that would be needed to remove the observed trend in gm with pCO2 are shown in Supplementary Fig. S8. Introducing a value for Vpr implies decoupling Vp from Cm (gm). In other words, the required Vp value to support the measured A could be achieved by choosing the adequate Vpr rather than by varying Cm. This would also further complicate estimations of ϕ from Δ13C as Vpr is not often measured and is not incorporated into the Δ13C models.
Our calculations assume that theoretical models of photosynthesis and discrimination represent the actual photosynthetic process; any inaccuracy in the models will introduce error in the calculated gm. We have evaluated one common modelling simplification, the effect of CA limitation, and also the impact of uncertainty on input parameters. Additionally, we have used two contrasting species to illustrate the sensitivity of ϕ to gm. Although a complete analysis of ϕ is beyond the scope of this work, this should be undertaken in future studies together with investigations on PEP regeneration limitations. Other future foci for research include: investigating in vivo and in vitro Vpmax values and variation across species and environmental conditions; and compiling leaf structure, CA, aquaporins, or other data that could reveal potential mechanisms behind observed gm patterns.
Supplementary data
Supplementary data are available at JXB online.
Methods S1. Model of 13C discrimination in C4 species.
Table S1. Gas exchange values for Ci and A, and calculated values for Cm and CA-lim gm in Setaria viridis and Zea mays at 25 °C and variable CO2 supply.
Fig. S1. Cm across Ci in Setaria viridis at three temperatures, and in Zea mays at 25 °C.
Fig. S2. Description of the models used to evaluate the effect of gm in calculations of ϕ.
Fig. S3. Sensitivity of calculations of CA-lim gm in Setaria viridis to uncertainty in input parameters.
Fig. S4. Impact of Rd and b′3 in the calculation of CA-lim gm in Setaria viridis at 25 °C.
Fig. S5. Measured versus modeled response of A to Ci at 25 °C in Setaria viridis and Zea mays for different values of Vpmax and gm.
Fig. S6. Values for in vivo Vpmax across Ci in Setaria viridis calculated when CA-lim gm is constant with pCO2.
Fig. S7. Vh across Ci in Setaria viridis at three temperatures.
Fig. S8. Values for Vpr across Ci in Setaria viridis calculated when CA-lim gm is constant with pCO2.
Acknowledgments
This research was supported by the Division of Chemical Sciences, Geosciences and Biosciences, Office of Basic Energy Sciences, Photosynthetic Systems through DE-SC0001685 and with instrumentation from an NSF Major Research Instrumentation grant #0923562. We thank an anonymous reviewer for valuable comments that improved this manuscript.
References
- Arnau J, Bono R, Vallejo G. 2009. Analyzing small samples of repeated measures data with the mixed-model adjusted F test. Communications in Statistics - Simulation and Computation 38, 1083–1103. [Google Scholar]
- Bailey KJ, Gray JE, Walker RP, Leegood RC. 2007. Coordinate regulation of phosphoenolpyruvate carboxylase and phosphoenolpyruvate carboxykinase by light and CO2 during C4 photosynthesis. Plant Physiology 144, 479–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbour MM, Evans JR, Simonin KA, von Caemmerer S. 2016. Online CO2 and H2O oxygen isotope fractionation allows estimation of mesophyll conductance in C4 plants, and reveals that mesophyll conductance decreases as leaves age in both C4 and C3 plants. New Phytologist 210, 875–889. [DOI] [PubMed] [Google Scholar]
- Bellasio C, Griffiths H. 2014. Acclimation to low light by C4 maize: implications for bundle sheath leakiness. Plant, Cell & Environment 37, 1046–1058. [DOI] [PubMed] [Google Scholar]
- Bongi G, Loreto F. 1989. Gas-exchange properties of salt-stressed olive (Olea europea L.) leaves. Plant Physiology 90, 1408–1416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boyd RA, Gandin A, Cousins AB. 2015. Temperature responses of C4 photosynthesis: biochemical analysis of Rubisco, phosphoenolpyruvate carboxylase, and carbonic anhydrase in Setaria viridis. Plant Physiology 169, 1850–1861. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bunce JA. 2010. Variable responses of mesophyll conductance to substomatal carbon dioxide concentration in common bean and soybean. Photosynthetica 48, 507–512. [Google Scholar]
- Cousins AB, Badger MR, von Caemmerer S. 2006. Carbonic anhydrase and its influence on carbon isotope discrimination during C4 photosynthesis. Insights from antisense RNA in Flaveria bidentis. Plant Physiology 141, 232–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cousins AB, Badger MR, von Caemmerer S. 2008. C4 photosynthetic isotope exchange in NAD-ME- and NADP-ME-type grasses. Journal of Experimental Botany 59, 1695–1703. [DOI] [PubMed] [Google Scholar]
- Douthe C, Dreyer E, Epron D, Warren CR. 2011. Mesophyll conductance to CO2, assessed from online TDL-AS records of ¹³CO2 discrimination, displays small but significant short-term responses to CO2 and irradiance in Eucalyptus seedlings. Journal of Experimental Botany 62, 5335–5346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards GE, Walker DA. 1983. C3, C4: Mechanisms, and cellular and environmental regulation of photosynthesis. Oxford, UK: Blackwell Scientific Publications. [Google Scholar]
- Evans JR. 1983. Nitrogen and photosynthesis in the flag leaf of wheat (Triticum aestivum L.). Plant Physiology 72, 297–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans JR, Sharkey TD, Berry JA, Farquhar GD. 1986. Carbon isotope discrimination measured concurrently with gas exchange to investigate CO2 diffusion in leaves of higher plants. Australian Journal of Plant Physiology 13, 281–292. [Google Scholar]
- Evans JR, Terashima I. 1988. Photosynthetic characteristics of spinach leaves grown with different nitrogen treatments. Plant and Cell Physiology 29, 157–165. [Google Scholar]
- Evans JR, von Caemmerer S. 1996. Carbon dioxide diffusion inside leaves. Plant Physiology 110, 339–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farquhar GD. 1983. On the nature of carbon isotope discrimination in C4 species. Australian Journal of Plant Physiology 10, 205–226. [Google Scholar]
- Farquhar GD, Cernusak LA. 2012. Ternary effects on the gas exchange of isotopologues of carbon dioxide. Plant, Cell & Environment 35, 1221–1231. [DOI] [PubMed] [Google Scholar]
- Farquhar GD, Sharkey TD. 1982. Stomatal conductance and photosynthesis. Annual Review of Plant Physiology 33, 317–345. [Google Scholar]
- Flexas J, Diaz-Espejo A, Galmés J, Kaldenhoff R, Medrano H, Ribas-Carbo M. 2007. Rapid variations of mesophyll conductance in response to changes in CO2 concentration around leaves. Plant, Cell & Environment 30, 1284–1298. [DOI] [PubMed] [Google Scholar]
- Flexas J, Ribas-Carbó M, Diaz-Espejo A, Galmés J, Medrano H. 2008. Mesophyll conductance to CO2: current knowledge and future prospects. Plant, Cell & Environment 31, 602–621. [DOI] [PubMed] [Google Scholar]
- Furumoto T, Izui K, Quinn V, Furbank RT, von Caemmerer S. 2007. Phosphorylation of phosphoenolpyruvate carboxylase is not essential for high photosynthetic rates in the C4 species Flaveria bidentis. Plant Physiology 144, 1936–1945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghannoum O. 2009. C4 photosynthesis and water stress. Annals of Botany 103, 635–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghannoum O, Conroy JP. 1998. Nitrogen deficiency precludes a growth response to CO2 enrichment in C3 and C4Panicum grasses. Australian Journal of Plant Physiology 25, 627–636. [Google Scholar]
- Ghannoum O, von Caemmerer S, Barlow EWR, Conroy JP. 1997. The effect of CO2 enrichment and irradiance on the growth, morphology and gas exchange of a C3 (Panicum laxum) and a C4 (Panicum antidotale) grass. Australian Journal of Plant Physiology 24, 227–237. [Google Scholar]
- Gillon JS, Yakir D. 2000a. Internal conductance to CO2 diffusion and C18OO discrimination in C3 leaves. Plant Physiology 123, 201–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillon JS, Yakir D. 2000b. Naturally low carbonic anhydrase activity in C4 and C3 plants limits discrimination against C18OO during photosynthesis. Plant, Cell & Environment 23, 903–915. [Google Scholar]
- Gu L, Sun Y. 2014. Artefactual responses of mesophyll conductance to CO2 and irradiance estimated with the variable J and online isotope discrimination methods. Plant, Cell & Environment 37, 1231–1249. [DOI] [PubMed] [Google Scholar]
- Hassiotou F, Ludwig M, Renton M, Veneklaas EJ, Evans JR. 2009. Influence of leaf dry mass per area, CO2, and irradiance on mesophyll conductance in sclerophylls. Journal of Experimental Botany 60, 2303–2314. [DOI] [PubMed] [Google Scholar]
- Hatch MD. 1987. C4 photosynthesis: a unique blend of modified biochemistry, anatomy and ultrastructure. Biochemical and Biophysical Acta 895, 81–106. [Google Scholar]
- Hatch MD, Burnell JN. 1990. Carbonic anhydrase activity in leaves and its role in the first step of C4 photosynthesis. Plant Physiology 93, 825–828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hatch MD, Slack CR, Johnson HS. 1967. Further studies on a new pathway of photosynthetic carbon dioxide fixation in sugar-cane and its occurrence in other plant species. The Biochemical Journal 102, 417–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henderson SA, von Caemmerer S, Farquhar GD. 1992. Short-term measurements of carbon isotope discrimination in several C4 species. Australian Journal of Plant Physiology 19, 263–285. [Google Scholar]
- Jenkins CL, Furbank RT, Hatch MD. 1989. Mechanism of C4 photosynthesis: a model describing the inorganic carbon pool in bundle sheath cells. Plant Physiology 91, 1372–1381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolbe AR, Cousins AB. 2018. Mesophyll conductance in Zea mays responds transiently to CO2 availability: implications for transpiration efficiency in C4 crops. New Phytologist. In press. doi:10.1111/nph.14942. [DOI] [PubMed] [Google Scholar]
- Kromdijk J, Griffiths H, Schepers HE. 2010. Can the progressive increase of C4 bundle sheath leakiness at low PFD be explained by incomplete suppression of photorespiration?Plant, Cell & Environment 33, 1935–1948. [DOI] [PubMed] [Google Scholar]
- Kromdijk J, Ubierna N, Cousins AB, Griffiths H. 2014. Bundle-sheath leakiness in C4 photosynthesis: a careful balancing act between CO2 concentration and assimilation. Journal of Experimental Botany 65, 3443–3457. [DOI] [PubMed] [Google Scholar]
- Leakey ADB, Bernacchi CJ, Dohleman FG, Ort DR, Long SP. 2004. Will photosynthesis of maize (Zea mays) in the US Corn Belt increase in future [CO2] rich atmospheres? An analysis of diurnal courses of CO2 uptake under free-air concentration enrichment (FACE). Global Change Biology 10, 951–962. [Google Scholar]
- Loreto F, Harley PC, Di Marco G, Sharkey TD. 1992. Estimation of mesophyll conductance to CO2 flux by three different methods. Plant Physiology 98, 1437–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markelz RJ, Strellner RS, Leakey AD. 2011. Impairment of C4 photosynthesis by drought is exacerbated by limiting nitrogen and ameliorated by elevated [CO2] in maize. Journal of Experimental Botany 62, 3235–3246. [DOI] [PubMed] [Google Scholar]
- Osborn HL, Alonso-Cantabrana H, Sharwood RE, Covshoff S, Evans JR, Furbank RT, von Caemmerer S. 2017. Effects of reduced carbonic anhydrase activity on CO2 assimilation rates in Setaria viridis: a transgenic analysis. Journal of Experimental Botany 68, 299–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peisker M. 1986. Models of carbon metabolism in C3–C4 intermediate plants as applied to the evolution of C4 photosyntheis. Plant, Cell & Environment 9, 627–635. [Google Scholar]
- Peisker M, Henderson SA. 1992. Carbon: terrestrial C4 plants. Plant, Cell & Environment 15, 987–1004. [Google Scholar]
- Pengelly JJ, Sirault XR, Tazoe Y, Evans JR, Furbank RT, von Caemmerer S. 2010. Growth of the C4 dicot Flaveria bidentis: photosynthetic acclimation to low light through shifts in leaf anatomy and biochemistry. Journal of Experimental Botany 61, 4109–4122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sage RF. 2004. The evolution of C4 photosynthesis. New Phytologist 161, 341–370. [DOI] [PubMed] [Google Scholar]
- Steduto P, Katerji N, Puertos-Molina H, Ünlü M, Mastrorilli M, Rana G. 1997. Water-use efficiency of sweet sorghum under water stress conditions. Gas-exchange investigations at leaf and canopy scales. Field Crops Research 54, 221–234. [Google Scholar]
- Stryer L. 1988. Biochemistry. New York: W. H. Freeman. [Google Scholar]
- Tazoe Y, von Caemmerer S, Badger MR, Evans JR. 2009. Light and CO2 do not affect the mesophyll conductance to CO2 diffusion in wheat leaves. Journal of Experimental Botany 60, 2291–2301. [DOI] [PubMed] [Google Scholar]
- Tazoe Y, von Caemmerer S, Estavillo GM, Evans JR. 2011. Using tunable diode laser spectroscopy to measure carbon isotope discrimination and mesophyll conductance to CO2 diffusion dynamically at different CO2 concentrations. Plant, Cell & Environment 34, 580–591. [DOI] [PubMed] [Google Scholar]
- Tholen D, Ethier G, Genty B, Pepin S, Zhu XG. 2012. Variable mesophyll conductance revisited: theoretical background and experimental implications. Plant, Cell & Environment 35, 2087–2103. [DOI] [PubMed] [Google Scholar]
- Tholen D, Zhu XG. 2011. The mechanistic basis of internal conductance: a theoretical analysis of mesophyll cell photosynthesis and CO2 diffusion. Plant Physiology 156, 90–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ubierna N, Gandin A, Boyd RA, Cousins AB. 2017. Temperature response of mesophyll conductance in three C4 species calculated with two methods: 18O discrimination and in vitro Vpmax. New Phytologist 214, 66–80. Corrigendum. New Phytologist 217: 956–959. [DOI] [PubMed] [Google Scholar]
- Ubierna N, Sun W, Cousins AB. 2011. The efficiency of C4 photosynthesis under low light conditions: assumptions and calculations with CO2 isotope discrimination. Journal of Experimental Botany 62, 3119–3134. [DOI] [PubMed] [Google Scholar]
- Ubierna N, Sun W, Kramer DM, Cousins AB. 2013. The efficiency of C4 photosynthesis under low light conditions in Zea mays, Miscanthus × giganteus and Flaveria bidentis. Plant, Cell & Environment 36, 365–381. [DOI] [PubMed] [Google Scholar]
- von Caemmerer S. 2000. Biochemical models of leaf photosynthesis. Collingwood, Australia: CSIRO publishing. [Google Scholar]
- von Caemmerer S, Ghannoum O, Pengelly JJ, Cousins AB. 2014. Carbon isotope discrimination as a tool to explore C4 photosynthesis. Journal of Experimental Botany 65, 3459–3470. [DOI] [PubMed] [Google Scholar]
- Warren CR. 2008. Stand aside stomata, another actor deserves centre stage: the forgotten role of the internal conductance to CO2 transfer. Journal of Experimental Botany 59, 1475–1487. [DOI] [PubMed] [Google Scholar]
- Warren CR, Ethier GJ, Livingston NJ, Grant NJ, Turpin DH, Harrison DL, Black TA. 2003. Transfer conductance in second growth Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco) canopies. Plant, Cell & Environment 26, 1215–1227. [Google Scholar]
- Yin X, van der Putten PE, Driever SM, Struik PC. 2016. Temperature response of bundle-sheath conductance in maize leaves. Journal of Experimental Botany 67, 2699–2714. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.