Abstract
Mathematical models of cardiac action potentials have become increasingly important in the study of heart disease and pharmacology, but concerns linger over their robustness during long periods of simulation, in particular due to issues such as model drift and non-unique steady states. Previous studies have linked these to violation of conservation laws, but only explored those issues with respect to charge conservation in specific models. Here, we propose a general and systematic method of identifying conservation laws hidden in models of cardiac electrophysiology by using bond graphs, and develop a bond graph model of the cardiac action potential to study long-term behaviour. Bond graphs provide an explicit energy-based framework for modelling physical systems, which makes them well suited for examining conservation within electrophysiological models. We find that the charge conservation laws derived in previous studies are examples of the more general concept of a ‘conserved moiety’. Conserved moieties explain model drift and non-unique steady states, generalizing the results from previous studies. The bond graph approach provides a rigorous method to check for drift and non-unique steady states in a wide range of cardiac action potential models, and can be extended to examine behaviours of other excitable systems.
Keywords: bond graph, cardiac electrophysiology, conservation law
1. Introduction
Models of the cardiac action potential have been developed to study cardiac diseases, such as arrhythmia [1–3], ischaemia [4] and acidosis [5]. Increasing model complexity has led to concerns over the occurrence of drift and non-unique steady states [6–8], particularly for extensions of the DiFrancesco & Noble [9] and Luo–Rudy [1,3] models. While solutions to these issues have been proposed using conservation principles [10,11], they have not been universally applied for more recent models, many of which still use non-conservative stimulus currents that predispose them to drift [12–14]. More recently, the Food and Drug Administration (FDA) has initiated plans to use cardiac action potential models to assess potential drug side-effects on cardiac instability through the human ether-à-go-go-related gene (hERG) K+ channel. Thus, with an increasing emphasis on model robustness and accuracy, there is a renewed incentive to resolve the issues of drift and non-unique steady states [15,16].
Drift is the failure of a model to reach a consistent limit cycle when simulated over long periods, and is often caused by a non-conservative stimulus containing current with no charge carrier [6,10]. Hund et al. [10] derived a charge conservation law, and found that non-conservative stimulus currents violate this conservation law, hence they proposed K+ ions as the current charge carrier to resolve this. A related issue in many models where drift has been resolved is that steady-state limit cycles under constant pacing depend upon the initial conditions and are therefore non-unique [7,8,10]. Thus, depending on the initial conditions, the same model may lead to different conclusions. Like drift, authors have suggested that charge conservation can constrain initial conditions such that they lead to the same steady state [8,10,11].
While the studies by Hund et al. [10] and Livshitz & Rudy [11] suggest measures to eliminate drift and attain a unique steady state by using conservation laws, their analyses are limited in their scope and not a comprehensive solution for all models. Because existing studies [10,11] explore charge conservation only in specific models, and the conservation laws were derived from physical intuition rather than a principled mathematical approach, it is difficult to generalize their findings to other models where charge conservation is routinely neglected. Furthermore, because these studies focus only on conservation of charge, they may miss other conservation laws relevant for long-term behaviour, such as those corresponding to ions, ion channels and buffers. A general approach is, therefore, desirable to deal with the issues of drift and steady states in a more systematic manner and for a broader range of models.
To facilitate a general approach, we propose the use of bond graphs which explicitly model energy transfer across physical systems to ensure compliance with conservation principles. Bond graphs were initially invented to model hydroelectric systems [17] and they have subsequently been extended to model chemical [18], biochemical [19,20] and electrochemical systems [21]. As with all physical systems, biological processes must obey the fundamental principles of physics and thermodynamics [22]; therefore, bond graphs are well suited for constraining models of biological systems to physically plausible solutions [23], and also for inferring the energetic cost of biological processes [21,23–25]. Because the bond graph representation emphasizes analogies between different physical domains, electrophysiological systems can be analysed as an analogous biochemical system with a stoichiometric matrix that describes the stoichiometry of each reaction within its columns [20,26–28]. In this context, the ‘conservation principle’ described in earlier studies is an example of the more general principle of a conserved moiety in metabolic and bond graph analysis [23,29].
In this study, we develop an abridged bond graph model of the cardiac action potential and outline a general approach to study the effects of conserved moieties on drift and steady-state behaviour. Our bond graph model simulates the essential features of the cardiac action potential, and because bond graphs are energy-based this easily provides an estimate of the energetic cost (in Joules) of the cardiac action potential. Our analysis reveals conservation of charge as one of the conserved moieties of our model, along with other conserved moieties corresponding to ions, channels, transporters and buffers. We observed that our model solution was subject to drift when the stimulus current violated any conservation laws corresponding to the conserved moieties, and that changes to the initial conditions led to different steady states if the value of any conserved moiety was changed. To demonstrate that our approach is general, we analyse variants of our bond graph model where different ions have been fixed at a constant concentration (corresponding to ‘chemostats’). It should be noted that fixing an ion concentration can change the conserved moieties of a system, therefore influencing a model's susceptibility to drift and non-unique steady states. The bond graph approach is a useful and general method to identify and interpret conservation principles, and it can link conserved moieties to individual steady states. Our approach can be used to automatically derive charge conservation laws that are frequently neglected in existing models of cardiac electrophysiology, and we build upon existing reports [10,11] to propose solutions for drift and non-unique steady states which work for all cardiac action potential models that can be represented using bond graphs.
2. Methods
(a). Model components
To study the issues of drift and non-unique steady states, we built an abridged bond graph model of the cardiac action potential, with the minimal number of channels and pumps required to simulate the essential features of a cardiac action potential, and maintain ionic concentrations over long periods of simulation. We note that a series of mathematical equations can only be described using bond graphs if they describe a thermodynamically consistent system, and that no existing model of cardiac electrophysiology is entirely thermodynamically consistent. As seen in Gawthrop et al. [21], an exact translation of existing ion channel models into the bond graph framework is generally not possible. Therefore, for some transport processes and particularly for ion channels, it was necessary to build new models under the bond graph framework, although their parameters and structure can be chosen based on equations in existing models. Accordingly, many of the essential components of our model were based primarily on the Luo–Rudy 1994 dynamic model [1], although it is possible to use other models and/or model more sub-cellular processes. We argue in §2c that some aspects of the equations for the ion channels described in the Luo and Rudy model are not thermodynamically consistent, and unable to be represented as bond graphs. We describe our approach to modelling ion channels in §2d. As we use simple and elementary bond graph structures based on physical principles, our bond graph representation of ion channels is a physically constrained approximation of the equations described in Luo and Rudy, although it is still able to simulate the essential features of the cardiac action potential.
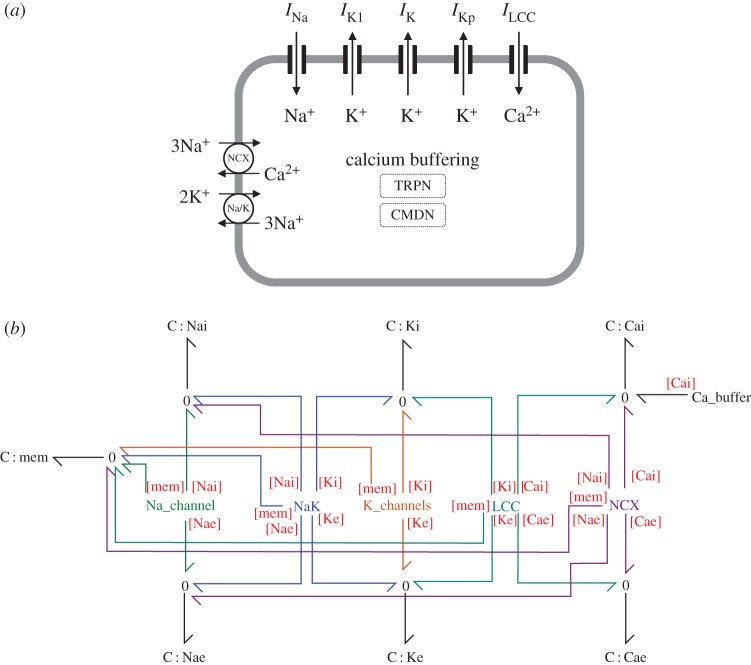
Model components are shown in figure 1a, together with the overall bond graph structure (figure 1b). Ion channels and Ca2+ buffering components were based upon their representations in Luo & Rudy [1]. The L-type Ca+ channel in the Luo–Rudy model is permeable to calcium, sodium and potassium, but we neglected its sodium conductance as this has a relatively small contribution to the action potential. The Na+/K+ ATPase model was based on the model by Terkildsen et al. [4], with modifications suggested by Pan et al. [30] to allow conversion into a bond graph model. The equation for the Na+–Ca2+ exchanger (NCX) current in Luo and Rudy did not have an obvious correspondence to a bond graph structure, thus we modelled this component using a simple bond graph module that was fitted to experimental data [31,32]. The general approach for modelling ion channels is described later in the methods, with details on the other components, as well as further detail on ion channel modelling given in the electronic supplementary material.
Figure 1.
Action potential model. (a) Cell schematic, (b) overall bond graph structure. The bond graph modules Na_channel, NaK, K_channels, LCC, NCX and Ca_buffer contain more detailed aspects of the bond graph structure which are described further in the Methods and electronic supplementary material. Coloured bonds link bond graph modules to the appropriate chemical species. Definitions: INa, sodium current; IK1, time-independent K+ current; IK, time-dependent K+ current; IKp, plateau K+ current; ILCC, L-type Ca2+ current; NCX, Na+–Ca2+ exchanger; Na/K, Na+/K+ ATPase; TRPN, troponin; CMDN, calmodulin. (Online version in colour.)
(b). Bond graph modelling
Here, we briefly outline bond graph components as used in electrophysiological modelling. For a more comprehensive introduction, the texts by Gawthrop & Smith [33] and Borutzky [34] provide detailed descriptions of bond graph theory, and Gawthrop & Bevan [35] provide a short tutorial for engineers. Theory for bond graph modelling of biochemical systems can be found in [19,20,23,36].
Bond graphs consist of components (representing physical objects and processes), bonds (representing the transfer of energy) and junctions (representing network structure). Each bond carries two variables: an effort e and a flow f , such that their product determines the power of the bond (i.e. p = ef). Thus, bond graphs explicitly account for energy transfer, and are thermodynamically consistent. Because effort and flow are generalized variables, they can represent quantities from a variety of physical systems, including mechanical (e = force (N), f = velocity (m s−1)), electrical (e = voltage (V), f = current (A)) and hydraulic systems (e = pressure (Pa), f = volumetric flow rate (m3 s−1)) [34].
The network structure of a bond graph is specified by 0 and 1 junctions. The 0 (or effort) junctions specify that efforts of all connected bonds are equal, and thus to ensure conservation of energy through this junction, the flows of the bonds must sum to zero. In the electrical and hydraulic domains, 0 junctions represent parallel connections, whereas they represent series connections in the mechanical domain. By a similar principle, 1 (or flow) junctions specify that the flows of all connected bonds are equal, ensuring that their efforts sum to zero. Thus, 1 junctions correspond to series connections in the electrical and hydraulic domains, and parallel connections in the mechanical domain.
To illustrate the use of a bond graph for electric circuit analysis, we consider the electric circuit where two capacitors are connected to a resistor in series (figure 2a). All components are linear, described by the following equations:
| 2.1 |
The 1 junction enforces Kirchhoff's voltage law, such that:
| 2.2 |
Combining these equations gives rise to a system of the first-order differential equations:
| 2.3 |
and
| 2.4 |
It should be noted that in this example, the R and C components are linear. More generally (as required in biochemical and electrophysiological systems), bond graphs allow the definition of components with nonlinear constitutive equations to give rise to nonlinear ordinary differential equations (ODEs) that adhere to thermodynamic and physical constraints [34].
Figure 2.
Conceptual representations of physical systems. (a) A bond graph for the illustrated simple electric circuit with two capacitors and a resistor in series. (b) A bond graph analogous to the electric circuit in (a) can also represent the chemical reaction . (c) Bond graphs can also model interaction of components in both the chemical and physical domains, such as the transport of an ion across a membrane. (d) Transport of an ion across a membrane through an ion channel involves gating which modulates the rate of reaction. Thus the ion channel is analogous to a potentiometer. (Online version in color.)
More recently, bond graphs have been extended to model biochemical systems [19,20] where the chemical potential μ (J mol−1) is the effort variable, and molar flow rate v (mol s−1) is the flow variable. As temperature and pressure are assumed to be constant in biochemical systems, the measure of thermodynamic potential μ corresponds to Gibbs free energy [37]. For bond graph modelling of more general systems where temperature and pressure change, the reader is directed to the text by Thoma & Bouamama [38].
Because mass action equations are nonlinear in general, nonlinear components are required to model biochemical systems. Each chemical species is represented as a capacitor. However, in contrast to the electrical domain, the constitutive equation for the capacitor representing each species is logarithmic:
| 2.5 |
where x (mol) is the molar amount of the species, K (mol−1) is a species thermodynamic constant, R = 8.314 Jmol−1K−1 is the gas constant and T is the absolute temperature of the system. Reactions are modelled as two-port resistors using the Marcelin–de Donder equation as the constitutive equation:
| 2.6 |
where κ (mol s−1) is a reaction rate constant and Af (J mol−1) and Ar (J mol−1) are the forward and reverse affinities, respectively. The two affinities represent the potential energies present in the reactants and products, and the reaction proceeds in the direction of decreasing potential. As illustrated by the example in figure 2b, the reaction has a physical analogy to figure 2a, with the same equivalent electric circuit. By using the constitutive equations in equations (2.5) and (2.6), the reaction velocity for the bond graph model follows mass-action kinetics:
| 2.7 |
where the forward and reverse rate constants are k+ = κ1Ka and k− = κ1Kb. For more general chemical reaction networks, 1 junctions describe the presence of multiple reactants or products in a single reaction, whereas 0 junctions describe the involvement of a single species in multiple reactions [20]. For some models, we may wish to keep the amount x of a species constant and this is achieved by defining the species as a ‘chemostat’ [39]. Because chemostats can be interpreted as an external flow that balances internal flows, they require energy to be pumped into (or out of) the system [23].
The bond graph framework for biochemistry can be extended to electrochemical systems [21] as demonstrated in figure 2c, which models the transport of a positively charged species X across a membrane. It should be noted that chemical species are described with C components that have a logarithmic association, whereas the C component corresponding to the (electric) membrane potential has a linear constitutive relationship. A transformer (TF) is used to convert the membrane voltage into an equivalent chemical potential through Faraday's constant F = 96485 C mol−1, such that:
| 2.8 |
and
| 2.9 |
Thus, the reaction velocity is:
| 2.10 |
By setting v = 0 the familiar Nernst equation for the equilibrium potential can be derived [21]:
| 2.11 |
where the final equality results from the relation KiWi = KeWe, where Wi and We are the intracellular and extracellular volumes, respectively [21]. Therefore, the thermodynamic consistency of the bond graph approach enforces constraints on the equilibrium of the ion channel. However, it should be noted that where electrical circuit representations of the membrane Nernst potential use voltage sources, the bond graph approach necessarily accounts for possible changes in ionic concentrations, and thus this ‘voltage source’ is split into two capacitors that provide an equivalent voltage difference.
We chose to represent ion channels such that conductance was modulated by membrane voltage, both directly and indirectly through gating processes. A bond graph representation for this relationship is given in figure 2d. As shown, this model has the same electrical representation as figure 2c however it uses a variable resistor. The bond graph representation contains the same states, with C : xi, C : xe, and C : mem (with a transformer) connected through 0 junctions. In this case however, the Re components that describe the constitutive relation have been changed, such that Re_GHK : r1 is connected to an additional effort that modulates its velocity, and the gating affinity Ag is added to both the forward and reverse affinities to describe changes in permeability due to gating. Further detail on modelling ion channels using bond graphs is given in §2d.
(c). Modelling approach
Because bond graphs constrain the equations of a model to ensure thermodynamic consistency, they only allow the representation of the subset of general mathematical models that are thermodynamically consistent. In such models, dissipative processes such as reactions and ionic currents can only proceed in the direction of decreasing chemical or electrochemical potential, and when there is no potential gradient (i.e. the process is at equilibrium), the process must stop. However, many existing models of cardiac electrophysiology are not constrained to ensure this behaviour, and in some cases, they describe physically infeasible systems that create energy out of nowhere [20]. Therefore, many existing models do not have a direct bond graph representation [23]. An advantage of the bond graph approach is that the discipline required to convert an existing model into a bond graph helps to highlight thermodynamic issues and inconsistencies in existing models that would have otherwise been missed or ignored (see Gawthrop et al. [23] for an example of this process applied to a model of glycolysis). For the currents in this study, the Luo–Rudy equations for the time-dependent K+ and L-type Ca2+ channels are not thermodynamically consistent, and therefore cannot be directly converted into a bond graph model. As shown in equation (2.11), a consequence of the thermodynamic consistency of the bond graph framework is that there is a constraint on the equilibrium point for each ion channel that is determined by the Nernst equation. As the equilibrium points of the time-dependent K+ and L-type Ca2+ channels do not correspond to the Nernst potential (see electronic supplementary material, A.1.3 and A.1.5), they are not thermodynamically consistent and therefore their equations cannot be translated into a dissipative bond graph component. These issues were addressed by finding a thermodynamically consistent approximation that satisfies the Nernst equation. A second issue is that it is difficult to simultaneously model open-channel currents and channel gating using the elementary components, described in §2b and figure 2, thus we approximated these relations using the components described in that section rather than using more complicated components. Therefore, rather than attempting to reproduce the Luo–Rudy equations exactly, we built a bond graph structure as implied by the equations in the Luo and Rudy model, and chose parameters of our bond graph model to fit aspects of the Luo–Rudy model as closely as possible, specifically the current-voltage (I-V) curves and gating parameters. For all other components conversion into a bond graph model was more straightforward, and we used the methods of Gawthrop et al. [23]. Further information on the bond graph model, and parameter identification is given in the electronic supplementary material.
(d). Ion channel modelling
(i). Bond graph structure.
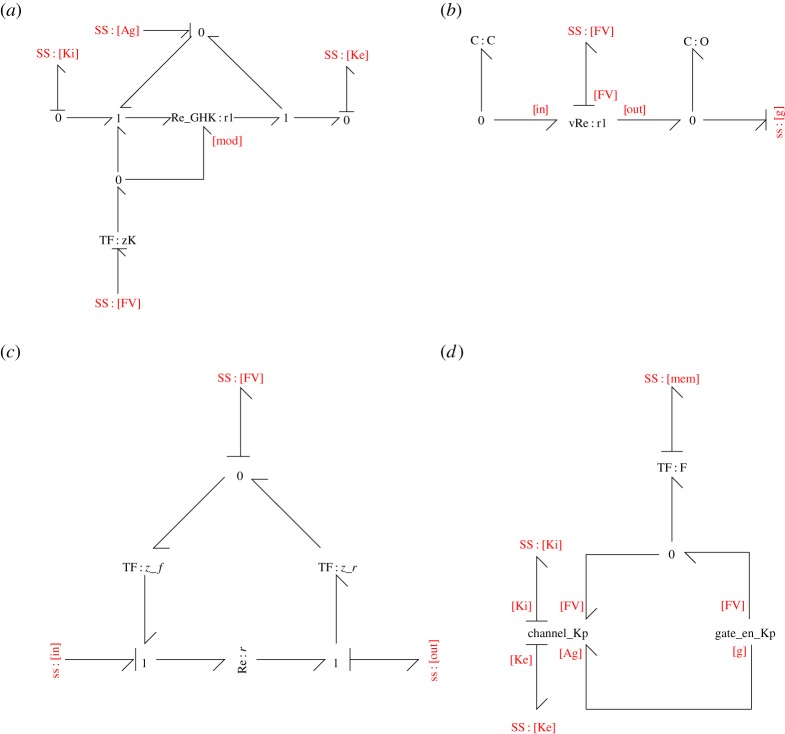
In this section, we discuss decisions made in developing models of ion channels. The bond graph structure for the Kp channel is shown in figure 3. The other channels have similar structures that follow from the discussion in this section.
Figure 3.
The bond graph model of a plateau K+ channel. (a) The channel_Kp module describes the current through the ion channel. (b) The gate_en_Kp contains the states required for gating. (c) The vRe module contains a voltage-dependent reaction used to describe channel state transitions. (d) The channel current and gating modules are combined into an ion channel model (Kp_channel). (Online version in colour.)
(ii). Current–voltage relations.
While thermodynamic properties can be used to determine how membrane voltage and ionic concentrations relate at equilibrium, they do not specify behaviour away from equilibrium. For this purpose, the current-voltage (I-V) relationship defines how the membrane voltage relates to the current through a specific channel. In many electrophysiology models [1], currents through ion channels are described through the use of linear I-V relationships based on empirical fits to data rather than fundamental physical principles. Using bond graphs, it is difficult to incorporate the effects of gating using a linear I-V equation. While linear I-V equations can be thermodynamically consistent provided they satisfy the Nernst equation in equation (2.11), and such equations can be represented by using a linear R component, the modulation of its conductance would require the use of signal bonds that do not necessarily represent physical processes [34]. Therefore, we use the Goldman–Hodgkin–Katz (GHK) equation to model ion channels, as it enables relatively simple incorporation of ion channel gating as a physics-based biochemical module [21]. The GHK equation defines a nonlinear relationship between current I and membrane voltage V :
| 2.12 |
where ci and ce are the ion's intracellular and extracellular concentrations, respectively [40]. In a bond graph, the GHK equation for current can be described by a modulated Re component with a single modulator (see figure 2d, left panel and figure 3a), using the constitutive equation from Gawthrop et al. [21]:
| 2.13 |
As discussed in Gawthrop et al. [21], setting
| 2.14 |
| 2.15 |
| 2.16 |
gives rise to the GHK equation.
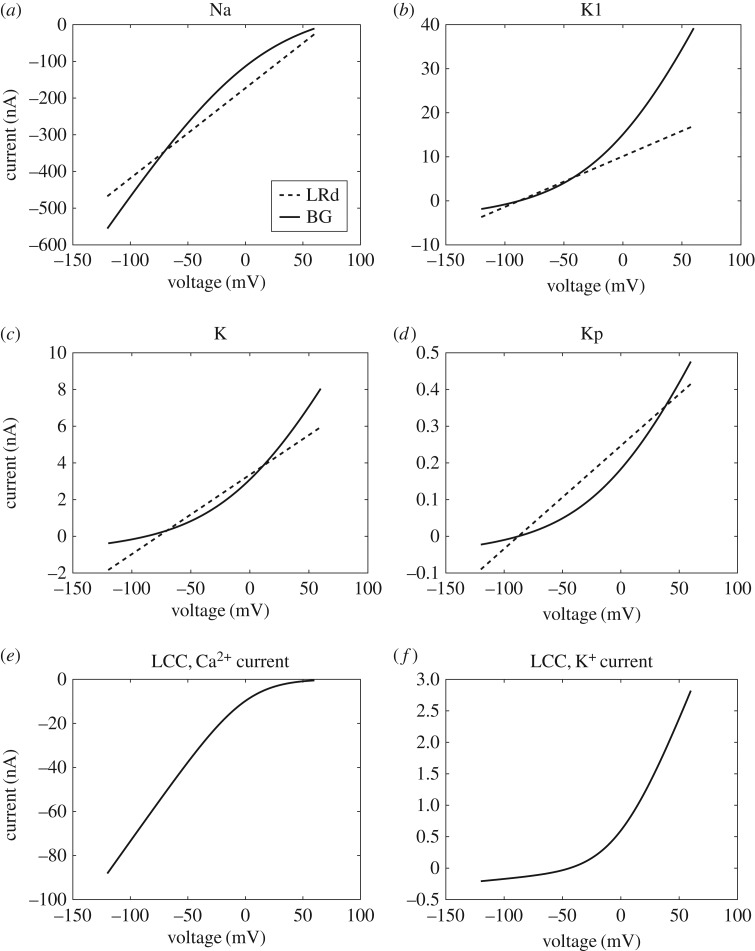
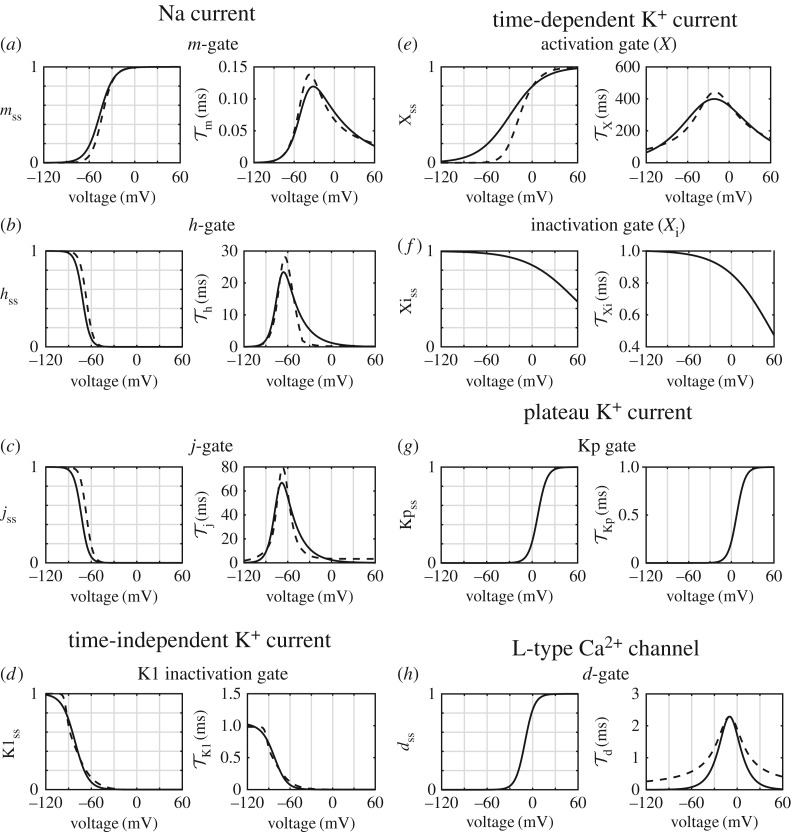
As many ion channels in the Luo–Rudy model are described using a linear I-V relationship, the use of GHK equations requires approximation. A comparison of the resulting I-V curves is given in figure 4. Details of the fitting process, as well as the fitted bond graph parameters, are given in the electronic supplementary material. The Na+ channel I-V curves appeared to match reasonably well (figure 4a), with some discrepancies at positive membrane potentials. For K+ channels (figure 4b–d), we attempted to optimize the fit across voltages that correspond to their physiological function, so that their currents would be most similar to those of Luo and Rudy when the ion channels are open. Accordingly, for IK1 (−90 mV≤V < − 30 mV), IK (−20 mV≤V ≤30 mV) and IKp (V > 0 mV) the I-V curves matched reasonably well in these regions. Discrepancies occurred outside these ranges of voltages, but appeared to only cause minor differences to the currents. In their implementation of IK, Luo & Rudy [1] use a thermodynamically inconsistent I-V equation where the current is non-zero at the Nernst potential for K+. Despite this, bond graph parameters could still be chosen to give a reasonable fit to this I-V equation (figure 4c). Because the Luo–Rudy model based their L-type Ca2+ I-V curves on the GHK equation, there was a far closer match between the bond graph and Luo–Rudy models for these currents, (figure 4e,f ) and the K+ curve was matched exactly (figure 4f ).
Figure 4.
Comparison of I-V curves between the Luo–Rudy (LRd) and bond graph (BG) models. (a) INa, (b) IK1, (c) IK, (d) IKp, (e) ICa,L, (f) IK,L. The standard concentrations in Luo & Rudy [1] ([Na+i] = 10 mM, [Na+e] = 140 mM, [K+i] = 145 mM, [K+e] = 5.4 mM, [Ca+i] = 0.12 μM, [Ca+e] = 1.8 mM) were used to match I-V curves.
(iii). Modulation.
While the I-V curves describe currents through open ion channels, a formulation for gating is required to describe the number of open ion channels at any given time. In the Hodgkin–Huxley framework, gating is modelled as differential equations that give the proportion of open gates at any given time. We incorporated the effects of gating through a gating affinity Ag, which is added to both the forward and reverse affinities of a reaction (figure 3a) to modulate its rate without changing the equilibrium [21].
(iv). State models.
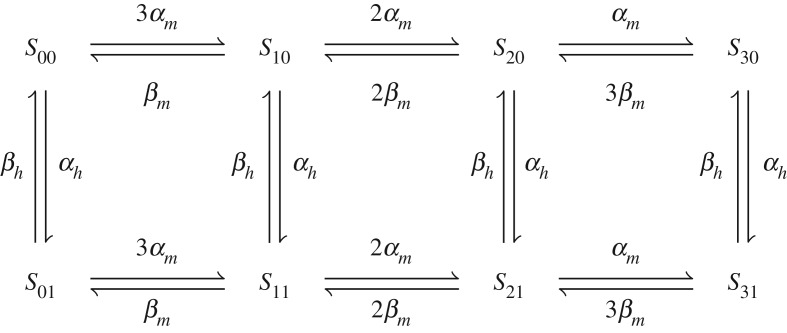
Ion channel models must account for gating and bond graphs require the use of physical components to achieve this. We model gating as transitions between channel states, known in the literature as Markov models [41,42]. To illustrate, we use the example of a typical Na+ channel in which the current I is described by the equation
| 2.17 |
where is the current when all channels are open. This can be described using the reaction scheme in figure 5, where S31 represents the open channel. Because individual channel states are modelled, the current depends only on the amount of S31 and not any of the other closed states. Thus, incorporation into the gating framework described above is intuitive; each state represents a structural conformation of the ion channel and the number of channels in each state is explicitly tracked, facilitating a simple approach to account for the energetics of gating under varying ion channel densities.
Figure 5.
Channel states of a Na+ channel.
(v). Voltage dependence of state transitions.
The transition rates between open and closed states are voltage dependent for ion channels. Hodgkin–Huxley models describe state transitions using ODEs of the form
| 2.18 |
where g is a gating variable such as m, h or n. In typical Hodgkin–Huxley models, these rates α(V ) and β(V ) are modelled using mathematical expressions on the basis of empirical fits to data. However, the gate transitions of the ion channels described in this study are voltage-dependent, thus they must result from the movement of charge through an electric field [43]. Accordingly, due to the physics-based nature of bond graphs, the open and closed states of channels must be explicitly modelled as physical components with a restricted set of constitutive equations. We note that the equations used to fit to data are not necessarily thermodynamically consistent. This is particularly common for fits to experimental measurements that do not capture the equilibria of the processes examined. Therefore, because common expressions for α(V ) and β(V ) do not obey the laws of thermodynamics, bond graphs are unable to perfectly replicate existing mathematical expressions used for ion channel transition rates. We chose to model state transitions by using the module described in figure 3b, which results in an exponential voltage-dependence for both the forward and reverse reactions. In the case of the plateau K+ channel, the rate of transition from the closed state (C) to the open state (O) is as follows:
| 2.19 |
where
| 2.20 |
and
| 2.21 |
The parameters α0, zf, β0 and zr are fitted against mathematical equations in the original model, and then used to determine the bond graph parameters. It is acceptable to fit the kinetic parameters α0 and β0 to reduce computation time as the equilibrium points of state transitions are not specified. The incorporation of voltage-dependence for the f-gate was more involved, and discussed in further detail in the electronic supplementary material.
To assess the quality of fit, we compare steady-state open probabilities gss = α(V )/(α(V ) + β(V )) and time constants τ = 1/(α(V ) + β(V )) (figure 6). The curves for gss and τ were generally in agreement; however, there were some exceptions. In particular, time constants for the Na+ channel gates have lower peaks in the bond graph model when compared to the Luo–Rudy model (figure 6a–c), but this did not appear to significantly affect Na+ channel function as the peaks were all decreased by a similar proportion, facilitating coordination between opening and closing. Similarly, the time constant τd (figure 6h) was lower in the bond graph model for some voltages, but given that discrepancies occur at time constants much smaller than the time course of a cardiac action potential we expect that the effects would be negligible. Finally, for the time-dependent K+ current Xss is substantially higher at negative voltages so that the bond graph model can provide a better match at positive voltages (figure 6e). The effects of this difference are partially offset by the lower GHK current at negative voltages which are still above the Nernst potential of K+ (figure 4c).
Figure 6.
Fits for bond graph (BG) parameters against corresponding gating equations from the Luo–Rudy (LRd) model. Steady-state open probabilities are shown on the left panels, and time constants are shown on the right. The bond graph equations are plotted with solid lines, and the Luo and Rudy equations in dashed lines. Gates include (a) m, sodium activation; (b) h, sodium inactivation; (c) j, slow sodium inactivation; (d) K1, time-independent K+ activation; (e) X, time-dependent K+ activation; (f) , time-dependent K+ inactivation; (g) Kp, plateau K+ activation; (h) d, L-type Ca2+ channel activation. Note that the and Kp gates were originally formulated as steady-state equations, thus time constants are shown only for matched bond graph parameters.
(e). Finding conserved moieties
Within a biochemical model, conserved moieties are chemical structures that are neither created, removed nor broken down. A common example in energy-dependent metabolic networks is the adenosine moiety found in AMP, ADP and ATP [23,29]. Mass balance specifies that the total amount of each conserved moiety remains constant, and if information on the molecular structure of each species of a reaction network is available, these conservation laws can be derived by counting the number of moieties across all species [29]. In practice, many models do not contain this structural information and this approach cannot be used; however, the conservation laws still hold. Here, we outline a method to find conserved moieties using stoichiometric information rather than chemical structures.
Models of cardiac electrophysiology can be represented by the differential equation
| 2.22 |
where X(t) is a vector of each state (such as species, or charge difference across a membrane), N is the stoichiometric matrix [20,26–28] and V(X) is a vector of fluxes (such as reaction velocities or ion channel currents) [20,26,44], which is, in general, a nonlinear function of X. If the model contains chemostats, the entries of X, and rows of N corresponding to the chemostats are deleted prior to performing the above analysis [39]. Using results from biochemical systems [20], if g is a row vector in the left nullspace of N, i.e. gN = 0, then
| 2.23 |
Therefore, the linear combination gX is constant for the duration of the simulation. We call the linear combination of species represented by gX a conserved moiety. The space of all conserved moieties can be described by a left nullspace matrix G, whereby linear combinations of the rows of G give all possible conserved moieties gX [45,46]. Because the left nullspace of N is a vector subspace and the rows of G form a basis for this subspace, G accounts for all conservation laws. A further advantage of using the left nullspace matrix is that it does not require information on chemical structures. The left nullspace matrix for any given system is generally not unique; however, there are many well-established techniques for calculating nullspace matrices [47], specialized approaches for finding meaningful conserved moieties in biochemical networks [29,48,49] as well as methods for finding conserved moieties from the junction structure of a bond graph [36]. In this study, we chose conserved moieties with clear physical interpretations [49], but our conclusions hold regardless of our choice of the left nullspace matrix.
(f). Stimulus currents
The cardiac action potential model was stimulated using a constant current stimulus that contained enough charge to raise the membrane potential by 30 mV over 0.1 ms. The non-conservative stimulus currents consist of non-specific charge that is not carried by any specific ion. As recommended by Kneller et al. [8], conservative stimulus currents contained K+ ions as the charge carrier.
3. Results
(a). Simulation of a single action potential
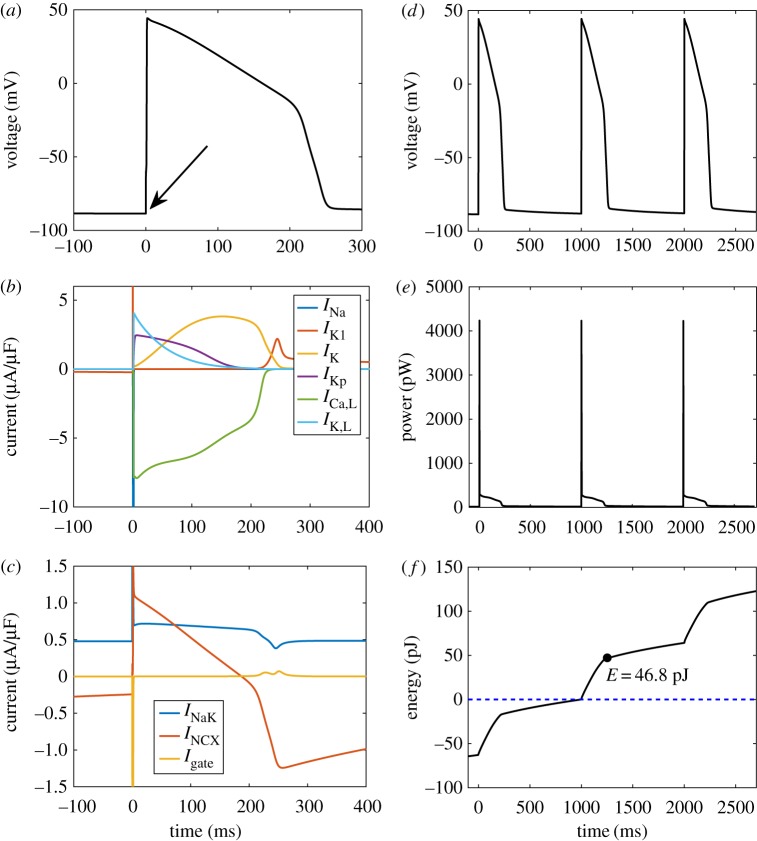
To verify that our bond graph model reproduced the features of a typical action potential, we simulated the model over a single beat (figure 7a–c). The membrane potential (figure 7a, with stimulation indicated by the arrow) resembled a typical cardiac action potential, with a distinct peak and plateau phase. The contributions of ion channel currents reproduce some common features of cardiac action potentials (figure 7b). Once the action potential is initiated by a stimulus current, the sodium current INa briefly activates to give rise to a voltage spike. Following this, the plateau phase occurs where depolarizing L-type Ca2+ currents oppose the repolarizing K+ currents IK and IKp. Towards the end of the action potential, IK1 activates to restore the resting potential [50]. Our model also simulates the reversal of NCX current across the action potential, and the consistent outward current of the Na+/K+ ATPase to maintain ionic gradients (figure 7c). As a consequence of incorporating the voltage-dependence of gating transitions in a physical framework, transitions between channel states are associated with a gating current resulting from the movement of such charged residues. Our model reveals that the total gating current across all channels Igate has minimal contribution to total current (figure 7c).
Figure 7.
A simulation of the cardiac action potential using a bond graph model. (a) Membrane voltage, following stimulation with a conservative stimulus current (arrow); (b) ion channel currents; (c) transporter and gating currents; (d) membrane voltage over three cycles, for comparison with (e) and (f); (e) power consumption; (f) energy dissipated, with the variable E representing the energy consumption over the duration of the action potential. The model was run initially for 300 ms to allow the membrane potential and channel gates to stabilize. The intracellular ion concentrations were dynamic variables with initial concentrations [Na+i] = 10 mM, [K+i] = 145 mM and [Ca+i] = 0.12 μM. Constant concentrations were [Na+e] = 140 mM, [K+e] = 5.4 mM, [Ca+e] = 1.8 mM, [MgATP] = 6.95 mM, [MgADP] = 0.035 mM, [Pi] = 0.3971 mM and pH = 7.095. T = 310 K. (Online version in colour.)
Figure 7e shows the power consumption of the membrane model over three cardiac cycles which was integrated to estimate the energetic cost of the cardiac action potential (figure 7f ). Note that energy continues to be consumed even during the resting state due to the presence of currents associated with ion transporters. Thus, while energy is predominantly consumed during the action potential, there is a positive gradient between action potentials (figure 7f ). By setting the energy consumption at the start of the second action potential to zero (figure 7f , dotted blue line), we calculated the energetic cost over the duration of the action potential to be 46.8 pJ. As the capacitive area of membrane for this model is 1.534 × 10−4 cm2, the energy consumed per unit membrane area is 305 nJ cm−2. When compared to Gawthrop et al.'s [21] estimate of 173 nJ cm−2 for the energetic cost of an action potential in the giant axon of a squid, the cardiac action potential uses 76% more energy. The main reason for this difference is that in contrast to a neuron, the cardiac action potential contains a plateau phase with opposing currents. Despite the relatively slow rate of change in voltage, the Ca2+ and K+ currents remain relatively high; therefore, a large amount of energy is dissipated during the plateau phase.
(b). Chemostats influence the conserved moieties of cardiac action potential models
Because the earliest models of the cardiac action potential did not include active transporters, they used constant intracellular concentrations to maintain ionic gradients across multiple cardiac cycles [9,51]. Later models incorporated ion transporters, allowing them to represent physiological conditions with dynamic intracellular ion concentrations, and constant extracellular ion concentrations to model washout from the circulatory system [1,3]. Under ischaemic conditions, washout is greatly inhibited, thus models of ischaemia use dynamic extracellular ion concentrations [4]. We investigated the issue of drift in three classes of model: those with (A) dynamic ion concentrations on both sides of the membrane, representing models of myocytes under ischaemic conditions; (B) dynamic intracellular ion concentrations but constant extracellular ion concentrations, representing models of myocytes under physiological conditions; and (C) constant ion concentrations, representing models without transporters.
We used our bond graph model to represent these classes of models, selecting ions to fix at constant concentrations that resulted in three variants representative of the classes listed above. Thus, variant A represents models of cardiomyocytes under ischaemic conditions [4], variant B represents models of cardiomyocytes under physiological conditions [1,3] and variant C represents models without ion transporters [9,51]. Conserved moieties of each variant were found using the left nullspace matrix of the stoichiometric matrix (table 1), and these include for example, the total amount of K1 channel (moiety 1). Because the channel is neither synthesized nor degraded in our model, the total amount of channel, i.e. the sum of its closed (CK1) and open (OK1) states, remains constant over the course of a simulation.
Table 1.
Conserved moieties associated with chemostat selection. Across some biochemical subgroups (moiety), there are constraints (conserved quantity) on a corresponding sum of species representing the total of the moiety. The conserved quantities remain constant over the course of a simulation. Q represents contributions of other species to charge imbalance across the membrane. The symbol Σ represents charge contributions from Markov states of channels and transporters. The definition of Σ, and all species can be found in the electronic supplementary material and code.
| moiety | conserved quantity | |
|---|---|---|
| conserved moieties common to all variants (A,B,C) | ||
| 1 | K1 channel | CK1 + OK1 |
| 2 | K channel | S00,K + S10,K + S20,K + S01,K + S11,K + S21,K |
| 3 | Kp channel | CKp + OKp |
| 4 | Na channel | S000,Na + S100,Na + S200,Na + S300,Na + S010,Na + S110,Na + S210,Na + S310,Na + S001,Na + S101,Na + S201,Na + S301,Na + S011,Na + S111,Na + S211,Na + S311,Na |
| 5 | LCC | S000,LCC + S010,LCC + S020,LCC + S100,LCC + S110,LCC + S120,LCC + S001,LCC + S011,LCC + S021,LCC + S101,LCC + S111,LCC + S121,LCC |
| 6 | Na+/K+ ATPase | P1NaK + P2NaK + P3NaK + P4NaK + P5NaK + P6NaK + P7NaK + P8NaK + P9NaK + P10NaK + P11NaK + P12NaK + P13NaK + P14NaK + P15NaK |
| 7 | NCX | P1NCX + P2NCX + P3NCX + P4NCX + P5NCX + P6NCX |
| 8 | troponin | TRPN + TRPNCa |
| 9 | calmodulin | CMDN + CMDNCa |
| dynamic ion concentrations (A) | ||
| chemostats | MgADP, MgATP, Pi, H+ | |
| 10 | K+ ion | K+i + K+e + 2P1NaK + P2NaK + P12NaK + 2P13NaK + 2P14NaK +2P15NaK |
| 11 | Na+ ion | Na+i + Na+e + P4NaK + 2P5NaK + 3P6NaK + 3P7NaK + 3P8NaK + 2P9NaK + P10NaK + 3P1NCX + 3P6NCX |
| 12 | Ca2+ ion | Ca2+i + Ca2+e + 2S001,LCC + 2S011,LCC + 2S021,LCC + 2S101,LCC + 2S111,LCC + 2S121,LCC + P3NCX + P4NCX + TRPNCa + CMDNCa |
| 13 | charge | Q − K+i − Na+i − 2Ca2+i + 2TRPN + 2CMDN + Σ |
| dynamic intracellular ion concentrations (B) | ||
| chemostats | MgADP, MgATP, Pi, H+, K+e, Na+e, Ca2+e | |
| 10 | charge | Q − K+i − Na+i − 2Ca2+i + 2TRPN + 2CMDN + Σ |
| constant ion concentrations (C) | ||
| chemostats | MgADP, MgATP, Pi, H+, K+i, K+e, Na+i, Na+e, Ca2+i, Ca2+e | |
Similarly, moiety 10 for variant (A) represents the total amount of K+ ions, which includes intracellular K+, extracellular K+ and the K+ ions bound to Na+/K+ ATPase. The total amount of K+ is constant when ion concentrations are dynamic. However, because fixing the concentration of K+ requires an additional external flux, the conservation law is broken in variants (B) and (C). Because the membrane capacitance is included in the stoichiometry of the system, our method automatically identifies a charge conservation law (moiety 13 for variant (A), and moiety 10 for variant (B)).
While it is reassuring that our approach reveals the obvious conserved moieties described above, it also reveals the nontrivial charge conserved moiety that is missed by many existing cardiac electrophysiology models. The overall amount of intracellular charge can be described as a sum of contributions from intracellular K+, Na+, Ca2+ (and its buffers) and Markov states from ion channels and transporters (Σ), similar to forms found in previous studies [10,52]. It should be noted, however, that when all ion concentrations were held constant, charge conservation was broken, as indicated by the absence of a conserved charge moiety in the bottom partition of table 1. In general, holding the concentration of a species constant breaks conservation laws [39] and the number of conserved moieties progressively decreases as more ion concentrations are modelled as chemostats. We discuss the consequences of this in latter sections.
(c). Non-conservative stimulus currents cause drift in models with a chargeconservation law
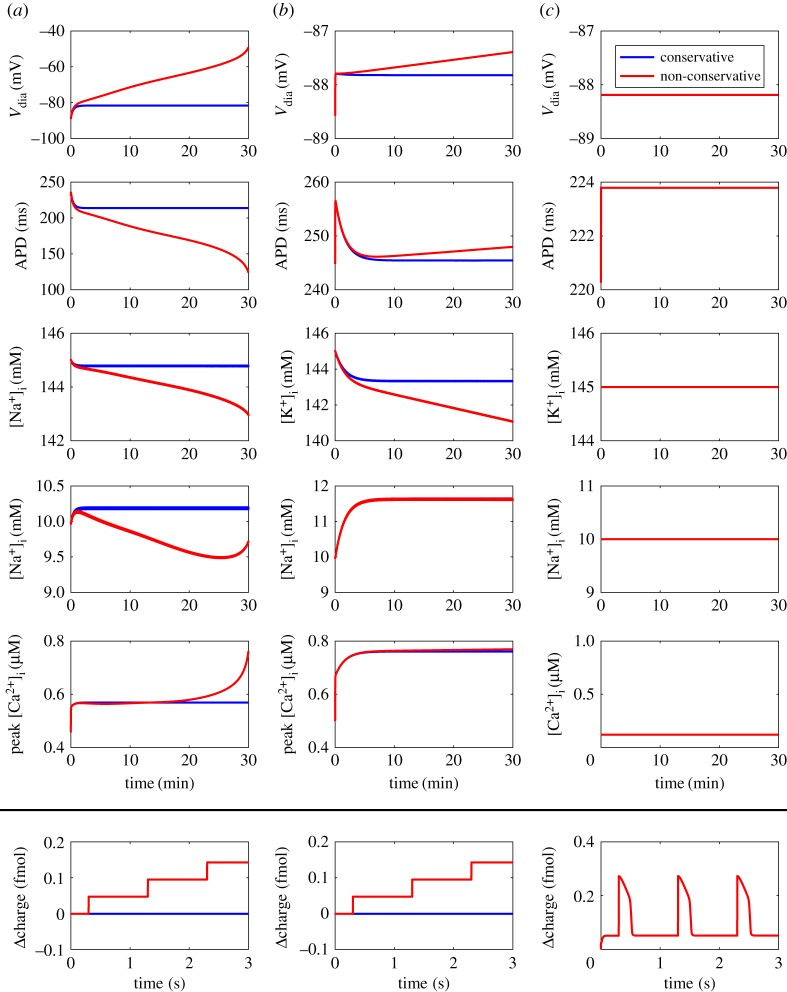
An important feature of cardiac electrophysiology models is that they must be simulated for extended periods to examine physiologically relevant changes in behaviour, thus we tested how the type of stimulus current affected each variant of the cardiac action potential model by pacing at 1 Hz for 30 min. As illustrated (figure 8a,b), a non-conservative stimulus resulted in drift when the model had dynamic ion concentrations either for all compartments, or only within the intracellular compartment. The drift was particularly pronounced when all ion concentrations were dynamic (figure 8a), as extracellular concentrations changed faster than intracellular concentrations. In contrast, the model was resistant to drift from a non-conservative stimulus when all ion concentrations were held constant (figure 8c).
Figure 8.
Effect of stimulus type and variable ion concentrations on drift in the bond graph model. (a) Dynamic ion concentrations; (b) Dynamic intracellular ion concentrations; (c) Constant ion concentrations. Results are shown for stimuli that conserve overall charge (blue) and those that do not conserve charge (red). Non-conservative stimulus currents contain non-specific charge, and conservative stimulus currents contain charge and potassium ions. Charge values are given as differences from the initial value of . . Definitions: , diastolic membrane potential; APD, action potential duration at 90% repolarization. (Online version in colour.)
These results suggested that drift arose due to violations of the conserved charge moiety. Charge is a conserved moiety (table 1) in model variants where drift occurred with a non-conservative stimulus. In this situation, non-conservative stimulus currents cause drift because every stimulus causes a stepwise increase in the value of the conserved charge moiety (figure 8a,b bottom panels). However, because conservation laws are broken as more species are represented as chemostats [39], charge is no longer a conserved moiety when all ion concentrations are constant (table 1). Thus, an observation which may not be obvious to intuition is that under these conditions charge is no longer constant between stimuli, and therefore free to return to its original value after each stimulus (figure 8c, bottom panel), allowing such models to achieve a steady-state limit cycle.
Using the observations from the bottom row of figure 8, it is possible to develop a systematic and automated check for drift. Let vs be a row matrix representing the stoichiometry of the stimulus current (with chemostats removed), Ncd be the stoichiometric matrix after removing rows corresponding to chemostats, and G be the left nullspace matrix of Ncd. As seen in this section, a stimulus current will cause drift if it results in any change to the conserved moieties GX. Therefore to avoid altering any of the conserved moieties, the stimulus current must have zero contribution to them, i.e. Gvs = 0 (or equivalently, vs needs to lie in the image of Ncd). Thus, the model drifts if Gvs≠0.
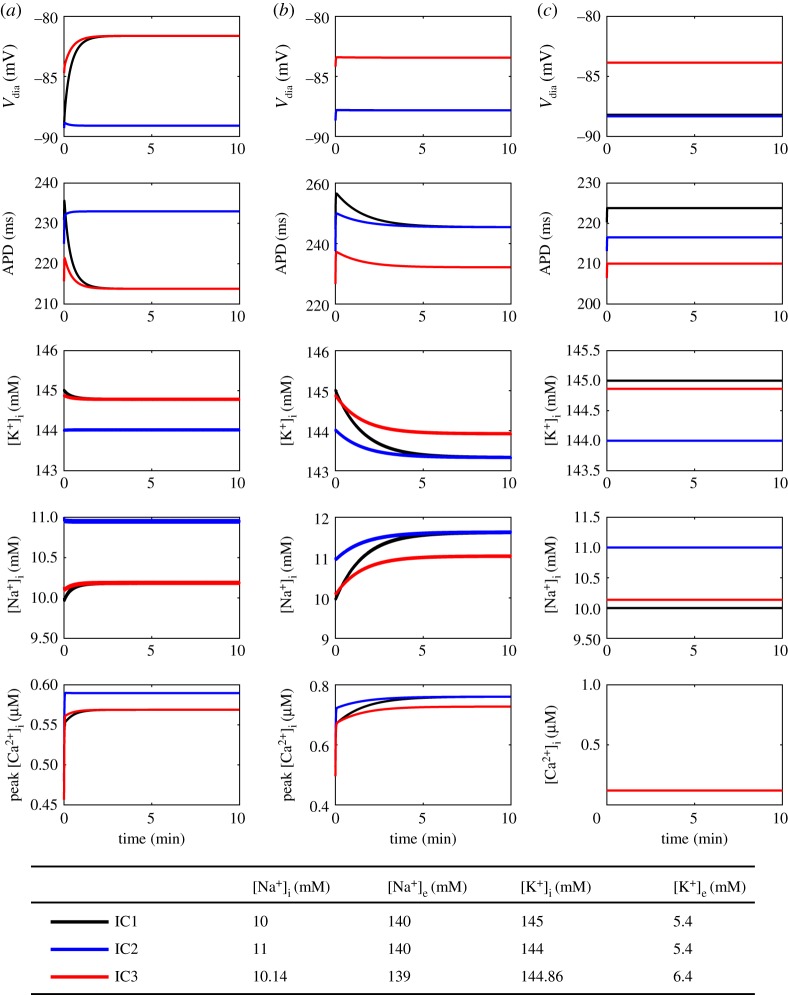
(d). Initial conditions influence steady states through conserved moieties and chemostats
Next, for different sets of conserved moieties (as determined by constrained/dynamic ionic concentrations) we tested how the steady-state behaviour of the cardiac action potential was altered under three different initial conditions (figure 9). The first set of initial conditions (IC1) are common values for comparison (figure 5; at bottom). IC2 is the same as IC1 but with 1mM intracellular K+ exchanged for 1 mM of intracellular Na+, such that charge is conserved but K+ and Na+ are not conserved. Similarly, IC3 is the same as IC1, but with some K+ extruded and an equal amount of Na+ moved into the cell such that charge, Na+, and K+ are all conserved. When all ion concentrations are dynamic, IC1 and IC3 lead to the same steady state, but IC2 results in a different steady state (figure 9a). If only intracellular ion concentrations are dynamic, however, IC1 and IC2 result in identical steady states, but IC3 leads to a different steady state (figure 9b). Finally, keeping all ion concentrations constant leads to different steady states for all initial conditions (figure 9c).
Figure 9.
Effect of initial conditions on steady-state behaviour. (a) Dynamic ion concentrations; (b) Dynamic intracellular ion concentrations; (c) Constant ion concentrations. The models were paced at 1 Hz for 30 min using a conservative stimulus current. [MgATP] = 6.95 mM, [MgADP] = 0.035 mM, [Pi] = 0.3971 mM, pH = 7.095, T = 310 K. Definitions: Vdia, diastolic membrane potential; APD, action potential duration at 90% repolarization. (Online version in colour.)
These results demonstrate that the summed amount for each conserved moiety and/or chemostat value determines the steady-state behaviour of cardiac action potential models. To investigate this further, we calculated the values for conserved moieties and chemostats that resulted from each initial condition (table 2; differences from IC1 indicated in italics). For two sets of initial conditions to achieve identical steady states, all conserved moieties and chemostats must have the same value. Thus, under dynamic ion concentrations (figure 9a), IC3 results in the same steady state as IC1 because all conserved moieties have been preserved (table 2), whereas IC2 causes a different steady state because the K+ and Na+ conserved moieties take on different values. Similarly, when only intracellular ion concentrations are dynamic, IC2 preserves the value of all conserved moieties and chemostats, but IC3 changes the values of the chemostats corresponding to extracellular Na+ and K+ concentrations (table 2), hence the different steady state. When all ion concentrations were held constant, changes in the chemostat values (table 2) were associated with different steady states for all three initial conditions (figure 9c).
Table 2.
The values of conserved moieties and chemostats under different initial conditions. All values are in fmol. Chemostats are indicated with (cs). Values different from IC1 are shown in italics.
| lvalue |
|||
|---|---|---|---|
| moiety/chemostat | IC1 | IC2 | IC3 |
| dynamic ion concentrations (A) | |||
| K+ | 5538.1 | 5500.1 | 5538.1 |
| Na+ | 1105.6 | 1143.6 | 1105.6 |
| charge | −5882.2 | −5882.2 | −5882.2 |
| dynamic intracellular ion concentrations (B) | |||
| K+e (cs) | 27.98 | 27.98 | 38.35 |
| Na+e (cs) | 5510 | 5510 | 715.12 |
| charge | −5882.2 | −5882.2 | −5882.2 |
| constant ion concentrations (C) | |||
| K+e (cs) | 27.98 | 27.98 | 38.35 |
| Na+e (cs) | 725.48 | 725.48 | 715.12 |
| K+i (cs) | 5510 | 5472 | 5500 |
| Na+i (cs) | 380 | 418 | 390.36 |
4. Discussion
In this study, we developed a bond graph model of the cardiac action potential with the aim of resolving the issues of drift and non-unique steady states. Analysis using conserved moieties enabled the discovery of all conservation laws within the model, including the charge conservation law neglected by many existing studies. In addition to the conservation of charge law from previous studies [10,52,53], we found conservation laws corresponding to ions, states of Markov models of channels and transporters, and buffers, demonstrating the comprehensiveness of our approach. Because the bond graph approach requires species and processes to be resolved in biophysical detail, calculation of conservation laws is more straightforward than working purely with the mathematical equations of a model. Two key advantages of our approach over existing analyses are that it reveals all conservation laws in a comprehensive and systematic manner, and that it is general for all models of the cardiac action potential that can be represented as bond graphs. As a result, our approach can be scaled to more complex cardiac models without manual examination of the equations of a model to identify each individual conservation law, and the nontrivial charge conservation law will be accounted for when it appears as a conserved moiety. When simulated over long periods with a non-conservative stimulus, our bond graph model displayed solution drift, but it became resistant to drift when ion concentrations were held constant, demonstrating that changes in the value of a conserved charge moiety drive model drift. We also found that two sets of initial conditions can lead to different steady states if the values of their corresponding conserved moieties and chemostats are different, suggesting a strong link between conserved moieties and the steady-state limit cycles of cardiac action potential models. To demonstrate that our approach is general, we tested how the selection of chemostats (i.e. fixed concentrations) influenced drift and steady states by using variants of our model that were representative of existing models in the literature. Our approach highlights the subtle but relevant observation that holding ion concentrations constant changes the conserved moieties of the model, which in turn has an effect on the susceptibility of a model to drift and non-unique steady states. Because chemostats represent connections between a system and its external environment, they are essential to coupling together biological processes [23]. The coupling of biological processes generally causes changes in the conservation laws of a system which may be difficult to capture through observation. Our approach using bond graphs provides a systematic method of dealing with changes to conservation laws as a result of coupling models together.
(a). Drift
When paced with a non-conservative stimulus, variants of the model with a charge conservation law (A and B) underwent drift (figure 8a,b) consistent with previous studies on the Luo–Rudy model [10,11]. Our observations also explain why models with constant ion concentrations (similar to variant C) are more likely to be resistant to drift [10]. By observing changes in the charge conserved moiety, the bond graph approach attributes drift to regular perturbations in charge that cannot be restored due to the presence of a conservation law. Whereas previous analyses relied solely on intuition to derive a conservation law corresponding to charge [10,11], we note that our approach automatically derives this conservation law, and can also detect other conservation laws that may be relevant for drift.
We note that in order to avoid drift, all conserved moieties (and not only the conserved moiety corresponding to charge) must be preserved by the stimulus current. However, in the examples explored in this study, we found that the stimulus currents preserved the value of all conserved moieties apart from charge, and therefore were not plotted. While intuition may suggest that modelling a stimulus current with K+ would cause an accumulation of intracellular K+, the K+ is passively transported back through K+ channels. Furthermore, the total amount of K+ (the relevant conserved moiety) remains constant because the loss of K+ from the extracellular side is offset by accumulation on the intracellular side. By contrast, for charge conservation in variants A and B, the model contains no mechanism to reverse the change in charge difference caused by the non-conservative current, thus drift results.
As demonstrated, the bond graph method requires construction of a stoichiometric matrix, providing a simple approach to check whether a stimulus current will cause drift. While it is common practice to use K+ as the charge carrier for stimulus currents, it is likely that multiple species contribute to the current [8,10]. Thus, the automated approach suggested here is well suited for checking whether more complex stimulus currents satisfy conservation of charge, as well as other conservation laws within the model. It should be noted, however, that while a model satisfying Gvs = 0 will not drift due to violating conservation laws, drift may still occur due to an imbalance of currents throughout the action potential, for instance, in the absence of Na+/K+ ATPase, the ionic gradients would gradually disappear in a model with dynamic ion concentrations.
Finally, we believe that this analysis provides a link between the issues of drift and steady states. Our models show that drift due to a non-conservative stimulus current can be attributed to changes in the value of the charge conserved moiety with every stimulus, and accordingly the steady state of the model changes. Model drift then occurs as the solution continually chases a moving steady state.
(b). Effects of initial conditions on steady states
We also found that initial conditions of cardiac action potential models change their steady states through the values of chemostats and conserved moieties (figure 9 and table 2). Accordingly, the same perturbation to initial conditions can have different effects on the steady state depending on which species are held constant. Therefore, in addition to ensuring that the concentration of ions is physiological, care should be taken to correctly initialize each state of buffers and Markov models of ion channels and ion transporters, as they may contain a significant fraction of total ion abundance. For example, Ca2+ buffers and SERCA can sequester a significant amount of Ca2+ and they should be initialized with the correct amount of bound Ca2+ when multi-state models are used [54]. We note that the difficulty of manually deriving conservation laws increases exponentially as models of cardiac electrophysiology become more complex, and we believe that our approach extends on existing analyses [10,11] to provide a general method for assessing steady-state behaviour by comparing the values of conserved moieties and chemostats that result from each initial condition.
In the field of biochemical network analysis, there is a well-established dependence of quiescent steady states on conserved moieties, and numerous mathematical techniques for assessing the uniqueness and stability of these steady states have been developed [55,56]. However, the influence of conserved moieties on limit cycles in an oscillating system that is regularly stimulated has yet to be investigated. Our results hint at similarities between these two fields, and while we only tested the uniqueness of steady states using relatively small perturbations to the initial conditions, it is possible that a set of conserved moieties may have multiple steady states, and greater perturbations may lead to other limit cycles.
(c). The ‘differential’ and ‘algebraic’ methods
The discovery of conservation principles in cardiac electrophysiology has led to a debate over whether to use the differential or algebraic methods of simulation [7,10,11,52,53]. The differential method is the calculation of membrane voltage by integrating total current, and the algebraic method is the calculation of membrane voltage using an algebraic relationship derived from charge conservation. We chose the differential method over the algebraic method because it better supports model reuse and modularity - in particular it is easier to modify the equations to select different species as chemostats, and to combine equations when two models are coupled. We note, however, that the algebraic method may reduce computational complexity [10,20]. In bond graph modelling, the algebraic method can be implemented by using conserved moieties to turn the system of ODEs into an index-0 differential algebraic equation (DAE) (eqn 3.48 of [20]). This method generalizes existing algebraic methods to reduce the system of differential equations by using all conserved moieties and not just the conserved charge moiety. While we did not use the algebraic approach, we emphasize that the choice of method relates to numerical approaches for model simulation rather than the underlying physics of the system [10]. Therefore, the differential and algebraic methods are equivalent in conservative systems provided that the initial conditions and values of conserved moieties are consistent.
(d). Integration into whole-cell models
Our bond graph model of the cardiac action potential is the first step towards a fully integrated whole-cell bond graph model of a cardiomyocyte that couples electrophysiology, signalling, metabolism and mechanics. As energy drives all biological processes, and energy supply can be limited under certain pathophysiological states, it is of interest to examine how cardiomyocytes allocate their energy, and also to estimate the efficiency of processes that are essential for cardiomyocyte function [57,58]. Modelling studies for the energetic regulation of a cardiac cell exist across the literature [58], but while some components used in these models are thermodynamically consistent [59,60], existing whole-cell models are neither energy-based nor thermodynamically consistent throughout the entire model. Furthermore, because existing experimental and modelling studies use ATP consumption as a proxy for energy consumption, they can only estimate the energy consumption of major energy sinks: the Na+/K+ ATPase, SERCA and crossbridge cycling [58,61]. A bond graph approach may thus provide more detailed insights into how a cardiac cell uses energy downstream of ATP hydrolysis processes, and help to identify energy-consuming processes. Because the bond graph approach is energy-based, it not only provides the necessary constraints to develop a thermodynamically consistent model, but also allows us to directly assess energy consumption of the model (in Joules). We found that when normalized against membrane area, the cardiac action potential consumes approximately 76% more energy than an action potential in the axon of a giant squid. To the authors' knowledge, this is the first account of energy consumed by electrochemical processes during the cardiac action potential.
(e). Limitations
A limitation of our approach is that the physical constraints imposed by the bond graph approach prevent the direct translation of existing models of cardiac electrophysiology into bond graphs. This points at thermodynamic issues that exist within existing models of cardiac electrophysiology; while many models contain components that are thermodynamically consistent, the authors are not aware of any models that are entirely thermodynamically consistent. Nonetheless, the inability to perfectly replicate properties of existing models as bond graphs impedes the creation of bond graph models of cardiac electrophysiology, as it requires new models to be built from the bottom up with existing equations only used as guides for parameter fitting. As a result of this limitation, our bond graph model represents only a subset of the ion transport processes within a cardiomyocyte, and only approximates the behaviour described in existing models. While our model is able to reproduce many essential features of the action potential, it is unlikely to be physiologically realistic under conditions different to those used for our fitting process. Thus in future studies, it would be interesting to explore the use of more complex bond graph components to generate more physiologically realistic models. We chose to use a restricted set of components and constitutive equations to keep the model simple, although the bond graph framework is flexible enough to account for a wider range of equations provided that they are thermodynamically consistent. While many ion channels (including those for INa, IK1 and IKp in the Luo and Rudy model) are modelled using linear I-V relationships, the choice of I-V relationship is generally chosen on the basis of providing an empirical fit to data rather than as a result of physical principles. Thus, a more ideal approach would be to use nonlinear bond graph components derived from physical principles, and fit their parameters directly to experimental data. Additionally, empirical equations for gating transition parameters are generally not expressed in a thermodynamic framework, and are therefore impossible to replicate exactly with a bond graph model. We used a simple gating mechanism to reduce equation complexity while maintaining thermodynamic consistency; however, the quality of fit could be improved by using more complicated gating mechanisms, or other thermodynamically consistent constitutive equations.
Because of physical restrictions imposed by the bond graph framework, we were forced to model ion channels and transporters using Markov states to faithfully represent their underlying physics. However, this produced a model that had numerous states compared to the number of biological processes. While it is reassuring to find that our method of identifying conserved moieties remained robust despite this complexity, simulation of the model was computationally expensive. For the purpose of integrating this action potential model into a larger whole-cell model, it would be useful to have simple model components that reduce computational cost. While current methods for reducing biochemical models in the bond graph framework are not advanced enough to apply to the biological components in this study, we note that bond graphs provide a useful foundation for applying model simplification while ensuring that thermodynamic consistency is maintained [20].
We also decided to limit the transport processes included in our model to those considered essential for producing a cardiac action potential, while maintaining a limit cycle using dynamic ion concentrations. Our bond graph model omitted many ionic currents due to their small amplitudes; however, these channels may have greater contributions under conditions which vary from those tested here. Thus, an obvious extension of this work would be the integration of other electrogenic processes within the cardiac membrane. It would be interesting to investigate whether coupling other models requires further tuning of parameters [62], and whether the presence of physical bond graph parameters changes this process. A related limitation is that our model does not account for ion concentrations such as H+ and Cl−, as well as pH buffers [5]. While including these ions and their transporters would lead to a more accurate model, the omission of these ions did not cause inconsistencies in the conservation laws described in this study. These ions were assumed to be membrane impermeable in our model, and thus their constant contributions to the membrane potential were accounted for in the initial value of the charge conserved moiety. Similar to how calcium and its buffers were accounted for in our current approach (table 1), our bond graph approach is sufficiently general to account for other ions and their buffers.
When formulating the structure and parameters for a bond graph model of the cardiac action potential (or most other biological processes), it is possible to either fit against existing mathematical models or the underlying experimental measurements. For all processes in this study excluding the NCX, we developed our bond graph model to reproduce the behaviour of an existing model, in an attempt to re-use existing knowledge about these processes. This approach poses constraints on the bond graph structure used, especially for gating structure. Therefore, it would be interesting to develop an approach that assesses bond graph structures as well as bond graph parameters, based on their fits to data [62]. Such an approach may provide a better fit to the data, and uncover insights into the physical mechanisms of ion channels.
5. Conclusion
In this study, we have developed a bond graph model of the cardiac action potential and used this to explore the issues of drift and non-unique steady states. We demonstrate that the analysis of conserved moieties generalizes the concept of charge conservation used in earlier studies, and found that changes in conserved moieties can explain drift as well as changes in steady-state behaviour. Importantly, holding ion concentrations constant can have significant consequences on both drift and steady states as they change the conserved moieties in the model. Our approach to resolving drift and non-unique steady states is sufficiently general that it can be applied to any bond graph model of the cardiac action potential model. We hope that the bond graph approach outlined here will prove useful for the development of future cardiac electrophysiology models, and eventually whole-cell models of the cardiomyocyte.
Supplementary Material
Data accessibility
The code associated with this study is available from GitHub (https://github.com/uomsystemsbiology/bond_graph_cardiac_AP), and archived on Zenodo (https://doi.org/10.5281/zenodo.1172205) [63]. The repository contains Matlab (The MathWorks, Natick, MA) code that generates the figures, CellML code containing parameters, initial conditions and equations of the model, and full details of the bond graph structure.
Author's contributions
M.P., P.J.G., J.C. and E.J.C. developed the theory. M.P. performed the research. K.T. provided conceptual advice and helped interpret the results. All authors contributed to the text of the manuscript and gave final approval for publication.
Competing interests
We have no competing interests.
Funding
M.P. acknowledges the financial support provided by an Australian Government Research Training Program Scholarship. P.J.G. thanks the Melbourne School of Engineering for its support via a Professorial Fellowship. K.T. is supported by the Heart Foundation of New Zealand (Research Fellowship 1692) and the Marsden Fund Council from Government funding, managed by Royal Society Te Aprangi (Marsden Fast-Start UOA1703. This research was in part conducted and funded by the Australian Research Council Discovery Projects funding scheme (project DP170101358).
References
- 1.Luo CH, Rudy Y. 1994. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ. Res. 74, 1071–1096. (doi:10.1161/01.RES.74.6.1071) [DOI] [PubMed] [Google Scholar]
- 2.Luo CH, Rudy Y. 1994. A dynamic model of the cardiac ventricular action potential. II. Afterdepolarizations, triggered activity, and potentiation. Circ. Res. 74, 1097–1113. (doi:10.1161/01.RES.74.6.1097) [DOI] [PubMed] [Google Scholar]
- 3.Faber GM, Rudy Y. 2000. Action potential and contractility changes in [Na+]i overloaded cardiac myocytes: a simulation study. Biophys. J. 78, 2392–2404. (doi:10.1016/S0006-3495(00)76783-X) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Terkildsen JR, Crampin EJ, Smith NP. 2007. The balance between inactivation and activation of the Na+-K+ pump underlies the triphasic accumulation of extracellular K+ during myocardial ischemia. Am. J. Physiol. - Heart C. 293, H3036–H3045. (doi:10.1152/ajpheart.00771.2007) [DOI] [PubMed] [Google Scholar]
- 5.Crampin EJ, Smith NP. 2006. A dynamic model of excitation-contraction coupling during acidosis in cardiac ventricular myocytes. Biophys. J. 90, 3074–3090. (doi:10.1529/biophysj.105.070557) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Guan S, Lu Q, Huang K. 1997. A discussion about the DiFrancesco–Noble model. J. Theor. Biol. 189, 27–32. (doi:10.1006/jtbi.1997.0486) [DOI] [PubMed] [Google Scholar]
- 7.Fraser JA, Huang CLH. 2007. Quantitative techniques for steady-state calculation and dynamic integrated modelling of membrane potential and intracellular ion concentrations. Prog. Biophys. Mol. Biol. 94, 336–372. (doi:10.1016/j.pbiomolbio.2006.10.001) [DOI] [PubMed] [Google Scholar]
- 8.Kneller J, Ramirez RJ, Chartier D, Courtemanche M, Nattel S. 2002. Time-dependent transients in an ionically based mathematical model of the canine atrial action potential. Am. J. Physiol. - Heart Circulat. Physiol. 282, H1437–H1451. (doi:10.1152/ajpheart.00489.2001) [DOI] [PubMed] [Google Scholar]
- 9.DiFrancesco D, Noble D. 1985. A model of cardiac electrical activity incorporating ionic pumps and concentration changes. Phil. Trans. R. Soc. Lond. B 307, 353–398. (doi:10.1098/rstb.1985.0001) [DOI] [PubMed] [Google Scholar]
- 10.Hund TJ, Kucera JP, Otani NF, Rudy Y. 2001. Ionic charge conservation and long-term steady state in the Luo—Rudy dynamic cell model. Biophys. J. 81, 3324–3331. (doi:10.1016/S0006-3495(01)75965-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Livshitz L, Rudy Y. 2009. Uniqueness and stability of action potential models during rest, pacing, and conduction using problem-solving environment. Biophys. J. 97, 1265–1276. (doi:10.1016/j.bpj.2009.05.062) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Aslanidi OV, Boyett MR, Dobrzynski H, Li J, Zhang H. 2009. Mechanisms of transition from normal to reentrant electrical activity in a model of rabbit atrial tissue: interaction of tissue heterogeneity and anisotropy. Biophys. J. 96, 798–817. (doi:10.1016/j.bpj.2008.09.057) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Carro J, Rodríguez JF, Laguna P, Pueyo E. 2011. A human ventricular cell model for investigation of cardiac arrhythmias under hyperkalaemic conditions. Phil. Trans. R. Soc. A 369, 4205–4232. (doi:10.1098/rsta.2011.0127) [DOI] [PubMed] [Google Scholar]
- 14.Grandi E, Pasqualini FS, Bers DM. 2010. A novel computational model of the human ventricular action potential and Ca transient. J. Mol. Cell. Cardiol. 48, 112–121. (doi:10.1016/j.yjmcc.2009.09.019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sager PT, Gintant G, Turner JR, Pettit S, Stockbridge N. 2014. Rechanneling the cardiac proarrhythmia safety paradigm: a meeting report from the Cardiac Safety Research Consortium. Am. Heart J. 167, 292–300. (doi:10.1016/j.ahj.2013.11.004) [DOI] [PubMed] [Google Scholar]
- 16.Colatsky T, Fermini B, Gintant G, Pierson JB, Sager P, Sekino Y, Strauss DG, Stockbridge N. 2016. The Comprehensive in Vitro Proarrhythmia Assay (CiPA) initiative—Update on progress. J. Pharmacol. Toxicol. 81, 15–20. (doi:10.1016/j.vascn.2016.06.002) [DOI] [PubMed] [Google Scholar]
- 17.Paynter HM. 1961. Analysis and design of engineering systems. Cambridge, MA: MIT Press. [Google Scholar]
- 18.Borutzky W, Dauphin-Tanguy G, Thoma JU. 1995. Advances in bond graph modelling: theory, software, applications. Math. Comput. Simulat. 39, 465–475. (doi:10.1016/0378-4754(95)00106-6) [Google Scholar]
- 19.Oster GF, Perelson AS, Katchalsky A. 1973. Network thermodynamics: dynamic modelling of biophysical systems. Q. Rev. Biophys. 6, 1–134. (doi:10.1017/S0033583500000081) [DOI] [PubMed] [Google Scholar]
- 20.Gawthrop PJ, Crampin EJ. 2014. Energy-based analysis of biochemical cycles using bond graphs. Proc. R. Soc. Lond. A 470, 20140459 (doi:10.1098/rspa.2014.0459) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gawthrop PJ, Siekmann I, Kameneva T, Saha S, Ibbotson MR, Crampin EJ. 2017. Bond graph modelling of chemoelectrical energy transduction. IET Syst. Biol. 11, 127–138. (doi:10.1049/iet-syb.2017.0006) [Google Scholar]
- 22.Omholt SW, Hunter PJ. 2016. The Human Physiome: a necessary key for the creative destruction of medicine. Interface Focus 6, 20160003 (doi:10.1098/rsfs.2016.0003) [Google Scholar]
- 23.Gawthrop PJ, Cursons J, Crampin EJ. 2015. Hierarchical bond graph modelling of biochemical networks. Proc. R. Soc. A 471, 20150642 (doi:10.1098/rspa.2015.0642) [Google Scholar]
- 24.Gawthrop PJ. 2017. Bond graph modeling of chemiosmotic biomolecular energy transduction. IEEE Trans. Nanobiosci. 16, 177–188. (doi:10.1109/TNB.2017.2674683) [DOI] [PubMed] [Google Scholar]
- 25.Gawthrop PJ, Crampin EJ. 2017. Energy-based analysis of biomolecular pathways. Proc. R. Soc. A 473, 20160825 (doi:10.1098/rspa.2016.0825) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Beard DA, Liang Sd, Qian H. 2002. Energy balance for analysis of complex metabolic networks. Biophys. J. 83, 79–86. (doi:10.1016/S0006-3495(02)75150-3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Beard DA, Babson E, Curtis E, Qian H. 2004. Thermodynamic constraints for biochemical networks. J. Theor. Biol. 228, 327–333. (doi:10.1016/j.jtbi.2004.01.008) [DOI] [PubMed] [Google Scholar]
- 28.van der Schaft A, Rao S, Jayawardhana B. 2013. On the mathematical structure of balanced chemical reaction networks governed by mass action kinetics. SIAM J. Appl. Math. 73, 953–973. (doi:10.1137/11085431X) [Google Scholar]
- 29.Haraldsdóttir HS, Fleming RMT. 2016. Identification of conserved moieties in metabolic networks by graph theoretical analysis of atom transition networks. PLoS Comput. Biol. 12, e1004999 (doi:10.1371/journal.pcbi.1004999) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pan M, Gawthrop PJ, Cursons J, Tran K, Crampin EJ.2017. The cardiac Na+/K+ ATPase: an updated, thermodynamically consistent model. (http://arxiv.org/abs/1711.00989. )
- 31.Kimura J, Miyamae S, Noma A. 1987. Identification of sodium-calcium exchange current in single ventricular cells of guinea-pig. J. Physiol. (Lond.) 384, 199–222. (doi:10.1113/jphysiol.1987.sp016450) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Beuckelmann DJ, Wier WG. 1989. Sodium-calcium exchange in guinea-pig cardiac cells: exchange current and changes in intracellular Ca2+. J. Physiol. (Lond.) 414, 499–520. (doi:10.1113/jphysiol.1989.sp017700) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gawthrop P, Smith L. 1996. Metamodelling: for bond graphs and dynamic systems. Prentice Hall International Series in Systems and Control Engineering London, New York: Prentice Hall. [Google Scholar]
- 34.Borutzky W. 2010. Bond graph methodology. Berlin, Germany: Springer. [Google Scholar]
- 35.Gawthrop P, Bevan G. 2007. Bond-graph modeling. IEEE Control Syst. 27, 24–45. (doi:10.1109/MCS.2007.338279) [Google Scholar]
- 36.Gawthrop PJ. 2017. Bond-graph modelling and causal analysis of biomolecular systems. In Bond graphs for modelling, control and fault diagnosis of engineering systems (ed. W Borutzky), pp. 587–623. Cham, Switzerland: Springer (doi:10.1007/978-3-319-47434-2_16)
- 37.Atkins PW, De Paula J. 2006. Physical chemistry for the life sciences. Oxford, UK/New York, NY: Oxford University Press/W.H. Freeman. [Google Scholar]
- 38.Thoma J, Bouamama BO. 2000. Modelling and simulation in thermal and chemical engineering. Berlin, Germany: Springer. [Google Scholar]
- 39.Polettini M, Esposito M. 2014. Irreversible thermodynamics of open chemical networks. I. Emergent cycles and broken conservation laws. J. Chem. Phys. 141, 024117 (doi:10.1063/1.4886396) [DOI] [PubMed] [Google Scholar]
- 40.Keener J, Sneyd J. 2009. Mathematical physiology. Interdisciplinary Applied Mathematics, vol. 8/1. New York, NY: Springer.
- 41.Rudy Y, Silva JR. 2006. Computational biology in the study of cardiac ion channels and cell electrophysiology. Q. Rev. Biophys. 39, 57–116. (doi:10.1017/S0033583506004227) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Fink M, Noble D. 2009. Markov models for ion channels: versatility versus identifiability and speed. Phil. Trans. R. Soc. A 367, 2161–2179. (doi:10.1098/rsta.2008.0301) [DOI] [PubMed] [Google Scholar]
- 43.Hodgkin AL, Huxley AF. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (Lond.) 117, 500–544. (doi:10.1113/jphysiol.1952.sp004764) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Liebermeister W, Uhlendorf J, Klipp E. 2010. Modular rate laws for enzymatic reactions: thermodynamics, elasticities and implementation. Method. Biochem. Anal. 26, 1528–1534. (doi:10.1093/bioinformatics/btq141) [DOI] [PubMed] [Google Scholar]
- 45.Palsson B. 2006. Systems biology: properties of reconstructed networks. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 46.Klipp E. 2009. Systems biology: a textbook. New York, NY: Wiley-VCH. [Google Scholar]
- 47.Anton H, Rorres C. 2014. Elementary linear algebra: applications version. Hoboken, NJ: John Wiley & Sons Inc. [Google Scholar]
- 48.Schuster S, Hilgetag C. 1995. What information about the conserved-moiety structure of chemical reaction systems can be derived from their stoichiometry? J. Phys. Chem. 99, 8017–8023. (doi:10.1021/j100020a026) [Google Scholar]
- 49.Schuster S, Höfer T. 1991. Determining all extreme semi-positive conservation relations in chemical reaction systems: a test criterion for conservativity. J. Chem. Soc. Faraday Trans. 87, 2561–2566. (doi:10.1039/FT9918702561) [Google Scholar]
- 50.Noble D, Rudy Y. 2001. Models of cardiac ventricular action potentials: iterative interaction between experiment and simulation. Phil. Trans. R. Soc. Lond. A 359, 1127–1142. (doi:10.1098/rsta.2001.0820) [Google Scholar]
- 51.Luo CH, Rudy Y. 1991. A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction. Circ. Res. 68, 1501–1526. (doi:10.1161/01.RES.68.6.1501) [DOI] [PubMed] [Google Scholar]
- 52.Varghese A, Sell GR. 1997. A conservation principle and its effect on the formulation of Na–Ca exchanger current in cardiac cells. J. Theor. Biol. 189, 33–40. (doi:10.1006/jtbi.1997.0487) [DOI] [PubMed] [Google Scholar]
- 53.Endresen LP, Hall K, Høye JS, Myrheim J. 2000. A theory for the membrane potential of living cells. Eur. Biophys. J. 29, 90–103. (doi:10.1007/s002490050254) [DOI] [PubMed] [Google Scholar]
- 54.Higgins ER, Cannell MB, Sneyd J. 2006. A buffering SERCA pump in models of calcium dynamics. Biophys. J. 91, 151–163. (doi:10.1529/biophysj.105.075747) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Gross E, Harrington HA, Rosen Z, Sturmfels B. 2016. Algebraic systems biology: a case study for the Wnt pathway. B. Math. Biol. 78, 21–51. (doi:10.1007/s11538-015-0125-1) [DOI] [PubMed] [Google Scholar]
- 56.Feliu E, Wiuf C. 2012. Variable elimination in chemical reaction networks with mass-action kinetics. SIAM J. Appl. Math. 72, 959–981. (doi:10.1137/110847305) [DOI] [PubMed] [Google Scholar]
- 57.Neubauer S. 2007. The failing heart—an engine out of fuel. Eng. J. Med. 356, 1140–1151. (doi:10.1056/NEJMra063052) [DOI] [PubMed] [Google Scholar]
- 58.Tran K, Loiselle DS, Crampin EJ. 2015. Regulation of cardiac cellular bioenergetics: mechanisms and consequences. Physiol. Rep. 3, e12464 (doi:10.14814/phy2.12464) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Tran K, Smith NP, Loiselle DS, Crampin EJ. 2009. A thermodynamic model of the cardiac sarcoplasmic/endoplasmic Ca2+ (SERCA) pump. Biophys. J. 96, 2029–2042. (doi:10.1016/j.bpj.2008.11.045) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Smith NP, Crampin EJ. 2004. Development of models of active ion transport for whole-cell modelling: cardiac sodium–potassium pump as a case study. Prog. Biophys. Mol. Biol. 85, 387–405. (doi:10.1016/j.pbiomolbio.2004.01.010) [DOI] [PubMed] [Google Scholar]
- 61.Schramm M, Klieber HG, Daut J. 1994. The energy expenditure of actomyosin-ATPase, Ca2+-ATPase and Na+, K+-ATPase in guinea-pig cardiac ventricular muscle. J. Physiol. 481, 647–662. (doi:10.1113/jphysiol.1994.sp020471) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Babtie AC, Stumpf MPH. 2017. How to deal with parameters for whole-cell modelling. J. R. Soc. Interface 14, 20170237 (doi:10.1098/rsif.2017.0237) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Pan M, Gawthrop PJ, Tran K, Cursons J, Crampin EJ. 2018. Supporting code for ‘Bond graph modelling of the cardiac action potential: implications for drift and non-unique steady states’ Zenodo. (doi:10.5281/zenodo.1172205) [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Pan M, Gawthrop PJ, Tran K, Cursons J, Crampin EJ. 2018. Supporting code for ‘Bond graph modelling of the cardiac action potential: implications for drift and non-unique steady states’ Zenodo. (doi:10.5281/zenodo.1172205) [DOI] [PMC free article] [PubMed]
Supplementary Materials
Data Availability Statement
The code associated with this study is available from GitHub (https://github.com/uomsystemsbiology/bond_graph_cardiac_AP), and archived on Zenodo (https://doi.org/10.5281/zenodo.1172205) [63]. The repository contains Matlab (The MathWorks, Natick, MA) code that generates the figures, CellML code containing parameters, initial conditions and equations of the model, and full details of the bond graph structure.