Estimating SNP-Based Heritability and Genetic Correlation in Case-Control Studies Directly and with Summary Statistics

Abstract

Methods that estimate SNP-based heritability and genetic correlations from genome-wide association studies have proven to be powerful tools for investigating the genetic architecture of common diseases and exposing unexpected relationships between disorders. Many relevant studies employ a case-control design, yet most methods are primarily geared toward analyzing quantitative traits. Here we investigate the validity of three common methods for estimating SNP-based heritability and genetic correlation between diseases. We find that the phenotype-correlation-genotype-correlation (PCGC) approach is the only method that can estimate both quantities accurately in the presence of important non-genetic risk factors, such as age and sex. We extend PCGC to work with arbitrary genetic architectures and with summary statistics that take the case-control sampling into account, and we demonstrate that our new method, PCGC-s, accurately estimates both SNP-based heritability and genetic correlations and can be applied to large datasets without requiring individual-level genotypic or phenotypic information. Finally, we use PCGC-s to estimate the genetic correlation between schizophrenia and bipolar disorder and demonstrate that previous estimates are biased, partially due to incorrect handling of sex as a strong risk factor.

Introduction

Much of the theory underlying methods for estimating two key measures of disease genetic architecture, SNP-based heritability and genetic correlation, was designed for cohort studies of quantitative phenotypes. Consequently, when applied to studies of categorical traits, these methods may contain unacknowledged biases that may affect estimation accuracy.

The problem of accurately estimating SNP-based heritability and genetic correlation is usually translated into questions about variance and covariance components in properly defined mathematical models. A commonly held misconception states that variance components can be accurately calculated in case-control studies by virtue of applying a correction factor to results derived under a quantitative trait framework.^{1, 2, 3, 4} However, this is not true when risk factors (including risk variants) exert a strong influence on disease risk. In this paper we examine the validity of approaches for estimating heritability, genetic covariance, and correlation (covariance standardized to a [−1, 1] scale) in case-control studies of disease.

Broadly speaking, there are three common approaches for carrying out these tasks. The first is based on restricted maximum likelihood estimation (REML) in the linear mixed model (LMM)⁵ framework and is implemented in some widely used tools.^{6, 7, 8} This approach has been extensively applied to heritability estimation^{1, 5, 7} and to genetic correlation estimation.^{7, 9, 10, 11}

The second approach is based on regression of phenotype correlations on genotype correlations and relies on less restrictive assumptions than the LMM approach. This approach was originally designed for quantitative phenotypes, in which case it is known as Haseman-Elston (HE) regression.^{12, 13} It has recently been adapted for case-control studies, in which case it is called PCGC.^{14, 15} A common misconception states that PCGC is the same as HE regression (up to a scaling factor), but this equivalence holds only in the absence of covariates.¹⁴ Rather than being an extension of HE regression, PCGC was carefully derived from first principles to apply to all relevant situations in case-control studies. In this paper we extend PCGC to also estimate genetic correlation and to accommodate arbitrary genetic architectures.

The third approach is the family of linkage disequilibrium score regression (LDSC) methods, which estimate heritability and genetic correlation while accounting for LD,^{2, 16} and have recently been applied to numerous large-scale studies.^{17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33} LDSC is attractive because it requires only publicly available summary statistics from genetic studies, thereby avoiding privacy and logistical concerns.³⁴ Other summary-statistics-based methods have also been proposed recently but we focus on LDSC, as alternative methods cannot be applied in the presence of LD³ or are not directly designed for categorical phenotypes.^{4, 35, 36}

Here we examine all three approaches under a common set of assumptions that is shared by all of them. We demonstrate that even when these assumptions hold, LDSC and REML yield biased estimates in the presence of covariates representing major risk factors such as sex and age, due to incorrect modeling of case-control ascertainment. In contrast, PCGC remains unbiased under all settings. We further develop a new version of PCGC, called PCGC-s, that can work with summary statistics that explicitly take the case-control sampling into account.

We demonstrate the value of PCGC-s by investigating the genetic correlation between schizophrenia and bipolar disorder and between type 1 diabetes and coronary artery disease. We demonstrate that the estimates of both quantities are severely biased under alternative methods, partially due to incorrect handling of sex—an important risk factor. Finally, we provide best practice recommendations depending on the available data and the trait characteristics.

Material and Methods

Underlying Mixed Effects Model

We adopt the theoretical framework of the liability threshold model,^{37, 38} which is the same model assumed by REML¹ and LDSC² for analysis of case-control studies. This model assumes that every individual i has a latent normally distributed liability value for trait t, $a_t^i$, such that case subjects of trait t are individuals whose liability exceeds a given cutoff.

We additionally assume that the liability of trait t can be decomposed into three terms corresponding to a covariates effect $q_t^i$, a genetic effect $g_t^i$, and an environmental effect $e_t^i$, $a_t^i=q_t^i+g_t^i+e_t^i$, such that the vectors of covariate effects ${\mathit{q}}_t={\left[q_t^1,\dots ,q_t^n\right]}^T$, of genetic effects ${\mathit{g}}_t={\left[g_t^1,\dots ,g_t^n\right]}^T$, and of environmental effects ${\mathit{e}}_t={\left[e_t^1,\dots ,e_t^n\right]}^T$ are given by:

$${\mathit{q}}_t={\mathit{C}}_t{\mathit{\beta }}_t$$

$${\mathit{g}}_t\sim \mathcal{N}\left(0;{\sigma }_{gt}^2{\mathit{G}}_t\right)$$

$${\mathit{e}}_t\sim \mathcal{N}\left(0;\left(1-{\sigma }_{gt}^2\right)\mathit{I}\right).$$

Here, ${\mathit{C}}_t$ is a design matrix of covariates, ${\mathit{\beta }}_t$ is a column vector of fixed effects, ${\mathit{G}}_t$ is a matrix of genetic similarity coefficients (defined below), ${\sigma }_{gt}^2$ is a genetic variance parameter, and $\mathit{I}$ is the identity matrix. The matrix ${\mathit{G}}_t$ is typically given by ${\mathit{G}}_t={\mathit{X}}_t\mathit{W}{\mathit{X}}_t^T,$ where ${\mathit{X}}_t$ is an $n\times m$ matrix of m standardized single-nucleotide polymorphisms (SNPs), and $\mathit{W}$ is an $m\times m$ diagonal weighting matrix, which assigns different weights to different SNPs. This definition can accommodate any linear genetic architecture; it includes the standard model used by common REML software packages^{6, 7} and by LDSC^{2, 16} under the special case $\mathit{W}=\left(1/m\right)\mathit{I}$. However, it can also accommodate minor allele frequency (MAF)-dependent and LD-dependent architectures,^{8, 39} which correspond to a suitable choice of $\mathit{W}$ (Supplemental Methods).

Under these assumptions, every individual i has an observed affection status indicator for trait t, $y_t^i$, such that $y_t^i=1$ if and only if $a_t^i>{\tau }_t$, where ${\tau }_t={\text{Φ}}^{-1}\left(1-K_t\right)+\text{E}{\left[{\mathit{C}}_t\right]}^T{\mathit{\beta }}_t$ is the affection cutoff for trait t with prevalence $K_t$, and where ${\text{Φ}}^{-1}(\cdot )$ is the inverse cumulative standard normal density.

For a pair of traits t₁, t₂, the concatenated liabilities vector follows a multivariate normal distribution,

$$\left[\begin{array}{c}{\mathit{a}}_{t_1}\\ {\mathit{a}}_{t_2}\end{array}\right]\sim \mathcal{N}\left(\left[\begin{array}{c}{\mathit{C}}_{t_1}{\mathit{\beta }}_{t_1}\\ {\mathit{C}}_{t_2}{\mathit{\beta }}_{t_2}\end{array}\right],\left[\begin{array}{cc}{\sigma }_{g{t}_1}^2{\mathit{G}}_{t_1}+\left(1-{\sigma }_{g{t}_1}^2\right){\mathit{I}}_{t_1}& {\rho }_{t_1,t_2}{\mathit{G}}_{t_1,t_2}\\ {\rho }_{t_1,t_2}{\left({\mathit{G}}_{t_1,t_2}\right)}^T& {\sigma }_{g{t}_2}^2{\mathit{G}}_{t_2}+\left(1-{\sigma }_{g{t}_2}^2\right){\mathit{I}}_{t_2}\end{array}\right]\right),$$

where ${\mathit{G}}_{t_1,t_2}={\mathit{X}}_{t_1}\mathit{W}{\mathit{X}}_{t_2}^T$ is the matrix of between-study genetic similarity coefficients (i.e., the genetic similarity coefficients between each individual in study 1 and each individual in study 2), ${\rho }_{t_1,t_2}$ is the genetic covariance, and ${\mathit{I}}_{t_1},{\mathit{I}}_{t_2}$ are identity matrices of suitable dimensions.

The quantities we investigate in this paper are defined as follows:

• (a)The SNP-based heritability of trait t, defined as $h_t^2\triangleq \text{var}\left(g_t^i\right)/\text{var}\left(a_t^i\right)$.
• (b)The SNP-based genetic covariance of two traits t₁, t₂, defined as ${\rho }_{t_1,t_2}\triangleq \text{cov}\left(g_{t_1}^i,g_{t_2}^i\right)$.
• (c)The SNP-based genetic correlation of two traits t₁, t₂, defined as $r_g\triangleq {\rho }_{t_1,t_2}/\sqrt{\text{var}\left(g_{t_1}^i\right)\text{var}\left(g_{t_2}^i\right)}$.

In the remainder of this article we use the shortened terms “heritability,” “genetic covariance,” and “genetic correlation” for brevity.

The Effect of Ignoring Covariates

The main contribution of PCGC-s over LDSC is its ability to account for covariates. Although it is rarely possible to measure all covariates affecting the trait of interest, covariates with a strong effect (such as the effect of sex on coronary artery disease) are often measured. This raises the question of whether omission of such important covariates affects heritability and genetic correlation estimates. We prove in the Supplemental Methods that if a method can provide unbiased estimates in settings with no covariates, it can also provide unbiased estimates in settings with covariates by simply ignoring these covariates, assuming that the covariate effects are (1) normally distributed and (2) uncorrelated with the genetic effect. The main idea behind the derivation is that the environmental effect represents the aggregated effect of unmeasured covariates and can thus absorb the effect of omitted covariates when these assumptions hold.

The assumption of normality approximately holds if a trait is influenced by a large number of covariates with small effects, owing to the central limit theorem. However, many traits are strongly influenced by a small number of non-normally distributed covariates, such as sex. Heritability estimates with omitted covariates can become inaccurate in the presence of such strong covariates. In contrast, genetic correlation is accurately estimated in the simulations even in the presence of strong non-normal covariates, suggesting that the errors in the estimation of genetic covariance and genetic variance approximately cancel out when dividing one by the other. However, this observation is currently unsupported by statistical theory.

The assumption that covariates are uncorrelated with the genetic effect is often violated when using heritable covariates, such as genetic principal components. This problem can be circumvented by regressing the omitted covariates out of the genotypes and correcting the individual-level affection cutoffs prior to parameter estimation or to computing summary statistics (Supplemental Methods). We caution that regression of covariates out of binary phenotypes as suggested in Bulik-Sullivan⁴⁰ can yield incorrect estimates in case-control studies, even for genetic correlation (as verified in the Results).

Marginal and Conditional Heritability

An important point often overlooked in heritability estimation is that covariates such as sex and age also contribute to the liability variance. Since the liability is non-identifiable, it is typically assumed to have a unit variance when conditioning on measured covariates. The liability is defined as $a_t^i=g_t^i+e_t^i+{\left({\mathit{C}}_t^i\right)}^T{\mathit{\beta }}_t$, and thus its marginal variance is given by $\text{var}\left[g_t^i+e_t^i\right]+\text{var}\left[{\left({\mathit{C}}_t^i\right)}^T{\mathit{\beta }}_t\right]=1+\text{var}\left[{\left({\mathit{C}}_t^i\right)}^T{\mathit{\beta }}_t\right]$ (assuming that covariates are uncorrelated with the genetic effects). Consequently, heritability is given by ${\sigma }_{gt}^2/\left(1+\text{var}\left({\left({\mathit{C}}_t^i\right)}^T{\mathit{\beta }}_t\right)\right)$ (Supplemental Methods). Alternatively, one could assume that the marginal variance is 1, in which case the conditional variance is smaller than 1.

In practice, many studies define the genetic variance ${\sigma }_{gt}^2$ as the heritability, even in the presence of covariates. We therefore denote the former definition as marginal heritability and the latter definition as conditional heritability, because the latter definition uses the variance of the liability conditional on measured covariates.

In this paper we consider marginal heritability for two reasons: (1) this definition is arguably more natural, as different studies using different covariates are ultimately interested in estimating the same quantity; and (2) LDSC tends to severely underestimate the conditional heritability (as compared to less severe overestimation of marginal heritability). Therefore, we do not consider estimation of conditional heritability further in this paper.

PCGC-s with No Covariates

PCGC with no covariates estimates ${\rho }_{t_1,t_2}$ by regressing standardized phenotypic correlations ${\tilde{y}}_{t_1}^i{\tilde{y}}_{t_2}^j$ on genetic similarity coefficients $G_{t_1,t_2}^{i,j}$ and then dividing the resulting estimator by a constant $f\left(t_1,t_2\right)$ (Supplemental Methods). This estimation encapsulates both genetic covariance and heritability, which for a trait t with no covariates is given by ${\rho }_{t,t}$.

The PCGC estimator can be computed without individual-level data by using the following two summary statistics:

$$z_t^k\triangleq \frac{1}{\sqrt{n_t}}\sum _{i=1}^{n_t}{\tilde{y}}_t^i{X}_t^{k,i}$$

$${\hat{r}}_t^{k,h}\triangleq \frac{1}{n_t}\sum _{i=1}^{n_t}{X}_t^{k,i}{X}_t^{h,i},$$

where n_t is the sample size of study t and $X_t^{k,i}$ is the value of the k^th variant of individual i in study t, after standardization. It is also possible to use logistic regression-based or other types of summary statistics, but this constitutes an approximation (Supplemental Methods).

Using these quantities and denoting $S_{t_1,t_2}$ as the set of all pairs of indices i, j that refer to the same individual shared between the two studies, the PCGC estimator can be written as:

$${\hat{\rho }}_{t_1,t_2}^{\text{pcgc}-\text{s}}\triangleq \frac{1}{f\left(t_1,t_2\right)}\frac{\frac{\sqrt{n_{t_1}{n}_{t_2}}}{m}{\sum }_{k=1}^m{z}_{t_1}^k{z}_{t_2}^k-{\sum }_{\left(i,j\right)\in S_{t_1,t_2}}{G}_{t_1,t_2}^{i,j}\left({\tilde{y}}_{t_1}^i{\tilde{y}}_{t_2}^j\right)}{\frac{n_{t_1}{n}_{t_2}}{m^2}{\sum }_{k,h=1}^m{\hat{r}}_{t_1}^{k,h}{\hat{r}}_{t_2}^{k,h}-{\sum }_{\left(i,j\right)\in S_{t_1,t_2}}{\left(G_{t_1,t_2}^{i,j}\right)}^2},$$

where m is the number of variants and $f\left(t_1,t_2\right)$ is given by:$f\left(t_1,t_2\right)=\frac{\sqrt{P_{t_1}\left(1-P_{t_1}\right)P_{t_2}\left(1-P_{t_2}\right)}\varphi \left({\tau }_{t_1}\right)\varphi \left({\tau }_{t_2}\right)}{K_{t_1}\left(1-K_{t_1}\right)K_{t_2}\left(1-K_{t_2}\right)}.$

Here, K_t and P_t are the prevalence of trait t and the case-control proportion of study t, respectively, ${\tau }_t={\text{Φ}}^{-1}\left(1-K_t\right)$ is the liability cutoff, and $\varphi (\cdot )$, $\text{Φ}(\cdot )$ are the density and cumulative distribution of the standard normal distribution, respectively.

The resulting estimator approximately coincides with the LDSC estimator if there are no overlapping individuals (i.e., individuals that are included in both studies) and the in-sample LD estimates in both studies are the same as in the reference population used by LDSC.⁴⁰ The extension to estimating multiple variance components or for using MAF and LD-dependent genetic architectures is straightforward (Supplemental Methods).

The second term of the numerator and of the denominator can be computed by research groups with access to the genotypes and phenotypes of overlapping individuals, which often consist of control cohorts, or can be approximated via the approximation $G_{t_1,t_2}^{i,j}\approx 1.0$ for overlapping individuals, as done implicitly in LDSC.² However, we caution that even minor deviations (which can occur for example by regressing principal components out of genotypes) can affect the approximation (Supplemental Methods).

A particularly convenient property of ${\hat{\rho }}_{t_1,t_2}^{\text{pcgc}-\text{s}}$ in the absence of covariates is that when estimating the genetic correlation, all terms dependent on the trait prevalence vanish. This is convenient because the true trait prevalence is often not known with certainty.

PCGC-s with Covariates

In the presence of covariates, PCGC estimates ${\rho }_{t_1,t_2}$ by regressing ${\tilde{y}}_{t_1}^i{\tilde{y}}_{t_2}^j$ on $G_{t_1,t_2}^{i,j}{Q}_{t_1,t_2}^{i,j}$, where $Q_{t_1,t_2}^{i,j}$ is a quantity that depends on the covariates of individuals i and j, and so the regression constant is different for every pair of individuals.¹⁴ The corresponding PCGC-s estimator is given by:

$${\hat{\rho }}_{t_1,t_2}^{\text{pcgc}-\text{covar}-\text{s}}\triangleq \frac{\frac{1}{m}{\sum }_{k=1}^m{z}_{t_1}^{k,\text{covar}}{z}_{t_2}^{k,\text{covar}}-{\sum }_{\left(i,j\right)\in S_{t_1,t_2}}{\tilde{y}}_{t_1}^i{\tilde{y}}_{t_2}^j{G}_{t_1,t_2}^{i,j}{Q}_{t_1,t_2}^{i,j}}{\frac{1}{m^2}{\sum }_{k,h=1}^m{\hat{r}}_{t_1}^{k,h,\text{covar}}{\hat{r}}_{t_2}^{k,h,\text{covar}}-{\sum }_{\left(i,j\right)\in S_{t_1,t_2}}{\left(G_{t_1,t_2}^{i,j}{Q}_{t_1,t_2}^{i,j}\right)}^2}.$$

The above quantities are defined as follows:

$$z_t^{k,\text{covar}}\triangleq \sum _{i=1}^{n_t}{\tilde{y}}_t^i{X}_t^{k,i}\sum _{\text{a}=0}^1{\text{u}}_{\text{t},\text{a}}^i$$

$${\hat{r}}_t^{k,h,\text{covar}}\triangleq \sum _{i=1}^{n_t}{X}_t^{k,i}{X}_t^{h,i}\sum _{\text{a},\text{b}=0}^1{\text{u}}_{\text{t},\text{a}}^{\text{i}}{\text{u}}_{\text{t},\text{b}}^{\text{i}}$$

$$Q_{t_1,t_2}^{i,j}\triangleq \sum _{a,b=0}^1{u}_{t_1,a}^i{u}_{t_2,b}^j,\text{where}{\text{u}}_{\text{t},0}^i,{\text{u}}_{\text{t},1}^j\text{are}\text{given}\text{by:}$$

$${\text{u}}_{\text{t},0}^{\text{i}}\triangleq \frac{\varphi \left({\tau }_t^i\right)}{\sqrt{P_t^i\left(1-P_t^i\right)}\left(K_t^i+\left(1-K_t^i\right)\frac{K_t\left(1-P_t\right)}{P_t\left(1-K_t\right)}\right)}\frac{K_t\left(1-P_t\right)}{P_t\left(1-K_t\right)}{P}_t^i$$

$${\text{u}}_{\text{t},1}^{\text{j}}\triangleq \frac{\varphi \left({\tau }_t^j\right)}{\sqrt{P_t^j\left(1-P_t^j\right)}\left(K_t^j+\left(1-K_t^j\right)\frac{K_t\left(1-P_t\right)}{P_t\left(1-K_t\right)}\right)}\left(1-P_t^j\right).$$

Here, $K_t^i$ is the probability of individual i being a case conditional on her covariates, $P_t^i$ is the probability of individual i being a case conditional on her covariates and on being ascertained into the study, and ${\tau }_t^i={\text{Φ}}^{-1}\left(1-K_t^i\right)$ is the liability cutoff of individual i conditional on her covariates.

The full derivation, extensions for multiple variance components and for MAF and LD-dependent architectures, and an approximation that requires a single summary statistic instead of using ${\hat{r}}_t^{k,h,\text{covar}}$ (which requires a number of statistics equal to the number of pairs of variants) are provided in the Supplemental Methods.

As in the case of no covariates, the second term of the numerator and denominator can be computed by research groups with access to overlapping individuals, which often consist of control cohorts. Third parties with no access to overlapping individuals can approximate the terms on the right-hand sides of the numerator and the denominator given appropriate summary statistics (Supplemental Methods).

Results

We are interested in estimating the following quantities (see Material and Methods for exact definitions): (a) heritability, the fraction of liability variance explained by genetics; (b) genetic covariance, the covariance between the genetic components of two traits on the liability scale; and (c) genetic correlation, the genetic covariance standardized to a [−1,1] scale.

We are concerned with the three following questions:

• 1.Can quantities (a)–(c) be estimated reliably given genotypic and phenotypic data?
• 2.Can quantities (a)–(c) be estimated reliably given summary statistics via LDSC?
• 3.Can quantities (a)–(c) be estimated reliably given summary statistics via an alternative method?

The answers to questions 1 and 2 are summarized in Table S1. Briefly, PCGC is the only method that can estimate all quantities of interest under all investigated settings. REML provides inconsistent estimates of quantities (a) and (b) and empirically provides consistent estimates of quantity (c). LDSC can provide consistent estimates of quantities (a) and (b) in the absence of covariates and provides consistent estimates of quantity (c) when no covariates are included in the analysis. To answer question 3, we present a reformulation of PCGC called PCGC-s that can estimate quantities (a)–(c) reliably using only summary statistics, both with and without covariates (Supplemental Methods).

Simulation Studies

We conducted simulation studies to investigate the behavior of the evaluated methods in case-control studies; such simulations require first obtaining a very large pool with hundreds of thousands of individuals, and then sampling a small fraction of case subjects according to the trait prevalence.^{1, 14, 16, 41}

Our simulations were based on the liability threshold model. Briefly, for every non-genetic covariate k we sampled two independent effect for two different traits (t₁ and t₂), denoted as ${\beta }_{t_1}^k,$ ${\beta }_{t_2}^k$, from a normal distribution. In addition, for every SNP j we sampled two correlated effect sizes, $b_{t_1}^j,b_{t_2}^j$. A subset of these effects were equal to zero (determined according to the desired trait polygenicity). Every other pair of effects was sampled independently from a bivariate normal distribution, whose covariance matrix was determined according to the desired heritabilities and genetic correlation of the two traits. In most simulations the variance of all pairs of effects was the same, though we also evaluated MAF and LD-dependent architectures, as described below.

For every individual i, we generated a vector of uniformly spaced SNPs whose LD decays exponentially with distance, denoted as ${\mathit{x}}^i$, and a vector of independent covariates denoted as ${\mathit{c}}^i$. Finally, for every individual i and for every trait $t\in \left\{t_1,t_2\right\}$, we generated (1) a normally distributed environmental effect $e_t^i$; (2) a liability given by $a_t^i={\left({\mathit{x}}^i\right)}^T{\mathit{b}}_t+{\left({\mathit{c}}^i\right)}^T{\mathit{\beta }}_t+e_t^i$; and (3) a case/control label, where case subjects are individuals with $a_t^i>{\tau }_t$, with ${\tau }_t$ being the empirical 1 − K_t percentile of the liabilities in the population, and K_t is the prevalence of trait t. We kept on sampling individuals until obtaining the desired number of case and control subjects. The full simulation details are provided in the Supplemental Methods.

Our simulations span a wide range of scenarios, with various levels of prevalence, heritability, genetic correlation, sample sizes, number of SNPs, number of covariates, LD patterns, fraction of shared controls, and trait polygenicity. In each experiment we varied one or more of the above parameters while keeping the others fixed. The default simulation parameters used 1% prevalence, 50% heritability, and 50% genetic correlation, with each study having 2,000 case subjects, 1,000 unique and 1,000 overlapping control subjects, and 10,000 SNPs whose LD decays exponentially with distance, and with a correlation of between 25% and 90% between consecutive SNPs (consequently, the correlation between every pair of SNPs separated by at least 25 SNPs is <0.001 in all settings). In most simulations all SNPs influenced the phenotype, though we verified that relaxing this assumption does not affect the results (see details below). 100 simulations were conducted for each unique combination of settings.

The examined methods included (1) PCGC-s; (2) PCGC-s-LD, which is an approximate version of PCGC-s that uses external LD estimates (but uses data about overlapping individuals; Supplemental Methods); (3) LDSC with omitted covariates (LDSC-omit); and (4) REML, using the implementation in GCTA⁶ (exact execution details are provided in the Supplemental Methods). Note that PCGC-s is exactly equivalent to PCGC when all required summary statistics are provided. LDSC-omit refers to LDSC that does not include any covariates in the analysis and was used because explicit inclusion of covariates can lead to highly biased estimates, as demonstrated below. In most simulations LDSC-omit was based on our own implementation, to avoid confounding the analysis by implementation details. Specifically, our implementation of LDSC-omit used a predetermined intercept and did not weight summary statistics by their posterior variance, similarly to PCGC-s-LD (see Discussion for elaboration on these issues). In additional simulations described below, we demonstrated that when using the ldsc software instead of our own implementation, LDSC-omit became less accurate.

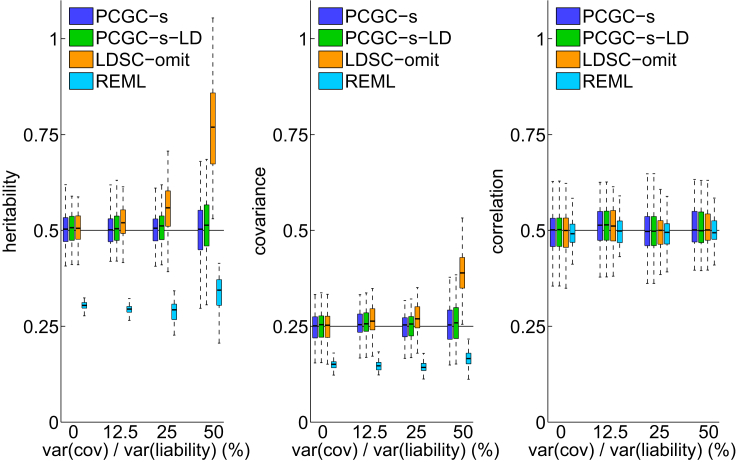
Our first experiment examined the impact of covariate effect magnitude on the estimation of heritability, genetic covariance, and genetic correlation. We simulated datasets with five binary covariates that explained various fractions of the liability variance, where the first covariate accounted for 95% of the aggregated covariates effect. All methods estimated correlation well, but PCGC-s and PCGC-s-LD were the only methods that estimated the two other quantities accurately (Figure 1). Both PCGC-s and PCGC-s-LD estimated heritability significantly more accurately than LDSC-omit (p < 2.1 × 10⁻², p < 1.7 × 10⁻⁶, p < 6.5 × 10⁻²⁴ for covariates explaining 12.5%, 25%, and 50% of the liability variance, respectively; binomial test for PCGC-s-LD; PCGC-s results were effectively the same). The accuracy of LDSC-omit improved as effect sizes became smaller; LDSC-omit and PCGC give very similar estimates in the absence of covariates, as expected from theory (Supplemental Methods). REML consistently underestimated heritability despite using the correction for case-control ascertainment implemented in GCTA.¹ We note that the extent of under-estimation by REML is not fixed with a known ratio but depends on various unknown parameters.¹⁴ We also obtained similar results when ignoring the contribution of covariates to the liability variance (Material and Methods, Figure S1).

Figure 1.

The Effect of Covariate Strength

PCGC-s and PCGC-s-LD estimate all parameters accurately under all settings; LDSC-omit estimates of heritability and genetic covariance become increasingly inaccurate as the covariates strength increases; REML misestimates heritability and genetic covariance under all settings. All methods estimate genetic correlation accurately. The black horizontal lines indicate the true parameter values. 100 experiments were performed for each unique combination of settings, and each study included 2,000 case subjects and 2,000 control subjects.

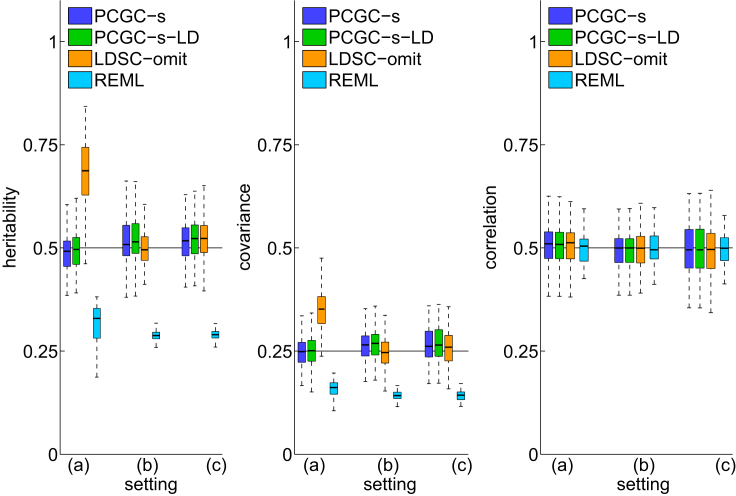
The next experiment examined the implications of having normal versus non-normal covariate effects, by considering three settings: (1) a single binary covariate, (2) a single normally distributed covariate, and (3) 20 equally strong binary covariates. In all settings the covariates jointly explained 40% of the liability variance. Setting 1 encodes a non-normal aggregated effect, whereas settings 2 and 3 encode a normal and an approximately normal effect (owing to the central limit theorem), respectively. In setting 1, LDSC-omit was substantially less accurate than PCGC-s (p < 3.21 × 10⁻¹⁹; binomial test) and PCGC-s-LD (p < 2.73 × 10⁻²⁰; binomial test), because its underlying model is violated in the presence of strong non-normally distributed covariates (Figure 2, Material and Methods). The bias of LDSC-omit decreased when decreasing the magnitude of the covariate effects, similarly to the results shown in Figure 1.

Figure 2.

The Effect of the Covariate Effects Distribution

Setting (a) includes a single binary covariate; setting (b) includes a single normally distributed covariate; setting (c) includes 20 binary variables with equal strength, yielding an approximately normal aggregated effect owing to the central limit theorem. PCGC-s and PCGC-s-LD are the only methods that accurately estimate heritability and genetic covariance in setting (a), where the covariates effects distribution is far from normal. 100 experiments were performed for each unique combination of settings, and each study included 2,000 case subjects and 2,000 control subjects.

In additional experiments, we simulated data with one strong and four weak binary covariates as in the first experiment, where the covariates jointly explained 25% of the liability variance, and verified that the results remained similar under various levels of heritability (Figure S2), genetic correlation (Figure S3), prevalence (Figure S4), LD (Figure S5), fraction of shared controls (Figure S6), numbers of covariates (Figure S7), sample sizes (Figure S8), numbers of simulated causal SNPs (Figure S9), and trait polygenicity (Figure S10). We also explored running LDSC-omit using the ldsc software (Figure S11) and using logistic regression-based summary statistics (Figures S12 and S13).

We also examined the effect of using LDSC without omitting covariates, by regressing measured covariates out of the phenotypes and genotypes prior to computing summary statistics, as previously recommended.^{16, 40} Our results demonstrate that LDSC estimates are severely down-biased in this setting, with an average bias of more than 10% in heritability and covariance estimation, and of more than 5% in correlation estimation, under realistic settings (Figures S14 and S15).

Next, we performed a set of experiments with a MAF and LD-dependent genetic architectures. Specifically, we simulated phenotypes according to the LDAK model,⁸ which replaces the standard genetic similarity matrix ${\mathit{G}}_t={\mathit{X}}_t{\mathit{X}}_t^T/m$ with the matrix ${\mathit{G}}_t={\mathit{X}}_t\mathit{W}{\mathit{X}}_t^T/M$, where $\mathit{W}=\text{diag}\left[{\left(p^j\left(1-p^j\right)\right)}^{0.75}{w}^j\right]$, p^j is the MAF of SNP j, w^j minimizes the L₂ norm of $\left(1-{\sum }_{k=1}^m{\left(r^{k,j}\right)}^2{w}^k\right)$, and $M={\sum }_k{W}_{kk}$. All methods yielded biased estimates of heritability and genetic covariance when using the incorrect genetic similarity matrix ${\mathit{G}}_t={\mathit{X}}_t{\mathit{X}}_t^T/m$ (Figure S16). However, PCGC-s and PCGC-s-LD became unbiased when using the correct genetic similarity matrix, whereas the other methods remained biased even when using the correct genetic similarity matrix (Figure S17). Interestingly, all methods yielded empirically unbiased estimates of genetic correlation even when using an incorrect model, suggesting that the approximation errors cancel themselves out, similarly to the patterns observed when not correctly modeling case-control ascertainment. A numerical summary of all the results reported in this section is provided in Table S2.

Finally, we note that PCGC-s-LD is highly computationally efficient. Since PCGC-s-LD uses only summary statistics, it can perform estimation for data with millions of variants and hundreds of thousands of individuals in less than 1 hr (results not shown).

Estimating the Genetic Architecture of Schizophrenia and Bipolar Disorder

To demonstrate the behavior of the methods on real data, we studied the heritability and genetic correlation of schizophrenia (SCZ)⁴² and bipolar disorder (BP).⁴³ To prevent confounding due to population stratification,⁴⁴ we restricted the analysis to two highly concordant Swedish datasets consisting of 1,745 SCZ-affected case subjects, 1,268 BP-affected case subjects, and 6,293 control subjects, 2,566 of which are shared between the studies^{42, 43} (Supplemental Methods). The covariates included 10 principal components and sex, which is a major risk factor for both diseases.

The PCGC-s heritability estimates for SCZ and BP were 39.2% and 41.7%, respectively. The estimated genetic correlation was 42.4%, which is substantially lower than previous estimates of 68% using REML¹⁰ and 79% using LDSC.² We further verified that when omitting covariates, the PCGC-s estimates increased to 60%, suggesting that incorrect treatment of non-genetic risk factors can lead to inflated estimates. When invoking LDSC on the same data using the ldsc software, the estimated correlation could not be computed when omitting covariates due to negative estimated heritabilities and was 15.8% when regressing the covariates out of the phenotypes (Table 1). We also estimated the heritabilities and genetic correlation under the LDAK model⁸ and obtained very similar estimates (Table S3). Namely, the heritability estimates for SCZ and BP were 40.0% and 46.1%, respectively, and the estimated genetic correlation was 43.8%. Overall, we conclude that improper handling of covariates and of sample overlap in case-control studies can lead to substantially biased estimates and to incorrect conclusions regarding the genetic architecture of genetic diseases.

Table 1.

Results of Real Data Analysis of Psychiatric Disorders

Covariates		SCZ		BP		Correlation
		${\hat{\mathbf{\sigma }}}_{\mathbf{g}}^{\mathbf{2}}$	${\hat{\mathbf{h}}}^{\mathbf{2}}$	${\hat{\mathbf{\sigma }}}_{\mathbf{g}}^{\mathbf{2}}$	${\hat{\mathbf{h}}}^{\mathbf{2}}$
Omitted	PCGC-s	0.127 (0.059)	0.127 (0.059)	0.259 (0.044)	0.259 (0.044)	0.561 (0.149)
	PCGC-s-LD	0.139 (0.047)	0.139 (0.047)	0.282 (0.057)	0.282 (0.057)	0.602 (0.178)
	LDSC-omit	0.467 (0.101)	0.467 (0.101)	0.293 (0.109)	0.293 (0.109)	0.451 (0.190)
	LDSC-omit +intercept	0.467 (0.101)	0.467 (0.101)	0.293 (0.109)	0.293 (0.109)	–
Included	PCGC-s	0.399 (0.068)	0.392 (0.062)	0.426 (0.051)	0.417 (0.045)	0.437 (0.077)
	PCGC-s-LD	0.438 (0.059)	0.430 (0.049)	0.465 (0.059)	0.455 (0.058)	0.424 (0.084)
	LDSC	0.412 (0.084)	0.405 (0.070)	0.356 (0.105)	0.348 (0.103)	0.527 (0.176)
	LDSC+intercept	0.412 (0.084)	0.405 (0.077)	0.356 (0.105)	0.349 (0.093)	0.158 (0.112)

Shown are the estimated values of the genetic variance ${\sigma }_g^2$ (also termed the conditional heritability in this paper), the marginal heritability h² (which is equal to ${\sigma }_g^2$ when no covariates are present and smaller than ${\sigma }_g^2$ in the presence of covariates) and the genetic correlation. Standard errors were computed via a block jackknife of 200 blocks of consecutive SNPs. LDSC+intercept is the LDSC estimator when fitting an intercept from the data.² LDSC-omit is different from PCGC-s-LD with omitted covariates because of differences in the predetermined intercept value due to normalization (Supplemental Methods). LDSC results were computed using the ldsc software. Values marked with “–” could not be computed because of negative or illegal parameter estimates.

Estimating the Genetic Architecture of Type 1 Diabetes and Coronary Artery Disease

To further evaluate PCGC-s, we studied the correlation between type 1 diabetes (T1D) and coronary artery disease (CAD), using data from the Wellcome Trust Case Control Consortium 1 (WTCCC1).⁴⁵ It is known that T1D is associated with an increased risk for CAD,⁴⁶ but the role of genetics in this association is not clear. We chose to explore this example because of the expected impact of covariates on the result: T1D is very strongly affected by SNPs in the major histocompatibility complex (MHC) region, and sex is a major risk factor for CAD. We thus modeled the effects of these risk factors as fixed rather than random and investigated the implications of inclusion and exclusion of these covariates. The analysis details are provided in the Supplemental Methods.

The results demonstrated the existence of a positive genetic correlation between T1D and CAD and corroborated the simulation studies (Table 2, Table S4). As expected, inclusion of covariates had a minor effect on PCGC-s estimates, decreasing the heritability estimate for T1D from 23.7% to 18.3% and for CAD from 40.5% to 39.9%, and slightly increasing the genetic correlation estimate from 18.1% to 19.2%. The LDSC heritability estimates for T1D and CAD when omitting covariates (35% and 58.8%, respectively) were greater than those of PCGC-s (consistent with our simulation results) and the correlation estimate was also greater (28.4%). LDSC heritability estimates were nonsensical (non-positive or greater than one) when including covariates or fitting an intercept rather than using a predetermined one. REML estimation of genetic correlation using gcta failed to converge.

Table 2.

Results of Real Data Analysis of T1D and CAD

Covariates		T1D		CAD		Correlation
		${\hat{\mathbf{\sigma }}}_{\mathbf{g}}^{\mathbf{2}}$	${\hat{\mathbf{h}}}^{\mathbf{2}}$	${\hat{\mathbf{\sigma }}}_{\mathbf{g}}^{\mathbf{2}}$	${\hat{\mathbf{h}}}^{\mathbf{2}}$
Omitted	PCGC-s	0.237 (0.044)	0.237 (0.044)	0.405 (0.063)	0.405 (0.063)	0.181 (0.115)
	PCGC-s-LD	0.245 (0.045)	0.245 (0.045)	0.420 (0.065)	0.420 (0.065)	0.181 (0.115)
	LDSC-omit	0.350 (0.046)	0.350 (0.046)	0.588 (0.066)	0.588 (0.066)	0.284 (0.074)
	LDSC-omit +intercept	0.013 (0.105)	0.013 (0.105)	0.020 (0.109)	0.020 (0.109)	–
Included	PCGC-s	0.241 (0.066)	0.183 (0.050)	0.435 (0.070)	0.399 (0.062)	0.192 (0.139)
	PCGC-s-LD	0.250 (0.069)	0.190 (0.052)	0.451 (0.065)	0.413 (0.060)	0.191 (0.139)
	LDSC	−1.75 (0.038)	–	−0.33 (0.058)	–	–
	LDSC+intercept	−0.03 (0.046)	–	−0.07 (0.09)	–	–

The table fields are the same as in Table 1. LDSC results are based on our own implementation to provide a detailed comparison with PCGC-s that is not confounded by implementation details. Results using the ldsc software are provided in Table S4.

We conclude that accounting for covariates can substantially affect heritability and genetic correlation estimates. However, we caution that the results are sensitive to preprocessing of the data (Tables S5–S7, Supplemental Methods; see Discussion). We also present genetic correlation estimates between all phenotypes included in the WTCCC1 study, confirming some well-known significant correlations, such as between hypertension and coronary artery disease; and others that have been tentatively suggested in the literature, such as between rheumatoid arthritis and coronary artery disease^{47, 48} (Table S8).

Discussion

Our major conclusions regarding the existing approaches can be summarized as follows. (1) REML severely misestimates heritability and genetic covariance in case-control studies under all settings (as has been pointed out previously^{7, 14, 41}). In settings without binary covariates, REML accurately estimates genetic correlation, but it can become slightly biased in the presence of such covariates. (2) LDSC estimates are accurate in the absence of covariates but can become biased in the presence of binary covariates with strong effects. Importantly, regressing covariates out of phenotypes prior to running LDSC can lead to a very severe bias and should always be avoided. We further caution that the software implementation of LDSC can lead to different estimates than those of PCGC-s even in the absence of covariates due to different data preprocessing procedures, as discussed below. (3) PCGC accurately estimates all quantities of interest directly or with summary statistics. (4) Standard summary statistics cannot be used to estimate genetic correlation for traits with binary non-genetic risk factors; we propose here a novel formulation of privacy-preserving summary statistics which can be used for this task.

Another potentially problematic aspect of genetic correlation estimation is analysis of cohorts from ancestrally divergent populations. Our preliminary analysis demonstrated that analysis of such cohorts can lead to inflated and unstable genetic correlation estimates for all methods, even when using a large number of PCs as covariates (results not shown). We therefore opted to focus our analysis on two Swedish cohorts. Previous estimates of the genetic correlation between schizophrenia and bipolar disorder were based on cohorts from divergent European populations, which may be another reason for the large difference between our estimates and previous ones.^{2, 10, 44}

When comparing different methods, it is important to distinguish between the underlying mathematics and the software implementation. Even though PCGC-s and LDSC are roughly equivalent in the absence of covariates, the software implementation of PCGC-s is careful to perform case-control-aware data preprocessing (e.g., avoiding in-sample SNP standardization, and avoid assuming that the diagonal of the genetic similarity matrix is exactly 1.0; Supplemental Methods). This can lead to major differences between the estimates of the software implementations in real data analysis. We therefore recommend that researchers use our software implementation of PCGC-s for analysis of case-control studies regardless of the presence of covariates, because PCGC-s is careful to preprocess case-control data correctly.

An important issue often raised in the context of heritability estimation regards the validity of the assumed model. One specific concern concerns the use of allele frequency and LD-dependent architectures.^{8, 39, 49, 50} While important, this concern is not directly related to our results, as PCGC-s can accommodate arbitrary linear genetic architectures (Supplemental Methods). Additional concerns include the difference between “SNP heritability” and “narrow sense heritability” which assumes that all causal SNPs are measured^{7, 51} and the potentially larger difference between narrow sense heritability and the true genetic heritability in the presence of non-additive effects.⁵² These concerns are well founded and should certainly be addressed in practice. However, they are not directly related to our study, which focuses on the performance of different methods when the model assumed by these methods (liability threshold model and additivity) holds. We believe our conclusion, that commonly used methods can be biased under their own modeling assumptions, is of major interest even given the concerns about the validity of the assumptions themselves.

An important question that has been debated recently concerns the relationship between causal effect sizes and MAF and LD patterns.^{8, 39, 49} PCGC-s can be readily modified to use any linear genetic architecture and can thus accommodate different genetic architectures. Several researchers recently advocated comparing between different models via the data likelihood,⁸ but unfortunately exact likelihood estimation is infeasible in ascertained case-control studies. The determination of genetic architectures under case-control studies is therefore a potential line of future work.

Finally, the LDSC framework includes several techniques not considered in this work: estimation of the contribution of functional annotations to the liability variance,⁵³ improved estimation by weighting of summary statistic,¹⁶ and fitting an intercept from the data rather than using a predetermined one.¹⁶ The first technique can be readily adapted into the PCGC-s framework (Supplemental Methods). We do not recommend using the other techniques in case-control studies, as the derivations underlying these techniques assume an additive phenotype with genotype-environment independence. Adapting these procedures into case-control studies under a formal theoretical framework remains a potential avenue for future work.

Declaration of Interests

The authors declare no competing interests.

Published: July 5, 2018

Web Resources

• PCGC-s, https://github.com/omerwe/PCGCs