Abstract
Prostate-associated gene 4 (PAGE4) is an intrinsically disordered protein implicated in prostate cancer. The stress-response kinase homeodomain-interacting protein kinase 1 (HIPK1) phosphorylates two residues in PAGE4, serine 9 and threonine 51. Phosphorylation of these two residues facilitates the interaction of PAGE4 with activator protein-1 (AP-1) transcription factor complex to potentiate AP-1's activity. In contrast, hyperphosphorylation of PAGE4 by CDC-like kinase 2 (CLK2) attenuates this interaction with AP-1. Small-angleX-ray scattering and single-molecule fluorescence resonance energy transfer measurements have shown that PAGE4 expands upon hyperphosphorylation and that this expansion is localized to its N-terminal half. To understand the interactions underlying this structural transition, we performed molecular dynamics simulations using Atomistic AWSEM, a multi-scale molecular model that combines atomistic and coarse-grained simulation approaches. Our simulations show that electrostatic interactions drive transient formation of an N-terminal loop, the destabilization of which accounts for the dramatic change in size upon hyperphosphorylation. Phosphorylation also changes the preference of secondary structure formation of the PAGE4 ensemble, which leads to a transition between states that display different degrees of disorder. Finally, we construct a mechanism-based mathematical model that allows us to capture the interactions of different phosphoforms of PAGE4 with AP-1 and its downstream target, the androgen receptor (AR)—a key therapeutic target in prostate cancer. Our model predicts intracellular oscillatory dynamics of HIPK1-PAGE4, CLK2-PAGE4, and AR activity, indicating phenotypic heterogeneity in an isogenic cell population. Thus, conformational switching of PAGE4 may potentially affect the efficiency of therapeutically targeting AR activity.
Keywords: intrinsically disordered protein, PAGE4, AWSEM, order–disorder transition, non-genetic heterogeneity
Introduction
A significant fraction (≈ 15%–30%) of proteins lack a stable structure, at least when they are not bound to an interaction partner or ligand [1–5]. Such unstructured proteins populate a diverse ensemble of interconverting conformations in order to function and, thus, they are referred to as intrinsically disordered proteins (IDPs). Despite their lack of rigid structure, IDPs are involved in regulation, signaling, and control of information flow in the cell. Binding to multiple partners and high-specificity/low-affinity interactions play crucial roles in the functions of IDPs [6,7]. Disorder enables IDPs to participate in both one-to-many and many-to-one signaling [3,8]. However, when overexpressed or aberrantly expressed, IDPs are prone to engage in promiscuous interactions that lead to various pathological conditions [9,10].
Complete structural characterization of IDPs has, in general, remained intractable to classical biophysical methods. Therefore, mechanistic insight into how IDPs function is currently limited to only a few examples. Prostate-associated gene 4 (PAGE4) is an IDP that has been relatively well characterized both structurally and functionally. PAGE4 has the hallmarks of a proto-oncogene: while it is highly expressed during its development in the fetal prostate [11,12], it is aberrantly expressed in the diseased gland where it plays an important role in tumorigenesis [11].
PAGE4 is also a stress-response factor [11] and functions as transcriptional coactivator in prostate cancer (PCa) cells where it can potentiate transactivation by c-Jun [12]. The proto-oncogenec-Jun heterodimerizes with c-Fos to form the activator protein-1 (AP-1) transcription factor complex that can negatively regulate the activity of androgen receptor (AR) in PCa cells [13,14]. Furthermore, in PCa cells, PAGE4 is phosphorylated by the stress-response kinase homeodomain-interacting protein kinase 1 (HIPK1). Phosphorylation of PAGE4 by HIPK1 occurs predominantly at Thr51 and, to a significantly lower level, at Ser9 [15]. PAGE4 can also be hyperphosphorylated by another kinase named CDC-like kinase 2 (CLK2) [16]. Cell-based studies have revealed that phosphorylation of PAGE4 by the two kinases leads to opposing functions. Thus, while HIPK1-phosphorylated PAGE4 (HIPK1-PAGE4) potentiates c-Jun, CLK2-phosphorylated PAGE4 (CLK2-PAGE4) attenuates c-Jun activity [16]. Biophysical measurements employing small-angleX-ray scattering (SAXS), single-molecule fluorescence resonance energy transfer (smFRET), and NMR indicate that HIPK1-PAGE4 exhibits a relatively compact conformational ensemble that binds AP-1, whereas CLK2-PAGE4 is more expanded and resembles a random coil with reduced affinity for AP-1 [16]. Although these experiments indicate that different phosphoforms of PAGE4 have different sizes and functions, the molecular details of the critical interactions within PAGE4 that are responsible for such conformational changes have, until now, remained unclear.
To investigate the structural details during the change in the size of PAGE4 upon phosphorylation and to overcome the temporal and spatial resolution limits associated with SAXS and smFRET experiments [17–19], we have used molecular dynamics (MD) simulations with an optimized protein folding landscape model. The Associative memory, Water mediated, Structure and Energy Model (AWSEM)[20] is based on the principles of the energy landscape theory of protein folding and is optimized using a quantitative formulation of the principle of minimal frustration [21–23]. AWSEM has been effective in moderate resolution protein structure prediction and accurate identification of protein–protein binding interfaces [20,24]. Moreover, when combined with energy landscape analyses, AWSEM can elucidate the molecular mechanisms underlying the regulation of cellular responses [25]. An important component of the AWSEM force field, called the associative memory term, models local structural preferences by searching for protein fragments in the Protein Data Bank (PDB) [26] that have sequences that are locally similar to those in the protein being simulated.
Recently, we developed a multi-scale atomistic AWSEM model (AAWSEM) [27], which harnesses the power of all-atomexplicit-solvent simulations to directly generate atomistic structures that can be used as fragments by the associative memory term of AWSEM. AAWSEM can reliably fold both α-exclusive proteins [27] and α/β proteins [28]. AAWSEM is especially useful for investigating disordered proteins such as PAGE4 because the PDB often lacks adequate protein fragments for modeling the local structural preferences of IDPs. In addition, the coarse-grained nature of AAWSEM makes it suitable for fully sampling the part of the conformational space corresponding to the functional states of IDPs, which is significantly larger for disordered proteins than it is for folded proteins.
Here, we performed simulations with AAWSEM to investigate the interactions underlying the structural transitions between the PAGE4 conformational ensembles. Consistent with the experimental findings, our simulations show a change in the size of PAGE4 upon phosphorylation. By analyzing contact formation in all phosphoforms of PAGE4, we see that the formation and destabilization of an N-terminal loop is the predominant source of this variation in size. After gaining insights into the differences between the conformational ensembles of different forms of PAGE4 (wild type, i.e., non-phosphorylated WT-PAGE4, double-phosphorylated HIPK1-PAGE4, and hyper-phosphorylated CLK2-PAGE4), we developed a mechanism-based mathematical model to describe how switching from one form to another (e.g. from HIPK1-PAGE4 to CLK2-PAGE4) can affect the dynamics of the PAGE4/AP-1/AR regulatory circuit. The oscillations observed in this circuit suggest that PAGE4 conformational dynamics may contribute to phenotypic plasticity and, thus, influence the efficacy of therapeutic targeting of AR in PCa.
Results
The sequence properties of PAGE4
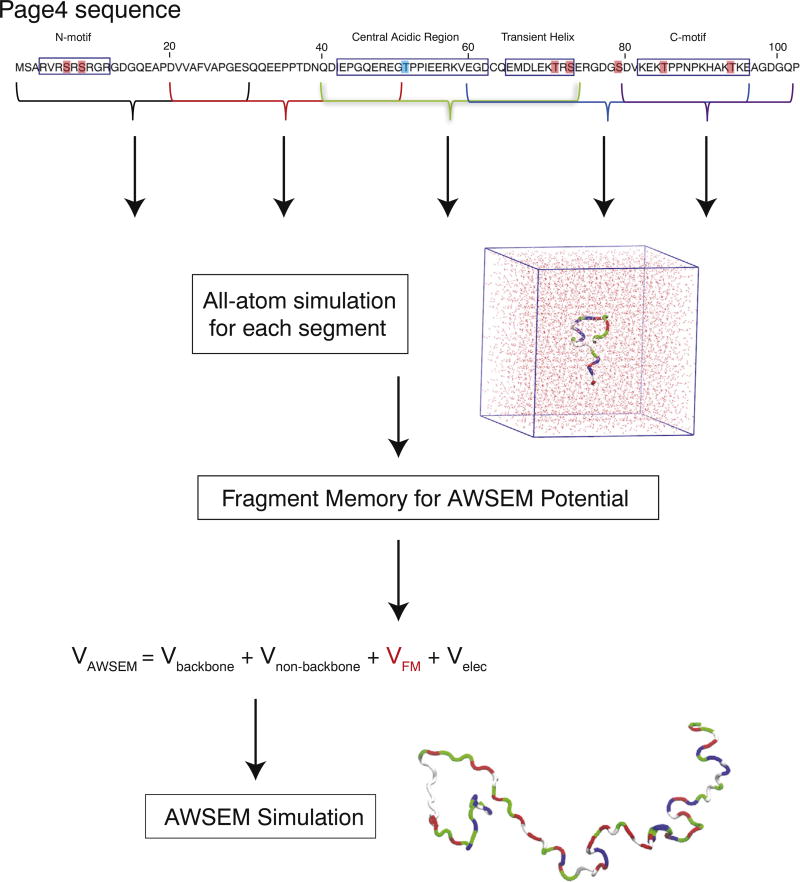
PAGE4 is a 102-residue disordered protein. Simple considerations of mean hydrophobicity [29] and net charge often suffice for predicting whether a protein will be intrinsically disordered [30], and we find that all phosphoforms of PAGE4 are predicted to be disordered according to these parameters (Fig. S1). Most of the residues in PAGE4 are predicted to have a greater than 50% chance of adopting a random coil conformation by secondary structure prediction tools [31] (except for residues Cys63 and Gln64, which are predicted to be helical and are located in the region that is experimentally found to exhibit transient helicity) (Fig. 1). PAGE4 is also a highly charged proteins, with a total of 16 postively charged residues and 24 negatively charged residues, resulting in a net charge of −8e. The charged residues are not evenly distributed. The N-motif (residues 4 to 12) and C-motif (residues 82 to 95) are positively charged, and there is a central acidic region (residues 43 to 62) that is negatively charged. Also, there is a nine-residue region (residues 65 to 73) that can transiently adopt a helical conformation as shown by NMR [32]. HIPK1 phosphorylates two sites in PAGE4—a partial phosphorylation at Ser9 (30 % ~ 40% occurrence, within the N-motif) and a nearly complete phosphorylation of Thr51 (>95% occurrence, within the central acidic region) [32]. CLK2 phosphorylates eight sites of PAGE4, with most of them undergoing nearly complete phosphorylation: Ser7 (>95%), Ser9 (>95%), Thr51 (>95%), Thr71 (50%), Ser73 (75%), Ser79 (50%), Thr85 (>95%), and Thr94 (60%) [16]. Since both Ser7 and Ser9 reside in the N-motif, and Thr85 and Thr94 reside in the C-motif, the hyperphosphorylation neutralizes the N-motif and the C-motif. On the other hand, Thr51 resides in the central acidic region, and Thr71 and Ser73 reside in the transiently helical region. The phosphorylation of Thr51, Thr71 and Ser73 changes the local conformational preferences of the residues in those regions, contributing to a shift of the structural ensemble.
Fig. 1.
The sequence of PAGE4 and a schematic summary of the AAWSEM simulation protocol. The sites phosphorylated by HIPK1 are highlighted in blue; those phosphorylated by CLK2 are highlighted in red. All phosphoforms of PAGE4 were separated into five segments of approximately 30 residues each that preserve the previously identified motifs: Segment 1 (residues 1 to 30), Segment 2 (residues 20 to 50), Segment 3 (residues 40 to 74), Segment 4 (residues 60 to 96), and Segment 5 (residues 80 to 102). Each segment was simulated in an explicit-solvent environment using continuous simulated tempering (CST) [33]. The structural ensemble consisting of structures sampled by CST at temperatures between 293 and 330K was clustered into subensembles and passed as fragment memories to the AWSEM model for the coarse-grained level simulations of the entire PAGE4. A representative structure of PAGE4 colored by residue type (non-polar residues white, basic residues blue, acidic residues red and polar residues green [36]) is shown at the bottom. The PAGE4 sequence representation at the top is adapted from [16].
Phosphorylation by HIPK1 and CLK2 changes the size of PAGE4
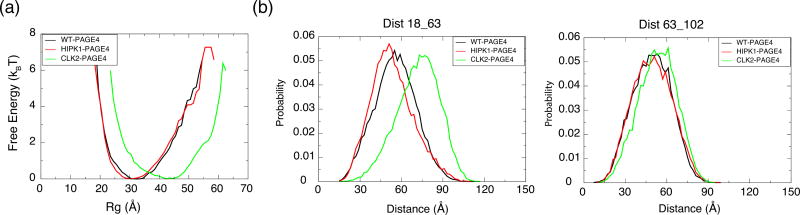
Our simulations indicate that PAGE4 changes in size upon being phosphorylated. The overall size of the protein can be measured using the radius of gyration (Rg). The preference of each phosphoform for adopting a structure of a particular overall size is captured by the free energy profiles as a function of Rg (Fig. 2a). It is clear from the free energy profiles that CLK2-PAGE4 is more expanded compared with HIPK1-PAGE4 and that HIPK1-PAGE4 is slightly more compact than WT-PAGE4.
Fig. 2.
Size and distance measurements of PAGE4 ensembles from simulations. (a) The free energy profiles as a function of the radius of gyration (Rg) of the simulated phosphoforms of PAGE4. (b) The probability distributions of site-specific distances between two residues that were previously measured in smFRET experiments. (left) residue 18 and 63; (right) residue 63 and 102.
In order to further quantify the size of different phosphoforms of PAGE4—WT-PAGE4, HIPK1-PAGE4 and CLK2-PAGE4—and to compare these sizes with experimental measurements [16], we calculated the average Rg of each form of PAGE4. The calculated 〈Rg〉 values for the three phosphoforms of PAGE4 are presented in the second column of Table 1. The simulations qualitatively reproduce the changes in size upon phosphorylation seen in the SAXS experiments [16]. Moreover, the calculated 〈Rg〉 is quantitatively close to the experimental values (Table 1). As a side comment, the Rg values of disordered proteins are sometimes estimated by assuming a random-coil model with parameters that have been fitted using data collected from several IDPs [33,35] (Eq. (1)).
| (1) |
Table 1.
A summary of the size measurements of the PAGE4 phosphoforms from both the AAWSEM simulations and the SAXS and smFRET experiments
| SAXS 〈Rg〉 (Å) | FRET efficiency 〈E〉 | FRET RMS Dist (Å) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||
| Res. 18–63 | Res. 63–102 | Res. 18–63 | Res. 63–102 | |||||||
|
|
|
|
|
|
||||||
| EXPa | SIMb | EXP | SIM | EXP | SIM | EXP | SIM | EXP | SIM | |
| Wild-type form | 36 ± 1.1 | 32.9 | 0.55 | 0.48 | 0.64 | 0.60 | 56 | 57.4 | 50 | 51.2 |
| HIPK1 form | 34.7 ± 1.2 | 32.1 | 0.52 | 0.53 | 0.63 | 0.60 | 59 | 55.6 | 50 | 51.4 |
| CLK2 form | 49.8 ± 1.9 | 41.8 | 0.35 | 0.22 | 0.58 | 0.52 | 75 | 73.4 | 55 | 54.8 |
EXP, experimental results [16].
SIM, simulation results (this study).
In Eq. (1), N the number of residues, R0 = 2.54 Å, and ν = 0.522. Using Eq. (1) to estimate the Rg of PAGE4 yields a value of ≈ 28A. Therefore, this generic estimate fails to capture the overall dimensions of PAGE4, and we see that all three forms of PAGE4 are more expanded than other IDPs with the same number of residues.
Phosphorylation-induced expansion of PAGE4 is localized to the N-terminal half
In addition to information about the overall size of PAGE4 obtained through analysis of SAXS experiments, smFRET experiments provide further insight into the changes in size of the N-terminal and C-terminal halves of PAGE4 upon phosphorylation [16]. The smFRET experiments showed that the size of the N-terminal half of the protein, as measured by the distance between the donor and acceptor dyes that were attached to residues 18 and 63 (Dist18_63), had a much larger increase in the hyper-phosphorylated form (56 to 75 Å) than in its double-phosphorylated form (56 to 59 Å). In comparison, the size of the C-terminal half of PAGE4 is less sensitive to phosphorylation. The distance between residues 63 and 102 (Dist63_102) changes from 50 to 55 Å (Table 1) upon hyperphosphorylation, and there is not a significant change in the size of the C-terminal half of PAGE4 upon double-phosphorylation. These distance changes were inferred based on a large decrease of FRET efficiency upon hyper-phosphorylation, and we provide both distance and efficiency comparisons between our simulations and the corresponding experiments in Table 1 (columns 3, 4).
Our simulations yield distances that are similar to the distances inferred from experiment (Fig. 2b and Table 1). Since the AAWSEM model represents each amino acid using only three explicitly simulated atoms (Cα, Cβ, and O atoms), we approximated the distance between the probes attached to the two residues by the distance between their Cα atoms. In good agreement with experiment, our simulations show that Dist18_63 changes from 57.4 Å in WT-PAGE4 to 73.4 Å in CLK2-PAGE4, while Dist63_102 changes from 51.4 to 54.8 Å. By converting the distances observed in our simulations to FRET efficiencies using a Förster radius of 52.4 Å [16], we also reproduce the decrease in the average FRET efficiency measured for N-terminal PAGE4 upon hyper-phosphorylation (from 0.48 for WT-PAGE4 to 0.22 for CLK2-PAGE4).
The structural expansion in the N-terminus of PAGE4 upon hyperphosphorylation is associated with the loss of loop formation
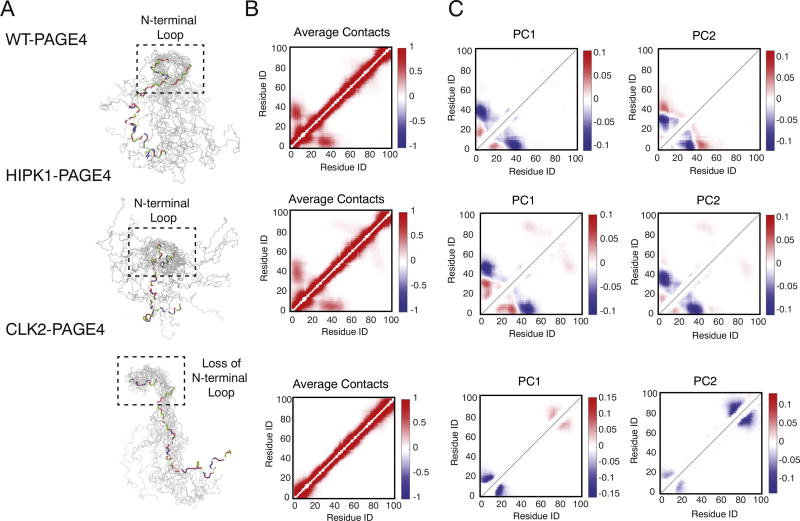
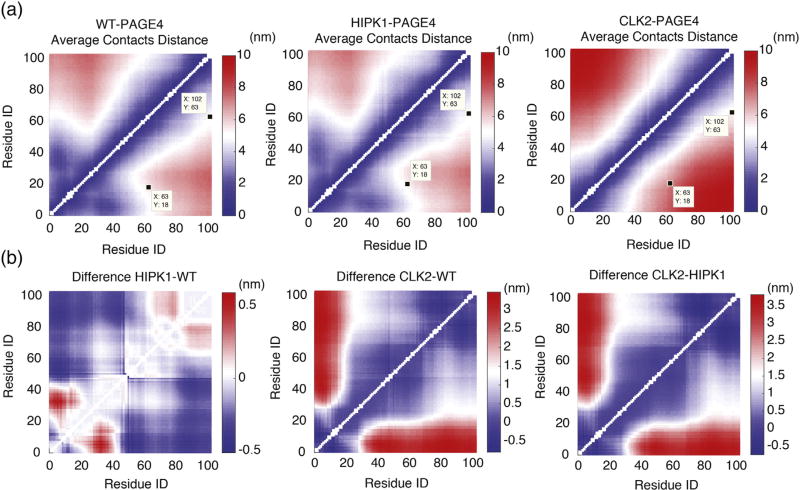
Our simulations enable us to probe the structural details of PAGE4 conformational heterogeneity. Contact formation analysis of the ensembles of simulated structures shows that the expansion of PAGE4 upon hyperphosphorylation is caused by the loss of an N-terminal loop between the N-motif and the central acidic region (Fig. 3). The N-motif has an excess of basic residues in both WT-PAGE4 and HIPK1-PAGE4, which allows the N-motif to easily interact with the central acidic region around residue 40. These specific interactions lead to frequent loop formation. In contrast, the N-motif is neutralized upon hyperphosphorylation, which causes a loss of this loop formation and, ultimately, to a more expanded CLK2-PAGE4. To visualize this loop formation, we plot the average probabilities of contact formation of all phosphoforms of PAGE4 from the AAWSEM simulations (Fig. 3). Since the electrostatic interactions were modeled using a screened Debye–Huckel potential with a Debye length of 10.0 Å (see Materials and Methods, The AAWSEM Force Field for more details), we used the cutoff value of 20.0 Å between the Cβ atoms for creating the contact maps in Fig. 3. This choice of a relatively large cut-off value for the definition of a contact allows us to capture the electrostatic interactions between residues before the interactions between the residues decay to 20% of their value at the Debye length. Also, since we are mostly interested in non-local interactions, contacts are defined only for the residues that are at least three residues apart from each other in sequence. As shown in Fig. 3b, in both WT-PAGE4 and HIPK1-PAGE4, the N-motif region has a non-zero probability for forming contacts with the central acidic region, while no such contacts are formed in CLK2-PAGE4. There are also interactions being formed between the C-motif and the central acidic region in WT-PAGE4 and HIPK1-PAGE4, although the frequency of contact formation between the C-motif and the central acidic region is lower than that of the N-motif and the central acidic region. In addition, we have analyzed the average distance between each pair of residues in all of the simulated PAGE4 ensembles (Fig. 4a). The differences between these predicted average distances (Fig. 4b) can be used to select pairs of residues to label in future smFRET experiments that can best reveal the change of PAGE4 size upon phosphorylation.
Fig. 3.
The structural ensembles of different phosphoforms of PAGE4 collected from the AAWSEM simulations. (a) Representative structures from the structural ensembles generated by AAWSEM. Randomly picked structures are aligned to minimize the RMSDs between their N-motifs [36]. It is clear that the N-terminal loop forms in the WT- and HIPK1-PAGE4, while no loops are formed in the CLK2-PAGE4. (b) The average contact maps generated based on the simulated ensembles. The color bar shows the probability of contact formation. There are non-zero probabilities for interactions between the N-motif and the central acidic region as well as the C-motif and the central acidic region. (c) The top two principal component modes generated by the contact-based principal component analysis. We plot the coefficients of the first two principal components PC1 and PC2.
Fig. 4.
The average distance of residue pairs are calculated from simulations. (a) The average distance between each pair of residues calculated from our simulations for three phosphoforms of PAGE4. The residues pairs probed by the FRET experiment [16] are labeled. (b) The difference in average distance between residue pairs among three phosphoforms of PAGE4.
Although the average contact map shows a higher likelihood of N-terminal loop formation inWT-PAGE4 and HIPK1-PAGE4 as compared to CLK2-PAGE4, it does not capture any information regarding the correlated motions sampled during the simulations. To further understand the collective conformational movements, we performed principal component analysis (PCA) based on the contact maps of the simulated structures. The contact PCA approach used here is similar to that used in previous studies [37,38]. We plot the coefficients of the top two principal components. Large coefficients correspond to contacts that vary more in that principal mode, and the relative sign of any two coefficients indicates whether the corresponding contacts form in a correlated or anti-correlated manner in that mode. In WT-PAGE4 and HIPK1-PAGE4, PC1 shows correlated contact formation between residues in the N-motif and the central acidic region (the blue halo between residues ~10 and residues ~50 in Fig. 3c), indicative of frequent loop formation in the N-terminal half of PAGE4. In contrast, in CLK2-PAGE4, correlated contact formation occurs only among residues that are close in sequence. Interestingly, we also observe correlated contact formation between the C-motif and the central acidic region in HIPK1-PAGE4. The principal component coefficients of this motion have the opposite sign to those in the N-motif (the red halo between residues ~50 and residues ~90 in Fig. 3c), and are weaker than the coefficients corresponding to contacts between the N-motif and the central acidic region. The observed PCA patterns thus suggest competitive and anti-correlated contact formation between the central acidic region and either the N-motif or the C-motif, both of which “take turns” forming a loop with the central acidic region. These long-range interactions are also observed in Fig. 4a and were detected experimentally as shown in, for example, Fig. 7 of [32]. The observation of loop formation hints at a fly-casting motion that is frequently observed in the study of disordered proteins [39–41].
Fig. 7.
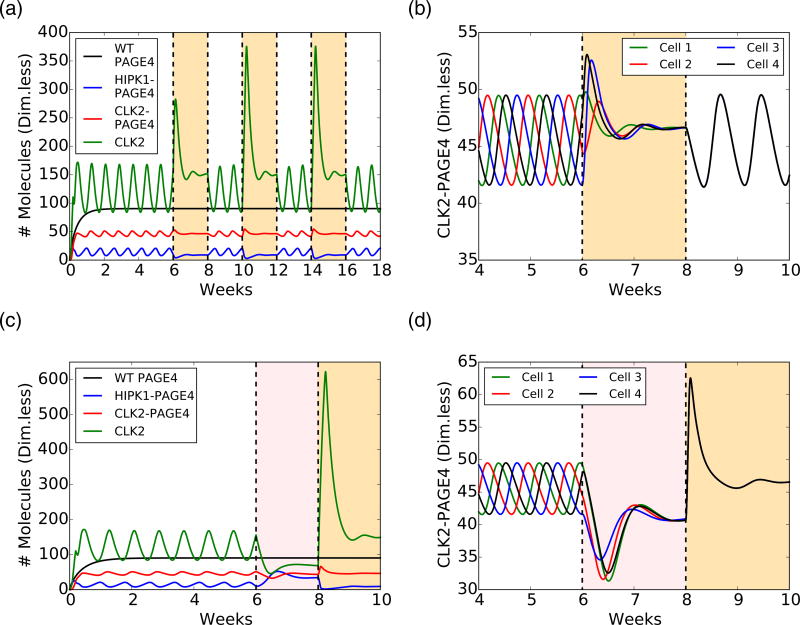
Intermittent ADT and BAT temporarily quench oscillations and synchronize the cell population's phenotypic dynamics. (a) Temporal dynamics of WT-PAGE4, HIPK1-PAGE4, CLK2-PAGE4, and CLK2 under intermittent ADT. In the simulation, ADT was applied and removed at regular intervals of 2 weeks (the orange-shaded areas indicate when the therapy is on). (b) Temporal dynamics of CLK2-PAGE4 in four different unsynchronized cells (i.e., the oscillations of CLK2-PAGE4 are not in phase). A 2-weeks pulse of ADT synchronizes the cellular dynamics across the population. (c) Temporal dynamics under BAT. The pink-shaded area indicates the 2 weeks of AR overexpression, while the orange-shaded area depicts the subsequent 2 weeks of ADT. Oscillations are quenched in 4 weeks of treatment, but after 2 weeks, levels of HIPK1-PAGE4 decrease, while levels of CLK2-PAGE4 increase. After 2 weeks of ADT, the levels are similar to those observed in continuous ADT. (d) Similar to intermittent ADT, BAT synchronizes cellular dynamics. In all plots, concentrations of WT-PAGE4, HIPK1-PAGE4, CLK2-PAGE4, and CLK2 are represented in arbitrary dimensionless units.
Changes in turn-like structures upon phosphorylation
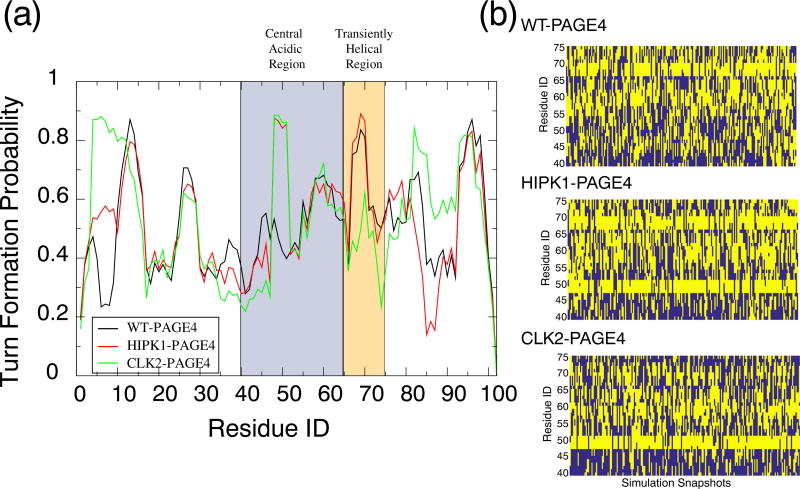
In addition to indicating the expansion of PAGE4 upon hyperphosphorylation, NMR experiments suggested that a more compact structure of HIPK1-PAGE4 is accompanied by an increase of turn-like structures in the central acidic region [32]. Our simulations indeed find an increase of turn structure in this region (Fig. 5). The most prominent increase in turn structure occurs between Arg48 and Thr51, where the probability of forming a turn structure increases from 40% (in WT-PAGE4) to 80% (in HIPK1-PAGE4, Fig. 5a). This increase in turn-like structures is probably due to the phosphorylation of Thr51. The simulations also display a more populated turn structure in the same region upon hyperphosphorylation. Because no other residues close to Thr51 are further phosphorylated upon hyperphosphorylation, CLK2-PAGE4 shares the same structural features as HIPK1-PAGE4 in the central acidic region.
Fig. 5.
Turn-like structure propensity of the PAGE4 phosphoforms. (a) The probability for each residue to adopt a turn-like structure. The central acidic region and transiently helical region are shaded in blue and orange, respectively. The secondary structure was calculated using the Stride algorithm [42]. (b) The dynamics of turn formation per residue during the simulations of each phosphoform of PAGE4. We only show the residues in the central acidic region and the transiently helical region. A yellow block indicates that the residue was identified by Stride to be in a turn structure, while blue means that it was not.
Two other residues in the transiently helical region (Thr71 and Ser73) are further phosphorylated by CLK2. Phosphorylation of Thr71 and Ser73 causes a reduction of turn structure in this region (Fig. 5a). The simulation time trace of turn-like structures in this region also changes upon phosphorylation (Fig. 5b). The change of turn-like structure signifies a transient order–disorder transition in this local region. It has been hypothesized that the binding site for the AP-1 complex is located in this region of PAGE4 [32]. Therefore, our simulations suggest that the hyperphosphorylation of PAGE4 by CLK2 results in a loss of order in the transient helix, which may then be responsible for a decrease in binding affinity between PAGE4 and the AP-1 complex.
Implications of switching between CLK2-PAGE4 and HIPK1-PAGE4 for plasticity in PCa cells
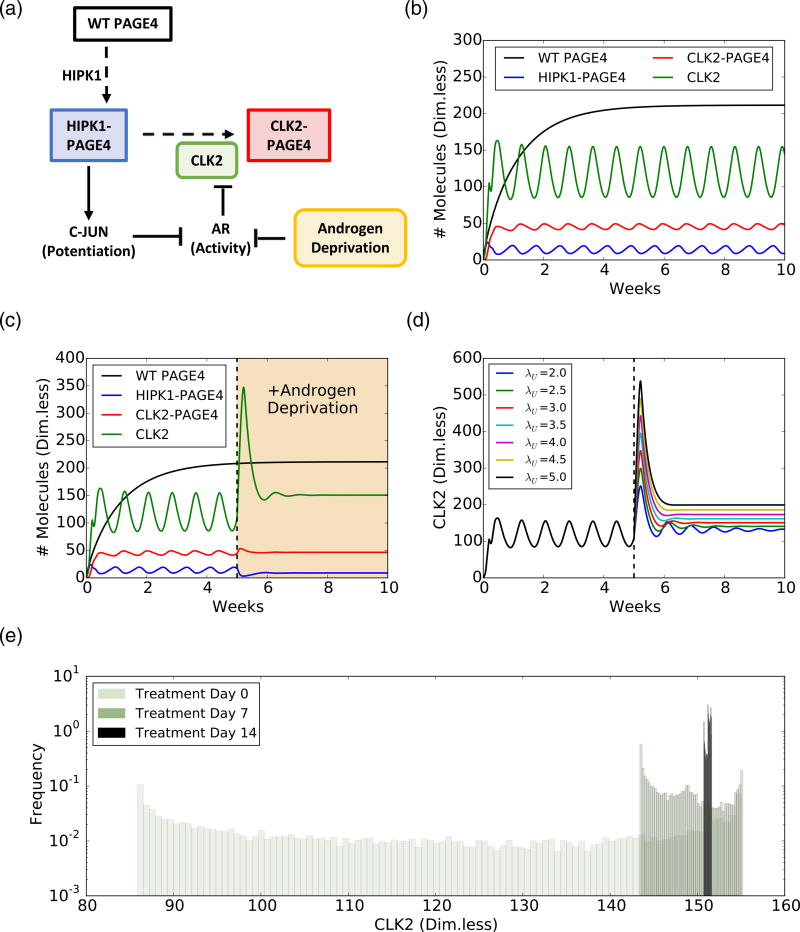
To investigate the consequences of PAGE4 structural dynamics in modulating cellular plasticity, we constructed a coarse-grained mathematical model of PAGE4 intracellular dynamics and its interactions with the AP-1/AR signaling axis (Fig. 6a). The model considers the three relevant PAGE4 phosphoforms (WT-PAGE4, HIPK1-PAGE4 and CLK2-PAGE4) and the enzymes catalyzing the reactions that convert WT-PAGE4 into the doubly-phosphorylated and hyperphosphorylated forms (HIPK1, CLK2). As mentioned previously, HIPK1-PAGE4 and CLK2-PAGE4 have significant differences in their potentiation of c-Jun and binding to AP-1. Because c-Jun potentiation can indirectly increase the level of CLK2, a negative feedback loop is formed that can give rise to oscillatory behavior of the levels of HIPK1-PAGE4, CLK2-PAGE4, and, consequently, AR activity [16]. Our previous modeling efforts have shown that this PAGE4/AP-1/AR circuit can generate oscillations between an androgen-dependent phenotype (characterized by high levels of HIPK1-PAGE4) and an androgen-independent phenotype (characterized by high levels of CLK2-PAGE4) [16]. Here, we extend this model by including the temporal dynamics of WT-PAGE4 and modeling different hormone-deprivation treatments for PCa (see Materials and Methods, Mathematical model for the PAGE4/AP-1/AR regulatory axis for further details). The extended model exhibits similar phenotypic oscillations between a (high HIPK1-PAGE4, low CLK2-PAGE4) state and a (low HIPK1-PAGE4, high CLK2-PAGE4) state when no treatment was applied (Fig. 6b) in quite a robust manner; varying the model parameters by 10-fold still results in a model that exhibits oscillations (Fig. S4A, B).
Fig. 6.
Androgen deprivation suppresses phenotypic oscillations and eliminates heterogeneity in a PCa cell population, as predicted by a mathematical model. (a) Schematic of the PAGE4 phosphorylation circuit and its connection with androgen resistance. WT-PAGE4 is double phosphorylated by HIPK1 enzyme, and the resulting HIPK1-PAGE4 complex can be hyperphosphorylated via the CLK2 enzyme. Furthermore, HIPK1-PAGE4 regulates CLK2 via the intermediates c-Jun and AR. The cell under hormonal therapy is deprived of androgen, thereby decreasing AR activity. (b) Temporal dynamics of the intra-cellular levels of WT-PAGE4, HIPK1-PAGE4, CLK2-PAGE4, and CLK2. Without ADT, the oscillatory behavior exhibits a period of approximately 1 week. (c) ADT (orange-shaded area) quenches oscillations within approximately 2 weeks. (d) Temporal dynamics of the CLK2 cellular level for various CLK2 production rate fold-changes λU due to ADT. Any fold-change greater than or equal to 2 is sufficient to quench the oscillations. The value used in panel C is 3. (e) Distribution of CLK2 cellular level in a simulated cohort of 10000 PCa cells. Before treatment (day 0), the distribution spans over the whole range of CLK2 levels observed in the single cell simulation of panel B. After one week of treatment (day 7), the distribution considerably narrows. At day 14 of treatment, all cells have a similar level of CLK2. In all plots, the concentrations of WT-PAGE4, HIPK1-PAGE4, CLK2-PAGE4, and CLK2 are represented in arbitrary dimensionless units.
First, we establish the period of oscillation to be approximately a week (Fig. 6b). This timescale arises from estimated half-life of non-phosphorylated, that is, WT-PAGE4 (≈150 h) [15], and is comparable to various hormone-deprivation treatments applied in the clinic [43,44], which motivated us to investigate the effect of various therapies. As a next step, we considered a constant inhibitory signal acting on the AR to simulate the effect of continuous Androgen Deprivation Therapy (ADT)—the standard care of therapy for over 75 years for locally advanced and/or metastatic PCa [43]. ADT quenched the oscillations and pushed the cells into a resistant phenotype (Fig. 6c). Quenching of oscillations is sensitive to the assumed fold-change in the decrease of AR activity levels, but only depended weakly on the specific mathematical form chosen to model ADT (Figs. 6d and S3C, D).
Next, we simulated continuous ADT in a cohort of 10,000 independent PCa cells. In this cohort, each cell displays oscillations with the same period, but they are not synchronized; that is, their oscillations have a non-zero phase difference. Therefore, the distribution of intracellular levels of CLK2 is quite broad before ADT is applied (Fig. 6e, day 0). After a week of therapy, the heterogeneity is considerably decreased, and after 2 weeks, all cells present similar levels of CLK2 (compare the distribution of CLK2 levels in day 0, day 7, and day 14 in Fig. 6e). Thus, ADT for a period of 2 weeks can not only quench the oscillations but also limit phenotypic heterogeneity significantly in an isogenic PCa cell population. It should be noted that our model focuses on cells that are not killed by therapeutic treatment. Thus, on one hand, cells with an androgen-dependent phenotype are highly likely to be killed by ADT, and on the other, ADT limits phenotypic heterogeneity among the cells that are not killed by ADT. A corollary implication that follows is that the population now turns more homogeneous comprising of androgen-independent cells.
Motivated by these results, we implemented an intermittent ADT treatment [43], where cells are periodically exposed to ADT for a limited time (2 weeks on–2 weeks off). Oscillations disappeared during the cycles of ADT but re-emerged once ADT was removed (Fig. 7a). Intriguingly, intermittent ADT coupled the oscillations of unsynchronized cells. We set up a simulation of four unsynchronized cells and tracked their level of CLK2-PAGE4. The oscillations became synchronized after the first round of ADT because the treatment pushed all cells to a similar state (Fig. 7b). Furthermore, we varied the duration of ADT pulses and discovered that a single pulse with a duration as short as 4 days could synchronize cells in the model (Fig. S5). Such synchronization can limit the phenotypic heterogeneity in cells that survive androgen deprivation. Intermittent androgen deprivation (IAD) therapy has been studied both in xenografts and in the clinic with varying time periods of androgen deprivation and the drug holiday in between [45]. Our model simulations offer a plausible explanation as to why the period of androgen deprivation should be at least on the order of a few weeks in length.
Lastly, we considered the bipolar androgen treatment (BAT), another novel treatment for PCa [43]. This therapy consists of 4 weeks of ADT with an AR overexpression signal that was on for the first 2 weeks. BAT suppressed oscillations during both treatment phases, but the cell was pushed to different states (Fig. 7c). The activation of AR and the consequent inhibition of CLK2 enforced a higher level of HIPK1-PAGE4. Conversely, the last 2 weeks of ADT led to the already observed resistant phenotype with low HIPK1-PAGE4 (compare pink-shaded and orange-shaded regions in Fig. 7c). Similar to the intermittent ADT case, BAT synchronized phenotypic oscillations of otherwise unsynchronized cells by quenching the oscillatory dynamics of the PAGE4/AP-1/AR circuit (Fig. 7d). Therefore, our results showed that, similar to ADT, both BAT and IAD can reduce phenotypic heterogeneity in a PCa cell population. Thus, ADT, BAT, and IAD likely make the cell populations more vulnerable to therapeutic strategies.
Discussion
PAGE4 is a prototypical IDP with pleiotropic functions. Despite being considered to be almost entirely disordered based on data obtained using various biophysical measurements [46], our simulations show that PAGE4 has functionally important structural features that are modulated by phosphorylation.
While the biophysical experimental techniques used previously to discern the various PAGE4 conformational ensembles are routinely used to study IDPs, as far as we are aware, they have not been used in parallel to make measurements of the same IDP under identical experimental conditions. Furthermore, quite remarkably, the structural data collected on PAGE4 show a very high level of agreement not only among the different biophysical techniques used but also between the theoretically computed and experimentally observed values.
Although the biophysical techniques employed can correctly capture some ensemble-based properties of PAGE4 such as the size and the distance in between two smFRET probes, there is still a gap between the highest time resolution that can be achieved experimentally and that of the structural dynamics of proteins. This problem is especially prominent for a protein that is highly disordered and exists as an ensemble of rapidly interconverting conformers. In this case, MD simulations with an optimized coarse-grainedforce field provide us with additional structural details on the various phosphoforms of PAGE4. Our MD simulations accurately reproduce the ensemble averaged features of PAGE4 in both the unphosphorylated and phosphorylated states. This consistency provides strong evidence that our model is able to correctly represent the structural ensembles seen experimentally.
Frequent N-terminal loop formation in both WT-PAGE4 and HIPK1-PAGE4, as seen in our PCA analysis, is reminiscent of the “fly-casting” mechanism that has been proposed for other disordered proteins [39–42]. Fly-casting proteins typically have a relatively unstructured state with a large capture radius. This disordered state binds weakly at a relatively large distance, followed by folding as the protein approaches the binding site, analogous to a fly-casting motion. The structural plasticity of the protein allows for a combination of binding and folding motions, which facilitates protein-DNA recognition. PAGE4 is a highly charged molecule and, therefore, it is possible that PAGE4 can bind to both c-Jun of the AP-1 protein complex and DNA (the AP-1 binding site on the promoter). The regular dynamic motion of the N-terminal portion and the frequent loop formation could enlarge the capture radius for PAGE4 to find its binding partner, which would increase the rate of c-Jun transactivation. CLK2-PAGE4 loses this regular motion, which is replaced by a more disordered N-terminal motion. The loss of specificity may lead to a reduced binding affinity of PAGE4 [16] to AP-1, which eventually results in the degradation of PAGE4 itself.
Our simulations also indicate an increase of turn-like structure in the central acidic region upon double-phophorylation and hyperphosphorylation. We also see a loss of turn-like structure in the transient helical region upon hyperphosphorylation. Consistent with the former observation, a recent NMR study [32] suggested that an increase of turn-like structure in the central acidic region was the source of a slightly more compact structure of HIPK1-PAGE4. The loss of turn structure in the transient helix indicates a partial order–disorder transition. The order–disorder transition has been previously shown to be a part of protein function to lower the free energy barrier and increase the kinetic rate of conformational rearrangements [47–50]. Here, this transition offers another way by which phosphorylation modulates the binding affinity of PAGE4 to the AP-1 protein complex. Because the transiently helical region was previously suspected to be a potential binding site of the AP-1 complex [32], this order–disorder transition can serve to disrupt the binding site, leading to the release of AP-1 upon PAGE4 hyperphosphorylation and the attenuation in c-Jun potentiation. This conjecture is based entirely on the structural analysis of PAGE4. Further studies including simulations of binding of PAGE4 to the AP-1 complex along with the cognate DNA binding site are currently underway.
To gain insights into the functional implications of the conformational dynamics of PAGE4 in PCa management, we designed a coarse-grained mathematical model. The main goal of the model was to discern how the different conformational ensembles of PAGE4 may modulate androgen insensitivity in PCa cells through their opposite interactions with the AP-1/AR axis. Our model predicted oscillations in the levels of the different PAGE4 conformational ensembles as well as in HIPK1, CLK2 and AR activity. These oscillations occur on a timescale of a week, which corresponds to approximately the half-life of WTPAGE4. These observations support our previous experimental observations that cells in an isogenic population may exhibit phenotypes with varying androgen deprivation sensitivities [51]. Therefore, it is plausible that, in addition to extrinsic signals, phenotypic plasticity can also arise from intracellular dynamics [52,53], in this case, by “conformational noise” [53,55] emerging from switching between different conformational states of PAGE4. Moreover, cells in a given population likely oscillate with some phase difference between each other, giving rise to non-genetic heterogeneity, a burgeoning therapeutic challenge in PCa [56,57]. A recent study [58] shows that phosphorylation in Hsf1 (Heat Shock Factor 1) can generate non-genetic heterogeneity and antifungal resistance, further strengthening our argument.
According to our model, all therapies—continuous ADT, IAD, and BAT—eliminated the oscillations and pushed cells toward a resistant phenotype. Furthermore, the treatments largely diminished phenotypic heterogeneity in a cohort of PCa cells within 2 weeks. A limitation of our model is that we do not consider cell death being induced by any of the therapies; in other words, the model predictions mentioned above are only for a subset of cells that are not killed during therapeutic treatment. Extending this mathematical formalism to a population-level approach that considers accelerated cell death in the presence of hormonal treatments [59] would represent a step forward toward formulating predictions of potential clinical relevance, especially given that ADT has remained the standard of care for metastatic and locally advanced PCa for over 75 years. Oscillations were rescued when the inhibition on AR during IAD was removed. However, due to limited phenotypic heterogeneity, the cell population oscillated in phase after the treatment was applied. The perfect synchronization observed here can potentially also be disrupted by noise and biological effects beyond what is considered in the model. However, the hormonal treatment [60] could introduce a coherence time or window where the intracellular temporal dynamics of different cells appear correlated. Such predictions that can be experimentally validated using live-cell reporters for AR activity are currently being explored in our laboratories.
Materials and Methods
The AAWSEM force field
We used a recently developed model, AAWSEM, for our simulations of the structures of the various phosphoforms of PAGE4. AAWSEM is a variant of AWSEM. Details of AAWSEM have been given elsewhere [27,28]. Here, we only briefly summarize this forcefield. The AWSEM Hamiltonian is a coarse-grainedforce field that represents the backbone structure of the simulated proteins using three atoms per residue: the Cα, Cβ, and O atoms. The positions of all of the other backbone atoms can be calculated on the fly by assuming an ideal planar peptide bond geometry. The AWSEM Hamiltonian can be decomposed into four components (Eq. (2)).
| (2) |
In Eq. (2), Vnon − backbone = Vcontact + Vburial + VHB. The Vbackbone term dictates the backbone geometry of the protein. The Vnon − backbone term describes the residue-residue interactions that are not related to backbone connectivity. The Vburial term is a many-body term that depends on the density of the immediate environs surrounding each residue. The VHB hydrogen bonding term and the VFM fragment memory term determine the secondary structures preferred by the protein. VHB can be informed by a secondary structure prediction [31,61]. The Vcontact = Vdirect + Vwater is a contact term describing the tertiary interactions between each pair of residues that are separated by more than 9 residues along the sequence. It is composed of two terms. captures the direct protein–protein interaction. describes the water-mediated and protein-mediated interactions. The γ parameters were optimized based on a database of training structures culled from the PDB. The quantity that was maximized during the optimization was the ratio of the folding temperature to the glass transition temperature, Tf/Tg [62–64]. The fragment based associative memory term, VFM, is of the form , where σij = |i − j|0.15 is a sequence separation-dependent interaction well width. The rijs are the cartesian distances between the Cα and Cβ atoms of two residues i and j. is the corresponding distance in the memory structures. VFM guides the local-in-sequence interactions of the Cα and Cβ atoms and can be based on fragments obtained in one of two ways. In conventional AWSEM simulations, VFM comes from searching the PDB for structures that share a similar sequence with the simulated sequence locally. In AAWSEM, VFM comes from exhaustive all-atomexplicit-solvent simulations. Since disordered proteins do not usually have solved structures in the PDB database, here we chose to use atomistic simulations to obtain the fragment memory structures.
In the original version of AAWSEM, the full sequence of a protein was initially segmented in overlapping parts based on the output from secondary structure prediction tools such as PSSpred [31]. Then, the segments were simulated using an all-atom model in explicit solvent. Here, since PAGE4 is predicted by PSSpred to be almost completely disordered, we segmented it according to the empirical motifs that have been annotated in the literature [32]. The segmentation scheme is shown in Fig. 1. Segments were simulated with an enhanced sampling method known as CST [33,65] to achieve an equilibrated structural ensemble. CST was performed in a temperature range of 293–350K and the structures that were sampled at temperatures below 330K were selected for structural clustering. After the clustering of structures by the “single linkage” algorithm, the central structure of each cluster was selected as a memory structure. The weight of the VFM term was assigned according to the size of each structural cluster.
The Velec electrostatic term is the screened Debye–Huckel interaction, which approximates the screening effect of charge–charge interactions in solution. The details of this term were described in a separate paper [66]. The form of Velec is given in Eq. (3).
| (3) |
In Eq. (3), KElec = (4πε0)−1 = 332.24 kcal · Å · mol−1 · e−2 and εr is the dielectric constant of the media. qi and qj are the charges of the residues i and j. is the Debye length where I is the ionic strength of the solution. Following the previous study, we used εr = 80.0 and lD = 10.0 Å throughout our simulations to mimic typical physiological conditions. Cscaling is a constant that we introduced in this study for tuning the relative strength of the electrostatic potential compared with other energy terms of the AWSEM Hamiltonian. In this study, we performed simulations with Cscaling = 1.0, 2.0, and 4.0. We found that the simulations with Cscaling = 4.0 matched the experimental results quantitatively [16]. Smaller values of Cscaling resulted in qualitative agreement between simulations and experiments but poorer quantitative agreement (see the Supporting Information Fig. S2, Table S1). Thus, the analyses throughout the main text are based on the Cscaling = 4.0 simulations. We used the same value of Cscaling to study different phosphorylated forms of PAGE4. Thus, the changes in the conformational preferences of PAGE4 upon phosphorylation are true predictions of this model. We performed simulations in a neutral pH environment by setting the charges of Glu (glutamic acid) and Asp (asparic acid) residues to −1e, while those of Arg (arginine) and Lys (lysine) residues were set to +1e.
Calculation of free energy profiles and expectation values
The free energy F was calculated as F = − kBT log (P) where P is the probability for the protein to have a specific value of the Rg. Expectation values of Rg were calculated using Eq. (4).
| (4) |
In Eq. (4), p(Rg) is the probability density as a function of Rg.
Treatment of phosphorylation
Approaches to simulate phosphorylation have been studied in previous work using the AMH model [37,38], which was the predecessor of AWSEM model. In a previous approach, the phosphorylated residues were simulated as “super-charged” glutamic acid (Glu) residues. We adopted the same method in this study, where both the phosphorylated Ser (serine) and phosphorylated Thr (threonine) were simulated as a Glus. Since the pKAs of phospho-serine and phospho-threonine were determined to be less than 7 in experiment [67], we simulated the phosphorylated residues with a charge of −2e. Furthermore, because the phosphorylation probability was found to be variable among the different forms of PAGE4, we multiplied the charge by its phosphorylation probability to reflect this variability. For example, the Ser9 was shown by experiment to have a 30 % ~ 40% probability to be phosphorylated in HIPK1-PAGE4, so it was simulated as Glu with a charge of 35 % × (− 2) = − 0.7 e. In the all-atomexplicit-solvent simulations, the phosphoserine and phosphothreonine were simulated by adding phosphoryl groups onto Ser and Thr and simulated under the CHARMM36 potential [68].
The change of water mediated interaction for disordered proteins
The γ parameters in Vcontact of the AWSEM potential were previously optimized in a self-consistent way to maximize the foldability of proteins [62–64]. The optimization was performed to maximize the Tf/Tg, or, equivalently, the ratio of the energy gap δE = Aγ and the roughness of the landscape ΔE = γBγ. Here A and γ are vectors, and B is a matrix. The elements of A and B are defined as shown in Eq. (5).
| (5) |
In Eq. (5), φi is the functional form of a particular type of interaction. The “mg” stands for “molten globule” and “n” stands for “native”. The optimization objective is the functional , which is maximized by γ ∝ B−1A. In practice, the γ parameters were determined in a self-consistent way by iterating between simulating to generate a set of molten-globule structural decoys and recalculating the γ parameters until the γ vector converges. Additionally, the collapse temperature of the simulated proteins is related to the γ parameters by Tc = A′γ, whose elements are , where N is the number of residues. The degree of collapse of proteins in a simulation with a fixed temperature can be controlled by changing Tc. Our simulation with the default γ parameters showed an overly compact structure of PAGE4 compared to the available experimental data (Table S2 and Fig. S3). Therefore, we can changed the degree of collapse of simulated proteins by shifting the γ parameters. We shifted the γ parameters of Vcontact to make the AWSEM potential more repulsive. All γ parameters are shifted by a constant −0.7 in all of our simulations, which ensured that the simulated ensemble of WT-PAGE4 had a similar Rg to that measured from the SAXS experiments [16]. We used the same γ values in all of our simulations. In this way, any difference of Rgs between the three phosphoforms of PAGE4 in our simulations comes from the effect of phosphorylation.
Details of atomistic simulations
The atomistic simulations were performed for the segments of PAGE4 in an explicit-solvent environment (Fig. 1). We used the CST [33] method to speed up the sampling. The temperature was continuously changed according to CST's prescriptions in the range from T = 293 ~ 350K, and detailed balance was maintained throughout the simulations. The atomistic simulation were carried out with a time step of 2.0 fs. The simulated system was neutralized and put into physiological conditions (an ionic concentration of 0.15 M) using Na+ and Cl− ions. For each segment, we performed a total of 1 µs of atomistic simulation with the CHARMM36m force field, which is a modified version of the CHARMM36 force field that has been shown to better reproduce conformational ensembles of IDPs [69]. After the simulations, we used only structures sampled when the temperature T was less than 330K to feed into the AWSEM VFM potential. We also disregarded the first 25 ns of each simulation, which was required for convergence of the CST algorithm.
Mathematical model for the PAGE4/AP-1/AR regulatory axis
We modeled the PAGE4 circuit depicted in Fig. 6a by extending the mathematical framework formulated by Kulkarni et al. [16]. The temporal dynamics of WT-PAGE4 (PU), HIPK1-PAGE4 (PM), CLK2-PAGE4 (PH), and the CLK2 enzyme (C) in the PCa cell is shown in Eqs. (6)–(9).
| (6) |
| (7) |
| (8) |
| (9) |
In Eqs. (6)–(9), (gU, gM, gH, gC) and (kU, kM, kH, kC) are basal production and degradation rates. The term represents the conversion of WT-PAGE4 (PU) to HIPK1-PAGE4 (PM) via enzymatic activity of HIPK1 (H). Here, A represents the threshold level for the catalytic reaction. Similarly, represents the conversion of HIPK1-PAGE4 (PM) to CLK2-PAGE4 (PH) via the enzyme CLK2 (C) and threshold B. PM regulates C via the intermediates c-Jun and AR activity. This interaction is modeled via the shifted Hill function [52] , where λC is the production rate fold-change of C in the presence of HIPK1-PAGE4, nC is the Hill coefficient regulating the fold-change dependence on PM, PM0 is a threshold concentration for Cactivation, and PM (t − τd) is the level of PM at time t − τd. The delay term τd considers the intermediate steps in the signaling.
The androgen treatments effectively regulate CLK2 via the modulation on AR activity (see Fig. 6a), and were therefore modeled with the term H+ (U, U0, nU, λU). U, U0, nU, λU are the treatment level, the threshold for treatment activation, the Hill coefficient and the fold-change in production rate of CLK2, respectively. The fold-change for CLK2 production rate was λU > 1 for ADT (inhibition of AR and, therefore, activation of CLK2) and λU < 1 for the overexpression phase of BAT (overexpression of AR, inhibition of CLK2).
A dimensionless version of Eqs. (6)–(9) was used for the numerical solution of the model. The Supplementary Information provides details about the dimensionless model (Section “Dimensionless model”), the model's parameters (Section “Parameters estimation”), and the numerical solution (Section “Details on numerical simulation”).
Supplementary Material
Acknowledgments
This work is supported by the Center for Theoretical Biological Physics sponsored by the NSF (Grant PHY-1427654), NSF-MCB1241332 and by NSF-CHE1614101. We also wish to acknowledge support from National Institutes of Healthgrants GM062154 (J.O.) and CA181730 (J.O. and P.K.). G.R. was supported by JC Bose Fellowship and SERB Centre for Mathematical Biology Phase II grant. M.K.J. was supported by a Gulf Coast Consortia on the Computational Cancer Biology Training Program (CPRIT Grant No. RP170593). We also would like to thank Prof. Peter Wolynes for the insightful discussions.
Abbreviations used
- IDPs
intrinsically disordered proteins
- PAGE4
prostate-associated gene 4
- PCa
prostate cancer
- AP-1
activator protein-1
- AR
androgen receptor
- HIPK1
homeodomain-interacting protein kinase 1
- CLK2
CDC-like kinase 2
- SAXS
small-angle X-ray scattering
- smFRET
single-molecule fluorescence resonance energy transfer
- MD
molecular dynamics
- AWSEM
Associative memory, Water mediated, Structure and Energy Model
- CST
continuous simulated tempering
- PCA
principal component analysis
- ADT
androgen deprivation therapy
- IAD
intermittent androgen deprivation
- BAT
bipolar androgen treatment.
Footnotes
Appendix A. Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jmb.2018.05.011.
References
- 1.Wright PE, Dyson H. Intrinsically unstructured proteins: re-assessing the protein structure-function paradigm. J. Mol. Biol. 1999 Oct.293:321–331. doi: 10.1006/jmbi.1999.3110. [DOI] [PubMed] [Google Scholar]
- 2.Dunker A, Lawson J, Brown CJ, Williams RM, Romero P, Oh JS, Oldfield CJ, Campen AM, Ratliff CM, Hipps KW, Ausio J, Nissen MS, Reeves R, Kang C, Kissinger CR, Bailey RW, Griswold MD, Chiu W, Garner EC, Obradovic Z. Intrinsically disordered protein. J. Mol. Graph. Model. 2001 Feb.19:26–59. doi: 10.1016/s1093-3263(00)00138-8. [DOI] [PubMed] [Google Scholar]
- 3.Uversky VN. Dancing protein clouds: the strange biology and chaotic physics of intrinsically disordered proteins. J. Biol. Chem. 2016 Mar.291:6681–6688. doi: 10.1074/jbc.R115.685859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.DeForte S, Uversky VN. Order, disorder, and everything in between. Molecules (Basel, Switzerland) 2016 Aug.21 doi: 10.3390/molecules21081090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Leuenberger P, Ganscha S, Kahraman A, Cappelletti V, Boersema PJ, von Mering C, Claassen M, Picotti P. Cell-wide analysis of protein thermal unfolding reveals determinants of thermostability. Science. 2017 Feb.355:eaai7825. doi: 10.1126/science.aai7825. [DOI] [PubMed] [Google Scholar]
- 6.Uversky VN. Unusual biophysics of intrinsically disordered proteins. Biochim. Biophys. Acta Protein Proteomics. 2013 May;1834:932–951. doi: 10.1016/j.bbapap.2012.12.008. [DOI] [PubMed] [Google Scholar]
- 7.Uversky VN. Intrinsic disorder-based protein interactions and their modulators. Curr. Pharm. Des. 2013;19(23):4191–4213. doi: 10.2174/1381612811319230005. [DOI] [PubMed] [Google Scholar]
- 8.Oldfield CJ, Dunker AK. Intrinsically disordered proteins and intrinsically disordered protein regions. Annu. Rev. Biochem. 2014 Jun;83:553–584. doi: 10.1146/annurev-biochem-072711-164947. [DOI] [PubMed] [Google Scholar]
- 9.Vavouri T, Semple JI, Garcia-Verdugo R, Lehner B. Intrinsic protein disorder and interaction promiscuity are widely associated with dosage sensitivity. Cell. 2009 Jul;138:198–208. doi: 10.1016/j.cell.2009.04.029. [DOI] [PubMed] [Google Scholar]
- 10.Marcotte EM, Tsechansky M. Disorder, promiscuity, and toxic partnerships. Cell. 2009 Jul;138:16–18. doi: 10.1016/j.cell.2009.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zeng Y, Gao D, Kim JJ, Shiraishi T, Terada N, Kakehi Y, Kong C, Getzenberg RH, Kulkarni P. Prostate-associated gene 4 (PAGE4) protects cells against stress by elevating p21 and suppressing reactive oxygen species production. Am. J. Clin. Exp. Urol. 2013;1(1):39–52. [PMC free article] [PubMed] [Google Scholar]
- 12.Rajagopalan K, Qiu R, Mooney SM, Rao S, Shiraishi T, Sacho E, Huang H, Shapiro E, Weninger KR, Kulkarni P. The stress-response protein prostate-associated gene 4, interacts with c-Jun and potentiates its transactivation. Biochim. Biophys. Acta. 2014 Feb.1842:154–163. doi: 10.1016/j.bbadis.2013.11.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sato N, Sadar MD, Bruchovsky N, Saatcioglu F, Rennie PS, Sato S, Lange PH, Gleave ME. Androgenic induction of prostate-specific antigen gene is repressed by protein–protein interaction between the androgen receptor and AP-1/c-Jun in the human prostate cancer cell line LNCaP. J. Biol. Chem. 1997 Jul;272:17485–17494. doi: 10.1074/jbc.272.28.17485. [DOI] [PubMed] [Google Scholar]
- 14.Tillman K, Oberfield JL, Shen XQ, Bubulya A, Shemshedini L. c-Fos dimerization with c-Jun represses c-Jun enhancement of androgen receptor transactivation. Endocrine. 1998 Oct.9:193–200. doi: 10.1385/ENDO:9:2:193. [DOI] [PubMed] [Google Scholar]
- 15.Mooney SM, Qiu R, Kim JJ, Sacho EJ, Rajagopalan K, Johng D, Shiraishi T, Kulkarni P, Weninger KR. Cancer/testis antigen PAGE4, a regulator of c-Jun transactivation, is phosphorylated by homeodomain-interacting protein kinase 1, a component of the stress-response pathway. Biochemistry. 2014 Mar.53:1670–1679. doi: 10.1021/bi500013w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kulkarni P, Jolly MK, Jia D, Mooney SM, Bhargava A, Kagohara LT, Chen Y, Hao P, He Y, Veltri RW, Grishaev A, Weninger K, Levine H, Orban J. Phosphorylation-induced conformational dynamics in an intrinsically disordered protein and potential role in phenotypic heterogeneity. Proc. Natl. Acad. Sci. U. S. A. 2017 Mar.114:E2644–E2653. doi: 10.1073/pnas.1700082114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Reinartz I, Sinner C, Nettels D, Stucki-Buchli B, Stockmar F, Panek PT, Jacob CR, Nienhaus GU, Schuler B, Schug A. Simulation of FRET dyes allows quantitative comparison against experimental data. The Journal of Chemical Physics. 2018;148:123321. doi: 10.1063/1.5010434. [DOI] [PubMed] [Google Scholar]
- 18.Zheng W, Zerze GH, Borgia A, Mittal J, Schuler B, Best RB. Inferring properties of disordered chains from FRET transfer efficiencies. The Journal of Chemical Physics. 2018;148:123329. doi: 10.1063/1.5006954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zheng W, Best RB. An extended Guinier analysis for intrinsically disordered proteins. J. Mol. Biol. 2018 Mar; doi: 10.1016/j.jmb.2018.03.007. (in press) [DOI] [PMC free article] [PubMed]
- 20.Davtyan A, Schafer NP, Zheng W, Clementi C, Wolynes PG, Papoian GA. AWSEM-MD: protein structure prediction using coarse-grained physical potentials and bioinformatically based local structure biasing. J. Phys. Chem. B. 2012 Jul;116:8494–8503. doi: 10.1021/jp212541y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc. Natl. Acad. Sci. U. S. A. 1987 Nov.84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Leopold PE, Montal M, Onuchic JN. Protein folding funnels: a kinetic approach to the sequence-structure relationship. Proc. Natl. Acad. Sci. 1992 Sept.89:8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins. 1995 Mar.21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 24.Zheng W, Schafer NP, Davtyan A, Papoian GA, Wolynes PG. Predictive energy landscapes for protein–protein association. Proc. Natl. Acad. Sci. 2012 Nov.109:19244–19249. doi: 10.1073/pnas.1216215109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Potoyan DA, Zheng W, Komives EA, Wolynes PG. Molecular stripping in the NF-κB/IκB/DNA genetic regulatory network. Proc. Natl. Acad. Sci. 2016 Jan.113:110–115. doi: 10.1073/pnas.1520483112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Res. 2000 Jan.28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen M, Lin X, Zheng W, Onuchic JN, Wolynes PG. Protein folding and structure prediction from the ground up: the atomistic associative memory, water mediated, structure and energy model. J. Phys. Chem. B. 2016 Aug.120:8557–8565. doi: 10.1021/acs.jpcb.6b02451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chen M, Lin X, Lu W, Onuchic JN, Wolynes PG. Protein folding and structure prediction from the Ground Up II: AAWSEM for α/β proteins. J. Phys. Chem. B. 2017 Apr.121:3473–3482. doi: 10.1021/acs.jpcb.6b09347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kyte J, Doolittle RF. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 1982 May;157:105–132. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
- 30.Uversky VN, Gillespie JR, Fink AL. Why are “natively unfolded” proteins unstructured under physiologic conditions? Proteins Struct. Funct. Genet. 2000 Nov.41:415–427. doi: 10.1002/1097-0134(20001115)41:3<415::aid-prot130>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 31.Yan R, Xu D, Yang J, Walker S, Zhang Y. A comparative assessment and analysis of 20 representative sequence alignment methods for protein structure prediction. Sci. Rep. 2013 Dec.3 doi: 10.1038/srep02619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.He Y, Chen Y, Mooney SM, Rajagopalan K, Bhargava A, Sacho E, Weninger K, Bryan PN, Kulkarni P, Orban J. Phosphorylation-induced conformational ensemble switching in an intrinsically disordered cancer/testis antigen. J. Biol. Chem. 2015 Oct.290:25090–25102. doi: 10.1074/jbc.M115.658583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhang C, Ma J. Enhanced sampling and applications in protein folding in explicit solvent. J. Chem. Phys. 2010 Jun;132:244101. doi: 10.1063/1.3435332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Flory PJ. Principles of Polymer Chemistry. Vol. 19. Cornell Univ. Press; Ithaca, NY: 2006. print ed. (OCLC: 254754780) [Google Scholar]
- 35.Bernad P, Blackledge M. A self-consistent description of the conformational behavior of chemically denatured proteins from NMR and small angle scattering. Biophys. J. 2009 Nov.97:2839–2845. doi: 10.1016/j.bpj.2009.08.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996 Feb.14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 37.Shen T, Zong C, Hamelberg D, McCammon JA, Wolynes PG. The folding energy landscape and phosphorylation: modeling the conformational switch of the NFAT regulatory domain. FASEB J. 2005 Sept.19:1389–1395. doi: 10.1096/fj.04-3590hyp. [DOI] [PubMed] [Google Scholar]
- 38.Lätzer J, Shen T, Wolynes PG. Conformational switching upon phosphorylation: a predictive framework based on energy landscape principles. Biochemistry. 2008 Feb.47:2110–2122. doi: 10.1021/bi701350v. [DOI] [PubMed] [Google Scholar]
- 39.Shoemaker BA, Portman JJ, Wolynes PG. Speeding molecular recognition by using the folding funnel: the fly-casting mechanism. Proc. Natl. Acad. Sci. 2000 Aug.97:8868–8873. doi: 10.1073/pnas.160259697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Levy Y, Onuchic JN, Wolynes PG. Fly-casting in protein–DNA binding: frustration between protein folding and electrostatics facilitates target recognition. J. Am. Chem. Soc. 2007 Jan.129:738–739. doi: 10.1021/ja065531n. [DOI] [PubMed] [Google Scholar]
- 41.Trizac E, Levy Y, Wolynes PG. Capillarity theory for the fly-casting mechanism. Proc. Natl. Acad. Sci. 2010 Feb.107:2746–2750. doi: 10.1073/pnas.0914727107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Frishman D, Argos P. Knowledge-based protein secondary structure assignment. Proteins Struct. Funct. Genet. 1995 Dec.23:566–579. doi: 10.1002/prot.340230412. [DOI] [PubMed] [Google Scholar]
- 43.Kratiras Z, Konstantinidis C, Skriapas K. A review of continuous vs intermittent androgen deprivation therapy: redefining the gold standard in the treatment of advanced prostate cancer. Myths, facts and new data on a perpetual dispute. Int. Braz. J. Urol. 2014 Feb.40:3–15. doi: 10.1590/S1677-5538.IBJU.2014.01.02. (discussion 15) [DOI] [PubMed] [Google Scholar]
- 44.Schweizer MT, Antonarakis ES, Wang H, Ajiboye AS, Spitz A, Cao H, Luo J, Haffner MC, Yegnasubramanian S, Carducci MA, Eisenberger MA, Isaacs JT, Denmeade SR. Effect of bipolar androgen therapy for asymptomatic men with castration-resistant prostate cancer: Results from a pilot clinical study. Sci. Transl. Med. 2015 Jan.7:269ra2. doi: 10.1126/scitranslmed.3010563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Buchan NC, Goldenberg SL. Intermittent androgen suppression for prostate cancer. Nat. Rev. Urol. 2010 Oct.7:552–560. doi: 10.1038/nrurol.2010.141. [DOI] [PubMed] [Google Scholar]
- 46.Zeng Y, He Y, Yang F, Mooney SM, Getzenberg RH, Orban J, Kulkarni P. The cancer/testis antigen prostate-associated gene 4 (PAGE4) is a highly intrinsically disordered protein. J. Biol. Chem. 2011 Apr.286:13985–13994. doi: 10.1074/jbc.M110.210765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Miyashita O, Onuchic JN, Wolynes PG. Nonlinear elasticity, protein quakes, and the energy landscapes of functional transitions in proteins. Proc. Natl. Acad. Sci. 2003 Oct.100:12570–12575. doi: 10.1073/pnas.2135471100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Okazaki K-i, Koga N, Takada S, Onuchic JN, Wolynes PG. Multiple-basin energy landscapes for large-amplitude conformational motions of proteins: structure-based molecular dynamics simulations. Proc. Natl. Acad. Sci. 2006 Aug.103:11844–11849. doi: 10.1073/pnas.0604375103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Whitford PC, Sanbonmatsu KY, Onuchic JN. Biomolecular dynamics: order–disorder transitions and energy landscapes. Rep. Prog. Phys. 2012 Jul;75:076601. doi: 10.1088/0034-4885/75/7/076601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lin X, Eddy NR, Noel JK, Whitford PC, Wang Q, Ma J, Onuchic JN. Order and disorder control the functional rearrangement of influenza hemagglutinin. Proc. Natl. Acad. Sci. 2014 Aug.111:12049–12054. doi: 10.1073/pnas.1412849111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Terada N, Shiraishi T, Zeng Y, Aw-Yong K-M, Mooney SM, Liu Z, Takahashi S, Luo J, Lupold SE, Kulkarni P, Getzenberg RH. Correlation of Sprouty1 and Jagged1 with aggressive prostate cancer cells with different sensitivities to androgen deprivation. J. Cell. Biochem. 2014 Sept.115:1505–1515. doi: 10.1002/jcb.24805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lu M, Jolly MK, Levine H, Onuchic JN, Ben-Jacob E. MicroRNA-based regulation of epithelial-hybrid-mesenchymal fate determination. Proc. Natl. Acad. Sci. 2013 Nov.110:18144–18149. doi: 10.1073/pnas.1318192110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Jolly MK, Jia D, Boareto M, Mani SA, Pienta KJ, Ben-Jacob E, Levine H. Coupling the modules of EMT and stemness: a tunable stemness window model. Oncotarget. 2015 Sept.6 doi: 10.18632/oncotarget.4629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Rangarajan N, Fox Z, Singh A, Kulkarni P, Rangarajan G. Disorder, oscillatory dynamics and state switching: the role of c-Myc. J. Theor. Biol. 2015 Dec.386:105–114. doi: 10.1016/j.jtbi.2015.09.013. [DOI] [PubMed] [Google Scholar]
- 55.Mooney SM, Jolly MK, Levine H, Kulkarni P. Phenotypic plasticity in prostate cancer: role of intrinsically disordered proteins. Asian J. Androl. 2016 Oct.18:704–710. doi: 10.4103/1008-682X.183570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Brock A, Huang S. Precision oncology: between vaguely right and precisely wrong. Cancer Res. 2017 Dec.77:6473–6479. doi: 10.1158/0008-5472.CAN-17-0448. [DOI] [PubMed] [Google Scholar]
- 57.Jia D, Jolly MK, Kulkarni P, Levine H. Phenotypic plasticity and cell fate decisions in cancer: insights from dynamical systems theory. Cancers. 2017 Jun;9:70. doi: 10.3390/cancers9070070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zheng X, Beyzavi A, Krakowiak J, Patel N, Khalil AS, Pincus D. Hsf1 phosphorylation generates cell-to-cell variation in Hsp90 levels and promotes phenotypic plasticity. Cell Rep. 2018 Mar.22:3099–3106. doi: 10.1016/j.celrep.2018.02.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hirata Y, Tanaka G, Bruchovsky N, Aihara K. Mathematically modelling and controlling prostate cancer under intermittent hormone therapy. Asian J. Androl. 2012 Mar.14:270–277. doi: 10.1038/aja.2011.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Hirata Y, Akakura K, Higano CS, Bruchovsky N, Aihara K. Quantitative mathematical modeling of PSA dynamics of prostate cancer patients treated with intermittent androgen suppression. J. Mol. Cell Biol. 2012 Jun;4:127–132. doi: 10.1093/jmcb/mjs020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Drozdetskiy A, Cole C, Procter J, Barton GJ. JPred4: a protein secondary structure prediction server. Nucleic Acids Res. 2015 Jul;43:W389–W394. doi: 10.1093/nar/gkv332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Koretke KK, Luthey-Schulten Z, Wolynes PG. Self-consistently optimized energy functions for protein structure prediction by molecular dynamics. Proc. Natl. Acad. Sci. U. S. A. 1998 Mar.95:2932–2937. doi: 10.1073/pnas.95.6.2932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Papoian GA, Ulander J, Wolynes PG. Role of water mediated interactions in protein–protein recognition landscapes. J. Am. Chem. Soc. 2003 Jul;125:9170–9178. doi: 10.1021/ja034729u. [DOI] [PubMed] [Google Scholar]
- 64.Schafer NP, Kim BL, Zheng W, Wolynes PG. Learning to fold proteins using energy landscape theory. Isr. J. Chem. 2014 Aug.54:1311–1337. doi: 10.1002/ijch.201300145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zang T, Yu L, Zhang C, Ma J. Parallel continuous simulated tempering and its applications in large-scale molecular simulations. J. Chem. Phys. 2014 Jul;141:044113. doi: 10.1063/1.4890038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Tsai M-Y, Zheng W, Balamurugan D, Schafer NP, Kim BL, Cheung MS, Wolynes PG. Electrostatics, structure prediction, and the energy landscapes for protein folding and binding: electrostatic energy landscapes for folding and binding. Protein Sci. 2016 Jan.25:255–269. doi: 10.1002/pro.2751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Xie Y, Jiang Y, Ben-Amotz D. Detection of amino acid and peptide phosphate protonation using Raman spectroscopy. Anal. Biochem. 2005 Aug.343:223–230. doi: 10.1016/j.ab.2005.05.038. [DOI] [PubMed] [Google Scholar]
- 68.Mallajosyula SS, Guvench O, Hatcher E, MacKerell AD. CHARMM additive all-atom force field for phosphate and sulfate linked to carbohydrates. J. Chem. Theory Comput. 2012 Feb.8:759–776. doi: 10.1021/ct200792v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Huang J, Rauscher S, Nawrocki G, Ran T, Feig M, de Groot BL, Grubmüller H, MacKerell AD. CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nat. Methods. 2017 Jan.14:71–73. doi: 10.1038/nmeth.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.