Dynamic Clustering of Dyneins on Axonal Endosomes: Evidence from High-Speed Darkfield Imaging

Abstract

One of the fundamental features that govern the cooperativity of multiple dyneins during cargo trafficking in cells is the spatial distribution of these dyneins on the cargo. Geometric considerations and recent experiments indicate that clustered distributions of dyneins are required for effective cooperation on micron-sized cargos. However, very little is known about the spatial distribution of dyneins and their cooperativity on smaller cargos, such as vesicles or endosomes <200 nm in size, which are not amenable to conventional immunostaining and optical trapping methods. In this work, we present evidence that dyneins can dynamically be clustered on endosomes in response to load. Using a darkfield imaging assay, we measured the repeated stalls and detachments of retrograde axonal endosomes under load with <10 nm localization accuracy at imaging rates up to 1 kHz for over a timescale of minutes. A three-dimensional stochastic model was used to simulate the endosome motility under load to gain insights on the mechanochemical properties and spatial distribution of dyneins on axonal endosomes. Our results indicate that 1) the distribution of dyneins on endosomes is fluid enough to support dynamic clustering under load and 2) the detachment kinetics of dynein on endosomes differs significantly from the in vitro measurements possibly due to an increase in the unitary stall force of dynein on endosomes.

Introduction

Cytoplasmic dynein drives the long-distance trafficking of various cellular cargos toward the minus-ends of microtubules in eukaryotic cells (1, 2, 3, 4, 5). Though dynein is a weak motor with a modest stall force of 1.1 pN in vitro, the collective function of multiple dyneins can generate forces up to 20 pN on large cargos in cells (6, 7). Dynein-specific properties like adaptable stepping, convex force-velocity relationship, and catch-bond detachment kinetics make it highly conducive for dyneins to work cooperatively as a team (7). This cooperation is fundamental for the diverse range of dynein-driven processes in cells, besides cargo trafficking, that entail mechanical forces higher than a few pN.

An important facet governing the cooperative function of cargo-bound dyneins is the spatial distribution of dyneins on cargo, which determines the number of dyneins that are geometrically active (i.e., can bind to the microtubule) simultaneously and can cooperate effectively. Erickson and coworkers used simulations to show that the geometric activity and cooperation between motors is facilitated by clustered distribution of motors for large micron-sized cargos (8). Recently, Rai and coworkers used optical trapping, immunostaining, and pharmacological studies to show that clustered distribution of dyneins on late phagosomes (1–2 μm in size) is critical for the phagosome trafficking in cells (9). They also discussed the structural interactions that cluster dyneins within cholesterol microdomains on the phagosomes. It is very likely that the functional relevance for dynein clustering and the underlying clustering mechanism is cargo specific.

The importance of dynein clustering for effective cooperation on micron-sized cellular cargos is quite apparent from the geometric considerations of dynein length and cargo size (8, 9). However, not much is known about the spatial distribution of dyneins and their cooperativity on smaller cargos like vesicles or endosomes around 100–200 nm in size. Optical trapping approaches that measure the cumulative force of dyneins on cargos are limited to just a few large micron-sized cargos (6, 7, 10, 11). Further, optical traps can only probe the geometrically active motor forces and cannot report directly on the spatial distribution of dyneins on the cargo. Probing the spatial distribution of dyneins on such small cargos in cells is also not practical with immunostaining methods (12). New approaches are therefore needed to study smaller cellular cargos for better insights into the cellular mechanisms assisting the clustering and cooperativity of dyneins. In this work, we present experimental data and model simulations to support a hypothesis that dyneins can dynamically be clustered on endosomes in cells based on new experimental data on endosomes under load in axons and three-dimensional (3D) model simulations.

Our recent studies indicate that the robust long-distance retrograde transport of endosomes, as small as 100–200 nm, along the axons of neurons is driven cooperatively by multiple dyneins (13, 14). We also reported an approach that permitted us to study the retrograde endosome transport under load. Specifically, we showed that retrograde endosomes carrying fluorescent nanoparticles could be tethered in axons stochastically depending on the laser illumination power (14). Though the tether mechanism is not yet clear, the elastic tether force opposes the dyneins hauling the endosomes, resulting in repeated stalls and detachments of endosomes that are remarkably similar to the records of cargos under load in optical traps (7). The repeated stall/detachment profiles of the endosomes under load are expected to be sensitive to the spatial distribution and detachment kinetics of dyneins on endosomes. However, fluorescence-based imaging limited the number of stalls/detachments seen per endosome due to photobleaching and irreversible endosome stalling at the laser power required for good spatiotemporal resolution. In this work, we report a low-power darkfield imaging assay for the long-term tracking of retrograde endosomes, carrying gold nanoparticles, with <10 nm spatial resolution at imaging rates up to 1 kHz. This method permitted us in a few cases to capture hundreds of stalls and detachments of the same endosome under load and made single-endosome mechanical analysis possible. We then formulated a 3D stochastic model, which incorporates the translational, rotational, and thermal motions of the endosome driven by multiple dyneins and the dynamics of dynein-endosome contact positions, to simulate the endosome stalls and detachments under load. Our model is successful in quantitatively simulating all the features and statistics of the experimental stall/detachment profiles and gave insights on the mechanochemical properties and spatial distribution of dyneins on endosomes. Based on these results, we hypothesize that dyneins can dynamically be clustered on endosomes in response to load. The dynamic clustering of dyneins can be a particularly efficient mechanism for smaller cargos, but larger cargos may need additional structural interactions, as is the case for phagosomes (9).

Methods

Conjugation of gold nanoparticles with wheat germ agglutinin

Streptavidin functionalized gold nanoparticles (GNPs in phosphate-buffered saline (PBS), 80 nm) were purchased from Nanopartz (Loveland, CO). The GNPs were coated with wheat germ agglutinin (WGA) using biotin-avidin covalent interaction to obtain GNP-WGA as follows. In a typical conjugation procedure, 20 μL of the GNPs in PBS (1 nM) is sonicated for 10 s, and 8 μL of biotin-WGA (1 μM) is added and the mixture is left standing for 30 min. The GNPs were then spun down by centrifugation at 3000 rpm for 10 min, and the supernatant with unconjugated WGA was discarded (repeated twice). The GNP-WGA conjugate was then made up in 20 μL culture medium and was briefly sonicated for 10–15 s before adding to the dorsal root ganglion (DRG) neuron culture.

Microfluidic device for DRG neuron culture compatible with darkfield imaging

The use of microfluidic devices for primary neuron culture had been documented by us elsewhere (15, 16). These devices, made of polydimethyl siloxane (PDMS), were typically ∼5 mm in thickness and were compatible with objective-based oblique illumination fluorescence imaging of axonal transport. In this work, we used PDMS devices ∼1 mm in thickness compatible with dark field imaging of axonal transport (see below). The device fabrication was as reported before, but in this study, we used an 8:1 weight ratio of silicone elastomer and curing agent to enhance the mechanical stability of the thinner PDMS devices. DRG neurons were cultured in these devices as reported earlier, and we used mature DRG cultures (7–10 days old) for the transport studies.

Dark field imaging of GNP-endosome transport in microfluidic DRG neuron cultures

We customized an inverted microscope (Nikon Eclipse Ti-U; Nikon, Tokyo, Japan) for the dark field imaging of GNP-endosomes in axons with high spatial localization accuracy (<10 nm) at imaging rates up to 1 kHz. Briefly, unpolarized white light from a halogen lamp is focused by a high numerical aperture condenser (NA = 1.4) through a light stop that selects highly oblique rays to illuminate the sample. An adjustable NA objective (NA ∼0.8–1.25) collects only the scattered light, which is spectrally filtered (selecting 550–650 nm) and focused onto a fast sCMOS camera. We obtained the localization accuracy (<10 nm, Fig. S1) of our imaging system from the position uncertainty of GNPs stuck on cover slips, as detailed in the literature (17).

The axon terminals or cell bodies in the microfluidic culture were selectively incubated with GNP-WGA (0.5 nM), which was washed off using culture medium after 30 min. Shortly before imaging, the culture medium was replaced with CO₂ independent medium, and the culture was capped on top with a cover slip to form a ∼1 mm thick microfluidic device compatible with the working distance of the high-NA condenser and dark filed imaging. The culture was imaged on a water-heated custom microscope stage set to maintain the culture at 31°C. Maintaining the culture at physiological temperature 37°C required heating the optical components, which are in oil contact, to >45°C and was hence not preferred. Imaging was started typically 2 h after the incubation start and restricted to <45 min session. Time-lapse videos of endosome transport were acquired at 100–1000 frames per second with the illumination power in the range of 0.25–1 mW/cm².

3D stochastic model simulation of GNP-endosome motion and detachments

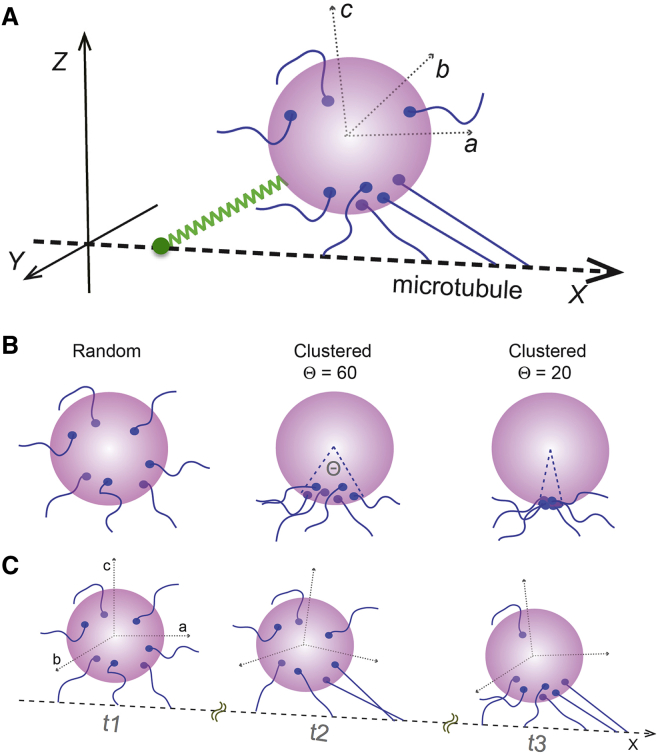
We built a 3D stochastic model, based on earlier models (8, 13) with key modifications, to simulate the collective function of dyneins on endosomes under load (Fig. 4). Briefly, our model considers a stable number of dyneins, distributed randomly or in a clustered geometry, on a spherical endosome connected to the microtubule (along the x axis of laboratory frame). The dynamics of individual dyneins, which determine the endosome motion, are governed by their microtubule-binding, unbinding, forward- or backward-stepping rates that include the load dependence of velocities and detachment kinetics. The endosome motion is separated into translational and rotational components, and the thermal fluctuations on endosome are explicitly incorporated in both these components. In addition, our model also considers the fluidity of dynein-distribution on endosomes under load by incorporating the motor-endosome contact point diffusion and drift under mechanical torque on the endosome surface. To simulate the tethered endosome motility, we modeled the tether as a linear-elastic spring docking the endosome to the microtubule. The elastic tether buckles freely but exerts a restoring force when stretched beyond its rest length. The cooperative function of dyneins moving the tethered endosome against this restoring force results in repeated stalls and detachments, which are quantified and compared to experimental data. Most of the parameters in our model are constrained by experimental data from this study or from literature (7, 18). A detailed description of the model, the Monte Carlo simulation algorithm, and the parameter selection is given in the Supporting Material.

Figure 4.

3D model for simulating the tethered endosome dynamics. (A) A schematic of the endosome with multiple dyneins in our 3D model is shown (see Methods and Supporting Material). (X, Y, Z) is the laboratory frame and (a, b, c) is the endosome frame of reference. (B) Random-fixed and clustered-fixed spatial distributions of dyneins on endosomes are shown. (C) Fluid distribution of dyneins on endosomes, which permits the dynein-endosome contacts to diffuse and slide under mechanical torque, is shown. To see this figure in color, go online.

Results

Darkfield imaging of retrograde axonal endosome transport in microfluidic neuron cultures

Enhanced accuracy and time resolution

In earlier studies, we reported the real-time tracking of retrograde axonal endosome transport using receptor-mediated endocytosis of WGA-coated fluorescent quantum dots/nanoparticles and fluorescence imaging in microfluidic neuron cultures (13, 14). Using intensely fluorescent nanoparticles (100 nm), we reported a localization accuracy of ∼25 nm at 150 Hz imaging rate and a laser illumination power of 45 W/cm². Here, we tracked the retrograde transport of endosomes carrying gold nanoparticles (GNPs, 80 nm) using darkfield imaging as described in Methods. The extremely high scattering cross section of GNPs in the visible range improved the localization accuracy to <10 nm at imaging rates up to 1 kHz and low illumination power of <1mW/cm² (Fig. S1). Further, the low power darkfield illumination is noninvasive and enabled us to track the same GNP-endosome for tens of minutes without any degradation in GNP scattering. The imaging frame rate in our experiments is limited by the size of imaging field, which was 14 × 140 μm² for 1 kHz frame rate.

Axonal transport imaging

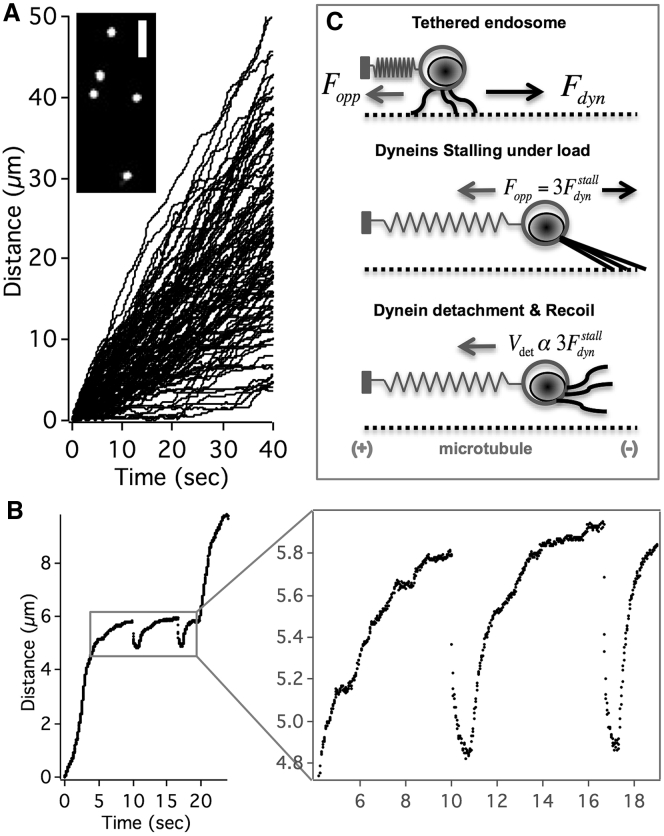
The strong scattering signal from GNPs allowed us to visualize the GNP-endosome transport in axons directly from the eyepiece of microscope, which made it convenient to select the regions of interest to be imaged. The imaging was carried out in axonal segments far from (hundreds of microns) the terminals and cell bodies, following distal incubation of WGA-GNPs. We observed robust internalization and fast retrograde transport of GNPs in axons within an hour of incubating with 0.5 nM WGA-GNP. The GNP-endosome motion is highly processive and almost unidirectional in retrograde direction (Fig. 1 A; Video S1). Most endosomes traversed the imaging field of view (140 μm) with no indication of detachment from the microtubules and diffusion within axons. The transport pattern of GNP-endosome transport is comparable to that of quantum dot-endosomes (13) indicating that the GNP is not perturbing the mechanics of endosome transport. The predominant unidirectionality makes the retrograde GNP-endosome transport in axons a fitting system to study the mechanics of multiple dyneins in cells.

Figure 1.

Retrograde GNP-endosomes under load. (A) Unidirectional trajectories of retrograde GNP-endosomes in axons captured by darkfield imaging are shown. The inset shows a snapshot of GNP-endosomes transporting in axons. Scale bars, 3 μm. (B) Gradual stalls and fast reversals (“jumps”) exhibited by GNP-endosomes in axons are shown. (C) The elastic tether model explains the endosome jumps as the gradual stalling and detachment of dyneins under load.

Video S1. Retrograde Transport of GNP-Endosomes Recorded at 100 fps by Darkfield Imaging

The movie is played at 3× the original speed. Movie dimensions are 3 x 16 μm².

Tethering of endosomes and long-term imaging of endosome jumps

Recently, we developed a technique termed nanoparticle-assisted optical tethering of endosomes (NOTE) in axons (14). Specifically, we showed that retrograde endosomes carrying fluorescent nanoparticles (30–100 nm) could become stochastically tethered to the microtubule during transport, depending on the fluorescence laser illumination power. We find that a few of the retrogradely moving GNP-endosomes (<5% at 1 mW/cm²) also behaved similarly, as if they were docked to the microtubule by an elastic tether (Fig. 1 B; Video S2). The opposing force from the elastic tether resulted in these GNP-endosomes gradually stalling and snapping back due to the lead-dyneins detaching from the microtubule (Fig. 1 C). The gradual stalls and fast reversals, referred to as “endosome jumps,” are remarkably similar to the records of cellular cargos in optical traps (7) and contain valuable information on the collective function of dyneins on the endosomes under load. In the case of endosomes with fluorescent nanoparticles (14), the endosomes typically became stationary after a few jumps at the laser illumination power of 45 W/cm² and the imaging resolution degraded within a few minutes due to photobleaching. In contrast, at the low power darkfield illumination, the GNP-endosomes often resumed retrograde transport after a few jumps and in a few cases exhibited tens to hundreds of jumps at the same axonal location over tens of minutes of imaging (Video S3). Such long-term tracking of the sequential stalls and detachments of the same GNP-endosome with darkfield imaging made it possible for us to undertake single-endosome and individual motor motility analysis as detailed below.

Video S2. Retrograde Moving GNP-Endosome Exhibiting a Couple of Gradual Stalls and Detachments before Resuming the Normal Retrograde Transport

Retrograde moving GNP-endosome exhibits a couple of gradual stalls and detachments (‘jumps’) and resumes normal retrograde transport. The movie is acquired at 500 fps and is played at the original speed. Movie dimensions are 3 × 12 μm².

Video S3. Retrograde Moving GNP-Endosome Exhibiting a Series of Stalls and Detachments

Retrograde GNP-endosome exhibiting a series of stalls and detachments (‘jumps’). The movie is acquired at 500 fps and is played at the original speed. Movie dimensions are 2 × 5 μm². 17 × 43.

Retrograde endosome transport under load: single-endosome analysis

Endosome jump sizes

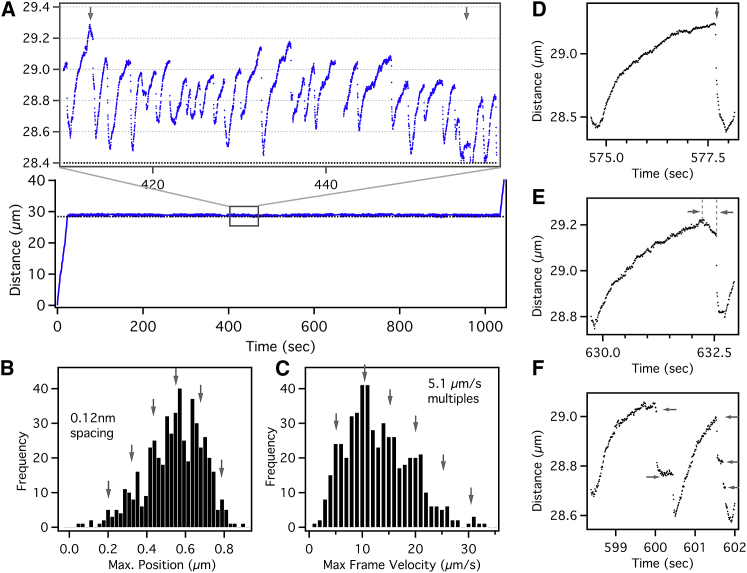
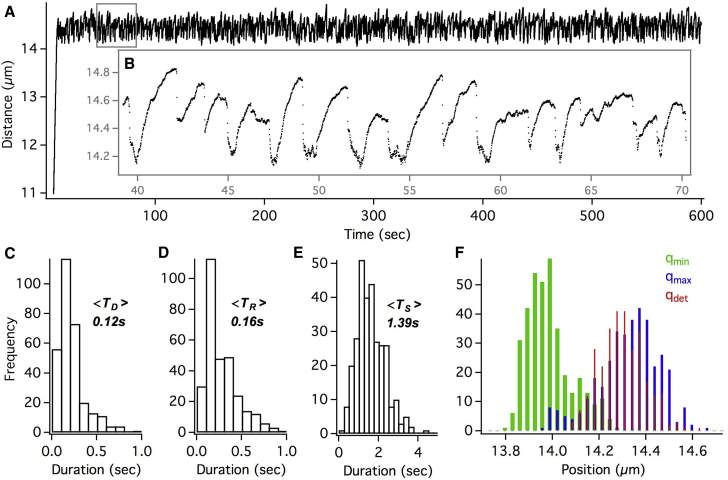
Fig. 2 A shows a retrograde moving endosome exhibiting hundreds of jumps at the same axonal location over 18 min of imaging at 100 fps before resuming normal retrograde transport. This trajectory is extracted from multiple sequential videos with drift correction using stationary scattering objects within the videos as internal references. We then estimated the endosome jump size as the difference between the maximum position reached within each jump event and the approximated tether location (dotted line in Fig. 2 A). The endosome exhibits a wide range of jump sizes from 110 to 900 nm, as shown in Fig. 2 B, which indicates the activity of multiple dyneins stochastically sharing the load on endosome. We note that the jump sizes are approximate since the tether location is not precisely known and some residual drift within the trajectory cannot be ruled out altogether. Nonetheless, the distribution of jump sizes exhibited an apparent peak multiplicity of ∼120 nm (Fig. S5 D). Assuming the 120 nm jumps are single dynein events, we can infer the cooperative activity of ∼8 dyneins on the endosome.

Figure 2.

(A) Repeated stalls and detachments of a retrograde GNP-endosome under load. The black dotted line is the estimated location of the tether. (B) Histogram of endosome jump size, obtained as the maximum distance covered within each jump relative to the tether location, exhibits peak multiplicity of ∼120 nm. (C) Histogram of maximum frame velocity (V_maxf) within each jump exhibits peak multiplicity of ∼5.1 μm/s. (D) Sudden detachment recoil profile is shown. (E) Delayed detachment recoil profile is shown. (F) Sequential detachment recoil profile is shown. To see this figure in color, go online.

Recoil velocities

Similar conclusion can be reached from the recoil velocity of the stalled endosome upon detachment, which is related to the cumulative stall force of lead-dyneins. Fig. 2 C shows the distribution of the maximal frame velocity (V_maxf obtained for each endosome jump as the maximal frame-to-frame distance covered per unit time during recoil) of the recoiling endosome within each jump. This distribution ranged up to 35 μm/s and exhibited a discrete peak structure with a multiplicity of ∼5.1 μm/s (Fig. S5 E). It can be shown (Supporting Material) that V_maxf is linearly related to the instantaneous detachment velocity (V_detach), which is proportional to the cumulative stall force of the lead-dyneins (14). Therefore, the peak multiplicity in Fig. 2 C can be attributed to the cooperative activity of at least six dyneins stochastically sharing the load on the endosome. Notably, while the recoil velocity distribution averages around the activity of two to three dyneins, the jump size distribution averages around the activity of four to five dyneins. It is plausible that some of the endosome jumps exhibit much lower V_maxf than expected due to the endosome recoil profiles being abruptly interrupted as detailed below.

Recoil profiles

We see a wide range of recoil profiles following dynein detachment over these hundreds of endosome jumps. In many cases the recoil profile is a sharp exponential decay (Fig. 2 D), indicating that the detachment of multiple lead dyneins happens in quick succession. The fast exponential recoil of the endosome after lead-dynein detachment is often interrupted within 40 –60 ms, possibly by the presence of lagging microtubule-bound dyneins or by the rebinding of detached dyneins to the microtubule. On average, the complete endosome recoil lasted ∼180 ms before dynein driven retrograde movement resumed for the next stall/jump. Interestingly, we also see delayed detachment profiles, although less frequently, as shown in Fig. 2 E. Such profiles likely arise due to partial detachment of lead-dyneins followed by the backward stepping of remaining lead-dyneins under superstall load before detaching from the microtubule. Occasionally, we see sequential detachment of dyneins apparent as a step pattern in the recoil profile (Fig. 2 F).

Sequential stalls/detachments

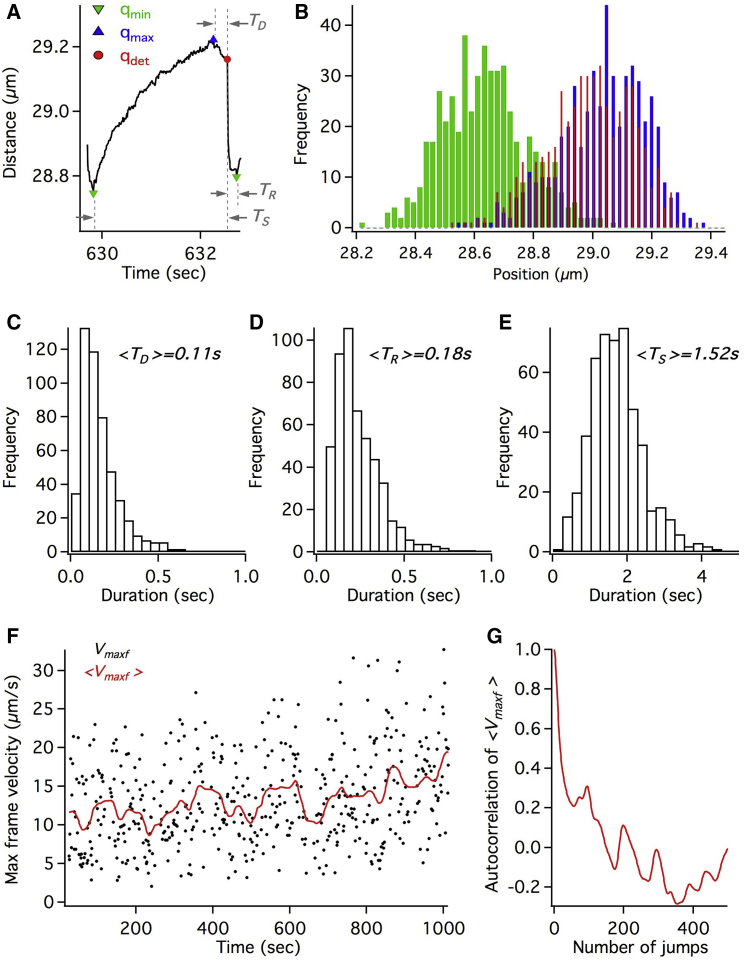
In order to quantify the repeated stall and detachment profiles, we used an automated sliding window analysis to identify the maximal position (q_max) reached within a stall event, the detachment position (q_det) after the stall, and the minimum position (q_min) reached after the detachment (Fig. 3 A; Fig. S2). Fig. 3 B shows the histograms of the minima, maxima, and detachment positions within each jump for the endosome in Fig. 2. We then quantified the stalls/detachments in terms of three statistical metrics namely the stall duration (T_S), the detachment duration (T_D), and the recoil duration (T_R), as shown in Fig. 3 A. The distributions of these dynamic variables are shown in Fig. 3, C–E and the mean statistics are summarized in Table 1. These distributions, obtained from sequential stalls/detachments of the endosome over a long time, can provide valuable insights on the mechanochemical properties and spatial distribution of dyneins on the endosome by guiding accurate models.

Figure 3.

Single endosome statistics obtained from the multiple endosome jumps in Fig 2. (A) A depiction of the stall duration T_S, detachment duration T_D, and the recoil duration T_R, based on the minimal (q_min), maximal (q_max), and detachment (q_det) positions within the endosome jump is shown. (B) Histograms of q_min, q_max, and q_det positions are shown. The distributions of T_D, T_R, and T_S are shown in (C), (D), and (E), respectively. (F) The maximum frame velocity V_maxf within each successive jump is shown as a function of time (black markers). The moving average <V_maxf > (red line) shows the dynamic variation of detachment velocities over a span of minutes. (G) The autocorrelation of <V_maxf > is shown.

Table 1.

3D Model Simulation of the Tethered Single Endosome Dynamics

	Model	Detach Kinetics	Dynein Dist.	TD (s)	TR (s)	TS (s)	Vmaxf (μm/s)	Ld
	endosome: Fig. 2			0.11	0.18	1.52	11.6
A	IVT, Nd = 8	CB	random	0.14	0.13	1.10	4.21	1.96
B	IVT, Nd = 8	EXPN		0.08	0.11	0.75	6.21	1.68
C	IVT, Nd = 6	CB	Θ = 5	0.17	0.12	1.14	4.04	3.11
D	IVT, Nd = 6	EXPN		0.10	0.11	1.06	10.0	3.10
E	IVT, Nd = 6	CB	Θ = 30	0.17	0.12	1.06	3.94	3.01
F	IVT, Nd = 6	EXPN		0.11	0.10	1.01	9.87	2.93
G	IVT, Nd = 6	CB	Θ = 90	0.17	0.12	0.98	4.50	2.65
H	IVT, Nd = 6	EXPN		0.09	0.14	0.87	7.15	2.75
I	IVT, Nd = 8	CB	fluid	0.30	0.21	1.71	3.79	3.08
J	IVT, Nd = 8	EXPN		0.05	0.15	0.87	8.58	1.88
K	HS, Nd = 8	EXPN	random	0.11	0.13	0.95	5.84	1.91
L	HS, Nd = 6		Θ = 60	0.24	0.12	2.49	12.8	4.20
M	HS, Nd = 6		Θ = 90	0.24	0.12	2.43	10.8	4.12
N	HS, Nd = 6		Θ = 180	0.19	0.12	1.65	8.90	3.30
O	HS, Nd = 8		fluid	0.12	0.16	1.39	10.1	2.88
P	HS, Nd = 10			0.13	0.12	1.50	11.7	3.51

From Figs. 2 and 3. For each simulation resulting in multiple endosome jumps, we computed the averages of detachment duration T_D, recoil duration T_R, stall duration T_S, maximal frame velocity V_maxf, and the load sharing dyneins L_d. The mean of these averages from eight different simulations for each condition are tabulated above. The standard errors in these values are ∼10% of the values. All simulations in this table are run with an endosome size of 150 nm, dynein binding rate of 5/s, and unloaded dynein detachment rate of 0.4/s. The dynein-motor contact diffusion constant used for the fluid distribution is 0.01 μm²/s. See Supporting Material for additional information on the simulation and model parameters. CB, catch-bond kinetics; EXPN, exponential kinetics; HS, high stall force model with dynein stall force = 2.5 pN; IVT, in vitro model with dynein stall force = 1.25 pN.

Gradual variations in motor forces

An intriguing feature in the repeated detachments of the endosome in Fig. 2 is the gradual variation of the detachment velocities (i.e., cumulative dynein forces) over a timescale of minutes. Fig. 3 F shows the maximal frame velocity V_maxf within each successive jump (black markers) in Fig. 2, which highlights the stochastic variation in the lead-dyneins sharing load. On the other hand, the rolling average of V_maxf (red curve in Fig. 3 F) reveals two notable features. Firstly, there is a gradual variation in the average <V_maxf> over a series of 100–200 detachments as seen from the autocorrelation of <V_maxf> in Fig. 3 G. Secondly, there is a gradual increase in <V_maxf> over the timescale of 1000 s until the endosome eventually broke free and resumed retrograde transport. These observations suggest that the cumulative dynein forces acting on the endosome are dynamic and can gradually evolve over a timescale of minutes. Recently, there have been a few studies probing the collective forces of dyneins on large cellular cargos using calibrated optical traps (6, 7, 9). However, none of the studies probed the same cargo over a long period of time. Our results suggest that such long time trapping studies could be valuable in understanding the dynamic nature of the cargo transport machinery. We note that the single-endosome motility analysis presented above is also done on a few other endosomes exhibiting repeated stalls and detachments. Fig. S3 shows another representative example of an endosome, imaged at 500 fps, exhibiting ∼200 jumps over 14 min.

3D stochastic model simulations of multi-dynein endosome transport under load

In order to analyze the single-endosome stalls/detachments we built a 3D stochastic model, based on the prototype by Erickson and coworkers (8), to simulate the endosome motility under elastic load (see Methods and Supporting Material). In our Monte Carlo model simulations, an endosome driven by multiple dyneins is linked to the microtubule by an elastic tether that exerts a restoring force when stretched beyond its rest length (Fig. 4 A). The collective function of dyneins against the restoring force of the tether results in repeated endosome stalls and detachments, which can be quantified and compared to the experimental data.

The key model parameters are the endosome size, axonal viscosity, number of dyneins, tether stiffness, mechanochemical properties of dyneins, and the spatial distribution of dyneins on the endosome. For a given endosome exhibiting tens of stalls and detachments, most of these model parameters can be estimated from the experimental data as detailed below and in the Supporting Material. Within the constraints of experimental data, we extensively analyzed a few specific considerations in our simulations including 1) the stall force and detachment kinetics of dyneins on endosomes, 2) the spatial distribution of dyneins on endosomes (Fig. 4 B), and 3) the diffusion of motor-endosome contact positions on the endosome surface (Fig. 4 C). Our model simulations successfully replicated the variety of experimental stall and detachment profiles as well as the overall single-endosome experimental statistics (Fig. 5) to aid our understandings on the collective function of dyneins on endosomes (detailed below).

Figure 5.

High stall force model simulation with fluid distribution of dyneins on endosome (Table 1, row O). (A) Simulated trajectory of the tethered endosome exhibiting repeated stalls and detachments is shown. (B) Zooming into the endosome jumps shows key features like sudden, delayed, and sequential detachment profiles. The distributions of T_D, T_R, and T_S for the simulated endosome jumps are shown in (C), (D), and (E), respectively. (F) Histograms of q_min, q_max, and q_det positions for the simulated endosome jumps are shown. To see this figure in color, go online.

In vitro mechanochemical properties cannot simulate experimental stall/detachment profiles

First, we tried to simulate the main statistical metrics quantifying the single-endosome stalls and detachments (i.e., stall duration T_S, detachment duration T_D, and recoil duration T_R) in Fig. 2, by constraining the mechanochemical properties of dynein in the model to in vitro measurements (18). Specifically, the unitary stall force of dynein (F_s = 1.25 pN), the load dependence of dynein-stepping rates, and catch-bond detachment kinetics are fixed to in vitro measurements (Supporting Material). We estimated the other model parameters from the experimental data as follows. 1) The forward/backward stepping rates can be estimated from the net velocity of freely moving endosomes before the initiation of jumps. 2) Considering the jump size of 120 nm as a single dynein event, the tether stiffness is given by k = F_s/120, where F_s is the single dynein stall force. 3) We then fit a few jumps with uninterrupted exponential recoil profiles to extract the damping constant k/γ (Eq. S1) and thereby the friction coefficient γ using k from the previous step. 4) From the effective axonal viscosity (0.05–0.2 Ns/m²) and known γ, we can estimate the endosome size using the Stokes relation. 5) From the peak structure in jump sizes and detachment velocities, we can estimate the number of cooperating dyneins on the endosome to be ∼8. Our simulations spanned a reasonable range of model parameters around these experimental estimates (Table 1).

Our simulations show that the in vitro model has significant limitations in replicating the experimental metrics (Table 1, rows A–J). Basically, the dynein detachment under load in the in vitro model is too fast for efficient cooperation between dyneins and resulted in the average stall durations 40–50% lower than the experiment. Decreasing the detachment rate to enhance the dynein cooperativity, on the other hand, resulted in delayed detachment profiles with average detachment durations twofold higher than the experiment. Further, the histograms of the minima, maxima, and detachment positions within each jump obtained from the model simulations showed significant qualitative differences with experiment (Fig. S4). We tried an extensive set of considerations, including different spatial distributions of dyneins on endosome (Fig. 4, B and C) and relaxed scans of parameters around the experimentally determined estimates. However, the simulated stall duration, detachment duration, and detachment velocity were not simultaneously consistent with experimental data using the in vitro stall force and detachment kinetics of dynein. For instance, clustering the dyneins within a narrow sector on the endosome increases dynein cooperation and the stall duration but results in significantly delayed detachments and rapidly interrupted recoil profiles that are qualitatively inconsistent with experimental data (Fig. S4). We also explored single-rate exponential detachment kinetics as well as a wide range of parameters within catch-bond detachment kinetics with minimal improvement in model performance. Although the exponential kinetics fit the detachment duration and detachment velocity reasonably well, the stall duration is underestimated by 30–50%.

We then tried a modified set of mechanochemical properties (i.e., the high stall force model) based on the in vivo force measurements on lipid droplet system (11, 18, 19). Specifically, we used a higher unitary stall force of 2.5 pN and single-rate exponential detachment kinetics for dynein (Supporting Material). Interestingly, we observed a very good fit to not only the averages but also the distributions of different metrics quantifying the experimental stalls and detachments using the high stall force model simulations with exponential detachment kinetics (Table 1, rows O–P). The averages of stall duration, detachment duration, recoil duration, and detachment velocity could all be simulated with <15% error using the experimentally constrained parameters. Fig. 5 A shows the simulated trajectory of a tethered endosome (Table 1, row O) exhibiting repeated stalls and detachments. Further, notable experimental features like the shoulders in stall profiles and the sudden, delayed, and sequential detachment profiles, etc., are all borne out by model simulations (Fig. 5 B). These results indicate that the detachment kinetics of dynein on endosomes differs substantially from in vitro measurements, within the accuracy of our model. A plausible reason could be the difference in stall force of dynein on endosome, which parametrically affects the detachment kinetics (7, 18). It is also plausible that a pair of dyneins could function as a unit with a unitary stall force of ∼2.5 pN and significantly altered detachment kinetics.

Spatial distribution of dyneins on the endosome in 3D model simulations

In analyzing the efficacy of the in vitro (1.25 pN) and high stall force (2.5 pN) models, we tried several considerations for the spatial distribution of dyneins on endosomes including random-fixed, cluster-fixed, and fluid distributions (Fig. 4, B and C). Briefly, for the random-fixed distribution, dyneins are randomly distributed and the dynein-endosome contact positions are fixed on the endosome surface during the simulation. For the cluster-fixed distribution, the dynein-endosome contact positions are randomly distributed and fixed on a spherical sector of the endosome surface subtending an angle Θ (range of 0–π radians) at the center of the endosome. For the fluid distribution, the dynein-endosome contact positions were allowed to diffuse (D = 0.001–0.1 μm²/s) and drift with torque on the endosome surface (Fig. 4 C). The statistics of simulated endosome stalls and detachments over a long time are highly sensitive to the nature of dynein distribution as detailed below.

Fixed distributions of dyneins on endosomes are not consistent with experimental data

Random-fixed distribution. The geometric activity of dyneins, and hence their cooperativity, is sensitive to the spatial distribution of dyneins even on endosomes as small as 150 nm and the random-fixed distribution is not conducive for dynein cooperativity. For a tethered 150 nm endosome with eight randomly distributed dyneins, the average number of dyneins sharing the load at detachment is <2. In order to have four dyneins cooperating on average, as seen in the experimental data (14), we need a total of 20 dyneins randomly distributed on the endosome (in vitro model). This is implausible based on immunostaining studies (12, 20), which indicate that the maximum number of dyneins on neuronal vesicles is <12. The observation that the number of cooperating dyneins on axonal endosomes (∼4 on average (14)) is comparable to the total number of dyneins (∼5–7 on average (12, 20)) indicates some degree of dynein clustering even on the endosomes as small as 100–200 nm.

Cluster-fixed distribution. We then analyzed the cluster-fixed distributions of dyneins on endosome with Θ ranging from π/30 (all dyneins at one point) to π (all dyneins in one hemisphere). As expected, the dynein cooperativity is enhanced with decreasing Θ due to an increasing number of dyneins that are geometrically active simultaneously. For a tethered 150 nm endosome with eight dyneins, the average number of dyneins sharing load at detachment is 4 for Θ = π/30, 3.9 for Θ = π/6, 3.8 for Θ = π/3, 3.6 for Θ = π/2, and 2.2 for Θ = π. However, the stalls and detachment profiles for low Θ values are inconsistent with the experimental data for both the in vitro (Table 1, rows C–H) and high stall force (Table 1, rows L–N) models. Clustering the dyneins on a narrow sector (Θ < π/3) not only increased the detachment duration (80–100% greater than seen in experiment) but also decreased the recoil duration (40% < experiment) due to fast rebinding of dyneins, which are all geometrically active. Further, clustered distributions with low Θ resulted in a narrow distribution of large stalls due to uniform cooperativity and a bimodal distribution of minima between stalls due to frequently interrupted recoil profiles (Fig. S4), which clearly contrast the experimental data (Fig. 3 B). These results suggest that the dyneins are neither randomly distributed nor clustered at a spot (or too narrowly, as in Θ < π/4) on the endosome.

The high stall force model with clustered dynein distribution overestimates both the detachment duration and the stall duration (Table 1, rows L–N) due to enhanced cooperative activity. We then considered the possibility that the spatial distribution of dyneins is dynamically evolving as opposed to being fixed at the initially recruited positions on endosome surface. It is plausible that the dynein-endosome contact positions are not rigidly fixed and retain some degree of mobility on endosome surface. We hypothesized that this scenario would result in partial clustering of dyneins to intermediate Θ (π/4–π/2) on endosomes, which might not only fit the data better but also explain the dynamic long time variations in detachment velocities seen in experiments. We therefore explored the fluid-distribution model where the dynein-endosome contact positions are allowed to diffuse and drift under mechanical torque (Supporting Material).

Fluid distribution of dynein-endosome contacts leads to dynein clustering on endosomes

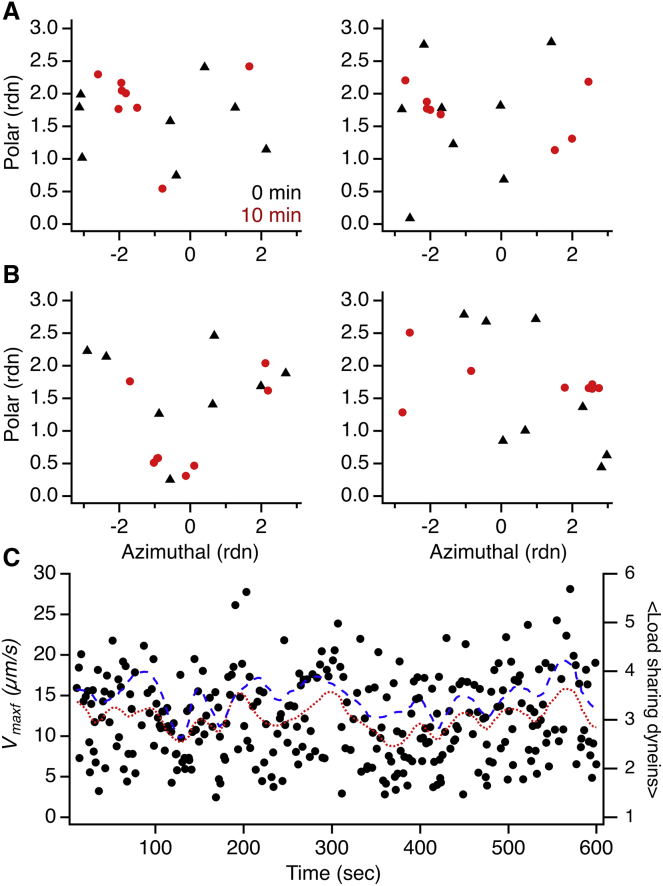
With the fluid distribution, we first asked if the repeated stalls and detachments of dyneins on tethered endosomes could result in the spatial reorganization of dyneins on endosome surface. To this end, we simulated the dynamics of a tethered endosome (150 nm size, with eight dyneins) with the dynein-endosome contact diffusion constant in the range of D = 0.001–0.1 μm²/s. Starting with randomly distributed dyneins, we monitored the spatial distribution of dyneins on the tethered endosome after 10 min of repeated stalls and detachments. Interestingly, in quite a few cases, we observed partial spatial pooling of dyneins (as in Fig. 4 C) on the endosome surface (Fig. 6, A and B). This can be rationalized as follows. Endosomes driven by multiple dyneins tend to maintain a stable orientation with respect to the microtubule for sustained periods of time. The asymmetric positioning of the microtubule can pool dyneins on the endosome surface due to two factors, including 1) the duty ratio of dyneins (microtubule binding/unbinding rate ratio >5) prevents the geometrically active dyneins diffusing away from the region on endosome surface closer to the microtubule and 2) the torques exerted at the dynein-endosome contact positions, for dyneins under load, slide the contacts closer to the microtubule. Of course, the fluctuations of endosome orientation can prolong the timescale for spatial clustering and may also result in multiple clusters depending on the endosome size and viscosity. These results demonstrate that dyneins can dynamically be clustered on the endosome surface in response to load.

Figure 6.

Dynamic clustering of dyneins on tethered endosomes shown by high stall force model simulation with fluid distribution of dyneins on 150 nm endosomes. (A) The spatial distribution of dyneins on endosome is shown by plotting the endosome body coordinates (polar versus azimuthal angles) for each dynein-endosome contact position. The initial distribution is shown in black (filled triangles), and the distribution after 10 min of stalls/detachments is shown in red (filled circles). D = 0.001 μm²/s (B), same as in (A), except D = 0.01 μm²/s. (C) Dynamic variation in motor detachment velocities (V_maxf as black markers and <V_maxf> as red line/dotted line) over a span of minutes from simulation is shown (Table 1, row P). The <V_maxf> shows a clear correlation with the average number of load sharing dyneins (blue line/dashed line). To see this figure in color, go online.

We then analyzed the tethered endosome stalls and detachments over a long time with fluid distribution of dyneins. The model simulations with fluid dynein distribution (high stall force model) were quite successful in replicating the experimental data with minimal modification of the experimentally determined parameters (Fig. 2), as mentioned in the earlier section on in vivo model simulations (Fig. 5; Table 1). Notably, the simulations also show the dynamic variations in detachment velocities over a span of minutes, which correlate well with the number of load-sharing dyneins (Fig. 6 C). The quantitative accuracy of these model simulations supports the hypothesis that the dynamic clustering of dyneins could be a viable mechanism to facilitate the cooperativity of dyneins on axonal endosomes.

Discussion

The collective function of dyneins is fundamental for the retrograde transport of a diverse range of cellular cargos with different sizes and motility regimes. Broadly, the cooperativity of multiple dyneins is governed by several factors, including 1) molecular adaptations of dynein (7, 18), 2) intracellular regulators modifying single dynein properties (21, 22, 23), and 3) mechanisms controlling the spatial assembly of dyneins on cellular cargos (9). Although there is extensive research in literature focused on the first two factors, our understanding of the spatial assembly of dyneins on cellular cargos is limited to specific micron-sized cargos. Probing the spatial assembly of dyneins on smaller cellular cargos is not practical with direct approaches like optical trapping and immunostaining. In this work, we combined a new darkfield imaging assay and 3D stochastic models to analyze the spatial assembly and collective function of dyneins on retrograde endosomes in axons. Our results suggest that the dyneins are assembled in a semiclustered geometry even on endosomes as small as 100–200 nm. Further, we show that such a semiclustered distribution on endosomes can arise from dynamic clustering of dyneins during active transport under load, which can be an efficient mechanism for smaller cargos. The high-accuracy tracking of GNP-endosome motility under load and the quantitative accuracy of our model simulations provide a better understanding of the spatial distribution and mechanochemical properties of dyneins endosomes.

Dynamic clustering of dyneins on cellular cargos: a generic mechanism?

Proteins and lipid microdomains are known to undergo diffusion in the cell membrane, with the diffusion constant ranging from 0.01 to 0.1 μm²/s. It is therefore plausible that the dynein-endosome contact positions are not completely rigid and retain some degree of mobility on the endosome surface. As a consequence, mechanical torques at dynein-endosome contact positions for stretched dyneins under load could result in the contacts sliding and clustering on endosome surface proximal to the microtubule. Our simulations show that even with highly constrained dynein-endosome contact diffusion (0.001 μm²/s), dyneins can dynamically assemble into semiclustered geometries on the endosome in response to load.

The dynamic clustering can be a particularly efficient mechanism for small cellular cargos with a high geometrically active/inactive surface area ratio than larger cargos. However, dynamic clustering by itself may not be enough to support the high cooperativity of dyneins seen on micron-sized cellular cargos. Intracellular force measurements show that the collective forces on micron-sized cargos can be up to 20 pN, indicating the cooperativity of around 10–15 dyneins. Additional structural interactions may be necessary for large cellular cargos to keep all the dyneins clustered within one or more tight spots on cargo for high cooperativity. Recent work by Rai and coworkers demonstrated that the dyneins are spatially clustered on micron-sized late phagosomes in cells (9). More importantly, they also elucidated the likely structural interactions responsible for the clustering of dyneins within cholesterol microdomains on phagosomes. The fact that uniformly distributed dyneins on early phagosomes evolve into clustered distributions on late phagosomes indicates that the dynein-phagosome contacts are mobile before being trapped into tight spots by structural interactions (9). From a general perspective, the clustering mechanism could be cargo-specific and cargo size-dependent. It is quite plausible that a combination of dynamic clustering and cargo-specific structural interactions shape the assembly of dyneins on large cellular cargos.

Evidence for dynamic clustering of motors on cellular cargos under load could also be noted from other experimental data. Soppina and coworkers showed that large bidirectional endosomes in cells were enlongated during pauses, resulting from tugs of war between teams of kinesins and dyneins (24). This indicates that the dyneins were not only clustered to cooperatively withstand the kinesin forces but also positioned spatially opposite to kinesins. Whereas structural interactions can be attributed to the clustering of dyneins, it is hard to rationalize the relative positioning of opposing motor teams. Such polarized spatial assembly of kinesins and dyneins on endosomes could potentially result from dynamic clustering under opposing load.

Recently, there were a few studies probing the collective forces of dyneins on populations of large cellular cargos using calibrated optical traps (6, 7, 9). However, there was no study probing the forces on the same cargo over long times, which is important to distinguish the stochastic and long-time dynamic variations in the collective mechanics of dyneins. Although some long time variations can be attributed to regulatory interactions coupled with cargo maturation, our results suggest that some dynamic variation can also result from fluid distributions of dyneins on cargos.

Mechanochemical properties of dyneins on endosomes

In vitro measurements from several groups have established the stall force of dynein (1.1–1.25 pN) and the catch-bond detachment kinetics of dynein at superstall load (6, 7, 10, 18). However, force measurements on a few large cellular cargos reveal system-dependent stall force of dynein in cells. Shubeita and coworkers, studying lipid droplet transport in vivo, show that the stall force of dynein is 2.5 pN (11). This is substantiated by other independent studies on lipid droplets in vivo (19). On the other hand, Rai and coworkers showed that the unit stall force of retrograde phagosomes in cells is 2.2 pN. This was interpreted as a pair of dyneins recruited by Rab7, thereby giving a stall force of 1.1 pN for dynein on phagosomes (7). The mechanical properties of dyneins extracted by modeling the single GNP-endosome jumps under load could therefore extend the current knowledge on the system dependence of dynein properties in cells.

A notable feature of our single-endosome data analysis based on tens of endosome stalls and detachments is that many model parameters (number of active motors, tether stiffness, friction coefficient, dynein velocity) can be roughly estimated from the experimental data. Further, there are several statistical metrics to be fit simultaneously, which is a rigorous test for different models. Within the accuracy of our 3D model, our results show that the in vitro model (1.25 pN stall force, in vitro detachment kinetics) has severe drawbacks, whereas the high stall force model (2.5 pN stall force) is reasonably accurate in simulating the experimental data. We note that the quantitative accuracy of high stall force model is not necessarily conclusive evidence for the stall force of dynein being 2.5 pN on endosomes. However, in conjunction with the results on lipid droplet system, it lends further credence to the presumed cargo dependence of dynein mechanical properties in cells. Our simulations indicate that the detachment kinetics of dyneins on endosomes differ significantly from in vitro measurements. It is plausible that this could be due to 1) altered mechanochemical properties of dynein complexes on endosome or 2) the function of a pair of dyneins as a unit with twice the stall force of a dynein and modified detachment kinetics. It was reported that the formation of dynein-dynactin-BICD2 complex increases human dynein’s force production to 4.3 pN (25). Further, a recent study shows that dynactin can recruit a second dynein that elevates the stall force and speed of the complex (26).

It is also worth discussing the caveats and limitations of our 3D model. Firstly, it is evident from the data reported earlier (14) and in this work that the endosome jumps are the result of an opposing force on the dyneins driving the endosome. However, the biochemical origins of this force are yet to be established. Understanding the mechanical nature of the force (beyond the simple elastic tether model) would be imperative to improve and substantiate the model simulations. Secondly, our model does not include any regulatory interactions between dyneins and adaptors or between the protofilament structure of the microtubule and protofilament switching of dyneins. It is plausible that such interactions play a critical role in altering the mechanochemical properties in cells as mentioned above (25, 26). Thirdly, we note that the Brownian diffusion of dynein-endosome contacts is a simplification made to highlight the principle of dynamic clustering. However, the timescale of dynamic clustering and the eventual spatial distribution of motors could be modulated by structural domains on the cargo based on the size and specifics of cellular cargos.

Author Contributions

P.D.C. designed the research, carried out the experiments, formulated the model and ran the simulations, and wrote the manuscript. B.C. designed the research and wrote the manuscript. D.L.C. and L.K. carried out the experiments.

Editor: Julie Biteen.