DISTRIBUTED TESTING AND ESTIMATION UNDER SPARSE HIGH DIMENSIONAL MODELS

Abstract

This paper studies hypothesis testing and parameter estimation in the context of the divide-and-conquer algorithm. In a unified likelihood based framework, we propose new test statistics and point estimators obtained by aggregating various statistics from k subsamples of size n/k, where n is the sample size. In both low dimensional and sparse high dimensional settings, we address the important question of how large k can be, as n grows large, such that the loss of efficiency due to the divide-and-conquer algorithm is negligible. In other words, the resulting estimators have the same inferential efficiencies and estimation rates as an oracle with access to the full sample. Thorough numerical results are provided to back up the theory.

1. Introduction

In recent years, the field of statistics has developed apace in response to the opportunities and challenges spawned from the ‘data revolution’, which marked the dawn of an era characterized by the availability of enormous datasets. An extensive toolkit of methodology is now in place for addressing a wide range of high dimensional problems, whereby the number of unknown parameters, d, is much larger than the number of observations, n. However, many modern datasets are instead characterized by n and d both large. The latter presents intimidating practical challenges resulting from storage and computational limitations, as well as numerous statistical challenges (Fan et al., 2014). It is important that statistical methodology targeting modern application areas does not lose sight of the practical burdens associated with manipulating such large scale datasets. In this vein, incisive new algorithms have been developed for exploiting modern computing architectures and recent advances in distributed computing. These algorithms enjoy computational or communication efficiency and facilitate data handling and storage, but come with a statistical overhead if inappropriately tuned.

With increased mindfulness of the algorithmic difficulties associated with large datasets, the statistical community has witnessed a surge in recent activity in the statistical analysis of various divide and conquer (DC) algorithms, which randomly partition the n observations into k subsamples of size n_k = n/k, construct statistics based on each subsample, and aggregate them in a suitable way. In splitting the dataset, a single, very large scale estimation or testing problem with computational complexity O(γ(n)), for a given function γ(·) that depends on the underlying problem, is transformed into k smaller problems with computational complexity O(γ(n/k)) on each machine. What get lost in this process are the interactions of split subsamples in each machine. They are not recoverable without additional rounds of communication or without additional communication between the machines. Since every additional split of the dataset incurs some efficiency loss, it is of significant practical interest to derive a theoretical upper bound on the number of subsamples k that delivers the same asymptotic statistical performance as the practically unavailable “oracle” procedure based on the full sample.

We develop communication efficient generalizations of the Wald and Rao’s score tests for the sparse high dimensional scheme, as well as communication efficient estimators for the parameters of the sparse high dimensional and low dimensional linear and generalized linear models. In all cases we give the upper bound on k for preserving the statistical error of the analogous full sample procedure. While hypothesis testing in a low dimensional context is straightforward, in the sparse high dimensional setting, nuisance parameters introduce a non-negligible bias, causing classical low dimensional theory to break down. In our high dimensional Wald construction, the phenomenon is remedied through a debiasing of the estimator, which gives rise to a test statistic with tractable limiting distribution, as documented in the k = 1 (no sample split) setting in Zhang and Zhang (2014) and van de Geer et al. (2014). For the high dimensional analogue of Rao’s score statistic, the incorporation of a correction factor increases the convergence rate of higher order terms, thereby vanquishing the effect of the nuisance parameters. The approach is introduced in the k = 1 setting in Ning and Liu (2014), where the test statistic is shown to possess a tractable limit distribution. However, the computation complexity for the debiased estimators increases by an order of magnitude, due to solving d high-dimensional regularization problems. This motivates us to appeal to the divide and conquer strategy.

We develop the theory and methodology for DC versions of these tests. In the case of k = 1, each of the above test statistics can be decomposed into a dominant term with tractable limit distribution and a negligible remainder term. The DC extension requires delicate control of these remainder terms to ensure the error accumulation remains sufficiently small so as not to materially contaminate the leading term. We obtain an upper bound on the number of permitted subsamples, k, subject to a statistical guarantee. More specifically, we find that the theoretical upper bound on the number of subsamples guaranteeing the same inferential or estimation efficiency as the whole-sample procedure is $k=o({(\mathit{s}logd)}^{-1}\sqrt{n})$ in the linear model, where s is the sparsity of the parameter vector. In the generalized linear model the scaling is $k=o({((s\vee s_1)logd)}^{-1}\sqrt{n})$, where s₁ is the sparsity of the inverse information matrix.

For sparse high dimensional estimation problems, we use the same debiasing technique introduced in the high dimensional testing problems to obtain a thresholded divide and conquer estimator that achieves the full sample minimax rate. The appropriate scaling is found to be $k=O(\sqrt{n/(s^{2}logd)})$ for the estimation of the sparse parameter vector in the high dimensional linear model and $k=O(\sqrt{n/({(s\vee s_1)}^{2}logd)})$ for the high dimensional generalized linear model. Moreover, we find that the loss incurred by the divide and conquer strategy, as quantified by the distance between the DC estimator and the full sample estimator, is negligible in comparison to the statistical error of the full sample estimator provided that k is not too large. In the context of estimation, the optimal scaling of k with n and d is also developed for the low dimensional linear and generalized linear model. This theory is of independent interest. It also allows us to study a refitted estimation procedure under a minimal signal strength assumption.

1.1. Related Literature

A partial list of references covering DC algorithms from a statistical perspective is Chen and Xie (2012), Zhang et al. (2013), Kleiner et al. (2014), Liu and Ihler (2014) and Zhao et al. (2014a). The closest works to ours are Zhang et al. (2013), Lee et al. (2015) and Rosenblatt and Nadler (2016). Zhang et al. (2013) consider the distributed estimator for kernel ridge regression. In the context of d < n, Zhang et al. (2013) propose the distributed estimator by averaging the kernel ridge regression estimators for each data split. They obtain an explicit upper bound on the number of splits yielding the minimax optimal rates for the mean squared error. However, it is not straightforward to generalize their estimator to the high dimensional setting. In an independent work, Lee et al. (2015) propose the same debiasing approach of van de Geer et al. (2014) to allow aggregation of local estimates on distributed data splits in the context of sparse high dimensional linear and generalized linear models. Though using different techniques of proofs, the conclusions of Lee et al. (2015) in terms of the optimal choice of tuning parameter scaling and the upper bound on the permissible number of sample splits is of the same order. Our work differs from theirs in two aspects: (1) our work also contributes to the distributed testing in sparse high dimensional models and (2) we propose a refitted distributed estimator which has the oracle rate. Our results on hypothesis testing reveal a different phenomenon to that found in estimation, as we observe through the different requirements on the scaling of k. On the estimation side, our results also differ from those of Lee et al. (2015) in that our additional refitting step allows us to achieve the oracle rate. Rosenblatt and Nadler (2016) consider the distributed empirical risk minimization for M-estimators. They require the dimension of the interest parameter to satisfy the scaling condition d/n → κ ∈ (0, 1), which rules out the d ≫ n case. They quantify the accuracy loss over the full sample estimator in terms of the number of splits.

1.2. Organization of the paper

The rest of the paper is organized as follows. Section 2 collects notation and details of a generic likelihood based framework. Section 3 covers testing, providing high dimensional DC analogues of the Wald test (Section 3.1) and Rao’s score test (Section 3.2), in each case deriving a tractable limit distribution for the corresponding test statistic under standard assumptions. Section 4 covers distributed estimation, proposing an aggregated estimator of the unknown parameters of linear and generalized linear models in low dimensional and sparse high dimensional scenarios, as well as a refitting procedure that improves the estimation rate, with the same scaling, under a minimal signal strength assumption. Section 5 provides numerical experiments to back up the developed theory. In Section 6 we discuss our results together with remaining future challenges. Proofs of our main results are collected in Section 7, while the statement and proofs of a number of technical lemmas are deferred to the Supplementary Material.

2. Background and Notation

We first collect the general notation, before providing a formal statement of our statistical problems. More specialized notation is introduced in context.

2.1. Generic Notation

We adopt the common convention of using bold-face letters for vectors only, while regular font is used for both matrices and scalars. |·| denotes both absolute value and cardinality of a set, with the context ensuring no ambiguity. For x = (x₁, …, x_d)^T ∈ ℝ^d, and 1 ≤ q ≤ ∞, we define ${\Vert \mathit{x}\Vert }_q={({\sum }_{j=1}^d{\mid x_j\mid }^q)}^{1/q}$, ||x||₀ = |supp(x)|, where supp(x) = {j : x_j ≠ 0}. Write ||x||_∞ = max_1≤j≤d |x_j|, while for a matrix M = [M_jk], let ||M||_max = max_j,k |M_jk|, ||M||₁ = Σ_j,k |M_jk|. For any matrix M we use M_ℓ to index the transposed ℓ^th row of M and [M]_ℓ to index the ℓ^th column. The sub-Gaussian norm of a scalar random variable X is defined as ||X||_ψ2 = sup_q≥1 q^−1/2(𝔼|X|^q)^1/q. For a random vector X ∈ ℝ^d, its sub-Gaussian norm is defined as ||X||_ψ2 = sup_{x∈𝕊^d−1}||〈X, x〉||_ψ2, where 𝕊^d−1 denotes the unit sphere in ℝ^d. Let I_d denote the d × d identity matrix; when the dimension is clear from the context, we omit the subscript. We also denote the Hadamard product of two matrices A and B as A ∘ B and (A ∘ B)_jk = A_jkB_jk for any j, k. {e₁, …, e_d} denotes the canonical basis for ℝ^d. For a vector v ∈ ℝ^d and a set of indices 𝒮 ⊆ {1, …, d}, v_𝒮 is the vector of length |𝒮| whose components are {v_j : j ∈ 𝒮}. Additionally, for a vector v with j^th element v_j, we use the notation v_−j to denote the remaining vector when the j^th element is removed. With slight abuse of notation, we write v = (v_j, v_−j) when we wish to emphasize the dependence of v on v_j and v_−j individually. The gradient of a function f(x) is denoted by ∇f(x), while ∇_xf(x, y) denotes the gradient of f(x, y) with respect to x, and ${\nabla }_{\mathit{xy}}^{2}f(\mathit{x},\mathit{y})$ denotes the matrix of cross partial derivatives with respect to the elements of x and y. For a scalar η, we simply write f′(η) := ∇_ηf(η) and $f^{″}(\eta ):={\nabla }_{\eta \eta }^{2}f(\eta )$. For a random variable X and a sequence of random variables, {X_n}, we write X_n ⇝ X when {X_n} converges weakly to X. If X is a random variable with standard distribution, say F_X, we simply write X_n ⇝ F_X. Given a, b ∈ ℝ, let a ∨ b and a ∧ b denote the maximum and minimum of a and b. We also make use of the notation a_n ≲ b_n (a_n ≳ b_n) if a_n is less than (greater than) b_n up to a constant, and a_n ≍ b_n if a_n is the same order as b_n.

2.2. General Likelihood based Framework

Let ${({\mathit{X}}_1^T,Y_1)}^T,\dots ,{({\mathit{X}}_n^T,Y_n)}^T$ be n i.i.d. copies of the random vector (X^T, Y)^T, whose realizations take values in ℝ^d × 𝒴. Write the collection of these n i.i.d. random couples as $\mathcal{D}=\{{({\mathit{X}}_1^T,Y_1)}^T,\dots ,{({\mathit{X}}_n^T,Y_n)}^T\}$ with Y = (Y₁, …, Y_n)^T and X = (X₁, …,X_n)^T ∈ ℝ^n×d. Conditional on X_i, we assume Y_i is distributed as F_β^* for all i ∈ {1, …, n}, where F_β^* is a known distribution parameterized by a sparse d-dimensional vector β^* and has a density or mass function f_β^*. We thus define the negative log-likelihood function, ℓ_n(β), as

$${\ell }_n(\mathit{\beta })=\frac{1}{n}\sum _{i=1}^n{\ell }_i(\mathit{\beta })=-\frac{1}{n}\sum _{i=1}^{n}log{f}_{\mathit{\beta }}(Y_i\mid {\mathit{X}}_i).$$ (2.1)

We use J^* = J(β^*) to denote the information matrix and Θ^* to denote (J^*)⁻¹, where $J(\mathit{\beta })=\mathbb{E}[{\nabla }_{\mathit{\beta }\mathit{\beta }}^2{\ell }_n(\mathit{\beta })]$.

For testing problems, our goal is to test $H_0:{\beta }_v^{\ast }={\beta }_v^H$ for a specific fixed index v ∈ {1, …, d}. We partition β^* as ${\mathit{\beta }}^{\ast }={({\beta }_v^{\ast },{\mathit{\beta }}_{-v}^{\ast T})}^T\in {ℝ}^d$, where ${\mathit{\beta }}_{-v}^{\ast }\in {ℝ}^{d-1}$ is a vector of nuisance parameters and ${\beta }_v^{\ast }$ is the parameter of interest. To handle the curse of dimensionality, we exploit a penalized M-estimator defined as,

$${\widehat{\mathit{\beta }}}^{\lambda }=\underset{\mathit{\beta }}{\text{argmin}}\{{\ell }_n(\mathit{\beta })+{\mathcal{P}}_{\lambda }(\mathit{\beta })\},$$ (2.2)

with P_λ(β) a sparsity inducing penalty function with a regularization parameter λ. Examples of P_λ(β) include the convex ℓ₁ penalty, ${\mathcal{P}}_{\lambda }(\mathit{\beta })=\lambda {\Vert \mathit{\beta }\Vert }_1=\lambda {\sum }_{j=1}^d\mid {\beta }_j\mid$ which, in the context of the linear model, gives rise to the Lasso estimator (Tibshirani, 1996),

$${\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\lambda }=\underset{\mathit{\beta }}{\text{argmin}}\left\{\frac{1}{2n}{\Vert \mathit{Y}-X\mathit{\beta }\Vert }_2^2+\lambda {\Vert \mathit{\beta }\Vert }_1\right\}.$$ (2.3)

Other penalties include folded concave penalties such as the smoothly clipped absolute deviation (SCAD) penalty (Fan and Li, 2001) and minimax concave MCP penalty (Zhang, 2010), which eliminate the estimation bias and attain the oracle rates of convergence (Loh and Wainwright, 2013; Wang et al., 2014a). The SCAD penalty is defined as

$${\mathcal{P}}_{\lambda }(\mathit{\beta })=\sum _{j=1}^d{p}_{\lambda }({\beta }_j),\text{where}{p}_{\lambda }(t)={\int }_0^{\mid t\mid }\left\{\lambda 𝟙(z\le \lambda )+\frac{a\lambda -z}{a-1}𝟙(z>\lambda )\right\}dz,$$ (2.4)

for a given parameter a > 0 and MCP penalty is given by

$${\mathcal{P}}_{\lambda }(\mathit{\beta })=\sum _{j=1}^d{p}_{\lambda }({\beta }_j),\text{where}{p}_{\lambda }(t)=\lambda {\int }_0^{\mid t\mid }{\left(1-\frac{z}{\lambda b}\right)}_{+}dz$$ (2.5)

where b > 0 is a fixed parameter. The only requirement we have on P_λ(β) is that it induces an estimator satisfying the following condition.

Condition 2.1

For any δ ∈ (0, 1), if $\lambda \asymp \sqrt{log(d/\delta )/n}$,

$$\mathbb{P}\left({\Vert {\widehat{\mathit{\beta }}}^{\lambda }-{\mathit{\beta }}^{\ast }\Vert }_1>{\mathit{Csn}}^{-1/2}\sqrt{log(d/\delta )}\right)\le \delta ,$$ (2.6)

where s is the sparsity of β^*, i.e., s = ||β^*||₀.

Condition 2.1 is crucial for the theory developed in Sections 3 and 4. Under suitable conditions on the design matrix X, it holds for the Lasso, SCAD and MCP. See Bühlmann and van de Geer (2011); Fan and Li (2001); Zhang (2010) respectively and Zhang and Zhang (2012).

The DC algorithm randomly and evenly partitions 𝒟 into k disjoint subsets 𝒟₁, …,𝒟_k, so that $\mathcal{D}={\cup }_{j=1}^k{\mathcal{D}}_j$, 𝒟_j ∩𝒟_ℓ = Ø for all j, ℓ ∈ {1, …, k}, and |𝒟₁| = |𝒟₂| = ··· = |𝒟_k| = n_k = n/k, where it is implicitly assumed that n can be divided evenly. Let ℐ_j ⊂ {1, …, n} be the index set corresponding to the elements of 𝒟_j. Then for an arbitrary n × d matrix A, A^(j) = [A_iℓ]_{i∈ℐj,1≤ℓ≤d}. For an arbitrary estimator τ̂, we write τ̂ (𝒟_j) when the estimator is constructed based only on 𝒟_j. Finally, we write ${\ell }_{n_k}^{(j)}(\mathit{\beta })={\sum }_{i\in {\mathcal{I}}_j}{\ell }_i(\mathit{\beta })$ to denote the negative log-likelihood function based on 𝒟_j.

While the results of this paper hold in a general likelihood based framework, for simplicity we state conditions at the population level for the generalized linear model (GLM) with canonical link. A much more general set of statements appear in the auxiliary lemmas upon which our main results are based. Under GLM with the canonical link, the response follows the distribution,

$$f_n(\mathit{Y};X,{\mathit{\beta }}^{\ast })=\prod _{i=1}^{n}f(Y_i;{\eta }_i^{\ast })=\prod _{i=1}^n\left\{c(Y_i)exp\left[\frac{Y_i{\eta }_i^{\ast }-b({\eta }_i^{\ast })}{\varphi }\right]\right\},$$ (2.7)

where ${\eta }_i^{\ast }={\mathit{X}}_i^T{\mathit{\beta }}^{\ast }$. The negative log-likelihood corresponding to (2.7) is given, up to an affine transformation, by

$${\ell }_n(\mathit{\beta })=\frac{1}{n}\sum _{i=1}^n-Y_i{\mathit{X}}_i^T\mathit{\beta }+b({\mathit{X}}_i^T\mathit{\beta })=\frac{1}{n}\sum _{i=1}^n-Y_i{\eta }_i+b({\eta }_i)=\frac{1}{n}\sum _{i=1}^n{\ell }_i(\mathit{\beta }),$$ (2.8)

and the gradient and Hessian of ℓ_n(β) are respectively

$$\nabla {\ell }_n(\mathit{\beta })=-\frac{1}{n}{X}^T(\mathit{Y}-\mathit{\mu }(X\mathit{\beta }))\text{and}{\nabla }^2{\ell }_n(\mathit{\beta })=\frac{1}{n}{X}^{T}D(X\mathit{\beta })X,$$

where μ(β) = (b′(η₁), …, b′(η_n))^T and D(β) = diag{b″(η₁), …, b″(η_n)}. In this setting, $J(\mathit{\beta })=\mathbb{E}[b^{″}({\mathit{X}}_1^T\mathit{\beta }){\mathit{X}}_1{\mathit{X}}_1^T]$ and $J^{\ast }=\mathbb{E}[b^{″}({\mathit{X}}_1^T{\mathit{\beta }}^{\ast }){\mathit{X}}_1{\mathit{X}}_1^T]$.

3. Divide and Conquer Hypothesis Tests

In the context of the two classical testing frameworks, the Wald and Rao’s score tests, our objective is to construct a test statistic S̄_n with low communication cost and a tractable limiting distribution F. From this statistic we define a test of size α of the null hypothesis, $H_0:{\beta }_v^{\ast }={\beta }_v^H$, against the alternative, $H_1:{\beta }_v^{\ast }\ne {\beta }_v^H$, as a partition of the sample space described by

$$T_n^{\alpha }=\{\begin{array}{ll}0\hfill & \text{if}\mid {\overline{S}}_n\mid \le F^{-1}(1-\alpha /2)\hfill \\ 1\hfill & \text{if}\mid {\overline{S}}_n\mid >F^{-1}(1-\alpha /2)\hfill \end{array}$$ (3.1)

for a two sided test.

3.1. Two Divide and Conquer Wald Type Constructions

For the high dimensional linear model, Zhang and Zhang (2014), van de Geer et al. (2014) and Javanmard and Montanari (2014) propose methods for debiasing the Lasso estimator with a view to constructing high dimensional analogues of Wald statistics and confidence intervals for low-dimensional coordinates. As pointed out by Zhang and Zhang (2014), the debiased estimator does not impose the minimum signal condition used in establishing oracle properties of regularized estimators (Fan and Li, 2001; Fan and Lv, 2011; Loh and Wainwright, 2015; Wang et al., 2014b; Zhang and Zhang, 2012) and hence has wider applicability than those inferences based on the oracle properties. The method of van de Geer et al. (2014) is appealing in that it accommodates a general penalized likelihood based framework, while the Javanmard and Montanari (2014) approach is appealing in that it optimizes asymptotic variance and requires a weaker condition than van de Geer et al. (2014) in the specific case of the linear model. We consider the DC analogues of Javanmard and Montanari (2014) and van de Geer et al. (2014) in Sections 3.1.1 and 3.1.2 respectively.

3.1.1. Lasso based Wald Test for the Linear Model

The linear model assumes

$$Y_i={\mathit{X}}_i^T{\mathit{\beta }}^{\ast }+{\epsilon }_i,$$ (3.2)

where ${\{{\epsilon }_i\}}_{i=1}^n$ are i.i.d. with 𝔼(ε_i) = 0 and variance σ². For concreteness, we focus on a Lasso based method, but our procedure is also valid when other pilot estimators are used. We describe a modification of the bias correction method introduced in Javanmard and Montanari (2014) as a means to testing hypotheses on low dimensional coordinates of β^* via pivotal test statistics.

On each subset 𝒟_j, we compute the debiased estimator of β^* as in Javanmard and Montanari (2014) as

$${\widehat{\mathit{\beta }}}^d({\mathcal{D}}_j)={\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\lambda }({\mathcal{D}}_j)+\frac{1}{n_k}{M}^{(j)}{\left(X^{(j)}\right)}^T\left(Y^{(j)}-X^{(j)}{\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\lambda }({\mathcal{D}}_j)\right),$$ (3.3)

where the superscript d is used to indicate the debiased version of the estimator, $M^{(j)}={({\mathbf{m}}_1^{(j)},\dots ,{\mathbf{m}}_d^{(j)})}^T$ and m_v is the solution of

$${\mathbf{m}}_v^{(j)}=\underset{\mathbf{m}}{\text{argmin}}{\mathbf{m}}^T{\widehat{\mathrm{\sum }}}^{(j)}\mathbf{m}\text{s.t.}{\Vert {\widehat{\mathrm{\sum }}}^{(j)}\mathbf{m}-{\mathit{e}}_v\Vert }_{\infty }\le {\vartheta }_1,{\Vert X^{(j)}\mathbf{m}\Vert }_{\infty }\le {\vartheta }_2.$$ (3.4)

The choice of tuning parameters ϑ₁ and ϑ₂ is discussed in Javanmard and Montanari (2014) and Zhao et al. (2014a) and they suggest to choose ${\vartheta }_1\asymp \sqrt{logd/n}$, ϑ₂n^−1/2 = o(1). In the context of our DC procedure, ϑ₁ and ϑ₂ rely on k and should be chosen as ${\vartheta }_1\asymp \sqrt{\mathit{k}logd/n}$, ϑ₂n^−1/2 = o(1), as quantified in Theorem 3.3. Above, ${\widehat{\mathrm{\sum }}}^{(j)}={n_k}^{-1}{\sum }_{i\in {\mathcal{I}}_j}{\mathit{X}}_i^{(j)}{\mathit{X}}_i^{(j)T}$ is the sample covariance based on 𝒟_j, whose population counterpart is $\mathrm{\sum }=\mathbb{E}({\mathit{X}}_1{\mathit{X}}_1^T)$ and M^(j) is its regularized inverse. The second term in (3.3) is a bias correction term, while ${\sigma }^2{\mathbf{m}}_v^{(j)T}{\widehat{\mathrm{\sum }}}^{(j)}{\mathbf{m}}_v^{(j)}/n_k$ is shown in Javanmard and Montanari (2014) to be the variance of the v^th component of β̂^d(𝒟_j). The parameter ϑ₁, which tends to zero, controls the bias of the debiased estimator (3.3) and the optimization in (3.4) minimizes the variance of the resulting estimator.

Solving d optimization problems in (3.4) increases an order of magnitude of computation complexity even for k = 1. Thus, it is necessary to appeal to the divide and conquer strategy to reduce the computation burden. This gives rise to the question how large k can be in order to maintain the same statistical properties as the whole sample one (k = 1).

Because our DC procedure gives rise to smaller samples, Σ̂ is singular. This singularity does not pose a statistical problem but it does make the optimization problem ill-posed. To overcome the singularity in Σ̂ and the resulting instability of the algorithm, we propose a change of variables. More specifically, noting that M^(j) is not required explicitly, but rather the product M^(j)(X^(j))^T, we propose

$${\mathit{b}}_v^{(j)}=\underset{\mathit{b}}{\text{argmin}}\frac{{\mathit{b}}^{(j)T}{\mathit{b}}^{(j)}}{n_k}\text{s.t.}{\Vert \frac{X^{(j)T}{\mathit{b}}^{(j)}}{n_k}-{\mathit{e}}_v\Vert }_{\infty }\le {\vartheta }_1,{\Vert {\mathit{b}}^{(j)}\Vert }_{\infty }\le {\vartheta }_2,$$ (3.5)

from which we construct M^(j)(X^(j))^T = B^T, where B = (b₁, …, b_d). The algorithm in equation (3.5) is crucial to the success of our procedure in practice.

The following conditions on the data generating process and the tail behavior of the design vectors are imposed in Javanmard and Montanari (2014). Both conditions are used to derive the theoretical properties of the DC Wald test statistic based on the aggregated debiased estimator, ${\overline{\mathit{\beta }}}^d=k^{-1}{\sum }_{j=1}^k{\widehat{\mathit{\beta }}}^d({\mathcal{D}}_j)$.

Condition 3.1

${\{(Y_i,{\mathit{X}}_i)\}}_{i=1}^n$ are i.i.d. and Σ satisfies 0 < C_min ≤ λ_min(Σ) ≤ λ_max(Σ) ≤ C_max.

Condition 3.2

The rows of X are sub-Gaussian with ||X_i||_ψ2 ≤ κ, i = 1, …, n.

Note that under the two conditions above, there exists a constant κ₁ > 0 such that ${\Vert {\mathit{X}}_1{\mathrm{\sum }}^{-\frac{1}{2}}\Vert }_{{\psi }_2}\le {\kappa }_1$. Without loss of generality, we set κ₁ = κ. Our first main theorem provides the relative scaling of the various tuning parameters involved in the construction of β̄^d.

Theorem 3.3

Suppose Conditions 2.1, 3.1 and 3.2 are fulfilled. Suppose $\mathbb{E}[{\epsilon }_1^4]<\infty$ and choose ϑ₁, ϑ₂ and k such that ${\vartheta }_1\asymp \sqrt{\mathit{k}logd/n}$, ϑ₂n^−1/2 = o(1) and $k=o({(\mathit{s}logd)}^{-1}\sqrt{n})$. For any v ∈ {1, …, d}, we have

$$\sqrt{n}\frac{1}{k}\sum _{j=1}^k\frac{{\widehat{\beta }}_v^d({\mathcal{D}}_j)-{\beta }_v^{\ast }}{{\widehat{Q}}_v^{(j)}}⇝N(0,{\sigma }^2),$$ (3.6)

where ${\widehat{Q}}_v^{(j)}={({\mathbf{m}}_v^{(j)T}{\widehat{\mathrm{\sum }}}^{(j)}{\mathbf{m}}_v^{(j)})}^{1/2}$.

Theorem 3.3 entertains the prospect of a divide and conquer Wald statistic of the form

$${\overline{S}}_n=\sqrt{n}\frac{1}{k}\sum _{j=1}^k\frac{{\widehat{\beta }}_v^d({\mathcal{D}}_j)-{\beta }_v^H}{\overline{\sigma }{({\mathbf{m}}_v^{(j)T}{\widehat{\mathrm{\sum }}}^{(j)}{\mathbf{m}}_v^{(j)})}^{1/2}}$$ (3.7)

for ${\beta }_v^{\ast }$, where σ̄ is an estimator for σ based on the k subsamples. On the left hand side of equation (3.7) we suppress the dependence on v to simplify notation. As an estimator for σ, a simple suggestion with the same computational complexity is σ̄ where

$${\overline{\sigma }}^2=\frac{1}{k}\sum _{j=1}^k{\widehat{\sigma }}^2({\mathcal{D}}_j)\text{and}{\widehat{\sigma }}^2({\mathcal{D}}_j)=\frac{1}{n_k}\sum _{i\in {\mathcal{I}}_j}{(Y_i^{(j)}-{\mathit{X}}_i^{(j)T}{\widehat{\mathit{\beta }}}_{\text{Lasso}}^{\lambda }({\mathcal{D}}_j))}^2.$$ (3.8)

One can use the refitted cross-validation procedure of Fan et al. (2012) to reduce the bias of the estimate. In Lemma 3.4 we show that with the scaling of k and λ required for the weak convergence results of Theorem 3.3, consistency of σ̄² is also achieved.

Lemma 3.4

Suppose 𝔼[ε_i|X_i] = 0 for all i ∈ {1, …, n}. Then with $\lambda \asymp \sqrt{\mathit{k}logd/n}$ and $k=o\left(\sqrt{n}{(\mathit{s}logd)}^{-1}\right)$, |σ̄² − σ²| = o_ℙ(1).

With Lemma 3.4 and Theorem 3.3 at hand, we establish in Corollary 3.5 the asymptotic distribution of S̄_n under the null hypothesis $H_0:{\beta }_v^{\ast }={\beta }_v^H$. This holds for each component v ∈ {1, …, d}.

Corollary 3.5

Suppose Conditions 3.1 and 3.2 are fulfilled, $\mathbb{E}[{\epsilon }_1^4]<\infty$, and λ, ϑ₁ and ϑ₂ are chosen as $\lambda \asymp \sqrt{\mathit{k}logd/n},{\vartheta }_1\asymp \sqrt{\mathit{k}logd/n}$ and ϑ₂n^−1/2 = o(1). Then provided $k=o({(\mathit{s}logd)}^{-1}\sqrt{n})$, under $H_0:{\beta }_v^{\ast }={\beta }_v^H$, we have

$$\underset{n\to \infty }{lim}\mid \mathbb{P}({\overline{S}}_n\le t)-\mathrm{\Phi }(t)\mid =0,$$ (3.9)

where Φ(·) is the cdf of a standard normal distribution.

3.1.2. Wald Test in the Likelihood Based Framework

An alternative route to debiasing the Lasso estimator of β^* is the one proposed in van de Geer et al. (2014). Their so called desparsified estimator of β^* is more general than the debiased estimator of Javanmard and Montanari (2014) in that it accommodates generic estimators of the form (2.2) as pilot estimators, but the latter optimizes the variance of the resulting estimator. The desparsified estimator for subsample 𝒟_j is

$${\widehat{\mathit{\beta }}}^d({\mathcal{D}}_j)={\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)-{\widehat{\mathrm{\Theta }}}^{(j)}\nabla {\ell }_{n_k}^{(j)}({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)),$$ (3.10)

where Θ̂^(j) is a regularized inverse of the Hessian matrix of second order derivatives of ${\ell }_{n_k}^{(j)}(\mathit{\beta })$ at β̂^λ(𝒟_j), denoted by ${\widehat{J}}^{(j)}={\nabla }^2{\ell }_{n_k}^{(j)}({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j))$. We will make this explicit in due course. The estimator resembles the classical one-step estimator (Bickel, 1975), but now in the high-dimensional setting via regularized inverse of the Hessian matrix Ĵ^(j), which reduces to the empirical covariance of the design matrix in the case of the linear model. From equation (3.10), the aggregated debiased estimator over the k subsamples is defined as ${\overline{\mathit{\beta }}}^d=k^{-1}{\sum }_{j=1}^k{\widehat{\mathit{\beta }}}^d({\mathcal{D}}_j)$.

We now use the nodewise Lasso (Meinshausen and Bühlmann, 2006) to approximately invert Ĵ^(j) via L₁-regularization. The basic idea is to find the regularized invert row by row via a penalized L₁-regression, which is the same as regressing the variable X_v on X_−v but expressed in the sample covariance form. For each row v ∈ 1, …, d, consider the optimization

$${\widehat{\mathit{\kappa }}}_v({\mathcal{D}}_j)=\underset{\mathit{\kappa }\in {ℝ}^{d-1}}{\text{argmin}}\left({\widehat{J}}_{vv}^{(j)}-2{\widehat{J}}_{v,-v}^{(j)}\mathit{\kappa }+{\mathit{\kappa }}^T{\widehat{J}}_{-v,-v}^{(j)}\mathit{\kappa }+2{\lambda }_v{\Vert \mathit{\kappa }\Vert }_1\right),$$ (3.11)

where ${\widehat{J}}_{v,-v}^{(j)}$ denotes the v^th row of Ĵ^(j) without the (v, v)^th diagonal element, and ${\widehat{J}}_{-v,-v}^{(j)}$ is the principal submatrix without the v^th row and v^th column. Introduce

$${\widehat{C}}^{(j)}:=\left(\begin{array}{cccc}1& -{\widehat{\kappa }}_{1,2}({\mathcal{D}}_j)& \dots & -{\widehat{\kappa }}_{1,d}({\mathcal{D}}_j)\\ -{\widehat{\kappa }}_{2,1}({\mathcal{D}}_j)& 1& \dots & -{\widehat{\kappa }}_{2,d}({\mathcal{D}}_j)\\ ⋮& ⋮& \ddots & ⋮\\ -{\widehat{\kappa }}_{d,1}({\mathcal{D}}_j)& -{\widehat{\kappa }}_{d,2}({\mathcal{D}}_j)& \dots & 1\end{array}\right)$$ (3.12)

and Ξ̂^(j) = diag(τ̂₁(𝒟_j), …, τ̂_d(𝒟_j)), where ${\widehat{\tau }}_v{({\mathcal{D}}_j)}^2={\widehat{J}}_{vv}^{(j)}-{\widehat{J}}_{v,-v}^{(j)}{\widehat{\mathit{\kappa }}}_v({\mathcal{D}}_j)$. Θ̂^(j) in equation (3.10) is given by

$${\widehat{\mathrm{\Theta }}}^{(j)}={({\widehat{\mathrm{\Xi }}}^{(j)})}^{-2}{\widehat{C}}^{(j)},$$ (3.13)

and we define ${\widehat{\mathbf{\Theta }}}_v^{(j)}$ as the transposed v^th row of Θ̂^(j).

Theorem 3.8 establishes the limit distribution of the term,

$${\overline{S}}_n=\sqrt{n}\frac{1}{k}\sum _{j=1}^k\frac{{\widehat{\beta }}_v^d({\mathcal{D}}_j)-{\beta }_v^H}{\sqrt{{\mathrm{\Theta }}_{vv}^{\ast }}}$$ (3.14)

for any v ∈ {1, …, d} under the null hypothesis $H_0:{\beta }_v^{\ast }={\beta }_v^H$. This provides the basis for the statistical testing based on divide-and-conquer. We need the following condition. Recall that J^* = 𝔼[∇_ββℓ_n(β^*)] and consider the generalized linear model (2.7).

Condition 3.6

(i) ${\{(Y_i,{\mathit{X}}_i)\}}_{i=1}^n$ are i.i.d., 0 < C_min ≤ λ_min(Σ) ≤ λ_max(Σ) ≤ C_max, λ_min(J^*) ≥ L_min > 0, ||J^*||_max < U₁ < ∞. (ii) For some constant M < ∞, ${max}_{1\le i\le n}\mid {\mathit{X}}_i^T{\mathit{\beta }}^{\ast }\mid \le M$ and max_1≤i≤n ||X_i||_∞ ≤ M. (iii) There exist finite constants U₂, U₃ > 0 such that b″(η) < U₂ and b‴(η) < U₃ for all η ∈ ℝ.

The same assumptions appear in van de Geer et al. (2014). In the case of the Gaussian GLM, the condition on λ_min(J^*) reduces to the requirement that the covariance of the design has minimal eigenvalue bounded away from zero, which is a standard assumption. We require ||J^*||_max < ∞ to control the estimation error of different functionals of J^*. The restriction in (ii) on the covariates and the projection of the covariates are imposed for technical simplicity; it can be extended to the case of exponential tails (see Fan and Song, 2010). Note that $\text{Var}(Y_i)=\varphi b^{″}({\mathit{X}}_i^T{\mathit{\beta }}^{\ast })$ where ϕ is the dispersion parameter in (2.7), so b″(η) < U₂ essentially implies an upper bound on the variance of the response. In fact, Lemma E.2 shows that b″(η) < U₂ can guarantee that the response is sub-Gaussian. b‴(η) < U₃ is used to derive the Lipschitz property of $b^{″}({\mathit{X}}_i^T\mathit{\beta })$ with respect to β as shown in Lemma E.5. We emphasize that no requirement in Condition 3.6 is specific to the divide and conquer framework.

The assumption of bounded design in (ii) can be relaxed to the sub- Gaussian design. However, the price to pay is that the allowable number of subsets k is smaller than the bounded case, which means we need a larger sub-sample size. To be more precise, the order of maximum k for the sub-Gaussian design has an extra factor, which is a polynomial of $\sqrt{logd}$, compared to the order for the bounded design. This logarithmic factor comes from different Lipschitz properties of $b^{″}({\mathit{X}}_i^T\mathit{\beta })$ in the two designs, which is fully explained in Lemma E.5 in the Supplementary Material. In the following theorems, we only present results for the case of bounded design for technical simplicity.

In addition, recalling that Θ^* = (J^*)⁻¹, where $J^{\ast }:=J({\mathit{\beta }}^{\ast })=\mathbb{E}[{\nabla }_{\mathit{\beta }\mathit{\beta }}^2{\ell }_n({\mathit{\beta }}^{\ast })]$, we impose Condition 3.7 on Θ^* and its estimator Θ̂.

Condition 3.7

(i) ${min}_{1\le v\le d}{\mathrm{\Theta }}_{vv}^{\ast }>{\theta }_{min}>0$. (ii) ${max}_{1\le i\le n}{\Vert {\mathit{X}}_i^T{\mathbf{\Theta }}^{\ast }\Vert }_{\infty }\le M$. (iii) For v = 1, …, d, whenever ${\lambda }_v\asymp \sqrt{\mathit{k}logd/n}$ in (3.11), we have

$$\mathbb{P}\left({\Vert {\widehat{\mathbf{\Theta }}}_v-{\mathbf{\Theta }}_v^{\ast }\Vert }_1\ge C{s}_1\sqrt{logd/n}\right)\le d^{-1},$$

where C is a constant and s₁ is such that ${\Vert {\mathbf{\Theta }}_v^{\ast }\Vert }_0\precsim s_1$ for all v ∈ {1, …, d}.

Part (i) of Corollary 3.7 ensures that the variances of each component of the debiased estimator exist, guaranteeing the existence of the Wald statistic. Parts (ii) and (iii) are imposed directly for technical simplicity. Results of this nature have been established under a similar set of assumptions in van de Geer et al. (2014) and Negahban et al. (2009) for convex penalties and in Wang et al. (2014a) and Loh and Wainwright (2015) for folded concave penalties.

As a step towards deriving the limit distribution of the proposed divide and conquer Wald statistic in the GLM framework, we establish the asymptotic behavior of the aggregated debiased estimator ${\overline{\beta }}_v^d$ for every given v ∈ [d].

Theorem 3.8

Under Conditions 2.1, 3.6 and 3.7, with $\lambda \asymp \sqrt{\mathit{k}logd/n}$, we have

$${\overline{\beta }}_v^d-{\beta }_v^{\ast }=-\frac{1}{k}\sum _{j=1}^k{\widehat{\mathbf{\Theta }}}_v^{(j)T}\nabla {\ell }_{n_k}^{(j)}({\mathit{\beta }}^{\ast })+o_{\mathbb{P}}(n^{-1/2})$$ (3.15)

for any k ≪ d satisfying $k=o\left({((s\vee s_1)logd)}^{-1}\sqrt{n}\right)$, where ${\widehat{\mathbf{\Theta }}}_v^{(j)}$ is the transposed v^th row of Θ̂^(j).

The proof of Theorem 3.8 shows that for the Wald test procedure, the divide and conquer estimator ${\overline{\beta }}_v^d$ is asymptotically as efficient as the full sample estimator β̂_v, i.e.,

$$\underset{n\to \infty }{lim}\frac{\text{Var}({\overline{\beta }}_v^d)}{\text{Var}({\widehat{\beta }}_v^d)}-1=0.$$

A corollary of Theorem 3.8 provides the asymptotic distribution of the Wald statistic in equation (3.14) under the null hypothesis.

Corollary 3.9

Let S̄_n be as in equation (3.14), with ${\mathrm{\Theta }}_{vv}^{\ast }$ replaced with an estimator Θ̃_vv. Then under the conditions of Theorem 3.8 and $H_0:{\beta }_v^{\ast }={\beta }_v^H$, provided |Θ̃_vv − Θ_vv| = o_ℙ(1) under the scaling $k=o\left({((s\vee s_1)logd)}^{-1}\sqrt{n}\right)$, we have

$$\underset{n\to \infty }{lim}\underset{t\in ℝ}{sup}\mid \mathbb{P}({\overline{S}}_n\le t)-\mathrm{\Phi }(t)\mid =0.$$

Remark 3.10

Although Theorem 3.8 and Corollary 3.9 are stated only for the GLM, their proofs are in fact an application of two more general results. Further details are available in Lemmas E.7 and E.8 in the Supplementary Material.

We return to the issue of estimating ${\mathrm{\Theta }}_{vv}^{\ast }$ in Section 4, where we introduce a consistent estimator of ${\mathrm{\Theta }}_{vv}^{\ast }$ that preserves the scaling of Theorem 3.8 and Corollary 3.9.

3.2. Divide and Conquer Score Test

In this section, we use ∇_vf(β) and ∇_−vf(β) to denote, respectively, the partial derivative of f with respect to β_v and the partial derivative vector of f with respect to β_−v. ${\nabla }_{vv}^{2}f(\mathit{\beta }),{\nabla }_{v,-v}^{2}f(\mathit{\beta }),{\nabla }_{-v,v}^{2}f(\mathit{\beta })$ and ${\nabla }_{-v,-v}^{2}f(\mathit{\beta })$ are analogously defined.

In the low dimensional setting (where d is fixed), Rao’s score test of $H_0:{\beta }_v^{\ast }={\beta }_v^H$ against $H_1:{\beta }_v^{\ast }\ne {\beta }_v^H$ is based on ${\nabla }_v{\ell }_n({\beta }_v^H,{\stackrel{\sim }{\mathit{\beta }}}_{-v})$ , where β̃_−v is a constrained maximum likelihood estimator of ${\mathit{\beta }}_{-v}^{\ast }$, constructed as ${\stackrel{\sim }{\mathit{\beta }}}_{-v}={\text{argmin}}_{{\mathit{\beta }}_{-v}}{\ell }_n({\beta }_v^H,{\mathit{\beta }}_{-v})={\text{argmax}}_{{\mathit{\beta }}_{-v}}\{-{\ell }_n({\beta }_v^H,{\mathit{\beta }}_{-v})\}$. If H₀ is false, imposing the constraint postulated by H₀ significantly violates the first order conditions from M-estimation with high probability; this is the principle underpinning the classical score test. Under regularity conditions, it can be shown (e.g. Cox and Hinkley, 1974) that

$$\sqrt{n}({\nabla }_v{\ell }_n({\beta }_v^H,{\stackrel{\sim }{\mathit{\beta }}}_{-v}))J_{v\mid -v}^{\ast -1/2}⇝N(0,1),$$

where $J_{v\mid -v}^{\ast }$ is given by $J_{v\mid -v}^{\ast }=J_{v,v}^{\ast }-{\mathit{J}}_{v,-v}^{\ast }{J}_{-v,-v}^{\ast -1}{\mathit{J}}_{-v,v}^{\ast }$, with $J_{v,v}^{\ast },{\mathit{J}}_{v,-v}^{\ast },J_{-v,-v}^{\ast }$ and ${\mathit{J}}_{-v,v}^{\ast }$ the partitions of the information matrix J^* = J(β^*),

$$J(\mathit{\beta })=\left(\begin{array}{cc}{J}_{v,v}& {\mathit{J}}_{v,-v}\\ {\mathit{J}}_{-v,v}& J_{-v,-v}\end{array}\right)=\left(\begin{array}{cc}\mathbb{E}{\nabla }_{v,v}^2{\ell }_n(\mathit{\beta })& \mathbb{E}{\nabla }_{v,-v}^2{\ell }_n(\mathit{\beta })\\ \mathbb{E}{\nabla }_{-v,v}^2{\ell }_n(\mathit{\beta })& \mathbb{E}{\nabla }_{-v,-v}^2{\ell }_n(\mathit{\beta })\end{array}\right).$$ (3.16)

The problems associated with the use of the classical score statistic in the presence of a high dimensional nuisance parameter are brought to light by Ning and Liu (2014), who propose a remedy via the decorrelated score. The problem stems from the inversion of the matrix $J_{-v,-v}^{\ast }$ in high dimensions. The decorrelated score is defined as

$$S({\beta }_v^{\ast },{\mathit{\beta }}_{-v}^{\ast })={\nabla }_v{\ell }_n({\beta }_v^{\ast },{\mathit{\beta }}_{-v}^{\ast })-{\mathit{w}}^{\ast T}{\nabla }_{-v}{\ell }_n({\beta }_v^{\ast },{\mathit{\beta }}_{-v}^{\ast }),$$ (3.17)

where ${\mathit{w}}^{\ast T}={\mathit{J}}_{v,-v}^{\ast }{J}_{-v,-v}^{\ast -1}$. For a regularized estimator ŵ of w^*, to be defined below, we consider the score estimator

$$\widehat{S}({\beta }_v^{\ast },{\widehat{\mathit{\beta }}}_{-v}^{\lambda })={\nabla }_v{\ell }_n({\beta }_v^{\ast },{\widehat{\mathit{\beta }}}_{-v}^{\lambda })-{\widehat{\mathit{w}}}^T{\nabla }_{-v}{\ell }_n({\beta }_v^{\ast },{\widehat{\mathit{\beta }}}_{-v}^{\lambda }).$$ (3.18)

Hence, provided w^* is sufficiently sparse to avoid excessive noise accumulation, we are able to achieve consistency of ŵ under the high dimensional setting, ultimately giving rise to a tractable limit distribution of a suitable rescaling of $\widehat{S}({\beta }_v^{\ast },{\widehat{\mathit{\beta }}}_{-v}^{\lambda })$. Since ${\beta }_v^{\ast }$ is restricted under the null hypothesis, $H_0:{\beta }_v^{\ast }={\beta }_v^H$, the statistic in (3.18) is accessible once H₀ is imposed. As Ning and Liu (2014) point out, w^* is the solution to

$${\mathit{w}}^{\ast }=\underset{\mathit{w}}{\text{argmin}}\mathbb{E}{[{\nabla }_v{\ell }_n({\beta }_v^H,{\mathit{\beta }}_{-v}^{\ast })-{\mathit{w}}^T{\nabla }_{-v}{\ell }_n({\beta }_v^H,{\mathit{\beta }}_{-v}^{\ast })]}^2$$

under $H_0:{\beta }_v^{\ast }={\beta }_v^H$.

Our divide and conquer score statistic under $H_0:{\beta }_v^{\ast }={\beta }_v^H$ is

$$\overline{S}({\beta }_v^H)=\frac{1}{k}\sum _{j=1}^k{\widehat{S}}^{(j)}\left({\beta }_v^H,{\widehat{\mathit{\beta }}}_{-v}^{\lambda }({\mathcal{D}}_j)\right),\text{where}$$ (3.19)

${\widehat{S}}^{(j)}\left({\beta }_v,{\widehat{\mathit{\beta }}}_{-v}^{\lambda }({\mathcal{D}}_j)\right)={\nabla }_v{\ell }_{n_k}^{(j)}\left({\beta }_v,{\widehat{\mathit{\beta }}}_{-v}^{\lambda }({\mathcal{D}}_j)\right)-\widehat{\mathit{w}}{({\mathcal{D}}_j)}^T{\nabla }_{-v}{\ell }_{n_k}^{(j)}\left({\beta }_v,{\widehat{\mathit{\beta }}}_{-v}^{\lambda }({\mathcal{D}}_j)\right)$ and we estimate w^* using the Dantzig selector of Candes and Tao (2007)

$$\begin{gathered} \widehat{\mathit{w}}({\mathcal{D}}_j)=\underset{\mathit{w}}{\text{argmin}}{\Vert \mathit{w}\Vert }_1, \\ \text{s.t.}{\Vert {\nabla }_{-v,v}^2{\ell }_{n_k}^{(j)}\left({\widehat{\beta }}_v^{\lambda }({\mathcal{D}}_j),{\widehat{\mathit{\beta }}}_{-v}^{\lambda }({\mathcal{D}}_j)\right)-{\mathit{w}}^T{\nabla }_{-v,-v}^2{\ell }_{n_k}^{(j)}\left({\widehat{\beta }}_v^{\lambda }({\mathcal{D}}_j),{\widehat{\mathit{\beta }}}_{-v}^{\lambda }({\mathcal{D}}_j)\right)\Vert }_{\infty }\le \mu . \end{gathered}$$

Theorem 3.11

Let Ĵ_v|−v be a consistent estimator of $J_{v\mid -v}^{\ast }$ and

$$S^{(j)}({\beta }_v^H,{\mathit{\beta }}_{-v}^{\ast })={\nabla }_v{\ell }_{n_k}^{(j)}({\beta }_v^H,{\mathit{\beta }}_{-v}^{\ast })-{\mathit{w}}^{\ast T}{\nabla }_{-v}{\ell }_{n_k}^{(j)}({\beta }_v^H,{\mathit{\beta }}_{-v}^{\ast }).$$

Suppose ||w^*||₁ ≲ s₁ and Conditions 2.1 and 3.6 are fulfilled. Then under $H_0:{\beta }_v^{\ast }={\beta }_v^H$ with $\lambda \asymp \mu \asymp \sqrt{\mathit{k}logd/n}$,

$$\begin{gathered} \sqrt{n}\overline{S}({\beta }_v^H)=\sqrt{n}\frac{1}{k}\sum _{j=1}^k{S}^{(j)}({\beta }_v^H,{\mathit{\beta }}_{-v}^{\ast })+o_{\mathbb{P}}(1) \\ \text{and}\underset{n\to \infty }{lim}\underset{t\in ℝ}{sup}|\mathbb{P}\left(\sqrt{n}·\overline{S}({\beta }_v^H){\widehat{J}}_{v\mid -v}^{-1/2}\le t\right)-\mathrm{\Phi }(t)|=0, \end{gathered}$$

for any k ≪ d satisfying $k=o\left({((s\vee s_1)logd)}^{-1}\sqrt{n}\right)$, where $\overline{S}({\beta }_v^H)$ is defined in equation (3.19).

Remark 3.12

By the definition of w^* and the block matrix inversion formula for Θ^* = (J^*)⁻¹, sparsity of w^* is implied by sparsity of Θ^* as assumed in van de Geer et al. (2014) and Condition 3.7 of Section 3.1.2. In turn, ||w^*||₀ ≲ s₁ implies ||w^*||₁ ≲ s₁ provided that the elements of w^* are bounded.

Remark 3.13

Although Theorem 3.11 is stated in the penalized GLM setting, the result holds more generally; further details are available in Lemma E.13 in the Supplementary Material.

To maintain the same computational complexity, an estimator of the conditional information needs to be constructed using a DC procedure. For this, we propose to use

$${\overline{J}}_{v\mid -v}=k^{-1}\sum _{j=1}^k\left({\nabla }_{v,v}^2{\ell }_{n_k}^{(j)}({\overline{\beta }}_v^d,{\overline{\mathit{\beta }}}_{-v})-{\overline{\mathit{w}}}^T{\nabla }_{-v,v}^2{\ell }_{n_k}^{(j)}({\overline{\beta }}_v^d,{\overline{\mathit{\beta }}}_{-v})\right),$$

where the divide and conquer estimator ${\overline{\beta }}_v^d=k^{-1}{\sum }_{j=1}^k{\widehat{\beta }}_v^d({\mathcal{D}}_j),{\overline{\mathit{\beta }}}_{-v}=k^{-1}{\sum }_{j=1}^k{\widehat{\mathit{\beta }}}_{-v}^{\lambda }({\mathcal{D}}_j)$ and $\overline{\mathit{w}}=k^{-1}{\sum }_{j=1}^k\widehat{\mathit{w}}({\mathcal{D}}_j)$. Note that for certain v, the communication cost for calculating J̄_v|−v is not high, since all the involved quantities ${\{{\nabla }_{v,v}^2{\ell }_{n_k}^{(j)}({\overline{\beta }}_v^d,{\overline{\mathit{\beta }}}_{-v})\}}_{j=1}^k,{\{{\nabla }_{-v,v}^2{\ell }_{n_k}^{(j)}({\overline{\beta }}_v^d,{\overline{\mathit{\beta }}}_{-v})\}}_{j=1}^k$ and ${\{\widehat{\mathit{w}}({\mathcal{D}}_j)\}}_{j=1}^k$ are scalars, d-dimensional vectors and d-dimensional vectors respectively. The communication cost is thus of order O(kd). We do not communicate the entire huge hessian matrix here.

Lemma 3.14

Suppose ||w^*||₁ = O(s₁) and Conditions 2.1 and 3.6 are fulfilled. Then for any k ≪ d satisfying $k=o\left({((s\vee s_1)logd)}^{-1}\sqrt{n}\right),\mid {\overline{J}}_{v\mid -v}-J_{v\mid -v}^{\ast }\mid =o_{\mathbb{P}}(1)$.

By Lemma 3.14, we show that J̄_v|−v is consistent and can be applied to Theorem 3.11.

4. Accuracy of Distributed Estimation

This section focuses on high-dimensional (d ≫ n) divide-and-conquer estimators for linear and generalized linear models. As explained below Theorem 3.8 in Section 3, the efficiency loss from the divide-and-conquer process is asymptotically zero. This motivates us to consider ||β̄^d − β̂^d||, the loss incurred by the divide and conquer strategy in comparison with the practically unavailable full sample debiased estimator β̂^d, where ||·|| is certain norm. Indeed, it turns out that, for k not too large, β̄^d − β̂^d appears only as a higher order term in the decomposition of β̄^d − β^* and thus ||β̄^d − β̂^d|| is negligible compared to the statistical error, ||β̂^d − β^*||. In other words, the divide-and-conquer errors are statistically negligible.

Compared with calculating the full sample debiased Lasso estimator, our proposed DC strategy enjoys computational advantages since it is highly parallel and each subsample problem has a much smaller scale than the full sample problem given a suitably large k. However, relative to just the full sample penalized M-estimator (e.g., Lasso), distributed point estimation does not entail a computational gain like distributed testing, since our distributed algorithm requires debiasing each component of the Lasso estimator and hence brings high expense of computation. The bottleneck of computation of our DC procedure comes from the d extra debiasing steps. To mitigate this problem, we can actually debias each component of β̂ in a parallel fashion. According to the optimization procedures (3.4) and (3.11), debiasing one component of the Lasso estimator is entirely independent of the debiasing of another component. Therefore, as long as each branch computer in the cluster shares the sub-dataset 𝒟_j and the Lasso estimator β̂^(j), they can work in parallel and collectively return to a central server all the components of the debiased Lasso estimator. This parallelization reduces the time complexity significantly.

When the minimum signal strength is sufficiently strong, thresholding β̄^d achieves exact support recovery, motivating a refitting procedure based on the low dimensional selected variables. As a means to understanding the theoretical properties of this refitting procedure, as well as for independent interest, we develop new theories and methodologies for the low dimensional (d < n) linear and generalized linear models in Appendixes A and B in the Supplementary Material respectively. We show that simple averaging of low dimensional OLS or GLM estimators (denoted uniformly as β̂^(j), without superscript d as debiasing is not necessary) suffices to preserve the statistical error, i.e., achieving the same statistical accuracy as the estimator based on the full sample. This is because, in contrast to the high dimensional setting, parameters are not penalized in the low dimensional case. With β̄ the average of β̂^(j) over the k machines and β̂ the full sample counterpart (k = 1), we derive the rate of convergence of ||β̄ − β̂||₂. Refitted estimation using only the selected covariates allows us to eliminate the log d term in the statistical rate of convergence of the estimator under high-dimensional settings. We present theoretical results on the refitting estimation as corollaries to the low-dimensional regression results in Appendixes A and B in the Supplementary Material.

4.1. The High-Dimensional Linear Model

Recall that the high dimensional DC estimator is ${\overline{\mathit{\beta }}}^d=k^{-1}{\sum }_{j=1}^k{\widehat{\mathit{\beta }}}^d({\mathcal{D}}_j)$, where β̂^d(𝒟_j) for 1 ≤ j ≤ k is the debiased estimator defined in (3.3). We also denote the debiased Lasso estimator using the entire dataset as ${\widehat{\mathit{\beta }}}^d={\widehat{\mathit{\beta }}}^d({\cup }_{j=1}^k{\mathcal{D}}_j)$. The following lemma shows that not only is β̄^d asymptotically normal, it approximates the full sample estimator β̂^d so well that it has the same statistical error as β̂^d provided the number of subsamples k is not too large.

Lemma 4.1

Consider the linear model (3.2). Under the Conditions 3.1 and 3.2, if λ, ϑ₁ and ϑ₂ are chosen as $\lambda \asymp \sqrt{\mathit{k}logd/n},{\vartheta }_1\asymp \sqrt{\mathit{k}logd/n}$ and ϑ₂n^−1/2 = o(1), we have with probability 1 − c/d,

$${\Vert {\overline{\mathit{\beta }}}^d-{\widehat{\mathit{\beta }}}^d\Vert }_{\infty }\le C\frac{\mathit{sk}logd}{n}\text{and}{\Vert {\overline{\mathit{\beta }}}^d-{\mathit{\beta }}^{\ast }\Vert }_{\infty }\le C\left(\sqrt{\frac{logd}{n}}+\frac{\mathit{sk}logd}{n}\right).$$ (4.1)

Remark 4.2

The term $\sqrt{logd/n}$ in (4.1) is the estimation error of ||β̂^d − β^*||_∞, while the term (sk log d)/n is the rate of the distance between the divide and conquer estimator and the full sample estimator. Lemma 4.1 does not rely on any specific choice of k. However, in order for the aggregated estimator β̄^d to attain the same ||·||_∞ norm estimation error as the full sample Lasso estimator, β̂_Lasso, the required scaling is $k=O(\sqrt{n/(s^{2}logd)})$. This is a weaker scaling requirement than that of Theorem 3.3 because the latter entails a guarantee of asymptotic normality, which is a stronger result. It is for the same reason that our estimation results only require O(·) scaling whilst those for testing require o(·) scaling.

Rosenblatt and Nadler (2016) show that in the high-dimensional regime where d/n_k → κ ∈ (0, 1), the divide and conquer procedure suffers from first-order accuracy loss. This seems a contradiction to our result, since our dimension is even higher than their context, but we have no first-order accuracy loss while averaging debiased estimators based on subsamples, as long as we have an appropriate number of data splits. In fact, in the highdimensional sparse linear regression, the intrinsic dimension is the sparsity s rather than d, which is regarded instead as the ambient dimension. The sparsity assumption changes the original high-dimensional problem to be an intrinsically low-dimensional one and thus allows us to escape from any first-order accuracy loss of the divide and conquer procedure. Given s = o(n_k), we can treat high-dimensional sparse linear regression approximately as the classical linear regression setting where d = o(n_k). Hence we expect no first-order accuracy loss from the divide and conquer procedure here.

Although β̄^d achieves the same rate as the Lasso estimator under the infinity norm, it cannot achieve the minimax rate in ℓ₂ norm since it is not a sparse estimator. To obtain an estimator with the ℓ₂ minimax rate, we sparsify β̄^d by hard thresholding. For any β ∈ ℝ^d, define the hard thresholding operator 𝒯_ν such that the j^th entry of 𝒯_ν(β) is

$${[{\mathcal{T}}_{\nu }(\mathit{\beta })]}_j={\mathit{\beta }}_j𝟙\{\mid {\mathit{\beta }}_j\mid \ge \nu \},\text{for}1\le j\le d.$$ (4.2)

According to (4.1), if ${\mathit{\beta }}_j^{\ast }=0$, we have $\mid {\overline{\mathit{\beta }}}_j^d\mid \le C(\sqrt{logd/n}+\mathit{sk}logd/n)$ with high probability. The following theorem characterizes the estimation error, ||𝒯_ν(β̄^d) − β^*||₂, and divide and conquer error, ||𝒯_ν(β̄^d) − 𝒯_ν(β̂^d)||₂, of the thresholded estimator 𝒯_ν(β̄^d).

Theorem 4.3

Under the linear model (3.2), suppose Conditions 3.1 and 3.2 are fulfilled and choose $\lambda \asymp \sqrt{\mathit{k}logd/n},{\vartheta }_1\asymp \sqrt{\mathit{k}logd/n}$ and ϑ₂n^−1/2 = o(1). Take the parameter of the hard threshold operator in (4.2) as $\nu =C_0\sqrt{logd/n}$ for some sufficiently large constant C₀. If the number of subsamples satisfies $k=O(\sqrt{n/(s^{2}logd)})$, for large enough d and n, we have with probability 1 − c/d,

$$\begin{gathered} {\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathcal{T}}_{\nu }({\widehat{\mathit{\beta }}}^d)\Vert }_2\le C\frac{s^{3/2}\mathit{k}logd}{n},{\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathit{\beta }}^{\ast }\Vert }_{\infty }\le C\sqrt{\frac{logd}{n}} \\ \text{and}{\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathit{\beta }}^{\ast }\Vert }_2\le C\sqrt{\frac{\mathit{s}logd}{n}}. \end{gathered}$$

Remark 4.4

In fact, in the proof of Theorem 4.3, we show that if the thresholding parameter ν satisfies ν ≥ ||β̄^d − β^*||_∞, we have ${\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathit{\beta }}^{\ast }\Vert }_2\le 2\sqrt{2s}·\nu$; it is for this reason that we choose $\nu \asymp \sqrt{logd/n}$. Unfortunately, the constant is difficult to choose in practice. In the following paragraphs we propose a practical method to select the tuning parameter ν.

Let (M^(j)X^(j)T)_ℓ denote the transposed ℓ^th row of M^(j)X^(j)T. Inspection of the proof of Theorem 3.3 reveals that the leading term of $\sqrt{n}{\Vert {\overline{\mathit{\beta }}}^d-{\mathit{\beta }}^{\ast }\Vert }_{\infty }$ satisfies

$$T_0=\underset{1\le \ell \le d}{max}\frac{1}{\sqrt{k}}\sum _{j=1}^k\frac{1}{\sqrt{n_k}}{(M^{(j)}{X}^{(j)T})}_{\ell }^T{\mathit{\epsilon }}^{(j)}.$$

Chernozhukov et al. (2013) propose the Gaussian multiplier bootstrap to estimate the quantile of T₀. Let ${\{{\xi }_i\}}_{i=1}^n$ be i.i.d. standard normal random variable independent of ${\{(Y_i,{\mathit{X}}_i)\}}_{i=1}^n$. Consider the statistic

$$W_0=\underset{1\le \ell \le d}{max}\frac{1}{\sqrt{k}}\sum _{j=1}^k\frac{1}{\sqrt{n_k}}{(M^{(j)}{X}^{(j)T})}_{\ell }^T({\widehat{\mathit{\epsilon }}}^{(j)}\circ {\mathit{\xi }}^{(j)}),$$

where ε̂^(j) ∈ ℝ^n_k is an estimator of ε^(j) such that for any i ∈ ℐ_j, ${\widehat{\epsilon }}_i^{(j)}=Y_i^{(j)}-{\mathit{X}}_i^{(j)}\widehat{\mathit{\beta }}({\mathcal{D}}_j)$, and ξ^(j) is a subvector of ${\{{\xi }_i\}}_{i=1}^n$ with indices in ℐ_j. Recall that “∘” denotes the Hadamard product. The α-quantile of W₀ conditioning on ${\{Y_i,{\mathit{X}}_i\}}_{i=1}^n$ is defined as c_W0(α) = inf{t | ℙ(W₀ ≤ t | Y, X) ≥ α}. We estimate c_W0(α) by Monte-Carlo and thus choose ${\nu }_0=c_{W_0}(\alpha )/\sqrt{n}$. This choice ensures

$${\Vert {\mathcal{T}}_{{\nu }_0}({\overline{\mathit{\beta }}}^d)-{\mathit{\beta }}^{\ast }\Vert }_2=O_{\mathbb{P}}(\sqrt{\mathit{s}logd/n}),$$

which coincides with the ℓ₂ convergence rate of the Lasso.

Remark 4.5

Lemma 4.1 and Theorem 4.3 show that if the number of subsamples satisfies $k=o(\sqrt{n/(s^{2}logd)}),{\Vert {\overline{\mathit{\beta }}}^d-{\widehat{\mathit{\beta }}}^d\Vert }_{\infty }=o_{\mathbb{P}}\left(\sqrt{logd/n}\right)$ and ${\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathcal{T}}_{\nu }({\widehat{\mathit{\beta }}}^d)\Vert }_2=o_{\mathbb{P}}(\sqrt{\mathit{s}logd/n})$, and thus the error incurred by the divide and conquer procedure is negligible compared to the statistical minimax rate. The reason for this contraction phenomenon is that β̄^d and β̂^d share the same leading term in their Taylor expansions around β^*. The difference between them is only the difference of two remainder terms which has a smaller order than the leading term. We uncover a similar phenomenon in the low dimensional case covered in Appendix A in the Supplementary Material. However, in the low dimensional case ℓ₂ norm consistency is automatic while the high dimensional case requires an additional thresholding step to guarantee sparsity and, consequently, ℓ₂ norm consistency.

4.2. The High-Dimensional Generalized Linear Model

We generalize the DC estimation of the linear model to GLM. Recall that β̂^d(𝒟_j) is the de-biased estimator defined in (3.10) and the aggregated estimator is ${\overline{\mathit{\beta }}}^d=k^{-1}{\sum }_{j=1}^k{\widehat{\mathit{\beta }}}^d({\mathcal{D}}_j)$. We still denote ${\widehat{\mathit{\beta }}}^d={\widehat{\mathit{\beta }}}^d({\cup }_{j=1}^k{\mathcal{D}}_j)$. The next lemma bounds the error incurred by splitting the sample and the statistical rate of convergence of β̄^d in terms of the infinity norm.

Lemma 4.6

Consider the generalized linear model (2.7) with canonical link. Under Conditions 2.1, 3.6 and 3.7, for β̂^λ with $\lambda \asymp \sqrt{\mathit{k}logd/n}$, we have with probability 1 − c/d, there exists a constant C > 0, such that

$${\Vert {\overline{\mathit{\beta }}}^d-{\widehat{\mathit{\beta }}}^d\Vert }_{\infty }\le C\frac{(s\vee s_1)\mathit{k}logd}{n},{\Vert {\overline{\mathit{\beta }}}^d-{\mathit{\beta }}^{\ast }\Vert }_{\infty }\le C\left(\sqrt{\frac{logd}{n}}+\frac{(s\vee s_1)\mathit{k}logd}{n}\right).$$

Remark 4.7

The term $\sqrt{logd/n}$ in above is the estimation error of ||β̂^d − β^*||_∞, while the error term (s ∨ s₁)k log d/n is attributable to the distance between β̄^d and β̂^d.

Applying a similar thresholding step as in the linear model, we quantify the ℓ₂-norm estimation error, ||𝒯_ν(β̄^d) − β^*||₂ and the distance between the divide and conquer estimator and full sample estimator ||𝒯_ν(β̄^d) − 𝒯_ν(β̂^d)||₂.

Theorem 4.8

For the GLM (2.7), under Conditions 2.1 – 3.7, choose $\lambda \asymp \sqrt{\mathit{k}logd/n}$ and ${\lambda }_v\asymp \sqrt{\mathit{k}logd/n}$. Take the parameter of the hard threshold operator in (4.2) as $\nu =C_0\sqrt{logd/n}$ for some sufficiently large constant C₀. If the number of subsamples satisfies $k=O(\sqrt{n/({(s\vee s_1)}^{2}logd)})$, for large enough d and n, we have with probability 1 − c/d,

$$\begin{gathered} {\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathcal{T}}_{\nu }({\widehat{\mathit{\beta }}}^d)\Vert }_2\le C\frac{(s\vee s_1)s^{1/2}\mathit{k}logd}{n},{\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathit{\beta }}^{\ast }\Vert }_{\infty }\le C\sqrt{\frac{logd}{n}} \\ \text{and}{\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathit{\beta }}^{\ast }\Vert }_2\le C\sqrt{\mathit{s}logd/n}. \end{gathered}$$ (4.3)

Remark 4.9

As in the case of the linear model, Theorem 4.8 reveals that the loss incurred by the divide and conquer procedure is negligible compared to the statistical minimax estimation error provided $k=o\left(\sqrt{n/{(s_1\vee s)}^2\mathit{s}logd}\right)$.

A similar proof strategy to that of Theorem 4.8 allows us to construct an estimator of ${\mathrm{\Theta }}_{vv}^{\ast }$ that achieves the required consistency with the scaling of Corollary 3.9. Our estimator is Θ̃_vv: = [𝒯_ζ(Θ̄)]_vv, where $\overline{\mathrm{\Theta }}=k^{-1}{\sum }_{j=1}^k{\widehat{\mathrm{\Theta }}}^{(j)}$ and 𝒯_ζ(·) is the thresholding operator defined in equation (4.2) with $\zeta =C_1\sqrt{logd/n}$ for some sufficiently large constant C₁.

Corollary 4.10

Under the conditions and scaling of Theorem 3.8, $|{\stackrel{\sim }{\mathrm{\Theta }}}_{vv}-{\mathrm{\Theta }}_{vv}^{\ast }|=o_{\mathbb{P}}(1)$.

Substituting this estimator in Corollary 3.9 delivers a practically implementable test statistic based on $k=o\left({((s\vee s_1)logd)}^{-1}\sqrt{n}\right)$ subsamples.

Remark 4.11

Notice that point estimation requires less stringent scaling of k than hypothesis testing in both the linear and generalized linear models. This is because the testing and estimation require different rates for the higher order term Δ in the decomposition

$$\sqrt{n}({\overline{\mathit{\beta }}}^d-{\mathit{\beta }}^{\ast })=\mathit{Z}+\mathbf{\Delta },$$

where Z is the leading term contributing to the asymptotic normality of $\sqrt{n}({\overline{\mathit{\beta }}}^d-{\mathit{\beta }}^{\ast })$. For hypothesis testing, we need ${\Vert \mathbf{\Delta }/\sqrt{n}\Vert }_{\infty }=o_P(1/\sqrt{n})$ to guarantee the asymptotic normality. For estimation, we need ${\Vert \mathbf{\Delta }\sqrt{n}\Vert }_{\infty }=o_P(\sqrt{logd/n})$ to match the minimax rate of ||β̄^d − β^*||_∞. Therefore, the number of splits k for testing is more stringent by a factor of $1/\sqrt{logd}$ than in estimation.

5. Simulations

In this section, we illustrate and validate our theoretical findings through simulations. For hypothesis testing, we use QQ plots to compare the distribution of p-values for divide and conquer test statistics to their theoretical uniform distribution. We also investigate the estimated type I error and power of the divide and conquer tests. For estimation, we validate our claim in the beginning of Section 4 that the loss incurred by the divide and conquer strategy is negligible compared with the statistical error of the corresponding full sample estimator in the high dimensional case. Specifically, we compare the performance of the divide and conquer thresholding estimator of Section 4.1 with the full sample Lasso and the average Lasso over subsamples. An analogous empirical verification of the theory is performed for the low dimensional case as well; we put it in Appendixes C and D of the Supplementary Material.

5.1. Results on Hypothesis Testing

We explore the probability of rejection of a null hypothesis of the form $H_0:{\beta }_1^{\ast }=0$ when data ${(Y_i,{\mathit{X}}_i)}_{i=1}^n$ are generated according to the linear model,

$${\mathit{Y}}_i={\mathit{X}}_i^T{\mathit{\beta }}^{\ast }+{\epsilon }_i,{\epsilon }_i~N\left(0,{\sigma }_{\epsilon }^2\right),$$

where ${\sigma }_{\epsilon }^2=1$ and

$${\mathit{\beta }}^{\ast }={({\beta }_1^{\ast },\underset{d-s-1}{\underbrace{0,\cdots ,0}},\underset{s}{\underbrace{1,\cdots ,1}})}^T,$$

where d = 5000 and s = 3. In each Monte Carlo replication, we split the initial sample of size n into k subsamples of size n/k. In particular we choose n = 5000 and k ∈ {1, 2, 5, 10, 20, 25, 40, 50, 100, 200, 500}. The number of Monte Carlo replications is 500. Using β̂_Lasso as a preliminary estimator of β^*, we construct Wald and Rao’s score test statistics as described in Sections 3.1.2 and 3.2 respectively.

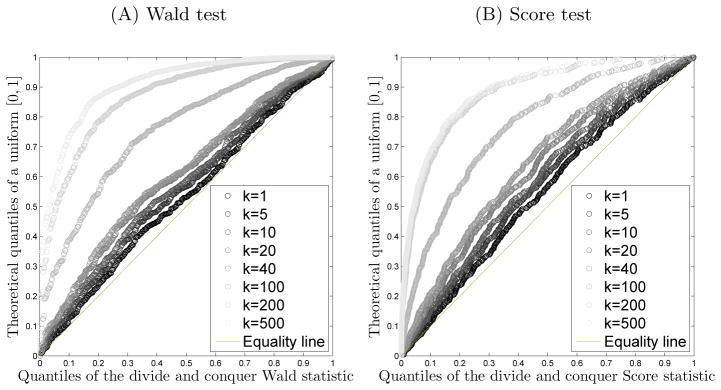
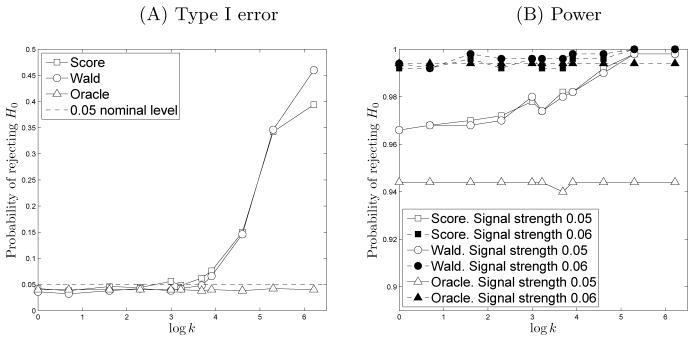
Panels (A) and (B) of Figure 1 are QQ plots of the p-values of the divide and conquer Wald and score test statistics under the null hypothesis against the theoretical quantiles of of the uniform [0,1] distribution for eight different values of k. For both test constructions, the distributions of the p-values are close to uniform and remain so as we split the data set. When k ≥ 100, the distribution of the corresponding p-values deviates from the uniform distribution visibly, as expected from the theory developed in Sections 3.1.2 and 3.2. Panel (A) of Figure 2 shows that, for both test constructions, when the number of splits k ≤ 50, the empirical level of the test is close to both the nominal α = 0.05 level and the level of the full sample oracle OLS estimator which knows the true support of β^*. On the other hand, the type I error increases dramatically when k is larger than 50. This is consistent with asymptotic normality of the test statistics we established when k is controlled appropriately. Panel (B) of Figure 2 displays the power of the test for two different signal strengths, ${\beta }_1^{\ast }=0.05$ and 0.06. We see that the power for the Score and Wald tests improves when the signal strength goes from 0.05 to 0.06. In addition, we find that the power is high regardless of how large k is. However, Figure 2(A) shows that the Type I error is large when k is large, which makes the tests invalid. Therefore, these results illustrate that the Type I and II errors are controllable when the number of splits k is relatively small. We also record the wall time for computation for these k’s in Table 1. The wall time is computed by taking the maximal time taken for each split and averaged over replications.

Fig 1.

QQ plots of the p-values of the Wald (A) and score (B) divide and conquer test statistics against the theoretical quantiles of the uniform [0,1] distribution under the null hypothesis.

Fig 2.

(A) Estimated probabilities of type I error for the Wald and score tests as a function of k. (B) Estimated power with signal strength 0.05 and 0.06 for the Wald, and score tests as a function of k.

Table 1.

Computation time for the divide and conquer testing and estimation, where k = 1 corresponds to the non-splitting case and k > 1 corresponds to the distributed case.

k	1	2	5	10	20	25	50	100	200
Score test (s)	364.39	73.22	35.09	23.61	23.56	20.78	24.13	37.53	64.67
Wald test (s)	426.23	68.95	19.66	10.09	6.70	5.71	3.88	2.60	1.91
𝒯ν(β̄d)(103s)	61.50	30.00	7.92	6.58	4.48	2.94	2.64	2.11	1.66
Split Lasso (s)	89.18	32.02	34.57	6.47	4.87	4.16	2.56	1.92	2.64

5.2. Results on Estimation

In this section, we turn our attention to experimental validation of our divide and conquer estimation theory, focusing first on the low dimensional case and then on the high dimensional case.

5.2.1. The High Dimensional Linear Model

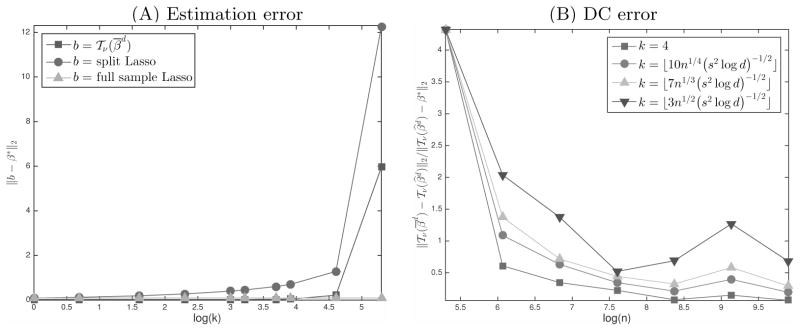
We now consider the same setting of Section 5.1 with n = 5000, d = 5000 and ${\beta }_j^{\ast }=10$ for all j in the support of β^*. In this context, we analyze the performance of the thresholded averaged debiased estimator of Section 4.1. Figure 3(A) depicts the average over 100 Monte Carlo replications of ||b − β^*||₂ for three different estimators: debiased divide-and-conquer b = 𝒯_ν(β̄^d), the Lasso estimator based on the whole sample b = β̂_Lasso and the estimator obtained by naïvely averaging the Lasso estimators from the k subsamples b = β̄_Lasso. The parameter ν is taken as $\nu =\sqrt{logd/n}$ in the specification of 𝒯_ν(β̄^d). As expected, the performance of β̄_Lasso deteriorates sharply as k increases. 𝒯_ν(β̄^d) outperforms β̂_Lasso as long as k is not too large. This is expected because, for sufficiently large signal strength, both β̂_Lasso and 𝒯_ν(β̄^d) recover the correct support, however 𝒯_ν(β̄^d) is unbiased for those ${\beta }_j^{\ast }$ in the support of β^*, whilst β̂_Lasso is biased. Figure 3(B) shows the error incurred by the divide and conquer procedure ||𝒯_ν(β̄^d) − 𝒯_ν(β̂^d)||₂ relative to the statistical error of the full sample estimator, ||𝒯_ν(β̄^d) − β^*||₂, for four different scalings of k. We observe that, with $k\asymp O(\sqrt{n/s^{2}logd})$, the relative error incurred by the divide and conquer procedure can hardly converge. This is consistent with Theorem 4.3. Given the lower bound of statistical error of the full sample Lasso estimator β̂, From Theorem 4.3 we derive that

Fig 3.

(A): Statistical error of the DC estimator, split Lasso and the full sample Lasso for k ∈ {1, 2, 5, 10, 20, 25, 40, 50, 100, 200} when n = 5000, d = 5000. (B): Euclidean norm difference between the DC thresholded debiased estimator and its full sample analogue.

$$\frac{E{\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathcal{T}}_{\nu }({\widehat{\mathit{\beta }}}^d)\Vert }_2^2}{E{\Vert {\mathcal{T}}_{\nu }({\widehat{\mathit{\beta }}}^d)-{\mathit{\beta }}^{\ast }\Vert }_2^2}\le \frac{s^2{k}^{2}logd}{n}.$$

When $k\asymp O(\sqrt{n/s^{2}logd})$, the righthand side is an O(1) term. Therefore the line with inverted triangles in Figure 3(B) implies that the statistical error rate we developed in Theorem 4.3 is tight. We also record the wall time for estimation computation for these k’s in Table 1. The wall time is computed by taking the maximal time taken for each splits and averaged over replications. We notice that the computation time decreases with k at first due to the parallel algorithm. However, for the score test and split Lasso, the time becomes increasing when k is large, this is because the computation time to aggregate results from different splits is no longer negligible for very large k’s.

6. Discussion

With the advent of the data revolution comes the need to modernize the classical statistical tool kit. For very large scale datasets, distribution of data across multiple machines is the only practical way to overcome storage and computational limitations. It is thus essential to build aggregation procedures for conducting inference based on the combined output of multiple machines. We successfully achieve this objective, deriving divide and conquer analogues of the Wald and score statistics and providing statistical guarantees on their performance as the number of sample splits grows to infinity with the full sample size. Tractable limit distributions of each DC test statistic are derived. These distributions are valid as long as the number of subsamples, k, does not grow too quickly. In particular, $k=o\left({((s\vee s_1)logd)}^{-1}\sqrt{n}\right)$ is required in a general likelihood based framework. If k grows faster than ${((s\vee s_1)logd)}^{-1}\sqrt{n}$, remainder terms become nonnegligible and contaminate the tractable limit distribution of the leading term. When attention is restricted to the linear model, a faster growth rate of $k=o\left({(\mathit{s}logd)}^{-1}\sqrt{n}\right)$ is allowed.

The divide and conquer strategy is also successfully applied to estimation of regression parameters. We obtain the rate of the loss incurred by the divide and conquer strategy. Based on this result, we derive an upper bound on the number of subsamples for preserving the statistical error. For low-dimensional models, simple averaging is shown to be effective in preserving the statistical error, so long as k = O(n/d) for the linear model and $k=O(\sqrt{n}/d)$ for the generalized linear model. For high-dimensional models, the debiased estimator used in the Wald construction is also successfully employed, achieving the same statistical error as the Lasso based on the full sample, so long as $k=O(\sqrt{n/s^{2}logd})$.

Our contribution advances the understanding of distributed inference in the presence of large scale and distributed data, but there is still a great deal of work to be done in the area. We focus here on the fundamentals of hypothesis testing and estimation in the divide and conquer setting. Beyond this, there is a whole tool kit of statistical methodology designed for the single sample setting, whose split sample asymptotic properties are yet to be understood.

7. Proofs

In this section, we present the proofs of the main theorems appearing in Sections 3 and 4. The statements and proofs of several auxiliary lemmas appear in the Supplementary Material. To simplify notation, we take ${\beta }_v^H=0$ without loss of generality.

7.1. Proofs for Section 3.1

The proof of Theorem 3.3, relies on the following lemma, which bounds the probability that optimization problems in (3.4) are feasible.

Lemma 7.1

Assume $\mathrm{\sum }=\mathbb{E}({\mathit{X}}_i{\mathit{X}}_i^T)$ satisfies C_min < λ_min(Σ) ≤ λ_max(Σ) ≤ C_max as well as ||Σ^−1/2X₁||_ψ2 = κ, then we have

$$\mathbb{P}\left(\underset{j=1,\dots ,k}{max}{\Vert M^{(j)}{\widehat{\mathrm{\sum }}}^{(j)}-I\Vert }_{max}\le a\sqrt{\frac{logd}{n}}\right)\ge 1-2k{d}^{-c_2},$$

where $c_2=\frac{a^2{C}_{min}}{24e^2{\kappa }^4{C}_{max}}-2$.

Proof

The proof is an application of the union bound in Lemma 6.2 of Javanmard and Montanari (2014).

Proof of Theorem 3.3

For 1 ≤ j ≤ k, let $\sqrt{n_k}({\widehat{\mathit{\beta }}}^d({\mathcal{D}}_j)-{\mathit{\beta }}^{\ast })={\mathit{Z}}^{(j)}+{\mathbf{\Delta }}^{(j)}$, where ${\mathit{Z}}^{(j)}=\frac{1}{\sqrt{n_k}}{M}^{(j)}{X}^{(j)T}{\mathit{\epsilon }}^{(j)}$. From Theorem F.1, we know that as long as ${\mathbf{m}}_v^{(j)T}{\widehat{\mathbf{\sum }}}^{(j)}{\mathbf{m}}_v^{(j)}\ge c>0$ holds uniformly for j = 1, …, d,

$$\overline{\mathbf{\Delta }}:=\sqrt{n}\frac{1}{k}\sum _{j=1}^k\frac{{\mathrm{\Delta }}_v^{(j)}}{{\widehat{Q}}^{(j)}}=o_{\mathbb{P}}(1).$$

Then we define

$${\overline{V}}_n:=\sqrt{n}\frac{1}{k}\sum _{j=1}^k\frac{Z_v^{(j)}}{{\widehat{Q}}^{(j)}}=\sum _{j=1}^k\sum _{i\in {\mathcal{I}}_j}{\xi }_{iv}^{(j)},\text{where}{\xi }_{iv}^{(j)}:=\frac{{\mathbf{m}}_v^{(j)T}{\mathit{X}}_i^{(j)}{\epsilon }_i^{(j)}}{{\left(n{\mathbf{m}}_v^{(j)T}{\widehat{\mathrm{\sum }}}^{(j)}{\mathbf{m}}_v^{(j)}\right)}^{1/2}}.$$

We now establish the asymptotic normality of V̄_n by verifying the requirements of the Lindeberg-Feller central limit theorem (e.g. Kallenberg, 1997, Theorem 4.12). By the fact that ε_i is independent of X for all i and 𝔼[ε_i] = 0,

$$\begin{gathered} \mathbb{E}({\xi }_{iv})=\mathbb{E}(\mathbb{E}({\xi }_{iv}^{(j)}\mid X))=\mathbb{E}\left\{\mathbb{E}\left[{\mathbf{m}}_v^{(j)T}{\mathit{X}}_i^{(j)}{\epsilon }_i^{(j)}/{\left(n{\mathbf{m}}_v^{(j)T}{\widehat{\mathrm{\sum }}}^{(j)}{\mathbf{m}}_v^{(j)}\right)}^{1/2}\mid X\right]\right\} \\ =\mathbb{E}\left\{{\left(n{\mathbf{m}}_v^{(j)T}{\widehat{\mathrm{\sum }}}^{(j)}{\mathbf{m}}_v^{(j)}\right)}^{-1/2}{\mathbf{m}}_v^{(j)T}{\mathit{X}}_i^{(j)}\mathbb{E}\left({\epsilon }_i^{(j)}\right)\right\}=0. \end{gathered}$$

By independence of ${\{{\epsilon }_i\}}_{i=1}^n$ and the definition of Σ̂^(j), we also have

$$\begin{gathered} \text{Var}\left({\overline{V}}_n\mid X\right)=\sum _{j=1}^k\sum _{i\in {\mathcal{I}}_j}\text{Var}\left({\xi }_{iv}^{(j)}\mid X\right) \\ =\frac{1}{n}\sum _{j=1}^k{\left({\mathbf{m}}_v^{(j)T}{\widehat{\mathrm{\sum }}}^{(j)}{\mathbf{m}}_v^{(j)}\right)}^{-1}\sum _{i\in {\mathcal{I}}_j}{\mathbf{m}}_v^{(j)T}{\mathit{X}}_i^{(j)}{\mathit{X}}_i^{(j)T}{\mathbf{m}}_v^{(j)}\text{Var}\left({\epsilon }_i^{(j)}\mid X\right)={\sigma }^2. \end{gathered}$$

Therefore we have

$$\text{Var}({\overline{V}}_n)=\mathbb{E}(\text{Var}({\overline{V}}_n\mid X))+\text{Var}(\mathbb{E}({\overline{V}}_n\mid X))={\sigma }^2.$$

It only remains to verify the Lindeberg condition, i.e.,

$$\underset{k\to \infty }{lim}\underset{n_k\to \infty }{lim}\frac{1}{{\sigma }^2}\sum _{j=1}^k\sum _{i\in {\mathcal{I}}_j}\mathbb{E}\left[{({\xi }_{iv}^{(j)})}^2𝟙\{\mid {\xi }_{iv}^{(j)}\mid >\epsilon \sigma \}\right]=0,\forall \epsilon >0,$$ (7.1)

whose verification is relegated to the Appendix E of the Supplementary Material. Finally we reach the conclusion by the Slutsky’s Theorem.

Proof of Corollary 3.5

Let ${\mathcal{F}}_n:=\{{\mathit{m}}_v^{(j)T}{\widehat{\mathbf{\sum }}}^{(j)}{\mathit{m}}_v^{(j)}\ge c>0,j=1,\dots ,k\}$, where n is the total sample size. According to Theorem 3.3, when ℱ_n holds, we have

$$\underset{n\to \infty }{lim}\mathbb{P}({\overline{S}}_n\le t\mid \mathit{X})-\mathrm{\Phi }(t)=0.$$

From the proof of Lemma 13 in Javanmard and Montanari (2014), lim_n→∞ ℙ(ℱ_n) = 1. For any t ∈ ℝ and δ > 0, by applying dominating convergence Theorem to 𝟙{|ℙ(S̄_n ≤ t | X) − Φ(t)| > δ and ℱ_n holds}, we have

$$\underset{n\to \infty }{lim}\mathbb{P}(\mid \mathbb{P}({\overline{S}}_n\le t\mid \mathbf{X})-\mathrm{\Phi }(t)\mid >\delta )=0.$$

According to the dominate convergence theorem, since ℙ(S̄_n ≤ t | X) ∈ [0, 1], we have

$$\underset{n\to \infty }{lim}\mathbb{P}({\overline{S}}_n\le t)=\underset{n\to \infty }{lim}\mathbb{E}[\mathbb{P}({\overline{S}}_n\le t\mid \mathbf{X})]=\mathbb{E}[\underset{n\to \infty }{lim}\mathbb{P}({\overline{S}}_n\le t\mid \mathbf{X})]=\mathrm{\Phi }(t).$$

Therefore, we complete the proof of the corollary.

The proofs of Theorem 3.8 and Corollary 3.9 are stated as an application of Lemmas E.7 and E.8 in the Supplementary Material, which apply under a more general set of requirements. We present the proof of Theorem 3.8 below and defer Corollary 3.9 to Appendix E in the Supplementary Materials.

Proof of Theorem 3.8

We verify (A1)–(A4) of Lemma E.7. For (A1), decompose the object of interest as

$$\frac{1}{n_k}{\Vert X^{(j)}{\widehat{\mathrm{\Theta }}}^{(j)}\Vert }_{max}=\frac{1}{n_k}{\Vert X^{(j)}\left({\widehat{\mathrm{\Theta }}}^{(j)}-{\mathrm{\Theta }}^{\ast }\right)\Vert }_{max}+\frac{1}{n_k}{\Vert X^{(j)}{\mathrm{\Theta }}^{\ast }\Vert }_{max}={\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2,$$

where Δ₁ can be further decomposed and bounded by

$$\begin{gathered} \frac{1}{n_k}{\Vert X^{(j)}\left({\widehat{\mathrm{\Theta }}}^{(j)}-{\mathrm{\Theta }}^{\ast }\right)\Vert }_{max}=\frac{1}{n_k}\underset{1\le i\le n}{max}\underset{1\le v\le d}{max}\left[\mid {\mathit{X}}_i^{(j)T}\left({\widehat{\mathbf{\Theta }}}_v^{(j)}-{\mathbf{\Theta }}_v^{\ast }\right)\mid \right] \\ \le \frac{1}{n_k}\underset{1\le i\le n}{max}{\Vert {\mathit{X}}_i\Vert }_{\infty }\underset{1\le v\le d}{max}{\Vert {\widehat{\mathbf{\Theta }}}_v^{(j)}-{\mathbf{\Theta }}_v^{\ast }\Vert }_1. \end{gathered}$$

We have

$$\mathbb{P}({\mathrm{\Delta }}_1>q/2)\le \mathbb{P}\left(\underset{1\le v\le d}{max}{\Vert {\widehat{\mathbf{\Theta }}}_v^{(j)}-{\mathbf{\Theta }}_v^{\ast }\Vert }_1>\frac{n}{kM}\frac{q}{2}\right)<\psi$$

and by Condition 3.7, ψ = o(d⁻¹) = o(k⁻¹) for any $q\ge 2{\mathit{CMs}}_1{(k/n)}^{3/2}·\sqrt{logd}$, a fortiori for q a constant. Since X_i is sub-Gaussian, a matching probability bound can easily be obtained for Δ₂, thus we obtain

$$\mathbb{P}(n_k^{-1}{\Vert X^{(j)}{\widehat{\mathrm{\Theta }}}^{(j)}\Vert }_{max})\le 2\psi$$

for ψ = o(k⁻¹). (A2) and (A3) of Lemma E.7 are applications of Lemmas E.3 and E.4 respectively. To establish (A4), observe that

$$\left({\widehat{\mathbf{\Theta }}}_v^{(j)T}{\nabla }^2{\ell }_{n_k}^{(j)}\left({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)\right)-{\mathit{e}}_v\right)={\mathrm{\Delta }}_1+{\mathrm{\Delta }}_2+{\mathrm{\Delta }}_3,$$

where ${\mathrm{\Delta }}_1={\left({\widehat{\mathbf{\Theta }}}_v^{(j)}-{\mathbf{\Theta }}_v^{\ast }\right)}^T{\nabla }^2{\ell }_{n_k}^{(j)}\left({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)\right),{\mathrm{\Delta }}_2={\mathbf{\Theta }}_v^{\ast T}\left({\nabla }^2{\ell }_{n_k}^{(j)}({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j))-{\nabla }^2{\ell }_{n_k}^{(j)}({\mathit{\beta }}^{\ast })\right)$ and ${\mathrm{\Delta }}_3={\mathbf{\Theta }}_v^{\ast T}{\nabla }^2{\ell }_{n_k}^{(j)}({\mathit{\beta }}^{\ast })-{\mathit{e}}_v$. We thus consider |Δ_ℓ(β̂^λ(𝒟_j) − β^*)| for ℓ = 1, 2, 3.

$$\begin{gathered} \mid {\mathrm{\Delta }}_2({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)-{\mathit{\beta }}^{\ast })\mid =\left|\frac{1}{n_k}\sum _{i\in {\mathcal{I}}_j}{\mathbf{\Theta }}_v^{\ast T}{\mathbf{X}}_i{\mathit{X}}_i^T({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)-{\mathit{\beta }}^{\ast })[b^{″}({\mathit{X}}_i^T{\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j))-b^{″}({\mathit{X}}_i^T{\mathit{\beta }}^{\ast })]\right| \\ \le U_3\underset{1\le i\le n}{max}\mid {\mathbf{\Theta }}_v^{\ast T}{\mathit{X}}_i\mid \frac{1}{n_k}{\Vert X({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)-{\mathit{\beta }}^{\ast })\Vert }_2^2. \end{gathered}$$

$\mathbb{P}\left({\Vert X\left({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)-{\mathit{\beta }}^{\ast }\right)\Vert }_2^2\succsim n^{-1}\mathit{sk}log(d/\delta )\right)<\delta$ by Lemma E.4, thus ℙ(|Δ₂ · (β̂^λ(𝒟_j) − β^*)| > t) < δ for t ≍ MU₃n⁻¹sk log(d/δ). Invoking Hölder’s inequality, Hoeffding’s inequality and Condition 2.1, we also obtain, for t ≍ n⁻¹sk log(d/δ),

$$\begin{gathered} \mathbb{P}\left(\mid {\mathrm{\Delta }}_3({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)-{\mathit{\beta }}^{\ast })\mid >t\right) \\ \le \mathbb{P}\left({\Vert {\mathbf{\Theta }}_v^{\ast T}\left(\frac{1}{n_k}\sum _{i\in {\mathcal{I}}_j}{b}^{″}({\mathit{X}}_i^T{\mathit{\beta }}^{\ast }){\mathit{X}}_i{\mathit{X}}_i^T\right)-{\mathit{e}}_v\Vert }_{max}{\Vert {\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)-{\mathit{\beta }}^{\ast }\Vert }_1>t\right). \end{gathered}$$

Therefore ℙ(|Δ₂(β̂^λ(𝒟_j) − β^*)| > t) < 2δ. Finally, with t ⑍ n⁻¹(s ∨ s₁)k log(d/δ),

$$\mathbb{P}\left(\mid {\mathrm{\Delta }}_1({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)-{\mathit{\beta }}^{\ast })\mid >t\right)\le \mathbb{P}\left(\frac{1}{n_k}{\Vert \sum _{i\in {\mathcal{I}}_j}{X}_i^T\left({\widehat{\mathbf{\Theta }}}_v-{\mathbf{\Theta }}_v\right)b^{″}({\mathit{X}}_i^T{\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j))\Vert }_2{\Vert X^{(j)T}\left({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)-{\mathit{\beta }}^{\ast }\right)\Vert }_2>t\right),$$

hence ℙ(|Δ₁(β̂^λ(𝒟_j) − β^*)| > t) < 2δ. This follows because by Lemma E.4,

$$\mathbb{P}({\Vert \frac{1}{n_k}{X}^{(j)}({\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j)-{\mathit{\beta }}^{\ast })\Vert }_2\succsim n^{-1/2}\sqrt{\mathit{sk}log(d/\delta )}<\delta$$

and by Lemma C.4 of Ning and Liu (2014),

$$\mathbb{P}\left({\Vert \frac{1}{n_k}\sum _{i\in {\mathcal{I}}_j}{X}_i^T\left({\widehat{\mathbf{\Theta }}}_v-{\mathbf{\Theta }}_v\right)b^{″}({\mathit{X}}_i^T{\widehat{\mathit{\beta }}}^{\lambda }({\mathcal{D}}_j))\Vert }_2\succsim n^{-1/2}\sqrt{s_1\mathit{k}log(d/\delta )}\right)<\delta .$$

7.2. Proofs for Theorems in Section 3.2

The proof of Theorem 3.11 relies on several preliminary lemmas, collected in Appendix E in the Supplementary Material. Without loss of generality we set $H_0:{\beta }_v^{\ast }=0$ to ease notation.

Proof of Theorem 3.11

Since $\overline{S}(0)=k^{-1}{\sum }_{j=1}^k{\widehat{S}}^{(j)}(0,{\widehat{\mathit{\beta }}}_{-v}^{\lambda }({\mathcal{D}}_j))$, and (B1)–(B4) of Condition E.9 in the Supplementary Material are fulfilled under Conditions 3.6 and 2.1 by Lemma E.10 (see Appendix E in the Supplementary Material). The proof is now simply an application of Lemma E.13 in the Supplementary Material with ${\beta }_v^{\ast }=0$ under the restriction of the null hypothesis.

Proof of Lemma 3.14

The proof is an application of Lemma E.16 in the Supplementary Material, noting that (B1)–(B5) of Condition E.9 in the Supplementary Material are fulfilled under Conditions 3.6 and 2.1 by Lemmas E.10 and E.11 in the Supplementary Material.

7.3. Proofs for Theorems in Section 4

Recall from Section 2 that for an arbitrary matrix M, M_ℓ denotes the transposed ℓ^th row of M and [M]_ℓ denotes the ℓ^th column of M.

Proof of Theorem 4.3

By Lemma 4.1 and $k=O(\sqrt{n/(s^{2}logd)})$, there exists a sufficiently large C₀ such that for the event $\mathcal{E}:=\{{\Vert {\overline{\mathit{\beta }}}^d-{\mathit{\beta }}^{\ast }\Vert }_{\infty }\le C_0\sqrt{logd/n}\}$, we have ℙ(ℰ) ≥ 1 − c/d. We choose $\nu =C_0\sqrt{logd/n}$, which implies that, under ℰ, we have ν ≥ ||β̄^d − β^*||_∞.

Let 𝒮 be the support of β^*. The derivations in the remainder of the proof hold on the event ℰ. Observe ${\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}_{{\mathcal{S}}^c}^d)=\mathbf{0}$ as ${\Vert {\overline{\mathit{\beta }}}_{{\mathcal{S}}^c}^d\Vert }_{\infty }\le \nu$. For j ∈ 𝒮, if $\mid {\mathit{\beta }}_j^{\ast }\mid \ge 2\nu$, we have $\mid {\overline{\mathit{\beta }}}_j^d\mid \ge \mid {\beta }_j^{\ast }\mid -\nu \ge \nu$ and thus $\mid {\mathcal{T}}_{\nu }({\overline{\beta }}_j^d)-{\beta }_j^{\ast }\mid =\mid {\overline{\beta }}_j^d-{\beta }_j^{\ast }\mid \le \nu$. While if $\mid {\beta }_j^{\ast }\mid <2\nu ,\mid {\mathcal{T}}_{\nu }({\overline{\beta }}_j^d)-{\beta }_j^{\ast }\mid \le \mid {\beta }_j^{\ast }\mid \vee \mid {\overline{\beta }}_j^d-{\beta }_j^{\ast }\mid \le 2\nu$. Therefore, on the event ℰ,

$$\begin{gathered} {\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathit{\beta }}^{\ast }\Vert }_2={\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}_{\mathcal{S}}^d)-{\mathit{\beta }}_{\mathcal{S}}^{\ast }\Vert }_2\le 2\sqrt{s}\nu \\ \text{and}{\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathit{\beta }}^{\ast }\Vert }_{\infty }={\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}_{\mathcal{S}}^d)-{\beta }_{\mathcal{S}}^{\ast }\Vert }_{\infty }\le 2\nu . \end{gathered}$$

The statement of the theorem follows because $\nu =C_0\sqrt{logd/n}$ and ℙ(ℰ) ≥ 1 − c/d. Following the same reasoning, on the event ${\mathcal{E}}^{\prime }:=\mathcal{E}\cup \{{\Vert {\widehat{\mathit{\beta }}}^d-{\mathit{\beta }}^{\ast }\Vert }_{\infty }\le C_0\sqrt{logd/n}\}\cup \{{\Vert {\widehat{\mathit{\beta }}}^d-{\widehat{\mathit{\beta }}}^d\Vert }_{\infty }\le C_{0}sk\text{log}d/n\}$, we have

$$\begin{gathered} {\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)-{\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}^d)\Vert }_2={\Vert {\mathcal{T}}_{\nu }({\overline{\mathit{\beta }}}_{\mathcal{S}}^d)-{\mathcal{T}}_{\nu }({\widehat{\mathit{\beta }}}_{\mathcal{S}}^d)\Vert }_2 \\ \le {\Vert {\overline{\mathit{\beta }}}_{\mathcal{S}}^d-{\widehat{\mathit{\beta }}}_{\mathcal{S}}^d\Vert }_2\le \sqrt{s}{\Vert {\overline{\mathit{\beta }}}_{\mathcal{S}}^d-{\widehat{\mathit{\beta }}}_{\mathcal{S}}^d\Vert }_{\infty }\le C{s}^{3/2}\mathit{k}logd/n. \end{gathered}$$

As Lemma 4.1 also gives ℙ(ℰ′) ≥ 1 − c/d, the proof is complete.

Proof of Corollary 4.10

By an analogous proof strategy to that of Theorem 4.8, $|{[{\mathcal{T}}_{\zeta }(\overline{\mathrm{\Theta }})]}_{vv}-{\mathrm{\Theta }}_{vv}^{\ast }|=O_p\left(\sqrt{n^{-1}logd}\right)=o_{\mathbb{P}}(1)$ under the conditions of the Corollary provided $k=o\left({((s\vee s_1)logd)}^{-1}\sqrt{n}\right)$.