Estimating causal effects from a randomized clinical trial when noncompliance is measured with error

SUMMARY

Noncompliance or non-adherence to randomized treatment is a common challenge when interpreting data from randomized clinical trials. The effect of an intervention if all participants were forced to comply with the assigned treatment (i.e., the causal effect) is often of primary scientific interest. For example, in trials of very low nicotine content (VLNC) cigarettes, policymakers are interested in their effect on smoking behavior if their use were to be compelled by regulation. A variety of statistical methods to estimate the causal effect of an intervention have been proposed, but these methods, including inverse probability of compliance weighted (IPCW) estimators, assume that participants’ compliance statuses are reported without error. This is an untenable assumption when compliance is based on self-report. Biomarkers (e.g., nicotine levels in the urine) may provide more reliable indicators of compliance but cannot perfectly discriminate between compliers and non-compliers. However, by modeling the distribution of the biomarker as a mixture distribution and writing the probability of compliance as a function of the mixture components, we show how the probability of compliance can be directly estimated from the data even when compliance status is unknown. To estimate the causal effect, we develop a new approach which re-weights participants by the product of their probability of compliance given the observed data and the inverse probability of compliance given confounders. We show that our proposed estimator is consistent and asymptotically normal and show that in some situations the proposed approach is more efficient than standard IPCW estimators. We demonstrate via simulation that the proposed estimator achieves smaller bias and greater efficiency than ad hoc approaches to estimating the causal effect when compliance is measured with error. We apply our method to data from a recently completed randomized trial of VLNC cigarettes.

1. Introduction

Twenty years ago, Benowitz and Henningfield (1994) argued the addictive properties of cigarettes could be eliminated if the nicotine content were reduced to 0.4–0.5 milligrams (mg) per gram of tobacco. In the United States, the Family Smoking Prevention and Tobacco Control Act provides the Food and Drug Administration (FDA) with the regulatory authority to limit the nicotine content of cigarettes to lower levels (but not zero) if such a regulation is likely to improve public health. As smoking remains the United States’ leading cause of preventable death (U.S. Department of Health and Human Services, 2014), nicotine reduction could have a substantial public health impact. However, evidence for the effectiveness of such a policy is limited.

We recently reported the results of The Center for The Evaluation of Nicotine in Cigarettes, project 1 (CENIC-p1), a 6-week randomized trial evaluating the effect of nicotine reduction on tobacco use and dependence (Donny and others, 2015). Current smokers (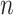 = 839) were randomized equally to one of seven groups consisting of a usual brand control condition or experimental cigarettes with nicotine content ranging from 15.8 mg per gram of tobacco (normal nicotine controls) to 0.4 mg per gram of tobacco. In addition, the investigators included a group that received cigarettes with 0.4 mg of nicotine per gram of tobacco with high tar to understand the effect of tar yield on cigarette use and dependence when nicotine content is reduced. Participants were instructed to smoke only those cigarettes provided in the trial and were considered non-compliant if they smoked cigarettes not provided by the trial (i.e., non-study commercial cigarettes). Although they were not given incentives to avoid smoking non-study commercial cigarettes, they were encouraged to honestly report their smoking behavior and were allowed to complete the trial regardless of compliance. During Week 6 of the study, smokers randomized to the lowest nicotine condition had significantly reduced tobacco use, dependence, and nicotine exposure compared to the usual brand and normal nicotine control conditions.

The results of CENIC-p1 provide empirical support for nicotine reduction as a regulatory strategy, but they must be interpreted cautiously due to substantial noncompliance to randomized treatment assignment. For example, among participants randomized to smoke very low nicotine content (VLNC) cigarettes (cigarettes with 0.4 mg of nicotine per gram of tobacco), 39% reported smoking at least 1 non-study cigarette during week 6, and 80% reported smoking at least 1 non-study cigarette at some point during the trial. A per protocol analysis, that is, analyzing only compliant participants, is problematic because compliance status is confounded, and compliers may differ systematically from non-compliers. The primary analysis of CENIC-p1 followed the intention-to-treat (ITT) principle and analyzed the data from all participants according to their randomized treatment assignment regardless of their compliance. An ITT analysis provides an unbiased estimator of the effect of a treatment or intervention when it is used in an environment (e.g., target population, level of non-compliance, etc.) similar to the clinical trial environment (Hernán and Hernández-Díaz, 2012). However, if the nicotine content of cigarettes were limited by regulation, and smokers no longer had legal access to standard commercial cigarettes, the effect of nicotine reduction on smoking behavior may be different than in the trial.

Our goal is to estimate the effect of smoking VLNC cigarettes on cigarette consumption and other measures of smoking behavior (dependence, withdrawal, etc.) in the hypothetical world where a regulatory body has reduced the nicotine content of cigarettes, and normal nicotine content commercial cigarettes are no longer available. In the language of clinical trials, we wish to estimate the effect of smoking VLNC cigarettes in the presence of complete compliance, that is, the causal effect (Bellamy and others, 2007). Methods for estimating the causal effect of an intervention in the presence of noncompliance are well-established and include inverse probability of compliance weighted (IPCW) estimators (Hernán and Robins, 2006; Cain and Cole, 2009), principal stratification (Frangakis and Rubin, 2002), structural nested models estimated by G-estimation (Robins, 1994), and instrumental variable approaches (Angrist and others, 1996).

Existing methods for estimating causal effects in the presence of noncompliance assume that investigators know, without error, whether or not a participant was compliant. In the context of randomized tobacco trials, like CENIC-p1, self-reported compliance is subject to error and recall bias, and analyzing biomarkers of nicotine exposure has been suggested as an alternate approach to identify non-compliant participants (Benowitz and others, 2015). One recent study (Denlinger and others, 2016) evaluating biomarkers of nicotine exposure in participants exclusively smoking cigarettes with 0.4 mg per gram of tobacco found that the 95th percentile for total nicotine equivalents (TNEs, a biomarker of short-term nicotine exposure that measures most nicotine metabolites) was 6.41 nmol/mL. Yet among the CENIC-p1 participants randomized to the 0.4 mg per gram of tobacco arm, 63% of participants who self-reported full compliance during Week 6 had TNE greater than 6.41 nmol/mL (Nardone and others, 2016). This demonstrates that self-reported compliance can substantially misclassify whether or not participants were compliant to their randomized treatment assignment. Although certain biomarkers (e.g., TNE) may suggest that a participant’s self-reported compliance status is incorrect, no biomarker of nicotine exposure perfectly discriminates between compliers and non-compliers.

We propose a novel estimator of the causal effect from a randomized clinical trial when compliance status is measured with error. In contrast to existing methods, our estimator explicitly accounts for the potential for misclassification of compliers and non-compliers. Although we treat compliance status as an unobserved variable, we show how to weight participants by the product of their probability of compliance given the observed data and the inverse probability of compliance given confounders, resulting in a consistent and asymptotically normal estimator of the causal effect. Our simulation results illustrate that in finite samples our estimator outperforms ad hoc causal methods which ignore the error in compliance status by using either self-reported data or by using an estimated indicator of compliance. When there is a perfect discriminator of compliers and non-compliers, our estimator reduces to the standard IPCW estimator.

2. Causal effect estimators

2.1. Potential outcomes and target of inference

We consider a hypothetical randomized clinical trial, where 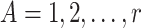denotes the treatment group, which we assume is randomized. Let be a measure (without error) of noncompliance with 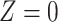indicating full compliance and increasing 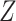indicating greater noncompliance. For example, 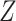may be the number of non-study commercial cigarettes smoked in week 6 of CENIC-p1 or the number of pills not taken in a therapeutic clinical trial. Define the compliance indicator 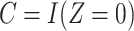, and note that 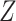and 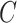are not directly observed if noncompliance is measured with error. Define 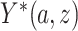to be the outcome of a randomly-selected participant if, possibly contrary to fact, we set 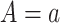and 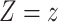. Because for each participant we do not observe 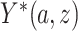for all 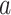and 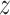, 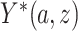is a potential outcome. For CENIC-p1, 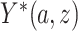is the number of study cigarettes with nicotine content 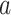smoked per day in week 6 of the study if the participant were to smoke 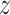non-study cigarettes per day. The target of inference is 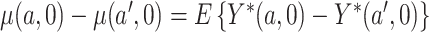, the expected difference of the outcome among randomized treatment groups 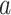and 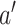if all participants were to be compliant. In the context of mediation literature, 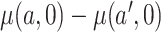is known as the controlled direct effect (Pearl, 2001), that is, the treatment effect when the mediator, number of non-study cigarettes, is set at the fixed value of 0.

2.2. Observed data

Let 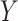be the observed outcome for a randomly-selected participant. Define the self-reported compliance indicator variable 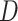, with 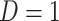indicating the participant reports full compliance and 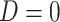indicating that the participant reports any noncompliance. Let 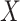be a vector of patient variables, and let 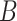be a biomarker indicating exposure to the treatment 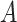. In the context of CENIC-p1, 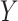is the number of study cigarettes smoked per day during week 6 of the trial, 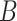is a biomarker of nicotine exposure (e.g., TNE or cotinine) measured during week 6, 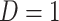if the participant reports smoking 0 non-study cigarettes during week 6, and 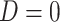if the participant reports smoking any non-study cigarettes during week 6. Note that participants self-report 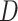, and this may be subject to error and recall biases.

2.3. Identifying assumptions

To relate the distribution of the observed data to the distribution of the potential outcome 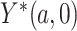in the case where 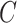is observed, we make the following identifying assumptions (Robins and Hernán, 2008). First, we assume that we have measured enough covariates such that the compliance status is conditionally ignorable. That is, we assume the probability that a participant is compliant depends only on the observed covariates 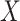and 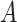and not additionally on any potential outcomes; this implies that 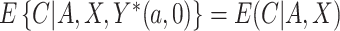(no unmeasured confounders assumption). Although there may be additional variables associated with 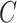, for example, the biomarker 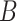, we assume that there are no additional confounders aside from 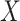. Second, we assume that 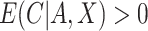for all 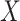and 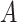, that is, there is positive probability of complying with the randomized treatment assignment within all levels of the confounders (positivity assumption). Finally, we assume that if 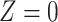and 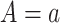, then 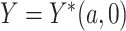, that is, if a participant is compliant with the trial protocol, then her observed outcome is the same as it would be if the participant were forced to be compliant with the trial protocol (consistency assumption). When 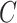is unobserved, additional assumptions will be necessary and will be stated where required.

2.4. Proposed estimators

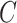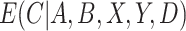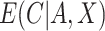We have stressed that may not be directly observed due to measurement error or misclassification, but assume for now that and are known. We discuss in Section 3 how these expectations can be estimated even though 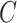is unobserved. We can estimate 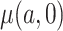by solving the following estimating equation:

$$\sum _{i=1}^n\frac{E\left(C_i|A_i,B_i,X_i,Y_i,D_i\right)}{E\left(C_i|A_i,X_i\right)}\left\{Y_i-\mu (a,0)\right\}I(A_i=a)=0.$$ (2.1)

A similar estimator could be constructed for 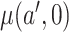, and the difference in those estimators could be used to estimate the treatment effect.

The estimating function with weights 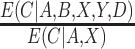is similar to a standard IPCW estimator with weights 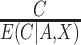, but we have replaced the numerator with the conditional expected value of compliance instead of an indicator variable for compliance status. Note that if all participants self-reported compliance without error, or if there exists a biomarker that can perfectly discriminate compliers from non-compliers, then 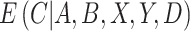equals 0 or 1, and the estimating function in Equation (2.1) simplifies to the standard IPCW estimating function. Although it is not obvious that we can obtain valid inference without observing 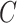, we show in Section 4 that, under suitable regularity conditions, 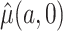, the solution to the estimating equation, is a consistent and asymptotically normal estimator of 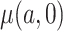. Because our estimator has an expectation, rather than an indicator variable, in the numerator to account for potential misclassification, we refer to the estimator as the Compliance Unsure RE-weighted estimator, or CURE estimator.

3. Estimating the weights

In practice, 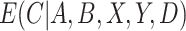and 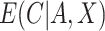are usually unknown and must be estimated. To estimate these, we begin by re-writing 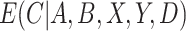as a function of components that can be estimated directly from the observed data. We then show how auxiliary data, if available, can be used to obtain a more precise estimate of 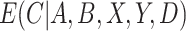. Finally, we discuss how 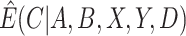, the estimate of 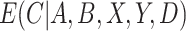, can be used to estimate .

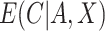3.1. Estimating the numerator of the weights

First, using Bayes’ Theorem, we can write 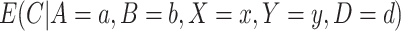as:

$$\frac{f(b|a,x,y,d,c=1;\xi )\cdot \rho (a,x,y,d;\alpha )}{f(b|a,x,y,d,c=1;\xi )\cdot \rho (a,x,y,d;\alpha )+f(b|a,x,y,d,c=0;\xi )\cdot \left\{1-\rho (a,x,y,d;\alpha )\right\}},$$ (3.1)

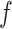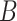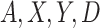where is the conditional density of given , and 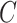indexed by parameter vector 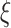, and 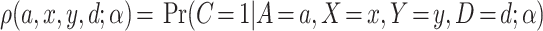indexed by parameter vector 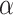. Rewriting the expectation shifts the goal from estimating the conditional expectation of 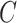to estimating the conditional distribution of 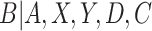. Note that 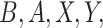and 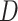are all observed random variables, which allows us to directly estimate the density of as the mixture density

$$\begin{array}{rr}\hfill g(b|a,x,y,d;\xi ,\alpha )& \hspace{0.17em}=\rho (a,x,y,d;\alpha )\cdot f(b|a,x,y,d,c=1;\xi )+\left\{1-\rho (a,x,y,d;\alpha )\right\}\hfill \\ & \hspace{0.17em}\cdot f(b|a,x,y,d,c=0;\xi ).\hfill \end{array}$$ (3.2)

Thus, although we do not observe C, we can estimate 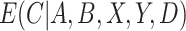by estimating the conditional density of 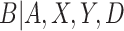. The maximum likelihood estimators of 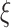and 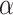solve the score equations

$$\sum _{i=1}^n\frac{\mathrm{\partial }}{\mathrm{\partial }({\xi }^T,{\alpha }^T{)}^T}\log g(B_i|A_i,X_i,Y_i,D_i;\xi ,\alpha )=0.$$ (3.3)

As is frequently the case with mixture distributions, Equation (3.3) may be difficult to solve directly. In that case, we can find the maximum likelihood estimates using the expectation-maximization (EM) algorithm (Dempster and others, 1977). In Section A of the supplementary material available at Biostatistics online, we give details of the EM algorithm updates for 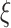and .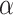

Equations (3.1)–(3.3) can sometimes be simplified based on the scientific problem. For example, in some applications it may be reasonable to simplify the modeling assumptions of the conditional density of 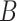. 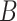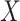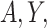In particular, according the directed acyclic graph (DAG) in Section B of the supplementary materials available at Biostatistics online, which is one plausible DAG for the CENIC-p1 data, may be conditionally independent of given and 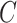. We note that this assumption is testable using observed data so the data analyst does not need to a priori assume the correct causal structure. Additionally, it may be reasonable to assume that if 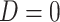, that is, the participant reports noncompliance with the study protocol, then 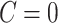without error. That is, participants may not erroneously report noncompliance because in most trials there is usually no incentive to be non-compliant. This would imply that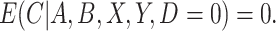

3.2. Incorporating compliance information from an auxiliary study

Estimating mixture distributions is challenging in practice due to difficulties in identifying the underlying component densities. An advantage to estimating the mixture distribution of 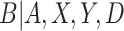for CENIC-p1 is the presence of an auxiliary study to evaluate biomarkers of nicotine exposure in fully compliant participants. Denlinger and others (2016) present data on biomarkers of nicotine exposure for 23 smokers who volunteered to be sequestered in a hotel for four nights with access to only cigarettes with 0.4 mg nicotine per gram of tobacco. These participants are known to be compliant, and their data can be used in conjunction with the data from CENIC-p1 to estimate the density of the biomarker in compliers. This will enhance our ability to identify the underlying components of the mixture distribution for 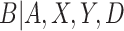. While these auxiliary data may seem unique to CENIC-p1, similar data arise in other settings. For example, pharmacokinetic/pharmacodynamic data from early-phase clinical trials could be used to help identify compliers in a phase III therapeutic clinical trial. In our application, we do not want to include these individuals’ outcomes, 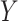, in estimation of the causal effect due to differences in smoking behavior between participants in the auxiliary and primary studies, but we do expect the distribution of 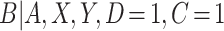to be consistent across studies. This is known as the transportability assumption in the measurement error literature (Carroll and others, 2006).

Let 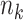denote the number of participants in the auxiliary study, let 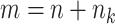, and define the indicator variable 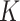that equals 1 if the participant is included in the auxiliary data or 0 if the participant is included in the main trial. We can incorporate the auxiliary data when estimating 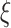and 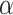by solving the score equations

$$\sum _{i=1}^m\frac{\mathrm{\partial }}{\mathrm{\partial }({\xi }^T,{\alpha }^T{)}^T}\left\{(1-K_i)\cdot \log g(B_i|A_i,X_i,Y_i,D_i;\xi ,\alpha )+K_i\cdot \log f(B_i|A_i,X_i,Y_i,d=1,c=1;\xi )\right\}=0.$$ (3.4)

3.3. Estimating the denominator of the weights

In most applications, the denominator of the weights will be unknown and must be estimated. Because the denominator must be between 0 and 1, we specify a regression model 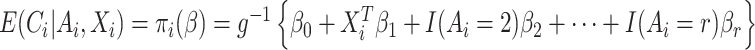, where 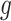is a link function that maps from (0, 1) to 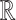, such as the logit or probit link, and 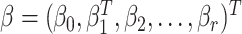is a vector of unknown regression coefficients. If 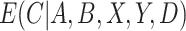were known, we could estimate 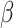by solving the estimating equation

$$\sum _{i=1}^m(1-K_i)\frac{\left\{E(C_i|A_i,B_i,X_i,Y_i,D_i;\xi ,\alpha )-{\pi }_i(\beta )\right\}}{{\pi }_i(\beta )\left\{1-{\pi }_i(\beta )\right\}}\frac{\mathrm{\partial }{\pi }_i(\beta )}{\mathrm{\partial }{\beta }^T}=0.$$ (3.5)

That is, 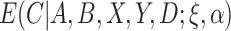is the “response” of the regression model. Note that 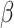can be estimated using standard software, for example, using the glm function in R. Because 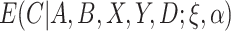is between 0 and 1, this is analogous to modeling proportions in a logistic or probit model. In the case that 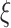and 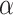are unknown, we can stack Equations (3.4) and (3.5) and solve jointly, which is equivalent to replacing 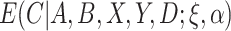in Equation (3.5) with the estimated expectation .

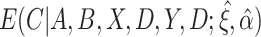4. Asymptotic properties of the CURE estimator

In discussing the asymptotic properties of the proposed estimator, for simplicity we assume there are no auxiliary data of the type described in Section 3.2 and consider only a single-arm trial with 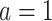for all participants, but the results easily generalize to multi-arm trials. Under the assumptions in Section 2.3, the estimating function has expectation equal to 0. The key to demonstrating this is to note that in expectation, our proposed estimator is equivalent to an IPCW estimator in which the compliance status is known without error:

$$\begin{array}{rr}\hfill E\left[\frac{E\left(C_i|B_i,X_i,Y_i,D_i\right)}{E\left(C_i|X_i\right)}\left\{Y_i-\mu (1,0)\right\}\right]& \hspace{0.17em}=E\left[\frac{C_i}{E\left(C_i|X_i\right)}\left\{Y_i-\mu (1,0)\right\}\right]\hfill \\ & \hspace{0.17em}=E\left[\frac{E\left\{C_i|X_i,Y_i^{\ast }(1,0)\right\}}{E\left(C_i|X_i\right)}\left\{{Y^{\ast }}_i(1,0)-\mu (1,0)\right\}\right]\hfill \\ & \hspace{0.17em}=E\left[\frac{E(C_i|X_i)}{E\left(C_i|X_i\right)}\left\{{Y^{\ast }}_i(1,0)-\mu (1,0)\right\}\right]=0.\hfill \end{array}$$ (4.1)

The 1st equality follows from iterated expectation. At this step, the argument of the expectation is now equivalent to the case when 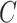is known without error, and the remaining equalities follow from assumptions stated in Section 2.3: the 2nd follows from the consistency assumption and iterated expectation, and the 3rd follows from the no unmeasured confounders assumption. Note that the result in Equation (4.1) hold even if 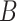is null. That is, we do not need to measure a biomarker of exposure and could replace 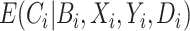with 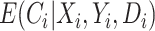and the estimating function would still have expectation equal to zero. Nevertheless, conditioning on 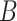allows us to incorporate auxiliary compliance data as described in Section 3.2. Furthermore, including a biomarker of compliance improves the discrimination between the compliers and non-compliers which will improve the computational stability of the estimates in the mixture distribution in Equation (3.2).

We can simultaneously estimate 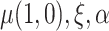, and 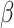by stacking the estimating equations given in Equations (2.1), (3.4), and (3.5). Let 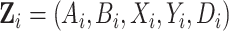be the observed data on participant 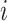and 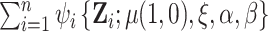denote the stacked estimating function. We showed above that the first component of 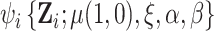has expectation 0; the components corresponding to 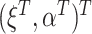and 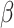have expectation 0 due to being score functions of a log likelihood and of a generalized linear model, respectively. The fact that the stacked estimating function has expectation 0 implies that, under suitable regularity conditions,

$$\sqrt{n}\left[{\left\{\hat{\mu }(1,0),{\hat{\xi }}^T,{\hat{\alpha }}^T,{\hat{\beta }}^T\right\}}^T-{\left\{\mu (1,0),{\xi }^T,{\alpha }^T,{\beta }^T\right\}}^T\right]\stackrel{D}{⟶}N\left(0,U^{-1}V(U^{-1}{)}^T\right),$$

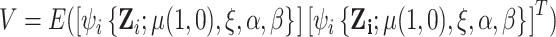where and 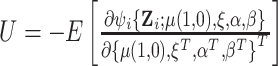. The sandwich covariance matrix 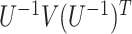can be estimated using the empirical averages for 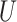and 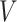(see, e.g., Stefanski and Boos (2002)) or with the bootstrap (Efron, 1979).

Note that unlike IPCW estimators when 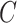is known where only the model for 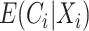must be correctly specified, the CURE estimator also relies on correctly specifying the distribution of the mixture components in Equation (3.2) to obtain consistent and asymptotically normal estimators.

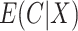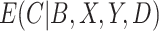We compare the relative efficiency of the CURE estimator to the standard IPCW estimator when compliance is observed in order to understand the consequences of measuring compliance with error. If and are known and do not need to be estimated, then the CURE estimator is more efficient than the standard IPCW estimator with weights 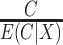. To see this, first note that 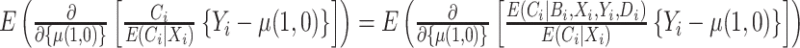, so the difference in the limiting variance of the estimators is due to differences in the variances of the estimating function. Next, we can write

$$\text{var}\left[\frac{C_i}{E(C_i|X_i)}\left\{Y_i-\mu (1,0)\right\}\right]=\text{var}\left[\frac{C_i-E(C_i|B_i,X_i,Y_i,D_i)+E(C_i|B_i,X_i,Y_i,D_i)}{E(C_i|X_i)}\left\{Y_i-\mu (1,0)\right\}\right].$$

Then, because

$$\begin{array}{rr}& \text{cov}\left[\frac{C_i-E(C_i|B_i,X_i,Y_i,D_i)}{E(C_i|X_i)}\left\{Y_i-\mu (1,0)\right\},\frac{E(C_i|B_i,X_i,Y_i,D_i)}{E(C_i|X_i)}\left\{Y_i-\mu (1,0)\right\}\right]\hfill \\ & \hspace{0.17em}=E\left(\left[\frac{E(C_i|B_i,X_i,Y_i,D_i)-E(C_i|B_i,X_i,Y_i,D_i)}{E(C_i|X_i)}\left\{Y_i-\mu (1,0)\right\}\right]\frac{E(C_i|B_i,X_i,Y_i,D_i)}{E(C_i|X_i)}\left\{Y_i-\mu (1,0)\right\}\right)\hfill \\ & \hspace{0.17em}=0\hfill \end{array}$$

by iterated expectation, the variance of the estimating function with weights 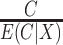is

$$\begin{array}{rr}& \text{var}\left[\frac{C_i}{E(C_i|X_i)}\left\{Y_i-\mu (1,0)\right\}\right]\hfill \\ & \hspace{0.17em}=\text{var}\left[\frac{E(C_i|B_i,X_i,Y_i,D_i)}{E(C_i|X_i)}\left\{Y_i-\mu (1,0)\right\}\right]+\text{var}\left[\frac{C_i-E(C_i|B_i,X_i,Y_i,D_i)}{E(C_i|X_i)}\left\{Y_i-\mu (1,0)\right\}\right]\hfill \\ & \hspace{0.17em}\ge \text{var}\left[\frac{E(C_i|B_i,X_i,Y_i,D_i)}{E(C_i|X_i)}\left\{Y_i-\mu (1,0)\right\}\right].\hfill \end{array}$$

Thus, if all expectations are known and do not need to be estimated, the CURE estimator is more efficient asymptotically than the standard IPCW estimator. To gain some intuition for why this occurs, consider the case where compliance has no effect on the outcome: the CURE estimator gains efficiency by simply taking a sample average of the outcome among participants randomized to group 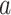to estimate 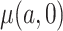, whereas the IPCW estimator excludes participants who are non-compliant even though compliance has no effect on the outcome. As the effect of compliance on the outcome strengthens, 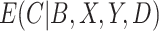approaches an indicator function and the CURE estimator approaches the standard IPCW estimator. In general, the CURE estimator borrows more data from the non-compliers as the effect of compliance decreases, which increases efficiency over the IPCW estimator.

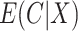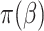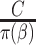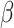A natural question is how estimating the weights impacts the variances of the estimators. Here, we use notation consistent with the generalized linear model notation introduced previously, and we remind the reader that can be written as . When the weights are , and must be estimated jointly with 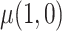, the asymptotic variance of 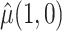is

$$E\left[\frac{{\left\{{Y^{\ast }}_i(1,0)-\mu (1,0)\right\}}^2}{{\pi }_i(\beta )}\right]-H_1{H}_2^{-1}{H}_1^T,$$

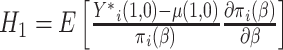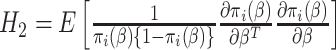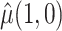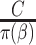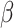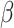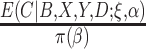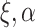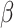where and . This interesting result shows that the variance of with weights is reduced when is estimated compared to when is known (Lunceford and Davidian, 2004). When the weights are , when , and must be estimated jointly with 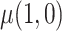, and when there are no auxiliary data to use in estimating the parameters of the mixture density (3.2), then the large sample variance of 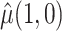is

$$\begin{array}{rr}& E\left[\frac{E(C_i|B_i,X_i,Y_i,D_i{)}^2}{{\pi }_i(\beta {)}^2}{\left\{Y_i-\mu (1,0)\right\}}^2\right]+2\left[\begin{array}{cc}\hfill \left(-H_3{H}_4^{-1}+H_1{H}_2^{-1}{H}_5{H}_4^{-1}\right)& \left(-H_1{H}_2^{-1}\right)\hfill \end{array}\right]\left[\begin{array}{c}\hfill H_6^T\\ \hfill H_7^T\end{array}\right]\hfill \\ & \hspace{0.17em}+\left[\begin{array}{cc}\hfill \left(-H_3{H}_4^{-1}+H_1{H}_2^{-1}{H}_5{H}_4^{-1}\right)& \left(-H_1{H}_2^{-1}\right)\hfill \end{array}\right]\left[\begin{array}{cc}\hfill H_4& H_8\hfill \\ \hfill H_8^T& H_9\hfill \end{array}\right]\left[\begin{array}{c}\hfill {\left(-H_3{H}_4^{-1}+H_1{H}_2^{-1}{H}_5{H}_4^{-1}\right)}^T\\ \hfill {\left(-H_1{H}_2^{-1}\right)}^T\end{array}\right],\hfill \end{array}$$ (4.2)

where

$$\begin{array}{rr}\hfill H_3& \hspace{0.17em}=-E\left[\frac{Y_i-\mu (1,0)}{{\pi }_i(\beta )}\frac{\mathrm{\partial }E(C_i|B_i,X_i,Y_i,D_i)}{\mathrm{\partial }({\xi }^T,{\alpha }^T)}\right]\hfill \\ \hfill H_4& \hspace{0.17em}=E\left[\frac{\mathrm{\partial }\log g(B_i|X_i,Y_i,D_i;\xi ,\alpha )}{\mathrm{\partial }({\xi }^T,{\alpha }^T{)}^T}\frac{\mathrm{\partial }\log g(B_i|X_i,Y_i,D_i;\xi ,\alpha )}{\mathrm{\partial }({\xi }^T,{\alpha }^T)}\right]\hfill \\ \hfill H_5& \hspace{0.17em}=-E\left[{\pi }_i(\beta )\left\{1-{\pi }_i(\beta )\right\}\frac{\mathrm{\partial }{\pi }_i(\beta )}{\mathrm{\partial }{\beta }^T}\frac{\mathrm{\partial }E(C_i|B_i,X_i,Y_i,D_i)}{\mathrm{\partial }({\xi }^T,{\alpha }^T)}\right]\hfill \\ \hfill H_6& \hspace{0.17em}=E\left[\frac{C_i\left\{{Y^{\ast }}_i(1,0)-\mu (1,0)\right\}}{{\pi }_i(\beta )}\frac{\mathrm{\partial }\log g(B_i|X_i,Y_i,D_i;\xi ,\alpha )}{\mathrm{\partial }({\xi }^T,{\alpha }^T)}\right]\hfill \\ \hfill H_7& \hspace{0.17em}=E\left[\frac{E(C_i|B_i,X_i,Y_i,D_i)\left\{Y_i-\mu (1,0)\right\}\left\{E(C_i|B_i,X_i,Y_i,D_i)-{\pi }_i(\beta )\right\}}{{\pi }_i(\beta {)}^2\left\{1-{\pi }_i(\beta )\right\}}\frac{\mathrm{\partial }{\pi }_i(\beta )}{\mathrm{\partial }\beta }\right]\hfill \\ \hfill H_8& \hspace{0.17em}=E\left[\frac{E(C_i|B_i,X_i,Y_i,D_i)-{\pi }_i(\beta )}{{\pi }_i(\beta )\left\{1-{\pi }_i(\beta )\right\}}\frac{\mathrm{\partial }\log g(B_i|X_i,Y_i,D_i;\xi ,\alpha )}{\mathrm{\partial }({\xi }^T,{\alpha }^T{)}^T}\frac{\mathrm{\partial }{\pi }_i(\beta )}{\beta }\right]\hfill \\ \hfill H_9& \hspace{0.17em}=E\left[\frac{{\left\{E(C_i|B_i,X_i,D_i,Y_i)-{\pi }_i(\beta )\right\}}^2}{{\left[{\pi }_i(\beta )\left\{1-{\pi }_i(\beta )\right\}\right]}^2}\frac{\mathrm{\partial }{\pi }_i(\beta )}{\mathrm{\partial }{\beta }^T}\frac{\mathrm{\partial }{\pi }_i(\beta )}{\mathrm{\partial }\beta }\right]\hfill \end{array}$$

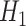and and 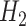were defined previously. The last term in (4.2) is positive because it is a quadratic form of a positive semi-definite matrix, but the middle term does not have this property and is neither clearly positive nor clearly negative under all conditions. Thus, although estimating the weights for the IPCW estimator is guaranteed to increase the asymptotic efficiency of 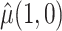, there is no such guarantee for the CURE estimator. If 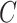were observed and 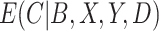were estimated using a regression model in the CURE estimator, then we could make a definitive statement about the impact of estimating 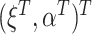on the limiting variance of 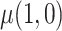, but this is not possible when 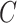is not observed and we used the approach described in Section 3. Also note that the information matrix 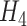will contain more information when auxiliary data are incorporated as described in Section 3.2, but this may be beneficial only for estimation of the mixture density (3.2) in small samples, not for asymptotic efficiency of .

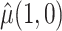5. Simulation study

We designed a simulation study to test the finite-sample properties of the proposed estimator. For simplicity, we consider a scenario in which all participants are assigned a single treatment, 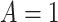, and only estimate 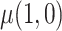, rather than a difference in means between two treatment groups. To facilitate data generation, define 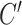as a latent continuous measure of compliance. We generated 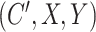from a multivariate normal distribution with mean vector 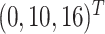and covariance matrix 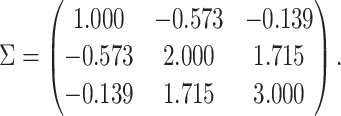We define the compliance indicator 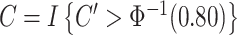, where 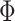is the standard normal cumulative distribution function. This gives 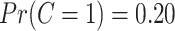, consistent with the preliminary estimates of the compliance rate from CENIC-p1 (Nardone and others, 2016). We simulated 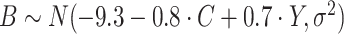with two values of 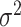, 0.818 and 0.663, to give an area under the receiver operating characteristic (ROC) curve of 0.8 or 0.9, respectively, for discriminating between compliers and non-compliers. We let 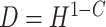, where 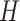is a Bernoulli random variable with success probability 0.3 independent of other data, so that those truly compliant (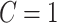) always self-report compliance and for non-compliant participants (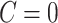) 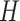is an indicator of whether or not non-compliance was reported with error. The data generated are consistent with the DAG shown in the supplementary material Section B available at Biostatistics online, which is one possible DAG for the CENIC-p1 data. 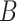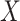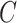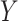Note that the DAG implies that and are conditionally independent given and (and 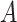, which here has only one level).

We considered sample sizes of 225 (roughly the number of participants randomized to the VLNC cigarettes in CENIC-p1), 500, and 1,000 and also included data from an auxiliary study in which participants are known to be compliant as described in Section 3.2 equal to 10% of the size of the main clinical trial.

We compared five estimators of 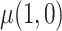: (i) a per protocol estimator based on self-reported compliance; (ii) an inverse probability weighted (IPW) estimator based on self-reported compliance with weights equal to 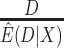; (iii) an IPW estimator with weights equal to 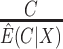; (iv) a cutoff IPW estimator that first estimates 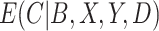using the methods described in Section 3.1, defines 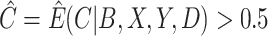, and then uses the weights 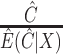; and (v) the CURE estimator with weights 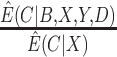. Although we have argued the IPW estimator cannot be used in CENIC-p1, we include it for comparison to illustrate the cost of relying on imperfect measures of compliance. We assumed that 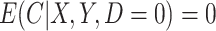, and observations with 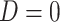did not contribute to estimation of the mixture distribution. To estimate 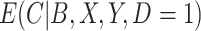in the cutoff IPW and CURE estimators, we assumed simple linear regression models with normal residuals for 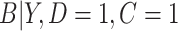and 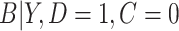; to estimate 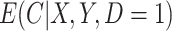we assumed a generalized linear model with probit link. To improve computation time, we used a single set of starting values for the EM algorithm which were estimated parameters from models fit using the actual compliance 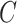. In applications, when 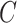is unknown to the analyst and cannot be used to generate starting values, the EM algorithm may require multiple iterations with different starting values to find the global maximum of the likelihood, but the simulation nevertheless gave good results using only this one set of starting values for each iteration. For the self-reported IPW, cutoff IPW, and CURE estimators, the denominator of the weights was estimated using a generalized linear model with probit link where the outcome is the numerator of the weights. We used the bootstrap percentile method with 1,000 bootstrap re-sampled data sets to compute 95% confidence intervals (CI).

Table 1 shows the simulation results. Overall, the CURE estimator has very small bias for both area under the curve (AUC) of 0.8 and 0.9. With AUC of 0.8, the CURE estimator has higher mean squared error than per protocol or IPW based on self-report, but with sample size 1,000 the mean squared error is smaller; with AUC of 0.9, the CURE estimator has lower mean squared error for sample sizes 500 and 1,000. The per protocol and self-report IPW estimators show bias that is not attenuated with increasing sample size and coverage probabilities which are not close to the nominal level. The cutoff IPW estimator has low bias, but, surprisingly, for each sample size and AUC level, the CURE estimator has much smaller mean squared error and coverage probability closer to the nominal 0.95 level. Unsurprisingly, the CURE estimator has higher mean squared error than the IPW estimator, but the mean squared error of the CURE estimator approaches that of the IPW estimator as the AUC increases. The simulation results demonstrate that the CURE estimator has better small sample performance than per protocol and self-report IPW when there is potential for misclassification. Furthermore, the CURE estimator performs better than an ad hoc estimator that uses IPW with an estimated indicator variable of compliance.

Table 1.

Simulation results

n	Estimator	Bias	MC SD	Mean SE	CP	MSE
225	Per Protocol	0.629	0.173	0.174	0.045	0.426
	Self-Report IPW	0.403	0.155	0.154	0.257	0.187
	IPW	0.035	0.330	0.278	0.905	0.110
	Cutoff IPW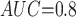	0.140	0.860	0.740	0.978	0.758
	CURE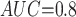	0.119	0.768	0.689	0.976	0.603
	Cutoff IPW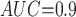	0.037	0.605	0.574	0.972	0.367
	CURE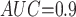	0.033	0.523	0.518	0.970	0.274
500	Per Protocol	0.636	0.114	0.117	0.000	0.417
	Self-Report IPW	0.405	0.101	0.103	0.024	0.174
	IPW	0.015	0.209	0.196	0.926	0.044
	Cutoff IPW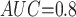	0.010	0.665	0.659	0.983	0.442
	CURE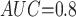	0.047	0.530	0.571	0.978	0.283
	Cutoff IPW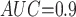	0.021	0.368	0.419	0.982	0.136
	CURE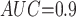	0.021	0.277	0.344	0.965	0.077
1000	Per Protocol	0.633	0.086	0.082	0.000	0.408
	Self-Report IPW	0.405	0.071	0.072	0.000	0.169
	IPW	0.009	0.154	0.143	0.937	0.024
	Cutoff IPW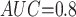	0.070	0.480	0.531	0.983	0.235
	CURE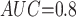	0.011	0.325	0.418	0.979	0.106
	Cutoff IPW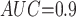	0.053	0.244	0.279	0.977	0.062
	CURE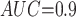	0.007	0.173	0.208	0.963	0.030

Subscripts indicate the area under the ROC curve for discriminating compliers from non-compliers. MC SD, Monte Carlo standard deviation of the estimator; Mean SE, mean estimated standard error of the estimator; CP, coverage probability of 95% CI, MSE: mean squared error.

6. Application to the CENIC-p1 data

We applied the CURE estimator to estimate the causal effect of VLNC cigarettes on the number of cigarettes smoked per day using data from CENIC-p1. Although CENIC-p1 was a 6-week trial, for simplicity we are only concerned with compliance and outcomes collected in the last week. In this analysis, we let 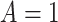if the participant was randomized to smoke VLNC cigarettes (0.4 mg nicotine per gram of tobacco, high and low tar groups combined) and let 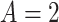if randomized to smoke usual brand cigarettes. All other notation in this application is defined in Section 2.

The goal of this analysis is to estimate the causal contrast 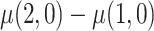, the expected reduction in cigarettes smoked per day during week 6 if smoking only VLNC cigarettes versus smoking usual brand cigarettes. We estimate the causal effect by estimating 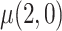and 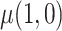separately and taking their difference. The usual brand group is meant to represent smoking behavior with commercially available cigarettes and, in that sense, participants in this group were never treated as non-compliant, and 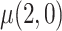was estimated using the sample average of the total number of cigarettes smoked per day during week 6 (i.e., study plus non-study cigarettes). We consider the four estimators for 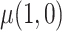discussed in the simulation study (excluding IPW because 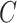is unobserved) and include the ITT estimator for comparison.

As in the simulation, we assumed that 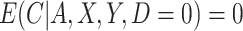, and participants with 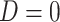did not contribute to estimation of the mixture distribution. Using the biomarker log(TNE) measured at week 6 as the (only) biomarker 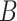of exposure, we estimated the probability of compliance for participants self-reporting compliance (i.e., 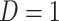) following the approach in Section 3.1. Specifically, in fitting the mixture distribution in Equation (3.2), we assume a simple linear regression model with normally distributed errors for 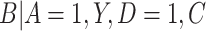with no shared parameters between the different levels of 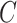. 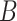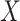As in the simulation, we assume that and are conditionally independent given 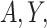and 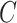, consistent with the DAG in Section B of the supplementary material available at Biostatistics online. We assumed a logistic regression model for 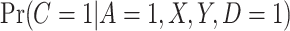, where the confounders 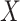included age, level of addiction (baseline cigarettes per day and log of TNE), measures of withdrawal (Minnesota Nicotine Withdrawal Scale at week 5 and maximum acute withdrawal), and satisfaction with and craving for VLNC (Cigarette Evaluation Scale and Questionnaire of Smoking Urges at week 5) and normal nicotine cigarettes (Questionnaire of Smoking Urges at week 5). We incorporated the data for the 23 participants from Denlinger and others (2016) who were known to be compliant to aid in estimating the parameters of the mixture distribution as described in Section 3.2. Multiple sets of starting values were tried for the EM algorithm, and we used those values which gave the lowest negative log likelihood. We estimated the denominator 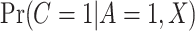following the approach of Section 3.3 using a logit link with the same predictors 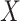described above. All CIs were estimated using the non-parametric bootstrap percentile method with 1,000 bootstrap resamples.

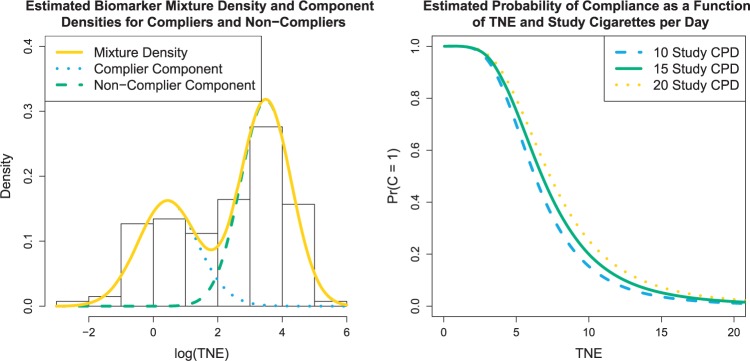
For the VLNC group, 137 of 222 (61.7%) participants self-reported compliance during week 6. The left panel of Figure 1 shows a histogram of 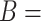log(TNE) for the self-reported compliers in the treatment group, the estimated mixture distribution, and the complier and non-complier component distributions, which supports our parametric assumptions for the components of the mixture distribution. The right panel shows the probability of compliance as a function of TNE and 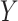, the self-reported number of cigarettes per day. We estimate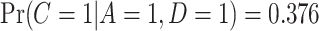d , and 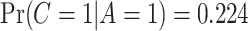, indicating a substantial proportion of self-reported compliers were non-compliant. Estimated coefficients and parameters for the numerator and denominator of the weights and 95% bootstrap CIs can be found in Section C of the supplementary material available at Biostatistics online. We also include a table giving some summary statistics of baseline characteristics, confounders, and the biomarker Week 6 log(TNE).

Fig. 1.

Left: histogram of 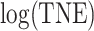, the biomarker of nicotine exposure, for the self-reported compliers randomized to smoke cigarettes with 0.4 mg nicotine per gram tobacco in the CENIC-p1 trial. The estimated mixture distribution (solid line) and the distribution of each of the mixture components (dashed and dotted lines) is overlaid. Right: probability a participant who self-reported compliance was actually compliant as a function of TNE and number of self-reported study cigarettes smoked per day.

Table 2 shows the estimated causal effect of VLNC cigarettes on number of cigarettes smoked per day. The cutoff IPW gives the most optimistic estimate of the causal effect of the treatment, while the CURE estimate is more conservative. In contrast, the per protocol and self-report IPW estimators give similar and more modest estimates of the treatment effect. Although the CURE and cut-off IPW estimates are similar, note that the length of the 95% CI is much wider for the cut-off IPW estimator than for the CURE estimator.

Table 2.

Point estimates, standard error (SE) of the estimators, and 95% CI of the estimated causal effect for each estimator

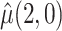
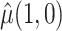
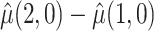
Estimator				SE	95% CI
ITT	22.18	15.37	6.81	1.57	(3.78, 10.07)
Causal estimators
Per protocol	22.18	15.12	7.07	1.80	(3.61, 10.63)
Self-report IPW	22.18	15.19	6.99	1.67	(3.66, 10.38)
Cutoff IPW	22.18	14.83	7.35	3.03	(1.64, 12.99)
CURE	22.18	14.98	7.20	2.79	(2.01, 12.46)

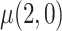: mean cigarettes smoked per day for the usual brand group; 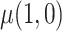: mean cigarettes smoked per day for the VLNC group if all participants were to be compliant.

We typically expect the ITT estimator to be more conservative than estimators of the causal effect. Although the ITT estimator was in fact more conservative than the causal estimator, the difference is small considering the large proportion of noncompliance. While this may seem counterintuitive, the impact of non-compliance may be different compared to other clinical trials of medication. In the case of medication, we expect a monotone dose-response relationship, and non-compliance with the medication should dilute the treatment effect by reducing the dose received. Here, on the one hand, non-compliant use of high nicotine cigarettes could actually reduce the need for study cigarettes more than the study cigarette itself (e.g., by more effectively alleviating withdrawal). Consequently, one might expect the number of study cigarettes smoked per day to be lower in non-compliant participants than it would be if they were forced to be compliant. On the other hand, non-compliance is also associated with individuals who find VLNC cigarettes particularly unsatisfying. Such individuals might be less inclined to continue to smoke or would smoke less if forced to be compliant.

The results presented here require us to assume that we have correctly modeled the numerator and denominator of the weights and should be interpreted cautiously. Like all models, the assumptions must be considered when interpreting outcomes, and convergent analyses should be used to clarify the likely mechanism whenever possible. Finally, it is important to note that in a regulatory environment in which VLNC cigarettes were the only legally available cigarettes, we would expect that the proportion of smokers using only VLNC cigarettes would be substantially higher than in CENIC-p1, but there would still likely be some use of cigarettes with higher nicotine content (e.g., hoarding, black market).

7. Discussion

Methods for estimating causal effects from randomized clinical trials when there is noncompliance frequently rely on imperfect measures of compliance. Estimators that do not acknowledge the error in the measures of compliance will result in biased estimators of the causal effect. We developed a causal estimator that accounts for uncertainty in compliance status by re-weighting a typical IPCW estimator by a participant’s probability of compliance given a biomarker of compliance, the outcome of interest, and confounders. Although we treated the true compliance status as unobserved, we showed the probability of compliance can be estimated by assuming the distribution of the biomarker follows a mixture distribution with separate components for compliers and non-compliers. The simulation demonstrates that our proposed estimator has little bias, good coverage probability, and smaller mean squared error than an ad hoc estimator.

The methods developed here have particular relevance to and were motivated by regulatory tobacco research. There is usually substantial noncompliance in regulatory tobacco trials due to the availability of commercial tobacco products. The causal analysis using the methods we have developed, as compared to an ITT analysis, is likely to better estimate the effect we would observe if regulations changing the nicotine composition in cigarettes were enacted. However, our proposed method also has broad applicability for clinical trials conducted in other therapeutic areas. The method is particularly attractive in cases where investigators rely on imperfect measures of compliance, such as participants’ self-report (e.g., pill counts, timeline follow back, etc.) because the method explicitly accounts for the uncertainty of compliance status.

The preceding has assumed that either the outcome 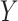is not subject to measurement/self-report error or that one is interested in the average causal effect on self-reported outcomes. We show in Section D of the supplementary material available at Biostatistics online that if the observed outcome is subject to measurement error, the proposed approach will estimate the causal effect if there were no measurement error under mild assumptions.

Others have investigated the effect of and possible solutions to mediation estimators when the mediator (e.g., compliance to randomized treatment group) is measured with error (Valeri and others, 2014; Ogburn and Vander Weele, 2012). Most prior work has examined the effect on regression-based estimators as opposed to our IPW framework. Additionally, our approach makes minimal assumptions about measurement error. In particular, we do not need to assume that self-reported compliance (i.e., the covariate measured with error) is a surrogate for true compliance for valid inference. 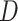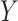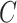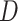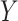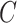That is, the method does not require that is conditionally independent of given or that is conditionally independent of given and .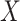

There are several limitations to our approach. First, estimating the parameters of the mixture distributions may be computationally challenging, resulting in unstable parameter estimates. In our simulation, we relied on an auxiliary data set that included data from participants whose compliance was known. However, such data sources are frequently available in other settings as well, such as in pharmacokinetic/pharmacodynamic studies. Second, we only considered compliance and outcomes during week 6 of the CENIC-p1 trial. This was done mainly for simplicity, however, and we could develop a longitudinal extension of the estimator, which is a likely subject of future work. Finally, inverse probably weighted estimators are known to be inefficient. The efficiency of the CURE estimator could likely be improved through an augmented weighted estimator (Tsiatis, 2006).

Causal inference methods frequently rely on poor measures of compliance. Our causal estimator weights participants by the product of their probability of compliance given the biomarker of treatment exposure and the inverse probability of compliance given confounders. Our approach suggests that, rather than improving methods of eliciting compliance status from participants, perhaps a more fruitful of area of research is in developing biomarkers of exposure. We restricted our attention to IPCW-like weights and developed the method for a point exposure study, but future work may develop causal estimators in other settings. Our hope is that the proposed methods becomes a standard analysis by investigators estimating causal effects from clinical trials.

8. Software

The R code for the simulation and an example data set with analysis is available for download at https://github.com/jeffrey-boatman/cure-estimator.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This research was partially funded by NIH grants R03-DA041870 and U54-DA031659 from the National Institute on Drug Abuse and FDA Center for Tobacco Products (CTP). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or FDA CTP.