An Alternative Robust Estimator of Average Treatment Effect in Causal Inference

Summary

The problem of estimating the average treatment effects is important when evaluating the effectiveness of medical treatments or social intervention policies. Most of the existing methods for estimating the average treatment effect rely on some parametric assumptions about the propensity score model or the outcome regression model one way or the other. In reality, both models are prone to misspecification, which can have undue influence on the estimated average treatment effect. We propose an alternative robust approach to estimating the average treatment effect based on observational data in the challenging situation when neither a plausible parametric outcome model nor a reliable parametric propensity score model is available. Our estimator can be considered as a robust extension of the popular class of propensity score weighted estimators. This approach has the advantage of being robust, flexible, data adaptive and it can handle many covariates simultaneously. Adopting a dimension reduction approach, we estimate the propensity score weights semiparametrically by using a nonparametric link function to relate the treatment assignment indicator to a low-dimensional structure of the covariates which are formed typically by several linear combinations of the covariates. We develop a class of consistent estimators for the average treatment effect and study their theoretical properties. We demonstrate the robust performance of the estimators on simulated data and a real data example of investigating the effect of maternal smoking on babies’ birth weight.

1. Introduction

Estimating the average treatment effect is important in comparing different medical treatments, social programs and intervention policies. The problem is challenging when the data come from an observational study instead of a randomized experiment. Direct differencing of the sample averages is susceptible to confounding bias, which is caused by imbalances in baseline covariate distributions between the treatment group and the control group.

Under the commonly imposed no unmeasured confounder assumption (Rosenbaum and Rubin (1983); De Luna et al. (2011)), a variety of methods have been proposed to consistently estimate the average treatment effect. The class of doubly robust (DR) estimators (Scharfstein et al. (1999); Robins and Rotnitzky (2001); Bang and Robins (2005); Rubin and van der Laan (2008); Cao et al. (2009); Tan (2010); Rotnitzky et al. (2012); van der Laan and Rose (2011); Vansteelandt et al. (2012); van der Laan (2015); Benkeser (2016), among others) have been particularly popular due to their double protection against model misspecification.

For most practitioners, the application of DR estimation often adopts parametric specification of both the propensity score model and the outcome regression model, hereafter referred to as parametric DR. The parametric DR estimators are consistent when either the parametric propensity score model or the parametric outcome regressions model is correctly specified. However, Carpenter et al. (2006), Kang and Schafer (2007) and Vansteelandt et al. (2012) observed that the finite-sample bias can be amplified when one of the working models is misspecified and the bias of parametric DR estimators can be severe if both models are slightly misspecified. Vermeulen and Vansteelandt (2015) recently proposed a novel generic strategy for bias reduction under misspecification of both models. Vermeulen and Vansteelandt (2016) further explored the use of data-adaptive estimators in constructing bias-reduced doubly robust estimation. These estimators provide very useful improvement over standard parametric DR estimators, but still need at least one working model to be correctly specified using a parametric model.

Motivated by the practical concern of bias reduction, we propose an alternative approach by directly considering estimators of average treatment effects that are consistent in a larger class of semiparametric propensity score models. The semiparametric class we study imposes a semiparametric structure for the propensity score model while imposing no structure for the outcome regression model. As a direct consequence, our proposed estimator is expected to be consistent for many distributions where most of the standard parametric DR estimators would become inconsistent. This will be demonstrated by the numerical results in Section 4. Furthermore, we derive the asymptotic normality of the proposed estimator for the average treatment effect, which remains valid for this general class of semiparametric distributions.

There has been growing recent interest in relaxing the parametric specification of working models in parametric DR. Hirano et al. (2003) and Wang et al. (2010) considered nonparametric approach for estimating the propensity score. However, the nonparametric approach is not feasible when many covariates are present due to the curse of dimensionality. Imai and Ratkovic (2014) introduced covariate balancing propensity score as a method that is robust to mild misspecification of the parametric propensity score model. McCaffrey et al. (2004); Ridgeway and McCaffrey (2007); Petersen et al. (2007); Westreich et al. (2010); Lee et al. (2010) explored machine learning approaches for modeling the propensity score but have not studied the asymptotic properties of the resulted average treatment effect estimator. In a sequence of impressive work, Van der Laan and his coauthors proposed and carefully studied targeted maximum likelihood estimators (TMLE) which incorporates the state-of-art of machine learning and uses an ensemble of models. See van der Laan and Rubin (2006), the recent manuscript of van der Laan and Rose (2011) and the references therein. van der Laan (2014) showed that a double targeting can guarantee that the bias of the estimator of the target parameter is of second order and hence asymptotically linear. van der Laan (2015) further proposed a general one-step targeted minimum loss-based estimator based on an initial estimator of the nuisance parameters defined by a loss-based super-learner and proved that this one-step TMLE is asymptotically efficient. The latter estimator is understandably more computationally intensive than our proposed approach as it involves multiple tuning parameters and requires cross-validation.

The approach we propose can be viewed as a middle ground between the parametric DR and the nonparametric DR. Compared to parametric DR, our method does not rely on parametric specification of the propensity score model or the outcome regression model. In fact, we do not attempt to model the outcome at all, and only model the propensity score semiparametrically, hence it is more robust as far as the dependence on the propensity score model is concerned. Compared to the nonparametric DR, it has the advantage of being able to handle many covariates. Specifically, we relax the commonly imposed parametric assumption on the propensity score model by only assuming the probability of assigning the treatment depends on the p-dimensional covariate vector X through several linear combinations ℬ^TX, where ℬ is a p × d matrix with d < p. We then estimate this conditional probability by employing a nonparametric link function. Note that much work exists in studying how to model the relation between a binary response and many covariates, see for example, Pregibon (1980), Koenker and Yoon (2009), Li et al. (2016). The special case of d = 1 yields the single index model and is especially well studied (Härdle et al., 2004). As an intermediate model for the propensity score in the treatment effect estimation, our semiparametric approach for estimating the propensity score is most closely related to the sufficient dimension reduction literature (Cook, 1998) and is of independent interest. Existing methods for estimating the dimension reduction space such as sliced inverse regression (SIR)(Li, 1991), sliced average variance estimation (SAVE) (Cook and Weisberg, 1991), directional regression (Li and Wang, 2007), generalized directional regression (Li and Dong, 2009; Dong and Li, 2010) have two limitations in relation to our problem. First, they rely mainly on a linearity condition and/or a constant variance condition, i.e. E(X | ℬ^TX) being a linear function of ℬ^TX and var(X | ℬ^TX) being a constant matrix, or their generalized form, which may not hold in our problem. Second, they require a reversal of the relation between X and T, i.e. they require to compute expectations of the functions of the covariates X conditional on T. Because T only has two values, each expectation will generate only two different values, which is not sufficient for subsequent operations of these methods. This hampers the direct application of these methods. On the other hand, other methods based on nonparametric regression (Xia, 2007) and semiparametric regression (Ma and Zhu, 2012, 2013) exist, but they also need to be adapted instead of directly applied to estimating the propensity score which concerns binary response.

The rest of the paper is organized as follows. In Section 2, we introduce the multi-index semiparametric estimator of the propensity score function and a robust estimator of the average treatment effect. In Section 3, we study the asymptotic properties of the estimators. Simulation studies are conducted and presented in Section 4. We illustrate the usefulness of the method in a real data example of analyzing effect of maternal smoking on babies’ birth weight in Section 5 and conclude the paper with a brief discussion in Section 6. The Appendix contains the derivation of the efficient score function and the proof of Theorem 1. The regularity conditions, proofs of Lemmas and additional numerical results are given in the online supplementary document.

2. A robust estimator of the average treatment effect

2.1 Notation and setup

We consider the popular setting of a binary treatment T (T = 1 for treatment and 0 for control). To estimate the treatment effect, we adopt the potential or counterfactual outcome framework (Neyman et al., 1990; Rubin, 1974). Let Y*(1) be the outcome of the subject had s/he (possibly counter to fact) received treatment; and Y*(0) be the outcome of the subject has s/he (possibly counter to fact) received non-treatment. Our goal is to estimate the average treatment effect

$$\tau =E\{Y^{\ast }(1)-Y^{\ast }(0)\}.$$

The difficulty of the problem arises because for each individual in the sample, we observe either Y*(1) or Y*(0), but not both. The observed outcome is Y = TY*(1) + Y*(0)(1 − T), that is, the observed outcome is the potential outcome corresponding to the treatment the subject actually receives, which is often referred to as the consistency assumption in causal inference (Rubin, 1986).

Given data from an observational study {Y_i, T_i, X_i}, i = 1, …, n, where Y_i is the response of the ith subject, T_i is the binary treatment indicator, X_i is a vector of covariates, we are interested in estimating the average causal effect of the treatment. Direct differencing the sample averages of the treatment and control groups often leads to a biased estimator of τ in observational studies as the two groups often differ in some covariates that are associated with both the treatment and outcome. Let π(X) = P(T = 1|X) be the propensity score function and assume that the unconfoundedness given X assumption is satisfied, that is {Y*(1), Y*(0)} ⊥ T|X, or the treatment assignment is independent of the potential outcomes given the covariates. Rosenbaum and Rubin (1983) showed that adjusting for propensity score can completely remove the confounding bias from the difference in covariates.

Hahn (1998) derived the semiparametric efficiency bound for estimating τ in the general model where only the independence between treatment and potential outcomes given covariates is assumed. The propensity score can be used in different ways to obtain a consistent estimator for the average treatment effect. Hahn (1998) also proposed an estimator that achieves the semiparametric efficiency bound, but his estimator involves estimating E(YT|X), E{Y (1 − T)|X} and π(X). Hirano et al. (2003) further showed that a simpler estimator that only estimates π(X) nonparametrically can also achieve the semiparametric efficiency bound. However, these nonparametric estimators suffer from the curse of dimensionality in real data analysis even with a moderate amount of covariates such as four covariates.

In practice, existing work on causal inference usually adopts a parametric approach to modeling the propensity score function. For example, logistic models are frequently used to model disease occurrence in case-control studies (Prentice and Pyke, 1979; Chatterjee and Carroll, 2005; Lin and Zeng, 2009; Ma and Carroll, 2016), in missing probability problem (Rubin, 1976; Rubin and Little, 2002), and even in survival models (Efron, 1988). However, the parametric approach is prone to model misspecification and can result in substantial bias.

The crux of our robust estimator of the average treatment effect is to develop a flexible estimator of the propensity score function. Instead of the parametric logistic regression model for the propensity score function, we assume

$$\text{pr}(T=1|\mathbf{X}=\mathbf{x})=\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}\mathbf{x})\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}\mathbf{x})\}},$$ (2.1)

where X ∈ ℛ^p, ℬ ∈ ℛ^p×d and η is an arbitrary unspecified function. Note that we use the logit link function here for parameterization purpose to ensure that the depicted probability function takes values between 0 and 1. As the function η is completely unspecified, our model allows the probability of being assigned to the treatment to depend on several linear combinations of X in a nonparametric fashion. In contrast, the popular logistic regression model assumes this probability to depend on one particular linear combination of X in a known parametric fashion.

2.2 Flexible estimation of the propensity score

To obtain a more concise form, we rewrite (2.1) equivalently as

$$\text{pr}(T=t|\mathbf{X}=\mathbf{x})=\frac{\text{exp}\{t\eta ({ℬ}^{\mathrm{T}}\mathbf{x})\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}\mathbf{x})\}}.$$ (2.2)

The log-likelihood function of ℬ and η is ${\sum }_{i=1}^n(t_i\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)-\text{log}[1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}])$. For identifiability of ℬ, we require ℬ to have the form $ℬ={({\mathbf{I}}_d,{ℬ}_l^{\mathrm{T}})}^{\mathrm{T}}$, where the upper submatrix I_d is the d × d identity matrix while the lower submatrix ℬ_l is an arbitrary (p − d) × d matrix. To estimate the semiparametric propensity score function, we need to estimate ℬ_l and the unknown function η, the former of which contains p_t = (p − d)d free parameters while the latter can be viewed as an infinite dimensional parameter, where the subindex in p_t stands for “total”. In the sequel, for notational convenience, for any arbitrary p × d matrix ℬ, we define the concatenation of the columns contained in the lower p − d rows of ℬ as vecl(ℬ) = vec(ℬ_l) = (β_d+1,1, …β_p,1, …β_d+1,d, …β_p,d)^T where “vec” stands for vectorization while “vecl” is the vectorization of the lower part of the original matrix.

Our approach of estimation relies on first deriving the influence function using the geometric technique (Bickel et al., 1993; Tsiatis, 2006). In the Appendix, we derive the efficient score function with respect to ℬ:

$$\begin{gathered} {\mathbf{S}}_{\text{eff}}(t_i,{\mathbf{x}}_i,{ℬ}^{\mathrm{T}}{\mathbf{x}}_i,\eta ,\mathit{\eta }\prime ) \\ =\text{vecl }(\{{\mathbf{x}}_i-E({\mathbf{X}}_i|{ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}[t_i-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}}). \end{gathered}$$ (2.3)

We use the Nadaraya-Watson kernel estimator to estimate E(X_i | ℬ^Tx_i), that is,

$$\hat{E}(\mathbf{X}|{ℬ}^{\mathrm{T}}\mathbf{x})=\frac{{\sum }_{i=1}^n{\mathbf{x}}_i{K}_h({ℬ}^{\mathrm{T}}{\mathbf{x}}_i-{ℬ}^{\mathrm{T}}\mathbf{x})}{{\sum }_{i=1}^n{K}_h({ℬ}^{\mathrm{T}}{\mathbf{x}}_i-{ℬ}^{\mathrm{T}}\mathbf{x})},$$ (2.4)

where h is a bandwidth and K is a multivariate kernel function, K_h(·) = K(·/h)/h^d. Neither η nor η′ is known in a real data analysis. To deal with this complexity, in the following we borrow the idea of locally efficient and adaptively efficient estimators in general and especially in Ma and Zhu (2012) and consider two different options, which lead to two different estimators of ℬ.

First, we consider an estimator of ℬ based on a posited form of η, denoted as η*, which may not be identical to η. The corresponding derivative is denoted by η*′. This yields the locally efficient score function

$$\begin{gathered} {\mathbf{S}}_{\text{eff}}^{\ast }(t_i,{\mathbf{x}}_i,ℬ,{\eta }^{\ast },{\mathit{\eta }}^{\ast \prime }) \\ =\text{vecl }(\{{\mathbf{x}}_i-E({\mathbf{X}}_i|{ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}[t_i-\frac{\text{exp}\{{\eta }^{\ast }({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}{1+\text{exp}\{{\eta }^{\ast }({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}]{\mathit{\eta }}^{\ast \prime }{({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}}). \end{gathered}$$ (2.5)

Obviously, there are many different choices of η, as long as η* is a smooth function of ℬ^Tx. For example, when we choose ${\eta }^{\ast }({ℬ}^{\mathrm{T}}\mathbf{x})={\mathbf{1}}_d^{\mathrm{T}}{ℬ}^{\mathrm{T}}\mathbf{x}$ where 1_d is a length d vector of ones. Then η*′(ℬ^Tx) = 1_d. The locally efficient estimator of ℬ solves the estimating equation

$$\sum _{i=1}^n\text{vecl}[\{{\mathbf{x}}_i-\hat{E}({\mathbf{X}}_i|{ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}\{t_i-\frac{\text{exp}({\mathbf{1}}_d^{\mathrm{T}}{ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}{1+\text{exp}({\mathbf{1}}_d^{\mathrm{T}}{ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}\}{\mathbf{1}}_d^{\mathrm{T}}]=\mathbf{0}.$$ (2.6)

We denote this estimator by ℬ̂₁.

Next, we consider estimating η(ℬ^Tx_i) and its first derivative nonparametrically to obtain an adaptively efficient estimator of ℬ. We adopt the local linear kernel method to estimate η(ℬ^Tx) and its first derivative, which solves

$$\sum _{i=1}^n[t_i-\frac{\text{exp}\{b_0+{\mathbf{b}}_1^{\mathrm{T}}({ℬ}^{\mathrm{T}}{\mathbf{x}}_i-{ℬ}^{\mathrm{T}}{\mathbf{x}}_0)\}}{1+\text{exp}\{b_0+{\mathbf{b}}_1^{\mathrm{T}}({ℬ}^{\mathrm{T}}{\mathbf{x}}_i-{ℬ}^{\mathrm{T}}{\mathbf{x}}_0)\}}]K_h({ℬ}^{\mathrm{T}}{\mathbf{x}}_i-{ℬ}^{\mathrm{T}}{\mathbf{x}}_0)=0$$ (2.7)

$$\sum _{i=1}^n[t_i-\frac{\text{exp}\{b_0+{\mathbf{b}}_1^{\mathrm{T}}({ℬ}^{\mathrm{T}}{\mathbf{x}}_i-{ℬ}^{\mathrm{T}}{\mathbf{x}}_0)\}}{1+\text{exp}\{b_0+{\mathbf{b}}_1^{\mathrm{T}}({ℬ}^{\mathrm{T}}{\mathbf{x}}_i-{ℬ}^{\mathrm{T}}{\mathbf{x}}_0)\}}]({ℬ}^{\mathrm{T}}{\mathbf{x}}_i-{ℬ}^{\mathrm{T}}{\mathbf{x}}_0)K_h({ℬ}^{\mathrm{T}}{\mathbf{x}}_i-{ℬ}^{\mathrm{T}}{\mathbf{x}}_0)=\mathbf{0}.$$ (2.8)

The estimators b̂₀ and b̂₁ are the estimators of η and η′ at ℬ^Tx₀, respectively. We can vary x₀ to obtain estimates of the functions at various values. We write the resulting estimators as η̂(·, ℬ) and η̂′(·, ℬ), which can be considered as profiled estimators for η and η′. We subsequently plug η̂(·, ℬ), η̂′(·, ℬ), Ê(X | ℬ^Tx) into (2.3) and solve for ℬ to obtain the efficient estimator, which we denote by ℬ̂₂.

2.3 Robust estimation of the average treatment effect

To estimate the average treatment effect robustly, we propose to use

$$\hat{\tau }=\frac{1}{n}\sum _{i=1}^n\{\frac{T_i{Y}_i}{\hat{\pi }(X_i)}-\frac{(1-T_i)Y_i}{1-\hat{\pi }(X_i)}\},$$ (2.9)

where π̂(X_i) is obtained from the semiparametric model (2.1) and estimated using either of the two options discussed in Section 2.2. Algorithm 1 below depicts the detailed steps of obtaining the estimator τ̂ when the locally efficient estimator of π(X_i) is used (i.e., based on ℬ̂₁). The algorithm based on ℬ̂₂ is similar. The above procedure can be considered as an extension of the celebrated Horvitz–Thompson inverse probability weighted estimator (Horvitz and Thompson, 1952), which was originally developed for survey sampling.

The proposed estimator enjoys nice robustness properties. It is more flexible than the parametric propensity score model and hence is less prone to misspecification. It also does not propose any outcome regression models, which leads to computational simplicity. One can further pursue a double robust estimator by augmenting the estimator we propose. It could further improve estimation efficiency at the price of more complex modeling and/or computation. The estimator can accommodate a large number of covariates. Note that although nonparametric smoothing is used to estimate π(X_i), the smoothing is implemented with respect to ℬ^Tx. Under the dimension reduction assumption, it is often sufficient to consider a small d in practice; our estimator does not face the kind of curse of dimensionality that prevents the practical implementation of the estimators in Hahn (1998) and Hirano et al. (2003). Furthermore, we allow the covariate X to include both continuous and discrete or categorical variables without imposing any distributional assumptions on the covariate.

Algorithm 1.

Robust estimator of the average treatment effect

Input: {Yi, Ti, Xi}, i = 1, …, n, where Yi is the response of the ith subject, Ti is a binary treatment indicator (Ti = 1 for treatment and 0 for control), Xi is a vector of covariates.

Output: Estimator τ̂.

1: Use (2.6) to obtain a local efficient estimator of ℬ, denoted as ℬ̃ via, for example, choosing ${\eta }^{\ast }({ℬ}^{\mathrm{T}}\mathbf{x})={\mathbf{1}}_d^{\mathrm{T}}{ℬ}^{\mathrm{T}}\mathbf{x}$.

2: Perform nonparametric estimation of η(ℬTxi) and its first derivative η′(ℬTxi) by implementing (2.7). Write the resulting estimator as η̂(ℬTxi, ℬ) and η̂′(ℬTxi, ℬ).

3: Perform nonparametric estimation of E(Xi | ℬTxi). Write the resulting estimator as Ê(ℬTxi).

4: Plug η̂(·, ℬ), η̂′(·, ℬ) and Ê(·) in to Seff and solve the estimating equation $$\sum _{i=1}^n{\mathbf{S}}_{\text{eff}}(y_i,{\mathbf{x}}_i,ℬ,\hat{\eta },\hat{\mathit{\eta }}\prime ,\hat{E})=\mathbf{0},$$ using ℬ̃ as starting value, to obtain the efficient estimator ℬ̂.

5: Repeat Step 2 to obtain the final estimator of η(·) and form π̂(Xi) = 1 − 1/[1 + exp{η̂(ℬ̂Tx)}].

6: return $\hat{\tau }=n^{-1}{\sum }_{i=1}^n\{\frac{T_i{Y}_i}{\hat{\pi }(X_i)}-\frac{(1-T_i)Y_i}{1-\hat{\pi }(X_i)}\}$.

Remark 1

A technical detail involved in the nonparametric step of the above procedure is bandwidth selection. Through extensive numerical experimentation, we find that the ℬ estimation procedure is quite insensitive to the bandwidth, while inference precision could be affected by the bandwidth. Thus, guided by the theoretical properties (see Lemma 1, Lemma 2 and the regularity conditions C4), we recommend simply setting the bandwidth to be var(‖X_i‖₂)n^−1/5 throughout the estimation of ℬ, and use a leave-one-out cross-validation procedure to obtain the smoothing parameter h in estimating η after fixing ℬ̂. The same bandwidth then can be used in the inference procedure.

3. Asymptotic Properties

We now study the asymptotic properties of the estimators for the propensity score function for the robust estimator of the average treatment effect. The regularity conditions that are needed for the theoretical development are given in the online Supplementary Materials. Condition C1 consists of some standard requirements on the univariate and multivariate kernel functions. Condition C4 contains some mild requirement on the bandwidth. Conditions C2–C3 and C5–C8 contain the boundedness, smoothness and invertibility of several functions or matrices. All these conditions are very mild.

First, we study the asymptotic properties of ℬ̂₁, the nonparametric estimators of η, η′ and ℬ̂₂ discussed in Section 2.2. The results are summarized in Lemmas 1 and 2 below. The proofs are relegated to the online Supplementary Materials.

Lemma 1

Let ℬ̂₁ be the estimator defined in Section 2.2. Under the regularity conditions (C1)–(C6), ℬ̂₁ is locally efficient. As n → ∞,

$$\sqrt{n}\{\text{vecl}({\widehat{ℬ}}_1)-\text{vecl}(ℬ)\}\to N\{\mathbf{0},{\mathbf{A}}^{-1}\mathbf{G}{({\mathbf{A}}^{-1})}^{\mathrm{T}}\}$$

in distribution, where

$$\begin{gathered} \mathbf{A}=E\left\{\frac{\partial }{\partial {(\text{vecl }ℬ)}^{\mathrm{T}}}\text{vecl }\right(\{{\mathbf{X}}_i-E({\mathbf{X}}_i|{ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}[T_i-\frac{\text{exp}\{{\eta }^{\ast }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{{\eta }^{\ast }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}\left] \\ {\mathit{\eta }}^{\ast \prime }{({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}}\right)\}, \end{gathered}$$

$$\mathbf{G}=E\left\{\text{vecl }{(\{{\mathbf{X}}_i-E({\mathbf{X}}_i|{ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}[T_i-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)}^{\mathrm{T}})}^{\otimes 2}\right\}.$$

Here and throughout the paper, a^⊗2 ≡ aa^T.

Lemma 2

Assume the regularity conditions (C1)–(C4) and (C7)–(C8) hold. The local linear kernel estimators of η̂(ℬ^Tx) and η̂′(ℬ^Tx) defined in Section 2.2 satisfy

$$E\{\hat{\eta }({ℬ}^{\mathrm{T}}\mathbf{x})\}-\eta ({ℬ}^{\mathrm{T}}\mathbf{x})=O(h^m),E\{\hat{\mathit{\eta }}\prime ({ℬ}^{\mathrm{T}}\mathbf{x})\}-\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}\mathbf{x})=O(h^m),$$

$$\text{var}\{\hat{\eta }({ℬ}^{\mathrm{T}}\mathbf{x})\}=O_p\{{({\mathit{\text{nh}}}^d)}^{-1}\},\text{ var}\{\hat{\mathit{\eta }}\prime ({ℬ}^{\mathrm{T}}\mathbf{x})\}=O_p\{{({\mathit{\text{nh}}}^{d+2})}^{-1}\}.$$

Furthermore, ℬ̂₂ defined in Section 2.2 is efficient and satisfies

$$\sqrt{n}\{\text{vecl}({\widehat{ℬ}}_2)-\text{vecl}({ℬ}_2)\}\to N(\mathbf{0},{\mathbf{V}}^{-1})$$

in distribution as n → ∞, where

$$\begin{gathered} \mathbf{V}=E\{{\mathbf{S}}_{\text{eff}}{(T_i,{\mathbf{X}}_i,{ℬ}^{\mathrm{T}}{\mathbf{X}}_i,\eta ,\mathit{\eta }\prime ,E)}^{\otimes 2}\} \\ =E\left\{\text{vecl }{(\{{\mathbf{X}}_i-E({\mathbf{X}}_i|{ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}[T_i-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)}^{\mathrm{T}})}^{\otimes 2}\right\}. \end{gathered}$$

We provide the asymptotic property of the average treatment estimator τ̂ defined in Section 2.3, where the propensity is based on the dimension reduction estimation. We adopt two standard assumptions in causal inference, i.e., no unmeasured confounding and positivity.

Theorem 1

Under the regularity conditions (C1)–(C8), when n → ∞ the estimator π̂ from (2.9) based on ℬ̂₂ satisfies

$$\sqrt{n}(\hat{\tau }-\tau )\to N(0,{\sigma }^2)$$

in distribution, where ${\sigma }^2={\sigma }_{\text{eff}}^2+{\mathbf{a}}^{T}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}\mathbf{a}$, with

$${\sigma }_{\text{eff}}^2=\text{var }\left[\right\{\frac{T_i{Y}_i}{\pi ({\mathbf{X}}_i)}-\frac{(1-T_i)Y_i}{1-\pi ({\mathbf{X}}_i)}-\tau \}-\{\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\}\{T_i-\pi ({\mathbf{X}}_i)\}],$$

$$\mathbf{a}=E([Y_{i1}\{1-\pi ({\mathbf{X}}_i)\}+Y_i^{\ast }(0)\pi ({\mathbf{X}}_i)]\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\otimes {\mathbf{X}}_{\mathit{\text{iL}}}).$$

Remark 2

In the above asymptotic variance expression, ${\sigma }_{\text{eff}}^2$ is the optimal estimation variance (Hahn, 1998; Hirano et al., 2003) when the propensity is completely unknown and estimated purely nonparametrically. The additional term is the price we pay when we use a dimension reduction procedure to estimate π instead of doing it fully nonparametrically. In other words, our estimator is in general not efficient.

Regarding the theoretical efficiency bound in estimating a treatment effect, whether the propensity score is completely known or completely unknown, the efficiency bound in estimating the average treatment effect is the same as is given in Hahn (1998). In our context, the propensity score is partially known, in that we know it has the dimension reduction structure. Thus, the efficiency bound in estimating the treatment effect should be in between the completely known and completely unknown cases, and hence is also the same as that given in Hahn (1998).

Regarding achieving optimal efficiency, if inverse probability weighting method is used, the efficiency bound is only achieved if the propensity score is estimated nonparametrically, regardless of whether the true propensity score is known or not known (Hirano et al., 2003). Thus, in the setting where the propensity score is partially known, the efficiency bound is still only achieved if the estimator ignores the fact that the propensity score is partially known and is estimated nonparametrically. If instead the known knowledge about the propensity is used in the estimator, then the asymptotic efficiency is strictly larger than the efficiency bound.

However, estimating the propensity score nonparametrically is often infeasible in practice, especially when there are many covariates. Thus, a natural compromise is to adopt as flexible a model as possible, such as the dimension reduction model, to facilitate the propensity score estimation, which provides a trade-off between efficiency and practical applicability.

4. Monte Carlo studies

4.1 A simulation study on estimating the propensity score function

We first conduct a simulation study to investigate the performance of the flexible semiparametric estimators proposed in Section 2.2 for the propensity score.

We generate the vector of covariates X = (X₁, X₂, X₃, X₄, X₅, X₆)^T as follows. The covariates X₁ and X₂ are generated from independent standard normal distributions. We let X₃ = 0.2X₁+0.2(X₂+2.0)², X₄ = 0.1+0.2(X₁+X₂)+0.3(X₁+1)², and generate X₅ and X₆ independently from Bernoulli distribution with success probability exp(X₃)/{1 + exp(X₃)} and exp(X₄)/{1 + exp(X₄)}, respectively. In (2.2), we consider the following two different functional forms:

• Setting (1): η(ℬ^Tx) = sin(ℬ^Tx),

  where d = 1 and ℬ = (1.0, −1.2, 0.8, −1.7, −1.5, 0.5)^T.

• Setting (2): $\eta ({ℬ}^{\mathrm{T}}\mathbf{x})=\text{sin}({ℬ}_1^{\mathrm{T}}\mathbf{x})+\text{sin}({ℬ}_2^{\mathrm{T}}\mathbf{x})$, where d = 2,

  ℬ₁ = (1.0, 0.0, 1.2, 0.8, −1.2, 0.8)^T and ℬ₂ = (0.0, 1.0, 1.3, 0.7, 1.1, −0.7)^T.

For comparison purposes, we implement the oracle estimator and compare with our proposed semiparametric estimators ℬ̂₁ and ℬ̂₂. The oracle estimator assumes the functional form of η in (2.2) is known, although E(x| ℬ^Tx) is still estimated through the kernel regression in (2.4). Even though the oracle estimator is unrealistic, it provides a benchmark since it is the best performance one could expect to obtain. The local estimator ℬ̂₁ replaces η with a mis-specified function in the estimation procedure and estimates E(x| ℬ^Tx) nonparametrically. We posit the models η*(ℬ^Tx) = sin(ℬ^Tx + 0.8) − 0.3 and ${\eta }^{\ast }({ℬ}^{\mathrm{T}}\mathbf{x})=\text{sin}({ℬ}_1^{\mathrm{T}}\mathbf{x}+0.5)+\text{cos}({ℬ}_2^{\mathrm{T}}\mathbf{x}-0.5)$ for setting (1) and (2), respectively. The efficient estimator ℬ̂₂ does not use any posited model for η. Instead, we estimate E(x| ℬ^Tx), η and η′ through nonparametric regression, i.e. we followed the algorithm described in Section 2. The efficient estimator ℬ̂₂ is more computationally involved since it solves estimating equations to obtain the nonparametric components η and η′ at n locations inside the search for ℬ which does not have a closed form. To alleviate the computational burden, we performed the nonparametric estimation on a set of grid points and then performed a linear interpolation for d = 1 and a bilinear interpolation for d = 2 to obtain the values at each ℬ̂^(k)T x_i, where ℬ̂^(k) represents the kth iteration of the estimated ℬ̂ during solving the estimating equation in Step 4 of the algorithm in Section 2.

We repeat each experiment 1000 times with sample size n = 500 and 1000, respectively. The results are summarized in Table 1 for setting (1) and Table 2 for setting (2). From Table 1, we observe that the performance of both ℬ̂₁ and ℬ̂₂ is close to that of the oracle estimator. All estimators have very small bias for both sample sizes. The results in the table also provide the median of the estimated standard errors using the results in Lemma 1 and Lemma 2 and the empirical coverage probability of the 95% confidence intervals. These results indicate that the asymptotic normal approximation is accurate for the sample sizes. We observe similar performance in Table 2. The standard errors of the ℬ̂₁ and ℬ̂₂ become smaller as the sample size grows and the confidence interval coverage probabilities become closer to the nominal level.

Table 1.

The median and the sample standard errors (std) for various estimates, and the inference results, respectively, the average of the estimated standard deviation ( $\widehat{\text{std}}$) and the coverage of the estimated 95% confidence interval (CI) of the oracle estimator and the efficient estimator of ℬ in simulated example 1.

		ℬ2	ℬ3	ℬ4	ℬ5	ℬ6
	True	−1.2	0.8	−1.7	−1.5	0.5
Oracle n=500	median	−1.2000	0.7760	−1.6932	−1.5000	0.4964
	$\widehat{\text{std}}$	0.3044	0.3885	0.2019	0.3854	0.3117
	std	0.3406	0.4116	0.2300	0.3800	0.3670
	CI	0.9320	0.9230	0.9220	0.9610	0.9630
Local n=500	median	−1.0224	0.6503	−1.7137	−1.4016	0.4694
	$\widehat{\text{std}}$	0.2897	0.3431	0.2411	0.5357	0.3581
	std	0.3726	0.4450	0.3736	0.5194	0.4415
	CI	0.8680	0.8830	0.8660	0.9440	0.9300
Efficient n=500	median	−1.2155	0.8105	−1.6986	−1.5037	0.5070
	$\widehat{\text{std}}$	0.5674	0.7080	0.3036	0.5353	0.4337
	std	0.4735	0.4813	0.4129	0.5211	0.5074
	CI	0.9750	0.9860	0.8850	0.9540	0.9440
Oracle n=1000	median	−1.1879	0.8133	−1.6843	−1.5061	0.5000
	$\widehat{\text{std}}$	0.2106	0.2444	0.1435	0.2684	0.2097
	std	0.2405	0.2906	0.1506	0.2924	0.2234
	CI	0.9400	0.9310	0.9400	0.9510	0.9640
Local n=1000	median	−1.1802	0.7920	−1.6926	−1.3853	0.4710
	$\widehat{\text{std}}$	0.2369	0.2463	0.1419	0.2748	0.2196
	std	0.2720	0.2755	0.1874	0.2931	0.2698
	CI	0.9240	0.9430	0.9430	0.9210	0.9450
Efficient n=1000	median	−1.1936	0.8030	−1.6999	−1.4953	0.4966
	$\widehat{\text{std}}$	0.3963	0.3656	0.1712	0.3716	0.2364
	std	0.2561	0.2337	0.1724	0.3168	0.2165
	CI	0.9590	0.9720	0.9400	0.9320	0.9520

Table 2.

The median and the sample standard errors (std) for various estimates, and the inference results, respectively, the median of the estimated standard deviation ( $\widehat{\text{std}}$) and the coverage of the estimated 95% confidence interval (CI) of the oracle estimator and the efficient estimator, of ℬ in simulated example 2.

		ℬ13	ℬ14	ℬ15	ℬ16	ℬ23	ℬ24	ℬ25	ℬ26
	True	1.2	0.8	−1.2	0.8	1.3	0.7	1.1	−0.7
Oracle n=500	median	1.1874	0.8112	−1.1817	0.8318	1.3251	0.7152	1.0779	−0.7113
	$\widehat{\text{std}}$	0.2085	0.2057	0.3807	0.3622	0.2215	0.2251	0.3949	0.3704
	std	0.2703	0.2861	0.4262	0.4070	0.2873	0.2871	0.4411	0.4085
	CI	0.9380	0.9260	0.9570	0.9610	0.9290	0.9230	0.9690	0.9580
Local n=500	median	1.1939	0.7960	−1.1061	0.8663	1.3070	0.6214	1.2427	−0.7372
	$\widehat{\text{std}}$	0.3259	0.3271	0.5747	0.5526	0.4377	0.4376	0.8213	0.7297
	std	0.3440	0.3748	0.5479	0.5553	0.5138	0.4981	0.7111	0.6871
	CI	0.9270	0.9210	0.9610	0.9700	0.9110	0.9670	0.9490	0.9390
Efficient n=500	median	1.2292	0.8759	−1.2214	0.8315	1.3566	0.7002	1.0998	−0.7723
	$\widehat{\text{std}}$	0.7113	0.6808	0.6997	0.7027	0.6757	0.5555	0.6938	0.6622
	std	0.6104	0.4356	0.4836	0.4129	0.5529	0.5078	0.5195	0.4764
	CI	0.9200	0.9700	0.9770	0.9930	0.9540	0.9260	0.9630	0.9690
Oracle n=1000	median	1.1928	0.8154	−1.2070	0.8194	1.3053	0.7098	1.0877	−0.6931
	$\widehat{\text{std}}$	0.1460	0.1423	0.2620	0.2458	0.1437	0.1447	0.2629	0.2435
	std	0.1742	0.1710	0.2852	0.2700	0.1690	0.1647	0.2778	0.2591
	CI	0.9610	0.9480	0.9560	0.9610	0.9420	0.9540	0.9540	0.9650
Local n=1000	median	1.2028	0.7792	−1.0987	0.8109	1.3363	0.6012	1.3007	−0.7161
	$\widehat{\text{std}}$	0.2224	0.1970	0.3610	0.3381	0.2816	0.2865	0.6493	0.5385
	std	0.2551	0.2402	0.4031	0.3784	0.2226	0.3547	0.5111	0.4654
	CI	0.9450	0.9440	0.9470	0.9550	0.9490	0.9670	0.9620	0.9550
Efficient n=1000	median	1.2208	0.8606	−1.2053	0.8055	1.3637	0.7079	1.0827	−0.7109
	$\widehat{\text{std}}$	0.4734	0.4541	0.3217	0.3032	0.4532	0.3743	0.4572	0.3026
	std	0.4529	0.3142	0.3351	0.2927	0.4261	0.2521	0.3789	0.2716
	CI	0.9230	0.9730	0.9380	0.9450	0.9310	0.9780	0.9570	0.9660

4.2 Additional Simulations

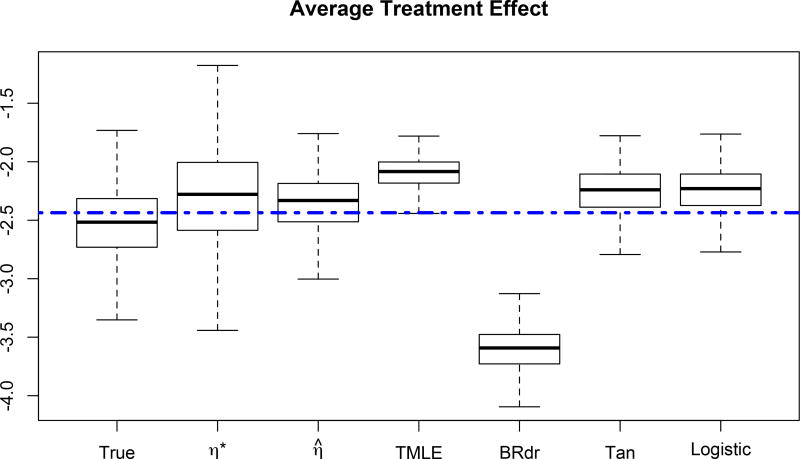
We further compare the performance of estimators for higher dimensional covariates where p = 10. In dimension reduction literature, p = 10 is considered to be rather high dimension. See Ma and Zhu (2012) for an investigation of covariate dimension issues. We independently generate X₁, X₂ from Uniform(0, 1), X₃ and X₇ from Normal(0, 0.5²), X₄ from Normal(0, 1). Then we form X₅ = X₁+X₂X₄, X₆ = −X₂+X₁X₃, X₈ = (X₄−X₂)X₁−X₇, X₉ = X₁X₇−X₃ and X₁₀ = X₂X₈−X₉. Further we explore the situation which the covariate dimension cannot be much reduced. We set the true propensity score function to be $\text{pr}(T=1|\mathbf{X})=1-{[1+\text{exp}\{0.1\sqrt{|X_5-X_4^2|}-\text{cos}(X_2{X}_8)-X_1\text{ exp}(X_6)-(X_3-X_9)X_7+\text{exp}(-X_{10})\}]}^{-1}$ and the true outcome function to be $Y=-T\text{ exp}(-X_{10})+\text{sin}(X_1+X_2)-X_3^2-\text{cos}(X_4)-X_5+X_7\text{log}(X_6^2)-\text{cos}(X_8)-T|X_9|$. We now examine the performance of various method in terms of estimating the average treatment effect. To implement our semiparametric estimator, we set d = 1, which is certainly not the case in the true model, and investigated the locally efficient estimation procedure, where we posit a mis-specified model η*(ℬ^Tx) = 0.4 cos(ℬ^Tx). This η*(·) restricts the function value to [−0.4, 0.4] while the true value is out of this range. We summarize the estimated average treatment effect in Figure (1), where “true” represents the result when the true propensity score is used, “η*” is the from the semiparametric estimator when “η*(·)” is used in the local estimation of ℬ, “η̂” is when the link function η is estimated as described in the efficient estimator procedure. We also compare our semiparametric approach with targeted maximum likelihood estimation (TMLE) (van der Laan and Rubin, 2006), the biased reduced double robust (BRdr) estimator proposed by Vermeulen and Vansteelandt (2015), Tan’s improved method (Tan) (Tan, 2006, 2010), and the standard method where the propensity score is estimated via logistic regression (Logistic). From the data generating process described above, it is clear that neither the propensity score model nor the outcome model is a generalized linear model. In implementing the TMLE method, rather than providing a model for either the propensity score or the outcome, we allow the TMLE algorithm to call the powerful SuperLearner to estimate these two quantities in a data adaptive fashion. Our implementation of BRdr estimator is also data adaptive, please see Vermeulen and Vansteelandt (2015) for detail. To estimate the propensity scores, a logistic regression model is assumed according to Tan’s description of the method. In contrast, Tan’s method uses generalized linar model (glm) in estimating the treatment outcome, hence the outcome model is misspecified since the true model here is not a glm. From Figure (1), although the TMLE method has the smallest variance, it is severely biased. BRdr, Tan and Logistic are also biased.

Figure 1.

Average treatment effect when p = 10, no dimension reduction is possible and the outcome is $Y=-T\text{ exp}(-X_{10})+\text{sin}(X_1+X_2)-X_3^2-\text{cos}(X_4)-X_5+X_7\text{log}(X_6^2)-\text{cos}(X_8)-T|X_9|$. Dimension reduction model is used by setting d = 1. The dashed line is the true average treatment effect.

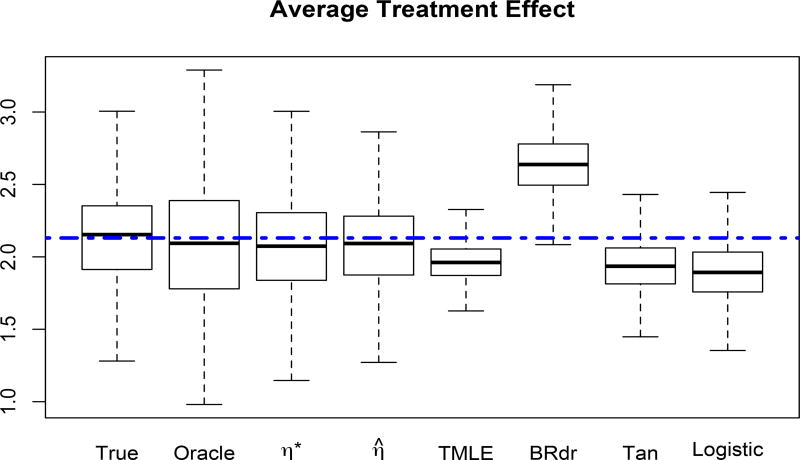
We further examine the situation when the covariate dimension indeed can be reduced to d = 1. Specifically, we set ℬ = (1.0, −0.4, 0.4, −0.2, −0.2, 0.4, 0.3, −0.3, −0.6, −0.6)^T and the true η function η(ℬ^Tx) = exp(0.5 ℬ^Tx) cos(ℬ^Tx) to generate the treatment T, where x is generated in the same way as before. We generate the outcome from the model $Y=\text{exp}(T+X_{10})+\text{sin}(X_1)X_2+X_3^2-\text{cos}(X_4-X_5)+\text{log}(X_6^2)X_7+X_8-{\mathit{\text{TX}}}_9$. We implemented the same estimators as before, and added an oracle estimator where the true η is used in estimating ℬ. From the results in Figure 2, we see that the semiparametric methods still outperform other estimators.

Figure 2.

Average treatment effect when p = 10, dimension reduction structure valid for d = 1 and the outcome is $Y=\text{exp}(T+X_{10})+\text{sin}(X_1)X_2+X_3^2-\text{cos}(X_4-X_5)+\text{log}(X_6^2)X_7+X_8-{\mathit{\text{TX}}}_9$. The dashed line is the true average treatment effect.

4.3 Comparison of several methods in data by Kang-Schafer

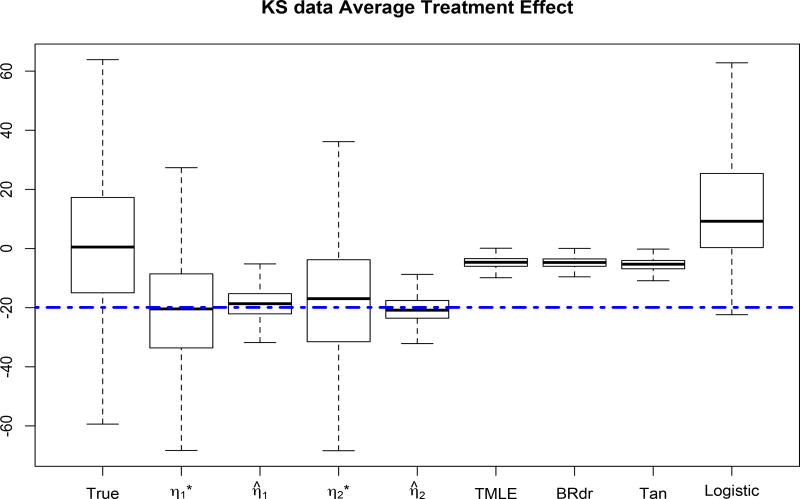
Finally, we examine the efficient and locally efficient estimator on the data generated following Kang and Schafer (2007). Specifically, we generated (Z₁, Z₂, Z₃, Z₄)^T from Normal(0, I₄) and then form x₁ = exp(z₁/2), x₂ = z₂/{1 + exp(z₁)}, x₃ = (z₁z₃/25 + 0.6)³, x₄ = (z₂ + z₄ + 20)²/400. The outcome model is generated as y = 210+27.4z₁+13.7z₂+13.7z₃+13.7z₄+ε, where ε ~ N(0, 1) and the true propensity function is π = expit(−z₁+0.5z₂−0.25z₃−0.1z₄). We use the observable data (Y_i, T_i, X_i) for i = 1, 2, ⋯, n to estimate the propensity score π̂_i for i = 1, 2, ⋯, n, then calculate the average treatment effect τ̂. The performance of the average treatment effect can be found in Figure (3), where “True” refers to the average treatment effect calculated from an inverse probability weighted method where the true weight is used. Both the locally efficient and efficient estimators yield reasonable results in comparison with other methods, regardless of whether d = 1 or d = 2.

Figure 3.

Average treatment effect on Kang and Schafer data. ${\eta }_1^{\ast }$ and η̂₁ are for d = 1. ${\eta }_2^{\ast }$ and η̂₂ are for d = 2. The dashed line is the true average treatment effect.

5. A real data example

We next apply the proposed semiparametric methods to analyze the average effect of maternal smoking on babies’ birth weight. The Low Birth Weight data constitute observations from mothers in Pennsylvania, USA and contain birth information on 4642 infants (Cattaneo, 2010). This dataset was originally used by Almond et al. (2005). The outcome of interest Y is infant birth weight measured in grams. The binary variable T denotes the mother’s smoking status (1 = smoking, 0 = nonsmoking). The covariates include mother’s age, mother’s marital status, an indicator variable for alcohol consumption during pregnancy, an indicator for whether there was a previous birth where the newborn died, mother’s education, father’s education, number of prenatal care visits, mother’s race, indicator of first born baby and months since last birth (monthslb).

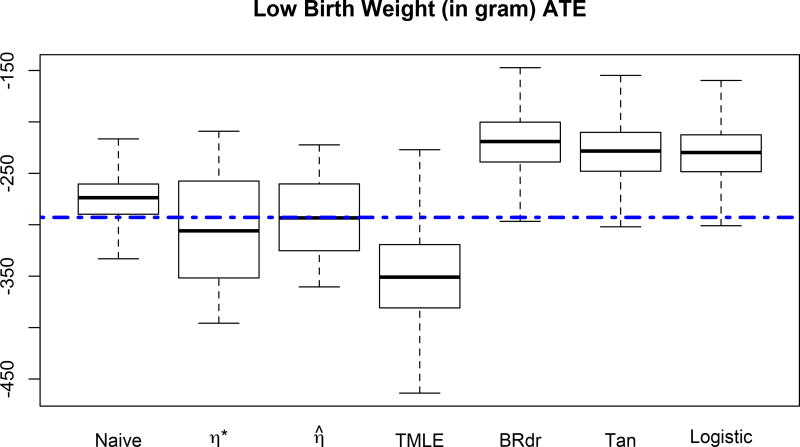
Based on data from the 4642 infants, the naive average weight difference of the two groups of babies belonging to smoking and non-smoking mothers yields −275.25 grams. Considering that this naive result is not necessarily a valid estimator of the causal result of smoking on birth weight, we next studied the proposed estimators. Specifically, we compare three estimators of average treatment effect discussed in the Section 4: “Logistic”, τ̂₁ and τ̂₂. The estimated propensity score functions are summarized in Table 3. The estimated average treatment difference corresponding to “Logistic”, τ̂₁ and τ̂₂ are −352.08, −295.77 and −306.32 grams, respectively. In addition, we compare the average causal effect with Tan’s improved method, TMLE and BRdr. The results indicate that maternal smoking has a negative impact on babies’ birth weight. The estimate average treatment differences are summarized in Table 4 along with the mean and standard deviation from 1000 bootstrap samples for each method. The bootstrap average treatment effect from the seven approaches can be found in Figure (4). Note that the estimator using propensity score estimated by logistic regression is substantially different from τ̂₁ and τ̂₂. This suggests logistic regression may not provide an adequate model for the propensity score function.

Table 3.

Low Birth Weight data Example.

	Naive			Local			Efficient
	Est	Std	P-value	Est	Std	P-value	Est	Std	P-value
(Intercept)	0.9848	0.2631	0.0002
age	1.0021	0.3607	0.0055
mmarried	−0.9480	0.1030	0.0000	−0.8020	0.2187	0.0002	−1.6922	0.3537	0.0000
alcohol	1.5886	0.1844	0.0000	1.5021	0.4156	0.0003	2.7014	0.4683	0.0000
deadkids	0.3893	0.0909	0.0000	0.4070	0.1232	0.0010	0.4980	0.1554	0.0014
medu	−0.0964	0.0190	0.0000	−0.0675	0.0281	0.0164	−0.2066	0.0571	0.0003
fedu	−0.0426	0.0118	0.0003	−0.0499	0.0182	0.0061	−0.1067	0.0369	0.0038
nprenatal	−0.0299	0.0111	0.0071	−0.0346	0.0141	0.0143	−0.0513	0.0221	0.0204
monthslb	0.0062	0.0015	0.0000	0.0062	0.0019	0.0012	0.0097	0.0028	0.0007
mrace	0.6888	0.1184	0.0000	0.7607	0.2093	0.0003	1.1446	0.2421	0.0000
fbaby	−0.2574	0.1059	0.0150	−0.2728	0.1181	0.0209	−0.3799	0.1881	0.0435

Table 4.

Average treatment difference in the Low Birth Weight data. Bootstrap mean (BS mean) and Bootstrap std (BS std). Bootstrap sample B = 1000.

	Naive	Efficient	Local	Logistic	TMLE	BRdr	Tan
Estimate	−275.25	−295.77	−306.32	−352.08	−219.96	−228.89	−230.57
BS mean	−275.10	−292.85	−304.69	−352.11	−219.69	−229.33	−231.34
BS std	21.36	38.62	54.50	46.78	29.50	29.34	27.66

Figure 4.

Bootstrap Average Treatment Effect. The dashed line is the mean of the average treatment effect calculated from the efficient estimation procedure.

6. Conclusion and discussions

In this paper, we propose a semiparametric approach to estimating the average treatment effect. The approach is less prone to propensity score model misspecification compared to the logistic regression based inverse probability weighted estimators, which have dominant roles in causal inference. A parametric propensity score model (e.g., logistic regression model) is certainly a lot more informative than a semiparametric model such as the dimension reduction model we propose, but it also bears a greater risk of being misspecified. If the parametric propensity score model is misspecified, then the resulting estimation of the average treatment effect is inconsistent. Furthermore, the semiparametric estimator does not rely on specification of the outcome regression model, and hence is attractive when a reliable outcome regression model is hard to obtain and/or compute, such as when studying treatment effects on complex diseases. We note that if one is willing to propose outcome models and carry more computation, then further extending our method to a doubly robust estimator could bring additional benefit such as efficiency gain.

It is of interest to investigate whether a dimension reduction propensity score model will always lead to more efficient treatment effect estimation than a parametric one, in the case that both models are correct. However, we find that it is not true in general. The relation can go either way, and it depends on the specific models. We summarize the results in Lemma 3 in the online Supplementary Materials.

Not able to find any definitive relation between the dimension reduction model and a general parametric model, we further investigate the situation of nested models. For the sake of comparing two models that are both correct, this certainly makes much sense. To this end, the model will be the same as in (2.2), except that now η is a known function. Unfortunately, even for this case, as shown in the online Supplementary Materials, there is no definitive relation we can claim. Thus, even when the parametric model is a submodel of the dimension reduction model, there is no definitive relation between the two estimators of the average treatment effect based on the two models. Our intuition is that not only the model makes a difference, but also the specific estimator used in the propensity score model has a role to play. The overall picture is unclear and is potentially very complex; much work is needed to fully understand these relations and can lead to interesting research results.

Finally, even though our initial intention is to overcome the potential issue of mis-specification of both the propensity score model and the outcome regression model through employing a more relaxed modeling strategy of the former and giving up modeling of the latter, and subsequently proposing inverse property weighting, double robust estimator can be used in combination with our method to further gain efficiency. As it is well known in the original form of the double robust estimator, in combination with the semiparametric propensity score model, when the treatment response is modeled correctly, the method will be more efficient than our method. If the treatment response is modeled incorrectly, depending on how “wrong” the model is, the method could be less efficient than our method. However, if the method of Tan (2010) is adopted, in combination with the semiparametric propensity score model, one can always obtain a more efficient estimator than our method, regardless of whether the treatment response is modeled correctly or not. Thus, to achieve improved efficiency, one can strive to propose a “good” model for the treatment response, and further perform additional computation to obtain the correlation adjustment required in Tan (2010).

Appendix

A.1 Derivation of the efficient score function

Taking derivative with respect to ℬ of the logarithm of the probability density function function, it is easy to verify that the score function with respect to ℬ is

$$\mathbf{S}{}_{ℬ}(T_i,{\mathbf{x}}_i,{ℬ}^{\mathrm{T}}{\mathbf{x}}_i,\eta ,\mathit{\eta }\prime )=\text{vecl }\left({\mathbf{x}}_i\right[T_i-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}}).$$

The efficient score is the residual after projecting the score vector with respect to ℬ onto the nuisance tangent space Λ (Tsiatis, 2006). The nuisance tangent space, denoted Λ, is the mean-squared closure of all nuisance tangent spaces of all parametric submodels. We can verify that

$$\mathrm{\Lambda }=\left(\right[T-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}\mathbf{X})\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}\mathbf{X})\}}]\mathbf{a}({ℬ}^{\mathrm{T}}\mathbf{X}):\forall \mathbf{a}({ℬ}^{\mathrm{T}}\mathbf{X})\in {ℛ}^{(p-d)\times d})$$

We then obtain its orthogonal complement

$$\begin{gathered} {\mathrm{\Lambda }}^{\perp }=[\mathbf{f}(Y,\mathbf{X}):\forall \mathbf{f}\in R^{(p-d)d}s.t.E\{\mathbf{f}(1,\mathbf{X})|T=1,{ℬ}^{\mathrm{T}}\mathbf{X}\}\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}\mathbf{X})\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}\mathbf{X})\}} \\ =F\{\mathbf{f}(0,\mathbf{X})|T=0,{ℬ}^{\mathrm{T}}\mathbf{X}\}]. \end{gathered}$$

We now write

$$\begin{gathered} \mathbf{S}{}_{ℬ}(T_i,{\mathbf{x}}_i,{ℬ}^{\mathrm{T}}{\mathbf{x}}_i,\eta ,\mathit{\eta }\prime ) \\ =\text{vecl }\left({\mathbf{x}}_i\right[T_i-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}}) \\ =\text{vecl }(E(\mathbf{X}|{ℬ}^{\mathrm{T}}\mathbf{x})[T_i-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}}) \\ +\text{vecl }(\mathbf{x}-E(\mathbf{X}|{ℬ}^{\mathrm{T}}\mathbf{x})[T_i-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}}). \end{gathered}$$

We can readily verify that

$$\text{vecl }(E(\mathbf{X}|{ℬ}^{\mathrm{T}}\mathbf{x})[T_i-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}})\in \mathrm{\Lambda }$$

and

$$\text{vecl }(\mathbf{x}-E(\mathbf{X}|{ℬ}^{\mathrm{T}}\mathbf{x})[T_i-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}})\in {\mathrm{\Lambda }}^{\perp },$$

hence this yields the desired result.

A.2 Proof of Theorem 1

From (2.9), we write

$$\begin{gathered} n^{1/2}(\hat{\tau }-\tau ) \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n\{\frac{Y_i{T}_i}{\pi ({\mathbf{X}}_i)}-\frac{Y_i(1-T_i)}{1-\pi ({\mathbf{X}}_i)}-\tau \}+\frac{1}{\sqrt{n}}\sum _{i=1}^n\{\frac{Y_i{T}_i}{\hat{\pi }({\mathbf{X}}_i)}-\frac{Y_i{T}_i}{\pi ({\mathbf{X}}_i)}-\frac{Y_i(1-T_i)}{1-\hat{\pi }({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{1-\pi ({\mathbf{X}}_i)}\} \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n\{\frac{Y_i{T}_i}{\pi ({\mathbf{X}}_i)}-\frac{Y_i(1-T_i)}{1-\pi ({\mathbf{X}}_i)}-\tau \} \\ +\frac{1}{\sqrt{n}}\sum _{i=1}^n[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}\{\pi ({\mathbf{X}}_i)-\hat{\pi }({\mathbf{X}}_i)\}-\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}\{\hat{\pi }({\mathbf{X}}_i)-\pi ({\mathbf{X}}_i)\}] \\ +O_p\left[\frac{1}{\sqrt{n}}\sum _{i=1}^n{\{\hat{\pi }({\mathbf{X}}_i)-\pi ({\mathbf{X}}_i)\}}^2\right] \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n\{\frac{Y_i{T}_i}{\pi ({\mathbf{X}}_i)}-\frac{Y_i(1-T_i)}{1-\pi ({\mathbf{X}}_i)}-\tau \}-\frac{1}{\sqrt{n}}\sum _{i=1}^n[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}]\{\hat{\pi }({\mathbf{X}}_i)-\pi ({\mathbf{X}}_i)\} \\ +O_p(n^{1/2}{h}^{2m}+n^{-1/2}{h}^{-d}). \end{gathered}$$

Now

$$\begin{gathered} \frac{1}{\sqrt{n}}\sum _{i=1}^n[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}]\{\hat{\pi }({\mathbf{X}}_i)-\pi ({\mathbf{X}}_i)\} \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}][\frac{\text{exp}\{\hat{\eta }({\widehat{ℬ}}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\hat{\eta }({\widehat{ℬ}}^{\mathrm{T}}{\mathbf{X}}_i)\}}-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}] \\ =T_1+T_2+T_2, \end{gathered}$$

where

$$T_1=\frac{1}{\sqrt{n}}\sum _{i=1}^n[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}][\frac{\text{exp}\{\eta ({\widehat{ℬ}}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\eta ({\widehat{ℬ}}^{\mathrm{T}}{\mathbf{X}}_i)\}}-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}],$$

$$T_2=\frac{1}{\sqrt{n}}\sum _{i=1}^n[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}][\frac{\text{exp}\{\hat{\eta }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\hat{\eta }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}],$$

$$\begin{gathered} T_3=\frac{1}{\sqrt{n}}\sum _{i=1}^n[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}][\frac{\text{exp}\{\hat{\eta }({\widehat{ℬ}}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\hat{\eta }({\widehat{ℬ}}^{\mathrm{T}}{\mathbf{X}}_i)\}}-\frac{\text{exp}\{\eta ({\widehat{ℬ}}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\eta ({\widehat{ℬ}}^{\mathrm{T}}{\mathbf{X}}_i)\}}] \\ -\frac{1}{\sqrt{n}}\sum _{i=1}^n[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}][\frac{\text{exp}\{\hat{\eta }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\hat{\eta }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}]. \end{gathered}$$

It is easy to see that

$$\begin{gathered} T_3 \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}]\frac{\partial }{\partial ℬ}[\frac{\text{exp}\{\hat{\eta }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\hat{\eta }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}]|}_{ℬ={ℬ}^{\ast }} \\ (\widehat{ℬ}-ℬ) \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n{[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}]{(\frac{\text{exp}\{\hat{\eta }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}\hat{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)}{{[1+\text{exp}\{\hat{\eta }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}]}^2} \\ -\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}\eta \prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)}{{[1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}]}^2})}^{\mathrm{T}}|}_{ℬ={ℬ}^{\ast }}\otimes {\mathbf{X}}_{\mathit{\text{iL}}}^{\mathrm{T}}\sqrt{n}\text{vecl}(\widehat{ℬ}-ℬ) \\ =o_p(1), \end{gathered}$$

where the last equality is because $\sqrt{n}\text{vecl}(\widehat{ℬ}-ℬ)=O_p(1)$ based on Lemma 2, and because of the consistency of η̂, η̂′ established in Lemma 2.

It is also easy to see that

$$\begin{gathered} T_1=\frac{1}{n}\sum _{i=1}^n[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}]\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}\eta \prime {({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)}^{\mathrm{T}}}{{[1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}]}^2}\otimes {\mathbf{X}}_{\mathit{\text{iL}}}^{\mathrm{T}}\sqrt{n}\text{vecl}(\widehat{ℬ}-ℬ)+o_p(1) \\ =E\left(\right[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}]\pi ({\mathbf{X}}_i)\{1-\pi ({\mathbf{X}}_i)\}\eta \prime {({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)}^{\mathrm{T}}\otimes {\mathbf{X}}_{\mathit{\text{iL}}}^{\mathrm{T}}) \\ \times \frac{1}{\sqrt{n}}\sum _{i=1}^{n}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}})}^{-1}{\mathbf{S}}_{\text{eff}}({\mathbf{X}}_i,T_i)+o_p(1) \\ =E([Y_i^{\ast }(1)\{1-\pi ({\mathbf{X}}_i)\}+Y_i^{\ast }(0)\pi ({\mathbf{X}}_i)]\eta \prime {({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)}^{\mathrm{T}}\otimes {\mathbf{X}}_{\mathit{\text{iL}}}^{\mathrm{T}})\frac{1}{\sqrt{n}}\sum _{i=1}^{n}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}})}^{-1}{\mathbf{S}}_{\text{eff}}({\mathbf{X}}_i,T_i) \\ +o_p(1) \\ ={\mathbf{a}}^{\mathrm{T}}\frac{1}{\sqrt{n}}\sum _{i=1}^{n}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}{\mathbf{S}}_{\text{eff}}({\mathbf{X}}_i,T_i)+o_p(1), \end{gathered}$$

where $Y_i^{\ast }(1)$ and $Y_i^{\ast }(0)$ are potential outcomes under treatment and no treatment respectively, and we used the independence assumption between potential outcomes and treatment in the second last equality.

We now analyze T₂. To this end, with the same notation as in the proof of Lemma 2 in the online supplement,

$$\begin{gathered} T_2=\frac{1}{\sqrt{n}}\sum _{i=1}^n[\frac{Y_i{T}_i}{{\pi }^2({\mathbf{X}}_i)}+\frac{Y_i(1-T_i)}{{\{1-\pi ({\mathbf{X}}_i)\}}^2}][\frac{\text{exp}\{\hat{\eta }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\hat{\eta }({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}}] \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n[\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}]\{\hat{H}({\mathbf{t}}_i)-H({\mathbf{t}}_i)\}. \end{gathered}$$

Here again we used the independence assumption in the last equality. We consider Ĥ (t_i) as the direct kernel estimator of H(t_i), i.e. $\hat{H}({\mathbf{t}}_i)=\{{\sum }_{j=1}^n{K}_h({\mathbf{t}}_j-{\mathbf{t}}_i)Y_j\}/\{{\sum }_{j=1}^n{K}_h({\mathbf{t}}_j-{\mathbf{t}}_i)\}$.

We further obtain

$$\begin{gathered} T_2=\frac{1}{n^{3/2}}\sum _{i=1}^n\sum _{j=1}^n\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\}\{\frac{K_h({\mathbf{t}}_j-{\mathbf{t}}_i)Y_j}{n^{-1}{\sum }_{k=1}^n{K}_h({\mathbf{t}}_k-{\mathbf{t}}_i)}-H({\mathbf{t}}_i)\} \\ =\frac{1}{n^{3/2}}\sum _{i=1}^n\sum _{j=1}^n\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\}[\frac{K_h({\mathbf{t}}_j-{\mathbf{t}}_i)Y_j}{f({\mathbf{t}}_i)}\{1-\frac{n^{-1}{\sum }_{k=1}^n{K}_h({\mathbf{t}}_k-{\mathbf{t}}_i)-f({\mathbf{t}}_i)}{f({\mathbf{t}}_i)}\} \\ -H({\mathbf{t}}_i)]+O_p(n^{1/2}{h}^{2m}+n^{-1/2}{h}^{-d}) \\ =\frac{1}{n^{3/2}}\sum _{i=1}^n\sum _{j=1}^n\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\}\{\frac{K_h({\mathbf{t}}_j-{\mathbf{t}}_i)Y_j}{f({\mathbf{t}}_i)}-H({\mathbf{t}}_i)\} \\ -\frac{1}{n^{3/2}}\sum _{i=1}^n\sum _{j=1}^n\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\}H({\mathbf{t}}_i)\left\{\frac{K_h({\mathbf{t}}_j-{\mathbf{t}}_i)-f({\mathbf{t}}_i)}{f({\mathbf{t}}_i)}\right\}+o_p(1) \\ =\frac{1}{n^{3/2}}\sum _{i=1}^n\sum _{j=1}^n\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\}[\frac{K_h({\mathbf{t}}_j-{\mathbf{t}}_i)}{f({\mathbf{t}}_i)}\{Y_j-H({\mathbf{t}}_i)\}]+o_p(1) \\ =n^{-1/2}\sum _{i=1}^n\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\}E[\frac{K_h({\mathbf{t}}_j-{\mathbf{t}}_i)}{f({\mathbf{t}}_i)}\{Y_j-H({\mathbf{t}}_i)\}|{\mathbf{t}}_i,T_i] \\ +n^{-1/2}\sum _{j=1}^{n}E(\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\}[\frac{K_h({\mathbf{t}}_j-{\mathbf{t}}_i)}{f({\mathbf{t}}_i)}\{Y_j-H({\mathbf{t}}_i)\}]|{\mathbf{t}}_j,Y_j) \\ -n^{1/2}E\left(\right\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\left\}\right[\frac{K_h({\mathbf{t}}_j-{\mathbf{t}}_i)}{f({\mathbf{t}}_i)}\{Y_j-H({\mathbf{t}}_i)\}\left]\right)+o_p(1) \\ =n^{-1/2}\sum _{j=1}^{n}E\left(\right\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\left\}\right[\frac{K_h({\mathbf{t}}_j-{\mathbf{t}}_i)}{f({\mathbf{t}}_i)}\{Y_j-H({\mathbf{t}}_i)\}]|{\mathbf{t}}_j,Y_j)+o_p(1) \\ =n^{-1/2}\sum _{i=1}^n\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\}\{T_i-H({\mathbf{t}}_i)\}+o_p(1) \\ =n^{-1/2}\sum _{i=1}^n\{\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\}\{T_i-\pi ({\mathbf{X}}_i)\}+o_p(1). \end{gathered}$$

Combining the above results regarding T₁, T₂ and T₃, we obtain

$$\begin{gathered} n^{1/2}(\hat{\tau }-\tau ) \\ =\frac{1}{\sqrt{n}}\sum _{i=1}^n\left[\right\{\frac{Y_i{T}_i}{\pi ({\mathbf{X}}_i)}-\frac{Y_i(1-T_i)}{1-\pi ({\mathbf{X}}_i)}-\tau \}-\{\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\}\{T_i-\pi ({\mathbf{X}}_i)\}] \\ -{\mathbf{a}}^{\mathrm{T}}\frac{1}{\sqrt{n}}\sum _{i=1}^{n}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}{\mathbf{S}}_{\text{eff}}({\mathbf{X}}_i,T_i)+o_p(1). \end{gathered}$$ (A.1)

Comparing with the results in Hirano et al. (2003), it is now clear that the component in (A.1) is the efficient influence function, while the remaining component in the expansion of n^1/2(τ̂ − τ) is the difference between the influence functions of our estimator and the efficient estimator, hence is orthogonal to the efficient influence function. In fact the orthogonality is also easily checked by direct calculation.

A.3 Statement of Lemma 3

Lemma 3

Assume the treatment allocation is independent of the potential treatment outcome given the covariates. Assume further that the probability of treatment is bounded away from 0 and 1. Assume a parametric model π(X_i, γ) with true parameter value γ₀. Then when n → ∞, the estimator τ̂ from (2.9) satisfies $\sqrt{n}(\hat{\tau }-\tau )\to N(0,{\sigma }^2)$, where ${\sigma }^2={\sigma }_{\text{eff}}^2+E(B_i^2)$ where ${\sigma }_{\text{eff}}^2$ is the same as in Theorem 1, and $B_i=\{\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\}\{T_i-\pi ({\mathbf{X}}_i)\}-E\left(\right[\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\left]\frac{\partial \pi ({\mathbf{X}}_i,\mathit{\gamma })}{\partial {\mathit{\gamma }}_0}\right)\varphi ({\mathbf{X}}_i,T_i)$, where ϕ(X_i, T_i) is the influence function of γ̂.

A.4 Comparing average treatment effect estimators for nested propensity models

When η is a known function, the efficient score function for ℬ is

$$\begin{gathered} {\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}(y_i,{\mathbf{x}}_i,{ℬ}^{\mathrm{T}}{\mathbf{x}}_i)=\text{vecl }\left({\mathbf{x}}_i\right[y_i-\frac{\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}{1+\text{exp}\{\eta ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\}}]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}}) \\ =\text{vecl }[{\mathbf{x}}_i\{y_i-\pi ({\mathbf{X}}_i)\}\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)}^{\mathrm{T}}] \\ =\{y_i-\pi ({\mathbf{X}}_i)\}\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{x}}_i)\otimes {\mathbf{x}}_{\mathit{\text{iL}}}, \end{gathered}$$

and the efficient influence function is $E{({\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}^{\mathrm{T}})}^{-1}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}$. Using the results in Lemma 3, we have

$$\begin{gathered} B_i=\{\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\}\{T_i-\pi ({\mathbf{X}}_i)\} \\ -E\left(\right[\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}]\pi ({\mathbf{X}}_i)\{1-\pi ({\mathbf{X}}_i)\}\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)}^{\mathrm{T}}\otimes {\mathbf{X}}_{\mathit{\text{iL}}}^{\mathrm{T}})E{({\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}^{\mathrm{T}})}^{-1}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}} \\ =\{\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\}\{T_i-\pi ({\mathbf{X}}_i)\} \\ -E([Y_i^{\ast }(1)\{1-\pi ({\mathbf{X}}_i)\}+Y_i^{\ast }(0)\pi ({\mathbf{X}}_i)]\mathit{\eta }\prime {({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)}^{\mathrm{T}}\otimes {\mathbf{X}}_{\mathit{\text{iL}}}^{\mathrm{T}})E{({\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}^{\mathrm{T}})}^{-1}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}} \\ =\{\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\}\{T_i-\pi ({\mathbf{X}}_i)\}-{\mathbf{a}}^{\mathrm{T}}E{({\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}^{\mathrm{T}})}^{-1}\{\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\otimes {\mathbf{X}}_{\mathit{\text{iL}}}\}\{T_i-\pi ({\mathbf{X}}_i)\}, \end{gathered}$$

Now let

$$\begin{gathered} C_i\equiv B_i+{\mathbf{a}}^{\mathrm{T}}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}{\mathbf{S}}_{\text{eff}}({\mathbf{X}}_i,T_i) \\ =\{\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\}\{T_i-\pi ({\mathbf{X}}_i)\}-{\mathbf{a}}^{\mathrm{T}}E{({\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}^{\mathrm{T}})}^{-1}\{\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\otimes {\mathbf{X}}_{\mathit{\text{iL}}}\}\{T_i-\pi ({\mathbf{X}}_i)\} \\ +{\mathbf{a}}^{\mathrm{T}}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}\{\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\otimes \{{\mathbf{X}}_{\mathit{\text{iL}}}-E({\mathbf{X}}_{\mathit{\text{iL}}}|{ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}\{T_i-\pi ({\mathbf{X}}_i)\} \\ =\left[\right\{\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\}-{\mathbf{a}}^{\mathrm{T}}E{({\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}^{\mathrm{T}})}^{-1}\{\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\otimes {\mathbf{X}}_{\mathit{\text{iL}}}\} \\ +{\mathbf{a}}^{\mathrm{T}}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}\{\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\otimes \{{\mathbf{X}}_{\mathit{\text{iL}}}-E({\mathbf{X}}_{\mathit{\text{iL}}}|{ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}]\{T_i-\pi ({\mathbf{X}}_i)\}. \end{gathered}$$

Now, following the previous notation to let t_i = ℬ^TX_i, and H(t_i) = π(X_i),

$$\begin{gathered} E\{C_i{\mathbf{a}}^{\mathrm{T}}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}{\mathbf{S}}_{\text{eff}}({\mathbf{X}}_i,T_i)\} \\ =E\left(\right[\{\frac{Y_i^{\ast }(1)}{\pi ({\mathbf{X}}_i)}+\frac{Y_i^{\ast }(0)}{1-\pi ({\mathbf{X}}_i)}\}-{\mathbf{a}}^{\mathrm{T}}E{({\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}^{\mathrm{T}})}^{-1}\{\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\otimes {\mathbf{X}}_{\mathit{\text{iL}}}\} \\ +{\mathbf{a}}^{\mathrm{T}}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}\{\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\otimes \{{\mathbf{X}}_{\mathit{\text{iL}}}-E({\mathbf{X}}_{\mathit{\text{iL}}}|{ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}]{\{T_i-\pi ({\mathbf{X}}_i)\}}^2 \\ \times {\mathbf{a}}^{\mathrm{T}}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}\{\mathit{\eta }\prime ({ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\otimes \{{\mathbf{X}}_{\mathit{\text{iL}}}-E({\mathbf{X}}_{\mathit{\text{iL}}}|{ℬ}^{\mathrm{T}}{\mathbf{X}}_i)\}) \\ =E\left(\right[\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\}-{\mathbf{a}}^{\mathrm{T}}E{({\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}^{\mathrm{T}})}^{-1}\{\mathit{\eta }\prime ({\mathbf{t}}_i)\otimes {\mathbf{X}}_{\mathit{\text{iL}}}\} \\ +{\mathbf{a}}^{\mathrm{T}}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}\mathit{\eta }\prime ({\mathbf{t}}_i)\otimes \{{\mathbf{X}}_{\mathit{\text{iL}}}-E({\mathbf{X}}_{\mathit{\text{iL}}}|{\mathbf{t}}_i)\}]H({\mathbf{t}}_i)\{1-H({\mathbf{t}}_i)\} \\ \times {\mathbf{a}}^{\mathrm{T}}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}\mathit{\eta }\prime ({\mathbf{t}}_i)\otimes \{{\mathbf{X}}_{\mathit{\text{iL}}}-E({\mathbf{X}}_{\mathit{\text{iL}}}|{\mathbf{t}}_i)\}) \\ =E\left(\right[\{\frac{Y_i^{\ast }(1)}{H({\mathbf{t}}_i)}+\frac{Y_i^{\ast }(0)}{1-H({\mathbf{t}}_i)}\}-{\mathbf{a}}^{\mathrm{T}}\{E{({\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}{\stackrel{\sim }{\mathbf{S}}}_{\text{eff}}^{\mathrm{T}})}^{-1}-E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}\}\mathit{\eta }\prime ({\mathbf{t}}_i)\otimes \{{\mathbf{X}}_{\mathit{\text{iL}}}-E({\mathbf{X}}_{\mathit{\text{iL}}}|{\mathbf{t}}_i)\}] \\ \times H({\mathbf{t}}_i)\{1-H({\mathbf{t}}_i)\}{\mathbf{a}}^{\mathrm{T}}E{({\mathbf{S}}_{\text{eff}}{\mathbf{S}}_{\text{eff}}^{\mathrm{T}})}^{-1}\mathit{\eta }\prime ({\mathbf{t}}_i)\otimes \{{\mathbf{X}}_{\mathit{\text{iL}}}-E({\mathbf{X}}_{\mathit{\text{iL}}}|{\mathbf{t}}_i)\}), \end{gathered}$$

which is not necessarily zero. Thus, there is no definitive relation we can say even when the parametric model is a submodel of the dimension reduction model.