Abstract
Under different environmental stresses, bacteria optimize the allocation of cellular resources through a variety of mechanisms. Recently, researchers have used phenomenological models to quantitatively characterize the allocation of bacterial protein resources under metabolic and translational limitations. Some stresses interfere with protein maturation, thereby enhancing the expression of chaperones and proteases. However, the reallocation of protein resources caused by such environmental stresses has not been modeled quantitatively. Here, we developed a dynamic model of coarse-grained protein resource fluxes based on a self-replicator that includes protein maturation and degradation. Through flux balance analysis, it produces a constrained optimization problem that can be solved analytically. Accordingly, we predicted protein allocation fractions as functions of growth rate under different limitations, which are basically in line with empirical data. We cultured Escherichia coli in media containing different concentrations of chloramphenicol, acetic acid, and paraquat and measured the functional relationship between the expression level of β-galactosidase driven by a constitutive promoter and the bacterial growth rate, respectively. Taking into account the possible mode of stress limitation on the fluxes, our model reproduces this experimentally measured relationship. In addition, our model is in good agreement with the experimental relationship between growth rate and proteome fraction of unnecessary protein in E. coli, considering the unoptimized upregulation of chaperones with useless protein overexpression. The results provide a more systematic view of bacterial stress adaptation that may help in designing for bioengineering or medical interventions.
Introduction
Bacteria have to adapt to various stresses such as nutrient limitation, heat/cold shock, acidic/alkaline stress, oxidative damage, and high osmolarity, so they have evolved a variety of corresponding response mechanisms to counteract or alleviate these stresses (1, 2, 3, 4). These response mechanisms can be well tuned to overcome different stresses to maintain the necessary cellular physiology. However, the production of response proteins is a burden to cell growth and reproduction. This leads to a balance of resource allocation between reproduction and maintenance/repair (5). Inducing bacterial stress responses under these conditions eventually leads to reallocation of cellular protein resources (6), with preference given to growth rate maximization (7). Molecular chaperones and proteases are important for protein quality control (8, 9). Many environmental factors such as temperature, pH, free radicals, hydrostatic pressure, and osmolarity can affect the processes of protein folding and assembly (2), and abnormalities in these factors can interfere with protein maturation. To resist this effect, bacteria will express more chaperones and proteases. This will lead to the proportion of chaperones and proteases in the proteome rising to a degree that cannot be ignored (10, 11, 12, 13, 14, 15). This study aims to quantitatively characterize bacterial protein allocation under nonlethal stress conditions, especially when the protein maturation process is impaired. We will highlight the role of chaperones and proteases in protein quality control and protein allocation.
The process of cell growth can be regarded as a process of “self-replication,” and the cell is a “self-replicator.” A simple self-replicator is that ribosomes translate themselves as well as other proteins (16, 17). In the past ∼10 years, many models based on such a self-replicator have been constructed that phenomenologically describe the dependence of some physiological factors (e.g., transcription/translation rate, mRNA/protein level, resource allocation) on bacterial growth rate (e.g., (16, 18, 19, 20, 21, 22, 23, 24, 25)). In these models, proteins are usually divided into different classes according to their function and trends under different growth conditions (e.g., (19, 20, 21, 22)). In the model of Scott et al. (19), proteins were divided into three classes: 1) R, ribosomal and other ribosome-affiliated proteins; 2) Q, proteins unaffected by translation inhibition; and 3) P, the remainder. They considered the self-replicator to be the case in which ribosomes synthesize either themselves or other proteins (Fig. 1 A). They found that the fraction of the total protein mass occupied by the Q sector is nearly 50% independent of the growth rate, whereas the fractions for the R and P sectors are linearly correlated with the growth rate under nutrient/translational limitations, which are the so-called “growth laws” (17, 19). The growth laws indicate that bacteria need to be assigned more resources to protein synthesis, i.e., more ribosomes are reallocated to produce themselves with either the increase of metabolic rate or the decrease of translation rate. Within their framework, we developed a coarse-grained protein resource flux balance model to elucidate how bacterial cells allocate protein resources, especially when environmental stress is affecting protein maturation.
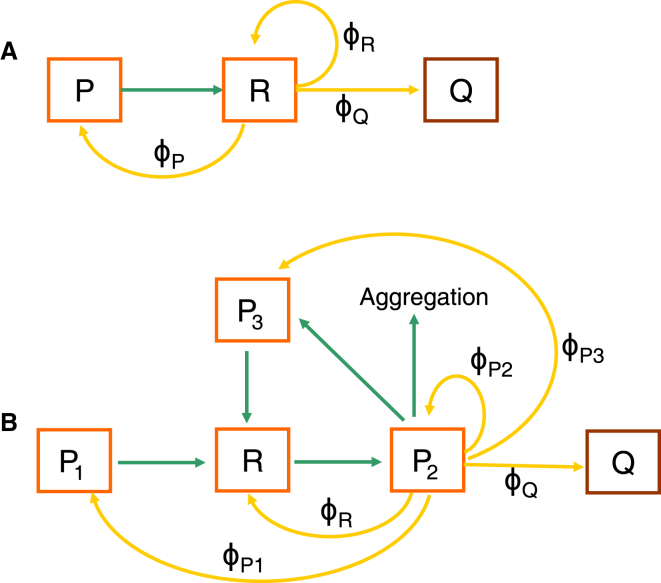
Figure 1.
Schematic illustration of protein self-replicator. (A) An illustration for the model of Scott et al. (19) is shown. The proteome is partitioned into Q (housekeeping and growth rate-independent proteins), R (ribosome-affiliated proteins) and P (proteins belonging to neither Q nor R). R-class proteins are partly used for synthesizing themselves and partly for other proteins. The green line denotes the resource flows from nutrients to AAs by P. Yellow lines indicate proteins that are synthesized by R and allocated to R, P, and Q with fractions ϕR, ϕP, and ϕQ. (B) An illustration of our model is shown. The proteome is partitioned into Q, R, P1 (P-class proteins required by AA supply), P2 (chaperones and other proteins catalyzing protein maturation), and P3 (proteases and other proteins promoting protein degradation). P2-class proteins are partly used for maturating themselves and partly for others. Green lines indicate AA supply (from P1 to R), polypeptide translation (from R to P2), aberrant protein formation (from P2 to P3 or protein aggregation), and aberrant protein degradation into AAs (from P3 to R), respectively. Yellow lines denote proteins that are matured by P2 and allocated to Q, R, P1, P2, and P3 with fractions ϕQ, ϕR, ϕP1, ϕP2, and ϕP3. ϕX (∈ {Q, R, P, P1, P2, P3}) denotes the fraction of total native proteins devoted to X-class proteins.
To construct our model, we considered a more complete self-replicator, which includes not only nutrient uptake, metabolism, and translation but also protein maturation, degradation, and aggregation (Fig. 1 B). Different environmental pressures may have different effects on these processes, resulting in the redistribution of protein resources in these processes. Therefore, this extended self-replication model can describe how different allocations of protein resources under environmental stress lead to different steady-state growth rates. A diagram of coarse-grained protein resource fluxes can describe the advanced self-replicator (Fig. 2), in which the flux rates can be represented as functions of the concentrations or proteome fractions of protein classes. Flux balance analysis (FBA) is widely used in studying bacterial metabolism (26), and recently it has been extended to describe resource allocation between cellular processes beyond metabolism (7, 21, 22, 27). The extended self-replication model of protein resource fluxes may give a series of steady-state growth rates under a fixed condition. Because bacteria with higher growth rates are more likely to survive because of higher evolutionary adaptability in common nonlethal (e.g., weakly acidic or oxidative) environments. Therefore, we used the growth rate as the objective function of optimization in the analysis. By FBA, we derived the optimal protein allocation to achieve the maximal growth rate.
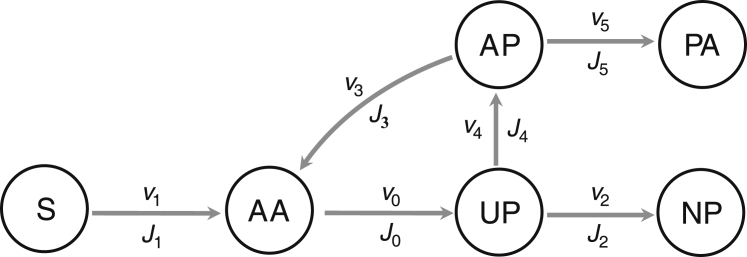
Figure 2.
Schematic illustration of protein resource fluxes in bacteria. AAs inside the cell come from the uptake and metabolism of the nutritional substrate (S) via P1 (flagella, transporters, metabolic enzymes, and their affiliated proteins) or from the degradation of aberrant proteins via P3 (proteases and their affiliated proteins). The former is defined as AA supply flux (v1, J1) and the latter as the degradation flux (v3, J3). AAs are translated into polypeptides via R (ribosome-affiliated proteins), defined as translation flux (v0, J0). Unfolded polypeptides (UP) mature as native proteins via P2 (chaperones and other proteins promoting protein maturation) or mistakenly mature as aberrant proteins (AP) because of the lack of P2. The former is defined as normal maturation flux (v2, J2) and the latter as aberrant maturation flux (v4, J4). APs can also form protein aggregates spontaneously, defined as the aggregation flux (v5, J5). Here, vi denotes the total flux rate and Ji (, where Mc denotes total cell mass and i ∈ {0, 1, 2, 3, 4, 5}) denotes flux rate per unit cell mass. Each flux can be represented as a function of the concentration or proteome fraction of related proteins.
Our model predicted how the optimal protein allocation changes with the growth rate as a flux capacity (flux rate constant) is reduced, based on which two general characteristics of the bacterial stress adaptation can be drawn. With reasonably selected parameters, the proteome fractions of chaperone-like proteins and protease-like proteins under nutrient and translation limitations agree well with the genome-wide proteomic data (22, 28, 29, 30). These two fractions are close to 5 and 0%, respectively, basically regardless of growth rate. Furthermore, we predicted a significant increase in the mass fraction of chaperone-like proteins occupying the proteome under the protein maturation stress, which is roughly in line with the transcriptomic/proteomic data (11, 30, 31, 32, 33, 34). To test the model, we experimentally measured the changes in the expression level of lacZ driven by a constitutive promoter (PLtetO1 (35)) with the growth rate under translational, acidic, and oxidative stress, respectively. With reasonable consideration of the way in which the stress conditions affect flux capacities, our model fits well with the experimental data. The results under the acidic and oxidative stresses imply a mixed limitation on both flux capacities of amino acid supply and protein maturation. Inspired by the observed upregulation of chaperone proteins in response to overexpression of unnecessary proteins (e.g., (36, 37)), we hypothesized that a part of the chaperones are not optimized, and their proteome fraction increases with the proteome fraction of unnecessary protein. Combining this hypothesis with our model, we made a prediction of the relationship between growth rate and proteome fraction of useless proteins, which is in good agreement with the experimental data (36, 38). Importantly, we predicted that the fraction of overexpressed useless proteins at zero-growth rate is at ∼30%, which is also consistent with empirical data (36, 38). Finally, we discussed the common molecular mechanisms that allow protein reallocation and the possible effect of the toxicity of protein aggregates on protein allocation.
Materials and Methods
In experiments, we used Escherichia coli strain MGIBKYPLtetO1-lacZ from Terence Hwa’s lab (19). This strain was constructed from wild-type E. coli K12 MG1655 by deleting lacI, lacY, galK, and ryhB and replacing PlacZY|A with PLtetO1 (19). We cultivated the bacteria with four different M9 media: M9 + (0.5% w/v) Gluc, M9 + (0.5% w/v) Glyc, M9 + (0.5% w/v) Gluc + (0.2% w/v) cAA, and M9 + (0.5% v/v) Glyc + (0.2% w/v) cAA. Here, M9 is a minimal medium containing 1× M9 salts (1 L: 17.096 g Na2HPO4.12H2O, 3 g KH2PO4, 0.5 g NaCl, and 1 g NH4Cl, dissolved in double distilled water (ddH2O)), 2 mM MgSO4, and 0.1 mM CaCl2 (39), and cAA, Gluc, and Glyc denote casein acids hydrolysate, glucose, and glycerol, respectively. Experimental cultures were grown in a 48-well plate (Corning Costar; Corning, Corning, NY) shaken at 180 rotations per minute and 37°C. The optical density at 600 nm (OD600) was measured at more than three time points in the exponential phase, from which we derived the growth rate. In the β-galactosidase assay, culture quantification, culture permeabilization, and β-galactosidase reaction were all performed in 96-well plates. We used o-nitrophenyl-β-D-galactopyranoside as the substrate of β-galactosidase. The product o-nitrophenol was monitored by measuring the optical density at 405 nm (OD405). Both OD600 and OD405 were measured with a Wallac Victor3 1420 multilabel counter (PerkinElmer Life Sciences, Waltham, MA). Each measurement for OD600 was repeated three times. Our experimental procedure was adapted from the literature (19, 40, 41). Details of the procedure and data processing methods are presented in the Supporting Materials and Methods.
Results
A flux-balance-optimization model for protein allocation
Bacteria produce proteins from raw nutrients through several major systems composed mainly of proteins (1, 2, 4) (see Supporting Materials and Methods; Fig. S1). These systems include the chemotaxis and nutrient uptake system (flagella and transporters), catabolic system, biosynthetic system, translation system (ribosomes and accessory proteins), protein maturation system (molecular chaperones and other protein factors benefiting protein maturation), and aberrant protein degradation system (proteases and other affiliated proteins). The newly produced proteins are in turn distributed to those systems described above for subsequent protein production. The production and allocation of proteins constitute a self-replicator (Fig. 1). We divide native proteins into five classes (sectors) by extending the partition of Scott et al. (19), redefining Q-class proteins as proteins that are not affected by the stresses considered in this study (with proteome fraction ϕQ) and subdividing P-class proteins into three smaller classes: P1 includes proteins belonging to the chemotaxis/nutrient uptake/metabolic (amino acid supply) system (with proteome fraction ϕP1), P2 includes proteins belonging to the protein maturation system (with proteome fraction ϕP2), and P3 includes proteins belonging to the protein degradation system (with proteome fraction ϕP3). We still use R to indicate ribosomal and ribosome-affiliated proteins (with proteome fraction ϕR). Now the normalization constraint becomes (ϕQ, ϕR, ϕP1, ϕP2, ϕP3 ≥ 0).
Without lethal stress, bacterial cells can replicate themselves continuously, i.e., their components (such as the proteome) make themselves by utilizing extracellular nutrients. Fig. 2 shows the protein resource conversion flows in our extended self-replication model. There are six different forms of protein resources: nutritional substrate (S), amino acid (AA), unfolded nascent polypeptide (UP), normally matured native protein (NP), abnormally matured aberrant protein (AP), and protein aggregate (PA), corresponding to six different fluxes between them: AA supply flux (v1, J1), translation flux (v0, J0), UP normal maturation flux (v2, J2), UP aberrant maturation flux (v4, J4), AP degradation flux (v3, J3), and AP aggregation flux (v5, J5). In general, the growth rate is the optimization objective for the bacteria at the steady-state. In our model, it is equivalent to maximizing the UP normal maturation flux (J2) (see below). Here, we aim to find the optimal allocation of proteome through FBA using growth rate as the objective function.
The evolution of the amount of various protein resources over time can be represented by
| (1) |
where the mass vector M = (MAA, MUP, MAP, MPA, MNP)T, the conversion flux rate vector v = (v0, v1, v2, v3, v4, v5)T, and the stoichiometric matrix
| (2) |
When bacteria grow in the steady-state exponential phase, it results in dM/dt = μM, where μ indicates the growth rate. Together with Eq. 1, Sv = μM is given. We denote the total mass of cells as Mc. Then we denote the flux rate per cell mass (hereinafter referred to as “flux” for convenience) as Ji, i.e., Ji = vi/Mc and denote the fraction of cell mass devoted to component X (hereinafter referred to as the concentration of component X) as ψX, i.e., ψX = MX/Mc where i ∈ {0,1,2,3,4,5} and X ∈ {all forms of protein resources}. Furthermore, the flux vector J and the concentration vector satisfy
| (3) |
Note that the cell mass in this study excludes the mass of protein aggregates. Protein aggregates as wastes of protein resource inside the cell do not contribute to the reactions behind the fluxes that determine cell growth. The concentration of protein resource X (ψX) here actually reflects the mass ratio of X to all the usable substances in the cells (including normal proteins, RNA, DNA, etc.) Moreover, protein aggregates can occupy isolated spaces, for example, in the form of insoluble inclusion bodies (42). Excluding the mass of protein aggregates from the cell mass is equivalent to excluding their occupied volume from the total cell volume under the consideration of constant density (43). It is reasonable to refer to the concentration of component X in the remaining (connected) space.
Next, we express each flux Ji (i ∈ {0,1,2,3,4,5}) as a function of the level or relative level of each class (sector) proteins. Based on empirical evidence (19, 21, 22, 44), AA supply flux can be viewed as a linear function of the concentration of P1-class proteins, i.e.,
| (4) |
where k1 represents the bacterial “AA supply capacity,” which reflects the nutrient quality. Notice that here we set the vertical intercept to zero, which is exactly what Scott et al. (19) did. The basal expression levels (independent of the growth rate) of the enzymes in AA supply process are considered as a part of the Q sector. An intuitive understanding of this linear relationship is that a key enzyme (or an entire pathway) is the rate-limiting factor that ultimately determines the rate of AA production as a bottleneck (19). The translation flux (J0) is linearly dependent on the number of active ribosomes and is therefore proportional to the concentration of active R-class proteins, i.e.,
| (5) |
where k0 indicates “translational capacity” and ψ0 is the mass fraction of inactive R-class proteins (19, 22). In protein folding, the AA sequence determines the main folding pathway, whereas molecular chaperones and other affiliated proteins (P2-class proteins) play an auxiliary role by assisting the UPs to fold correctly or rescuing misfolded polypeptides back to a normal intermediate state (9, 45). P2-class proteins are hereinafter referred to simply as “chaperones.” In bacterial cells, translation usually consumes more protein resources than maturation. To use resources more efficiently, the strategy adopted by the bacteria is to make as many as possible UPs into functional proteins. This means that the maturation process should be exceedingly efficient, which requires that chaperones are expressed enough to fully fulfill the auxiliary role. Therefore, the rate of protein maturation (either normally or aberrantly) should be limited by the level of UPs, and then we simply assume that both the UP normal maturation flux (J2) and UP aberrant maturation flux (J4) linearly depend on the concentration of UPs, i.e., J2 ∝ ψUP and J4 ∝ ψUP. The mechanism of chaperones influencing protein maturation is complicated. In general, the more chaperones are able to help, the more UPs fold into native structures and will saturate when the number of chaperones reaches a certain value. To avoid the complex calculations but capture the saturation effect of chaperones, we assume that J2 and J4 are the Michaelis-Menten functions of the concentration of all chaperones (ψP2), i.e., J2 ∝ ψP2/(Km + ψP2) and J4 ∝ Km/(Km + ψP2). Here, Km is equilibrium constant, which represents the degree of difficulty in folding an UP into an NP. Based on the above description, we finally write J2 and J4 as
| (6) |
and
| (7) |
where k2 and k4 are rate constants for successful and aberrant maturations, respectively. Notice that k2, k4, and Km can be integrated as one parameter (see ϕm as below) given the constraints on J2 and J4. Chaperones help bacteria to fold as many UPs as possible into functional proteins, but too many chaperones are a burden on the growth of bacteria. To get the maximal growth rate, the bacteria need an appropriate ψP2, i.e., ψP2 should be chosen to be small enough to make ψP2/(Km + ψP2) as close to one as possible. In the absence of maturation stress, Km is approximately equal to zero, so even a small ψP2 is sufficient to make , and thus J2 ≈ J0 and J4 ≈ 0. Under the stress that affects protein maturation (such as thermal, acidic or oxidative stress), UPs are harder to fold into NPs without the help of chaperones and Km will be raised. To meet the requirements of bacterial growth, bacteria need to allocate more resources to molecular chaperones, which means ψP2 will increase. The difference in the means of limitation between AA supply flux and protein maturation flux indicate that proteins are produced in a way of “strict flow in and loose flow out.” Similar to the AA supply process, protein degradation can also be regarded as rate limiting at some protease concentrations, and then AP degradation flux (J3) is proportional to the concentration of proteases and other proteins promoting the degradation of abnormally folding polypeptides (P3-sector proteins), i.e.,
| (8) |
where k3 denotes “AP degradation capacity.” P3-sector proteins are hereinafter referred to simply as “proteases.” If we can ensure that J3 turns off when the growth medium is not too poor and there is no strict limitation on the AA supply flux, our main results are not sensitive to using different relations between J3 and ψP3. Protein aggregation is more likely a spontaneous (enzyme-free) process, so the aggregation flux (J5) can be expressed as a function of the concentration of aberrant proteins (ψAP) independent of the concentration of each sector protein. The significance of this flux to our model is reflected in the constraint
| (9) |
AAs, UPs, and APs are intermediate products in the fluxes system. The bacteria need to utilize protein resources economically. AA pools are well controlled by negative and positive feedback loops in the balance of AA supply flux and translation flux (19). The amount of free AAs just needs to meet the requirement of ongoing translation, so the free AAs should not occupy a high proportion of cell mass. This is supported by experimental evidence. Free building blocks (AAs, deoxynucleoside triphosphates, ribonucleoside triphosphates, etc.) for macromolecules occupy 2.5% of the dry mass for E. coli B/r strain with a doubling time of 40 min (1), which indicates that the proportion of AAs should be less than 2.5%. With the help of chaperones and folding catalysts, the folding time of UPs should mostly be shorter than one bacterial generation. However, the majority of mature proteins have half-lives of 5–20 h over several generations (8). Therefore, the fraction of cell mass for UPs should be quite small relative to that for mature proteins. APs can interfere with normal physiological processes, so the bacteria should aggregate or degrade them quickly once they are formed (see the Discussion and the Supporting Materials and Methods). Therefore, we neglect the terms μψAA, μψUP, and μψAP in Eq. 3. We substitute JiψNP for Ji (i ∈ {0,1,2,3,4,5}) in the above equations and define ϕX as the fraction of the proteome mass that the X mass occupies (referred to simply as the proteome or mass fraction of X hereinafter), i.e., ϕX = ψX/ψNP, where X is one form of protein resource. Furthermore, with Eq. 3, we rewrite Eqs. 4, 5, 6, 7, and 8 as
| (10) |
| (11) |
| (12) |
| (13) |
and
| (14) |
where ϕm = k4Km/(k2ψNP), reflecting the frustration level of protein maturation. Notice that constraints J0 = J2 + J4 and μ = J2 have been used here. We assume that the mass fraction of normal proteins in the cell mass (ψNP) does not change with the growth rate much under the stresses considered in this study. Thus, the change of ϕm due to the (small) change of ψNP can be neglected. Notice that cell mass excludes the mass of protein aggregates in our definition (see above). Then the change in the mass of protein aggregates even under the maturation stress will not affect ψNP much. The below results are consistent with this assumption (see Fig. S2). Based on this assumption, ϕm is basically independent of k0 and k1. We use 1/ϕm to indicate “UP maturation capacity.” The corresponding constraints are
| (15) |
| (16) |
| (17) |
and
| (18) |
In stress conditions, bacteria redistribute protein resources for the fastest growth rate, and the problem of the allocation of protein resources in the stressful environment becomes a constrained optimization problem in which the growth rate is the objective function. Here, we need to derive the optimal protein allocation by maximizing the growth rate (μ = μmax). This optimization problem can be analytically solved by the method of dimensionality reduction (see the procedure and the optimal solution in the Supporting Materials and Methods).
To analyze a particular stress with our model, we need to know exactly how the stress suppresses the fluxes. The main assumptions and parameters for the specific stresses studied here are listed in Table S1. Some of the parameters are fixed based on literature (19): ϕ∗ = 0.55, ϕ0 = 0.066, k0 = 6 h−1 (no translation limitation), and k1 = 1.3 h−1 (for M9 + Glyc), 2 h−1 (for M9 + Gluc and M63 + Gluc), 2.6 h−1 (for M9 + cAA + Glyc), 3.34 h−1 (for M9 + cAA + Gluc and M63 + cAA + gluc), or 20 h−1 (for Neidhardt’s rich defined media + Gluc) (no AA supply limitation). ϕm and k3 are fixed to reasonably agree with experimental data: ϕm = 0.0061 and k3 = 0.3h−1. Additional parameters for fitting experimental data are given in the figure captions.
The model needs to be further clarified in the following aspects. First, there are two different types of protein degradation: housekeeping and regulatory (8, 46). The degradation of APs in our model mainly refers to the housekeeping type. Second, growth-rate-dependent proteins may be regulated both in number and in activity. In our model, inactive proteins are regarded as non-native (aberrant); in other words, all NPs are considered as active. So those proteins that regulate protein activity also belong to the P2 class (chaperone-like proteins). Third, “growth-rate independent” in this study refers to “not affected by the stresses under consideration.” Fourth, under intense (lethal) stress, some parameters (such as mass fraction of housekeeping proteins ϕQ) may significantly depend on growth rate, and even DNA may be damaged to cause SOS response (47). Here, we only consider weak (nonlethal) stress. Fifth, recently, the rate of translational elongation has been found to depend on the growth rate under changes in nutrient composition (20, 25). We considered the dependence of translational elongation rate on growth rate in our model, and the results did not change much (see Fig. S5).
The model predicts optimal allocation of proteins under the limitation on flux capacity
The rigorous analytical solution to the above optimization problem shows how protein allocation and growth rate depend on flux capacities (see Supporting Materials and Methods). Environmental stress suppresses a flux by reducing its capacity, and the stronger the stress, the smaller the flux capacity. Using this relationship, we can derive from the analytic solution the effect of the stress intensity on protein resource allocation and growth rate. Table 1 summarizes how the maximal growth rate (μmax) and the optimal mass fraction of each class of proteins (,,,) change as one of the flux capacities (k0, k1, 1/ϕm, and k3) decreases. It shows that the flux suppressed by the stress will occupy a higher fraction of the protein, whereas some of other fluxes will occupy lower fractions accordingly. For example, the mass fraction of ribosome-affiliated proteins increases with decreasing translation capacity k0 but decreases with decreasing AA supply capacity k1, whereas the mass fraction of AA-supply-required proteins changes inversely. In addition, the growth rate is always declining as the flux capacity is limited. With only one exception—when AA supply capacity is higher than AP degradation capacity (k1 > k3)—the limitation on AP degradation capacity (k3) does not affect the growth rate.
Table 1.
The Model Predicts the Changes of the Optimal Allocation Fractions , , , and and Maximized Growth Rate μmax with the Flux Capacities k0, k1, k3, and 1/ϕm
, and – indicate increasing, decreasing and constant, respectively.
Keeping k1 > k3.
Little stress on protein maturation, namely, ϕm ∼ 0.
If k1 > k0k3/(k3 + 2k0), take “”; if k1 < k0k3/(k3 + 2k0), take “.”
According to the analytic solution, the optimal allocation fractions of the proteome can be expressed as explicit functions of the maximized growth rate μmax (see the Supporting Materials and Methods). For example, under the condition of k1 > k3, and can be formalized as linear functions of μmax no matter whether k1 or k0 is reduced (AA supply or translation limitation), i.e.,
| (19) |
| (20) |
and
| (21) |
| (22) |
where A = (ϕm + ϕ∗∗)1/2, and ϕ∗∗ = ϕ∗ − ϕ0. If ϕm = 0 (i.e., no frustration in protein maturation), we have A = B = ϕ∗∗1/2, and then the linear functions shown by Eqs. 19, 20, 21, and 22 degenerate into the Scott-Hwa growth laws (17, 19): . Beyond the Scott-Hwa growth laws , our model gives that both mass fractions of chaperones and proteases ( and ) are independent of growth rate (the former is a function of ϕm, and the latter is zero) when k1 or k0 decreases under the condition k1 > k3. Moreover, our model predicts a linear correlation between the mass fraction of each class of proteins and the growth rate under the protein maturation stress (see Supporting Materials and Methods; Figs. 3 and S3).
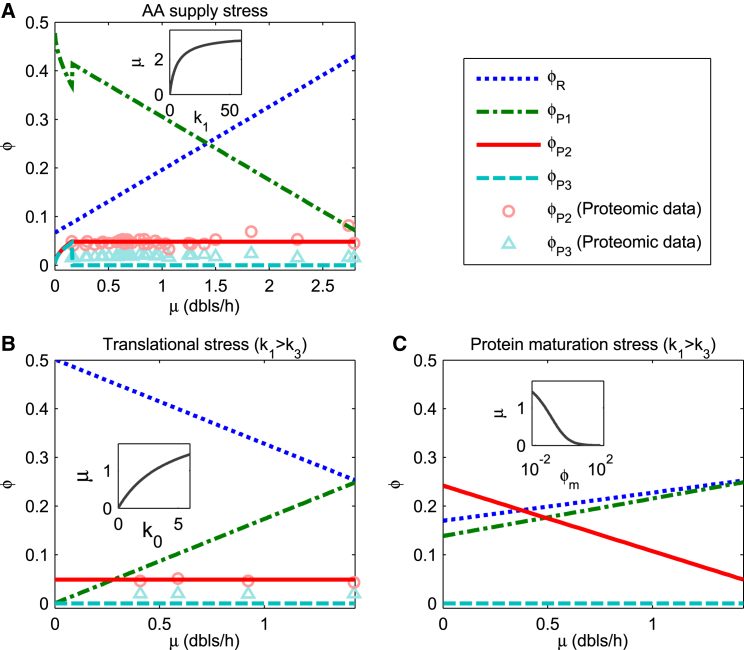
Figure 3.
The model predicts the relation of protein allocation fractions and the growth rate when one flux capacity (k1, k0, or 1/ϕm) is reduced by the stress. Insets present the decrease of growth rate with flux capacity limitation, in which units of μ, k1, k0, and ϕm are doublings/hour (dbls/h), h−1, h−1, and 1, respectively. ϕR, ϕP1, ϕP2, and ϕP3 indicate proteome fractions of ribosome-affiliated proteins (R class), AA-supply-required proteins (P1 class), chaperone-like proteins (P2 class), and protease-like proteins (P3 class), respectively. The experimental data for ϕP2 (circles) and ϕP3 (triangles) are obtained with the classification of Proteomaps (49); those in (A) are based on the proteomic data of (22, 28, 29, 30), and those in (B) are based on (22). Common parameters: ϕ∗ = 0.55, ϕ0 = 0.066, k3 = 0.3 h−1. (A) AA supply stress is shown by k1 decreasing. Parameters: k0 = 6 h−1 and ϕm = 0.0061. (B) Translational stress is displayed by k0 decreasing (k1 > k3). Parameters: k1 = 4.5 h−1 and ϕm = 0.0061. (C) Protein maturation stress is reflected by ϕm increasing (k1 > k3). Parameters: k0 = 6 h−1 and k1 = 4.5 h−1. To see this figure in color, go online.
Assigning empirical or properly chosen values to the parameters (see the model section), we obtain the quantitative relation between the mass fraction (, also simplified as ϕX, X ∈ {R, P1, P2, P3}) of each class of proteins and growth rate (μmax, also simplified as μ) under the stress of limiting flux capacity k0, k1, or 1/ϕm, as shown in Figs. 3 and S3. Under AA supply stress (k1 decreasing), the mass fraction of ribosome-affiliated proteins linearly increases with the growth rate (μmax), whereas the mass fraction of AA-supply-required proteins linearly decreases except at extremely small growth rates (Fig. 3 A). Under translational stress (k0 decreasing), linearly or approximately linearly decreases with μmax, whereas linearly increases (Figs. 3 B and S3 B). Figs. 3, A and B and S3, A and B also show the mass fraction of chaperones and proteases (i.e., ) is much smaller than that of ribosome-affiliated and AA-supply-required proteins . These results, obtained with a small ϕm (=0.0061), are in line with those of Scott et al. (19).
Interestingly, Fig. 3 A shows that there is a jump in protein allocation at a growth rate of 0.15 doublings/h (also see Fig. S3). When the growth rate is smaller than this jump point, both mass fractions of chaperones and proteases ( and ) increase with the growth rate. When the growth rate exceeds the jump point, the mass fraction of chaperones is saturated, whereas the mass fraction of proteases drops to zero immediately. The shift of is in line with the fact that most proteins are stable when E. coli cells grow in a nutrient-rich environment, but these “stable” proteins are prone to degradation in starvation (46). The jump results from the switching of AP degradation process. If AA supply capacity (k1) is higher than AP degradation capacity (k3), it is more efficient to produce AAs via metabolism than via the degradation of aberrant proteins. At this time, the bacteria will switch off the AP degradation process (i.e., J3 = 0) and transfer the cost of P3-sector proteins totally to P2 sector. As a result, APs will tend to aggregate. In the opposite case, the bacteria will express enough proteases to degrade all the APs to compensate for the lack of AAs produced via metabolism. In real bacterial cells, the “jump” might be smoothed out because our model is a coarse-grained model; many details about the bacteria are not taken into account, and the bacteria may not always proliferate at the maximal rate because of environmental variability (48). By analyzing the proteomic data (22, 28, 29), we found that the mass fraction of chaperones and folding catalysts (classified by Proteomaps (49)) in the proteome is around 5%, and the mass fraction of peptidases (proteases) is around 2%. Moreover, both of these fractions are substantially independent of growth rates under various conditions that limit AA supply (by changing composition or concentration of nutrients or titrating a permease for carbon source or a key enzyme in an anabolic pathway) or limit the translation (induced by chloramphenicol). By choosing k3 and ϕm properly, our results are in good agreement with the above proteomic analysis (see Fig. 3, A and B): the mass fraction of chaperones is always ∼5% and that of proteases is always ∼0% in the case k1 > k3. It suggests that the consideration of protein quality control in our model and the choice of parameters (ϕm and k3) are reasonable. The extra 2% protease fraction in the empirical data points to the existence of a basal level of the proteases. From Table 1, we know the influence of the perturbations of ϕm and k3 on the above results. Under the condition of k1 > k3, when ϕm is perturbed, the proteome fraction of chaperones changes in the same direction as ϕm and the proteome fractions of AA-supply-required proteins and ribosome-affiliated proteins change in the opposite direction of ϕm, whereas the fraction of proteases remains constant. When k3 is lower than k1, the perturbation of k3 does not affect protein allocation, but when k3 is higher than k1, it affects the jump point and protein allocation.
Under the stress (e.g., thermal, acidic, and oxidative stresses) of interfering protein maturation, ϕm is raised, so the mass fraction of chaperones (ϕP2) should increase as well (see Figs. 3 C and S3 C; Table 1). Figs. 3 C and S3 C present the quantitative relationship between protein allocation and growth rate under the protein maturation stress (ϕm increasing) for the cases of k1 > k3 and k1 < k3, respectively. When AA supply capacity is larger than AP degradation capacity (k1 > k3), the mass fraction of proteases is zero, i.e., , and decreasing the growth rate (from 1.44 to 0 doublings/h), the mass fraction of chaperones will linearly increase (from ∼5% to ∼25%), whereas both mass fractions of ribosome-affiliated proteins and AA-supply-required proteins ( and ) will linearly decrease (see Fig. 3 C). These relations, as the important predictions of our model, indicate that the expression of chaperones, proteases, and other affiliated proteins can be upregulated to maximize the growth rate under the maturation stress, and meanwhile, that of ribosomal proteins, metabolic enzymes, etc. should be downregulated according to resource reallocation. Fig. 4 shows that a higher fraction of the translation flux will flow to the aberrant maturation flux with increasing intensity of maturation stress, which indicates that a remarkable proportion of UPs mature abnormally under the strong maturation stress even if chaperones are expressed at a high level. In addition, Fig. 4 shows that the aberrant maturation flux (J4) 100% shifts to the aggregation flux (J5) when k1 > k3, which is in line with the above results (see the results when k1 < k3 in the Supporting Materials and Methods and Fig. S4 therein).
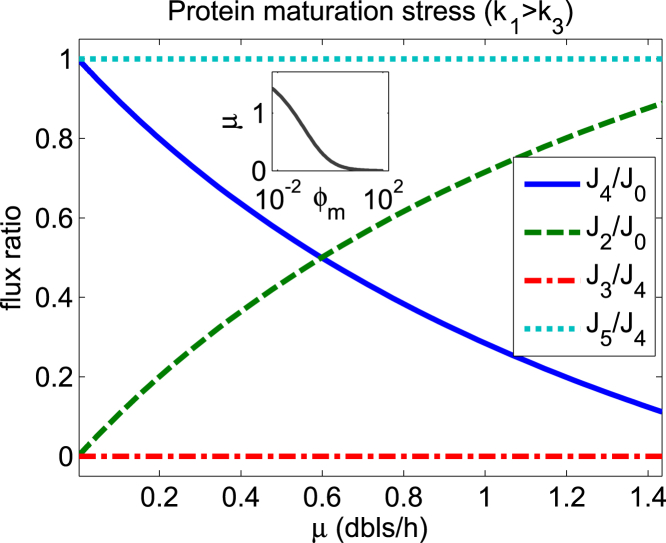
Figure 4.
Translation flux shifts from the normal maturation flux to the aberrant maturation flux under protein maturation stress (ϕm increasing). J0: translation flux; J2: normal maturation flux; J4: aberrant maturation flux; J3: degradation flux; J5: aggregation flux. J2/J0 and J4/J0 indicate fractions of UPs matured normally and abnormally, respectively. J3/J4 and J5/J4 indicate fractions of APs degraded and aggregating, respectively. Notice that J2/J0 + J4/J0 = 1 and J3/J4 + J5/J4 = 1. The plot shows that J2/J0 decreases with the maturation stress (minimum = 0), whereas J4/J0 increases (maximum = 1) with the maturation stress. When AA supply capacity is bigger than the degradation capacity (k1 > k3), AP degradation flux is switched off and all the aberrantly matured proteins aggregate. Parameters are the same as those used in Fig. 3C. To see this figure in color, go online.
Genome-wide transcriptomic/proteomic data show that the expression of some chaperones increases significantly in response to acidic stress (11, 31), oxidative stress (32), and thermal stress (33, 34). The transcriptomic data from Tucker et al. (31) show that periplasmic acid stress chaperones hdeA and hdeB are upregulated more than 10-fold, and cbpA (co-chaperone of DnaK), is increased fivefold at pH = 4.5 relative to pH = 7.4. Allen and Griffiths (32), with their microarray data, revealed that the expression of at least three chaperone genes (hdeA, clpB, and dnaK) has a 1.5- to 4-fold change upon exposure of exponentially growing cells to 2.5 mM hydrogen peroxide or 300 mM paraquat. Foshag et al. (33) found five chaperones (GroEL, GroES, DnaK, GrpE, and SecA) increased 3- to 10-fold in 42°C-heat-shocked S30 lysates. Notice that some chaperones may not be detected/recognized in the above genome-wide data. Therefore, it is very likely that the mass fraction of all chaperones (including chaperone-like proteins) in the proteome increases significantly under the protein maturation stresses (such as acidic, oxidative, and thermal stresses). Schmidt et al. (30) in 2016 measured the abundance of >2300 proteins under 20 steady-state conditions. With the classification of Proteomaps (49), we computed the mass fraction of chaperones (including folding catalysts) and that of proteases (peptidases) under these conditions. With varying nutrient sources or using glucose-limited chemostat (17 conditions), the mass fractions are ∼5% and ∼2% respectively, which is in agreement with above results from other proteomic data, except that the mass fraction of chaperones is ∼8% with the complex medium LB. Interestingly, the mass fraction of chaperones increases significantly (55 and 35% respectively) in presence of the weak thermal (42°C) and acidic stresses (pH = 6), which is in line with our results about the maturation stress.
Based on the above results in line with the literature (e.g., (19, 21, 22)), we summarize two general characteristics of bacterial cells under stress: 1) environmental stress usually creates a bottleneck somewhere in protein production, resulting in slower cell growth; and 2) the bacteria can reallocate protein resource among fluxes to maximize the growth rate within constraints. Stress-targeted flux occupies an increased proteome fraction (may increase from a negligible fraction to a remarkable fraction), and other fluxes occupy decreased proteome fractions correspondingly.
The model quantifies the change of β-galactosidase concentration from a constitutive promoter with the growth rate under translational, acidic, and oxidative stresses
The linear relationships as shown in Fig. 3 C are the predictions for the pure maturation stress, under which the maturation of all the proteome sectors is restricted to the same extent. However, the maturation stresses available for the current experiments (e.g., thermal, acidic, or oxidative stress) may not act on only one flux, and therefore protein allocation is probably not linearly correlated with the growth rate. Different proteins differ in their maturation pathways with the help of different molecular chaperones (9). The usual maturation stress probably does not have a common intensity for all the proteins, i.e., proteins from different sectors may have different sensitivities to the stress. In addition to the limitation on the maturation process, the stress may also hinder other processes in which some sensitive proteins play important roles. The genome-wide transcriptomic/proteomic data show that some metabolic enzymes, like chaperones, are produced at higher levels under thermal, acidic, or oxidative stress (11, 30, 31, 32, 33, 34). Moreover, the rate-limiting enzymes are widespread in the AA supply process. It is likely that one of the upregulated metabolic enzymes determines the rate of AA supply under the usual maturation stress. Therefore, the usual maturation stress probably limits both the protein maturation process and the AA supply process, with the former being direct and the latter being indirect. To explain our experimental results under acidic and oxidative stresses, the effects of stress on both flux capacities need to be considered.
We measured the expression level of β-galactosidase constitutively driven by promoter PLetO1 (35) in E. coli as a function of growth rate under translational (induced by chloramphenicol), acidic (induced by acetic acid), and oxidative (induced by paraquat) stresses, respectively. As Scott et al. (19) did, β-galactosidase driven by a constitutive promoter can be regarded as a P1-class protein, and the mass fraction of β-galactosidase can be assumed to be proportional to that of AA-supply-required proteins (P1 sector), i.e., ϕZ ∝ ϕP1. Considering that the change of cell mass is mainly reflected in proteins and RNA (43), we can derive ϕNP ∝ 1/(ρ + ϕR) with ρ = 0.76 (19), which is in agreement with empirical data for various nutrients and different chloramphenicol concentrations (see the Supporting Materials and Methods and Fig. S7 therein). Integrating above formulas with Z ∝ ψZ = ϕZψNP, we can represent β-galactosidase concentration Z as a function of mass fractions of ribosome-affiliated proteins and AA-supply-required proteins (ϕR and ϕP1) (see the Supporting Materials and Methods):
| (23) |
where ρ = 0.76 (19) and C is constant. This formula connects the experimental variable Z with theoretical variables ϕP1 and ϕR. Considering how the stress changes flux capacities, our optimization model combined with Eq. 23 yields comparable results to the experimental data (see Figs. 5 and S8).
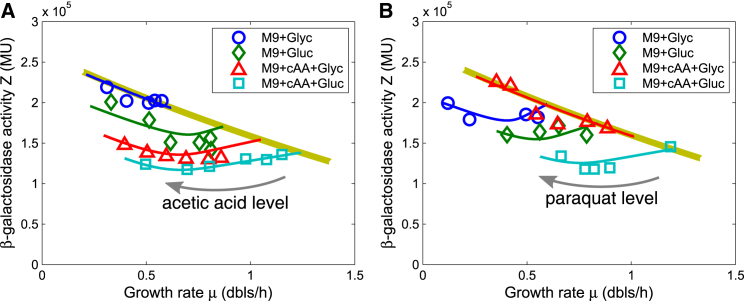
Figure 5.
β-galactosidase activity (concentration) from a constitutive promoter (PLtetO1) as a function of growth rate under the stress induced by acetic acid or paraquat is well fitted with the model. Circles, diamonds, triangles, and squares denote experimental results for the bacteria grown in four different growth media (M9 + Glyc, M9 + Gluc, M9 + cAA + Glyc, and M9 + cAA + Gluc) with various sublethal levels of acetic acid or paraquat. Corresponding experimental data are presented in Tables S2 and S3. Blue, green, red, and cyan lines show theoretical results under the acidic or oxidative stress, and yellow lines indicate those under AA supply stress. Parameters: ϕ∗ = 0.55, ϕ0 = 0.066, k0 = 6 h−1, = 1.3 h−1 (blue line), 2 h−1 (green line), 2.6 h−1 (red line), or 3.34 h−1 (cyan line), = 0.0061, k3 = 0.3 h−1, β = 5, C = 5 × 105 Miller units. (A) Results under the stress of acetic acid are shown. Kx = 0.1 (blue line), 5 (green line), 15 (red line), or 25 (cyan line). (B) Results under the stress of paraquat are shown. Kx = 9 (blue line), 12 (green line), 0.1 (red line), or 15 (cyan line).
Chloramphenicol-induced translation inhibition can be represented by a decrease in translational capacity k0 (19). To obtain theoretical results in agreement with experimental data, we determined ϕ∗, ϕ0, k1 (under translation limitation), and k0 (under nutrient limitation) based on the literature (19) and set ϕm and k3 as the values from fitting the proteomic data (see above). In addition, we fixed the scaling factor C (in Eq. 23) by fitting the experimental β-galactosidase concentration as a function of growth rate. As shown in Fig. S8, our model well fitted β-galactosidase concentration as a function of growth rate under chloramphenicol limitation with various growth media. However, it seems that the experimental β-galactosidase concentration may not convert to zero at the zero-growth rate as we predict. This may indicate that β-galactosidase has a nonzero basal expression level that could be regarded as part of housekeeping the Q sector. We have overlooked this possible impact here because it is not our focus of concern, nor does it affect our main results. Fig. S8 B, converted from theoretical curves in Fig. S8 A with Eq. 23, shows a linear relationship between the mass fraction of AA-supply-required proteins (ϕP1) and growth rate under translation inhibition as an echo of the results of Scott et al. (19).
For acidic/oxidative stress, our experimental results (see Fig. 5) show that β-galactosidase concentration basically decreases and then increases to some extent with the level of the inducer (acetic acid or paraquat). It is impossible to explain this phenomenon if we only consider that the maturation flux capacity is affected. According to the manner and effect of action, we classify the effects of acidic/oxidative stress on the maturation (folding, assembly, activation, etc.) process of proteins as direct and indirect. In general, maturation stress affects the folding of UPs into functional proteins: the nonspecific frustration on the maturation of the entire proteome becomes a bacterial growth bottleneck, and we call this effect a direct effect. Bacteria will use protein quality-control systems to deal with this effect. The damage or activity reduction of some specific key protein caused by the stress will affect the key biochemical process(es) in the important pathway(s), and thus this protein becomes the bottleneck restricting bacterial cell growth. We refer to this effect of maturation stress as an indirect effect. A variety of rate-limiting enzymes exist in the AA supply process, and empirical data show that expressions of some metabolic enzymes are also increased in response to acidic or oxidative stress (11, 30, 31, 32). Moreover, only AA supply stress can induce an increase in the concentration of AA-supply-required proteins according to Fig. 3. Therefore, one of the simplest and most natural ideas is that the acidic/oxidative stress acts on the AA supply process by influencing some important proteins in this process. Based on this viewpoint, both AA supply flux and UP normal maturation flux are limited by the acidic/oxidative stress, which is reflected in our model by the reduction of flux capacities k1 and 1/ϕm. We define the stress intensity (x) by
| (24) |
where represents the values in the absence of oxidative/acidic stress. In general, the stress intensity x is a function of the concentration of the inducer (here, acetic acid or paraquat), and x = 0 if there is no inducer. The acidic/oxidative stress acts on the AA supply flux by affecting the enzymes, and enzyme-catalyzed biochemical reaction rates can often be written in the form of a Hill function. Therefore, a reasonable choice of the relationship between AA supply capacity k1 and stress intensity x is
| (25) |
where represents the values in the absence of oxidative/acidic stress and Kx and β denote the equilibrium constant and Hill coefficient, respectively. Although we do not know the exact relationship between stress intensity and inducer concentration, for each value of stress intensity x, we can calculate the optimal protein allocation and growth rate and then get the value of β-galactosidase concentration. Finally, we can get protein allocation and β-galactosidase concentration as functions of growth rate. To compare with the experimental results, we set ϕ∗, ϕ0, , k0, , k3, and C as the same values as those for the corresponding parameters under chloramphenicol limitation and fixed Kx and β (in Eq. 23) by fitting the experimental relationship of β-galactosidase concentration and growth rate. Fig. 5 shows our model can well fit the experimental β-galactosidase concentration as a function of growth rate under the acidic and oxidative stresses induced by acetic acid and paraquat, respectively. Furthermore, the results also show that the relationship between β-galactosidase concentration and growth rate is also dependent on the growth medium. It suggests that the bacteria grown in different growth media choose different AA supply pathways with different acidic/oxidative sensitivities. Astonishingly, the curves in Fig. 5 for M9 + Glyc under acetic acid stress and M9 + cAA + Glyc under paraquat stress overlap with the nutrient line. This means that in both cases, the limitation on AA supply flux completely overwhelms the limitation on the maturation flux because of the supersensitivity of some key AA supply enzyme(s).
The model well characterizes the effects of overexpression of unnecessary protein on growth rate
Earlier experiments show that many chaperones (e.g., DnaK, DnaJ, GrpE, HtpG, and GroEL) are upregulated in response to overexpression of an unnecessary protein (e.g., (36, 37)). With two-dimensional polyacrylamide gels, Dong et al. (36) found that DnaK and GroEL increase around 90 and 27%, respectively, in the level in response to overexpression of either ΔEF-Tu or β-galactosidase. DNA microarray data of Oh and Liao (37) show that dnaK, dnaJ, grpE, and htpG are upregulated two- to eightfold under the overexpression of the α-subunit of the luciferase heterodimer. The upregulation of chaperones can be qualitatively interpreted with our model. Bacteria cannot distinguish the unnecessary protein from useful proteins at the translation level. In order not to waste translation costs, whether it is a useful or useless protein, the bacterium should try its best to help the UPs correctly folded into the native structures. Producing unnecessary proteins, although taking up cellular resources, has no use in cell growth. When unnecessary proteins are overexpressed, the same translation costs are paid while the proportion of functional proteins obtained is reduced. This is similar to the cells facing maturation stress. Similarly, chaperones will be upregulated in response to overexpression of unnecessary proteins. Because chaperones are able to have a non-neglectable mass fraction in the proteome (see our above results), it is meaningful to consider the effect of their upregulation in illuminating the physiological change of the bacteria with overexpressed unnecessary protein.
Overexpression of unnecessary proteins will inhibit bacterial cell growth, which is well known in synthetic biology and biotechnology (19, 21, 22, 23, 36, 38, 43, 50). From empirical data, the growth rate shows a nonlinear decrease as the mass fraction of the unnecessary protein in the whole proteome increases, and the ratio reaches a maximum of ∼30 at the zero-growth rate (36, 38). But the Scott-Hwa model and other extended versions predict an exactly linear relation and a zero-growth ratio between 40 and 50 (17, 19, 21, 22, 23). The nonlinear behavior and a smaller zero-growth ratio in empirical data probably result from the effect of upregulation of chaperones accompanying the overexpression of unnecessary protein that is unconsidered in previous models. Here, we integrate this effect into our model to provide a more in-depth explanation of the empirical results.
Overexpression of the unnecessary protein directly affects three fluxes: translation flux (J0), normal maturation flux (J2), and aberrant maturation flux (J4) (see the Supporting Materials and Methods). For convenience, we consider that the useless protein has the same level of maturation frustration (ϕm) as the useful proteins. Under this consideration, we do not need to distinguish the useless protein from useful proteins, and the model can be still described by Eqs. 10, 11, 12, 13, 14, 15, 16, 17, and 18, but the normalization condition shown by Eq. 17 should be changed to
| (26) |
where ϕU ≥ 0. We also modeled the situation in which the maturation frustration level of the useless protein differs from that of useful proteins (see the Supporting Materials and Methods), for which the results vary little if the maturation frustration level of the useless protein is not much higher than that of useful proteins.
As mentioned above, chaperones are upregulated as unneeded protein is overexpressed. The upregulation of chaperones does not come from the direct limitation on the UP maturation process. Instead, it comes from the limitation on the maturation flux for useful proteins due to the occupation of resources by the useless protein. The most economical way is to use all chaperones for useful proteins. Overexpression of unnecessary proteins in experiments is artificially controlled, so upregulation of chaperones is not fully optimized. At least a portion of the chaperones are used for the maturation of unneeded proteins, which are not well optimized and are only related to the amount of unnecessary protein. For the sake of convenience, we assume that the mass fraction of unoptimized chaperones are linearly related to the mass fraction of overexpressed unnecessary protein (ϕU). The chaperones used for the maturation of useful proteins also come from these useful proteins, and the bacteria will optimize the proteome fraction for this portion of chaperones to achieve optimal growth rates. Therefore, we can assign the mass fraction of all chaperones (ϕP2) to an unoptimizable part (proportional to ϕU) and an optimizable part , represented by
| (27) |
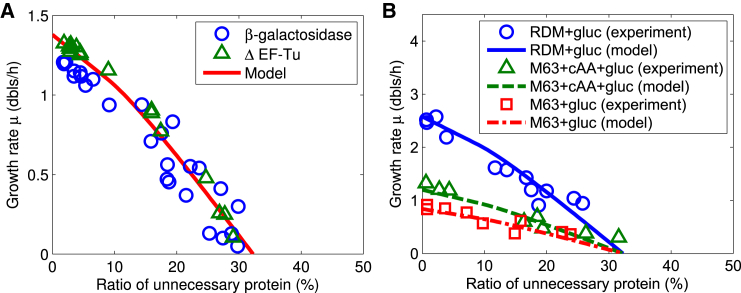
where and α is constant. Notice that here ϕP2 ≥ αϕU, i.e., chaperones have a minimal mass fraction αϕU. When α = 0 and ϕm ≈ 0, our model is equivalent to that of Scott et al. (19). The relationship between the mass fraction of unoptimized chaperones and ϕU may actually be more complicated, in which case we consider Eq. 27 as a linear approximation of this relationship. The optimization goal is still to maximize the growth rate μ. Furthermore, we only consider k1 > k3 because it usually holds in bacteria. Then we can analytically solve the optimization problem in a one-dimensional space (see Supporting Materials and Methods). From the analytic solution (see Supporting Materials and Methods), we can get the maximal proteome fraction of unnecessary protein ϕU at zero-growth rate, i.e., . With α = 0.5, our theoretical results (Fig. 6) fit well with experimental data of Dong et al. (36) and Scott et al. (19). These results reproduce the nonlinear relationship of growth rate and the proteome fraction of unnecessary protein ϕU and also give the maximal fraction of unnecessary protein , approximately equal to the 30% obtained directly from the data by experiments (36, 38). From the analytic solution (see the Supporting Materials and Methods) and Fig. S9, the mass fraction of chaperones (ϕP2) decreases a little bit and then increases with the mass fraction of useless protein (ϕU), whereas mass fractions of R-class and P1-class proteins both decrease. This is in line with the experimental evidence that many heat-shock proteins (chaperone-like proteins) are upregulated, whereas ribosomes, some elongation factors, and some metabolic enzymes are expressed less under overexpression of unneeded proteins (36, 37, 38).
Figure 6.
Empirical relations of growth rate and proteome fraction of overexpressed unnecessary protein are completely elucidated with our model, which indicates a significant effect of the upregulation of chaperone proteins. Global parameters: ϕ∗ = 0.55, ϕ0 = 0.066, k0 = 6, ϕm = 0.0061, k3 = 0.3 h−1, α = 0.5. (A) The model well fits the experimental data of Dong et al. (36) with overexpression of β-galactosidase or ΔEF-Tu. k1 = 4.2 h−1. (B) The model well fits the experimental data of Scott et al. (19) with overexpression of β-galactosidase in different growth media (Neidhardt’s rich defined media + Gluc, M63 + cAA + Gluc, and M63 + Gluc; see details in (19)). k1 = 20 h− (solid line), 3.34 h−1 (dashed line), or 2 h−1 (dash-dot line). To see this figure in color, go online.
Discussion
The acidic or oxidative stress can hinder the maturation of many proteins, which will induce higher expressions of some chaperones and proteases (10, 11, 13, 14, 15). When the stress is strong, the maturation of some vulnerable proteins will mostly fail even if chaperones are expressed at high levels. We propose that the most vulnerable key proteins belong to the P1 class (AA-supply-required proteins) because, first of all, P1-class proteins such as metabolic enzymes have greater diversity and variability than other proteins. Second, only the limitation on AA supply flux leads to the increased expression of P1-class proteins. We do not rule out the possibility that acidic/oxidative stress inhibits other processes such as translation. But even if there is such an effect, we still believe that it does not overwhelm the effects on the maturation process and AA supply process. The Scott-Hwa model (17, 19) has been extended to study more detailed effects of the limitations on AA supply and translation processes (20, 21, 22, 25) or to investigate the effects of energy dissipation (23). We have considered the dependence of translational elongation rate on growth rate (20, 25) in our model, but we have not found any significant change in the results (see Fig. S5). Further decomposition of AA supply flux (21, 22) brings further partition of AA-supply-required proteins, but its consideration in our model does not affect the results on mass fractions of chaperones and proteases. Energy-molecule ATP is also a limiting factor that controls the choice of metabolic strategies and the rate of metabolic overflow (16, 23). In our model, such energy limitations can be roughly reflected in the change of flux capacity k1.
More systematic experiments can be carried out under acidic/oxidative stress conditions to test the broad conclusions of this work and even go beyond this study. For example, the mass ratio between RNA and protein can be measured as was done by Scott et al. (19) to check the change of proteome fraction of ribosome-affiliated proteins (ϕR) predicted in this research. The linear relationships that we predicted under the maturation stress (shown in Fig. 3 C) may be observed in some well-designed experiments, for example, using a special chemical to limit the folding of all proteins to a similar degree. In addition, more detailed genome-wide proteomic data than before can be obtained with high-throughput techniques (e.g., mass spectrometry) to check the predictions on a larger scale.
Here, we studied the phenomenological relationships between bacterial protein allocation and growth rate under nonlethal stress conditions. The elucidation of molecular mechanisms behind these relations is another important issue. A common mechanism of achieving protein reallocation is the alarmone ppGpp-mediated stringent response, in which ribosomal proteins are inhibited by ppGpp at the transcriptional level or autorepressed at the translation level because of ppGpp inhibiting rRNA synthesis (51, 52). ppGpp emerges in response to multiple stresses, and it probably inhibits synthesis of other R-class (ribosome-affiliated) proteins as well as ribosomal proteins directly or indirectly. Another important way to adjust protein allocation is regulating the competition between sigma factors by global regulators, such as ppGpp, Rsd, and 6S RNA (5, 53, 54, 55, 56). In bacterial stress response, usually, numerous active alternative σ factors will emerge. Thereby some stress proteins whose transcription promoters are recognized by these alternative σ factors will be produced at a higher level, whereas housekeeping σ factor (σD) and housekeeping proteins will be negatively regulated in some way. Therefore, bacterial protein allocation is probably mainly adjusted by regulating the competition between σ factors for core RNA polymerases and the competition between messenger RNAs for ribosomes in stress adaptation (see the Supporting Materials and Methods).
The effects of protein aggregate from the aggregation flux were not taken into account in our above model. Protein aggregate, as a waste of protein resources in the cell, may be also an aging factor because of its certain toxicity to bacterial cells (42, 57, 58). So, protein aggregate may also affect protein allocation and cell growth via a feedback loop. Our model can be improved to give a possible explanation of effects of protein aggregates on protein allocation (see the Supporting Materials and Methods). The results show that if the toxicity of protein aggregates is high enough, bacteria will degrade all the APs without the jump that takes place in the relation of protein allocation and growth rate. If the toxicity of protein aggregates is small, the bacterium will either degrade all APs or allow all of them to aggregate, and which way it chooses is determined by physiological conditions (see the Supporting Materials and Methods). Inclusion body, as a form of protein aggregate, was observed in normally growing cells (42, 59), indicating that protein aggregates are not highly harmful to bacterial cells. Actually, the larger interference area of dispersed aberrant polypeptides causes their toxicity to be stronger than their aggregates. It indicates that the aggregation is another effective manner to lessen the exposed toxicity of dispersed aberrant polypeptides. Therefore, the degradation and the aggregation are two complementary strategies to handle the toxic APs. The degradation can eliminate the toxicity thoroughly, and its product (AAs) can be reused by cells, but it requires extra protein resources (proteases). The aggregation is mainly spontaneous, but it produces waste containing some toxicity. Bacterial cells need to choose a better strategy according to environmental conditions.
Conclusions
In this research, we investigated the allocation of bacterial proteins under nonlethal stress conditions, especially those that hinder the maturation of proteins, by performing a coarse-grained FBA of a self-replication model. Considering the role of protein quality control in protein allocation, we extend the model of Scott et al. (19), which is used to phenomenologically study the allocation of protein resources between metabolism and translation. From our model, maximizing the growth rate during the steady-state exponential growth determines the relationship of protein allocation and growth rate in bacteria under nonlethal stress conditions. Our model gives a mostly linear dependence of proteome fractions of ribosome-affiliated proteins and AA-supply-required proteins on growth rate, which is in agreement with empirical relationships found by changing nutrient quality or translational rate (19). Moreover, we discover a nonmonotonic relationship between the concentration of a constitutive protein (β-galactosidase) and growth rate under acidic/oxidative stress: β-galactosidase concentration tends to decrease and then increase with the stress intensity. The results imply that some proteins working in AA supply flux are more vulnerable to the acidic/oxidative stress than others. So, if the stress is strong enough, the limitation on AA supply flux will overwhelm that on the maturation flux. According to our model, the blockages in AA supply and protein maturation cause divergent dependences of the proteome fraction of AA-supply-required proteins on the growth rate. So, the concerted action of these two blockages leads to the convex relation of β-galactosidase activity versus growth rate (Fig. 5). Considering that the mass fraction of chaperones and chaperone-affiliated proteins includes an unoptimized part that is proportional to that of the overexpressed useless protein, we obtain a sublinear relationship between growth rate and the mass ratio of the unnecessary protein to total proteins and the zero-growth mass ratio around 30%. These results are in better agreement with the experimental data (36, 38) than those from previous models (17, 19, 21, 22, 23). Our model suggests that when a synthetic gene is overexpressed for bioengineering applications, there is an extra limitation on the bacterial growth rate. This extra limitation could be overcome by a systematic alteration of the genome to control the proteome fraction of chaperones and chaperone-affiliated proteins.
In addition to the specific stresses we studied here (e.g., acidic stress, oxidative stress, and overexpression of unnecessary protein), other stresses (such as thermal and antibiotic stresses) are also worth researching with experiments and coarse-grained models for understanding resource-allocation strategies of bacterial cells more widely. Many molecular chaperones and proteases are notably upregulated in heat-shock response (12, 33, 34). Moreover, some antibiotics can interfere with proteolytic machinery (60). Therefore, it is necessary to consider protein quality control for characterizing bacterial adaptation to thermal and some antibiotic stresses. Chen et al. (34) recently, with a genome-scale model integrating protein folding with metabolism and gene expression, predicted that the mass fraction of chaperones has a significant increase under thermal stress. The increase of the mass fraction of chaperones they predicted (18-fold) at 45°C in comparison with 37°C is much higher than that we predicted (fourfold as the maximum) under protein maturation stress (see Fig. 3 C). The difference is partly because we have not yet considered possible dependences of the parameters (e.g., flux capacities) on the temperature in our model. Another reason is that their detailed model may not be complete. More relevant experiments are needed to support the theoretical prediction of the effect of thermal stress.
The quantitative research on protein allocation will help us to understand how a microorganism (e.g., pathogenic bacteria and engineering bacteria) adapts to a stressful environment (e.g., addition of antibiotics and overexpression of synthetic genes) in a systematic and quantitative way, which will eventually pave the way for rational design for improved therapeutic interventions and biotechnology.
Author Contributions
Q.Z. and H.S. designed the research. Q.Z. and H.S. constructed the model. Q.Z. performed analytic derivation and experiments. R.L., J.L., and H.S. provided technical support and conceptual advice. Q.Z. and H.S. analyzed the results and wrote the manuscript.
Acknowledgments
We thank Terence Hwa for providing E. coli strain MGIBKYPLtetO1-lacZ and Weimou Zheng, Marco Cosentino Lagomarsino, Bianca Sclavi, and Malik Yousuf for helpful discussion.
The work was supported by the Strategic Pilot Project of Chinese Academy of Sciences (XDA17010504), the National Natural Science Foundation of China (grant nos.11774359, 11747601, and 11274320) and the Interdisciplinary Innovation Team of Chinese Academy of Sciences (no. 2060299).
Editor: Anatoly Kolomeisky.
Footnotes
Supporting Materials and Methods, nine figures, and four tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30869-5.
Contributor Information
Qing Zhang, Email: qzhang@itp.ac.cn.
Hualin Shi, Email: shihl@itp.ac.cn.
Supporting Citations
References (61, 62, 63, 64, 65, 66, 67, 68) appear in the Supporting Material.
Supporting Material
References
- 1.Neidhardt F.C., Ingraham J.L., Schaechter M. Volume 20. Sinauer Sunderland; Sunderland, MA: 1990. Physiology of the Bacterial Cell: a Molecular Approach. [Google Scholar]
- 2.Neidhardt F.C., Curtiss R., III, Ingraham J.L. Escherichia coli and Salmonella: Cellular and Molecular Biology. In: Lin E.C.C., Low K.B., Umbarger H.E., editors. Second edition. American Society for Microbiology; Washington, DC: 1996. [Google Scholar]
- 3.Gama-Castro S., Salgado H., Collado-Vides J. RegulonDB version 9.0: high-level integration of gene regulation, coexpression, motif clustering and beyond. Nucleic Acids Res. 2016;44:D133–D143. doi: 10.1093/nar/gkv1156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Keseler I.M., Mackie A., Karp P.D. The EcoCyc database: reflecting new knowledge about Escherichia coli K-12. Nucleic Acids Res. 2017;45:D543–D550. doi: 10.1093/nar/gkw1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nyström T. Growth versus maintenance: a trade-off dictated by RNA polymerase availability and sigma factor competition? Mol. Microbiol. 2004;54:855–862. doi: 10.1111/j.1365-2958.2004.04342.x. [DOI] [PubMed] [Google Scholar]
- 6.Han M.J., Lee S.Y. The Escherichia coli proteome: past, present, and future prospects. Microbiol. Mol. Biol. Rev. 2006;70:362–439. doi: 10.1128/MMBR.00036-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Goelzer A., Fromion V. Bacterial growth rate reflects a bottleneck in resource allocation. Biochim. Biophys. Acta. 2011;1810:978–988. doi: 10.1016/j.bbagen.2011.05.014. [DOI] [PubMed] [Google Scholar]
- 8.Maurizi M.R. Proteases and protein degradation in Escherichia coli. Experientia. 1992;48:178–201. doi: 10.1007/BF01923511. [DOI] [PubMed] [Google Scholar]
- 9.Hartl F.U., Bracher A., Hayer-Hartl M. Molecular chaperones in protein folding and proteostasis. Nature. 2011;475:324–332. doi: 10.1038/nature10317. [DOI] [PubMed] [Google Scholar]
- 10.Farr S.B., Kogoma T. Oxidative stress responses in Escherichia coli and Salmonella typhimurium. Microbiol. Rev. 1991;55:561–585. doi: 10.1128/mr.55.4.561-585.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Maurer L.M., Yohannes E., Slonczewski J.L. pH regulates genes for flagellar motility, catabolism, and oxidative stress in Escherichia coli K-12. J. Bacteriol. 2005;187:304–319. doi: 10.1128/JB.187.1.304-319.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guisbert E., Yura T., Gross C.A. Convergence of molecular, modeling, and systems approaches for an understanding of the Escherichia coli heat shock response. Microbiol. Mol. Biol. Rev. 2008;72:545–554. doi: 10.1128/MMBR.00007-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Malki A., Le H.T., Richarme G. Solubilization of protein aggregates by the acid stress chaperones HdeA and HdeB. J. Biol. Chem. 2008;283:13679–13687. doi: 10.1074/jbc.M800869200. [DOI] [PubMed] [Google Scholar]
- 14.Hong W., Wu Y.E., Chang Z. Chaperone-dependent mechanisms for acid resistance in enteric bacteria. Trends Microbiol. 2012;20:328–335. doi: 10.1016/j.tim.2012.03.001. [DOI] [PubMed] [Google Scholar]
- 15.Dahl J.U., Gray M.J., Jakob U. Protein quality control under oxidative stress conditions. J. Mol. Biol. 2015;427:1549–1563. doi: 10.1016/j.jmb.2015.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Molenaar D., van Berlo R., Teusink B. Shifts in growth strategies reflect tradeoffs in cellular economics. Mol. Syst. Biol. 2009;5:323. doi: 10.1038/msb.2009.82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Scott M., Hwa T. Bacterial growth laws and their applications. Curr. Opin. Biotechnol. 2011;22:559–565. doi: 10.1016/j.copbio.2011.04.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zaslaver A., Kaplan S., Itzkovitz S. Invariant distribution of promoter activities in Escherichia coli. PLoS Comput. Biol. 2009;5:e1000545. doi: 10.1371/journal.pcbi.1000545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Scott M., Gunderson C.W., Hwa T. Interdependence of cell growth and gene expression: origins and consequences. Science. 2010;330:1099–1102. doi: 10.1126/science.1192588. [DOI] [PubMed] [Google Scholar]
- 20.Klumpp S., Scott M., Hwa T. Molecular crowding limits translation and cell growth. Proc. Natl. Acad. Sci. USA. 2013;110:16754–16759. doi: 10.1073/pnas.1310377110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.You C., Okano H., Hwa T. Coordination of bacterial proteome with metabolism by cyclic AMP signalling. Nature. 2013;500:301–306. doi: 10.1038/nature12446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hui S., Silverman J.M., Williamson J.R. Quantitative proteomic analysis reveals a simple strategy of global resource allocation in bacteria. Mol. Syst. Biol. 2015;11:784. doi: 10.15252/msb.20145697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Basan M., Hui S., Hwa T. Overflow metabolism in Escherichia coli results from efficient proteome allocation. Nature. 2015;528:99–104. doi: 10.1038/nature15765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Weiße A.Y., Oyarzún D.A., Swain P.S. Mechanistic links between cellular trade-offs, gene expression, and growth. Proc. Natl. Acad. Sci. USA. 2015;112:E1038–E1047. doi: 10.1073/pnas.1416533112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dai X., Zhu M., Hwa T. Reduction of translating ribosomes enables Escherichia coli to maintain elongation rates during slow growth. Nat. Microbiol. 2016;2:16231. doi: 10.1038/nmicrobiol.2016.231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kauffman K.J., Prakash P., Edwards J.S. Advances in flux balance analysis. Curr. Opin. Biotechnol. 2003;14:491–496. doi: 10.1016/j.copbio.2003.08.001. [DOI] [PubMed] [Google Scholar]
- 27.Mori M., Hwa T., Marinari E. Constrained allocation flux balance analysis. PLoS Comput. Biol. 2016;12:e1004913. doi: 10.1371/journal.pcbi.1004913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Valgepea K., Adamberg K., Vilu R. Escherichia coli achieves faster growth by increasing catalytic and translation rates of proteins. Mol. Biosyst. 2013;9:2344–2358. doi: 10.1039/c3mb70119k. [DOI] [PubMed] [Google Scholar]
- 29.Li G.W., Burkhardt D., Weissman J.S. Quantifying absolute protein synthesis rates reveals principles underlying allocation of cellular resources. Cell. 2014;157:624–635. doi: 10.1016/j.cell.2014.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schmidt A., Kochanowski K., Heinemann M. The quantitative and condition-dependent Escherichia coli proteome. Nat. Biotechnol. 2016;34:104–110. doi: 10.1038/nbt.3418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tucker D.L., Tucker N., Conway T. Gene expression profiling of the pH response in Escherichia coli. J. Bacteriol. 2002;184:6551–6558. doi: 10.1128/JB.184.23.6551-6558.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Allen K.J., Griffiths M.W. Impact of hydroxyl- and superoxide anion-based oxidative stress on logarithmic and stationary phase Escherichia coli O157:H7 stress and virulence gene expression. Food Microbiol. 2012;29:141–147. doi: 10.1016/j.fm.2011.09.014. [DOI] [PubMed] [Google Scholar]
- 33.Foshag D., Henrich E., Bernhard F. The E. coli S30 lysate proteome: a prototype for cell-free protein production. N. Biotechnol. 2018;40:245–260. doi: 10.1016/j.nbt.2017.09.005. Published online September 21, 2017. [DOI] [PubMed] [Google Scholar]
- 34.Chen K., Gao Y., Palsson B.O. Thermosensitivity of growth is determined by chaperone-mediated proteome reallocation. Proc. Natl. Acad. Sci. USA. 2017;114:11548–11553. doi: 10.1073/pnas.1705524114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lutz R., Bujard H. Independent and tight regulation of transcriptional units in Escherichia coli via the LacR/O, the TetR/O and AraC/I1-I2 regulatory elements. Nucleic Acids Res. 1997;25:1203–1210. doi: 10.1093/nar/25.6.1203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dong H., Nilsson L., Kurland C.G. Gratuitous overexpression of genes in Escherichia coli leads to growth inhibition and ribosome destruction. J. Bacteriol. 1995;177:1497–1504. doi: 10.1128/jb.177.6.1497-1504.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Oh M.-K., Liao J.C. DNA microarray detection of metabolic responses to protein overproduction in Escherichia coli. Metab. Eng. 2000;2:201–209. doi: 10.1006/mben.2000.0149. [DOI] [PubMed] [Google Scholar]
- 38.Kurland C.G., Dong H. Bacterial growth inhibition by overproduction of protein. Mol. Microbiol. 1996;21:1–4. doi: 10.1046/j.1365-2958.1996.5901313.x. [DOI] [PubMed] [Google Scholar]
- 39.Sambrook J., Russell D. Third Edition. Cold Spring Harbor Laboratory Press; Cold Spring Harbor, NY: 2001. Molecular Cloning: A Laboratory Manual. [Google Scholar]
- 40.Zhang X., Bremer H. Control of the Escherichia coli rrnB P1 promoter strength by ppGpp. J. Biol. Chem. 1995;270:11181–11189. doi: 10.1074/jbc.270.19.11181. [DOI] [PubMed] [Google Scholar]
- 41.Shetty, R. P. 2008. Applying engineering principles to the design and construction of transcriptional devices. PhD thesis (Massachusetts Institute of Technology).
- 42.Lindner A.B., Madden R., Taddei F. Asymmetric segregation of protein aggregates is associated with cellular aging and rejuvenation. Proc. Natl. Acad. Sci. USA. 2008;105:3076–3081. doi: 10.1073/pnas.0708931105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Basan M., Zhu M., Hwa T. Inflating bacterial cells by increased protein synthesis. Mol. Syst. Biol. 2015;11:836. doi: 10.15252/msb.20156178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hermsen R., Okano H., Hwa T. A growth-rate composition formula for the growth of E.coli on co-utilized carbon substrates. Mol. Syst. Biol. 2015;11:801. doi: 10.15252/msb.20145537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gething M.-J., Sambrook J. Protein folding in the cell. Nature. 1992;355:33–45. doi: 10.1038/355033a0. [DOI] [PubMed] [Google Scholar]
- 46.Miller C.G. Protein degradation and proteolytic modification. In: Neidhardt F.C., Curtiss III R., editors; Umbarger H.E., editor. Escherichia coli and Salmonella: Cellular and Molecular Biology. Second Edition. Volume 1. American Society for Microbiology; 1996. pp. 938–954. [Google Scholar]
- 47.Michel B. After 30 years of study, the bacterial SOS response still surprises us. PLoS Biol. 2005;3:e255. doi: 10.1371/journal.pbio.0030255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Acar M., Mettetal J.T., van Oudenaarden A. Stochastic switching as a survival strategy in fluctuating environments. Nat. Genet. 2008;40:471–475. doi: 10.1038/ng.110. [DOI] [PubMed] [Google Scholar]
- 49.Liebermeister W., Noor E., Milo R. Visual account of protein investment in cellular functions. Proc. Natl. Acad. Sci. USA. 2014;111:8488–8493. doi: 10.1073/pnas.1314810111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bentley W.E., Mirjalili N., Kompala D.S. Plasmid-encoded protein: the principal factor in the “metabolic burden” associated with recombinant bacteria. Biotechnol. Bioeng. 1990;35:668–681. doi: 10.1002/bit.260350704. [DOI] [PubMed] [Google Scholar]
- 51.Paul B.J., Ross W., Gourse R.L. rRNA transcription in Escherichia coli. Annu. Rev. Genet. 2004;38:749–770. doi: 10.1146/annurev.genet.38.072902.091347. [DOI] [PubMed] [Google Scholar]
- 52.Kaczanowska M., Rydén-Aulin M. Ribosome biogenesis and the translation process in Escherichia coli. Microbiol. Mol. Biol. Rev. 2007;71:477–494. doi: 10.1128/MMBR.00013-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Farewell A., Kvint K., Nyström T. Negative regulation by RpoS: a case of sigma factor competition. Mol. Microbiol. 1998;29:1039–1051. doi: 10.1046/j.1365-2958.1998.00990.x. [DOI] [PubMed] [Google Scholar]
- 54.Abee T., Wouters J.A. Microbial stress response in minimal processing. Int. J. Food Microbiol. 1999;50:65–91. doi: 10.1016/s0168-1605(99)00078-1. [DOI] [PubMed] [Google Scholar]
- 55.Jishage M., Kvint K., Nyström T. Regulation of ς factor competition by the alarmone ppGpp. Genes Dev. 2002;16:1260–1270. doi: 10.1101/gad.227902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Grigorova I.L., Phleger N.J., Gross C.A. Insights into transcriptional regulation and σ competition from an equilibrium model of RNA polymerase binding to DNA. Proc. Natl. Acad. Sci. USA. 2006;103:5332–5337. doi: 10.1073/pnas.0600828103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Stewart E.J., Madden R., Taddei F. Aging and death in an organism that reproduces by morphologically symmetric division. PLoS Biol. 2005;3:e45. doi: 10.1371/journal.pbio.0030045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Maisonneuve E., Ezraty B., Dukan S. Protein aggregates: an aging factor involved in cell death. J. Bacteriol. 2008;190:6070–6075. doi: 10.1128/JB.00736-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Maisonneuve E., Fraysse L., Dukan S. Existence of abnormal protein aggregates in healthy Escherichia coli cells. J. Bacteriol. 2008;190:887–893. doi: 10.1128/JB.01603-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Brötz-Oesterhelt H., Beyer D., Labischinski H. Dysregulation of bacterial proteolytic machinery by a new class of antibiotics. Nat. Med. 2005;11:1082–1087. doi: 10.1038/nm1306. [DOI] [PubMed] [Google Scholar]
- 61.Bremer H., Dennis P. Feedback control of ribosome function in Escherichia coli. Biochimie. 2008;90:493–499. doi: 10.1016/j.biochi.2007.10.008. [DOI] [PubMed] [Google Scholar]
- 62.Bremer H., Dennis P.P. Modulation of chemical composition and other parameters of the cell by growth rate. In: Neidhardt F.C., Curtiss III R., editors; Umbarger H.E., editor. Escherichia coli and Salmonella: Cellular and Molecular Biology. Second Edition. Volume 2. American Society for Microbiology; 1996. pp. 1553–1569. [Google Scholar]
- 63.Campbell E.A., Westblade L.F., Darst S.A. Regulation of bacterial RNA polymerase σ factor activity: a structural perspective. Curr. Opin. Microbiol. 2008;11:121–127. doi: 10.1016/j.mib.2008.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Conway T., Schoolnik G.K. Microarray expression profiling: capturing a genome-wide portrait of the transcriptome. Mol. Microbiol. 2003;47:879–889. doi: 10.1046/j.1365-2958.2003.03338.x. [DOI] [PubMed] [Google Scholar]
- 65.Iwakura Y., Ito K., Ishihama A. Biosynthesis of RNA polymerase in Escherichia coli. I. Control of RNA polymerase content at various growth rates. Mol. Gen. Genet. 1974;133:1–23. doi: 10.1007/BF00268673. [DOI] [PubMed] [Google Scholar]
- 66.Sharma U.K., Chatterji D. Transcriptional switching in Escherichia coli during stress and starvation by modulation of sigma activity. FEMS Microbiol. Rev. 2010;34:646–657. doi: 10.1111/j.1574-6976.2010.00223.x. [DOI] [PubMed] [Google Scholar]
- 67.Sidgwick N.V., Aldous W.M. CVIII.-Influence of position on the solubility and volatility of the mono-and di-nitrophenols. J. Chem. Soc. Trans. 1921;119:1001–1012. [Google Scholar]
- 68.Taniguchi Y., Choi P.J., Xie X.S. Quantifying E. coli proteome and transcriptome with single-molecule sensitivity in single cells. Science. 2010;329:533–538. doi: 10.1126/science.1188308. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.