Contact Potential for Structure Prediction of Proteins and Protein Complexes from Potts Model

Abstract

The energy function is the key component of protein modeling methodology. This work presents a semianalytical approach to the development of contact potentials for protein structure modeling. Residue-residue and atom-atom contact energies were derived by maximizing the probability of observing native sequences in a nonredundant set of protein structures. The optimization task was formulated as an inverse statistical mechanics problem applied to the Potts model. Its solution by pseudolikelihood maximization provides consistent estimates of coupling constants at atomic and residue levels. The best performance was achieved when interacting atoms were grouped according to their physicochemical properties. For individual protein structures, the performance of the contact potentials in distinguishing near-native structures from the decoys is similar to the top-performing scoring functions. The potentials also yielded significant improvement in the protein docking success rates. The potentials recapitulated experimentally determined protein stability changes upon point mutations and protein-protein binding affinities. The approach offers a different perspective on knowledge-based potentials and may serve as the basis for their further development.

Introduction

Computer simulations are essential for studying biological macromolecules, including proteins. Along with the search space sampling, the energy function is the key component of modeling. The energy function can be either derived from the general physical principles (like a number of popular force fields (1, 2, 3, 4)) or based on diverse sets of known protein structures (various knowledge-based or statistical potentials (5, 6, 7, 8)). Statistical potentials provide the balance between accuracy and computational efficiency. Thus, they are successfully applied to many problems, such as discrimination of the native structure from decoys (9, 10), fold recognition (11), structure prediction (12), protein docking (13, 14, 15) and design (16, 17), and prediction of protein stability and affinity (18, 19, 20). Simplified energy models provide insight into general principles of protein folding and binding (21, 22, 23, 24).

One of the common approaches to developing statistical potentials is to calculate the probability of various structural features observed in a set of experimental protein structures relative to a reference state (7, 25). The probability is subsequently converted into energy using the inverse Boltzmann relation (7). However, the choice of the reference state, which serves as an imaginary protein model without interactions, is not a well-defined problem, and a number of approximations have been proposed. Among them are averaging (26), finite ideal-gas (10), spherical noninteracting (27), atom-shuffled (28), random-walk chain (29), and quasichemical (6) approximations. A different strategy for deriving statistical potentials is based on optimization of the energy parameters to maximize recognition of the native structure from a set of decoys (30, 31, 32). Despite the success of statistical potentials in various applications, their physical interpretation is not quite clear (33, 34, 35). Thus, derivation of the potential that provides fundamental and transparent insight is highly desirable.

Many problems that require describing direct (microscopic) interactions of objects (atoms, particles, etc.) from observation of microscopic configurations of the system of these objects can be successfully tackled by inverse statistical mechanics approaches (see (36, 37, 38) and references therein). In particular, the Ising (39) and Potts (40) models were used to study the collective behavior of neurons (41, 42), infer gene-interaction networks from experimentally observed transcription profiles (43), predict residue-residue contacts from multiple sequence alignments (37, 44, 45), study protein fitness landscapes (46, 47), and infer epistatic effects from fitness (48). Interaction parameters in these models are often recovered using the maximal entropy principle (49), resulting in the least structured (i.e., most generic) model that is still consistent with the experimental data. In this study, we show that inverse statistical mechanics formalism applied to the Potts model can be used to construct both residue-residue and atom-atom contact potentials, with the latter outperforming most existing energy functions in a number of tests. A closely related approach has already been utilized to derive residue-residue statistical contact potentials (50, 51, 52). However, these studies have not gained much attention, most likely because they were discussed from a different perspective, i.e., protein evolution and design, and no detailed analysis of the performance of the constructed potentials in protein structural modeling has been reported. In this article, we bridge this gap and show that the inverse Potts inference can be applied to construct simple but effective residue-residue and atom-atom contact potentials, with the latter performing on par with the best existing statistical potentials. The effectiveness of the potentials is attributed to 1) the consistent estimation of the energy parameters by the pseudolikelihood maximization approach and 2) explicit treatment of one-body energies at the learning stage.

Materials and Methods

Contact energies

Graph representation of protein structure

Noncovalent interactions in a protein can be modeled by a simple contact potential, suggesting that if two structural elements (called here interaction centers) are closer in space than a cutoff distance d_max, then these elements contribute some distance-independent value to the total energy. The interaction center can be the center of mass of a residue (for residue-residue potentials) or a single heavy atom (for atom-atom potentials). The number of distinct types of interaction centers (hereafter denoted as q) can vary depending on the level of generalization. In this study, we consider one residue-residue (RRCE20) and three atom-atom (AACE18, AACE20, and AACE167) contact potentials (RRCE and AACE are residue-residue and atom-atom contact energies, respectively; the summary description of the potentials is in Table 1). In the AACE18 potential, the atoms are grouped according to their physicochemical properties (19), yielding q = 18 distinct atom types. For the AACE20 potential, all heavy atoms in a residue are grouped together, resulting in q = 20 atom types. In the most detailed AACE167 potential, each heavy atom in the 20 residue types is considered separately, yielding q = 167 atom types. Hydrogen atoms or different protonation states of titratable amino acids were not considered.

Table 1.

Four Types Of Contact Potentials

Potential	Interaction centers	Number of Interaction Center Types, q	Description of Types	Number of Parameters
RRCE20	residue centroids	20	20 standard amino acids	230
AACE18	heavy atoms	18	18 atom types from (19)	189
AACE20	heavy atoms	20	20 standard amino acids	230
AACE167	heavy atoms	167	all heavy atoms in 20 standard amino acids	14,195

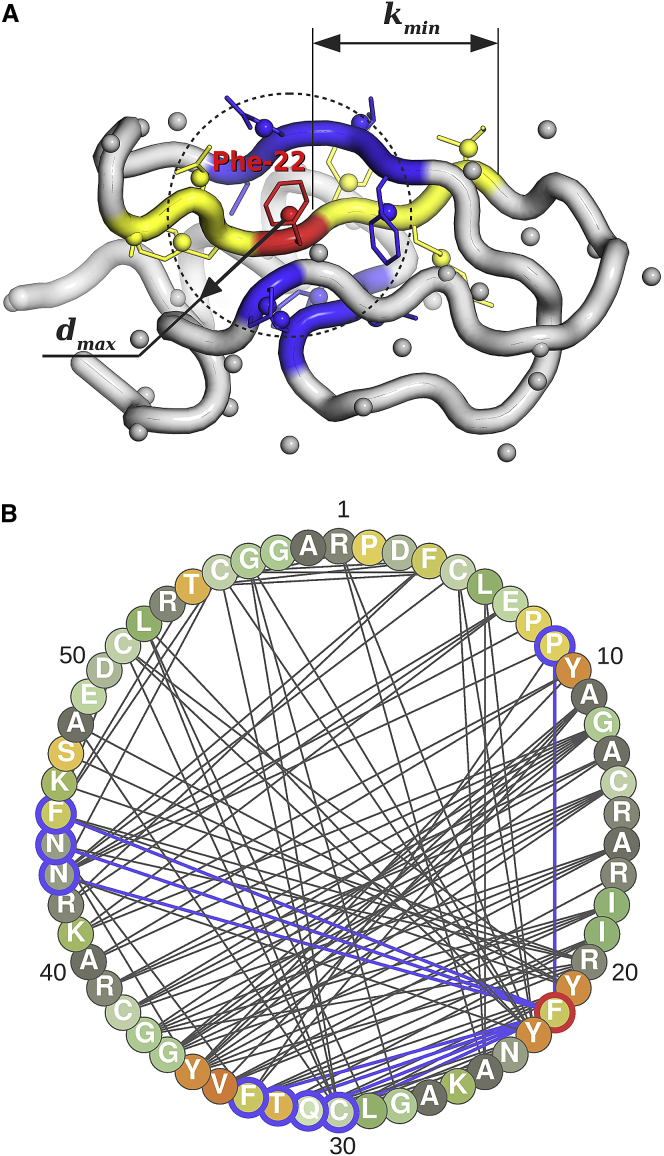
For the applications discussed in this work, it is sufficient to represent a single protein structure by an undirected graph G_p(V_p,E_p) (Fig. 1). In such a graph, the set of nodes V_p = {v_i} includes all interaction centers for a protein p. The set of edges E_p = {e_ij} comprises connections between interaction centers i and j, which are 1) closer in space than a cutoff distance d_max and 2) separated by at least k_min residues in the protein sequence (Fig. 1 A). For a given protein, the number of nodes L is fixed, but the number of edges may vary with the protein conformation. The only free parameters are d_max and k_min. Their optimal values are to be determined by the benchmarking. Besides k_min, there are no other assumptions on the protein topology (e.g., information on the intraresidue connectivity is not used).

Figure 1.

Graphical model of protein 3D structure. (A) A cartoon representation of the 58-residue bovine pancreatic trypsin inhibitor mutant 1G6X is shown. Residue centroids are shown by small spheres. Blue parts are an example of residue neighborhood, showing all residues with centroids within d_max = 7 Å from Phe22 (in red). Residues in yellow are within k_min = 3 positions in sequence from Phe22 and are not included in its neighborhood when calculating the parameters of the potential. (B) The graph G_p(V_p,E_p) is a simplified representation of the BPTI mutant structure at d_max = 7 Å and k_min = 3. Phe22 and its neighbors have red and blue borders, respectively. Nodes of the graph are color-coded according to the amino acid type to indicate their state.

Energy of protein

Each node in the graph G_p(V_p,E_p) can adopt one of q possible states (q is determined solely by the type of the potential; in this study, q = 18, 20, or 167; see Table 1). For clarity, a state of graph G_p(V_p,E_p) is denoted by the same letters as the graph vertices {v_i}, giving a vector

$$\overrightarrow{\mathbf{v}}=\left(v_1,\dots ,v_i,\dots ,v_L\right),$$ (1)

which is composed of integer numbers v_i ∈ (1,...,k,...,q), associated with atom (residue) types of the graph nodes. To derive the contact potentials, we introduce one- and two-body energy terms to account for self-energies and energies of contacting atom (residue) pairs within the protein. Thus, each graph node i of type v_i can be associated with one of q possible numbers $h_{v_i}$ from vector

$$\overrightarrow{\mathbf{h}}=\left(h{}_1,\dots ,h_k,\dots ,h_q\right).$$ (2)

In turn, each edge, e_ij, can be attributed to one of q × q values $J_{v_i,v_j}$ from a symmetric matrix

$$\mathbf{J}=\left(\begin{array}{lllll}{J}_{11}\hfill & \cdots \hfill & J_{1k}\hfill & \cdots \hfill & J_{1q}\hfill \\ ⋮\hfill & \ddots \hfill & ⋮\hfill & ⋰\hfill & ⋮\hfill \\ J_{k1}\hfill & \cdots \hfill & J_{kk}\hfill & \cdots \hfill & J_{kq}\hfill \\ ⋮\hfill & ⋰\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ J_{q1}\hfill & \cdots \hfill & J_{qk}\hfill & \cdots \hfill & J_{qq}\hfill \end{array}\right),$$ (3)

depending on types v_i and v_j of nodes i and j, respectively. For every type of potential, there are unique sets of $\overrightarrow{\mathbf{h}}$ and J parameters shared by all nodes and edges of the graph. However, each protein has a unique graph G_p(V_p,E_p) and atom (residue) type assignment vector $\overrightarrow{\mathbf{v}}$, which are solely determined by the conformation and amino acid composition of that protein.

Summation over the nodes and edges of the graph G_p(V_p,E_p) yields an expression for the energy of the protein

$$U\left(\overrightarrow{\mathbf{v}}\right)=\sum _{\left\{v_i\right\}}{h}_{v_i}+\sum _{\left\{e_{ij}\right\}}{J}_{v_i,v_j}.$$ (4)

It is similar to the expression for the energy (Hamiltonian) of the q-state generalized Potts model in statistical physics (40), in which pairwise interactions depend on the states of the interacting sites and the local fields (or self-energies) act on the single sites of the system.

For a fixed graph G_p(V_p,E_p) (i.e., fixed protein conformation), the probability of state $\overrightarrow{\mathbf{v}}$ is given by the Boltzmann (Gibbs) distribution

$$P\left(\overrightarrow{\mathbf{v}}\right)=\frac{1}{Z}\exp \left(-\beta U\left(\overrightarrow{\mathbf{v}}\right)\right),$$ (5)

where β is a scaling factor (which, in statistical physics, means the inverse energy of thermal fluctuations at temperature T, β = 1/RT), and Z is the statistical sum over the set of all possible system states $\left\{\overrightarrow{\mathbf{v}}\right\}$:

$$Z=\sum _{\left\{\overrightarrow{\mathbf{v}}\right\}}\exp \left(-\beta U\left(\overrightarrow{\mathbf{v}}\right)\right).$$ (6)

Parameters $\overrightarrow{\mathbf{h}}$ and J (Eqs. 2 and 3) are not known a priori but can be inferred from a large set of known protein structures (see below). Probability distribution in Eq. 5 is also known as Markov random field (53) on graph G_p(V_p,E_p).

Pseudolikelihood approximation

Because native protein sequences are close to optimal for their three-dimensional structures (54), for a given structure of a protein, an accurate energy model should assign highest probability to the native sequence compared to any non-native one. This concept, for example, helps in protein design when one tries to find a sequence that best fits a given protein fold (55). In terms of the energy function (Eq. 4), the task can be formulated as an optimization problem of finding values of $\overrightarrow{\mathbf{h}}$ (Eq. 2) and J (Eq. 3) that maximize the probability of observing the native state

$$P\left({\overrightarrow{\mathbf{v}}}_{\mathrm{nat}}\right)=\underset{\left\{\overrightarrow{\mathbf{v}}\right\}}{\max }\left(P\left(\overrightarrow{\mathbf{v}}\right)\right).$$ (7)

However, the optimization problem (Eq. 7) cannot be solved directly because of the combinatorial complexity of the partition function (Eq. 6). To make the problem tractable, the probability function (Eqs. 5 and 6) for the native state (sequence) is approximated by a product of local conditional probabilities (pseudolikelihoods)

$$\mathit{P}\left({\overrightarrow{\mathbf{v}}}_{\text{nat}}\right)\approx \prod _i\frac{\exp \left(-\beta \mathit{U}\left({\mathit{v}}_{\mathit{i},\text{nat}}\right)\right)}{\sum _{\mathit{k}=1}^{\mathit{q}}\exp \left(-\beta \mathit{U}\left({\mathit{v}}_{i,k}\right)\right)},$$ (8)

where multiplication is performed over all atoms (residues) and summation in the denominator is over all possible q states of a single interaction center. U(v_i,k) is the “energy” of a single interaction center, or G_p(V_p,E_p) node, in state k

$$U\left(v_{i,k}\right)=h_k+\sum _{\left\{e_{ij}\right\}}{J}_{k{k}^{\text{'}}},$$ (9)

where summation is performed over all other nodes in G_p(V_p,E_p) connected to node i by an edge. The temperature factor β = 1 is used throughout the work. In the pseudolikelihood approximation, all nodes are in the native states, and only the state of a current node varies to calculate the “pseudo”-statistical sum (denominator in Eq. 8). The pseudolikelihoods are known to provide asymptotically consistent estimates of parameters $\overrightarrow{\mathbf{h}}$ and J (56) and are successfully applied to large sample size problems in physics and biology (37, 51, 57).

In the above formalism, the optimization problem (Eq. 7) is reduced to solving the system of differential equations

$$\{\begin{array}{l}\frac{\partial \left(-\log \mathit{P}\left({\overrightarrow{\mathbf{v}}}_{\mathrm{nat}}\right)\right)}{\partial {\mathit{h}}_{\mathit{k}}}=0,\mathit{k=}\mathrm{1}\mathit{,}\dots \mathit{,q}\hfill \\ ⋮\hfill \\ \frac{\partial \left(-\log \mathit{P}\left({\overrightarrow{\mathbf{v}}}_{\mathrm{nat}}\right)\right)}{\partial {\mathit{J}}_{\mathit{k}{\mathit{k}}^{\text{'}}}}=0,\mathit{k=}\mathrm{1}\mathit{,}\dots \mathit{,q}\mathrm{and}{\mathit{k}}^{\mathit{\text{'}}}\mathit{=}\mathrm{1}\mathit{,}\dots \mathit{,q}\hfill \end{array}.$$ (10)

For convenience, in the analytical deduction of the derivatives in Eq. 10, we used negative pseudo-log-likelihoods. More details of the pseudolikelihood optimization are in the Supporting Materials and Methods.

The solution to system of equations (Eq. 10) within the graph G_p(V_p,E_p) would provide $\overrightarrow{\mathbf{h}}$ and J specific only for one protein. To obtain generic potentials, we solved the system of equations (Eq. 10) for a composite graph G(V,E) constructed by joining graphs G_p(V_p,E_p) for all individual proteins in a large set of protein structures (details on this “training” set are in Materials and Methods). The product in Eq. 8 runs over all nodes in that composite graph, whereas all other considerations remain the same.

Once $\overrightarrow{\mathbf{h}}$ and J values are obtained for the training set, only the J matrix, which constitutes the contact potential, is applied to several problems in protein modeling (see Results). The role of self-energies $\overrightarrow{\mathbf{h}}$ is to provide an accurate estimation of J (also discussed in the Results).

It is worth noting that in terms of the graph representation, the development of “classical” statistical potentials is usually limited to collecting information on the number of nodes in the composite graph in state k and the number of edges connecting nodes in states k and k′ without solving Eq. 10.

Training set of protein structures

To calculate the Potts parameters $\overrightarrow{\mathbf{h}}$ and J, a nonredundant training set of 6338 protein chains was collected by the Protein Sequence Culling Server (58). Only x-ray structures with resolution ≤2.0 Å, R-factor ≤0.25, and ≥40 residues per chain were selected. Redundancy was removed at 25% sequence identity cutoff. Individual chains were extracted from Protein Data Bank (PDB) asymmetric units, and missing heavy atoms were restored by the PDB2PQR software (59) using CHARMM topology parameters (1). Alternative residue conformations, if present in the original PDB structure, were removed by the same PDB2PQR program. Nineteen chains from the initial pool of 6338 structures could not be processed either because of multiple models in the original PDB file or a large number of missing heavy atoms (>10%). These structures were left out from the consideration, yielding the final set of 6319 chains from 6092 different PDB entries.

Parameters of the contact potential

At each value of the distance cutoff d_max (from 4 to 15 Å, with 0.1 Å step) and sequence separation k_min (from 1 to 10, with step 1), we built the graph G(V,E) for 6319 single protein structures from the training set. Minimization of the objective function (Eq. 8) with derivatives (Eq. 10) was performed by the in-house C program specifically designed for this purpose. The GNU Scientific Library (http://www.gnu.org/software/gsl/) implementation of the quasi-Newton Broyden-Fletcher-Goldfarb-Shanno method (60) (bgfs2 module of the GNU Scientific Library) was used. Minimization started with all the target parameters set to zero and proceeded iteratively until the norm of the gradient achieved the absolute tolerance of 10⁻³.

CASP decoys

Decoys for near-native structure detection were compiled from all tertiary structure predictions submitted to Critical Assessment of Structure Prediction (CASP) rounds X and XI (61, 62). Following the CASP practice, the models were analyzed at the level of evaluation units, or domains, assigned by the assessors. To make the energy estimates consistent, partial models with incomplete chains were removed from the pool of decoys. Overall, 224 domains from 172 protein chains were selected for testing. PDB files of models and the tables with models’ parameters and ranking according to global distance test, total score (GDT_TS) (63) were downloaded from the CASP repository (http://predictioncenter.org/download_area/).

Scoring of CASP decoys

Performance of different energy functions on the CASP decoys were assessed in terms of the Z-score, defined as the distance (measured in standard deviations) between the energy of the best (highest GDT_TS score) model U_b (or the native structure) calculated by the tested function and the mean energy of all decoy structures $\langle U\rangle$

$$\text{Z}\text{-}\text{score}=\frac{U_b-\langle U\rangle }{\sigma },$$ (11)

where σ is the standard deviation of energy U (given by the tested function) for all decoys in the set. In addition to the Z-score (Eq. 11), we also used the Pearson correlation coefficient between energies and GDT_TS scores of the models, as well as the normalized rank of the best-energy model

$$1-R=1-\frac{R_{\text{GDT\_TS}}}{N_{\text{tot}}},$$ (12)

where R_{GDT_TS} is the rank by the GDT_TS score of the best-energy model, and N_tot is the total number of the models in the set. The form 1 − R was used to transform the normalized rank to the increasing function of the scoring method effectiveness.

For the assessment of the potentials, the energy of a protein model was calculated by simple summation of the inferred couplings J over all pairs (i,j) of interaction centers that are consistent with distance cutoff d_max used to derive the potential

$$U_p=\sum _{\left(i,j\right)}{J}_{v_i,v_j}.$$ (13)

The sum over the self-energies (local fields) $\overrightarrow{\mathbf{h}}$ was omitted in Eq. 13 because it does not depend on the protein conformation and thus does not affect ranking of the model structures. Subscripts v_i, v_j enumerate types of atoms (residues) i and j, respectively (v_i ∈ 1,2,...,q, where q = 18, 20, or 167 depending on the contact potential type; see Table 1).

Data set of point mutations

To evaluate applicability of the contact potentials to prediction of the change in the folding free energy ΔΔG upon mutations, we used a data set of 2648 point mutations for 131 globular proteins with experimentally resolved x-ray or NMR structure, for which mutation-induced change in protein stability was determined experimentally (64). The set is derived from the ProTherm database (65). 235 mutations in the set originate from NMR structures (12 distinct PDB IDs) with the number of models from 5 to 46. Because the data set contains experimentally resolved structures for the wild-type proteins (those deposited in the PDB) only, the structure of a mutant was obtained by manual replacement of the corresponding side chain. The replacement was followed by the SCWRL4 (66) repacking of the residues within 6 Å distance to the mutated residue (the residue-residue distance defined as any atom to any atom of the two residues). To compensate for possible biases introduced by SCWRL4, the same relaxation procedure was applied to the same residues of the wild-type structure. For each mutated residue X, relative solvent exposure was calculated as the ratio between the absolute solvent-accessible surface area (SASA) of this residue in the wild-type structure and the reference SASA for this type of residue in the Gly-X-Gly tripeptide (67). A residue was considered to be at the surface if >20% of its SASA was exposed.

Assuming that the folding free energy of a protein is proportional to its internal energy in the folded state, ΔΔG_calc was approximated by the difference in internal energies (Eq. 13) of the mutant and the wild-type:

$$\mathit{\Delta \Delta }{G}_{\text{calc}}=U_{\text{mut}}-U_{\text{WT}}.$$ (14)

Docking decoys

The initial set of 1020 binary protein-protein complexes, for which the structures of the complex (in PDB biological assembly) and the structure of both unbound components are available, was generated by the ProPairs tool (68) run locally on a PDB snapshot with the default parameters. The set was postprocessed to retain only pairs with a high similarity of bound and unbound partners (sequence identity >96% and coverage >80% (69)), which reduced the set size to 427. Additional purging of structurally similar (template modeling-score (70) >0.8) and large (>2500 residues per interactor) complexes yielded the final set of 396 complexes (Dockground Benchmark 4.0 (71) http://dockground.compbio.ku.edu). For comparison, we also used 230 protein-protein complexes in the docking Benchmark 5.0 from Weng’s group (69).

The unbound proteins from both benchmarks were docked by the fast Fourier transform rigid-body docking program GRAMM (72, 73) at low resolution, with 3.5 Å grid step and 10° angular interval. The top 100,000 matches per complex, ranked solely by the shape complementarity, were compared to the reference complex obtained by structural superposition of the unbound monomers onto corresponding proteins in the co-crystallized complex. The quality of the docking models was assessed by the Critical Assessment of Predicted Interactions (CAPRI) criteria (74) (Table S1). Docking success rate was defined as the fraction of complexes for which at least one successful prediction (defined at different accuracy categories) was in the top n predictions. The docking predictions were further reranked by the energy of the proteins A and B interface U_AB, calculated (similarly as for individual proteins; see Eq. 13) by summing up the couplings J over all pairs (i ∈ A, j ∈ B) of the interchain contacts closer in space than d_max:

$$U_{\text{AB}}=\sum _{\left(i\in A,j\in B\right)}{J}_{v_i,v_j}.$$ (15)

The predicted matches were clustered to identify the most probable hit within each putative docking funnel. Only one lowest energy prediction from each cluster was selected.

Affinity benchmark

To access how U_AB (Eq. 15) correlates with the protein-protein binding affinities, the set of 92 protein-protein complexes with known co-crystallized structures and experimentally determined binding affinities ΔG_exp was selected from the Affinity Benchmark version 2.0 (69). We considered only the rigid-body cases—those without significant conformational changes upon binding. Such cases were defined as bound/unbound interface root mean-square distance < 1.5 Å and fraction of non-native contacts (the number of non-native residue-residue contacts in the predicted complex divided by the total number of contacts in that complex (74)) < 0.4.

Energy functions

For comparison, we tested the following knowledge-based energy functions: discrete optimized protein energy (DOPE) (27), distance-scaled, finite ideal-gas reference (DFIRE) (10), dipolar DFIRE (dDFIRE) (75, 76), random walk (RW) and RWplus (29), generalized orientation-dependent all-atom potential (GOAP) (77), OPUS-PSP (78), RF-HA-SRS (28), and RF-CB-SRS-OD (79). DOPE, DFIRE, RW, and RF-HA-SRS are all-heavy-atom distance-dependent potentials, whereas RWplus, dDFIRE, and GOAP have an additional orientation-dependent term. OPUS-PSP is an orientation-dependent contact potential defined for blocks of side-chain atoms. RF-CB-SRS-OD is a residue-level distance- and orientation-dependent energy function. In addition, a simple residue-residue contact potential by Miyazawa and Jernigan MJ3h (80) was also tested because of its best performance in scoring of protein docking decoys (81, 82).

Results and Discussion

Parameters of the contact potentials

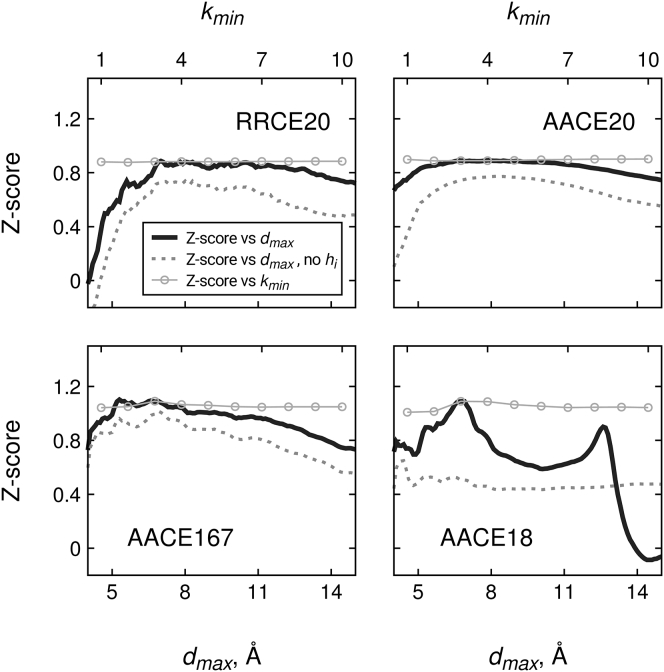
Different distance cutoffs d_max and sequence separations k_min may result in a different graph model for the protein structure (Fig. 1) and thus in different sets of local fields $\overrightarrow{\mathbf{h}}$ and couplings J that maximize the likelihood function (Eq. 8). To find the optimal d_max and k_min values, we derived our four potentials RRCE20, AACE20, AACE167, and AACE18 (Table 1) using 1110 various d_max and k_min combinations (see Materials and Methods). The performance of the potentials was evaluated by discriminating best models from the CASP decoys (Figs. 2 and S1).

Figure 2.

Performance of residue-residue and atom-atom contact potentials in best-model structure recognition from CASP decoys. Statistical potentials derived at different values of sequence separation k_min and distance cutoff d_max were used to score models of 224 protein domains submitted to CASP rounds X and XI. Performance is measured as Z-score of the highest GDT_TS score model averaged over all 224 evaluation units. The solid line shows distance dependence of the Z-scores (bottom horizontal axis) at the optimal sequence separation k_min = 3. Performance of the potentials derived without local fields $\overrightarrow{\mathbf{h}}$ is shown by the dashed lines. Thin gray lines with circles show the Z-score dependence on the sequence separation k_min (top horizontal axis) at d_max = 8.0 Å (RRCE20, AACE20) and d_max = 6.9 Å (AACE167, AACE18). The plots are cross-sections of the heat maps in Fig. S1 at specific values of sequence separation k_min and distance cutoff d_max.

All four potentials performed poorly when contacts between residues adjacent in the sequence $\left(k_{min}\mathrm{\gtrsim }1\right)$ were considered in the derivation of the contact energies. Residues that are close in sequence are close in space primarily because of the covalent bonds. Thus, taking such contacts into account obscures the treatment of nonbonded interactions, especially at smaller d_max (83). As d_max increases, more interacting pairs contribute to the potentials, and the relative contribution of sequence-adjacent residues declines rapidly. However, with complete exclusion of the sequence-adjacent residues, some portion of the nonbonded interaction energy remains unaccounted for, causing a drop, albeit slight, in the performance. The optimal performance was observed at k_min = 3. Thus, the potentials derived at this k_min value were used in the further analysis unless stated otherwise. Despite high correlation of the RRCE20 contact energies and the well-known Miyazawa-Jernigan matrix MJ3h (80) (R = 0.90), the former still shows better decoy discrimination by all three measures (Fig. 4).

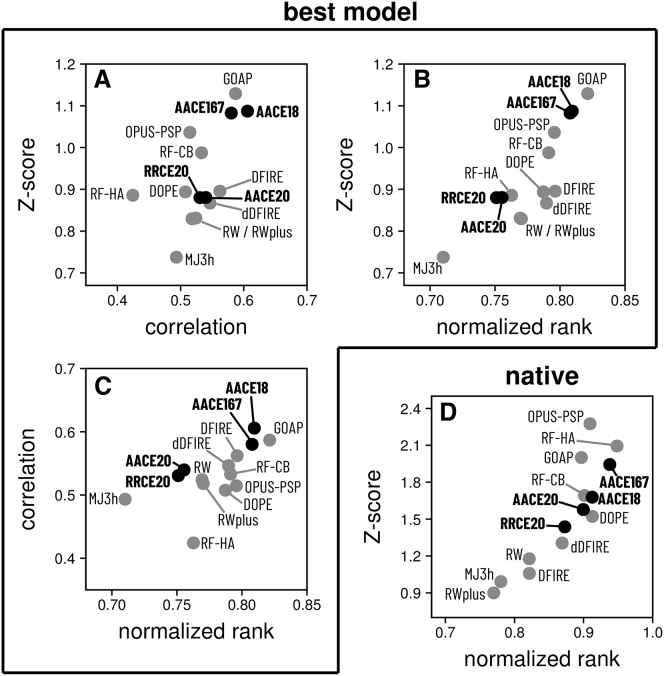
Figure 4.

Performance of various energy functions in the best-model structure recognition from CASP decoys. The best model’s Z-score, its normalized rank 1 − R, and Pearson’s correlation coefficient r of the energy score and GDT_TS score of models, all averaged over 224 CASP decoy sets, are shown for different scoring functions on scatter plots (A)–(C) (one plot per each combination of the above three assessment scores). For comparison, average Z-scores and normalized ranks for the native structure are shown on plot (D).

The RRCE20 and AACE20 potentials showed very similar trends with varying d_max. This suggested that if all atoms within one residue are assigned to one type, the way of calculating contacts (either between residue centroids or between residue heavy atoms) has a negligible effect on the energy function. The optimal performance for these potentials was achieved within a broad d_max interval (6–11 Å). If the protein heavy atoms were split into 167 different types, the trend remained similar. However, the best performance is observed at lower d_max = 5 ÷ 8 Å; Z-score increases significantly from 0.89 to 0.88 for RRCE20 and AACE20, respectively, to 1.09 for AACE167.

The distinct feature of the AACE18 potential is the two sharp peaks of enhanced performance (in terms of Z-score, quantitatively similar to the performance of the much more complex AACE167) at d_max ∼ 6.9 and ∼12.6 Å (Fig. 2 D). The exact reason for the two-peak distribution is not clear because the statistical potential parameters are derived from a self-consistent solution of the system of equations (10), in which elucidating the effect of a particular factor is nontrivial if possible at all. However, the peaks do not appear when the potential is derived using a reduced model (leaving out $h_{v_i}$ terms in Eqs. 4 and 9; dashed lines in Fig. 2 D). This points to an important interconnectivity between one- and two-body energies, which substantially elevates the efficiency of the potential at certain d_max. Generally, the reduced model yields significantly less effective contact potentials (the dashed lines in Fig. 2 are all below the solid lines). AACE18 correlates poorly (R = 0.43) with the original atomic contact energies from (19).

The convergence analysis of the inferred energy parameters showed that they are already close to optimal. Thus, further increase in the number of structures deposited to PDB can only marginally improve the potentials (Figs. S2 and S3).

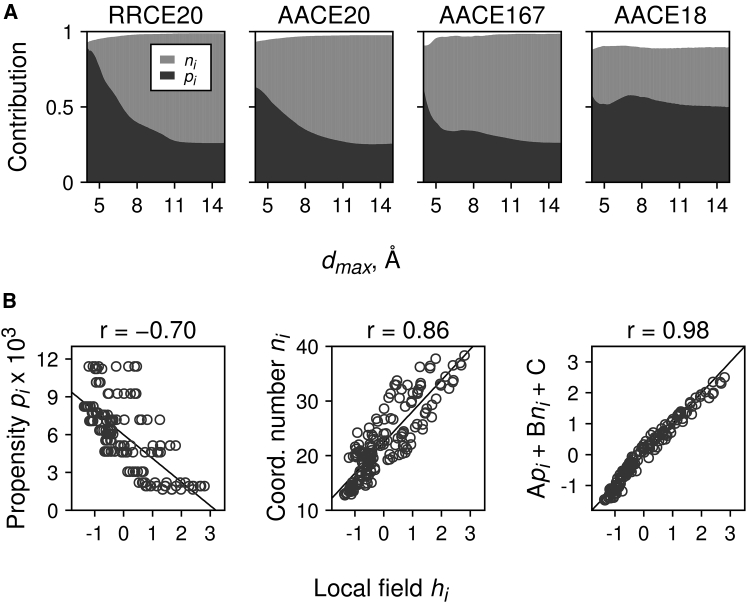
Local fields

After the local fields $\overrightarrow{\mathbf{h}}$ and couplings J are learned by solving the system of equations (Eq. 10), one-body terms (or self-energies) can be omitted in protein structure energy estimates and scoring applications (Eqs. 13, 14, and 15). Nevertheless, the local fields are essential internal parameters of the model at the learning stage (Eqs. 7, 8, and 9), boosting the effectiveness of the resulting two-body energies J (dashed and solid lines in Fig. 2). Below, we provide a detailed analysis of how the trained h_k parameters are related to the basic features of individual interaction center types.

Empirically, we found that the one-body energies $\overrightarrow{\mathbf{h}}$ can be described by a linear combination of two interaction centers features (Fig. 3 B, rightmost panel)

$$h_k=a\times p_k+b\times n_k+c,$$ (16)

where p_k and n_k are the propensity (frequency of occurrence) and the average coordination number (in graph terminology, the average number of node neighbors in the graph G(V,E) connected by an edge) for the interaction centers of type k in the training set, respectively. The coordination number is inversely related to the exposure of the interaction center to the solvent because the interface atoms or residues have less contact with other interaction centers than those in the protein core.

Figure 3.

Properties of the local fields $\overrightarrow{\mathbf{h}}$. (A) The contribution (relative importance) of atom propensities p_k and average coordination numbers n_k to local fields $\overrightarrow{\mathbf{h}}$ for the least-squares linear model (Eq. 16) with varying cutoff distance d_max is shown, calculated for RRCE20, AACE20, AACE167, and AACE18 potentials, respectively. The data was obtained by the averaging-over-orderings method by Lindeman et al. (94) as implemented in the relaimpo package (95) for R statistical computing language. (B) As an example, h_k correlations with atom propensities p_k and coordination numbers n_k and their linear combination (Eq. 16) are shown for the AACE167 potential derived at d_max = 6.9 Å and k_min = 3.

The two parameters p_k and n_k contribute ≥90% to the fields $\overrightarrow{\mathbf{h}}$ for all potentials and d_max (Fig. 3, A–D). For the RRCE20 and AACE20 potentials (Fig. 3, A and B), the propensities contribute significantly more at smaller distances, whereas at larger d_max, the coordination numbers become more important. The AACE167 potential showed qualitatively similar behavior. The main difference was that contribution of the propensities became larger at significantly smaller d_max (a steep dark-gray peak on the left-hand side of Fig. 3 A). The AACE18 potential showed distinctly different patterns (Fig. 3 A, rightmost panel). For this potential, the relative importance of p_k and n_k weakly depends on d_max, and the propensities generally have a higher contribution to local fields than the coordination numbers (e.g., at optimal d_max = 6.9 Å, n_k-values contribute ∼65 and 36% to the local fields for the AACE167 and AACE18 potentials, respectively).

Discrimination of protein near-native structures

The quality of knowledge-based energy functions is often assessed by their ability to recognize the native structure or the best model in a set of decoys (9, 84, 85). Models submitted to the CASP competition (86) are believed to be the most challenging (87) and have been recently used by others to benchmark their statistical potentials (79, 88). Thus, we tested our four potentials on the CASP decoys from rounds X and XI of the competition (61, 62). Identifying the best model from the decoys (that also corresponds to the real-case modeling scenario, when the native structure is not known) is generally more challenging than identifying the native structure (79, 87). This is also the case for our potentials: Z-scores for the best model are on average in the 0.9–1.1 range, whereas corresponding numbers for the native structure are 0.6–0.8 Z-score units higher (Fig. S4). Although discrimination of the best model is significantly harder than that of the native structure (which also substantially complicates comparison of different scoring functions), it is more relevant to the real-case scenario when only the models, but not the native structure, are available. Thus, unlike a number of other studies on scoring functions, we focused our analysis on the ability of the potentials to discriminate the best model and compared their performance to 10 state-of-the-art knowledge-based energy functions (Fig. 4).

In terms of the Z-score (Eq. 11), the AACE18 and AACE167 potentials are among the top ones, only behind GOAP (77). Assessment by the normalized rank (Eq. 12) also puts AACE18 and AACE167 on top of the list (1 − R = 0.809 and 0.808, respectively), only slightly behind GOAP (1 − R = 0.821). High correlation of energy and structural accuracy scores of the decoys indicates good scoring (77). In this respect, AACE18 shows the best performance (the average correlation coefficient 0.606), followed by GOAP (0.587) and AACE167 (0.585) (Fig. 4). These values are similar to correlations reported elsewhere (e.g., (77)). Statistical analysis reveals, however, that the differences between AACE18, AACE167, and GOAP are marginal and all three potentials have comparable performance, significantly better than the other tested energy functions (Table S2). The other two assessment scores (Z-score and normalized rank) are not as discriminative (see corresponding p-values in Table S2). However, they still place AACE18 and AACE167 among the top ones, only slightly behind GOAP. The way to establish exact ranking for the 14 potentials is not obvious. However, consistency between the three assessment scores should indicate that GOAP, AACE18, and AACE167 are the three best-performing energy functions in the best-model discrimination test. In discrimination of the native structure test (Fig. 4 D), the performance order is slightly different, with OPUS-PSP and RF-HA-SRS on top of the list by the Z-score, followed by GOAP and AACE167. This suggests that some energy functions are more tuned for high-resolution decoys but are less successful in discriminating models of moderate accuracy. In this respect, AACE167 is more sensitive in selecting the native structure compared to AACE18 (Fig. 4 D).

The residue-level RRCE20 and AACE20 potentials perform poorly by all measures, suggesting the need for atomic details for effective contact potentials. On the other hand, our contact potentials AACE18 and AACE167, which are quite simple (e.g., no distance or orientation dependency), are sufficient for capturing most structural details of the protein models, which usually is achieved by much more complex energy functions.

Protein stability changes upon point mutations

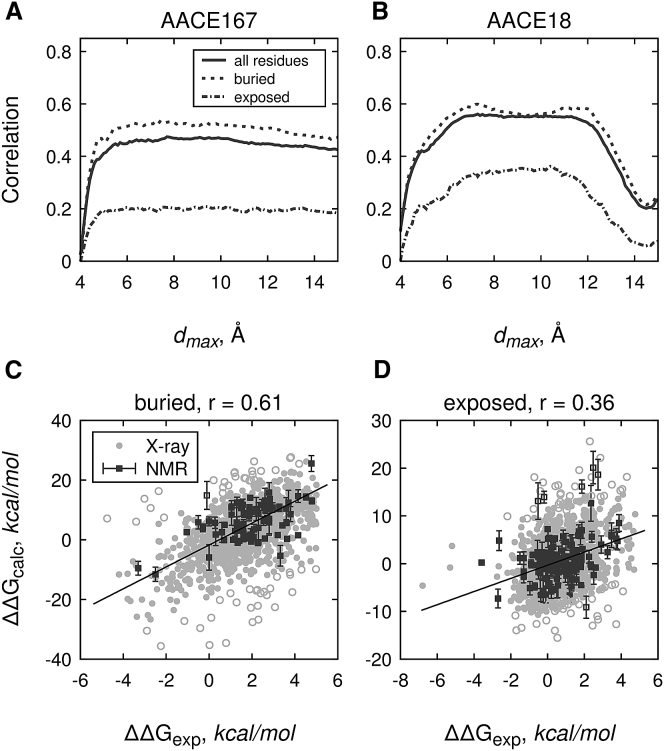
The top-performing AACE18 and AACE167 potentials were further tested for their ability to predict the change in protein stability ΔΔG upon single mutation (see Materials and Methods). The testing was done on the benchmark set of 2648 point mutations (64) in terms of Pearson’s r for correlation of the calculated ΔΔG_calc (Eq. 14) and experimental ΔΔG_exp, separately for the buried and the exposed residues at various distance cutoffs d_max (Fig. 5). Correlations were calculated after removal of outliers, which include all points with deviations from the least-squares linear fit outside a 2.5–97.5% range. Surface residues are generally more susceptible to structural variations because their side chains are less constrained by the neighbors. In addition, there is a significant solvent contribution to their energetics. These effects are especially hard to account for by any energy function. Indeed, both potentials had a significant drop in performance (by ∼50% in terms of r) for the surface residues compared to the performance for the buried residues (Fig. 5, A and B). Overall, the AACE167 performance almost saturates at r ∼0.45 for d_max > 5 Å. However, the predictions for the surface residues are much less accurate compared to the predictions for the buried ones (r ∼0.2 and 0.5, respectively). For d_max < 5 Å, the performance drops almost to zero regardless of the residue exposure to solvent.

Figure 5.

Prediction of protein stability changes upon point mutations by the AACE167 and AACE18 potentials. Experimentally determined ΔΔG values for 2648 point mutations from 131 proteins are correlated with the ones calculated by AACE167 (A) and AACE18 (B) potentials at different cutoff distances d_max. As an example, correlations for the AACE18 potential at d_max = 6.9 Å and k_min = 3 are shown separately for (C) buried (relative SASA ≤ 0.2, 1429 residues) and (D) exposed residues (relative SASA > 0.2, 1219 residues), respectively. Light gray circles correspond to the x-ray structures. Dark gray squares are based on multimodel NMR structures and show calculated ΔΔG values averaged over all states, with the error bars showing standard deviations. All points with deviations from the least-squares linear fit (solid black lines) not falling into (0.025, 0.975) percentile range were treated as outliers, shown by open circles/squares.

The AACE18 energy function also has generally better predictions for the buried residues than for the exposed ones. However, the performance is not constant at d_max > 5 Å (Fig. 5 B). Similar to the best-model recognition from the CASP decoys (Fig. 2 D), the elevated r values are observed for the buried residues at two d_max values, 7 and 12 Å. For the surface residues, however, such peaks are not observed, and the best recapitulation of the experimental energies is achieved at d_max ∼ 8 ÷ 11 Å (Fig. 5 B). Interestingly, this d_max region coincides with the region of lower performance on the buried residues. This distance range roughly corresponds to the water-mediated interactions (89), which indicates that solvent effects are better treated by the simpler AACE18 rather than by the more complicated AACE167 potential.

An example of correlation between ΔΔG_exp and ΔΔG_calc calculated by the AACE18 potential for buried and exposed residues (Fig. 5, C and D) indicates that NMR structures yield slightly more accurate ΔΔG_calc estimates than the x-ray structures (r = 0.65 vs. 0.58 for buried and 0.38 vs. 0.34 for exposed residues, correspondingly). This might be related to a more adequate environment of the NMR models and to averaging over the ensemble of all models in the PDB entry. However, a direct comparison is problematic because the sets of NMR and x-ray structures consist of different proteins.

In comparison with other energy functions, AACE18 potential is ranked sixth, with r_AACE18 = 0.554 compared to r_dDFIRE = 0.591 of the top performing dDFIRE (Fig. S6 A, one-sided p-value = 0.023 at 95% confidence). However, the difference in correlations between the first five energy functions is not statistically significant (p-value = 0.189 between the first—dDFIRE—and the fifth—DOPE). The performance of the other three potentials, AACE167, AACE20, and RRCE20, is significantly worse (Fig. S6 A).

Contact potentials in protein docking

Predicting protein-protein complexes from the structures of the individual monomers (protein docking) remains a challenging problem in computational structural biology because of a fine balance between different factors (shape complementarity, solvent and electrostatic effects, conformational changes, etc.) that enable specific binding but are hard to accurately account for. Thus, the protein docking problem is often addressed by coarse-grained approaches, at least at the initial modeling stages (90).

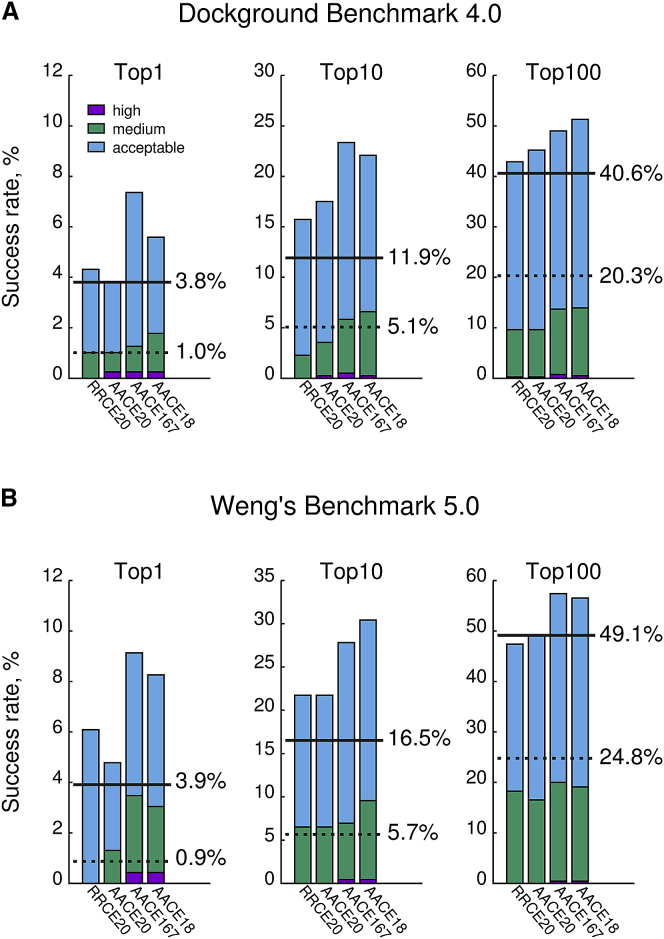
We tested how well our contact potentials score the low-resolution docking predictions by GRAMM (72, 73) (Figs. 6 and S5). Models of complexes were assessed according to the CAPRI criteria (Table S1). Predictions with acceptable and better quality were considered successful. Similar to the CASP decoys (Fig. S1), the best discrimination of the near-native models is achieved at the distance cutoffs d_max = 6.9 Å for AACE167 and AACE18 potentials and d_max = 8.0 Å for RRCE20 and AACE20. However, the best performance is achieved at larger sequence separation k_min = 5. All four energy functions, in most cases, outperform the Miyazawa-Jernigan MJ3h statistical potential (80), which has been recently shown to be one of the top-performing scoring functions in protein docking (81). The largest improvement over MJ3h is achieved by the atom contact potentials AACE167 and AACE18. The AACE18 also proved its efficiency in discriminating near-native docking matches in a recent joint CASP/CAPRI round of the CASP12 competition (91).

Figure 6.

Scoring of low-resolution docking decoys. The top 100,000 matches per complex with highest shape complementarity score from GRAMM were evaluated by RRCE20, AACE20, AACE167, and AACE18 contact potentials, followed by L-root-mean-square-deviation-based clustering with 10 Å radius, for (A) Dockground Benchmark 4 and (B) Weng’s Benchmark 5. The lowest energy model from each cluster was further assessed by the CAPRI criteria (see Table S1). The docking success rate for 1, 10, and 100 best scored clusters was calculated (bars). Dashed lines are the baselines of the success rates when models are ranked according to the raw shape complementarity. Solid lines are docking success rates attained by the Miyazawa-Jernigan MJ3h statistical potential.

Interestingly, the reference structure often has a higher (worse) energy score than the top near-native docking clusters (Fig. S7). This is likely caused by atom clashes in the reference structure obtained by simple structural superimposition of the unbound monomers onto corresponding bound conformations. Our docking protocol, albeit low resolution, is able to find better-scoring near-native matches. The true native conformation is generally scored higher in the case of AACE18 and in particular AACE167 potentials (Fig. S7), suggesting that taking into account protein flexibility might further improve the ranking. However, as Fig. S7 shows, selection of the native conformation from the docking decoys is still difficult. Similar success rates were reported previously for popular protein-protein docking scoring functions ZRANK (92) and integration of residue- and atom-based potentials for docking (93).

Correlation with protein binding affinity

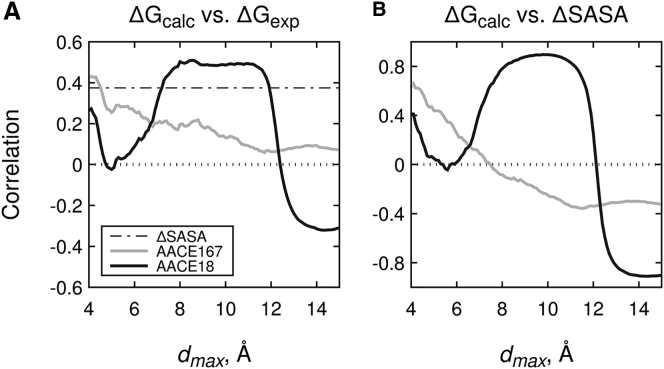
Finally, we analyzed correlation of the interchain energy U_AB (Eq. 15) or ΔG_calc calculated by the atom AACE18 and AACE167 potentials at various distance cutoffs d_max for the protein complexes in the affinity benchmark (69), with the experimentally determined binding affinities ΔG_exp (Figs. 7 and S6 B). The experimental binding free energies were recapitulated significantly worse by the more complex AACE167 potential than by the simpler AACE18 (Fig. 7 A). Even a naïve ΔG predictor, which approximates binding free energy by the change in the SASA (ΔSASA) upon complex formation, outperformed AACE167 at almost all d_max (except small d_max ∼ 4 Å). At the same time, AACE18 again performed significantly better at d_max = 8 ÷ 11 Å than at other distances, which correlates with the data on the point mutations for the exposed residues (Fig. 5 B). In this d_max range, the AACE18 energies tend to be highly correlated with ΔSASA (Fig. 7 B), which is not the case for the more complex AACE167. This indicates that desolvation effects are largely captured by the AACE18 potential, albeit in a simple form ΔG_desolvation ∼ ΔSASA. However, AACE18 performance is still superior to the naïve ΔSASA predictor (Fig. 7 A) as well as all other energy functions tested on the affinity benchmark (r_AACE18 = 0.508, followed by the DFIRE potential with r_DFIRE = 0.445; Fig. S6 B). In comparison, specialized affinity prediction algorithms still have a better performance, with correlations up to r = 0.53 for the full set and r = 0.75 for rigid-body cases (69).

Figure 7.

Prediction of proteins binding affinities by AACE167 and AACE18 potentials. (A) Experimentally determined binding free energies (ΔG_exp) for 92 rigid-body complexes from affinity benchmark 2 are correlated with the ones calculated (ΔG_calc) by the AACE167 and AACE18 potentials with varying cutoff distances d_max. Dashed line at 0.375 show performance of a naïve predictor, which approximates binding free energy by the change in solvent-accessible surface area (ΔSASA) upon complex formation. (B) The correlation of calculated binding free energies ΔG_calc and ΔSASA values is shown.

Conclusions

In summary, we presented a framework for generating semiempirical general-purpose contact potentials for proteins structure modeling. The potentials are derived from the Potts model by solving the inverse statistical physics problem. The model contains only two adjustable parameters, interaction distance cutoff d_max and separation in the sequence for the interacting units (residues or atoms) k_min. No other assumptions on the protein topology or information on intraresidue connectivity were used. Unlike many other statistical potentials, our derivation scheme explicitly includes one-body energy terms, which are shown to be a significant component of the model, boosting the effectiveness of the derived potentials.

The potentials were derived purely from the structural data in the PDB and are completely independent of any reference state. The results showed that they are successful not only in recognizing near-native models of individual proteins but also in scoring of protein docking decoys, recapitulating the experimental binding energies, and predicting stability changes upon point mutations. Such transferability of atomic potentials is strongly dependent on the assignment of the atom types. Among three considered assignment schemes, the grouping of atoms according to their physicochemical properties yielded consistently top-performing AACE18 potential. Interestingly, despite the effectiveness of the most detailed AACE167 potential in scoring of CASP decoys, it was much less effective at recapitulating experimental free energies. Large number of atom types enables fine-tuning of the AACE167 potential to achieve high decoy discrimination rate. However, at the same time, it affects its transferability to other applications.

It should be also noted that even for the most effective AACE18 potential, it is hard, if possible at all, to use one optimal contact distance d_max for all applications. For example, for discrimination of the structural decoys (for both the individual proteins and the protein complexes), the optimal d_max value was 6.9 Å. However, d_max = 8.0 Å yielded better correlation with the experimentally determined binding free energies. This discrepancy was shown to be at least partially related to the solvent effects, which are not explicitly taken into account by our model.

Overall, it is quite remarkable that in a wide range of protein structure modeling applications, simple contact potentials with no distance or orientation dependencies are sufficient for the same or better performance than much more complex knowledge-based energy functions used in the field. However, such simplicity may also pose limitations to the potentials applicability, e.g., in structure refinement, because of the lack of sensitivity to small changes in atom-atom distances inherent to the contact potentials. Complementing contact potentials with other scoring terms (e.g., the extent of clashes, surface area, etc.) is one way to overcome this problem, which has been explored by us in CASP-CAPRI competition (91).

In the future, we plan further development of the statistical potentials by incorporating distance dependence and solvent effects as well as exploring higher-order interactions (e.g., including three-body terms in Eq. 4). We will also explore different atom types, including hydrogen atoms and different protonation states of the titratable residues. On the learning side, more thorough selection of the training set, as well as inclusion of the interchain contacts from biological assemblies in PDB, could also lead to better contact energy estimates. All these questions can be addressed within the approach presented in this work.

The potentials are available at http://vakser.compbio.ku.edu/main/resources.php

Author Contributions

I.A. was responsible for concept, design, acquisition, analysis and interpretation of data, and writing of the manuscript. P.J.K. was responsible for supervision, analysis and interpretation of data, and writing of the article. I.A.V. was responsible for supervision, analysis and interpretation of data, and writing of the article. All authors read and approved the final manuscript.

Editor: Amedeo Caflisch.