Abstract
Reaction-equilibrium constants determine the metabolite concentrations necessary to drive flux through metabolic pathways. Group-contribution methods offer a way to estimate reaction-equilibrium constants at wide coverage across the metabolic network. Here, we present an updated group-contribution method with 1) additional curated thermodynamic data used in fitting and 2) capabilities to calculate equilibrium constants as a function of temperature. We first collected and curated aqueous thermodynamic data, including reaction-equilibrium constants, enthalpies of reaction, Gibbs free energies of formation, enthalpies of formation, entropy changes of formation of compounds, and proton- and metal-ion-binding constants. Next, we formulated the calculation of equilibrium constants as a function of temperature and calculated the standard entropy change of formation using a model based on molecular properties. The median absolute error in estimating was 0.013 kJ/K/mol. We also estimated magnesium binding constants for 618 compounds using a linear regression model validated against measured data. We demonstrate the improved performance of the current method (8.17 kJ/mol in median absolute residual) over the current state-of-the-art method (11.47 kJ/mol) in estimating the 185 new reactions added in this work. The efforts here fill in gaps for thermodynamic calculations under various conditions, specifically different temperatures and metal-ion concentrations. These, to our knowledge, new capabilities empower the study of thermodynamic driving forces underlying the metabolic function of organisms living under diverse conditions.
Introduction
The First and Second Laws of Thermodynamics connect reaction-flux directions, metabolite concentrations, and reaction-equilibrium constants. An increasing number of systems biology methods have begun to take advantage of the intimate connection between thermodynamics and metabolism to obtain insights into the function of metabolic networks. These methods have been used in a number of applications, including the calculation of thermodynamically feasible optimal states (1, 2), the identification of thermodynamic bottlenecks in metabolism (3, 4), and the constraint of kinetic constants via Haldane relationships (5).
To perform thermodynamic analyses on metabolic networks, it is necessary to have values for the equilibrium constants of reactions carrying flux in the network. Experimentally, the equilibrium constant of a reaction is determined by calculating the mass action ratio (the ratio of product to substrate concentrations), also called the reaction quotient, when the reaction is at equilibrium. A collection of experimentally measured equilibrium constants for over 600 reactions has been published in the National Institute of Standards and Technology (NIST) Thermodynamics of Enzyme-Catalyzed Reactions database (TECRdb) (6). However, the equilibrium constants of the majority of known metabolic reactions are still unmeasured, making computational estimation necessary. The most commonly used approach for estimating thermodynamic constants in aqueous solutions is the group-contribution method (7, 8). This method is based on the simplifying assumption that the Gibbs energy of formation of a compound is based on the sum of the contributions of its composing functional groups, which are independent of each other. The contribution of each group can be estimated through linear regression, using existing data on and the Gibbs energies of reactions .
Recent iterations of group-contribution methods for reactions in aqueous solutions have incorporated pH corrections into estimations of equilibrium constants (9) and improved accuracy by taking advantage of fully defined reaction-stoichiometric loops forming First Law energy-conservation relationships within the training data (10). These methods also have begun to take advantage of computational chemistry software to estimate the pKa-values of compounds as part of thermodynamic parameter estimation. However, a number of issues remain for thermodynamic estimation of reaction-equilibrium constants in metabolic networks, including 1) significant estimation errors in many cases, which may be attributed to a number of factors, including missing or erroneous reaction conditions; and 2) the lack of an established method to handle correction of thermodynamic data with respect to temperature changes across conditions. Additionally, existing group-contribution methods have not taken into account the substantial metal-ion binding of many metabolites at physiological ion concentrations, although established theory exists to correct reaction-equilibrium constants for metal-ion binding when ion-dissociation constants are available (11).
The geochemistry field has developed a sophisticated theory to handle thermodynamic variables as a function of temperature for a wide variety of compounds in aqueous solutions (12, 13, 14, 15, 16, 17, 18). The parameters used to calculate thermodynamic transformation across temperature are specific for different compounds. However, the available literature only covers less than half of the compounds in the NIST TECRdb. Therefore, the estimation of a large number of compound-specific parameters is required. It is possible to use a group-contribution approach by incorporating these parameters into the formulation of and fitting them against experimental data at different temperatures. However, because of the lack of data in necessary depth and resolution, the parameter estimation procedure on the fully parameterized thermodynamic model can suffer from significant error due to overfitting of parameters. Therefore, a simplified approach with fewer parameters to transform across temperature is desirable.
In this study, we extend the capabilities of computational estimation of reaction-equilibrium constants for metabolic networks. We first curate the NIST TECRdb of reaction-equilibrium constants to obtain missing reaction conditions and correct any other errors. We further incorporate additional thermodynamic data, including and data related to proton and metal-ion binding, from a number of other sources (11, 19, 20, 21, 22, 23). The equilibrium constants and -values are commonly used as the training data for group contribution. The proton- and metal-ion-binding data are required to transform across different pH and metal-ion concentrations. To enable the calculation of equilibrium constants as a function of temperature, we adapt the thermodynamic theory from the geochemistry literature (12, 13, 14, 15, 16, 17, 18) given certain simplifying assumptions. The thermodynamic parameters required for such calculation, of aqueous species, are estimated through a regression model using various molecular descriptors. Next, to fill gaps in the magnesium-binding correction of equilibrium constants, we estimate magnesium-binding constants for 618 compounds using molecular descriptors and magnesium-binding groups defined based on known magnesium-binding compounds. Finally, we incorporate these new data and functionalities into the most recently published group-contribution framework, termed the component contribution (10), to obtain a new group-contribution estimator for reaction-equilibrium constants with expanded capabilities.
Materials and Methods
Workflow for estimation of equilibrium constants
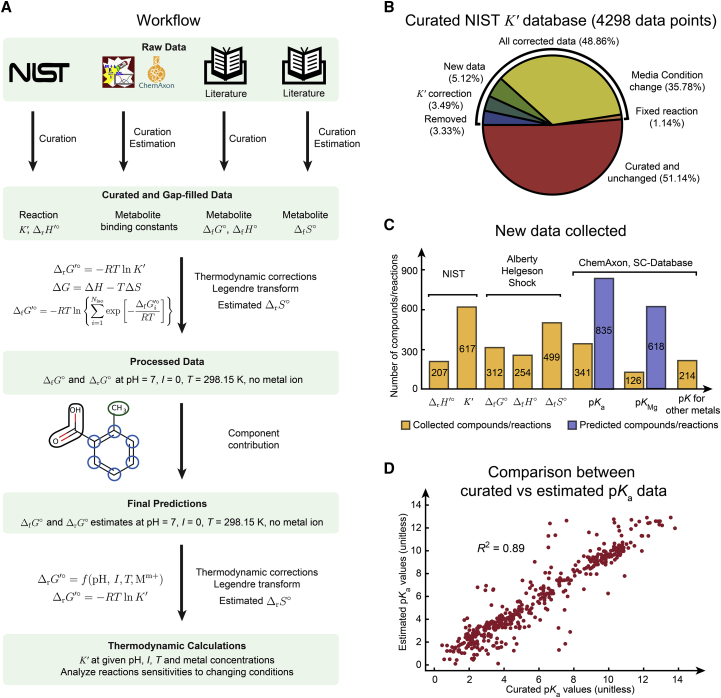
We first introduce the workflow for estimation of equilibrium constants illustrated in Fig. 1 A. The following sections expand upon the workflow in greater detail. We collected and curated 4298 equilibrium constants (K′) for 617 unique reactions measured under different conditions (temperature, pH, ionic strength, metal-ion concentrations) as the training data set for the current group-contribution method (Fig. 1 B). We also collected -values from multiple sources as the training data (11, 19, 20). We collected and curated stability constants of metal-ion complexes from the International Union of Pure and Applied Chemistry (IUPAC) Stability Constants Database (SC-database) and from various literature sources and online databases (11, 19, 20) (Fig. 1 C). To complete the necessary thermodynamic transformations to reference conditions, we estimated different thermodynamic properties for compounds for which data were not available. We estimated pKa-values using ChemAxon (Budapest, Hungary) (http://www.chemaxon.com). We used regression models to estimate magnesium binding constants (pKMg) and based on collected data.
Figure 1.
Estimation of reaction-equilibrium constants. (A) The workflow of data curation and parameter fitting for equilibrium constant estimation is given. (B) The results of curation of equilibrium constants from the NIST TECRdb are given. (C) New thermodynamic properties generated, either collected from sources shown or computationally estimated, are given. (D) A comparison between curated pKa data from the IUPAC SC-database as well as literature with computationally estimated pKa-values from ChemAxon is shown. To see this figure in color, go online.
First, we transformed all measurements to the same reference conditions at 298.15 K, pH 7, 0 M ionic strength, and no metal concentration. We applied a Legendre transform to account for the different ion-binding states of each compound as in the previous component-contribution method (10). The transformation of the Gibbs free energy of reaction across pH and ionic strength is also based on the previous method. However, we used the Davies equation rather than the extended Debye-Hückel equation to calculate activity coefficients of electrolyte solutions, as the Davies equation was used in the previous work for thermodynamic transformations across temperature (12, 13, 14, 15). The transformation of Gibbs free energy of reaction across different metal concentrations is based on the formulation described by Alberty (11, 24). The transformation of Gibbs free energy of reaction across temperature is based on adapted thermodynamic theory from the geochemistry literature (12, 13, 14, 15) with simplifying assumptions. The relevant equations and theory above can be found in the Supporting Materials and Methods.
Using and data at reference conditions, we applied the component contribution method by Noor et al. (10) and obtained estimates of and at reference conditions. Using these values, as well as the estimated to transform across temperature (more details in Results) and other thermodynamic transformations applied in the previous work (10), we are able to calculate the equilibrium constant of a given reaction at defined temperature, pH, and ionic strength.
Curation of the IUPAC SC-database
The IUPAC SC-database contains ion-binding data, i.e., dissociation/binding/stability constants, under various conditions from primary literature. Additionally, the database contains several different annotations for the binding of protons and metal ions to specific aqueous species. When the ligand is a proton, the related dissociation constant is a pKa constant, whereas when the ligand is a metal ion such as magnesium, the dissociation constant is a pKMg (modified to the specific ion) constant. For each compound of interest, we categorized the available binding data specific to each ion-bound state. We then corrected binding data to 0 M ionic strength using the Davies equation (25). For each ion-binding reaction, we calculated the median of all available binding data as the value utilized in the fitting (Table S1, tabs 4, 5, and 7).
Features and data used in regression models to estimate pKMg and
For estimation of pKMg, we included a total of 140 data points (Table S1, tab 5) and 128 molecular descriptors as features for regression models. The molecular descriptors included magnesium binding groups identified from existing pKMg data (Table S1, tab 8), the charge of the compound excluding any magnesium binding groups, sums of partial charge and numbers of different types of atoms, and several additional molecular descriptors from ChemAxon and RDkit. For estimation of , we included 762 data points (Table S1, tab 3) and 195 features including group decompositions, sums of partial charge and numbers of different types of atoms, and molecular descriptors from ChemAxon and RDkit. The molecular descriptors of compound were estimated with Calculator Plugins, Marvin 16.11.21, 2016, ChemAxon (http://www.chemaxon.com) and RDKit: open-source cheminformatics (http://www.rdkit.org). The full list of molecular descriptors used can be found in Table S1, tab 15.
Comparison of regression methods using nested 10-fold cross-validation
We tested six different regression methods to estimate pKMg and . These methods are ridge regression, lasso regression, elastic net regularization, random forests, extra trees, and gradient boosting. We applied nested 10-fold cross-validation to compare the performance of these regression methods. The specific implementation of nested 10-fold cross-validation involves generating an outer loop and inner loop of cross-validation. The outer loop separates the whole dataset into 10 folds, with one fold for testing and the rest for training in each iteration. The training data in each iteration is further separated into 10 folds, and cross-validation is performed in the inner loop to select the optimal model hyperparameters through grid search (Table S1, tab 16). We repeated the nested 10-fold cross-validation on each regression method five different times by splitting the data into different subdivisions.
We then assessed model performance through the median absolute residual of testing errors calculated from the outer loop, for a total of 50 folds (10 folds × 5 repetitions). The testing errors calculated here also reflect how well the model generalizes on unseen data and are thus used as a metric to evaluate model performance. We also evaluated model stability by calculating the relative standard deviation (RSD, SD/mean) of hyperparameters selected by the inner loop for a total of 50 folds (10 folds × 5 repetitions). We evaluated both testing error and the RSD of hyperparameters when selecting the final regression model to use. For every fitting procedure, we applied standardization on both the training and testing set using the mean and SD of features calculated from the training set.
The regression models, including linear models, tree-based methods, and gradient boosting, were implemented using the Python package scikit-learn 0.19.1 (26).
Lasso regression for estimation of pKMg and
Based on the evaluation of different regression methods through nested 10-fold cross-validation (more details in Results), we used lasso regression as the model to estimate pKMg and . Specifically, the objective function to minimize is
| (1) |
where y is the vector of data with length , X is the matrix with features in the row corresponding to each data point, w is the vector of coefficients of the model, and α is a constant that tunes the degree of the penalty.
We repeated 10-fold cross-validation 100 times on pKMg and data sets, respectively, to find the optimal α-values that lead to the lowest testing errors. We then constructed a lasso-regression-based estimator for each pKMg and dataset using the selected α-value and applying standardization on the dataset.
Comparison of previous and current group-contribution method
We compared how the previous (10) and the current group-contribution methods perform at different temperatures. Because the previous group-contribution method does not involve an explicit term to correct for at different temperatures, we were only able to substitute different temperatures in thermodynamic transformations and Legendre transform (Eqs. S8 and S9, the RT term) as the temperature transformation on . On the other hand, the current method includes an explicit term besides the RT term to calculate at different temperatures. Using the two methods, we calculated -values of all the TECRdb data measured at different temperatures and the absolute residual of the estimated -values against experimental data.
We then performed 10-fold cross-validation on the 432 reactions that overlapped between the previous and the current group-contribution method. Specifically, we first transformed experimentally measured data to the reference state (298.15 K, pH 7, 0 M ionic strength), with different sequential modifications on this procedure (based on the previous method). These modifications include updated media conditions, the Davies equation to correct for the effect of ionic strength, new compound groups, temperature correction, and metal correction. For each set of -values obtained, we calculated the median of all data points in each unique reaction, and performed 10-fold cross-validation on those 432 -values. We repeated this procedure 100 times by splitting the data into different subdivisions. We then calculated the median absolute residual of 100 repetitions for each reaction.
Additionally, we also compared how well the two methods perform on the 185 new reactions collected in this work. The first method is based on the previous work by Noor et al. (10), whereas the second method in the current work is similar to the first but has several modifications, including updated media conditions, the Davies equation, new compound groups, and the temperature correction. We fit the group-contribution model using both methods with -values of the original 432 overlapping reactions as training data and calculated the absolute residual in predicting for the 185 new reactions as the testing set.
Calculation of standard entropy change of formation
The standard entropy change of formation of the compound is not directly available. Given the type of data available, it can be calculated either from and the standard enthalpy of formation of the compound
| (2) |
or from the standard molar entropy of the compound
| (3) |
where is the standard molar entropy of the element composing the compound and is the number of atoms for the element .
Implementation and availability of source code
The updated group-contribution method has been implemented in Python 2.7.6. The source code is available on GitHub (https://github.com/bdu91/group-contribution), together with detailed instructions on how to install it and examples using the package.
Results
Collection and curation of thermodynamic data
The workflow for estimating reaction-equilibrium constants under given pH, temperature, ionic strength, and metal-ion concentrations is demonstrated in Fig. 1 A (Materials and Methods). To obtain the necessary data for this estimation, we curated a number of databases and primary literature sources. First of all, from the NIST TECRdb (https://randr.nist.gov/enzyme) (6), we obtained measured equilibrium constants (K′) and enthalpies of reactions for 617 and 207 unique reactions, respectively. Noticing a number of gaps in experimental conditions and other minor issues, we curated a total of 4298 measured K′ data from the NIST TECRdb. This curation effort resulted in 48.9% corrected data entries, including updated experimental media conditions (35.78%), addition of new data (5.12%), correction of K′-values (3.49%), removal of problematic data (3.33%) (examples in Table S1, tab 13), and correction of reaction formulae (1.14%) (Fig. 1 B).
Next, we collected data on standard Gibbs free energies of formation , standard enthalpies of formation , and standard entropy of formation changes for 312, 254, and 499 unique compounds, respectively (Fig. 1 C). data are usually not directly measured but instead are calculated from either and data or standard molar entropy (S°) of the compound (Materials and Methods). The above data are from multiple sources: Thermodynamics of Biochemical Reactions by Alberty (11), the SUPCRT92 database (19), and the Organic Compounds Hydration Properties Database (20).
Lastly, we collected and curated pKa data for 341 compounds, magnesium binding constants for 126 compounds, and other metal-type binding constants for 214 compounds (including cobalt, iron, zinc, sodium, potassium, manganese, calcium, and lithium) from the IUPAC SC-database and primary literature (21, 22, 23) (Fig. 1 C). We also predicted pKa data for 835 compounds using ChemAxon (http://www.chemaxon.com) (Fig. 1 C). We compared the collected pKa data and the predicted values from ChemAxon for the same compounds (Fig. 1 D). We found that the differences between the collected and predicted pKa-values can be as large as 5.84 (unitless), with a median of 0.42 (unitless). This error is a large enough difference to substantially alter the major protonation states for metabolites containing groups with pKa-values around physiological pH. We examined the specific cause of the largest discrepancies and found that they are due to issues such as assignment of the pKa-value to the wrong charged form by ChemAxon (e.g., 4-oxo-L-proline) or error in calculating pKa-values related to particular molecular moieties, such as nitrogenous bases and nitrogen atoms on unsaturated rings (e.g., 2′-deoxyguanosine 5′-monophosphate, xanthine-8-carboxylate, deaminocozymase). We thus used measured pKa data when available. All collected and curated data can be found in Table S1, tabs 1–7.
Thermodynamic parameters for transformation of across temperature
We then sought to develop the capability to calculate standard transformed Gibbs energy of reaction as a function of temperature. Specifically, we adapted theory from the geochemistry literature under constant enthalpy and entropy assumptions (12, 13, 14, 15), as well as the assumption that the contribution of heat capacity to change in Gibbs energy over temperature is negligible compared to the contribution of entropy (derivation in Supporting Materials and Methods). Thus, we obtained a simple linear formulation of at a given temperature T using the standard entropy change of reaction at a reference (298.15 K) (derivation in Supporting Materials and Methods):
| (4) |
As (we use in later references because is the only condition of interest, and the same for ) of reactions can be calculated from the of the compounds involved, we sought to construct a regression model to estimate -values. Besides collecting 669 -values for 499 compounds at different protonation states (Table S1, tab 3) as training data, we also collected -values from multiple sources. These -values are effectively linear combinations of -values and can also be used as training data for estimation. From the NIST TECRdb, we selected reactions with K′ data measured under at least four different temperatures. We then calculated the of each reaction using the of the reaction at different temperatures based on Eq. 4, obtaining 51 -values. Next, we picked reactions in the NIST TECRdb with both and data available and calculated their -values, obtaining 41 additional data points. Together, we obtained a total of 762 data points for estimation.
Estimation of standard entropy change of formation
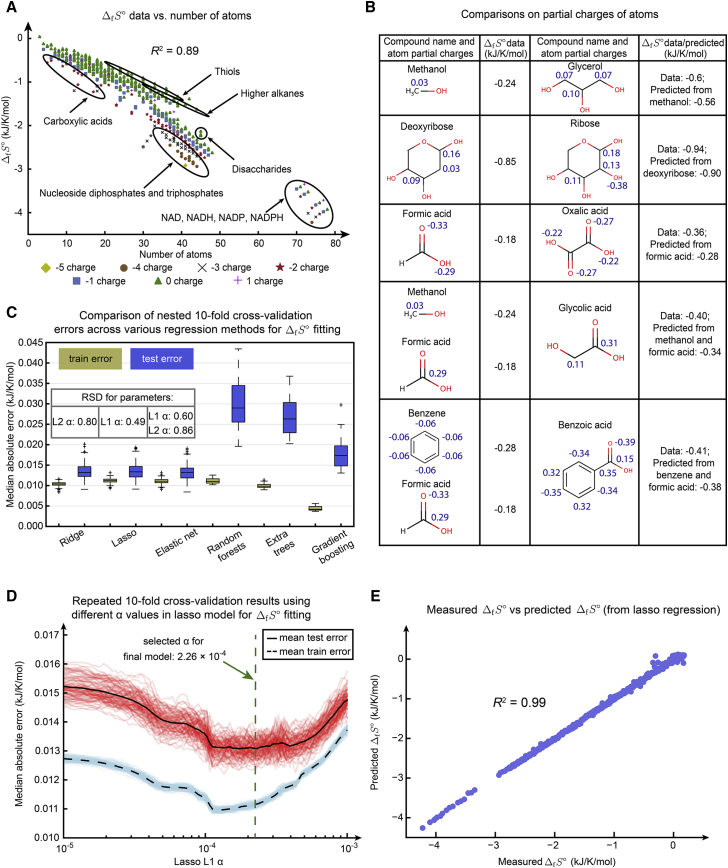
We found that simple molecular descriptors, notably the number of atoms in the compound and the compound charge, were highly useful as predictors for . Specifically, we found data to be highly correlated simply with the total numbers of atoms in the compound, with an R2 of 0.89 (Fig. 2 A). The data as a function of atom number are separated into two main clusters, one of which contains aqueous species with large atom numbers and large absolute -values (oxidized nicotinamide adenine dinucleotide, reduced nicotinamide adenine dinucleotide, oxidized nicotinamide adenine dinucleotide phosphate, reduced nicotinamide adenine dinucleotide phosphate). The other cluster contains a wide variety of aqueous species, with a few categories labeled in Fig. 2 A. We noticed clear separations among aqueous species with −5, −4, −3, and −2 charge, but less so for those with −1, 0, and +1 charge (Fig. 2 A). We found the trend between and number of atoms exists even more strongly among compounds within the same homologous series, in which the compound structures differ only by the number of CH2 units in the main carbon chain. Specifically, -value decreases by ∼0.11 kJ/K/mol with every additional CH2 unit. This trend was observed in a number of homologous series including alkanes, alkenes, alkynes, aldehydes, single carboxylic acids, amines, amides, and thiols. However, the change in with respect to the number of atoms across different homologous series is inconsistent, thus requiring additional molecular descriptors.
Figure 2.
Estimation of standard entropy change of formation ΔfS°. (A) ΔfS° versus number of atoms is shown. The compounds with different charges are encoded with different colored symbols. We also labeled compounds belonging to the same category or containing the same functional groups. (B) Comparisons of partial charges of atoms between compounds are shown. Each row contains a pair of compounds and their ΔfS° data. In each pair, the ΔfS° of the latter compound can be predicted from that of the former compound(s) based on the difference in atom number. The partial charges of atoms that are different within each pair are marked in blue. (C) Training and testing errors of nested 10-fold cross-validation (repeated five different times) on ΔfS° data using six different regression methods are shown. We also used relative standard deviation (RSD, SD/mean to assess the relative variability of linear regression model parameters selected by the inner loops of nested cross-validation. (D) A selection of parameters in the lasso regression using 10-fold cross-validation on all ΔfS° data is shown. We repeated 10-fold cross-validation 100 times and calculated training (blue) and testing (red) errors at α from 10−5 to 10−3. The mean training and testing errors are shown in dashed and solid black lines. The selected α at the lowest mean testing error is 2.26 × 10−4 (unitless). (E) A comparison of 762 measured ΔfS° training data versus predicted ΔfS°-values from the final lasso-regression model. To see this figure in color, go online.
As an additional descriptor, we found that partial charge of atoms can help distinguish from different homologous series. For example, the carbon atoms in glycerol (alcohol containing multiple hydroxyl groups) have larger partial charges than those in methanol (alcohol containing a single group). The prediction of glycerol from methanol based on their difference in atom numbers yielded a smaller absolute -value than the actual glycerol data (Fig. 2 B) (calculation in Table S1, tab 9). The correlation of larger partial charges of carbon atoms with larger absolute is also observed in other pairs in Fig. 2 B (deoxyribose versus ribose, methanol + formic acid versus glycolic acid, benzene + formic acid versus benzoic acid). Besides carbon atoms, we also found differences in partial charges of oxygen atoms to be associated with differences, as shown between formic acid and oxalic acid (Fig. 2 B). After these observations, we included the sums of absolute partial charge of each type of atom as molecular descriptors for the regression model.
In addition to partial charge, we also considered a number of other molecular descriptors from ChemAxon and RDkit (Materials and Methods). We obtained a total of 195 features and 762 data for regression models. We performed nested 10-fold cross-validation to compare between multiple regression models (Fig. 2 C). We selected lasso regression as the final model to use, because it has significantly smaller testing errors compared to more complex methods and the least variation in parameters selected from cross-validation compared to other linear regression methods (Fig. 2 C). Using parameters selected from cross-validation on the entire dataset (Fig. 2 D), we constructed a lasso-regression model and predicted 672 -values (Table S1, tab 17). We obtained 121 predictive variables from the final lasso model, including 1) the number of carbon, hydrogen, and oxygen atoms; 2) the partial charge of hydrogen and oxygen atoms; 3) the formal charge of the compound; 4) the presence of phosphate groups; and 5) the solvent-accessible surface area. The median absolute residual of the lasso-regression model for estimation is 0.013 kJ/K/mol (Fig. 2 C). Because -values are linear combinations of -values, we used the final lasso-regression model to estimate the -values for all 617 reactions in the TECRdb (Table S1, tab 10).
Evaluation of temperature-dependent estimation of
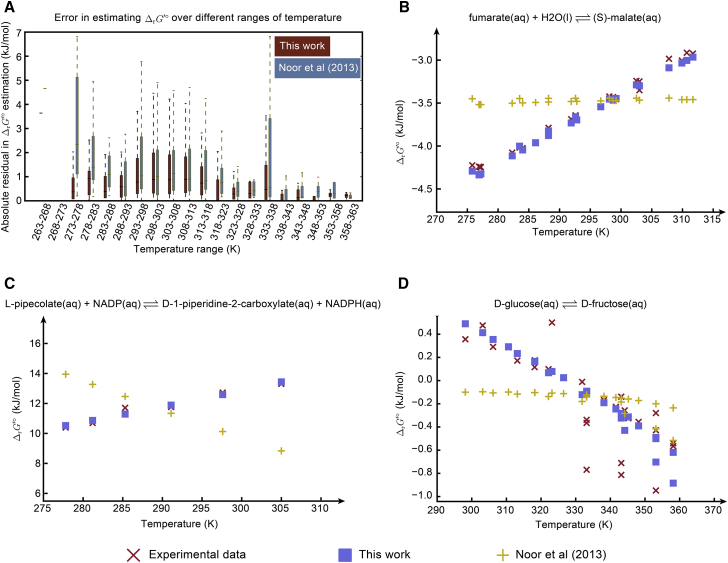
We next evaluated the performance of our method in estimating at different temperatures. We calculated -values of all the K′ data measured at different temperatures in the TECRdb using the current method with estimated -values and the previous group-contribution method (10). We calculated the absolute residuals of estimation and compared the two methods across temperature. We found that our method resulted in smaller residuals than the previous method in all temperature ranges (Fig. 3 A). This result is also confirmed in different reactions for which we identified series of K′ data measured at different temperatures. In all those cases, our estimated across temperature agreed well with the experimental data, in contrast to the estimations by the previous method (Fig. 3, B–D). Additionally, we found the temperature-dependent estimation of to be quite robust in the temperature range of available data in the TECRdb (0–90°C), which covers the living conditions of most organisms. Examining reactions for which -values are predicted to be sensitive to change in temperature (large / ratio), a number of interesting cases in central metabolism were identified, including malate dehydrogenase, amino acid transaminase, and transketolase (Table S1, tab 14).
Figure 3.
Evaluation of temperature-dependent estimation of ΔrG′°. (A) A comparison of absolute residuals on estimating ΔrG′° at different temperatures between the previous group-contribution method (10) and the current method is shown. For all the TECRdb data measured at different temperatures, we estimated the ΔrG′°-values using the previous method and the current method and calculated the absolute residual against experimental data. For clarity in comparison, we divided the entire temperature range into windows with 5 K difference. (B) Estimated ΔrG′°-values for the fumarate hydratase reaction at different temperatures using the previous method and the current method are given. (C) Estimated ΔrG′°-values for the 1-piperidine-2-carboxylate reductase reaction at different temperatures using the previous method and the current method are given. (D) Estimated ΔrG′°-values for the xylose isomerase reaction at different temperatures using the previous method and the current method are given. To see this figure in color, go online.
Estimation of unknown magnesium binding constants
In addition to its dependence on temperature, the standard transformed Gibbs free energy of the compound can also depend on pH and the concentrations of metal ions because of the presence of different protonation states and various metal bound species. Specifically, can be calculated based on the standard transformed Gibbs energies of its different ion bound states (, , etc.) through Legendre transform (11).
| (5) |
The equation can be rewritten as
| (6) |
where is the Gibbs energy of a particular ion-bound state (typically with the least hydrogens and metal ions bound). The Gibbs energy of a specific ion-bound state can then be written in terms of and the binding polynomial ,
| (7) |
where Pi is expressed in terms of the proton concentration and metal-ion concentration as well as the binding constants of successive proton- and metal-ion-binding steps to obtain the ith ion-bound state (11) (derivation in Supporting Materials and Methods). Therefore, metal-binding constants are important parameters that affect and subsequently reaction-equilibrium constants.
We focused on magnesium binding, because the magnesium ion is well-known to bind to various metabolites and its binding to ATP and other phosphate-containing compounds has been characterized experimentally (27, 28). However, magnesium-binding data is still lacking for a large number of compounds that contain similar structural groups to those known to bind magnesium, suggesting that many more compounds may have substantial magnesium binding than have been measured.
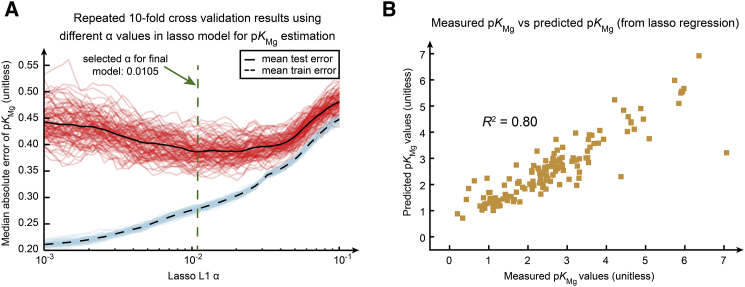
Based on the structures of compounds with known magnesium binding, we determined 31 magnesium-binding groups (Table S1, tab 8), most of which are phosphate and carboxyl groups. We were unable to determine the specific binding groups for certain categories of compounds that were measured to complex with magnesium, including nucleobases, ribonucleosides, and purine derivatives. To try to capture metabolite properties responsible for Mg binding in these cases, we added molecular properties (Materials and Methods) as additional descriptors. Together, we used 128 features and 140 measured magnesium-binding constants to construct several candidate regression models for the prediction of magnesium-dissociation constants. We performed nested 10-fold cross-validation to compare between multiple regression models (Fig. S2, A and B). We selected lasso regression as the best predictor because of its superior generalizability compared to more complex methods (Fig. S2 A) and stable model parameters across cross-validation replicates compared to other linear methods (Fig. S2 B). Using 140 measured magnesium-binding constants as training data, we constructed a lasso-regression model with parameters tuned through cross-validation (Fig. 4 A) and predicted 1707 magnesium-binding constants for aqueous species from 618 compounds (Table S1, tab 5). We obtained 35 predictive variables from the final lasso model, including the formal charge, the solvent-accessible surface area, the presence of various phosphate groups for magnesium binding, the partial charge of nitrogen atoms, the compound charge excluding its magnesium-binding groups, and the dipole moment of the molecule. We found 34 of the 618 compounds are predicted to bind to magnesium at physiological concentrations (2–3 mM) (29). The median absolute residual of the lasso-regression model for magnesium-binding-constant estimation is 0.39 (unitless), as calculated by the nested 10-fold cross-validation (Fig. S2 A).
Figure 4.
Estimation of compound magnesium binding constants (pKMg). (A) A selection of parameters in the lasso regression using 10-fold cross-validation on all pKMg data is given. We repeated 10-fold cross-validation 100 times and calculated training (blue) and testing (red) errors at α from 10−3 to 10−1. The mean training and testing errors are shown in dashed and solid black lines. The selected α at the lowest mean testing error is 0.0105 (unitless). (B) A comparison of 140 measured pKMg training data versus predicted pKMg-values from the final lasso-regression model is shown. To see this figure in color, go online.
Estimation of standard Gibbs free energy of reaction
Utilizing the curated and estimated datasets mentioned above, as well as the estimation of , we adapted the most recent group-contribution-based method, termed component contribution (10), to calculate reaction-equilibrium constants for a set of 617 unique reactions in the NIST TECRdb. Besides the addition of transformation of across temperature, we also included 17 novel group definitions to account for compounds with new functional groups not covered by the previous component-contribution method. The novel group definitions can be found in Table S1, tab 11. Additionally, we used the Davies equation (25) rather than the extended Debye-Hückel equation (used in the previous component-contribution method (10)) to correct for the effect of ionic strength, as the Davies equation was used in the previous work on temperature-dependent thermodynamic calculations (12, 13, 14, 15). We also showed that the Davies equation was slightly more effective in correcting data at high ionic strength compared to the extended Debye-Hückel equation (Fig. S5). On top of the new functionalities, we also added additional -values for 185 reactions and -values for 178 compounds over the dataset used in the previous method.
We compared the accuracy of the updated component-contribution method with the previous work using repeated 10-fold cross-validation (Materials and Methods) for a set of 432 overlapping reactions (10). We applied the modifications mentioned above sequentially on the framework to examine how each new functionality affects the estimation error globally (Fig. S4 A). We first noted that the updated media conditions increased the median absolute residual of estimation (6.21 kJ/mol), which we found to be due to the addition of data at high ionic strength (>0.5 M, beyond the working range of the Davies equation). Removal of those data resulted in similar errors as in the previous work (5.95 kJ/mol). We found a modest decrease in median absolute residual with the additional group definitions (5.82 kJ/mol) and capability to transform Gibbs energy of reaction across temperature (5.71 kJ/mol) (Fig. S4 A). Surprisingly, we observed a considerable increase in error (6.47 kJ/mol) after applying the correction on magnesium concentration globally (Fig. S4 A). We investigated this issue in detail and found that problems related to inconsistency in measured K′ data (involving magnesium binding) and report of total magnesium concentration can be major sources of error, even though the correction works with well curated data (Supporting Materials and Methods). Therefore, we proceed by omitting the global correction on magnesium concentration from our procedure.
Additionally, we compared our method to the most recent method by predicting for 185 new reactions collected in this work, using the 432 overlapping previous reactions as training data. We found the median absolute residual from the current method (8.17 kJ/mol) is notably smaller than that from the previous work (11.47 kJ/mol) (Fig. S4 B).
To summarize, we included the Davies equation, new group definitions, and temperature transformation capabilities but not the magnesium correction in our final group-contribution framework. We used the equilibrium constants from the TECRdb and the collected -values as the training data (Table S1, tabs 1and 3). Additionally, we used the collected pKa data from the SC-database when possible and estimated the rest using ChemAxon (Table S1, tab 4). Overall, our method led to improved performance compared to the most recent group-contribution method while adding the capability to correct equilibrium constants with respect to temperature and substantially expanding the scope of predictions and thermodynamic datasets used in estimation.
Discussion
In this work, we expanded the scope of thermodynamic calculations to more compounds and reactions with both curated and estimated data and also extended the group-contribution methods for estimating reaction-equilibrium constants to account for variations in temperature. We first collected and curated thermodynamic data including K′, , ,,, and various ion-binding constants from a number of databases. We then applied an existing thermodynamic theory with simplifying assumptions to enable the calculation of Gibbs free energy of reaction across temperature and estimated the necessary parameters using a linear regression model. We also estimated magnesium-binding constants for 618 compounds using molecular descriptors and magnesium-binding groups based on existing binding data. With new capabilities and new data, we utilized an updated group-contribution method to calculate equilibrium constants with improved accuracy over previous work.
The curation of the NIST TECRdb revealed that fully specified media conditions, which influence the ionic strength and metal-ion-concentration corrections, were often lacking. Surprisingly, curating the literature and filling in media conditions did not improve the resulting fit on the estimation of equilibrium constants, with one possible cause that we added data at high ionic strengths that exceed the intended range of the Davies and Debye-Hückel models for chemical activity. Another possible source of error could be related to the relatively simple model used to account for the effect of ionic strength on activity coefficients of aqueous electrolytes. The Davies equation fails to account for specific interactions between various ions present in solution and is unable to calculate activity coefficients at temperatures other than 298.15 K. Equations with a more comprehensive handling of these thermodynamic theories are established (12, 13, 14, 15, 30, 31) but require substantially more data than is currently available for the vast majority of compounds.
Utilizing reasonable assumptions of constant enthalpy and entropy over the range of biological interest, we formulated a simplified approach to calculate temperature transformation of Gibbs energy of reaction and reduced the number of parameters needed for estimation drastically. With the incorporation of temperature transformation capabilities, we obtained similar errors in estimating compared to the previous method (10) (Fig. S4 A). Such similar errors seem to be largely due to the fact that most of the data were measured not far from 298.15 K (83.5% of the data were measured under 295.15–313.15 K), resulting in a minor change in correction of K′ to the reference conditions. However, we do predict large changes in the Gibbs energy of many reactions at high temperatures (approaching 373 K), which thus may be significant for high-interest thermophilic organisms such as those living in hot springs and hydrothermal vents.
The compound-specific parameter required for temperature transformation in our simplified model is , which is missing for a large number of compounds in the TECRdb. Using a regression model, we predicted of a comprehensive collection of compounds with high accuracy by identifying key chemical properties such as number of atoms and partial charge. The linear correlation of other thermodynamic properties (e.g., standard molar entropy, standard partial molal volume, ) with number of atoms has been demonstrated in previous work (32, 33, 34, 35), but only for compounds in the same homologous series. We found the partial charge of atoms to be useful to distinguish from different homologous series, possibly because of the fact that the partial charge of atoms of the aqueous species influences its interaction with surrounding water molecules. The regression model was unable to clearly differentiate of compounds within certain categories, however, such as monosaccharides and disaccharides. For example, the differences in for fructose, mannose, and sorbose are around 10 to 20 J/K/mol, whereas the model only predicts up to 5 J/K/mol difference because of their similar chemical properties. Such error is not evident when evaluating the accuracy of estimation, as of monosaccharides are around 1000 J/K/mol. However, when calculating of the isomerization reaction between monosaccharides, we found that the errors of prediction, though small compared to -values, are significant compared to the calculated -values. We observed this issue to be prevalent for a number of reactions in the NIST TECRdb. Thus, identification of new molecular properties or additional features describing group interactions to more accurately differentiate these complex carbohydrates can be a productive next step to improve estimation. Additionally, the error in estimation can be incorporated into the calculation of confidence intervals developed by the previous method (10), offering the capability to assess the error in estimating at different temperatures.
We demonstrated that magnesium-binding groups (specifically the phosphate groups) that could be identified from known magnesium-binding compounds are useful features to estimate magnesium-binding constants with good accuracy. However, we found a number of compounds that complex with magnesium do not contain the binding groups we defined. These compounds include nucleobases, ribonucleosides, deoxyribonucleosides, purine derivatives, and small chemicals such as ammonia, thiocyanate, and urea. Currently, we use molecular properties to describe their binding to magnesium. Such an issue in identifying the chemical moiety responsible for magnesium binding can still make it difficult to extend our predictions to new compounds with similar structures as the compounds described above. The approach of estimating magnesium-binding constants can also be applied to other metals. However, we did not perform such predictions here because of the scarcity of binding data available for other metals.
We found the overall error in estimating increases with the incorporation of magnesium correction using curated and predicted magnesium binding data (Fig. S4 A). We identified inconsistency in K′ data (with magnesium binding involved) to be one primary source of error. Another source of error can be due to the uncertainty in estimation of magnesium-binding constants and missing binding data for other metals. Additionally, most measurements only reported total metal-ion concentrations, whereas the metal-correction formulation uses free-metal-ion concentrations. Therefore, additional effort is necessary to calculate free-metal-ion concentrations from measured data. Because of the lack of binding data and uncertainty in estimated data, an iterative approach might be taken in which free-metal-ion concentrations calculated using the current binding data are applied to optimize the binding data, which are then fed into the calculation of free-metal-ion concentrations.
The current work expands opportunities toward an understanding of thermodynamic factors underlying metabolic network and function in biological systems. This area has generated a number of exciting results, such as the discovery that amino acid biosynthesis, which is endergonic at surface conditions, is exergonic under the conditions of life in hydrothermal vents (36). Another recent effort proposed proteomic constraints because of thermodynamic bottlenecks as a critical factor underlying metabolic pathway choice (4). As methods for estimating the thermodynamic properties of metabolic networks continue to improve, these efforts are likely to be increasingly fruitful in uncovering the physical constraints driving the function and evolution of metabolic networks.
Conclusion
The work here provides an updated group-contribution method with an expanded set of thermodynamic data and extended capabilities to calculate equilibrium constants as a function of temperature. We collected and curated thermodynamic data for compounds and reactions from a number of databases and primary literature sources. We established a simple yet well-justified framework, which includes formulations derived from existing theory and the necessary parameters , to calculate equilibrium constants as a function of temperature. We also used molecular properties and magnesium binding groups defined from existing data to estimate magnesium-binding constants for 618 compounds through a linear regression model. Taken together, this work fills a gap in previous group-contribution methods to calculate equilibrium constants to temperature conditions and better correct for magnesium-ion binding. These efforts should facilitate the growing number of applications to apply thermodynamic principles to better understand cell metabolism.
Author Contributions
B.D. and D.C.Z. conceived and designed the study. B.D., Z.Z., S.G., J.T.Y., and D.C.Z. collected the data. B.D. and D.C.Z. performed the analysis. B.D., Z.Z., S.G., J.T.Y., B.O.P., and D.C.Z. wrote the manuscript. B.D. and J.T.Y. wrote the Supporting Materials and Methods. All authors read and approved the final content.
Acknowledgments
We would like to thank Nikolaus Sonnenschein for valuable discussions. We would also like to thank the reviewers for their thoughtful comments.
This work was supported by the Novo Nordisk Foundation Grant Number NNF10CC1016517.
Editor: Daniel Beard.
Footnotes
Supporting Materials and Methods, six figures, and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30524-1.
Supporting Citations
References (37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53) appear in the Supporting Material.
Supporting Material
References
- 1.Henry C.S., Broadbelt L.J., Hatzimanikatis V. Thermodynamics-based metabolic flux analysis. Biophys. J. 2007;92:1792–1805. doi: 10.1529/biophysj.106.093138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hamilton J.J., Dwivedi V., Reed J.L. Quantitative assessment of thermodynamic constraints on the solution space of genome-scale metabolic models. Biophys. J. 2013;105:512–522. doi: 10.1016/j.bpj.2013.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kümmel A., Panke S., Heinemann M. Putative regulatory sites unraveled by network-embedded thermodynamic analysis of metabolome data. Mol. Syst. Biol. 2006;2:2006.0034. doi: 10.1038/msb4100074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Noor E., Bar-Even A., Milo R. Pathway thermodynamics highlights kinetic obstacles in central metabolism. PLoS Comput. Biol. 2014;10:e1003483. doi: 10.1371/journal.pcbi.1003483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Beard D.A., Vinnakota K.C., Wu F. Detailed enzyme kinetics in terms of biochemical species: study of citrate synthase. PLoS One. 2008;3:e1825. doi: 10.1371/journal.pone.0001825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Goldberg R.N., Tewari Y.B., Bhat T.N. Thermodynamics of enzyme-catalyzed reactions--a database for quantitative biochemistry. Bioinformatics. 2004;20:2874–2877. doi: 10.1093/bioinformatics/bth314. [DOI] [PubMed] [Google Scholar]
- 7.Mavrovouniotis M.L. Group contributions for estimating standard gibbs energies of formation of biochemical compounds in aqueous solution. Biotechnol. Bioeng. 1990;36:1070–1082. doi: 10.1002/bit.260361013. [DOI] [PubMed] [Google Scholar]
- 8.Jankowski M.D., Henry C.S., Hatzimanikatis V. Group contribution method for thermodynamic analysis of complex metabolic networks. Biophys. J. 2008;95:1487–1499. doi: 10.1529/biophysj.107.124784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Noor E., Bar-Even A., Milo R. An integrated open framework for thermodynamics of reactions that combines accuracy and coverage. Bioinformatics. 2012;28:2037–2044. doi: 10.1093/bioinformatics/bts317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Noor E., Haraldsdóttir H.S., Fleming R.M. Consistent estimation of Gibbs energy using component contributions. PLoS Comput. Biol. 2013;9:e1003098. doi: 10.1371/journal.pcbi.1003098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Alberty R.A. John Wiley & Sons; Hoboken, NJ: 2003. Thermodynamics of Biochemical Reactions. [Google Scholar]
- 12.Helgeson H.C., Kirkham D.H. Theoretical prediction of the thermodynamic behavior of aqueous electrolytes at high pressures and temperatures; I, Summary of the thermodynamic/electrostatic properties of the solvent. Am. J. Sci. 1974;274:1089–1198. [Google Scholar]
- 13.Helgeson H.C., Kirkham D.H. Theoretical prediction of the thermodynamic behavior of aqueous electrolytes at high pressures and temperatures; II, Debye-Huckel parameters for activity coefficients and relative partial molal properties. Am. J. Sci. 1974;274:1199–1261. [Google Scholar]
- 14.Helgeson H.C., Kirkham D.H. Theoretical prediction of the thermodynamic properties of aqueous electrolytes at high pressures and temperatures. III. Equation of state for aqueous species at infinite dilution. Am. J. Sci. 1976;276:97–240. [Google Scholar]
- 15.Helgeson H.C., Kirkham D.H., Flowers G.C. Theoretical prediction of the thermodynamic behavior of aqueous electrolytes by high pressures and temperatures; IV, calculation of activity coefficients, osmotic coefficients, and apparent molal and standard and relative partial molal properties to 600 degrees C and 5kb. Am. J. Sci. 1981;281:1249–1516. [Google Scholar]
- 16.Shock E.L., Helgeson H.C. Calculation of the thermodynamic and transport properties of aqueous species at high pressures and temperatures: correlation algorithms for ionic species and equation of state predictions to 5 kb and 1000°C. Geochim. Cosmochim. Acta. 1988;52:2009–2036. [Google Scholar]
- 17.Plyasunov A.V., Shock E.L. Correlation strategy for determining the parameters of the revised Helgeson-Kirkham-Flowers model for aqueous nonelectrolytes. Geochim. Cosmochim. Acta. 2001;65:3879–3900. [Google Scholar]
- 18.Plyasunov A.V., Connell J.P.O., Shock E.L. Semiempirical equation of state for the infinite dilution thermodynamic functions of hydration of nonelectrolytes over wide ranges of temperature and pressure. Fluid Phase Equilib. 2001;183:133–142. [Google Scholar]
- 19.Johnson J.W., Oelkers E.H., Helgeson H.C. SUPCRT92: a software package for calculating the standard molal thermodynamic properties of minerals, gases, aqueous species, and reactions from 1 to 5000 bar and 0 to 1000°C. Comput. Geosci. 1992;18:899–947. [Google Scholar]
- 20.Plyasunova N.V., Plyasunov A.V., Shock E.L. Database of thermodynamic properties for aqueous organic compounds. Int. J. Thermophys. 2004;25:351–360. [Google Scholar]
- 21.Pettit L.D., Powell K.J. The IUPAC stability constants database. Chemistry International – Newsmagazine for IUPAC. 2006;28:14–15. [Google Scholar]
- 22.Kortüm G., Andrussow K. Butterworths; London, UK: 1961. Dissociation Constants of Organic Acids in Aqueous Solution. [Google Scholar]
- 23.Perrin D.D. Butterworths; London, UK: 1965. Dissociation Constants of Organic Bases in Aqueous Solution. [Google Scholar]
- 24.Alberty R.A. Effect of pH and metal ion concentration on the equilibrium hydrolysis of adenosine triphosphate to adenosine diphosphate. J. Biol. Chem. 1968;243:1337–1343. [PubMed] [Google Scholar]
- 25.Davies C.W. 397. The extent of dissociation of salts in water. Part VIII. An equation for the mean ionic activity coefficient of an electrolyte in water, and a revision of the dissociation constants of some sulphates. J. Chem. Soc. 1938;0:2093–2098. [Google Scholar]
- 26.Pedregosa F., Varoquaux G., Duchesnay É. Scikit-learn: machine learning in python. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]
- 27.Goldberg R.N., Tewari Y.B. Thermodynamics of the disproportionation of adenosine 5′-diphosphate to adenosine 5′-triphosphate and adenosine 5′-monophosphate. I. Equilibrium model. Biophys. Chem. 1991;40:241–261. doi: 10.1016/0301-4622(91)80024-l. [DOI] [PubMed] [Google Scholar]
- 28.Larson J.W., Tewari Y.B., Goldberg R.N. Thermochemistry of the reactions between adenosine, adenosine 5′-monophosphate, inosine, and inosine 5′-monophosphate; the conversion of d-histidine to (urocanic acid+ammonia) J. Chem. Thermodyn. 1993;25:73–90. [Google Scholar]
- 29.Cayley S., Lewis B.A., Record M.T., Jr. Characterization of the cytoplasm of Escherichia coli K-12 as a function of external osmolarity. Implications for protein-DNA interactions in vivo. J. Mol. Biol. 1991;222:281–300. doi: 10.1016/0022-2836(91)90212-o. [DOI] [PubMed] [Google Scholar]
- 30.Pitzer K.S., Kim J.J. Thermodynamics of electrolytes. IV. Activity and osmotic coefficients for mixed electrolytes. J. Am. Chem. Soc. 1974;96:5701–5707. [Google Scholar]
- 31.Elizalde M.P., Aparicio J.L. Current theories in the calculation of activity coefficients-II. Specific interaction theories applied to some equilibria studies in solution chemistry. Talanta. 1995;42:395–400. doi: 10.1016/0039-9140(95)01422-8. [DOI] [PubMed] [Google Scholar]
- 32.Helgeson H.C. Calculation of the thermodynamic properties and relative stabilities of aqueous acetic and chloroacetic acids, acetate and chloroacetates, and acetyl and chloroacetyl chlorides at high and low temperatures and pressures. Appl. Geochem. 1992;7:291–308. [Google Scholar]
- 33.Shock E.L. Organic acids in hydrothermal solutions: standard molal thermodynamic properties of carboxylic acids and estimates of dissociation constants at high temperatures and pressures. Am. J. Sci. 1995;295:496–580. doi: 10.2475/ajs.295.5.496. [DOI] [PubMed] [Google Scholar]
- 34.Schulte M.D., Rogers K.L. Thiols in hydrothermal solution: standard partial molal properties and their role in the organic geochemistry of hydrothermal environments. Geochim. Cosmochim. Acta. 2004;68:1087–1097. [Google Scholar]
- 35.Schulte M.D., Shock E.L. Aldehydes in hydrothermal solution: standard partial molal thermodynamic properties and relative stabilities at high temperatures and pressures. Geochim. Cosmochim. Acta. 1993;57:3835–3846. doi: 10.1016/0016-7037(93)90337-v. [DOI] [PubMed] [Google Scholar]
- 36.Amend J.P., Shock E.L. Energetics of amino acid synthesis in hydrothermal ecosystems. Science. 1998;281:1659–1662. doi: 10.1126/science.281.5383.1659. [DOI] [PubMed] [Google Scholar]
- 37.Ono K., Yanagida K., Soda K. Alanine racemase of alfalfa seedlings (Medicago sativa L.): first evidence for the presence of an amino acid racemase in plants. Phytochemistry. 2006;67:856–860. doi: 10.1016/j.phytochem.2006.02.017. [DOI] [PubMed] [Google Scholar]
- 38.Woolf B. Some enzymes in B. coli communis which act on fumaric acid. Biochem. J. 1929;23:472–482. doi: 10.1042/bj0230472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Quastel J.H., Woolf B. The equilibrium between l-aspartic acid, fumaric acid and ammonia in presence of resting bacteria. Biochem. J. 1926;20:545–555. doi: 10.1042/bj0200545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Siekevitz P., Potter V.R. The adenylate kinase of rat liver mitochondria. J. Biol. Chem. 1953;200:187–196. [PubMed] [Google Scholar]
- 41.Nishizuka Y., Takeshita M., Hayaishi O. beta-Alanine-alpha-alanine transaminase of Pseudomonas. Biochim. Biophys. Acta. 1959;33:591–593. doi: 10.1016/0006-3002(59)90166-0. [DOI] [PubMed] [Google Scholar]
- 42.Nixon P.F., Blakley R.L. Dihydrofolate reductase of Streptococcus faicium. II. Purification and some properties of two dihydrofolate reductases from the amethopterin-resistant mutant Streptococcus faecium var. Durans strain A. J. Biol. Chem. 1968;243:4722–4731. [PubMed] [Google Scholar]
- 43.Blasi F., Fragomele F., Covelli I. Thyroidal phenylpyruvate tautomerase. Isolation and characterization. J. Biol. Chem. 1969;244:4864–4870. [PubMed] [Google Scholar]
- 44.Haagensen P., Karlsen L.G., Villadsen J. The kinetics of penicillin-V deacylation on an immobilized enzyme. Biotechnol. Bioeng. 1983;25:1873–1895. doi: 10.1002/bit.260250715. [DOI] [PubMed] [Google Scholar]
- 45.Hassan Ansari N.C.P., Stevens L. Effects of high concentrations of proteins on the equilibrium and kinetic properties of four enzymes. Biochem. Soc. Trans. 1985;13:362. [Google Scholar]
- 46.Huber R.E., Hurlburt K.L. Reversion reactions of β-galactosidase (Escherichia coli) Arch. Biochem. Biophys. 1986;246:411–418. doi: 10.1016/0003-9861(86)90487-x. [DOI] [PubMed] [Google Scholar]
- 47.Johansson E., Hedbys L., Svensson S. Studies of the reversed α-mannosidase reaction in high concentrations of mannose. Enzyme Microb. Technol. 1989;11:347–352. [Google Scholar]
- 48.Hori N., Watanabe M., Mikami Y. The effects of organic solvent on the ribosyl transfer reaction by thermostable purine nucleoside phosphorylase and pyrimidine nucleoside phosphorylase from bacillus stearothermophilus JTS 859. Biocatalysis. 1991;4:297–304. doi: 10.1016/0168-1656(91)90003-e. [DOI] [PubMed] [Google Scholar]
- 49.Manchester J., Walkup G., You Z. Evaluation of pKa estimation methods on 211 druglike compounds. J. Chem. Inf. Model. 2010;50:565–571. doi: 10.1021/ci100019p. [DOI] [PubMed] [Google Scholar]
- 50.Settimo L., Bellman K., Knegtel R.M. Comparison of the accuracy of experimental and predicted pKa values of basic and acidic compounds. Pharm. Res. 2014;31:1082–1095. doi: 10.1007/s11095-013-1232-z. [DOI] [PubMed] [Google Scholar]
- 51.Newville M., Stensitzki T., Nelson A. Astrophysics Source Code Library; 2016. Lmfit: Non-Linear Least-Square Minimization and Curve-Fitting for Python.https://lmfit.github.io/lmfit-py/ [Google Scholar]
- 52.Levenberg K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944;2:164–168. [Google Scholar]
- 53.Marquardt D. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963;11:431–441. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.