Abstract
When an atrial cell is paced rapidly, calcium (Ca) waves can form on the cell boundary and propagate to the cell interior. These waves are referred to as “triggered waves” because they are initiated by Ca influx from the L-type Ca channel and occur during the action potential. However, the consequences of triggered waves in atrial tissue are not known. Here, we develop a phenomenological model of Ca cycling in atrial myocytes that accounts for the formation of triggered waves. Using this model, we show that a fundamental requirement for triggered waves to induce abnormal electrical activity in tissue is that these waves must be synchronized over large populations of cells. This is partly because triggered waves induce a long action potential duration (APD) followed by a short APD. Thus, if these events are not synchronized between cells, then they will on average cancel and have minimal effects on the APD in tissue. Using our computational model, we identify two distinct mechanisms for triggered wave synchronization. The first relies on cycle length (CL) variability, which can prolong the CL at a given beat. In cardiac tissue, we show that CL prolongation leads to a substantial amplification of APD because of the synchronization of triggered waves. A second synchronization mechanism applies in a parameter regime in which the cell exhibits stochastic alternans in which a triggered wave fires, on average, only every other beat. In this scenario, we identify a slow synchronization mechanism that relies on the bidirectional feedback between the APD in tissue and triggered wave initiation. On large cables, this synchronization mechanism leads to spatially discordant APD alternans with spatial variations on a scale of hundreds of cells. We argue that these spatial patterns can potentially serve as an arrhythmogenic substrate for the initiation of atrial fibrillation.
Introduction
The beating of the heart requires the coordination between electrical activity across the cell membrane and mechanical contraction (1). This process is mediated by voltage-sensitive calcium (Ca) channels that open in response to an action potential (AP). The Ca that enters the cell through these channels then diffuses and binds to ryanodine receptors (RyRs), which themselves open in a Ca-dependent manner. RyR channels are arranged in tight clusters of 10–100 channels that release Ca into the cytosol from Ca stored in the sarcoplasmic reticulum (SR). The released Ca then diffuses and signals mechanical contraction at the myofilaments, after which it is pumped back into the SR via the SR Ca2+-ATPase (SERCA) uptake channel allowing the process to repeat again on the next beat. It is this Ca cycling processes that mediates the coupling between electrical activity at the cell membrane and mechanical contraction of the cell.
Recently, there has been a great deal of work implicating Ca cycling as a possible player in the initiation and maintenance of atrial fibrillation (AF) (2, 3, 4). Optical mapping of AF in a range of animal models reveals the presence of triggered activity that is likely caused by a disruption in the Ca cycling system (5). In particular, it is generally believed that spontaneous Ca waves within atrial cells can induce membrane depolarization, which can evolve into an ectopic excitation (4, 6). These ectopic sources are arrhythmogenic because they can initiate an ill-timed beat with a high propensity for wave break. Alternatively, an ectopic region will disrupt repolarization and therefore induce repolarization heterogeneities, which can induce wave break of the following paced beat. Thus, unstable Ca cycling is a potential candidate for the aperiodic electrical activity that underlies AF.
In a recent study, we (7) demonstrated that atrial myocytes from the dog heart are prone to a particular type of Ca wave. We found that when an atrial myocyte is rapidly paced then Ca waves propagate inside the cell between paced beats. These waves are referred to as triggered waves because they occurred during the AP, in sharp contrast to spontaneous Ca waves, which are typically observed after a pause longer than the pacing period (8) and during Ca overload conditions. Shiferaw et al. (9) applied computational modeling to show that triggered waves are fundamentally due to the unique spatial architecture of atrial myocytes. In particular, these cells lack a well-developed transverse tubule (TT) structure, and therefore, the bulk of Ca signaling between L-type Ca channel (LCC) and RyR channels occurs at the cell boundary (10, 11). Thus, under normal conditions, Ca is released because of Ca sparks that occur at the cell boundary, which then diffuse to the cell interior. However, under rapid pacing conditions, RyR clusters in the cell interior become more sensitized so that sparks at the cell boundary can nucleate Ca waves that propagate to the cell interior. These triggered Ca waves are likely highly arrhythmogenic because they occur during pacing and can therefore induce triggered activity, which may have a higher likelihood of producing wave break because of the short coupling intervals between paced beats. Also, triggered waves disrupt the process of Ca cycling and can therefore lead to aperiodic Ca responses that will feed back on the AP duration (APD) to induce heterogeneities that can form a substrate for arrhythmia.
The goal of this study is to develop a phenomenological model of an atrial cell, which can be used to model voltage and Ca in cardiac tissue simulations. This model will account for the experimentally observed triggered waves while being computationally tractable for simulations of hundreds of thousands of electrotonically coupled cells that are paced for many beats. A fully detailed three-dimensional (3D) model of Ca cycling (12, 13, 14), which reproduces triggered Ca waves, requires the simulation of roughly 105 ion channels, which makes it computationally demanding to simulate cardiac tissue. Here, we apply a population-based approach that keeps track only of key variables such as the number of Ca sparks and the global average Ca concentration within various compartments in the cell. This model accounts for the stochastic properties of triggered and spontaneous Ca waves and can be used to explore how Ca waves can induce excitations in cardiac tissue. Using this model, we will address the fundamental question of how stochastic triggered waves can induce arrhythmogenic electrical activity in tissue. Our main finding is that voltage perturbations in tissue depend crucially on the synchronization of triggered waves. This synchronization can occur via two distinct mechanisms. In the first case, we show that a modest increase in cycle length (CL) at one beat can lead to an elevated SR load on the next beat, which in turn will tend to synchronize triggered waves on that beat. Based on this mechanism, we show that variability in CL can substantially amplify the effect of triggered waves on the APD in cardiac tissue. The reason for this is that a triggered wave typically prolongs the APD on the same beat but then shortens the APD on the next because the previous diastolic interval (DI) is shorter. If triggered waves are not synchronized, then spatial averaging due to electrotonic coupling leads to a cancelation between the long and short APD. However, even a small degree of synchronization between cells can negate this cancelation effect and amplify APD variations in tissue. In the second case, we show that upon rapid pacing, triggered Ca waves can enter an “alternans” mode in which a triggered wave occurs, with high likelihood, only on every other beat. This response is consistent with our previous experimental findings in which alternans of this form are readily observed in the presence of isoproterenol and caffeine (7). When these triggered wave alternans occur, gradual feedback between the Ca transient and APD leads to a synchronization process that forces the triggered waves to occur in phase i.e., at the same beat. This mechanism leads to tissue scale patches of synchronized triggered waves that form spatially discordant APD alternans. Using our computational model, we explore these synchronization mechanisms and comment on their role in the initiation of AF.
Methods
Population-based model of spark activation
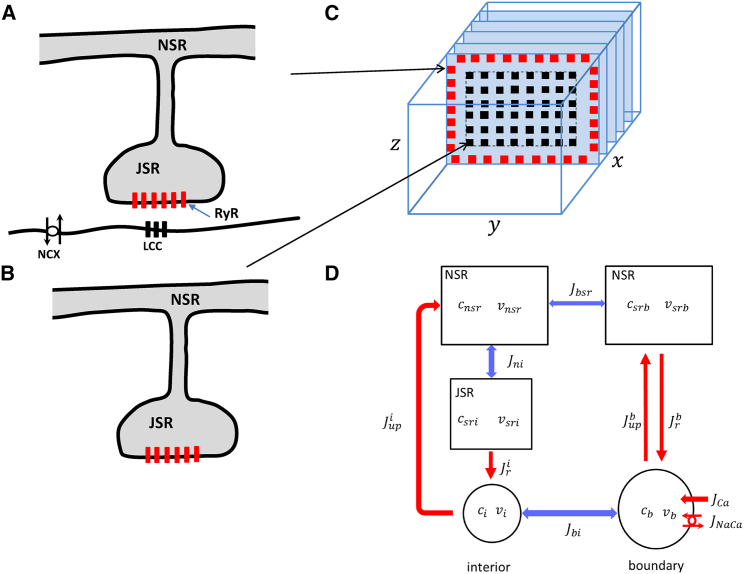
Atrial myocytes lack a well-defined TT system so that the bulk of Ca signaling between RyR and LCCs occurs at the cell boundary. Thus, we can divide the RyR clusters in the cell in to the following two groups: 1) a population of RyR clusters, referred to as junctional clusters (Fig. 1 A), where LCCs are in close proximity (∼10 nm) and which are mostly located near the cell boundary (Fig. 1 C); and 2) nonjunctional RyR clusters (Fig. 1 B) in the cell interior, which are far from LCCs. Nonjunctional clusters have a minimal spacing in the range of ∼100–500 nm (15, 16) and therefore sense Ca that has to diffuse a distance longer than this scale. In this study, we will denote the total number of junctional and nonjunctional clusters to be and respectively. To model Ca release, we will denote to be the number of nonjunctional clusters at which Ca is being released because of a Ca spark at time . Similarly, we will keep track of the number of sparks at junctional clusters denoted as . The total number of sparks in the cell is then given by Ca sparks are formed and extinguished in their respective volumes according to the reaction scheme
| (1) |
where 0 denotes an “off” cluster that is shut, and 1 denotes an “on” cluster at which Ca is being released because of a spark. The rate at which Ca sparks are activated at nonjunctional and junctional clusters is given by and , respectively, and with corresponding extinction rates and .
Figure 1.
An illustration of the spatial architecture of Ca signaling in an atrial myocyte. (A) Junctional RyR clusters are in close proximity to LCCs on the cell membrane. The JSR protrudes from the NSR and forms synapse-like regions where Ca signaling takes place. The NaCa exchanger (NCX) regulates intracellular Ca by pumping out the Ca that enters the cell via the LCC. (B) A nonjunctional RyR cluster that is found in the cell interior is shown. (C) The spatial distribution of junctional and nonjunctional RyR clusters in a 3D atrial myocyte model is shown. (D) A reduced compartment model of the atrial cell architecture is shown. We divide the boundary of the cell into the total SR volume , which is the sum of the total JSR and NSR volumes. The average Ca concentration in this volume is denoted by . The total cytosol on the cell boundary has volume and concentration . The currents linking these two spaces are the Ca release due to a population of sparks on the boundary and the uptake pump current , which replenishes the boundary SR. The cell interior is divided into the total NSR, JSR, and cytosolic volumes, with concentrations , and respectively. Ca release from the JSR to the cytosol is due to the interior sparks with total current , whereas denotes the total uptake current. The currents , , and are diffusive currents proportional to the concentration difference between adjoining compartments. To see this figure in color, go online.
To model subcellular Ca dynamics, we will simulate the time evolution of the number of sparks using a phenomenological approach. To do this, we first pick a sufficiently small time step interval such that the reaction rates are effectively constant during this interval. Then, if we have sparks in the cell interior and cluster sites at which a Ca spark can occur, the number of new sparks in the cell interior will be the number of successes in trials given a success probability . Similarly, the number of sparks that extinguish will be the number of success in trials with probability . Therefore, the number of Ca sparks in the cell interior will evolve according to
| (2) |
where
| (3) |
| (4) |
and where is a random number picked from a binomial distribution with a success probability p and number of trails n. In a similar fashion, we can model the time evolution of boundary sparks by simply replacing the spark transition rates and the total number of clusters. This approach captures the stochasticity of spark recruitment and extinction by modeling these events as independent probabilistic events. To describe correlations between transition events, the spark activation rates, and , are taken to be a nonlinear function of the state of the system, i.e., the Ca concentrations and the number of active sparks in the interior and boundary . In this manner, we can model the complex spatiotemporal dynamics of Ca cycling using a phenomenological approach that describes only the number of sparks in the cell.
Cell compartmentalization and Ca cycling
To model Ca dynamics, we apply a phenomenological approach in which the spark rates described above are dependent on the internal Ca concentrations in the cell. To proceed, we divide the cell into an interior region in which the bulk of RyR clusters are nonjunctional and a boundary region composed of junctional RyR clusters (Fig. 1 C). Furthermore, we divide the cell interior and boundary into distinct volumes, which are illustrated in Fig. 1 D. Here, each volume corresponds to the total volume of a given compartment in the cell. In particular, the cell interior will be divided into the network SR (NSR) with volume , which is the total volume of the NSR in the cell, the total junctional SR (JSR) volume , and the total bulk cytosol volume . For example, if there are JSR compartments in the cell then , where is the volume of the JSR compartment in the cell. To track concentrations in these volumes, we denote to be the average total Ca concentration in volume , and will denote the corresponding average free concentration. Thus, we let be average free Ca concentration in the volume , and are the average free concentrations in volume . Similarly, the boundary region will be divided accordingly into a cytosolic volume with average free concentration and total volume and the SR with average concentration and total volume . For convenience, we will lump JSR and NSR and refer to the total volume of this space as the SR. We do this because the Ca released at the boundary is tightly controlled by the LCC current, and the diffusional delay between the NSR and JSR regions does not play an important role in the dynamics. The total Ca concentrations then obey the following Ca flux equations:
| (5) |
| (6) |
| (7) |
| (8) |
and
| (9) |
where the definitions and descriptions of the fluxes are given in Table 1. For clarity, we note here that each flux refers to the total flux because of the thousands of channels connected to the indicated subcellular volume. For example, , where is the flux because of the SERCA pump residing in the cell interior. Also, release from the SR into the boundary volume will have the form
| (10) |
where is the fraction of boundary clusters with an active spark and where is a constant representing the aggregate current flux. Similarly, release from the JSR into the interior cytosol will have the form
| (11) |
where and where is a proportionality constant. Details of the model equations after suitable rescaling of volume factors, along with a treatment of the relevant Ca buffers, is given in the Supporting Materials and Methods.
Table 1.
Description of Ca fluxes in the Phenomenological Model
| Flux | Description |
|---|---|
| Total RyR flux from the boundary SR to the boundary cytosolic space. | |
| Total uptake flux from cytosol to SR on the boundary. | |
| Total RyR flux from JSR to cytosolic space in the cell interior. | |
| Total uptake flux from cytosol into the bulk NSR in the cell interior. | |
| Total diffusive flux from boundary to interior cytosol. | |
| Total diffusive flux from boundary to interior NSR. | |
| Total diffusive flux from NSR to JSR in cell interior. | |
| Total LCC current at cell boundary. | |
| Total NaCa exchanger current at the cell boundary. |
A population-based model of the LCC Markov model
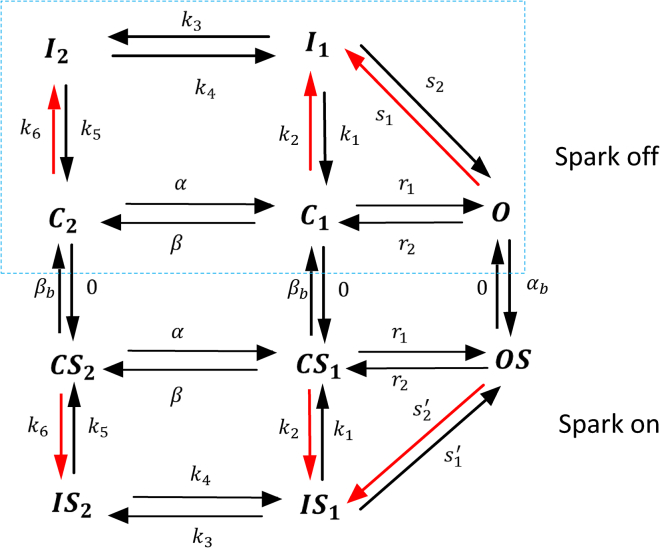
To model the LCC current, we develop a Markovian model based on that introduced by Mahajan et al. (17). A challenge of applying a Markovian approach is that the Ca sensed by LCCs is highly nonuniform in the cell because some channels are in the vicinity of Ca sparks and others are not. To solve this problem, we split our population of LCCs into two groups of Markov states. The first group, which we will refer to as the “spark off” group, is shown inside the dashed box (Fig. 2) and represents LCCs that are far from active sparks. The Markov states describing these channels consist of two closed states , one open state , and two inactive states , with red arrows denoting Ca-dependent rates. Because these channels are not in the vicinity of a Ca spark, their Ca-dependent transition rates depend only on the diastolic Ca concentration in the cell, which will be set at [Ca] = 0.1 μM. On the other hand, LCCs that are in the same junctional space of an active sparks (“spark on”) are described by Markov states which are regulated by a local Ca concentration that is substantially larger [Ca] = 100 μM. These channels undergo much faster Ca-induced inactivation. The transition rates between groups of channels is then easily modeled by letting open LCCs in the “spark off” group transition to the “spark on” group at a rate that is simply the spark recruitment rate . Similarly, the reverse transition will be set to the rate that sparks extinguish . This approach accounts for the known relationship between the inactivation of the whole cell LCC current and the amount of Ca released into the cell (1). Here, this coupling is modeled by keeping track of the population of LCCs that are regulated by a high or low local Ca concentration due to local Ca sparks. Detailed model parameters describing the channel transitions rates are given in the Supporting Materials and Methods.
Figure 2.
Markovian model of the LCC current. Markov states in the dashed box (spark off) represent channels facing low Ca (0.1 μM), whereas channels outside the box (spark on) face a Ca spark with high local Ca (100 μM). Red lines indicate Ca-dependent rates. To see this figure in color, go online.
The rate of spark recruitment at junctional clusters
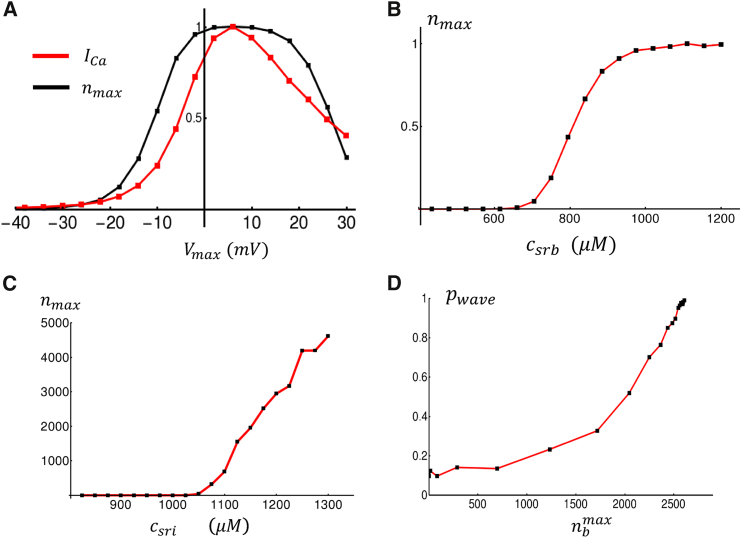
In this section, we develop a phenomenological model of the spark recruitment and extinction rates. To guide in the model construction, we will rely on a physiologically based atrial cell model developed previously by Shiferaw et al. (9). In this model, which is based on a ventricular cell model attributable to Restrepo et al. (12, 13), Ca cycling is described by stochastic simulation of thousands of individual ion channels, which are distributed in a 3D grid representing the cell. Here, we will apply this model to develop a simplified model of the spark recruitment rate. As a starting point, we will first consider the rate of spark recruitment at junctional sites near the cell boundary. To assess the dependence of the spark rate on system parameters, we consider the response of the cell to a rectangular AP clamp from to . We apply this voltage clamp and measure the peak number of Ca sparks that are recruited at the cell boundary during a 200-ms duration at In Fig. 3 A, we plot peak and the peak number of sparks recruited in the cell as a function of . We find that the maximal number of sparks mirrors the peak Ca entry into the cell. This relationship is well known in the experimental literature and is referred to as graded release (1). To model this effect, we will take the spark recruitment rate to be proportional to the Ca influx due to open LCCs that are not facing an active Ca spark. Thus, we let , where is the fraction of LCCs in the open state O (see Fig. 2), and is the current through an open LCC. To complete our phenomenological model, we note that spark recruitment should be highly sensitive to the SR Ca load. This is because the SR load dictates the gradient of Ca across RyR channels and therefore sensitizes the channel to Ca. Furthermore, RyR channels themselves are directly sensitive to luminal Ca concentration in the SR. To analyze this effect, we again apply our 3D computational model to determine the relationship between spark recruitment and SR load. In Fig. 3 B, we plot the maximal number of Ca sparks at junctional sites that are elicited in response to our rectangular voltage clamp. Indeed, we find that spark recruitment at junctional sites is small for SR loads below a threshold ∼800 μM and then increases substantially as the SR load is increased above threshold. To capture these relationships phenomenologically, we will take a junctional spark rate of the form
| (12) |
where is a proportionality constant such that is in units of sparks/ms. To model the SR load dependence, we use a sigmoid function of the form
| (13) |
so that the spark rate is negligible for JSR loads smaller than and increases in a nonlinear fashion, dictated by the Hill coefficient . Finally, we will take our extinction rate to be , where is roughly the average spark lifetime (∼20–50 ms).
Figure 3.
Dependence of boundary Ca release on system parameters. (A) The red line shows peak in response to a rectangular voltage clamp from = −85 mV to the indicated . Here, the current is normalized to its maximal value. The black line indicates the maximal number of Ca sparks evoked at junctional sites , normalized to the maximal number of sparks recruited. The initial SR load is set to 1000 μM with a voltage held at for 10 ms, after which the voltage is raised to for 200 ms. The spark number is the maximal number of sparks recruited in the 200 ms duration at . A plot of spark number represents the average of 10 independent simulations. (B) The maximal number of Ca sparks evoked at junctional sites in response to a rectangular voltage clamp to = 0 mV, plotted as a function of the initial SR concentration is shown. Here, we have normalized the y axis to the maximal number of sparks recruited at an SR load of 1200 μM. Plots represent the average of 10 independent simulations. (C) A plot of the maximal number of Ca sparks at nonjunctional sites in response to an AP clamp is shown. Each point shown is the average over 100 independent simulations at the given initial SR load. (D) A plot of versus the maximal number of boundary sparks recruited. To vary the number of sparks recruited, we scale from 10 to 150%. At a fixed strength, we compute using 100 independent simulations. To see this figure in color, go online.
The rate of spark recruitment at nonjunctional clusters
To model spark recruitment at nonjunctional clusters, we develop a phenomenological model that accounts for Ca wave activation in the cell interior. Our experimental observations and computational modeling of the 3D cell model reveal that, during pacing, Ca waves can propagate from the boundary into the cell interior (9). This typically occurs under rapid pacing in which the Ca content of the SR is large so that RyR clusters are sufficiently sensitized to support a propagating wave. Under these conditions, Ca waves are nucleated at the cell boundary because of Ca sparks that occur at junctional sites. To gain further insight into this nucleation process, we apply our detailed model to determine how propagating waves in the interior depend on model parameters. To determine these relationships, we drive our 3D cell model with a standard AP clamp waveform (Eq. S61). We then measure the relationship between Ca sparks recruited at the cell boundary and the interior. In Fig. 3 C, we plot the maximal number of interior Ca sparks recruited as a function of the SR load. Indeed, we find that for low SR loads, Ca waves do not propagate in the cell interior, and there is a negligible number of Ca sparks in the cell. However, for SR loads above ∼1000 μM, we find that Ca waves begin to propagate in the cell interior, and the number of Ca sparks increases substantially with increasing load. Similarly, in Fig. 3 D, we plot the probability that a Ca wave propagates in the cell, denoted as , as a function of the maximal number of Ca sparks recruited at the cell boundary. To vary Ca spark recruitment at the boundary, we vary the conductance from 10 to 150%. If the number of nonjunctional sparks exceeded 500 after the AP upstroke, then we say that a Ca wave propagated in the cell interior. Empirically, we found that 500 sparks resulted in a convenient threshold to distinguish between fluctuations due to spontaneous Ca sparks and a full Ca wave that propagated in the cell. We then compute as the number of simulation runs a wave occurred divided by the total number of simulations. In this case, we compute from 100 independent runs at varying conductances. In Fig. 3 D, we plot as a function of the maximal number of boundary sparks recruited. Indeed, we find that increases with the number of Ca sparks recruited at junctional sites. This result demonstrates that the probability of wave nucleation in the cell interior is tightly controlled by Ca release at the boundary.
To model the essential features of this process using our simplified spark-rate approach, we note that 1) the spark rate must couple to the number of Ca sparks recruited at the cell boundary such that an increase of will promote the nucleation of a wave that activates interior sites; 2) once a sufficient amount of nonjunctional sparks are triggered, the number of sparks will then increase further as a propagating wave proceeds to activate more sparks; and 3) finally, as indicated by Fig. 3 C, spark recruitment in the interior should also have a nonlinear threshold dependence on the SR load. To capture these features, we will model the nonjunctional spark rate using a phenomenological function of the form
| (14) |
Here, the coupling between the fraction of active boundary sites and the rate of spark recruitment in the interior is governed by a function of the form
| (15) |
so that nonjunctional sparks are ignited at a rate that increases with the fraction of activated boundary clusters . Here, denotes the threshold for excitation from the boundary, and gives a measure of the nonlinearity of the activation process. Now, once sparks are formed in the interior, they can then propagate and recruit more sparks provided a wave nucleation threshold has been crossed. To model this effect, we will take
| (16) |
where is the nucleation threshold and where is the Hill coefficient that characterizes the nonlinearity. Thus, a Ca wave is said to occur when , and the internal spark rate is substantially increased. Here, and are adjustable constants that parametrize the relative strength of boundary-activated sparks and sparks activated by the Ca wave. Finally, we also introduce a nonlinear SR load dependence given by
| (17) |
which ensures that Ca waves occur mostly above a threshold . We point out here that Ca waves can be formed if increases above the threshold because of stochastic fluctuations alone. This scenario corresponds to the well-known spontaneous Ca waves that occur during Ca overload conditions and in the absence of LCC triggering. Hence, both spontaneous and triggered waves can be described using the phenomenological spark rate given by Eq. 14.
Results
Model response to pacing with atrial AP model
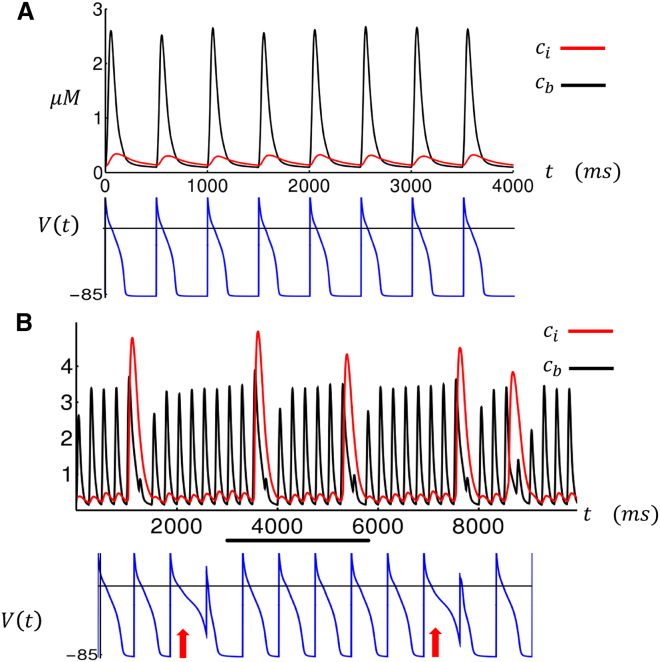
To model rapid pacing, we have integrated our Ca cycling equations with the major ion currents from the Grandi et al. (18) human atrial cell model. In particular, we incorporate their ion current formulations for the fast Na current , the rapidly activating delayed rectifier current , the slowly activating delayed rectifier current , the ultrarapid delayed rectifier current , the inward rectifier current , the transient outward current , the exchange current , and finally, the NaCa exchanger (NCX) current . All Ca cycling components of the original Grandi et al. (18) AP model have been replaced with the Ca cycling equations given in Eqs. 5, 6, 7, 8, and 9. In Fig. 4 A, we plot the steady-state boundary cytosolic Ca concentration , along with the internal concentration , at a pacing CL of 500 ms. Here, we see that tracks the periodic AP, whereas Ca release at the interior is small. Under these conditions, we find that the spark activation rate in the cell interior is small so that the fraction of internal sparks is below the wave activation threshold , and no triggered waves occur in the cell interior. Now, when the cell is rapidly paced at CL = 250 ms, Ca release at the interior then exhibits large intermittent release events (Fig. 4 B, red line) where the Ca transient in the interior rises substantially. These release events correspond to large increases in the fraction of activated sparks , which represents the effect of triggered Ca wave propagation in atrial myocytes. Closer inspection shows that these excitations are due to a larger recruitment of boundary sparks, which is due to the increased SR loading at rapid pacing rates, which initiate regenerative spark activation in the cell interior. Furthermore, our computational model indicates that these large Ca release events induce fluctuations in the APD. In particular, we find that the APD is prolonged on the beats in which the Ca release is large, which is because of the increased inward on that beat. Consequently, the next APD is smaller (Fig. 4 B, bottom trace) because of the reduction of the previous DI, which leads to less time for recovery of the LCCs. Thus, large Ca release events in the interior lead to a sequence of long-short (LS) APD fluctuations.
Figure 4.
Cytosolic Ca transient in the cell interior and boundary as a function of time. Here, the cell is paced for 100 beats to reach a steady state, after which we plot the Ca concentrations and membrane voltage. In (A), CL = 500 ms, and in (B), CL = 250 ms. For (B), the voltage trace corresponds to the beats indicated by the black horizontal line. The APD at which a large Ca release occurred is indicated with a red arrow. To see this figure in color, go online.
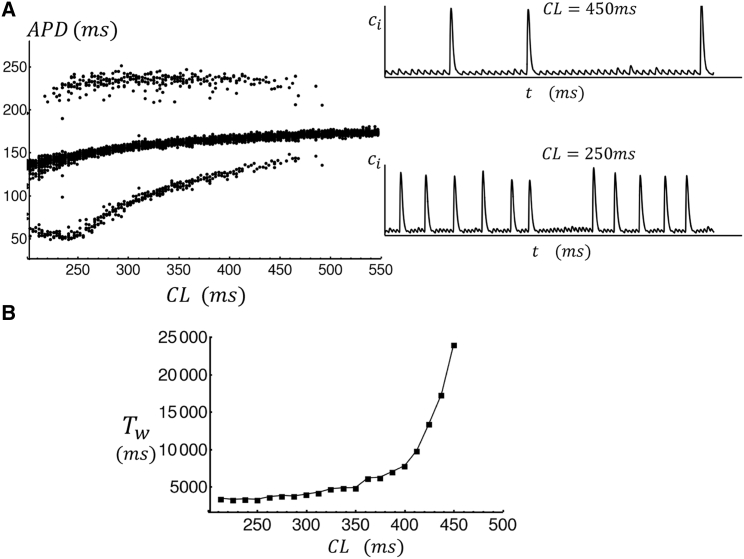
To further explore the system response to rapid pacing, in Fig. 5 A, we plot the APD for the last 40 beats of a simulation of 200 beats for a range of CL. Here, we find that stochastic APD fluctuations due to triggered waves begin to occur for CLs below ∼500 ms. The frequency of these events increases as the CL is decreased, such that at CL = 450 ms pacing (see inset) there are triggered release events every 20–40 beats, whereas at CL = 250 ms, these events are more frequent. To characterize the statistics of APD fluctuations in Fig. 5 B, we compute the mean waiting time between internal Ca release events. Here, we find that the timing to a triggered wave increases exponentially with increasing CL. This result is qualitatively similar to experimental measurements of triggered waves in isolated cells from a normal dog atria (7). There, it was found that rapid pacing increases the wave frequency so that a triggered wave was observed every few beats at CLs in the range of 200–300 ms.
Figure 5.
(A) Steady-state APD as a function of CL. In this simulation, we pace the cell for 200 beats, at a given CL, and then plot the APD for the last 30 beats. The APD is computed as the duration between stimulus time and when = −50 mV during repolarization. The inset shows example traces of the interior Ca concentration at CL = 450 ms and CL = 250 ms. (B) The mean waiting time between large Ca release events as a function of pacing CL. The mean waiting time was computed by pacing to a steady state and then measuring the time to the next triggered wave after t = 1000 ms. A triggered wave is designated to occur when > 0.8 μM. The mean waiting time is computed by averaging over 200 independent simulations.
Alternans
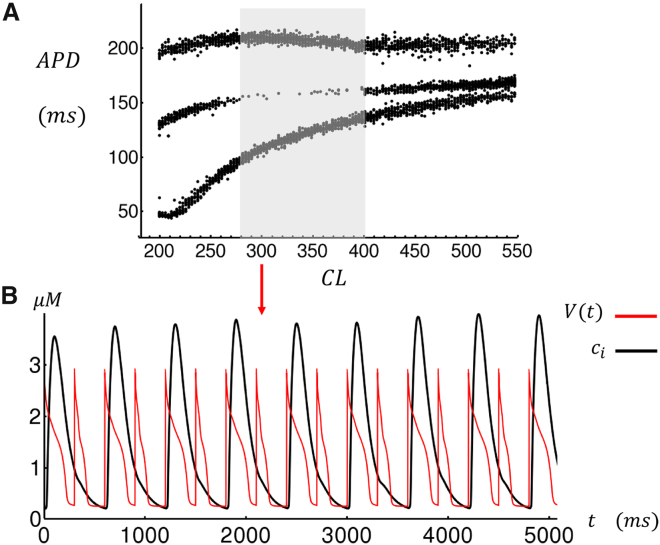
Our computational model can be used to explore Ca cycling dynamics in atrial myocytes under a variety of experimental conditions. In a previous study (7) on dog atrial myocytes, we showed that upon the application of isoproterenol and caffeine, these myocytes exhibited Ca transient alternans when they were paced at rapid rates. A close inspection of the corresponding line scan images reveals that these alternans are due to synchronized wave activation, which occurs only on alternate beats. Using our phenomenological model, we find an alternans regime at rapid pacing rates after decreasing the threshold , which increases the coupling between internal and boundary sites. This change is motivated by a variety of previous experimental findings showing that both isoproterenol and caffeine likely increase the open probability of RyR, which should increase the likelihood of wave propagation. In Fig. 6 A, we show the bifurcation diagram of the model when we reduce the threshold for boundary activation from to , while keeping all other parameters the same as that used in Fig. 5 A. Here, we find that there is a range of CLs (shaded region) at which the APD alternates, on average, from a long to short APD. In Fig. 6 B, we show the Ca transient along with the membrane voltage at CL = 300 ms, which indicates that during alternans the large internal Ca release occurs only on alternate beats. In this case, the underlying mechanism for alternans is straightforward. Effectively, a triggered excitation occurs in the cell interior at a given beat but fails on the next because of insufficient recovery time of the SR load. To confirm this physical picture, we have also applied our detailed 3D computational model to image subcellular Ca during alternans. Indeed, we find that at rapid rates the system readily exhibits sustained alternans in which wave propagation only occurs on alternate beats (see Fig. S1). Finally, in Fig. S2, we present, to our knowledge, new confocal line scan imaging data showing this alternans mode in a dog atrial cell in heart failure.
Figure 6.
(A) The steady-state APD is shown for the last 30 beats after pacing to a steady state for 200 beats. Sustained APD alternans are observed during the range of CLs indicated by the shaded area. (B) The time course of steady-state and when the cell is paced at CL = 300 ms. Note that Ca release occurs only every other beat. All model parameters are the same as that used in Fig. 5 with the exception of the threshold , which has been reduced from 0.5 to 0.44. To see this figure in color, go online.
Synchronization of Ca waves in tissue
Our model simulations reveal that the initiation of triggered waves is a stochastic process. Thus, in cardiac tissue with thousands of coupled myocytes, it is unclear how these stochastic events can summate to induce triggered activity. More precisely, electrical coupling between myocytes will simply average the voltage over the electrotonic length and therefore substantially minimize APD fluctuations due to triggered waves. Furthermore, we note from Fig. 4 B that a triggered Ca wave leads to a LS APD sequence. This implies that if two neighboring cells undergo a triggered excitation on alternate beats then electrical coupling will average the long and short APD so that the average APD will be substantially smaller than if both excitations occur on the same beat. Therefore, for triggered waves to be arrhythmogenic, it is essential for them to be synchronized in tissue over thousands to millions of cells.
Synchronization due to CL perturbation
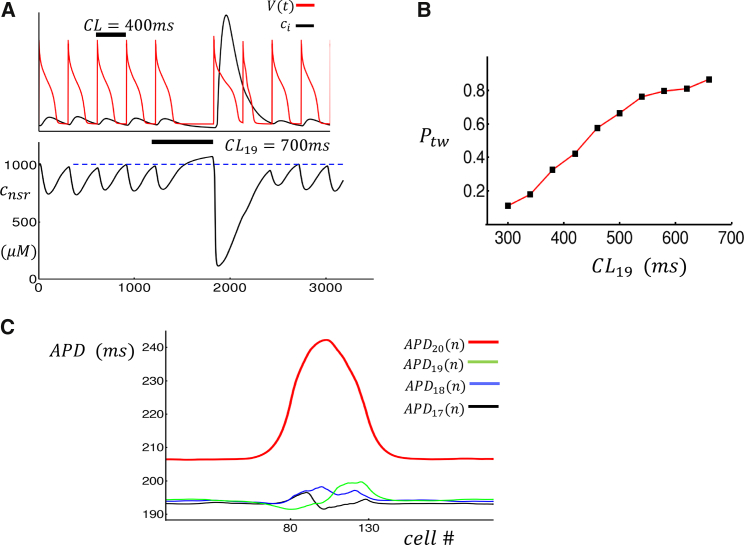
In this study, we propose two distinct synchronization mechanisms that substantially amplify the effect of triggered waves in cardiac tissue. The first mechanism is based on the observation that a prolongation of the pacing CL will lead to an increased SR load at the beginning of the next beat, because there will be more time for SERCA to load Ca into the SR. Therefore, we expect that triggered excitations in atrial myocytes will be more synchronized after a fluctuation that increases the CL. In Fig. 7 A, we show that an increase in CL from 400 to 700 ms leads to a triggered excitation on the next beat. By plotting the interior NSR load during the prolonged beat, we confirm that the SR load is larger at the time of the next stimulus after a CL prolongation. Thus, the probability of a triggered excitation is increased because the SR is more primed for wave propagation. In Fig. 7 B, we pace a cell for 20 beats at CL = 300 ms and compute the probability of a triggered excitation on the 20th beat as a function of the CL on the 19th beat (CL19). We find that increases as CL19 is increased above the baseline CL. The effect of this increased synchronization in cardiac tissue is substantial. In Fig. 7 C, we show the spatial distribution of APD when a cable of cells is paced at CL = 300 ms and with a prolonged CL19 = 450 ms. Here, model parameters are chosen so that the middle 50 cells (80–130) exhibit triggered waves at the baseline pacing of CL = 300 ms, whereas cells outside do not exhibit triggered waves. To accomplish this, we set the threshold for excitation to be for cells prone to triggered waves and otherwise. Fig. 7 C shows the APD distribution for the four last beats showing that the prolonged CL dramatically amplifies the APD variation on the next beat (APD20). In this case, we find that triggered excitations in the “unhealthy” patch lead to APD fluctuations that are ∼5 ms, whereas after the prolonged beat, this change is amplified to ∼30 ms. We point out that APD fluctuations in the unhealthy patch during the base CL pacing can fluctuate above or below the APD of normal cells. This is because a triggered excitation leads to a LS sequence, and in the absence of synchronization, the spatial average can be either above or below the APD in the absence of the triggered excitation. Therefore, partial synchronization of the healthy patch over one beat leads to a substantial effect in tissue by negating this cancellation effect. This result implies that the effect of triggered waves on cardiac tissue is highly sensitive to variations in CL.
Figure 7.
The response of the system to a prolongation of CL. (A) Atrial cell model paced at CL = 400 ms followed by a prolonged beat with CL19 = 700 ms is shown. The bottom trace shows the NSR load inside the cell as a function of time. (B) The probability of triggered wave as a function of prolonged beat duration CL19 is shown. The cell is paced for 20 beats at CL = 300 ms, and is computed on the 20th beat. The criterion for excitation is that > 0.8 μM during the 20th beat. (C) A plot of the APD on a cable of 210 cells that is paced at CL = 300 ms with CL19 = 450 ms is shown. Cells from 80 to 130 are set with = 0.5 and = 0.6 otherwise (i.e., triggered waves only occur on the central patch). In this simulation, we solve the cable equation for voltage with = 5 × 10−4 cm2/ms, space step = 0.015 cm, and time step dt = 0.1 ms. To see this figure in color, go online.
Synchronization due to bidirectional feedback
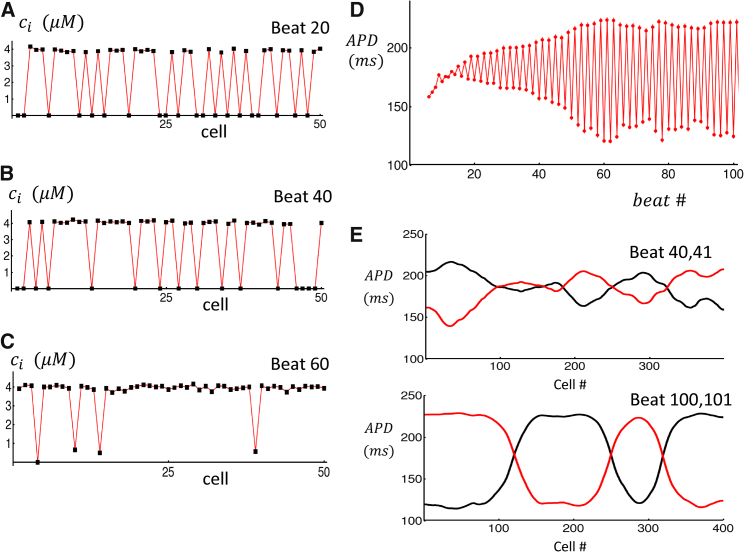
A second mechanism for wave synchronization occurs when cells are in the alternans regime. In this parameter regime, we find that the bidirectional coupling between Ca release and APD can gradually force a population of coupled cells to fire triggered waves on the same beat. In Fig. 8, A–C, we show the peak of the interior Ca concentration , at the indicated beat number, on a cable of 50 electrically coupled cells. Here, we pace all cells in the cable at CL = 300 ms and choose parameters identical to Fig. 6 A so that all cells are in the triggered alternans regime. In this simulation, a triggered Ca release in the cell interior leads to a large peak ∼4 μM, whereas a beat in which no internal release occurs has a much smaller peak Ca ( ∼0.2 μM). After pacing for many beats, we find that the triggered release events become gradually more synchronized so that after 60 beats most cells have a triggered excitation on the same beat (Fig. 8 C). For the same simulation, we have also computed the APD at a specific cell (Fig. 8 D). Our simulations show that APD alternans amplitude grows with beat number as the cell is paced. This is expected because the synchronization of triggered waves on the cable will lead to a larger effect on the APD. In Fig. 8 E, we show the spatial distribution of APD on a cable of 400 cells that has been paced for 100 beats. At beats 40 and 41, we find a random pattern of APD fluctuations due to stochastic triggered waves that are spatially averaged by the electrical coupling between cells. At beats 100 and 101, we find that the cable has self-organized into synchronized regions of a size ∼100 cells. Within these regions, triggered Ca release is synchronized, and the amplitude of APD alternans is large. Thus, when each individual cell exhibits triggered wave alternans, then the longtime evolution of a piece of tissue exhibits spatially discordant alternans, in which the phase of alternans changes over a characteristic length scale that is much larger than a single cell.
Figure 8.
Synchronization of triggered waves due to bidirectional feedback with APD. (A–C) Black squares denote the peak of the Ca transient on a cable of 50 cells at beats 20, 40, and 60. (D) APD at cell 10 as a function of beat number is shown. (E) APD on two alternate beats as a function of cell number on a cable of 400 cells is shown. Traces show APD at beat 40 and 41, and bottom traces shows beat 100 and 101. To see this figure in color, go online.
Discussion
In this study, we have developed a computationally tractable model of Ca cycling in atrial myocytes. The main feature of this model is that it accounts for the unique spatial architecture of these cells, which do not have a well-developed TT system. Thus, Ca signaling in atrial cells occurs mainly at the cell boundary at junctional clusters where RyR and LCCs are in close proximity. However, the large number of nonjunctional RyRs in the cell interior can fire Ca sparks so that propagating Ca waves can be triggered by excitations at the cell boundary. The essential feature of these waves is that they are initiated by LCC openings and can therefore occur during pacing. It is this feature that makes them particularly arrhythmogenic because they can disrupt the rhythmic beating of the cell. Here, we have developed a phenomenological model that describes triggered waves by keeping track of the number of Ca sparks at both junctional and nonjunctional sites. In this approach, a triggered wave is modeled as an autocatalytic event in which the number of sparks at nonjunctional sites increases, leading to a rise in the Ca concentration in the cell interior. This process is coupled to Ca sparks at junctional sites at the cell boundary so that during pacing the cell interior behaves as a stochastic excitable system that is driven periodically. Our model accounts for the stochastic nature of the release process by modeling spark activation and extinction as a binomial random process. In this way, we are able to model experimentally measured features of triggered waves such as their stochasticity and nonlinear dependence on SR load. This phenomenological approach leads to a substantial decrease in computational cost, as compared to detailed 3D computational models that simulate the stochastic dynamics of hundreds of thousands of individual ion channels. Thus, the model developed here can be implemented to study 3D atrial tissue involving millions of electrically coupled cells.
At the single-cell level, our model allows us to study Ca cycling in atrial myocytes under rapid pacing conditions. The main result is that during rapid pacing the SR Ca load increases, which promotes the formation of triggered waves. These triggered waves are stochastic, and so the appropriate way to characterize their timing is by computing the mean waiting time (Fig. 5 B). Our simulations reveal that the mean waiting time decreases exponentially as the cell is paced faster. This result is consistent with experiments in dog atrial cells, which show that triggered waves occur with greater frequency at rapid pacing rates (7) but are essentially never observed at slow pacing rates. Furthermore, we find that if a triggered wave occurs at a given beat then the APD on that beat is prolonged because of the increased inward current due to NaCa exchanger. This APD prolongation leads to a shortened DI and therefore a shortened APD on the next beat because the LCC current will be reduced because of the lesser time for recovery from inactivation. Therefore, a triggered wave leads to a LS sequence of APD, which will be arrhythmogenic because an early afterdepolarization can potentially occur at the long APD and therefore initiate a propagating beat. Also, if the triggered wave is substantially delayed then it can occur during the DI and generate inward currents that can potentially trigger a premature excitation (i.e., a delayed afterdepolarization). Our computational model also revealed that the excitation of triggered waves is a highly nonlinear process, which makes an atrial myocyte prone to alternans. In this model, an alternans response occurs at rapid rates when the nonlinear activation of the cell interior is engaged. In this case, a mode can occur in which a Ca wave is triggered only at every other beat. This pattern has been observed experimentally under exposure to isoproterenol or caffeine (7), which are known to increase RyR open probability and Ca waves. In the Supporting Materials and Methods, we also show a line scan image showing clear triggered wave alternans in dog atrial cells in heart failure (Fig. S2). It is likely that in heart failure the RyR open probability is also increased, which engages the nonlinearity that leads to alternans. These results indicate that the architecture of atrial myocytes makes them particularly prone to alternans given the nonlinear dependence of triggered wave nucleation on key factors such as the SR load and the likelihood of sparks at junctional clusters.
The primary goal of this study was to develop a computational model that can be used to explore how triggered waves can induce electrical excitations on the tissue scale. A crucial finding of our simulations is that synchronization of triggered waves in a population of cells is essential for arrhythmogenic perturbations of membrane voltage to occur. This is true because triggered waves are stochastic; therefore, in the absence of synchronization, the net effect in tissue will be for electronic effects to simply average out excitations at the cell scale. During pacing, we expect that voltage diffuses during one paced beat a distance of roughly ξ =, where = is the effective diffusion coefficient of voltage in cardiac tissue. Thus, we expect the AP to be averaged out over a length scale ξ ∼1–5 nm, which in 3D tissue, corresponds to a volume containing several hundred thousand cells. Thus, randomly occurring triggered waves will be spatially averaged, and tissue scale APD fluctuations will be small. Furthermore, we note that in response to a triggered wave, the APD of a single cell will alternate in a LS sequence. Thus, if triggered waves are randomly timed then the long and short APDs will tend to cancel in a population of cells. Therefore, it is absolutely crucial for triggered waves to be synchronized to significantly perturb the voltage of a mass of cardiac tissue.
To achieve synchronization, we have explored two distinct mechanisms. The first relies on the prolongation of the CL on a given beat, which leads to a larger SR load on the next beat and therefore a larger number of triggered waves. This effect is substantial on a one-dimensional cable in which a segment is vulnerable to triggered waves. Here, we find that CL prolongation at a given beat dramatically amplifies the amplitude of the local APD by synchronizing local release events. In effect, the synchronized response to a CL prolongation negates the cancellation of randomly timed LS APD perturbations. Here, we point out that this effect is not restricted to atrial tissue but can also be applied to the ventricle. In the ventricle, we do not expect triggered waves because TTs are highly developed, and there is little space for triggered excitations to form. In that case, arrhythmogenic activity is likely driven by spontaneous Ca waves, which typically occurs during the DI. In this case, it is clear that if these spontaneous waves are to induce tissue scale excitations, they will have to be highly synchronized. Our findings suggest that a prolongation of CL will likely synchronize Ca release activity by forcing all cells in the tissue to a acquire a higher SR load on the same beat. In the clinical setting, there is some evidence that large variations in CL are associated with the onset of spontaneous arrhythmias (19, 20, 21). In particular, several studies have shown that ventricular tachycardia in some patients tends to occur immediately after a long inter beat interval (19). In other cases, there is evidence that ventricular tachycardia occurs with higher likelihood after a short-long inter beat interval that is caused by an early premature ventricular contraction followed by a long interval due to a missed sinus beat (20). Our analysis suggests that such a sequence is highly arrhythmogenic because the resulting large variations in CL will synchronize Ca waves after the long pause. Thus, our study indicates that Ca wave synchronization may be crucial to understand the initiation of some spontaneous cardiac arrhythmias.
The second mechanism for triggered wave synchronization occurs when the single cell exhibits triggered wave alternans. When this occurs, we find that the bidirectional feedback between the APD and Ca cycling can lead to a gradual synchronization of triggered waves over many beats. The underlying mechanism for this has been described previously in a study by Sato et al. (22). To explain this mechanism in this context, let us first identify the two possible triggered wave sequences as follows: phase 1: triggered wave–no wave–triggered wave–no wave and phase 2: no wave–triggered wave–no wave–triggered wave.
Now, when a population of cells is paced, we will have a random collection of cells in phase 1 and cells in phase 2. Let us assume that so that there are more cells in phase 1. If this occurs, then the APD will alternate by a small amount in synchrony with phase 1. Now, the APD will feed back on triggered waves on the next beat because the DI is smaller, and the probability of triggered waves on the next beat will be reduced. In this way, the APD will gradually synchronize triggered waves so that after many beats segments of a long cable will tend to form regions of synchronized triggered waves on a length scale comparable to ∼ξ. Given that the phase of a given synchronized region is sensitive to the initial distribution of alternans phase, then we expect that these synchronized patterns will tend to form out-of-phase regions on the length scale ξ (i.e., the system will form spatially discordant alternans with a wavelength set by the electrotonic coupling). Thus, at a steady state, we expect large APD fluctuations because triggered waves will be synchronized over hundreds of thousands of cells.
The synchronization mechanisms introduced here are crucial for subcellular Ca cycling activity to induce arrhythmia triggers on the tissue scale. In particular, spatially discordant alternans of APD in cardiac tissue is highly arrhythmogenic for two reasons. Firstly, we expect that a synchronized region of triggered waves will induce substantially larger inward currents, which can initiate an early afterdepolarization or delayed afterdepolarization, depending on the average timing of the triggered Ca waves. Thus, we expect that focal excitations in tissue will originate from patches where triggered waves occur effectively in unison. Secondly, spatially discordant alternans introduce large dynamical heterogeneities in cardiac tissue (23, 24). In effect, as shown in Fig. 8 E, the APD can vary substantially near the nodes that separate out-of-phase regions. This heterogeneity is expected to be highly arrhythmogenic because a triggered excitation from a focal source will then tend to break in the regions of large APD and propagate in regions where APD is reduced. Finally, we highlight the general picture that triggered wave alternans are particularly dangerous because their presence leads to a dramatic simplification of the system dynamics in which cells can lie in one of two possible dynamical states that differ only by a phase. It is this reduction of the range of dynamical possibilities that allows the APD synchronization mechanism to take effect and therefore amplify the resulting tissue scale voltage perturbations. Our work indicates that perhaps it is this feature of alternans that explains their strong correlation to arrhythmias in a wide range of contexts (25). Finally, we stress the fact that the mechanisms described here are robust in the sense that they do not depend on the detailed mechanisms of calcium-induced-calcium release and Ca wave propagation in atrial myocytes. The essential requirement is simply that Ca waves propagate in the cell and that their occurrence is regulated by the membrane voltage via the L-type Ca current. Thus, we expect the mechanisms proposed here to be relevant in a more general context in which Ca waves occur and are sensitive to changes in the membrane voltage.
Author Contributions
Y.S., G.L.A., and J.A.W. designed research, performed research, contributed analytic tools, analyzed data, and wrote the article.
Acknowledgments
Y.S. thanks Enric Alvarez-Lacalle for helpful discussions.
This work was supported by the National Heart, Lung, and Blood Institute grant RO1HL101196 (Y.S. and J.A.W.). Part of this work has been completed at the Kavli Institute of Theoretical Physics. This research was supported in part by the National Science Foundation grant No. NSF PHY-1748958, National Institutes of Health grant No. R25GM067110, and the Gordon and Betty Moore Foundation grant No. 2919.01.
Editor: Eric Sobie.
Footnotes
Supporting Materials and Methods, two figures, and four tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30967-6.
Supporting Material
References
- 1.Bers D.M. Kluwer Academic Publishers; Boston, MA: 2001. Excitation-Contraction Coupling and Cardiac Contractile Force. [Google Scholar]
- 2.Heijman J., Voigt N., Dobrev D. Calcium handling and atrial fibrillation. Wien. Med. Wochenschr. 2012;162:287–291. doi: 10.1007/s10354-012-0109-9. [DOI] [PubMed] [Google Scholar]
- 3.Nattel S. New ideas about atrial fibrillation 50 years on. Nature. 2002;415:219–226. doi: 10.1038/415219a. [DOI] [PubMed] [Google Scholar]
- 4.Dobrev D., Wehrens X.H.T. Calcium-mediated cellular triggered activity in atrial fibrillation. J. Physiol. 2017;595:4001–4008. doi: 10.1113/JP273048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Landstrom A.P., Dobrev D., Wehrens X.H.T. Calcium signaling and cardiac arrhythmias. Circ. Res. 2017;120:1969–1993. doi: 10.1161/CIRCRESAHA.117.310083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Blatter L.A. The intricacies of atrial calcium cycling during excitation-contraction coupling. J. Gen. Physiol. 2017;149:857–865. doi: 10.1085/jgp.201711809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Aistrup G.L., Arora R., Wasserstrom J.A. Triggered intracellular calcium waves in dog and human left atrial myocytes from normal and failing hearts. Cardiovasc. Res. 2017;113:1688–1699. doi: 10.1093/cvr/cvx167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Izu L.T., Wier W.G., Balke C.W. Evolution of cardiac calcium waves from stochastic calcium sparks. Biophys. J. 2001;80:103–120. doi: 10.1016/S0006-3495(01)75998-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shiferaw Y., Aistrup G.L., Wasserstrom J.A. Mechanism for triggered waves in atrial myocytes. Biophys. J. 2017;113:656–670. doi: 10.1016/j.bpj.2017.06.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Arora R., Aistrup G.L., Wasserstrom J.A. Regional distribution of T-tubule density in left and right atria in dogs. Heart Rhythm. 2017;14:273–281. doi: 10.1016/j.hrthm.2016.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Trafford A.W., Clarke J.D., Dibb K.M. Calcium signalling microdomains and the t-tubular system in atrial mycoytes: potential roles in cardiac disease and arrhythmias. Cardiovasc. Res. 2013;98:192–203. doi: 10.1093/cvr/cvt018. [DOI] [PubMed] [Google Scholar]
- 12.Restrepo J.G., Weiss J.N., Karma A. Calsequestrin-mediated mechanism for cellular calcium transient alternans. Biophys. J. 2008;95:3767–3789. doi: 10.1529/biophysj.108.130419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Restrepo J.G., Karma A. Spatiotemporal intracellular calcium dynamics during cardiac alternans. Chaos. 2009;19:037115. doi: 10.1063/1.3207835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Qu Z., Nivala M., Weiss J.N. Calcium alternans in cardiac myocytes: order from disorder. J. Mol. Cell. Cardiol. 2013;58:100–109. doi: 10.1016/j.yjmcc.2012.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Franzini-Armstrong C., Protasi F., Tijskens P. The assembly of calcium release units in cardiac muscle. Ann. N. Y. Acad. Sci. 2005;1047:76–85. doi: 10.1196/annals.1341.007. [DOI] [PubMed] [Google Scholar]
- 16.Franzini-Armstrong C., Protasi F., Ramesh V. Shape, size, and distribution of Ca(2+) release units and couplons in skeletal and cardiac muscles. Biophys. J. 1999;77:1528–1539. doi: 10.1016/S0006-3495(99)77000-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mahajan A., Shiferaw Y., Weiss J.N. A rabbit ventricular action potential model replicating cardiac dynamics at rapid heart rates. Biophys. J. 2008;94:392–410. doi: 10.1529/biophysj.106.98160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Grandi E., Pandit S.V., Bers D.M. Human atrial action potential and Ca2+ model: sinus rhythm and chronic atrial fibrillation. Circ. Res. 2011;109:1055–1066. doi: 10.1161/CIRCRESAHA.111.253955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Viskin S., Fish R., Barron H.V. Arrhythmias in the congenital long QT syndrome: how often is torsade de pointes pause dependent? Heart. 2000;83:661–666. doi: 10.1136/heart.83.6.661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gomes J.A., Alexopoulos D., Suh K. The role of silent ischemia, the arrhythmic substrate and the short-long sequence in the genesis of sudden cardiac death. J. Am. Coll. Cardiol. 1989;14:1618–1625. doi: 10.1016/0735-1097(89)90005-3. [DOI] [PubMed] [Google Scholar]
- 21.el-Sherif N., Gough W.B., Restivo M. Reentrant ventricular arrhythmias in the late myocardial infarction period: mechanism by which a short-long-short cardiac sequence facilitates the induction of reentry. Circulation. 1991;83:268–278. doi: 10.1161/01.cir.83.1.268. [DOI] [PubMed] [Google Scholar]
- 22.Sato D., Bers D.M., Shiferaw Y. Formation of spatially discordant alternans due to fluctuations and diffusion of calcium. PLoS One. 2013;8:e85365. doi: 10.1371/journal.pone.0085365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hayashi H., Shiferaw Y., Qu Z. Dynamic origin of spatially discordant alternans in cardiac tissue. Biophys. J. 2007;92:448–460. doi: 10.1529/biophysj.106.091009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mironov S., Jalife J., Tolkacheva E.G. Role of conduction velocity restitution and short-term memory in the development of action potential duration alternans in isolated rabbit hearts. Circulation. 2008;118:17–25. doi: 10.1161/CIRCULATIONAHA.107.737254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Rosenbaum D.S., Jackson L.E., Cohen R.J. Electrical alternans and vulnerability to ventricular arrhythmias. N. Engl. J. Med. 1994;330:235–241. doi: 10.1056/NEJM199401273300402. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.