Jackknife approach to the estimation of mutual information

Significance

As a fundamental concept in information theory, mutual information has been commonly applied to quantify the dependence between variables. However, existing estimations have unstable statistical performance since they involve a set of tuning parameters. We develop a jackknife approach that does not incur predetermined tuning parameters. The proposed approach enjoys several appealing theoretical properties and has stable numerical performance.

Abstract

Quantifying the dependence between two random variables is a fundamental issue in data analysis, and thus many measures have been proposed. Recent studies have focused on the renowned mutual information (MI) [Reshef DN, et al. (2011) Science 334:1518–1524]. However, “Unfortunately, reliably estimating mutual information from finite continuous data remains a significant and unresolved problem” [Kinney JB, Atwal GS (2014) Proc Natl Acad Sci USA 111:3354–3359]. In this paper, we examine the kernel estimation of MI and show that the bandwidths involved should be equalized. We consider a jackknife version of the kernel estimate with equalized bandwidth and allow the bandwidth to vary over an interval. We estimate the MI by the largest value among these kernel estimates and establish the associated theoretical underpinnings.

A key issue in data science is how to measure the dependence between two random variables. Pearson’s correlation coefficient (1) provides a powerful measure for linear dependence, but it is incapable of detecting nonlinear association (2, 3). Thus, many other measures have been introduced to quantify complex dependence. For example, Gretton et al. (4) proposed a kernel-based independence criterion that uses the squared Hilbert–Schmidt norm of the cross-covariance operator. Székely, Rizzo, and Bakirov (5) introduced the distance correlation (dCor) which does not involve any nonparametric estimation and is free of tuning parameters. Heller, Heller, and Gorfine (6) proposed a rank-based distance measure which demonstrates good numerical performance. Although many different measures have been proposed, the mutual information introduced by Claude Shannon in 1948 (7) is not replaceable and is still of great research interest. As a fundamental measure of dependence, mutual information (MI) possesses several desirable properties and can be interpreted intuitively (8). These advantages secure MI as a very powerful measure of nonlinear dependence with very wide applications in data analysis. As such, studies have focused on its mathematical properties and its estimation efficiency (2, 9, 10).

For continuous data, there are three typical groups of estimation for MI. The first group is the “bins” method that discretizes the continuous data into different bins and estimates MI from the discretized data (11, 12). The asymptotic performance for this bins method is systematically analyzed in ref. 13. The second group is based on estimates of probability density functions, for example, the histogram estimator of ref. 14, the kernel density estimator (KDE) of ref. 15, the B-spline estimator of ref. 16, and the wavelet estimator of ref. 17. To reduce the bias at the boundary region, ref. 18 introduced the mirrored KDE and derived its exponential concentration bound. Recently, ref. 19 further applied the ensemble method in kernel estimation and derived the ensemble estimator. The third group is based on the relationship between the MI and entropies. One of the most popular estimations in this group is the k-nearest neighbors (kNN) estimator introduced in ref. 20, which was extended in ref. 10, leading to the introduction of the Kraskov–Stögbauer–Grassberger (KSG) estimator. This estimator is further discussed in refs. 21–23.

Although many different approaches have been considered, the estimation of MI, especially for continuous data, relies heavily on the choice of the tuning parameters involved such as the number of bins, the bandwidth in kernel density estimation, and the number of neighbors in the kNN estimator. As a consequence, the corresponding estimators may be very unstable or seriously biased. However, little research has been done on the selection of these parameters. In this paper, we focus on the KDE approach (24, 25), which involves at least four bandwidth matrices. Experience with tests for independence suggests that the bandwidths should be set equal. Equalization of bandwidths also helps us reduce the bias at the boundary region and thus improve the efficiency of estimation. To free the estimation from bandwidth selection, we consider a jackknife version of MI (called JMI) and show that JMI has asymptotically a unique maximum with respect to the equalized bandwidth. We adopt the maximum value as our estimator of MI and provide the necessary statistical underpinnings. Interestingly, for the very special case of independent random variables, JMI enjoys a consistency rate higher than that of root-n. Numerically, we compare the estimation efficiency of JMI vs. that of other estimation methods that include the mixed KSG of ref. 23, the copula-based KSG of ref. 21, and other KDE methods. We also construct a test for independence (2, 3, 26) based on the JMI and compare it with several popular methods, such as the dCor of ref. 5, the maximal information coefficient (MIC) of ref. 9, and the Heller–Heller–Gorfine (HHG) test of ref. 6. These comparisons demonstrate the superior performance of JMI.

MI and Its Kernel Estimation

Consider two random variables $\mathbf{X}={\left(X_1,X_2,\dots ,X_P\right)}^{\prime }$ and $\mathbf{Y}={\left(Y_1,Y_2,\dots ,Y_Q\right)}^{\prime }$. Let us focus on the case that their joint probability density function exists. MI is defined as

$$MI\left(\mathbf{X},\mathbf{Y}\right)=E\left\{\log \frac{f_{\mathbf{X}\mathbf{Y}}\left(\mathbf{X},\mathbf{Y}\right)}{f_{\mathbf{X}}\left(\mathbf{X}\right)f_{\mathbf{Y}}\left(\mathbf{Y}\right)}\right\},$$

where $f_{\mathbf{X}}$, $f_{\mathbf{Y}}$, and $f_{\mathbf{X}\mathbf{Y}}$ are the density functions of $\mathbf{X}$, $\mathbf{Y}$, and $\left(\mathbf{X},\mathbf{Y}\right)$, respectively. This definition can be easily extended to other types of random variables that may not have density functions (13). As a measure of complex dependence, MI possesses the following desirable properties. It is always nonnegative, i.e., $MI\left(\mathbf{X},\mathbf{Y}\right)\ge 0,$ and equality holds if and only if the two variables are independent. Moreover, the stronger is the dependence between two variables, the larger is the MI. MI is also invariant under strictly monotonic variable transformations. More recently, Kinney and Atwal (2) proved that MI satisfies the so-called self-equitability, indicating that MI places the same importance on linear and nonlinear dependence.

Let $S=\left\{\left({\mathbf{x}}_i,{\mathbf{y}}_i\right),i=1,\dots ,n\right\}$ with ${\mathbf{x}}_i={\left(x_{i1},x_{i2},\dots ,x_{iP}\right)}^{\prime }$ and ${\mathbf{y}}_i={\left(y_{i1},y_{i2},\dots ,y_{iQ}\right)}^{\prime }$ be independent samples from $\left(\mathbf{X},\mathbf{Y}\right)$. Let $|\cdot |$ represent the determinant of a matrix. Consider the following multivariate KDEs:

$$\begin{array}{ccc}\hfill {\widehat{f}}_{\mathbf{X},{\mathbf{H}}_{\mathbf{X}}}\left(\mathbf{x}\right)& =\hfill & \frac{1}{n}\sum _{j=1}^n{\mathbf{K}}_{{\mathbf{H}}_{\mathbf{X}}}^P\left({\mathbf{x}}_j-\mathbf{x}\right);\hfill \\ \hfill {\widehat{f}}_{\mathbf{Y},{\mathbf{H}}_{\mathbf{Y}}}\left(\mathbf{y}\right)& =\hfill & \frac{1}{n}\sum _{j=1}^n{\mathbf{K}}_{{\mathbf{H}}_{\mathbf{Y}}}^Q\left({\mathbf{y}}_j-\mathbf{y}\right);\hfill \\ \hfill {\widehat{f}}_{\mathbf{X}\mathbf{Y},{\mathbf{B}}_{\mathbf{X}},{\mathbf{B}}_{\mathbf{Y}}}\left(\mathbf{x},\mathbf{y}\right)& =\hfill & \frac{1}{n}\sum _{j=1}^n{\mathbf{K}}_{{\mathbf{B}}_{\mathbf{X}}}^P\left({\mathbf{x}}_j-\mathbf{x}\right){\mathbf{K}}_{{\mathbf{B}}_{\mathbf{Y}}}^Q\left({\mathbf{y}}_j-\mathbf{y}\right).\hfill \end{array}$$

Here ${\mathbf{H}}_{\mathbf{X}}$, ${\mathbf{H}}_{\mathbf{Y}}$, ${\mathbf{B}}_{\mathbf{X}}$, and ${\mathbf{B}}_{\mathbf{Y}}$ are diagonal bandwidth matrices with ${\mathbf{H}}_{\mathbf{X}}=diag\left(h_{{\mathrm{X}}_1}^2,h_{{\mathrm{X}}_2}^2,\dots ,h_{{\mathrm{X}}_P}^2\right)$, ${\mathbf{H}}_{\mathbf{Y}}=diag\left(h_{{\mathrm{Y}}_1}^2,h_{{\mathrm{Y}}_2}^2,\dots ,h_{{\mathrm{Y}}_Q}^2\right)$, ${\mathbf{B}}_{\mathbf{X}}=diag\left(b_{{\mathrm{X}}_1}^2,b_{{\mathrm{X}}_2}^2,\dots ,b_{{\mathrm{X}}_P}^2\right)$, and ${\mathbf{B}}_{\mathbf{Y}}=diag\left(b_{{\mathrm{Y}}_1}^2,b_{{\mathrm{Y}}_2}^2,\dots ,b_{{\mathrm{Y}}_Q}^2\right)$; typically, for diagonal matrix $\mathbf{A}$, ${\mathbf{K}}_{\mathbf{A}}^P\left(\mathbf{x}\right)=|\mathbf{A}{|}^{-1/2}{\mathbf{K}}^P\left({\mathbf{A}}^{-1/2}\mathbf{x}\right)$, where ${\mathbf{K}}^P$ is a P-dimensional symmetric density function with ${\mathbf{K}}^P\left(\mathbf{x}\right)=\prod _{p=1}^{P}K\left(x_p\right)$. Based on these estimators, the KDE of MI is

$${Î}_1\left({\mathbf{B}}_{\mathbf{X}},{\mathbf{B}}_{\mathbf{Y}},{\mathbf{H}}_{\mathbf{X}},{\mathbf{H}}_{\mathbf{Y}}\right)=\frac{1}{n}\sum _{i=1}^n\log \frac{{\widehat{f}}_{\mathbf{X}\mathbf{Y},{\mathbf{B}}_{\mathbf{X}},{\mathbf{B}}_{\mathbf{Y}}}\left({\mathbf{x}}_i,{\mathbf{y}}_i\right)}{{\widehat{f}}_{\mathbf{X},{\mathbf{H}}_{\mathbf{X}}}\left({\mathbf{x}}_i\right){\widehat{f}}_{\mathbf{Y},{\mathbf{H}}_{\mathbf{Y}}}\left({\mathbf{y}}_i\right)}.$$ [1]

This estimator is consistent under some mild conditions. However, as pointed out by ref. 15, its numerical performance is heavily influenced by the choice of bandwidths. Another problem is the notorious boundary effect, which becomes more serious as ${\widehat{f}}_{\mathbf{X},{\mathbf{H}}_{\mathbf{X}}}\left({\mathbf{x}}_i\right)$ and ${\widehat{f}}_{\mathbf{Y},{\mathbf{H}}_{\mathbf{Y}}}\left({\mathbf{y}}_i\right)$ appear in the denominator.

In checking the independence between $\mathbf{X}$ and $\mathbf{Y}$, we usually compare the product of frequencies in hypercubes ${\mathcal{D}}_{\mathbf{X}}=\left\{{\mathbf{x}}_i:|x_{ip}-x_p|<h_{{\mathrm{X}}_p},p=\mathrm{1,2},\dots ,P\right\}$ and ${\mathcal{D}}_{\mathbf{Y}}=\left\{{\mathbf{y}}_i:|y_{iq}-y_q|<h_{{\mathrm{Y}}_q},q=\mathrm{1,2},\dots ,Q\right\}$ with the frequency in their intersection ${\mathcal{D}}_{\mathbf{X}}\cap {\mathcal{D}}_{\mathbf{Y}}=\left\{\left({\mathbf{x}}_i,{\mathbf{y}}_i\right):|x_{ip}-x_p|<h_{{\mathrm{X}}_p},|y_{iq}-y_q|<h_{{\mathrm{Y}}_q},p=\mathrm{1,2},\dots ,P,q=\mathrm{1,2},\dots ,Q\right\}$. Let $\#$ denote the number of elements in a set. By taking ${\mathbf{K}}^P\left(\mathbf{x}\right)=\prod _{p=1}^P\left[{\mathbf{1}}_{\left(\left|x_p\right|\le 1\right)}/2\right]$, where ${\mathbf{1}}_A$ is the indicator function of set $A$, those frequencies are, respectively,

$$\begin{array}{ccc}\hfill \frac{\#{\mathcal{D}}_{\mathbf{X}}}{n}& =\hfill & \frac{2^P}{n}\sum _{i=1}^n\prod _{p=1}^{P}K\left(\frac{x_{ip}-x_p}{h_{{\mathrm{X}}_p}}\right)=2^P|{\mathbf{H}}_{\mathbf{X}}{|}^{1/2}{\widehat{f}}_{\mathbf{X},{\mathbf{H}}_{\mathbf{X}}}\left(\mathbf{x}\right),\hfill \\ \hfill \frac{\#{\mathcal{D}}_{\mathbf{Y}}}{n}& =\hfill & \frac{2^Q}{n}\sum _{i=1}^n\prod _{q=1}^{Q}K\left(\frac{y_{iq}-y_q}{h_{{\mathrm{Y}}_q}}\right)=2^Q|{\mathbf{H}}_{\mathbf{Y}}{|}^{1/2}{\widehat{f}}_{\mathbf{Y},{\mathbf{H}}_{\mathbf{Y}}}\left(\mathbf{y}\right),\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \frac{\#\left({\mathcal{D}}_{\mathbf{X}}\cap {\mathcal{D}}_{\mathbf{Y}}\right)}{n}& =\hfill & \frac{2^{P+Q}}{n}\sum _{i=1}^n\prod _{p=1}^{P}K\left(\frac{x_{ip}-x_p}{h_{{\mathrm{X}}_p}}\right)\prod _{q=1}^{Q}K\left(\frac{y_{iq}-y_q}{h_{{\mathrm{Y}}_q}}\right)\hfill \\ \hfill & =\hfill & 2^{P+Q}{\left(\left|{\mathbf{H}}_{\mathbf{X}}\right|\left|{\mathbf{H}}_{\mathbf{Y}}\right|\right)}^{1/2}{\widehat{f}}_{\mathbf{X}\mathbf{Y},{\mathbf{H}}_{\mathbf{X}},{\mathbf{H}}_{\mathbf{Y}}}\left(\mathbf{x},\mathbf{y}\right).\hfill \end{array}$$

Thus, the ratio of comparison is

$$\frac{\#\left({\mathcal{D}}_{\mathbf{X}}\cap {\mathcal{D}}_{\mathbf{Y}}\right)/n}{\#{\mathcal{D}}_{\mathbf{X}}/n\#{\mathcal{D}}_{\mathbf{Y}}/n}=\frac{{\widehat{f}}_{\mathbf{X}\mathbf{Y},{\mathbf{H}}_{\mathbf{X}},{\mathbf{H}}_{\mathbf{Y}}}\left(\mathbf{x},\mathbf{y}\right)}{{\widehat{f}}_{\mathbf{X},{\mathbf{H}}_{\mathbf{X}}}\left(\mathbf{x}\right){\widehat{f}}_{\mathbf{Y},{\mathbf{H}}_{\mathbf{Y}}}\left(\mathbf{y}\right)}.$$

Note that the bandwidth matrices corresponding to $\mathbf{X}$ in both estimators of $f_{\mathbf{X}}$ and $f_{\mathbf{X},\mathbf{Y}}$ are the same, and the same is true for the case of $\mathbf{Y}$. We therefore argue that ${\mathbf{B}}_{\mathbf{X}}={\mathbf{H}}_{\mathbf{X}}$ and ${\mathbf{B}}_{\mathbf{Y}}={\mathbf{H}}_{\mathbf{Y}}$ should be imposed on the KDE. With these equalizations of bandwidths, the joint and marginal densities are well defined; i.e., $\int {\widehat{f}}_{\mathbf{X}\mathbf{Y},{\mathbf{H}}_{\mathbf{X}},{\mathbf{H}}_{\mathbf{Y}}}\left(\mathbf{x},\mathbf{y}\right)d\mathbf{x}={\widehat{f}}_{\mathbf{Y},{\mathbf{H}}_{\mathbf{Y}}}\left(\mathbf{y}\right)$ and $\int {\widehat{f}}_{\mathbf{X}\mathbf{Y},{\mathbf{H}}_{\mathbf{X}},{\mathbf{H}}_{\mathbf{Y}}}\left(\mathbf{x},\mathbf{y}\right)d\mathbf{y}={\widehat{f}}_{\mathbf{X},{\mathbf{H}}_{\mathbf{X}}}\left(\mathbf{x}\right)$, which is an important feature in the definition of MI. Another important motivation for equalizing the bandwidths is that it can automatically reduce the estimation bias at the boundary region; see theoretical justification in the next section.

Jackknife Estimation of MI

Marginal transformation is an efficient way to improve the estimation of ref. 1 and to reduce the technical complexity (27, 28). We consider the uniform transformation $\mathbf{U}={\left(U_1,U_2,\dots ,U_P\right)}^{\prime }={\left(F_{X_1}\left(X_1\right),F_{X_2}\left(X_2\right),\dots ,F_{X_P}\left(X_P\right)\right)}^{\prime }$ and $\mathbf{V}={\left(V_1,V_2,\dots ,V_Q\right)}^{\prime }={\left(F_{Y_1}\left(Y_1\right),F_{Y_2}\left(Y_2\right),\dots ,F_{Y_Q}\left(Y_Q\right)\right)}^{\prime }$, where $F_{X_p},p=\mathrm{1,2},\dots ,P$ and $F_{Y_q},q=\mathrm{1,2},\dots ,Q$ are the cumulative distribution functions of $X_p$ and $Y_q$, respectively. It is easy to see that $MI\left(\mathbf{U},\mathbf{V}\right)=MI\left(\mathbf{X},\mathbf{Y}\right).$ Use $c_{\mathbf{U}}\left(\mathbf{u}\right),c_{\mathbf{V}}\left(\mathbf{v}\right)$ and $c_{\mathbf{U}\mathbf{V}}\left(\mathbf{u},\mathbf{v}\right)$ to denote the copula density functions of $\mathbf{U}$, $\mathbf{V}$, and $\left(\mathbf{U},\mathbf{V}\right)$, respectively. For observed data, the corresponding transformation is ${\left({\mathbf{u}}_i^{\star },{\mathbf{v}}_i^{\star }\right)}^{\prime }={\left(u_{i1}^{\star },\dots ,u_{iP}^{\star },v_{i1}^{\star },\dots ,v_{iQ}^{\star }\right)}^{\prime }={\left(F_{X_1,n}\left(x_1\right),\dots ,F_{X_P},n\left(x_P\right),F_{Y_1,n}\left(y_1\right),\dots ,\hspace{0.17em}{F}_{Y_Q,n}\left(y_Q\right)\right)}^{\prime }$with $F_{X_p,n},p=\mathrm{1,2},\dots ,P$ and $F_{Y_q,n},q=\mathrm{1,2},\dots ,Q$ denoting the empirical cumulative distribution functions of $\left\{x_{ip},i=1,\dots ,n\right\}$ and $\left\{y_{iq},i=1,\dots ,n\right\}$, respectively.

A main problem with the KDE is the selection of bandwidths. In the literature, many selection methods have been proposed (29–31). Although good properties have been proved for these selectors in the estimation of density function, applying them to the estimation of MI does not work well (15, 32).

Jackknife Estimation.

Note that MI is zero when the two random variables are independent, and generally bigger MIs imply stronger dependence. Thus, the bandwidths should be selected to maximize MI to detect possible dependence. This idea was also applied in statistical tests (33, 34). However, maximizing MI tends to overfit the MI, making it possibly infinite. Instead, we use the jackknife estimation (27, 35). Let

$${Î}_2\left({\mathbf{B}}_{\mathbf{U}},{\mathbf{B}}_{\mathbf{V}},{\mathbf{H}}_{\mathbf{U}},{\mathbf{H}}_{\mathbf{V}}\right)=\frac{1}{n}\sum _{i=1}^n\log \frac{{ĉ}_{\mathbf{U}\mathbf{V},{\mathbf{B}}_{\mathbf{U}},{\mathbf{B}}_{\mathbf{V}}}^{\backslash i}\left({\mathbf{u}}_i^{\star },{\mathbf{v}}_i^{\star }\right)}{{ĉ}_{\mathbf{U},{\mathbf{H}}_{\mathbf{U}}}^{\backslash i}\left({\mathbf{u}}_i^{\star }\right){ĉ}_{\mathbf{V},{\mathbf{H}}_{\mathbf{V}}}^{\backslash i}\left({\mathbf{v}}_i^{\star }\right)}$$ (2)

with bandwidth matrices ${\mathbf{H}}_{\mathbf{U}}=diag\left(h_{{\mathrm{U}}_1}^2,h_{{\mathrm{U}}_2}^2,\dots ,h_{{\mathrm{U}}_P}^2\right)$, ${\mathbf{H}}_{\mathbf{V}}=diag\left(h_{{\mathrm{V}}_1}^2,h_{{\mathrm{V}}_2}^2,\dots ,h_{{\mathrm{V}}_Q}^2\right)$, ${\mathbf{B}}_{\mathbf{U}}=diag\left(b_{{\mathrm{U}}_1}^2,b_{{\mathrm{U}}_2}^2,\dots ,b_{{\mathrm{U}}_P}^2\right)$, ${\mathbf{B}}_{\mathbf{V}}=diag\left(b_{{\mathrm{V}}_1}^2,b_{{\mathrm{V}}_2}^2,\dots ,b_{{\mathrm{V}}_Q}^2\right)$, and

$$\begin{array}{ccc}\hfill {ĉ}_{\mathbf{U},{\mathbf{H}}_{\mathbf{U}}}^{\backslash i}\left(\mathbf{u}\right)& =\hfill & \frac{1}{n-1}\sum _{j\ne i}{\mathbf{K}}_{{\mathbf{H}}_{\mathbf{U}}}^P\left({\mathbf{u}}_j^{\star }-\mathbf{u}\right);\hfill \\ \hfill {ĉ}_{\mathbf{V},{\mathbf{H}}_{\mathbf{V}}}^{\backslash i}\left(\mathbf{v}\right)& =\hfill & \frac{1}{n-1}\sum _{j\ne i}{\mathbf{K}}_{{\mathbf{H}}_{\mathbf{V}}}^Q\left({\mathbf{v}}_j^{\star }-\mathbf{v}\right);\hfill \\ \hfill {ĉ}_{\mathbf{U}\mathbf{V},{\mathbf{B}}_{\mathbf{U}},{\mathbf{B}}_{\mathbf{V}}}^{\backslash i}\left(\mathbf{u},\mathbf{v}\right)& =\hfill & \frac{1}{n-1}\sum _{j\ne i}{\mathbf{K}}_{{\mathbf{B}}_{\mathbf{U}}}^P\left({\mathbf{u}}_j^{\star }-\mathbf{u}\right){\mathbf{K}}_{{\mathbf{B}}_{\mathbf{V}}}^Q\left({\mathbf{v}}_j^{\star }-\mathbf{v}\right).\hfill \end{array}$$

We estimate MI by the maximum of ${Î}_2\left({\mathbf{B}}_{\mathbf{U}},{\mathbf{B}}_{\mathbf{V}},{\mathbf{H}}_{\mathbf{U}},{\mathbf{H}}_{\mathbf{V}}\right)$. With four bandwidth matrices as arguments, this maximization is not easy. However, as suggested above, the bandwidths in the calculation should be set equal. The bias expansion in Theorem 1 also indicates that this equalization of bandwidths in Eq. 2 is helpful for counteracting boundary bias.

For theoretical analysis, we define an “oracle” estimator

$${Î}_0=\frac{1}{n}\sum _{i=1}^n\log \frac{c_{\mathbf{U}\mathbf{V}}\left({\mathbf{u}}_i,{\mathbf{v}}_i\right)}{c_{\mathbf{U}}\left({\mathbf{u}}_i\right)c_{\mathbf{V}}\left({\mathbf{v}}_i\right)}.$$

Note that ${Î}_0$ is exactly 0 when the two variables are independent and, by the central limit theorem, it is root-n consistent when $0<MI<\infty$ and ${E\left[\log \frac{c_{\mathbf{U}\mathbf{V}}\left(\mathbf{U},\mathbf{V}\right)}{c_{\mathbf{U}}\left(\mathbf{U}\right)c_{\mathbf{V}}\left(\mathbf{V}\right)}\right]}^2<\infty$. As ${Î}_0$ is actually not obtainable, hereafter we use it only as a benchmark for asymptotic analysis.

Theorem 1.

Under general regularity conditions (SI Appendix, section C, Assumptions A.1, A.2, A.5, and A.6) on functions $K$, $c_{\mathbf{U}}$, $c_{\mathbf{V}}$, and $c_{\mathbf{U}\mathbf{V}}$ and bandwidth matrices, we have

$$\begin{array}{ccc}\hfill & \hfill & \frac{1}{n}\sum _{i=1}^n\log {ĉ}_{\mathbf{U}\mathbf{V},{\mathbf{B}}_{\mathbf{U}},{\mathbf{B}}_{\mathbf{V}}}^{\backslash i}\left({\mathbf{u}}_i^{\star },{\mathbf{v}}_i^{\star }\right)-\frac{1}{n}\sum _{i=1}^n\log c_{\mathbf{U}\mathbf{V}}\left({\mathbf{u}}_i,{\mathbf{v}}_i\right)\hfill \\ \hfill & \hfill & =-C_1\left[\sum _{p=1}^P{b}_{{\mathrm{U}}_p}+\sum _{q=1}^Q{b}_{{\mathrm{V}}_q}\right]+o_P\left(\sum _{p=1}^P\left|b_{{\mathrm{U}}_p}\right|+\sum _{q=1}^Q\left|b_{{\mathrm{V}}_q}\right|\right),\hfill \end{array}$$

where $C_1$ is given in in SI Appendix, Eq.S1. Furthermore,

$$\begin{array}{ccc}\hfill & \hfill & {Î}_2\left({\mathbf{H}}_{\mathbf{U}},{\mathbf{H}}_{\mathbf{V}},{\mathbf{B}}_{\mathbf{U}},{\mathbf{B}}_{\mathbf{V}}\right)-{Î}_0\hfill \\ \hfill & =\hfill & C_1\left[\sum _{p=1}^P\left(h_{{\mathrm{U}}_p}-b_{{\mathrm{U}}_p}\right)+\sum _{q=1}^Q\left(h_{{\mathrm{V}}_q}-b_{{\mathrm{V}}_q}\right)\right]\hfill \\ \hfill & \hfill & +o_P\left(\sum _{p=1}^P\left(\left|h_{{\mathrm{U}}_p}\right|+\left|b_{{\mathrm{U}}_p}\right|\right)+\sum _{q=1}^Q\left(\left|h_{{\mathrm{V}}_q}\right|+\left|b_{{\mathrm{V}}_q}\right|\right)\right).\hfill \end{array}$$

The first part of Theorem 1 indicates that a kernel-based estimate of a copula density has a bias of the same order as the bandwidth. It is caused by the boundary points since the kernel density estimation has a much faster consistency rate for the interior points (36). The second part concerns ${Î}_2$, which involves a divisor in the form of a product of two marginal copula densities; it shows that its bias depends on the difference of bandwidths, i.e., $h_{{\mathrm{U}}_p}-b_{{\mathrm{U}}_p}$ and $h_{{\mathrm{V}}_q}-b_{{\mathrm{V}}_q}$. If the commonly used selectors (24, 25, 31, 37) are adopted to select the bandwidths separately, then $b_{{\mathrm{U}}_p}$ and $b_{{\mathrm{V}}_q}$ are of order $n^{-1/\left(P+Q+4\right)}$ while $h_{{\mathrm{U}}_p}$ and $h_{{\mathrm{V}}_q}$ are of order $n^{-1/\left(P+4\right)}$ and $n^{-1/\left(Q+4\right)}$, respectively. Consequently, the kernel estimator of MI with those bandwidths would suffer a bias of order $n^{-1/\left(P+Q+4\right)}$. However, if we equalize the bandwidths, ${\mathbf{B}}_{\mathbf{U}}={\mathbf{H}}_{\mathbf{U}}\text{and}{\mathbf{B}}_{\mathbf{V}}={\mathbf{H}}_{\mathbf{V}},$ the leading term in the bias will be eliminated automatically. To further simplify the bandwidth selection, we also restrict ${\mathbf{H}}_{\mathbf{U}}=h^2{\mathbf{I}}_P$ and ${\mathbf{H}}_{\mathbf{V}}=h^2{\mathbf{I}}_Q$ with ${\mathbf{I}}_n$ the $n\times n$ identity matrix. This restriction is reasonable since each component of $\mathbf{U}$ and $\mathbf{V}$ is uniformly distributed on $\left[\mathrm{0,1}\right]$ after the transformation. Thus, we consider a jackknife estimator of MI with one common bandwidth,

$${Î}_3\left(h\right)=\frac{1}{n}\sum _{i=1}^n\log \frac{{ĉ}_{\mathbf{U}\mathbf{V},h^2{\mathbf{I}}_P,h^2{\mathbf{I}}_Q}^{\backslash i}\left({\mathbf{u}}_i^{\star },{\mathbf{v}}_i^{\star }\right)}{{ĉ}_{\mathbf{U},h^2{\mathbf{I}}_P}^{\backslash i}\left({\mathbf{u}}_i^{\star }\right){ĉ}_{\mathbf{V},h^2{\mathbf{I}}_Q}^{\backslash i}\left({\mathbf{v}}_i^{\star }\right)}.$$

Our final estimator is

$$\widehat{JMI}\left(\mathbf{X},\mathbf{Y}\right)={\text{max}}_{h>0}\left[{Î}_3\left(h\right)\right].$$

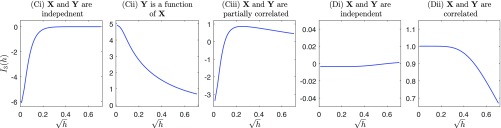
Since this estimation procedure involves a maximization problem, the existence of a global maximum is crucial for computation. With a different relationship between $\mathbf{X}$ and $\mathbf{Y}$, the objective function ${Î}_3\left(h\right)$ possesses three typical shapes: (i) When $\mathbf{X}$ and $\mathbf{Y}$ are independent of each other, ${Î}_3\left(h\right)$ is an increasing function bounded by 0 as in Fig. 1 Ci; the maximum is achieved with a large $h$ and tends to 0. (ii) When $\mathbf{X}$ and $\mathbf{Y}$ are functionally dependent (i.e., one is a function of the other), the objective function is monotone decreasing as in Fig. 1 Cii, suggesting a zero-valued bandwidth and that the estimated information tends to infinity. (iii) When $\mathbf{X}$ and $\mathbf{Y}$ are partially correlated, ${Î}_3\left(h\right)$ is a unimodal function as shown in Fig. 1 Ciii. These shapes are further justified by Theorem 2. In particular, when $\mathbf{X}$ and $\mathbf{Y}$ are partially correlated, Theorem 2 indicates that the unique maximum is achieved at $h\propto n^{-1/\left(P+Q+3\right)}$.

Fig. 1.

Typical shapes of function ${Î}_3\left(h\right)$. In Ci, Cii, and Ciii, at least one of $\mathbf{X}$ and $\mathbf{Y}$ is a continuous variable; in Di and Dii, both $\mathbf{X}$ and $\mathbf{Y}$ are discrete.

Theorem 2.

Under general regularity conditions (SI Appendix, section C, Assumptions A.1, A.5, and A.7) on functions $K$, $c_{\mathbf{U}}$, $c_{\mathbf{V}}$, and bandwidth,

• a)if $MI<\infty$ and $c_{\mathbf{U}\mathbf{V}}$ satisfies the regularity condition A.2 in SI Appendix, section C, then

$${Î}_3\left(h\right)-{Î}_0=-\frac{C_2}{2}{h}^3-\frac{C_3}{2n{h}^{P+Q}}+o_P\left(h^3+\frac{1}{n{h}^{P+Q}}\right),$$

where $C_2$ and $C_3$ are two nonnegative constants given in SI Appendix, section C. In particular, $C_2=0$ when $\mathbf{X}$ and $\mathbf{Y}$ are independent.

• b)If $MI=\infty$, and $\mathbf{X}$ and $\mathbf{Y}$ are functionally dependent and satisfy regularity condition A.3 in SI Appendix, section C, then

$${Î}_3\left(h\right)=min\left(P,Q\right)\log \frac{1}{h}+o_P\left(\log \frac{1}{h}\right).$$

Although JMI is defined for continuous random variables, it also applies to the discrete random variables and mixed random variables (with neither purely continuous distributions nor purely discrete distributions). If both $\mathbf{X}$ and $\mathbf{Y}$ are discrete, ${Î}_3\left(h\right)$ depends on $h$ as shown in Fig. 1 Di or Dii: If they are independent, ${Î}_3\left(h\right)$ changes only marginally with $h$; otherwise ${Î}_3\left(h\right)$ remains unchanged when $h$ is smaller than a certain value and is decreasing thereafter, suggesting any bandwidth that is small enough will give the same estimator. If $\mathbf{X}$ and $\mathbf{Y}$ have a mixture of continuous components and discrete components, ${Î}_3\left(h\right)$ depends on $h$ in the same way as in Fig. 1 Ci, Cii, and Ciii. More details about extension of JMI to discrete case can be found in SI Appendix, section G.

Compared with existing methods such as mirrored KDE (18), ensemble KDE (19), copula-based KSG (21), and mixed KSG (23), the $\widehat{JMI}\left(\mathbf{X},\mathbf{Y}\right)$ has several advantages. First, it is more computationally efficient since only one common bandwidth is introduced. Second, the procedure is completely data driven, and we provide a stable selection procedure for bandwidth $h$ so that no tuning parameter needs to be predetermined. Third, our method does not necessitate boundary correction and yet it retains the same estimation efficiency because the boundary biases are eliminated automatically. Finally and most importantly, taking the unique maximum value makes $\widehat{JMI}\left(\mathbf{X},\mathbf{Y}\right)$ numerically stable.

Consistency of the Estimation.

We have the following results for the consistency of our estimator.

Theorem 3.

Under general regularity conditions (SI Appendix, section C, Assumptions A.1, A.5, and A.8) on functions $K$, $c_{\mathbf{U}}$, $c_{\mathbf{V}}$, and bandwidth,

• a)if $MI<\infty$and $c_{\mathbf{U}\mathbf{V}}$ satisfies regularity condition A.2 in SI Appendix, section C, then

$$\widehat{JMI}\left(\mathbf{X},\mathbf{Y}\right)-{Î}_0=O_P\left(n^{-3/\left(P+Q+3\right)}\right);$$

• b)if $MI=\infty$and $c_{\mathbf{U}\mathbf{V}}$ satisfies regularity condition A.4 in SI Appendix, section C, then

$$\widehat{JMI}\left(\mathbf{X},\mathbf{Y}\right)\to \infty ,\hspace{0.17em}a.s..$$

Note that ${Î}_0$ is the oracle estimator of MI with root-n consistency. When $X$ and $Y$ are both univariate random variables, Theorem 3a indicates that JMI has, in general, the same root-n consistency as ${Î}_0$, which is the minimax rate (38) for estimating MI. Interestingly, for the special case when $X$ and $Y$ are independent, ${Î}_0=0$ and the estimator converges to 0 at rate $n^{-3/5}$, which is even faster than root-n. We exploit this faster consistency rate for the independent case to yield a test for independence with high local power as shown in SI Appendix, section F.

Test for Independence

The proposed JMI estimator is a natural test statistic for independence. Tests based on asymptotic distributions require data with large sample size. In contrast, the permutation technique can give a precise distribution for even small samples (39–41). For a random sample of $n$ observations, $S=\left\{\left({\mathbf{x}}_i,{\mathbf{y}}_i\right),i=1,\dots ,n\right\}$, from $\left(\mathbf{X},\mathbf{Y}\right)$, let $\delta \left(1\right),\delta \left(2\right),\dots ,\delta \left(n\right)$ be a random permutation of $\mathrm{1,2},\dots ,n$. Based on data $S_1=\left\{\left({\mathbf{x}}_i,{\mathbf{y}}_{\delta \left(i\right)}\right),i=1,\dots ,n\right\}$, calculate the jackknife estimator, denoted by ${\widehat{JMI}}_1$. On repeating the above procedure $N$ times, $T=\left\{{\widehat{JMI}}_k,k=1,\dots ,N\right\}$ are obtained. The distribution of $\widehat{JMI}$, under the null hypothesis $H_0$, can be approximated by the empirical distribution of $T$. At significance level $\alpha$, we reject the null hypothesis when $\widehat{JMI}$ based on the original data is greater than the (1$-\alpha$)th quantile of $T$.

Simulation Study

Estimation of MI.

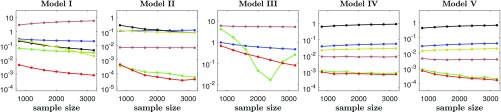
In this section, we compare the efficiency of the JMI estimator with that of existing estimators of MI. As shown in ref. 23, the mixed KSG has the best performance among the three kNN-based estimators they considered and outperforms the partitioning method in their simulation studies. We thus include the mixed KSG as a representative of kNN-based methods in the comparison. As the copula-based KSG (21) makes the same marginal transformation as ours, it is also included in the comparison. To illustrate the stability of the bandwidth selection of JMI, we compare its performance with that of mirrored KDE (18) and other KDE methods that select bandwidths, respectively, by the rule-of-thumb method (THUMB) and the plug-in method (PLUG-IN). We use the same models as in ref. 23 and their variations for multivariate cases, all together nine models, to evaluate the estimation methods. Details of these models are listed in SI Appendix, section D. Similar to ref. 23, the mean-squared errors (MSEs) of different methods for different models and sample sizes are calculated based on 250 replications. The results for the first five models are plotted in Fig. 2, while those for the other four models are shown in SI Appendix, section E. It can be seen that the other KDE methods have much bigger MSE than JMI, possibly due to the fact that unequalized bandwidths tend to cause boundary estimation bias. Copula-based KSG also performs badly as it is not applicable directly to discrete random variables. Mixed KSG shows satisfactory performance in all of the models but is worse than JMI, especially for models I and III. In comparison, our JMI has the smallest MSE for almost all models across different sample sizes, indicating its superior performance.

Fig. 2.

In each panel, the lines represent MSEs of different estimation methods based on 250 replications. Correspondence between colors and the methods are as follows: JMI in red, mixed KSG in green, rule of thumb KDE in blue, plug-in KDE in black, mirrored KDE in dark yellow, and copula-based KSG in brown. For model III, the plug-in method and the mirrored KDE method are not calculated due to their excessive computational complexity.

Test for Independence.

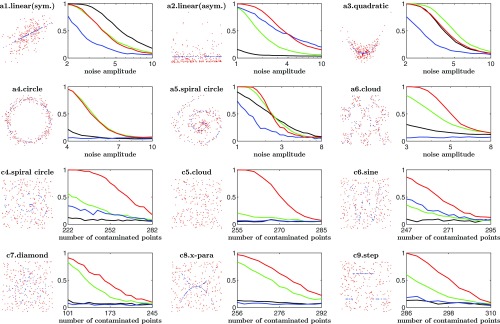
Many statistical tests have been proposed for independence. As demonstrated in ref. 3, HHG of ref. 6 usually has the best performance among all of the existing methods. To ease visualization, we include only dCor of ref. 5, HHG of ref. 6, and MIC of ref. 9 in this simulation study. We examine 16 models that were used in refs. 2, 3, and 6 which include both univariate models and multivariate models. For each model, we further consider the additive noise and the case where the data are contaminated with pure noise. Details of these models are listed in SI Appendix, section D. Similar to ref. 2, we simulate data with sample size $n=320$ and 25 different magnitudes of noise level. For models with additive noise, we increase the noise level by changing the noise ratio amplitude (NR), while for models with contaminations, we raise the noise level by introducing more contaminating observations. We plot the power curves for some of the results in Fig. 3, and the others are in SI Appendix, section E.

Fig. 3.

In each pair of panels, Left shows the model and the data, and Right shows the power of tests at significance level $\alpha =0.05$: Models a1–a6 with additive noise are in Upper panels, and models c4–c9 with contaminated noise are in Lower panels. For power curves, correspondence between colors and different methods is as follows: red for JMI, green for HHG, blue for MIC, and black for dCor.

We summarize the results as follows. dCor performs well only for linear models with symmetric additive noise, but poorly for the other models. Similar to results in refs. 2 and 3, MIC performs very well in testing independence for the high-frequency sine model but it fails in other models. In most cases, HHG has relatively better performance than MIC and dCor, which is consistent with the findings in ref. 3. Generally, JMI appears to be the most stable test for independence. It has similar performance to HHG for models with additive noise but has clear superiority for data with contaminated observations.

Discussion

In this paper, we have introduced a jackknife kernel estimation for the MI (JMI). Inspired by statistical tests for independence and guided by asymptotic analysis, we propose that the bandwidths involved in the estimation should be set equal. For measuring the dependence, we estimate the MI using its maximum value with respect to the equalized bandwidth. JMI is completely data driven and does not incur predetermined tuning parameters. It enjoys very good statistical properties such as automatic bias correction and high local power in testing for independence. The superiority of JMI is also demonstrated through simulation studies. We attribute the good performance of JMI to two factors: (i) the definition of MI itself and (ii) our estimation method that enjoys several advantages mentioned above.

Materials and Methods

“Mixed KSG” was calculated by the codes in ref. 23. “Copula-based KSG” was based on the algorithm described in ref. 21. “Mirrored KDE” was computed by the algorithm introduced in ref. 42. For the other methods, the simulations were conducted in R. “dCor” and “MIC” were estimated using packages “energy” and “Minerva,” respectively. The HHG test was carried out using the package “HHG.” For kernel methods, the rule of thumb used the optimal Gaussian bandwidth given in ref. 24; bandwidths for “PLUG-IN” were calculated using the package “ks.” “JMI” was calculated by the procedure discussed in SI Appendix, section B. For estimation efficiency, MSE for each model and sample size was calculated based on 250 replications. For the test of independence, we adopted the permutation test discussed above. For each sample, we randomly permuted observations of $\mathbf{Y}$ to generate samples under the null hypothesis. The power curve for each model and at each noise level was calculated based on 1,000 simulations. Our calculation codes are available at https://github.com/XianliZeng/JMI.