Photonic implementation of Majorana-based Berry phases

Experimental realization of Berry phases brings us closer to the exotic physics of Majorana fermions.

Abstract

Geometric phases, generated by cyclic evolutions of quantum systems, offer an inspiring playground for advancing fundamental physics and technologies alike. The exotic statistics of anyons realized in physical systems can be interpreted as a topological version of geometric phases. However, non-Abelian statistics has not yet been demonstrated in the laboratory. Here, we use an all-optical quantum system that simulates the statistical evolution of Majorana fermions. As a result, we experimentally realize non-Abelian Berry phases with the topological characteristic that they are invariant under continuous deformations of their control parameters. We implement a universal set of Majorana-inspired gates by performing topological and nontopological evolutions and investigate their resilience against perturbative errors. Our photonic experiment, though not scalable, suggests the intriguing possibility of experimentally simulating Majorana statistics with scalable technologies.

INTRODUCTION

The Berry phase is one of the most intriguing concepts in physics (1). It inspired numerous investigations toward theoretical frontiers with its possible generalizations (2) and technological applications in quantum computation (3). At the forefront of research in geometric evolutions is the controlled realization of anyonic statistics in condensed matter systems (4–6). This is manifested by the cyclic evolution of two anyonic quasiparticles braided around each other. The anyonic quasiparticles are deemed Abelian or non-Abelian depending on the possible geometric evolutions from the exchange being simple global phase factors or noncommuting unitaries, respectively. The statistical character of the exchange evolutions dictates that the resulting geometric phases are topologically robust. This robustness is a very desirable characteristic because it makes non-Abelian anyons a promising platform for fault-tolerant quantum computation (5–8). In the past decades, non-Abelian anyons have been extensively theorized in condensed matter systems (9–12). The most promising direction for realizing non-Abelian anyons is the investigation of Majorana zero modes (MZMs). There are already several positive signatures for the realization of MZMs in the laboratory (13–21). Nevertheless, the experimental realization of braiding operations is still a challenging open problem.

RESULTS

Encoding of MZM geometric evolutions

Here, we report the experimental quantum simulation of four MZM braiding evolutions encoded in an all-optical system (22). The MZMs are supported at the endpoints of two Kitaev chain models (KCMs) composed of fermions. To perform the encoding, we first transform the fermion system, with Hamiltonian H_KCM, to a spin-¹/₂ system, with Hamiltonian H_spin, through a unitary Jordan-Wigner (JW) transformation, U_JW (23, 24). The spin system is then encoded in the spatial modes of single photons (25).

Under the JW transformation, the local Hamiltonians are unitarily connected

$${\mathit{H}}_{\text{spin}}={\mathit{U}}_{\text{JW}}{\mathit{H}}_{\text{KCM}}{\mathit{U}}_{\text{JW}}^{†}$$ (1)

As a result, the time evolutions of the KCM and the spin system are identical when written in their corresponding basis states. The geometric phases that correspond to the braiding of MZMs are particular cases of time evolutions that are cyclic and adiabatic. Hence, the photonic system can simulate the statistical evolution of four MZMs by simulating the corresponding spin system. The possibility to generate an equivalent quantum evolution is in complete alignment with the spirit of quantum simulation (26). The unitary equivalence (Eq. 1) between the KCM and the spin system guarantees that the Berry phase obtained by evolving H_spin is non-Abelian and topological in nature. Our previous experiment simulated the exchange of two MZMs positioned at the endpoints of the same chain, thus realizing a topological Abelian Berry phase (25).

The topological character of the spin model results from the topological character of the KCM. In the latter model, the topological invariance corresponds to the invariance of the geometric evolution against perturbations that are local in position space. As the environment is assumed to act locally in space, the KCM is a promising candidate for performing fault-tolerant quantum computation. The unitary transformation U_JW inherits the spin model with topologically invariant geometric evolutions, but now with respect to perturbations that are local in the parametric space of the adiabatic evolution. As these perturbations are not necessarily local in the position space, they may not correspond to possible environmental errors in the spin system. In addition, in our photonic experiment, the resulting non-Abelian geometric phases are insensitive of the exact timing of each controlled evolution when it is large enough. This is a highly desirable characteristic that facilitates the experimental realization of the non-Abelian evolution with high fidelity.

By experimentally simulating the braiding of different pairs of MZMs, we can only realize Clifford gates (27), such as the Hadamard gate, $\mathit{H}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1& -1\\ 1& 1\end{array}\right)$, and the $(-\frac{\mathrm{\pi }}{4})$-phase gate, $\mathit{R}=\left(\begin{array}{cc}1& 0\\ 0& -\mathit{i}\end{array}\right)$, which are not universal for quantum computation (28). The inclusion of a non-Clifford gate, such as the $\frac{\mathrm{\pi }}{8}$-phase gate, $\mathit{T}=\left(\begin{array}{cc}1& 0\\ 0& {\mathit{e}}^{\mathit{i}\mathrm{\pi }/4}\end{array}\right)$, can resolve this problem (29). We experimentally simulate the $\frac{\mathrm{\pi }}{8}$-phase gate by moving two MZMs at the same site and exposing them to a controlled local perturbation. We experimentally demonstrate that, unlike the H and R topological gates, the $\frac{\mathrm{\pi }}{8}$-phase gate is not immune to local perturbations in MZMs B and C. Nevertheless, “magic state distillation” (30) can be used to produce error-corrected $\frac{\mathrm{\pi }}{8}$-phase gates from noisy ones. When access to an arbitrary number of Kitaev chains is possible, two-qubit topological gates can be realized by using the control procedures presented here.

Quantum gates based on MZM braiding

The smallest system of two connected Kitaev chains that remains fault-tolerant against local perturbations at all times during the braiding evolution is composed of six fermion sites (31). Using six, rather than five, sites guarantees that no pairs of MZMs ever meet at the same site, which would render them unprotected to local perturbations. Here, we describe these fermions through the canonical operators c_j and ${\mathit{c}}_{\mathit{j}}^{†}$, with positions j = 1,…, 6, where j = 1, 2 constitutes the first chain, j = 4, 5, 6 constitutes the second chain, and j = 3 corresponds to the link between them, as shown in Fig. 1. The KCM for the two chains is given in terms of Majorana operators, ${\mathrm{\gamma }}_{\mathit{j}\mathit{a}}={\mathit{c}}_{\mathit{j}}+{\mathit{c}}_{\mathit{j}}^{†}$ and ${\mathrm{\gamma }}_{\mathit{j}\mathit{b}}=\mathit{i}({\mathit{c}}_{\mathit{j}}^{†}-{\mathit{c}}_{\mathit{j}})$, by the Hamiltonian

$${\mathit{H}}_{{\mathrm{M}}_0}=\mathit{i}({\mathrm{\gamma }}_{1\mathit{b}}{\mathrm{\gamma }}_{2\mathit{a}}+{\mathrm{\gamma }}_{4\mathit{b}}{\mathrm{\gamma }}_{5\mathit{a}}+{\mathrm{\gamma }}_{5\mathit{b}}{\mathrm{\gamma }}_{6\mathit{a}})+\mathit{i}{\mathrm{\gamma }}_{3\mathit{a}}{\mathrm{\gamma }}_{3\mathit{b}}$$ (2)

The Majorana operators γ_m satisfy the relations ${\mathrm{\gamma }}_{\mathit{m}}^{†}={\mathrm{\gamma }}_{\mathit{m}}$ and γ_lγ_m + γ_mγ_l = 2δ_lm for l, m = 1a, 1b,..., 6a, 6b. Note that the particular operators γ_1a, γ_2b, γ_4a, and γ_6b are not present in Hamiltonian (Eq. 2), so $[{\mathit{H}}_{{\mathrm{M}}_0},{\mathrm{\gamma }}_{\mathit{j}}]=0$ for j = 1a, 2b, 4a, 6b. As a result, these Majorana modes have zero energy, giving rise to four endpoint MZMs, which we denote as A, B, C, and D in Fig. 1. The logical qubit states are taken to be |0_L〉 = |00_g〉 and |1_L〉 = |11_g〉 corresponding to the degenerate ground states of ${\mathit{H}}_{{\mathrm{M}}_0}$ with even fermion parity, given by |00_g〉 = Nf₁d₁f₂d₂d₃|vac〉 and $|{11}_{\mathrm{g}}\rangle ={\mathit{f}}_1^{†}{\mathit{f}}_2^{†}|{00}_{\mathit{g}}\rangle$, where f₁ = (γ_1a + iγ_2b)/2, f₂ = (γ_6b + iγ_4a)/2, d₁ = (γ_1b + iγ_2a)/2, d₂ = (γ_4b + iγ_5a)/2, and d₃ = (γ_5b + iγ_6a)/2. For convenience, we denote the appropriate normalization constant by N.

Fig. 1. The set of universal quantum gates.

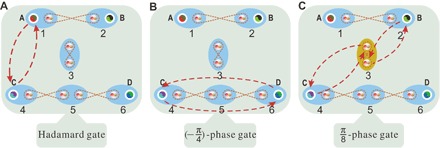
The Kitaev chains consist of six fermions (numbered from 1 to 6) with four endpoint MZMs A, B, C, and D, which can be used to demonstrate the universal gates. Each two Majorana fermions in the blue ellipse form a conventional fermion. The dashed lines between different Majorana fermions represent the initial interactions between them. (A) The anticlockwise braiding of MZMs A and C implements a Hadamard gate, H, acting on the logical basis. (B) The anticlockwise braiding of MZMs C and D implements a $(-\frac{\mathrm{\pi }}{4})$-phase gate, R, acting on the logical basis. (C) The real-time population-dependent evolution on MZMs B and C, which is realized by transporting the two MZMs to a single site (site 3 in our experiment) and applying a coupling between them, leads to a $\frac{\mathrm{\pi }}{8}$-phase gate, T, acting on the logical basis.

The Hadamard gate H on the logical qubit can be realized by the anticlockwise braiding of MZMs A and C positioned at sites 1 and 4, respectively, as shown in Fig. 1A. The transport of the MZMs around the chain network is performed by adiabatically evolving the system through the following sequence of Hamiltonians, ${\mathit{H}}_{{\mathrm{M}}_0}$, ${\mathit{H}}_{{\mathrm{h}}_1}$, ${\mathit{H}}_{{\mathrm{h}}_2}$, ${\mathit{H}}_{{\mathrm{h}}_3}$, and ${\mathit{H}}_{{\mathrm{M}}_0}$, where

$$\begin{array}{c}{\mathit{H}}_{{\mathrm{h}}_1}=\mathit{i}({\mathrm{\gamma }}_{1\mathit{b}}{\mathrm{\gamma }}_{2\mathit{a}}+{\mathrm{\gamma }}_{1\mathit{a}}{\mathrm{\gamma }}_{3\mathit{a}}+{\mathrm{\gamma }}_{5\mathit{b}}{\mathrm{\gamma }}_{6\mathit{a}})+\mathit{i}{\mathrm{\gamma }}_{4\mathit{a}}{\mathrm{\gamma }}_{4\mathit{b}},\\ {\mathit{H}}_{{\mathrm{h}}_2}=\mathit{i}({\mathrm{\gamma }}_{1\mathit{b}}{\mathrm{\gamma }}_{2\mathit{a}}+{\mathrm{\gamma }}_{1\mathit{a}}{\mathrm{\gamma }}_{3\mathit{a}}+{\mathrm{\gamma }}_{3\mathit{b}}{\mathrm{\gamma }}_{4\mathit{b}}+{\mathrm{\gamma }}_{5\mathit{b}}{\mathrm{\gamma }}_{6\mathit{a}}),\\ {\mathit{H}}_{{\mathrm{h}}_3}=\mathit{i}({\mathrm{\gamma }}_{1\mathit{b}}{\mathrm{\gamma }}_{2\mathit{a}}+{\mathrm{\gamma }}_{1\mathit{a}}{\mathrm{\gamma }}_{3\mathit{a}}+{\mathrm{\gamma }}_{4\mathit{b}}{\mathrm{\gamma }}_{5\mathit{a}}+{\mathrm{\gamma }}_{5\mathit{b}}{\mathrm{\gamma }}_{6\mathit{a}})\end{array}$$ (3)

Section S1B shows a depiction of the resulting MZM transportation. The ground states of these Hamiltonians have the MZMs located at the desired sites. Hence, braiding can be implemented by a set of consecutive imaginary-time evolution (ITE) operators, ${\mathit{e}}^{-{\mathit{H}}_{{\mathrm{M}}_0}\mathit{t}}$, ${\mathit{e}}^{-{\mathit{H}}_{{\mathrm{h}}_1}\mathit{t}}$, ${\mathit{e}}^{-{\mathit{H}}_{{\mathrm{h}}_2}\mathit{t}}$, ${\mathit{e}}^{-{\mathit{H}}_{{\mathrm{h}}_3}\mathit{t}}$, and ${\mathit{e}}^{-{\mathit{H}}_{{\mathrm{M}}_0}\mathit{t}}$, where t is taken to be large enough for these operators to faithfully represent projectors onto the corresponding ground states up to overall normalization (25). Because of the topological nature of the produced evolutions, the exact value of t does not matter as long as it is long enough to suppress the contribution from the excited states (see Materials and Methods and section S1A). The theoretically expected non-Abelian Berry phase resulting from this set of evolutions is given by $\mathit{H}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1& -1\\ 1& 1\end{array}\right)$ when written in the logical basis {|00_g〉, |11_g〉} (see Materials and Methods).

To realize the R gate on the logical qubit, we need to anticlockwise braid the MZMs C and D, as shown in Fig. 1B. The experimental simulation of the braiding evolution is performed by switching between the corresponding Majorana Hamiltonians ${\mathit{H}}_{{\mathrm{r}}_1}$, ${\mathit{H}}_{{\mathrm{r}}_2}$, and ${\mathit{H}}_{{\mathrm{r}}_3}$. This time evolution can be implemented by a set of consecutive ITE operators, ${\mathit{e}}^{-{\mathit{H}}_{{\mathrm{M}}_0}\mathit{t}}$, ${\mathit{e}}^{-{\mathit{H}}_{{\mathrm{r}}_1}\mathit{t}}$, ${\mathit{e}}^{-{\mathit{H}}_{{\mathrm{r}}_2}\mathit{t}}$, ${\mathit{e}}^{-{\mathit{H}}_{{\mathrm{r}}_3}\mathit{t}}$, and ${\mathit{e}}^{-{\mathit{H}}_{{\mathrm{M}}_0}\mathit{t}}$. The detailed process is given in section S1C. The resulting non-Abelian Berry phase is given by $\mathit{R}=\left(\begin{array}{cc}1& 0\\ 0& -\mathit{i}\end{array}\right)$ in the logical basis. The corresponding braiding with a single chain was realized in the study of Xu et al. (25). The Hermitian conjugate gates, H^† and R^†, are produced by reversing the orientation of the exchanging paths. Realizing the Hadamard gate, H, and the $(-\frac{\mathrm{\pi }}{4})$-phase gate, R, by braiding of MZMs demonstrates the non-Abelian character of the generated Berry phases. When these two operations are performed in reverse order, they give a different composite geometric evolution, because HR ≠ RH.

To realize the $\frac{\mathrm{\pi }}{8}$-phase gate, we place two MZMs at the same site and apply a local field. This causes the splitting of the ground-state degeneracy for a certain time, during which the appropriate dynamical phase factor is accumulated (29). In particular, we transport the B and C MZMs to site 3 by a set of ITE operations. Then, the population-dependent Hamiltonian H_e = − iγ_3aγ_3b is operated for a certain time τ, as shown in Fig. 1C. Last, the MZMs are transferred back to their initial position. The details of this process can be found in section S1D. During this evolution, the qubit states are transformed by $\mathit{M}=\left(\begin{array}{cc}\text{cos} \mathrm{\tau }& -\mathit{i}\text{sin} \mathrm{\tau }\\ -\mathit{i}\text{sin} \mathrm{\tau }& \text{cos} \mathrm{\tau }\end{array}\right)={\mathit{e}}^{-\mathit{i}{\mathrm{\sigma }}_{\mathit{x}}\mathrm{\tau }}$. With the help of the Hadamard gate, we can obtain the $\frac{\mathrm{\pi }}{8}$-phase gate as ${\mathit{H}}^{†}\mathit{M}\mathit{H}={\mathit{e}}^{-\mathit{i}\mathrm{\tau }}\left(\begin{array}{cc}1& 0\\ 0& {\mathit{e}}^{2\mathit{i}\mathrm{\tau }}\end{array}\right)$ by choosing the time to be $\mathrm{\tau }=\frac{\mathrm{\pi }}{8}$. This gate is not protected against noise perturbations acting on site 3 when both MZMs are positioned there. Moreover, unlike the braiding gates, the dynamical gate is sensitive to timing errors.

Spin encoding of two-chain system

To experimentally simulate the braiding evolutions of MZMs A and C, we transform the fermionic Hamiltonians ${\mathit{H}}_{{\mathrm{M}}_0}$, ${\mathit{H}}_{{\mathrm{h}}_1}$, ${\mathit{H}}_{{\mathrm{h}}_2}$, and ${\mathit{H}}_{{\mathrm{h}}_3}$ of Eqs. 2 and 3, via a JW transformation, into the equivalent spin Hamiltonians, H₀, H₁, H₂, and H₃, respectively, where

$$\begin{array}{c}{\mathit{H}}_0=-{\mathrm{\sigma }}_1^{\mathit{x}}{\mathrm{\sigma }}_2^{\mathit{x}}+{\mathrm{\sigma }}_3^{\mathit{z}}-{\mathrm{\sigma }}_4^{\mathit{x}}{\mathrm{\sigma }}_5^{\mathit{x}}-{\mathrm{\sigma }}_5^{\mathit{x}}{\mathrm{\sigma }}_6^{\mathit{x}},\\ {\mathit{H}}_1=-{\mathrm{\sigma }}_1^{\mathit{x}}{\mathrm{\sigma }}_2^{\mathit{x}}+{\mathrm{\sigma }}_1^{\mathit{y}}{\mathrm{\sigma }}_2^{\mathit{z}}{\mathrm{\sigma }}_3^{\mathit{x}}+{\mathrm{\sigma }}_4^{\mathit{z}}-{\mathrm{\sigma }}_5^{\mathit{x}}{\mathrm{\sigma }}_6^{\mathit{x}},\\ {\mathit{H}}_2=-{\mathrm{\sigma }}_1^{\mathit{x}}{\mathrm{\sigma }}_2^{\mathit{x}}+{\mathrm{\sigma }}_1^{\mathit{y}}{\mathrm{\sigma }}_2^{\mathit{z}}{\mathrm{\sigma }}_3^{\mathit{x}}+{\mathrm{\sigma }}_3^{\mathit{x}}{\mathrm{\sigma }}_4^{\mathit{y}}-{\mathrm{\sigma }}_5^{\mathit{x}}{\mathrm{\sigma }}_6^{\mathit{x}},\\ {\mathit{H}}_3=-{\mathrm{\sigma }}_1^{\mathit{x}}{\mathrm{\sigma }}_2^{\mathit{x}}+{\mathrm{\sigma }}_1^{\mathit{y}}{\mathrm{\sigma }}_2^{\mathit{z}}{\mathrm{\sigma }}_3^{\mathit{x}}-{\mathrm{\sigma }}_4^{\mathit{x}}{\mathrm{\sigma }}_5^{\mathit{x}}-{\mathrm{\sigma }}_5^{\mathit{x}}{\mathrm{\sigma }}_6^{\mathit{x}}\end{array}$$ (4)

During the adiabatic process, the spin system has the same spectrum as the fermion system at all times. Hence, both systems share the same time evolution operators when written in their corresponding basis (25). In particular, the non-Abelian geometric phase obtained during the transport of MZMs can be faithfully studied in the equivalent spin system. Because of the commutation relations between the terms of H₀, H₁, H₂, and H₃, the total process of ITE can be further simplified as${\mathit{e}}^{-{\mathit{H}}_0\mathit{t}}{\mathit{e}}^{-{\mathit{H}}_3\mathit{t}}{\mathit{e}}^{-{\mathit{H}}_2\mathit{t}}{\mathit{e}}^{-{\mathit{H}}_1\mathit{t}}|{\mathrm{\varphi }}_0\rangle ={\mathit{e}}^{-{\mathrm{\sigma }}_3^{\mathit{z}}\mathit{t}}{\mathit{e}}^{{\mathrm{\sigma }}_4^{\mathit{x}}{\mathrm{\sigma }}_5^{\mathit{x}}\mathit{t}}{\mathit{e}}^{-{\mathrm{\sigma }}_3^{\mathit{x}}{\mathrm{\sigma }}_4^{\mathit{y}}\mathit{t}}{\mathit{e}}^{-{\mathrm{\sigma }}_1^{\mathit{y}}{\mathrm{\sigma }}_2^{\mathit{z}}{\mathrm{\sigma }}_3^{\mathit{x}}\mathit{t}}{\mathit{e}}^{-{\mathrm{\sigma }}_4^{\mathit{z}}\mathit{t}}|{\mathrm{\varphi }}_0\rangle$, where |ϕ₀〉 is the ground state of H₀. To experimentally simulate the above dynamics, we need, in principle, a 2⁷-dimensional Hilbert space that corresponds to six spins for the chain network and an extra spin for implementing dissipation. However, because of the character of the ITE, we need to focus only on manipulations that act on the low-energy subspace, which is 2⁵-dimensional (see Materials and Methods). While our photonic simulator has limited scalability as it does not have a tensor product structure, we successfully managed to encode the full low-energy Hilbert space.

The experimental setup that realizes the adiabatic evolutions between the spin Hamiltonians (Eq. 4) and, as a consequence, the evolutions that correspond to the braiding of MZMs A and C is shown in Fig. 2. We encode the quantum states in the optical spatial modes of photons and manipulate them by beam displacers (BDs). A BD is a birefringent crystal, which separates light beams with horizontal and vertical polarizations by a certain displacement that depends on the length of the crystal (32). In our experiment, the polarization of the photons is used as the environmental degree of freedom for the realization of the ITE operations. The coupling between the spatial modes and the photon polarization is achieved using half-wave plates (HWPs) and quarter-wave plates (QWPs), which rotate the polarization of the corresponding modes. A dissipative evolution is accomplished in two steps. Initially, photons are passed through a polarizing beam splitter (PBS), which transmits the horizontal component and reflects the vertical one. Subsequently, photons with vertical polarization are completely dissipated, and only the ones with horizontal polarization are preserved. The resulting states correspond to the ground state of the spin chain system. In this way, the state |ϕ₀〉 is initially prepared and is then sent to the ITE operation of H₁, H₂, H₃, and H₀ for the braiding of A and C with the dynamical map shown in Fig. 2A. The ITE operations are realized in Fig. 2, B (see Materials and Methods) and C, with one of the detailed processes shown in Fig. 2E. The combination of HWPs and a QWP in Fig. 2F is used to exchange basis between Pauli operators σ_y and σ_x (σ_z). The setup of basis rotation shown in Fig. 2D is used to rotate the output state onto the same basis of the input state. During the experiment, we need to construct a stable interferometer with 16 spatial modes. The relative phases in the interferometer are compensated by inserting thin glasses in the corresponding paths (not shown in Fig. 2). The effective operator of our setup (with four input modes and four output modes) is reconstructed by quantum process tomography with 256 measurements (33). The experimental configurations that demonstrate the braiding of C and D and the $\frac{\mathrm{\pi }}{8}$-phase gate are similar to the one shown in Fig. 2A and are given in section S2 (A and B). Section S1I shows the cross-section images for the state evolution during the ITE operation.

Fig. 2. Experimental setup.

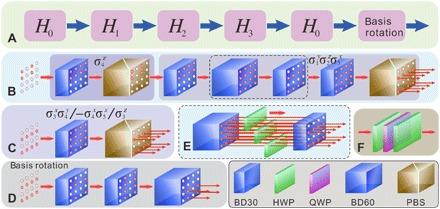
(A) ITEs between Hamiltonians that exchange MZMs A and C. (B) Setup to realize the ITE of H₁ (needs only ${\mathrm{\sigma }}_4^{\mathit{z}}$ and ${\mathrm{\sigma }}_1^{\mathit{y}}{\mathrm{\sigma }}_2^{\mathit{z}}{\mathrm{\sigma }}_3^{\mathit{x}}$). The state is initially prepared to be the ground state of H₀ involving four spatial modes, represented by solid circles. After rotation by BDs (BD30 with beams separated by 3.0 mm and BD60 with beams separated by 6.0 mm), HWPs, and QWPs and subsequent dissipation by PBSs, there are eight output spatial modes. One of the operation processes represented by the arrows is shown in (E), with HWPs set at different angles operating on different spatial modes. The combination of HWPs and a QWP in (F) is used to exchange basis between the Pauli operators σ_y and σ_x (σ_z). (C) Setup for the ITE of H₂ (needs only ${\mathrm{\sigma }}_3^{\mathit{x}}{\mathrm{\sigma }}_4^{\mathit{y}}$). The subsequent ITEs of H₃ (needs only $-{\mathrm{\sigma }}_4^{\mathit{x}}{\mathrm{\sigma }}_5^{\mathit{x}}$) and H₀ (needs only ${\mathrm{\sigma }}_3^{\mathit{z}}$) are similar to those of H₂. (D) The setup for basis rotation is used to rotate the output state along the same basis as the input state.

Realization of quantum gates

To characterize the quantum gates resulting from the braiding of MZMs, we experimentally reconstruct the whole density matrix in the basis of {|00_g〉, |01_g〉, |10_g〉, |11_g〉} (see Materials and Methods). The operators can be described in the 16-dimensional basis spanned by Σ^α ⊗ Σ^β, with Σ^α(β) being I, X, Y, and Z for α(β) = 0, 1, 2, 3, respectively, corresponding to the identity matrix and the three Pauli operators. The experimental result is shown in Fig. 3, A (real part) and B (imaginary part). The evolution corresponds to a Hadamard gate acting on the Majorana-based encoding qubit. To show this, we express the data in the logical basis {|00_g〉, |11_g〉}. The result for the corresponding implementation of $\mathit{H}=(\mathit{I}-\mathit{i}\mathit{Y})/\sqrt{2}$ is shown in Fig. 3, C (real part) and D (imaginary part). The overall fidelity of the Hadamard operator is 93.47 ± 0.02%. For the $\frac{\mathrm{\pi }}{8}$-phase gate, $\mathit{T}= \text{cos} \frac{\mathrm{\pi }}{8}\mathit{I}-\mathit{i}\text{sin} \frac{\mathrm{\pi }}{8}\mathit{X}$, the experimental fidelity is 92.57 ± 0.01%. The real and imaginary parts of the density matrix are shown in Fig. 4, A and B, respectively. The $(-\frac{\mathrm{\pi }}{4})$-phase gate, $\mathit{R}= \text{cos} \frac{\mathrm{\pi }}{4}\mathit{I}+\mathit{i}\text{sin} \frac{\mathrm{\pi }}{4}\mathit{Z}$, is further demonstrated with a fidelity of 93.44 ± 0.01%. All the density matrices corresponding to these operations are given in section S2D. The uncertainty in the fidelities is deduced from the Poissonian photon counting noise (25).

Fig. 3. Experimentally obtained density matrices for the Hadamard gate operation.

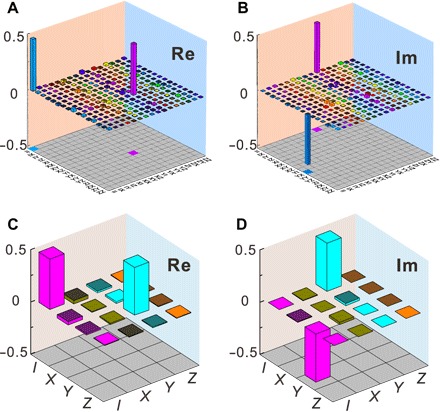
Real (Re) (A) and imaginary (Im) (B) parts of the Hadamard gate operator in the basis {|00_g〉, |01_g〉, |10_g〉, |11_g〉}. Real (C) and imaginary (D) parts of the Hadamard gate operator in the computational basis {|00_g〉, |11_g〉}. The measurement operators I, X, Y, and Z represent the identity, σ^x, σ^y, and σ^z, respectively.

Fig. 4. Experimental results of the effect phase and flip errors have during the $\frac{\mathrm{\pi }}{8}$-phase gate on the logical qubit encoded in the basis |00_g〉 and |11_g〉.

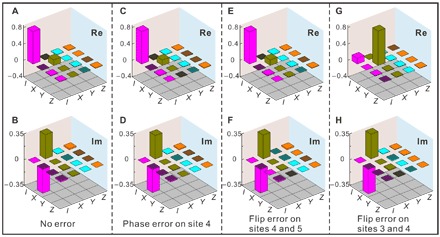
Real (A) and imaginary (B) parts of the density matrix without errors. Real (C) and imaginary (D) parts of the density matrix with phase error on site 4. Real (E) and imaginary (F) parts of the density matrix with flip error on sites 4 and 5. Real (G) and imaginary (H) parts of the density matrix with flip error on sites 3 and 4.

In our photonic experimental system, the main naturally occurring errors include the imperfect interference, the rotation errors of the wave plates, and the photon statistical fluctuation from the source. These errors are well under control, and they lead to the reduction of the fidelity (~93%). On the other hand, these fidelities are largely independent of the exact value of the imaginary time evolution parameter t as long as it is large enough to suppress contributions from excited states. Our numerical simulations show that the resulting evolutions stay unaffected even if we increase t by a factor of 2. In our experiment, the timing t depends on the ratio between the reflected and transmitted parts of the vertical polarization after the PBS in our experiment, which can be higher than 500:1.

Fault tolerance

During the realization of the H and R topological gates, the braided MZMs are never positioned at the same site. Thus, these gates are immune to arbitrary single-site perturbative errors in the MZM system (25). The $\frac{\mathrm{\pi }}{8}$-phase gate is not expected to be resilient against perturbations that act on site 3, where the two MZMs are brought together. These perturbations can lift the degeneracy of the logical basis states, thereby causing dephasing of the encoded quantum information.

In our experiment, the ITE operators not only drive the evolutions that result to quantum gates but also induce the effective interaction to supply the protection of the system. To experimentally probe this behavior, we add phase errors in the MZM system, realized by the spin operation (1 + σ^z)/2, acting on various sites during the control operations on the spin chains that give the $\frac{\mathrm{\pi }}{8}$-phase gate. The experimental setup is given in section S2B. The effective one-qubit gates in our scheme act on the space spanned by {|00_g〉, |11_g〉}. Figure 4 shows the final experimental density matrices with errors on different sites. For comparison, Fig. 4 (A and B) shows the real and imaginary parts of the density matrix after the implementation of the $\frac{\mathrm{\pi }}{8}$-phase gate without adding any errors at all. When local phase errors happen on site 4 during the gate manipulations, only one MZM is disturbed at a time and the operation remains unaffected. This resilience of the encoded information is shown in Fig. 4 (C and D). On the other hand, when the phase error is implemented on site 3, both MZMs are simultaneously disturbed. Hence, the final state is corrupted as the evolution is not topologically protected. A detailed analysis is given in section S1 (E and F).

Besides phase errors, we also consider flip errors. In the fermionic system, a flip error happens when a fermion erroneously tunnels between neighboring sites of the wire (31). This evolution can be exponentially suppressed by increasing the potential barrier between the two sites. In the spin system, flip errors are realized by (σ^yσ^y + σ^xσ^x)/2. These errors degrade the encoded information, only if the MZMs are positioned on the same or on neighboring sites to where the flip error acts. To demonstrate this, we implement a flip error between sites 4 and 5 when the MZMs are both on site 3. In this case, the operation remains unchanged, as shown in Fig. 4 (E and F). However, if the flip error acts on sites 3 and 4, while both MZMs are positioned on site 3, then the operation is corrupted, as shown in Fig. 4 (G and H). The theoretical analysis can be found in section S1 (G and H). Apart from the phase and flip errors that have their origin in the MZM system, the geometric phases are actually protected against all noise with ℤ₂ symmetry of the spin system.

DISCUSSION

In summary, we have experimentally demonstrated that it is, in principle, possible to implement non-Abelian Berry phases that simulate fault-tolerant quantum computation with MZMs. Our experiment is based on the dissipation method for the implementation of Berry phases introduced in our previous work (25). There, we experimentally simulate the evolutions of a single Kitaev chain corresponding to the exchange of its two endpoint MZMs and demonstrate the topological invariance of the resulting Abelian Berry phases. Here, we experimentally simulate the evolutions of two chains with four endpoint MZMs. This setup allows us to generate with high accuracy Berry phases that are both non-Abelian and topological in nature, mirroring the braiding statistics of MZMs. With these evolutions in hand, we can implement several quantum algorithms topologically, such as the Deutsch-Jozsa algorithm (34). A detailed protocol is given in section S1I. While our work simulates the evolution operator of Majorana braiding, the physical system we use is not the same but is unitarily equivalent to that of Majorana fermions. In our simulation, the obtained geometric phases are invariant under continuous variations of the control parameters, as is the case with the Majorana braiding. This invariance is of importance to quantum computation applications, as it provides stability against control errors of the experimental parameters.

When more than two Kitaev chains can be encoded, topological quantum computation with MZMs can be simulated by using exactly the same control procedures demonstrated here, applied to arbitrary pairs of chains. Because of the specific nature of our optical experiment, we are able to perform control operations with very high fidelity, but the scalability of our system is limited. Scalable MZM quantum computation can be experimentally simulated by translating our photonic simulator implementation to scalable systems, such as ion traps (35), ultracold atoms (36), and superconducting circuits (37) technologies, where the ITE dissipation methods have already been established.

MATERIALS AND METHODS

Performing ITE

Any pure state |ϕ〉 can be expressed in a complete set of eigenstates |e_k〉 of a certain Hamiltonian H as |ϕ〉 = ∑_kq_k|e_k〉, where q_k values represent the corresponding complex amplitudes. The ITE operator associated with H is given by exp(− Ht)∑_kq_k|e_k〉 = ∑_kq_k exp(− E_kt)|e_k〉, where E_k is the eigenvalue corresponding to |e_k〉. After the ITE, the amplitude q_k is changed to q_k exp(− E_kt). The decay of the amplitude depends exponentially on the energy: the higher the energy, the faster the decay of the amplitude. Therefore, for sufficiently large t, only the ground state of H (with lowest energy) survives with high fidelity.

The implementation of the ITE operations, used to perform the braiding, can be simplified as the terms of the corresponding Hamiltonians that commute with each other. For example, ${\mathit{e}}^{-{\mathit{H}}_0\mathit{t}}$ can be decomposed into ${\mathit{e}}^{{\mathrm{\sigma }}_5^{\mathit{x}}{\mathrm{\sigma }}_6^{\mathit{x}}\mathit{t}}{\mathit{e}}^{-{\mathrm{\sigma }}_3^{\mathit{z}}\mathit{t}}{\mathit{e}}^{{\mathrm{\sigma }}_4^{\mathit{x}}{\mathrm{\sigma }}_5^{\mathit{x}}\mathit{t}}{\mathit{e}}^{{\mathrm{\sigma }}_1^{\mathit{x}}{\mathrm{\sigma }}_2^{\mathit{x}}\mathit{t}}$. The ITE operator of each term can be directly implemented by local unitary operations and dissipation. To perform the dissipation in a controlled way, an environmental degree of freedom was introduced, which is appropriately coupled to the system. The total state of the system and its environment can be written as $|{\mathrm{\varphi }}_{\mathit{t}}\rangle =(|{\mathrm{\varphi }}_{\mathrm{g}}\rangle |0_{\mathit{e}}\rangle +|{\mathrm{\varphi }}_{\mathrm{g}}^{\perp }\rangle |1_{\mathit{e}}\rangle )/\sqrt{2}$, where $|{\mathrm{\varphi }}_{\mathrm{g}}^{\perp }\rangle$ denotes the states that are orthogonal to the ground state |ϕ_g〉 of the system. The environmental state |1_e〉 was dissipated during the evolution, and only |0_e〉 was preserved. Therefore, the ground state of the corresponding Hamiltonian was obtained.

Experimental procedure for implementing the ITE of H₁

Consider the eigenvectors $\{|\mathit{x}\rangle ,|\overline{\mathit{x}}\rangle \}$, $\{|\mathit{y}\rangle ,|\overline{\mathit{y}}\rangle \}$, and $\{|\mathit{z}\rangle ,|\overline{\mathit{z}}\rangle \}$ of the Pauli operators σ^x (X), σ^y (Y), and σ^z (Z), with eigenvalues {1, − 1}, respectively. Then, the ground state of H₀ in Eq. 4 is given by

$$\begin{array}{cc}\hfill |{\mathrm{\varphi }}_0\rangle =& \mathrm{\alpha }|{\mathit{x}}_1{\mathit{x}}_2{\overline{\mathit{z}}}_3{\mathit{x}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle +\mathrm{\beta }|{\overline{\mathit{x}}}_1{\overline{\mathit{x}}}_2{\overline{\mathit{z}}}_3{\mathit{x}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle \hfill \\ & +\mathrm{\mu }|{\mathit{x}}_1{\mathit{x}}_2{\overline{\mathit{z}}}_3{\overline{\mathit{x}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle +\mathrm{\nu }|{\overline{\mathit{x}}}_1{\overline{\mathit{x}}}_2{\overline{\mathit{z}}}_3{\overline{\mathit{x}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle \hfill \end{array}$$ (5)

where α, β, μ, and ν are complex amplitudes satisfying |α|² + |β|² + |μ|² + |ν|² = 1. Experimentally, the ground state (Eq. 5) of H₀ is represented as four spatial modes of single photons, as shown in the initial step of Fig. 2B. To evolve this state to the ground state of H₁, we only needed to implement the additional ITE operations of ${\mathrm{\sigma }}_4^{\mathit{z}}$ and ${\mathrm{\sigma }}_1^{\mathit{y}}{\mathrm{\sigma }}_2^{\mathit{z}}{\mathrm{\sigma }}_3^{\mathit{x}}$. Particle 4 is expressed in the basis $\{|\mathit{z}\rangle ,|\overline{\mathit{z}}\rangle \}$, as $|{\mathit{x}}_4\rangle =(|{\mathit{z}}_4\rangle +|{\overline{\mathit{z}}}_4\rangle )/\sqrt{2}$ and $|{\overline{\mathit{x}}}_4\rangle =(|{\mathit{z}}_4\rangle -|{\overline{\mathit{z}}}_4\rangle )/\sqrt{2}$. This change of basis transformation was implemented by HWPs in the initial four spatial modes. Eight spatial modes were created after splitting them by a BD30. The polarization of the terms with |z₄〉, which represent states with higher energy, was set to be vertical with HWPs. The polarization of the terms with $|{\overline{\mathit{z}}}_4\rangle$ was set to be horizontal.

The dissipative evolution was realized by passing photons through a PBS, where only four terms with horizontal polarization remain at the end. Similarly, for the ITE of ${\mathrm{\sigma }}_1^{\mathit{y}}{\mathrm{\sigma }}_2^{\mathit{z}}{\mathrm{\sigma }}_3^{\mathit{x}}$, the basis of particle 1 was rotated from $\{|\mathit{x}\rangle ,|\overline{\mathit{x}}\rangle \}$ to $\{|\mathit{y}\rangle ,|\overline{\mathit{y}}\rangle \}$ with the assistance of a combination of two HWPs and a QWP, as shown in Fig. 2F. Each of the spatial modes was horizontally split into two other modes with a BD30. For particle 2, the basis was rotated from $\{|\mathit{x}\rangle ,|\overline{\mathit{x}}\rangle \}$ to $\{|\mathit{z}\rangle ,|\overline{\mathit{z}}\rangle \}$. The eight spatial modes were further vertically split into 16 modes with a BD60. The terms with the same form were combined with a BD30. Last, the basis of particle 3 was changed to be $\{|\mathit{x}\rangle ,|\overline{\mathit{x}}\rangle \}$, in which 16 spatial modes were obtained with another BD30. After passing through a PBS, only the terms $\{|{\overline{\mathit{y}}}_1{\mathit{z}}_2{\mathit{x}}_3{\overline{\mathit{z}}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle$, $|{\overline{\mathit{y}}}_1{\overline{\mathit{z}}}_2{\overline{\mathit{x}}}_3{\overline{\mathit{z}}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle$, $|{\mathit{y}}_1{\overline{\mathit{z}}}_2{\mathit{x}}_3{\overline{\mathit{z}}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle$, $|{\mathit{y}}_1{\mathit{z}}_2{\overline{\mathit{x}}}_3{\overline{\mathit{z}}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle$, $|{\overline{\mathit{y}}}_1{\mathit{z}}_2{\mathit{x}}_3{\overline{\mathit{z}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle$, $|{\overline{\mathit{y}}}_1{\overline{\mathit{z}}}_2{\overline{\mathit{x}}}_3{\overline{\mathit{z}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle$, $|{\mathit{y}}_1{\overline{\mathit{z}}}_2{\mathit{x}}_3{\overline{\mathit{z}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle$ and $|{\mathit{y}}_1{\mathit{z}}_2{\overline{\mathit{x}}}_3{\overline{\mathit{z}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle \}$ remain, and the output state corresponds to the ground state of H₂. The ITE operations of the other Hamiltonians that are part of the cyclic evolution are found in section S1A.

After the basis rotation shown in Fig. 2D, the final state is expressed in the same basis as the initial state and takes the form

$$\begin{array}{cc}\hfill |{\mathrm{\varphi }}_4\rangle =& (\mathrm{\alpha }+\mathrm{\beta })|{\mathit{x}}_1{\mathit{x}}_2{\overline{\mathit{z}}}_3{\mathit{x}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle +(\mathrm{\mu }-\mathrm{\nu })|{\mathit{x}}_1{\mathit{x}}_2{\overline{\mathit{z}}}_3{\overline{\mathit{x}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle +\hfill \\ & (\mathrm{\beta }-\mathrm{\alpha })|{\overline{\mathit{x}}}_1{\overline{\mathit{x}}}_2{\overline{\mathit{z}}}_3{\mathit{x}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle +(\mathrm{\mu }+\mathrm{\nu })|{\overline{\mathit{x}}}_1{\overline{\mathit{x}}}_2{\overline{\mathit{z}}}_3{\overline{\mathit{x}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle \hfill \end{array}$$ (6)

To show the gate operation in the logical basis, we translated the basis by $|{\mathit{x}}_1{\mathit{x}}_2\rangle =(|0_{12}\rangle +|1_{12}\rangle )/\sqrt{2}$, $|{\overline{\mathit{x}}}_1{\overline{\mathit{x}}}_2\rangle =(|0_{12}\rangle -|1_{12}\rangle )/\sqrt{2}$, $|{\mathit{x}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle =(|0_{456}\rangle +|1_{456}\rangle )/\sqrt{2}$, and $|{\overline{\mathit{x}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle =(|1_{456}\rangle -|0_{456}\rangle )/\sqrt{2}$. The logical basis is given by $|{00}_{\mathrm{g}}\rangle =|0_{12}{0}_{456}\rangle |{\overline{\mathit{z}}}_3\rangle$, $|{01}_{\mathrm{g}}\rangle =|0_{12}{1}_{456}\rangle |{\overline{\mathit{z}}}_3\rangle$, $|{10}_{\mathrm{g}}\rangle =|1_{12}{0}_{456}\rangle |{\overline{\mathit{z}}}_3\rangle$, and $|{11}_{\mathrm{g}}\rangle =|1_{12}{1}_{456}\rangle |{\overline{\mathit{z}}}_3\rangle$. The initial state (ground state of H₀) is given in the logical basis by

$$\begin{array}{c}|{\mathrm{\varphi }}_0\rangle =(\mathrm{\alpha }+\mathrm{\beta }-\mathrm{\mu }-\mathrm{\nu })|{00}_{\mathrm{g}}\rangle +(\mathrm{\alpha }+\mathrm{\beta }+\mathrm{\mu }+\mathrm{\nu })|{01}_{\mathrm{g}}\rangle +\\ (\mathrm{\alpha }-\mathrm{\beta }-\mathrm{\mu }+\mathrm{\nu })|{10}_{\mathrm{g}}\rangle +(\mathrm{\alpha }-\mathrm{\beta }+\mathrm{\mu }-\mathrm{\nu })|{11}_{\mathrm{g}}\rangle \end{array}$$ (7)

where, for simplicity, we omitted the overall normalization. After the anticlockwise braiding, the final state becomes

$$|{\mathrm{\varphi }}_4\rangle =(\mathrm{\beta }-\mathrm{\mu })|{00}_{\mathrm{g}}\rangle +(\mathrm{\beta }+\mathrm{\mu })|{01}_{\mathrm{g}}\rangle +(\mathrm{\alpha }+\mathrm{\nu })|{10}_{\mathrm{g}}\rangle +(\mathrm{\alpha }-\mathrm{\nu })|{11}_{\mathrm{g}}\rangle$$ (8)

The unitary transformation that corresponds to the anticlockwise braiding of MZMs A and C reads

$$\mathit{U}=\frac{1}{\sqrt{2}}\left(\begin{array}{cccc}1& 0& 0& -1\\ 0& 1& -1& 0\\ 0& 1& 1& 0\\ 1& 0& 0& 1\end{array}\right)$$ (9)

written in the basis {|00_g〉, |01_g〉, |10_g〉, |11_g〉}. If we focus on the even fermion parity sector spanned by |00_g〉 and |11_g〉, the unitary transformation becomes

$$\mathit{U}=\frac{1}{\sqrt{2}}\left(\begin{array}{cc}1& -1\\ 1& 1\end{array}\right)$$ (10)

As a result, the braiding of A and C corresponds to a generalized form of the Hadamard gate operation, related to the standard Hadamard gate by U ⋅ R².

Experimental quantum process tomography

In our experiment, we used the quantum process tomography to identify the efficiency of the performed gate operations (33). The experimental measurement basis is chosen to be {hh, hv, vh, vv}, where h, v, r, and d represent the horizontal, vertical, right-hand circular, and diagonal polarizations, respectively. For each input state, we needed to reconstruct the final output state by two–qubit state tomography with 16 measurement configurations, as shown in fig. S13. To reconstruct the quantum process, we needed 16 different input states. As a result, there are 16² measurement settings. By expanding the output state $\mathcal{E}$(ρ) in terms of the Pauli basis operators {Ê_m} = {II, IX, IY, IZ, XI, XX, XY, XZ, YI, YX, YY, YZ, ZI, ZX, ZY, ZZ}, the quantum process can be expressed as $\mathcal{E}$(ρ) = ∑_mnχ_mnÊ_mρÊ_n^†. The physical process $\mathcal{E}$ is uniquely characterized by the 16-by-16 matrix χ.

In our experiment, the spin basis is represented as $\{|{\mathit{x}}_1{\mathit{x}}_2{\overline{\mathit{z}}}_3{\mathit{x}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle ,|{\overline{\mathit{x}}}_1{\overline{\mathit{x}}}_2{\overline{\mathit{z}}}_3{\mathit{x}}_4{\mathit{x}}_5{\mathit{x}}_6\rangle ,|{\mathit{x}}_1{\mathit{x}}_2{\overline{\mathit{z}}}_3{\overline{\mathit{x}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle ,|{\overline{\mathit{x}}}_1{\overline{\mathit{x}}}_2{\overline{\mathit{z}}}_3{\overline{\mathit{x}}}_4{\overline{\mathit{x}}}_5{\overline{\mathit{x}}}_6\rangle \}$, which corresponds to the polarization basis of {hh, hv, vh, vv}. The computation basis is chosen to be {|00_g〉, |01_g〉, |10_g〉, |11_g〉}. The transformation between the experimental basis and the computation basis is

$$\left(\begin{array}{c}|\mathit{h}\mathit{h}\rangle \\ |\mathit{h}\mathit{v}\rangle \\ |\mathit{v}\mathit{h}\rangle \\ |\mathit{v}\mathit{v}\rangle \end{array}\right)=\mathit{U}\left(\begin{array}{c}|{00}_{\mathrm{g}}\rangle \\ |{01}_{\mathrm{g}}\rangle \\ |{10}_{\mathrm{g}}\rangle \\ |{11}_{\mathrm{g}}\rangle \end{array}\right)=\frac{1}{2}\left(\begin{array}{cccc}1& 1& 1& 1\\ -1& 1& -1& 1\\ 1& 1& -1& -1\\ -1& 1& 1& -1\end{array}\right)\left(\begin{array}{c}|{00}_{\mathrm{g}}\rangle \\ |{01}_{\mathrm{g}}\rangle \\ |{10}_{\mathrm{g}}\rangle \\ |{11}_{\mathrm{g}}\rangle \end{array}\right)$$ (11)

The output state in the computation basis can be represented as

$$\mathcal{E}(\mathit{\rho }\prime )={\displaystyle \sum _{\mathit{i},\mathit{j}}}{\mathrm{\lambda }}_{\mathit{i}\mathit{j}}{\widehat{\mathit{E}}}_{\mathit{i}}\mathrm{\rho }\prime {\widehat{\mathit{E}}}_{\mathit{j}}^{†}$$ (12)

where

$${\mathrm{\lambda }}_{\mathit{i}\mathit{j}}={\displaystyle \sum _{\mathit{n},\mathit{m}}}{\mathrm{\chi }}_{\mathit{i}\mathit{j}}\mathit{T}\mathit{r}[({\mathit{U}}^{†}{\widehat{\mathit{E}}}_{\mathit{n}}\mathit{U}){\widehat{\mathit{E}}}_{\mathit{i}}]\mathit{T}\mathit{r}[({\mathit{U}}^{†}{\widehat{\mathit{E}}}_{\mathit{m}}\mathit{U}){\widehat{\mathit{E}}}_{\mathit{j}}]$$ (13)

A further restriction to the even parity sector can be performed by the projector P_e = (|00_g〉〈00_g| + |11_g〉〈11_g|)/2. This results in 4-by-4 reduced density matrices expressed in the logical basis {|00_g〉, |11_g〉}, as shown in Figs. 3 and 4.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/10/eaat6533/DC1

Section S1. Theoretical details

Section S2. Experimental details

Fig. S1. The circuit of one-step cooling algorithm.

Fig. S2. The process of anticlockwise braiding of MZMs A and C.

Fig. S3. The process of clockwise braiding of MZMs A and C.

Fig. S4. The process to anticlockwise braiding of MZMs C and D.

Fig. S5. The process of clockwise braiding of MZMs C and D.

Fig. S6. The process for implementing the phase gate based on the dynamics of MZMs.

Fig. S7. Spatial modes of the output states for the exchange of MZMs A and C.

Fig. S8. Spatial modes of the output states corresponding to the basis rotation.

Fig. S9. Spatial modes of the output states for the exchange of MZMs C and D.

Fig. S10. Spatial modes of the output states for the $\frac{\mathrm{\pi }}{8}$-phase operation.

Fig. S11. The process to implement the Deutsch-Jozsa algorithm with the braiding of MZMs.

Fig. S12. Experimental setup for the exchange of MZMs C and D.

Fig. S13. Experimental setup for the implementation of $\frac{\mathrm{\pi }}{8}$-phase gate and error operations.

Fig. S14. Experimental setup for the quantum process tomography.

Fig. S15. Experimental density matrices resulting from the $(-\frac{\mathrm{\pi }}{4})$-phase gate operation.

Fig. S16. Experimental density matrices resulting from the gate operations in the full basis.

Fig. S17. Experimental density matrices resulting from the $\frac{\mathrm{\pi }}{8}$-phase gate in the full basis.

Fig. S18. The state evolution in the Deutsch-Jozsa algorithm.

References (38, 39)