Probing molecular pathways for DNA orientational trapping, unzipping and translocation in nanopores by using a tunable overhang sensor

Abstract

Nanopores provide a unique single-molecule platform for genetic and epigenetic detection. The target nucleic acids can be accurately analyzed by characterizing their specific electric fingerprints or signatures in the nanopore. Here we report a series of novel nanopore signatures generated by target nucleic acids that are hybridized with a probe. A length-tunable overhang appended to the probe functions as a sensor to specifically modulate the nanopore current profile. The resulting signatures can reveal multiple mechanisms for the orientational trapping, unzipping, escaping and translocation of nucleic acids in the nanopore. This universal approach can be used to program various molecular movement pathways, elucidate their kinetics, and enhance the sensitivity and specificity of the nanopore sensor for nucleic acid detection.

Introduction

Nanopores provide a unique platform for single-molecule detection.^1–3 Individual DNA/RNA molecules that interact with a nanopore can specifically regulate the pores’ ionic current. Characterization of current fingerprints or signatures generated by target molecules enables us to electrically identify distinct molecular configurations and elucidate mechanisms for trapping,^4–6 unzipping,^7–12 unfolding^13,14 and translocation^15–17 of nucleic acid polymers in nanopores. Overall, nanopores are sensitive single-molecule identifiers for various genetic^5,18–22 and epigenetic^23–28 detection. The nanopore-based single-molecule mechanistic studies are also beneficial for biosensor development.^29–31 For example, complementary nucleic acid hybridization is a fundamental biochemical process and has been extensively utilized in developing electrochemical-based^32–36 and fluorescence-based sensors^37–39 and nanosensors.^40–42 Recently, we have developed a probe-based nanopore approach for microRNA detection.^24,43,44 Analysis of the signature generated by the microRNA probe hybrid in the nanopore allows single-molecule diagnostic detection of cancer-associated biomarkers in complex samples.²⁴ Therefore it is important to dissect the molecular mechanisms for these nanopore signatures.

In this report, we developed a novel sensing approach for simultaneously elucidating multiple mechanisms for DNA trapping, unzipping, escaping and translocation in the nanopore. We uncovered that a group of overhangs of different lengths appended to dsDNAs can generate a series of novel nanopore signatures that have not been reported previously. The investigation of these signatures would help us to understand a series of biophysical mechanisms: (1) how to manipulate the DNA trapping orientation? (2) What are the pathways for nucleic acid trapping, unzipping and translocation? (3) Are nucleic acids unzipped progressively or transiently? (4) How to modulate the unzipping occurrence and map the nanopore electric field intensity by using the overhang as a force sensor? (5) What is the kinetic pathway for DNA trapping and how to regulate the trapping efficiency by interplay of the overhang and voltage? These newly uncovered mechanisms provide guidelines for programming the nucleic acid–nanopore interactions, and are useful in optimizing nanopore biosensors.

Results and discussion

Signatures for DNA orientational trapping, unzipping and translocation

The first target we studied was C30. It comprises a 22 base-pair double-stranded domain that is appended with a 30 deoxycytidine overhang at the 3′ end of one strand (Table 1). The trapping of C30 from the cis opening of the α-hemolysin pore generated a large amount of long signatures (Fig. 1a). Over 95% of these signatures were Level-1 events with a relative conductance of 10% (I/I₀, where I and I₀ are currents of the block and the open pore) (Fig. 1b). As this conductance level is similar to that for the ssDNA translocation event (Fig. S1^†),^15,16 the Level-1 events should be generated by C30 that is trapped with its overhang threading into the β-barrel (~1.4–2.0 nm) and its double-stranded domain restricted in the nanocavity (~4.6 nm) of the pore (Fig. 1a model). The duration of Level-1 blocks (τ_off) was highly voltage-dependent (Fig. 1c). As the voltage increased from 100 mV to 180 mV, τ_off was exponentially shortened by 400-fold from 430 ± 70 ms to 1.0 ± 0.3 ms (Fig. S2^† for duration histograms). As in previous studies,^{7,9–12,45,46} such a τ_off–V relationship reveals a voltage-driven unzipping process. As expected, introducing mismatched base-pairs (C30-MM, Table 1) significantly destabilized the duplex, resulting in 10- to 100-fold shortening in τ_off at the same voltage (Fig. S3^†).^24,46 C30 also generated a small amount of Level-2 partial blocks with I/I₀ = 25%. The higher conductance of these signatures suggests that the β-barrel is not occupied. Thus the Level-2 events should be generated by C30 in the opposite trapping direction: its blunt end first enters the nanocavity (Fig. 1a model). The Level-2 conductance and the trapping orientation are in agreement with a previous study that a blunt-ended DNA in the nanocavity reduced the conductance to I/I₀ = 25–30%.⁴⁷ The previous studies have shown that structured nucleic acids such as the G-quadruplex aptamer^13,14 and hairpins^48,49 can be trapped in the nanocavity to partially block the pore conductance. At any voltage from +100 mV to +180 mV, the fraction of the Level-1 event was higher than the Level-2 event by more than 20-fold (Fig. 1b), indicating that the overhang is much more favorable over the blunt end when trapped in the pore. In addition to C30’s signatures, there were spike-like short blocks on the 100 ms scale (Fig. 1a). Based on the ssDNA translocation results (Fig. S1^†), they should have been generated by unhybridized ssDNA translocation through the pore (Fig. 1a model).

Table 1.

Sequences of DNAs used in this study

DNA	Sequence
C0	5′-TTAATGCTAATCGTGATAGGGG-3′a 3′-AATTACGATTAGCACTATCCCC-5′
C5	5′-TTAATGCTAATCGTGATAGGGG-3′ 3′-(C)5 AATTACGATTAGCACTATCCCC-5′
C8	5′-TTAATGCTAATCGTGATAGGGG-3′ 3′-(C)8 AATTACGATTAGCACTATCCCC-5′
C12	5′-TTAATGCTAATCGTGATAGGGG-3′ 3′-(C)12AATTACGATTAGCACTATCCCC-5′
C20	5′-TTAATGCTAATCGTGATAGGGG-3′ 3′-(C)20AATTACGATTAGCACTATCCCC-5′
C30	5′-TTAATGCTAATCGTGATAGGGG-3′ 3′-(C)30AATTACGATTAGCACTATCCCC-5′
C30-MM	5′-TTAATGTTAATCGCGATAGGGG-3′ 3′-(C)30AATTACGATTAGCACTATCCCC-5′

^aThe sequence of the short strand originates from microRNA miR155.

Fig. 1.

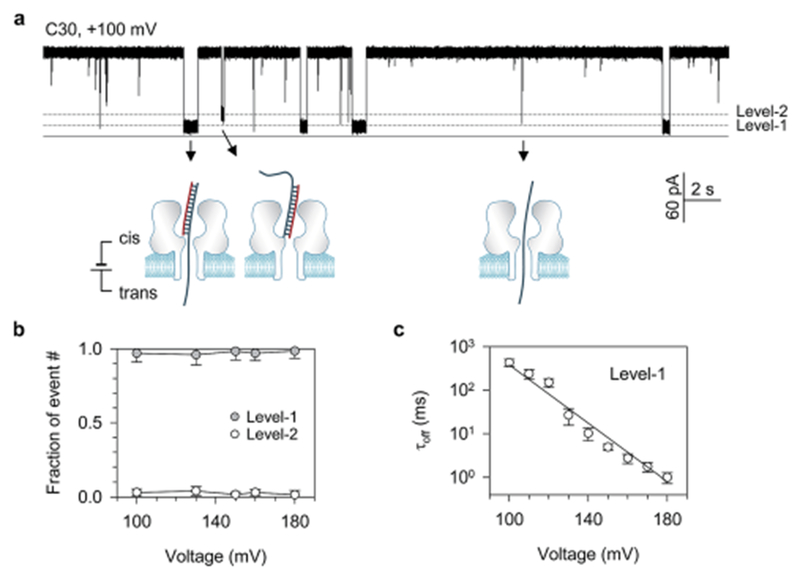
(a) Representative current trace showing the Level-1 and Level-2 events for trapping C30 in the pore from the cis side in both orientations, and short spikes for translocation of the unhybridized strands of C30. This current was recorded at +100 mV in 1 M KCl, 10 mM Tris (pH 7.5) and in the presence of 100 nM of each strand of C30 in the cis solution. The DNA sequences are shown in Table 1; (b) fractions of Level-1 and Level-2 events for C30 at various voltages. The majority of C30 block events were Level-1 events, indicating the preference for trapping the overhang over the blunt end in the pore; (c) duration of Level-1 events as a function of voltage applied. The duration–voltage correlation approximates to an exponential decay, indicating that the unzipping of C30 needs to overcome an energy barrier. The duration histograms for all voltages are illustrated in Fig. S2.^†

When examining closely, we uncovered that the Level-1 signatures were terminated in three distinct current patterns (Fig. 2a–c). The Level-1a block (Fig. 2a) was terminated with a short discrete half-block (A, 760 ± 58 μs) that was immediately followed by a downward ending spike (B, 180 ± 30 μs). The Level-1b block (Fig. 2b) only possessed the half-block shoulder at the terminal (A), but did not generate the ending spike (C). In a Level-1c event (Fig. 2c), the current at the event terminal was directly resumed to the open pore level without any intermediate state (D). Both Level-1b and 1c patterns can also be observed at higher filtering frequency (10 kHz) and higher data acquisition rate (100 kHz) (Fig. S5^†), suggesting that the missing of the shoulder (Fig. 2c) and ending spike (Fig. 2b and c) should not be caused by the filtering. We interpret the three terminal patterns as different DNA movement pathways in the pore. First, the duration of the three types of Level-1 events and their voltage-dependency were similar (Fig. S4^†), indicating that C30 is unzipped in all the three signatures. Upon unzipping, the dissociated long strand (52 nts) occupying the β-barrel first translocates through the pore. However, the dissociated short strand (22 nts) could move in three different ways. In a Level-1a block (Fig. 2a), the short strand temporarily resides in the wide nanocavity to form the half-block (A) and then passes through the β-barrel to generate the ending spike (B). This translocation is driven by a small voltage drop across the nanocavity, which is about 10% of the total voltage applied^29,30,50, and therefore should be weakly voltage-dependent. The model in Fig. 2a is consistent with the observation that the fraction of Level-1a events was slightly increased from (47 ± 6)% to (69 ± 6)% with voltage increasing from 100 mV to 180 mV (Fig. 2d). In a Level-1b event, the short strand staying in the nanocavity returns back to cis solution, rather than translocates through the pore. As a result, no ending spike can be generated. As the escaping is against the electric field, increasing the voltage should reduce the escaping chance. This is consistent with the finding that the fraction of Level-1b events gradually decreases from (19 ± 5)% at 100 mV to (9.2 ± 2.0)% at 180 mV. Unlike the Level-1a and -1b events, the Level-1c event without intermediate states (Fig. 2c) would correspond to another molecular pathway: the dissociated short strand does not reside in the nanocavity, but immediately follows the long strand to enter the β-barrel. Therefore, the β-barrel is always occupied (without a time gap) while both strands sequentially translocate through the pore. In a previous study on microRNA detection,²⁴ similar single-level long events have been observed and interpreted as the escape of the miRNA probe hybrid from the nanopore. We think that the modified model for this type of event as shown in Fig. 2c is more reasonable. As analyzed below, only blunt-ended dsDNA or that with a short overhang has a chance to escape. The long overhang of C30 prevents this duplex from escaping due to the high electric pulling force acting on it.

Fig. 2.

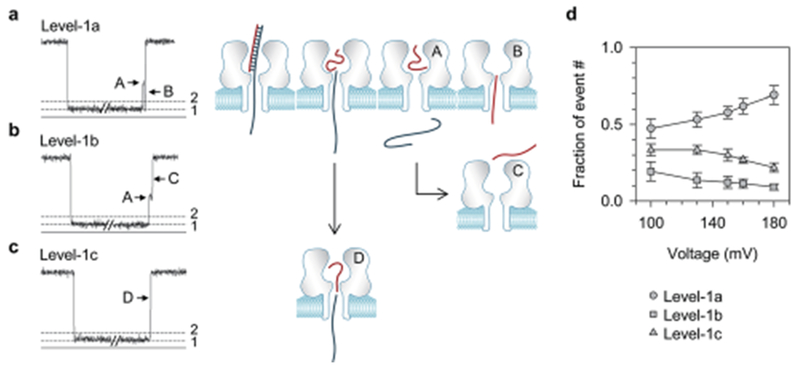
Three types of Level-1 events and the corresponding DNA movement pathways in the nanopore. (a–c) Current profiles for Level-1a (a), Level-1b (b) and Level-1c (c) events, and the corresponding models for different DNA movement pathways in the pore upon unzipping; (d) weak voltage-dependence of fractions of event numbers for the three types of Level-1 events.

In summary, the signature properties, including their current profiles, distributions, conductance and duration, are important markers useful in elucidating various molecular processes of DNA in nanopores, such as orientational trapping, unzipping, and molecular pathway. These signatures and their molecular mechanisms have not been reported in the past, although the nucleic acid unzipping has been extensively studied.^{7,8,10,12,46,47,49} Several previous studies were focused on the unzipping of hairpins.^10,12,49 Unlike the DNA duplex that splits into two strands, the single-stranded hairpin is limited to generate the multi-level signatures similar to what we found in Fig. 2.

Unzipping in the nanopore: long initiation and transient rapture

The signatures generated by C30 prove the occurrence of unzipping. However, these signatures cannot reveal how the DNA is unzipped. A specific question is whether the unzipping is a continuous process throughout the block or occurs in a transient, cooperative manner at the end of the block. We uncovered that the signature of DNA C0 (Table 1) can electrically “visualize” the unzipping kinetics, thereby elucidating the mechanism for dsDNA dehybridization. C0 trapped in the nanocavity produced a unique multi-level signature at high voltage (Fig. 3a for +150 mV and Fig. S6^† for +180 mV). Initially the conductance of the signature was kept at Level-2 for almost the entire block duration (A). As discussed for C30, this conductance level should be generated by the blunt-end C0 in the nanocavity without occupying the β-barrel, therefore suggesting that C0 is not dehybridized in this stage. However, at the end of the signature, the conductance was discretely decreased to Level-1 (B) for 920 ± 31 μs, then immediately increased to a half-block level (C), and finally decreased again to form an ending spike (D). We interpret that the transition from Level-2 to Level-1 (A → B) represents the start of C0 unzipping. As the initial dehybridized fragment enters the β-barrel, the signature goes into the Level-1 stage (B). When all the base-pairs are broken and the dissociated strand runs out of the pore, the Level-1 stage (B) is terminated. The duration of the Level-1 stage (B) suggests that a 22 base-pair DNA is raptured within 1 ms. The following half-block (C) and the ending spike (D) are similar to that observed in the C30’s Level-1a event (Fig. 2a). They should be formed by the complementary strand that resides shortly in the nanocavity (C) and finally passes through the β-barrel (D).

Fig. 3.

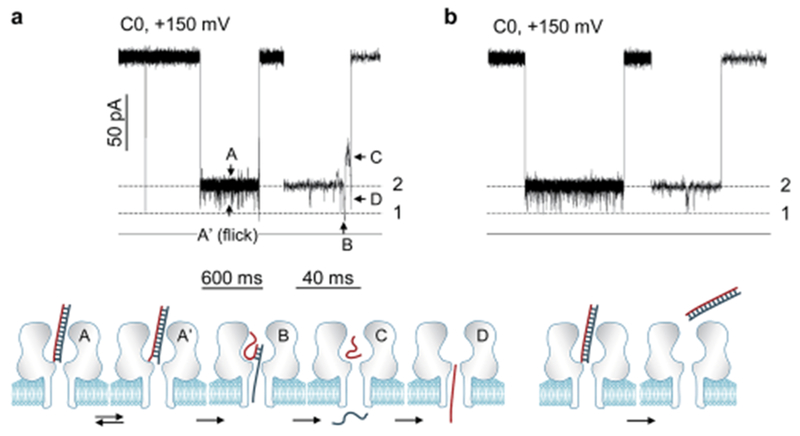
Dissection of the unzipping mechanism from the signatures of blunt-ended DNA C0. (a) Current profile of the C0 signature at +150 mV (top) and the corresponding molecular configuration change (bottom). The block profile includes a series of sequential stages, A′ ↔ A → B → C → D. The Level-1/Level-2 current transition (A → B) marks the beginning of unzipping, and stage B at Level-1 is the marker of the unzipping procedure. Such a signature reveals that DNA unzips in the nanopore transiently. A similar C0 signature having such an unzipping marker at +180 mV is shown in Fig. S6b;^† (b) current profile of a C0 signature without the unzipping marker. This signature represents that C0 escapes back to the cis solution without unzipping. A similar signature without the unzipping marker at +100 mV is shown in Fig. S6a.^†

The C0’s signature (Fig. 3a) demonstrates a transient, cooperative unzipping procedure in the nanopore. During the time before unzipping, the DNA retains its duplex form, but attempts to “initiate” the unzipping driven by the voltage. Before the unzipping starts, the base-pairs around the blunt end can also interact with the internal opening of the β-barrel, resulting in a series of Level-2-based downward current fiicks (A ↔ A′, Fig. 3a). Such an unzipping kinetics is similar to that observed using single-molecule pulling approaches.^51–53 The 1 ms DNA rapture time in the nanopore is also similar to the time scale for unzipping a 20 base-pair fragment using optical tweezers under a 10–20 pN pulling force.⁵³ Overall, the unzipping of DNA in the nanopore is a transient process. Once the unzipping is initiated from the end of the duplex, the remaining domain would be dehybridized cooperatively, with all base-pair hydrogen bonds broken instantly.

Regulation of unzipping by overhang length

The negatively charged DNA is pulled by the electric field in the nanopore to drive the unzipping. For DNA with an overhang, the pulling force is correlated with the amount of charges carried by the overhang. If this correlation is dissected, we would be able to use different length overhangs to modulate the driving force and thus program the unzipping. The overhang can also be used as a force sensor to probe the electric field distribution in the pore. To investigate the overhang length-regulated unzipping, we further studied targets C5, C8, C12 and C20, which contain 5, 8 12 and 20 deoxycytidines attached to the same 22 base-pair double-stranded domain. All the targets carrying an overhang generated both Level-1 (Fig. 4a) and Level-2 signatures, and more than 95% of total signatures were Level-1 (Fig. 4b), thus verifying the trapping preference for overhang over the blunt end into the α-hemolysin pore.

Fig. 4.

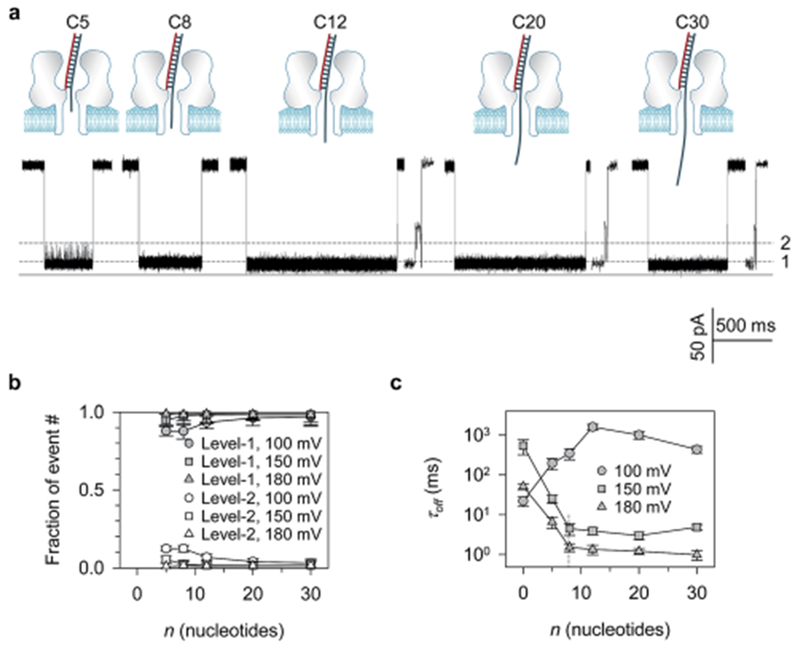
Modulation of DNA unzipping using overhangs with different base numbers. (a) Current profiles of Level-1 events for C5, C8, C12, C20 and C30 at +100 mV; (b) fractions of Level-1 versus Level-2 event numbers as a function of the overhang base number (n). Data at +100 mV, +150 mV and +180 mV are provided. Level-1 events always occur much more frequently than Level-2 events, confirming the preference for trapping the overhang over the blunt end into the nanopore; (c) block duration (τ_off) as a function of the overhang base number (n) at +100 mV, +150 mV and +180 mV. Histograms for duration distributions are shown in Fig. S7.^† The τ_off–n curves at +150 mV and +180 mV demonstrate a decaying phase followed by a constant phase with a transition at n = 8 (C8), inferring the overhang length-dependent electric driving force and the nanopore field distribution. The increase of τ_off with n for short overhangs at +100 mV infers the occurrence of escaping.

Fig. 4c shows the block duration (τ_off) as a function of the number of nucleotides in the overhang (n). Interestingly, τ_off demonstrates a two-phase correlation with n at high voltages. At +150 mV, τ_off was initially decreased sharply from 540 ± 170 ms for C0 to 4.5 ± 1.2 ms for C8. From C8, τ_off became overhang length-independent and slightly varied between 2.9 and 4.5 ms. A similar variation of τ_off was also found at +180 mV: a sharp decrease from 51 ± 19 ms for C0 to 1.5 ± 0.3 ms for C8, followed by a constant phase between 1.2 and 1.5 ms. In contrast, the τ_off–n relationship at low voltage such as +100 mV was different from +150 mV and +180 mV. Rather than shortening, τ_off was prolonged as n increased from C0 to C12, prior to the n-independent stage.

The two-phase regulation of block duration at high voltage is determined by the field distribution in the nanopore. If F is the force acting on the overhang, and the unzipping is assumed to overcome an energy barrier, the τ_off–F relationship can be simplified as τ_off(V) = τ_off(0)∙exp(−FΔx/k_BT), where Δx is the energy barrier width or the distance by which the molecule is separated along the reaction coordinate for dehybridization to occur, ^46,54 and τ_off(0) is the duration of C0. We also defined n_M as the maximum number of nucleotides that can be acted on by the electric field in the β-barrel. For an overhang with n < n_M, all of its nucleotides should be covered by the field. The driving force would be F = ΣqeE_i (i = 1, …, n), where qe is the effective charge per nucleotide, and E_i is the field intensity in the position of the i^th nucleotide. In a uniform field, F = nqeE, i.e. the force is proportional to the overhang length. This expression explains the observation that τ_off is almost exponentially shortened with increasing n from 0 (C0) to 8 (C8). For an n > n_M overhang, the terminal fragment of the overhang should extend out of the field, and should not be pulled by the field. This results in a maximal force F_M = n_MqeE, and a constant τ_off from C8 through C30. The critical point for this transition is n_M = 8 (C8). Assuming that there are 12 nucleotides spanning in the β-barrel,^7,15,49 this 8-nt overhang (C8) length is equivalent to approximately 2/3 of the total β-barrel length. The field intensity out of this range decays rapidly. This experimentally mapped This experimentally mapped field distribution is consistent with the molecular dynamics simulation result,⁵⁰ which shows that voltage is mainly dropped on the constrictive domain around the inner opening of the β-barrel. Assuming that the inter-base distance in a ssDNA is 0.5 nm,^15,46 the overhang length of C8 would be l_M = 4 nm. As E = V/l_M, the maximal force can be expressed as F_M = n_Mqe(V/l_M). Assuming q = 0.4 due to the shielding effect in high salt concentration,⁴⁶ and 90% of voltage is dropped on the β-barrel,²⁹ F_M would be 20 pN at 150 mV and 24 pN at 180 mV. For C5 with shorter overhang (n = 5), F is 13 pN at +150 mV and 15 pN at +180 mV. These unzipping forces are in agreement with the 10-20 pN level for unzipping determined using single-molecule pulling approaches.^51–53 At low voltage +100 mV, the DNAs carrying a shorter overhang (C0, C5 and C8) will be pulled by a reduced force, which gives these DNAs less chance to overcome the energy barrier for unzipping, and more chance to escape diffusively in the opposite direction. The DNA escape has been identified previously at low voltage (tens of mV),⁴⁶ which is equivalent to a short overhang to generate a small driving force. Similarly, the force on C5 at +100 mV is only 8.4 pN, lower than the 10–20 pN needed for unzipping. Currently, only the C0’s signatures can discriminate unzipping (Fig. 3a) and escaping (Fig. 3b, without Level-2 → Level-1 transition). With this capability, we determined the fraction of unzipping signatures, which increased with the voltage from zero at +100 mV and 57% at +150 mV to 79% at +180 mV.

In summary, the different length overhangs in the nanopore can be utilized to modulate the pulling force, and thus regulate the DNA unzipping and escaping. The overhang also acts as a force sensor to map the distribution of electric field intensity in the nanopore.

Diffusion-limited versus barrier-limited DNA trapping

Through signature characterization, we have elucidated a series of DNA mechanisms in nanopores. However, the above studies have not clarified how a DNA is trapped into the protein pore from the bulk solution. Understanding such a trapping mechanism would enable us to regulate and thus optimize the trapping efficiency for the improvement of the sensing throughput. For this purpose, we investigated the modulation of the DNA trapping process controlled by the overhang length. The result leads to the discovery of kinetic pathways for trapping DNA into the nanopore.

The trapping efficiency is measured by the trapping rate (or capture rate) k_on. The trapping of DNA in the nanopore involves two sequential steps: diffusive migration of a molecule from the bulk solution to the pore opening and the threading of a polymer into the pore (Fig. 5a). The diffusion step is biased by a weak electric field outside the pore opening,^5,55 while the threading step needs to overcome an energy barrier due to the nanopore confinement of the DNA end and/or DNA–pore interactions.⁵ The two sequential steps with their specific rate constants, k_dif and k_bar, contribute to the observed apparent trapping rate k_on as

$$k_{\text{on}}=\frac{k_{\mathrm{diff}}{k}_{\text{bar}}}{k_{\mathrm{diff}}+k_{\text{bar}}}$$ (1)

Fig. 5.

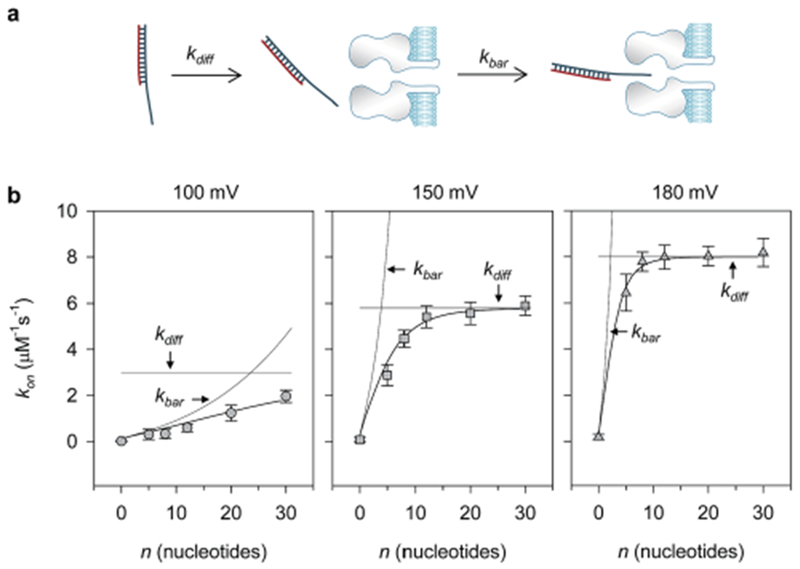
Dissection of the kinetic pathway for trapping DNA in the nanopore. (a) Diagram showing the two-step DNA trapping procedure: voltage-biased diffusion (k_dif) from solution to the pore opening, and threading pore by overcoming a barrier (k_bar). (b) Dissection of the apparent (observed) trapping rate (k_on) as a function of the overhang base number at +100 mV (left), +150 mV (middle) and +180 mV (right). The observed k_on–n relationships reveal the transition from k_bar-limited trapping to k_dif-limited trapping. k_bar was fitted using k_bar = A exp(Bn^0.5), a simplified expression from eqn (3) and (4), where n is the overhang base number, and A and B are voltage-dependent constants. k_dif at each voltage was a constant according to eqn (2). The observed trapping rate k_on was fitted using k_bar and k_dif according to eqn (1). At 100 mV, A = 0.1 μM⁻¹ s⁻¹, B = 0.7 and k_dif = 3.0 μM⁻¹ s⁻¹. At 150 mV, A = 0.32 μM⁻¹ s⁻¹, B = 1.5 and k_dif = 5.8 μM⁻¹ s⁻¹. At 180 mV, A = 0.41 μM⁻¹ s⁻¹, B = 2.2 and k_dif = 8.1 μM⁻¹ s⁻¹.

Fig. 5b shows the variation of k_on with the number of nucleotides in the overhang (n) at different voltages. At 100 mV, k_on was steadily enhanced from 0.016 ± 0.011 μM⁻¹∙s⁻¹ for C0 to 2.0 ± 0.3 μM⁻¹∙s⁻¹ for C30 (Fig. 5b, left). At 150 mV, however, k_on was sharply enhanced from 0.076 ± 0.04 μM⁻¹ s⁻¹ for C0 to 5.4 ± 0.5 μM⁻¹ s⁻¹ for C12, then was transitioned into an overhang length-independent phase (Fig. 5b, middle). At 180 mV, k_on was increased more steeply from 0.19 ± 0.11 μM⁻¹ s⁻¹ for C0 to 7.8 ± 0.4 μM⁻¹ s⁻¹ for C8, and then entered into a constant phase for C8 through C30 (Fig. 5b, right). This observation indicates an overhang length-regulated, voltage-modulated multi-step trapping procedure.

To dissect the overhang length-dependent trapping rate, we first analyzed how the two trapping steps are influenced by the overhang length. According to the model for trapping dsDNA in a solid nanopore,^5,55 the diffusion-limited rate k_diff is proportional to the voltage applied,⁵

$$k_{\mathrm{diff}}\propto (\pi d^2\mu ∕4l)V$$ (2)

where μ is the electrophoretic mobility of DNA in bulk solution and d and l are the diameter and length of the nanopore. As μ is independent of the DNA length, k_diff should be independent of the DNA length. In contrast to k_diff, the barrier-limited rate k_bar grows exponentially with voltage due to the need to overcome the energy barrier,

$$k_{\text{bar}}=k_{\mathrm{att}}\exp \left[\frac{\mathit{QV}-\Delta G}{k_{\mathrm{B}}T}\right]$$ (3)

where ΔG is the height of the threading barrier in the absence of voltage and Q is the effective charge of a DNA end segment, which is independent of the DNA length.⁵ The pre-factor k_att is an “attempt rate” at which the polymer attempts to climb the barrier, and can be expressed as,⁵

$$k_{\mathrm{att}}=C_0\exp \left[\frac{\mathit{eV}}{k_{\mathrm{B}}T}\frac{d^2}{\mathit{al}}{\left(\frac{n}{4n_{\mathrm{p}}}\right)}^{0.5}\right]$$ (4)

where n is the number of nucleotides in the overhang, n_p is the number of nucleotides in a DNA persistence length, and a is the length per nucleotide of DNA.⁵ This semi-quantitative model indicates that longer DNA would overcome the threading barrier at a higher rate.

We utilized the model described by eqn (1)–(4) to analyze the observed k_on–n relationships at different voltages (Fig. 5). When the voltage is fixed, k_diff should be a constant and independent of n (eqn (2)), while k_bar is increased as n increases with a slope factor of $\frac{\mathit{eV}}{k_{\mathrm{B}}T}\frac{d^2}{\mathit{al}}{\left(\frac{1}{4n_{\mathrm{p}}}\right)}^{0.5}$ (eqn (3) and (4)). At 100 mV, the fitted k_diff is 3.2 μM⁻¹ s⁻¹. Although k_bar increases with a slope factor of 0.7, it is still lower than k_diff for all the DNAs tested (k_bar < k_diff). Therefore, in the two-step pathway, the DNA trapping is dominated by k_bar (k_on ≈ k_bar). This explains why k_on is consistently increased with the overhang length (Fig. 5b, left). At higher voltage, for example 150 mV, the fitted k_diff reaches a higher level of 5.8 μM⁻¹ s⁻¹, while k_bar increases more sharply with a higher slope factor of 1.5. This allows k_bar to quickly catch up k_diff and becomes larger than k_diff as n increases (k_bar > k_diff). From n = 12 (C12), k_on is tuned from k_bar-limited to k_diff-limited and becomes a constant, leading to the observed two-phase k_on–n relationship (Fig. 5b, middle). Similarly, as the voltage is further increased to +180 mV, k_diff is enhanced to 8.1 μM⁻¹ s⁻¹, while k_bar grows more steeply with a slope factor of 2.2. This enables k_bar to catch up k_diff at a shorter overhang length, and finally transition of k_on from k_bar-dominating to k_diff-dominating at n = 8 (C8) (Fig. 5b, right).

Previous studies have indicated that the trapping of a ssDNA into the α-hemolysin protein pore (~2 nm) needs to cross a barrier,^56–59 but trapping a long dsDNA (4–6 kbp (ref. 60) and 48 kbp (ref. 61)) in wide solid pores (diameter >5 nm) is a diffusive process without crossing a barrier. Recently, a study using a sub 5 nm solid pore revealed the diffusion and threading steps during DNA trapping, and the extension of DNA length can change from the barrier-limited trapping to the diffusion-limited trapping.^5,55 A quantitative model has been established to analyze this procedure for trapping long dsDNAs of 400–50 000 bps in a solid nanopore⁵ in which the trapping rate transition occurs around 8000 bps. In the current study, we identified a similar two-step trapping in a 2 nm protein nano-pore, and demonstrated that the overhang base number can modulate the trapping kinetics. It should be noted that the transition from the barrier- to diffusion-limited rate occurs around 8–12 nucleotides (C8 to C12, Fig. 5, middle and right). This transition length is much shorter compared with several thousands of base-pairs in the solid nanopore.^5,55 This can be explained based on the large difference in the persistent length n_p between ssDNA (0.8 nm or 1.5 nts, ref. 62) and dsDNA (~150 bps) according to eqn (2)–(4).

In summary, the two-phase k_on–n relationship proves that the trapping of DNA in the protein nanopore involves two sequential processes, voltage-biased diffusion and barrier-limited threading. As the DNA length increases, the trapping procedure is transitioned from a barrier-limited trapping (rate is increased with the DNA length) to a diffusion-limited trapping (rate is independent of the DNA length) at a transition overhang length, and can be modulated by the voltage, which tends to shift the transition toward shorter overhangs.

Conclusions

We have utilized a series of DNAs that carry different length overhangs to mechanistically elucidate multiple DNA processes in the nanopores, including trapping, unzipping, escaping and translocation. The overhang performs multiple functions. It controls the DNA trapping orientation. Upon trapping in the pore, the overhang length determines the properties of the signatures. Dissection of these signatures reveals multiple molecular pathways for trapping, unzipping and translocation. The signatures clearly illustrate that DNA unzipping is a transient cooperative process. The overhang trapped in the pore acts as an electric field sensor, which can both modulate the DNA unzipping occurrence and probe the electric field distribution. The interplay of the overhang with voltage allows discrimination of the sequential DNA trapping steps, tracking their single-molecule kinetics and regulating the trapping efficiency. Overall, this is a universal approach to programming nucleic acids’ molecular processes for the optimization of biosensor performance.

Methods

The electrophysiology setup and the methods for nanopore experiments have been detailed previously.^13,24 Briefiy, the recording apparatus was composed of two chambers (cis and trans) that were partitioned with a Tefion film. The planar lipid bilayer of 1,2-diphytanoyl-sn-glycero-phosphatidylcholine (Avanti Polar Lipids) was formed spanning a 100–150 μm hole at the center of the partition. Both cis and trans chambers were filled with 1 M KCl buffered with 10 mM Tris and titrated to pH 7.5. All the solutions were filtered before use. Single α-hemolysin proteins were inserted into the bilayer from the cis side to form molecular pores. DNA oligonucleotides (Table 1) were synthesized and electrophoresis-purified by Integrated DNA Technologies Inc, CA. Before testing, the mixtures of ssDNAs were heated to 90 °C for 5 minutes, then gradually cooled down to room temperature and stored at 4 °C. In single-channel recording, the cis solution was grounded and the voltage was applied from the trans solution, so that a positive voltage can drive the translocation of a negatively charged DNA through the pore from cis to trans. Single-channel currents were recorded with an Axopatch 200A patch-clamp amplifier (Molecular Device Inc., former Axon Inc.), filtered with a built-in four pole low-pass Bessel filter at 5 kHz, and acquired with Clampex 9.0 software (Molecular Device Inc.) through a Digidata 1332 analog-to-digital converter (Molecular Devices) at a sampling rate of 20 kHz. To detect short intermediate states in a blocking event (Fig. S5^†), the current was filtered at 10 kHz and acquired at a sampling rate of 100 kHz. The data were analyzed using Clampfit 9.0 (Molecular Device Inc.), Excel (MicroSoft) and SigmaPlot (SPSS) software. The duration of DNA signatures (τ_off) was obtained from linear-binning duration histograms (e.g. Fig. S1^†) that were fitted with an exponential probability density function, or from logarithmic-binning duration histograms (e.g. Fig. S2, S4 and S7^†) fitted with a log-transformed exponential probability density function (in pClamp software). Log-binned histogram is suitable for separating events with large duration difference.⁶³ To obtain the dsDNA trapping rate (k_on) in the pore, we need to measure the frequency of their signature blocks. The frequency is the inverse of the time interval between adjacent dsDNA blocks (τ_on), which can be measured in pClamp. In practical measurement, the current traces also contained a small fraction of ssDNA translocation events, which needs to be removed when measuring τ_on. Because the time scale of translocation events (10–100 μs, ref. 15 and 16) is well separated from dsDNA blocks (1–1000 ms), the translocation short events can be removed by using 1 ms as the cut-off. In cases where the dsDNA event duration is short, such as at high voltage, the dsDNA block frequency can be obtained from the overall frequency multiplied by the fraction of the dsDNA blocks in the total block number. The fraction of dsDNA blocks can be obtained from the area covered by the blocks’ population in a duration histogram. Data presented were based on at least four independent experiments and are shown as mean ± SD. Experiments were conducted at 22 ± 1 °C.